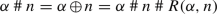Abstract
In this paper three main results are presented: a bijection between natural sums and natural products, the completion of the axioms of Carruth for natural sums, and a new characterization of the natural sums in terms of Klaua’s integral ordinals. After introducing some preliminary results, we present two lemmas and a proposition for the proof of the existence of a bijection between natural products and natural sums. Then we prove the incompleteness of Carruth’s axioms by providing two counterexamples, and complete Carruth’s axioms by adding a fifth axiom. Finally, we introduce a characterization of natural sums in terms of Klaua’s integral ordinals and present two families of natural sums, which differ from Hessenberg’s sum.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The first natural sum and product of ordinals, the so-called Hessenberg sum and Hessenberg product, were introduced by Hessenberg in [3]. The novelty of these operations on the ordinals were their improved algebraic properties with respect to the initial natural product and sum on the natural numbers. Although Hessenberg’s work was continued by Jacobsthal [4] by introducing the so-called Jacobstal product, Carruth [2] was the first to provide an axiomatisation for both the natural sums and products as well as showing that the Hessenberg sum is the smallest of all the natural sums and the highest of all the mixed sums. A further contribution characterising the Hessenberg sum as well as more general natural sums has been provided by Zuckerman [10].
In the recent literature, an infinitary version of the Hessenberg sum, were the Hessenberg sum is taken over all elements of a sequence of length \(\alpha \geqslant \omega \), has been used in the work of Väänanen and Wang [8] and Wang [9] and studied extensively by Lipparini in [6, 7].
The suitable algebraic properties of these natural operations have been also used in the construction for other algebraic structures. Klaua [5] developed the so-called ring of the integral ordinals and the field of the rational and real ordinals. Another field, the long real ordinals was also built and studied by Asperó and Tsaprounis [1], which is a complete ordered field (in contrast to Klaua’s ring).
2 Preliminaries
We start presenting the usual representation of the ordinals in terms of polynomials, which was first developed by Cantor.
Theorem 2.1
Any ordinal \(\alpha >0\) has a unique representation of the form

This representation is called the Cantor normal form, denoted \({ {\textsf {CNF}}}\).
The following is an auxiliary definition, which we introduce for the ease of the definition of natural sums; we call it the common normal representation with respect to two ordinals \(\alpha \) and \(\beta \).
Definition 2.2
Let \(\Omega \) be the class of ordinals and let \(\alpha ,\beta \in \Omega \) be two ordinals in \(\textsf {CNF}\), i.e.,

Furthermore, let \(\{\xi _k\,{:}\,0\leqslant k\leqslant l\}\) be an enumeration of \(\{\alpha _i\,{:}\,0\leqslant i\leqslant m\}\cup \{\beta _j\,{:}\,0\leqslant j\leqslant n\}\) such that \(\xi _0>\cdots >\xi _l\geqslant 0\).
Then, we refer to the common normal representation of \(\alpha \) and \(\beta \), denoted \(\textsf {CNR}(\alpha ,\beta )\), as:

where
Notice that the for any two ordinals \(\alpha ,\beta \) as above, their common normal representation  exists. Besides, the common representation is also unique since \(\{\xi _k\,{:}\,0\leqslant k\leqslant l\}\) is unique and the coefficients \({\hat{a}}_k\) and \({\hat{b}}_k\) are uniquely determined by the coefficients of Cantor’s normal form of \(\alpha \) and \(\beta \), respectively.
exists. Besides, the common representation is also unique since \(\{\xi _k\,{:}\,0\leqslant k\leqslant l\}\) is unique and the coefficients \({\hat{a}}_k\) and \({\hat{b}}_k\) are uniquely determined by the coefficients of Cantor’s normal form of \(\alpha \) and \(\beta \), respectively.
2.1 Natural sums and products
2.1.1 Hessenberg’s natural sum and product
We use the \(\textsf {CNR}\) and the \(\textsf {CNF}\) in order to define the so-called Hessenberg sum (see [3]), which is the first example of a natural sum and also the only example we could find in the literature.
Let \(\alpha \) and \(\beta \) be ordinals in \(\textsf {CNF}\), i.e.,

Furthermore, let  be
be  and
and  , respectively. Then we define the so-called Hessenberg sum, denoted \(\#\), of \(\alpha \) and \(\beta \) as:
, respectively. Then we define the so-called Hessenberg sum, denoted \(\#\), of \(\alpha \) and \(\beta \) as:

Now, we can define the product as the closed operation \(*\) by stipulating:

where \(\sum \) denotes the Hessenberg sum. Along the rest of the paper, we will always denote by \(\sum \) the Hessenberg sum over a sequence of ordinals.
2.1.2 Carruth’s axioms for natural sums and products
From the definition of Hessenberg’s natural sum and product, Carruth built his axioms for natural operations in 1941 (see [2]).
Carruth’s Axioms for Natural Sums 2.3
A natural sum is a closed binary operation \(+\) on the class of ordinals which satisfies the following conditions (for all ordinals \(\alpha ,\beta ,\gamma ,\delta \)):
- Axiom S 1.:
-
\(\alpha +\beta =\beta +\alpha \).
- Axiom S 2.:
-
\(\alpha +(\beta +\gamma )=(\alpha +\beta )+\gamma \).
- Axiom S 3.:
-
\(\alpha +0=0+\alpha =\alpha \).
- Axiom S 4.:
-
\(\alpha +\delta >\beta +\delta \) iff \(\alpha >\beta \).
Carruth’s Axioms for Natural Products 2.4
A natural product is defined as a closed operation \(\cdot \) on the class of ordinals, such that for the Hessenberg sum \(\mathbin {\#}\), the following conditions are satisfied (for all ordinals \(\alpha ,\beta ,\gamma ,\delta \)):
- Axiom P 1.:
-
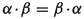 .
. - Axiom P 2.:
-
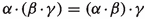 .
. - Axiom P 3.:
-
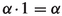 .
. - Axiom P 4.:
-
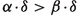 iff \(\alpha >\beta \).
iff \(\alpha >\beta \). - Axiom P 5.:
-
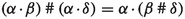 .
. - Axiom P 6.:
-
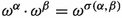 , where \(\sigma (\alpha ,\beta )\) is an ordinal depending on \(\alpha \) and \(\beta \).
, where \(\sigma (\alpha ,\beta )\) is an ordinal depending on \(\alpha \) and \(\beta \).
3 Bijection between natural sums and natural products
The first lemma guarantees that a natural sum can always be deduced from any natural product.
Lemma 3.1
If the operation “ \(\cdot \)” is a natural product and the function  is such that for every \(\alpha , \beta \in \Omega \),
is such that for every \(\alpha , \beta \in \Omega \),  , then \(\sigma (\alpha ,\beta )\) is a natural sum.
, then \(\sigma (\alpha ,\beta )\) is a natural sum.
Proof
First notice that the binary operation  , \((\alpha ,\beta )\mapsto \sigma (\alpha ,\beta )\) is well-defined by stipulating
, \((\alpha ,\beta )\mapsto \sigma (\alpha ,\beta )\) is well-defined by stipulating

We check now that \(\sigma \) meets the properties of a natural sum.
-
1.
Commutativity follows straightforward from Axiom P 1.
-
2.
If \(\alpha ,\beta \) and \(\delta \) are ordinals, by Axiom P 2 we have
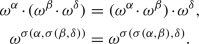
Hence, we have \(\sigma (\alpha ,\sigma (\beta ,\delta ))=\sigma (\sigma (\alpha ,\beta ),\delta )\), which shows that \(\sigma \) is associative.
-
3.
By Axiom P 3 and since \(\omega ^0=1\), we have
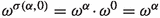 , and hence then \(\sigma (\alpha ,0)=\alpha \).
, and hence then \(\sigma (\alpha ,0)=\alpha \). -
4.
For any three ordinals \(\alpha ,\beta ,\delta \), the following are equivalent:
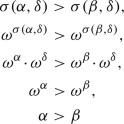
where the second and fourth equivalence follow from the strict monotonicity of the power function.\(\square \)
Below, we relax our notation slightly and allow that \(\omega ^{\alpha _k}\) is written after the integer \(a_k\).
Lemma 3.2
Let “ \(\cdot \)” denote any natural product. If \(\alpha \) and \(\beta \) are two ordinals with \( {\textsf {CNF}}\)  ,
,  , then
, then

where \(\sigma \) is the natural sum induced by the product “ \(\cdot \)” as in Lemma 3.1.
Proof
Notice first that the \(\textsf {CNF}\) is the Hessenberg natural sum of the terms \(a_k \omega ^{\alpha _k}\) and \(b_j \omega ^{\beta _j}\), respectively. By the distributive property of the natural product, we have:

Proposition 3.3
Let  be a natural sum. Then the binary operation “ \(\cdot \)” on
be a natural sum. Then the binary operation “ \(\cdot \)” on  defined by stipulating
defined by stipulating

is a natural product.
Proof
Axiom P 1, Axiom P 2, Axiom P 3, and Axiom P 6 are immediate from the definition of the product “ \(\cdot \)”. To see that “ \(\cdot \)” satisfies Axiom P 4, assume that  . Now, choose the \(\textsf {CNR}\) of \(\alpha ,\beta \) and the \(\textsf {CNF}\) for \(\delta \):
. Now, choose the \(\textsf {CNR}\) of \(\alpha ,\beta \) and the \(\textsf {CNF}\) for \(\delta \):
Then, the following are equivalent:

The first equivalence follows from the definition of the product. The second equivalence follows from the next argument. By the first equivalence, \(a_0d_0 \geqslant b_0d_0\) and hence either \(a_0>b_0\), in which case \(\alpha >\beta \), or \(a_0=b_0\). In the latter case, we define  and
and  . The first equivalence together with \(a_0=b_0\) implies
. The first equivalence together with \(a_0=b_0\) implies  .
.
We further iterate this reasoning for a general \(l\leqslant r\), given that  and \(a_i = b_i\), for any \(i\leqslant l\), where
and \(a_i = b_i\), for any \(i\leqslant l\), where

We obtain then \(a_{l+1}\geqslant b_{l+1}\). If \(a_{l+1}> b_{l+1}\), then \(\alpha >\beta \). Otherwise, \(a_{l+1} = b_{l+1}\). Hence, since  and \(a_i = b_i\) for any \(i\leqslant l\),
and \(a_i = b_i\) for any \(i\leqslant l\),  .
.
If there is no \(i<r\) such that \(a_i > b_i\), this iterating process ends after finite r steps and so we have defined the finite sequences \(\{ \alpha _l\}_{l\leqslant r}, \{ \beta _l\}_{l\leqslant r}\) and shown that \(a_i = b_i\) for any \(i\leqslant r\), which implies:

Such equality is a contradiction since  . Thus, there exists \(l_0\leqslant r\), such that \(a_i = b_i\), for any \(i\leqslant l_0\) and \(a_{l_0}\!>b_{l_0}\). In turn, this implies \(\alpha _{l_0}>\beta _{l_0}\) and \(\alpha _l > \beta _l\) for any \(l\leqslant l_0\). In particular, \(\alpha > \beta \).
. Thus, there exists \(l_0\leqslant r\), such that \(a_i = b_i\), for any \(i\leqslant l_0\) and \(a_{l_0}\!>b_{l_0}\). In turn, this implies \(\alpha _{l_0}>\beta _{l_0}\) and \(\alpha _l > \beta _l\) for any \(l\leqslant l_0\). In particular, \(\alpha > \beta \).
To see that “ \(\cdot \)” also satisfies Axiom P 5, we assume that the ordinals \(\alpha ,\beta ,\delta \) have the same representations as above. Thus, we have:

The previous results allow us to prove the following theorem.
Theorem 3.4
There is a bijection between the class of all natural sums and the class of all natural products.
Proof
Let  be the classes of all natural sums and all natural products, respectively, and let
be the classes of all natural sums and all natural products, respectively, and let  be the function which maps any natural sum \(\sigma \) to a natural product as in Lemma 3.2.
be the function which maps any natural sum \(\sigma \) to a natural product as in Lemma 3.2.
\(\Gamma \) is well-defined by Proposition 3.3, because for any  , \(\Gamma (\sigma )\) is a natural product. If there were
, \(\Gamma (\sigma )\) is a natural product. If there were  such that
such that
for any \(\alpha ,\beta \in \Omega \) then \(\delta _1 = \delta _2\) by the definition of a natural product.
Furthermore, the function \(\Gamma \) is injective by Lemma 3.1. The surjectivity is assured by Lemmas 3.1 and 3.2, since each natural product in  defines a unique natural sum in
defines a unique natural sum in  . \(\square \)
. \(\square \)
4 The need for a new axiom
Natural sums, as any type of ordinal sum, were initially defined as those sums which preserve the properties of Peano’s sum on \({\mathbb {N}}\), extending such sum to all ordinals.
Below, we present two examples that show how Carruth’s axioms for natural sums 2.3 allow the existence of sums that do not preserve Peano’s sum on \({\mathbb {N}}\). We argue that hence the axioms for natural sums are incomplete and provide an additional axiom that excludes such degenerate sums—completing the axioms for natural sums.
Example 4.1
Let \(\alpha ,\beta \) be two ordinals. Then, we define the sum by setting

where \(\mathbin {\#}\) denotes Hessenberg’s sum. It is easy to see that the defined sum satisfies Axiom S 1–Axiom S 4.
However, this is a sum where the successor ordinal \(\alpha ^+\) of \(\alpha \) is not \(\alpha +1\). In particular, \(n+1=n\mathbin {\#}2\) for any \(n\in {\mathbb {N}}-\{0\}\).
Example 4.2
If \(\alpha ,\beta \) are two different ordinals, we define the sum by setting.

The sum is well-defined and Axiom S 1 and Axiom S 3 follow immediately from the definition.
For associativity, let \(\alpha ,\beta ,\gamma \) be any three ordinals. Consider the following three cases:
-
If \(\alpha ,\beta ,\gamma \geqslant 2\), then
$$\begin{aligned} \alpha +(\beta +\gamma )= & {} \alpha +(\beta \mathbin {\#}\gamma \mathbin {\#}2)= \alpha \mathbin {\#}\beta \mathbin {\#}\gamma +4\\= & {} (\alpha \mathbin {\#}\beta \mathbin {\#}2)+\gamma =(\alpha +\beta )+\gamma . \end{aligned}$$ -
If \(\alpha ,\beta \geqslant 2\) and \(\gamma =1\), then
$$\begin{aligned} \alpha +(\beta +1)=\alpha +(\beta \mathbin {\#}2)=\alpha \mathbin {\#}\beta \mathbin {\#}4 =(\alpha \mathbin {\#}\beta \mathbin {\#}2)+1=(\alpha +\beta )+\gamma . \end{aligned}$$ -
If \(\alpha \geqslant 2\) and \(\beta =\gamma =1\), then
$$\begin{aligned} (\alpha +\beta )+\gamma =\alpha +1\mathbin {\#}2=\alpha \mathbin {\#}4=\alpha +2=\alpha +(1+1). \end{aligned}$$
In any other case, at least one of the ordinals \(\alpha ,\beta ,\gamma \) is equal to 0 and associativity holds.
For Axiom S 4, we pursue a similar proof by cases. Since in the definition above, the sum has been established by giving a definition of the form \(\alpha +\beta =\alpha \mathbin {\#}\beta \mathbin {\#}R(\alpha ,\beta )\) with \(R(\alpha ,\beta )\) some ordinal that depends on \(\alpha ,\beta \), we have:
This is fulfilled in our definition, since for \(\alpha ,\beta \geqslant 2\) we have
and therefore, Axiom S 4 holds.
These examples show that such axioms open up the concept of natural sum (of ordinals) which does not preserve the standard sum on \({\mathbb {N}}\). Following the initial definitions given by Hessenberg and Jakobstal, in order to preserve the ordinal sum on \({\mathbb {N}}\), we propose the following axiom — due to obvious reasons, we call it Successor Axiom.
Successor Axiom
For all natural sums  and \(\alpha \in \Omega \), it holds
and \(\alpha \in \Omega \), it holds
Proposition 4.3
If  is a natural sum with respect to Carruth’s Axioms and for any ordinal \(\alpha \) we have
is a natural sum with respect to Carruth’s Axioms and for any ordinal \(\alpha \) we have  , then, for any limit ordinal \(\eta \) and for any \(m\in {\mathbb {N}}\) we have:
, then, for any limit ordinal \(\eta \) and for any \(m\in {\mathbb {N}}\) we have:

In particular,  for any \(m,n\in {\mathbb {N}}\) and “ \(+\)” denoting the standard sum.
for any \(m,n\in {\mathbb {N}}\) and “ \(+\)” denoting the standard sum.
Proof
Let \(\eta \) be any limit ordinal. Then we have  . If we assume
. If we assume  , then
, then  , so, the proof follows by induction. \(\square \)
, so, the proof follows by induction. \(\square \)
Before we prove the next result, let us first briefly introduce the so-called Presburger Arithmetic:
Presburger Arithmetic
The language of the Presburger arithmetic contains the elements 0 and 1, and the binary operation “ \(+\)” such that the following axioms are fulfilled for any \(x,y\in {\mathbb {N}}\):
- PA \({}_{1}\).:
-
For each \(x\in {\mathbb {N}}\) we have \(0\ne x+1\).
- PA \({}_{2}\).:
-
If \(x+1=y+1\) then \(x=y\).
- PA \({}_{3}\).:
-
\(x+0=x\).
- PA \({}_{4}\).:
-
\(x+(y+1)=(x+y)+1\).
- PA \({}_{5}\).:
-
For any first-order formula \(\varphi \) in the language of Presburger arithmetic with a free variable x:
$$\begin{aligned} \bigl (\varphi (0) \wedge \forall x\bigl (\varphi (x) \rightarrow \varphi (x+1)\bigr )\bigr ) \rightarrow \forall y\,\varphi (y). \end{aligned}$$
Interestingly, we see that the inclusion of the Successor Axiom is crucial for natural sums to become Presburger sums.
Proposition 4.4
Let \(+\) denote any natural sum following Carruth’s axioms
-
(1)
If the sum “ \(+\)” satisfies additionally the Successor Axiom, then it builds a Presburger Arithmetic.
-
(2)
Carruth’s Axioms for natural sums are not sufficient to obtain the Presburger Arithmetic.
Proof
(1) We prove each axiom of Presburger Arithmetic separately.
PA \({}_{1}\): If \(0=x+1\) for some \(x\in {\mathbb {N}}\), then by \({\textsf {Axiom S}\textsf {4}}\), \(x+1 < 1\) implies \(x<0\).
PA \({}_{2}\): This axiom follows again from \({\textsf {Axiom S}\textsf {4}}\), since \(x>y\) implies \(x+1>y+1\).
PA \({}_{3}\) & PA \({}_{4}\): These axioms follow straightforward from \({\textsf {Axiom S}\textsf {3}}\) and \({\textsf {Axiom S}\textsf {2}}\), respectively.
PA \({}_{4}\): Notice that for any  there exists an \(\alpha \in {\mathbb {N}}\) such that \(y=\alpha \mathbin {\#}1 = \alpha +1\). Thus, if for any first-order formula \(\varphi \) in the Presburger Arithmetic we have \(\varphi (0)\) and for any x we have \(\varphi (x)\rightarrow \varphi (x+1)\), then for any \(y\in {\mathbb {N}}\) we have \(\varphi (y)\) (notice that any y is a successor except for \(y = 0\)).
there exists an \(\alpha \in {\mathbb {N}}\) such that \(y=\alpha \mathbin {\#}1 = \alpha +1\). Thus, if for any first-order formula \(\varphi \) in the Presburger Arithmetic we have \(\varphi (0)\) and for any x we have \(\varphi (x)\rightarrow \varphi (x+1)\), then for any \(y\in {\mathbb {N}}\) we have \(\varphi (y)\) (notice that any y is a successor except for \(y = 0\)).
(2) We consider the natural sum  given in Example 4.2, i.e., without the Successor Axiom. With this sum, 1 is not the successor of any element, since for any \(z\in {\mathbb {N}}\),
given in Example 4.2, i.e., without the Successor Axiom. With this sum, 1 is not the successor of any element, since for any \(z\in {\mathbb {N}}\),  . Hence, for some first-order formula \(\varphi \),
. Hence, for some first-order formula \(\varphi \),
does not imply \(\forall y\varphi (y)\), since \(\varphi (y)\) might be false for \(y=1\). \(\square \)
5 Characterization of natural sums
In this section, we would like to give a different approach to the natural sums. For this, we will make use of the results of Dieter Klaua [5], who extended the class of the ordinals with Hessenberg’s sum and product to the ring G of the so-called integral ordinals. We will see that embedding the ordinals into G can be beneficial for generating natural sums, since ordinals can then be subtracted.
5.1 The ring of integral ordinals
We next provide a slightly more general result, based on the work of Klaua, allowing for the construction of any rings with the natural products instead for only those rings that extend the Hessenberg product. We start by introducing the equivalence relation upon we build the elements of the ring G. Since the ordinals play the same role in the ring G as the natural numbers play in the ring \(\mathbb {Z}\), we call them natural ordinals. The class of all natural ordinals (i.e., the class \(\Omega \)), is denoted \({\mathbb {N}}_{\Omega }\).
Given some natural ordinals \(\gamma _1,\delta _1,\gamma _2,\delta _2\in {\mathbb {N}}_{\Omega }\), we define the following equivalence relation:
where \(\mathbin {\#}\) is the Hessenberg sum. For natural ordinals \(\gamma ,\delta \in {\mathbb {N}}_{\Omega }\), let \(G(\gamma ,\delta )\) be the class of all pairs  such that \((\gamma ,\delta )\sim _G (\gamma '\!,\delta ')\). Each equivalence class \(G(\gamma ,\delta )\) is an integral ordinal and the class of integral ordinals will be denoted by G. Now, from each integral ordinal \(G(\gamma ,\delta )\) we choose a representative \(\alpha \in G(\gamma ,\delta )\) and define
such that \((\gamma ,\delta )\sim _G (\gamma '\!,\delta ')\). Each equivalence class \(G(\gamma ,\delta )\) is an integral ordinal and the class of integral ordinals will be denoted by G. Now, from each integral ordinal \(G(\gamma ,\delta )\) we choose a representative \(\alpha \in G(\gamma ,\delta )\) and define  . Furthermore, the class of integral ordinals \([\alpha ]\) where \(\alpha =(\gamma ,\delta )\) and \(\gamma \geqslant \delta \) is denoted by \(G_{\Omega }\). Notice that the elements of \(G_{\Omega }\) correspond to the elements of \({\mathbb {N}}_{\Omega }\).
. Furthermore, the class of integral ordinals \([\alpha ]\) where \(\alpha =(\gamma ,\delta )\) and \(\gamma \geqslant \delta \) is denoted by \(G_{\Omega }\). Notice that the elements of \(G_{\Omega }\) correspond to the elements of \({\mathbb {N}}_{\Omega }\).
Now, we define a ring structure on the class G:
Definition 5.1
For \(i=1,2\) let \(\alpha _i=(\gamma _i,\delta _i)\).
-
1.
The order relation \(\leqslant _G\) on G is defined by stipulating
$$\begin{aligned} {[}\alpha _1]\leqslant _G[\alpha _2]\quad \Longleftrightarrow \quad \gamma _1\mathbin {\#}\delta _2 \leqslant \gamma _2\mathbin {\#}\delta _1. \end{aligned}$$ -
2.
The sum \([\alpha _1]+[\alpha _2]\) is defined by stipulating
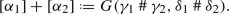
With respect to the sum “\(+\)” we have the neutral element \(0_G=G(0,0)\), and for each integral ordinal \([\alpha ]=G(\gamma ,\delta )\) we have that
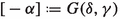 is the inverse of \([\alpha ]\), i.e., \([-\alpha ]+[\alpha ]=0_G\).
is the inverse of \([\alpha ]\), i.e., \([-\alpha ]+[\alpha ]=0_G\). -
3.
The product
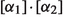 is defined by stipulating
is defined by stipulating 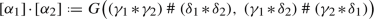
where \(*\) is any natural product. With respect to the product “\(\;\cdot \)” we have the neutral element
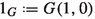 .
.
For the sake of simplicity we identify integral ordinals \([\alpha ]\) with \(\alpha \). As an immediate consequence of the definitions we have the following results analogous to the ones obtained in [5].
Proposition 5.2
-
1.
The relation \(\leqslant _G\) is well-defined and a total order.
-
2.
The integral sum is well-defined and has the following properties:
-
(a)
\(\alpha +0=0+\alpha =\alpha \).
-
(b)
\(\alpha +(\beta +\gamma )=(\alpha +\beta )+\gamma \).
-
(c)
\(\alpha +\beta =\beta +\alpha \).
-
(d)
If \(\alpha _1<\alpha _2\), then \(\alpha _1+\beta <\alpha _2+\beta \), for any integral ordinal \(\beta \).
-
(e)
\(\alpha +(-\alpha )=0\).
-
(a)
-
3.
The integral product is well-defined and has the following properties:
-
(a)
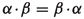 .
. -
(b)
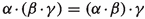 .
. -
(c)
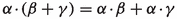 .
. -
(d)
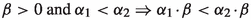 .
. -
(e)
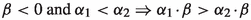 .
. -
(f)
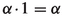 .
. -
(g)
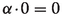 .
.
-
(a)
Properties 2.(a)–(e) imply that \((G,+,0_G)\) has a group structure due to the commutativity, associativity, existence of an identity element and cancellability of the sum. In addition, Properties 3.(a)–(g) guarantee the structure of a commutative ring for \((G,+,\,\cdot ,0_G,1_G)\). As a further consequence of Proposition 5.2 and analogously as in [5] we obtain the following
Corollary 5.3
The structure \((G,+,\,\cdot ,0_G,1_G)\) is an integral domain.
Proof
Let \([\alpha _1], [\alpha _2]\in G\) be such that \([\alpha _i] = G(\beta _i,\gamma _i)\) for \(\beta _i, \gamma _i\in \Omega \) and \(i=1,2\). If we assume  , then we obtain the following identities, which are equivalent:
, then we obtain the following identities, which are equivalent:

By assumption, for \(i=1,2\) we have \(G(\beta _i,0) > rless G(\gamma _i,0)\), since otherwise, \(\beta _i = \gamma _i\) which implies \([\alpha _i] = 0\). Hence, if \(G(\beta _1, 0 ) > rless G(\gamma _1, 0)\) by Property 3.(f) of Proposition 5.2, we obtain that  , arriving at a contradiction with identity (1). \(\square \)
, arriving at a contradiction with identity (1). \(\square \)
Last, we give a key result whose proof can be found in [5]:
Proposition 5.4
There is an embedding of the natural ordinals in the ring G of the integral ordinals.
5.2 Main results
Now we are able to introduce the characterization of natural sums. We will make use of the following auxiliary
Lemma 5.5
If  denotes any natural sum on the natural ordinals, then
denotes any natural sum on the natural ordinals, then

where \(\mathbin {\#}\) denotes Hessenberg’s sum and \(R(\alpha ,\beta )\) is an integral ordinal (depending on \(\alpha \) and \(\beta \)).
Proof
Since \(R(\alpha ,\beta )\) is arbitrary, this is just a consequence of Proposition 5.4 with  . \(\square \)
. \(\square \)
We will characterize now the function  ,
,  . In particular, we shall present axioms for the integral ordinal \(R(\alpha ,\beta )\) for natural sums.
. In particular, we shall present axioms for the integral ordinal \(R(\alpha ,\beta )\) for natural sums.
The function  satisfies the following conditions:
satisfies the following conditions:
-
1.
\(R(\alpha ,\beta )=R(\beta ,\alpha )\): Since
 is commutative, we have
is commutative, we have 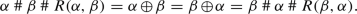
-
2.
For any ordinals \(\alpha ,\beta ,\gamma \) we have
$$\begin{aligned} R(\alpha ,\beta )\mathbin {\#}R\bigl (\alpha \mathbin {\#}\beta \mathbin {\#}R(\alpha ,\beta ),\gamma \bigr ) = R(\beta ,\gamma )\mathbin {\#}R\bigl (\alpha ,\beta \mathbin {\#}\gamma \mathbin {\#}R(\beta ,\gamma )\bigr ). \end{aligned}$$Since
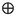 is associative, we have
is associative, we have 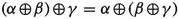 . So, on the one hand we have
. So, on the one hand we have 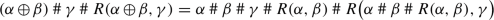
and on the other hand we have
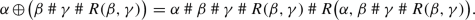
-
3.
For all ordinals \(\alpha \) we have \(R(\alpha ,0)=0\), which follows from \(G(\alpha ,\alpha ) = 0_G\) and Definition 5.1.
-
4.
For any ordinals \(\alpha ,\beta ,\delta \) with \(\alpha >\beta \) we have \(R(\alpha ,\delta )-R(\beta ,\delta )>\beta -\alpha \): The following statements are equivalent:
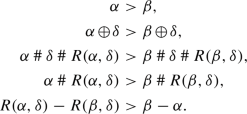
So, since
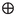 satisfies Axiom S 4, we have \(R(\alpha ,\delta )-R(\beta ,\delta )>\beta -\alpha \).
satisfies Axiom S 4, we have \(R(\alpha ,\delta )-R(\beta ,\delta )>\beta -\alpha \). -
5.
If the natural sum
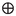 satisfies the \(\textsf {Successor Axiom}\), then for all ordinals \(\alpha \) and all \(n\in {\mathbb {N}}\) we have \(R(\alpha ,n)=0\): Since
satisfies the \(\textsf {Successor Axiom}\), then for all ordinals \(\alpha \) and all \(n\in {\mathbb {N}}\) we have \(R(\alpha ,n)=0\): Since 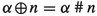 , we have
, we have 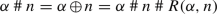
which implies \(R(\alpha ,n)=0\).
Proposition 5.6
The following conditions are necessary and sufficient for  , such that
, such that  , where
, where  , is a natural sum which satisfies Carruth’s and the Successor Axiom:
, is a natural sum which satisfies Carruth’s and the Successor Axiom:
-
(a)
For any ordinals \(\alpha ,\beta \) we have \(R(\alpha ,\beta )=R(\beta ,\alpha )\).
-
(b)
For any ordinals \(\alpha ,\beta ,\gamma \) we have
$$\begin{aligned} R(\alpha ,\beta )\mathbin {\#}R\bigl (\alpha \mathbin {\#}\beta \mathbin {\#}R(\alpha ,\beta ),\gamma \bigr ) = R(\beta ,\gamma )\mathbin {\#}R\bigl (\alpha ,\beta \mathbin {\#}\gamma \mathbin {\#}R(\beta ,\gamma )\bigr ). \end{aligned}$$ -
(c)
For any ordinal \(\alpha \) and any \(n\in {\mathbb {N}}\) we have \(R(\alpha ,n)=0\).
-
(d)
For any ordinals \(\alpha ,\beta ,\delta \) with \(\alpha >\beta \) we have \(R(\alpha ,\delta )-R(\beta ,\delta )>\beta -\alpha \).
Proof
Above we have seen that the conditions are necessary, So, it remains to show that the conditions are also sufficient.
(a) \(R(\alpha ,\beta )=R(\beta ,\alpha )\) implies that  is commutative.
is commutative.
(b) \(R(\alpha ,\beta )\mathbin {\#}R(\alpha \mathbin {\#}\beta \mathbin {\#}R(\alpha ,\beta ),\gamma ) = R(\beta ,\gamma )\mathbin {\#}R(\alpha ,\beta \mathbin {\#}\gamma \mathbin {\#}R(\beta ,\gamma ))\) implies that  is associative.
is associative.
(c) \(R(\alpha ,n)=0\) implies that  satisfies \({\textsf {Axiom S}\textsf {3}}\) and the \(\textsf {Successor Axiom}\).
satisfies \({\textsf {Axiom S}\textsf {3}}\) and the \(\textsf {Successor Axiom}\).
(d) If \(\alpha >\beta \), then \(R(\alpha ,\delta )-R(\beta ,\delta )>\beta -\alpha \) implies that  satisfies \({\textsf {Axiom S}\textsf {4}}\). \(\square \)
satisfies \({\textsf {Axiom S}\textsf {4}}\). \(\square \)
We now present a simple example for a natural sum obtained by using the characterization above.
Example 5.7
Let  be defined by stipulating
be defined by stipulating

Then  is a natural sum which satisfies the Successor Axiom:
is a natural sum which satisfies the Successor Axiom:
To see this, by Proposition 5.6 it is enough to show that \(R(\alpha ,\beta )\) satisfies (a)–(d): Conditions (a), (c), (d) are easily verified. For Condition (b) we consider the following four cases:
-
\(R(\alpha ,\beta )=\omega = R(\alpha \mathbin {\#}\beta \mathbin {\#}R(\alpha ,\beta ),\gamma )\): In this case we have that none of \(\alpha ,\beta ,\gamma \) belongs to \({\mathbb {N}}\), which implies that \(R(\beta ,\gamma )=\omega = R(\alpha ,\beta \mathbin {\#}\gamma \mathbin {\#}R(\beta ,\gamma ))\), and therefore we get
$$\begin{aligned} R(\alpha ,\beta )\mathbin {\#}R\bigl (\alpha \mathbin {\#}\beta \mathbin {\#}R(\alpha ,\beta ),\gamma \bigr ) =\omega \mathbin {\#}\omega = R(\beta ,\gamma )\mathbin {\#}R\bigl (\alpha ,\beta \mathbin {\#}\gamma \mathbin {\#}R(\beta ,\gamma )\bigr ). \end{aligned}$$ -
\(R(\alpha ,\beta )=0\) and \(R(\alpha \mathbin {\#}\beta \mathbin {\#}R(\alpha ,\beta ),\gamma )=\omega \): In this case we have that either \(\alpha \in {\mathbb {N}}\) or \(\beta \in {\mathbb {N}}\) and that \(\gamma \notin {\mathbb {N}}\). If \(\alpha \in {\mathbb {N}}\) and \(\beta \notin {\mathbb {N}}\), then \(R(\beta ,\gamma )=\omega \) and \(R(\alpha ,\beta \mathbin {\#}\gamma \mathbin {\#}R(\beta ,\gamma ))=0\), and if \(\alpha \notin {\mathbb {N}}\) and \(\beta \in {\mathbb {N}}\), then \(R(\beta ,\gamma )=0\) and \(R(\alpha ,\beta \mathbin {\#}\gamma \mathbin {\#}R(\beta ,\gamma ))=\omega \), and therefore we get
$$\begin{aligned} R(\alpha ,\beta )\mathbin {\#}R\bigl (\alpha \mathbin {\#}\beta \mathbin {\#}R(\alpha ,\beta ),\gamma \bigr ) =\omega = R(\beta ,\gamma )\mathbin {\#}R\bigl (\alpha ,\beta \mathbin {\#}\gamma \mathbin {\#}R(\beta ,\gamma )\bigr ). \end{aligned}$$ -
\(R(\alpha ,\beta )=\omega \) and \(R(\alpha \mathbin {\#}\beta \mathbin {\#}R(\alpha ,\beta ),\gamma )=0\): This case is similar to the previous case.
-
\(R(\alpha ,\beta )=0=R(\alpha \mathbin {\#}\beta \mathbin {\#}R(\alpha ,\beta ),\gamma )\): In this case we have that either \(\alpha \in {\mathbb {N}}\) or \(\beta \in {\mathbb {N}}\) and \(\gamma \in {\mathbb {N}}\). Since \(\gamma \in {\mathbb {N}}\), we have \(R(\beta ,\gamma )=0\), and since either \(\alpha \) or \(\beta \mathbin {\#}\gamma \) belongs to \({\mathbb {N}}\), we have \(R(\alpha ,\beta \mathbin {\#}\gamma \mathbin {\#}R(\beta ,\gamma ))=0\), and therefore we get
$$\begin{aligned} R(\alpha ,\beta )\mathbin {\#}R\bigl (\alpha \mathbin {\#}\beta \mathbin {\#}R(\alpha ,\beta ),\gamma \bigr ) =0= R(\beta ,\gamma )\mathbin {\#}R\bigl (\alpha ,\beta \mathbin {\#}\gamma \mathbin {\#}R(\beta ,\gamma )\bigr ). \end{aligned}$$
Example 5.7 shows that there are natural sums satisfying the \(\textsf {Successor Axiom}\) which are different from the Hessenberg sum.
References
Asperó, D., Tsaprounis, K.: Long reals. J. Log. Anal. 10, Art. No. 1 (2018)
Carruth, P.W.: Arithmetic of ordinals with applications to the theory of ordered Abelian groups. Bull. Amer. Math. Soc. 48(4), 262–271 (1942)
Hessenberg, G.: Grundbegriffe der Mengenlehre. Vandenhoeck & Ruprecht, Göttingen (1906)
Jacobsthal, E.: Zur Arithmetik der transfiniten Zahlen. Math. Ann. 67(1), 130–144 (1909)
Klaua, D.: Konstruktion ganzer, rationaler und reeller Ordinalzahlen und die diskontinuierliche Struktur der transfiniten reellen Zahlenräume. Schriftenreihe Inst. Math. Deutsch. Akad. Wiss. Berlin, Heft 8. Akademie, Berlin (1961)
Lipparini, P.: An infinite natural sum. Math. Log. Q. 62(3), 249–257 (2016)
Lipparini, P.: Some transfinite natural sums. Math. Log. Q. 64(6), 514–528 (2018)
Väänänen, J., Wang, T.: An Ehrenfeucht–Fraïssé game for \(L_{\omega _1 \omega }\). Math. Log. Q. 59(4–5), 357–370 (2013)
Wang, T.: An Ehrenfeucht–Fraïssé Game for \(L_{\omega _1 \omega }\). MSc Thesis, Universiteit van Amsterdam (2012)
Zuckerman, M.M.: Natural sums of ordinals. Fund. Math. 77(3), 289–294 (1973)
Funding
Open access funding provided by Swiss Federal Institute of Technology Zurich.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Halbeisen, L., Pérez-Velasco, P.P. On Carruth’s axioms for natural sums and products. European Journal of Mathematics 9, 97 (2023). https://doi.org/10.1007/s40879-023-00696-z
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40879-023-00696-z




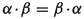 .
.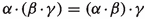 .
.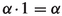 .
.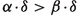 iff
iff 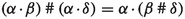 .
.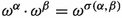 , where
, where 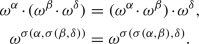
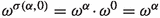 , and hence then
, and hence then 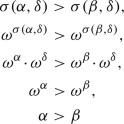
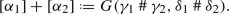
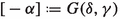 is the inverse of
is the inverse of 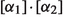 is defined by stipulating
is defined by stipulating 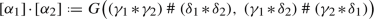
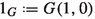 .
.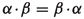 .
.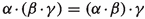 .
.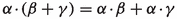 .
.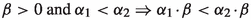 .
.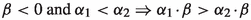 .
.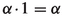 .
.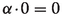 .
. is commutative, we have
is commutative, we have 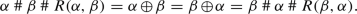
 is associative, we have
is associative, we have 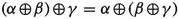 . So, on the one hand we have
. So, on the one hand we have 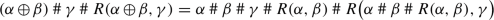
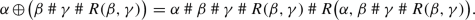
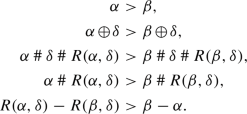
 satisfies
satisfies  satisfies the
satisfies the 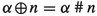 , we have
, we have