Abstract
We provide a new, self-contained proof of the classification of homogeneous 3-Sasakian manifolds, which was originally obtained by Boyer et al. (J Reine Angew Math 455:183–220, [10]). In doing so, we construct an explicit one-to-one correspondence between simply connected homogeneous 3-Sasakian manifolds and simple complex Lie algebras via the theory of root systems. We also discuss why the real projective spaces are the only non-simply connected homogeneous 3-Sasakian manifolds and derive the famous classification of homogeneous positive quaternionic Kähler manifolds due to Alekseevskii (Funct Anal Appl 2(2):106–114, [2]) from our results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
3-Sasakian geometry is arguably one of the most important odd-dimensional geometries. It provides a rich source of compact Einstein manifolds, lies “sandwiched” between the famous hyperkähler, quaternionic Kähler (qK) and Kähler–Einstein geometries and also has several links to algebraic geometry [9].
The history of the classification of homogeneous manifolds with these interrelated geometries is rather long and complicated, as it involves work from as early as 1961 [6] and as recently as 2020 [11]. In this article, we would like to summarize, revisit and improve upon these results by proving the following
Theorem 1.1
There is a one-to-one correspondence between simply connected homogeneous 3-Sasakian manifolds and simple complex Lie algebras.
Given a complex simple Lie algebra  , choose a maximal root \(\alpha \) of
, choose a maximal root \(\alpha \) of  and let
and let  denote the direct sum of the subspace \( \ker \alpha \) and the root spaces of roots perpendicular to \( \alpha \). Let
denote the direct sum of the subspace \( \ker \alpha \) and the root spaces of roots perpendicular to \( \alpha \). Let  and
and  be the compact real forms of
be the compact real forms of  and
and  , respectively, and write
, respectively, and write  for the compact real form of the
for the compact real form of the  -subalgebra defined by \( \alpha \). Let B denote the Killing form of
-subalgebra defined by \( \alpha \). Let B denote the Killing form of  , set
, set  and consider the reductive complement
and consider the reductive complement  . Let G be the simply connected Lie group with Lie algebra
. Let G be the simply connected Lie group with Lie algebra  and let \( H \subset G \) be the connected subgroup with Lie algebra . Define a G-invariant Riemannian metric g on \( M = G/H \) by extending the inner product on
and let \( H \subset G \) be the connected subgroup with Lie algebra . Define a G-invariant Riemannian metric g on \( M = G/H \) by extending the inner product on  given by
given by

Consider a basis \( X_1,X_2,X_3 \) of  satisfying the commutator relations \( [X_i,X_j] = 2 \varepsilon _{ijk} X_k \) and extend
satisfying the commutator relations \( [X_i,X_j] = 2 \varepsilon _{ijk} X_k \) and extend  to a G-invariant vector field \( \xi _i \) on M. Let \(\eta _i\) denote the metric dual of \(\xi _i\) and \(\varphi _i \) the G-invariant endomorphism field defined by extending
to a G-invariant vector field \( \xi _i \) on M. Let \(\eta _i\) denote the metric dual of \(\xi _i\) and \(\varphi _i \) the G-invariant endomorphism field defined by extending

Then, \((g,\xi _i,\eta _i,\varphi _i)_{i=1,2,3}\) is a G-invariant 3-Sasakian structure on M.
Conversely, given a simply connected homogeneous 3-Sasakian manifold M, represented as the quotient \({\widetilde{G}}/{\widetilde{H}}\), where \( {\widetilde{G}} \) is a connected Lie group acting effectively on M, then \({\widetilde{G}} = \textrm{Aut}_0(M)\), the connected component of the 3-Sasakian automorphism group of M, and M is the unique space associated with the complexification of the Lie algebra of \( {\widetilde{G}} \).
Using this characterization, we rediscover the list of homogeneous 3-Sasakian manifolds as given by Boyer, Galicki and Mann:
Corollary 1.2
Every homogeneous 3-Sasakian manifold \( M = G/H \) (not necessarily simply connected) is isomorphic to one of the following spaces:

To avoid redundancy, we need to assume \( n \geqslant 0 \), \( m \geqslant 3 \) and \( k \geqslant 7 \).
As a consequence, we also arrive at the complete list of homogeneous positive qK manifolds as discovered by Alekseevskii:
Corollary 1.3
Every homogeneous positive qK manifold is isometric to one of the spaces

where the Riemannian metric and quaternionic structure are also determined by Theorem 1.1 via the so-called Konishi bundle (see Proposition 2.7 and Sect. 11 for details).
The discussion of Theorem 1.1 and its consequences will be divided into several sections: We begin by recalling basic definitions and features of 3-Sasakian geometry in Sect. 2. We then summarize the history of the classification (Sect. 3) and introduce a certain  -grading of semisimple complex Lie algebras based on their root systems (Sect. 4). The first half of the proof of Theorem 1.1 is given in Sect. 5, where we construct homogeneous 3-Sasakian manifolds from simple Lie algebras. The centerpiece of this article is the converse argument in Sect. 6. For reasons that will become apparent during the construction, the special case of the exceptional Lie algebra
-grading of semisimple complex Lie algebras based on their root systems (Sect. 4). The first half of the proof of Theorem 1.1 is given in Sect. 5, where we construct homogeneous 3-Sasakian manifolds from simple Lie algebras. The centerpiece of this article is the converse argument in Sect. 6. For reasons that will become apparent during the construction, the special case of the exceptional Lie algebra  needs to be relegated to Sect. 7. We complete the proof of Theorem 1.1 by showing that no proper subgroup of the identity component
needs to be relegated to Sect. 7. We complete the proof of Theorem 1.1 by showing that no proper subgroup of the identity component  of the automorphism group can act transitively in Sect. 8. In Sect. 9 we compute the isotropy groups described in Corollary 1.2 explicitly for the classical spaces and Lie theoretically via Borel–de Siebenthal theory in the exceptional cases. In Sect. 10, we show that the only non simply connected homogeneous 3-Sasakian manifolds are the real projective spaces \({\mathbb {R}}P^{4n+3}\) which are the \({\mathbb {Z}}_2\)-quotient of the previously described space
of the automorphism group can act transitively in Sect. 8. In Sect. 9 we compute the isotropy groups described in Corollary 1.2 explicitly for the classical spaces and Lie theoretically via Borel–de Siebenthal theory in the exceptional cases. In Sect. 10, we show that the only non simply connected homogeneous 3-Sasakian manifolds are the real projective spaces \({\mathbb {R}}P^{4n+3}\) which are the \({\mathbb {Z}}_2\)-quotient of the previously described space  . Finally, since our arguments are independent of the classification of homogeneous positive qK manifolds, they allow for an alternative proof of the latter (Sect. 11).
. Finally, since our arguments are independent of the classification of homogeneous positive qK manifolds, they allow for an alternative proof of the latter (Sect. 11).
2 Fundamentals of 3-Sasakian geometry
3-Sasakian geometry may be approached from a variety of different starting points, including but not limited to: qK and hyperkähler geometry, Einstein geometry, spin geometry and certain areas of algebraic geometry. For the sake of brevity, we decided to limit the exposition in this article to the necessary minimum. The interested reader is referred to the comprehensive monograph [9, Chapters 6, 8, 13].
Definition 2.1
A Sasakian structure is a tuple  , where \( \xi \) is a unit length Killing vector field, the one form
, where \( \xi \) is a unit length Killing vector field, the one form  , the endomorphism field \( \varphi = - \nabla ^g \xi \) and the following curvature condition is satisfied:
, the endomorphism field \( \varphi = - \nabla ^g \xi \) and the following curvature condition is satisfied:

We refer to the objects \( \xi ,\eta \) and \( \varphi \) as the Reeb vector field, contact form and almost complex structure of the Sasakian structure.
Remark 2.2
The definition entails several important identities. Other common definitions of Sasakian manifolds in the literature are usually some selection of these. For  we have
we have

We also remark that the Reeb vector field \( \xi \) is characterized uniquely by the properties  ,
,  and that the cone over a Sasakian manifold admits a Kähler structure.
and that the cone over a Sasakian manifold admits a Kähler structure.
Definition 2.3
A 3-Sasakian structure is a tuple  such that each \( (M,g,\xi _i,\eta _i,\varphi _i) \) is a Sasakian structure and \( g(\xi _i,\xi _j) = \delta _{ij} \), \( [\xi _i,\xi _j] = 2 \varepsilon _{ijk} \xi _k \), where \( \varepsilon _{ijk} \) denotes the Levi-Civita symbol and (i, j, k) is a permutation of (1, 2, 3).
such that each \( (M,g,\xi _i,\eta _i,\varphi _i) \) is a Sasakian structure and \( g(\xi _i,\xi _j) = \delta _{ij} \), \( [\xi _i,\xi _j] = 2 \varepsilon _{ijk} \xi _k \), where \( \varepsilon _{ijk} \) denotes the Levi-Civita symbol and (i, j, k) is a permutation of (1, 2, 3).
Remark 2.4
For any cyclic permutation (i, j, k) of (1, 2, 3) the definition implies the compatibility conditions

The cone over a 3-Sasakian manifold admits a hyperkähler structure.
Proposition 2.5
([9, Corollary 13.2.3]) Every 3-Sasakian manifold M of dimension \( 4n+3 \) is Einstein with Einstein constant \( 2(2n+1) \). Moreover, if M is complete, it is compact with finite fundamental group.
Definition 2.6
A 3-Sasakian isomorphism between 3-Sasakian manifolds \( (M,g,\xi _i,\eta _i,\) \(\varphi _i) \) and  is an isometry
is an isometry  which satisfies one of the three equivalent conditions
which satisfies one of the three equivalent conditions  ,
,  or
or  for \( i = 1,2,3 \). We will mostly be interested in the case
for \( i = 1,2,3 \). We will mostly be interested in the case  , in which we call \( \phi \) a 3-Sasakian automorphism of M.
, in which we call \( \phi \) a 3-Sasakian automorphism of M.
We denote the group of all such transformations by  and call M a homogeneous 3-Sasakian manifold if
and call M a homogeneous 3-Sasakian manifold if  acts transitively. Homogeneous 3-Sasakian manifolds are in particular Riemannian homogeneous and thus, complete and compact. The Lie algebra
acts transitively. Homogeneous 3-Sasakian manifolds are in particular Riemannian homogeneous and thus, complete and compact. The Lie algebra  consists of the Killing vector fields
consists of the Killing vector fields  such that
such that  ,
,  and
and  for \( i =1,2,3 \).
for \( i =1,2,3 \).
Proposition 2.7
([9, Theorem 13.3.13 & Proposition 13.4.5]) The Reeb vector fields \( \xi _1,\xi _2,\xi _3 \) of a 3-Sasakian manifold M generate a 3-dimensional foliation  , whose space of leaves
, whose space of leaves  is a positive (i.e. its scalar curvature is positive) qK orbifold.
is a positive (i.e. its scalar curvature is positive) qK orbifold.
If M is a homogeneous 3-Sasakian manifold, then  is a locally trivial Riemannian fibration over a homogeneous positive qK manifold with fiber
is a locally trivial Riemannian fibration over a homogeneous positive qK manifold with fiber  or
or  .
.
3 History of the classification
The earliest result concerning our topic was the classification for the related notion of (compact simply connected) homogeneous complex contact manifolds (so-called  -spaces) by Boothby in 1961 [6], who showed that these are in one-to-one correspondence to simple complex Lie algebras. The much more famous next step was the work of Wolf and Alekseevskii on qK manifolds in the 1960s. First, Wolf showed in 1961 that there is a one-to-one correspondence between
-spaces) by Boothby in 1961 [6], who showed that these are in one-to-one correspondence to simple complex Lie algebras. The much more famous next step was the work of Wolf and Alekseevskii on qK manifolds in the 1960s. First, Wolf showed in 1961 that there is a one-to-one correspondence between  -spaces and compact simply connected symmetric positive qK manifolds [17, Theorem 6.1].
-spaces and compact simply connected symmetric positive qK manifolds [17, Theorem 6.1].
Boothby and Wolf already emphasized the importance of the maximal root in the root system of a simple Lie algebra, which will also play a key role in our construction: Wolf demonstrated that the compact simply connected symmetric positive qK manifolds are precisely of the form \( G/N_G(K) \), where G is a compact simple Lie group and \( N_G(K) \) denotes the normalizer of the subgroup K corresponding to the compact real form of the subalgebra generated by the root spaces of a maximal root and its negative. These manifolds became known as Wolf spaces. As we will show in this article, the simply connected homogeneous 3-Sasakian manifolds are of the form \( G/(C_G(K))_0 \), where \( (C_G(K))_0 \) is the identity component of the centralizer \( C_G(K) \) of K in G. In 1968 Alekseevskii fully classified compact homogeneous positive qK manifolds by demonstrating that they are necessarily of the form \( G/N_G(K) \) [2, Theorem 1].
By 1994, Boyer, Galicki and Mann transferred these results to the 3-Sasakian realm [10]. They combined the classification of homogeneous positive qK manifolds with Proposition 2.7 to obtain the following diffeomorphism type classification:
Theorem 3.1
([10, Theorem C]) Every homogeneous 3-Sasakian manifold \( M = G/H \) (not necessarily simply connected) is precisely one of the following:

To avoid redundancy, we need to assume \( n \geqslant 0 \), \( m \geqslant 3 \) and \( k \geqslant 7 \).
They also provided a more precise description of the 3-Sasakian structures in the four classical cases via 3-Sasakian reduction [10].
In 1996, Bielawski [5] described the Riemannian structure on these spaces uniformly. Both for his result and for several later discussions, we need to recall the following construction: As was first described systematically by Kobayashi and Nomizu [14], the study of G-invariant geometric objects on a reductive homogeneous space \( M = G/H = G/G_p \) can be greatly simplified by instead considering  -invariant algebraic objects on a fixed reductive complement
-invariant algebraic objects on a fixed reductive complement  of
of  in
in  . More precisely, the map
. More precisely, the map  , \( X \mapsto {\overline{X}}_p \) (where \( {\overline{X}}_p \) denotes the fundamental vector field of the left G-action at p) is an isomorphism that allows us to translate between
, \( X \mapsto {\overline{X}}_p \) (where \( {\overline{X}}_p \) denotes the fundamental vector field of the left G-action at p) is an isomorphism that allows us to translate between  -invariant tensors on
-invariant tensors on  and the restriction of G-invariant tensor fields to \( T_pM \).
and the restriction of G-invariant tensor fields to \( T_pM \).
While actually working on a more algebro-geometric problem (singularities of nilpotent varieties) and employing very different methods (e.g. Nahm’s differential equation), Bielawski obtained the following
Theorem 3.2
([5, Theorem 4]) For every homogeneous 3-Sasakian manifold \( M = G/H \) with reductive decomposition  , there is a natural decomposition
, there is a natural decomposition  such that the metric on M corresponds to an inner product on
such that the metric on M corresponds to an inner product on  of the form
of the form

where B denotes the Killing form of  and \( c > 0 \) is some constant.
and \( c > 0 \) is some constant.
In 2020, the work of Draper, Ortega and Palomo gave a new hands-on description of homogeneous 3-Sasakian manifolds [11]. Their study was based on the following
Definition 3.3
([11, Definition 4.1]) A 3-Sasakian datum is a pair  of real Lie algebras such that
of real Lie algebras such that
-
 is a
is a  -graded compact simple Lie algebra whose even part is a sum of two commuting subalgebras,
-graded compact simple Lie algebra whose even part is a sum of two commuting subalgebras, 
-
there exists an
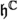 -module W such that the complexified
-module W such that the complexified 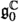 -module
-module  is isomorphic to the tensor product of the natural
is isomorphic to the tensor product of the natural  -module \({\mathbb {C}}^2\) and W:
-module \({\mathbb {C}}^2\) and W: 
Their main result is the following
Theorem 3.4
([11, Theorem 4.2]) Let \( M = G/H \) be a homogeneous space such that H is connected and the Lie algebras  constitute a 3-Sasakian datum. Consider the reductive complement
constitute a 3-Sasakian datum. Consider the reductive complement  and let
and let  denote the standard basis of
denote the standard basis of  and \( \xi _1, \xi _2, \xi _3 \) the corresponding G-invariant vector fields on M. If g and \( \varphi _i \) are the Riemannian metric and endomorphism fields described in Theorem 1.1 and
and \( \xi _1, \xi _2, \xi _3 \) the corresponding G-invariant vector fields on M. If g and \( \varphi _i \) are the Riemannian metric and endomorphism fields described in Theorem 1.1 and  , then the tuple \( (M,g,\xi _i,\eta _i, \varphi _i)_{i=1,2,3} \) constitutes a homogeneous 3-Sasakian structure.
, then the tuple \( (M,g,\xi _i,\eta _i, \varphi _i)_{i=1,2,3} \) constitutes a homogeneous 3-Sasakian structure.
Furthermore, they conducted a case-by-case study to show that every compact simple Lie algebra admits a 3-Sasakian datum, thus providing a detailed analysis of one homogeneous 3-Sasakian structure (it is, at this point, not clear if there could be more than one such structure on a given space) on each of the diffeomorphism types discovered by Boyer, Galicki and Mann.
We finish this section by giving an overview of the structure of our proof of Theorem 1.1: In Sect. 5, we first describe a way to construct a simply connected homogeneous 3-Sasakian manifold from a simple complex Lie algebra  and a maximal root \( \alpha \) of
and a maximal root \( \alpha \) of  . More precisely, we first utilize the theory of root systems to generate a complexified version
. More precisely, we first utilize the theory of root systems to generate a complexified version  of a 3-Sasakian datum. We then pass to the compact real forms
of a 3-Sasakian datum. We then pass to the compact real forms  to obtain a “real” 3-Sasakian datum in the sense of Definition 3.3 and apply Theorem 3.4.
to obtain a “real” 3-Sasakian datum in the sense of Definition 3.3 and apply Theorem 3.4.
For the converse argument in Sects. 6 and 7, we start with a simply connected homogeneous 3-Sasakian manifold \( M = G/H \), where G is a compact simply connected Lie group acting almost effectively and transitively on M via 3-Sasakian automorphisms. We prove that the Lie algebra  and its complexification
and its complexification  are simple and that the 3-Sasakian structure gives rise to a maximal root \( \alpha \) of
are simple and that the 3-Sasakian structure gives rise to a maximal root \( \alpha \) of  . We can therefore apply the previous construction and then show that this yields the same 3-Sasakian structure that we started with.
. We can therefore apply the previous construction and then show that this yields the same 3-Sasakian structure that we started with.
Sect. 8 completes the proof of Theorem 1.1 by showing that no subgroup of \( \textrm{Aut}_0(M) \) can act transitively. In particular, this proves that any two homogeneous 3-Sasakian manifolds \(M=G/H\),  associated with two different simple complex Lie algebras
associated with two different simple complex Lie algebras  are not isomorphic.
are not isomorphic.
4 Root system preliminaries
Later on, we will need certain basic facts about root systems, which we decided to collect in this section: Let  be a (finite-dimensional) semisimple complex Lie algebra. Its Killing form is non-degenerate and thus gives rise to an isomorphism
be a (finite-dimensional) semisimple complex Lie algebra. Its Killing form is non-degenerate and thus gives rise to an isomorphism  and a non-degenerate, symmetric bilinear form
and a non-degenerate, symmetric bilinear form  on
on  . We fix a Cartan subalgebra
. We fix a Cartan subalgebra  and denote the corresponding root system and root spaces by
and denote the corresponding root system and root spaces by  and
and  for
for  , respectively.
, respectively.
Each root \( \alpha \in \Phi \) has an associated coroot  defined as the unique element of
defined as the unique element of  satisfying \( \alpha (H_\alpha ) = 2 \). Furthermore,
satisfying \( \alpha (H_\alpha ) = 2 \). Furthermore,  is a subalgebra of
is a subalgebra of  which is isomorphic to
which is isomorphic to  . This isomorphism can be made explicit by choosing an
. This isomorphism can be made explicit by choosing an  -triple, i.e. vectors
-triple, i.e. vectors  satisfying the commutation relations
satisfying the commutation relations
Moreover, it can be shown that for any root \( \alpha \in \Phi \) and any linear form  :
:

In particular, \( c_{\alpha \beta } = 0 \) if and only if \( \alpha \) and \( \beta \) are perpendicular to each other (with respect to  ). In case \( \beta \) is also a root, \( c_{\alpha \beta } \) is an integer, which we will call the Cartan number of \( \beta \) with respect to \( \alpha \). Fixing a root \( \alpha \in \Phi \), we can therefore decompose
). In case \( \beta \) is also a root, \( c_{\alpha \beta } \) is an integer, which we will call the Cartan number of \( \beta \) with respect to \( \alpha \). Fixing a root \( \alpha \in \Phi \), we can therefore decompose

Since \( c_{\alpha \beta } \) is linear in \( \beta \), this decomposition is in fact a  -grading, i.e.
-grading, i.e.  . We also note that
. We also note that  is precisely the k-eigenspace of
is precisely the k-eigenspace of  . One can visualize this grading using parallel copies of hyperplanes perpendicular to \( \alpha \), e.g. for the root system \( A_2 \):
. One can visualize this grading using parallel copies of hyperplanes perpendicular to \( \alpha \), e.g. for the root system \( A_2 \):

The structure of this grading is related to the notion of maximality of the root \( \alpha \): Assuming we have chosen a set \( \Delta \subset \Phi \) of simple roots, we may introduce a partial order \( \leqslant \) on \( \Phi \) by stipulating that \( \alpha \leqslant \beta \) if and only if \( \beta - \alpha \) is a linear combination of roots in \( \Delta \) with non-negative coefficients. A root \( \alpha \in \Phi \) is called maximal if there is a choice of simple roots such that there is no strictly larger root than \( \alpha \) with respect to the induced partial order. The following lemma was adapted from [17, Theorem 4.2]:
Lemma 4.1
For any root \( \alpha \in \Phi \), the following statements are equivalent:
-
(i)
\( \alpha \) is maximal.
-
(ii)
\( |c_{\alpha \beta }| \leqslant 2 \) for all roots \( \beta \in \Phi \) and \( c_{\alpha \beta } = \pm 2 \) if and only if \( \beta = \pm \alpha \).
Proof
(i) \(\Rightarrow \) (ii): It is well known that for  , the Cartan number is given by \( c_{\alpha \beta } = p-q \), where \( p,q \in {\mathbb {N}}_0 \) are the greatest non-negative integers such that \( \beta + r \alpha \in \Phi \) for every \( r \in \{-p, \ldots , q\} \) [13, Proposition 2.29]. Suppose there was some
, the Cartan number is given by \( c_{\alpha \beta } = p-q \), where \( p,q \in {\mathbb {N}}_0 \) are the greatest non-negative integers such that \( \beta + r \alpha \in \Phi \) for every \( r \in \{-p, \ldots , q\} \) [13, Proposition 2.29]. Suppose there was some  such that \( c_{\alpha \beta } \geqslant 2 \). Then \( p \geqslant 2 \), so that \( \beta - \alpha , \beta -2\alpha \in \Phi \) and their negatives \( \alpha - \beta , 2\alpha -\beta \in \Phi \) are roots. In fact, \( \alpha - \beta \) has to be a non-negative linear combination of simple roots (for some choice of simple roots with respect to which \( \alpha \) is maximal), since otherwise \( \beta > \alpha \). But then \( 2\alpha -\beta \geqslant \alpha \) and maximality of \( \alpha \) would imply \( 2 \alpha - \beta = \alpha \), i.e. \( \beta = \alpha \). For
such that \( c_{\alpha \beta } \geqslant 2 \). Then \( p \geqslant 2 \), so that \( \beta - \alpha , \beta -2\alpha \in \Phi \) and their negatives \( \alpha - \beta , 2\alpha -\beta \in \Phi \) are roots. In fact, \( \alpha - \beta \) has to be a non-negative linear combination of simple roots (for some choice of simple roots with respect to which \( \alpha \) is maximal), since otherwise \( \beta > \alpha \). But then \( 2\alpha -\beta \geqslant \alpha \) and maximality of \( \alpha \) would imply \( 2 \alpha - \beta = \alpha \), i.e. \( \beta = \alpha \). For  such that \( c_{\alpha \beta } \leqslant -2 \), we apply this argument to \( -\beta \).
such that \( c_{\alpha \beta } \leqslant -2 \), we apply this argument to \( -\beta \).
(ii) \(\Rightarrow \) (i): We may choose a set of simple roots \(\Delta \) in such a way that \( c_{\alpha \beta } \geqslant 0 \) for all \( \beta \in \Delta \). This can be achieved by first choosing positive roots using a slight perturbation of the hyperplane perpendicular to \( \alpha \). Let \( \beta \in \Phi \) such that \( \beta \geqslant \alpha \), i.e. \( \beta -\alpha = \sum _{i=1}^n \lambda _i \alpha _i \), where \( \lambda _i \geqslant 0 \) and \( \alpha _i \in \Delta \). Then,
Hypothesis (ii) then implies \( \beta = \alpha \), so that \( \alpha \) is maximal.\(\square \)
Finally, we remark that in an irreducible root system \( \Phi \), the maximal root is unique up to the action of the Weyl group: This follows because in an irreducible root system, the maximal root is uniquely determined after choosing simple roots, and any two choices of simple roots can be mapped to each other by the Weyl group.
5 Constructing homogeneous 3-Sasakian manifolds from simple Lie algebras
Our goal in this section is the following construction:
Theorem 5.1
Let  be a simple complex Lie algebra, \( \alpha \) a maximal root in its root system,
be a simple complex Lie algebra, \( \alpha \) a maximal root in its root system,  the compact real form of
the compact real form of  and
and  the compact real form of the subalgebra
the compact real form of the subalgebra  . Let G denote the simply connected Lie group with Lie algebra
. Let G denote the simply connected Lie group with Lie algebra  , K the connected subgroup with Lie algebra
, K the connected subgroup with Lie algebra  and \( H = (C_G(K))_0 \) the identity component of the centralizer \( C_G(K) \) of K in G. Then, the simply connected homogeneous space \( M = G/H \) admits a homogeneous 3-Sasakian structure whose tensors are given by Theorem 1.1. All possible choices of a maximal root lead to isomorphic 3-Sasakian manifolds.
and \( H = (C_G(K))_0 \) the identity component of the centralizer \( C_G(K) \) of K in G. Then, the simply connected homogeneous space \( M = G/H \) admits a homogeneous 3-Sasakian structure whose tensors are given by Theorem 1.1. All possible choices of a maximal root lead to isomorphic 3-Sasakian manifolds.
Definition 5.2
A complex 3-Sasakian datum is a pair  of complex Lie algebras such that
of complex Lie algebras such that
-
 is a
is a  -graded simple Lie algebra whose even part is a sum of two commuting subalgebras,
-graded simple Lie algebra whose even part is a sum of two commuting subalgebras, 
-
there exists a
 -module W such that
-module W such that  as
as  -modules.
-modules.
Remark 5.3
We formulated the above definition in the given way because it allows us to branch off into two cases: Our primary interest in this article will be to consider the compact real forms  of
of  which then form a 3-Sasakian datum in the sense of Definition 3.3. On the other hand, one may also look at the real form
which then form a 3-Sasakian datum in the sense of Definition 3.3. On the other hand, one may also look at the real form  of
of  given by
given by  , to obtain a generalized 3-Sasakian datum in the sense of [1]. These give rise to homogeneous negative 3-\( (\alpha ,\delta ) \)-Sasakian manifolds by a construction similar to Theorem 3.4, compare [1, Theorem 3.1.1].
, to obtain a generalized 3-Sasakian datum in the sense of [1]. These give rise to homogeneous negative 3-\( (\alpha ,\delta ) \)-Sasakian manifolds by a construction similar to Theorem 3.4, compare [1, Theorem 3.1.1].
Proposition 5.4
Let  be a simple complex Lie algebra and \( \alpha \in \Phi \) a maximal root in its root system. Set
be a simple complex Lie algebra and \( \alpha \in \Phi \) a maximal root in its root system. Set  as well as
as well as

Then,  is a complex 3-Sasakian datum.
is a complex 3-Sasakian datum.
Proof
Using the  -grading from Sect. 4, we let
-grading from Sect. 4, we let

Since \(|c_{\alpha \beta }| \leqslant 2 \) for all \( \beta \in \Phi \) by Lemma 4.1, we have  . Because
. Because  and
and  are comprised of the
are comprised of the  with even and odd k respectively, this decomposition is in fact a
with even and odd k respectively, this decomposition is in fact a  -grading. We claim that
-grading. We claim that

as a direct sum of Lie algebras, where  . Since \( c_{\alpha \beta } = \pm 2 \) if and only if \( \beta = \pm \alpha \), we have the following vector space decompositions:
. Since \( c_{\alpha \beta } = \pm 2 \) if and only if \( \beta = \pm \alpha \), we have the following vector space decompositions:

In order to show that  is indeed a subalgebra of
is indeed a subalgebra of  , note that
, note that  for any \( \beta , \gamma \in \Phi _0 \). Now if \( \beta + \gamma \) is a root, then \( \beta + \gamma \in \Phi _0 \), so
for any \( \beta , \gamma \in \Phi _0 \). Now if \( \beta + \gamma \) is a root, then \( \beta + \gamma \in \Phi _0 \), so  . If \( \beta + \gamma \) is not a root and not zero, then
. If \( \beta + \gamma \) is not a root and not zero, then  . If \( \beta + \gamma = 0 \), then
. If \( \beta + \gamma = 0 \), then  because \( \beta \in \Phi _0 \). To check that
because \( \beta \in \Phi _0 \). To check that  and
and  commute, we recall that
commute, we recall that  is a subset of
is a subset of  . For \( \beta \in \Phi _0 \), we have
. For \( \beta \in \Phi _0 \), we have  , so
, so  and
and  commute.
commute.
We now verify the second condition from Definition 5.2 for the  -module
-module  . We choose an
. We choose an  -triple \( (X_\alpha , Y_\alpha , H_\alpha ) \) and identify it (in order) with the three standard matrices
-triple \( (X_\alpha , Y_\alpha , H_\alpha ) \) and identify it (in order) with the three standard matrices

This fixes isomorphisms  and
and  . We consider the following linear map:
. We consider the following linear map:

If \( \beta \in \Phi \) is such that \( c_{\alpha \beta } = -1 \), then \( \beta + \alpha \) must be a root and  . This shows that
. This shows that  and, by extension, \( \Psi \) are linear isomorphisms. It remains to be shown that \( \Psi \) preserves the
and, by extension, \( \Psi \) are linear isomorphisms. It remains to be shown that \( \Psi \) preserves the  -module structure, where
-module structure, where  acts on
acts on  via the above fixed isomorphism. We remind the reader of the commutator relations in (1).
via the above fixed isomorphism. We remind the reader of the commutator relations in (1).
If  , then
, then  preserves the decomposition
preserves the decomposition  . Since
. Since  and
and  are commuting subalgebras of
are commuting subalgebras of  , so are their respective adjoint subrepresentations,
, so are their respective adjoint subrepresentations,

Here,  denotes the adjoint representation of
denotes the adjoint representation of  on W, while in the following equations it will signify the standard representation of
on W, while in the following equations it will signify the standard representation of  on
on  . Finally, we check the representation of the basis \( (X_\alpha , Y_\alpha , H_\alpha ) \) of
. Finally, we check the representation of the basis \( (X_\alpha , Y_\alpha , H_\alpha ) \) of  :
:

By the Jacobi identity,

Ultimately,

\(\square \)
Proof of Theorem 5.1
Starting from a simple complex Lie algebra  and a maximal root \( \alpha \), Proposition 5.4 yields a complex 3-Sasakian datum
and a maximal root \( \alpha \), Proposition 5.4 yields a complex 3-Sasakian datum  . As mentioned in Remark 5.3, the compact real forms
. As mentioned in Remark 5.3, the compact real forms  constitute a “real” 3-Sasakian datum in the sense of Definition 3.3 and Theorem 3.4 endows \( M = G/H \) with a homogeneous 3-Sasakian structure. Since
constitute a “real” 3-Sasakian datum in the sense of Definition 3.3 and Theorem 3.4 endows \( M = G/H \) with a homogeneous 3-Sasakian structure. Since  and thus
and thus  , it follows that \( H = (C_G(K))_0 \).\(\square \)
, it follows that \( H = (C_G(K))_0 \).\(\square \)
Example 5.5
Let us illustrate the construction using the special case  : Here, the only simple Lie algebras are
: Here, the only simple Lie algebras are  ,
,  and
and  , corresponding (in order) to the root systems \( A_2, C_2 \) and \( G_2 \). The diagrams on the next page depict the subalgebras
, corresponding (in order) to the root systems \( A_2, C_2 \) and \( G_2 \). The diagrams on the next page depict the subalgebras  and
and  from the proposition in these three cases.
from the proposition in these three cases.
The corresponding homogeneous 3-Sasakian manifolds are (in order) the Aloff–Wallach space  the 7-sphere
the 7-sphere  and the exceptional space
and the exceptional space  .
.
We finish this section by showing that the maximal root is in fact an auxiliary choice:
Lemma 5.6
All possible choices of a maximal root in Proposition 5.4 lead to isomorphic 3-Sasakian manifolds.

Proof
Let  be a simple complex Lie algebra,
be a simple complex Lie algebra,  its compact real form, G the corresponding simply connected Lie group and \( T \subset G \) a maximal torus. Let
its compact real form, G the corresponding simply connected Lie group and \( T \subset G \) a maximal torus. Let  denote two maximal roots in the root system \( \Phi \) of
denote two maximal roots in the root system \( \Phi \) of  with respect to the Cartan subalgebra given by the complexification of the Lie algebra of T. As mentioned at the end of Sect. 4, the maximal root of \( \Phi \) is unique up to the action of the Weyl group \( W(G) = N_G(T)/T \), so there is a representative \( w \in N_G(T) \) such that
with respect to the Cartan subalgebra given by the complexification of the Lie algebra of T. As mentioned at the end of Sect. 4, the maximal root of \( \Phi \) is unique up to the action of the Weyl group \( W(G) = N_G(T)/T \), so there is a representative \( w \in N_G(T) \) such that  .
.
Because the Weyl group acts orthogonally on the root system,  maps the
maps the  -grading
-grading  with respect to \( \alpha \) to the grading
with respect to \( \alpha \) to the grading  with respect to
with respect to  . This implies that
. This implies that  , where
, where  are the compact real forms of the subalgebras
are the compact real forms of the subalgebras  considered in Proposition 5.4. Consequently,
considered in Proposition 5.4. Consequently,  for the corresponding connected subgroups
for the corresponding connected subgroups  and we have a well-defined diffeomorphism
and we have a well-defined diffeomorphism  ,
,  . One easily checks from the definitions in Theorem 1.1 that this map is a 3-Sasakian isomorphism.\(\square \)
. One easily checks from the definitions in Theorem 1.1 that this map is a 3-Sasakian isomorphism.\(\square \)
6 Deconstructing homogeneous 3-Sasakian manifolds
This section is the centerpiece of the article, where we explain a crucial step in the proof of Theorem 1.1, namely:
Theorem 6.1
Every simply connected homogeneous 3-Sasakian manifold arises from the construction described in Sect. 5.
From now on, let  denote a simply connected homogeneous 3-Sasakian manifold and let G be a compact simply connected Lie group acting almost effectively (i.e. the kernel of the action is discrete and hence finite) and transitively on M by 3-Sasakian automorphisms. We will show that the Lie algebra
denote a simply connected homogeneous 3-Sasakian manifold and let G be a compact simply connected Lie group acting almost effectively (i.e. the kernel of the action is discrete and hence finite) and transitively on M by 3-Sasakian automorphisms. We will show that the Lie algebra  of G and its complexification
of G and its complexification  are simple and describe how the 3-Sasakian structure gives rise to a maximal root \( \alpha \) of
are simple and describe how the 3-Sasakian structure gives rise to a maximal root \( \alpha \) of  with respect to a suitably chosen Cartan subalgebra. We can then apply the construction from Sect. 5 and prove that this yields the same 3-Sasakian structure that we started with.
with respect to a suitably chosen Cartan subalgebra. We can then apply the construction from Sect. 5 and prove that this yields the same 3-Sasakian structure that we started with.
The prototypical example to have in mind is where G is the universal cover of  , the identity component of the 3-Sasakian automorphism group of M. By Proposition 2.5, M is compact, so by the Myers–Steenrod theorem, the isometry group
, the identity component of the 3-Sasakian automorphism group of M. By Proposition 2.5, M is compact, so by the Myers–Steenrod theorem, the isometry group  of M is a compact Lie group. The subgroup
of M is a compact Lie group. The subgroup  of 3-Sasakian automorphisms of M is clearly closed and thus also a compact Lie group. Since M is connected, the identity component
of 3-Sasakian automorphisms of M is clearly closed and thus also a compact Lie group. Since M is connected, the identity component  still acts transitively. The universal cover of
still acts transitively. The universal cover of  acts almost effectively, transitively and by 3-Sasakian automorphisms. It will follow from the results that we are about to prove that the universal cover of
acts almost effectively, transitively and by 3-Sasakian automorphisms. It will follow from the results that we are about to prove that the universal cover of  is also compact.
is also compact.
Later on, we will show that, in fact, the effectively acting quotient of any group G satisfying the above assumptions is automatically the full identity component  of the automorphism group.
of the automorphism group.
Since G is compact, its Lie algebra  is reductive, i.e. decomposes as a direct sum of a semisimple subalgebra and its center
is reductive, i.e. decomposes as a direct sum of a semisimple subalgebra and its center  . We first show that
. We first show that  itself is semisimple.
itself is semisimple.
Lemma 6.2
For  , the fundamental vector fields satisfy the equation
, the fundamental vector fields satisfy the equation
Notably, evaluating the left-hand side at a point \( p \in M \) depends on \( {\overline{X}}, {\overline{Y}}\) only through their values at p, while the right-hand side a priori depends on the values in a neighborhood of p.
Proof
The standard formula for the exterior derivative reads
The Leibniz rule for the Lie derivative implies

where  because G acts by 3-Sasakian automorphisms. Applying the same reasoning to the second term yields \( {\overline{Y}}(\eta _i({\overline{X}})) = - \eta _i([{\overline{X}},{\overline{Y}}]) \). \(\square \)
because G acts by 3-Sasakian automorphisms. Applying the same reasoning to the second term yields \( {\overline{Y}}(\eta _i({\overline{X}})) = - \eta _i([{\overline{X}},{\overline{Y}}]) \). \(\square \)
Proposition 6.3
The Lie algebra  has trivial center and is therefore semisimple.
has trivial center and is therefore semisimple.
Proof
Let  be such that \( X \ne 0 \). Since G acts almost effectively, there is a point \( p \in M \) such that \( {\overline{X}}_p \ne 0 \) and thus an index \( i \in \{1,2,3\} \) such that \( {\overline{X}}_p \) is not proportional to \( (\xi _i)_p \). We show that there exists some
be such that \( X \ne 0 \). Since G acts almost effectively, there is a point \( p \in M \) such that \( {\overline{X}}_p \ne 0 \) and thus an index \( i \in \{1,2,3\} \) such that \( {\overline{X}}_p \) is not proportional to \( (\xi _i)_p \). We show that there exists some  satisfying \( \eta _i (\overline{[X,Y]}_p) \ne 0 \), which implies \( [X,Y] \ne 0 \): Because G acts transitively, we may choose some
satisfying \( \eta _i (\overline{[X,Y]}_p) \ne 0 \), which implies \( [X,Y] \ne 0 \): Because G acts transitively, we may choose some  such that \( {\overline{Y}}_p = \varphi _i {\overline{X}}_p \). From the previous lemma, we have
such that \( {\overline{Y}}_p = \varphi _i {\overline{X}}_p \). From the previous lemma, we have
One of the Sasaki equations in Remark 2.2 reads \( \varphi _i^2 {\overline{X}}_p = {}- {\overline{X}}_p + P_i {\overline{X}}_p \), where \( P_i \) denotes the orthogonal projection to the line through \( (\xi _i)_p \). Hence,
Remark 6.4
The compactness assumption fails for homogeneous negative 3-\((\alpha ,\delta )\)-Sasakian manifolds. Thus, unlike with the construction in the previous section, a classification cannot be achieved by the method described here. Indeed, in [1] homogenoeus negative 3-\((\alpha ,\delta )\)-Sasakian manifolds with a transitive action by a non-semisimple Lie group are constructed.
Since  is now both semisimple and the Lie algebra of a compact Lie group, its Killing form B is negative definite. We fix a point \( p \in M \) and let
is now both semisimple and the Lie algebra of a compact Lie group, its Killing form B is negative definite. We fix a point \( p \in M \) and let  denote its isotropy group. We write \( \theta :G \rightarrow M\),
denote its isotropy group. We write \( \theta :G \rightarrow M\),  for the orbit map, which has surjective differential
for the orbit map, which has surjective differential  , \(X \mapsto {\overline{X}}_p \). Let
, \(X \mapsto {\overline{X}}_p \). Let  denote the pullback of the contact form along the orbit map, which we may view — depending on the context — as either a linear form on
denote the pullback of the contact form along the orbit map, which we may view — depending on the context — as either a linear form on  or as a left-invariant differential one-form on G. In their seminal 1958 article [7], Boothby and Wang exhibited the following results
or as a left-invariant differential one-form on G. In their seminal 1958 article [7], Boothby and Wang exhibited the following results
Lemma 6.5
([7, Lemmata 2, 3, 4]) The one-form \( \alpha _i \) is  -invariant, satisfies
-invariant, satisfies  and \( d\alpha _i \) has rank \( 4n+2 \). Furthermore, the Lie algebra of the subgroup
and \( d\alpha _i \) has rank \( 4n+2 \). Furthermore, the Lie algebra of the subgroup  is given by \( \ker d\alpha _i \), contains
is given by \( \ker d\alpha _i \), contains  and has dimension
and has dimension  .
.
We now let  denote the Killing dual of \( \alpha _i \), i.e.
denote the Killing dual of \( \alpha _i \), i.e.  and consider
and consider  .
.  -invariance of B implies that
-invariance of B implies that  and
and  coincide, so
coincide, so

Proposition 6.6
The fundamental vector fields \( \overline{X_i} \) coincide with the Reeb vector fields \( \xi _i \) at the point p and obey the same commutator relations \( [X_i,X_j] = 2\varepsilon _{ijk}X_k \), where (i, j, k) is a permutation of (1, 2, 3).
Proof
Clearly,  , so that
, so that  . Furthermore, we have \( 1 = \alpha _i( X_i) = (\eta _i)_p(\overline{X_i})_p \). Thus, \( (\overline{X_i})_p \) satisfies the uniquely defining equations of the Reeb vector \( (\xi _i)_p \). Phrased differently, \( X_i \) (viewed as a left-invariant vector field on G) and \( \xi _i \) are \( \theta \)-related. Consequently, the Lie brackets \( [X_i,X_j] \) and \( [\xi _i, \xi _j] = 2\varepsilon _{ijk} \xi _k \) are also \( \theta \)-related and in particular, \( \overline{[X_i, X_j]}_p = 2\varepsilon _{ijk} (\xi _k)_p = 2\varepsilon _{ijk} (\overline{X_k})_p \). Hence, \( [X_i,X_j] \) and \( 2\varepsilon _{ijk} X_k \) could only differ by an element of
. Furthermore, we have \( 1 = \alpha _i( X_i) = (\eta _i)_p(\overline{X_i})_p \). Thus, \( (\overline{X_i})_p \) satisfies the uniquely defining equations of the Reeb vector \( (\xi _i)_p \). Phrased differently, \( X_i \) (viewed as a left-invariant vector field on G) and \( \xi _i \) are \( \theta \)-related. Consequently, the Lie brackets \( [X_i,X_j] \) and \( [\xi _i, \xi _j] = 2\varepsilon _{ijk} \xi _k \) are also \( \theta \)-related and in particular, \( \overline{[X_i, X_j]}_p = 2\varepsilon _{ijk} (\xi _k)_p = 2\varepsilon _{ijk} (\overline{X_k})_p \). Hence, \( [X_i,X_j] \) and \( 2\varepsilon _{ijk} X_k \) could only differ by an element of  . But
. But  and
and  , so that also
, so that also  . \(\square \)
. \(\square \)
Let  be a maximal Abelian subalgebra of
be a maximal Abelian subalgebra of  . Since
. Since  , it follows that
, it follows that  is a maximal Abelian subalgebra of
is a maximal Abelian subalgebra of  . In particular, \( {{\,\textrm{rk}\,}}G = {{\,\textrm{rk}\,}}H +1 \). The Riemannian metric g corresponds to an
. In particular, \( {{\,\textrm{rk}\,}}G = {{\,\textrm{rk}\,}}H +1 \). The Riemannian metric g corresponds to an  -invariant and thus also
-invariant and thus also  -invariant inner product on a reductive complement of our choice. The following lemma states that this inner product is even
-invariant inner product on a reductive complement of our choice. The following lemma states that this inner product is even  -invariant:
-invariant:
Lemma 6.7
For all  , we have
, we have
Proof
Since \( \overline{X_i} \) is a Killing vector field (G acts isometrically) that coincides with \( \xi _i \) at p, we obtain
Because the Levi-Civita connection \( \nabla \) is metric and torsion free and all G-fundamental fields commute with \( \xi _i \) (G acts by 3-Sasakian automorphisms), we have
Finally,  and
and  is skew-symmetric.\(\square \)
is skew-symmetric.\(\square \)
We now move on to the complex picture and let  and
and  . Let us consider the vectors
. Let us consider the vectors  defined by
defined by

which satisfy the commutation relations
Proposition 6.8
The linear form \( \alpha \) is a root of  with respect to
with respect to  , whose root space is given by
, whose root space is given by  . Furthermore,
. Furthermore,  and
and  is the coroot of \( \alpha \).
is the coroot of \( \alpha \).
Proof
Firstly, \( [H_\alpha ,X_\alpha ] = 2X_\alpha = \alpha (H_\alpha ) X_\alpha \). Since \( X_2, X_3 \) commute with  , the vector \( X_\alpha \) commutes with
, the vector \( X_\alpha \) commutes with  and in particular with
and in particular with  . Likewise,
. Likewise,  vanishes on
vanishes on  , so that \( \alpha \) vanishes on
, so that \( \alpha \) vanishes on  and in particular on
and in particular on  . \(\square \)
. \(\square \)
Let  denote the root system of
denote the root system of  with respect to
with respect to  . We consider the
. We consider the  -grading of
-grading of  introduced in Sect. 4, viz.
introduced in Sect. 4, viz.

Lemma 6.9
The 0- and \( \pm 2 \)-components of the grading are given by  and
and  , respectively.
, respectively.
Proof
 . Suppose there was a root \( \beta \ne \alpha \) such that \( c_{\alpha \beta } = 2 \). Then \( \langle \beta , \alpha \rangle > 0 \) and \( \beta - \alpha \) was a root satisfying \( c_{\alpha (\beta - \alpha )} = 0 \). We would need to have
. Suppose there was a root \( \beta \ne \alpha \) such that \( c_{\alpha \beta } = 2 \). Then \( \langle \beta , \alpha \rangle > 0 \) and \( \beta - \alpha \) was a root satisfying \( c_{\alpha (\beta - \alpha )} = 0 \). We would need to have  , but
, but  and
and  ,
,  . \(\square \)
. \(\square \)
Proposition 6.10
The Lie algebras  and
and  are simple.
are simple.
Proof
The semisimple Lie algebra  decomposes as a direct sum
decomposes as a direct sum  of simple ideals. Since the Killing form of
of simple ideals. Since the Killing form of  is negative definite, the same applies to the ideals
is negative definite, the same applies to the ideals  , which thus cannot be the realification of a complex Lie algebra. Therefore, their complexifications are also simple and yield a similar decomposition
, which thus cannot be the realification of a complex Lie algebra. Therefore, their complexifications are also simple and yield a similar decomposition  into simple ideals [13, Theorem 6.94]. Accordingly, the root system is a disjoint union \( \Phi = \Phi _1 \sqcup \cdots \sqcup \Phi _m \). We claim that
into simple ideals [13, Theorem 6.94]. Accordingly, the root system is a disjoint union \( \Phi = \Phi _1 \sqcup \cdots \sqcup \Phi _m \). We claim that  (and hence
(and hence  ), where i is the unique index such that \( \alpha \in \Phi _i \).
), where i is the unique index such that \( \alpha \in \Phi _i \).
For \( j \ne i \), the ideal  commutes with
commutes with  , so
, so  . Since
. Since  is an ideal and G is connected, it follows that
is an ideal and G is connected, it follows that  for all \( g \in G \). Because the G-action is almost effective, we must have
for all \( g \in G \). Because the G-action is almost effective, we must have  .\(\square \)
.\(\square \)
It is well-known that for any root system \( \Phi \) and any roots \( \alpha ,\beta \in \Phi \), the Cartan numbers are bounded by \( |c_{\alpha \beta }| \leqslant 3 \). Furthermore, the only irreducible case where \( |c_{\alpha \beta }| = 3 \) occurs is when  , \( \alpha \) is one of the short roots and \( \beta \) is the long root that forms an angle of 150 (210) degrees with \( \alpha \). We relegate the proof that this case cannot actually occur in our situation to the next section.
, \( \alpha \) is one of the short roots and \( \beta \) is the long root that forms an angle of 150 (210) degrees with \( \alpha \). We relegate the proof that this case cannot actually occur in our situation to the next section.
In all the remaining cases, we have therefore shown that \( \alpha \) is a maximal root (cf. Lemma 4.1), so we may carry out the construction from Sect. 5. We now prove that the 3-Sasakian structure obtained this way indeed coincides with the original one we started with. We simplify the analysis by studying the reductive complement  .
.
Lemma 6.11
The reductive complement  decomposes B-orthogonally as
decomposes B-orthogonally as

Proof
\( \supset \): Clearly, \( X_1,X_2,X_3 \) are B-orthogonal to  . For
. For  with \( \beta + \gamma \ne 0 \), the subspaces
with \( \beta + \gamma \ne 0 \), the subspaces  and
and  are
are  -orthogonal. This implies that for all \( \beta \in \Phi \) with \( c_{\alpha \beta } =1 \), the subspaces
-orthogonal. This implies that for all \( \beta \in \Phi \) with \( c_{\alpha \beta } =1 \), the subspaces  are also
are also  -orthogonal to
-orthogonal to  .
.
\( \subset \): By Sect. 6.9, both sides of the equation have dimension \( 4n+3 \).\(\square \)
We can compare the structure tensors of the two 3-Sasakian structures in question via the isomorphism  , \( X \mapsto {\overline{X}}_p \). Proposition 6.6 has already shown that the vectors \( X_i \) correspond to the Reeb vector fields \( \xi _i \). Looking back at Theorem 1.1, equality of the contact forms is equivalent to the following
, \( X \mapsto {\overline{X}}_p \). Proposition 6.6 has already shown that the vectors \( X_i \) correspond to the Reeb vector fields \( \xi _i \). Looking back at Theorem 1.1, equality of the contact forms is equivalent to the following
Lemma 6.12
 .
.
Proof
By definition,  . We have
. We have

We also have \( B(X_2,X_2) = B(X_3,X_3) = - 4(n+2) \), since we could have used the same arguments for a maximal torus of e.g. the form  . \(\square \)
. \(\square \)
Because the contact forms coincide, so do their differentials, which are the fundamental 2-forms. Since the Riemannian metrics are determined by the fundamental 2-forms together with the almost complex structures, it suffices to show that the latter coincide. Let  denote the
denote the  -invariant endomorphism of
-invariant endomorphism of  corresponding to the G-invariant endomorphism field \( \varphi _i \), i.e.
corresponding to the G-invariant endomorphism field \( \varphi _i \), i.e.  . Looking back at Theorem 1.1, the claim reduces to showing that
. Looking back at Theorem 1.1, the claim reduces to showing that

The first equation is clear from Proposition 6.6 and the 3-Sasaki equations in Remark 2.4.
Proposition 6.13
The almost complex structures of the two 3-Sasakian structures in question coincide.
Proof
We first claim that \( L_1 \) is not only  - but even
- but even  -invariant, i.e. that the endomorphisms \( L_1 \) and
-invariant, i.e. that the endomorphisms \( L_1 \) and  commute on
commute on  . For all
. For all  , we have
, we have
In the second equation, we used that  corresponds to an almost complex structure on
corresponds to an almost complex structure on  which is compatible with the common fundamental 2-form \( d\eta _1 \). The last equation follows from Lemma 6.7. This shows that
which is compatible with the common fundamental 2-form \( d\eta _1 \). The last equation follows from Lemma 6.7. This shows that  on
on  and consequently,
and consequently,  .
.
Let \( \beta \) be a root such that \( c_{\alpha \beta } = 1 \). Since  leaves
leaves  invariant, so does
invariant, so does  . Because \( L_1 \) is
. Because \( L_1 \) is  -invariant,
-invariant,  is
is  -invariant and thus also leaves
-invariant and thus also leaves  invariant. Now,
invariant. Now,  and
and  are
are  -linear maps on the one-dimensional subspace
-linear maps on the one-dimensional subspace  which square to
which square to  , so they must be given by multiplication with \( \pm i \). Since both endomorphisms commute with complex conjugation, they act on
, so they must be given by multiplication with \( \pm i \). Since both endomorphisms commute with complex conjugation, they act on  by multiplication with \( \mp i \). Therefore, \( L_1 \) and
by multiplication with \( \mp i \). Therefore, \( L_1 \) and  coincide on
coincide on  up to sign. We finish the proof that
up to sign. We finish the proof that  on
on  by observing that for
by observing that for  , Lemma 6.2 implies
, Lemma 6.2 implies
Again, we can repeat the arguments for the maximal tori  , \( i =2,3\). Even though the root spaces look differently then, the subalgebra
, \( i =2,3\). Even though the root spaces look differently then, the subalgebra  is still the same because it can be defined independently of the maximal torus as the B-orthogonal complement of
is still the same because it can be defined independently of the maximal torus as the B-orthogonal complement of  in
in  by virtue of Lemma 6.11. This proves that the almost complex structures in question also coincide for \( i =2,3 \).\(\square \)
by virtue of Lemma 6.11. This proves that the almost complex structures in question also coincide for \( i =2,3 \).\(\square \)
Remark 6.14
In later sections, instead of working with the simply connected, almost effectively acting Lie group G with Lie algebra  , we may sometimes turn to a non-simply connected (possibly effectively acting) group \( {\widetilde{G}} \) with Lie algebra
, we may sometimes turn to a non-simply connected (possibly effectively acting) group \( {\widetilde{G}} \) with Lie algebra  . For
. For  , using
, using  instead of
instead of  allows us to describe the corresponding coset space more explicitly via matrices. If we consider a description \( {\widetilde{G}}/{\widetilde{H}} \), then the isotropy group of the G-action on \( {\widetilde{G}}/{\widetilde{H}} \) is given by the connected subgroup \( H \subset G \) whose Lie algebra coincides with that of \( {\widetilde{H}} \). This follows from the fact that M is simply connected via the long exact sequence of homotopy groups. Hence, \( {\widetilde{G}}/{\widetilde{H}} \) and G/H are governed by the same Lie algebraic data and are therefore isomorphic homogeneous 3-Sasakian manifolds.
allows us to describe the corresponding coset space more explicitly via matrices. If we consider a description \( {\widetilde{G}}/{\widetilde{H}} \), then the isotropy group of the G-action on \( {\widetilde{G}}/{\widetilde{H}} \) is given by the connected subgroup \( H \subset G \) whose Lie algebra coincides with that of \( {\widetilde{H}} \). This follows from the fact that M is simply connected via the long exact sequence of homotopy groups. Hence, \( {\widetilde{G}}/{\widetilde{H}} \) and G/H are governed by the same Lie algebraic data and are therefore isomorphic homogeneous 3-Sasakian manifolds.
7 Why the short root of  cannot occur
cannot occur
We need to fill the final gap left in the proof of Theorem 6.1 in the previous section:
Proposition 7.1
Even in the case of a homogeneous 3-Sasakian manifold with automorphism algebra  , the root described in Sect. 6 is maximal.
, the root described in Sect. 6 is maximal.
For the sake of contradiction, let us assume that \( \alpha \) was one of the short roots of  . Again, we consider the reductive complement
. Again, we consider the reductive complement  as well as the maps
as well as the maps  , \( X \mapsto {\overline{X}}_p \) and
, \( X \mapsto {\overline{X}}_p \) and  . Using the same arguments as in the proof of Lemma 6.11, we obtain the B-orthogonal decomposition
. Using the same arguments as in the proof of Lemma 6.11, we obtain the B-orthogonal decomposition

Under the isomorphism  , this induces a decomposition of the tangent space:
, this induces a decomposition of the tangent space:

where  .
.
Lemma 7.2
The above decomposition of \( T_pM \) is \( g_p \)-orthogonal.
Proof
If  , then
, then
Hence, each \( V_\beta \) is \( g_p \)-orthogonal to \( \langle \xi _1,\xi _2,\xi _3\rangle \). If \( \beta _1, \beta _2 \) are roots such that \( \beta _1 \ne -\beta _2 \), then there exists some  such that \( \beta _1(X) \ne -\beta _2(X) \). We extend \( \psi \) and \( g_p \) complex (bi-)linearly, let
such that \( \beta _1(X) \ne -\beta _2(X) \). We extend \( \psi \) and \( g_p \) complex (bi-)linearly, let  ,
,  and complexify Lemma 6.7 to obtain
and complexify Lemma 6.7 to obtain

Since \( \beta _1(X) \ne -\beta _2(X) \), it follows that  and
and  are \( g_p \)-orthogonal. This implies that for \( \beta \ne \pm \gamma \), the subspaces \( V_\beta \) and \( V_\gamma \) are \( g_p \)-orthogonal.\(\square \)
are \( g_p \)-orthogonal. This implies that for \( \beta \ne \pm \gamma \), the subspaces \( V_\beta \) and \( V_\gamma \) are \( g_p \)-orthogonal.\(\square \)
Lemma 7.3
For all  , we have
, we have
Proof
By virtue of Lemma 6.2,

Lemma 7.4
For any root \( \beta \in \Phi \), we have  .
.
Proof
Let \( \gamma \in \Phi \) be such that \( \gamma \ne \sigma \alpha + \tau \beta \) for all \( \sigma , \tau \in \{\pm 1\} \). Then, \( \sigma \beta +\tau \gamma \not \in \{\pm \alpha \} \) for all \( \sigma , \tau \in \{\pm 1\} \). Consequently, the subspace  is
is  - orthogonal to
- orthogonal to  and thus also to \( X_2 = i(X_\alpha +Y_\alpha ) \) (see the equations above Proposition 6.8). The previous lemma now implies that \( \varphi _2 V_\beta \) is \( g_p \)-orthogonal to \( V_\gamma \). The claim then follows from Lemma 7.2.\(\square \)
and thus also to \( X_2 = i(X_\alpha +Y_\alpha ) \) (see the equations above Proposition 6.8). The previous lemma now implies that \( \varphi _2 V_\beta \) is \( g_p \)-orthogonal to \( V_\gamma \). The claim then follows from Lemma 7.2.\(\square \)
Proof of Preposition 7.1
Let us label some of the roots of  according to the following diagram:
according to the following diagram:

Lemma 7.4 implies that \( \varphi _2V_\beta \subset V_\gamma \). Since \( \varphi _2 \) is injective on the horizontal space, we in fact have \( \varphi _2V_\beta = V_\gamma \). Another application of Lemma 7.4 yields  . If we can show that there exists some \( Y \in V_\gamma \) such that \( \varphi _2Y \) has a non-trivial \( V_\delta \)-component, then we arrive at a contradiction to the fact that
. If we can show that there exists some \( Y \in V_\gamma \) such that \( \varphi _2Y \) has a non-trivial \( V_\delta \)-component, then we arrive at a contradiction to the fact that  on \( V_\beta \).
on \( V_\beta \).
Let \( Z^* \) denote the complex conjugate of a vector  . We can choose
. We can choose  ,
,  in such a way that
in such a way that
We note that
and
Lemma 7.3 finally implies that \( \varphi _2Y \) has a \( V_\delta \)-component for  .\(\square \)
.\(\square \)
8 Why no proper subgroup of  acts transitively
acts transitively
We have shown that any simply connected homogeneous 3-Sasakian manifold M is obtained from a complex 3-Sasakian datum as explained in Sect. 5. Hence, M can be written as G/H, where G is a simply connected compact simple Lie group. As G is simple, we pass to the effectively acting finite quotient \( {\widetilde{G}} \) which is then a subgroup of  . We can now write \( M = {\widetilde{G}} /{\widetilde{H}} \). Below we show that
. We can now write \( M = {\widetilde{G}} /{\widetilde{H}} \). Below we show that  . This concludes Theorem 1.1 as M determines its 3-Sasakian datum.
. This concludes Theorem 1.1 as M determines its 3-Sasakian datum.
Proposition 8.1
If a subgroup \({\widetilde{G}}\subset \textrm{Aut}_0(M)\) acts transitively on a simply connected homogeneous 3-Sasakian manifold M, then \({\widetilde{G}}=\textrm{Aut}_0(M)\).
Proof
We show that the Lie algebra  of \({\widetilde{G}}\) is tied to purely geometric data of M. Recall the setup from Theorem 1.1: We have a reductive decomposition
of \({\widetilde{G}}\) is tied to purely geometric data of M. Recall the setup from Theorem 1.1: We have a reductive decomposition  , where
, where  and
and  , where
, where  corresponds to the Reeb vector fields \(\xi _i\) and
corresponds to the Reeb vector fields \(\xi _i\) and  . Note that we have the commutator relations (cf. Proposition 5.4)
. Note that we have the commutator relations (cf. Proposition 5.4)

Consider the subspace  . Using the commutator relations we find that this is an ideal in
. Using the commutator relations we find that this is an ideal in  and thus (Proposition 6.10) already
and thus (Proposition 6.10) already  itself. Hence, the knowledge of
itself. Hence, the knowledge of  embedded in the Lie algebra of Killing vector fields
embedded in the Lie algebra of Killing vector fields  on M via \(X \mapsto {\overline{X}}\) alone determines
on M via \(X \mapsto {\overline{X}}\) alone determines  .
.
We now characterize  as the subset of Killing fields whose covariant derivatives satisfy a certain behavior at \( o = e{\widetilde{H}} \). By analogy, recall that in a symmetric space, the analogue of
as the subset of Killing fields whose covariant derivatives satisfy a certain behavior at \( o = e{\widetilde{H}} \). By analogy, recall that in a symmetric space, the analogue of  can be characterized as the Killing fields whose covariant derivative vanishes at o. Let \(\nabla \) be the Levi-Civita connection on M, and
can be characterized as the Killing fields whose covariant derivative vanishes at o. Let \(\nabla \) be the Levi-Civita connection on M, and  the associated Nomizu operator defined by
the associated Nomizu operator defined by
It satisfies

see [11, Theorem 4.2]. Thus, by definition of the Nomizu operator, we have
which means that

for  and
and

for  , where we used Lemma 6.2 in the last equation. Hence, the fundamental vector field of
, where we used Lemma 6.2 in the last equation. Hence, the fundamental vector field of  satisfies
satisfies

for all \(v\in T_oM\) and where  denotes the projection of v to
denotes the projection of v to  . Note that \((\nabla {\overline{Y}})_o\) depends only on the value
. Note that \((\nabla {\overline{Y}})_o\) depends only on the value  . We now consider the maps
. We now consider the maps

where the first map is  and the second is evaluation at o. The evaluation map is injective, as for Killing fields \(Y_1,Y_2\) in the middle space with \((Y_1)_o = (Y_2)_o\), by Property (2) also \((\nabla Y_1)_o = (\nabla Y_2)_o\), which implies that \(Y_1 = Y_2\). Since
and the second is evaluation at o. The evaluation map is injective, as for Killing fields \(Y_1,Y_2\) in the middle space with \((Y_1)_o = (Y_2)_o\), by Property (2) also \((\nabla Y_1)_o = (\nabla Y_2)_o\), which implies that \(Y_1 = Y_2\). Since  both maps are isomorphisms. Thus,
both maps are isomorphisms. Thus,

Therefore we have shown that every connected Lie group \( {\widetilde{G}} \) with Lie algebra  acting effectively and transitively on M has the same Lie algebra, namely
acting effectively and transitively on M has the same Lie algebra, namely  . The corresponding connected subgroup of
. The corresponding connected subgroup of  is then
is then  .\(\square \)
.\(\square \)
9 Determining the isotropy
Having proven Theorem 1.1, we now derive the precise list given in Corollary 1.2. By Theorems 5.1 and 6.1 any simply-connected homogeneous 3-Sasakian manifold can be written in the form G/H, where G is a simply-connected simple Lie group and \(H = (C_G(K))_0\), where \(K\subset G\) is the connected subgroup with Lie algebra  determined by a maximal root. In this section, we will determine the isotropy groups H, thereby proving Corollary 1.2 in the simply connected case. The classical cases are dealt with in the following
determined by a maximal root. In this section, we will determine the isotropy groups H, thereby proving Corollary 1.2 in the simply connected case. The classical cases are dealt with in the following
Proposition 9.1
For  and
and  , the isotropy groups are given by
, the isotropy groups are given by  and
and  , respectively.
, respectively.
Proof
We use the explicit description of the root systems of the compact groups provided in [16, Chapter 11].
 : We may choose the maximal root \( \alpha \) such that
: We may choose the maximal root \( \alpha \) such that  (by letting \( \alpha = \gamma _{n+1} \) in Tapp’s notation). Accordingly,
(by letting \( \alpha = \gamma _{n+1} \) in Tapp’s notation). Accordingly,

 : We may choose \( \alpha \) such that
: We may choose \( \alpha \) such that  (by letting \( \alpha = \alpha _{m-1,m} \) in Tapp’s notation). Accordingly,
(by letting \( \alpha = \alpha _{m-1,m} \) in Tapp’s notation). Accordingly,

 : We recall that there are two embeddings
: We recall that there are two embeddings  , depending on whether
, depending on whether  is viewed as acting on
is viewed as acting on  by multiplication from the left or right, respectively. We may choose \( \alpha \) such that
by multiplication from the left or right, respectively. We may choose \( \alpha \) such that  (by letting \( \alpha = \alpha _{[k/2]-1,[k/2]} \) in Tapp’s notation). Accordingly,
(by letting \( \alpha = \alpha _{[k/2]-1,[k/2]} \) in Tapp’s notation). Accordingly,

We now present a different method based on Borel–de Siebenthal theory, which allows us to first understand the isotopy algebra  in the exceptional cases:
in the exceptional cases:
Using the same notation as before, we let  be a maximal Abelian subalgebra and consider the maximal Abelian subalgebra
be a maximal Abelian subalgebra and consider the maximal Abelian subalgebra  of
of  . Let \(\alpha \) denote the maximal root that vanishes on
. Let \(\alpha \) denote the maximal root that vanishes on  . We fix a set of positive roots of
. We fix a set of positive roots of  using a slight perturbation of the hyperplane perpendicular to the maximal root \(\alpha \). By intersecting this hyperplane with
using a slight perturbation of the hyperplane perpendicular to the maximal root \(\alpha \). By intersecting this hyperplane with  , we also obtain a notion of positive root for
, we also obtain a notion of positive root for  . By the very definition of root spaces, as
. By the very definition of root spaces, as  commutes with \(X_1\), any root of
commutes with \(X_1\), any root of  becomes, by extending it by 0 on \(X_1\), a root of
becomes, by extending it by 0 on \(X_1\), a root of  .
.
Proposition 9.2
The simple  -roots are precisely those simple
-roots are precisely those simple  -roots perpendicular to \(\alpha \).
-roots perpendicular to \(\alpha \).
Proof
By our notions of positivity, any  -simple root is also
-simple root is also  -simple: If an
-simple: If an  -root is the sum of two positive
-root is the sum of two positive  -roots, both of them have to lie in the hyperplane perpendicular to \(\alpha \). Conversely, recall that by Proposition 5.4 the roots of
-roots, both of them have to lie in the hyperplane perpendicular to \(\alpha \). Conversely, recall that by Proposition 5.4 the roots of  are exactly those roots \(\beta \) perpendicular to the maximal root \(\alpha \).\(\square \)
are exactly those roots \(\beta \) perpendicular to the maximal root \(\alpha \).\(\square \)
We can thus determine the isotropy type of H by deleting the nodes in the Dynkin diagram of G corresponding to simple roots that are not perpendicular to \(\alpha \). For each simple G, these were determined by Borel and de Siebenthal in [8]: In the table on p. 219 they draw the Dynkin diagrams for every simple  , extended by the lowest root (denoted P in their notation). In order to find the isomorphism type of H one therefore only needs to erase this lowest root, as well as all roots connected to it. As an example, consider the Dynkin diagram of \(E_6\):
, extended by the lowest root (denoted P in their notation). In order to find the isomorphism type of H one therefore only needs to erase this lowest root, as well as all roots connected to it. As an example, consider the Dynkin diagram of \(E_6\):

Deleting \(\alpha \) as well as the unique simple root connected to it results in the Dynkin diagram of  : The homogeneous 3-Sasakian manifold corresponding to \(E_6\) is
: The homogeneous 3-Sasakian manifold corresponding to \(E_6\) is  .
.
Remark 9.3
If one removes only the nodes in the Dynkin diagram of G that are connected to \(\alpha \), and not \(\alpha \) itself, one obtains the Dynkin diagram of the normalizer \(N_G(K)\), which then yield the Wolf spaces \(G/N_G(K)\). Note that by the list in [8], in all cases except  the maximal root \(\alpha \) is connected to only one other node, which means that in these cases the groups H and \(N_G(K)\) are semisimple, whereas in the case
the maximal root \(\alpha \) is connected to only one other node, which means that in these cases the groups H and \(N_G(K)\) are semisimple, whereas in the case  the groups H and \(N_G(K)\) have a one-dimensional center. Furthermore, in the cases except
the groups H and \(N_G(K)\) have a one-dimensional center. Furthermore, in the cases except  , the normalizer \(N_G(K)\) is a maximal subgroup of maximal rank: the types of such groups are exactly those that were classified by Borel and de Siebenthal in [8]: Given a simple compact Lie group G, one adds the lowest root to the Dynkin diagram and removes one other simple root from it.
, the normalizer \(N_G(K)\) is a maximal subgroup of maximal rank: the types of such groups are exactly those that were classified by Borel and de Siebenthal in [8]: Given a simple compact Lie group G, one adds the lowest root to the Dynkin diagram and removes one other simple root from it.
Going through the list in [8], one obtains the Lie algebras of the isotropy groups of the homogeneous spaces occurring in Corollary 1.2. As we determined the isotropy groups in the classical cases above, in order to finish the proof of this corollary in the simply connected case, we only need to argue that in the exceptional cases the isotropy groups are simply connected. Ishitoya and Toda showed in [12, Corollary 2.2] that in the cases \(G=G_2, F_4, E_6, E_7, E_8\), we have  , which is, because G is simply connected, equivalent to
, which is, because G is simply connected, equivalent to  . (See also [8, Remarque II, p. 220] for how to compute the fundamental group of a maximal subgroup of G of maximal rank.) Moreover, by [12, Theorem 2.1] the normalizer \(N_G(K)\) is of the form
. (See also [8, Remarque II, p. 220] for how to compute the fundamental group of a maximal subgroup of G of maximal rank.) Moreover, by [12, Theorem 2.1] the normalizer \(N_G(K)\) is of the form  , which then implies that H is simply connected.
, which then implies that H is simply connected.
10 Why  is the only non-simply connected homogeneous 3-Sasakian manifold
is the only non-simply connected homogeneous 3-Sasakian manifold
Having treated the simply connected case of Corollary 1.2, our goal is now to prove the following
Theorem 10.1
The only homogeneous 3-Sasakian manifolds which are not simply connected are the real projective spaces 
Let \( M = G/{\overline{H}} \) be a homogeneous 3-Sasakian manifold (not necessarily simply connected), where G is a simply connected compact Lie group and \( {\overline{H}} \) is possibly disconnected. The universal cover of \( G/{\overline{H}} \) is given by G/H, where H denotes the identity component of \( {\overline{H}} \), and the homogeneous 3-Sasakian structure lifts to the simply connected space G/H. As shown in Sect. 6, the automorphism group G has to be simple. The vectors  from Sect. 6 span a subalgebra
from Sect. 6 span a subalgebra  and we let \(K \subset G \) denote the corresponding connected subgroup.
and we let \(K \subset G \) denote the corresponding connected subgroup.
Since H is the identity component of \( {\overline{H}}\), we have \( {\overline{H}} \subset N_G(H) \). Furthermore, the 3-Sasakian structure descends from G/H to \( G/{\overline{H}} \), so \( {\overline{H}} \subset C_G(K) \). Conversely, any subgroup \( {\overline{H}} \subset N_G(H) \cap C_G(K) \) containing H allows us to define a 3-Sasakian structure on \( G/{\overline{H}}\). Summarizing, the non-simply connected quotients of a given simply connected homogeneous 3-Sasakian manifold G/H are classified by the subgroups of the group
Thus, it suffices to show that this quotient is  for
for  and trivial otherwise.
and trivial otherwise.
Lemma 10.2
The numerator \( N_G(H) \cap C_G(K) \) is the subgroup generated by \( H \cup Z(K) \).
Proof
Clearly, \( H \cup Z(K) \subset N_G(H) \cap C_G(K) \). The vector  is the infinitesimal generator of a circle subgroup \( S_1 \subset K \). Since
is the infinitesimal generator of a circle subgroup \( S_1 \subset K \). Since  and the centralizer of any torus (not necessarily maximal) in a compact connected Lie group is always connected, it follows that \( C_G(S_1) \) is the subgroup generated by \( H \cup S_1 \). Consequently, any \( g \in C_G(K) \subset C_G(S_1) \) can be represented as \( g = hg_1 \) for some \( h \in H \), \( g_1 \in S_1 \). Since \( H \subset C_G(K) \), we have \( g_1 = h^{-1}g \in C_G(K) \cap K = Z(K) \).\(\square \)
and the centralizer of any torus (not necessarily maximal) in a compact connected Lie group is always connected, it follows that \( C_G(S_1) \) is the subgroup generated by \( H \cup S_1 \). Consequently, any \( g \in C_G(K) \subset C_G(S_1) \) can be represented as \( g = hg_1 \) for some \( h \in H \), \( g_1 \in S_1 \). Since \( H \subset C_G(K) \), we have \( g_1 = h^{-1}g \in C_G(K) \cap K = Z(K) \).\(\square \)
Proposition 10.3
The quotient  and trivial otherwise.
and trivial otherwise.
Proof
By the previous lemma, it suffices to check if Z(K) is contained in H.
 : We have already seen in Sect. 9 that the center
: We have already seen in Sect. 9 that the center  is not contained in
is not contained in  .
.
 : We have also shown that in this case
: We have also shown that in this case  is contained in
is contained in  .
.
 : We have seen that for
: We have seen that for  , the center
, the center  is contained in
is contained in  We now transfer this statement to
We now transfer this statement to  : Denote the universal covering map by
: Denote the universal covering map by  . First, we observe that the connected subgroup of
. First, we observe that the connected subgroup of  that maps onto a block-diagonally embedded
that maps onto a block-diagonally embedded  is
is  , for \(r\geqslant 4\): this is because
, for \(r\geqslant 4\): this is because  is 2-connected for \(r\geqslant 4\), hence equal to
is 2-connected for \(r\geqslant 4\), hence equal to  by the long exact sequence in homotopy. Thus, for \(k\geqslant 7\), the subgroups
by the long exact sequence in homotopy. Thus, for \(k\geqslant 7\), the subgroups  and
and  lift to
lift to  and
and  , respectively. As \(\pi \) is a \(2\,{:}\,1\)-covering, the group covering
, respectively. As \(\pi \) is a \(2\,{:}\,1\)-covering, the group covering  is
is  , where the
, where the  quotient means that the nontrivial elements in the kernels of the respective projections are identified. Now,
quotient means that the nontrivial elements in the kernels of the respective projections are identified. Now,  . This implies that the center of
. This implies that the center of  is contained in
is contained in  .
.
\( G = G_2, F_4, E_6, E_7, E_8 \): Ishitoya and Toda showed that the subgroup U of the corresponding symmetric base space G/U has to be of the form  and that the center
and that the center  is contained in H [12, Theorem 2.1].\(\square \)
is contained in H [12, Theorem 2.1].\(\square \)
11 Deriving the classification of homogeneous positive qK manifolds
We end this article by showing that the classification of homogeneous positive qK manifolds in Sect. 1.3, which had originally been the stepping stone for the classification of homogeneous 3-Sasakian manifolds, can in turn be derived from our results.
Let B be a positive qK manifold. We recall that qK manifolds may be characterized by a subbundle \( Q \subset \text {End} \, TB \) of the endomorphism bundle which admits a local frame satisfying the multiplication rules of the quaternions. In her 1975 article [15], Konishi showed that the  - principal fibre bundle \( P \rightarrow B \) of oriented orthonormal frames of Q admits a 3-Sasakian structure. This construction is known as the Konishi bundle over B and constitutes the inverse of the fibration introduced in Proposition 2.7. Another natural and interesting bundle over B is the unit sphere bundle
- principal fibre bundle \( P \rightarrow B \) of oriented orthonormal frames of Q admits a 3-Sasakian structure. This construction is known as the Konishi bundle over B and constitutes the inverse of the fibration introduced in Proposition 2.7. Another natural and interesting bundle over B is the unit sphere bundle  in Q, known as the twistor fibration. Its total space Z is both a complex contact manifold and a Fano variety [9, Chapters 12, 13].
in Q, known as the twistor fibration. Its total space Z is both a complex contact manifold and a Fano variety [9, Chapters 12, 13].
A qK automorphism of B is an isometry \( \phi :B \rightarrow B \) such that conjugation with its differential \( d\phi \) leaves the bundle Q invariant. We call B a homogeneous qK manifold if there is a Lie group G acting transitively on B by qK automorphisms. We first show the following
Proposition 11.1
The Konishi bundle over a simply connected homogeneous positive qK manifold is a homogeneous 3-Sasakian manifold.
Let B be a simply connected homogeneous positive qK manifold, so that we may write \( B = G/U \), where G is simply connected and U is connected. Because G acts on B by qK automorphisms, the G-action lifts to the Konishi bundle P. In particular, the isotropy group U acts on the fiber F of P over the identity coset \( eU \in B \).
Choose and fix a frame \( p \in F \). This allows us to identify F with  via the orbit bijection
via the orbit bijection  ,
,  . The
. The  -left action on itself by left multiplication now induces a left action on F (which depends on the choice of p), viz.
-left action on itself by left multiplication now induces a left action on F (which depends on the choice of p), viz.  . Since the U-action commutes with the
. Since the U-action commutes with the  -right action on F, there exists a homomorphism \( \rho :U \rightarrow V \) onto a subgroup
-right action on F, there exists a homomorphism \( \rho :U \rightarrow V \) onto a subgroup  (again, all depending on p) such that
(again, all depending on p) such that  for all \( q \in F \), namely
for all \( q \in F \), namely  . Clearly,
. Clearly,  .
.
Lemma 11.2
\( d = 3\).
Proof
Let us first assume that \( d = 0 \). Then, the connected group U would act trivially on F. Hence, we would obtain a well-defined global section \( B \rightarrow P\),  , meaning that the principal fiber bundle P was trivial. But the first Pontryagin class \( p_1(P) \) of P is (up to a factor) given by the class of the fundamental 4-form \( \Omega \in \Omega ^4(B) \) of B and is therefore non-trivial [4, Proposition 14.92].
, meaning that the principal fiber bundle P was trivial. But the first Pontryagin class \( p_1(P) \) of P is (up to a factor) given by the class of the fundamental 4-form \( \Omega \in \Omega ^4(B) \) of B and is therefore non-trivial [4, Proposition 14.92].
If we suppose that \( d = 1 \), then V is a connected one-dimensional subgroup of  and is thus comprised of rotations around a fixed axis
and is thus comprised of rotations around a fixed axis  . Choose a point \( x \in L \cap S^2 \). We view the frame \( p \in F \) as a linear isometry
. Choose a point \( x \in L \cap S^2 \). We view the frame \( p \in F \) as a linear isometry  and consider the mapping \( B \rightarrow Z \),
and consider the mapping \( B \rightarrow Z \),  . This map is well-defined because
. This map is well-defined because

We would thus obtain a global section of the twistor fibration, which is impossible on compact positive qK manifolds [3, Theorem 3.8].\(\square \)
Proof of Proposition 11.1
From the previous lemma, we know that U acts transitively on F and consequently, G acts transitively on P. This action preserves the 3-Sasakian structure, since the Reeb vector fields are (by construction of the Konishi bundle) the infinitesimal generators of the  -action, which commutes with G. \(\square \)
-action, which commutes with G. \(\square \)
Proof of of Corollary 1.3
By Proposition 11.1, the Konishi bundle P over a simply connected homogeneous positive qK manifold B is a homogeneous 3-Sasakian manifold, i.e. one of the manifolds listed in Corollary 1.2. Dividing P by the action of the group \( K \subset G \) from the previous sections, we obtain the list in Corollary 1.3. The statement about the Riemannian metric and quaternionic structure follows from the fact that the Konishi bundle is a Riemannian fibration.
Let us now assume that \( {\overline{B}} = G/{\overline{U}} \) was a non-simply connected homogeneous positive qK manifold, where \( {\overline{U}} \) is disconnected. Then, \( {\overline{B}} \) is finitely covered by \( B = G/U \), where U denotes the identity component of \( {\overline{U}} \). The qK structure lifts from \( {\overline{B}} \) to B and the Konishi bundles \( P, {\overline{P}} \) over \( B, {\overline{B}} \) form a diagram

We obtain the existence of the dashed equivariant map \( P \rightarrow {\overline{P}} \), so that \( {\overline{P}} \) is a non-simply connected homogeneous 3-Sasakian manifold. By Theorem 10.1, \( {\overline{P}} \) can only be  which leads to the same quotient
which leads to the same quotient  as
as  \(\square \)
\(\square \)
References
Agricola, I., Dileo, G., Stecker, L.: Homogeneous non-degenerate \(3- (\alpha,\delta )\)-Sasaki manifolds and submersions over quaternionic Kähler spaces. Ann. Global Anal. Geom. 60(1), 111–141 (2021)
Alekseevsky, D.V.: Compact quaternion spaces. Funct. Anal. Appl. 2(2), 106–114 (1968)
Alekseevsky, D.V., Marchiafava, S., Pontecorvo, M.: Compatible almost complex structures on quaternion Kähler manifolds. Ann. Global Anal. Geom. 16(5), 419–444 (1998)
Besse, A.L.: Einstein Manifolds. Classics in Mathematics. Springer, Berlin (2008). Reprint of the (1987 )edition
Bielawski, R.: On the hyper-Kähler metrics associated to singularities of nilpotent varieties. Ann. Global Anal. Geom. 14(2), 177–191 (1996)
Boothby, W.M.: Homogeneous complex contact manifolds. In: 1961 Proceedings of Symposia in Pure Mathematics, vol. III, pp. 144–154. American Mathematical Society, Providence (1961)
Boothby, W.M., Wang, H.C.: On contact manifolds. Ann. Math. 68(3), 721–734 (1958)
Borel, A., De Siebenthal, J.: Les sous-groupes fermés de rang maximum des groupes de Lie clos. Comment. Math. Helv. 23, 200–221 (1949)
Boyer, C.P., Galicki, K.: Sasakian Geometry. Oxford Mathematical Monographs. Oxford University Press, Oxford (2008)
Boyer, C.P., Galicki, K., Mann, B.M.: The geometry and topology of 3-Sasakian manifolds. J. Reine Angew. Math. 455, 183–220 (1994)
Draper, C., Ortega, M., Palomo, F.J.: Affine connections on 3-Sasakian homogeneous manifolds. Math. Z. 294(1–2), 817–868 (2020)
Ishitoya, K., Toda, H.: On the cohomology of irreducible symmetric spaces of exceptional type. J. Math. Kyoto Univ. 17(2), 225–243 (1977)
Knapp, A.W.: Lie Groups Beyond an Introduction. Progress in Mathematics, vol. 140. Birkhäuser, Boston (1996)
Kobayashi, S., Nomizu, K.: Foundations of Differential Geometry. Vol. II. Wiley Classics Library. Wiley, New York (1996). Reprint of the 1969 original publication
Konishi, M.: On manifolds with Sasakian 3-structure over quaternion Kaehler manifolds. Kōdai Math. Semin. Rep. 26, 194–200 (1974/75)
Tapp, K.: Matrix Groups for Undergraduates. Student Mathematical Library, vol. 79, 2nd edn. American Mathematical Society, Providence (2016)
Wolf, J.A.: Complex homogeneous contact manifolds and quaternionic symmetric spaces. J. Math. Mech. 14, 1033–1047 (1965)
Acknowledgements
The third named author thanks Ilka Agricola and Cristina Draper for fruitful discussions about the subject.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Leon Roschig is supported by the German Academic Scholarship Foundation.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Goertsches, O., Roschig, L. & Stecker, L. Revisiting the classification of homogeneous 3-Sasakian and quaternionic Kähler manifolds. European Journal of Mathematics 9, 11 (2023). https://doi.org/10.1007/s40879-023-00601-8
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40879-023-00601-8




 is a
is a  -graded compact simple Lie algebra whose even part is a sum of two commuting subalgebras,
-graded compact simple Lie algebra whose even part is a sum of two commuting subalgebras, 
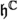 -module W such that the complexified
-module W such that the complexified 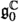 -module
-module  is isomorphic to the tensor product of the natural
is isomorphic to the tensor product of the natural  -module
-module 
 is a
is a  -graded simple Lie algebra whose even part is a sum of two commuting subalgebras,
-graded simple Lie algebra whose even part is a sum of two commuting subalgebras, 
 -module W such that
-module W such that  as
as  -modules.
-modules. cannot occur
cannot occur acts transitively
acts transitively is the only non-simply connected homogeneous 3-Sasakian manifold
is the only non-simply connected homogeneous 3-Sasakian manifold