Ample simplicial complexes

Abstract

Motivated by potential applications in network theory, engineering and computer science, we study r-ample simplicial complexes. These complexes can be viewed as finite approximations to the Rado complex which has a remarkable property of indestructibility, in the sense that removing any finite number of its simplexes leaves a complex isomorphic to itself. We prove that an r-ample simplicial complex is simply connected and 2-connected for r large. The number n of vertexes of an r-ample simplicial complex satisfies $\exp \bigl (\Omega \bigl (\frac{2^r}{\sqrt{r}}\bigr )\bigr )$. We use the probabilistic method to establish the existence of r-ample simplicial complexes with n vertexes for any $n>r 2^r 2^{2^r}$. Finally, we introduce the iterated Paley simplicial complexes, which are explicitly constructed r-ample simplicial complexes with nearly optimal number of vertexes.

1 Introduction

Modern network science uses simplicial complexes of high dimension for modelling complex networks consisting of a vast number of interacting entities: while pairwise interactions can be recorded by a graph, the higher order interactions between the entities require the language of simplicial complexes of dimension greater than 1. We refer the reader to a recent survey [4] with many interesting references including applications to social systems, neuroscience, ecology, and to biological sciences.

Viewing simplicial complexes as representing networks raises new interesting questions about their geometry and topology. Motivated by this viewpoint, we study in this paper a special class of simplicial complexes representing “stable and resilient” networks, in the sense that small alterations of the network have limited impact on its global properties (such as connectivity and high connectivity).

In [21] the authors investigated a remarkable simplicial complex X (called the Rado complex) which is “totally indestructible” in the following sense: removing any finite number of simplexes of X leaves a simplicial complex isomorphic to X. Unfortunately, X has infinite (countable) number of vertexes and cannot be practically implemented. In the present paper we study finite simplicial complexes which can be viewed as approximations to the Rado complex X. We call such complexes r-ample, where $r\geqslant 1$ is an integer characterising the depth or level of ampleness. The Rado complex is the only simplicial complex on countably many vertexes which is $\infty$-ample. The finite simplicial complexes which we study in this paper have a limited amount of ampleness and a limited amount of indestructibility. The formal definition of r-ampleness requires the existence of all possible extensions of simplicial subcomplexes of size at most r.

We believe that r-ample finite simplicial complexes, with r large, can serve as models for very resilient networks in real life applications.

One of the results of [21] states that the geometric realisation of the Rado complex is homeomorphic to the infinite dimensional simplex and hence it is contractible. A related mathematical object is the medial regime random simplicial complex [19] which, as we show in this paper, is r-ample, with probability tending to one.

It was proven in [19] that the medial regime random simplicial complex is simply connected and has vanishing Betti numbers in dimensions $\leqslant \log _2 \ln n$. For these reasons one expects that any r-ample simplicial complex is highly connected, for large r. This question is discussed below in Sect. 4.

Analogues of the ampleness property of this paper have been studied for graphs, hypergraphs, tournaments, and other structures, in combinatorics and in mathematical logic. In the literature a variety of terms have been used: r-existentially completeness, r-existentially closedness, r-e.c. for short [9, 13], and also the Adjacency Axiom r [5, 6], an extension property [18], property P(r) [7, 11]. This property intuitively means that you can get anything you want, it is also referred to as the Alice Restaurant Axiom [41, 43], and sometimes just as random. Here we use the term r-ample.

The plan of this paper is as follows. In Sect. 2 we give the main definition and discuss several examples.

In Sect. 3 we discuss the resilience properties of r-ample complexes; our main result, Theorem 3.1, gives a bound on the family of simplexes ${\mathscr {F}}$ such that removing ${\mathscr {F}}$ reduces the level of ampleness by at most k. A significant role in this estimate is played by the Dedekind number which equals the number of simplicial complexes on k vertexes; good asymptotic approximations for the Dedekind number are known, see Sect. 2.

In Sect. 4 we show that r-ample simplicial complexes are simply connected and 2-connected, for suitable values of r. Note that the Rado complex is contractible and hence one expects that any r-ample complex is k-connected for $r>r(k)$, for some $r(k)<\infty$. We do not know if this is true in general, however we are able to analyse the cases $k=1$ and $k=2$.

In Sect. 5 we construct ample simplicial complexes using the probabilistic method. We show that for every $r \geqslant 5$ and for any $n \geqslant r2^r2^{2^{r}}$, there exists an r-ample simplicial complex having exactly n vertexes, see Proposition 5.4.

In the final Sect. 6 we construct an explicit family, in the spirit of Paley graphs, of r-ample simplicial complexes on $\exp (O(r2^r))$ vertices. We do not know if this construction gives smaller r-ample complexes than in our probabilitic existence proof. The lower bound $\exp \bigl (\Omega \bigl (2^r/\sqrt{r}\bigr )\bigr )$ follows from Corollary 2.6. The construction of this section uses sophisticated tools of number theory.

2 Definitions and first examples

First we fix our notations and terminology. The symbol V(X) denotes the set of vertices of a simplicial complex X. If $U\subseteq V(X)$ is a subset we denote by $X_U$ the induced subcomplex on U, i.e., $V(X_U)=U$ and a set of points of U forms a simplex in $X_U$ if and only if it is a simplex in X.

An embedding of a simplicial complex A into X is an isomorphism between A and an induced subcomplex of X.

The join of simplicial complexes X and Y is denoted $X \,{*}\,Y$; recall that the set of vertexes of the join is $V(X)\sqcup V(Y)$ and the simplexes of the join are simplexes of the complexes X and Y as well as simplexes of the form $\sigma \tau =\sigma \,{*}\,\tau$ where $\sigma$ is a simplex in X and $\tau$ is a simplex in Y. The simplex $\sigma \tau =\sigma \,{*}\,\tau$ has as its vertex set the union of vertexes of $\sigma$ and of $\tau$. The symbol CX stands for the cone over X. For a vertex $v\in V(X)$ the symbol $\mathrm{lk}_X(v)$ denotes the link of v in X, i.e., the subcomplex of X formed by all simplexes $\sigma$ which do not contain v but such that $\sigma v=\sigma \,{*}\, v$ is a simplex of X.

Here is our main definition.

Definition 2.1

Let $r\geqslant 1$ be an integer. A nonempty simplicial complex X is said to be r-ample if for each subset $U\subseteq V(X)$ with $|U|\leqslant r$ and for each subcomplex $A\subseteq X_U$ there exists a vertex $v\in V(X) - U$ such that

$$\begin{aligned} \mathrm{lk}_X(v)\cap X_U = A. \end{aligned}$$

(2.1)

We say that X is ample or $\infty$-ample if it is r-ample for every $r\geqslant 1$.

The condition (2.1) can equivalently be expressed as

$$\begin{aligned} X_{U\cup \{v\}} = X_U \cup (v\,{*}\, A). \end{aligned}$$

Obviously, no finite simplicial complex can be $\infty$-ample. In [21] it was shown that there exists a unique, up to isomorphism, $\infty$-ample simplicial complex X on countably many vertices. The 1-skeleton of X is the well-known Rado graph [12, 17, 39]. The complex X (called the Rado complex in [21]) possesses remarkable stability properties, for example removing from X any finite set of simplexes leaves a simplicial complex isomorphic to X.

Later in this paper we show that for any integer r there exist finite r-ample simplicial complexes and we give probabilistic as well as explicit deterministic constructions.

It is clear that r-ampleness depends only on the r-dimensional skeleton.

To be 1-ample a simplicial complex must have no isolated vertexes and no vertexes connected to all other vertexes.

A 1-ample complex has at least four vertexes and Fig. 1 shows two such examples.

Fig. 1

1-ample complexes

A 2-ample complex is connected since for any pair of vertexes there must exist a vertex connected to both, i.e., the complex must have diameter $\leqslant 2$. A 2-ample complex is also twin-free in the sense that no two vertexes have exactly the same link. The following example shows that a 2-ample simplicial complex may be not simply connected.

Example 2.2

Consider a 2-dimensional simplicial complex X having 13 vertexes labelled by integers $0, 1, 2, \dots , 12$. A pair of vertexes i and j is connected by an edge iff the difference $i-j$ is a square modulo 13, i.e., if

$$\begin{aligned} i-j \equiv \pm 1, \pm 3, \pm 4 \mod 13. \end{aligned}$$

The 1-skeleton of X is a well-known Paley graph of order 13, see [9]. Next we add 13 triangles

$$\begin{aligned} i,\; i+1,\; i+4, \quad \text{ where } \;\; i=0, 1, \dots , 12. \end{aligned}$$

We claim that the obtained complex X is 2-ample. The verification amounts to the following: for any two vertices v, w, there exist vertexes adjacent to both v and w, vertexes adjacent to neither v nor w, vertexes adjacent to v but not to w and vertexes adjacent to w but not to v. Moreover, any edge lies both on single filled and unfilled triangles. Indeed, an edge $i, i+1$ lies in the triangle $i, i+1, i+4$ (filled) as well as in the triangle $i-3, i, i+1$ (unfilled). Informally, the filled triangles can be characterised by the identity $1+3=4$ and the unfilled by $3+1=4$.

We note that X can be obtained from the triangulated torus with 13 vertexes, 39 edges and 26 triangles (see Fig. 2) by removing 13 white triangles of type $i, i+3$, $i+4$. From this description it is obvious that X collapses onto a graph and calculating the Euler characteristic we find $b_0(X)=1,$ $b_1(X)= 14$ and $b_2(X)=0$.

The following lemma gives an equivalent criterion for r-ampleness.

Fig. 2

The simplicial complex of Example 2.2 can be obtained from the triangulated torus with 13 vertices, 39 edges and 26 triangles, by removing 13 triangles of type $\{i, i+3, i+4\}$

Lemma 2.3

A simplicial complex X is r-ample if and only if for every pair (A, B) consisting of a simplicial complex A and an induced subcomplex B of  A, satisfying $|V(A)|\leqslant r+1$, and for every embedding $f_B$ of B into X, there exists an embedding $f_A$ of A into X extending $f_B$.

Proof

Clearly the property described in Lemma 2.3 implies r-ampleness and we only need to show the inverse. Suppose that X is r-ample and let (A, B) be a pair consisting of a simplicial complex A with $|V(A)|\leqslant r+1$ and its induced subcomplex B. We can find a chain of subcomplexes

$$\begin{aligned} B=B_0\subset B_1\subset B_2\subset \cdots \subset B_k=A \end{aligned}$$

where each subcomplex $B_{i+1}$ is obtained from $B_i$ by adding a vertex $v_{i+1}$ and attaching a cone $v_{i+1}\,{*}\, Y_i$ where $Y_i\subset B_i$ is a subcomplex. Here $V(B_i)\leqslant r$ for any i. Once $B=B_0$ is identified with an induced subcomplex of X we may apply inductively the definition to extend this embedding to an embedding of A.$\square$

Applying Lemma 2.3 in the case when B is a single vertex, we obtain:

Corollary 2.4

If X is r-ample then any simplicial complex on at most $r+1$ vertexes can be embedded into X.

Corollary 2.5

The dimension of an r-ample simplicial complex X is at least r.

We shall denote by $M'(n)$ the number of simplicial complexes with vertexes from the set $\{1, 2, \dots , n\}$. The number $M'(n)+1=M(n)$ is known as the Dedekind number, see [28], it equals the number of monotone Boolean functions of n variables and has some other combinatorial interpretations, for example, it equals the number of antichains in the set of n elements. A few first values of the “reduced Dedekind number” $M'(n)$ are $M'(1)=2$, $M'(2)=5$, $M'(3)=19$. For general $n\geqslant 2$, $M'(n)$ admits estimates

$$\begin{aligned} {\left( {\begin{array}{c}n\\ \lfloor n/2 \rfloor \end{array}}\right) } \leqslant \log _2 (M'(n)) \leqslant {\left( {\begin{array}{c}n\\ \lfloor n/2 \rfloor \end{array}}\right) \biggl (1+O\biggl (\frac{\log n}{n}\biggr )\biggr )}. \end{aligned}$$

(2.2)

The lower bound in (2.2) is easy: one counts only the simplicial complexes of dimension less than or equal to $\lfloor n/2 \rfloor -1$ having the full $(\lfloor n/2 \rfloor -2)$-dimensional skeleton;¹ the number of such subcomplexes obviously equals $2^{\left( {\begin{array}{c}n\\ \lfloor n/2 \rfloor \end{array}}\right) }$. Indeed, any such simplicial complex is given by an arbitrary selection of simplexes of dimension $\lfloor n/2 \rfloor -1$.

The upper bound in (2.2) was obtained in [28]. We shall also mention that

$$\begin{aligned} {\left( {\begin{array}{c}n\\ \lfloor n/2 \rfloor \end{array}}\right) } \sim \sqrt{\frac{2}{\pi n}}\cdot 2^n, \end{aligned}$$

(2.3)

as follows from the Stirling formula. Thus,

$$\begin{aligned} \log _2 \log _2 (M'(n)) = n - \frac{1}{2} \log _2 n +O(1). \end{aligned}$$

Corollary 2.6

An r-ample simplicial complex contains at least

$$\begin{aligned} M'(r)+r \geqslant 2^{\left( {\begin{array}{c}r\\ \lfloor r/2\rfloor \end{array}}\right) } +r \end{aligned}$$

vertexes.

Proof

Let X be an r-ample complex. Using Lemma 2.4 we can embed into X an $(r\,{-}\,1)$-dimensional simplex $\Delta$ having r vertexes. Applying Definition 2.1, for every subcomplex A of $\Delta$ we can find a vertex $v_A$ in the complement of $\Delta$ having A as its link intersected with $\Delta$. The number of subcomplexes A is $M'(r)$ and we also have r vertexes of $\Delta$ which gives the estimate.$\square$

The following lemma gives information about local structure of r-ample complexes.

Lemma 2.7

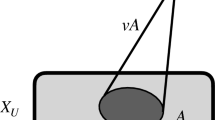
Let X be an r-ample simplicial complex. Then any simplicial map $f:K\rightarrow X$, where $|V(K)|\leqslant r$, is null-homotopic.

Proof

The set $U=f(V(k))\subset V(X)$ has cardinality $\leqslant r$ and applying Definition 2.1 we can find a vertex $v\in V(X)-U$ such that $X_{U\cup \{v\}} =v\,{*}\, X_U$ (cone over $X_U$). Thus we see that $f:K\rightarrow X$ factorises through a map with values in the cone $v\,{*}\, X_U$ which is contractible and hence f is null-homotopic.$\square$

We finish this section with the following observation.

Proposition 2.8

The link of a vertex in an r-ample simplicial complex is $(r\,{-}\,1)$-ample. More generally, the link of every k-dimensional simplex in an r-ample complex is $(r\,{-}\,k\,{-}\,1)$-ample.

Proof

We consider the case $k=0$ first. Let $v\in V(X)$ be a vertex and let L denote the link of v in X. Let (A, B) be a pair consisting of a simplicial complex A and its induced subcomplex B where $|V(A)|\leqslant r$. Consider the pair (CA, CB) consisting of cones with apex w. Note that CB is an induced subcomplex of CA and $|V(CA)|\leqslant r+1$. Since $v \,{*}\, L \subseteq X$, any embedding $f_B:B\rightarrow L$ can be extended to an embedding $f_{CB}:CB\rightarrow X$ where w is mapped into v. Since X is r-ample, applying Lemma 2.3 we can find an embedding $f_{CA}:CA\rightarrow X$ extending $f_{CB}$. Then the restriction $f_{CA}|A$ is an embedding $A\rightarrow L$ extending $f_B$.

The case when $k>0$ is similar. Let $\sigma$ be a k-simplex in X and let L denote its link. Consider a pair (A, B) with $|V(A)|\leqslant r-k$, an induced subcomplex B of A and an embedding $f_B:B\rightarrow L$. Consider the joins $A'\!=A\,{*}\, \sigma$ and $B'\!=B\,{*}\, \sigma$ and note that $V(A') \leqslant r+1$ and $B'$ is an induced subcomplex of $A'$. By Lemma 2.3 the join embedding $f_{B'}\!=f_B\,{*}\, 1:B'=B\,{*}\, \sigma \rightarrow L\,{*}\, \sigma$ can be extended to an embedding $f_{A'}:A'\! \rightarrow L\,{*}\, \sigma$ which restricts to an embedding $f_A:A\rightarrow L$ extending $f_B$.$\square$

3 Resilience of ample complexes

In this section we present a few results characterising “resilience”  of r-ample simplicial complexes: small perturbations to the complex reduce its ampleness in a controlled way and hence many important geometric properties pertain.

The perturbations that we have in mind are as follows. If X is a simplicial complex and ${\mathscr {F}}$ is a finite set of simplexes of X, one may consider the simplicial complex Y obtained from X by removing all simplexes of ${\mathscr {F}}$ as well as all simplexes which have faces belonging to ${\mathscr {F}}$. We shall say that Y is obtained from X by removing the set of simplexes $\mathscr {F}$.

Below we assume that ${\mathscr {F}}$ is “small” and X is “large”; we are interested in situations when Y preserves certain properties of X despite “the damage” caused by removing the family of simplexes $\mathscr {F}$.

We shall characterise the size of ${\mathscr {F}}$ by the following numbers. We denote by $v({\mathscr {F}})$ the cardinality of the set $\bigcup _{\sigma \in {\mathscr {F}}}V(\sigma )$; this is the number of vertexes incident to the simplexes of ${\mathscr {F}}$. Besides, we denote by $|{\mathscr {F}}|$ the cardinality of ${\mathscr {F}}$ and by $\dim \,({\mathscr {F}})=\sum _{\sigma \in {\mathscr {F}}} \dim \sigma$ the “total dimension” of ${\mathscr {F}}$. Clearly,

$$\begin{aligned} v({\mathscr {F}}) \leqslant |{\mathscr {F}}| +\dim \,({\mathscr {F}}) \end{aligned}$$

(3.1)

and the equality happens iff the simplexes of ${\mathscr {F}}$ are pairwise disjoint.

Theorem 3.1

Let X be an r-ample simplicial complex and let Y be obtained from X by removing a set ${\mathscr {F}}$ of simplexes. Then Y is $(r\,{-}\,k)$-ample provided that

$$\begin{aligned} v({\mathscr {F}}) < M'(k)+k. \end{aligned}$$

(3.2)

In particular, taking into account (3.1) and (2.2), the complex Y is $(r\,{-}\,k)$-ample if

$$\begin{aligned} |{\mathscr {F}}|+ \dim \,({\mathscr {F}}) < 2^{\left( {\begin{array}{c}k\\ \lfloor k/2\rfloor \end{array}}\right) }+k . \end{aligned}$$

Proof

Without loss of generality we may assume that ${\mathscr {F}}$ forms an anti-chain, i.e., no simplex of ${\mathscr {F}}$ is a proper face of another simplex of ${\mathscr {F}}$. Indeed, if $\sigma _1\subset \sigma _2$, where $\sigma _1, \sigma _2\in {\mathscr {F}}$, we can remove $\sigma _2$ from ${\mathscr {F}}$ without affecting the complex Y.

Consider a vertex $v\in V(Y)$ and its links $\mathrm{lk}_Y(v)\subset \mathrm{lk}_X(v)$ in Y and in X, correspondingly. Denote by $\mathscr {F}_v$ the set of simplexes $\sigma \subset \mathrm{lk}_X(v)$ such that either $\sigma \in {\mathscr {F}}$ or $v\sigma \in {\mathscr {F}}$. As follows directly from the definitions, $\mathrm{lk}_Y(v)$ is obtained from $\mathrm{lk}_X(v)$ by removing the set of simplexes ${\mathscr {F}}_v$.

Represent ${\mathscr {F}}$ as the disjoint union

$$\begin{aligned} {\mathscr {F}} = {\mathscr {F}}_0\sqcup {\mathscr {F}}_{1}, \end{aligned}$$

where ${\mathscr {F}}_0$ is the set of zero-dimensional simplexes from ${\mathscr {F}}$ and ${\mathscr {F}}_{1}$ is the set of simplexes in ${\mathscr {F}}$ having dimension $\geqslant 1$. Denote by

$$\begin{aligned} W_0=\bigcup _{\sigma \in {\mathscr {F}}_0} V(\sigma ) \quad \text{ and }\quad W_1=\bigcup _{\sigma \in {\mathscr {F}}_1}V(\sigma ) \end{aligned}$$

the sets of zero-dimensional simplexes and the set of vertexes of simplexes of positive dimension in ${\mathscr {F}}$. Note that $W_0\cap W_1=\varnothing$ due to our anti-chain assumption. Besides, $V(Y)=V(X)-W_0$ and therefore $W_1\subset V(Y)$.

Let $U\subset V(Y)$ be a subset and let $v\in V(Y)$ be a vertex such that: (a) $v\notin W_1$ and (b) the set $\mathrm{lk}_X(v)\cap X_U$ is a subcomplex of $Y_U$. Then

$$\begin{aligned} \mathrm{lk}_Y(v)\cap Y_U = \mathrm{lk}_X(v)\cap X_U. \end{aligned}$$

(3.3)

Indeed, we have $\mathrm{lk}_X(v)\cap Y_U =\mathrm{lk}_Y(v)\cap Y_U$ because of our assumption (a) and $\mathrm{lk}_X(v)\cap Y_U = \mathrm{lk}_X(v)\cap X_U$ because of (b).

Let k be an integer satisfying (3.2) and let $U\subset V(Y)$ be a subset with $|U|\leqslant r-k$. Given a subcomplex $A\subset Y_{U}$, we want to show the existence of a vertex $v\in V(Y)-U$ such that

$$\begin{aligned} \mathrm{lk}_Y(v)\cap Y_{U} =A. \end{aligned}$$

(3.4)

This would mean that our complex Y is $(r\,{-}\,k)$-ample.

Consider the induced subcomplex $X_{U}$ which obviously contains A as a subcomplex. Consider also the abstract simplicial complex

$$\begin{aligned} K=X_{U}\cup (A\,{*}\, \Delta ), \end{aligned}$$

where $\Delta$ is an abstract full simplex on k vertexes. Note that K has at most r vertexes, $X_{U}$ is an induced subcomplex of K and it is naturally embedded into X. Using the assumption that X is r-ample and applying Lemma 2.3, we can find an embedding of K into X extending the identity map of $X_{U}$. In other words, we can find k vertexes $v_1, \dots , v_k\in V(X)-U$ such that for a simplex $\tau$ of $X_{U}$ and for any nonempty subset

$$\begin{aligned} \tau '\!\subset \{v_1, \dots , v_k\}=U' \end{aligned}$$

one has $\tau \tau ' \in X$ if and only if $\tau \in A$. If one of these vertexes $v_i$ lies in $V(Y)-W_1$ then (using (3.3))

$$\begin{aligned} \mathrm{lk}_Y(v_i)\cap Y_{U}=\mathrm{lk}_X(v_i)\cap X_{U}=A \end{aligned}$$

and we are done. Thus, without loss of generality, we can assume that

$$\begin{aligned} U'\!\subset W_0\cup W_1. \end{aligned}$$

Let $Z\subset \Delta$ be an arbitrary simplicial subcomplex. We may use the r-ampleness of X and apply Definition 2.1 to the subcomplex $A\sqcup Z$ of $X_{U\cup U'}$. This gives a vertex $v_Z\in V(X)-(U\cup U')$ satisfying

$$\begin{aligned} \mathrm{lk}_{X}(v_Z) \cap X_{U\cup U'} =A\sqcup Z \end{aligned}$$

and in particular,

$$\begin{aligned} \mathrm{lk}_{X}(v_Z) \cap X_{U} =A. \end{aligned}$$

(3.5)

For distinct subcomplexes $Z, Z'\subset \Delta$ the points $v_Z$ and $v_{Z'}$ are distinct and the cardinality of the set $\{v_Z; Z\subset \Delta \}$ equals $M'(k)$. Noting that (3.5) is a subcomplex of $Y_U\subset X_U$ and comparing (3.3), (3.4), (3.5), we see that our statement would follow once we know that the vertex $v_Z$ lies in $V(Y) -W_1$ at least for one subcomplex Z.

Let us assume the contrary, i.e., $v_Z \in (W_0\cup W_1) - U'$ for every subcomplex $Z\subset \Delta$. The cardinality of the set $\{v_Z\}$ equals $M'(k)$ and the cardinality of the set $(W_0\cup W_1) - U'$ equals $v({\mathscr {F}}) - k$ and we get a contradiction with our assumption (3.2).$\square$

Corollary 3.2

Let X be an r-ample simplicial complex and let Y be obtained from X by removing a set ${\mathscr {F}}$ of simplexes. Denote by $a_i$ the number of i-dimensional simplexes in ${\mathscr {F}}$ where $i=0, 1, \dots$. Then:

• (a) If $r\geqslant 3$ and $a_0+2a_1 < M'(r-2) +r-2$ then Y is path-connected. In particular, Y is path-connected if

  $$\begin{aligned} a_0+2a_1 < 2^{\left( {\begin{array}{c}r-2\\ \lfloor r/2\rfloor -1\end{array}}\right) } + r-2. \end{aligned}$$

• (b) If $r\geqslant 5$ and $a_0+2a_1 +3a_2 < M'(r-4) +r-4$ then Y is simply connected. In particular, Y is simply connected if

  $$\begin{aligned} a_0+2a_1 +3a_2 < 2^{\left( {\begin{array}{c}r-4\\ \lfloor r/2\rfloor -2\end{array}}\right) } + r-4. \end{aligned}$$

• (c) If $r\geqslant 19$ and $a_0+2a_1 +3a_2+4a_3< M'(r-18) +r-18$ then Y is 2-connected. In particular, Y is 2-connected if

  $$\begin{aligned} a_0+2a_1 +3a_2+4a_3 < 2^{\left( {\begin{array}{c}r-18\\ \lfloor r/2\rfloor -9\end{array}}\right) } + r-18. \end{aligned}$$

Proof

Claim (a) follows from Theorem 3.1 and from the observation that a 2-ample complex is connected. Claim (b) follows from Theorem 3.1 and Proposition 4.1; claim (c) follows from Theorems 3.1 and 4.2. Here we also use the fact that i-connectedness (where $i\geqslant 0$) depends only on the $(i\,{+}\,1)$-dimensional skeleton of a simplicial complex.$\square$

4 Higher connectivity of ample complexes

It is natural to ask whether the geometric realisation of an r-ample simplicial complex is highly connected, i.e., has vanishing homotopy groups below certain dimension. The motivation for this question comes from the fact that an r-ample finite simplicial complex can be viewed as an approximation to the Rado simplicial complex whose geometric realisation is homeomorphic to an infinite dimensional simplex and hence is contractible [21].

Fig. 3

The process of constructing the bounding disc in a 5-ample complex as detailed in the proof of Proposition 4.1

Recall that a simplicial complex Y is m-connected if for every triangulation of the i-dimensional sphere $S^i$ with $i\leqslant m$ and for every simplicial map $\alpha :S^i\rightarrow Y$ there exists a triangulation of the disc $D^{i+1}$ extending the given triangulation of the sphere $S^i=\partial D^{i+1}$ and a simplicial map $\beta :D^{i+1}\rightarrow Y$ extending $\alpha$. A 1-connected complex is also said to be simply connected.

Proposition 4.1

For $r\geqslant 4$, any r-ample simplicial complex Y is simply connected. Moreover, any simplical loop $\alpha :S^1\rightarrow Y$ with n vertexes in an r-ample complex Y bounds a simplicial disc $\beta :D^2\rightarrow Y$ where $D^2$ is a triangulation of the disc having n boundary vertexes, at most $\bigl \lceil \frac{n-3}{r-3}\bigr \rceil$ internal vertexes and at most $\bigl \lceil \frac{n-3}{r-3}\bigr \rceil \cdot (r-1)+1$ triangles.

Proof

If $n\leqslant r$ we may simply apply the definition of r-ampleness and find an extension $\beta :D^2\rightarrow Y$ with a single internal vertex. If $n>r$ we may apply the definition of r-ampleness to any arc consisting of r vertexes, see Fig. 3. This reduces the length of the loop by $r-3$ and performing $\bigl \lceil \frac{n-r}{r-3}\bigr \rceil$ such operations we obtain a loop of length $\leqslant r$ which can be filled by a single vertex. The number of internal vertexes of the bounding disc will be $\bigl \lceil \frac{n-r}{r-3}\bigr \rceil +1= \bigl \lceil \frac{n-3}{r-3}\bigr \rceil$.

To estimate the number of triangles we note that on each intermediate step of the process described above we add $r-1$ triangles and on the final step we may add at most r triangles. This leads to the upper bound $\bigl \lceil \frac{n-r}{r-3}\bigr \rceil \cdot (r-1) +r= \bigl \lceil \frac{n-3}{r-3}\bigr \rceil \cdot (r-1)+1$.$\square$

Currently we have no examples of 3-ample complexes which are not simply connected. The 2-ample complex of Example 2.2 is not simply connected.

Next we state our result on 2-connectivity of r-ample complexes:

Theorem 4.2

For $r\geqslant 18$, every r-ample simplicial complex is 2-connected.

In the proof (which is given below) we shall use the following property of triangulations of the 2-sphere. By the degree $d_v$ of a vertex v of a triangulation $\Sigma$ of $S^2$ we understand the number of edges incident to v.

Lemma 4.3

In any triangulation $\Sigma$ of the 2-dimensional sphere there exist two adjacent vertexes v and w satisfying $d_v\leqslant 11$ and $d_w\leqslant 11$.

Proof of Lemma 4.3

Recall that for any triangulation $\Sigma$ of the 2-sphere one has the following relation:

$$\begin{aligned} \sum _v\, \biggl (1-\frac{d_v}{6}\biggr ) =2, \end{aligned}$$

(4.1)

where v runs over all vertexes of $\Sigma$ and $d_v$ denotes the degree of the vertex v. Formula (4.1) is well-known, it follows from the Euler formula $V-E+F=2$ by observing that $E=\frac{1}{2} \sum _v d_v$ and $F= \frac{1}{3} \sum _v d_v$. Formula (4.1) can be viewed as a combinatorial version of the Gauss–Bonnet theorem.

Let A stand for the set of vertexes $v\in V(\Sigma )$ satisfying $d_v\leqslant 11$ and let B denote the complementary set consisting of vertexes with $d_v\geqslant 12$. Denote also

$$\begin{aligned} C_A=\sum _{v\in A}\, \biggl (1-\frac{d_v}{6}\biggr ), \quad C_B=\sum _{v\in B} \,\biggl (1-\frac{d_v}{6}\biggr ), \end{aligned}$$

the contributions of both sets into the sum (4.1). Since $d_v\geqslant 3$ we have $1-\frac{d_v}{6}\leqslant \frac{1}{2}$ and hence

$$\begin{aligned} C_A \leqslant \frac{1}{2}\, |A|. \end{aligned}$$

Besides, $1-\frac{d_v}{6}\leqslant -1$ for $v\in B$ and therefore

$$\begin{aligned} C_B \leqslant {} -|B|, \quad C_A +C_B =2, \quad |A|+|B|=V. \end{aligned}$$

From these relations one obtains

$$\begin{aligned} |A|\geqslant \frac{2}{3}\,(V+2). \end{aligned}$$

(4.2)

Next we claim that there must exist an edge e with both endpoints in A, i.e., having degree $\leqslant 11$. Assuming the contrary, every triangle of the triangulation $\Sigma$ would have at most one vertex of degree $\leqslant 11$ and since the minimal degree is 3, using (4.2), we obtain that the number of triangles would be at least

$$\begin{aligned} 3\,{\cdot }\, \frac{2}{3}\,(V+2)=2V+4. \end{aligned}$$

However this contradicts the well-known relation $F=2V-4$ for the total number of triangles.$\square$

We shall also need the following simple lemma:

Lemma 4.4

Let D be a triangulated 2-dimensional disk and let $L=\partial D$ be its boundary circle. Assume that the length (i.e. the number of edges) of L is at least 7 and D has at most one internal vertex. Then there exists a pair of boundary vertexes $x, y\in L$ satisfying $d_L(x, y)\geqslant 3$ and such that they can be connected by a simplicial simple arc $\alpha$ in D with $\partial \alpha = \{x, y\}= \alpha \cap \partial D$. Here $d_L(x, y)$ denotes the distance between x and y along the boundary L, i.e., the number of edges in the shortest simplicial path in L connecting x and y.

Proof

Let us first consider the case when D has no internal vertexes. Denoting the length |L| of the boundary by n, we see that there are $n-3$ internal arcs (as follows from the Euler formula). We want to show that there exists an internal arc such that its end points x, y satisfy $d_L(x, y)\geqslant 3$. Assuming that $d_L(x, y)= 2$ for any internal arc, we may cut D along an arbitrary internal arc which produces a triangle and a triangulated disk $D'$ with $|L'|=n-1$ where $L'\!=\partial D'$. If we knew that our statement is true for $D'$ we could find vertexes $x, y\in L'$ satisfying $d_{L'}(x, y)\geqslant 3$ such that x, y are the endpoints of an internal arc of $D'$. Then $d_L(x,y)\geqslant d_{L'}(x, y) \geqslant 3$. This argument shows that without loss of generality we may assume that the length of L is exactly 7 but in this case one can see that our statement holds by examining a few explicit cases; see the left part of Fig. 4.

Consider now the case when D has a single internal vertex, denoted v. The vertex v is connected to at least three other vertexes $a, b, c\in L$. Let $d_L(a, c)$ be the maximal among the three numbers $d_L(a, b)$, $d_L(a, c)$, $d_L(b, c)$. Then either $d_L(a, b) + d_L(b, c) +d_L(a,c) = |L|$ or $d_L(a, c) = d_L(a, b) +d_L(b,c)$. In the first case one obtains $d_L(a, c)\geqslant 3$ (since $|L|\geqslant 7$) and we are done, as we can take for $\alpha$ the arc $av+vc$. In the second case we may similarly treat the case $d_L(a, c)\geqslant 3$ and we are left with the possibility $d_L(a, c)=2$ and hence $d_L(a, b)=1$ and $d_L(b, c)=1$. Cutting along the arc $av+vc$ produces two triangulated disks, each with no internal vertexes, one having four vertexes and the other, denoted $D'$, having |L| vertexes. We see that $|\partial D'|\geqslant 7$ and hence we may apply the previous case of the lemma, i.e., we can find two vertexes $x, y\in \partial D'\!=L'$ connected by an internal arc such that $d_{L'}(x, y)\geqslant 3$. We are done if none of the points x, y equal v. However if $x=v$ we may consider the pair $y, b\in L$ since $d_L(y, b)=d_{L'}(y, v) \geqslant 3$ and the points y, b are connected by the arc $\alpha = yv + vb$. See Fig. 4, right.$\square$

Fig. 4

Triangulated disks with no internal vertexes (left) and one internal vertex (right)

Proof of Theorem 4.2

We shall assume the contrary and arrive to a contradiction. Let Y be an 18-ample simplicial complex which is not 2-connected. From Proposition 4.1 we know that Y is simply connected. Let M(Y) denote the smallest number of vertexes in a triangulation $\Sigma$ of the sphere $S^2$ admitting a simplicial essential (i.e. not null-homotopic) map $f:\Sigma \rightarrow Y$. By the well-known Simplicial Approximation Theorem, M(Y) is finite. Lemma 2.7 implies $V(\Sigma )\geqslant 19$ for every simplicial essential map $f:\Sigma \rightarrow Y$ and hence $M(Y)\geqslant 19$.

Let $f:\Sigma \rightarrow Y$ be an essential simplicial minimal map, i.e. $V(\Sigma )=M(Y)$. We shall use the following geometric property of the triangulation $\Sigma$ of $S^2$, its “roundness”,  which is described below. Suppose that $L\subset \Sigma$ is a simple simplicial loop of length $|L|\leqslant 18$, i.e., L contains at most 18 edges. Clearly, L divides the sphere $\Sigma$ into two triangulated disks $D_1$ and $D_2$; each of these disks having |L| boundary vertexes and possibly a number of internal vertexes. We claim that at least one of the disks $D_1$, $D_2$ has at most one internal vertex. Indeed, suppose that each of the disks $D_1$ and $D_2$ has $\geqslant 2$ internal vertexes. Let $D=a\,{*}\, L$ be the cone with apex a and base L. We can form two triangulated spheres $\Sigma _1 = D_1\cup D$ and $\Sigma _2=D_2\cup D$ and each of these spheres has strictly smaller number of vertexes than $\Sigma$ (since D has a single internal vertex and each of the disks $D_1$, $D_2$ has at least two internal vertexes). Next we observe that each of the spheres $\Sigma _1$ and $\Sigma _2$ can be mapped simplicially into Y so that at least one of the maps $\Sigma _1\rightarrow Y$ or $\Sigma _2\rightarrow Y$ is essential. Indeed, consider the image $f(L)\subset Y$ of the loop L in Y. It is a subcomplex with at most 18 vertexes and by 18-ampleness of Y we can find a vertex $u\in V(Y)$ such that $u\,{*}\, f(L)\subset Y$. Now we may extend the map $f:\Sigma \rightarrow Y$ onto the disk $D=a\,{*}\, L$ by mapping a onto u and extending this map onto the cone by linearity. We obtain a simplicial map $g:\Sigma \cup D\rightarrow Y$ extending f and the restrictions $g_1=g|_{\Sigma _1}:\Sigma _1\rightarrow Y$ and $g_2=g|_{\Sigma _2}:\Sigma _2\rightarrow Y$ are the desired simplicial maps. Since $\Sigma _1\cup \Sigma _2=\Sigma \cup D$ and $\Sigma _1\cap \Sigma _2= D$ is contractible, we see that g is essential (as $f=g|_\Sigma$ is essential) and hence at least one of the maps $g_1$, $g_2$ is essential. Thus, we arrive at a contradiction with the minimality of f.

Next we invoke Lemma 4.3 which gives us two adjacent vertexes v and w of $\Sigma$, each having degree at most 11. Let e be the edge connecting v and w. Consider the subset U of the surface $\Sigma$ which is the union of all triangles which have nontrivial intersection with e. The boundary $\partial U$ is a closed curve (potentially with some identifications, see below) formed by $d_v +d_w-4\leqslant 11+11-4 =18$ edges and the interior of U is the union of $d_v+d_w-2$ triangles.

Fig. 5

Triangles incident to an edge on the surface

The edge e is incident to two triangles; we shall denote by $\alpha$ and $\beta$ the vertexes of these two triangles which are not incident to e, see Fig. 5.

Let us assume first that the links of the vertexes v and w satisfy

$$\begin{aligned} \mathrm{lk}_\Sigma (v)\cap \mathrm{lk}_\Sigma (w) =\{\alpha , \beta \}. \end{aligned}$$

Then U is a triangulated disk with $\leqslant 18+2=20$ vertexes, among them two are internal, as shown on Fig. 5.

Suppose now that there exists a vertex $a\in \mathrm{lk}_\Sigma (v)\cap \mathrm{lk}_\Sigma (w)$ which is distinct from $\alpha$ and $\beta$. Then the path $L =av+vw+wa$ is a simplicial loop on $\Sigma$ which divides the surface $\Sigma$ into two disks. By the roundness property of $\Sigma$, one of these two disks must have at most one internal vertex. In fact, the only possibility is that L bounds a disk with one internal vertex and L cannot be the boundary of a triangle: otherwise the edge e would belong to three different triangles. It is easy to see that this internal vertex must be either $\alpha$ or $\beta$, as there are exactly two triangles incident to e, see Fig. 6. In this case $\alpha$ becomes an internal vertex of U.

For similar reasons it might happen that both vertexes $\alpha$ and $\beta$ are internal vertexes of U.

The argument above shows that any vertex lying in $\mathrm{lk}_\Sigma (v)\cap \mathrm{lk}_\Sigma (w)$, which is distinct from $\alpha$ and $\beta$, belongs to a triangular simplicial loop surrounding either $\alpha$ or $\beta$ and containing the edge vw (similarly the loop $av+ vw+wa$ shown on Fig. 6). This implies that the intersection $\mathrm{lk}_\Sigma (v)\cap \mathrm{lk}_\Sigma (w)$ may contain at most four vertexes.

Fig. 6

Disk U with three internal vertexes

Potentially it might happen that $U=\Sigma$, i.e. $\partial U=\varnothing$. Then all vertexes of $\Sigma$, other than $v, \ w$, lie in the intersection $\mathrm{lk}_\Sigma (v)\cap \mathrm{lk}_\Sigma (w)$. Using the above arguments, we see that in this case $V(\Sigma )\leqslant 6$, which contradicts our assumption $V(\Sigma )\geqslant 19$.

The remaining possibility is that $U\subset \Sigma$ is a subcomplex, it has either 2, 3 or 4 internal vertexes and its total number of vertexes is at most 20.

The closure of the complement of U is in $\Sigma$ another disk, $U'$, and applying the roundness property of $\Sigma$, we conclude that that $U'$ has at most one internal point. Thus, we see that the triangulation $\Sigma$ must have at most 21 vertexes in total, and using Corollary 2.7 we obtain that $|V(\Sigma )|$ must be equal to one of the three numbers: 19, 20 or 21.

Using this observation we conclude that the length $\ell = |L|$ of the boundary $L=\partial U=\partial U'$ should satisfy $14 \leqslant \ell \leqslant 18$.

Finally we show that there must exist a simplicial simple closed curve $L'$ on $\Sigma$ dividing the sphere $\Sigma$ into two disks, each having more than one internal points, and this violates the roundness of $\Sigma$ and gives a contradiction. The curve $L'$ is the union of two arcs $L'\!=A\cup A'$ where $A\subset U$ and $A'\!\subset U'$. We first construct the arc $A'\!\subset U'$; we only must ensure that (c) the endpoints of $A'$ divide the boundary L into two arcs, each of length $\geqslant 3$. The existence of such an arc follows from Lemma 4.4. Once the arc $A'\!\subset U'$ satisfying (c) is constructed we connect its endpoints (lying on the boundary $L=\partial U$) by a simple simplicial arc A in U; it is clear from Figs. 5 and 6 that any two points on the boundary can be connected by such an arc in U.

The vertexes of L distinct from two vertexes $\partial A=\partial A'$ are internal vertexes of the disks on which the sphere $\Sigma$ is divided by the circle $L'$; the condition (c) ensures that at least two vertexes lie in each connected component of $\Sigma - L'$. This contradicts the roundness property of $\Sigma$ and completes the proof of Theorem 4.2.$\square$

We tend to believe that in general, for every $k\geqslant 1$ there exists r(k) such that every r-ample simplicial complex is k-connected provided that $r\geqslant r(k)$. We know that $r(1) \leqslant 4$ and $r(2)\leqslant 18$.²

5 Large random simplicial complex is ample

In this section we show that a large random simplicial complex is r-ample with probability tending to 1. This result implies the existence of r-ample finite simplicial complexes, we also use it to estimate the minimal number of vertexes an r-ample complex must possess.

First we recall a model of random simplicial complexes developed in [19, 20]; it is a generalisation of the well-known Linial–Meshulam model.

Let $\Delta _n$ denote the simplex on the vertex set $[n]=\{1, 2, \dots , n\}$. Suppose that for every simplex $\sigma \subset \Delta _n$ we are given a probability parameter $p_\sigma \in [0,1]$. We shall use the notation $q_\sigma =1-p_\sigma$. For a subcomplex $Y\subset \Delta _n$ we shall denote by F(Y) the set of faces of Y and by E(Y) the set of external faces of Y, i.e., simplexes $\sigma \subset \Delta _n$ such that $\partial \sigma \subset Y$ and $\sigma \not \subset Y$. Next we describe a probability measure on the set of all simplicial subcomplexes of $\Delta _n$; in terminology of [20] it is the lower measure (as opposed to an upper measure). The probability of a simplicial subcomplex $Y\subset \Delta _n$ is given by

$$\begin{aligned} P(Y)\, =\!\! \prod _{\sigma \in F(Y)}\!\! p_\sigma \,\cdot \!\!\! \prod _{\sigma \in E(Y)}\!\! q_\sigma . \end{aligned}$$

(5.1)

The intuitive meaning of this probability measure can be described as follows. One constructs a random complex Y inductively, by first selecting a random set of vertexes, adding randomly a set of edges, then a set of 2-simplexes and so on. On each step, once the k-dimensional skeleton $Y^{k}$ has been constructed, one adds external $(k\,{+}\,1)$-dimensional simplexes of $Y^k$ at random, each with its own probability $p_\sigma$, independently of the other simplexes. We refer to [20] for more detail and justification.

In this section we shall assume that the parameters $p_\sigma$ are in the medial regime, which means that the probability parameters $p_\sigma$ satisfy

$$\begin{aligned} p_\sigma \in [p, 1-p], \end{aligned}$$

(5.2)

where $p\in (0, 1/2]$ does not depend on n. (Note however that in Remark 5.2 we relax this assumption.) Paper [19] contains information about geometry and topology of medial regime random simplicial complexes; in particular, it is shown that a random simplicial complex in the medial regime is simply connected and has vanishing Betti numbers below dimension $\sim \log \log n,$ asymptotically almost surely.

Proposition 5.1

For every integer $r\geqslant 1$, the probability that a medial regime random simplicial complex is r-ample tends to one, as $n\rightarrow \infty$.

Proof

We estimate probability that a random complex Y is not r-ample. Let us make the following choices: a subset $U\subset [n]$ of cardinality $|U|\leqslant r$, a subcomplex $Z\subset \Delta _n$ with $V(Z)=U$, a subcomplex $A\subset Z$ and a vertex $v\in [n]- U$. Consider the following events:

$$\begin{aligned} W_U&= \{Y\subset \Delta _n\mid U\subset V(Y)\},\\ W_{U,Z}&=\{Y\subset \Delta _n\mid \, U\subset V(Y), \, Y_U=Z\}, \end{aligned}$$

and

$$\begin{aligned} W_{U,Z,A, v} = \bigl \{Y\subset \Delta _n\mid U\cup \{v\} \subset V(Y), \, Y_{U\cup \{v\}}=Z\cup (A \,{*}\, v)\bigr \}. \end{aligned}$$

Note that

$$\begin{aligned} W_U=\bigsqcup _Z\, W_{U,Z} \end{aligned}$$

is the disjoint union where Z runs over all subcomplexes of $\Delta _n$ satisfying $V(Z)=U$. Consider also the complement $W_{U,Z,A,v}^{\mathrm{c}}$ of $W_{U,Z,A,v}$ in $W_{U, Z}$, i.e.

$$\begin{aligned} W_{U,Z,A,v}^{\mathrm{c}} = W_{U, Z} - W_{U,Z,A,v}. \end{aligned}$$

A simplicial complex $Y\subset \Delta _n$ belongs to $W^\mathrm{c}_{U,Z,A, v}$ iff $U\subset V(Y)$ and $Y_U=Z$ and either $v\notin V(Y)$ or $v\in V(Y)$ and $\mathrm{lk}_Y(v)\cap Y_U\not = A$. We see that for $|U|\leqslant r$ any complex Y lying in the intersection

$$\begin{aligned} \bigcap _{v\in [n]-U}\!\!\!W^{\mathrm{c}}_{U,Z,A,v} \end{aligned}$$

is not r-ample. Moreover, the set ${\mathscr {N}}$ of all not r-ample simplicial complexes $Y\subset \Delta _n$, $Y\not =\varnothing$, coincides with

$$\begin{aligned} {\mathscr {N}} \, = \!\!\bigcup _{1\leqslant |U|\leqslant r} \biggl (\bigsqcup _{Z}\,\biggl (\bigcup _{A\subset Z}\biggl (\bigcap _{v\in [n]-U} \!\! W^{\mathrm{c}}_{U,Z,A,v}\biggr )\biggr )\biggr ). \end{aligned}$$

We denote

$$\begin{aligned} {\mathscr {N}}_{U, Z}\, = \bigcup _{A\subset Z}\biggl (\bigcap _{v\in [n]-U}\!\! W^{\mathrm{c}}_{U,Z,A,v}\biggr ) \end{aligned}$$

and ${\mathscr {N}}_{U} =\bigsqcup _Z {\mathscr {N}}_{U, Z}$. Then $\mathscr {N}= \bigcup _U {\mathscr {N}}_{U},$ where $|U|\leqslant r$.

We claim that the conditional probability equals

$$\begin{aligned} P(W_{U,Z,A,v}\, |\, W_{U,Z})= p_v\cdot \!\! \prod _{\sigma \in F(A)}\!\! p_{v\sigma }\cdot \!\! \prod _{\sigma \in E(A|Z)}\!\!q_{v\sigma }. \end{aligned}$$

(5.3)

Here $v\sigma$ denotes the join $v\,{*}\, \sigma$ and E(A|Z) denotes the set of simplexes $\sigma \in F(Z)-F(A)$ such that $\partial \sigma \subset A$. Indeed, the condition $Y_U=Z$, which appears in the definition of the set $W_{U, Z}$, can equivalently be expressed as

$$\begin{aligned} Z\subset Y\subset Z\,{*}\, \Delta _{U^\mathrm{c}}\end{aligned}$$

where $\Delta _{U^{\mathrm{c}}}\subset \Delta _n$ denotes the simplex spanned by the complementary set of vertexes $U^{\mathrm{c}}=[n]-U$.

We shall use [20, Corollary 5.6 (1)] (see also [16, Lemma 2.2]) which states that for given subcomplexes $A\subset B\subset \Delta _n$ satisfying $E(B)\subset E(A)$ the probability that a random complex Y contains A and is contained in B (i.e. $A\subset Y\subset B$) equals

$$\begin{aligned} \prod _{\sigma \in F(A)}\!\!p_\sigma \,\cdot \!\! \prod _{\sigma \in E(B)}\!\! q_\sigma . \end{aligned}$$

(5.4)

Formally in [20] it was assumed that $B\subset \partial \Delta _n$ which excludes the case $B=\Delta _n$. However all statements of [20, Section 5] and their proofs remain true without this assumption (which was imposed in [16] to study Alexander duality).

It is easy to see that

$$\begin{aligned} E(Z)= E(Z\,{*}\, \Delta _{U^{\mathrm{c}}})\sqcup U^{\mathrm{c}} \end{aligned}$$

where $U^{\mathrm{c}}$ stands for the set of 0-dimensional simplexes $\{\{v\}; v\in U^{\mathrm{c}}\}$. Equivalently, we can write $E(Z\,{*}\, \Delta _{U^{\mathrm{c}}})= E(Z) - U^{\mathrm{c}}$. We see that formula (5.4) is applicable and we get

$$\begin{aligned} P(W_{U, Z})\, = \!\prod _{\sigma \in F(Z)}\!\! p_\sigma \cdot \!\!\prod _{\sigma \in E(Z)-U^{\mathrm{c}}}\!\! q_\sigma . \end{aligned}$$

(5.5)

Similarly, repeating the above arguments with Z replaced by $Z'\!=Z\cup (v\,{*}\, A)$ one finds

$$\begin{aligned} P(W_{U, Z, A, v})\, =\! \prod _{\sigma \in F(Z')} \!\!p_\sigma \cdot \!\!\prod _{\sigma \in E(Z')-U'^{\mathrm{c}}}\!\! q_\sigma , \end{aligned}$$

where $U'\!=U\cup \{v\}$ and $U'^{\mathrm{c}}$ denotes the complement $[n] - U'$. Finally, noting that

$$\begin{aligned} F(Z')-F(Z) = \{v\}\cup \{v\sigma ; \sigma \in F(A)\} \end{aligned}$$

and

$$\begin{aligned} (E(Z')-U'^{\mathrm{c}})-(E(Z)-U^{\mathrm{c}}) =E(Z') - (E(Z)-\{v\})= \{v\sigma ; \sigma \in E(A\,{|}\,Z)\}, \end{aligned}$$

we arrive at the formula for the conditional probability (5.3).

Since $|F(A)|+|E(A|Z)|\leqslant 2^r-1$ (note that by definition a simplex is a nonempty subset of the vertex set), using the medial regime assumption (5.2), we obtain

$$\begin{aligned} P(W_{U,Z,A,v} \mid W_{U,Z}) \geqslant p^{2^r }\!. \end{aligned}$$

(5.6)

Hence the complement $W_{U,Z,A,v}^c$ of $W_{U,Z,A,v}$ in $W_{U, Z}$ satisfies

$$\begin{aligned} P(W_{U,Z,A,v}^{\mathrm{c}}\mid W_{U,Z}) \leqslant 1-p^{2^r }\!. \end{aligned}$$

Next we observe that the family of events $\{W_{U,Z,A,v}\}_{v\in U^{\mathrm{c}}}$ is collectively conditionally independent over $W_{U,Z}$. Indeed, for every subset $J\subset U^{\mathrm{c}}$ one can compute the conditional probability of the intersection

$$\begin{aligned} \begin{aligned} P\biggl (\bigcap _{v\in J}W_{U,Z,A,v}\, |\, W_{U,Z}\biggr )&= \prod _{v\in J} \,\biggl (p_v\cdot \!\!\prod _{\sigma \in F(A)} \!\!p_{v\sigma }\cdot \!\! \prod _{\sigma \in E(A|Z)}\!\!q_{v\sigma }\biggr )\\&= \prod _{v\in J} P(W_{U,Z,A,v}\, |\, W_{U,Z}) \end{aligned} \end{aligned}$$

(5.7)

by applying the above arguments to the complex $Z_J =Z\cup \bigcup _{v\in J} (v\,{*}\, A)$. In more detail, the intersection $\bigcap _{v\in J}W_{U,Z,A,v}$ coincides with the set of complexes $Y\subset \Delta _n$ satisfying

$$\begin{aligned} Z_J\subset Y\subset Z_J\,{*}\, \Delta _{(U^\mathrm{c}-J)}. \end{aligned}$$

(5.8)

Here $\Delta _{(U^c-J)}$ denotes the simplex spanned by the set $U^{\mathrm{c}}-J=[n]-V(Z_J)$. Since, as above,

$$\begin{aligned} E(Z_J\,{*}\, \Delta _{(U^{\mathrm{c}}-J)})= E(Z_J)-(U^{\mathrm{c}}-J) \subset E(Z_J), \end{aligned}$$

we see that formula (5.4) applies to (5.8). Using the equations

$$\begin{aligned} F(Z_J)-F(Z)&= \bigsqcup _{v\in J}\,\bigl (\{v\}\cup \{v\sigma ; \sigma \in F(A)\}\bigr ),\\ E(Z_J) - (E(Z) -J)&= \bigsqcup _{v\in J}\,\{v\sigma ; \sigma \in E(A|Z)\} \end{aligned}$$

and taking into account (5.5) we obtain (5.7).

Hence we get using (5.6),

$$\begin{aligned} P\biggl (\bigcap _{v\in [n]-U} \!\! W_{U,Z,A,v}^{\mathrm{c}} \mid W_{U,Z}\biggr )&\,= \!\!\prod _{v\in [n]-U}\!\! P(W^{\mathrm{c}}_{U,Z,A,v}\mid W_{U,Z})\\&\,\leqslant \bigl (1-p^{2^r }\bigr )^{n-|U|}\leqslant \bigl (1-p^{2^r }\bigr )^{n-r} \end{aligned}$$

and therefore

$$\begin{aligned} P({\mathscr {N}}_{U, Z}\,{|}\, W_{U,Z}) = P\biggl (\bigcup _A \bigcap _{v} \, W_{U,Z,A,v}^{\mathrm{c}} \mid W_{U,Z}\biggr ) \leqslant 2^{2^r}\bigl (1-p^{2^r }\bigr )^{n-r}, \end{aligned}$$

where A runs over subcomplexes of Z (the number of such subcomplexes is clearly bounded above by $2^{2^r}$).

Since ${\mathscr {N}}_U = \bigsqcup _Z {\mathscr {N}}_{U,Z}$ and $W_U = \bigsqcup _Z W_{U,Z}$, we obtain

$$\begin{aligned} P({\mathscr {N}}_U)\leqslant \max _Z P({\mathscr {N}}_{U,Z}\,{|}\, W_{U,Z}) \leqslant 2^{{2^r}} \bigl (1-p^{2^r}\bigr )^{n -r}. \end{aligned}$$

And finally, we obtain the following upper bound for the probability of the set ${\mathscr {N}}=\bigcup _U {\mathscr {N}}_{U}$ of all nonempty simplicial subcomplexes of $\Delta _n$ which are not r-ample:

$$\begin{aligned} \begin{aligned} P({\mathscr {N}}) \leqslant \sum _{j=1}^r {\left( {\begin{array}{c}n\\ j\end{array}}\right) } \cdot 2^{2^{r}}\bigl (1-p^{2^r }\bigr )^{n-r}\! \leqslant n^r\!\cdot 2^{2^{r}}\bigl (1-p^{2^r }\bigr )^{n-r}.\end{aligned} \end{aligned}$$

(5.9)

Clearly, for $n\rightarrow \infty$ the expression (5.9) tends to zero. Note also that the probability of the empty simplicial complex is bounded above by $(1-p)^n$ and tends to 0. $\square$

Remark 5.2

The above arguments prove that the conclusion of Proposition 5.1 holds under a slightly weaker assumption, namely $p_\sigma \in [p, 1-p]$ where $p=p(n)>0$ satisfies

$$\begin{aligned} p^{{2^r }} = \frac{r\ln n +\mu }{n} \end{aligned}$$

with $\mu =\mu (n)$ an arbitrary sequence tending to $\infty$. Examples satisfying the above condition are $p=1/n^\alpha$ with $\alpha \in (0, 2^{-r})$ and $p=1/\ln n$, the latter choice works for any r.

Remark 5.3

The arguments of the proof of Proposition 5.1 work without any change if one alters the medial regime assumption by requiring that $p_v=1$ for every vertex $v\in [n]$ while $p_\sigma \in [p, 1-p]$ for $\dim \sigma >0$. Formula (5.1) implies that in this case the probability measure is supported on the set of simplicial complexes $Y\subset \Delta _n$ with $V(Y)=[n]$, i.e. having exactly n vertexes. This observation will be used below in the proof of Proposition 5.4

Proposition 5.4

For every $r \geqslant 5$ and for every $n \geqslant r2^r2^{2^{r}}$, there exists an r-ample simplicial complex having exactly n vertexes.

Proof

The expression (5.9) is an upper bound of the probability that a medial regime random complex on n vertexes is not r-ample. Clearly, if for some n the RHS of (5.9) is smaller than 1 then an r-ample complex exists. The expression (5.9) is bounded above by

$$\begin{aligned} n^r 2^{2^r}e^{-p^{2^r}\cdot (n-r)}= n^r e^{-np^{2^r}}\!\!\cdot 2^{2^r}e^{rp^{2^r}} \end{aligned}$$

and taking the logarithm we obtain the following inequality:

$$\begin{aligned} np^{2^r} \!-r\ln n > 2^r \ln 2+ rp^{2^r} \end{aligned}$$

(5.10)

which guarantees the existence of an r-ample complex on n vertexes. Below we shall set $p=1/2$. The function $n\mapsto np^{2^r} -r\ln n$ is monotone increasing for $n>r2^{2^r}$ and therefore we only need to show that (5.10) is satisfied for $n=r2^r2^{2^r}\!$. The inequality (5.10) turns into

$$\begin{aligned} r2^r(1-\ln 2) -r^2 \ln 2 -r\ln r> 2^r \ln 2+ r2^{-2^r} \end{aligned}$$

which is equivalent to

$$\begin{aligned} r(1-\ln 2) -\ln 2 > \frac{r^2 \ln 2 +r\ln r}{2^r} + r2^{-2^r-r}. \end{aligned}$$

(5.11)

Given that $\ln 2\simeq 0.6931$, it is easy to see that (5.11) is satisfied for any $r\geqslant 5$. Indeed, one checks by a direct computation that (5.11) is satisfied for $r=5$; however, as a function of $r\geqslant 5$, the LHS of (5.11) is increasing while the RHS is decreasing.$\square$

As a byproduct, we also obtain the following result about 2-connectivity of random simplicial complexes in the medial regime.

Corollary 5.5

Every medial regime random simplicial complex [19] is 2-connected, asymptotically almost surely.

Proof

This follows from Proposition 5.1 and Theorem 4.2.$\square$

Connectivity and simple connectivity of the medial regime random simplicial complexes and vanishing of the Betti numbers were shown in [19]; the vanishing of the second homotopy group was not previously known.

6 Explicit construction of ample complexes

The random construction above shows the existence of r-ample simplicial complexes for every r. However, it does not tell us how to construct an r-ample complex explicitly. In this section we define a deterministic family of complexes that are guaranteed to be r-ample.

Our construction uses ideas from number theory, and generalises the classical Paley graph. In Definitions 6.3–6.5, we introduce the Iterated Paley Simplicial Complex $X_{n,p}$ on n vertices, for every odd prime power n and odd prime p dividing $(n-1)$. But first, we state the main theorem of the section.

Theorem 6.1

Let $r \in {\mathbb {N}}$. Every Iterated Paley Simplicial Complex $X_{n,p}$ with $p>2^{2^r+2r}$ and $n>r^2p^{2r}$ is r-ample.

Theorem 6.1 is proven below, after the definition of $X_{n,p}$. After the proof, we discuss the selection of the prime parameters n and p, so that r-ample complexes can be constructed for every r. We prove the following corollary:

Corollary 6.2

For every sufficiently large r, there exists an r-ample Iterated Paley Complex $X_{n,p}$ on $n=2^{(2+o(1))r2^r}$ vertices.

To summarise, a complex with less than

$$\begin{aligned} 2^{\left( {\begin{array}{c}r\\ \lfloor r/2\rfloor \end{array}}\right) } \sim 2^{\sqrt{\frac{2}{\pi }}\cdot \frac{2^r}{\sqrt{r}}} \end{aligned}$$

vertexes cannot be r-ample (as follows from formula (2.3) and Corollary 2.6); the probabilistic construction of Proposition 5.4 gives an r-ample complex on $n_r= 2^{2^r (1+o(1))}$ vertexes; the Iterated Payley complex is larger, it has approximately $\sim (n_r)^{2r}$ vertexes, according to Corollary 6.2.

Before proceeding to the definition of Iterated Paley Simplicial Complexes, we discuss the context in which they have emerged. The uninterested reader may skip to Definition 6.3 without loss of continuity.

The Paley graph and the Paley tournament are long known to satisfy the corresponding r-ampleness property [5, 8, 23]. Their vertices are the elements of a finite field ${\mathbb {F}}_n$, with an edge from x to y if and only if $(y-x)$ is a quadratic residue [36, in matrix form]. More generally, these constructions exhibit numerous important properties typical to their random counterparts, and are accordingly called pseudorandom or quasirandom [1, 34]. However, these provably r-ample graphs and tournaments are nearly square the size of those probabilistically shown to be r-ample. Understanding such gaps between randomized and explicit solutions is a recurring theme in the study of combinatorial structures and computational complexity.

The most straightforward extension of Paley’s graph to higher dimensions is by including a d-dimensional face $x_0 x_1 \cdots x_d$ if $x_0+x_1+\dots +x_d$ is a quadratic residue. Hypergraphs with $(d\,{+}\,1)$-edges constructed by this rule are known to possess some quasirandom properties [14, 25, 31]. They also yield large cosystoles in simplicial complexes, pertinent to d-dimensional coboundary expansion over ${\mathbb {F}}_2$, by Kozlov and Meshulam, see [30]. However, they fail to be ample. Indeed, if four vertices satisfy $a+b=c+d$, then abx is a face if and only if cdx is a face, hence some extensions of such a foursome are not available. All the explicit constructions considered in the study of quasirandom hypergraphs break down when it comes to r-ampleness.

Our new construction combines three generalizations of Paley graphs. First, if $m\,{|}\,(n-1)$ then, rather than quadratic residues in ${\mathbb {F}}_n$, one may determine adjacency by means of the multiplicative subgroup of m-th powers and its cosets. Having similar quasirandom properties [2, 27], such graphs proved useful in Ramsey theory [15, 24, 42]. They appear also in the classification of graphs with strong symmetries [32, 37].

Second, instead of defining hyperedges by summing $x_0+\dots +x_d$, one may use the Vandermonde determinant,

$$\begin{aligned} \Delta (x_0,\dots ,x_d)\, {:}{=}\!\!\prod \limits _{0 \leqslant i<j \leqslant d}\!\!\!(x_i-x_j). \end{aligned}$$

This is an appealing route because such products are compatible with the multiplicative nature of the above subgroups. Hypergraphs produced this way [22, 29, 38] are known to have several nice properties, but not r-ampleness.

The final and novel ingredient in our construction is the repeated use of Paley-like motifs. Faces are selected according to certain cosets of p-power residues mod n, and those cosets in turn correspond to quadratic residues mod p. For this reason, we name such constructions Iterated Paley. The need for this duplexity will be clarified in the ampleness proof.

We now formalize the foregoing description. For the following set of definitions, fix an odd prime power n, an odd prime p that divides $n-1$, and a primitive element g in the finite field ${\mathbb {F}}_n$.

Definition 6.3

For n, p, g as above, let

$$\begin{aligned} Q_{n,p} \,{:}{=}\,\bigl \{g^{\alpha } \mid \alpha \equiv \beta ^2 \bmod p, \;\text {for}\; \alpha ,\beta \in {\mathbb {Z}} \bigr \} \subset {\mathbb {F}}_n. \end{aligned}$$

Remark

Since $p\,|\,(n-1)$, we have a multiplicative subgroup $H = \langle g^p \rangle$ of index p in ${\mathbb {F}}_n^{\times } = \langle g \rangle$, and a group isomorphism ${\mathbb {F}}_n^{\times }/H \rightarrow ({\mathbb {F}}_p,+)$ taking $g H \mapsto 1$. The set $Q_{n,p}$ is the union of H-cosets that correspond to quadratic residues mod p. Hence, it contains about half the elements of the field,

$$\begin{aligned} |Q_{n,p}| = \frac{p+1}{2p}\,(n-1). \end{aligned}$$

Definition 6.4

The Iterated Paley Hypergraph $H_{n,p}$ has ${\mathbb {F}}_n$ as its vertex set, and a subset $\{x_1, x_2, \dots , x_t\}$ forms a hyperedge if

$$\begin{aligned} \prod _{1\leqslant i<j\leqslant t}\!\!\!(x_i-x_j) \in Q_{n,p}. \end{aligned}$$

Remark

Note that $(-1)=g^{(n-1)/2}$, and $(n-1)/2\equiv 0 \bmod p$ since p is odd, hence $(-1)\in H = \langle g^p \rangle$. Therefore, the condition in the definition of $H_{n,p}$ does not depend on the order of the vertices $x_1, x_2, \dots , x_t$. Note also that all n singletons $\{x\}$ are hyperedges, because $1 = g^0 \in Q_{n,p}$.

The Iteretad Paley Hypergraph might not be a simplicial complex, as it is not necessarily closed downward. We thus consider the largest simplicial complex contained in it, defined as follows.

Definition 6.5

The Iterated Paley Simplicial Complex $X_{n,p}$ has ${\mathbb {F}}_n$ as its vertex set, and a set $\{x_1, x_2, \dots , x_t\}$ forms a simplex if for every subset $\{x_{s_1}, x_{s_2}, \dots , x_{s_k}\} \subseteq \{x_1, x_2, \dots , x_t\}$,

$$\begin{aligned} \prod _{1\leqslant i<j\leqslant k}\!\!\bigl (x_{s_i}-x_{s_j}\bigr ) \in Q_{n,p}. \end{aligned}$$

Remark

The definitions of $Q_{n,p}$ and thereby $H_{n,p}$ and $X_{n,p}$ depend on the choice of primitive element $g \in {\mathbb {F}}_n$. Any other primitive element $h = g^\alpha \in {\mathbb {F}}_n$ gives the same construction if $\alpha$ is a quadratic residue mod p, and a different one if not. The two constructions are not isomorphic in general. Our results apply to either choice.

Remark

Note that $H_{n,p}$ and $X_{n,p}$ are invariant under a rather large group of symmetries $\{x \mapsto ax+b \,{|}\, a \in H, b \in {\mathbb {F}}_n\}$.

Before proving Theorem 6.1, we sketch the idea of the proof via a simple example: accommodating one 3-ampleness challenge, posed by three vertices $a,b,c \in X = X_{n,p}$. Given a, b, c, suppose that we are looking for another vertex $x \in X$ such that, say, $ax,bx,cx,abx,bcx \in X$ and $acx,abcx \not \in X$.

We find x in two stages. First we decide on three suitable H-cosets $g^{\alpha }H, g^{\beta }H$, $g^{\gamma }H$, where $H=\langle g^p \rangle$ as before. Then we find $x \in {\mathbb {F}}_n$ such that $(x-a) \in g^{\alpha }H$, $(x-b) \in g^{\beta }H$, and $(x-c) \in g^{\gamma }H$. Such an x exists by extending the uncorrelation property of squares, from Paley graphs. Specifically, three different additive translations of p-power cosets must intersect in $n/p^3 \pm O(\sqrt{n})$ elements.

Without knowing better, we pick $\alpha , \beta , \gamma \in {\mathbb {F}}_p$ one-by-one. The requirement $ax \in X$ implies that $\alpha$ must be a square, which gives $\lceil p/2 \rceil$ options. A short calculation shows that $bx, abx \in X$ require both $\beta$ and $\beta +\delta$ to be squares, where $\delta$ is determined by $(a-b)g^{\alpha } \in g^{\delta }H$. This has $p/2^2\pm O(\sqrt{p})$ solutions by the same ampleness property of Paley graphs. The requirements $cx,bcx \in X$ and $acx,abcx \not \in X$ give four constraints: $\gamma$ and $\gamma + \delta _b$ are squares while $\gamma + \delta _a$ and $\gamma + \delta _{ab}$ are nonsquares, where $\delta _a,\delta _b,\delta _{ab}$ are known from $a,b,c,\alpha ,\beta$. This is satisfied by $p/2^4\pm O(\sqrt{p})$ elements of ${\mathbb {F}}_p$, by the same reason that Paley graphs are 4-ample.

One has to be a bit careful to avoid contradictions between requirements. For example, $\delta _a=\delta _b$ might mean no solution for $\gamma$. The proof will avoid such problematic cases with advance planning. On the other hand, sometimes we can take shortcuts. For example, $acx \not \in X$ makes $abcx \not \in X$ come for free. We will not rely on such considerations, as they would not simplify the argument in general. That makes our proof apply to hypergraphs too.

With the above example in mind, we begin with a formal proof of Theorem 6.1. We first formalize the idea that at every step we have an abundance of choices for the witness to ampleness, with differences lying in the necessary cosets. The following lemma generalizes a property of Paley graphs and tournaments [5, 8, 23] to characters of order m.

Lemma 6.6

In a finite field ${\mathbb {F}}_q$, let $A \,{\subset }\, {\mathbb {F}}_q^{\times }$ be a proper multiplicative subgroup of index m. Given d cosets of A,

$$\begin{aligned} A_1, A_2, \dots , A_d \in {\mathbb {F}}_q^{\times }/A \end{aligned}$$

and pairwise distinct elements

$$\begin{aligned} c_1,c_2,\dots ,c_d \in {\mathbb {F}}_q \end{aligned}$$

the number of elements $x \in {\mathbb {F}}_q$ satisfying

$$\begin{aligned} (x-c_1) \in A_1, \quad (x-c_2) \in A_2, \quad \dots , \quad (x-c_d) \in A_d \end{aligned}$$

is at least

$$\begin{aligned} \frac{q}{m^d} - (d-1)\sqrt{q} - \frac{d}{m}. \end{aligned}$$

This lemma basically says that different additive translates of cosets of m-power residues are “mutually uncorrelated”. Their intersection is of order $q/m^d$ as expected from random subsets, up to an error term of about $d\sqrt{q}$. A proof of Lemma 6.6 is given in Appendix A.

Proof of Theorem 6.1

Let $X = X_{n,p}$ be as in Definition 6.5. Consider a set of vertices $\sigma = \{x_1,\dots ,x_d\} \subseteq {\mathbb {F}}_n = V(X)$. Throughout this proof, $\sigma$ is assumed to be nonempty. The Vandermonde determinant of $\sigma$ in ${\mathbb {F}}_n$ falls into one of the p cosets of $H = \langle g^p \rangle$,

$$\begin{aligned} \Delta (\sigma )\, = \,\pm \!\!\!\!\prod _{1 \leqslant i < j \leqslant d}\!\!\! (x_i - x_j) \in g^{\alpha (\sigma )}H. \end{aligned}$$

The exponent $\alpha (\sigma ) \in \{0,1,\dots ,p-1\}$ is uniquely determined for every $\sigma$, because $\pm 1 \in H$. In view of the remark following Definition 6.3, we regard $\alpha (\sigma )$ as an element of ${\mathbb {F}}_p$.

Recall that a simplex $\sigma \in X$ if and only if for all $\tau \subseteq \sigma$ the Vandermonde determinant $\Delta (\tau ) \in Q_{n,p}$. That is equivalent to $\alpha (\tau ) \in Q_p \cup \{0\}$, where

$$\begin{aligned} Q_p \,{:}{=}\, \bigl \{\beta ^2 \,{|}\, \beta \in {\mathbb {F}}_p^{\times }\bigr \} \end{aligned}$$

$Q_p$ is the multiplicative subgroup of quadratic residues mod p. The coset of quadratic nonresidues is denoted by $Q_p^{\mathrm{c}} \,{:}{=}\, {\mathbb {F}}_p^\times \,{\setminus }\, Q_p$.

To verify that X is r-ample, consider a set $U \subset {\mathbb {F}}_n$ of r vertices, and a subcomplex $Y \subseteq X_U$. We seek a vertex $x \in {\mathbb {F}}_n \,{\setminus }\, U$ such that for every $\sigma \in X_U$ the simplex $\sigma x \in X$ if and only if $\sigma \in Y$. Here $\sigma x$ stands for the simplex $\sigma \cup \{x\}$.

By the above characterization of the simplices of X, it is sufficient for the desired vertex x to solve the following set of $2^r-1$ constraints:

For every hypergraph Y on every set of r vertices $U \subset {\mathbb {F}}_n$, we show that this problem is indeed satisfiable.

We rewrite the above constraints on x. Clearly, the Vandermonde determinant of $\sigma x$ decomposes as follows:

$$\begin{aligned} \Delta (\sigma x)\, = \pm \!\!\!\!\prod _{1 \leqslant i < j \leqslant d}\!\!\! (x_i - x_j) \, \prod _{v \in \sigma }\, (x - v) = {}\pm \Delta (\sigma ) \prod _{v \in \sigma } \Delta (vx) . \end{aligned}$$

Applying the quotient map ${\mathbb {F}}_n^{\times } \rightarrow {\mathbb {F}}_n^{\times } / H \xrightarrow {\sim } {\mathbb {F}}_p$ such that $gH \mapsto 1$ yields the following congruence in ${\mathbb {F}}_p$:

$$\begin{aligned} \alpha (\sigma x) \equiv \alpha (\sigma ) + \sum _{v \in \sigma } \alpha (vx). \end{aligned}$$

We introduce r new variables, $\xi _v \in {\mathbb {F}}_p$ for each $v \in U$, related to x via $\xi _v = \alpha (vx)$, and obtain an equivalent reformulation of ($\star$), with the $r+1$ variables $\xi _v \in {\mathbb {F}}_p$ and $x \in {\mathbb {F}}_n$.

$$\begin{aligned}&\alpha (\sigma ) + \sum _{v \in \sigma } \xi _v \;\in \; {\left\{ \begin{array}{ll}\, Q_p &{} \text {if}\; \sigma \in Y, \\ \, Q_p^{\mathrm{c}} &{} \text {if}\; \sigma \not \in Y \end{array}\right. }\quad \text {for all}\;\;\sigma \subseteq U, \end{aligned}$$

(I)

$$\begin{aligned}&(x - v) \in g^{\xi _v} H \quad \text {for all}\;\;v \in U. \end{aligned}$$

(II)

We now show that given any assignment to the r variables $\{\xi _v\}$, there exists $x \in {\mathbb {F}}_n$ that satisfies (II). Indeed, applying Lemma 6.6 with $q=n$, $A=H$, $m=p$, and $d=r$, the number of $x \in {\mathbb {F}}_n$ satisfying $(x-v) \in g^{\xi _v}H$ for every $v \in U$ is at least

$$\begin{aligned} \frac{n}{p^r} - (r-1)\sqrt{n} - \frac{r}{p}\,. \end{aligned}$$

Since $n > r^2p^{2r}$, this lower bound is positive, and there exists at least one such solution $x \in {\mathbb {F}}_n \,{ \setminus }\, U$. This reduces the problem to finding $\{\xi _v\}$ that satisfy (I).

Let $U = \{u_1,\dots ,u_r\}$ in arbitrary order. Given $\sigma \subseteq U$, its last vertex $u_i$ in this sequence is called the top vertex of $\sigma$. To be precise, $u_i \in \sigma$ and $u_j \not \in \sigma$ for $j > i$. Since the constraints in (I) are labeled by $\sigma \subseteq U$ and include the variables $\xi _v$ for $v \in \sigma$, we determine $\xi _{u_1}, \dots , \xi _{u_r}$ inductively, selecting each $\xi _{u_i}$ according to the constraints where $u_i$ is the top vertex. We abbreviate $\xi _i = \xi _{u_i}$ as no confusion can arise.

Supposing $\xi _{1},\dots ,\xi _{{i-1}}$ are determined, the next variable $\xi _{i}$ has to satisfy the $2^{i-1}$ constraints where $u_i$ is the top vertex.

where

$$\begin{aligned} \delta (\sigma )\, {:}{=}\, \alpha (\sigma ) + \!\!\sum _{v \in \sigma {\setminus } u_i} \!\!\xi _v \in {\mathbb {F}}_p \end{aligned}$$

is already known from the variables determined earlier than $\xi _i$.

Before invoking Lemma 6.6 to show that $\xi _{i}$ exists, one has to make sure that all $\delta (\sigma )$ in ($\star \star$) are distinct. This requires some care when selecting $\xi _{1},\dots ,\xi _{{i-1}}$. Suppose that $u_i \in \sigma \cap \sigma '$ is the common top vertex of $\sigma$ and $\sigma '$, and $u_j \in \sigma {\setminus } \sigma '$ is the top vertex of their difference $\sigma \triangle \sigma ' \!= (\sigma \,{\setminus }\, \sigma ') \cup (\sigma ' \,{\setminus }\, \sigma )$. Then the condition $\delta (\sigma ) \ne \delta (\sigma ')$ takes the form

$$\begin{aligned} \xi _{j} \,\ne \, \biggl (\alpha (\sigma ')\, +\!\! \sum _{v \in (\sigma ' {\setminus } \sigma )} \!\!\xi _{v}\biggr ) - \biggl ( \alpha (\sigma )\, + \!\!\sum _{v \in (\sigma {\setminus } \sigma ') {\setminus } u_j} \!\!\!\!\xi _{v}\biggr ). \end{aligned}$$

Since the value on the right-hand side is known when selecting $\xi _{j}$ it can be avoided as long as there are enough other options supplied by Lemma 6.6. The number of forbidden values for $\xi _{j}$ is at most the number of such pairs of simplices, $\{\sigma , \sigma '\}$, with common top vertex $u_i$ and top “differentiating” vertex $u_j$. The number of these pairs is

$$\begin{aligned} \bigl (2^{j-1}\bigr )^2 \bigl (2^{r-j} - 1\bigr ) < 2^{r+j-2}. \end{aligned}$$

To sum up, in order to enable solutions for all $\xi _{i}$ we will actually find $2^{r+j-2}$ potential solutions for every variable $\xi _{j}$, and proceed with one that evades collisions among $\delta (\sigma )$ as shown above.

We thus assume by induction that $\xi _1,\dots ,\xi _{i-1}$ are given and the $2^{i-1}$ constraints in ($\star \star$) have distinct translations $\delta (\sigma )$, and apply Lemma 6.6 with $q=p$, $A=Q_p$, $m=2$, and $d=2^{i-1}$. This guarantees at least

$$\begin{aligned} \frac{p}{2^{2^{i-1}}} - \bigl ({2^{i-1}}-1\bigr ) \sqrt{p} - \frac{{2^{i-1}}}{2} \end{aligned}$$

possible values for the variable $\xi _{i}$. Since $p > 2^{2^r + 2r}$ and $i \leqslant r$, this number is greater than

$$\begin{aligned} 2^{2^{r-1}+2r}-(2^{r-1}-1)\, 2^{2^{r-1}+r} - 2^{r-2} \geqslant 2^{2^{r-1}+2r-1} \geqslant 2^{r+i-2} \end{aligned}$$

for all $i \leqslant r$, as required.

In conclusion, there exist $\xi _{1},\dots ,\xi _{r} \in {\mathbb {F}}_p$ satisfying ($\star \star$) for every i, and hence also (I). As shown above, this yields a vertex $x \in {\mathbb {F}}_n$ that satisfies (II) and hence $\mathrm{lk}_X(x) \cap X_U = Y$ as required.$\square$

In the rest of this section, we discuss the selection of parameters n and p for r-ample Iterated Paley Simplicial Complexes.

The construction requires two primes satisfying $n \equiv 1 \bmod p$, that are large enough as in Theorem 6.1. Given a prime p, the existence of arbitrarily large primes $n \in p{\mathbb {N}}+1$ is a special case of the classical Dirichlet Theorem. This case actually follows from an elementary argument. For $N > p$, let n be a prime divisor of $M = 1 + N! + \dots + (N!)^{p-1} = ((N!)^p-1)/(N!-1)$. Since $n\,{|}\,((N!)^p-1)$, necessarily $n>N$. If $N! \equiv _n 1$ then $M \equiv _n p$, which is ruled out by $n\,{|}\,M$. Therefore, $N! \not \equiv _n 1$ while $(N!)^p \equiv _n 1$. By Lagrange’s theorem, $p\,{|}\,(n-1)$, as desired.

However, in order to establish our quantitative result, Proposition 6.2, we need a prime n roughly of order $p^{2r}$. Dirichlet’s theorem asserts that about $1/(p-1)$ of all primes are contained in the arithmetic progression $p{\mathbb {N}}+1$, in an appropriate sense of asymptotic density [26]. The following lemma uses quantitative estimates of the “error term” to bound the gaps between these primes, which provides such a prime n that is not too large.

Lemma 6.7

There exists a constant P, such that for every prime $p>P$ and every $M \geqslant p^8$ there exists a prime $n \equiv 1\bmod p$ in the interval

$$\begin{aligned} M \;<\; n \;<\; \sqrt{p} \,M \end{aligned}$$

Proof

For a and q coprime, the number of primes less than or equal to x that are congruent to $a \bmod q$ is denoted

$$\begin{aligned} \pi (x; q, a) = \bigl |\{n\leqslant x : n\text { is prime, } n \equiv a\bmod q\}\bigr | \end{aligned}$$

Bounds on this number under various assumptions on the relation between q and x are given by the Brun–Titchmarsh theorem and the Siegel–Walfisz theorem. By recent improved bounds due to Maynard [35, Theorems 1, 2], there exist effectively computable positive constants Q and R, such that if $q\geqslant Q$ and $x\geqslant q^8$ then

$$\begin{aligned} \frac{R\,\log q}{\sqrt{q}}\cdot \frac{x}{\phi (q)\log x}< \pi (x; q, a) < \frac{2\, \mathrm {Li}(x)}{\phi (q)}. \end{aligned}$$

Here $\phi (q) = |\{a < q\,{ :}\, (a,q)=1\}|$ is Euler’s totient function, and the function $\mathrm {Li}\,(x) = \int _2^x \tfrac{dt}{\log t} \sim \tfrac{x}{\log x}$ is the Eulerian logarithmic integral. In fact, $\text {Li}\,(x) < \tfrac{3x}{2\log x}$ will suffice for our needs.

Letting $q=p$ and $a=1$, it follows for any $p > P = \max \,(Q, \exp \,(4/R))$ and $M > p^8$ that

$$\begin{aligned} \pi (M;p,1) \;<\; \frac{3M}{(p-1) \log M}< \frac{R\,\log p\,\sqrt{p}\,M}{\sqrt{p}\,(p-1) \log \,(\sqrt{p}\,M)} \;<\; \pi (\sqrt{p}M;p,1). \end{aligned}$$

The middle inequality is verified by

$$\begin{aligned} \frac{3 \log \, (\sqrt{p}\,M)}{R\,\log p \, \log M}< \frac{3}{R\,\log p}\,\biggl (\frac{1}{16} + 1\biggr ) < 1 . \end{aligned}$$

Since $\pi (M;p,1) < \pi (\sqrt{p}M;p,1)$, there exists at least one prime $n \equiv 1 \bmod p$ between M and $\sqrt{p}M$, as required.$\square$

Proof of Corollary 6.2

We now show there exist parameters satisfying the assumptions $p > 2^{2^r+2r}$ and $n > r^2 p^{2r}$ of Theorem 6.1, and $n = 2^{(2+o(1))r2^r}$.

In selecting p, we can just rely on Bertrand’s postulate, i.e., for every $N \in {\mathbb {N}}$ there exists a prime between N and 2N. Thus, there exists a prime p in the range

$$\begin{aligned} 2^{2^r+2r}\!< p < 2^{2^r+2r+1}\!. \end{aligned}$$

Suppose that r is large enough so that p satisfies Lemma 6.7. We pick a prime $n \equiv 1 \bmod p$ in the range

$$\begin{aligned} r^2p^{2r}\!< n < r^2p^{2r+1/2}\!. \end{aligned}$$

Therefore, for r sufficiently large, there exists an r-ample Iterated Paley Simplicial Complex $X_{n,p}$, on at most

$$\begin{aligned} n < r^2 2^{(2^r+2r+1)(2r+{1}/{2})} = 2^{2r2^r(1+o(1))} \end{aligned}$$

vertices.$\square$

Remark 6.8

Finally, we note that the construction of $X_{n,p}$ is explicit at least in the following sense.

Given $r \in {\mathbb {N}}$, one can find suitable primes p and $n = \exp (O(r2^r))$ and a primitive $g \in {\mathbb {F}}_n$ in $\text {poly}\,(n)$ time. One can also decide whether a given face belongs to the r-dimensional skeleton of $X_{n,p}$ in $\text {poly}\,(n)$ time.

These rough estimates leave some room for improvement, as the description of $X_{n,p}$ and such a face are in fact poly-logarithmic in n. Assuming the generalized Riemann hypothesis, or heuristics on the distribution of primes, may help in selecting p, n, and g. We do not pursue this matter here.

7 Proof of Lemma 6.6

Following works on Paley graphs and tournaments [5, 8, 23], we use character sums to prove Lemma 6.6. A multiplicative character of a finite field ${\mathbb {F}}_q$ is a map $\chi :{\mathbb {F}}_q \rightarrow {\mathbb {C}}$, such that $\chi (0)=0$, $\chi (1)=1$, and $\chi (ab)=\chi (a)\,\chi (b)$ for every $a,b \in {\mathbb {F}}_q$. Since $\chi$ is a homomorphism between the multiplicative groups, its image is all m-th roots of unity, where $m = (q-1)/|\mathrm{ker}\, \chi |$ is called the order of $\chi$.

The following estimate of character sums is based on the work of André Weil [10, 40]. This formulation appears in [33, Theorem 5.41] or [26, Theorem 11.23].

Theorem A.1

(Weil) Let $\chi$ be a character of order $m > 1$ of a finite field ${\mathbb {F}}_q$, and let f(x) be a polynomial over ${\mathbb {F}}_q$, that cannot be written as an m-th power, $c\,{\cdot }\, g(x)^m$. If f(x) has at most d distinct roots in a splitting field, then

$$\begin{aligned} \biggl |\sum _{x \in {\mathbb {F}}_q} \!\chi (f(x)) \biggr | \leqslant (d-1)\sqrt{q}. \end{aligned}$$

Proof of Lemma 6.6

Let $\alpha$ be a primitive element in ${\mathbb {F}}_q$, and let $\omega = e^{2 \pi i / m}$. In terms of the subgroup A of index m, we define the multiplicative order-m character $\chi (x) = \omega ^{t}$ for every $x \in \alpha ^{t}A$ and $t \in {\mathbb {Z}}_m = {\mathbb {Z}}/m{\mathbb {Z}}$, and as usual set $\chi (0)=0$.

Let $A_1,\dots ,A_d$ be A-cosets, and $c_1,\dots ,c_d$ be distinct field elements, as in the lemma. We define $t_1, \dots , t_d \in {\mathbb {Z}}_m$ such that $A_i = \alpha ^{t_i}A$, and consider the function

$$\begin{aligned} S(x) =\prod \limits _{i=1}^{d} \biggl ( \sum \limits _{j = 0}^{m-1} \bigl (\omega ^{-t_i}\chi (x-c_i)\bigr )^{j} \biggr ). \end{aligned}$$

If x satisfies $(x-c_i) \in \alpha ^{t_i}A$ then $\chi (x-c_i) = \omega ^{t_i}$ and the i-th factor equals m. If $(x-c_i) \notin \alpha ^{t_i}A$ and $x\not =c_i$, the i-th factor is a sum of m consecutive powers of a nontrivial m-th root of unity, which vanishes. In the case $x=c_i$ the i-th factor equals  1. It follows that $S(x)=m^d$ for every x that is counted in the lemma. For any other x the function S attains $S(x)=0$, apart from $x \in \{c_1,\dots ,c_d\}$ where $|S(x)| \leqslant m^{d-1}$. In conclusion, if N denotes the number of $x \in {\mathbb {F}}_q$ that satisfy $(x-c_i) \in \alpha ^{t_i}A = A_i$ for all $i \in \{1,\dots ,d\}$, then

$$\begin{aligned} \biggl |\sum \limits _{x \in {\mathbb {F}}_q} S(x) \biggr | \leqslant N m^d + d m^{d-1}. \end{aligned}$$

On the other hand, we may expand the sum over S(x) into $m^d$ different sums of characters:

$$\begin{aligned} \sum \limits _{x \in {\mathbb {F}}_q} S(x)&= \sum \limits _{x \in {\mathbb {F}}_q} \, \prod \limits _{i=1}^{d} \,\biggl ( \sum \limits _{j = 0}^{m-1} \omega ^{-j t_i} \chi (x-c_i)^j \biggr ) \\&= \sum \limits _{x \in {\mathbb {F}}_q} \sum _{j_1 \dots j_d} \biggl (\prod \limits _{i=1}^d\omega ^{-j_i t_i}\biggr ) \prod \limits _{i=1}^d \chi (x-c_i)^{j_i} \\&=\!\! \sum _{j_1 \dots j_d}\!\! \omega ^{-\sum _i j_i t_i} \sum \limits _{x \in {\mathbb {F}}_q} \!\! \chi \biggl (\prod \limits _{i=1}^d (x-c_i)^{j_i} \biggr ). \end{aligned}$$

The first term, which corresponds to $(j_1,\dots ,j_d) = (0,\dots ,0)$, is equal to q. Recall that $c_1,\dots ,c_d$ are pairwise distinct and $\max _ij_i < m$. By Weil’s Theorem, it follows that each one of the other $m^d-1$ terms is bounded in absolute value by $(d-1)\sqrt{q}$. Therefore, by the triangle inequality,

$$\begin{aligned} \biggl |\sum \limits _{x \in {\mathbb {F}}_q}\!\! S(x) \biggr | \geqslant q - (m^d-1)(d-1)\sqrt{q}. \end{aligned}$$

The lemma now follows by combining the two estimates of the sum, and solving for N.$\square$

Added in August 2021. This paper was published as a preprint in December 2020; in March, 2021 Jonathan A. Barmak published an interesting preprint [3] in which he improved the threshold for 2-connectivity given by Theorem 4.2 and answered positively our question stated at the end of Sect. 4.

Data sharing not applicable to this article as no datasets were generated or analysed during the current study.