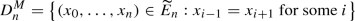Abstract
We verify that for a finite simplicial complex X and for piecewise linear loops on X, the “thin” loop space is a topological group of the same homotopy type as the space of continuous loops. This turns out not to be the case for the higher loops.





Similar content being viewed by others
Notes
In fact in [7] this is used as a definition of PL; i.e., a PL map is a simplicial map between some subdivisions.
Note that in the case of Milnor’s construction, see Sect. 8.1, if we set the degenerate set there to be
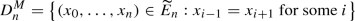
then the homotopy F does not leave \(D^M_n\) invariant. A different approach for contractibility is required.
References
Arens, R., Dugundji, J.: Topologies for function spaces. Pacific J. Math. 1(1), 5–31 (1951)
Badzioch, B.: Recognition principle for generalized Eilenberg–Mac Lane spaces. In: Aguad, J., Broto, C., Casacuberta, C. (eds.) Cohomological Methods in Homotopy Theory. Progress in Mathematics, vol. 196, pp. 21–26. Birkhäuser, Basel (2001)
Bahri, A., Cohen, F.R.: On “small geodesics” and free loop spaces (2008). arXiv:0806.0637
Barrett, J.W.: Holonomy and path structures in general relativity and Yang–Mills theory. Internat. J. Theoret. Phys. 30(9), 1171–1215 (1991)
Brazas, J., Fabel, P.: On fundamental groups with the quotient topology. J. Homotopy Relat. Struct. 10(1), 71–91 (2015)
Browder, W.: Homology operations and loop spaces. Illinois J. Math. 4(3), 347–357 (1960)
Buchstaber, V.M., Panov, T.E.: Toric Topology. Mathematical Surveys and Monographs, vol. 204. American Mathematical Society, Providence (2015)
Caetano, A., Picken, R.F.: An axiomatic definition of holonomy. Internat. J. Math. 5(6), 835–848 (1994)
Dold, A., Lashof, R.: Principal quasi-fibrations and fibre homotopy equivalence of bundles. Illinois J. Math. 3, 285–305 (1959)
Ferry, S.: Geometry Topology Notes. http://sites.math.rutgers.edu/~sferry/ps/geotop.pdf
Fritsch, R., Piccinini, R.A.: Cellular Structures in Topology. Cambridge Studies in Advanced Mathematics, vol. 19. Cambridge University Press, Cambridge (1990)
Gajer, P.: Higher holonomies, geometric loop groups and smooth Deligne cohomology. In: Brylinski, J.-L., et al. (eds.) Advances in Geometry. Progress in Mathematics, vol. 172, pp. 195–235. Birkhäuser, Boston (1999)
Griffiths, H.B.: The fundamental group of two spaces with a common point. Quart. J. Math. Oxford 5, 175–190 (1954)
Hansen, V.L.: On the homotopy type of certain spaces of differentiable maps. Math. Scan. 30, 75–87 (1972)
Hatcher, A.: Algebraic Topology. Cambridge University Press, Cambridge (2002)
Hirsch, M.W.: Differential Topology. Graduate Texts in Mathematics, vol. 33. Springer, New York (1994)
Hu, S.: Theory of Retracts. Wayne State University Press, Detroit (1965)
Klein, J.R.: The dualizing spectrum of a topological group. Math. Ann. 319(3), 421–456 (2001)
Kobayashi, S.: La connexion des variétés fibrées. II. C. R. Acad. Sci. Paris 238, 443–444 (1954)
Lefschetz, S.: Introduction to Topology. Princeton Mathematical Series, vol. 11. Princeton University Press, Princeton (1949)
Mackaay, M., Picken, R.: Holonomy and parallel transport for abelian gerbes. Adv. Math. 170(2), 287–339 (2002)
Mann, K.: Diffeomorphism groups of balls and spheres. New York J. Math. 19, 583–596 (2013)
May, J.P.: The Geometry of Iterated Loop Spaces. Lectures Notes in Mathematics, vol. 271. Springer, Berlin (1972)
Milnor, J.: Universal bundles. I. Ann. Math. 63, 272–284 (1956)
Mitchell, S.A.: A filtration of the loops on \({\rm SU}(n)\) by Schubert varieties. Math. Z. 193(3), 347–362 (1986)
Palais, R.S.: Homotopy theory of infinite dimensional manifolds. Topology 5, 1–16 (1966)
Rourke, C.P., Sanderson, B.J.: Introduction to Piecewise-Linear Topology. Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 69. Springer, New York (1972)
Smale, S.: Regular curves on Riemannian manifolds. Trans. Amer. Math. Soc. 87(2), 492–512 (1958)
Spanier, E.H.: Algebraic Topology. McGraw-Hill, New York (1966)
Stasheff, J.: “Parallel” transport—revisited. Mat. Contemp. 41, 191–204 (2012)
Strickland, N.P.: The category of CGWH spaces. https://neil-strickland.staff.shef.ac.uk/courses/homotopy/cgwh.pdf
Tapp, K.: Differential Geometry of Curves and Surfaces. Undergraduate Texts in Mathematics. Springer, Cham (2016)
Teleman, C.: Généralisation du groupe fondamental. Ann. Sci. École Norm. Sup. 3(77), 195–234 (1960)
Acknowledgements
We thank the organizers of LICMAA’2015 in Beirut, Lebanon, for inciting us to work on this project. We also thank Ali Maalaoui for earlier discussions around the topic. We finally thank the referee for his/her remarks.
Author information
Authors and Affiliations
Corresponding author
Additional information
In fond memory of Ştefan Papadima
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Group models for loop spaces
Appendix: Group models for loop spaces
The loop space \(\Omega (X)\) is an H-space which is associative only up to homotopy, and more generally an \(A_\infty \) space [30]. It is of interest in both homotopy theory and geometry to replace \(\Omega (X)\) by a weakly homotopic space that is a topological group. We list below the various known ways to do this.
1.1 Combinatorial models
Milnor in [24] is perhaps the earliest to have exhibited such a group replacement for \(\Omega (X)\) when X is of the homotopy type of a connected countable complex. For X a countable simplicial complex, consider \(S_k\) as in (2) and define

where \((x_0,\ldots , x_{i-1}, x_i, \ldots , x_n)\sim (x_0,\ldots , x_{i-1},\widehat{x}_i,x_{i+1},\ldots , x_n)\) whenever the triple \(x_{i-1}=x_i\) or \(x_{i-1}=x_{i+1}\). Then \(M(X)=\lim M_n\) is the group of a universal bundle, thus it is weakly homotopy equivalent to \(\Omega (X)\). Our model in this paper S(X) has the advantage of being homeomorphic to the thin loop space for piecewise linear loops. Note that there is a homomorphism of topological groups \(M(X)\rightarrow \omega (X)\).
Another model appears in [3] in the case X is a Riemannian manifold. The loop space model by Bahri and Cohen is obtained by considering composable small geodesics.
1.2 Simplicial (Kan) model
Let X be a based space which is of the homotopy type of a CW complex. Take the simplicial total singular complex SX of X which is a based simplical set. The Kan loop group GSX of SX is then a simplicial group and its geometric realization |GSX| is a topological group object in the category of compactly generated spaces. This is a model for the loop space. This is discussed in [18].
The generality of this model allows us to deduce for example that any strictly associative monoid (or H-space) such that \(\pi _0\) is a group can be “rigidified” to a topological group; that is is weakly homotopy equivalent to a topological group. Indeed for such spaces, Dold and Lashof show the existence of a classifying space \(B_X\) and a weak homotopy equivalence \(X\rightarrow \Omega (B_X)\). One then uses the above construction to replace the loop space up to equivalence by a topological group.
Note that May has another model that produces this time a topological monoid weakly equivalent to any \(A_\infty \)-space [23, Theorem 13.5].
1.3 The “geometric model”
Lefschetz [20, Chapter V, Section 4] and Kobayashi introduce the earliest known thin loop models for piecewise smooth loops on smooth manifolds. Teleman in [33] introduces a similar model which is a quotient of \(P(M,x_0)\), the space of piecewise smooth paths starting at \(x_0\), by three equivalence relations and uses this model to classify bundles. Gajer introduces a similar model in [12, Section 1.3], which with the first relation ensuring that in the quotient space G(M), the product of loops is associative, \(\sim _2\) ensures that the class of the constant map is the identity in G(M), and the final relation \(\sim _3\) implies that \([\gamma ^{-1}]\) is a genuine inverse for \([\gamma ]\), much as in our Sect. 3. However, the proof is not quite complete, see Remark 5.6.
1.4 The Quillen model
Let \(X=G\) be a simply-connected Lie group with simple Lie algebra, and let \(G_{{\mathbb {C}}}\) be its complexification. An “algebraic loop” in \(G_{{\mathbb {C}}}\) is a regular map \({{\mathbb {C}}}^*\!\rightarrow G_{{\mathbb {C}}}\) (i.e., a morphism of algebraic varieties). The set of all such loops is denoted by \({\widetilde{G}}_{{\mathbb {C}}}\). One then sets

This is an algebraic group. By a theorem of Quillen and Garland–Raghunathan, the restriction map to \(S^1\) yields a homotopy equivalence \(\Omega _{\mathrm{alg}}(G)\simeq \Omega (G)\) (one reference is [25]).
Rights and permissions
About this article
Cite this article
Ghazel, M., Kallel, S. Thin loop groups. European Journal of Mathematics 6, 864–887 (2020). https://doi.org/10.1007/s40879-019-00396-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-019-00396-7