Abstract
We describe the sixth worst singularity that a plane curve of degree \(d\geqslant 5\) could have, using its log canonical threshold at the point of singularity. This is an extension of a result due to Cheltsov (J Geom Anal 27(3):2302–2338, 2017) wherein the five lowest values of log canonical thresholds of a plane curve of degree \(d \geqslant 3\) were computed. These six small log canonical thresholds, in order, are 2 / d, \(({2d-3})/{(d-1)^2}\), \(({2d-1})/(d^2-d)\), \(({2d-5})/({d^2-3d+1})\), \(({2d-3})/(d^2-2d)\) and \(({2d-7})/({d^2-4d+1})\). We give examples of curves with these values as their log canonical thresholds using illustrations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \(C_d \subset {\mathbb {P}}^2\) be a reduced plane curve of degree d over \({\mathbb {C}}\) and P be a point on \(C_d\). We aim to address the following question:
Question 1.1
Given a curve \(C_d\) of fixed degree d, what is the worst singularity that the curve can have at the point P?
We can use various parameters to measure the singularity at the point P, such as multiplicity of the curve at P, \(\mathrm{mult}_P(C_d)\), Milnor number, \(\mu (P)\), or log canonical threshold of the curve at P,  . In this paper, we will use
. In this paper, we will use  to answer the above question. Recall that
to answer the above question. Recall that

By [4, Exercise 6.18] and [4, Lemma 6.35], we have

This implies that the smaller the value of  , the worse the singularity of the curve \(C_d\) at P.
, the worse the singularity of the curve \(C_d\) at P.
In order to answer Question 1.1 for \(d \leqslant 4\), the values of log canonical threshold of a given reduced curve \(C_d\) at P were computed.
Example 1.2
If \(d=1\) or \(d=2\), then  .
.
Example 1.3
If \(d=3\), then  is one of \(\{ 1, {5}/{6}, {3}/{4}, {2}/{3}\}\). The worst singularity corresponds to
is one of \(\{ 1, {5}/{6}, {3}/{4}, {2}/{3}\}\). The worst singularity corresponds to  and in this case, \(C_d\) is a union of three lines intersecting at P (example of such a curve is \(xy(x-y)=0\)). Examples of curves with the given values of log canonical threshold (2 / 3, 3 / 4 , 5 / 6, 1, resp.) are illustrated in Fig. 1.
and in this case, \(C_d\) is a union of three lines intersecting at P (example of such a curve is \(xy(x-y)=0\)). Examples of curves with the given values of log canonical threshold (2 / 3, 3 / 4 , 5 / 6, 1, resp.) are illustrated in Fig. 1.
Example 1.4
(Erik Paemurru) Let \(C_4\) be a quartic curve. Then  is one of \(\{ 1, {5}/{6}, {3}/{4}, {7}/{10}, {9}/{14}, {5}/{8}, {2}/{3}, {3}/{5}, {7}/{12}, {5}/{9}, {1}/{2} \}\). The worst singularity occurs when
is one of \(\{ 1, {5}/{6}, {3}/{4}, {7}/{10}, {9}/{14}, {5}/{8}, {2}/{3}, {3}/{5}, {7}/{12}, {5}/{9}, {1}/{2} \}\). The worst singularity occurs when  and in this case \(C_4\) is a union of four lines passing through P (example of such a curve is \(xy(x-y)(x+y)=0\)) as illustrated in Fig. 2.
and in this case \(C_4\) is a union of four lines passing through P (example of such a curve is \(xy(x-y)(x+y)=0\)) as illustrated in Fig. 2.
For curves \(C_d\) with \(d \leqslant 3\),  corresponds uniquely to a type of singularity of \(C_d\) at the point P. When \(d=4\), this is not the case. For example, both the curves illustrated in Fig. 3 have
corresponds uniquely to a type of singularity of \(C_d\) at the point P. When \(d=4\), this is not the case. For example, both the curves illustrated in Fig. 3 have  but have very different singularities at P.
but have very different singularities at P.
All the three parameters mentioned earlier give the same answer to Question 1.1, since mult\(_P(C_d) \leqslant d\), \(\mu (P) \leqslant (d-1)^2\), with \(\mathrm{mult}_P(C_d) = d\), \(\mu (P)=(d-1)^2\) if and only if \(C_d\) is a union of d lines. The following theorem proves that computing the log canonical threshold of the curve at P also gives the same answer to the above question.
Theorem 1.5
([2, Theorem 4.1]) One has  and the equality holds if and only if \(C_d\) is a union of d lines passing through P.
and the equality holds if and only if \(C_d\) is a union of d lines passing through P.
We can then ask the following question:
Question 1.6
What is the second worst singularity at the point P?
While examples given above answer this question for curves of degree \(d\leqslant 4\), [1] answers this question for degree \(d\geqslant 5\) curves. To present this answer, we introduce certain types of singularities in Sect. 2 and we call these types of singularities \({\mathbb {K}}_n, {\mathbb {T}}_n, \widetilde{{\mathbb {K}}}_n, \widetilde{{\mathbb {T}}}_n, {\mathbb {M}}_n, \widetilde{{\mathbb {M}}}_n, \widehat{{\mathbb {M}}}_n\), where \(n=\mathrm {mult}_P(C_d)\). In [1], the following result was obtained.
Theorem 1.7
Suppose \(d \geqslant 5\) and  . Then the curve \(C_d\) has singularities of type \({\mathbb {T}}_{d-1},{\mathbb {K}}_{d-1},\widetilde{{\mathbb {T}}}_{d-1},\widetilde{{\mathbb {K}}}_{d-1}\) at P and the values of their log canonical thresholds at P are \(({2d-3})/{(d-1)^2}< ({2d-1})/(d^2-d)< ({2d-5})/({d^2-3d+1}) < ({2d-3})/(d^2-2d)\), respectively.
. Then the curve \(C_d\) has singularities of type \({\mathbb {T}}_{d-1},{\mathbb {K}}_{d-1},\widetilde{{\mathbb {T}}}_{d-1},\widetilde{{\mathbb {K}}}_{d-1}\) at P and the values of their log canonical thresholds at P are \(({2d-3})/{(d-1)^2}< ({2d-1})/(d^2-d)< ({2d-5})/({d^2-3d+1}) < ({2d-3})/(d^2-2d)\), respectively.
This result and Theorem 1.5 give the five worst singularities of the curve \(C_d\). In this paper, we describe the sixth worst one. To be precise we prove
Theorem 1.8
Suppose \(d \geqslant 5\) and

Then the curve \(C_d\) has singularity of type \({\mathbb {M}}_{d-1}\), \(\widetilde{{\mathbb {M}}}_{d-1}\) or \(\widehat{{\mathbb {M}}}_{d-1}\) at the point P with  .
.
In the case of \(d=5\), one can hope to determine all possible values of log canonical threshold of quintic curves, like in the case of \(d=4\) this was done in Example 1.4.
In Sect. 3 we present preliminary results used in the Proof of Theorem 1.8, while the proof itself is given in Sect. 4.
2 Cusps and other singularities
Let C be a reduced curve on a smooth surface S and P be a point on C. We are interested in singularities of the curve C at the point P. In this section, we introduce various types of singularities which we denote by \({\mathbb {T}}_n,{\mathbb {K}}_n,\widetilde{{\mathbb {T}}}_n,\widetilde{{\mathbb {K}}}_n,{\mathbb {M}}_n,\widetilde{{\mathbb {M}}}_n\) and \(\widehat{{\mathbb {M}}}_n\), where \(n=\mathrm {mult}_P(C)\). We aim to describe geometric properties of the curve C having one of these types of singularities at P.
Let \(f_1:S_1 \rightarrow S\) be the blow-up of S at the point P. Let \(C^1\) be the proper transform in \(S_1\) of the curve C and \(E_1\) be the exceptional divisor of the blow-up.
2.1 Singularities of type \({\mathbb {K}}_n\) (cusps)
A curve C having singularity of type \({\mathbb {K}}_n\) can be defined with the help of its geometric properties as given below. These singularities are also called cusps.
-
\(\mathrm {mult}_P(C)=n \geqslant 2\),
-
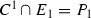 ,
, -
\(C^1\) intersects \(E_1\) tangentially at \(P_1\) and is smooth at this point (Fig. 4).
Recall from [5, Theorem 1.1] that the log canonical threshold of a cuspidal curve is

Remark 2.1
Suppose \(S={\mathbb {P}}^2\). Let C be a curve of degree \(d \geqslant 3\) having a \({\mathbb {K}}_{n}\) singularity at P. Then \(n \leqslant d-1\). If \(n=d-1\), then the curve C is irreducible. Such curves do exist. For example, the curve given by \(zx^{d-1}+y^d=0\) has singularity of type \({\mathbb {K}}_{d-1}\) at the point  .
.
2.2 Singularities of type \({\mathbb {T}}_{n}\)
A curve C having singularity of type \({\mathbb {T}}_{n}\) at P can be defined using the following geometric properties:
-
\(\mathrm{mult}_{P}(C)=n \geqslant 3\),
-
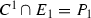 ,
, -
the point \(P_1\) is an ordinary double point of \(C^1\) (Fig. 5).
Remark 2.2
Suppose \(S={\mathbb {P}}^2\) and C is a curve of degree d. Let L be a line in \({\mathbb {P}}^2\) passing through P, whose proper transform \(L^1\) in \(S_1\) passes through \(P_1\). If the curve C has singularity of type \({\mathbb {T}}_n\), then \(C=L+Z\), where Z is an irreducible curve of degree \(d-1\) that does not contain L as an irreducible component. Since if not, then
which is absurd. Thus, \(C=L+Z\) and \(L \cap Z=P\) where Z has singularity of type \({\mathbb {K}}_{d-2}\) at the point P.
2.3 Singularities of type \(\widetilde{{\mathbb {T}}}_{n}\)
A curve C having singularity of type \(\widetilde{{\mathbb {T}}}_{n}\) at P can be defined using the following geometric properties:
-
\(\mathrm{mult}_{P}(C)=n \geqslant 4\),
-
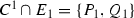 ,
, -
the point \(P_1\) is an ordinary double point of \(C^1\),
-
\(C^1\) intersects \(E_1\) transversally at \(Q_1\) and is smooth at this point (Fig. 6).
Remark 2.3
Suppose \(S={\mathbb {P}}^2\) and C is a curve of degree d. Let L be a line in \({\mathbb {P}}^2\) passing through the point P, whose proper transform \(L^1\) in \(S_1\) passes through the point \(P_1\). Similar computations as in Remark 2.2 imply \(C=Z+L\) so that \(L \cap Z=P\), where Z is an irreducible curve of degree \(d-1\) that does not contain L as an irreducible component and Z has singularity of type \(\widetilde{{\mathbb {K}}}_{d-2}\) at the point P, which is introduced in the next subsection.
2.4 Singularities of type \(\widetilde{{\mathbb {K}}}_{n}\)
A curve C with singularity of type \(\widetilde{{\mathbb {K}}}_{n}\) can be defined using the following geometric properties:
-
\(\mathrm{mult}_{P}(C)=n\geqslant 3\),
-
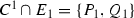 ,
, -
\(C^1\) intersects \(E_1\) tangentially at the point \(P_1\) and is smooth at this point,
-
\(C^1\) is smooth at \(Q_1\) and intersects \(E_1\) transversally at this point (Fig. 7).
Remark 2.4
Suppose \(S={\mathbb {P}}^2\) and C is a curve of degree d. Then C with a \(\widetilde{{\mathbb {K}}}_{d-1}\) singularity at P exists. Such a curve can be reducible, for example, \(y(x^{d-2}-y^{d-1})=0\) or can be irreducible, for example, \(x^{d-2}y+y^d+x^d=0\). If C is reducible, then \(C=L+Z\) where Z is a curve of degree \(d-1\) which does not contain L as an irreducible component and has singularity of type \({\mathbb {K}}_{d-2}\) at the point P.
2.5 Singularities of type \({\mathbb {M}}_{n}\)
A curve C with singularity of type \({\mathbb {M}}_{n}\) at P can be defined using the following geometric properties:
-
\(\mathrm{mult}_P(C)=n\geqslant 5\),
-
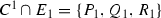 ,
, -
\(C^1\) is smooth at the points \(Q_1\) and \(R_1\) where it intersects transversally with \(E_1\),
-
the point \(P_1\) is an ordinary double point of \(C^1\) (Fig. 8).
Remark 2.5
Suppose \(S={\mathbb {P}}^2\) and C is a curve of degree d. A curve having singularity of type \({\mathbb {M}}_{d-1}\) at P exists, for example, \(x(x^2-y^2)(x^{d-4}-y^{d-3})=0\). It is reducible and thus \(C=Z+L\) where L is a line in S that contains the point P so that its proper transform \(L^1\) in \(S_1\) contains the point \(P_1\) and Z is an irreducible curve of degree \(d-1\) which does not contain L as an irreducible component.
2.6 Singularities of type \(\widetilde{{\mathbb {M}}}_n\)
A curve C with singularity of type \(\widetilde{{\mathbb {M}}}_n\) at P can be defined using the following geometric properties:
-
\(\mathrm {mult}_P(C)=n \geqslant 5\),
-
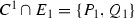 ,
, -
\(P_1\) is an ordinary double point of \(C^1\) with
 ,
, -
\(C^1\) intersects \(E_1\) tangentially at the point \(Q_1\) with
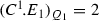 and is smooth at this point (Fig. 9).
and is smooth at this point (Fig. 9).
Remark 2.6
Suppose \(S={\mathbb {P}}^2\) and C is a curve of degree d. Then \(n=d-1\) is possible and a curve with singularity of type \(\widetilde{{\mathbb {M}}}_{d-1}\) exists. For example, \(y(zx^2+y^3)(zy^{d-4}+x^{d-3})=0\) has an \(\widetilde{{\mathbb {M}}}_{d-1}\) singularity at the point  . In this case, C is reducible and thus, \(C=L+Z\) where L is the line in S containing P such that its proper transform \(L^1\) passes through the point \(P_1\) in \(S_1\) and Z is a \(d-1\) degree irreducible curve that does not contain L as an irreducible component.
. In this case, C is reducible and thus, \(C=L+Z\) where L is the line in S containing P such that its proper transform \(L^1\) passes through the point \(P_1\) in \(S_1\) and Z is a \(d-1\) degree irreducible curve that does not contain L as an irreducible component.
2.7 Singularities of type \(\widehat{{\mathbb {M}}}_n\)
A curve C with singularity of type \(\widehat{{\mathbb {M}}}_n\) at P can be defined using the following geometric properties:
-
\(\mathrm {mult}_P(C)=n \geqslant 5\),
-
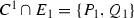 ,
, -
\(P_1\) is an ordinary double point of \(C^1\) with \((C_1.E_1)_{P_1}=n-2\),
-
\(Q_1\) is an ordinary double point of \(C^1\) with \((C_1.E_1)_{Q_1}=2\) (Fig. 10).
Remark 2.7
Suppose \(S={\mathbb {P}}^2\) and C is a curve of degree d with singularity of type \(\widehat{{\mathbb {M}}}_n\) at the point P. Then \(n=d-1\) is possible, for example, C given by \(x(zx^{d-4}+y^{d-3})(z^2y^2+x^4)=0\) has an \(\widehat{{\mathbb {M}}}_{d-1}\) singularity at the point  . That is, \(C=L+Z\) where L is a line in S that passes through the point P whose proper transform contains the point \(P_1\) and Z is an irreducible curve in S of degree \(d-1\) which does not contain L as an irreducible component.
. That is, \(C=L+Z\) where L is a line in S that passes through the point P whose proper transform contains the point \(P_1\) and Z is an irreducible curve in S of degree \(d-1\) which does not contain L as an irreducible component.
2.8 Defining equations
In this section, we describe a curve C having any of the above types of singularities using local equations. These descriptions actually are not essential to prove Theorem 1.8. Up to analytic change of coordinates, the equations of the curve C with the respective singularities are given below:
-
\(\mathbb {K}_n\): \(\displaystyle x^n+y^{n+1}+\sum _{{i=1}}^{n+1}\, a_ix^iy^{n+1-i}+\mathrm {H.O.T.}=0\),
-
\(\mathbb {T}_n\): \(\displaystyle x\biggl (x^{n-1}-y^{n}+\sum _{{i=2}}^{n+1}\, a_i x^{i-1}y^{n+1-i}+\mathrm {H.O.T}\biggr )=0\),
-
\(\widetilde{T}_n\): \(\displaystyle x\biggl (y(y^{n-1}-x^{n-2})+\sum _{{i=2}}^{n+1}\,a_i x^{i-1} y^{n+1-i}+\mathrm {H.O.T}\biggr )=0\),
-
\(\widetilde{K}_n\): \(\displaystyle y(x^{n-1}-y^{n})+\sum _{{i=1}}^{n+1}\,a_ix^{i-1}iy^{n+1-i}+\mathrm {H.O.T}=0\),
-
\(\mathbb {M}_n\):\(\displaystyle x\biggl ((x^2-y^2)(x^{n-3}-y^{n-2})+\!\!\!\sum _{{i=2, i \ne 3}}^{n} \!\!\! a_i x^i y^{n+1-i}+\mathrm {H.O.T}\biggr )=0\),
-
\(\widetilde{\mathbb {M}}_n\): \(\displaystyle y\biggl ((x^2+y^3)(y^{n-3}+x^{n-2})+\sum _{{i=1}}^{n-1}\, a_i x^i y^{n-i}+\!\!\!\! \sum _{{i=0 , i \ne n-2}}^{n+1}\!\!\!\!\!\! b_i x^i y^{n+1-i}+\mathrm {H.O.T}\biggr )=0\),
-
\(\widehat{\mathbb {M}}_n\): \(\displaystyle x\biggl ((x^{n-3}+y^{n-2})(y^2+x^4)+\!\!\!\sum _{{i=0 , i\ne 1}}^{n} \!\!\! a_i x^{i-1} y^{n+1-i}+ \sum _{{i=0}}^{n}\, b_i x^{i-1} y^{n+2-i}+\!\!\! \sum _{{i=0 , i \ne 5}}^{n+2}\!\!\!c_i x^{i-1} y^{n+3-i}+\mathrm {H.O.T}\biggr )=0\).
The above set of equations comprise an exhaustive list of curves C of a given degree with the various types of singularities, up to analytic change of coordinates and include the curves missing from the list in [1, Definition 1.9], as pointed out by the referee.
3 Preliminaries
Let S be a smooth surface and P be a point in S. Let D be an effective non-zero \({\mathbb {Q}}\)-divisor on the surface S. Then,
where each \(C_i\) is an irreducible curve on S and \(a_i \in {\mathbb {Q}}_{\geqslant 0}\).
Let \(\pi :{\widetilde{S}} \rightarrow S\) be a birational morphism such that \({\widetilde{S}}\) is smooth. One can then conclude that \(\pi \) is a composition of n blow-ups of points. For each \(C_i\), we denote its proper transform by \(\widetilde{C_i}\) and the exceptional curves of the blow-up by \(F_1, F_2,\dots , F_n\). Then,

where \(b_i \in {\mathbb {Q}}\). Suppose  is a divisor with simple normal crossings (SNC).
is a divisor with simple normal crossings (SNC).
Definition 3.1
([4, Definition 6.16]) The log pair (S, D) is said to be log canonical at P if the following conditions are satisfied:
-
\(a_i \leqslant 1\) for every \(C_i\) such that \(P \in C_i\),
-
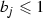 for every
for every 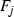 such that
such that 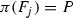 .
.
Similarly, the log pair (S, D) is said to be Kawamata log terminal at P if
-
\(a_i < 1\) for every \(C_i\) such that \(P \in C_i\),
-
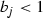 for every
for every 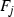 such that
such that  .
.
Let \(\pi _1:S_1 \rightarrow S\) be the blow-up of S at the point P and \(E_1\) be the exceptional curve of the blow-up. Let \(D^1\) be the proper transform of the divisor D on the surface \(S_1\) after blow-up. Let
This is called the log pull-back of the log pair (S, D). Observe that
This implies that the log pair (S, D) is not log canonical at P if \(\mathrm {mult}_P(D)>2\), and is not Kawamata log terminal if \(\mathrm {mult}_P(D) \geqslant 2\).
Remark 3.2
The log pair (S, D) is log canonical at the point P if and only if (\(S_1,D^{S_1})\) is log canonical at every point in \(E_1\). Similarly, the log pair (S, D) is Kawamata log terminal at the point P if and only if (\(S_1,D^{S_1}\)) is Kawamata log terminal at every point in \(E_1\).
Lemma 3.3
([4, Exercise 6.18]) Suppose (S, D) is not log canonical at P, then \(\mathrm {mult}_P(D)>1\). Similarly, if (S, D) is not Kawamata log terminal at P, then \(\mathrm {mult}_P(D) \geqslant 1\).
Let Z be an irreducible curve on S that contains the point P and is smooth at P. Suppose that Z is not contained in  . Let \(\mu \) be a non-negative rational number.
. Let \(\mu \) be a non-negative rational number.
Theorem 3.4
([3, Theorem 7], [4, Exercise 6.31], [6, Corollary 3.12]) Suppose the log pair \((S, \mu Z+D)\) is not log canonical (not Kawamata log terminal, resp.) at P and \(\mu \leqslant 1\) \((\mu <1\), resp.). Then \(\mathrm {mult}_P(D.Z)>1\).
Lemma 3.5
If (S, D) is not log canonical at P and \(\mathrm {mult}_P(D) \leqslant 2\), then there exists a unique point in \(E_1\) such that \((S_1,D^{S_1})\) is not log canonical at it. Similarly, if (S, D) is not Kawamata log terminal at P, and \(\mathrm {mult}_P(D)<2\), then there exists a unique point in \(E_1\) such that \((S_1,D^{S_1})\) is not Kawamata log terminal at it.
Proof
Suppose (S, D) is not log canonical at P and \(\mathrm {mult}_P(D) \leqslant \) 2 and suppose there exist two distinct points \(P_1\) and \(P_2\) in \(E_1\) at which \((S_1,D^{S_1})\) is not log canonical. Then,

by Theorem 3.4. Thus, Remark 3.2 proves the first assertion. Similarly we can prove the second assertion.\(\square \)
Lemma 3.6
([1, Lemma 2.14]) Suppose (S, D) is not Kawamata log terminal at P, and (S, D) is Kawamata log terminal in a punctured neighbourhood of the point P, then \(\mathrm {mult}_P(D)>1\).
Proof
Suppose \(\mathrm {mult}_P(D) \leqslant 1\). Let us seek for a contradiction. Since (S, D) is not Kawamata log terminal at P, we have that  is not Kawamata log terminal at some point \(P_1\in E_1\). From Lemma 3.5 we have that this point \(P_1\) is unique. This implies that \(\mathrm {mult}_{P}(D)>1\), by Lemma 3.3, which in turn contradicts our assumption.\(\square \)
is not Kawamata log terminal at some point \(P_1\in E_1\). From Lemma 3.5 we have that this point \(P_1\) is unique. This implies that \(\mathrm {mult}_{P}(D)>1\), by Lemma 3.3, which in turn contradicts our assumption.\(\square \)
Let \(Z_1\) and \(Z_2\) be irreducible curves on the surface S such that \(Z_1\) and \(Z_2\) are not contained in  and \(P \in Z_1 \cap Z_2\). Also, suppose that \(Z_1\) and \(Z_2\) are smooth at P and intersect transversally at P. Let \(\mu _1\) and \(\mu _2\) be non-negative rational numbers.
and \(P \in Z_1 \cap Z_2\). Also, suppose that \(Z_1\) and \(Z_2\) are smooth at P and intersect transversally at P. Let \(\mu _1\) and \(\mu _2\) be non-negative rational numbers.
Theorem 3.7
([3, Theorem 13]) If the log pair \((S, \mu _1Z_1+ \mu _2Z_2+D)\) is not log canonical at the point P, and \(\mathrm {mult}_P(D) \leqslant 1\), then \(\mathrm {mult}_P(D.Z_1) >2(1-\mu _2)\) or \(\mathrm {mult}_P(D.Z_2) >2(1-\mu _1)\) (or both). Similarly, if the log pair \((S, \mu _1Z_1+ \mu _2Z_2+D)\) is not Kawamata log terminal at the point P, and \(\mathrm {mult}_P(D)<1\), then \(\mathrm {mult}_P(D.Z_1) \geqslant 2(1-\mu _2)\) or \(\mathrm {mult}_P(D.Z_2) \geqslant 2(1-\mu _1)\) (or both).
4 Proof of the main result
Let us now prove the main result of the paper. Let \(C_d\) be a reduced curve of degree \(d \geqslant 5\) on a smooth surface S such that \(P \in C_d\) and let \(m_0=\mathrm {mult}_P(C_d)\). Suppose \(({2d-3})/(d^2-2d)<\mathrm {lct}_P(S,C_d) < ({2d-7})/({d^2-4d+1})\). This means that there exists \(\lambda < ({2d-7})/({d^2-4d+1})\) such that \((S,\lambda C_d)\) is not Kawamata log terminal at P. Let us also assume that \(m_0 \ne d\) and thus \(C_d\) is not a union of d lines. We want to show that the curve \(C_d\) has singularity of type \({\mathbb {M}}_{d-1},\widetilde{{\mathbb {M}}}_{d-1}\) or \(\widehat{{\mathbb {M}}}_{d-1}\) at the point P. It is important to notice that the arguments presented below are very similar to the arguments in [1]. Also, these are local arguments, i.e., it is not necessary for the curve \(C_d\) to be smooth everywhere outside of P. We assume that the respective divisors on the surface S at various levels are Kawamata log terminal (or log canonical) at a punctured neighbourhood of P.
Lemma 4.1
The following inequalities are used in the proof of the main result:
-
(i)
\(\lambda < {2}/({d-1})\),
-
(ii)
\(\lambda < ({2k+1})/{kd}\) , for \(k\in {\mathbb {Z}}_{>0}\) such that \(k \leqslant d-3\),
-
(iii)
\(\lambda < ({2k+1})/({kd+1})\) for \(k\in {\mathbb {Z}}_{>0}\) such that \(k\leqslant d-5\),
-
(iv)
\(\lambda <{3}/{d}\),
-
(v)
\(\lambda <{2}/({d-2})\),
-
(vi)
\(\lambda <{6}/({3d-4})\),
-
(vii)
\(\lambda < {5}/{2d}\).
The proof is straightforward.
We will now introduce some notations. Let \(S=S_0={\mathbb {P}}^2\) and  . Consider a sequence of blow-ups \(f_i:S_i \rightarrow S_{i-1}\) such that \(f_1\) is the blow-up of \(P_0=P\), \(f_2\) is the blow-up of the point \(P_1\), and so on, i.e., \(f_i\) is the blow-up of the point \(P_{i-1}\in S_{i-1}\). We have
. Consider a sequence of blow-ups \(f_i:S_i \rightarrow S_{i-1}\) such that \(f_1\) is the blow-up of \(P_0=P\), \(f_2\) is the blow-up of the point \(P_1\), and so on, i.e., \(f_i\) is the blow-up of the point \(P_{i-1}\in S_{i-1}\). We have
Also, let \(f:S_{k+1} \rightarrow S\) be the composition of the blow-ups, i.e., \(f=f_1\circ f_2 \circ \cdots \circ f_{k+1}\). The \(f_i\)-exceptional divisor during each blow-up is denoted by \(E_i\). The proper transform of the exceptional divisors  in \(S_i\) is denoted by
in \(S_i\) is denoted by  for all \(j < i\). Also, after the \(f_i\) blow-up, the curve \(C_d\) is denoted by \(C_d^i\) in \(S_i\). The divisors comprising of the curve and the exceptional curves on every floor \(S_i\) are together denoted by \(D^{S_i}\). We will explicitly describe how each of these points of blow-up are chosen.
for all \(j < i\). Also, after the \(f_i\) blow-up, the curve \(C_d\) is denoted by \(C_d^i\) in \(S_i\). The divisors comprising of the curve and the exceptional curves on every floor \(S_i\) are together denoted by \(D^{S_i}\). We will explicitly describe how each of these points of blow-up are chosen.
Since \((S,\lambda C_d\)) is not Kawamata log terminal at the point \(P\in C_d\), by Remark 3.2 one has that \((S_1,\lambda C_d^1+(\lambda m_0-1)E_1)\) is not Kawamata log terminal at some point in \(E_1\). Let this point be \(P_1\).
Lemma 4.2
\(\lambda m_0 <2\).
Proof
Since \(m_0 \leqslant d-1\), we have \(\lambda m_0 \leqslant \lambda (d-1)\). Using Lemma 4.1 (i), we get \(\lambda m_0 <2\).\(\square \)
From Lemma 3.5 this implies that the point \(P_1\) is a unique point on \(E_1\) at which \((S_1,D^{S_1})\), that is, \((S_1,\lambda C_d^1+(\lambda m_0-1)E_1)\) is not Kawamata log terminal.
Let L be the line in \({\mathbb {P}}^2\) whose proper transform, \(L^1\) in \(S_1\), contains the point \(P_1\).
Lemma 4.3
Suppose \(m_0=d-1\). Then L is an irreducible component of \(C_d\).
Proof
Observe that
If L is not an irreducible component of the curve \(C_d\), then we have
where \(m_1=\hbox {mult}_{P_1}(C_d^1)\). Thus we have \(m_0+m_1 \leqslant d\). \(P_1 \in C_d^1\), since if not, then \((S_1,(\lambda m_0-1)E_1)\) is not log canonical at the point \(P_1\), which is not possible since \(\lambda m_0-1<1\) from Lemma 4.2. Since \(m_0=d-1\), \(m_1=1\). Therefore, \(C_d^1\) is smooth at \(P_1\).
Let \(k=\mathrm{mult}_{P_1}(C_d^1.E_1)\). We claim that \(k>d-3\). Indeed, suppose \(k \leqslant d-3\). Since \((S_1, D^{S_1})\) is not Kawamata log terminal at the point \(P_1 \in E_1\), we have that \((S_2,D^{S_2})\) is not Kawamata log terminal at some point in \(E_2\), where
Let this point be \(P_2\). Note that all the coefficients of the curves in \(D^{S_2}\) are less than 1. In particular, we have
Thus, by Definition 3.1, \((S_3,D^{S_3})\) is not Kawamata log terminal at some point in \(E_3\). Let this point be \(P_3\). Thus, \(f_2\) is the blow-up of \(P_1 \in C^1 \cap E_1\), \(f_3\) is the blow-up of \(P_2 \in C^2 \cap E_2\), and so on. One then has the sequence as mentioned in (i).
We require \(k+1\) blow-ups to ensure simple normal crossing of the elements of the divisor over the point P. Here the points of blow-up are such that \(P_i=C^i \cap E_i\) and using the notations described earlier, we have
Let the coefficients of \(E_i^{k+1}\) in (2) be denoted by \(b_i\). Then since
is a divisor with simple normal crossings over P, at least one of \(b_i >1\) or \(b_{k+1}>1\). But the coefficients \(b_i\) are such that  for all \(j<i\) and we have
for all \(j<i\) and we have
from Lemma 4.1 (ii). That is, in particular  for all \(j<k+1\).
for all \(j<k+1\).
This contradiction implies that \(k > d-3\). We also know that
Therefore, these inequalities imply \(k=d-1\) or \(d-2\). Thus, when
-
\(k=d-1\), then \(C_d\) has singularity of type \({\mathbb {K}}_{d-1}\) at P (see Sect. 2.1).
-
\(k=d-2\), then \(C_d\) has singularity of type \(\widetilde{{\mathbb {K}}}_{d-1}\) at P (see Sect. 2.4).
If the curve \(C_d\) has either of the above singularities at the point P, then  or
or  , respectively. Since we assume
, respectively. Since we assume  , neither of these values for k are possible. Therefore, this contradiction implies that L is an irreducible component of the curve \(C_d\).\(\square \)
, neither of these values for k are possible. Therefore, this contradiction implies that L is an irreducible component of the curve \(C_d\).\(\square \)
Lemma 4.4
Suppose \(m_0=d-1\). Then \(C_d\) has singularity of type \({\mathbb {M}}_{d-1}\), \(\widetilde{{\mathbb {M}}}_{d-1}\) or \(\widehat{{\mathbb {M}}}_{d-1}\) at the point P.
Proof
From Lemma 4.3 we know that L is an irreducible component of the curve \(C_d\), i.e., we have \(C_d=C_{d-1}+L\) where \(C_{d-1}\) is an irreducible curve of degree \(d-1\) which does not contain L as an irreducible component. Let \(n_0=\mathrm {mult}_{P}(C_{d-1})\). Since \(m_0=\mathrm {mult}_P(C_d)=d-1\), we have \(n_0=m_0-1=d-2\) .
Let \(f_1:S_1 \rightarrow S\) be the blow-up at the point P and \(n_1=\mathrm {mult}_{P_1}(C_{d-1}^1)\). We have \(n_1=m_1-1\). We also have \(P_1 \in C_{d-1}^1\) since if not, it would mean that \((S_1, \lambda L^1+(\lambda (d-1)-1)E_1)\) is not log canonical at the point \(P_1\) which is a contradiction since \(\lambda <1 \) and \(\lambda (d-1)-1<1\) and  are SNC divisors over \(P_1\). Thus, \(n_1 \geqslant 1\).
are SNC divisors over \(P_1\). Thus, \(n_1 \geqslant 1\).
Consider

that is, \(n_0+n_1 \leqslant d-1\) and since \(n_0=d-2\), we have \(n_1=1\). Thus the curve \(C_{d-1}^1\) is smooth at \(P_1\).
Let \(k=\mathrm {mult}_{P_1}(C_{d-1}^1.E_1)\). We claim \(k> d-5\). Instead, suppose \(k \leqslant d-5\), then using similar computations as in Lemma 4.3, after \(k+1\) blow-ups, we get

where \((S_{k+1},D^{S_{k+1}})\) is not Kawamata log terminal at some point in \(E_{k+1}\), which we take to be \(P_{k+1}\). Here again, f is a composition of \(k+1\) blow-ups and \(b_i\) are the coefficients of \(E_i^{k+1}\) in the above equation.
Since the curves in the divisor
intersect at simple normal crossing at the point P after \(k+1\) blow-ups, one of these coefficients should be such that \(b_i > 1\) or \(b_{k+1}>1\) but we have

from Lemma 4.1 (iii) and the coefficients are such that  for all \(j<i\). In particular,
for all \(j<i\). In particular,  for all \(j<k+1\). This contradiction implies \(k>d-5\). We also know that
for all \(j<k+1\). This contradiction implies \(k>d-5\). We also know that
Thus, these inequalities imply that \(k=d-2\) or \(d-3\) or \(d-4\). Thus, when
-
\(k=d-2\), \(C_d\) has singularity of type \({\mathbb {T}}_{d-1}\) at P (see Sect. 2.2),
-
\(k=d-3\), \(C_d\) has singularity of type \(\widetilde{{\mathbb {T}}}_{d-1}\) at P (see Sect. 2.3).
If \(C_d\) has either one of the above singularities at the point P, then  or
or  , respectively. Since we assume that \(\mathrm {lct}_P({\mathbb {P}}^2,C_d) >({2d-3})/(d^2-2d)\), these values of k are not possible. Thus \(k=d-4\), i.e., \(C_d\) has singularity of type \({\mathbb {M}}_{d-1}\), \(\widetilde{{\mathbb {M}}}_{d-1}\) or \(\widehat{{\mathbb {M}}}_{d-1}\) at P.\(\square \)
, respectively. Since we assume that \(\mathrm {lct}_P({\mathbb {P}}^2,C_d) >({2d-3})/(d^2-2d)\), these values of k are not possible. Thus \(k=d-4\), i.e., \(C_d\) has singularity of type \({\mathbb {M}}_{d-1}\), \(\widetilde{{\mathbb {M}}}_{d-1}\) or \(\widehat{{\mathbb {M}}}_{d-1}\) at P.\(\square \)
Observe that Lemmas 4.3 and 4.4 complete the proof of the main result if \(m_0=d-1\). In the remaining part of the section, we will prove that \(m_0 \leqslant d-2\) is not possible. In particular, we prove the following proposition.
Proposition 4.5
If \(m_0 \leqslant d-2\), then \(\mathrm {lct}_P(S, C_d) \geqslant {2}/({d-1})\).
This in turn proves that for our choice of \(\lambda \) and the assumption that \((S,\lambda C_d)\) is not Kawamata log terminal at P, \(m_0 \leqslant d-2\) is not possible, since \(\lambda <{2}/({d-1})\). Let us prove this proposition by the method of contradiction.
Proof
Suppose \(m_0 \leqslant d-2\) and  . Let \(\mu ={2}/({d-1})\). Then \((S,\mu C_d\)) is not log canonical, in particular, is not Kawamata log terminal at a point, say P. Let us now obtain the necessary contradiction.
. Let \(\mu ={2}/({d-1})\). Then \((S,\mu C_d\)) is not log canonical, in particular, is not Kawamata log terminal at a point, say P. Let us now obtain the necessary contradiction.
Claim 1
The line L is not an irreducible component of the curve \(C_d\).
Proof
We shall prove this by contradiction. Suppose L is an irreducible component of the curve \(C_d\). Then \(C_d=L+C_{d-1}\), where \(C_{d-1}\) is an irreducible curve of degree \(d-1\) in \({\mathbb {P}}^2\) and does not contain L as an irreducible component. Let \(f_1:S_1 \rightarrow S\) be the blow-up at the point P in \(C_d\). Let \(n_0=\mathrm {mult}_P(C_{d-1})\).
Since \((S, \mu C_{d-1}+\mu L)\) is not log canonical at P, we have that \((S_1, \mu C_{d-1}^1 + \mu L^1 +(\mu (n_0+1)-1)E_1)\) is not log canonical at some point in \(E_1\). We choose this point to be \(P_1\). Let \(n_1=\mathrm {mult}_{P_1}(C_{d-1}^1)\). Consider
which implies that \(n_0+n_1 \leqslant d-1\). But \(n_0=m_0-1\leqslant d-3\), using our assumption.
Also, \(2n_1 \leqslant n_0+n_1\) which implies \(2n_1 \leqslant d-1\). We can then conclude that \(\mu n_1 \leqslant 1\). We also have \(L^1\) and \(E_1\) smooth at \(P_1\) and intersecting transversally at \(P_1\). Thus applying Theorem 3.7, we get

which implies that \(\mu (d-1) > 2\) or

which implies that \(\mu (n_0+2)> 2\).
The two inequalities in (3) and (4) imply that \(\mu (d-1) > 2\) which is absurd. Thus, L is not an irreducible component of \(C_d\). \(\blacksquare \)
Since L is not an irreducible component of the curve \(C_d\), from the computations in (1) we can also assume that \(m_0+m_1 \leqslant d\).
Since \((S,\mu C_d)\) is not log canonical at the point P and since \(\mu <1\), we have that \((S_1,\mu C_d^1+ (\mu m_0-1)E_1)\) is not log canonical at some point in \(E_1\), say \(P_1\). We also have
for \(d\geqslant 5\). Thus, from Lemma 3.5 there exists a unique point in \(E_2\), say \(P_2\), such that \((S_2, \mu C_d^2 +(\mu m_0-1)E_1^2+(\mu (m_0+m_1)-2)E_2)\) is not log canonical at \(P_2\).
We know that \(P_2 \in C_d^2\), since if not, it would imply \((S_2,(\mu m_0-1)E_1^2+(\mu (m_0+m_1)-2)E_2)\) is not log canonical at the point \(P_2\). This is not possible since \(\mu m_0-1<1\), \(\mu (m_0 +m_1)-2 \leqslant \mu d -2 <1\), and \(E_1^2,E_2\) are SNC divisors at \(P_2\).
Claim 2
\(P_2 \notin E_1^2\).
Proof
Suppose \(P_2 \in E_1^2\). Observe that
so that \(C_d^2.E_1^2=C_d^1.E_1-m_1 E_2.E_1^2=m_0-m_1\).
Also, since \(P_2 \in C_d^2 \cap E_1^2 \cap E_2\), we have \(m_2=\mathrm {mult}_{P_2}(C_d^2) \leqslant (C_d^2.E_1^2)\). Therefore, \(m_2 \leqslant m_0-m_1\). Since \(m_2 \leqslant m_1\), we have \(2m_2 \leqslant m_1+m_2 \leqslant m_0\) which implies

From Lemma 4.1 (v), we have
We also know that \(E_1^2\) and \(E_2\) are smooth at \(P_2\) and intersect transversally at \(P_2\).
Since \((S_2, \mu C_d^2 + (\mu m_0-1)E_1^2+(\mu (m_0+m_1)-2)E_2)\) is not log canonical at the point \(P_2\), Theorem 3.7 implies \(\mu (m_0-m_1) =\mu C_d^2.E_1^2 > 2(3-\mu (m_0+m_1))\) or \(\lambda m_1=\lambda C_d^2.E_2 > 2(2-\lambda m_0)\). That is, \(\mu (3m_0+m_1) > 6\) or \(\mu (2m_0+m_1) > 4\). We have
Using the above equations (5) and (6), both of the above mentioned inequalities obtained from using Theorem 3.7 result in contradiction, hence proving our claim that \(P_2 \notin E_1^2\). \(\blacksquare \)
Claim 3
\(P_2 \notin L^2\).
Proof
Suppose \(P_2 \in L^2\). Since L is not an irreducible component of \(C_d\), we have  and this implies that \(m_0+m_1+m_2 \leqslant d\). Also, applying Lemma 3.3, we get \(\mu d \geqslant \mu (m_0+m_1+m_2)>3\) which results in a contradiction since \(\mu d < 3\). Thus, \(P_2 \ne L^2 \cap E_2\). \(\blacksquare \)
and this implies that \(m_0+m_1+m_2 \leqslant d\). Also, applying Lemma 3.3, we get \(\mu d \geqslant \mu (m_0+m_1+m_2)>3\) which results in a contradiction since \(\mu d < 3\). Thus, \(P_2 \ne L^2 \cap E_2\). \(\blacksquare \)
Thus, we have that \((S_2, \mu C_d^2+(\mu (m_0+m_1)-2)E_2)\) is not log canonical at the point \(P_2\). Then from Remark 3.2, \((S_3, \mu C_d^3+(\mu (m_0+m_1)-2)E_2^3+(\mu (m_0+m_1+m_2)-3)E_3)\) is not log canonical at some point in \(E_3\), say \(P_3\).
We have \(2m_1 \leqslant m_0+m_1 \leqslant d,\) and
Therefore \(\mu (m_0+m_1+m_2)-3 \leqslant 1\).
\(P_3 \in C_d^3\), since if not, then this would imply that \((S_3,(\mu (m_0+m_1)-2)E_2^3+(\mu (m_0+m_1+m_2)-3)E_3) \) is not log canonical at the point \(P_3\). But since the coefficients of \(E_i\leqslant 1\) and \(E_2^3,E_3\) are SNC divisors over the point \(P_3\), this is not possible.
Claim 4
\(P_3 \notin E_2^3\).
Proof
Suppose \(P_3 \in E_2^3\). Observe that
We thus have
Therefore, Theorem 3.4 implies
which implies \(\mu (m_0+2m_1)>4\). From (7) we know that \(\mu (m_0+2m_1)\leqslant 4\). This contradiction proves our claim. \(\blacksquare \)
Therefore, the log pair \((S_3, \mu C_d^3+(\mu (m_0+m_1+m_2)-3)E_3)\) is not log canonical, at the point \(P_3\). Thus from Remark 3.2, \((S_4,\mu C_d^4+ (\mu (m_0+m_1+m_2)-3)E_3^4+(\mu (m_0+m_1+m_2+m_3)-4)E_4)\) is not log canonical at a point \(P_4 \in E_4\). We have
Thus,
Claim 5
\(P_4 \notin E_3^4\).
Proof
Suppose \(P_4 \in E_3^4\). From inequality (8), \(m_0+m_1+2m_2 < {5}/{\mu }\). Also, observe that
so that \(C_d^4.E_3^4=m_2-m_3\). Then from Theorem 3.4 we have
which implies

This contradicts inequality in (8). Thus \(P_4 \notin E_3^4\). \(\blacksquare \)
Thus, (\(S_4, \mu C_d^4+(\mu (m_0+m_1+m_2+m_3)-4)E_4)\) is not log canonical at the point \(P_4\). From Lemma 3.6, we have
which implies

Now using (9) and a geometric construction of a special curve in \(S_4\) we will try to arrive at a contradiction. We may assume that the line L is given by \(x=0\) and  . Let \({\mathscr {C}}\) be the conic in \({\mathbb {P}}^2\) that is given by
. Let \({\mathscr {C}}\) be the conic in \({\mathbb {P}}^2\) that is given by
where \(A,B \in {\mathbb {C}}\) and \(B \ne 0\). Then \({\mathscr {C}}\) is smooth and is tangent to the line L. Denote the proper transform of \({\mathscr {C}}\) in \(S^i\) by \({\mathscr {C}}^i\). It follows from Claims 2, 3, 4 and 5, that there exist A and \(B\ne 0\) such that \({\mathscr {C}}^i\) on \(S^i\) contain \(P_i\) for \(i=1,2,3\). So we can assume that A, B are chosen this way. Then we have
Thus the pencil \(\vert {\mathscr {C}}^4 \vert \) does not have base points.
Also, let \({\mathscr {L}}\) be a pencil of conics in \({\mathbb {P}}^2\) given by
where \(s,t\in {\mathbb {C}}\). It is generated by 2L and \({\mathscr {C}}\).
Let \(\phi _{\vert {\mathscr {C}}^4 \vert }:S^4 \rightarrow {\mathbb {P}}^1\) be the morphism defined by the pencil \(\vert {\mathscr {C}}^4 \vert \). Similarly, let \( \phi _{{\mathscr {L}}}:{\mathbb {P}}^2 \dashrightarrow {\mathbb {P}}^1 \) be the rational map defined by the pencil \({\mathscr {L}}\). These make the following diagram commutative:

Choose a curve \(Z^4\) in \(\vert {\mathscr {C}}^4 \vert \) that passes through the point \(P_4\). Then \(Z^4\) is a smooth irreducible curve. Let the proper transform of \(Z^4\) in \({\mathbb {P}}^2\) be denoted by Z. Thus Z is a smooth conic in the pencil \({\mathscr {L}}\). Suppose Z is not an irreducible component of the curve \(C_d\), then we have
Equations (9) and (10) result in a contradiction since \(\mu < {5}/({2d})\).
Thus, \(C_d=Z+C_{d-2}\) where \(C_{d-2}\) is an irreducible curve of degree \(d-2\) which does not contain the conic Z as an irreducible component.
Let \(C_{d-2}^1,C_{d-2}^2,C_{d-2}^3,C_{d-2}^4\) be the proper transforms of the curve \(C_{d-2}\) on the surfaces \(S_1, S_2, S_3\) and \(S_4\), respectively. Denote by \(n_0=\mathrm {mult}_P(C_{d-2})\), \(n_1=\mathrm {mult}_{P_1}(C_{d-2}^1)\), \(n_2=\mathrm {mult}_{P_2}(C_{d-2}^2)\), \(n_3=\mathrm {mult}_{P_3}(C_{d-2}^3)\), and \(n_4=\mathrm {mult}_{P_4}(C_{d-2}^4)\). Thus \((S_4, \mu C_{d-2}^4 +\mu Z^4 +((\mu (n_0+n_1+n_2+n_3+4)-4)E_4\)) is not log canonical at \(P_4\).
Applying Theorem 3.4 to the above gives \(\mu (2(d-2)-n_0-n_1-n_2-n_3)+\mu (n_0+n_1+n_2+n_3+4)-4>1\), which implies \(\mu > {5}/({2d})\). But \(\mu < {5}/({2d})\) and thus this contradiction proves the proposition.\(\square \)
This in turn proves that \(m_0\leqslant d-2\) is not possible for the chosen value of \(\lambda \), hence completing the Proof of Theorem 1.8.
References
Cheltsov, I.: Worst singularities of plane curves of given degree. J. Geom. Anal. 27(3), 2302–2338 (2017)
Cheltsov, I.A.: Log canonical thresholds on hypersurfaces. Sb. Math. 192(7–8), 1241–1257 (2001)
Cheltsov, I.: Del Pezzo surfaces and local inequalities. In: Cheltsov, I., et al. (eds.) Automorphisms in Birational and Affine Geometry. Springer Proceedings in Mathematics and Statistics, vol. 79, pp. 83–101. Springer, Cham (2014)
Kollár, J., Smith, K.E., Corti, A.: Rational and Nearly Rational Varieties. Cambridge Studies in Advanced Mathematics, vol. 92. Cambridge University Press, Cambridge (2004)
Kuwata, T.: On log canonical thresholds of reducible plane curves. Amer. J. Math. 121(4), 701–721 (1999)
Shokurov, V.V.: Three-dimensional log perestroikas. Russian Acad. Sci. Izv. Math. 40(1), 95–202 (1993)
Acknowledgements
The author would like to thank Erik Paemurru for his valuable comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Viswanathan, N. Lowest log canonical thresholds of a reduced plane curve of degree d. European Journal of Mathematics 6, 1216–1235 (2020). https://doi.org/10.1007/s40879-019-00374-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-019-00374-z








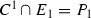 ,
,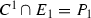 ,
,
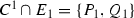 ,
,
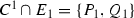 ,
,
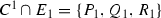 ,
,
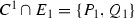 ,
, ,
,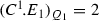 and is smooth at this point (Fig.
and is smooth at this point (Fig. 
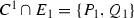 ,
,
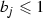 for every
for every 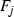 such that
such that 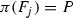 .
.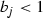 for every
for every 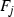 such that
such that  .
.