Abstract
It is known that the moduli space of smooth Fano–Mukai fourfolds \(V_{18}\) of genus 10 has dimension one. We show that any such fourfold is a completion of \({\mathbb {C}}^4\) in two different ways. Up to isomorphism, there is a unique fourfold \(V_{18}^{{\mathrm {s}}}\) acted upon by \({\mathrm{SL}}_2({\mathbb {C}})\). The group  is a semidirect product
is a semidirect product  . Furthermore, \(V_{18}^{{\mathrm {s}}}\) is a \({\mathrm{GL}}_2({\mathbb {C}})\)-equivariant completion of \({\mathbb {C}}^4\), and as well of \({\mathrm{GL}}_2({\mathbb {C}})\). The restriction of the \({\mathrm{GL}}_2({\mathbb {C}})\)-action on \(V_{18}^{{\mathrm {s}}}\) to
. Furthermore, \(V_{18}^{{\mathrm {s}}}\) is a \({\mathrm{GL}}_2({\mathbb {C}})\)-equivariant completion of \({\mathbb {C}}^4\), and as well of \({\mathrm{GL}}_2({\mathbb {C}})\). The restriction of the \({\mathrm{GL}}_2({\mathbb {C}})\)-action on \(V_{18}^{{\mathrm {s}}}\) to  yields a faithful representation with an open orbit. There is also a unique, up to isomorphism, fourfold \(V_{18}^{\mathrm a}\) such that the group
yields a faithful representation with an open orbit. There is also a unique, up to isomorphism, fourfold \(V_{18}^{\mathrm a}\) such that the group  is a semidirect product
is a semidirect product  . For a Fano–Mukai fourfold \(V_{18}\) isomorphic neither to \(V_{18}^{{\mathrm {s}}}\), nor to \(V_{18}^{\mathrm a}\), the group
. For a Fano–Mukai fourfold \(V_{18}\) isomorphic neither to \(V_{18}^{{\mathrm {s}}}\), nor to \(V_{18}^{\mathrm a}\), the group  is a semidirect product of \(({{\mathbb {G}}}_{\mathrm {m}})^2\) and a finite cyclic group whose order is a factor of 6. Besides, we establish that the affine cone over any polarized Fano–Mukai variety \(V_{18}\) is flexible in codimension one, and flexible if \(V_{18}=V_{18}^{{\mathrm {s}}}\).
is a semidirect product of \(({{\mathbb {G}}}_{\mathrm {m}})^2\) and a finite cyclic group whose order is a factor of 6. Besides, we establish that the affine cone over any polarized Fano–Mukai variety \(V_{18}\) is flexible in codimension one, and flexible if \(V_{18}=V_{18}^{{\mathrm {s}}}\).

Similar content being viewed by others
Notes
Cf. Lemma 5.4.
Such cones are the only cubic cones in V, see 4.5. Hence in the sequel we call them simply cubic cones. We will show that any smooth variety \(V_{18}\) contains a cubis scroll or a cubic cone.
In [41, Corollary 5.13] we constructed a pair (V, S) such that \(S\in {\mathscr {S}}(V)\) is a smooth cubic scroll.
In fact, \(s_t\) is the exceptional section of a surface \(\widetilde{S}_t\cong \mathbb {F}_3\) in \({{\mathscr {L}}}(V)\). The restriction \(s|_{\widetilde{S}_t}:\widetilde{S}_t\rightarrow S_t\) is the minimal resolution of singularity of the cubic cone \(S_t\).
The cubic cones \(S\subset V\) such that \((\Upsilon ,J_S)\) is of type 4.3 (ii) correspond actually to the two outer \((-1)\)-vertices in diagram (10.1.1). The two inner \((-1)\)-vertices in (10.1.1) correspond to the cubic cones \(S\subset V\) with \((\Upsilon ,J_S)\) of type 4.3 (iii); see Remark 13.3.2.
Alternatively, one can notice that the cones \(S_1\) and \(S_2\) correspond to the disjoint exceptional sections of the components \(\mathscr {F}_1\) and \(\mathscr {F}_2\) of \(\Sigma _{\mathrm {s}}(V)\). It follows that \(S_1\cap S_2\) is zero-dimensional, hence empty since
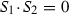 in \(H^*(V,\mathbb {Z})\), see Proposition 9.6 and Corollary 9.7.4.
in \(H^*(V,\mathbb {Z})\), see Proposition 9.6 and Corollary 9.7.4.
References
Akhiezer, D.N.: Lie Group Actions in Complex Analysis. Aspects of Mathematics, vol. E27. Friedr. Vieweg & Sohn, Braunschweig (1995)
Andreatta, M., Wiśniewski, J.A.: On contractions of smooth varieties. J. Algebraic Geom. 7(2), 253–312 (1998)
Arzhantsev, I., Flenner, H., Kaliman, S., Kutzschebauch, F., Zaidenberg, M.: Flexible varieties and automorphism groups. Duke Math. J. 162(4), 767–823 (2013)
Bourbaki, N.: Lie Groups and Lie Algebras. Chapters 4–6. Elements of Mathematics (Berlin). Springer, Berlin (2002) (Translated from the 1968 French original by Andrew Pressley)
Chriss, N., Ginzburg, V.: Representation Theory and Complex Geometry. Modern Birkhäuser Classics. Birkhäuser, Boston (2010) (Reprint of the 1997 edn.)
Collingwood, D.H., McGovern, W.M.: Nilpotent Orbits in Semisimple Lie Algebras. Van Nostrand Reinhold Mathematics Series. Van Nostrand Reinhold, New York (1993)
Coray, D.F., Tsfasman, M.A.: Arithmetic on singular Del Pezzo surfaces. Proc. London Math. Soc. (3) 57(1), 25–87 (1988)
Demazure, M.: Automorphismes et déformations des variétés de Borel. Invent. Math. 39(2), 179–186 (1977)
Dolgachev, I.V.: Classical Algebraic Geometry. Cambridge University Press, Cambridge (2012)
Eisenbud, D., Harris, J.: On varieties of minimal degree (A centennial account). In: Bloch, S.J. (ed.) Algebraic Geometry, Bowdoin, 1985. Proceedings of the Symposium Pure Mathematics, vol. 46.1, pp. 3–13. American Mathematical Society, Providence (1987)
Eisenbud, D., Van de Ven, A.: On the normal bundles of smooth rational space curves. Math. Ann. 256(4), 453–463 (1981)
Ekedahl, T., Laksov, D.: Two “generic” proofs of the spectral mapping theorem. Amer. Math. Monthly 111(7), 572–585 (2004)
Fu, B., Hwang, J.-M.: Isotrivial VMRT-structures of complete intersection type. Asian J. Math., special issue dedicated to Ngaiming Mok’s 60th birthday (2016, to appear). arXiv:1608.00846
Fujita, T.: On the structure of polarized manifolds with total deficiency one. II. J. Math. Soc. Japan 33(3), 415–434 (1981)
Furushima, M.: Complex analytic compactifications of \(\mathbf{C}^3\). Compositio Math. 76(1–2), 163–196 (1990)
Furushima, M.: The complete classification of compactifications of \(\mathbf{C}^3\) which are projective manifolds with the second Betti number one. Math. Ann. 297(4), 627–662 (1993)
Griffiths, Ph., Harris, J.: Principles of Algebraic Geometry. Wiley, New York (1994) (Reprint of the 1978 original)
Hirzebruch, F.: Some problems on differentiable and complex manifolds. Ann. Math. 60, 213–236 (1954)
Hochschild, G.: Introduction to Affine Algebraic Groups. Holden-Day, San Francisco (1971)
Humphreys, J.E.: Linear Algebraic Groups. Graduate Texts in Mathematics, vol. 21. Springer, New York (1975)
Hwang, J.-M., Mok, N.: Deformation rigidity of the rational homogeneous space associated to a long simple root. Ann. Sci. Éc. Norm. Supér. (4) 35(2), 173–184 (2002)
Iskovskikh, V.A.: Fano threefolds. I. Izv. Ross. Akad. Nauk SSSR Ser. Mat. 41(3), 516–562 (1977) (in Russian)
Iskovskikh, V.A., Prokhorov, Yu.G.: Fano Varieties. In: Parshin, A.N., Shafarevich, I.R. (eds.) Algebraic Geometry V. Encyclopaedia of Mathematical Sciences, vol. 47. Springer, Berlin (1999)
Kapustka, M., Ranestad, K.: Vector bundles on Fano varieties of genus ten. Math. Ann. 356(2), 439–467 (2013)
Kishimoto, T., Prokhorov, Yu., Zaidenberg, M.: \(\mathbb{G}_{{\rm a}}\)-actions on affine cones. Transform. Groups 18(4), 1137–1153 (2013)
Kodaira, K.: Holomorphic mappings of polydiscs into compact complex manifolds. J. Differential Geom. 6, 33–46 (1971/72)
Kurtzke Jr., J.F.: Centralizers of irregular elements in reductive algebraic groups. Pacific J. Math. 104(1), 133–154 (1983)
Kuznetsov, A.G., Prokhorov, YuG, Shramov, C.A.: Hilbert schemes of lines and conics and automorphism groups of Fano threefolds. Japan J. Math. 13(1), 109–185 (2018)
Landsberg, J.M., Manivel, L.: On the projective geometry of rational homogeneous varieties. Comment. Math. Helv. 78(1), 65–100 (2003)
Matsushima, Y.: Sur la structure du groupe d’homéomorphismes analytiques d’une certaine variété kählérienne. Nagoya Math. J. 11, 145–150 (1957)
Michałek, M., Perepechko, A., Süss, H.: Flexible affine cones and flexible coverings. Math. Z. (2016, to appear). arXiv:1612.01144v1
Mostow, G.D.: Fully reducible subgroups of algebraic groups. Amer. J. Math. 78, 200–221 (1956)
Mukai, Sh.: Curves, \(K3\) surfaces and Fano \(3\)-folds of genus \(\leqslant 10\). In: Hijikata, H., et al. (eds.) Algebraic Geometry and Commutative Algebra, vol. I, pp. 357–377. Kinokuniya, Tokyo (1988)
Mukai, Sh.: Biregular classification of Fano \(3\)-folds and Fano manifolds of coindex \(3\). Proc. Nat. Acad. Sci. USA 86(9), 3000–3002 (1989)
Peternell, T., Schneider, M.: Compactifications of \(\mathbf{C}^3\). I. Math. Ann. 280(1), 129–146 (1988)
Piontkowski, J., Van de Ven, A.: The automorphism group of linear sections of the Grassmannians \({\mathbb{G}} (1, N)\). Doc. Math. 4, 623–664 (1999)
Prokhorov, YuG: Fano threefolds of genus \(12\) and compactifications of \(\mathbb{C}^3\). St. Petersburg Math. J. 3(4), 855–864 (1992)
Prokhorov, YuG: Compactifications of \(\mathbf{C}^4\) of index \(3\). In: Tikhomirov, A., Tyurin, A. (eds.) Algebraic Geometry and its Applications (Yaroslavl, 1992). Aspects of Mathematics, vol. E25, pp. 159–169. Vieweg, Braunschweig (1994)
Prokhorov, YuG: On \(G\)-Fano threefolds. Izv. Math. 79(4), 795–808 (2015)
Prokhorov, YuG: Singular Fano threefolds of genus \(12\). Sb. Math. 207(7), 983–1009 (2016)
Prokhorov, Yu., Zaidenberg, M.: New examples of cylindrical Fano fourfolds. In: Masuda, K., et al. (eds.) Algebraic Varieties and Automorphism Groups. Advanced Studies in Pure Mathematics, vol. 75, pp. 443–464. Mathematical Society of Japan, Tokyo (2017)
Prokhorov, Yu., Zaidenberg, M.: Examples of cylindrical Fano fourfolds. Eur. J. Math. 2(1), 262–282 (2016)
Shokurov, V.V.: The existence of a straight line on Fano \(3\)-folds. Math. USSR-Izv. 15(1), 173–209 (1980)
Springer, T.A., Steinberg, R.: Conjugacy classes. Seminar on Algebraic Groups and Related Finite Groups. Lecture Notes in Mathematics, vol. 131, pp. 167–266. Springer, Berlin (1970)
Steinberg, R.: Regular elements of semisimple algebraic groups. Publ. Math. Inst. Hautes Études Sci. 25, 49–80 (1965)
Tevelev, E.A.: Projective Duality and Homogeneous Spaces. Encyclopaedia of Mathematical Sciences, vol. 133. Springer, Berlin (2005)
Tian, G.: Kähler-Einstein metrics on Fano manifolds. Japan J. Math. 10(1), 1–41 (2015)
Todd, J.A.: The locus representing the lines of four-dimensional space and its application to linear complexes in four dimensions. Proc. London Math. Soc. S2–30, 513–550 (1930)
Zaidenberg, M.G.: An analytic cancellation theorem and exotic algebraic structures on \(\mathbb{C}^n\), \(n\geqslant 3\). Colloque d’analyse complexe et géométrie. Astérisque 217(8), 251–282 (1993)
Acknowledgements
The paper started during the first author’s stay at the Institute Fourier, Grenoble, in June of 2016. He thanks the institute for its hospitality. The authors are grateful to Alexander Kuznetsov for useful discussions, to Michel Brion, Jun-Muk Hwang, and Laurent Manivel for important remarks around the material of Sect. 7, and to Ivan Arzhantsev and Alexander Perepechko for a pertinent remark concerning the material of Sect. 14. Our thanks are due also to the referee for his remarks improving the style of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Yuri Prokhorov was partially supported by the RFBR Grants 15-01-02164, 15-01-02158, and by the Russian Academic Excellence Project ‘5-100’.
Rights and permissions
About this article
Cite this article
Prokhorov, Y., Zaidenberg, M. Fano–Mukai fourfolds of genus 10 as compactifications of \({\mathbb {C}}^4\) . European Journal of Mathematics 4, 1197–1263 (2018). https://doi.org/10.1007/s40879-018-0244-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-018-0244-y
Keywords
- Fano variety
- Fourfold
- Compactification of \({\mathbb {C}}^n\)
- Sarkisov link
- Group action
- Automorphism group
- Affine cone



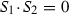 in
in