Abstract
We present some motivations and discuss various aspects of an approach to the Jacobian Conjecture in terms of irreducible elements and square-free elements.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Jacobian Conjecture is one of the most important open problems stimulating modern mathematical research [29]. Its long history is full of equivalent formulations and wrong proofs. In this article we give a survey of a new purely algebraic approach to the Jacobian Conjecture in terms of irreducible elements and square-free elements, based mainly on: the authors’ paper [20], de Bondt and Yan’s paper [7], authors’ paper [23], and the joint paper with Matysiak [22].
Let k be a field of characteristic zero. By  we denote the k-algebra of polynomials in n variables. Given polynomials
we denote the k-algebra of polynomials in n variables. Given polynomials  , by
, by  we denote their Jacobian determinant:
we denote their Jacobian determinant:

The Jacobian Conjecture was stated by Keller in 1939 for polynomials with integer coefficients [26]. For arbitrary field k of characteristic zero it asserts the following:
If polynomials
satisfy the Jacobian condition
, then
.
It is known [9] that formulations of the Jacobian Conjecture for various fields of characteristic zero (as well as for \({\mathbb {Z}}\)) are equivalent to each other. The conjecture can be expressed in terms of k-endomorphisms of the polynomial ring  :
:
If a k-endomorphism \(\varphi \) of
satisfies the Jacobian condition
, then it is an automorphism.
For more information on the Jacobian Conjecture we refer the reader to the van den Essen’s book [11].
A primary motivation of our approach can be found in a question of van den Essen and Shpilrain from 1997 [13, Problem 1], whether if a k-endomorphism of  over a field k of characteristic zero maps variables to variables, then it is an automorphism. A polynomial \(f\in k\) is called a variable if there exist polynomials
over a field k of characteristic zero maps variables to variables, then it is an automorphism. A polynomial \(f\in k\) is called a variable if there exist polynomials  such that
such that  . A positive solution of this problem was obtained by Jelonek [24, 25]. In 2006, Bakalarski proved an analogous fact for irreducible polynomials over \(\mathbb {C}\) ([5, Theorem 3.7], see also [1]). Namely, he proved that a complex polynomial endomorphism is an automorphism if and only if it maps irreducible polynomials to irreducible polynomials. One of the authors in 2013 obtained a characterization of k-endomorphisms of
. A positive solution of this problem was obtained by Jelonek [24, 25]. In 2006, Bakalarski proved an analogous fact for irreducible polynomials over \(\mathbb {C}\) ([5, Theorem 3.7], see also [1]). Namely, he proved that a complex polynomial endomorphism is an automorphism if and only if it maps irreducible polynomials to irreducible polynomials. One of the authors in 2013 obtained a characterization of k-endomorphisms of  satisfying the Jacobian condition as those mapping irreducible polynomials to square-free polynomials [20, Theorem 5.1]. This fact has been further generalized by de Bondt and Yan: they proved that mapping square-free polynomials to square-free ones is also equivalent to the Jacobian condition [7, Corollary 2.2].
satisfying the Jacobian condition as those mapping irreducible polynomials to square-free polynomials [20, Theorem 5.1]. This fact has been further generalized by de Bondt and Yan: they proved that mapping square-free polynomials to square-free ones is also equivalent to the Jacobian condition [7, Corollary 2.2].
We present our generalization of the Jacobian Conjecture for r polynomials  , where k is a field of characteristic zero and \(r\leqslant n\): if all jacobians (with respect to r variables) are relatively prime, then
, where k is a field of characteristic zero and \(r\leqslant n\): if all jacobians (with respect to r variables) are relatively prime, then  is algebraically closed in
is algebraically closed in  [23]. Next we present equivalent versions of this generalized Jacobian condition in terms of the mentioned k-subalgebra: all irreducible (resp. square-free) elements of
[23]. Next we present equivalent versions of this generalized Jacobian condition in terms of the mentioned k-subalgebra: all irreducible (resp. square-free) elements of  are square-free in
are square-free in  [23, Theorem 2.4]. Recall that an element \(a\in R\) is called square-free if it cannot be presented in the form \(a=b^2c\), where \(b,c\in R\) and b is non-invertible. It is reasonable to consider such properties in a general case, e.g. for subrings of unique factorization domains. In this case the property that square-free elements of a subring are square-free in the whole ring can be expressed in some factorial form [23, Theorem 3.4]. At the end we discuss possible directions of future research.
[23, Theorem 2.4]. Recall that an element \(a\in R\) is called square-free if it cannot be presented in the form \(a=b^2c\), where \(b,c\in R\) and b is non-invertible. It is reasonable to consider such properties in a general case, e.g. for subrings of unique factorization domains. In this case the property that square-free elements of a subring are square-free in the whole ring can be expressed in some factorial form [23, Theorem 3.4]. At the end we discuss possible directions of future research.
2 Freudenburg’s Lemma and its generalizations
A motivation for the main preparatory fact (Theorem 2.4) comes from generalizations of the following lemma of Freudenburg from [14].
Theorem 2.1
(Freudenburg’s Lemma) Given a polynomial  , let
, let  be an irreducible non-constant common factor of \({\partial f}/{\partial x}\) and \({\partial f}/{\partial y}\). Then there exists \(c\in \mathbb {C}\) such that g divides \(f+c\).
be an irreducible non-constant common factor of \({\partial f}/{\partial x}\) and \({\partial f}/{\partial y}\). Then there exists \(c\in \mathbb {C}\) such that g divides \(f+c\).
The assertion of the above statement can be strengthened in a way that if g is irreducible, then

Freudenburg needed this result to prove that if a polynomial of the form w(u, v), where u and v are variables, belongs to the ring of constants of some locally nilpotent derivation of the algebra  , then a variable also belongs to this ring. Van den Essen, Nowicki and Tyc obtained the following generalization of Freudenburg’s Lemma [12, Proposition 2.1].
, then a variable also belongs to this ring. Van den Essen, Nowicki and Tyc obtained the following generalization of Freudenburg’s Lemma [12, Proposition 2.1].
Theorem 2.2
(van den Essen, Nowicki, Tyc) Let k be an algebraically closed field of characteristic zero. Let Q be a prime ideal of the ring  and
and  . If for each i the partial derivative \({\partial f}/{\partial x_i}\) belongs to Q, then there exists \(c\in k\) such that \(f-c\in Q\).
. If for each i the partial derivative \({\partial f}/{\partial x_i}\) belongs to Q, then there exists \(c\in k\) such that \(f-c\in Q\).
They noted [12, Remark 2.4] that the assumption “k is algebraically closed” cannot be dropped: for \(f=x^3+3x\) and \(Q=(g)\), where \(g=x^2+1\), in  we have
we have  , but
, but  for any \(c\in {\mathbb {R}}\). The idea of a generalization (in [18]) to arbitrary field k of characteristic zero was to consider, instead of \(f-c\), a polynomial w(f), where w(T) is irreducible. In the mentioned example \(w(T)=T^2+4\) since
for any \(c\in {\mathbb {R}}\). The idea of a generalization (in [18]) to arbitrary field k of characteristic zero was to consider, instead of \(f-c\), a polynomial w(f), where w(T) is irreducible. In the mentioned example \(w(T)=T^2+4\) since  . In fact, Freudenburg’s Lemma was generalized to the case when the coefficient ring is a UFD of arbitrary characteristic.
. In fact, Freudenburg’s Lemma was generalized to the case when the coefficient ring is a UFD of arbitrary characteristic.
Theorem 2.3
([18, Theorem 3.1]) Let K be a unique factorization domain, let Q be a prime ideal of  . Consider a polynomial
. Consider a polynomial  such that \({\partial f}/{\partial x_i}\in Q\) for \(i=1,\ldots ,n\).
such that \({\partial f}/{\partial x_i}\in Q\) for \(i=1,\ldots ,n\).
-
(a)
If \(\mathrm{char\,}K=0\), then there exists an irreducible polynomial
 such that \(w(f)\in Q\).
such that \(w(f)\in Q\). -
(b)
If \(\mathrm{char\,}K=p>0\), then there exist
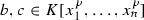 such that
such that  , \(b\not \in Q\) and \(bf+c\in Q\).
, \(b\not \in Q\) and \(bf+c\in Q\).
As a consequence we obtain (see [18, Proposition 3.3]) that if k is an arbitrary field of characteristic zero,  and g is irreducible, then
and g is irreducible, then

A generalization of Freudenburg’s Lemma to an arbitrary number of polynomials over a field of characteristic zero was obtained in [23]. Denote by  the Jacobian determinant of the polynomials \(f_1,\dots ,f_r\) with respect to
the Jacobian determinant of the polynomials \(f_1,\dots ,f_r\) with respect to  .
.
Theorem 2.4
([23, Theorem 2.3]) Let k be a field of characteristic zero, let \(f_1,\ldots \),  , \(\ldots ,x_n]\) be arbitrary polynomials, where
, \(\ldots ,x_n]\) be arbitrary polynomials, where  , and let
, and let  be an irreducible polynomial. The following conditions are equivalent:
be an irreducible polynomial. The following conditions are equivalent:
-
(i)
 for every
for every  ,
, -
(ii)
 for some irreducible polynomial
for some irreducible polynomial  ,
, -
(iii)
 for some square-free polynomial
for some square-free polynomial  .
.
The proof is based on the methods of proofs of earlier special cases: [20, Theorem 4.1] and de Bondt and Yan’s [7, Theorem 2.1].
Note also that a positive characteristic analog of Freudenburg’s Lemma for r polynomials in n variables was obtained in [21]. It was connected with a characterization of p-bases of rings of constants with respect to polynomial derivations.
3 A characterization of Keller maps
In this section we present the main result of [20] and its substantial extension by de Bondt and Yan from [7]. Note the following consequence of Theorem 2.4 in the case \(r=n\).
Theorem 3.1
([20, Corollary 4.2], [7, Corollary 2.2]) Let k be a field of characteristic zero. For arbitrary polynomials  the following conditions are equivalent:
the following conditions are equivalent:
-
(i)
 ,
, -
(ii)
the polynomial \(w(f_1,\dots ,f_n)\) is square-free for every irreducible polynomial
 ,
, -
(iii)
the polynomial \(w(f_1,\dots ,f_n)\) is square-free for every square-free polynomial
 .
.
The above equivalence can be expressed as a characterization of endomorphisms satisfying the Jacobian condition analogous to the characterization of automorphisms from Bakalarski’s theorem [5, Theorem 3.7].
Theorem 3.2
([20, Theorem 5.1], [7, Corollary 2.2]) Let k be a field of characteristic zero. Let \(\varphi \) be a k-endomorphism of the algebra of polynomials  . The following conditions are equivalent:
. The following conditions are equivalent:
-
(i)
 ,
, -
(ii)
for every irreducible polynomial
 the polynomial \(\varphi (w)\) is square-free,
the polynomial \(\varphi (w)\) is square-free, -
(iii)
for every square-free polynomial
 the polynomial \(\varphi (w)\) is square-free.
the polynomial \(\varphi (w)\) is square-free.
In this way we obtain a new equivalent formulation of the Jacobian Conjecture for an arbitrary field k of characteristic zero:
Every k-endomorphism of
mapping square-free polynomials to square-free polynomials is an automorphism.
There is a natural question if there exists a non-trivial example of an endomorphism satisfying condition (ii) such that \(\varphi (w)\) is reducible for some irreducible w. An affirmative answer to this question is equivalent to the negation of the Jacobian Conjecture [20, Section 6, Remark 1].
4 A generalization of the Jacobian Conjecture
In [23], we generalized the Jacobian Conjecture in the following way (recall that  denotes the Jacobian determinant of the polynomials \(f_1,\ldots ,f_r\) with respect to
denotes the Jacobian determinant of the polynomials \(f_1,\ldots ,f_r\) with respect to  ).
).
Conjecture
 For arbitrary polynomials
For arbitrary polynomials  , with k a field of characteristic zero and
, with k a field of characteristic zero and  , if
, if

then  is algebraically closed in
is algebraically closed in  .
.
Recall that by Nowicki’s characterization the above assertion means that R is a ring of constants of some k-derivation of  (see [28, Theorem 5.4], [27, Theorem 4.1.4], [10, 1.4]).
(see [28, Theorem 5.4], [27, Theorem 4.1.4], [10, 1.4]).
We have:
-
 implies the ordinary Jacobian Conjecture for r polynomials in r variables over k [23, Lemma 1.1],
implies the ordinary Jacobian Conjecture for r polynomials in r variables over k [23, Lemma 1.1], -
 is true ([4, Proposition 14], see also [17, a remark before Proposition 4.2]),
is true ([4, Proposition 14], see also [17, a remark before Proposition 4.2]), -
the reverse implication in
 need not to be true if \(r<n\), we may take for example \(f_1=x_1^2x_2\), \(f_2=x_3\), \(\dots \), \(f_r=x_{r+1}\) [23, Remark 1.2].
need not to be true if \(r<n\), we may take for example \(f_1=x_1^2x_2\), \(f_2=x_3\), \(\dots \), \(f_r=x_{r+1}\) [23, Remark 1.2].
5 Analogs of Jacobian conditions for subrings
In this section we present equivalent versions of the generalized Jacobian condition from Conjecture  in terms of irreducible elements as well as square-free elements. It is useful to introduce (following [19]) the notion of a “differential gcd” for r polynomials
in terms of irreducible elements as well as square-free elements. It is useful to introduce (following [19]) the notion of a “differential gcd” for r polynomials  , where
, where  :
:

The next theorem is a consequence of Theorem 2.4.
Theorem 5.1
Let k be a field of characteristic zero. Assume that polynomials  are algebraically independent over k. Then the following conditions are equivalent:
are algebraically independent over k. Then the following conditions are equivalent:
-
(i)
 ,
, -
(ii)
for every irreducible polynomial
 the polynomial \(w(f_1,\dots ,f_r)\) is square-free,
the polynomial \(w(f_1,\dots ,f_r)\) is square-free, -
(iii)
for every square-free polynomial
 the polynomial \(w(f_1,\dots ,f_r)\) is square-free.
the polynomial \(w(f_1,\dots ,f_r)\) is square-free.
Note that under the assumptions of the above theorem, a polynomial  is irreducible (square-free) if and only if \(w(f_1,\ldots ,f_r)\) is an irreducible (square-free) element of
is irreducible (square-free) if and only if \(w(f_1,\ldots ,f_r)\) is an irreducible (square-free) element of  . This allows us to express the above conditions in terms of the sets of irreducible elements (\(\mathrm{Irr\,}\)) and square-free elements (\(\mathrm{Sqf\,}\)) of the respective rings.
. This allows us to express the above conditions in terms of the sets of irreducible elements (\(\mathrm{Irr\,}\)) and square-free elements (\(\mathrm{Sqf\,}\)) of the respective rings.
Theorem 5.2
([23, Theorem 2.4]) Let  , where k is a field of characteristic zero. Assume that \(f_1,\ldots ,f_r\in A\) are algebraically independent over k. Put
, where k is a field of characteristic zero. Assume that \(f_1,\ldots ,f_r\in A\) are algebraically independent over k. Put  . Then the following conditions are equivalent:
. Then the following conditions are equivalent:
-
(i)
 ,
, -
(ii)
\(\mathrm{Irr\,}R\subset \mathrm{Sqf\,}A\),
-
(iii)
\(\mathrm{Sqf\,}R\subset \mathrm{Sqf\,}A\).
Therefore we may consider conditions (ii) and (iii) in a general case, when A is a domain (a commutative ring with unity without zero divisors) and R is a subring of A, and we may call them analogs of the Jacobian condition (i). Conjecture \(\text {JC}(r,n,k)\) motivated us to state the following question [23, Section 3].
A general question
Let R be a subring of a domain A such that
Under what conditions is R algebraically closed in A?
In particular, the ordinary Jacobian Conjecture for \(r=n\),  , where \(\mathrm{char\,}k=0\), asserts that if \(f_1,\dots ,f_n\in A\) are algebraically independent over k,
, where \(\mathrm{char\,}k=0\), asserts that if \(f_1,\dots ,f_n\in A\) are algebraically independent over k,  and \(\mathrm{Sqf\,}R\subset \mathrm{Sqf\,}A\), then \(R=A\).
and \(\mathrm{Sqf\,}R\subset \mathrm{Sqf\,}A\), then \(R=A\).
In order to understand a more general context of the conditions \(\mathrm{Irr\,}R\subset \mathrm{Sqf\,}A\) and \(\mathrm{Sqf\,}R\subset \mathrm{Sqf\,}A\), when R is a subring of a domain A, we can inscribe them into the following diagram of implications [22, Proposition 3.3].

By \(\mathrm{Prime\,}R\) we have denoted the set of all prime elements of R, by \(\mathrm{Gpr\,}R\) the set of (single) generators of principal radical ideals of R, and by \(\mathrm{Rdl\,}R\) (following [6, p. 67]) the set of radical ideals of R.
6 Factorial properties
Now we discuss factorial properties connected with inclusions \(\mathrm{Irr\,}R\subset \mathrm{Irr\,}A\) and \(\mathrm{Sqf\,}R\subset \mathrm{Sqf\,}A\), where R is a subring of a unique factorization domain A.
Recall that a subring R of a domain A such that for every \(x,y\in A\):

is called factorially closed. Rings of constants of locally nilpotent derivations in domains of characteristic zero are factorially closed (see [10, 15] for details). Note that according only to the multiplicative structure, a submonoid of a (commutative cancellative) monoid satisfying the above condition is called divisor-closed [16]. Denote by \(R^{*}\) the set of all invertible elements of a ring R. It is well known that a subring R of a unique factorization domain A such that  is factorially closed in A if and only if \(\mathrm{Irr\,}R\subset \mathrm{Irr\,}A\) (see [23, Lemma 3.2]).
is factorially closed in A if and only if \(\mathrm{Irr\,}R\subset \mathrm{Irr\,}A\) (see [23, Lemma 3.2]).
Under natural assumptions we can express also the condition \(\mathrm{Sqf\,}R\subset \mathrm{Sqf\,}A\) in a form of factoriality. If R is a domain, by \(R_0\) we denote its field of fractions.
Theorem 6.1
([23, Theorem 3.4]) Let A be a unique factorization domain. Let R be a subring of A such that  and \(R_0\cap A=R\). The following conditions are equivalent:
and \(R_0\cap A=R\). The following conditions are equivalent:
-
(i)
\(\mathrm{Sqf\,}R\subset \mathrm{Sqf\,}A\),
-
(ii)
for every \(x\in A\), \(y\in \mathrm{Sqf\,}A\), if
 , then \(x,y\in R\).
, then \(x,y\in R\).
If A is a UFD, then a subring R of A that fulfills condition (ii) of Theorem 6.1 we will call square-factorially closed in A. Condition (ii) has an advantage over condition (i) since it does not involve square-free elements of R. For example, one can define the square-factorial closure of a subring R in A as an intersection of all square-factorially closed subrings of A containing R.
There arise two questions concerning the condition \(\mathrm{Irr\,}R\subset \mathrm{Sqf\,}A\) in the case when A is a UFD. Firstly, is it equivalent to \(\mathrm{Sqf\,}R\subset \mathrm{Sqf\,}A\) under some natural assumptions (like  )? If such equivalence does not hold in general, can the condition \(\mathrm{Irr\,}R\subset \mathrm{Sqf\,}A\) be expressed in a form of factoriality, similarly to the above theorem?
)? If such equivalence does not hold in general, can the condition \(\mathrm{Irr\,}R\subset \mathrm{Sqf\,}A\) be expressed in a form of factoriality, similarly to the above theorem?
The notion of square-factorial closedness is relevant to the thoroughly studied notion of root closedness. Recall that a subring R of a ring A is called root closed in A if the following implication:

holds for every \(x\in A\) and \(n\geqslant 1\).
Theorem 6.2
([23, Theorem 3.6]) Let A be a unique factorization domain. Let R be a subring of A such that  and \(R_0\cap A=R\). If R is square-factorially closed in A, then R is root closed in A.
and \(R_0\cap A=R\). If R is square-factorially closed in A, then R is root closed in A.
An interesting task would be to investigate whether square-factorial closedness is stable under various operations and extensions. Such kind of results were obtained for example for root closedness (see [2, 3, 8, 30]). The latter is stable for instance under homogeneous grading and under passages to polynomial extension, to power series extension, to rational functions extension, to semigroup ring  , where \({\Gamma }\) is torsionless grading monoid. If for square-factorial closedness some property would not be valid in general, then under what additional assumptions it will? For example, stability of root closure under passage to power series extension is acquired by imposing the assumption that a subring R is von Neumann regular (see [30]) or
, where \({\Gamma }\) is torsionless grading monoid. If for square-factorial closedness some property would not be valid in general, then under what additional assumptions it will? For example, stability of root closure under passage to power series extension is acquired by imposing the assumption that a subring R is von Neumann regular (see [30]) or  (see [3]) as in Theorem 6.2. Another prospect for further research is to obtain relationships (similarly to Theorem 6.2) of square-factorial closedness with other notions, such as seminormality.
(see [3]) as in Theorem 6.2. Another prospect for further research is to obtain relationships (similarly to Theorem 6.2) of square-factorial closedness with other notions, such as seminormality.
References
Adjamagbo, K.: On isomorphisms of factorial domains and the Jacobian conjecture in any characteristic (2006). arXiv:math/0608008
Anderson, D.F.: Root closure in integral domains. J. Algebra 79(1), 51–59 (1982)
Angermüller, G.: Root closure. J. Algebra 90(1), 189–197 (1984)
Ayad, M.: Sur les polynômes \(f(X, Y)\) tels que \(K[f]\) est intégralement fermé dans \(K[X, Y]\). Acta Arith. 105(1), 9–28 (2002)
Bakalarski, S.: Jacobian problem for factorial varieties. Univ. Iagel. Acta Math. 44, 31–34 (2006)
Belluce, L.P., Di Nola, A., Ferraioli, A.R.: Ideals of MV-semirings and MV-algebras. In: Litvinov, G.L., Sergeev, S.N. (eds.) Tropical and Idempotent Mathematics and Applications. Contemporary Mathematics, vol. 616, pp. 59–75. American Mathematical Society, Providence (2014)
de Bondt, M., Yan, D.: Irreducibility properties of Keller maps. Algebra Colloq. 23(4), 663–680 (2016)
Brewer, J.W., Costa, D.L., McCrimmon, K.: Seminormality and root closure in polynomial rings and algebraic curves. J. Algebra 58(1), 217–226 (1979)
Connell, E., van den Dries, L.: Injective polynomial maps and the Jacobian Conjecture. J. Pure Appl. Algebra 28(3), 235–239 (1983)
Daigle, D.: Locally nilpotent derivations. Lecture Notes for the “September School of Algebraic Geometry” , Łukęcin, Poland, September 2003. http://aix1.uottawa.ca/~ddaigle/Lukecin03/LukecinDaigle.pdf
van den Essen, A.: Polynomial Automorphisms and the Jacobian Conjecture. Progress in Mathematics, vol. 190. Birkhäuser, Basel (2000)
van den Essen, A., Nowicki, A., Tyc, A.: Generalizations of a lemma of Freudenburg. J. Pure Appl. Algebra 177(1), 43–47 (2003)
van den Essen, A., Shpilrain, V.: Some combinatorial questions about polynomial mappings. J. Pure Appl. Algebra 119(1), 47–52 (1997)
Freudenburg, G.: A note on the kernel of a locally nilpotent derivation. Proc. Amer. Math. Soc. 124(1), 27–29 (1996)
Freudenburg, G.: Algebraic Theory of Locally Nilpotent Derivations. Encyclopaedia of Mathematical Sciences, vol. 136. Springer, Berlin (2006)
Geroldinger, A., Halter-Koch, F.: Non-unique Factorizations. Pure and Applied Mathematics, vol. 278. Chapman & Hall/CRC, Boca Raton (2006)
Jędrzejewicz, P.: Positive characteristic analogs of closed polynomials. Cent. Eur. J. Math. 9(1), 50–56 (2011)
Jędrzejewicz, P.: A characterization of one-element \(p\)-bases of rings of constants. Bull. Pol. Acad. Sci. Math. 59(1), 19–26 (2011)
Jędrzejewicz, P.: Jacobian conditions for \(p\)-bases. Comm. Algebra 40(8), 2841–2852 (2012)
Jędrzejewicz, P.: A characterization of Keller maps. J. Pure Appl. Algebra 217(1), 165–171 (2013)
Jędrzejewicz, P.: A characterization of \(p\)-bases of rings of constants. Cent. Eur. J. Math. 11(5), 900–909 (2013)
Jędrzejewicz, P., Matysiak, Ł., Zieliński, J.: On some factorial properties of subrings. Univ. Iagel. Acta Math. arXiv:1606.06592
Jędrzejewicz, P., Zieliński, J.: Analogs of Jacobian conditions for subrings. J. Pure Appl. Algebra 221(8), 2111–2118 (2017)
Jelonek, Z.: A solution of the problem of van den Essen and Shpilrain. J. Pure Appl. Algebra 137(1), 49–55 (1999)
Jelonek, Z.: A solution of the problem of van den Essen and Shpilrain II. J. Algebra 358, 8–15 (2012)
Keller, O.-H.: Ganze Cremona-Transformationen. Monatsh. Math. Phys. 47(1), 299–306 (1939)
Nowicki, A.: Polynomial Derivations and Their Rings of Constants. Nicolaus Copernicus University, Toruń (1994). http://www-users.mat.umk.pl/~anow/ps-dvi/pol-der.pdf
Nowicki, A.: Rings and fields of constants for derivations in characteristic zero. J. Pure Appl. Algebra 96(1), 47–55 (1994)
Smale, S.: Mathematical problems for the next century. Math. Intelligencer 20(2), 7–15 (1998)
Watkins, J.J.: Root and integral closure for \(R[[X]]\). J. Algebra 75(1), 43–58 (1982)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Jędrzejewicz, P., Zieliński, J. An approach to the Jacobian Conjecture in terms of irreducibility and square-freeness. European Journal of Mathematics 3, 199–207 (2017). https://doi.org/10.1007/s40879-017-0145-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-017-0145-5





 satisfy the Jacobian condition
satisfy the Jacobian condition
 , then
, then
 .
. satisfies the Jacobian condition
satisfies the Jacobian condition
 , then it is an automorphism.
, then it is an automorphism.
 such that
such that 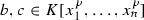 such that
such that  ,
,  for every
for every  ,
, for some irreducible polynomial
for some irreducible polynomial  ,
, for some square-free polynomial
for some square-free polynomial  .
. ,
, ,
, .
. ,
, the polynomial
the polynomial  the polynomial
the polynomial  mapping square-free polynomials to square-free polynomials is an automorphism.
mapping square-free polynomials to square-free polynomials is an automorphism.
 implies the ordinary Jacobian Conjecture for r polynomials in r variables over k [
implies the ordinary Jacobian Conjecture for r polynomials in r variables over k [ is true ([
is true ([ need not to be true if
need not to be true if  ,
, the polynomial
the polynomial  the polynomial
the polynomial  ,
, , then
, then