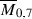Abstract
Fulton’s question about effective k-cycles on  for \(1<k<n-4\) can be answered negatively by appropriately lifting to
for \(1<k<n-4\) can be answered negatively by appropriately lifting to  the Keel–Vermeire divisors on
the Keel–Vermeire divisors on  . In this paper we focus on the case of 2-cycles on
. In this paper we focus on the case of 2-cycles on  , and we prove that the 2-dimensional boundary strata together with the lifts of the Keel–Vermeire divisors are not enough to generate the cone of effective 2-cycles. We do this by providing examples of effective 2-cycles on
, and we prove that the 2-dimensional boundary strata together with the lifts of the Keel–Vermeire divisors are not enough to generate the cone of effective 2-cycles. We do this by providing examples of effective 2-cycles on  that cannot be written as an effective combination of the aforementioned 2-cycles. These examples are inspired by a blow up construction of Castravet and Tevelev.
that cannot be written as an effective combination of the aforementioned 2-cycles. These examples are inspired by a blow up construction of Castravet and Tevelev.
Similar content being viewed by others
1 Introduction
An open problem in the birational geometry of  , the moduli space of stable n-pointed rational curves, is the F-conjecture. This conjecture claims that the cone
, the moduli space of stable n-pointed rational curves, is the F-conjecture. This conjecture claims that the cone  of effective curves, is generated by the numerical equivalence classes of 1-dimensional boundary strata, which are obtained by intersecting boundary divisors. This is known to be true if \(n\le 7\) (see [17]).
of effective curves, is generated by the numerical equivalence classes of 1-dimensional boundary strata, which are obtained by intersecting boundary divisors. This is known to be true if \(n\le 7\) (see [17]).
A similar question (which is known as Fulton’s question) was stated in [17] also for the cone  of effective k-cycles with \(1<k<n-3\):
of effective k-cycles with \(1<k<n-3\):

Denote by  the cone generated by the numerical equivalence classes of the k-dimensional boundary strata. Then the question is whether or not
the cone generated by the numerical equivalence classes of the k-dimensional boundary strata. Then the question is whether or not  is equal to
is equal to  . As Keel and Vermeire pointed out in the case of divisors (see [11, 22]), the cone
. As Keel and Vermeire pointed out in the case of divisors (see [11, 22]), the cone  is strictly contained in
is strictly contained in  , and one can see that
, and one can see that  for all \(1<k<n-4\) by appropriately lifting to
for all \(1<k<n-4\) by appropriately lifting to  the Keel–Vermeire divisors on
the Keel–Vermeire divisors on  (see Sect. 4, in particular Corollary 4.3). So the problem is to understand what lies in
(see Sect. 4, in particular Corollary 4.3). So the problem is to understand what lies in  (see [1, 3, 7, 14, 20] for the codimension 1 case). Recently, a lot of work has been done in order to understand the cones of effective and pseudoeffective cycles of higher codimension on projective varieties (see [4, 6, 9, 10, 18, 21]).
(see [1, 3, 7, 14, 20] for the codimension 1 case). Recently, a lot of work has been done in order to understand the cones of effective and pseudoeffective cycles of higher codimension on projective varieties (see [4, 6, 9, 10, 18, 21]).
We work over an algebraically closed field \(\mathbb {K}\) of any characteristic. The main result of this paper (Theorem 6.8) can be synthesized in the following statement.
Theorem
The 2-dimensional boundary strata on  together with the lifts of the Keel–Vermeire divisors on
together with the lifts of the Keel–Vermeire divisors on  are not enough to generate the cone
are not enough to generate the cone  .
.
The lifts of the Keel–Vermeire divisors are defined as the pushforwards with respect to the natural inclusion  of the Keel–Vermeire divisors on the boundary divisor \(D_{ab}\) (which is isomorphic to
of the Keel–Vermeire divisors on the boundary divisor \(D_{ab}\) (which is isomorphic to  ) for any \(\{a,b\}\subset \{1,\ldots ,7\}\). In this way we produce 315 extremal rays of
) for any \(\{a,b\}\subset \{1,\ldots ,7\}\). In this way we produce 315 extremal rays of  which lie outside of
which lie outside of  (see Proposition 5.4). Denote with
(see Proposition 5.4). Denote with  the cone generated by
the cone generated by  and by these lifts.
and by these lifts.
Examples of effective 2-cycles on  whose numerical equivalence classes do not lie in the cone
whose numerical equivalence classes do not lie in the cone  are produced using the following blow up construction of Castravet and Tevelev (see [2, Theorem 3.1]): take seven labeled points in \(\mathbb {P}^2\) which do not lie on a (possibly reducible) conic. Then the blow up of \(\mathbb {P}^2\) at these points can be embedded in
are produced using the following blow up construction of Castravet and Tevelev (see [2, Theorem 3.1]): take seven labeled points in \(\mathbb {P}^2\) which do not lie on a (possibly reducible) conic. Then the blow up of \(\mathbb {P}^2\) at these points can be embedded in  as an effective 2-cycle. Using this construction and considering particular arrangements of seven labeled points in \(\mathbb {P}^2\), we define what we call special hypertree surfaces on
as an effective 2-cycle. Using this construction and considering particular arrangements of seven labeled points in \(\mathbb {P}^2\), we define what we call special hypertree surfaces on  (see Definition 6.6), which are related to Castravet and Tevelev hypertrees (see [3]). In Theorem 6.8 we prove that the numerical equivalence class of a special hypertree surface does not lie in the cone
(see Definition 6.6), which are related to Castravet and Tevelev hypertrees (see [3]). In Theorem 6.8 we prove that the numerical equivalence class of a special hypertree surface does not lie in the cone  . This implies that
. This implies that  , which is our main result. An example of 7-points arrangement in \(\mathbb {P}^2\) which gives rise to a special hypertree surface on
, which is our main result. An example of 7-points arrangement in \(\mathbb {P}^2\) which gives rise to a special hypertree surface on  is the one shown in Fig. 1.Footnote 1
is the one shown in Fig. 1.Footnote 1
All the other special hypertree surfaces are obtained by permuting the labels of the points arrangement in Fig. 1. In Sect. 6.3 we show that there are 210 (resp. 30) distinct numerical equivalence classes of special hypertree surfaces on  if the characteristic of the base field is different from 2 (resp. equal to 2).
if the characteristic of the base field is different from 2 (resp. equal to 2).
Summing up, if we denote with  the cone generated by
the cone generated by  and by the numerical equivalence classes of the embedded blow ups of \(\mathbb {P}^2\) at seven points, we have the following chain of containments:
and by the numerical equivalence classes of the embedded blow ups of \(\mathbb {P}^2\) at seven points, we have the following chain of containments:

The second main result of this paper is an explicit description of the intersection theory of the 2-dimensional boundary strata on  . In Propositions 3.4 and 3.5 we give formulas that compute the intersection number of two 2-dimensional boundary strata on
. In Propositions 3.4 and 3.5 we give formulas that compute the intersection number of two 2-dimensional boundary strata on  . Then we study the numerical equivalence classes of these 2-cycles (see Propositions 3.7 and 3.8), and this, together with some recent results of Chen and Coskun in [4], allows us to give a complete description of the cone
. Then we study the numerical equivalence classes of these 2-cycles (see Propositions 3.7 and 3.8), and this, together with some recent results of Chen and Coskun in [4], allows us to give a complete description of the cone  (see Corollary 3.10). We also fully describe the bilinear form
(see Corollary 3.10). We also fully describe the bilinear form  given by the intersection product (see Propositions 3.11 and 3.12).
given by the intersection product (see Propositions 3.11 and 3.12).
In Sect. 2 we recall some basic facts and notations about  that are used in this paper. Section 3 contains the formulas for the intersection of two 2-dimensional boundary strata on
that are used in this paper. Section 3 contains the formulas for the intersection of two 2-dimensional boundary strata on  , and the complete study of the cone
, and the complete study of the cone  . In Sect. 4 there is a detailed description of the lifting technique, which is immediately applied in Sect. 5 to describe the lifts to
. In Sect. 4 there is a detailed description of the lifting technique, which is immediately applied in Sect. 5 to describe the lifts to  of the Keel–Vermeire divisors on
of the Keel–Vermeire divisors on  . Section 6 is where we discuss the embedded blow ups of \(\mathbb {P}^2\) in
. Section 6 is where we discuss the embedded blow ups of \(\mathbb {P}^2\) in  and where we prove our main theorem. In Sect. 7 we generalize the construction of the two cones
and where we prove our main theorem. In Sect. 7 we generalize the construction of the two cones  and
and  to any
to any  for \(n>7\). We also state some questions that will be the object of further investigation.
for \(n>7\). We also state some questions that will be the object of further investigation.
2 Preliminaries: boundary strata on \(\overline{M}_{0,n}\)
In this section we review some of the main definitions and facts about the boundary strata on  . For a more detailed discussion, see for example [17]. Equivalence between k-cycles on
. For a more detailed discussion, see for example [17]. Equivalence between k-cycles on  refers to numerical equivalence, which is the same as rational equivalence and algebraic equivalence by [16].
refers to numerical equivalence, which is the same as rational equivalence and algebraic equivalence by [16].
Definition 2.1
The irreducible components of the locus of points on  parametrizing stable n-pointed rational curves with at least \(n-3-k\) nodes, have dimension k and are called boundary k-strata. Codimension 1 (resp. 1-dimensional) boundary strata are also called boundary divisors (resp. F-curves).
parametrizing stable n-pointed rational curves with at least \(n-3-k\) nodes, have dimension k and are called boundary k-strata. Codimension 1 (resp. 1-dimensional) boundary strata are also called boundary divisors (resp. F-curves).
Definition 2.2
Given \(n\ge 3\) and \(0\le k\le n-3\), define  to be the cone generated by the equivalence classes of the boundary k-strata on
to be the cone generated by the equivalence classes of the boundary k-strata on  (V stands for “vital cycles”, as they were called in [17]).
(V stands for “vital cycles”, as they were called in [17]).
Notation
If n is a positive integer, then [n] denotes the set \(\{1,\ldots ,n\}\).
Combinatorial description of boundary divisors
There is a bijection between boundary divisors and partitions  , with \(2\le |I|\le n-2\). \(D_{I}=D_{I^\mathrm{c}}\) denotes the boundary divisor corresponding to the partition
, with \(2\le |I|\le n-2\). \(D_{I}=D_{I^\mathrm{c}}\) denotes the boundary divisor corresponding to the partition  . \(\delta _{I}=\delta _{I^\mathrm{c}}\) denotes the equivalence class of \(D_{I}\). For simplicity, the equivalence class of a boundary divisor will be called just boundary divisor.
. \(\delta _{I}=\delta _{I^\mathrm{c}}\) denotes the equivalence class of \(D_{I}\). For simplicity, the equivalence class of a boundary divisor will be called just boundary divisor.
Combinatorial description of equivalence classes of F-curves
There is a bijection between equivalence classes of F-curves and partitions of \([n]=\{1,\ldots ,n\}\) into four nonempty subsets (see [17, Lemma 4.3]). Given a partition  , we denote by \(F_{I_1,I_2,I_3,I_4}\) the equivalence class of the F-curves corresponding to that partition.
, we denote by \(F_{I_1,I_2,I_3,I_4}\) the equivalence class of the F-curves corresponding to that partition.
Every boundary stratum on  can be realized as the complete intersection of all the boundary divisors containing it as follows. Let B be a boundary stratum and let C(B) be the stable n-pointed rational curve corresponding to the generic point of B (C(B) has as many nodes as the codimension of B). If
can be realized as the complete intersection of all the boundary divisors containing it as follows. Let B be a boundary stratum and let C(B) be the stable n-pointed rational curve corresponding to the generic point of B (C(B) has as many nodes as the codimension of B). If  denotes the set of singular points of C(B), given
denotes the set of singular points of C(B), given  let \(T_p\) be the set of markings that are over one of the two connected components of the normalization of C(B) at p. Then we have that
let \(T_p\) be the set of markings that are over one of the two connected components of the normalization of C(B) at p. Then we have that

Moreover, since the boundary of  has normal crossings, we have that the equivalence class of B is the product of all \(\delta _{T_p}\) as p varies among the nodes of C(B).
has normal crossings, we have that the equivalence class of B is the product of all \(\delta _{T_p}\) as p varies among the nodes of C(B).
The last thing we want to recall is [16, Fact 4]: given two boundary divisors \(D_I, D_J\) on  , then
, then  , which by definition means
, which by definition means

3 The cone of boundary 2-strata on \(\overline{M}_{0,7}\)
The main object of our study is  , which is a subcone of the real vector space
, which is a subcone of the real vector space  (in Sect. 3.5 we show that
(in Sect. 3.5 we show that  ). We start by analyzing the subcone
). We start by analyzing the subcone  . The first thing we want to do is to give a combinatorial description of the boundary 2-strata on
. The first thing we want to do is to give a combinatorial description of the boundary 2-strata on  . After this, we study their intersections and their equivalence classes.
. After this, we study their intersections and their equivalence classes.
3.1 Combinatorial description of the boundary 2-strata on 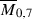
According to Definition 2.1, a boundary 2-stratum on  is the closure of the locus of points parametrizing stable 7-pointed rational curves of the shape shown in Fig. 2, where \(I\amalg J\amalg K\) is a given partition of [7]. Stability imposes that \(2\le |I|\le 4\), \(1\le |J|\le 3\) and \(2\le |K|\le 4\). Therefore: there is a bijection between set-theoretically distinct boundary 2-strata, and partitions
is the closure of the locus of points parametrizing stable 7-pointed rational curves of the shape shown in Fig. 2, where \(I\amalg J\amalg K\) is a given partition of [7]. Stability imposes that \(2\le |I|\le 4\), \(1\le |J|\le 3\) and \(2\le |K|\le 4\). Therefore: there is a bijection between set-theoretically distinct boundary 2-strata, and partitions
 of [7], with
\(2\le |I|\le 4\), \(1\le |J|\le 3\)
and
of [7], with
\(2\le |I|\le 4\), \(1\le |J|\le 3\)
and
 , modulo the equivalence relation
, modulo the equivalence relation
 .
.
With  we denote the boundary 2-stratum corresponding to the partition
we denote the boundary 2-stratum corresponding to the partition  of [7]. The equivalence class of \(s_{I,J,K}\) is denoted by \(\sigma _{I,J,K}\). Obviously, we have that
of [7]. The equivalence class of \(s_{I,J,K}\) is denoted by \(\sigma _{I,J,K}\). Obviously, we have that  . An easy combinatorial count tells us that there are 490 set-theoretically distinct boundary 2-strata \(s_{I,J,K}\). A similar description applies for codimension 2 boundary strata on
. An easy combinatorial count tells us that there are 490 set-theoretically distinct boundary 2-strata \(s_{I,J,K}\). A similar description applies for codimension 2 boundary strata on  for \(n\ge 8\). For general results about boundary strata of codimension 2 on
for \(n\ge 8\). For general results about boundary strata of codimension 2 on  , see [4, Section 6].
, see [4, Section 6].
3.2 Intersection of two distinct boundary 2-strata
Given \(\sigma _{I,J,K}\) and \(\sigma _{L,M,N}\), our goal is to compute the intersection  . This intersection is clearly zero, unless we require that the condition defined here below is satisfied.
. This intersection is clearly zero, unless we require that the condition defined here below is satisfied.
Definition 3.1
Consider two boundary 2-strata \(s_{I,J,K}\) and \(s_{L,M,N}\). Assume that

If this condition is satisfied, we write  .
.
Lemma 3.2
Let \(D_{I_1},D_{I_2}\) and \(D_{I_3}\) be three distinct boundary divisors on  such that
such that  for all \(\{a,b\}\subset \{1,2,3\}\). Then \(D_{I_1}\cap D_{I_2}\cap D_{I_3}\) is an F-curve.
for all \(\{a,b\}\subset \{1,2,3\}\). Then \(D_{I_1}\cap D_{I_2}\cap D_{I_3}\) is an F-curve.
Proof
Assume without loss of generality that \(I_1\cap I_2=\emptyset \). We know that  and
and  , therefore
, therefore
Among these 16 cases, the only possible are
Up to changing \(I_3\) with \(I_3^\mathrm{c}\), we just need to consider
Now, inspecting each one of these four cases, it is easy to see that the intersection \(D_{I_1}\cap D_{I_2}\cap D_{I_3}\) is an F-curve. \(\square \)
Lemma 3.3
Let \(s_{I,J,K}\) and \(s_{L,M,N}\) be two distinct boundary 2-strata on  satisfying the condition
satisfying the condition  . Then we can write
. Then we can write  where, either the four boundary divisors \(\delta _{I_1},\delta _{I_2},\delta _{I_3}\) and \(\delta _{I_4}\) are pairwise distinct, or exactly two of them are equal. In the latter case, we assume that \(I_3=I_4\). In any case, we assume that \(I_1\cap I_2=\emptyset \) and \(|I_1|\le |I_2|\).
where, either the four boundary divisors \(\delta _{I_1},\delta _{I_2},\delta _{I_3}\) and \(\delta _{I_4}\) are pairwise distinct, or exactly two of them are equal. In the latter case, we assume that \(I_3=I_4\). In any case, we assume that \(I_1\cap I_2=\emptyset \) and \(|I_1|\le |I_2|\).
Proof
Write  . Obviously \(\delta _I\ne \delta _K\) and \(\delta _L\ne \delta _N\). If two boundary divisors among \(\delta _I,\delta _K,\delta _L\) and \(\delta _N\) are equal, assume without loss of generality that \(\delta _K=\delta _L\). Then we must have that \(\delta _N\ne \delta _I\), or we would have \(s_{I,J,K}=s_{L,M,N}\). Also, \(\delta _N\ne \delta _K=\delta _L\). This proves that there can be at most two boundary divisors among \(\delta _I,\delta _K,\delta _L\) and \(\delta _N\) that are equal. So, let us write
. Obviously \(\delta _I\ne \delta _K\) and \(\delta _L\ne \delta _N\). If two boundary divisors among \(\delta _I,\delta _K,\delta _L\) and \(\delta _N\) are equal, assume without loss of generality that \(\delta _K=\delta _L\). Then we must have that \(\delta _N\ne \delta _I\), or we would have \(s_{I,J,K}=s_{L,M,N}\). Also, \(\delta _N\ne \delta _K=\delta _L\). This proves that there can be at most two boundary divisors among \(\delta _I,\delta _K,\delta _L\) and \(\delta _N\) that are equal. So, let us write  , where \(\{I,K,L,N\}=\{A,B,I_3,I_4\}\) and \(I_3=I_4\) in case two boundary divisors among \(\delta _I,\delta _K,\delta _L\) and \(\delta _N\) coincide. Finally, we can obviously rewrite
, where \(\{I,K,L,N\}=\{A,B,I_3,I_4\}\) and \(I_3=I_4\) in case two boundary divisors among \(\delta _I,\delta _K,\delta _L\) and \(\delta _N\) coincide. Finally, we can obviously rewrite  with \(I_1\cap I_2=\emptyset \) (here we use the hypothesis of lemma
with \(I_1\cap I_2=\emptyset \) (here we use the hypothesis of lemma  ) and \(|I_1|\le |I_2|\). \(\square \)
) and \(|I_1|\le |I_2|\). \(\square \)
Proposition 3.4
Let \(s_{I,J,K}\) and \(s_{L,M,N}\) be two distinct boundary 2-strata on  such that
such that  (otherwise, the intersection number
(otherwise, the intersection number  is trivially zero). Write
is trivially zero). Write  as prescribed by Lemma 3.3 (recall that in this lemma we assumed, among other things, that \(|I_1|\le |I_2|)\). Then
as prescribed by Lemma 3.3 (recall that in this lemma we assumed, among other things, that \(|I_1|\le |I_2|)\). Then

Proof
Let us make some preliminary observations. We have that

Define \(S=s_{I_1,(I_1\cup I_2)^\mathrm{c},I_2}\) and let  be the inclusion morphism. Using the projection formula, we obtain that
be the inclusion morphism. Using the projection formula, we obtain that

Now, for \(j=3,4\), \(i^*\delta _{I_j}=[D_{I_1}\cap D_{I_2}\cap D_{I_j}]\), where \(D_{I_1}\cap D_{I_2}\cap D_{I_j}\) is an F-curve by Lemma 3.2. So \(i^*\delta _{I_3}\) and \(i^*\delta _{I_4}\) are two equivalence classes of F-curves on the boundary 2-stratum S. There are two possibilities for S up to isomorphism.
-
(i)
If \(|I_1|=2\) and \(|I_2|\in \{2,4\}\), then
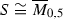 . By Kapranov’s blow up construction of
. By Kapranov’s blow up construction of  (see [15]), we know that
(see [15]), we know that 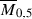 is isomorphic to the blow up of \(\mathbb {P}^2\) at four points in general linear position. Moreover, the F-curves of
is isomorphic to the blow up of \(\mathbb {P}^2\) at four points in general linear position. Moreover, the F-curves of 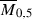 correspond to the exceptional divisors of the blow up, and the strict transforms of the lines spanned by the blown up points.
correspond to the exceptional divisors of the blow up, and the strict transforms of the lines spanned by the blown up points. -
(ii)
If \(|I_2|=3\) and \(|I_1|\in \{2,3\}\), then
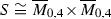 , which is isomorphic to
, which is isomorphic to 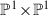 . An F-curve on S corresponds to a line on
. An F-curve on S corresponds to a line on  in the form
in the form  or
or 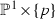 for some point \(p\in \mathbb {P}^1\).
for some point \(p\in \mathbb {P}^1\).
Observe that in case (i) (resp. case (ii)) the self-intersection of an F-curve is  (resp. 0), and in both cases two distinct F-curves intersect at one point if and only if their intersection number is 1.
(resp. 0), and in both cases two distinct F-curves intersect at one point if and only if their intersection number is 1.
Now, let us prove our intersection formula for  .
.
-
\(|I_1|=2\) and \(|I_2|=2\). Up to permuting the labels, we have that

where x and y are the nodes of the stable 7-pointed rational curve corresponding to the generic point of S. If \(\delta _{I_3}=\delta _{I_4}\), then
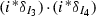 is equal to the self-intersection of an F-curve on
is equal to the self-intersection of an F-curve on  , which gives
, which gives  . So let us assume that \(\delta _{I_1},\delta _{I_2},\delta _{I_3}\) and \(\delta _{I_4}\) are pairwise distinct. Given \(j=3,4\), since
. So let us assume that \(\delta _{I_1},\delta _{I_2},\delta _{I_3}\) and \(\delta _{I_4}\) are pairwise distinct. Given \(j=3,4\), since  and
and  , then \(i^*\delta _{I_j}\) is equal to one of the following boundary divisors on
, then \(i^*\delta _{I_j}\) is equal to one of the following boundary divisors on  : $$\begin{aligned} \delta _{34},\quad \delta _{35},\quad \delta _{45}\quad \text {or}\quad \delta _{345}. \end{aligned}$$
: $$\begin{aligned} \delta _{34},\quad \delta _{35},\quad \delta _{45}\quad \text {or}\quad \delta _{345}. \end{aligned}$$If \(i^*\delta _{I_3}=\delta _{34},\delta _{35}\) or \(\delta _{45}\), then \(i^*\delta _{I_4}=\delta _{345}\) because
 and \(\delta _{I_3}\ne \delta _{I_4}\). If \(i^*\delta _{I_3}=\delta _{345}\), then \(i^*\delta _{I_4}\) has to be equal to \(\delta _{34},\delta _{35}\) or \(\delta _{45}\). In any case, \(\sigma _{I,J,K}\cdot \sigma _{L,M,N}=1\).
and \(\delta _{I_3}\ne \delta _{I_4}\). If \(i^*\delta _{I_3}=\delta _{345}\), then \(i^*\delta _{I_4}\) has to be equal to \(\delta _{34},\delta _{35}\) or \(\delta _{45}\). In any case, \(\sigma _{I,J,K}\cdot \sigma _{L,M,N}=1\). -
\(|I_1|=2\) and \(|I_2|=4\). We have isomorphisms
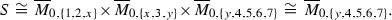
If \(\delta _{I_3}=\delta _{I_4}\), then again
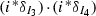 is equal to the self-intersection of an F-curve on
is equal to the self-intersection of an F-curve on 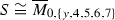 , which gives
, which gives 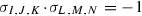 . Let us assume that \(\delta _{I_3}\ne \delta _{I_4}\). Given \(j=3,4\), then \(i^*\delta _{I_j}\) is equal to one of the following boundary divisors on
. Let us assume that \(\delta _{I_3}\ne \delta _{I_4}\). Given \(j=3,4\), then \(i^*\delta _{I_j}\) is equal to one of the following boundary divisors on 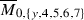 : $$\begin{aligned} \delta _{45},\;\; \delta _{46},\;\; \delta _{47},\;\; \delta _{56},\;\; \delta _{57},\;\; \delta _{67},\;\; \delta _{456},\;\; \delta _{457},\;\; \delta _{467}\;\; \text {or}\;\; \delta _{567}. \end{aligned}$$
: $$\begin{aligned} \delta _{45},\;\; \delta _{46},\;\; \delta _{47},\;\; \delta _{56},\;\; \delta _{57},\;\; \delta _{67},\;\; \delta _{456},\;\; \delta _{457},\;\; \delta _{467}\;\; \text {or}\;\; \delta _{567}. \end{aligned}$$If \(i^*\delta _{I_3}=\delta _{45},\delta _{46},\delta _{47},\delta _{56},\delta _{57}\) or \(\delta _{67}\), then assume up to a change of labels that \(i^*\delta _{I_3}=\delta _{45}\). In this case, \(i^*\delta _{I_4}=\delta _{67},\delta _{456}\) or \(\delta _{457}\). If \(i^*\delta _{I_3}=\delta _{456},\delta _{457},\delta _{467}\) or \(\delta _{567}\), assume up to a change of labels that \(i^*\delta _{I_3}=\delta _{456}\). Then \(i^*\delta _{I_4}\) has to be equal to \(\delta _{45},\delta _{46}\) or \(\delta _{56}\). Each one of these choices for \(i^*\delta _{I_3}\) and \(i^*\delta _{I_4}\) gives \(\sigma _{I,J,K}\cdot \sigma _{L,M,N}=1\).
-
\(|I_1|=2\) and \(|I_2|=3\). In this case we have

If \(\delta _{I_3}=\delta _{I_4}\), then
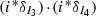 is equal to the self-intersection of an F-curve on
is equal to the self-intersection of an F-curve on 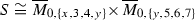 , which gives
, which gives  . Now consider the case \(\delta _{I_3}\ne \delta _{I_4}\). For \(j=3,4\), \(i^*\delta _{I_j}\) is equal to the equivalence class of one of the following divisors on
. Now consider the case \(\delta _{I_3}\ne \delta _{I_4}\). For \(j=3,4\), \(i^*\delta _{I_j}\) is equal to the equivalence class of one of the following divisors on  :
: 
Since
 , the only possibility for \(i^*\delta _{I_3}\) and \(i^*\delta _{I_4}\) is to belong to two different rulings of S. It follows that
, the only possibility for \(i^*\delta _{I_3}\) and \(i^*\delta _{I_4}\) is to belong to two different rulings of S. It follows that 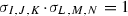 .
. -
\(|I_1|=3\) and \(|I_2|=3\). Then
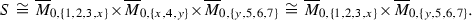
If \(\delta _{I_3}=\delta _{I_4}\), then
 is equal to the self-intersection of an F-curve on
is equal to the self-intersection of an F-curve on 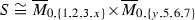 , which gives
, which gives  . For the case \(\delta _{I_3}\ne \delta _{I_4}\), given \(j=3,4\), \(i^*\delta _{I_j}\) is equal to the equivalence class of one of the following divisors on
. For the case \(\delta _{I_3}\ne \delta _{I_4}\), given \(j=3,4\), \(i^*\delta _{I_j}\) is equal to the equivalence class of one of the following divisors on  :
: 
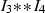 implies that \(i^*\delta _{I_3}\) and \(i^*\delta _{I_4}\) belong to two different rulings of S. In particular,
implies that \(i^*\delta _{I_3}\) and \(i^*\delta _{I_4}\) belong to two different rulings of S. In particular,  .
.
At this point, the claimed intersection formula sums up all the considerations we made so far. \(\square \)
3.3 Self-intersection of a boundary 2-stratum
We want to compute  . The idea is to find an appropriate Keel relation (see [16, p. 569, Theorem 1 (2)]) that allows us to replace \(\delta _I\) and reduce the calculation to the previous case.
. The idea is to find an appropriate Keel relation (see [16, p. 569, Theorem 1 (2)]) that allows us to replace \(\delta _I\) and reduce the calculation to the previous case.
Proposition 3.5
Let \(\sigma _{I,J,K}\) be the equivalence class of a boundary 2-stratum with \(|I|\le |K|\). Then
Proof
Up to relabeling the markings, it is enough to prove that \(\sigma _{12,3,4567}^2=0\), \(\sigma _{123,4,567}^2=\sigma _{12,34,567}^2=1\) and \(\sigma _{12,345,67}^2=2\).
-
 . Let us use the boundary relation
. Let us use the boundary relation 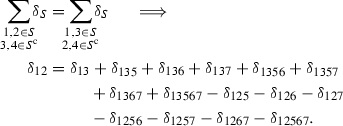
But now, if \(\delta _T\) is one of the boundary divisors that appear in the expression we just found for \(\delta _{12}\), then
 is false or
is false or 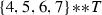 is false. Hence, \(\sigma _{12,3,4567}^2=0\).
is false. Hence, \(\sigma _{12,3,4567}^2=0\). -
 . Consider
. Consider 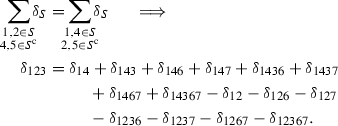
After replacing \(\delta _{123}\) with the new expression and distributing, we get
 .
. -
 . We use the following boundary relation:
. We use the following boundary relation: 
-
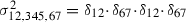 .
. 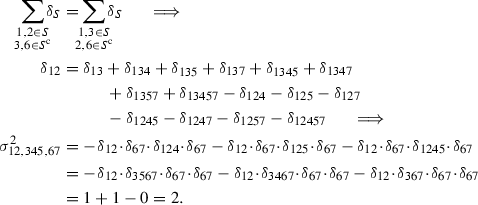
\(\square \)
Remark 3.6
As one of the referees pointed out, Proposition 3.5 can also be proved using [8, Lemma 3.5]. Say we want to compute \(\sigma _{I,J,K}^2\). Then, adopting the same notation used in [8, Lemma 3.5], one can take \(B=s_{I,J,K}\) and let \(X\rightarrow B\) be the pullback of the universal family on  with respect to the inclusion
with respect to the inclusion  . Then the intersection number \(\sigma _{I,J,K}^2\) can be computed using the formula provided at the end of [8, Lemma 3.5].
. Then the intersection number \(\sigma _{I,J,K}^2\) can be computed using the formula provided at the end of [8, Lemma 3.5].
3.4 Equivalence classes of boundary 2-strata
So far, we considered set theoretically distinct boundary 2-strata. However, we are interested in studying distinct equivalence classes of boundary 2-strata.
Proposition 3.7
Consider \(\sigma _{I,J,K}\) and \(\sigma _{L,M,N}\) with \(|I|\le |K|\), \(|L|\le |N|\) and \(s_{I,J,K}\ne s_{L,M,N}\). Then \(\sigma _{I,J,K}=\sigma _{L,M,N}\Leftrightarrow I\cup J=L\cup M\) and \(|I\cup J|=3\).
Proof
(\(\Leftarrow \)) Assume \(\{a,b,c,d,e,f,g\}=[7]\) and let \(I\cup J=\{a,b,c\}\). Consider the boundary divisor  . Let
. Let  be the usual projection morphism. If C is the stable 7-pointed rational curve corresponding to the generic point of \(D_{abc}\), assume the node of C and the labels b, c fixed on the twig which contains a, b and c. So we can think of a as parametrizing \(\mathbb {P}^1\), and therefore \(\pi ^{-1}(b)=s_{ab,c,defg}\), \(\pi ^{-1}(c)=s_{ac,b,defg}\). In conclusion, \(s_{ab,c,defg}\) and \(s_{ac,b,defg}\) are rationally equivalent.
be the usual projection morphism. If C is the stable 7-pointed rational curve corresponding to the generic point of \(D_{abc}\), assume the node of C and the labels b, c fixed on the twig which contains a, b and c. So we can think of a as parametrizing \(\mathbb {P}^1\), and therefore \(\pi ^{-1}(b)=s_{ab,c,defg}\), \(\pi ^{-1}(c)=s_{ac,b,defg}\). In conclusion, \(s_{ab,c,defg}\) and \(s_{ac,b,defg}\) are rationally equivalent.
(\(\Rightarrow \)) Let us prove the contrapositive. We proceed by enumerating all the possible cases.
-
(i)
\(|J|=3\). Then
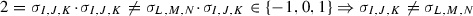 .
. -
(ii)
\(|I|=|J|=2\). Up to relabeling, we can assume that \(\sigma _{I,J,K}=\sigma _{12,34,567}\). The boundary 2-stratum \(\sigma _{L,M,N}\) can be in one of the following forms:
$$\begin{aligned} \sigma _{ab,cd,efg},\quad \sigma _{abc,d,efg}\quad \text {or}\quad \sigma _{ab,c,defg} \end{aligned}$$(\(\sigma _{ab,cde,fg}\) is excluded because of what we just discussed in (i)). In any case, we can write
 with \(|S|=4\). Therefore,
with \(|S|=4\). Therefore,  can be equal to just 0 or
can be equal to just 0 or 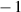 (more in detail, if
(more in detail, if  , then \(S=\{1,2,3,4\}\) and the intersection can be either 0 or
, then \(S=\{1,2,3,4\}\) and the intersection can be either 0 or  ). However
). However  , so \(\sigma _{12,34,567}\ne \sigma _{L,M,N}\).
, so \(\sigma _{12,34,567}\ne \sigma _{L,M,N}\). -
(iii)
\(|J|=1\) and \(|I|=3\). This case uses the same strategy we adopted in (ii).
-
(iv)
\(|J|=1\) and \(|I|=2\). We can assume \(\sigma _{I,J,K}=\sigma _{12,3,4567}\). Because of what we proved so far, we can assume that \(s_{L,M,N}=s_{ab,c,defg}\). By our hypotheses, we also have that \(s_{ab,c,defg}\) has to be different from \(s_{13,2,4567}\) and \(s_{23,1,4567}\). But now, up to permuting \(\{4,5,6,7\}\) and \(\{1,2\}\) (which leave \(\sigma _{12,3,4567}\) unchanged), there are few possibilities for \(\sigma _{ab,c,defg}\), which are
$$\begin{aligned}&\sigma _{12,4,3567},\quad \sigma _{13,4,2567},\quad \sigma _{14,2,3567}, \quad \sigma _{14,3,2567},\quad \sigma _{14,5,2367},\\&\sigma _{34,1,2567},\quad \sigma _{34,5,1267},\quad \sigma _{45,1,2367}, \quad \sigma _{45,3,1267},\quad \sigma _{45,6,1237}. \end{aligned}$$In each case, one can compute that \(\sigma _{ab,c,defg}\cdot \sigma _{45,123,67}=0\) using Proposition 3.4. But \(\sigma _{12,3,4567}\cdot \sigma _{45,123,67}=1\) again by Proposition 3.4, and therefore \(\sigma _{12,3,4567}\ne \sigma _{ab,c,defg}\).\(\square \)
Now, an easy count tells us that there are 420 distinct equivalence classes of boundary 2-strata on  . In addition, these 420 equivalence classes generate distinct rays in
. In addition, these 420 equivalence classes generate distinct rays in  as we prove in the next proposition.
as we prove in the next proposition.
Proposition 3.8
Distinct equivalence classes of boundary 2-strata on  generate distinct rays in the cone
generate distinct rays in the cone  .
.
Proof
We say that a boundary 2-stratum \(\sigma _{I,J,K}\) is of type (a, b, c) if \(\{a,b,c\}=\{|I|,|J|,|K|\}\). Let \(\alpha \) and \(\beta \) be two distinct boundary 2-strata on  . Assume by contradiction that we can find \(r\in \mathbb {R}_{>0}\), \(r\ne 1\), such that \(\alpha =r\beta \).
. Assume by contradiction that we can find \(r\in \mathbb {R}_{>0}\), \(r\ne 1\), such that \(\alpha =r\beta \).
There are three cases to discuss.
-
\(\alpha \) and \(\beta \) are not of type (2, 1, 4). Then \(\alpha ^2=r^2\beta ^2\ne 0\) by Proposition 3.5, so that \(r=\sqrt{\alpha ^2/\beta ^2}\). Considering all the possible cases for \(\alpha ^2\) and \(\beta ^2\), we see that \(r\in \bigl \{1/\sqrt{2},\sqrt{2}\bigr \}\), which cannot be because r has to be rational.
-
Exactly one among \(\alpha \) and \(\beta \) is of type (2, 1, 4). This is impossible because one side of the equality \(\alpha ^2=r^2\beta ^2\) would be zero and the other not.
-
Both \(\alpha \) and \(\beta \) are of type (2, 1, 4). Since \(\alpha \ne 0\), we can find a boundary 2-stratum \(\gamma \) such that
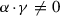 . According to Propositions 3.4 and 3.5, we must have that
. According to Propositions 3.4 and 3.5, we must have that 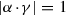 and
and 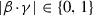 . In any case, the equality
. In any case, the equality  gives a contradiction.\(\square \)
gives a contradiction.\(\square \)
Recent work of Chen and Coskun (see [4]) shows that the 420 equivalence classes of boundary 2-strata on  generate extremal rays of
generate extremal rays of  .
.
Theorem 3.9
([4, Theorem 6.1]) Equivalence classes of boundary strata of codimension 2 on  are extremal in
are extremal in  .
.
To conclude, the next corollary completely describes the cone  and sums up what we know about
and sums up what we know about  so far.
so far.
Corollary 3.10
The cone  has at least 420 extremal rays, which are generated by the distinct equivalence classes of the boundary 2-strata on
has at least 420 extremal rays, which are generated by the distinct equivalence classes of the boundary 2-strata on  . In particular, the closed cone
. In particular, the closed cone  has exactly 420 extremal rays.
has exactly 420 extremal rays.
3.5 The intersection form 
The real vector space  is equipped with a symmetric bilinear form
is equipped with a symmetric bilinear form  given by the intersection between equivalence classes of 2-cycles. Since Q is nondegenerate, then Q has rank equal to
given by the intersection between equivalence classes of 2-cycles. Since Q is nondegenerate, then Q has rank equal to  .
.
Proposition 3.11
 .
.
Proof
Let \(\mathbb {K}\) be our base field. We know that the equivalence classes of the boundary 2-strata span  in any characteristic. Moreover, the linear dependence relations between the equivalence classes of the boundary 2-strata on
in any characteristic. Moreover, the linear dependence relations between the equivalence classes of the boundary 2-strata on  , only depend on the combinatorics of the intersection between the boundary 2-strata (that we just studied in Propositions 3.4 and 3.5), and all this does not depend on
, only depend on the combinatorics of the intersection between the boundary 2-strata (that we just studied in Propositions 3.4 and 3.5), and all this does not depend on  . Hence,
. Hence,  does not depend on the characteristic, and we can assume that \(\mathbb {K}=\mathbb {C}\).
does not depend on the characteristic, and we can assume that \(\mathbb {K}=\mathbb {C}\).
As a complex variety,  is an HI scheme. An HI scheme X is a scheme of characteristic zero such that the canonical map \(A_*(X)\rightarrow H_*(X;\mathbb {Z})\) from the Chow groups to the homology is an isomorphism (see [16, Appendix] for more details). It follows that the Chow group
is an HI scheme. An HI scheme X is a scheme of characteristic zero such that the canonical map \(A_*(X)\rightarrow H_*(X;\mathbb {Z})\) from the Chow groups to the homology is an isomorphism (see [16, Appendix] for more details). It follows that the Chow group  is isomorphic to the homology group
is isomorphic to the homology group  . Therefore, the dimension of
. Therefore, the dimension of  as a real vector space is equal to \(b_4\), the 4-th Betti number of
as a real vector space is equal to \(b_4\), the 4-th Betti number of  .
.
We can find \(b_4\) by computing  , the Poincaré polynomial of
, the Poincaré polynomial of  . We compute this polynomial by using a recursive formula in [5, Section 5], which gives the Poincaré polynomial of the space \(T_{d,n}\), the compact moduli space of stable n-pointed rooted trees of d-dimensional projective spaces. In our case,
. We compute this polynomial by using a recursive formula in [5, Section 5], which gives the Poincaré polynomial of the space \(T_{d,n}\), the compact moduli space of stable n-pointed rooted trees of d-dimensional projective spaces. In our case,  (see [5, Proposition 3.4.3]), and one can compute that
(see [5, Proposition 3.4.3]), and one can compute that  . \(\square \)
. \(\square \)
Proposition 3.12
The bilinear form Q has signature (86, 41).
Proof
The 420 equivalence classes of the boundary 2-strata span  . Therefore, we can choose 127 of these 2-cycles to form a basis for
. Therefore, we can choose 127 of these 2-cycles to form a basis for  , and a matrix representation for Q is given by the intersection matrix of these 127 equivalence classes of boundary 2-strata. Since this matrix just depends on the combinatorics of the intersection between the boundary 2-strata, we have that the signature of Q is independent of the characteristic of the base field. So let \(\mathbb {C}\) be our base field.
, and a matrix representation for Q is given by the intersection matrix of these 127 equivalence classes of boundary 2-strata. Since this matrix just depends on the combinatorics of the intersection between the boundary 2-strata, we have that the signature of Q is independent of the characteristic of the base field. So let \(\mathbb {C}\) be our base field.
With this assumption, we have that  is an HI scheme and a smooth manifold, implying that
is an HI scheme and a smooth manifold, implying that  . Using the Hodge–Riemann bilinear relations (see [12, Chapter 0]), one has that
. Using the Hodge–Riemann bilinear relations (see [12, Chapter 0]), one has that

where  is the index of
is the index of  (i.e. the number of positive eigenvalues minus the number of negative eigenvalues in a matrix representation of Q), and \(h^{p,q}\) the Hodge numbers of
(i.e. the number of positive eigenvalues minus the number of negative eigenvalues in a matrix representation of Q), and \(h^{p,q}\) the Hodge numbers of  .
.
Now, knowing that the Poincaré polynomial of  is
is  (see the proof of Proposition 3.11), and using the Hodge decomposition, we can compute that
(see the proof of Proposition 3.11), and using the Hodge decomposition, we can compute that

implying that the signature of Q is (86, 41). \(\square \)
Under a more arithmetic perspective, we can view Q as a bilinear form on  (which is torsion-free). In this case, Q is unimodular by Poincaré duality and odd by Proposition 3.5.
(which is torsion-free). In this case, Q is unimodular by Poincaré duality and odd by Proposition 3.5.
4 Lift of effective cycles
The technique we are about to describe allows to construct an effective k-cycle on  given an effective k-cycle on
given an effective k-cycle on  .
.
4.1 The lift construction
Let  be the map forgetting the
be the map forgetting the  -th label. Consider the boundary divisor \(D_{n,n+1}\) and let
-th label. Consider the boundary divisor \(D_{n,n+1}\) and let  be the inclusion morphism. The following varieties can be naturally identified:
be the inclusion morphism. The following varieties can be naturally identified:

and therefore we have a commutative diagram

Definition 4.1
If  , then
, then  will be called the lift of
\(\alpha \)
to
will be called the lift of
\(\alpha \)
to
 .
.
Observe that, instead of just considering \(D_{n,n+1}\), one can do a similar construction with any \(D_{ab}\), \(\{a,b\}\subset [n+1]\). As the following lemma explains, some of the properties of \(\alpha \) are preserved after we lift it.
Lifting Lemma
Let k and n be integers such that \(0<k<n-3\). Let \(\alpha \) be the equivalence class of an effective k-cycle on  . Consider the maps
. Consider the maps  and
and  as above. Then
as above. Then
-
(i)
if
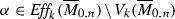 , then
, then 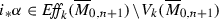 ;
; -
(ii)
if \(\alpha \) is extremal in
 , then
, then  is extremal in
is extremal in  .
.
Proof
(i) Assume by contradiction that  . Therefore we can write \(i_*\alpha =\sum _{j=1}^mr_j[Z_j]\), where \(r_j\in \mathbb {R}_{>0}\) and
. Therefore we can write \(i_*\alpha =\sum _{j=1}^mr_j[Z_j]\), where \(r_j\in \mathbb {R}_{>0}\) and  are boundary k-strata. But then
are boundary k-strata. But then  , because \(\pi _*[Z_j]\) is either zero or the equivalence class of a boundary k-stratum on
, because \(\pi _*[Z_j]\) is either zero or the equivalence class of a boundary k-stratum on  for all j. This is a contradiction.
for all j. This is a contradiction.
(ii) Assume that \(i_*\alpha =\sum _{j=1}^mr_j[Z_j]\), where \(r_j\in \mathbb {R}_{>0}\) and  are irreducible and effective k-cycles. We prove that \([Z_j]\) is proportional to \(i_*\alpha \) for all \(j=1,\ldots ,m\).
are irreducible and effective k-cycles. We prove that \([Z_j]\) is proportional to \(i_*\alpha \) for all \(j=1,\ldots ,m\).
Consider the reduction morphism  where \(\mathscr {A}\) is the weight data \((1/(n-1),\ldots ,1/(n-1),1,1)\) (see [13]). The exceptional locus of \(f_{\mathscr {A}}\) is exactly
where \(\mathscr {A}\) is the weight data \((1/(n-1),\ldots ,1/(n-1),1,1)\) (see [13]). The exceptional locus of \(f_{\mathscr {A}}\) is exactly  and \(f_{\mathscr {A}}(D_{n,n+1})\) is a point. In particular \(f_{\mathscr {A}*}i_*\alpha =0\), implying that
and \(f_{\mathscr {A}}(D_{n,n+1})\) is a point. In particular \(f_{\mathscr {A}*}i_*\alpha =0\), implying that
Since  is projective, we have that \(f_{\mathscr {A}*}[Z_j]=0\) for all j, which is equivalent to \(\dim f_{\mathscr {A}}(Z_j)<k\) for all j. This implies that, given any j, \(Z_j\subset D_{n,n+1}\). Define \(Z_j'=i^{-1}Z_j\), so that \(i_*[Z_j']=Z_j\), and therefore \(\sum _{j=1}^mr_j[Z_j']\) is an effective k-cycle on
is projective, we have that \(f_{\mathscr {A}*}[Z_j]=0\) for all j, which is equivalent to \(\dim f_{\mathscr {A}}(Z_j)<k\) for all j. This implies that, given any j, \(Z_j\subset D_{n,n+1}\). Define \(Z_j'=i^{-1}Z_j\), so that \(i_*[Z_j']=Z_j\), and therefore \(\sum _{j=1}^mr_j[Z_j']\) is an effective k-cycle on  such that
such that
The pushforward morphism \(i_*\) is injective on k-cycles, because  is the identity. It follows that \(\alpha =\sum _{j=1}^mr_j[Z_j']\), and hence each \([Z_j']\) is proportional to \(\alpha \) by the extremality of \(\alpha \) in
is the identity. It follows that \(\alpha =\sum _{j=1}^mr_j[Z_j']\), and hence each \([Z_j']\) is proportional to \(\alpha \) by the extremality of \(\alpha \) in  . In particular, each \([Z_j]\) has to be proportional to \(i_*\alpha \) for all j. \(\square \)
. In particular, each \([Z_j]\) has to be proportional to \(i_*\alpha \) for all j. \(\square \)
Alternatively, the following proposition can be used to prove the second part of the lifting lemma.
Proposition 4.2
([4, Proposition 2.5]) Let \(\gamma :Y\rightarrow X\) be a morphism between two projective varieties. Assume that \(A_k(Y)\rightarrow N_k(Y)\) is an isomorphism and that the composite \(\gamma _*:A_k(Y)\rightarrow A_k(X)\rightarrow N_k(X)\) is injective. Moreover, assume that \(f:X\rightarrow W\) is a morphism to a projective variety W whose exceptional locus is contained in \(\gamma (Y)\). If a k-dimensional subvariety \(Z\subset Y\) is an extremal cycle in \(Eff _k(Y)\) and if \(\dim \gamma (Z)-\dim f(\gamma (Z))>0\), then \(\gamma (Z)\) is also extremal in \(Eff _k(X)\).
Given this result, one can prove that \(i_*\alpha \) is extremal by taking  ,
,  , \(\gamma =i\),
, \(\gamma =i\),  with \(\mathscr {A}=(1/(n-1),\ldots ,1/(n-1),1,1)\), \(f=f_{\mathscr {A}}\) and \([Z]=\alpha \).
with \(\mathscr {A}=(1/(n-1),\ldots ,1/(n-1),1,1)\), \(f=f_{\mathscr {A}}\) and \([Z]=\alpha \).
4.2 Fulton’s question
The following question is attributed to Fulton.
Question
([17, Question 1.1]) Let \(0< k< n-3\). Is it true that  ?
?
Following [11, 22] notation, denote the previous question with \(F_k(0,n)\) (observe that the analogue question for \(k=0\) or \(k=n-3\) is trivial). \(F_1(0,5)\) is answered positively because  is a del Pezzo of degree 5. The answer to \(F_1(0,6)\) and \(F_1(0,7)\) is also yes, but this is a deep result of Keel and McKernan (see [17]). \(F_1(0,n)\) for \(n>7\) is an open question, and the conjecture that says \(F_1(0,n)\) has a positive answer for \(n>7\) is called the F-conjecture.
is a del Pezzo of degree 5. The answer to \(F_1(0,6)\) and \(F_1(0,7)\) is also yes, but this is a deep result of Keel and McKernan (see [17]). \(F_1(0,n)\) for \(n>7\) is an open question, and the conjecture that says \(F_1(0,n)\) has a positive answer for \(n>7\) is called the F-conjecture.
Keel and Vermeire showed that \(F_{n-4}(0,n)\) has a negative answer for all \(n\ge 6\) (see [11, 22]). This result, combined with the lifting lemma, clearly shows what is the answer to \(F_k(0,n)\) for \(1<k<n-4\).
Corollary 4.3
If \(1<k<n-4\), then \(F_k(0,n)\) has a negative answer, or in other words  .
.
Proof
We know that  from [11, 22]. Therefore, using the lifting lemma, we see that
from [11, 22]. Therefore, using the lifting lemma, we see that  . Now, by iterating this argument, we obtain that
. Now, by iterating this argument, we obtain that  . \(\square \)
. \(\square \)
5 Lifts to  of the Keel–Vermeire divisors on \(\overline{M}_{0,6}\)
of the Keel–Vermeire divisors on \(\overline{M}_{0,6}\)
The following description of the Keel–Vermeire divisors on  is convenient for us.
is convenient for us.
Definition 5.1
Assume \([6]=\{i,j,k,\ell ,m,q\}\). A divisor on  in the from
in the from

is called a Keel–Vermeire divisor on
 .
.
Properties of the Keel–Vermeire divisors on
\(\overline{M}_{0,6}\) A Keel–Vermeire divisor \(\delta _{mq,ij}^\mathrm{KV}\) on  is effective and cannot be written as an effective sum of boundary divisors. This is proved in [22] in characteristic zero, and one can see that it actually holds in any characteristic. It is also important for us to know that the Keel–Vermeire divisors on
is effective and cannot be written as an effective sum of boundary divisors. This is proved in [22] in characteristic zero, and one can see that it actually holds in any characteristic. It is also important for us to know that the Keel–Vermeire divisors on  are extremal in the cone
are extremal in the cone  in any characteristic. A proof of this can be found in [3]. Observe that \(\delta _{mq,ij}^\mathrm{KV}=\delta _{ij,mq}^\mathrm{KV}=\delta _{qm,ij}^\mathrm{KV}=\delta _{mq,ji}^\mathrm{KV}=\delta _{mq,k\ell }^\mathrm{KV}\), therefore there are 15 Keel–Vermeire divisors on
in any characteristic. A proof of this can be found in [3]. Observe that \(\delta _{mq,ij}^\mathrm{KV}=\delta _{ij,mq}^\mathrm{KV}=\delta _{qm,ij}^\mathrm{KV}=\delta _{mq,ji}^\mathrm{KV}=\delta _{mq,k\ell }^\mathrm{KV}\), therefore there are 15 Keel–Vermeire divisors on  .
.
One more property (but we do not use it in this paper) is that the Keel–Vermeire divisors together with the boundary divisors on  generate the cone
generate the cone  . This was first proved by Hassett and Tschinkel in [14]. An alternative proof of this fact can be found in [1] (actually, in [1] it is proved that the Cox ring of
. This was first proved by Hassett and Tschinkel in [14]. An alternative proof of this fact can be found in [1] (actually, in [1] it is proved that the Cox ring of  is generated by the sections of these divisors, which is a stronger condition).
is generated by the sections of these divisors, which is a stronger condition).
Now we want to lift the Keel–Vermeire divisors to  and give a combinatorial description of these lifts.
and give a combinatorial description of these lifts.
Proposition 5.2
Let \([7]=\{a,b,i,j,k,\ell ,m\}\). Then any lift to  of a Keel–Vermeire divisor on
of a Keel–Vermeire divisor on  can be written as the following linear combination of boundary 2-strata:
can be written as the following linear combination of boundary 2-strata:
Proof
Let us choose a boundary divisor \(D_{ab}\) on  . This can be identified with
. This can be identified with  , where x is an extra label. So, if we write
, where x is an extra label. So, if we write  , a Keel–Vermeire divisor on
, a Keel–Vermeire divisor on  is in the form
is in the form

If  is the natural inclusion, then the lift to
is the natural inclusion, then the lift to  of \(\delta _{mx,ij}^\mathrm{KV}\) is by definition
of \(\delta _{mx,ij}^\mathrm{KV}\) is by definition

Now, each one of the pushforwards appearing in the right hand side of the previous identity, can be computed by attaching along x a rational tail with the labels \(\{x,a,b\}\). By doing so, we obtain the claimed 2-cycle on  . \(\square \)
. \(\square \)
Notation
We use \(\sigma _{ab,m,ij}^\mathrm{KV}\) to denote the following lift to  of a Keel–Vermeire divisor on
of a Keel–Vermeire divisor on  :
:

The next lemma will be used several times.
Lemma 5.3
Let  be the map forgetting the label \(y\in [7]\), and let \(\sigma _{ab,m,ij}^\mathrm{KV}\) be a lift to
be the map forgetting the label \(y\in [7]\), and let \(\sigma _{ab,m,ij}^\mathrm{KV}\) be a lift to  of a Keel–Vermeire divisor on
of a Keel–Vermeire divisor on  . Then
. Then

Proof
First observe that

In the same way, one can prove that \(\pi _{b*}\sigma _{ab,m,ij}^\mathrm{KV}=\delta _{ma,ij}^\mathrm{KV}\).
Let  . Up to relabeling, we can assume that \(\sigma _{ab,m,ij}^\mathrm{KV}=\sigma _{67,5,12}^\mathrm{KV}\). Moreover, by the symmetries of the Keel–Vermeire divisors, we just have to prove our claim when \(y=5\) or \(y=1\). In the former case,
. Up to relabeling, we can assume that \(\sigma _{ab,m,ij}^\mathrm{KV}=\sigma _{67,5,12}^\mathrm{KV}\). Moreover, by the symmetries of the Keel–Vermeire divisors, we just have to prove our claim when \(y=5\) or \(y=1\). In the former case,

Finally, if \(y=1\), we have that

\(\square \)
Since we have \(\left( {\begin{array}{c}7\\ 2\end{array}}\right) \) choices for \(D_{ab}\) and 15 choices for a Keel–Vermeire divisor inside \(D_{ab}\), in total we have 315 lifts of Keel–Vermeire divisors to  . The question now is whether these 315 equivalence classes generate different extremal rays of
. The question now is whether these 315 equivalence classes generate different extremal rays of  . This is what we are about to prove.
. This is what we are about to prove.
Proposition 5.4
The 315 lifts to  of the Keel–Vermeire divisors on
of the Keel–Vermeire divisors on  generate distinct extremal rays of
generate distinct extremal rays of  that lie outside of
that lie outside of  .
.
Proof
The extremality of these rays and the fact that they lie outside of the cone  follow from our lifting lemma in Sect. 4. Let us prove that these rays are all distinct.
follow from our lifting lemma in Sect. 4. Let us prove that these rays are all distinct.
Consider two lifts of Keel–Vermeire divisors in the form \(\sigma _{ab,m,ij}^\mathrm{KV}\), \(\sigma _{ab,m',i'j'}^\mathrm{KV}\). Assume that \(\sigma _{ab,m,ij}^\mathrm{KV}=r\sigma _{ab,m',i'j'}^\mathrm{KV}\) for some \(r\in \mathbb {R}_{>0}\). Then we must have  which implies that \(\delta _{mb,ij}^\mathrm{KV}=\delta _{m'b,i'j'}^\mathrm{KV}\) because different Keel–Vermeire divisors generate different rays. In particular, \(\sigma _{ab,m,ij}^\mathrm{KV}=\sigma _{ab,m',i'j'}^\mathrm{KV}\). From this we conclude that lifts of different Keel–Vermeire divisors which are contained in the same boundary divisor give rise to distinct rays of
which implies that \(\delta _{mb,ij}^\mathrm{KV}=\delta _{m'b,i'j'}^\mathrm{KV}\) because different Keel–Vermeire divisors generate different rays. In particular, \(\sigma _{ab,m,ij}^\mathrm{KV}=\sigma _{ab,m',i'j'}^\mathrm{KV}\). From this we conclude that lifts of different Keel–Vermeire divisors which are contained in the same boundary divisor give rise to distinct rays of  .
.
Let us consider two distinct boundary divisors \(D_{ab}\) and \(D_{cd}\). Consider two lifts \(\sigma _{ab,m,ij}^\mathrm{KV}\) and \(\sigma _{cd,m',i'j'}^\mathrm{KV}\). Assume by contradiction that \(\sigma _{ab,m,ij}^\mathrm{KV}=r\sigma _{cd,m',i'j'}^\mathrm{KV}\) for some \(r\in \mathbb {R}_{>0}\). Since \(D_{ab}\) and \(D_{cd}\) are distinct, we can assume without loss of generality that \(a\notin \{c,d\}\). It follows that

which is a contradiction because a Keel–Vermeire divisor cannot be proportional to a boundary divisor. \(\square \)
Definition 5.5
Define  to be the cone generated by the boundary 2-strata on
to be the cone generated by the boundary 2-strata on  and the lifts to
and the lifts to  of the Keel-Vermeire divisors on
of the Keel-Vermeire divisors on  .
.
Corollary 5.6
The cone  has at least 735 extremal rays: 420 are generated by the boundary 2-strata and 315 are generated by the lifts of Keel–Vermeire divisors. In particular, the closed cone
has at least 735 extremal rays: 420 are generated by the boundary 2-strata and 315 are generated by the lifts of Keel–Vermeire divisors. In particular, the closed cone  has exactly 735 extremal rays.
has exactly 735 extremal rays.
Now our goal is to describe  outside of the cone
outside of the cone  . The first question that one may ask is whether or not
. The first question that one may ask is whether or not  is equal to
is equal to  . In what follows, we establish that these two cones are not equal.
. In what follows, we establish that these two cones are not equal.
6 Embedded blow ups of \(\mathbb {P}^2\) in \(\overline{M}_{0,n}\)
6.1 The blow up construction
In [2], Castravet and Tevelev give a way to embed  in
in  , where the embedding and the blow up depend on the choice of n points in \(\mathbb {P}^2\). Moreover, they tell us how the boundary divisors pullback under this embedding. Here is their construction.
, where the embedding and the blow up depend on the choice of n points in \(\mathbb {P}^2\). Moreover, they tell us how the boundary divisors pullback under this embedding. Here is their construction.
Theorem 6.1
([2, Theorem 3.1]) Suppose \(p_1,\ldots ,p_n\in \mathbb {P}^2\) are distinct points, and let \(U\subset \mathbb {P}^2\) be the complement of the union of the lines spanned by these points. Consider the morphism
defined as follows: given \(p\in U\), let \(F(p)=\bigl [(\mathbb {P}^1;\varphi _p(p_1),\ldots ,\varphi _p(p_n))\bigr ]\), where \(\varphi _p:\mathbb {P}^2\dashrightarrow \mathbb {P}^1\) is the projection from p. Then F extends to a morphism

If the points \(p_1,\ldots ,p_n\) do not lie on a (possibly reducible) conic, then F is a closed embedding. In this case the boundary divisors \(\delta _I\) of  pullback as follows: for each line L in our line arrangement, if \(I\subseteq [n]\) is such that \(p_i\in L\Leftrightarrow i\in I\), then \(F^*\delta _I=\widehat{L}_I\) (the strict transform of \(L_I)\) and (assuming \(|I|\ge 3)\)
\(F^*\delta _{I\setminus \{k\}}=E_k\), where \(k\in I\) and \(E_k\) is the exceptional divisor over \(p_k\). Other boundary divisors pullback trivially.
pullback as follows: for each line L in our line arrangement, if \(I\subseteq [n]\) is such that \(p_i\in L\Leftrightarrow i\in I\), then \(F^*\delta _I=\widehat{L}_I\) (the strict transform of \(L_I)\) and (assuming \(|I|\ge 3)\)
\(F^*\delta _{I\setminus \{k\}}=E_k\), where \(k\in I\) and \(E_k\) is the exceptional divisor over \(p_k\). Other boundary divisors pullback trivially.
In [2], this theorem is used to embed curves in  that are possible candidate to be counterexamples to the F-conjecture (later on in the paper, they show that these curves actually are not counterexamples by means of the “arithmetic break” technique).
that are possible candidate to be counterexamples to the F-conjecture (later on in the paper, they show that these curves actually are not counterexamples by means of the “arithmetic break” technique).
From now on, our attention is focused on this kind of embedded surfaces. Let us give a name to them.
Definition 6.2
Consider n points \(p_1,\ldots ,p_n\in \mathbb {P}^2\) that do not lie on a (possibly reducible) conic. Then, using Theorem 6.1, the embedded surface  will be called an embedded blow up of
\(\mathbb {P}^2\)
in
will be called an embedded blow up of
\(\mathbb {P}^2\)
in
 . The points \(p_1,\ldots ,p_n\) will be called the points associated to the embedded blow up.
. The points \(p_1,\ldots ,p_n\) will be called the points associated to the embedded blow up.
Remark 6.3
If \(\sigma \) is the equivalence class of an embedded blow up of \(\mathbb {P}^2\) in  , observe that the intersection properties of \(\sigma \) can be studied using the projection formula. Let \(\sigma _{I,J,K}\) be a codimension 2 boundary stratum on
, observe that the intersection properties of \(\sigma \) can be studied using the projection formula. Let \(\sigma _{I,J,K}\) be a codimension 2 boundary stratum on  . Then
. Then

Now, the intersection  is easy to compute because the two divisors \(F^*\delta _I\) and \(F^*\delta _K\) can be either zero, an exceptional divisor, or the strict transform of a line that is spanned by the n points in \(\mathbb {P}^2\).
is easy to compute because the two divisors \(F^*\delta _I\) and \(F^*\delta _K\) can be either zero, an exceptional divisor, or the strict transform of a line that is spanned by the n points in \(\mathbb {P}^2\).
It will be crucial to know that the Keel–Vermeire divisors on  can be realized as particular embedded blow ups of \(\mathbb {P}^2\). This is proved by Castravet and Tevelev in [3, Section 9] using irreducible hypertrees.
can be realized as particular embedded blow ups of \(\mathbb {P}^2\). This is proved by Castravet and Tevelev in [3, Section 9] using irreducible hypertrees.
Definition 6.4
Let \(n\ge 3\) and \(d\ge 1\). A hypertree \({\Gamma }=\{{\Gamma }_1,\ldots ,{\Gamma }_d\}\) on the set [n] is a collection of subsets of [n] such that the following conditions are satisfied:
-
any subset \({\Gamma }_j\) has at least three elements;
-
any \(i\in [n]\) is contained in at least two subsets \({\Gamma }_j\);
-
(convexity axiom)

-
(normalization)
$$\begin{aligned} n-2=\sum _{j\in [d]}(|{\Gamma }_j|-2). \end{aligned}$$
A hypertree is irreducible if all the inequalities in the convexity axiom are strict. A planar realization for a hypertree \({\Gamma }\) on the set [n] is a configuration of different points \(p_1,\ldots ,p_n\in \mathbb {P}^2\) such that, for any subset \(S\subsetneq [n]\) with at least three points, \(\{p_i\}_{i\in S}\) are collinear if and only if \(S\subseteq {\Gamma }_j\) for some j.
Remark 6.5
It turns out that, up to a change of labels, there is a unique irreducible hypertree on the set [6], and a planar realization for this is given by the intersection points of four lines in \(\mathbb {P}^2\) in general linear position. In [3, Section 9] is proved that the embedding in  of the blow up of \(\mathbb {P}^2\) at the six points of this planar realization gives a Keel–Vermeire divisor. Moreover, we can actually obtain all the 15 Keel–Vermeire divisors by labeling the six points appropriately.
of the blow up of \(\mathbb {P}^2\) at the six points of this planar realization gives a Keel–Vermeire divisor. Moreover, we can actually obtain all the 15 Keel–Vermeire divisors by labeling the six points appropriately.
The reason why we are interested in these embedded blow ups of \(\mathbb {P}^2\) in  is because they allow us to provide examples of effective 2-cycles whose equivalence classes do not lie in the cone
is because they allow us to provide examples of effective 2-cycles whose equivalence classes do not lie in the cone  . The examples we discuss are given by what we call special hypertree surfaces, which are related to Castravet and Tevelev irreducible hypertrees.
. The examples we discuss are given by what we call special hypertree surfaces, which are related to Castravet and Tevelev irreducible hypertrees.
6.2 Special hypertree surfaces on 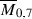
Definition 6.6
An embedded blow up of \(\mathbb {P}^2\) in  with associated points \(p_1,\ldots ,p_7\) will be called a hypertree surface on
with associated points \(p_1,\ldots ,p_7\) will be called a hypertree surface on
 if there exists \(y\in [7]\) such that \(p_1,\ldots ,\widehat{p}_y,\)
\(\ldots ,p_7\) is a planar realization for an irreducible hypertree on the set
if there exists \(y\in [7]\) such that \(p_1,\ldots ,\widehat{p}_y,\)
\(\ldots ,p_7\) is a planar realization for an irreducible hypertree on the set  . A hypertree surface will be called special if we can find three distinct such \(y\in [7]\).
. A hypertree surface will be called special if we can find three distinct such \(y\in [7]\).
Lemma 6.7
Let  be the equivalence class of a hypertree surface on
be the equivalence class of a hypertree surface on  . Then
. Then  .
.
Proof
Let \(p_1,\ldots ,p_7\in \mathbb {P}^2\) be the points associated to h and assume without loss of generality that the points \(p_1,\ldots ,p_6\) form a planar realization for an irreducible hypertree on the set [6]. Arguing by contradiction, let \(h=\sum \alpha _{I,J,K}\sigma _{I,J,K}\) for some coefficients \(\alpha _{I,J,K}\in \mathbb {R}_{\ge 0}\). If  is the morphism forgetting the 7-th label, we have that
is the morphism forgetting the 7-th label, we have that  . Now,
. Now,  can be either zero (for example
can be either zero (for example  ), or a boundary divisor (for example
), or a boundary divisor (for example  ). Therefore
). Therefore  is an effective sum of boundary divisors on
is an effective sum of boundary divisors on  . However, \(\pi _{7*}h\) can be thought of as the equivalence class of the surface in
. However, \(\pi _{7*}h\) can be thought of as the equivalence class of the surface in  obtained by embedding the blow up of \(\mathbb {P}^2\) at \(p_1,\ldots ,p_6\). But then
obtained by embedding the blow up of \(\mathbb {P}^2\) at \(p_1,\ldots ,p_6\). But then  has to be a Keel–Vermeire divisor (see Remark 6.5), implying that
has to be a Keel–Vermeire divisor (see Remark 6.5), implying that  cannot be written as an effective sum of boundary 2-strata. This gives a contradiction. \(\square \)
cannot be written as an effective sum of boundary 2-strata. This gives a contradiction. \(\square \)
Theorem 6.8
Let  be the equivalence class of a special hypertree surface on
be the equivalence class of a special hypertree surface on  . Then
. Then  .
.
Proof
Let \(p_1,\ldots ,p_7\in \mathbb {P}^2\) be the points associated to h. Up to relabeling, we can assume that \(y=5,6,7\) are such that \(p_1,\ldots ,\widehat{p}_y,\ldots ,p_7\) is a planar realization for an irreducible hypertree on the set  . Assume by contradiction that we can find nonnegative coefficients \(\alpha _{I,J,K}, \beta _{ab,m,ij}\) such that
. Assume by contradiction that we can find nonnegative coefficients \(\alpha _{I,J,K}, \beta _{ab,m,ij}\) such that

where  runs over the 15 lifts of the Keel–Vermeire divisors on \(D_{ab}\). Fix any coefficient \(\beta _{a'b',m',i'j'}\) (so that \(a',b',m',i'\) and \(j'\) are fixed indices). At least one number among 5, 6 and 7 is not contained in \(\{a',b'\}\). Assume without loss of generality that \(7\notin \{a',b'\}\). If we consider the morphism
runs over the 15 lifts of the Keel–Vermeire divisors on \(D_{ab}\). Fix any coefficient \(\beta _{a'b',m',i'j'}\) (so that \(a',b',m',i'\) and \(j'\) are fixed indices). At least one number among 5, 6 and 7 is not contained in \(\{a',b'\}\). Assume without loss of generality that \(7\notin \{a',b'\}\). If we consider the morphism  forgetting the 7-th label, using Lemma 5.3 we obtain that
forgetting the 7-th label, using Lemma 5.3 we obtain that

where  is a Keel–Vermeire divisor. The total coefficient of the boundary divisor \(\delta _{a'b'}\) in (1) is equal to a sum \((\cdots +\beta _{a'b',m',i'j'}+\cdots )\), where the terms of the sum are equal to some of the coefficients \(\alpha _{I,J,K}, \beta _{ab,m,ij}\). The Keel–Vermeire divisors are extremal in
is a Keel–Vermeire divisor. The total coefficient of the boundary divisor \(\delta _{a'b'}\) in (1) is equal to a sum \((\cdots +\beta _{a'b',m',i'j'}+\cdots )\), where the terms of the sum are equal to some of the coefficients \(\alpha _{I,J,K}, \beta _{ab,m,ij}\). The Keel–Vermeire divisors are extremal in  , therefore the coefficient of \(\delta _{a'b'}\) has to be zero. Since the terms in the sum \((\cdots +\beta _{a'b',m',i'j'}+\cdots )=0\) are nonnegative, it follows that \(\beta _{a'b',m',i'j'}=0\). But \(\beta _{a'b',m',i'j'}\) is arbitrary, so any coefficient \(\beta _{ab,m,ij}\) is equal to zero. This implies that
, therefore the coefficient of \(\delta _{a'b'}\) has to be zero. Since the terms in the sum \((\cdots +\beta _{a'b',m',i'j'}+\cdots )=0\) are nonnegative, it follows that \(\beta _{a'b',m',i'j'}=0\). But \(\beta _{a'b',m',i'j'}\) is arbitrary, so any coefficient \(\beta _{ab,m,ij}\) is equal to zero. This implies that  , which contradicts Lemma 6.7. \(\square \)
, which contradicts Lemma 6.7. \(\square \)
6.3 Classification of the special hypertree surfaces on 
Let us find all the possible special hypertree surfaces on  . We start by fixing a planar realization \(p_1,\ldots ,p_6\in \mathbb {P}^2\) for the irreducible hypertree given by
. We start by fixing a planar realization \(p_1,\ldots ,p_6\in \mathbb {P}^2\) for the irreducible hypertree given by
We consider permutations of these labels later on. Observe that the points \(p_1,\ldots ,p_6\) span seven lines: three of them contain exactly two labeled points, and the remaining four contain exactly three labeled points. Let X be the union of these seven lines. If  , this points and lines arrangement is shown below in Fig. 3 (\(\mathbb {K}\) is our base field).
, this points and lines arrangement is shown below in Fig. 3 (\(\mathbb {K}\) is our base field).
The characteristic 2 case is discussed separately at the end of this section. Therefore, for now assume that  .
.
Let us add a seventh point \(p_7\) to the configuration in Fig. 3. Take  . Then we cannot have a special hypertree surface, because if we drop a label \(y\in [6]\), the points \(p_1,\ldots ,\widehat{p}_y,\ldots ,p_7\) span at least five lines containing exactly two labeled points. Therefore we must have \(p_7\in X\).
. Then we cannot have a special hypertree surface, because if we drop a label \(y\in [6]\), the points \(p_1,\ldots ,\widehat{p}_y,\ldots ,p_7\) span at least five lines containing exactly two labeled points. Therefore we must have \(p_7\in X\).
Doing similar considerations, one can easily prove that \(p_7\) must lie in the intersection of at least two lines in X. Since \(p_7\) is distinct from \(p_1,\ldots ,p_6\), we have three possibilities for \(p_7\) (the lines in X intersect in 9 points). All three of these cases give a special hypertree surface, as shown in Fig. 4. The arrows show the three points \(p_y\) that can be dropped in order to get an irreducible hypertree on the set  . Consider the action
. Consider the action  induced by the natural action
induced by the natural action  . When a permutation \(\tau \in S_7\) acts on
. When a permutation \(\tau \in S_7\) acts on  , we write
, we write  . Let \(h_1\) be the equivalence class of the special hypertree surface obtained by using the top left points configuration in Fig. 4. Similarly, define \(h_2\) to be the equivalence class of the special hypertree surface obtained by using the top right configuration, and \(h_3\) the one obtained by using the bottom configuration in the same figure.
. Let \(h_1\) be the equivalence class of the special hypertree surface obtained by using the top left points configuration in Fig. 4. Similarly, define \(h_2\) to be the equivalence class of the special hypertree surface obtained by using the top right configuration, and \(h_3\) the one obtained by using the bottom configuration in the same figure.
First, observe that \(h_2\) belongs to the orbit of \(h_1\) under the \(S_7\)-action because  . Also \(h_3\) belongs to the orbit of \(h_1\), because
. Also \(h_3\) belongs to the orbit of \(h_1\), because  . Therefore, it is enough to consider the \(S_7\)-action on \(h_1\).
. Therefore, it is enough to consider the \(S_7\)-action on \(h_1\).
Let us find the stabilizer of \(h_1\) under the \(S_7\)-action. It is easy to find the following subgroup of \(\text {Stab}_{S_7}(h_1)\):

which is isomorphic to the dihedral group \(D_3\). It is less obvious to notice this other subgroup of the stabilizer

which is isomorphic to the Klein group  . To see why \(G_1,G_2\subseteq \text {Stab}_{S_7}(h_1)\), just take any \(\tau \in G_1\cup G_2\) and observe that
. To see why \(G_1,G_2\subseteq \text {Stab}_{S_7}(h_1)\), just take any \(\tau \in G_1\cup G_2\) and observe that  and \(h_1\) have the same intersection number with every boundary 2-stratum on
and \(h_1\) have the same intersection number with every boundary 2-stratum on  .
.
To show that \(\text {Stab}_{S_7}(h_1)\) is actually generated by \(G_1\) and \(G_2\), take any \(\tau \in \text {Stab}_{S_7}(h_1)\). Thinking of \(\tau \) as a bijection \(\tau :[7]\rightarrow [7]\), then \(\tau (\{3,4,7\})=\{3,4,7\}\). This is true because, in order to preserve the intersection numbers with the boundary 2-strata, we need to send a labeled point that lies on a line containing exactly two labeled points to a labeled point having the same property. In particular, we must have that \(\tau (\{1,2,5,6\})=\{1,2,5,6\}\). Therefore \(\tau \) acts by permuting the two sets \(\{3,4,7\}\) and \(\{1,2,5,6\}\) separately. Now there are two cases: \(\tau \) fixes 2 or not. In the first case, the only possibility for \(\tau \) is to be an element of \(G_1\). If \(\tau \) does not fix 2, then assume that \(\tau \) is the identity on \(\{3,4,7\}\) (we can assume this up to composing with an element of \(G_1\)). In this case, one can check that \(\tau \) must be an element of \(G_2\) in order to preserve the intersection numbers with the boundary 2-strata on  . Therefore, we just deduced that \(\text {Stab}_{S_7}(h_1)=\langle G_1,G_2\rangle \).
. Therefore, we just deduced that \(\text {Stab}_{S_7}(h_1)=\langle G_1,G_2\rangle \).
An easy count tells us that \(\langle G_1,G_2\rangle =24\), and therefore the orbit of \(h_1\) has \(7!/24=210\) distinct equivalence classes. As one can easily check, these classes generate distinct rays in  . The next proposition summarizes what we proved so far.
. The next proposition summarizes what we proved so far.
Proposition 6.9
In characteristic different from 2, there are 210 distinct equivalence classes of special hypertree surfaces on  . These classes generate 210 distinct rays of
. These classes generate 210 distinct rays of  which lie outside of the cone
which lie outside of the cone  .
.
Classification in characteristic 2
The discussion in characteristic 2 is essentially the same, but with the following exceptions. First of all, in Fig. 3, the seven lines intersect in seven points (one of which is unlabeled), giving the well known Fano configuration. Also in this case, \(p_7\) has to be the unlabeled point at the intersection of three lines, and therefore we produced only one special hypertree surface. Now, if we consider the \(S_7\)-action, it is straightforward to see that the stabilizer of the special hypertree surface we found is  , which has 168 elements. So, the analogue of Proposition 6.9 in characteristic 2 is the following.
, which has 168 elements. So, the analogue of Proposition 6.9 in characteristic 2 is the following.
Proposition 6.10
In characteristic 2, there are 30 distinct equivalence classes of special hypertree surfaces on  . These classes generate 30 distinct rays of
. These classes generate 30 distinct rays of  which lie outside of the cone
which lie outside of the cone  .
.
Remark 6.11
We do not know yet if the rays generated by the equivalence classes of the special hypertree surfaces are extremal in  , and certainly a proof or a disproof of the extremality of these rays would be a further step toward the understanding of the cone
, and certainly a proof or a disproof of the extremality of these rays would be a further step toward the understanding of the cone  .
.
Remark 6.12
We observed that the equivalence classes of the special hypertree surfaces are invariant with respect to a certain subgroup of \(S_7\). Given a subgroup G of \(S_n\), the idea of considering G-invariant sub-loci of  intersecting the interior \(M_{0,n}\) recently appeared in [19]. Also, the same idea was previously used to describe the Keel–Vermeire divisors (see [22, Section 3]).
intersecting the interior \(M_{0,n}\) recently appeared in [19]. Also, the same idea was previously used to describe the Keel–Vermeire divisors (see [22, Section 3]).
Remark 6.13
Consider the moduli space  , which is the quotient of
, which is the quotient of  by the natural action
by the natural action  . As we studied
. As we studied  , one can also consider
, one can also consider  . For a study of the pseudoeffective cone
. For a study of the pseudoeffective cone  see [10, Section 7.3].
see [10, Section 7.3].
Let us define the following subcone of  .
.
Definition 6.14
Define  to be the cone generated by the equivalence classes of the boundary 2-strata, the lifts of the Keel–Vermeire divisors on
to be the cone generated by the equivalence classes of the boundary 2-strata, the lifts of the Keel–Vermeire divisors on  and the embedded blow ups of \(\mathbb {P}^2\) in
and the embedded blow ups of \(\mathbb {P}^2\) in  .
.
It follows from what we proved that we have strict inclusions

7 Generalization to \(\overline{M}_{0,n}\) for any \(n>7\) and further questions
We can generalize our constructions for 2-cycles on  to any
to any  with \(n>7\). First, define
with \(n>7\). First, define  inductively to be the subcone of
inductively to be the subcone of  generated by
generated by  and by the lifts of the effective 2-cycles in
and by the lifts of the effective 2-cycles in  . Similarly, we can define
. Similarly, we can define  inductively to be the subcone of
inductively to be the subcone of  generated by
generated by  , by the lifts of the effective 2-cycles in
, by the lifts of the effective 2-cycles in  and by the embedded blow up of \(\mathbb {P}^2\) in
and by the embedded blow up of \(\mathbb {P}^2\) in  . Since we already know that
. Since we already know that  , it is not hard to see that we have the following strict inclusions:
, it is not hard to see that we have the following strict inclusions:

At this point, one can ask the following questions.
Question 7.1
Is  equal to
equal to  ?
?
Question 7.2
Is it possible to give examples of embedded blow ups of \(\mathbb {P}^2\) in  that generate extremal rays of
that generate extremal rays of  ?
?
Question 7.3
Is  equal to
equal to  ?
?
Notes
All the figures in this paper were realized using the software GeoGebra, Copyright International GeoGebra Institute, 2013.
References
Castravet, A.-M.: The Cox ring of \(\overline{M}_{0,6}\). Trans. Amer. Math. Soc. 361(7), 3851–3878 (2009)
Castravet, A.-M., Tevelev, J.: Rigid curves on \(\overline{M}_{0,n}\) and arithmetic breaks. In: Alexeev, V., et al. (eds.) Compact Moduli Spaces and Vector Bundles, Contemporary Mathematics, vol. 564, pp. 19–67. American Mathematical Society, Providence (2012)
Castravet, A.-M., Tevelev, J.: Hypertrees, projections, and moduli of stable rational curves. J. Reine Angew. Math. 675, 121–180 (2013)
Chen, D., Coskun, I.: Extremal higher codimension cycles on moduli spaces of curves. Proc. London Math. Soc. 111(1), 181–204 (2015)
Chen, L., Gibney, A., Krashen, D.: Pointed trees of projective spaces. J. Algebraic Geom. 18(3), 477–509 (2009)
Debarre, O., Ein, L., Lazarsfeld, R., Voisin, C.: Pseudoeffective and nef classes on abelian varieties. Compos. Math. 147(6), 1793–1818 (2011)
Doran, B., Giansiracusa, N., Jensen, D.: A simplicial approach to effective divisors in \(\overline{M}_{0,n}\) (2014). arXiv:1401.0350
Edidin, D.: The codimension-two homology of the moduli space of stable curves is algebraic. Duke Math. J. 67(2), 241–272 (1992)
Fulger, M.: The cones of effective cycles on projective bundles over curves. Math. Z. 269(1–2), 449–459 (2011)
Fulger, M., Lehmann, B.: Zariski decompositions of numerical cycle classes (2013). arXiv:1310.0538
Gibney, A., Keel, S., Morrison, I.: Towards the ample cone of \(\overline{M}_{g, n}\). J. Amer. Math. Soc. 15(2), 273–294 (2002)
Griffiths, P., Harris, J.: Principles of Algebraic Geometry. Wiley, New York (1994)
Hassett, B.: Moduli spaces of weighted pointed stable curves. Adv. Math. 173(2), 316–352 (2003)
Hassett, B., Tschinkel, Yu.: On the effective cone of the moduli space of pointed rational curves. In: Berrick, A.J., Leung, M.C., Xu, X. (eds.) Topology and Geometry: Commemorating SISTAG, Contemporary Mathematics, vol. 314, pp. 83–96. American Mathematical Society, Providence (2002)
Kapranov, M.M.: Veronese curves and Grothendieck–Knudsen moduli space \(\overline{M}_{0, n}\). J. Algebraic Geom. 2(2), 239–262 (1993)
Keel, S.: Intersection theory of moduli space of stable \(n\)-pointed curves of genus zero. Trans. Amer. Math. Soc. 330(2), 545–574 (1992)
Keel, S., McKernan, J.: Contractible extremal rays on \(\overline{M}_{0,n}\). In: Farkas, G., Morrison, I. (eds.) Handbook of Moduli. Vol. II. Advanced Lectures in Mathematics, vol. 25, pp. 115–130. International Press, Somerville (2013)
Lehmann, B.: Geometric characterizations of big cycles (2013). arXiv:1309.0880
Moon, H.-B., Swinarski, D.: Effective curves on \(\overline{M}_{0, n}\) from group actions. Manuscripta Math. 147 (1–2), 239–268 (2015)
Opie, M.: Extremal divisors on moduli spaces of rational curves with marked points (2013). arXiv:1309.7229
Tarasca, N.: Brill–Noether loci in codimension two. Compos. Math. 149(9), 1535–1568 (2013)
Vermeire, P.: A counterexample to Fulton’s conjecture on \(\overline{M}_{0, n}\). J. Algebra 248(2), 780–784 (2002)
Acknowledgments
The author would like to express gratitude to his advisor, Valery Alexeev, for his insightful comments and helpful discussions. He is also grateful to Angela Gibney for her great suggestions and support. Many thanks to Noah Giansiracusa, Daniel Krashen, Dino Lorenzini and Robert Varley for interesting discussions and for their helpful feedback. Gratitude also goes to Ana-Maria Castravet, Dawei Chen, Izzet Coskun and Jenia Tevelev for great discussions related to this paper. A special thanks to Ana-Maria Castravet for pointing out a mistake in the first version of this paper, and to Jenia Tevelev for a helpful discussion on Lemma 6.7. The author is also grateful to the referees for their careful reading of the paper and their comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Partially supported by the Office of the Graduate School of the University of Georgia.
Rights and permissions
About this article
Cite this article
Schaffler, L. On the cone of effective 2-cycles on  .
European Journal of Mathematics 1, 669–694 (2015). https://doi.org/10.1007/s40879-015-0072-2
.
European Journal of Mathematics 1, 669–694 (2015). https://doi.org/10.1007/s40879-015-0072-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-015-0072-2







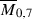
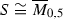 . By Kapranov’s blow up construction of
. By Kapranov’s blow up construction of  (see [
(see [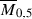 is isomorphic to the blow up of
is isomorphic to the blow up of 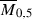 correspond to the exceptional divisors of the blow up, and the strict transforms of the lines spanned by the blown up points.
correspond to the exceptional divisors of the blow up, and the strict transforms of the lines spanned by the blown up points.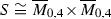 , which is isomorphic to
, which is isomorphic to 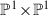 . An F-curve on S corresponds to a line on
. An F-curve on S corresponds to a line on  in the form
in the form  or
or 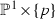 for some point
for some point 
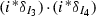 is equal to the self-intersection of an F-curve on
is equal to the self-intersection of an F-curve on  , which gives
, which gives  . So let us assume that
. So let us assume that  and
and  , then
, then  :
:  and
and 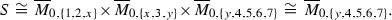
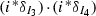 is equal to the self-intersection of an F-curve on
is equal to the self-intersection of an F-curve on 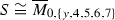 , which gives
, which gives 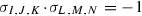 . Let us assume that
. Let us assume that 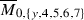 :
: 
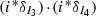 is equal to the self-intersection of an F-curve on
is equal to the self-intersection of an F-curve on 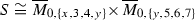 , which gives
, which gives  . Now consider the case
. Now consider the case  :
: 
 , the only possibility for
, the only possibility for 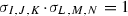 .
.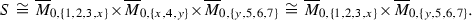
 is equal to the self-intersection of an F-curve on
is equal to the self-intersection of an F-curve on 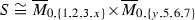 , which gives
, which gives  . For the case
. For the case  :
: 
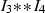 implies that
implies that  .
. . Let us use the boundary relation
. Let us use the boundary relation 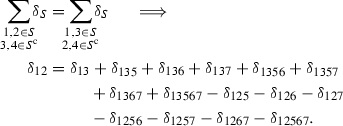
 is false or
is false or  is false. Hence,
is false. Hence,  . Consider
. Consider 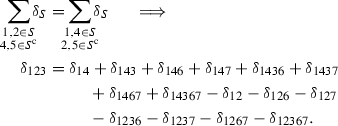
 .
. . We use the following boundary relation:
. We use the following boundary relation: 
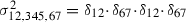 .
. 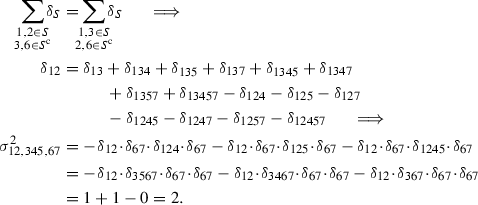
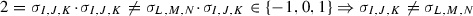 .
. with
with  can be equal to just 0 or
can be equal to just 0 or  (more in detail, if
(more in detail, if  , then
, then  ). However
). However  , so
, so 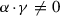 . According to Propositions
. According to Propositions 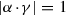 and
and 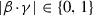 . In any case, the equality
. In any case, the equality  gives a contradiction.
gives a contradiction.
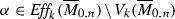 , then
, then 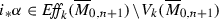 ;
; , then
, then  is extremal in
is extremal in  .
. of the Keel–Vermeire divisors on
of the Keel–Vermeire divisors on