Abstract
It is shown that if various cardinal invariants of the continuum related to \({\mathfrak {d}}\) are equal to \(\aleph _1\) then there is a non-trivial automorphism of \({\mathcal {P}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\). Some of these results extend to automorphisms of \({\mathcal {P}}(\kappa )/[\kappa ]^{<\kappa }\) if \(\kappa \) is inaccessible.
Similar content being viewed by others
1 Introduction
A fundamental result in the study of the Čech–Stone compactification, due to Rudin [7, 8], is that, assuming the Continuum Hypothesis, there are \(2^{\mathfrak {c}}\) autohomeomorphisms of  and, hence, there are some that are non-trivial in the sense that they are not induced by any one-to-one function on \({\mathbb {N}}\). While Rudin established his result by showing that for any two P-points of weight \(\aleph _1\) there is an autohomeomorphism sending one to the other, Parovičenko [6] showed that non-trivial autohomeomorphisms could be found by exploiting the countable saturation of the Boolean algebra of clopen subsets of
and, hence, there are some that are non-trivial in the sense that they are not induced by any one-to-one function on \({\mathbb {N}}\). While Rudin established his result by showing that for any two P-points of weight \(\aleph _1\) there is an autohomeomorphism sending one to the other, Parovičenko [6] showed that non-trivial autohomeomorphisms could be found by exploiting the countable saturation of the Boolean algebra of clopen subsets of  —this is isomorphic to the algebra \({\mathcal {P}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\). Indeed, the duality between Stone spaces of Boolean algebras and algebras of regular open sets shows that the existence of non-trivial autohomeomorphisms of
—this is isomorphic to the algebra \({\mathcal {P}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\). Indeed, the duality between Stone spaces of Boolean algebras and algebras of regular open sets shows that the existence of non-trivial autohomeomorphisms of  is equivalent to the existence of non-trivial isomorphisms of the Boolean algebra \({\mathcal {P}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\) to itself.
is equivalent to the existence of non-trivial isomorphisms of the Boolean algebra \({\mathcal {P}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\) to itself.
Notation 1.1
If A and B are subsets of \( \kappa \) let \(\equiv _\kappa \) denote the equivalence relation defined by  if and only if
if and only if  and
and  will denote the assertion that
will denote the assertion that  denote the equivalence class of A modulo \(\equiv _\kappa \) and let \({\mathcal {P}}(\kappa )/[\kappa ]^{<\kappa }\) denote the quotient algebra of the \({\mathcal {P}}(\kappa )\) modulo the congruence relation \(\equiv _\kappa \). If \(\kappa = \omega \) it is customary to use \(\equiv ^*\) instead of \(\equiv _\omega \) and \(\subseteq ^*\) instead of \(\subseteq _\omega \).
denote the equivalence class of A modulo \(\equiv _\kappa \) and let \({\mathcal {P}}(\kappa )/[\kappa ]^{<\kappa }\) denote the quotient algebra of the \({\mathcal {P}}(\kappa )\) modulo the congruence relation \(\equiv _\kappa \). If \(\kappa = \omega \) it is customary to use \(\equiv ^*\) instead of \(\equiv _\omega \) and \(\subseteq ^*\) instead of \(\subseteq _\omega \).
Notation 1.2
If f is a function defined on the set A and \(X\subseteq A\) then the notation f(X) will be used to denote \(\{f(x):x\in X\}\) in spite of the potential for ambiguity.
Definition 1.3
An isomorphism \({\Phi }:{\mathcal {P}}(\kappa )/[\kappa ]^{<\kappa }\rightarrow {\mathcal {P}}(\kappa )/[\kappa ]^{<\kappa }\) will be said to be trivial if there is a one-to-one function \(\varphi :\kappa \rightarrow \kappa \) such that \({\Phi }([A]_\kappa ) = [\varphi (A)]_\kappa \) for each \(A\subseteq \kappa \). The isomorphism \({\Phi }\) will be said to be somewhere trivial if there is some \(B\in [\kappa ]^\kappa \) and a one-to-one function \(\varphi :B\rightarrow \kappa \) such that \({\Phi }([A]_\kappa ) = [\varphi (A)]_\kappa \) for each \(A\subseteq B\) and \({\Phi }\) will be said to be nowhere trivial if it is not somewhere trivial.
The question of whether the Continuum Hypothesis, or some other hypothesis, is needed in order to find a non-trivial isomorphism of \({\mathcal {P}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\) to itself was settled in the affirmative by Shelah in [9]. The argument of [9] relies on an iterated oracle chain condition forcing to obtain a model where \(2^{\aleph _0} = \aleph _2\) and every isomorphism of \({\mathcal {P}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\) to itself is induced by a one-to-one function from \({\mathbb {N}}\) to \({\mathbb {N}}\). The oracle chain condition requires the addition of cofinally many Cohen reals and so \({\mathfrak {d}} = \aleph _2\) in this model. Subsequent work has shown that it is also possible to obtain that every isomorphism of \({\mathcal {P}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\) is trivial by other approaches [2, 10, 14] but these have always required \({\mathfrak {d}} > \aleph _1\) as well. However, it was shown in [11] that this cardinal inequality is not entailed by the non existence of nowhere trivial isomorphisms from \({\mathcal {P}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\) to itself—in the model obtained by iterating \(\omega _2\) times Sacks reals there are no nowhere trivial isomorphisms yet \({\mathfrak {d}} = \aleph _1\).
On the other hand, while we now know that the Continuum Hypothesis cannot be completely eliminated from Rudin’s result, perhaps it can be weakened to some other cardinal equality such as \({\mathfrak {d}} = \aleph _1\). It will be shown in this article that non-trivial isomorphisms of \({\mathcal {P}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\) to itself can indeed be constructed from hypotheses on cardinal arithmetic weaker than \(2^{\aleph _0} = \aleph _1\) and reminiscent of \({\mathfrak {d}} = \aleph _1\). However, it is shown in [3] that it is consistent with set theory that \({\mathfrak {d}}=\aleph _1\) yet all isomorphisms of \({\mathcal {P}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\) are trivial so some modification of the equality \({\mathfrak {d}} = \aleph _1\) will be required.
It will also be shown that natural generalizations of the arguments can be applied to the same question for \({\mathcal {P}}(\kappa )/[\kappa ]^{<\kappa }\) where \(\kappa \) is inaccessible. The chief interest here is that, unlike \({\mathcal {P}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\), the algebra \({\mathcal {P}}(\kappa )/[\kappa ]^{<\kappa }\) is not countably saturated if \(\kappa >\omega \)—to see this, simply consider a family \(\{A_n\}_{n\in \omega }\subseteq [\kappa ]^\kappa \) such that \(\bigcap _{n\in \omega } A_n=\varnothing \). In other words, Parovičenko’s transfinite induction argument to construct non-trivial isomorphisms from \({\mathcal {P}}(\kappa )/[\kappa ]^{<\kappa }\) to itself is not available and some other technique is needed.
The statement and proof of Lemma 2.1 is provided for all \(\kappa \) and we will apply both to the case that \(\kappa =\omega \) and to the case that \(\kappa \) is inaccessible. However, Lemma 3.2 deals only with the case that \(\kappa \) is inaccessible. It is somewhat simpler than the case for \(\omega \) and so is dealt with first because the general approach is similar in the \(\kappa = \omega \) case, but this case requires some technical details not needed in the inaccessible case.
2 A sufficient condition for a non-trivial isomorphism
The following lemma provides sufficient conditions for the existence of a non-trivial isomorphism of \({\mathcal {P}}(\kappa )/[\kappa ]^{<\kappa }\) to itself. The set theoretic requirements for the satisfaction of these conditions will be examined later. The basic idea of the lemma is that an isomorphism of \({\mathcal {P}}(\kappa )/[\kappa ]^{<\kappa }\) can be approximated by partitioning \(\kappa \) into small sets \(I_\nu \) and constructing isomorphisms from subalgebras of \({\mathcal {P}}(I_\nu )\) and taking the union of these. Unless the subalgebras of \({\mathcal {P}}(I_\nu )\) are all of \({\mathcal {P}}(I_\nu )\), this union will only be a partial isomorphism. Hence a \(\kappa ^+\) length sequence of ever larger families of subalgebras of \({\mathcal {P}}(I_\nu )\) is needed to obtain a full isomorphism. In order to guarantee that this isomorphism is not trivial the prediction principle described in hypothesis (H\(_3\)) of the lemma is needed.
Lemma 2.1
There is a non-trivial automorphism of \({\mathcal {P}}(\kappa )/[\kappa ]^{<\kappa }\) provided that there is a partition of \(\kappa \) by \(\{I_\nu \}_{\nu \in \kappa }\) such that
- \(({H}_1)\) :
-
\(|I_\nu |<\kappa \) for each \(\nu \in \kappa \).
- \(({H}_2)\) :
-
For each \(\xi \in \kappa ^+\) and \(\nu \in \kappa \) there is a Boolean subalgebra \({\mathfrak {B}}_{\xi ,\nu }\) of \({\mathcal {P}}(I_\nu )\) and an automorphism \({\Phi }_{\xi ,\nu }\) of \({\mathfrak {B}}_{\xi ,\nu }\).
- \(({H}_3)\) :
-
If \(\xi \in \eta \) then there is \(\iota \in \kappa \) such that \({\mathfrak {B}}_{\xi ,\nu }\subseteq {\mathfrak {B}}_{\eta ,\nu }\) and
 for all
for all 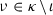 .
. - \(({H}_4)\) :
-
For any one-to-one \(F:\kappa \rightarrow \kappa \) there are \(\xi \in \kappa ^+\) and cofinally many \(\nu \in \kappa \) for which there is an atom \(a\in {\mathfrak {B}}_{\xi ,\nu }\) and \(\iota \in a\) such that \(F(\iota )\notin {\Phi }_{\xi ,\nu }(a)\).
- \(({H}_5)\) :
-
For any \(A\subseteq \kappa \) there are \(\xi \in \kappa ^+\) and \(\iota \) in \(\kappa \) such that \(A\cap I_\nu \in {\mathfrak {B}}_{\xi ,\nu }\) for all
 .
.
Proof
Define

and begin by observing that this is well defined. To see this, it must first be observed that given A and B such that  there is \(\alpha \in \kappa ^+\) such that for all \(\xi >\alpha \) and for all \(\nu \) in a final segment of \(\kappa \) the equation
there is \(\alpha \in \kappa ^+\) such that for all \(\xi >\alpha \) and for all \(\nu \) in a final segment of \(\kappa \) the equation
is defined and valid by hypothesis \((\hbox {H}_4)\). From hypothesis \((\hbox {H}_2)\) it then follows that if \(\xi \) and \(\eta \) are greater than \(\alpha \) then

and, hence, \({\Phi }([A]_\kappa )\) is well defined. Since each \({\Phi }_{\xi ,\nu }\) is an automorphism it follows that \({\Phi }\) is an automorphism of \({\mathcal {P}}(\kappa )/[\kappa ]^{<\kappa }\).
To see that \({\Phi }\) is non-trivial, suppose that there is a one-to-one function \(F:\kappa \rightarrow \kappa \) such that \( F( A)\in {\Phi }([A]_\kappa )\) for all \(A\subseteq \kappa \). Using hypothesis (H\(_3\)) choose \(\xi \in \kappa ^+\) for which there is \(Z\in [\kappa ]^\kappa \) and atoms \(a_\nu \in {\mathfrak {B}}_{\xi ,\nu }\) and \(j_\nu \in a_\nu \) such that \(F(j_\nu )\notin {\Phi }_{\xi ,\nu }(a_\nu )\) for each \(\nu \in Z\). Let \(W\in [Z]^\kappa \) be such that for each \(\nu \in W\), if \(F(j_\nu )\in I_\mu \) and \(\mu \ne \nu \) then \(\mu \notin W\). Let \(A= \bigcup _{\nu \in W}a_\nu \). It follows from hypothesis (H\(_2\)) that for any \(\eta \ge \xi \)

and, hence, \(F(A)\notin {\Phi }([A]_\kappa )\). \(\square \)
3 When are the hypotheses of Lemma 2.1 satisfied?
In answering a question of A. Blass concerning the classification of cardinal invariants of the continuum based on the Borel hierarchy Goldstern and Shelah introduced a family of cardinal invariants called \(\mathbf{c}(f,g)\) defined to be the least number of uniform trees with g-splitting needed to cover a uniform tree with f-splitting [4] and showed that uncountably many of these can be distinct simultaneously. The following definition is very closely related to this as well as to the notion of a slalom found in [1].
Definition 3.1
Given functions f and g from \({{\mathrm{\mathbf{cof}}}}(\kappa )\) to \(\kappa \) such that \(g(\xi )\) is a cardinal for each \(\xi \in {{\mathrm{\mathbf{cof}}}}(\kappa )\), let \({\mathfrak {d}}_{f,g}\) be the least cardinal of a family \({\mathcal {D}}\subseteq \prod _{\nu \in \kappa }[f(\nu )]^{g(\nu )}\) such that for every \(F\in \prod _{\nu \in \kappa }f(\nu )\) there is \(G\in {\mathcal {D}}\) such that \(F(\nu )\in G(\nu )\) for all \(\nu \). Given a uniform filter \({\mathcal {F}}\) on \(\kappa \) define \({\mathfrak {d}}_{f,g}({\mathcal {F}})\) to be the least cardinal of a family \({\mathcal {D}}\subseteq \prod _{\nu \in \kappa }[f(\nu )]^{g(\nu )}\) such that for every \(F\in \prod _{\nu \in \kappa }f(\nu )\) there is \(G\in {\mathcal {D}}\) and \(X\in {\mathcal {F}}\) such that \(F(\nu )\in G(\nu )\) for all \(\nu \in X\).
Lemma 3.2
Let \(\kappa \) be inaccessible and \(f:\kappa \rightarrow \kappa \) and \(g:\kappa \rightarrow \kappa \) be functions such that:
-
both f and g take their values in the set of cardinals,
-
\(\lim _{\nu \rightarrow \kappa }g(\nu ) = \kappa \),
-
\(2^{g(\nu )} < |f(\nu ) |\) for all \(\nu \in \kappa \),
-
\({\mathfrak {d}}_{2^f,g}({\mathcal {F}}) = \kappa ^+\) for some filter \({\mathcal {F}}\) generated by a \(\subseteq _\kappa \)-descending tower of length \(\kappa ^+\),
then the hypotheses of Lemma 2.1 hold.
Proof
Given the hypothesis, it may be assumed that there are \(\subseteq _\kappa \)-descending sets \(\{X_\xi \}_{\xi \in \kappa ^+}\subseteq {\mathcal {F}}\) and functions \(\{G_\xi \}_{\xi \in \kappa ^+}\subseteq \prod _{\nu \in \kappa }[2^{f(\nu )}]^{g(\nu )}\) such that for every \(F\in \prod _{\nu \in \kappa }2^{f(\nu )}\) there is \(\xi \in \kappa ^+\) such that \(F(\nu )\in G_\xi (\nu )\) for all \(\nu \) in a final segment of \(X_\xi \). (This is done simply by reindexing so that for all \(\xi \in \kappa ^+\) there are cofinally many \(\eta \in \kappa ^+\) such that \(G_\xi = G_\eta \).) Moreover, by a diagonal argument using the fact that \(\lim _{\nu \rightarrow \kappa }g(\nu )=\kappa \) it can be assumed that if \(\xi \in \eta \) then \(G_\xi (\nu ) \subseteq G_\eta (\nu )\) for a final segment of \(\nu \in X_\eta \). (This is the part of the argument that does not extend to the case \(\kappa = \omega \).)
Now let \(\{I_\nu \}_{\nu \in \kappa }\) partition \(\kappa \) so that \(|I_\nu | = f(\nu )\) and let \(\{\theta _{\iota ,\nu }\}_{\iota \in 2^{f(\nu )}}\) enumerate all permutations of \(I_\nu \). Let \(A_\nu :2^{f(\nu )}\rightarrow {\mathcal {P}}(I_\nu )\) be a bijection. Let \(A_{0,\nu }\) and \(A_{1,\nu }\) partition \(I_\nu \) into two sets of cardinality \(f(\nu )\) and let \(\varphi _{0,\nu }\) be an involution of \(I_\nu \) interchanging \(A_{0,\nu }\) and \(A_{1,\nu }\). For \(\nu \in X_0\) let \({\mathfrak {B}}_{0,\nu } = \{\varnothing , I_\nu , A_{0,\nu },A_{1,\nu }\}\) and let \({\Phi }_{0,\nu }\) be the automorphism of \({\mathfrak {B}}_{0,\nu }\) induced by \(\varphi _{0,\nu }\). For  let \({\mathfrak {B}}_{0,\nu } = {\mathcal {P}}(I_\nu )\) and let \({\Phi }_{0,\nu }\) be the identity. As the induction hypothesis assume condition (H\(_2\)) of Lemma 2.1 holds and that, in addition,
let \({\mathfrak {B}}_{0,\nu } = {\mathcal {P}}(I_\nu )\) and let \({\Phi }_{0,\nu }\) be the identity. As the induction hypothesis assume condition (H\(_2\)) of Lemma 2.1 holds and that, in addition,
-
\({\mathcal {A}}_{\xi ,\nu }\) are the atoms of \({\mathfrak {B}}_{\xi ,\nu }\) and \({\mathcal {A}}_{\xi ,\nu }\) generate \({\mathfrak {B}}_{\xi ,\nu }\),
-
\({\mathcal {A}}_{\xi ,\nu }\) is a partition of \(I_\nu \),
-
\(|{\mathcal {A}}_{\xi ,\nu }| \le 2^{g(\nu )}\) provided that \(\nu \in X_\xi \),
-
for \(\nu \in X_\xi \) there are involutions \(\varphi _{\xi ,\nu }\) of \(I_\nu \) that induce \({\Phi }_{\xi ,\nu }\).
If \({\mathfrak {B}}_{\xi ,\nu }, {\mathcal {A}}_{\xi ,\nu }, \varphi _{\xi ,\nu }\) and \({\Phi }_{\xi ,\nu }\) have been defined for all \(\xi \) less than the limit ordinal \(\eta \) then a standard diagonalization yields \({\mathfrak {B}}_{\eta ,\nu }, {{\mathcal {A}}}_{\eta ,\nu }, \varphi _{\eta ,\nu }\) and \({\Phi }_{\eta ,\nu }\).
Therefore assume that \({\mathfrak {B}}_{\xi ,\nu }, {\mathcal {A}}_{\xi ,\nu }, \varphi _{\xi ,\nu }\) and \({\Phi }_{\xi ,\nu }\) have been defined. Let \({\mathcal {A}}^*_{\xi +1,\nu }\) be the atoms generated by \({\mathcal {A}}_{\xi ,\nu }\) and \(\{A_\nu (\iota ),\varphi _{\xi ,\nu }(A_\nu (\iota ))\}_{\iota \in G_{\xi +1}(\nu )}\)—in other words, \({\mathcal {A}}^*_{\xi +1,\nu }\) consists of intersections of maximal centred subfamilies of

Observe that since the elements of \({\mathcal {A}}_{\xi ,\nu }\) are pairwise disjoint, at most one of them can belong to a centred family and so  for all \(\nu \) in a final segment of \( X_{\xi }\). Moreover, \({\mathcal {A}}^*_{\xi +1,\nu }\) is a partition of \(I_\nu \). Since \(f(\nu ) > 2^{g(\nu )}\) there must be for each \(\nu \in X_{\xi }\) some \(a_\nu \in {\mathcal {A}}^*_{\xi +1,\nu }\) such that \(|a_\nu | > g(\nu )\). For each \(\nu \in X_{\xi + 1}\) let \(\varphi :a_\nu \rightarrow \varphi _{\xi ,\nu }(a_\nu )\) be any bijection such that for each \(\iota \in G_{\xi +1}(\nu )\) there is some \(k_{\iota ,\nu }\in a_\nu \) such that \(\varphi (k_{\iota , \nu })\ne \theta _{\iota , \nu }(k_{\iota , \nu })\). Now for \(\nu \in X_{\xi + 1}\) let
for all \(\nu \) in a final segment of \( X_{\xi }\). Moreover, \({\mathcal {A}}^*_{\xi +1,\nu }\) is a partition of \(I_\nu \). Since \(f(\nu ) > 2^{g(\nu )}\) there must be for each \(\nu \in X_{\xi }\) some \(a_\nu \in {\mathcal {A}}^*_{\xi +1,\nu }\) such that \(|a_\nu | > g(\nu )\). For each \(\nu \in X_{\xi + 1}\) let \(\varphi :a_\nu \rightarrow \varphi _{\xi ,\nu }(a_\nu )\) be any bijection such that for each \(\iota \in G_{\xi +1}(\nu )\) there is some \(k_{\iota ,\nu }\in a_\nu \) such that \(\varphi (k_{\iota , \nu })\ne \theta _{\iota , \nu }(k_{\iota , \nu })\). Now for \(\nu \in X_{\xi + 1}\) let

and note that \({\mathcal {A}}_{\xi +1,\nu }\) is also a partition. Let \(\varphi _{\xi +1,\nu }\) be defined by

and let \({\Phi }_{\xi +1,\nu }\) be induced by \(\varphi _{\xi +1,\nu }\). Let \({\mathfrak {B}}_{\xi +1,\nu }\) be the Boolean algebra generated by the atoms \({\mathcal {A}}_{\xi +1,\nu }\). On the other hand, for  let \({\mathfrak {B}}_{\xi +1,\nu }={\mathcal {P}}(I_\nu )\) and let \({\Phi }_{\xi +1,\nu }\) be induced by \(\varphi _{\xi ,\nu }\). It is immediate for each \(\nu \in \kappa \) that \({\mathfrak {B}}_{\xi ,\nu }\subseteq {\mathfrak {B}}_{\xi +1,\nu }\) and that
let \({\mathfrak {B}}_{\xi +1,\nu }={\mathcal {P}}(I_\nu )\) and let \({\Phi }_{\xi +1,\nu }\) be induced by \(\varphi _{\xi ,\nu }\). It is immediate for each \(\nu \in \kappa \) that \({\mathfrak {B}}_{\xi ,\nu }\subseteq {\mathfrak {B}}_{\xi +1,\nu }\) and that  . Moreover,
. Moreover,
for all \(\nu \) in a final segment of \( X_{\xi +1}\) as required.
To see that hypothesis \((\hbox {H}_3)\) of Lemma 2.1 holds let \(F:\kappa \rightarrow \kappa \) be one-to-one. If there are cofinally many \(\nu \) such that there is \(z_\nu \in I_\nu \) such that \(F(z_\nu ) \notin I_\nu \) then let \(\xi =0\) and, without loss of generality, it may be assumed that \(z_\nu \) belongs to the atom \( A_{0,\nu }\) of \({\mathfrak {B}}_{0,\nu }\) for cofinally many \(\nu \). Since \(\varphi _{0,\nu }(A_{0,\nu }) = A_{1,\nu }\subseteq I_\nu \) it is clear that \(F(z_\nu )\notin \varphi _{0,\nu }(A_{0,\nu })\). If, on the other hand, \(F(I_\nu ) \subseteq I_\nu \) for all \(\nu \) in a final segment of \(\kappa \) then  for some \(J(\nu )\) also for a final segment. There is then some \(\xi \in \kappa ^+\) such that \(J(\nu )\in G_\xi (\nu )\) for all \(\nu \) in a final segment of \( X_\xi \) and it may as well be assumed that \(\xi \) is a successor. By construction, for all \(\nu \) in a final segment of \(X_\xi \) there is a singleton \(\{\iota \}\in {\mathcal {A}}_{\xi ,\nu }\) such that \({\Phi }_{\xi ,\nu }(\{\iota \}) = \{\varphi _{\xi ,\nu }(k)\}\) and \(\varphi _{\xi ,\nu }(\iota ) \ne \theta _{J(\nu ),\nu }(\iota ) = F(\iota )\).
for some \(J(\nu )\) also for a final segment. There is then some \(\xi \in \kappa ^+\) such that \(J(\nu )\in G_\xi (\nu )\) for all \(\nu \) in a final segment of \( X_\xi \) and it may as well be assumed that \(\xi \) is a successor. By construction, for all \(\nu \) in a final segment of \(X_\xi \) there is a singleton \(\{\iota \}\in {\mathcal {A}}_{\xi ,\nu }\) such that \({\Phi }_{\xi ,\nu }(\{\iota \}) = \{\varphi _{\xi ,\nu }(k)\}\) and \(\varphi _{\xi ,\nu }(\iota ) \ne \theta _{J(\nu ),\nu }(\iota ) = F(\iota )\).
Finally, to see that hypothesis \((\hbox {H}_4)\) of Lemma 2.1 holds let \(A\subseteq \kappa \). Let \(F\in \prod _{\nu \in \kappa }2^{f(\nu )}\) be such that \(A\cap I_\nu = A_\nu (F(\nu ))\) for all \(\nu \). By the hypothesis of Lemma 3.2 there is \(\xi \in \kappa ^+\) such that \(F(\nu )\in G_\xi (\nu )\) for all \(\nu \in X_\xi \). It follows that \(A\cap I_\nu = A_\nu (F(\nu )) \in {\mathfrak {B}}_\xi (\nu )\) for all \(\nu \) in a final segment of \(X_\xi \). Since \({\mathfrak {B}}_{\xi ,\nu } = {\mathcal {P}}(I_\nu )\) if \(\nu \notin X_\xi \) it follows that there is some \(\iota \in \kappa \) such that \( A\cap I_\nu \in {\mathfrak {B}}_{\xi ,\nu }\) for all \(\nu \ge \iota \). \(\square \)
4 The special case of \(\kappa = \omega \)
The proof of Lemma 3.2 does not apply to \(\kappa =\omega \) because it relies on the fact that  if \(\mu \) is an infinite cardinal. This is used to reduce to the case \(G_\xi (\nu )\subseteq G_\eta (\nu )\) for most \(\nu \) if \(\xi \in \eta \). The first part of the proof of Lemma 4.1 corrects this—the function f in its hypothesis can be thought of as yielding a sequence of integers approximating infinite cardinals—but the general outline of the proof is the same as that of Lemma 3.2.
if \(\mu \) is an infinite cardinal. This is used to reduce to the case \(G_\xi (\nu )\subseteq G_\eta (\nu )\) for most \(\nu \) if \(\xi \in \eta \). The first part of the proof of Lemma 4.1 corrects this—the function f in its hypothesis can be thought of as yielding a sequence of integers approximating infinite cardinals—but the general outline of the proof is the same as that of Lemma 3.2.
Lemma 4.1
If there are functions \(f:{\mathbb {N}}\rightarrow {\mathbb {N}}\) and \(g:{\mathbb {N}}\rightarrow {\mathbb {N}}\) such that for all \(k\in {\mathbb {N}}\)

and if \({\mathfrak {d}}_{f!,g}({\mathcal {F}}) = \aleph _1\) for some filter \({\mathcal {F}}\) generated by a \(\subseteq ^*\)-descending tower of length \(\omega _1\) then the hypotheses of Lemma 2.1 hold.
Proof
Given the hypothesis, it may be assumed that there are \(\subseteq ^*\)-descending sets \(\{X_\xi \}_{\xi \in \omega _1}\subseteq {\mathcal {F}}\) and functions \(\{G_\xi \}_{\xi \in \omega _1}\subseteq \prod _{n\in \omega }[f(n)!]^{g(n)}\) such that for every \(F\in \prod _{n\in \omega }f(n)!\) there is \(\xi \in \omega _1\) such that \(F(n)\in G_\xi (n)\) for all but finitely many \(n\in X_\xi \). (This is done simply by reindexing so that for all \(\xi \in \omega _1\) there are cofinally many \(\eta \in \omega _1\) such that \(G_\xi = G_\eta \).)
It will first be shown that it can be assumed that there are functions, \(\overline{g}\), \(h_\xi :{\mathbb {N}}\rightarrow {\mathbb {N}}\) and \(H_\xi \in \prod _{n\in {\mathbb {N}}}[f(n)!]^{h_\xi (n)} \) for \(\xi \in \omega _1\) such that
-
(a)
 ,
, -
(b)
if \(\xi \in \eta \in \omega _1\) then \(4h_\xi \le ^* h_\eta \le \overline{g}\),
-
(c)
if \(\xi \in \eta \in \omega _1\) then \(H_\xi (n)\subseteq H_\eta (n)\) for all but finitely many n,
-
(d)
if \(F\in \prod _{n\in {\mathbb {N}}}f(n)!\) and \(F(n)\in G_\xi (n)\) for all but finitely many \(n\in X_\xi \) then also \(F(n)\in H_\xi (n)\) for all but finitely many \(n \in X_\xi \).
To see this note that the hypothesis that  for all k makes it possible to choose \(h:{\mathbb {N}}\rightarrow {\mathbb {N}}\) such that
for all k makes it possible to choose \(h:{\mathbb {N}}\rightarrow {\mathbb {N}}\) such that

and \(\lim _{n\rightarrow \infty }h(n) = \infty \). Then find \(\overline{h}_\xi :{\mathbb {N}}\rightarrow {\mathbb {N}}\) for \(\xi \in \omega _1\) such that if \(\xi \in \eta \) then  for all but finitely many \(n\in {\mathbb {N}}\). Let
for all but finitely many \(n\in {\mathbb {N}}\). Let  and note that it can be assumed that
and note that it can be assumed that  for all \(n\in {\mathbb {N}}\). Define
for all \(n\in {\mathbb {N}}\). Define  and observe that if \(\xi \in \eta \in \omega _1\) then
and observe that if \(\xi \in \eta \in \omega _1\) then

for all but finitely many n.
Let \(H_0(n) = G_0(n)\). Given \(H_\xi \) satisfying conditions (c) and (d), define \(H_{\xi +1}(n) = H_\xi (n) \cup G_{\xi +1}(n)\) and note that

On the other hand, if \(\eta \) is a limit ordinal and \(H_\xi \) satisfying the desired requirements have been chosen for \(\xi \in \eta \), then a diagonalization argument yields \(H_\eta \) such that \(|H_\eta (n)| = h_\eta (n)\) and \(H_\xi (n)\subseteq H_\eta (n)\) for all but finitely many n for each \(\xi \in \eta \). Hence \(h_\xi \) and \(H_\xi \) satisfy conditions (b), (c) and (d).
Now let \(\{I_n\}_{n\in \omega }\) partition \({\mathbb {N}}\) so that \(|I_n | = f(n)\) and let \(\{\theta _{j,n}\}_{j\in f(n)!}\) enumerate all permutations of \(I_n\). Let \(A_n:f(n)!\rightarrow {\mathcal {P}}(I_n)\) be a surjection. Without loss of generality, f(n) is even for each n. So let \(A_{0,n}\) and \(A_{1,n}\) partition \(I_n\) into two equal sized sets and let \(\varphi _{0,n}\) be an involution of \(I_n\) interchanging \(A_{0,n}\) and \(A_{1,n}\). For \(n\in X_0\) let \({\mathfrak {B}}_{0,n} = \{\varnothing , I_n, A_{0,n},A_{1,n}\}\) and let \({\Phi }_{0,n}\) be the automorphism of \({\mathfrak {B}}_{0,n}\) induced by \(\varphi _{0,n}\). For  let \({\mathfrak {B}}_{0,n} = {\mathcal {P}}(I_n)\) and let \({\Phi }_{0,n}\) be the identity. As the induction hypothesis assume condition (H\(_3\)) of Lemma 2.1 holds and that, in addition,
let \({\mathfrak {B}}_{0,n} = {\mathcal {P}}(I_n)\) and let \({\Phi }_{0,n}\) be the identity. As the induction hypothesis assume condition (H\(_3\)) of Lemma 2.1 holds and that, in addition,
-
(e)
\({\mathcal {A}}_{\xi ,n}\) are the atoms of \({\mathfrak {B}}_{\xi ,n}\) and that \(|{\mathcal {A}}_{\xi ,n}| \le 2^{4h_\xi (n)}\) provided that \(n\in X_\xi \),
-
(f)
for \(n\in X_\xi \) there are involutions \(\varphi _{\xi ,n}\) of \(I_n\) that induce \({\Phi }_{\xi ,n}\).
If \({\mathfrak {B}}_{\xi ,n}, {\mathcal {A}}_{\xi ,n}, \varphi _{\xi ,n}\) and \({\Phi }_{\xi ,n}\) have been defined for all \(\xi \) less than the limit ordinal \(\eta \) then a standard diagonalization yields \({\mathfrak {B}}_{\eta ,n}, {\mathcal {A}}_{\eta ,n}, \varphi _{\xi ,n}\) and \({\Phi }_{\eta ,n}\).
Therefore assume that \({\mathfrak {B}}_{\xi ,n}, {\mathcal {A}}_{\xi ,n}, \varphi _{\xi ,n}\) and \({\Phi }_{\xi ,n}\) have been defined. Let \({\mathcal {A}}^*_{\xi +1,n}\) be the atoms generated by \({\mathcal {A}}_{\xi ,n}\) and \(\{A_n(j),\varphi _{\xi ,n}(A_n(j))\}_{j\in H_{\xi +1}(n)}\)—in other words, \({\mathcal {A}}^*_{\xi +1,n}\) consists of intersections of maximal centred subfamilies of  . Then
. Then

for all but finitely many \(n\in X_\xi \). Since  there must be some \(a_n\in {\mathcal {A}}^*_{\xi +1,n}\) such that \(|a_n| > \overline{g}(n)\) for each \(n\in X_{\xi }\). Let \(\varphi :a_n\rightarrow \varphi _{\xi ,n}(a_n)\) be any bijection such that for each \(n\in X_{\xi + 1}\) and each \(j\in H_{\xi +1}(n)\) there is some \(k_{j,n}\in a_n\) such that \(\varphi (k_{j,n})\ne \theta _{j,n}(k_{j,n})\). Now for \(n\in X_{\xi + 1}\) let \({\mathcal {A}}_{\xi +1,n} = {\mathcal {A}}^*_{\xi +1,n}\cup \{\{k_{j,n}\}:j\in H_{\xi +1}(n)\}\) and let \(\varphi _{\xi +1,n}\) be defined by
there must be some \(a_n\in {\mathcal {A}}^*_{\xi +1,n}\) such that \(|a_n| > \overline{g}(n)\) for each \(n\in X_{\xi }\). Let \(\varphi :a_n\rightarrow \varphi _{\xi ,n}(a_n)\) be any bijection such that for each \(n\in X_{\xi + 1}\) and each \(j\in H_{\xi +1}(n)\) there is some \(k_{j,n}\in a_n\) such that \(\varphi (k_{j,n})\ne \theta _{j,n}(k_{j,n})\). Now for \(n\in X_{\xi + 1}\) let \({\mathcal {A}}_{\xi +1,n} = {\mathcal {A}}^*_{\xi +1,n}\cup \{\{k_{j,n}\}:j\in H_{\xi +1}(n)\}\) and let \(\varphi _{\xi +1,n}\) be defined by

and let \({\Phi }_{\xi +1,n}\) be induced by \(\varphi _{\xi +1,n}\). Let \({\mathfrak {B}}_{\xi +1,n}\) be the Boolean algebra whose atoms are \({\mathcal {A}}_{\xi +1,n}\). On the other hand, for  let \({\mathfrak {B}}_{\xi +1,n}={\mathcal {P}}(I_n)\) and let \({\Phi }_{\xi +1,n}\) be induced by \(\varphi _{\xi ,n}\). It is immediate for each \(n\in \omega \) that \({\mathfrak {B}}_{\xi ,n}\subseteq {\mathfrak {B}}_{\xi +1,n}\) and that
let \({\mathfrak {B}}_{\xi +1,n}={\mathcal {P}}(I_n)\) and let \({\Phi }_{\xi +1,n}\) be induced by \(\varphi _{\xi ,n}\). It is immediate for each \(n\in \omega \) that \({\mathfrak {B}}_{\xi ,n}\subseteq {\mathfrak {B}}_{\xi +1,n}\) and that  . Moreover,
. Moreover,

for all but finitely many \(n\in X_{\xi +1}\) as required.
To see that hypothesis \((\hbox {H}_4)\) of Lemma 2.1 holds let \(F:{\mathbb {N}}\rightarrow {\mathbb {N}}\) be one-to-one. If there are infinitely many n such that there is \(z_n\in I_n\) such that \(F(z_n) \notin I_n\) then let \(\xi =0\) and, without loss of generality, it may be assumed that \(z_n\) belongs to the atom \( A_{0,n}\) of \({\mathfrak {B}}_{0,n}\) for infinitely many n. Since \(\varphi _{0,n}(A_{0,n}) = A_{1,n}\subseteq I_n\) it is clear that \(F(z_n)\notin \varphi _{0,n}(A_{0,n})\). If, on the other hand, \(F(I_n) \subseteq I_n\) for all but finitely many n then  for some J(n) also for all but finitely many n. By condition (d) there is some \(\xi \in \omega _1\) such that \(J(n)\in H_\xi (n)\) for all but finitely many \(n\in X_\xi \) and condition (c) allows the assumption that \(\xi \) is a successor. By construction, for all but finitely many \(n\in X_\xi \) there is a singleton \(\{k\}\in {\mathcal {A}}_{\xi ,n}\) such that \({\Phi }_{\xi ,n}(\{k\}) = \{\varphi _{\xi ,n}(k)\}\) and \(\varphi _{\xi ,n}(k) \ne \theta _{J(n),n}(k) = F(k)\).
for some J(n) also for all but finitely many n. By condition (d) there is some \(\xi \in \omega _1\) such that \(J(n)\in H_\xi (n)\) for all but finitely many \(n\in X_\xi \) and condition (c) allows the assumption that \(\xi \) is a successor. By construction, for all but finitely many \(n\in X_\xi \) there is a singleton \(\{k\}\in {\mathcal {A}}_{\xi ,n}\) such that \({\Phi }_{\xi ,n}(\{k\}) = \{\varphi _{\xi ,n}(k)\}\) and \(\varphi _{\xi ,n}(k) \ne \theta _{J(n),n}(k) = F(k)\).
Finally, to see that hypothesis \((\hbox {H}_5)\) of Lemma 2.1 holds let \(A\subseteq {\mathbb {N}}\). Let \(F\in \prod _{n\in {\mathbb {N}}}f(n)!\) be such that \(A\cap I_n = A_n(F(n))\) for all n. By the hypothesis of Lemma 3.2 there is \(\xi \in \omega _1\) such that \(F(n)\in G_\xi (n)\) for all \(n \in X_\xi \). From condition (d) it follows that \(F(n)\in H_\xi (n)\) for all but finitely many \(n \in X_\xi \). Since \({\mathfrak {B}}_{\xi ,n} = {\mathcal {P}}(I_n)\) if \(n\notin X_\xi \) it follows that \( A\cap I_n\in {\mathfrak {B}}_{\xi ,n}\) for all but finitely many \(n \in {\mathbb {N}}\). \(\square \)
Corollary 4.2
If \({\mathfrak {d}}_{f!,g} = \aleph _1\) then there is a non-trivial isomorphism of \({\mathcal {P}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\).
Proof
In this case let \({\mathcal {F}}\) be the co-finite filter and note it is generated by the constant \(\subseteq ^*\)-descending sequence all of whose terms are \(\omega \). \(\square \)
Corollary 4.3
If there is an \(\aleph _1\)-generated filter \({\mathcal {F}}\) such that \({\mathfrak {d}}_{f!,g}({\mathcal {F}}) = \aleph _1\ne {\mathfrak {d}}\) then there is a non-trivial isomorphism of \({\mathcal {P}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\).
Proof
Let \({\mathcal {F}}\) be generated by \(\{X_\xi \}_{\xi \in \omega _1}\). Use Rothberger’s argument and \( \aleph _1\ne {\mathfrak {d}}\) to construct a \(\subseteq ^*\)-descending sequence \(\{Y_\xi \}_{\xi \in \omega _1}\) all of whose terms are \({\mathcal {F}}\) positive and such that \(Y_\xi \subseteq X_\xi \). Let \({\mathcal {F}}'\) be generated by \(\{Y_\xi \}_{\xi \in \omega _1}\) and note that \({\mathfrak {d}}_{f!,g}({\mathcal {F}}') = \aleph _1\). \(\square \)
It has to be noted that the hypothesis of Corollary 4.3 is not vacuous in the sense that there are models of set theory in which it holds. For example, in the model obtained by iterating Miller reals \(\omega _2\) times the following hold:
-
\({\mathfrak {d}} = \aleph _2\) because the Miller reals themselves are unbounded by the ground model,
-
\({\mathfrak {d}}_{f,g} = \aleph _1\) for appropriate f and g because the Miller partial order satisfies the Laver property,
-
\(\mathfrak {u} = \aleph _1\) because P-points from the ground model generate ultrafilters in the extension.
However there does not seem to be any model demonstrating that the assumption that \(\aleph _1\ne {\mathfrak {d}}\) in Corollary 4.3 is essential. It is shown in [3] that it is consistent with set theory that \({\mathfrak {d}}=\aleph _1\) yet all automorphisms of \({\mathcal {P}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\) are trivial. However, \(\mathfrak {u} = \aleph _2\) in that model because random reals are added cofinally often.
5 Remarks and questions
The first thing to note is that there are models where \({\mathfrak {d}}_{f!,g}=\aleph _1< 2^{\aleph _0}\) for f and g satisfying the hypotheses of Lemma 4.1—for example, this is true in the model obtained by either iteratively adding \(\omega _2\) Sacks realsFootnote 1 or adding any number of Sacks reals, greater than \(\aleph _1\) of course, side-by-side. Of course \({\mathfrak {d}}=\aleph _1\) also in these models. It is therefore of interest to note that the Laver property implies that \({\mathfrak {d}}_{f!,g}=\aleph _1\) in the Laver model as well, yet \({\mathfrak {d}} = \aleph _2\) in this model. It should also be observed that it is possible for \({\mathfrak {d}}_{f,g}\) to be larger that \({\mathfrak {d}}\). For example, iteratively forcing \(\omega _2\) times with perfect trees T that are cofinally f branching will yield such a model.
To be a bit more precise, given \(f:\omega \rightarrow \omega \) define \({\mathbb {S}}(f)\) to consist of all trees \(T\subseteq \bigcup _{n\in \omega }\prod _{j\in n}f(j)\) such that or each \(t\in T\) there is \(s\supseteq t\) such that \(s^{\frown }\! j \in T\) for all \(j\in f(|s|)\). So Sacks forcing is just \({\mathbb {S}}(2)\) where 2 is the constant 2 function. The same proof as for Sacks forcing shows that \({\mathbb {S}}(f)\) is proper and adds no reals unbounded by the ground model. Iterating \({\mathbb {S}}(f)\) with countable support \(\omega _2\) times then yields model in which \({\mathfrak {d}} = \aleph _1\). However, if \(g:\omega \rightarrow \omega \) and \(\mathcal H\subseteq \prod _{n\in \omega }[f(n)]^{g(n)}\) has cardinality \(\aleph _1\) then there is some model containing g and \(\mathcal H\) and there is \(\mathrm{\Gamma }\in \prod _{n\in \omega } f(n)\) which is generic over this model. This generically ensures that for all \(h\in \mathcal H\) there is some j such that \(\mathrm{\Gamma }(j) \notin h(j)\).
The generalization of Sacks reals to uncountable cardinals in [5] establishes that the hypotheses of Lemma 3.2 can be satisfied for uncountable cardinals. Alternatively, one could iteratively force \(\kappa ^+\) times with the partial order \({\mathbb {P}}(f,g)\) consisting of pairs \((G,{\mathcal {F}})\) where \(|G| < \kappa \) and G is a function whose domain is a subset of \(\kappa \) and \(G(\xi ) \in [f(\xi )]^{g(\xi )}\) and \({\mathcal {F}}\subseteq \prod _{\xi \in \kappa }f(\xi )\) and \(|{\mathcal {F}}|<\kappa \) with the ordering defined by \((G,{\mathcal {F}})\le (G',{\mathcal {F}}')\) if
-
\(G\supseteq G'\),
-
\({\mathcal {F}} \supseteq {\mathcal {F}}'\),
-
if \(\xi \) is the in the domain of
 and \(f\in {\mathcal {F}}'\) then \(f(\xi ) \in G(\xi )\).
and \(f\in {\mathcal {F}}'\) then \(f(\xi ) \in G(\xi )\).
It is easy to see that \({\mathbb {P}}(f,g)\) is \(\kappa \)-closed and that if \(\mathrm{\Gamma }\subseteq {\mathbb {P}}(f,g)\) is generic then the domain of \(\bigcup _{(G,{\mathcal {F}})\in \mathrm{\Gamma }}G\) has cardinality \(\kappa \) and the family of such domains added iteratively will generate the necessary filter.
However, the following question does not seem to be answered.
Question 5.1
Is it consistent for an inaccessible cardinal \(\kappa \) that \({\mathfrak {d}}_{f,g}=\kappa ^+\) where \(f(\alpha ) =(2^{\aleph _\alpha })^+\) and \(g(\alpha ) = \aleph _\alpha \) yet \({\mathfrak {d}} (\kappa )> \kappa ^+\) where \({\mathfrak {d}} (\kappa )\) is the generalization of \({\mathfrak {d}}\) to \(\kappa \)?
It is worth observing that the isomorphism of Lemma 2.1 is trivial on some infinite sets—indeed, if \(\xi \in \kappa ^+\) and \(X\subseteq {\mathbb {N}}\) are such that \(\{x\}\) belongs to some \({\mathfrak {B}}_{\xi ,\nu }\) for each \(x\in X\) then \({\Phi }\) is trivial on \({\mathcal {P}}(X)\). However, if \(\mathcal {T}({\Phi })\) is defined to be the ideal  then \(\mathcal {T}({\Phi })\) is a small ideal in the sense that the quotient algebra \({\mathcal {P}}({\mathbb {N}})/\mathcal {T}({\Phi })\) has large antichains, even modulo the ideal of finite sets—in the terminology of [2], the ideal \(\mathcal {T}({\Phi })\) is not ccc by fin. To see this, simply observe that the proof of Lemma 4.1 actually shows that hypothesis (H\(_4\)) of Lemma 2.1 can be strengthened to: For any one-to-one \(F:{\mathbb {N}}\rightarrow {\mathbb {N}}\) there is \(\xi \in \kappa ^+\) such that for all but finitely many \(\nu \in \omega \) there is an atom \(a\in {\mathfrak {B}}_{\xi ,\nu }\) and \(\iota \in a\) such that \(F(\iota )\notin {\Phi }_{\xi ,\nu }(a)\). It follows that if \(Z\subseteq {\mathbb {N}}\) is infinite then \(Z^* = \bigcup _{\nu \in Z}I_\nu \notin \mathcal {T}({\Phi })\). Hence, if \({\mathcal {A}}\) is an almost disjoint family of subsets of \(\mathbb N\) then \(\{A^*:A\in {\mathcal {A}}\}\) is an antichain modulo the ideal of finite sets.
then \(\mathcal {T}({\Phi })\) is a small ideal in the sense that the quotient algebra \({\mathcal {P}}({\mathbb {N}})/\mathcal {T}({\Phi })\) has large antichains, even modulo the ideal of finite sets—in the terminology of [2], the ideal \(\mathcal {T}({\Phi })\) is not ccc by fin. To see this, simply observe that the proof of Lemma 4.1 actually shows that hypothesis (H\(_4\)) of Lemma 2.1 can be strengthened to: For any one-to-one \(F:{\mathbb {N}}\rightarrow {\mathbb {N}}\) there is \(\xi \in \kappa ^+\) such that for all but finitely many \(\nu \in \omega \) there is an atom \(a\in {\mathfrak {B}}_{\xi ,\nu }\) and \(\iota \in a\) such that \(F(\iota )\notin {\Phi }_{\xi ,\nu }(a)\). It follows that if \(Z\subseteq {\mathbb {N}}\) is infinite then \(Z^* = \bigcup _{\nu \in Z}I_\nu \notin \mathcal {T}({\Phi })\). Hence, if \({\mathcal {A}}\) is an almost disjoint family of subsets of \(\mathbb N\) then \(\{A^*:A\in {\mathcal {A}}\}\) is an antichain modulo the ideal of finite sets.
One should not, therefore, expect to get a nowhere trivial isomorphism by these methods. It is nevertheless, conceivable that there are some other cardinal invariants similar to \({\mathfrak {d}}_{f,g}\) that would, when small, imply the existence of nowhere trivial isomorhisms of \({\mathcal {P}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\). In this context it is interesting to note that it is at least consistent with small \({\mathfrak {d}}\) that there are nowhere trivial isomorphisms.
Proposition 5.2
It is consistent that \(\aleph _1 = {\mathfrak {d}} \ne 2^{\aleph _0}\) and there is a nowhere trivial isomorphism of \({\mathcal {P}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\).
Sketch of proof
The partial order defined in [12, Section 2, Definition 2.1] will be usedFootnote 2. Begin with a model V satisfying \(2^{\aleph _0} > \aleph _1\) and construct a tower of permutations \(\{(A_\xi ,F_\xi ,{\mathfrak {B}}_\xi )\}_{\xi \in \text {Lim}(\omega _1)}\) such that, letting  and \(\mathbb {P}_\eta \) be the finite support iteration of partial orders that are \({\mathbb {Q}}({\mathfrak {S}}_\xi )\) for \(\xi \in \text {Lim}(\eta )\) and Hechler forcing if \(\xi \) is a successor, the following holds for each \(\eta \) and G that is \(\mathbb {P}_{\omega _1}\) generic over V:
and \(\mathbb {P}_\eta \) be the finite support iteration of partial orders that are \({\mathbb {Q}}({\mathfrak {S}}_\xi )\) for \(\xi \in \text {Lim}(\eta )\) and Hechler forcing if \(\xi \) is a successor, the following holds for each \(\eta \) and G that is \(\mathbb {P}_{\omega _1}\) generic over V:
-
\(A_\eta = A_{{\mathfrak {S}}_\eta }[G\cap {\mathbb {Q}}({\mathfrak {S}}_\eta )]\),
-
\(F_\eta = F_{{\mathfrak {S}}_\eta }[G\cap {\mathbb {Q}}({\mathfrak {S}}_\eta )]\),
-
\({\mathfrak {B}}_\eta = {\mathcal {P}}({\mathbb {N}})\cap V[G\cap \mathbb {P}_\eta ]\).
The proof of [12, Theorem 2.1] shows that there is a nowhere trivial isomorphism of \({\mathcal {P}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\) in this model and, since \(\mathbb {P}_{\omega _1}\) is ccc, it is also true that \(2^{\aleph _0}\) remains larger than \(\aleph _1\) in the generic extension. The Hechler reals guarantee that \({\mathfrak {d}} = \aleph _1\). \(\square \)
It should also be noted that Lemma 2.1 actually yields \(2^{(\kappa ^+)}\) isomorphisms. It is shown in [13] that it is possible to have non-trivial isomorphisms of \({\mathcal {P}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\) without having \(2^{\mathfrak {c}}\) such isomorphisms. This motivates the following, somewhat vague, question.
Question 5.3
Can there be some variant of \({\mathfrak {d}}_{f,g}\) which, when small, yields a non-trivial isomorphism of \({\mathcal {P}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\) without yielding the maximal possible number of such?
Given the remarks following Corollary 4.3 it is natural to ask the following.
Question 5.4
Is it consistent that \({\mathfrak {d}}_{f!,g} = {\mathfrak {d}}\) for f and g satisfying the hypothesis of Lemma 4.1 and to have \(\mathfrak {u} = \aleph _1\) and to have that all isomorphisms of \({\mathcal {P}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\) are trivial?
As a final remark it will be noted that Corollary 4.2 shows that [12, Theorem 3.1] cannot be improved to show that in models obtained by iterating Sacks or Silver reals all isomorphisms of \({\mathcal {P}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\) are trivial because the equality \({\mathfrak {d}}_{f!,g}=\aleph _1\) holds in these models for the necessary f and g.
References
Bartoszyński, T., Judah, H.: Set Theory. On the Structure of the Real Line. A K Peters, Wellesley (1995)
Farah, I.: Analytic Quotients: Theory of Liftings for Quotients over Analytic Ideals on the Integers. Memoirs of the American Mathematical Society, vol. 148(702). American Mathematical Society, Providence (2000)
Farah, I., Shelah, S.: Trivial automorphisms. Israel J. Math. 201(2), 701–728 (2014)
Goldstern, M., Shelah, S.: Many simple cardinal invariants. Arch. Math. Logic 32(3), 203–221 (1993)
Kanamori, A.: Perfect-set forcing for uncountable cardinals. Ann. Math. Logic 19(1–2), 97–114 (1980)
Parovičenko, I.I.: On a universal bicompactum of weight \(\aleph \). Dokl. Akad. Nauk SSSR 150, 36–39 (1963)
Rudin, W.: Homogeneity problems in the theory of Čech compactifications. Duke Math. J. 23(3), 409–419 (1956)
Rudin, W.: Note of correction: “Homogeneity problems in the theory of Čech compactifications,” vol. 23 (1956), pp. 409–419. Duke Math. J. 23(6), 633 (1956)
Shelah, S.: Proper Forcing. Lecture Notes in Mathematics, vol. 940. Springer, Berlin (1982)
Shelah, S., Steprāns, J.: PFA implies all automorphisms are trivial. Proc. Amer. Math. Soc. 104(4), 1220–1225 (1988)
Shelah, S., Steprāns, J.: Somewhere trivial autohomeomorphisms. J. London Math. Soc. 49(3), 569–580 (1994)
Shelah, S., Steprāns, J.: Martin’s axiom is consistent with the existence of nowhere trivial automorphisms. Proc. Amer. Math. Soc. 130(7), 2097–2106 (2002)
Steprāns, J.: The autohomeomorphism group of the Čech–Stone compactification of the integers. Trans. Amer. Math. Soc. 355(10), 4223–4240 (2003)
Veličković, B.: OCA and automorphisms of \({\cal P}(\omega )/{\rm fin}\). Topology Appl. 49(1), 1–13 (1993)
Author information
Authors and Affiliations
Corresponding author
Additional information
Originally considered by the Central European Journal of Mathematics but withdrawn due to imposition of publishing fees and resubmitted to the European Journal of Mathematics.
The first author’s research for this paper was partially supported by the United States–Israel Binational Science Foundation (Grant No. 2006108), and by the National Science Foundation (Grant No. NSF-DMS 0600940). (It is number 990 on his list of papers.) The second author’s research for this paper was partially supported by NSERC of Canada.
Rights and permissions
About this article
Cite this article
Shelah, S., Steprāns, J. Non-trivial automorphisms of \({{\mathcal {P}}}({\mathbb {N}})/[{\mathbb {N}}]^{<\aleph _0}\) from variants of small dominating number. European Journal of Mathematics 1, 534–544 (2015). https://doi.org/10.1007/s40879-015-0058-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-015-0058-0




 for all
for all 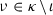 .
. .
. ,
, and
and