Introduction

The use of composite materials in the aerospace field has been growing exponentially within the last decades, due to their superior mechanical properties such as strength and stiffness to weight ratio: these properties allowed consistent decrease in weight and consequently strong performances improvement for the overall machine. Nonetheless, when compared to metals, composites are more sensitive to environmental conditions such as temperature or humidity, more likely to be damaged by fatigue loads in their early life [1] and more threatened by HVI (high-velocity impacts) and LVI (low-velocity impacts) events. In particular, the latter are the physical phenomena under examination in this study.

In the aerospace field impacts are one of the main responsible for delamination, the detaching of the plies due to loss of interface strength: bird strikes, debris, ice impacts are major concerns for aircrafts crashworthiness. Delamination leads to consistent drops in laminate mechanical properties and its presence is not always identifiable through standard inspection procedures, forcing to use NDT (Non-Destructive Inspection Techniques) [2, 3], expensive and hard to carry out for large and complex components. It’s then necessary to implement numerical models able to predict the phenomenon and anticipate its consequences. However, the problem is not trivial: as opposed to the so-called intralaminar damages such as matrix cracking, fiber debonding or compressive failure, this damage mechanism is driven by out-of-plane stresses and consequently the numerical modelization requires to take into account out-of-plane loads transferred between the layers by the adhesive interface. Commonly used modeling techniques are mainly the following two: 3D elements along with 3D material laws for the cohesive layer, the so-called CZM (Cohesive Zone Model) [4, 5]; interface modeling using contacts through the SSA (Stacked Shell Approach) [6].

The first option is in principle the most accurate, as able to describe the adhesive behavior and the delamination mechanism to the fullest. On the other hand, given the thin geometry of these laminates, mesh sizes required to get acceptable results need to be small [7], leading to high computational costs even for simple models. Furthermore, notable obstacles lie in the identification of the key parameters for the adhesives: comprehensive DCB (Double Cantilever Beam), ENF (End Notched Flexure) and MMB (Mixed Mode Bending) test campaigns to characterize the adhesive interface are needed, as the properties depend on both bonding and bonded material [8]. As a consequence, these tests are rather complex and reliable results are not always guaranteed.

The SSA significantly reduces the required computational time, but still needs complex calibration phase, for which the previously mentioned tests are needed. Moreover, contact parameters are highly sensitive to mesh size and loading conditions, leading to numerically unstable models [9]. These issues make this approach useful for small models subjected to controlled boundary conditions but hard to implement successfully for medium to large applications.

Summarizing, common feature of the two techniques is the modelization of each ply (or sub-laminate); though theoretically promising, both require high computing power and complex calibration phase. For large models standard practice is implementing one of these two approaches only in the impact region [10]: this compromise significantly reduces the computational effort but the instability issues remain and the applicability is limited to models for which the impact region is known a priori.

The alternative solution proposed here is an empirical damage criterion developed along the well-known equivalent shell approach, which consists in modeling the plies as unique shell parts with the properties of the whole laminate. The criterion is based on the assumption that comparing numerical intralaminar parameters with experimental data provided by NDT techniques, it is actually possible to find a relation between the two without considering the interlaminar adhesive properties. Therefore, an experimental LVI campaign on representative flat specimens were carried out and analyzed by means of NDI techniques; then the equivalent shell approach was exploited to build correspondent numerical models and impacts were simulated using the explicit solver LS-DYNA. Subsequently, a series of damage parameters were evaluated and a semi-empirical procedure to compute and represent the damaged region was developed and tuned by comparison with the NDT scans: said procedure consisted in identifying a threshold value for which a boundary between intact and damaged regions could be established.

Damage Model Foundations

The damage model on which the proposed criterion is primarily based on is the work carried out in the ’70s by Hashin, who developed the first 2D stress state failure model able to take into account the large part of composite damage mechanisms [11]; the results were published in 1980 and are briefly summarized below. Hashin considered four possible failure conditions:

  • Tensile fiber mode: valid for \(\sigma _{11}>0\), with \(\sigma _{A^{+}}\) tensile failure stress in fiber direction and \(\tau _{A}\) axial failure shear.

    $$\begin{aligned} \left( \frac{\sigma _{11}}{\sigma _{A^{+}}}\right) ^{2} + \left( \frac{\sigma _{12}}{\tau _{A}}\right) ^{2} = 1 \end{aligned}$$
    (1)

  • Fiber compressive mode: valid for \(\sigma _{11}<0\), with \(\sigma _{A^{-}}\) compressive failure stress in fiber direction (absolute value).

    $$\begin{aligned} \sigma _{11} + \sigma _{A^{-}} = 1 \end{aligned}$$
    (2)

  • Tensile matrix mode: valid for \(\sigma _{22}>0\), with \(\sigma _{T^{+}}\) tensile failure stress transverse to fiber direction.

    $$\begin{aligned} \left( \frac{\sigma _{22}}{\sigma _{T^{+}}}\right) ^{2} + \left( \frac{\sigma _{12}}{\tau _{A}}\right) ^{2} = 1 \end{aligned}$$
    (3)

  • Compressive matrix mode: valid for \(\sigma _{22}<0\), with \(\tau _{T}\) transverse failure shear and \(\sigma _{T^{-}}\) compressive failure stress transverse to fiber direction (absolute value).

    $$\begin{aligned} \left( \frac{\sigma _{22}}{\tau _{T}}\right) ^{2} + \left[ \left( \frac{\sigma _{T^{-}}}{2\tau _{T}}\right) ^{2} - 1\right] \left( \frac{\sigma _{22}}{\sigma _{T^{-}}}\right) + \left( \frac{\sigma _{12}}{\tau _{A}}\right) ^{2} = 1 \end{aligned}$$
    (4)

Hashin’s equations are valid for 2D stress state and do not consider interlaminar failure mechanisms. Other models came out since then, such as Chang-Chang’s and Puck-Shürman’s studies (resp. [12, 13]), but none of them were able to describe delamination without taking into account through-the-thickness stress.

Regarding damage, studies started in the ’90s and first authors were Matzenmiller et al. [14]. Their law, published in 1995 and from now on addressed here as MLT, is valid for 2D stress state in unidirectional laminates and is the second pillar of the criterion proposed in this research. Effective stress in the ply (\({\hat{\sigma }}_{ij}\)) shall be calculated taking into account the progressive damage, which is represented by 3 damage variables (\(w_{11}\), \(w_{22}\), \(w_{12}\), fiber, matrix and shear direction) through the damage operator \({\textbf {M}}\).

$$\begin{aligned} \sigma = \begin{Bmatrix} \sigma _{x} \\ \sigma _{y} \\ \tau \end{Bmatrix} \quad {\hat{\sigma }} = \begin{Bmatrix} \hat{\sigma _{x}} \\ \hat{\sigma _{y}} \\ {\hat{\tau }} \end{Bmatrix} \quad w = \begin{Bmatrix} w_{11} \\ w_{22} \\ w_{12} \end{Bmatrix} \end{aligned}$$
(5)
$$\begin{aligned} {\textbf {M}} = \begin{bmatrix} \frac{1}{1-w_{11}} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \frac{1}{1-w_{22}} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \frac{1}{1-w_{12}} \end{bmatrix} \end{aligned}$$
(6)
$$\begin{aligned} {\hat{\sigma }} = {\textbf {M}} \sigma \end{aligned}$$
(7)

In cases of full damage decoupling in the three directions, analytical solutions are possible: the authors obtained a strain dependent exponential function (\(\varepsilon\) and \(\varepsilon _{f}\) are respectively current and failure strain) whose curve slope is controlled by a material parameter (m). This function can be appreciated in Fig. 1 for different values of m; as in Matzenmiller’s work, strain is normalized with respect to Xt/E, respectively limit stress and elastic modulus.

$$\begin{aligned} w_{ij} = 1 - e^{-\frac{1}{me} \left( \frac{\varepsilon _{ij}}{\varepsilon _{f_{ij}}} \right) ^{m} } \end{aligned}$$
(8)
Fig. 1
figure 1

MLT damage equation, normalized strain vs damage parameter \(w_{ij}\)

Full size image

Full decoupling means that the effective stress \({\hat{\sigma }}_{ij}\) computed using Eq. 7 is dependent only on the damage value \(w_{ij}\). For example, effective stress in fibers direction will depend only on fiber damage while matrix and shear damage are not considered.

$$\begin{aligned} {\hat{\sigma }}_{11} = \frac{1}{1-w_{11}}\sigma _{11}+(0)*\sigma _{22}+(0)*\sigma _{12}=\frac{1}{1-w_{11}}\sigma _{11} \end{aligned}$$
(9)

While particularly novel at the time it was published, as of today the MLT damage models presented a series of limitations, widely addressed by Williams and Vaziri [15,16,17]. In the present work, first limitations to consider are the two-dimensional stress-state and decoupling constraints: being impacts multi-dimensional loading conditions, full decoupling is hard to accept from a theoretical point of view. Second limitation highlighted in the literature cited above lies in the m parameter identification procedure, which is complex and not always effective and must be repeated manually for each of the three stress directions: m is computed correlating the normalized stress-strain experimental curves with the numerical ones and adjusted consequently (Eq. 10, Fig. 2). While other composite damage models able to overcome some of the cited issues were developed after MLT’s studies (e.g. [13, 18]), to the authors knowledge none of them were able to describe delamination without taking into account out-of-plane interlaminar properties.

$$\begin{aligned} \frac{\sigma }{X_{t}} = e^{-\frac{1}{me} \left( \frac{\varepsilon }{\varepsilon _{f}} \right) ^{m}} \frac{\varepsilon }{\varepsilon _{f}} \end{aligned}$$
(10)
Fig. 2
figure 2

MLT damage equation, calibration of m parameter (the graph is re-created from [14])

Full size image

As the present work searches for a semi-empirical procedure to evaluate damage, the MLT equations were considered suitable: intended as cumulative damage indicators beyond their physical meaning, said equations provide a robust and reliable intralaminar damage function, which can be used as a starting point to develop a semi-empirical criterion reversing the experimental results. Throughout the paper, the term “semi-empirical” is used to underline the fact that the criterion makes use of well-known and tested parameters with strong physical and theoretical meaning, yet not sufficient to describe damage when out-of-plane stresses are involved: as mentioned in section “Introduction”, main assumption is that for the impact loading conditions at issue the interlaminar response can actually be considered related to the intralaminar behavior, and as a consequence the latter can be used to describe the other.

Experimental Campaign

As mentioned above, this study was centered on CFRP and GFRP composite laminates. Four lamination sequences and two kinds of plies were analyzed: detailed information are depicted in Tables 1 and 2, where t represents the ply thickness and T the laminate thickness. Specimens were flat panels of dimensions 200x200 mm.

Fig. 3
figure 3

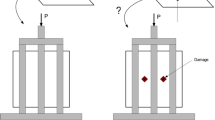
Test setup. The channel guiding the drop is a square aluminum tube with dimensions \(60\times 60\) mm; the frame details can be found in the related ASTM norm [19]. The accelerometer can be appreciated on the bottom right figure, glued to the upper part of the impactor

Full size image
Table 1 Test sessions–specimen details
Full size table
Table 2 Test sessions—test data
Full size table

The drop-test was executed following the indications of the related ASTM standard [19] (Fig. 3). The impactor was a steel sphere tightened to the bottom of a steel block, with an overall mass of 1.267 kg. A drop tower was used to guide the impactor fall and obtain meaningful impacts, vertical and centered on the plate.

Three impacts for each lamination sequence were performed; results were evaluated by means of impactor acceleration, measured by a piezoresistive accelerometer with sampling frequency set at 25 kHz.

The impact energies were chosen in order to provoke BVIDs (Barely Visible Impacts Damages) on the plates, as in case of penetration the breakage would have prevented the appreciation of the delamination mechanisms. In fact, as shown in Fig. 4, where some frames of one of the impact tests for the glass fiber laminates are depicted, the maximum deflection of the plate is under 5–10 mm. The impact speed was measured with a high speed camera recording at 9600 fps by means of the Time Of Flight principle.

Fig. 4
figure 4

Plate deflection

Full size image

To study the damaged surface NDT tests were carried out. All the panels were first analyzed before the impact by means of radiography scans, to seek for potential manufacturing defects, none of which were identified; then, ultrasound scans were performed on the impacted specimens to evaluate the damaged surface. Final surface were then extracted through image processing. Procedure for one of the glass cross-ply specimens can be appreciated in Fig. 5.

Fig. 5
figure 5

Glass cross-ply specimen 3, damaged surface: ultrasound scan and processed image

Full size image

Numerical Models

Model Setup

Numerical models were implemented in LS-DYNA starting from previous numerical activities, where materials had been characterized by means of static tests correlation following the ASTM norms for composite testing. Detailed information regarding static characterization were considered beyond the scope of this paper; however, brief overview of the material properties is reported in Tables 3 and 4.

Table 3 Material properties
Full size table
Table 4 Material properties
Full size table

The validated models exploited *MAT58 (LAMINATED_COMPOSITE_FABRIC) with thin shell elements (Belytschko–Leviatan formulation), with 4-points integration planes for accuracy improvement. In order to work on correlated material cards, the same material formulations were used. This choice was also driven by the peculiar damage formulation embedded in the keyword: *MAT58 output stresses are in fact the effective stresses corrected and adjusted using the MLT damage formulation, namely \({\hat{\sigma }}\) of Eq. 7. Furthermore, said material is able to produce as output the three in-plane damage variables \(w_{11}\), \(w_{22}\) and \(w_{12}\) which were used to write the proposed semi-empirical damage criterion.

The lamination sequence was obtained through the *PART_COMPOSITE card, exploiting linear laminated shell theory and allowing the choice of an arbitrary number of integration points through-the-thickness, with computational costs and accuracy consequently affected; for this study laminates were modeled assigning one integration plane for each layer.

Regarding the mesh size, major constraint was the static test mesh, which was regular at \(2\times 2\) mm: as some loading configurations had turned out to be severely mesh dependent (bending above all), going too far from that element size could have lead to unreliable results. After mesh sensitivity studies were performed, acceleration curves and damaged areas correlation results were satisfying for regular mesh sizes up to 3 mm.

Fig. 6
figure 6

Test setup—numerical model

Full size image

As the acceleration was directly measured on the impactor, the frame was modeled as a rigid plate simply supporting the specimen by means of a surface to surface contact; the clamps preventing in and out of plane translational motion in four points were obtained constraining the corresponding nodes on the panel in the three directions (Fig. 6). The impactor was modeled as a rigid sphere, as its dynamics and deformability were considered negligible with respect to the phenomenon under analysis. Acceleration measurement was then taken sampling the acceleration history of one node of the sphere at the same frequency used in the experimental campaign.

Damage Criterion

Regarding the damage model, the MLT law was exploited to identify a threshold value, unique for all materials and lamination sequences, able to establish the boundary between damaged and non-damaged status, both in-plane and through-the-thickness: this damaged status can be intended within the method as layer failure.

The proposed procedure to build the damage criterion is composed of three essential steps. First some intralaminar parameters have to be chosen: starting from the considerations provided in “Damage Model Foundations” section, the MLT damage variables \(w_{11}\), \(w_{22}\) and \(w_{12}\) were used, as particularly suited both for their strong physical meaning and their cumulative nature. Second, proposed definition for layer failure must be chosen. Here, it was defined as the overcoming of a limit value for at least one of the three damage variables; physically, the concept is similar to a cuboid-shaped failure surface: if the damage parameter overcomes the limit value in any of the three directions, the layer is considered failed. Last, the tuning procedure is implemented, where the chosen intralaminar parameters are analyzed to search for the layer failure limit value.

MLT variables were requested as output thanks to the capabilities of *MAT58, avoiding any need to calculate them using stresses and any problem linked with aliasing (thanks to their cumulative nature). Furthermore, the LS-DYNA solver automatically performs the computation of the m parameter (see “Damage Model Foundations” section), through the following analytical equations:

$$\begin{aligned} m_{11_{C,T}} = \frac{1}{\ln \left( \varepsilon _{11} \frac{E_{11}}{X_{C,T}} \right) } \end{aligned}$$
(11)
$$\begin{aligned} m_{22_{C,T}} = \frac{1}{\ln \left( \varepsilon _{22} \frac{E_{22}}{Y_{C,T}} \right) } \end{aligned}$$
(12)
$$\begin{aligned} m_{12} = \frac{1}{\ln \left( \varepsilon _{12} \frac{G_{12}}{S_{C}} \right) } \end{aligned}$$
(13)

where m is the material parameter, \(\varepsilon\) the strain respectively for fiber compression–tension, matrix compression–tension and shear, E the Young’s modulus, G the shear modulus, X the fiber stress limit (C–T compression–tension), Y the matrix stress limit (C–T compression–tension), S the shear stress limit. Comprehensive explanation of LS-DYNA solver behavior regarding the matter is found in [20, 21].

Using the LS-DYNA Scripting Command Language (.scl)—a C-like programming language runnable within the LsPrePost environment [22]—and Matlab, a numerical tool able to manage output data for each time state, element and integration point was developed. The procedure is explained hereunder:

  1. 1.

    choice of initial guess threshold;

  2. 2.

    extraction of the three damage variables (\(w_{11}\), \(w_{22}\), \(w_{12}\)) for each integration point, element, time state;

  3. 3.

    creation of an output file as follows:

    $$\begin{aligned} \begin{matrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \ldots \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 2 &{}\quad 0 &{}\quad \ldots \\ 0 &{}\quad 2 &{}\quad 0 &{}\quad 1 &{}\quad 3 &{}\quad 0 &{}\quad 3 &{}\quad 0 &{}\quad \ldots \\ 3 &{}\quad 2 &{}\quad 0 &{}\quad 1 &{}\quad 3 &{}\quad 0 &{}\quad 5 &{}\quad 1 &{}\quad \ldots \\ 3 &{}\quad 3 &{}\quad 0 &{}\quad 2 &{}\quad 5 &{}\quad 0 &{}\quad 5 &{}\quad 1 &{}\quad \ldots \\ 3 &{}\quad 3 &{}\quad 0 &{}\quad 2 &{}\quad 6 &{}\quad 0 &{}\quad 5 &{}\quad 1 &{}\quad \ldots \end{matrix} \end{aligned}$$
    (14)

    where values represent the total number of failed layers at each time state (row) for each element (column);

  4. 4.

    data processing, using two output variables:

    • leveled damage, representing the fraction of layers which had overcome the chosen threshold in at least one direction:

      $$\begin{aligned} dam_{lev}=\frac{total\, failed}{total} \end{aligned}$$
      (15)

    • binary damage, describing if at least one layer had overcome the chosen threshold in at least one direction:

      $$\begin{aligned} dam_{bin}= {\left\{ \begin{array}{ll} 0 &{}\quad \text { if nothing had failed} \\ 1 &{}\quad \text { if at least one layer had failed} \end{array}\right. } \end{aligned}$$
      (16)
  5. 5.

    total damaged area evaluation (through the binary damage), i.e. for a threshold equal to 0.95:

    $$\begin{aligned} A_{0.95} = \sum _{elements} \left( dam_{bin_{0.95}} * A_{element} \right) \end{aligned}$$
    (17)
  6. 6.

    LsPrePost User Fringe input files creation.

The process was repeated for a series of threshold values and ended when the best correlation with the experimental areas was found. This method gets more precise as element size decreases and/or damaged area increases, and its sensitivity is not one element nor the largest element, but a closed loop of elements which gets larger far from the impact point (Fig. 7).

Fig. 7
figure 7

Numerical sensitivity. As shown in picture b, the elements defining the numerical uncertainty are all the elements adjacent to the damaged surface. In this case, \(3\times 3\) mm elements: damaged area equal to 135 mm\(^2\), external adjacent elements 180 mm\(^2\), internal adjacent elements 108 mm\(^2\)

Full size image

As element size grows the difference between external and internal perimeter increases, causing consistent loss of accuracy. Being element results actually interpolated nodal results and being quadrilateral shells 4-nodes elements, the error is calculated taking 1/4th of the total elements adjacent to the perimeter.

Optimum Threshold Identification

Damaged surfaces were extracted through the procedure descripted in section “Damage Criterion”: binary damage was used to calculate five areas for each impact, for MLT damage thresholds from 0.94 to 0.98. Figure 8 shows the absolute errors (\(A_{num} - A_{exp}\)) for each combination of values for the most reliable mesh (regular squared, 2 mm): damaged surface errors of all the tests are plotted for damage thresholds 0.94, 0.95, 0.96, 0.97, 0.98. Mean errors ± their standard deviation are also shown for each limit value.

Fig. 8
figure 8

Optimum threshold identification: damage threshold evaluated vs absolute error with respect to the experimental surface; on the bottom mean error ± standard deviation. Data are reported for every specimen minus the UD carbon broken due to excessive impact energy

Full size image

Errors decrease as the MLT threshold increases, passing from positive values for .94 (larger areas compared to the experimental results) to negative values for .98 (smaller areas compared to the experimental results). The best results lie around 0.95, as for those values errors are distributed around zero. Thus .95 was chosen, resulting averagely in good correlation: 8 areas out of 11 were correlated within a range of ±50 mm\(^{2}\) uncertainty (numerical uncertainties were chosen based on the considerations above, section “Damage Criterion”, while experimental uncertainties are discussed below, section “Unidirectional Laminates”).

In other words, best correlation between experimental and numerical damaged surface was here obtained if layer failure defined as in section “Damage Criterion” is set to 95% of at least one MLT intralaminar damage variable.

Results and Discussion

The numerical models were validated in two phases: first by means of acceleration curvesFootnote 1 and in particular acceleration peaks, then through the damaged surface comparison to identify the damage threshold and calibrate the damage algorithm.Footnote 2 Results are reported here grouped by the damage mechanism involved: first the unidirectional plates, showing a matrix driven failure mechanism, then the cross-ply specimens, characterized by delamination and fiber breakage.

Unidirectional Laminates

Unidirectional laminates presented long cracks varying from 60 to 142 mm along the fiber direction. As shown in Fig. 9, here the main damage mechanism is tensile matrix failure along the fibers.

Fig. 9
figure 9

Unidirectional carbon and glass laminates: impacted specimens, processed ultrasonic scan, proposed numerical damage index (top to bottom)

Full size image

As reported in Fig. 10, carbon and glass unidirectional laminates presented good correlation in terms of acceleration curves. In particular, glass laminates showed peak relative errors under 5%, respectively 2.0, 0.6 and 3.3%. On the other hand, if carbon specimens showed good correlation for the first two impacts, for the third specimen the drop height turned out to be too low to get an effective measurement and was consequently discarded.

Fig. 10
figure 10

Acceleration curves correlation for UD laminates

Full size image

For the UD laminates, the evaluation of the experimental damaged area presented two major issues.

First, as appreciated in Fig. 9, the perimeter is not always clear nor well defined and multiple cracks may lead to incoherent choices. UD laminates show thin rectangular or even line-shaped damaged regions: these damages are only partially describable as surfaces. Second, surface values under examination are rather low: some specimens presented areas of 10 mm\(^{2}\); as areas increase as a function of R\(^2\), high uncertainty values are likely. One way to understand this problem is to imagine a 5 mm radius circular damaged surface, whose correspondent area would be 78.54 mm\(^2\): a 25% error would correspond to a positive error of 0.59 and negative error of 0.67 on radius, much lower values both in relative and absolute sense.

However, given the variety of shapes resulted from both experimental scans and numerical damage index, the radius could have been used effectively as error parameter only in a few of the cases reported in this section for UD laminates and in the next for cross-ply plates. In fact, the more the damage region description steps away from a circular shape, the less the radius is a representative and representable parameter. For this reason, and in order to provide uniformity on the uncertainty evaluation procedure throughout the work, it was decided to calculate the error with respect to the surface for both unidirectional and cross-ply specimens: an uncertainty value of \(\pm 25\%\) on the experimental areas was considered appropriate.

Results of the damaged surface correlation for both the unidirectional sets of specimens are shown in Fig. 11: despite the issues discussed above, overall correlation was satisfactory. For the carbon laminates, the second and third specimens presented good results within the uncertainty range, while the first one broke due to the high impact velocity and consequently the experimental damaged surface couldn’t be evaluated. Adequate results were recorded for the glass laminates except for the first case, in which the experimental area evaluation was particularly troublesome due to the almost pure matrix failure damage mechanism, leading to a line-shaped region.

Fig. 11
figure 11

Damaged area correlation for UD laminates, damaged surface vs impact energy

Full size image

Cross-Ply Laminates

Fig. 12
figure 12

Cross-ply carbon and glass laminates: impacted specimens, processed ultrasonic scan, proposed numerical damage index (left to right)

Full size image

As opposed to the UDs, the impact campaign on the cross-ply specimens identified delamination as the main damage mechanism (Fig. 12). Glass laminates presented elliptical dents without visible fiber breakage, characterized by the typical peanut-shaped delamination; carbon specimens presented multiple cracks in the first direction together with elliptical dents.

Fig. 13
figure 13

Acceleration curves correlation for cross-ply laminates

Full size image

As shown in Fig. 13 carbon and glass cross-ply laminates presented good correlation in terms of acceleration curves. In particular, carbon laminates presented acceleration relative errors under 10% for the first two impacts (2.7 and 6.4, respectively), while three glass specimens out of three correlated with relative errors under 5%: respectively 4.1, 3.1 and 0.2%.

In terms of damaged surface (Fig. 14), as values under examination are still rather low, relative considerations made in the previous paragraph for UD specimens are valid here: some specimens presented values comparable with the area of a few shell elements. Nonetheless, with respect to the UD laminates, the damaged surface evaluation process turned out to be more effective, as areas involved were better defined. In fact, cross-ply specimens showed improved results in terms of surface correlation: 5 numerical areas out of 6 follow experimental values within the chosen margin of error.

Fig. 14
figure 14

Damaged area correlation for cross-ply laminates, damaged surface vs impact energy

Full size image

Summary

Overall, data presented above show good correlation of the numerical models, both in terms of acceleration curve and proposed damage index.

Regarding acceleration curves, satisfactory results were especially obtained for glass specimens, as both unidirectional and cross-ply reported peak relative errors below 5%; nonetheless, good matching is obtained for carbon specimens, with the exception of high energy impacts (over 2 J): in those cases the high impact velocities provoked element deletion and consequent drop in acceleration. As main purpose of this first correlation phase was the validation of the models for low velocity impacts (BVIDs), aforementioned results were considered acceptable and material models reliable with respect to the scope of the work.

In terms of damage surface, the most satisfactory results were obtained for the cross-ply specimens. As mentioned in the previous paragraphs, the reason must be identified in the nature of the damaged surface shape: if rectangular/line-shaped areas driven by matrix failure were found on the unidirectional laminates, cross-ply plates reported elliptical shapes driven by the delamination mechanism; as these last shapes are much better defined and captured by a surface approach, correlation improved as well. In fact, for UD laminates, a one-dimensional approach based on the crack length would have resulted in better correlation, but a uniform definition of the error was considered essential. That said, the damage index proposed showed good capability to reproduce qualitatively and quantitatively the damage region within the chosen error.

Regarding the damage criterion itself, most notable result is that data highlighted above and in section “Optimum Threshold Identification” (Fig. 8) seem to show that a unique value of 95% over any of the three MLT damage variables is the optimum threshold, able to well reproduce the damage region for all the tested materials and lamination sequences.

Conclusions

This study was aimed to design a damage criterion able to show damage provoked by low velocity impact events on thin composite laminates, in particular CFRP and GFRP. The main focus was on trying to solve the widespread problem of delamination description for medium to large scale applications, in which the phenomenon is particularly hard to model with the state-of-the art techniques, usually leading to unfeasible computational costs and/or unstable models; a semi-empirical alternative procedure was here developed exploiting the MLT damage law, using a dedicated drop-weight impact test campaign for calibration. Good results were obtained both in terms of acceleration curves correlation and damaged surface comparison for almost every specimen.

As a concluding remark, the campaign and the damage criterion calibration showed that composite damage due to low velocity impact events can be described as a damaged surface without considering out-of-plane stresses even when delamination is involved, exploiting intralaminar damage parameters integrated with experimental results. The proposed solution provides a robust method which can be easily integrated to equivalent shell approaches and is in principle extendable to any CFRP/GFRP composite laminate: ultimately, the implementation of the criterion is reduced to setting one parameter only, the calibrated limit value over the damage parameters.

Nevertheless, the calibration of said limit value is not straightforward. When it comes to evaluate the damaged region two issues need to be addressed both in the experimental campaign and in the numerical analyses. First, as a function of the damage mechanisms involved the shape of the region might not be representable as a surface (e.g. the first specimen of UD glass), leading to incoherent choices. Second, the overall dimension of the region is a key element to have a reliable description of the surface itself: if values are too low the boundaries are hard to distinguish both from the experimental scans and the numerical analyses, leading to high uncertainties; in both the two phases, resolution becomes essential.

Consequently, best way to proceed to calibrate the criterion would be to choose stacking sequences and impact energies so that sufficiently large damaged regions are obtained in both directions, yet breakage of the specimen is avoided. When enough experimental data is collected, chosen intralaminar numerical parameters for each ply are computed and elaborated, calibrating a damage law with the procedure described in section “Damage Criterion” and section “Optimum Threshold Identification”. Based on the considerations of section “Damage Model Foundations” and the results presented above, it’s worth noting that if MLT variables were used throughout the work, other physical parameters could have been exploited, or other elaboration procedures and failure definitions applied with similar results. On the other hand, the choice of MLT damage parameters and layer failure as defined in section “Damage Criterion” proved to be beneficial thanks to their physical meaning and simple implementation procedures.

Given these considerations, the method proposed is particularly suited for large-scale applications, to reduce the high computational power required by more refined and accurate techniques such as CZM and SSA. Beside damage extension, the method provides also a parameter able to describe the level of damage through-the-thickness, or damage depth: the leveled damage, (section “Damage Criterion”), which might be validated through further impact tests campaigns and advanced NDI techniques. Focus must be put also on studying alternative damage formulations, such as the ones highlighted in [17, 18], and in the extension of the method to fabric composites. Further developments lie in the implementation of analogous procedures for hybrid solid-shell element formulations (e.g. LS-DYNA thick shells), exploiting their superior ability to capture the out-of-plane stresses and the low computational costs compared to the classical solid elements.