The drop-weight test (sometimes called the drop-hammer test) is superficially one of the simplest explosive sensitivity tests that can be conceived [1, 2]. At its most basic, it involves trapping a small sample of explosive between two parallel, hard, high melting-point and rigid surfaces, one of which is dropped from varying heights to compress the sample. The drop-height is varied until a defined level of explosive violence is obtained from the sample and this height is recorded as a figure of sensitivity (or insensitivity). Usually this threshold is for a 50% probability of a violent ignition (known as a “go”). This seeming simplicity obscures the fact that the process of producing chemical reactions in the explosive sample in this way involves a very complex series of events that are still not fully understood, but requires both high pressure and high shear rates.

Additionally, it is extremely uncommon that in day-to-day usage, transport or storage a thin layer of energetic material is ever trapped between two parallel, hard, high melting-point and rigid surfaces that then compress the material quickly enough for reaction to start. It is therefore both surprising and serendipitous that the drop-weight test has any real utility as a safety screening test.

Indeed, the very applicability of the test is somewhat suspect when it is realized that the ranking of individual explosives is often different depending on the machine design. Table 8.3 in Reference [2] succinctly summarizes the problem. In that table the absolute ranking of several common explosives are compared against four types of machine. The general ranking is consistent (e.g., TNT is always less sensitive than PETN), but in two cases RDX is less sensitive than HMX, while in one example that order is reversed and in another they are equal. Additionally, in four cases, lead azide is found to be more sensitive than PETN, but in one machine that order is also reversed and in another they are equal.

Significantly, a missed progressive propagation behavior in a drop-weight test at LANL was at least partly responsible for the death of a worker, Candelario Esquibel, in 1952. At that time LANL was searching for a material that was more sensitive than PETN but less sensitive than lead azide. An initially promising candidate was thallium azide. Historically at LANL the drop-weight sensitivity was the prime screening gate for material production scale-up and the drop-height numbers for thallium azide appeared acceptable. After drying a 50 lb batch in several porcelain-covered steel trays, Esquibel was killed when transferring the mixture out into glass storage vessels with an aluminum-alloy scoop. It is presumed that friction between the porcelain, the explosive crystals and the scoop was sufficient to result in an ignition, propagation and partial detonation of some or all of the material in one tray. It was determined that the detonation did not spread to other trays or storage vessels from estimates of the overall violence of the event.

It was later determined that the drop-weight height estimates for thallium azide were much too high and that small ignition events with only minimal consumption of material were actually occurring at significantly lower heights. Specifically, at that time, the “go” and “no-go” threshold was a subjective decision made by the operator in the control room listening to the bang via a microphone and audio amplifier in the drop-weight room. With this particular material, the drops sounded rather loud from very low heights, but only became comparable to normal “gos” in PETN, RDX and the like at heights normally associated with “safe” materials. In retrospect the 50% drop-height values should have raised concerns since the standard deviation in “go” heights was much greater than usual (presumably because some of the sample was always somewhat reacting) and the 50% drop-height value for thallium azide powder soaked with water was actually lower than the measurement for the dry powder–a very abnormal finding.

In essence, the drop-weight test is a dynamic high-pressure and high-shear experiment. The only reasonably common accident scenario with a similar ignition stimulus is moderate-velocity fragment impact, particularly of flat-faced fragments (moderate velocity in this case being fragments traveling at hundreds of meters per second). In this velocity regime the impact pressure in the explosive is too low for a prompt shock-to-detonation transition (SDT) process to occur. However, it is fast enough that high strain rates are created, both mechanical and inertial confinement effects are significant and the explosive is not in a state of stress equilibrium.

Nevertheless, the original purpose of the drop-weight test was to screen out explosive compounds that were unacceptably sensitive to accident scenarios and the resulting consequences. It is undeniable that there is a strong correlation between energetic materials that are sensitive to drop-weight impacts from small heights and those that kill or maim as a result of accidental initiation stimuli during processing, transportation or use. In this important, but limited, application the drop-weight test is an extremely valuable apparatus in the study of explosive safety. However, it does not directly measure any property related to SDT or thermal stability (in particular self-heating), an important safety property of home-made explosives (HMEs). So what is it actually measuring?

This article largely concerns drop-weight machines that place the samples between smooth and hardened-steel anvils, of which there are three common designs used in the West. The details of these designs are not reproduced here, but can be found in [2]. A fourth, and fairly common, machine design puts the sample on top of sandpaper that is then compressed by hardened-steel anvils. This method introduces yet another reaction mechanism to an already complex system.

The introduction of grit on the sandpaper increases the ease with which ignition sites form compared with smooth anvils. This is not from an explosive property, but results from the frictional heating of loose grit moving against the hard upper anvil during the impact. It is typically the frictionally heated loose and therefore mobile grit that forms the hot-spot, not the interaction of the flowing explosive with the much more numerous stationary grit particles. Thus, the quality of the sandpaper glue (i.e., quality of manufacture and batch-to-batch variation) and glue aging play a very significant role in the drop-weight sensitivity measured. Historically, testing locations have purchased one large batch of sandpaper that is used for many years, but then have noticed a significant change in drop-heights when the old batch is expended and a new one is used. The threshold in this form of the drop-weight is therefore more a function of sandpaper properties and the ignition temperature of the explosive than a fundamental measurement of the propensity for explosion in the material. The loose-grit frictional heating mechanisms are well summarized in Reference [3].

In concept, the drop-weight test uses the kinetic energy of the falling mass to start ignition in a small (25–40 mg) sample of energetic material by some undetermined mechanism and then allows the ignition (or ignitions) to rapidly propagate (explode) to some degree, creating an effect that can be measured. In many common explosives (e.g., PETN), it is found that a fairly distinct drop-height exists between essentially no reaction of the material and almost complete rapid deflagration of the majority of the sample. Only true primary explosives transition to a detonation under this stimulus. This is highly convenient since the violence of deflagrations are generally so limited even in the most powerful explosives that the steel anvils can be reused for multiple tests before requiring re-work. Thus, in many common explosives a clear distinction between a “no-go” (little to no reaction) and a “go” (clear reaction judged by a sound or light threshold) occurs. One historical problem with the drop-weight test has occurred when testing materials that for a small increment in drop-height do not exhibit such a clear and defined change in violence (e.g., thallium azide or HNS [4]).

It is therefore clear that the drop-weight is an integrated explosive test involving ignition of the explosive and propagation of the reaction. Significantly, the majority of explosives prone to accidental initiation, growth and detonation are also relatively easy to ignite and the reaction propagates easily (e.g., PETN). For this reason, the drop-weight is an efficient screen for those compounds but for others that ignite easily but propagate poorly (e.g., thallium azide), unless an experienced and informed operator pays attention, erroneous estimates of unusual explosive compounds’ sensitivity will be found.

The Mechanics of the Drop-Weight Apparatus

The numerous physical processes occurring during the few hundred microseconds duration of a drop-weight test are complex and interrelated, even in an inert specimen. It is therefore useful to model the response of notional inert samples in a simplified apparatus using a computer code. In this way the physical processes that affect energy transfer within the system could be understood. The Eulerian CTH code written by Sandia National Laboratory was chosen for this. The transfer of the original kinetic energy source (the dropping upper anvil) could be tracked and the material variables associated with both the anvils and the sample followed throughout the event (temperature, pressure, internal energy, kinetic energy, position and velocity) using virtual Lagrangian sensors (tracers) that move with the material they were originally embedded in. Such tracers were put into both the anvils and across the radius of the sample.

A simplified type 12 smooth hardened steel tooling arrangement was modeled with an effectively infinite lower anvil. The top 2.5 kg anvil had a velocity of 6 m \(\hbox {s}^{-1}\) representing a substantial drop-height typical of a test on TNT. The notional inert 16 mg sample was given the density and equation-of-state (EOS) of PMMA (a low sound speed, low density polymer).

Table 1 The drop-weight model conditions
Full size table

The four test cases run are shown in Table 1. Condition (A) was where the sample had zero shear strength (i.e., the model was fully hydrodynamic). In (B) the sample was elastic perfectly-plastic with a yield strength of 100 MPa, but a melt temperature of 400 K representing a low melting point solid such as inert PETN. In this model any material above the melt temperature instantly has zero shear strength. In (C) the same 100 MPa yield behavior was employed, but melting was totally suppressed representing a high melting point solid. Condition (D) was used to explore the concept of load-drop that is introduced in Sect. 2. For this reason it makes more sense to delay analysis of this model result until that section. The anvils had the equation-of-state of alloy steel and a hardness such that they remained fully elastic in all situations. Because the drop-weight creates a very narrow gap in which the sample flows, the uniform mesh resolution used (12.5 \(\upmu\)m) had to be fine, making this a large cylindrical axi-symmetric problem. The code ran on a Linux cluster with 448 processors and each model run took about 26 hours.

Fig. 1
figure 1

CTH model tracer location map and output. Temperature and radial velocity results for condition (a) are shown together with temperature, radial velocity and axial displacement for condition (b)

Full size image
Fig. 2
figure 2

CTH model output for conditions (C) and (D). Temperature, radial velocity and pressure results for condition (C) are shown together with pressure for condition (D)

Full size image

As the motion of the top anvil initially deforms the sample with strength (B), the temperature rises as it extrudes radially relatively slowly (1–10 m \(\hbox {s}^{-1}\)), see Fig. 1. Both pressure and temperature are greatest in the sample center and drop towards the edge. In the hydrodynamic sample (A) the pressure is low and the sample undergoes negligible heating at this stage. This results in little anvil deceleration occurring. By 300 \(\upmu\)s the anvils are less than 200 \(\upmu\)m apart. The rate of radial flow required for the anvils to close has been rising geometrically and sample inertia effects provide a substantial and increasing force that must be overcome. This causes the pressure in the sample to rise quickly and results in both anvils beginning to deform elastically. The radial velocity of the hydrodynamic sample (A) is greatest reaching \(\approx\) 400 m \(\hbox {s}^{-1}\) for an instant just before the lower anvil begins to significantly deform. The radial velocity of the sample with strength (B) is a little lower (\(\approx\) 300 m \(\hbox {s}^{-1}\)), but the edge sample temperature had already increased to within 20 K of melt. The added viscous heating from the brief rapid motion event creates a spatially variable melting process that influences the further viscous flow in a complex manner. That is, the material in the center is initially hotter, and indeed molten at this point, but is moving slowly, while the now hot but still solid material at the edge briefly moves, quickly creating significant strain heating which results in melting whereupon it loses strength, suppressing further heating.

The “noisy” signals, seen particularly in the temperature plot for (B), are due to the Lagrangian nature of the tracer and the presence of large gradients between model cells. This can result in the tracer hopping between cells with substantially different state variables and the apparent, but non-physical, oscillations shown result.

Once the lower anvil begins deforming elastically (shown only for (B)), it allows the top anvil together with the approximately constant thickness sample and lower anvil to effectively move together and this quickly reduces all the radial sample velocities to close to zero. It also effectively transfers the remaining kinetic energy of the top anvil to the lower one (the energy sink). Peak pressure (0.3–0.5 GPa) is reached at \(\approx\) 380 \(\upmu\)s and rebound begins at \(\approx\) 420 \(\upmu\)s. As the top anvil slows, the temperature in the hydrodynamic sample (A) quickly drops but does not in (B) where mixed molten and solid material regions exist. Once bounce occurs the elastic unloading process creates a second brief radial velocity flow event in both cases. This reaches velocities in excess of 100 m \(\hbox {s}^{-1}\), but under negligible pressure.

In both (A) and (B) the circumference area of the anvils touched very briefly at turn around time, but owing to the relatively low pressures imposed by the samples the contact area was relatively large and the steel-on-steel impact pressure was therefore also low.

Things are slightly different in the model with strength, but where melting is suppressed (C). Initially, of course, the behavior is similar to that of (B) until about 300 \(\upmu\)s. In this case, however, the homogeneous strength effects prevent the anvils ever getting closer than 300 \(\upmu\)m and the sample radial velocity only reaches a maximum value of 30 m \(\hbox {s}^{-1}\). This produces high temperatures in the center of the sample (550 K) but much lower ones at the edge (400 K). The resulting peak anvil pressure is much greater (3 GPa) producing significant bowing of the center of the anvil. In fact the sample forms an elliptical shape and allows the steel anvils to firmly touch at their circumference. In this model condition, peak pressure was not reached until 440 \(\upmu\)s and bounce did not occur until 510 \(\upmu\)s, significantly later than for conditions (A) and (B).

In summary, although the broad physical processes occurring in (A), (B) and (C) have similarities, the details vary depending on the constitutive properties of the sample. Principally, it was demonstrated that the shear strength and melting characteristics of the sample make a significant difference to the specific elastic deformation of the anvils and the flow velocities within the sample. Additionally, it was found that the motion of the lower anvil–influenced by the elastic and inertial effects in that location–was responsible for suppressing the rapid radial flow event in the sample. Because the radial flow is largely responsible for the thermomechanical conditions necessary for ignition, it explains why subtle differences in machine design will produce significantly different drop-weight results.

Among other physical aspects the model ignored were melt kinetics, heat transfer, molten viscosity, reaction chemistry, instability growth, sample work hardening and particle-particle interactions. Nevertheless, we believe that the simplified models adequately bracketed the broad range of responses likely in a real drop-weight test.

The Ignition Process in the Drop-Weight

Most drop-weight apparatuses are not instrumented and so it is impossible to detect at what stage of compression the ignition and subsequent propagation occurs. In badly designed machines there is significant bounce after impact and ignition can occur in either of two forms: only on the second lesser impact on damaged explosive, or twice if all of the material is not consumed in the first impact. Well-designed machines are “dead” and transfer almost all of the dropping mass momentum into the sample and lower assembly, resulting in very little bounce.

Drop-weight apparatuses used for most testing use steel anvils which provide no direct optical access to the impact process. An alternative design used principally for scientific investigation uses transparent anvils made either of toughened glass or sapphire to provide optical access [5, 6]. It is observed that the explosive sample is extensively deformed into an expanding thin disc prior to any sign of reaction. To a large extent, therefore, the form of the sample, a loose granular pile or a pellet, is irrelevant since the original morphology and geometry are destroyed early during the impact. This is a considerable advantage for safety testing since a pile of the test explosive can be laid approximately in the center of the anvil and so long as the total sample mass is consistent, broadly reproducible results are obtained.

As the explosive is compacted into the thin disc, many materials with low to moderate melting points as a result of viscoplastic heating are observed to melt and transition from opaque to clear (e.g., PETN) [5, 6]. Around the time this occurs the rate of radial expansion accelerates rapidly from meters per second to hundreds of meters per second. The pressure in such an expanding disc is very high (0.5–1 GPa) in the center and lower at the edges [5]. Materials with higher melting points are only observed to “plastically yield” at large deformation, but then rapidly accelerate radially to similar speeds as those that melt. If ignition occurs, it is usually towards the edges of the expansion where the velocity is greatest, the pressure lowest and is observed shortly (2–100 \(\upmu\)s) after the rapid radial acceleration occurs.

In a typical drop-weight apparatus, the load magnitude increases from zero to a maximum value and decays in an approximately sinusoidal manner and has a total duration of 0.25–0.75 ms [1, 5]. Machine designs that have been instrumented to measure the load during impact show that, in the vast majority of explosive materials where a marginal “go” occurs, the load climbs until reaching approximately 2/3 of the maximum for that drop-height prior to the rapid radial expansion phase. When the rapid expansion phase begins some researchers have measured a significant temporary drop in the load applied to the sample. Therefore, the abrupt unloading (load-drop) has been attributed to either sample melting or sintering and rapid plastic or viscous flow that occurs relatively late in the drop-weight energy transfer process [5, 6]. Ignition, if it occurs at all, is observed only after this load-drop and the delay is both explosive composition- and machine design-dependent.

Research on the load-drop phenomenon is limited and does not appear to have been studied since the results reported in [5]. It is clear that inert materials with high melting points (> 800 °C) give load-time traces that are very similar to drops with no sample present. That is, they show no load-drop since presumably no melting or sintering occurs. Inert materials with moderate melting temperatures (600–800 °C) show slight perturbations in the load-time history presumably from localized softening processes, but no load-drop. Some inert materials with low melting points (70–190 °C) and some explosives (e.g., tetryl, Composition B) show a distributed series of load fluctuations rather than a single abrupt one. Things get more complicated with other low and moderate melting point inert solids (200–600 °C) and most explosives. Some show a single abrupt load-drop, and in the case of explosives, reaction some time later, while others appear to undergo a deformation process that results in essentially no resistance being applied to the anvil and the load drops to zero before recovering. It is suspected that this apparent complete lack of resistance in some cases is purely an artifact of the design of the apparatus used in this study rather than an inherent property of explosives, although given the apparent significance of the load-drops in the ignition process, this needs further study before this can be asserted (Williamson DM (2019) Cavendish Laboratory, University of Cambridge, UK. Personal Communication).

If one imagines a strong sample in the drop-weight that suddenly loses all strength at some point during deformation, the results proposed in [5] might be expected to occur. The strong sample would initially create large deceleration forces on the upper anvil, which if suddenly removed by, for instance, an abrupt melting process, then the upper anvil would experience a minimal pressure condition until the continuing motion brought it back against liquid material trapped by the lower anvil and a rapid radial flow and higher pressure state was created. From that time on the response would be expected to follow the fully hydrodynamic condition (A) discussed in Sect. 1.

In an effort to simulate this effect, a strong sample with a yield strength of 500 MPa was given a melt temperature of only 400 K. The elastic perfectly-plastic flow criterion and the abrupt removal of shear strength at the melt temperature simulate the best possible circumstances to reveal such a load-drop. However, consulting the pressure time traces for condition (D) in Fig. 2 reveals that even under these seemingly ideal load-drop generating circumstances, the pressure profile is complex and highly spatially dependent. There is a large, but only slow, decline in pressure at the center of the sample that is not observed in the other model conditions; however, the more modest load-drops observed at different distances from the center do not occur all at the same time. Therefore the integrated pressure over the upper anvil face would not be expected to show any kind of abrupt load-drop event. This casts further doubt on the validity of the load-drop phenomenon and suggests it may have been an artifact of the specific apparatus design.

Ignition processes in the drop-weight, when they occur, are not initially observed to be widespread, but localized to one or more hot-spots that then grow (or quench). Indeed, it was the marked discrepancy in the simple calculation of the total energy in a drop-weight with respect to the energy required to homogeneously bulk-heat a typical sample of explosive to ignition that initially demonstrated that some isolated form of localization (hot-spots) must be occurring. The localizations generate discrete ignition sites that then propagate, rather than a distributed thermal explosion from uniform heating [6]. This hot-spot idea was later also applied to SDT events although SDT is unrelated to the drop-weight processes.

Thus, ignition in the drop-weight apparatus on smooth, hard, high-melting point anvils is driven by viscoplastic and possibly adiabatic shear-band heating from rapid radial expansion of the flowing explosive when the stress imparted by the anvils is much greater than the shear strength of the explosive [5,6,7,8,9]. Further, residual inhomogeneities in the explosive or the flow pattern (instabilities and non-uniformity in radial growth and jetting are usually observed) produce regions of localized heating that can ignite and propagate [5, 6].

Fig. 3
figure 3

An exaggerated sketch of the anvil deformation problem that can lead to extrusion into a narrowing gap. 1. Metal support. 2. Anvil (glass in this case). 3. Explosive sample. 4. Narrowing gap

Full size image

One known problem, particularly with transparent anvil drop-weights, is elastic bowing of the anvils from high pressures in the center of the sample and unloaded circumferences [10, 11]. Therefore as the force builds at the center of the anvil a variable gap is created into which the extruding explosive must be forced [6]. This is in addition to the previously discussed inertia and viscosity effects that also act to prevent unconstrained lateral expansion of the sample into a thin parallel gap. Figure 3 shows an exaggerated illustration of the effect. Because transparent anvil drop-weight designs can only support the anvils at the edges and the elastic moduli of glass is approximately three times lower than steel, the effect is usually more severe in these designs.

Measurement of Violence

As discussed previously, the drop-weight is an integrated ignition and propagation test to a defined level of violence. Currently, violence is usually quantified using a specific sound or light threshold and comparison with a reference compound (often dry PETN or RDX powder) performed at the same time. In this manner explosive material outliers or a change in the machine response are generally identified by knowledgeable operators.

Each energetic material has a different reaction propagation behavior after ignition has occurred. For example, TATB is both very difficult to ignite and propagates very poorly. HMTD (hexamethylene triperoxide diamine) has a very low spontaneous combustion temperature of 133 °C and is a primary explosive; by definition, it transitions from deflagration to detonation effectively instantaneously. This particular material often damages the drop-weight anvils even with very small test masses. Lead azide is interesting since it is remarkably thermally stable, having a spontaneous combustion temperature of 310 °C, but is a primary explosive. Other explosives can be easy to ignite, but propagate relatively poorly (e.g., thallium azide). On the other hand, due to its low melting temperature but high ignition temperature, TNT is fairly hard to ignite but then propagates relatively well. Generally, the drop-weight test is most repeatable for materials that either ignite easily and propagate rapidly (e.g., PETN) or are hard to ignite and propagate poorly (e.g., TATB).

It is important to bear in mind that, unlike secondary explosives, primary explosives may not need to flow under the action of the drop-weight to produce reaction. The action of slow crushing may be enough to induce detonation and so the fundamental mechanism of localization of energy may be different in primary explosives than the hot-spot model accepted for secondary explosives.

Figure 4 shows the results from two notional tests that are diagnosed using peak sound intensity. In (a), a well-behaved drop-weight explosive is shown with a very distinct jump in intensity at a specific height, representing the onset of almost complete combustion of the sample. The slight rise in intensity before and after represents the extra kinetic energy of the mass dropped from increasing height being converted to extra sound energy, independent of any test material present.

In contrast, Fig. 4b shows the result from a material that begins partial reaction at very low drop-heights, but the reaction subsequently quenches. This results in a continuum of violence magnitude up to quite large heights where 100% combustion occurs. In this type of material the drop-height threshold value is somewhat subjective in terms of its propensity for causing an accident, but not from a defined “go” to a “no-go” perspective identified from other tests on well-behaved materials (the dotted lines in Fig. 4).

A conservative accident-prevention criterion would be the elimination of ignition in the drop-weight test. The alternative chosen instead is to accept ignitions and then count on the somewhat stochastic nature of reaction quenching to prevent damage to equipment or people. In the example shown in Fig. 4b, the use of such a conservative criterion would result in a drop-height value just above the sound intensity that would be generated from tests on inert powders at equivalent heights (i.e., the machine self-noise).

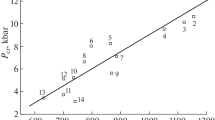
The notional plots for the hypothetical materials shown in Fig. 4 present an overly simplistic view of the stochastic nature of the drop-weight in real materials, but was drawn this way to more clearly reveal the trends. Figure 5 presents a summary of some real data using type 12A tooling (sandpaper) on a special batch of well-controlled RDX powder [12] where the 50% drop-height was measured to be \(37\pm 6\) cm. Although there is a clear overall upward trend in sound intensity with drop-height, the results from an individual drop can be highly misleading to an inexperienced operator. RDX is a fairly ideal material in the drop-weight test and yet there is significant scatter in the results.

Fig. 4
figure 4

a An exaggerated and simplified plot showing the response from a material well-suited to drop-weight sensitivity testing (e.g., PETN). b An exaggerated and simplified plot showing the response from a material less well-suited to drop-weight sensitivity testing (e.g., HNS, thallium azide)

Full size image
Fig. 5
figure 5

Example type 12A tooling drop-weight data (peak microphone voltage versus drop-height in cm) for a special batch of reference RDX made for machine calibration purposes. The defined “go” to “no-go” voltage threshold for this machine was found to be 1.3 V. Redrawn from [12]

Full size image

Growth and Propagation in the Drop-Weight

As Sect. 1 described, there is a gradient in the pressure state within the radially expanding explosive sample at ignition. Additionally, the anvils, either negligibly or significantly deformed, provide confinement to the reaction products from growing ignition sites. These effects combine to provide conditions conducive to reaction propagation in explosives since the flame front (heat) is maintained very close to the burning material. This occurs both from the applied physical pressure from the anvils and building pressure from combustion products having no ready path for release.

However, the loading duration in a typical drop-weight is 0.25–0.75 ms depending on the design and explosive material properties. Ignition is often observed to occur close to peak load (either before or after). As discussed in [1] this is poor experimental design since the elastic energy stored in the machine is close to a maximum value and the kinetic energy of the falling mass is close to zero at the time of the ignition and growth phase. Thus the elastic response of the apparatus therefore plays a key role in the result of the test.

Indeed, one of the authors is aware of a machine that started giving very irreproducible results before it was found that the bolts securing the lower anvil to the massive base plate had worked loose. Torquing the bolts fixed the problem, but looking back through the previous machine test entries, data for up to a year may have been suspect as the bolts were working slightly loose. This example illustrates the critical role that the elastic response of a drop-weight machine plays in the data accuracy and the need for frequent tests on samples with known responses in that machine.

It is therefore clear that the loading period of an individual drop machine is defined by its exact design, wear and maintenance and that these factors will greatly influence the data obtained. The loading period of a machine is an elastic response parameter and is therefore almost entirely independent of the drop-height, which alters only the magnitude of the peak sample pressure. This loading duration, or period, is important because in the majority of less sensitive explosives the deflagration growth phase is occurring as the machine is actually unloading the sample. Reduced pressure drops the reaction rate, lowers the amount of material consumed and makes less sound and light compared with a machine with a longer period dropped from the same height. This is one explanation for why the relative ranking of different explosives as well as the absolute drop-height values vary from machine to machine, even when they nominally have the same design [13].

It was mentioned earlier that the exact geometry and particle size of the test explosive sample is found to be relatively unimportant to the drop-height sensitivity measured, since the material is so heavily deformed prior to ignition that the starting configuration is largely irrelevant. This feature, allowing inexpensive and rapid sample throughput, is a mixed blessing. It is well known that particle size and morphology significantly affect the deflagration rate of explosive powders as well as their shock sensitivity [14]. These parameters are therefore critical in the deflagration-to-detonation (DDT) process, a common route to violent response after an accidental thermal stimulus. This important material-dependent factor is therefore absent in the drop-weight where propagation occurs only in a high-density material compact with very limited residual intergranular void space.

Drop-Weight Testing on Liquids

Water wetting of sensitive explosive powders is a common procedure both to mitigate electrostatic discharge (ESD) ignition concerns and to address United Nations (UN) transport by road sensitivity concerns. HMX with 2 wt% water added has been tested in the transparent anvil drop-weight and it is found that at this relatively low water concentration the ignition process was unaltered, but that the water inhibited propagation [5]. The effect of saturating HMX powder with water has not been tested to understand its effect on the ignition process although this is the common method of desensitizing bulk explosive powder for transport by road.

It has been demonstrated that the difference in drop-weight response between nitroglycerin without visible air bubbles and with them is up to a factor of 45 [3, 15, 16]. Indeed, this is the reason why large volumes of nitroglycerin should never be stored in pure liquid form. Further, it has been hypothesized that bubbles almost invisible to the naked eye may play a significant role in the apparent sensitivity of other liquid explosives to the drop-weight insult [3]. Good evidence has been found that this large sensitivity increase is due to adiabatic compression of the gas in the bubble during impact, and that the measured sensitivity increase correlates well with the ratio of specific heats of the gas in the bubble, which in turn affects the final collapsed state gas temperature [3, 16].

It is therefore important to understand that the measured 50% drop-weight height is likely to have larger statistical variability than solid explosives, since the content of minute air bubbles is likely to vary between samples, and that the sensitivity measured in relatively bubble-free drops is expected to be markedly different for those where they are deliberately introduced. Additionally, careful drop-weight operators need to take even greater care to maintain a consistent surface finish on the anvils when testing liquids rather than solids in an attempt to limit the inevitable variable effects from minute trapped gas bubbles.

It has been demonstrated by the use of a drop-weight apparatus with a small vacuum chamber surrounding the sample that the presence of entrained gas pockets in the drop-weight impact of powders do not provide the same ignition source as that found in liquids [17, 18].

Drop-Weight Design Limitations and Alternatives

Although the drop-weight test has a definite and valuable place as a ranking tool in terms of explosive safety, it is difficult to justify its use as a wider explosive research tool. Many researchers have attempted to do just this and correlate the drop-height metric with some other explosive property or to validate modeling efforts [19,20,21,22,23,24,25,26,27,28,29]. Since, as previously explained, the majority of very sensitive explosive compounds are easy to initiate and reaction propagates easily, and the majority of insensitive explosives are hard to initiate and propagate poorly, a generally correct trend is expected with respect to other physical properties or predictions. However, there will be important and possibly significant exceptions to this general rule.

For example, Reference [29] attempts to correlate a relatively simple chemical sensitivity model to the sensitivity of explosive compounds to the drop-weight. A large database of 258 results was initially available, although 212 were actually used after excluding several materials of the wrong sort and 8 “outliers”. A correlation coefficient (\(\hbox {R}^{2}\)) between the model predictions and data was initially 0.81 for those 212 compounds. However when the model was applied to another data set of 96 results, the correlation dropped to 0.60. By pruning out materials that did not fit well for various reasons, a final correlation coefficient of 0.69 was found for a selected 74 of those 96 compounds. It is therefore clear that the model has some correlation with drop-weight data, but there were many materials that did not fit so well. A significant question therefore remains: were the materials that did not fit the overall trend more interesting than those that did?

References [22, 23] also suggest removing outliers to improve correlation between the suggested fundamental “sensitivity index” (a modified oxygen balance) and the drop-height value for a given explosive. The reference also includes 50% drop-heights for many different explosive materials. Reference [20] correlates oxygen balance to the logarithm of the 50% drop-height with reasonable results except for three notable exceptions. Reference [27] correlates bond disassociation energy versus the logarithm of the 50% drop-height, but [26] suggests that the bond disassociation energy divided by the decomposition energy of the material correlates better. It is notable that several of the correlation papers lament the variability in the drop-weight results even when performed several times on their own machines. Some authors even blame the lack of better correlation with their suggested correlation metric to this variability. It is notable that the logarithm of the 50% drop-height is often chosen since this usually improves the visual correlation between the metric and the experimental data.

Finally, in Reference [19] a correlation is noted between the 50% drop-height and the temperature required for thermal explosion to occur in 250 \(\upmu\)s for that particular material since this is the total impact duration stated for the drop-weight machine used by the authors. This finding would appear to be dubious since as discussed previously, optical studies have revealed that initial ignition is driven by hot-spot processes, not volumetric thermal explosion.

As discussed, there are several deficiencies with the drop-weight test: (a) It does not rank “abnormal” materials well. In this case abnormal is defined as materials that ignite easily but propagate poorly or the rarer materials that ignite poorly but propagate easily. (b) The test is very machine design- and maintenance-dependent because the ignition and growth process occurs when the elastic energy in the machine is close to the maximum and the momentum in the falling mass is close to the minimum. Therefore, the growth process often occurs as the machine is unloading the sample and small variations may dramatically lower the resulting violence observed in some machines. (c) Information about the particle size and morphology and their effect on the DDT process, historically an important accident scenario, is not captured since the sample is homogenized by the large pressures imposed prior to ignition.

Reference [1] suggests a partial fix to (a) and (b) by measuring the impact energy to ignition for a composition in a modified drop-weight apparatus rather than the 50% drop-height to a defined level of violence. This is achieved relatively simply by attaching an accelerometer to the falling mass and greatly increasing the fall speed (20–40 m \(\hbox {s}^{-1}\)) using rubber bungee cords to accelerate the falling mass. In this way it was demonstrated that ignition occurred much earlier in the sample deformation process when the mass had been decelerated only slightly, the sample pressure was lower, the anvils were undeformed and the propagation phase occurred as the pressure was still increasing rather than decreasing. From measurements of the slight deceleration, the energy absorbed by the sample up to the point of ignition can be calculated easily and used as the sensitivity metric. Because propagation occurs during the still-increasing loading phase and was detected by photodiodes, the results are expected to be much less machine-dependent. The major disadvantages of this approach were the difficulty in making the accelerometer and cable attachment survive the higher impact speeds and the much greater wear-and-tear on the machine owing to the very large kinetic energies of the falling mass. Replacing the accelerometer with modern optical velocimetry techniques may reduce this experimental inconvenience by relocating the required diagnostics to a location away from the effects of reaction.

Differential scanning calorimetry (DSC) performed on different sample masses and at different heating rates can relatively easily measure the simple ignition kinetics of an explosive compound. A greater number of tests with modulated DSC (MDSC) can form a model of the self-heating kinetics that are relevant to cookoff accident scenarios. Samples would need to be run with both vented and sealed pans to understand the potential role of gas products that are auto-catalytic to the reaction chemistry. Thus, accurate, reliable and reproducible modern techniques are available that can quantify the ease of ignition (the first part of the drop-weight test). The methods cannot quantify the propensity for hot-spots to form under rapid radial expansion, but as noted earlier, this mode of accidental stimulus is actually rather rare in day-to-day use and storage.

The pressure-bomb strand-burner measures the rate of deflagration in a solid or powder explosive column as a function of externally applied gas pressure and, in more complex apparatus, initial temperature. This method can quantify the propensity for propagation of a burning front both as a function of confinement (applied gas pressure) and also actual particle morphology. This is equivalent to the second part of the drop-weight test process.

Although the combination of these laboratory tests is more time consuming and expensive than a single drop-weight series, with the exception of the ease of localization (hot-spots) under rapid flow, the combination potentially offers a way to independently measure both ignition and growth propensity in solid explosives. The DSC/MDSC measurements are equally valid in liquid explosives, but the issues associated with gas bubble adiabatic compression are not well addressed by this method or the strand-burner technique.

In summary, it appears that in too many situations a modification of the old adage, “If all you have is a drop hammer, then every explosive looks like a nail,” is true.