Abstract
Composite components regularly experience dynamic loads in service. Despite this, it is still difficult to obtain accurate mechanical properties of composite materials under high strain rate conditions. In this study, a new application of the Image-Based Inertial Impact (IBII) test methodology was developed, to generate an accurate in-plane transverse and shear moduli dataset from unidirectional (UD) off-axis composite specimens. The obtained dataset was consistent across different sample configurations, where results from the UD45\(^{\circ }\) off-axis specimens agreed well with the UD90\(^{\circ }\) values. Validation of the shear modulus identification was also undertaken by comparing the results from the UD90\(^{\circ }\) and UD45\(^{\circ }\) specimens with a multi-directional (MD) configuration. Here, it was found that MD±45\(^{\circ }\) specimen shear modulus values where marginally lower than that from the UD specimens, in accordance with the lower fibre volume fraction of the MD laminate. Low strain rate sensitivities in the \(0.5-2\times\)10\(^{3}\) \(\hbox {s}^{-1}\) regime evidenced in this work suggest previously published data (often from split-Hopkinson bar tests) may include both a material and system i.e. testing apparatus response.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
There are many examples of composite components being subjected to dynamic loads. In the aerospace industry, aircraft nose caps, wings and rear stabilisers can be impacted by a range of objects such as birds, hail or ice and runway debris. Design engineers regularly use a combination of experiments and finite element simulations in order to predict the response of these structures under impact conditions. The simulation’s ability to predict a realistic structural response hinges largely on the accuracy of the data used in the individual material models specified for the component. This is especially true for fibre reinforced polymer composite materials, where the resin dominant (i.e. transverse and shear) properties are generally considered rate sensitive [1].
One problem for simulation engineers utilising high strain rate material data is that there is significant scatter in published values. For example, in-plane transverse modulus strain rate sensitivities of Carbon Fibre Reinforced Polymer (CFRP) composites reported in literature are presented in Fig. 1a. Here, up to 20% variation in the reported values can be seen at strain rates below 10\(^{2}\) \(\hbox {s}^{-1}\). However, beyond 10\(^{2}\) \(\hbox {s}^{-1}\) the scatter is anywhere between – 20 and 40%. Scatter can also be seen in the reported shear modulus values from unidirectional (UD) samples, where at strain rates of 10\(^{3}\) \(\hbox {s}^{-1}\) UD45\(^{\circ }\) specimen results vary up to 40% as shown in Fig. 1b. Inconsistency was also found with the reported dynamic shear modulus from tests on multi-directional (MD) specimens, with one example reporting an increasing shear modulus with increasing strain rate [2] and another reporting practically no strain rate sensitivity [3] from ±45\(^{\circ }\) configurations. Therefore, when the same testing method is used to test similar materials in similar configurations at similar strain rates, different experimental campaigns yield conflicting results. Not all CFRP composites investigated utilised the same matrix system and therefore, some variation due to resin chemistry was expected. However, this alone does not account for the large scatter seen in Fig. 1. Furthermore, transverse and shear moduli results in Fig. 1 show a lack of data obtained at strain rates higher than a few hundred \(\hbox {s}^{-1}\). This is problematic for defence industry applications such as projectile/armour impact, where strain rates on the order of a few thousand \(\hbox {s}^{-1}\) are developed [4].
Percentage change in dynamic in-plane moduli relative to quasi-static values vs. strain rate for UD CFRP composites: a Transverse modulus from UD90\(^{\circ }\) specimens and b shear modulus from UD45\(^{\circ }\) and MD±45\(^{\circ }\) specimens. Circular markers represent tensile and square markers represent compressive test results, while solid markers are from MD±45\(^{\circ }\) specimens. Data obtained from composites with thermoset matrices in [2, 3, 5, 6, 7, 8, 9, 10, 11]
Many of the published results used high-speed hydraulic testing machines, drop towers or split-Hopkinson bars to generate data. These devices have one thing in common: they require the assumption of quasi-static equilibrium in the specimen in order to infer stress. In the case of the split-Hopkinson bar, this assumption is required to estimate specimen stress from strain gauges remotely mounted on the input and output bars. Unfortunately, for low wave-speed, quasi-brittle materials such as composites, quasi-static equilibrium is difficult to achieve at strain rates over a few hundred \(\hbox {s}^{-1}\) where inertial effects are significant [12, 13]. Short sample lengths are often used to reduce transient effects in split-Hopkinson bar tests [14]. However, quasi-static equilibrium is additionally difficult to achieve in split-Hopkinson tension bar experiments, which often require longer gauge length specimens that further delay equilibrium. Under these conditions it is difficult to obtain accurate quantitative modulus and failure stress data e.g. in [15].
Split-Hopkinson bar experiments also require the assumption of a 1D specimen loading in order to infer stress and calculate strain rate. This is one of the reasons why split-Hopkinson bar test configurations use long slender bars and well-machined, small diameter specimens: to reduce out of plane stresses [16]. During tests, radial friction is generated at the specimen/bar interfaces and within the specimen itself. Friction at the specimen/bar interface is generally reduced by applying grease at the specimen ends, however radial or out-of plane stresses within the specimen are not evaluated with traditional methods and can be significant at high strain rates [17]. In more recent times, full-field imaging techniques have been integrated in split-Hopkinson bar experiments [11,12,, 6, 18]. While this has improved strain measurement accuracy, inferring stress at high strain rates is still problematic because inertial effects are strong and the quasi-static equilibrium assumption is still required. Dispersion in the incident wave can induce multidimensional loading in the specimen and thus violate the 1D wave mechanics assumption [19]. Correction techniques such as that described in [20] can be used to account for wave dispersion, however these methods are still evolving [21]. Pulse shaping techniques that produce a ramped rather than a sharp rise in the incident pulse reduce dispersion [22], but ultimately limit achievable strain rates in tests.
Acknowledging that most dynamic data for CFRP composites were generated with the split-Hopkinson bar and that assumptions required for accurate results with the device can be violated with composites at high strain rates, scatter in the reported data is then expected. Ongoing requirements in pursuit of consistent high strain rate data for orthotropic composites have called for new experimental methods to be developed. New techniques based on full-field measurements have emerged [14, 23], with a recent example being the Image-Based Inertial Impact (IBII) test described in [19,20,26]. The IBII test uses ultra-high speed imaging, full-field measurements and the Virtual Fields Method (VFM) to obtain material properties under dynamic loads by using the inertial response of the material as a kind of embedded load-cell. Because the technique does not need to assume quasi-static equilibrium in the specimen, it is ideal for testing the high strain rate properties of materials, including composites. In fact, because the test is purely inertial, quasi-static equilibrium is never reached. The IBII test has been used to obtain the transverse modulus and failure stress of a UD CFRP composite in [26] and the interlaminar modulus and failure stress in [25]. A proof of concept evaluation of a single UD45\(^{\circ }\) composite specimen was conducted in [27], characterising transverse and shear moduli under a combined compression/shear state of stress. However, in that work experimental results were processed with smoothing parameters (see Sect. 3) based on the previous experimental campaign in [26]. Therefore, there is scope to extend the IBII test methodology to evaluate high strain rate modulus and failure stress properties of off-axis composites, using a range of specimen configurations and their respective optimised smoothing parameters.
This paper first describes the VFM theory used to identify the in-plane transverse and shear moduli from off-axis composites. Methods for the numerical implementation of the VFM equations then follow, and the kinematic field smoothing parameter optimisation procedure is outlined. Stress-strain curves and modulus values from UD90\(^{\circ }\), UD45\(^{\circ }\) and MD±45\(^{\circ }\) specimens are compared and related back to differences observed in the kinematic fields. Finally, modulus values from this study are compared to results in literature, where differences resulting from test methodology and strain rate regime are discussed.
Theory
The Virtual Fields Method
The VFM uses the principle of virtual work to establish equilibrium equations relating the internal and external forces on a solid deformable body under load. The principle of virtual work can be used to describe equilibrium of a solid body with density \(\rho\) in the absence of body forces as:
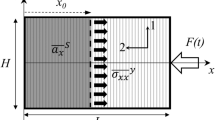
where \(\varvec{\sigma }\) is the stress tensor, \({\varvec{T}}\) is the traction vector and \({\varvec{a}}\) is the acceleration vector [28]. The virtual displacement vector is \(\varvec{u^{*}}\) and is related to the virtual strain tensor \(\varvec{\epsilon ^{*}}\) through \(\epsilon _{ij}^* = \frac{1}{2}( u_{i,j}^* + u_{j,i}^* ) \,\,,\,\, i,j = 1,2\). This equation is valid for any continuous and piecewise-differentiable virtual displacement field. The first term in Eq. 1 is the internal virtual work within the solid volume V, the second term is the external virtual work over the volume surface \(\delta V\) and the third term is the acceleration virtual work over V. Vector and tensor dot products are indicated by a full stop ‘.’ and a colon ‘:’, respectively. In this VFM application, we consider specimens impacted by a force F(t) depicted in Fig. 2 with the assumptions listed below:
-
1.
The specimen is in a state of 2D plane stress.
-
2.
Kinematic fields are constant through the specimen thickness.
-
3.
The specimen thickness is constant.
-
4.
The specimen density is constant in both space and time.
Assumptions 1–3 are made because the full-field measurement technique used here measures surface displacements. Additionally, the assumption of constant density is not completely necessary, but is employed as significant density variations or shock conditions are not expected here. When necessary, the density can be updated based on the measured strains, e.g. in [29]. If we apply the aforementioned assumptions and neglect body forces, the principle of virtual work given in Eq. 1 can be written in 2D as:
where all the terms were defined following Eq. 1, but in 2D the integrals are applied over the specimen surface area S and the specimen perimeter l. Lastly, the tensorial and vectorial fields are functions of both space and time, but the function notation has been omitted here for ease of writing the equations.
Two additional items are required to use Eq. 2 for material property identification. The first is to select a set of virtual fields and the second is to define a constitutive model. Here, rigid body virtual fields (with zero virtual strains) were selected, which cancel the internal virtual work and relate the external virtual work to the acceleration virtual work. This results in equations that relate stress averages along the specimen width to surface acceleration averages. A linear elastic constitutive model is assumed and the modulus is identified by fitting the average stress-strain response. This approach therefore gives the modulus as a function of position over the test duration.
Constitutive Model
Validation of the transverse modulus identification procedure utilising a linear elastic constitutive law for an impacted UD90\(^{\circ }\) specimen like that shown in Fig. 2a was outlined in [26]. Here, a linear elastic orthotropic constitutive model was selected as it is suitable for the early response of UD fibre composites. In the material coordinate system defined in Fig. 2b, the constitutive law for the transverse component of the UD45\(^{\circ }\) case takes the same form: \(\sigma _{22} = E_{22} \epsilon _{22}\). The only component expected to include any non-linearity is the shear term. However, this non-linearity is reduced with strain rate [7], so there should be an appreciable portion of the shear loading that is linear elastic. In both UD90\(^{\circ }\) and UD45\(^{\circ }\) cases, the constitutive law for the shear material response was obtained from the same linear elastic orthotropic constitutive law: \(\sigma _{12} = G_{12} \gamma _{12}\), where \(\gamma _{12}\) is the engineering shear strain equal to twice the tensorial shear strain (\(2\epsilon _{12}\)). Average stress and strain components obtained from IBII test specimens are used with these constitutive laws to reconstruct \(E_{22}\) and \(G_{12}\) moduli. The VFM equations used to determine the stress averages are derived next.
Schematic representation of IBII test specimens impacted by a force \(F_{x}(t)\) in the global \((x-y)\) and material (1–2) coordinate systems. The resulting normal stress \(\sigma _{22}\) and shear stress \(\sigma _{12}\) acting on a a UD90\(^{\circ }\) specimen vertical slice and a b UD45\(^{\circ }\) specimen angled slice at the position \(x_{0}\) from the specimen free edge
Virtual Fields for Modulus Identification
Previous implementations of the IBII test utilised rigid body virtual fields to identify the in-plane transverse modulus from UD90\(^{\circ }\) composite samples in [26] and the interlaminar modulus from through thickness samples in [25]. In this work, a similar approach was applied to UD45\(^{\circ }\) and UD90\(^{\circ }\) specimen configurations to obtain equations giving the average transverse and shear stress over the specimen surface.
Off-axis case: coordinate system rotation
For the off-axis case with the coordinate system orientation shown in Fig. 2b, the global acceleration and strain fields can be rotated into material coordinates using the standard rotation matrices, given here with the abbreviations \(s = sine\) and \(c = cosine\):
Off-axis case: transverse component
Consider the off-axis composite specimen in Fig. 2b. Here we apply a rigid body virtual field describing a rigid translation along the material 2−axis:
For this rigid body virtual field, the virtual strains are null and therefore the internal virtual work term in Eq. 2 is cancelled. Figure 2b shows the stress tensor components acting on the angled slice, which is combined with the acceleration vector and virtual field in the principle of virtual work (Eq. 2) resulting in the relationship:
Full-field measurements allow the integrals on the right and left sides of Eq. 6 to be approximated as discrete sums of the accelerations over S and the \(\sigma _{22}\) stresses over L, respectively. Substituting the specimen geometry and rearranging Eq. 6 then gives the transverse ‘stress gauge’ equation, provided that the grid of data points is regular in the 1–2 coordinate system:
where \(\overline{\sigma _{22}}^{L}\) is the average normal stress on an angled slice L shown in Fig. 2b. Additionally, \(\overline{a_{2}}^{S}\) is the surface average of the \(2-\)axis acceleration over the trapezoidal area from the free edge to the section of interest L. For the remainder of this paper, over-line notation represents the average component value over the region indicated by the superscript.
Off-axis case: shear component
Again, we consider the off-axis composite specimen in Fig. 2b and apply a rigid body virtual field, this time describing a rigid translation along the material 1−axis:
Similar to the process used for the transverse component, the stress tensor, acceleration vector and virtual fields are incorporated in the principle of virtual work (Eq. 2) leading to the relationship:
The integrals in Eq. 9 are again approximated as discrete sums over S to obtain the shear ‘stress gauge’ equation for an off-axis composite sample:
where \(\overline{\sigma _{12}}^{L}\) is the average shear stress acting over an angled slice L shown in Fig. 2b and \(\overline{a_{1}}^{S}\) is the average \(1-\)axis acceleration over S. Eq. 10 can also be applied to slices orthogonal to the slice shown in Fig. 2b to obtain the average shear stress.
Transverse case: transverse and shear components
The transverse case is just a ‘special’ case of the more general off-axis specimen considered previously. For the UD90\(^{\circ }\) specimen shown in Fig. 2a the rectangular surface area is given by \(S = Lx_{0}\). Substituting this into Eqs. 7 and 10 gives:
where \(\overline{\sigma _{22}}^{L}\) and \(\overline{\sigma _{12}}^{L}\) are the average normal and shear stresses on a vertical slice L as described in [24, 30].
Modulus Identification
For both specimen cases, the transverse constitutive law given previously \(\sigma _{22} = E_{22} \epsilon _{22}\) was used to obtain \(E_{22}\) from the linear elastic part of the \(\overline{\sigma _{22}}^L\) vs. \(\overline{\epsilon _{22}}^L\) response. Similarly, the shear constitutive law \(\sigma _{12} = G_{12} \gamma _{12}\) gives \(G_{12}\) over the linear portion of the \(\overline{\sigma _{12}}^{L}\) vs. \(\overline{\gamma _{12}}^{L}\) curves. For the UD90\(^{\circ }\) case, Eqs. 11 and 12 are valid for any transverse section of interest, so stress-strain curves can be plotted for any \(x_0\) coordinate on the specimen shown on Fig. 2a. This gives transverse and shear elastic moduli as a function of position along the specimen length. For the UD45\(^{\circ }\) case, Eqs. 7 and 10 are applied to angled slices that do not intersect the impact or free edges of the specimen. This was done to omit additional forces at the impact edge and low signal-to-noise ratio data at the free edge. Therefore, transverse and shear moduli obtained from off-axis samples are given as a function of \(x_{0}\) position over this domain. In the next section, the experimental method used for testing off-axis composite samples and the numerical implementation of the off-axis stress gauge equations are described.
Methodology
Quasi-Static Tests
Quasi-static tensile test specimens were cut from laminates made from Hexply M21/35%/268/T700GC UD pre-preg by Hexcel, France, consisting of M21 epoxy resin and T700GC carbon fibres. The laminates were made from 12 hand-layed plies, cured in an autoclave at the French aerospace laboratory (ONERA) in Lille. Appendix A gives the method and measurements used to calculate the laminate density of 1514 ± 20 kg.\(\hbox {m}^{-3}\). UD45\(^{\circ }\) tensile test specimens were cut from the UD0\(^{\circ }\) laminates by orientating the laminate fibres at 45\(^{\circ }\) to the specimen edges. Nominal specimen dimensions of 230 \(\times\) 25 \(\times\) 3 mm were achieved with a material cutting machine fitted with a diamond coated disc. Front and back surfaces of the specimens were lightly sanded using 500 grit sand paper, smoothing the peel-ply imprint so that the nominal specimen thickness was 3.14 mm. TML FRA-3-11 0\(^{\circ }\)/45\(^{\circ }\)/90\(^{\circ }\) rosette strain gauges were adhered to the front and back faces of the tensile specimens and aluminium tabs were bonded to the specimen ends as shown in Fig. 3a.
Tests were conducted on an Instron 5569 testing machine at 1 mm.\(\hbox {min}^{-1}\), loading the specimens within the elastic range to 4000 N and then unloading them at the same rate. Here, the goal was to obtain modulus properties so the specimens were not loaded to failure. Strain signal conditioning was achieved with a Strainsmart 8000 series transducer with a quarter-bridge configuration and 2 volts excitation for each individual gauge. In order to maximise the signal to noise ratio for each gauge, the 0\(^{\circ }\)/45\(^{\circ }\)/90\(^{\circ }\) rosette strain gauges were positioned with the first gauge aligned at 45\(^{\circ }\) to the material coordinate system. After the tests, the three normal strains from the rosette were converted to material coordinate strain components. Force readings from the load cell and the specimen cross sectional area were used to form the global coordinate stress tensor, which was transformed into material coordinates using the standard stress rotation matrix. The constitutive models defined in Sect. 2 were used to obtain the transverse and shear moduli via linear fits to the stress-strain curves, with the component strains taken as the average of the front and back measurements. Because both transverse and shear moduli were obtained from the UD45\(^{\circ }\) samples, UD90\(^{\circ }\) tests were not performed. In total, three specimens were tested six times each. Specimens were removed from the grips and re-gripped between each test and after the first three tests, the specimen was rotated 180\(^{\circ }\) i.e. upside-down. These practices were undertaken so that bias from gripping boundary conditions was minimised.
Dynamic Tests
IBII test specimens
UD90\(^{\circ }\) and UD45\(^{\circ }\) IBII test specimens were obtained by cutting rectangles from a UD0\(^{\circ }\) laminate, with the long edge at 90\(^{\circ }\) and 45\(^{\circ }\) to the laminate fibres, respectively. The IBII specimens were cut from a different plate to the quasi-static specimens, of which the density was calculated as 1575 ± 17 kg.\(\hbox {m}^{-3}\) (see Appendix A). MD\(\pm 45^{\circ }\) specimens were manufactured from 12 ply 0\(^{\circ }\)/90\(^{\circ }\) laminates with a density of 1530 ± 41 kg.\(\hbox {m}^{-3}\). Samples were cut from the laminates, aligning the specimen’s long rectangular edge at 45\(^{\circ }\) to the laminate fibres. Nominal dimensions of the IBII specimens were 70 \(\times\) 43 \(\times\) 3 mm and images of the finished UD90\(^{\circ }\) and UD45\(^{\circ }\) specimens are respectively shown in Figs. 3b, c. Note that a MD\(\pm 45^{\circ }\) specimen image is not shown as they appear identical to the UD45\(^{\circ }\) specimens. In the following sections of this paper, a naming convention is used to give results from a particular specimen type and number. For example, UD90-S3 refers to UD90\(^{\circ }\) specimen number three, UD45-S7 to UD45\(^{\circ }\) specimen number seven and MD45-S1 is MD±45\(^{\circ }\) specimen number one. After the specimen surfaces were lightly sanded, cleaned and dried, one specimen face was painted with a thin coat of white acrylic spray paint. A flat-bed printer was then used to print a regular grid of black squares over the specimen surface as shown in Fig. 4a, where the distance between the black squares (i.e. the grid pitch) was 0.9 mm. More information on the grid printing procedure can be found in [31].
IBII test set-up
In this work, the gas gun apparatus described in [31] was used to generate the dynamic loading required for the IBII tests. Before tests were conducted, a projectile/sabot assembly was loaded into the gas gun barrel and the pressure vessel was pressurised to the desired firing pressure to achieve a nominal velocity of 40 m.\(\hbox {s}^{-1}\). When the system was fired, a solenoid valve opened and the pressurised gas accelerated the projectile/sabot assembly down the gas gun barrel toward the target assembly. The target assembly consisted of a specimen bonded to a 45 mm diameter, 50 mm long right angled aluminium cylinder called a ‘wave guide’. In IBII tests, the purpose of the wave guide is to (1) hold the specimen and (2) provide good contact with the projectile, allowing the input pulse to load the specimen. The specimen and wave guide rested on a ‘v-shaped’ foam stand as shown in Fig. 4a and were encased by the target trap shown in Fig. 4b.
Imaging system
Specimen surface deformations were recorded with a Shimadzu HPV-X ultra-high speed video camera, with a framing rate of 2 MHz. Given that the camera records 128 images, the total recording time for each test was 64 \(\mu\)s. The camera has a pixel array size of 400 \(\times\) 250 pixels and was fitted with a Sigma 105 mm lens. The field of view encompassed the whole specimen, plus a 2 mm space at the free edge to ensure no data was lost because of the small amount of rigid body translation occurring during image capture. With the given imaging set-up and specimen grid pitch of 0.9 mm, the spatial frequency (often called sampling) recorded by the camera was 5 pixels per pitch. Table 1 gives a summary of the main imaging system and full-field measurement parameters. In addition, the flash light trigger time was selected so that the specimen was illuminated throughout the recorded portion of the test. Lastly, image distortions amplified by the presence of sharp edges (high image spatial frequencies) were reduced by using an optimal level of camera lens blur. Further details of the experimental set-up are given in [31]. Next, the full-field technique used to derive kinematic fields from the IBII tests is discussed.
The Grid Method
The Grid Method was used to calculate full-field displacements from specimen deformation images recorded during the tests. A thorough explanation and review of the Grid Method is detailed in [32] and therefore, only a summary of the main steps used in this application is given. For this work, a Matlab code containing the Grid Method procedure made freely available in [32] was used to calculate the displacement fields. The main steps in the Grid Method can be summarised as follows:
-
1.
Extract phase maps. A windowed discrete Fourier transform is used to calculate phase maps from the specimen grid deformation images recorded by the camera.
-
2.
Phase difference maps. Phase difference maps are calculated for each time step by subtracting the phase map from a reference undeformed grid (reference phase).
-
3.
Spatial phase unwrapping. Phase difference values should lie in the range of (-\(\pi\),+\(\pi\)) however, integers of 2\(\pi\) radians are added to phase jumps that occur outside this range. As described in [31], the Matlab code used to calculate phase maps in this work incorporates the phase unwrapping algorithm described in [32].
-
4.
Temporal phase unwrapping. Integers of 2\(\pi\) radians are added to the phase maps to remove distortions caused by phase differences outside the range of (-\(\pi\),+\(\pi\)) that may occur between frames. This can be due to both rigid body motion and deformation, meaning that temporal phase unwrapping is not necessarily uniform over the specimen.
-
5.
Displacement calculation. The iterative displacement calculation procedure outlined in [32] was used to correct for errors resulting from large displacements and grid defects. Here, the initial guess for the displacement calculation is obtained from the grid pitch p and the phase difference \(\varDelta \phi _{i}(t)\) maps using the equation:
$$\begin{aligned} u_{i}(t) = \frac{p}{2\pi }\varDelta \phi _{i}(t) \, \, , \, \, i=x,y \end{aligned}$$(13)
Strain and acceleration calculations
When using the Grid Method to derive displacement fields from grid images, edge effects from the windowed discrete Fourier transform cause one grid pitch worth of data at the specimen edges to be erroneous [31]. ‘Padding’ techniques that replace corrupted edge data with extrapolated values resulted in improved material property identification when using the VFM and Digital Image Correlation (DIC) in [33]. Therefore, the edge data extrapolation method developed in [25] was applied here. In this approach, one grid pitch worth of \(u_{x}\) displacement data on the impact and free (vertical) edges was first removed. Linear fits to the values five pixels (one grid pitch) in from the cropped edges are then extrapolated to populate the lost data. This operation was also performed on the top and bottom (horizontal) edges of the specimen on the \(u_{y}\) displacement fields.
After the edge padding procedure, Gaussian spatial smoothing was applied to reduce the random error on the strain calculations resulting from camera noise. Third order polynomial temporal smoothing was also used to mitigate the effects of camera noise on the acceleration fields. In general, smoothing with increasing kernel sizes reduces the random error, but increases the systematic error as the measurand peak values are ‘smeared’. An optimised combination of spatial and temporal kernels was determined using an image deformation study (discussed at the end of this Section). Spatial and temporal smoothing was applied to the raw displacement fields prior to deriving the strain and acceleration maps, respectively. Following smoothing, the strain fields were obtained by first order spatial differentiation and the accelerations by second order temporal differentiation of the displacement fields. These operations were performed using the centred finite difference approach implemented in Matlab’s gradient function. Note that the experimental processing code can be accessed from the digital dataset link given in Sect. 9.
Strain rate calculations
IBII test strain rates are heterogeneous in space and time. Peak average strain rates give the upper limit of the strain rate range experienced by the material, reported here as the maximum value from all specimen slices over the loading duration of the test. In order to give an indication of an ‘effective’ strain rate we define a second strain rate quantity, which is the strain-weighted strain rate:
with the loading duration being the time for the compressive or shear loading pulse to traverse the specimen length. Smoothing kernel edge effects were removed from the calculation by cropping the strain and strain rate fields by \(S_{k}\)/2 + one grid pitch from all edges, where \(S_{k}\) is the spatial smoothing kernel size in pixels.
Modulus identification for off-axis composites
The average acceleration components over S, \(\overline{a_{1}}^{S}\) and \(\overline{a_{2}}^{S}\) used in the ‘stress gauge’ equations given in Sect. 2 were determined for each recorded frame in four steps outlined below:
-
1.
Determine the linear equation of all angled slices in global coordinates, with one point for each pixel over the specimen height.
-
2.
Retain all acceleration data within the bounds of the free edges and the corresponding slice, as depicted in Fig. 5a.
-
3.
Average all acceleration data that is retained within the bounds.
-
4.
Repeat the procedure for all slices that do not intersect the impacted edge, as shown in Fig. 5b, where the number of measurement points on the diagram has been reduced for clarity.
One of the drawbacks of this method is that it results in a ‘staircase’ approximation of surface averaged accelerations, as indicated by the red region in Fig. 5b. However, this staircase approximation to the acceleration surface average was found to have minimal impact on the identification, as described in [30]. After the acceleration surface averages were calculated, the surface area S was determined for each specimen slice using the equation \(S = H(x_{0} + 0.5L \cos \theta )\), where H is the specimen height and recalling that \(x_{0}\) is the distance from the free-edge to the top corner of the slice, L is the slice length and \(\theta\) is the off-axis angle of the specimen. Lastly, the slice length L was calculated from the specimen geometry and the angle of the fibres using the trigonometric relationship \(L = H\sin \theta\). After \(\overline{a_{1}}^{S}\), \(\overline{a_{2}}^{S}\) and S were determined, \(\overline{\sigma _{22}}^{L}\) and \(\overline{\sigma _{12}}^{L}\) were calculated using Eqs. 7 and 10. Strain values at the pixel centroids were interpolated to the angled slices using the Matlab function scatteredInterpolant, as shown in the schematic given in Fig. 5c. \(\overline{\epsilon _{22}}^{L}\) and \(\overline{\gamma _{12}}^{L}\) were then calculated by averaging the interpolated strains over L. After the stress and strain averages on the angled slices were obtained, the transverse and shear moduli were calculated as described in Sect. 2. Equation 10 was also used to obtain the average shear stress over slices orthogonal to the specimen fibres, shown as dashed grey lines in Fig. 5b. Shear modulus values derived from the average stresses and strains along Slices 1 and Slices 2 are referred to as \(G_{12,\,Sl.\,1}\) and \(G_{12,\,Sl.\,2}\), respectively.
Schematic showing the a logical mask applied to an \(a_{1}\) acceleration field, where \(\overline{a_{1}}^{S}\) is the average of the unmasked data, b orthogonal 45\(^{\circ }\) slices on an off-axis specimen and the ‘staircase’ approximation of \(\overline{a_{1}}^{S}\) c strain interpolation operation for an arbitrary slice angle. Each schematic also applies to the \(a_{2}\) fields
Measurement resolution
Displacement, strain and acceleration resolutions were calculated by processing 128 static grid images with the same procedure used for the dynamic tests and taking the standard deviation (SD) of each field value over all 128 static images. Displacement resolution calculations were made using the raw displacement fields, whereas the strain and acceleration resolutions were calculated from smoothed fields. Table 2 lists the mean kinematic field resolutions for each specimen type, which were obtained from the average of the individual test values within the group.
Image Deformation Simulations
Previous work has shown that image deformation simulations are a useful tool for selecting optimal processing parameters for experiments based on full-field measurements [29,30,31,32,37]. In this work, image deformation procedures detailed in [24, 25, 31] were followed.
Image Deformation Procedure
The image deformation procedure began with a finite element simulation of a specimen impacted with an experimentally obtained loading pulse, similar to that in Fig. 14. Table 3 lists the simulation parameters in which ‘reference’ modulus values were specified in the material model. Before the simulation results were used in the image deformation process, a convergence study was undertaken to determine optimal mesh size and damping values. Displacement fields from the finite element simulation were imposed on a set of analytically-defined synthetic grid images, having the same size and grid properties as the experimental grids. The synthetic grids were then processed with the previously explained procedures.
Systematic error effects on the modulus identification were first assessed by processing the synthetic grids with a range of spatial smoothing kernel sizes, without noise. Systematic and random error effects were then assessed by processing the synthetic grids overlaid with 30 copies of Gaussian white noise, simulating camera noise present in the experimental modulus identification. Here, the noise amplitude was determined from the SD of noise grey levels present in 128 static experimental grid images. Analysis of the static images showed that the grey level noise had an average SD of 0.72% of the dynamic range, which was comparable to previous analysis in [25]. The noisy grid images were then processed with a range of spatial and temporal smoothing kernel sizes. The total error between the modulus value calculated for each kernel combination relative to the reference modulus is \(Err_{tot} = |Err_{sys}| + 2Err_{rand}\), where \(Err_{sys}\) is the systematic error:
where \(\overline{Q_{ii, ID}}\) is the mean identified modulus over 30 noise copies and \(Q_{ii,FE}\) is the reference modulus value specified in the finite element simulation material model. The random error is defined as the SD of the calculated modulus values over 30 noise copies, normalised by the reference modulus:
where \(N=30\) total iterations and \(Q^{k}_{ii, ID}\) is the modulus identified for the \(k^{th}\) iteration.
Image Deformation Results
For both specimen cases, the systematic error maps with and without noise were equivalent, indicating that the modulus identification was not influenced by noise. This result was expected given the linear elastic material model and therefore, the error maps presented here are for the noisy case. Figure 6a shows the systematic, random and total error on \(E_{22}\) for the UD90\(^{\circ }\) case, resulting from different spatial kernel \(S_{k}\) and temporal kernel \(T_{k}\) combinations. Here, the spatial and temporal kernels proportionately influence the total error, which was minimised to 0.02% with spatial and temporal kernels of 21 pixels and 15 frames, respectively. Therefore, this kernel combination (\(S_{k}\)=21 pixels, \(T_{k}\)=15 frames) was selected to process experimental results from the UD90\(^{\circ }\) specimens.
For the UD45\(^{\circ }\) case, Figs. 6b–d show the error variation resulting from different kernel combinations used in the identification of \(E_{22}\), \(G_{12,\,Sl.\,1}\) and \(G_{12,\,Sl.\,2}\), respectively. For a given temporal kernel size, the total error magnitude was more significantly influenced by increasing spatial kernel sizes in the UD45\(^{\circ }\) case compared to the UD90\(^{\circ }\) case. This may have been caused by the angled strain wave profile in the kinematic fields (shown in the next Section), resulting in a more distributed response over the ‘square’ smoothing kernel. In consideration of the total error plots for the off-axis case, it is clear that different kernel combinations are required to optimise each of the modulus components. Therefore, optimal smoothing was determined by selecting the temporal and spatial kernel combination that minimised the sum of the total errors from \(E_{22}\), \(G_{12,\,Sl.\,1}\) and \(G_{12,\,Sl.\,2}\), which was minimised to 0.94% with spatial and temporal kernels of 11 pixels and 25 frames, respectively. Therefore, the optimised smoothing parameters determined here (\(S_{k}\)=11 pixels, \(T_{k}\)=25 frames) were used to process the UD45\(^{\circ }\) case experimental data. It should be noted that for all cases, quite a large area in the plots produced low errors (dark blue zones). This was reassuring as it confirmed that the identification behaviour was rather stable over the range of smoothing kernel sizes assessed. However, without this study one could have ended up selecting harsher spatial smoothing leading to significantly larger errors, so this information is useful to make rational choices.
Systematic, random and total error plots (respectively \(Err_{sys}\), \(Err_{rnd}\) and \(Err_{tot}\)) resulting from different spatial \(S_{k}\) and temporal \(T_{k}\) kernel combinations: a \(E_{22}\) from the UD90\(^{\circ }\) case, together with b \(E_{22}\), c \(G_{12,\,Sl.\,1}\) and d \(G_{12,\,Sl.\,2}\) from the UD45\(^{\circ }\) case. The red cross gives the kernel combination that results in the lowest error for each error type
Experimental Results
Quasi-Static Tests
Figure 7a shows the transverse stress vs. strain response from the quasi-static tensile test on UD45\(^{\circ }\) Specimen 1. Here, the response was predominantly linear and the \(E_{22}\) modulus values were obtained from linear fits to a transverse strain value of 2.0 mm.\(\hbox {m}^{-1}\). Figure 7b shows the non-linear response from the shear stress vs. strain curve, where the non-linear onset strain was approximately 3.0 mm.\(\hbox {m}^{-1}\). This result is similar to that reported in [38], who obtained a non-linear onset strain of 2.5 mm.\(\hbox {m}^{-1}\) in similar tests on the same material in the MD±45\(^{\circ }\) configuration.
Table 4 gives the mean transverse and shear moduli obtained from six tests on each specimen. Transverse modulus values were corrected to account for fibre strains by fitting the \(\sigma _{22} - Q_{12} \epsilon _{11}\) vs. \(\epsilon _{22}\) response to obtain \(Q_{22}\) from which \(E_{22}\) was calculated using: \(E_{22} = Q_{22}(1-\nu _{12}\nu _{21})\). Here, \(Q_{12}\) was obtained from the relationship \(Q_{12} = \nu _{12}E_{22}/(1-\nu _{12}\nu _{21}\)), with \(\nu _{12} = 0.32\) and \(\nu _{21} = 0.019\). For brevity, modulus values from each test and specimen (total of 18 tests) are not listed here, but are available in the digital dataset. Mean modulus values from the three specimens were averaged to give a final mean \(E_{22}\) value of 8.30 GPa, obtained at a transverse strain rate of 6.86\(\times\)10\(^{-5}\) \(\hbox {s}^{-1}\), as listed at the bottom of Table 4. The final mean \(G_{12}\) value of 4.73 GPa obtained at an average shear strain rate of 1.1\(\times\)10\(^{-4}\) \(\hbox {s}^{-1}\) was consistent with that in [2], which was obtained from MD±45\(^{\circ }\) specimens made from the same material.
Dynamic Kinematic Fields
This section provides kinematic fields obtained from IBII tests on UD90\(^{\circ }\), UD45\(^{\circ }\) and MD±45\(^{\circ }\) specimens. Fields obtained from the UD90\(^{\circ }\) specimens are presented first because in this case, the material coordinates are orthogonal to the loading pulse and therefore, it is easier to follow wave progression in the specimen. Kinematic fields for the UD45\(^{\circ }\) and MD±45\(^{\circ }\) specimens are then presented and differences in the field evolutions are compared.
Kinematic fields: UD90\(^{\circ }\)
Figure 8 shows the \(u_{2}\) and \(u_{1}\) displacement fields at three time steps in the recorded loading history for UD90-S3. Evolution of the \(u_{2}\) wave front was mostly planar and aligned with the horizontal as shown in Fig. 8a. Angled wave fronts can be seen in the \(u_{1}\) fields in Fig. 8b, which resulted from a slight pitch misalignment between the projectile and the wave guide. This pitch misalignment generated a non-planar loading pulse, which induced non-symmetric \(u_{1}\) displacements across the specimen centre. Peak \(a_{2}\) and \(a_{1}\) values were on the order of \(5-7 \times 10^{6}\) m.\(\hbox {s}^{-2}\), as seen in Fig. 8c, d. Both acceleration field wave fronts were mostly planar, with the \(a_{1}\) profile being slightly angled, again due to the misaligned impact conditions.
At 20 \(\mu\)s the \(\epsilon _{22}\) wave front had reached the approximate specimen centre as shown in Fig. 9a, with peak values on the order of 20 mm.\(\hbox {m}^{-1}\) in compression. Previous testing on UD90\(^{\circ }\) specimens reported in [26] revealed low magnitude \(\epsilon _{11}\) strains due to the high stiffness in the fibre direction. Similar observations were made here and therefore, the UD90\(^{\circ }\) \(\epsilon _{11}\) fields are not shown, but are accessible from the digital dataset. A shear wave front can be seen in Fig. 9b, confirming observations made in the displacement and acceleration fields. This shear deformation arose from the slight impact misalignment, and in the present case, inadvertently enriched the test. Peak shear strains were on the order of 5–10 mm.\(\hbox {m}^{-1}\) and given their magnitude, it was possible to obtain the shear modulus from the UD90\(^{\circ }\) specimens. Compressive strain rates on the order of \(2 \times 10^{3}\) \(\hbox {s}^{-1}\) were present in the \({\dot{\epsilon }}_{22}\) fields shown in Fig. 9c. Similar peak values were obtained for the \({\dot{\gamma }}_{12}\) fields given in Fig. 9d.
Kinematic fields: UD45 \(^{\circ }\)
The \(u_{2}\) and \(u_{1}\) displacement fields from UD45-S7 are given in Fig. 10. As seen in Fig. 10a, the \(u_{2}\) wave front was approximately planar at 15 and 20 \(\mu\)s, and later developed a curved shape at 30 \(\mu\)s. Conversely, the \(u_{1}\) wave front was angled in-line with the specimen fibres, as shown in Fig. 10b. Similar peak \(u_{2}\) and \(u_{1}\) values were recorded, which was in contrast to the UD90-S3 \(u_{2}\) and \(u_{1}\) peak displacements that had dissimilar values. This result was expected because the 1-axis of the UD45\(^{\circ }\) specimens is closer to being axially-aligned with the loading pulse and therefore, displacements in this direction will be more significant compared to the UD90\(^{\circ }\) case. Fields for the \(a_{2}\) and \(a_{1}\) acceleration components are also shown in Fig. 10, where peak values were on the order of \(5-10 \times 10^{6}\) m.\(\hbox {s}^{-2}\). An angled wave profile aligned with the off-axis fibres developed for the \(a_{1}\) field at 20 \(\mu\)s, as shown in Figure 10d. Here, a tensile relief wave generated from the loading pulse can also be seen. Similar to the \(u_{2}\) fields, the \(a_{2}\) wave formation was initially planar, aligning itself with the fibres later in time.
Material coordinate strain and strain rate fields are given in Fig. 11, where peak compressive \(\epsilon _{22}\) values around 10 mm.\(\hbox {m}^{-1}\) are shown in Fig. 11a. Higher peak values around 20 mm.\(\hbox {m}^{-1}\) were obtained for the \(\gamma _{12}\) fields, which can be seen in Fig. 11b. Angled wave profiles in the \({\dot{\epsilon }}_{22}\) and \({\dot{\gamma }}_{12}\) fields at 20 and 30 \(\mu\)s can be seen in Fig. 11c, d, respectively. Peak strain rates for both the \({\dot{\epsilon }}_{22}\) and \({\dot{\gamma }}_{12}\) fields were on the order of \(2 \times 10^{3}\) \(\hbox {s}^{-1}\). The peak strain and strain rate values obtained from UD45-S7 were on a similar order of magnitude to UD90-S3. This was expected because both samples were loaded with similar impact velocities. However, for the UD90\(^{\circ }\) case the 2-axis response was stronger, as it was dominated by matrix compression. For the UD45\(^{\circ }\) case, the shear response was dominant and therefore, the 2-axis response was slightly lower. This explains why higher peak shear strains and strain rates were obtained from UD45-S7 compared to UD90-S3. Although, UD90\(^{\circ }\) samples impacted with a greater degree of projectile and wave guide misalignment will induce a strong shear response.
Kinematic fields: MD±45\(^{\circ }\)
For the MD±45\(^{\circ }\) specimens, the identification procedure will focus on obtaining the shear modulus, so only the kinematic field maps that are required for this are given here and the remaining fields can be found in the digital dataset. Displacement and acceleration fields for MD45-S1 are given in Fig. 12. As seen in Fig. 12a, the \(u_{2}\) field developed an angled wave front with an angle slightly greater than the + 45\(^{\circ }\) specimen fibres. This angled \(u_{2}\) wave formation was in contrast to the UD45\(^{\circ }\) specimen, which was more horizontal. Given the symmetry of the MD±45\(^{\circ }\) specimen, similar \(u_{2}\) and \(u_{1}\) displacement field patterns were expected. The \(a_{2}\) and \(a_{1}\) fields in Fig. 12c, d also show an angled wave front profile and have peak values around 5\(\times\)10\(^{6}\) \(\hbox {s}^{-1}\).
Strain and strain rate fields for MD45-S1 are given in Fig. 13. Similar to the UD45\(^{\circ }\) specimens, the \(\gamma _{12}\) field recorded peak values around 20 mm.\(\hbox {m}^{-1}\). However, the field was ‘X-shaped’ as shown in Fig. 13a, whereas the UD45\(^{\circ }\) field was angled and aligned with the laminate fibres. The \({\dot{\gamma }}_{12}\) wave profile had a similar shape to the \(\gamma _{12}\) field, as shown in Fig. 13b. Here, peak \({\dot{\gamma }}_{12}\) values were on the order of 2\(\times\)10\(^{3}\) \(\hbox {s}^{-1}\), which was similar to the UD45\(^{\circ }\) case. In the following Section, the acceleration and strain fields shown here were used to construct average stress-strain curves and identify modulus values from UD90\(^{\circ }\), UD45\(^{\circ }\) and MD±45\(^{\circ }\) specimens.
Dynamic Modulus Identification
Loading pulse
The average force acting on the specimen impact edge in the 2-axis direction \(\overline{F_{2}}^{L}\) was calculated from the specimen mass \(m_{s}\) and the average acceleration over the specimen surface \(\overline{a_{2}}^{s}\) using the equation \(\overline{F_{2}}^{L} = m_{s}\overline{a_{2}}^{s}\). At the same time, the average stress acting on the impact edge in the 2-axis direction \(\overline{\sigma _{22}}^{L}\) was obtained from Eq. 11. \(\overline{F_{2}}^{L}\) and \(\overline{\sigma _{22}}^{L}\) are plotted against time for the IBII test on UD90-S3 in Fig. 14, where peak compressive values were approximately 20 kN and 160 MPa, respectively. Multiple loading pulses were recorded due to wave reflections within the projectile, wave guide and specimen, as shown in Fig. 14.
Modulus identification: UD90 \(^{\circ }\)
Stress-strain curves obtained from slices at various \(x_{0}\) positions (distance from the specimen free-edge) for UD90-S3 are given in Fig. 15. Here, a linear loading in compression and unloading in tension was observed. All of the UD90\(^{\circ }\) samples failed during testing, as the loading pulse reflected from the specimen free-edge generating a concentrated tensile stress region, which exceeded the fracture stress of the specimen. Because the focus of this work was to obtain elastic modulus properties, the post-failure non-linear response was removed from the stress-strain curves. Peak transverse stress and strain values over the compressive loading were approximately 100–150 MPa and 10–15 mm.\(\hbox {m}^{-1}\), respectively.
Transverse modulus \(E_{22}\) values were obtained by linearly fitting the compressive stress-strain curves from each slice. Figure 16 gives \(E_{22}\) as a function of \(x_{0}\) position from six UD90\(^{\circ }\) specimens. Strain data on the edges of the sample is corrupted by smoothing edge effects and therefore, the average modulus for each sample was taken over the middle 50% of the sample length, as was done in [24, 26, 30]. Table 5 gives the mean transverse modulus value obtained from six tests as \(E_{22}\) = 10.2 GPa, with a COV of 1.52\(\%\), indicating excellent test-to-test repeatability. Similar to the quasi-static results, the IBII test \(E_{22}\) values listed in Table 5 were corrected to account for fibre strains. However, for the IBII tests the correction was applied using finite element model (see Sect. 3) \(\epsilon _{11}\) strains because of the low signal to noise ratio of the experimental \(\epsilon _{11}\) values. The quasi-static \(E_{22}\) value of 8.30 GPa obtained in this work was used to determine the percentage difference to the quasi-static value (\(\%\)Diff. to QS) of 22.3\(\%\).
Peak compressive average strain rates obtained during the loading portion of the test are also given in Table 5. From six tests, the mean peak average transverse strain rate was 2.41 \(\times\) 10\(^{3}\) \(\hbox {s}^{-1}\) and the shear value was lower at 1.34 \(\times\) 10\(^{3}\) \(\hbox {s}^{-1}\). This result was expected for the UD90\(^{\circ }\) specimens, given the transverse fibre orientation with respect to the loading pulse. Table 5 also lists the effective strain rates, where the mean transverse value of 0.932 \(\times\) 10\(^{3}\) \(\hbox {s}^{-1}\) was higher than the mean shear value of 0.421 \(\times\) 10\(^{3}\) \(\hbox {s}^{-1}\). As the strain rate fields are heterogeneous in both space and time (see Sect. 5, Dynamic kinematic fields), the effective strain rates were lower than the peak average values.
Equation 12 was used to calculate the average shear stress over the specimen height \(\overline{\sigma _{12}}^{L}\) from the \(a_{1}\) acceleration fields for the UD90\(^{\circ }\) specimens. Figure 17 shows the stress-strain curves, which were mostly linear but lower in magnitude compared to the transverse response. Linear fits to the shear stress-strain curves were used to obtain shear modulus values from each vertical specimen slice, which are plotted against \(x_{0}\) position for all specimens in Fig. 18. Modulus values from the middle 50% of slices were averaged to calculate \(G_{12}\) for each sample, as listed in Table 5. The mean \(G_{12}\) value from all specimens was 5.51 GPa with a COV of 2.30\(\%\), again indicating good repeatability between samples. Using the quasi-static \(G_{12}\) modulus value of 4.73 GPa, the \(\%\)Diff. to QS value was 16.6\(\%\).
Modulus identification: UD45 \(^{\circ }\)
Average transverse stress-strain curves at selected \(x_{0}\) distances from specimen UD45-S7 are given in Fig. 19. Similarly to results from UD90-S3, the transverse response from UD45-S7 was linear with peak compressive stresses reaching around 60 MPa. Small oscillations in the transverse stress-strain curves can be seen in Fig. 19, which resulted from the lower signal to noise ratio compared to the transverse response of the UD90\(^{\circ }\) samples. Again, linear fits over the compressive loading portion of the stress-strain curves were used to calculate the transverse modulus \(E_{22}\) for each slice. Red markers indicate the fitting regions for UD45-S7 in Fig. 19.
For the UD45\(^{\circ }\) case, the majority of (angled) slice data is located further away from the specimen’s impact and free edges and hence, less sensitive to spatial smoothing edge effects compared to the UD90\(^{\circ }\) case. Therefore, data from all slices was used for the modulus identification from the off-axis samples. Transverse modulus against position results from all UD45\(^{\circ }\) specimens are shown in Fig. 20. Table 6 gives the mean transverse modulus obtained from seven UD45\(^{\circ }\) tests as 9.91 GPa, with good consistency between samples denoted by the resulting COV of 3.36%. This \(E_{22}\) result was 19.4\(\%\) higher than the quasi-static reference value of 8.30 GPa listed in Table 4.
UD45-S7 average shear stress-strain curves at selected \(x_{0}\) positions from Slices 1 and Slices 2 are given in Fig. 21a, b, respectively. Here, some distinct differences between the transverse and shear material behaviour can be seen. Initially, the material response over the loading portion of the curve was linear and then turned non-linear. This type of behaviour was expected, as the shear response of fibre composites is generally found to be non-linear, with the non-linearity being attributed to micro-damage formation and other mechanisms [38]. As seen in Fig. 21a, the onset of non-linearity occurs between 10 and 15 mm.\(\hbox {m}^{-1}\) and is consistent with the results obtained in [38], where non-linear onset occurred at approximately 5 mm.\(\hbox {m}^{-1}\) at a strain rate of 5 \(\times\) 10\(^{1}\) \(\hbox {s}^{-1}\). With increasing strain rate, the non-linear response is delayed [9] and this explains the extended linear response observed in this study. The unloading behaviour was also predominantly linear and appears to have a slightly reduced stiffness compared to the linear portion of the compressive loading. In addition, there was a residual strain after the specimen had unloaded (at zero average shear stress). The lower unloading modulus and residual strain may indicate that the material has undergone micro-damage during the loading. However, physical evidence of damage is required to validate this hypothesis.
Linear fits to the loading portion of the shear stress-strain curves were used to determine the shear modulus for each \(x_{0}\) position on the specimen. Modulus fitting regions at various slices are shown as red markers in Fig. 21a, b, with the first point starting at the zero stress condition. Several approaches are possible to determine the upper limit of the fitting range. In this work, a progressive chord modulus procedure was used. Starting at the lower limit strain, chord modulus fits were made at progressively increasing strain values over the loading portion of the stress-strain curve, as shown in Fig. 22. The transition from linear to non-linear behaviour was determined by the point at which the chord modulus dropped below the average, over the shear loading pulse (with the initial data excluded). Data in the initial stages of loading were corrupted by noise, so values in the range of 2\(\times\) the shear strain noise floor were excluded from the average calculation. Sometimes the chord modulus fell below the mean before the transition because of noise present in the stress-strain curves, as seen in Fig. 22. Therefore, the onset of non-linearity was taken as the last chord modulus value that fell below the average. Finally, the shear modulus was determined from a linear fit through all data points in the linear range. As seen in Fig. 21a, the method used to determine the linear response fitting range was able to reasonably identify the onset of non-linearity in the stress-strain curves.
The average shear modulus as a function of \(x_{0}\) position from Slices 1 and Slices 2 for the UD45\(^{\circ }\) specimens is given in Fig. 23a and 23b, respectively. Table 6 lists the mean \(G_{12}\) values as 5.56GPa for Slices 1 and 5.31 GPa for Slices 2, calculated as the mean of seven test results. Good consistency between tests was obtained, evidenced by the low COV values of 2.52% and 3.58% for Slices 1 and Slices 2, respectively. Quasi-static \(G_{12}\) values from Table 4 were used to calculate shear strain rate sensitivities of 17.6\(\%\) and 12.3\(\%\) for Slices 1 and Slices 2, respectively. Strain rate data for the UD45\(^{\circ }\) specimens are also listed in Table 6 where as expected, the shear strain rates were higher than the transverse values.
Modulus identification: MD±45\(^{\circ }\)
As an additional validation of the method used to identify \(G_{12}\) from UD45\(^{\circ }\) specimens, shear moduli were obtained from MD±45\(^{\circ }\) specimens. Average shear stress and strain components were obtained from the two angled slices (see Figure 5b). Shear stress-strain curves from MD45-S1 at selected \(x_{0}\) positions from Slices 1 and 2 are shown in Fig. 24a, b, respectively. Here, the response was similar to the UD45\(^{\circ }\) specimens, however less residual strain was seen from the MD±45\(^{\circ }\) curves, noticeable when comparing Fig. 24a, b with Fig. 21a, b.
The progressive chord modulus method was also used for the MD±45\(^{\circ }\) \(G_{12}\) identification. Fig. 25a, b give the average shear modulus identified as a function of \(x_{0}\) position for Slices 1 and 2, respectively. Note that for Slices 2, \(x_{0}\) = 0 at the specimen impact edge (see Fig. 5b). Results from four IBII tests on MD±45\(^{\circ }\) specimens are listed in Table 7, giving shear modulus values of \(\hbox {G}_{12,Sl.\,1}\) = 5.06 GPa (COV = .65%) and \(\hbox {G}_{12,Sl.\,2}\) = 5.11 GPa (COV = 6.24%). Strain rate data in Table 7 shows similar peak average values from Slices 1 and 2 of 1.84 \(\times\) 10\(^{3}\) \(\hbox {s}^{-1}\) and 1.52 \(~\times\) 10\(^{3}\) \(\hbox {s}^{-1}\), respectively. As expected, the mean effective shear strain rate was lower, with a value of 1.04 \(~\times\) 10\(^{3}\) \(\hbox {s}^{-1}\).
Discussion
Transverse and shear moduli results from the different specimen configurations are now compared as a validation of the test methodology. The transverse stress gauge approach used to obtain the transverse modulus from UD45\(^{\circ }\) specimens had previously been evaluated with a single UD45\(^{\circ }\) CFRP specimen in [30]. This study extends the assessment to include a larger sample size and comparison to UD90\(^{\circ }\) \(E_{22}\) values, of which the transverse stress gauge methodology had already been experimentally validated in [26]. Figure 26a plots \(E_{22}\) values from the UD45\(^{\circ }\) and UD90\(^{\circ }\) specimens, with the mean UD90\(^{\circ }\) value being close to one SD away from the UD45\(^{\circ }\) result. Given the consistent results between the two sample laminate configurations, the transverse stress gauge method used to obtain the transverse modulus from UD45\(^{\circ }\) samples is considered experimentally validated.
Off-axis laminate configurations are typically used for shear modulus characterisation however, in this work UD90\(^{\circ }\) sample values were also obtained. As shown in Fig. 26b, the shear modulus from the UD90\(^{\circ }\) specimens was within one SD of the UD45\(^{\circ }\) result, when the two slice values are averaged. Therefore, the method of obtaining the shear modulus from UD90\(^{\circ }\) samples was experimentally verified.
Averaging values from Slices 1 and 2, the mean MD±45\(^{\circ }\) shear modulus was 6.4% lower than the UD45\(^{\circ }\) specimen result. The reduced MD±45\(^{\circ }\) modulus could be attributed to a lower fibre volume fraction caused by resin trapped at the ply interfaces during consolidation. This rationale was supported by the MD laminate’s reduced density value of 1530 kg.\(\hbox {m}^{-3}\), which was 2.9% lower than the UD laminate density of 1575 kg.\(\hbox {m}^{-3}\). Therefore, the lower MD±45\(^{\circ }\) shear modulus is consistent with the lower fibre volume fraction. Figure 26b shows a larger COV for the MD±45\(^{\circ }\) \(G_{12}\) values compared to the UD45\(^{\circ }\) and UD90\(^{\circ }\) specimens. This increased COV value was influenced by the higher \(G_{12}\) result from MD45-S1 (see Fig. 25a and 25b). At this stage the reason for this outlier is unknown.
Results from this study are now compared to tests on the same material in [2]. In that study, quasi-static \(E_{22}\) values from two specimens obtained at a strain rate of 9\(\times\)10\(^{-4}\) \(\hbox {s}^{-1}\) were averaged and are plotted in Fig. 26a. This average value of 7.98 GPa was 3.9% lower than that determined in this study (8.30 GPa). In [2], strains were measured on one side of the specimen whereas in this study, strains from both sides were averaged to remove the influence of bending on the modulus calculation. Therefore, it is possible that bias due to specimen bending could be included in the material response. Another reason for the variation could be due to the reduced laminate density of the quasi-static specimens evaluated in this work, which was measured as 1514 kg.\(\hbox {m}^{-3}\). Following the quasi-static result, \(E_{22}\) rises to around 10.2 GPa at 1.8\(\times\)10\(^{-3}\) \(\hbox {s}^{-1}\), which additionally corresponds to a change in test method from a standard test machine to a high-speed test machine. Thereafter, the results from [2] could be considered strain rate insensitive.
Transverse modulus values obtained from the UD90\(^{\circ }\) and UD45\(^{\circ }\) IBII tests are also plotted in Fig. 26a. When combined with the quasi-static values, the IBII results show an increasing strain rate sensitivity, which conforms to the understanding that the matrix dominant properties of composites are generally considered strain rate sensitive [1]. The strain rate insensitivity in [2] is largely influenced by the increased \(E_{22}\) obtained when changing the test method. At this stage, it is difficult to directly compare the strain rate sensitivities, as intermediate strain rate data was not obtained in this work. However, intermediate strain rate tests on the same material using an ultrasonic rig similar to that in [39] are currently being obtained in a separate study.
Quasi-static \(G_{12}\) data obtained from standard test machine tests on three specimens in [2] were averaged and plotted in Fig. 26b. Values obtained with a high-speed test machine at increasing strain rates are also given in Fig. 26b. Increasing strain rate sensitivity is seen moving from a strain rate of 5\(\times\)10\(^{-4}\) \(\hbox {s}^{-1}\) to around 1\(\times\)10\(^{-3}\) \(\hbox {s}^{-1}\), which like the transverse modulus data corresponds to a test method change. Given the spread in values, it is difficult to compare the results in [2] with the quasi-static value obtained in this study. Similar elastic limit strains were used to determine modulus values in both studies and therefore, variation in the modulus values due to the fitting ranges was assumed to be negligible. Differences here may again be attributed to the use of single-sided strain measurements, or a different mechanical response from the MD configuration tested in [2]. At higher strain rates, a positive strain rate sensitivity was obtained to a value of 6.6 GPa at 8.8\(\times\)10\(^{1}\) \(\hbox {s}^{-1}\). IBII test results from all three specimen configurations are also shown in Fig. 26b. When combined with the quasi-static data, results from this study also show a positive strain rate sensitivity, but at a lower rate compared to that in [2]. Again, it is difficult to assess the different strain rate sensitivities without intermediate data, however this will be available soon.
Positive \(E_{22}\) strain rate sensitivities of 22.3% and 19.4% above quasi-static values were obtained for the UD90\(^{\circ }\) and UD45\(^{\circ }\) samples, respectively. IBII tests on UD90\(^{\circ }\) CFRP composite specimens in [26] resulted in a \(E_{22}\) value of 7.9 GPa with strain rates around 2\(\times\)10\(^{3}\) \(\hbox {s}^{-1}\) (8% increase over the quasi static value). The same material was evaluated in the UD45\(^{\circ }\) configuration in [30], where the same \(E_{22}\) = 7.9 GPa value was obtained. In [26, 20], the composites utilised a low-temperature out-of-autoclave epoxy matrix, which may have behaved differently to the autoclave cured matrix used in samples evaluated here. Therefore, \(E_{22}\) values obtained in this work are reasonably consistent with the results from [26, 30].
Acknowledging differences in fibre and resin systems, transverse and shear moduli values obtained during this evaluation generally conform to published data from [10], where maximum strain rates were around a few hundred \(\hbox {s}^{-1}\). At this ‘lower end’ of the high strain rate regime, inertial effects are lower and the quasi-static equilibrium assumption used in the split-Hopkinson bar test may be more admissible. Further, strains reported in [10] were obtained from ‘on-sample’ full-field measurements using the DIC technique, which may have produced more realistic results compared to traditional split-Hopkinson bar analysis [40]. As seen in Fig. 1a, b, there was significant scatter in the published results, particularly at strain rates of 10\(^{2}\) \(\hbox {s}^{-1}\) and above. In this strain rate regime, inertial effects are stronger and the quasi-static equilibrium assumption can be violated. Therefore, it is difficult to make meaningful comparison with split-Hopkinson bar data obtained at strain rates higher than a few hundred \(\hbox {s}^{-1}\), because it is possible that inertial effects have influenced the result away from the ‘true’ material response.
Comparison of the a transverse and b shear modulus results from this study with data from [2]
Limitations and Future Work
Consideration of the test method limitations and their effect on the resulting modulus values is now given. Future research activities aiming to further understand the effects of these limitations and extend the universal nature of the technique are also discussed.
A key assumption of the IBII test method used here is that the kinematic fields are uniform through-thickness. The validity of this assumption was investigated in detail in [41] where a back-to-back imaging protocol was used. The results of this study showed that spurious out-of-plane loading due to projectile misalignment caused only a small bias on the elastic modulus identified when using the IBII method. When new alignment protocols were implemented (as was used in the present study) the bias on the modulus was almost completely suppressed. Given the linearity of the transverse response observed in all tests in this work, the impact of 3D effects on the results can be considered negligible.
In this evaluation, a non-linear shear response was obtained from the UD45\(^{\circ }\) IBII tests. The range over which linear fits to the shear stress-strain curves were made influenced the shear modulus value. Because the linear limit strain varied in space and time, chord moduli were progressively fit to the shear stress-strain curves and the linear limit was determined when the value fell below the average modulus from previous steps. This method was affected by noise induced oscillations in the shear response, which made the linear limit identification troublesome because the oscillations were often of similar magnitude to the non-linear onset strains. There is currently no efficient method to check every slice and time step to evaluate the linear elastic limit determined from the chord fitting method. Future work could therefore include image deformation studies, including a non-linear material model in the finite element simulations, which can be used to determine the linear fitting range for experimental results processing.
The shear modulus identification from UD90\(^{\circ }\) specimens was obtained from shear stresses and strains, generated from a pitch angle misalignment between the projectile and the wave guide during the tests. Here, the pitch angle misalignment was not intentional, so the resulting shear stress and strain magnitudes were low. In the future, it should be possible to design the test to intentionally use this misalignment to more strongly activate the shear response. This could be achieved using an appropriate finite element model to predict the loading from a misaligned projectile. Optimised smoothing parameters for experimental results processing could then be determined from image deformation studies.
The focus of the present work was to develop a method to accurately obtain transverse and shear moduli from off-axis specimens with the IBII technique. The next step would be extend this method to obtain the dynamic failure stress under a combined tension/shear or compression/shear loading. Mechanical properties associated with failure often require a more localised approach, because the stress state at the exact point of failure is required. As a first step, the Linear Stress Gauge (LSG) approach described in [26] could be applied to off-axis specimens in global coordinates, using the free-edge boundary conditions to populate the stress tensor. The stress tensor can then be rotated into material coordinates to obtain the transverse and shear failure stresses. However, this is only valid when failure occurs at the specimen edges, where y-axis stresses are zero and the full stress tensor can be obtained.
Alternative methods are possible for instances where the failure does not occur at the specimen edge. One option is to utilise angled slice boundary condition information together with rigid body virtual fields, to construct higher order (quadratic or cubic) approximations of the transverse and shear stress in the material coordinate system. Another option is to use the full-field accelerations to approximate the local equilibrium equation as described in [42]. Once the failure stress reconstruction methodology is determined, a range of off-axis specimens could be evaluated in IBII tests to populate a high strain rate failure envelope under combined tension/shear and compression/shear states of stress.
Shear stress-strain curves obtained in this work revealed different load and unload moduli together with a residual shear strain upon return to the zero stress condition. These observations most probably indicate the formation of damage and therefore, a shear damage model such as that reported in [43] could be adapted for this high strain rate application. Micrography of recovered specimens could then be used as experimental validation of the damage model, comparing the reduction in modulus with the percentage void increase in recovered impacted samples. Lastly, noise-optimised virtual fields could be used in the VFM to extract modulus data as in [25].
Conclusions
Results from this study have demonstrated that the IBII test methodology can accurately characterise the in-plane transverse and shear moduli of orthotropic composites in the \(0.5 - 2\times\)10\(^{3}\) \(\hbox {s}^{-1}\) strain rate regime. Three forms of experimental validation were achieved:
-
Seven tests on UD45\(^{\circ }\) specimens gave a mean transverse modulus value of \(E_{22}\) = 9.91 GPa (COV = 3.36\(\%\)), indicating good repeatability between specimens. This was similar to the mean UD90\(^{\circ }\) result of \(E_{22}\) = 10.2 GPa (COV = 1.52\(\%\)). Therefore, the IBII technique is capable of generating consistent in-plane transverse modulus values from samples with different off-axis fibre angles.
-
The shear modulus was also characterised during the UD90\(^{\circ }\) specimen tests, where the mean \(G_{12}\) value was 5.51 GPa (COV = 2.30\(\%\)), again indicating good specimen-to-specimen variability. This result was consistent with the mean \(G_{12}\) obtained from the UD45\(^{\circ }\) samples of 5.44 GPa (average of Slices 1 and 2). Therefore, the IBII technique can derive accurate shear modulus values from single tests on relatively easy to manufacture UD90\(^{\circ }\) specimens.
-
Four tests were performed on MD±45\(^{\circ }\) specimens, where the resulting shear modulus was 5.09 GPa (average of Slices 1 and 2). This was 6.4% lower than the UD45\(^{\circ }\) value and consistent with the reduced fibre volume fraction of the MD laminate, as evidenced by its lower density.
In consideration of the consistent results and experimental validation in this study, the IBII technique represents a suitable test method to use in pursuit of high strain rate modulus property identification for composite materials. The results presented here and in previous IBII studies, suggest that this test is a suitable candidate for a new standard high strain rate test for modulus identification. Undoubtedly, as camera technology improves the efficacy of the IBII method will also improve.
Data Provision
Data supporting this study are openly available and can be accessed from the University of Southampton repository here: http://dx.doi.org/10.5258/SOTON/D1527. The digital dataset contains the following:
-
1.
Raw experimental images for the dynamics tests and static images used for the measurement resolution analysis.
-
2.
Output from the data processing code for each sample tested including maps of all kinematic fields over the test duration.
-
3.
Quasi-static test data.
References
Kidane A, Gowtham H, Naik N (2017) Strain rate effects in polymer matrix composites under shear loading: a critical review. J Dyn Behav Mater 3(1):110–132
Berthe J, Brieu M, Deletombe E, Portemont G, Lecomte-Grosbras P, Deudon A (2013) Consistent identification of CFRP viscoelastic models from creep to dynamic loadings. Strain 49(3):257–266
Kwon J, Choi J, Huh H, Lee J (2017) Evaluation of the effect of the strain rate on the tensile properties of carbon-epoxy composite laminates. J Compos Mater 51(22):3197–3210
Anderson C, Walker J (1991) An examination of long-rod penetration. Int J Impact Eng 11(4):481–501
Melin L, Asp L (1999) Effects of strain rate on transverse tension properties of a carbon/epoxy composite: studied by moiré photography. Compos Part A 30(3):305–316
Taniguchi N, Nishiwaki T, Kawada H (2007) Tensile strength of unidirectional CFRP laminate under high strain rate. Adv Compos Mater 16(2):167–180
Schaefer J, Werner B, Daniel I (2017) Strain-rate-dependent failure criteria for composite laminates: application of the northwestern failure theory to multiple material systems. Technical Report SAND2017-3082C, Sandia National Laboratories, California, USA
Hsiao H, Daniel I (1998) Strain rate behavior of composite materials. Compos Part B 29(5):521–533
Hsiao H, Daniel I, Cordes R (1999) Strain rate effects on the transverse compressive and shear behavior of unidirectional composites. J Compos Mater 33(17):1620–1642
Koerber H, Xavier J, Camanho PP (2010) High strain rate characterisation of unidirectional carbon-epoxy IM7-8552 in transverse compression and in-plane shear using digital image correlation. Mech Mater 42(11):1004–1019
Daniel I, Werner B, Fenner J (2011) Strain-rate-dependent failure criteria for composites. Compos Sci Technol 71(3):357–364
Dioh N, Ivankovic A, Leevers P, Williams J (1995) Stress wave propagation effects in split Hopkinson pressure bar tests. Proc R Soc A 449(1936):187–204
Gama B, Gillespie J, Mahfuz H, Raines R, Haque A, Jeelani S, Bogetti T, Fink B (2001) High strain-rate behavior of plain-weave S2 glass/vinyl ester composites. J Compos Mater 35(13):1201–1228
Pierron F, Zhu H, Siviour C (2014) Beyond Hopkinson’s bar. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 372
Gilat A, Goldberg R, Roberts G (2002) Experimental study of strain-rate-dependent behavior of carbon/epoxy composite. Composites Sci Technol 62:1469–1476
Bourne N (2013) Materials in mechanical extremes. Cambridge University Press, New York, USA
Bertholf L, Karnes C (1975) Two-dimensional analysis of the split hopkinson pressure bar system. J Mech Physf Solids 23(1):1–19
Richter F, Köppe E, Daum W (2016) Tracking deformation history in split Hopkinson pressure bar testing. Mater Today 3(4):1139–1143
Davies R (1948) A critical study of the Hopkinson pressure bar. Philos Trans R Soc 240(821):375–457
Li Z, Lambros J (1999) Determination of the dynamic response of brittle composites by the use of the split Hopkinson pressure bar. Compos Sc Technol 59(7):1097–1107
Rigby S, Barr A, Clayton M (2018) A review of Pochhammer-Chree dispersion in the Hopkinson bar. Proc Inst Civil Eng 171(1):3–13
Chen W, Song B (2011) Split Hopkinson (Kolsky) bar design, testing and applications. Springer, New York
Pierron F (2008) Identification of materials mechanical properties from full-field measurements: latest advances in the virtual fields method. Appl Mech Mater 13–14:3–9
Fletcher L, Pierron F (2018) An image-based inertial impact (IBII) test for tungsten carbide cermets. J Dyn Behav Mater 4(4):481–504
Van Blitterswyk J, Fletcher L, Pierron F (2018) Image-based inertial impact test for composite interlaminar tensile properties. J Dyn Behav Mater 4(4):543–572
Fletcher L, Van-Blitterswyk J, Pierron F (2019) A novel image-based inertial impact (IBII) test for the transverse properties of composites at high strain rates. J Dyn Behav Mater 5(1):65–92
Fletcher L, Van-Blitterswyk J, Pierron F (2018) Combined shear/tension testing of fibre composites at high strain rates using an image-based inertial impact test. EPJ Web of Conferences, 183
Pierron F, Grédiac M (2012) The virtual fields method. Springer, New York
Koohbor B, Kidane A, Lu W-Y (2016) Characterizing the constitutive response and energy absorption of rigid polymeric foams subjected to intermediate-velocity impact. Polym Test 54:48–58
Pierron F, Fletcher L (2019) Generalized stress-strain curves for IBII tests on isotropic and orthotropic materials. J Dyn Behav Mater 5(2):180–193
Fletcher L, Van Blitterswyk J, Pierron F (2019) A manual for conducting image-based inertial impact (IBII) tests. University of Southampton, UK, Faculty of Engineering and Physical Sciences
Grédiac M, Sur F, Blaysat B (2016) The grid method for in-plane displacement and strain measurement: a review and analysis. Strain 52(3):205–243
Rossi M, Lava P, Pierron F, Debruyne D, Sasso M (2015) Effect of DIC spatial resolution, noise and interpolation error on identification results with the VFM. Strain 51(3):206–222
Lava P, Cooreman S, Coppieters S, De Strycker M, Debruyne D (2009) Assessment of measuring errors in DIC using deformation fields generated by plastic FEA. Optics Lasers Eng 47(7–8):747–753
Lava P, Cooreman S, Debruyne D (2010) Study of systematic errors in strain fields obtained via DIC using heterogeneous deformation generated by plastic FEA. Opt Lasers Eng 48(4):457–468
Rossi M, Pierron F (2012) On the use of simulated experiments in designing tests for material characterization from full-field measurements. Int J Solids Struct 49(3–4):420–435
Lukić B, Saletti D, Forquin P (2017) Use of simulated experiments for material characterization of brittle materials subjected to high strain rate dynamic tension. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 375(2085)
Castres M, Berthe J, Deletombe E, Brieu M (2017) Experimental evaluation of the elastic limit of carbon-fibre reinforced epoxy composites under a large range of strain rate and temperature conditions. Strain 53(6):1–10
Seghir R, Pierron F (2018) A novel image-based ultrasonic test to map material mechanical properties at high strain-rates. Exp Mech 58(2):183–206
Neumayer J, Kuhn P, Koerber H, Hinterhölzl R (2016) Experimental determination of the tensile and shear behaviour of adhesives under impact loading. J Adhesion 92(7–9):503–516
Van Blitterswyk J, Fletcher L, Pierron F (2020) The effect of out-of-plane loading on the image-based inertial impact (IBII) test. Strain, under review
Seghir R, Pierron F, Fletcher L (2019) Image-based stress field reconstruction in complex media. In Conference Proceedings of the Society for Experimental Mechanics Series, Greenville, USA
Chalal H, Avril S, Pierron F, Meraghni F (2006) Experimental identification of a nonlinear model for composites using the grid technique coupled to the virtual fields method. Compos Part A 37(2):315–325
Acknowledgements
The authors would like to thank Dr Julien Berthe at ONERA in Lille, France, for supplying the composite plates used for the specimens evaluated in this study. Thanks are also given to Dr Jared Van-Blitterswyk and Dr Xavier Regal for their help conducting the IBII tests.
Funding
EPSRC support is acknowledged by Professor Pierron and Dr Fletcher (Grant EP/L026910/1) and by Mr Parry (PhD studentship).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Density Calculations
Appendix A: Density Calculations
Density values were calculated from small samples cut from the same laminate that the IBII and quasi-static specimens were manufactured from. Surfaces of the density samples were first sanded to the same amount as the quasi-static and IBII test specimens. Each density sample mass was measured using a mass balance with a resolution of 1\(\times 10^{-4}\) grams. Six measurements of each specimen dimension were taken with a digital calliper with a resolution of ± 0.005 mm. The lower and upper geometric measurements were used to calculate the specimen’s (approximate) minimum and maximum volume. Maximum and minimum density values were calculated by dividing the specimen mass by the minimum and maximum volumes, respectively. Tables 8, 9 and 10 list the mean density value and standard deviation for each laminate.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Parry, S., Fletcher, L. & Pierron, F. The Off-Axis IBII Test for Composites. J. dynamic behavior mater. 7, 127–155 (2021). https://doi.org/10.1007/s40870-020-00271-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40870-020-00271-7