Image-Based Inertial Impact (IBII) Tests for Measuring the Interlaminar Shear Moduli of Composites

Abstract

The image-based inertial impact test has previously shown that inertial effects generated with high-strain-rate loading can be used to measure the dynamic constitutive properties of composites at strain rates on the order of $1600\,{\rm s}^{-1}$. This work represents an important next step in exploring the potential of this concept with two tests presented where loading heterogeneity is exploited to measure the interlaminar shear modulus and stress–strain behaviour at high strain rates. The first test configuration used a short-beam with asymmetric loading to activate the shear behaviour. The virtual fields method was used to directly identify the interlaminar shear modulus from heterogeneous full-field maps of strain and acceleration. Simulated experiments were used to optimise the test configuration, select optimal smoothing parameters, and quantify uncertainty from grid rotation on the shear modulus identifications. The test was validated experimentally with three different virtual fields identifying an average shear modulus ranging from 5.7 to 5.9 GPa measured at $1600\,{\rm s}^{-1}$, representing a 16–19% increase compared to quasi-static measurements. The shear modulus could also be identified from shear introduced into specimens tested in the standard, end-on interlaminar IBII configuration from slight in-plane misalignments of the impactor. The identified value of 5.6 GPa validates measurements from the first configuration and also demonstrates the capability to identify multiple interlaminar stiffness parameters from a single test.

Introduction

Due to the high specific stiffness and strength of polymer–matrix composites, there is an increasing desire to use thicker composite structures as lightweight alternatives to their metallic counterparts. In these cases, the interlaminar stresses become important to consider due to the relatively low strength and stiffness in these material planes, which leads to increased susceptibility to micro-cracking or delaminations, and premature failure of the material. Moreover, these structures are often subjected to dynamic loading (e.g., blast, crash, foreign object strike, etc.) where significant interlaminar stresses can develop over a range of strain rates [1,2,3]. Therefore, the reliability of numerical simulations hinges on the accuracy of models for the strain-rate sensitivity of interlaminar constitutive properties, which must be established experimentally. It is generally accepted that the interlaminar shear properties of polymer matrix composites under dynamic shear loading is different than under quasi-static conditions [4,5,6,7]. However, existing studies report highly scattered measurements of the interlaminar shear stiffness and strength [8, 9] making it very difficult to establish and quantify the effect of strain rate on these material properties.

The split-Hopkinson pressure bar (SHPB) apparatus is the most commonly used approach for measuring high-strain-rate shear properties. Since point measurements are used to infer the global response of the sample, two key assumptions must be made: (1) the specimen is in a state of uniform shear stress, and (2) that the loading is one-dimensional and satisfies quasi-static equilibrium conditions (inertia is negligible). Since there is no specific test method for obtaining these properties, researchers have considered a variety of specimen geometries that attempt to create a state of stress close to that of uniform shear so that properties can be derived from strain measurements on the input and output bars. Some examples include: the double V-notch shear test (Iosipescu) [10], single and double-lap joint shear test [4, 11, 12], short beam shear test [6], double notch shear test [6], and out-of-plane off-axis tests [13]. In a limited number of other studies thin tubular specimens have been machined and loaded with a torsional version of the SHPB [5, 7]. While this configuration is thought to provide loading that is closest to a state of pure shear, these studies suggest that measurements are highly sensitive to variation in specimen geometry (fillet radius, wall thickness), and layup orientation, leading to scatter in measurements of the interlaminar shear modulus.

The assumption that inertia can be neglected becomes questionable at strain rates above 100 s$^{-1}$ for materials with low wave speeds, such as polymer matrix composites [8, 14]. In these cases, it is unavoidable to have a period of loading where the stress state is heterogeneous [15, 16]. Until the inertial effects dampen out, the measurements from the input and output bars cannot be used to directly infer the response of the material. Some studies have implemented strain gauges directly onto the sample to try and improve the accuracy of strain measurements [11, 12]. However, the gains are marginal since assumptions are still made about the strain distribution, and reliable measurement of shear stress is still a problem. As a result, it is generally agreed that for such materials the SHPB cannot be used reliably for stiffness characterisation at low strains (< a few % strain) and strain rates above a few 100 s$^{-1}$ [14, 17,18,19].

Several recent studies have considered ultra-high-speed imaging and full-field measurements as an alternative way of characterising high-strain-rate material properties [20,21,22,23,24,25,26,27,28,29,30,31]. The virtual fields method (VFM) enables the inertial effects to be exploited with the specimen acting as a dynamic load cell, thus alleviating the requirement for external force measurement. This concept of using full-field measurements and the VFM for high-strain-rate stiffness identification was first validated by Moulart et al. [32] and Pierron and Forquin [20]. Follow on studies have resulted in the formalisation of the image-based inertial impact (IBII) test, which has been successfully demonstrated to measure high-strain-rate in-plane [21, 22, 24, 25] and interlaminar [26] properties of composites, and ceramics [27].

Development of the IBII test for interlaminar properties has so far been directed at tests suited to identifying the elastic modulus and tensile failure stress [26]. With the goal of complete interlaminar characterization, it is now desired to expand the test to develop a configuration that can be used to identify shear properties. Preliminary work [24] has demonstrated that the in-plane shear modulus and elastic modulus can be simultaneously identified using an edge-on impact configuration with fibres cut off-axis to the loading direction. While it would be ideal to extend the same concept for testing interlaminar specimens, this is challenging to do given the restriction on specimen length (limited by laminate thickness). Therefore, the purpose of this study is to develop an alternative IBII test that is better suited to small samples and directly provides the interlaminar shear modulus.

The IBII test configuration selected to activate the shear behaviour was similar to a short-beam-shear test, with full-field measurements and the virtual fields method used to directly identify the interlaminar shear modulus much like in [33,34,35]. Simulated experiments and image deformation were used to validate the proposed configuration, and evaluate the effect of camera resolution and grid rotation on the identification of the shear modulus. Synthetic image deformation was also used to select optimal smoothing parameters for processing experimental images and estimating uncertainty associated with the shear modulus identification. The IBII shear test concept was experimentally validated to show that the interlaminar shear modulus could be measured at strain rates on the order of 1600 s$^{-1}$. It was also found that the shear modulus could be identified from standard interlaminar IBII tension/compression specimens in [36] from shear introduced by slight pitch misalignment of the impactor, which agree well with the modulus identified using the presented test method.

Image-Based Inertial Impact (IBII) Test Principle and Theory

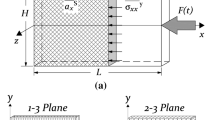
The basic idea behind the IBII test is to load the material at high strain rates using a stress wave generated by an impact with a projectile. Here, a simple rectangular geometry is used to exploit the compressive pulse loading and specimen inertia to generate shear in the region of the sample overhanging the waveguide (see Fig. 1). As the material adjacent to the waveguide is loaded by the pulse, the overhanging region will remain stationary until the axial pulse reaches the free edge allowing shear to build up in the region near the waveguide. A grid is deposited onto the sample and imaged with an ultra-high-speed camera to measure the dynamic, kinematic behaviour of the material. Displacement fields are used to compute strain and acceleration maps, which encode information about the material properties. Using the VFM it is possible to identify the interlaminar shear modulus directly from the fields as described in the following section.

Fig. 1

Generic configuration of proposed shear test using an overhanging impact specimen

The Virtual Fields Method (VFM)

The key concepts for applying the VFM in the IBII test is outlined in [26, 27] and therefore, only the relevant aspects to identifying the interlaminar shear moduli ($G_{13}$ or $G_{23}$) are included here. The reader is referred to [37] for a comprehensive description of the VFM. The principle of virtual work is satisfied with any virtual displacement fields that are continuous and piecewise differentiable. In this work, the following additional assumptions are made: (1) constant density and thickness in space; (2) kinematic fields are uniform in the thickness dimension of the sample; and (3) the specimen can be considered to be in a state of plane stress. Under these conditions, and neglecting body forces, the principle of virtual work takes the following form:

$$\begin{aligned} -\int _S {\varvec{\sigma }}:{\varvec{\epsilon}}^{*} dS + \int _{\delta l} {\user2{T}}\cdot {\user2{u}}^{*}dl = \rho \int _S{\user2{a}}\cdot {\user2{u}}^{*} dS \end{aligned}$$

(1)

where S denotes the surface of the region of interest, $\textit{\textbf{T}}$ is the Cauchy stress vector, which is applied to the in-plane boundaries denoted by l, ${\user2{u}}^{*}$ is the virtual displacement field, ${\varvec{\epsilon}}^{*}$ the virtual strain field and ${\varvec{\sigma}}$ the Cauchy stress tensor. Note that $:$ and $\cdot$ denote the dot product in matrix and vector forms, respectively. The left hand side of Eq. (1) represent the internal and external virtual work and the right hand side represents the virtual work of inertial forces.

Here, a linear elastic, orthotropic constitutive model is used. For the case of interlaminar shear, where the measurements are made in the material coordinates ($x-y$ aligned with $1-3$), the shear component is de-coupled from the in-plane stiffness components giving shear stress directly as a function of the engineering shear strain $\gamma _{xy}$, as $\sigma _{xy}$ = $G_{13}\gamma _{xy}$. Thus, the principle of virtual work reduces to:

$$\begin{aligned} -\int _S G_{13}\gamma _{xy}^{*}\gamma _{xy} dS + \int _{l}{\user2{T}} \cdot {\user2{u}}^{*}dl = \rho \int _S{\user2{a}}\cdot {\user2{u}}^{*} dS \end{aligned}$$

(2)

with $\gamma _{xy}^*$ = 2$\epsilon _{xy}^*$, the engineering virtual shear strain. Since $\textit{\textbf{a}}$ is non-negligible during the test there are a number of different ways in which $G_{13}$ can be identified. The first approach is to cancel out the contribution of internal virtual work and relate acceleration to stress through the external virtual work term since $\textit{\textbf{T}}$ = ${\varvec{\sigma}}\cdot{\user2{n}}$. In doing so, it is then possible to reconstruct stress–strain curves at different cross-sections in the sample with the initial slope of the curve used to identify $G_{13}$. The second approach is to eliminate the contribution of $\textit{\textbf{T}}$ (external virtual work) and directly identify $G_{13}$ from full-field shear strain and acceleration. Both approaches are described in the following sections. Note that Eq. (2) and the following theory is presented based on validation of the test using the 1–3 material plane. However, the same test principle and theory applies for the 2–3 material plane.

Shear Stress-Gauge Equation

Consider the portion of the sample overhanging the waveguide (Fig. 1), with the free body diagram shown in Fig. 2. The objective of the first approach is to identify the interlaminar shear modulus from the identified stress–strain behaviour similar to that presented in [21, 26, 27]. To do so, we select a simple rigid-body virtual field $(u_{x}^{*}=1, u_{y}^{*} =0)$ that removes the contribution of internal virtual work (i.e., $\epsilon _{ij}^{*}$ = 0). Substituting into Eq. (2) results in:

$$\begin{aligned} \int _{L} \sigma _{xy} dx = \rho \int _S a_{y} dS \end{aligned}$$

(3)

Fig. 2

Free-body diagram of impacted interlaminar shear sample. Fibres run parallel to the y-axis for the 1–3 material plane. Note that F(t) only represents the general orientation of the shear load imparted by the axial pulse and does not imply that the loading be strictly parallel to the x axis

which provides a direct relationship between virtual work from inertia and shear stress. Since strain and acceleration measurements are not continuous, and instead measured at discrete points on the surface, Eq. (3) must be approximated with discrete sums [21]. Doing so results in:

$$\begin{aligned} \overline{\sigma _{xy}}^{x} = \rho y_{o}\overline{a_{x}}^{S} \end{aligned}$$

(4)

which is henceforth referred to as the shear stress-gauge (SG) equation. In Eq. (4) the overline and superscript ‘S’ denotes the surface average between the top free edge and the cross-section of interest, and overline combined with superscript ‘x’ denotes the line average along the horizontal cross-section at $y_{0}$. The stress-gauge equation is used to reconstruct $\overline{\sigma _{xy}}^{x}$ at every cross-section for each acceleration field measured during the test. This is combined with average shear strain measured along the same cross-section ($\overline{\gamma _{xy}}^{x}$) to identify one point in the stress–strain space assuming $G_{13}$ is constant through the thickness for each slice. Performing this reconstruction for each frame populates the stress–strain response for the material. Taking the slope of a linear fitting to the initial part of the stress–strain curve provides a measurement of $G_{13}$. Since this information can be generated for each cross-section in the overhanging region of the sample, we obtain multiple measurements of the shear modulus, which can be compiled as a function of y to provide a spatial identification of the shear modulus.

Manually Selected Virtual Fields

The second approach assumes $G_{13}$ is constant in the specimen and uses full-field strain and acceleration maps for the identification. Since the distribution of the impact load at the bottom of the overhang is unknown, its contribution to external virtual work must be removed. To do so, the virtual displacement fields must be set to zero at y = H (see Fig. 2). One virtual field that satisfies this is $u_{x}^{*}$ = $y-H$, $u_{y}^{*}$ = 0, with the corresponding virtual strains of: $\epsilon _{xx}^{*}$ = $\epsilon _{yy}^{*}$ = 0 and $\gamma _{xy}^{*}$ = 1. Substituting this into Eq. (2) results in:

$$\begin{aligned} -G_{13}\int _S \gamma _{xy} dS = \rho \int _S a_{x}(y-H) dS \end{aligned}$$

(5)

By approximating integrals with discrete sums, the shear modulus $G_{13}$ can be calculated from a simple ratio of the weighted field-average of acceleration to field-average shear strain as:

$$\begin{aligned} G_{13} = -\frac{\rho \overline{a_{x}(y-H)}^{S_o}}{\overline{\gamma _{xy}}^{S_{o}}} \end{aligned}$$

(6)

where the overline superscripted with ‘$S_{o}$’ denotes averaging over the whole field of view. Note that Eq. (6) only applies for $\overline{\gamma _{xy}}^{S_{o}}$ not equal to zero. With this approach the interlaminar shear modulus $G_{13}$ is identified with Eq. (6) at every frame of the dynamic test. Since these virtual fields were selected manually based on intuition, Eq. (6) is henceforth referred to as the ‘manual VFM’ approach.

Special Optimised Virtual Fields

The virtual field selected in Sect. 2.1.2 represent one of an infinite number of virtual fields that remove the contribution of external virtual work. In the presence of noise, each set of virtual fields provides a different identification, each having variable sensitivity to noise. Avril et al. [38] showed that it is possible to automate the selection of ‘optimal’ virtual fields based such that stiffness parameter identifications have minimal sensitivity to strain noise. We adopt this procedure here to ensure that the virtual fields at each time step act as a near optimal spatial filter for the measurements, providing a higher weighting to regions where the shear components are most activated. In [25, 26] the general orthotropic, special optimised virtual fields approach was simplified for the direct identification of the interlaminar and transverse elastic modulus. Here we present a similar extension for the direct identification of the shear modulus.

The virtual fields are expanded using a piecewise virtual mesh which is formulated with only $u_{x}^*$ degrees of freedom. The $u_{x}^{*}$ degree of freedom is constant along x but allowed to vary along y (i.e., only virtual shear permitted) as:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{x}^{*}(x^{i},y^{j}) = u_{x}^{*}(x^{i+1},y^{j})\\ u_{x}^{*}(x^{i},y^{j}) \ne u_{x}^{*}(x^{i},y^{j+1}) \end{array}\right. } \end{aligned}$$

(7)

where i and j denote the column and row number of the virtual mesh, respectively. The $u_{y}^{*}$ virtual displacements were set to zero at all nodes, and both $u_{x}^{*}$ and $u_{y}^{*}$ were set to zero at the bottom of the region of interest to remove the virtual work contribution of the unknown loading as was done with the manual VFM approach. The general form of the resulting virtual displacement fields is shown schematically in Fig. 3.

Fig. 3

Virtual mesh for interlaminar shear modulus identification. Un-deformed mesh shown in grey. Note that the red arrows only indicate the general orientation of the shear load imparted by the axial pulse and does not imply that the loading be strictly parallel to the x axis

Starting from Eq. (2) the noise minimisation procedure was carried out in the same way as presented in [25, 38]. This generates a single set of optimal virtual field coefficients $({\textit{\textbf{Y}}}^{*} = [{\tilde{u}}_{1}^{*(1)} \dots {\tilde{u}}_{N}^{*(1)}])$ at each time step, which are used to find $G_{13}$ using the expression:

$$\begin{aligned} G_{13} = -\rho \frac{S}{N}\left[ \sum \limits _{i = 1}^{N} a_{x}^{i}{\textit{\textbf{Y}}}^{*}\right] \end{aligned}$$

(8)

where S denotes the surface area of the region of interest (given by $L \times H$) and N denotes the number of measurement points over that surface. In Eq. (8) it is assumed that the noise amplitude is much smaller than the magnitude of the measured strains, and integral quantities can be approximated by discrete sums. Using Eq. (8) it is possible to identify the shear modulus directly from full-field maps of $a_{x}$ acceleration. Since this virtual field provides the optimal identification, at least optimal in the sense of minimal sensitivity to strain noise, Eq. (8) is henceforth referred to as the optimised VFM approach. Note that in the manual and special optimised identification routines data is discarded within one pitch plus one spatial smoothing kernel along the bottom edge of the field of view to reduce filter edge effects.

Validity of Assumptions Tied to VFM Identifications

Some discussion is required regarding the validity of the underlying assumptions on which the above equations were formulated. From Eqs. (4), (6) and (8) one can see that stiffness and stress reconstructions are proportional to density so any variation between samples will scale the identifications accordingly. So long as thickness is constant along the sample, it cancels out in all expressions. If thickness and density vary along the length of the sample the uncertainty in stress reconstruction becomes more complex. However, it is probable that these effects are small given that measured thickness along the length of all samples tested here varied by no more than 1%, and density varied by as much as 2.5% (based on measurements from [26]).

A recent study has shown the 2D assumption does not hold well when there is angular misalignment in the impact chain and that this causes significant bias in stress reconstruction [36]. This was confirmed in [36] for end-on rectangular specimens using simultaneous, full-field measurements on the front and back faces. These measurements were then used to develop a set of diagnostics to identify when/where the 2D assumption breaks down.

Ideally, we would have back-to-back measurements to verify the 2D assumption for the overhanging shear configuration presented in this paper. Since this was not possible, we rely on the fact that we know the impact alignment is well controlled with our new alignment procedure [36] and that out-of-plane effects should be minimal with possible exception to regions near the where the load is introduced. However, this should be verified in the future with back-to-back measurements. Data from the edge-on test configuration presented in Sect. 8 was collected in [36] and diagnostics were used to check the validity of the 2D assumption over the region of the sample used for stiffness identification.

Numerical Test Design

Design Objectives

The objective was to design a test to characterise the high-strain-rate interlaminar shear modulus using a configuration that requires minimal preparation/machining while still enabling full-field measurements. To be consistent with previous tests in our laboratory with the interlaminar IBII method [26], we used the same 18 mm thick carbon/epoxy unidirectional pre-preg laminate (MTM45/AS4-1) supplied by Material Sciences Corp. For orthotropic materials the shear response in the material coordinates is de-coupled from the other in-plane stiffness parameters. Therefore, the shear modulus should be identifiable from any configuration where significant shear is generated.

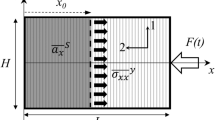
Following from the basic impact configuration in previous interlaminar IBII tests, the most intuitive configurations is to use a rectangular sample where part of it overhangs the waveguide in a type of ‘short-beam shear’ configuration. The dimensions most suitable to the given camera spatial resolution (400 × 250 pixels), and minimum printable grid pitch (0.337 mm) are 18 mm × 12 mm for the overhang part of the sample (for 7 pixels/period grid sampling). The design was simplified by replacing the projectile, waveguide and sabot with a uniform pulse loading over part of the specimen (as shown in Fig. 4) to better represent the experimentally-observed temporal evolution of the pulse. Using available waveguides and projectiles, the design space consisted of the two geometries listed in Table 1, and two pulse lengths, giving four total configurations.

Fig. 4

Simplified test configuration of proposed shear test with an applied pressure pulse used in design studies

Table 1 Specimen configurations considered in the design of an IBII shear test

Numerical Simulation

Each configuration was simulated in three-dimensions using ABAQUS/Explicit v.6.14-3. Eight-node brick elements with reduced integration (C3D8R) were used in all simulations. The time step was allowed to vary automatically, with outputs generated every $0.2\,{\upmu}{\text{s}}$ to represent imaging at 5 MHz with the Shimadzu HPV-X camera. A small amount of numerical damping ($\beta$) is required to control numerical, high frequency oscillations in explicit simulations. The mesh size and $\beta$ damping coefficient were selected through separate convergence studies. The optimal values were chosen based on convergence of the computed average shear stresses and the stress averages reconstructed using the stress-gauge equation (Eq. 4). These studies resulted in a mesh size of 0.2 mm and $\beta$ damping of $10^{-8}$ s. The material properties and relevant simulation parameters are listed in Table 2.

Table 2 Material properties and simulation parameters for the interlaminar shear IBII test

A $25\,\mu {\text{s}}$ pulse with an amplitude of 125 MPa was used to represent the loading from a 25 mm projectile travelling at $35\,{\text{m}}\, {\text{s}}^{-1}$ from [25]. The rise time is assumed to be half of the pulse period based on experimentally observed pulses. Similarly, the simulated pulse for a 10 mm long projectile is based on the experimental pulse measured in [26]. Both pulse profiles are shown in Fig. 5. The effect of sample geometry and pulse duration on the amount of shear generated in the sample are investigated in the following section.

Fig. 5

Simulated pulses applied uniformly on the face of the sample in contact with the waveguide

Effect of Geometry

The stress–strain space populated by each configuration (Fig. 6) was used as an initial metric to evaluate shear activation as a function of geometry and pulse duration. In general, Fig. 6 shows that the peak shear stress increases with increasing waveguide diameter and pulse duration. Configuration 1 with a $10\,\mu s$ pulse is the only configuration which creates a full load-unload cycle, which explains why a larger region of the stress–strain space is populated. This occurs because the specimen length and pulse are short enough that the shear wave reflected from the top and bottom edges causing the material to fully unload and re-load in shear. This is not observed in configuration 2 (Table 1) since the shear wave must travel further before it reflects from the bottom edge, thus limiting the amount of unloading that occurs within the simulated time frame.

Fig. 6

Full stress–strain space populated from all elements in the overhanging region of the sample for each configuration. Note that the stress–strain data are offset by $2\,{\text{mm}}\,{\text{m}}^{-1}$ for clarity and data within $1\,{\text{mm}} \times 1\,{\text{mm}}$ of the lower right corner of the sample are omitted to exclude the stress concentration. Note that configuration 2 with the $25\,\mu{\text{s}}$ pulse gives the highest peak shear stress

Increasing the specimen length provides some advantage for increased shear loading, but its effect is smaller than pulse duration. This is illustrated in Fig. 7 for configuration 2, which shows the temporal evolution of shear stress in the sample near the bottom of the overhang ($x = L/2$, $y = 0.95H$) for both pulses. For the $10\,\mu s$ pulse, $\sigma _{xy}$ monotonically increases up to a maximum at approximately $8\,\mu s$. The maximum shear stress is limited by the local $\sigma _{xx}$ becoming tensile as the reflected wave superimposes with the release wave on the back edge of the pulse. This is expected since the 10 mm projectile was designed to load the sample to failure in tension [26]. When the pulse is longer, the superposition of the reflected wave from the free edge and the incoming compressive pulse prevents full unloading and enables shear stress to continue to build up in the sample. In this case, peak shear stress rises by 40% by increasing the pulse length from 10 to $25\,{\upmu}{\text{s}}$. However, the extension of this is limited as simulations with a longer input pulse ($40\,{\upmu}{\text{s}}$) show little benefit in terms of increased peak shear stress. This is because unloading in shear occurs when the axial stress switches from compression to tension, which is a function of axial wave speed and specimen length. For pulse durations exceeding $25\,{\upmu}{\text{s}}$ the reflected waves superimpose at a similar time to form a tensile pulse with a greater amplitude than the input pulse, causing a decrease in shear loading.

Fig. 7

The effect of pulse duration on $\sigma _{xy}$ for configuration 2 at the bottom of the overhanging region ($x=L/2$, $y=0.95H$) for $10\,{\upmu}{\text{s}}$ and $25\,{\upmu}{\text{s}}$ pulses (pulse amplitude = 125 MPa)

The results from the first two studies show that a larger waveguide and longer sample offer some advantage for increasing the maximum shear stress generated in the sample, but the effect is relatively small compared to increasing the pulse duration from 10 to $25\,{\upmu}{\text{s}}$. Therefore, configuration 2 with a $25\,{\upmu}{\text{s}}$ pulse will be carried forward for experimental validation. Aside from slight improvements in shear activation, a larger waveguide offers a number of other practical benefits for implementation including: (1) easier specimen alignment on the waveguide and (2) better imaging resolution in alignment shots used to set the position of the support stand (see [40]). The complete experimental configuration is listed in Table 3. The target impact speed of $35\,{\text{m}}\,{\text{s}}^{-1}$ is based on previous tests with this waveguide-projectile configuration [25], which produced a compressive pulse amplitude of approximately 125 MPa. The following section focuses on the validation of the stiffness identification routines presented in Sect. 2 using simulated fields for the selected configuration.

Table 3 Selected experimental parameters for the interlaminar shear IBII test

Numerical Validation of Stiffness Identification Routines

Here, the stiffness identification routines described in Sect. 2 are validated using the kinematic fields extracted from the finite element model described in the previous section. The same simulation parameters from Table 2 were used with the specimen geometry listed in Table 3. Displacement, strain and acceleration fields were extracted at $0.2\,{\upmu}{\text{s}}$ time steps from the model, mimicking a sampling at a frame rate of 5 MHz consistent with current experimental capabilities. A sample of these fields is shown at the time corresponding to peak shear stress in Fig. 8.

Fig. 8

Simulated fields for the IBII shear specimen at the time step when peak shear stress is reached at the bottom of the overhang region (x = L/2, y = 0.95H): a $u_{x}$, b $u_{y}$, c $a_{x}$, d $a_{y}$, e $\epsilon _{xx}$, f $\epsilon _{yy}$, and g $\gamma _{xy}$

The acceleration fields ($a_{x}$) were processed using Eq. (4) to reconstruct average shear stress at each horizontal cross-section along the overhanging region of the sample. Combining average shear stress with average shear strain at each slice provides the shear stress-shear strain response. An example is shown at y = 0.95H in Fig. 9a. Using a linear regression to fit the stress–strain response, the spatial distribution of the shear modulus was extracted along the overhanging region as shown in Fig. 9b.

Fig. 9

a Reconstructed shear stress–shear strain curve at $y = 0.95H$, and b spatial identification of the shear modulus, $G_{13}$, by fitting the stress–strain curves with a linear regression model

The identification with the manual virtual fields and special optimised virtual fields are shown in Fig. 10a and Fig. 10b, respectively. A virtual mesh convergence study showed that the shear modulus could be identified with a virtual mesh as coarse as 1 $\times$ 2 elements, but the best temporal stability was obtained with a 1 $\times$ 5 mesh. Further refinement provided no benefit at the expense of increased processing time. At the start of the test both identifications are poor when the wave first enters the sample. The stability of the identification is also challenged past $17\,{\upmu}{\text{s}}$ due to low signal as the specimen unloads in shear. This has a larger effect on the manual virtual fields where both terms in Eq. (6) approach zero. This is because the manual virtual fields provide a static filter on the fields, whereas the special optimised virtual fields adjust in time according to the locations where strain signal is highest.

Fig. 10

Identification of the interlaminar shear modulus, $G_{13}$ from simulated strain and acceleration fields using: a manual virtual fields (Eq. 6), and b special optimised virtual fields (Eq. 8)

The results shown in Figs. 9 and 10 demonstrate that all stiffness identification methods are able to identify the reference modulus well within 1%. The simulation data serves as a perfect reference for validating the stiffness identification procedures. However, it does not account for experimental errors such as: spatial/temporal resolution of the camera, rigid-body rotation of the grid, and measurement noise. The effect of these parameters on each stiffness identification routine will be studied using synthetic image deformation as described in the following section.

Error Quantification Using Image Deformation

In this section image deformation simulations are used to explore the effect of experimental errors on the measured kinematic fields and identification of the shear modulus with the various VFM routines (Sect. 2.1). This section begins by describing the approach for reconstructing edge data, which differs from previous studies [25, 26], and then investigates the main source of systematic error (apart from the camera itself) of rigid body rotation of the grid. After this, the following section investigates the effects of camera resolution/noise as well as selection of optimal smoothing parameters. The general concepts of the image deformation procedure are provided below, but a full description of the process can be found in previous work [41,42,43]. The specific application of the image deformation procedure to the IBII test can be found in [26, 27, 40].

Image Deformation Procedure

The idea is to generate a set of synthetic grey level images of black-on-white grids that are representative of those captured in an experiment. Here we use an analytical function for the grey level intensity, and the super-sampling interpolation routine described in [40, 42, 44] to create the images. The simulated displacement fields from the FE model in Sect. 4 were encoded in these images based on an inter-frame time of $0.2\,{\upmu}{\text{s}}$ (frame rate of 5 MHz). All parameters required to generate the grid images are provided in Table A1 in Supplementary Material and the grid images are provided in the data repository references at the end of the article. Thirty combinations of grey-level noise were added to the images with an amplitude equivalent to that measured from a set of static grid images with the Shimadzu HPV-X camera. Each set of images were processed using a parametric sweep of spatial and temporal smoothing parameters. The systematic error ($e_{S}$) represents the difference between the mean identified stiffness parameter from the 30 cases of noise, and the reference stiffness in the FE model. Random error was defined as the standard deviation of the identification over the 30 cases of noise. The optimal parameters were chosen as those which minimised the total error defined as the absolute value of the systematic error plus or minus two times the random error ($e_{T}$ = max($|e_{S} + 2e_{R},e_{S} - 2e_{R}|$)). The errors were normalised by the reference shear modulus as was done in a previous study [26].

Shear Strain Reconstruction at Field Edges

Grey level images were processed using the same procedure as described in the flow chart in Fig. 5 of [26], which will be outlined here for completeness. From the grid method, we obtain phase maps which can be related to displacement with the known grid pitch. The raw displacement maps are processed in two different ways to obtain strains and accelerations. Strain fields are calculated by first spatially smoothing the displacement fields using a Gaussian filter followed by spatial differentiation with no temporal smoothing applied. The acceleration fields are calculated from displacements by applying a temporal filter (3rd order polynomial (Savitsky Golay)) before twice differentiating in time with no spatial smoothing applied.

The exception to the procedure in [26] in this work is the way shear strain maps are treated. Full-field displacements from the grid method are unreliable within one pitch of the edge of the grid. This data was replaced by using a linear extrapolation of the data within one pitch of the edge as discussed in [26]. Note that this reconstruction is performed only on the displacement fields prior to spatial or temporal smoothing. This reconstruction works well for reconstructing the edge data for all fields except $\gamma _{xy}$ since this is done independently for each row ($u_x$, $a_{x}$) or column ($u_{y}$, $a_{y}$), with no continuity enforced across the rows/columns. If the resulting artificial shear strains near the edge are left uncorrected, a bias is introduced into the identification routines. Therefore, edge effects are corrected on the derived strain fields using the free-edge boundary conditions (zero shear strain). Here we correct $\gamma _{xy}$ over one pitch plus half of the smoothing window width (since smoothing was applied to the displacement fields prior to spatial differentiation to obtain strains) by linearly extrapolating to zero strain at the free edges, based on the shear strains within one pitch of the corrupted data. The corrected strain fields are then used for stiffness identification.

Effect of Grid Rotation

Unlike previous tests where the grid remained aligned throughout the entire test, the loading in this case introduces rotation. This grid rotation creates a bias due to the fact that the phase in the x and y directions are computed in the camera coordinates, which remains fixed while the grid rotates [45]. Badulescu et al. [45] demonstrated that local grid rotations of $1^{\circ}$ tend to be problematic for accurate strain measurements. In this test grid rotation occurs locally as a result of shear deformation, and also globally when rigid-body rotation of the sample occurs. Image deformation simulations are used here as a tool to investigate the temporal evolution of rotation over the field of view, and quantify this effect on the measurement of the kinematic fields and stiffness identification routines.

Displacement fields derived from the grid method were used to obtain a map of local grid rotation ($\omega _{xy}$ = $1/2(\partial u_{x}/\partial y - \partial u_{y}/\partial x)$). This is shown at three time steps in Fig. 11. The rotation map at $8\,{\upmu}{\text{s}}$ (Fig. 11a) demonstrates that, prior to the onset of rigid-body rotation grid rotation is contained to the region closest to where the loading is applied. As the test progresses rigid-body rotation increases gradually from the impact edge (Fig. 11b), and eventually over the entire field of view. At $t = 18\,{\upmu}{\text{s}}$ (Fig. 11c) the majority of the field has rotated by nearly $0.7^{\circ }$, and near the impact edge up to $1^{\circ }$. This level of rotation is significant enough to bias full-field maps, as shown in [45]. However, the effect on identification of the shear modulus from the measured fields is non-trivial and requires careful consideration due to the potential compounding effect on strain and acceleration, from which stress is derived.

Fig. 11

Comparison of grid rotation with acceleration and strain fields at three time steps: a–c rotation calculated from grid method, d–f differences between acceleration from synthetic images and simulation, and g–i difference between shear strain from synthetic images and simulation

In order to visually quantify the bias induced by grid rotation on the underlying kinematics the fields taken directly from FE have been compared to those obtained by grid image deformation. It should be noted that these images also encode the systematic errors arising from the camera temporal/spatial resolution. Acceleration and strain fields derived from grid method displacements are compared to the simulated fields which are interpolated to the camera coordinates in Fig. 11d–f and g–i, respectively. From Fig. 11d–i it is clear that there is minimal bias in the calculation of strain and acceleration prior to the onset of rigid-body rotation (${\text{t}} = 8\,{\upmu}{\text{s}}$). For a period of time after the onset of rotation at the impact edge the difference between the fields from simulation and synthetic grid images is contained where shear loading is highest (up to $t=13\,{\upmu}{\text{s}}$). However, as rigid-body rotation ramps up, large differences are observed in shear strain fields and acceleration fields near the top edge at $t = 18\,{\upmu}{\text{s}}$.

While it would appear that grid rotation does not become problematic until late in the test, reconstructed shear stress–strain curves at different cross-sections indicate that the effects are measurable early on and that the effect varies with position as shown in Fig. 12. For $y/H = 0.90$, the reconstructed behaviour first diverges from the simulated response at approximately 13 MPa, whereas at $y/H = 0.3$ this occurs almost immediately. It was found that the divergence of the stress–strain response roughly correlated with a width-averaged rotation of $0.10^{\circ }$. When width-averaged rotation reached this value, local grid rotations near the impact edge approached $0.7{-}1^\circ$, at which point the bias becomes measurable in stress strain curves. This agrees with the local grid rotation threshold of $1^\circ$ cited by [45]. A width-averaged rotation of $0.10^{\circ }$ was used to threshold the stress–strain data at each section in the sample to mitigate the effect of grid rotation on the stiffness identification. Width-averaged rotation is used rather than a local rotation threshold to reduce sensitivity to noise and for consistency in the way stress–strain curves are constructed using width-averaged strain and stress (derived from acceleration).

Fig. 12

Shear stress–strain curves from noise-free image deformation simulations showing the bias caused by grid rotation at three cross-sections along the height of the sample. Note how the bias is more pronounced further from the impact

The identification of the shear modulus along the height of the sample using a rotation threshold of $0.10^{\circ }$ is shown in Fig. 13. Also shown is the identification from the full stress–strain response at each section to illustrate the reduction in bias by implementing a rotation threshold. The small oscillations in the identifications have a spatial frequency equal to that of the grid pitch and are believed to be caused by artificial fringes in the strain maps arising from grid rotation as discussed in [45]. Even with the rotation threshold, it is very difficult to identify stiffness from areas near the top edge of the sample, but it is identified reliably over roughly half of the sample closest to the top of the waveguide. With no rotation threshold the reference modulus is never identified successfully. Since rigid-body rotation begins once the compressive wave reaches the free edge at x = 0 (Fig. 1), which travels faster than the shear wave, the stress–strain response near to the top edge has more significant bias from rigid-body rotation. The signal-to-noise ratio in this region is also poorer than near the bottom of the sample, and therefore, the measurements are more sensitive to grid rotation. To reduce the systematic error on the identified shear modulus the spatial average is based on data from the lower half of the region of interest ($y/H = 0.5{-}0.85$). When no correction is applied the shear modulus is identified as 4.39 GPa (10% error), whereas the rotation threshold over a limited field of view results in an identified shear modulus of 4.76 GPa and a systematic error of 2.9%.

Fig. 13

Spatial identification of the shear modulus from synthetic images with no noise and no smoothing using the full stress–strain response, and with a width-averaged rotation threshold of $0.10^{\circ }$

Grid rotation influences the identifications with the manual and special optimised virtual fields in a similar way as shown in Fig. 14. The two virtual fields are able to identify the reference modulus over a very limited window from $t = 3{-}7\,{\upmu}{\text{s}}$, but the identifications rapidly decrease between $t = 7{-}9\,\mu {\text{s}}$ as the rigid-body rotation of the gauge region begins. Following this, the identifications are more stable but slowly decrease as the test progresses ($t = 10{-}20\,{\upmu}{\text{s}}$). As will be shown later, the narrow range of time where the reference modulus can be approximately resolved ($t = 3{-}7\,\mu {\text{s}}$) is much less evident in identifications from experimental images contaminated with noise. Therefore, when selecting optimal smoothing parameters, as discussed in the following section, the results are based on the time frame of $t = 10{-}20\,\mu {\text{s}}$ where the identifications are more robust. For noise-free images, the manual and special optimised virtual fields identify the shear modulus to be 4.45 GPa and 4.52 GPa, representing a bias of 9% and 8%, respectively.

In the following section the effects of grey level noise, and spatial and temporal smoothing are added to the synthetic images to quantify their effect on the identification of the shear modulus with each of the VFM routines. This provides a robust way to select optimal spatial and temporal smoothing parameters, and obtain estimates of uncertainty associated with identifications from experimental images.

Fig. 14

Temporal identifications of the interlaminar shear modulus using the manual and special optimised virtual fields approaches for synthetic images with no grey level noise

Selection of Optimal Smoothing Parameters

The spatial smoothing windows considered here range from 0 to 69 pixels (standard deviation ranging from 0 to 17 pixels), and the temporal windows ranged from 0 to 21 frames. Note that spatial smoothing is applied to the displacement fields prior to spatially differentiating to calculate strain, and temporal smoothing is applied separately to the raw displacement fields prior to temporally differentiating to obtain acceleration. Also recall that the identifications from special optimised and manual virtual fields are based on the simulated fields between 10 and 20 $\mu {\text{s}}$, and identifications from stress–strain curves are based on the response where width-average rotation is less than $0.10^{\circ }$. Total error maps for each of the identification procedures as a function of spatial and temporal smoothing windows are presented in Fig. 15.

Fig. 15

Image deformation sweep for selection of optimal smoothing parameters for processing experimental images—total error maps for the various identification approaches: a stress–strain curves (SG), b manual virtual fields (VF Man.), and c optimised virtual fields (VF Opt.). Note that the colour scale is different for each plot

The smoothing parameter sweep shows that the total error for all identification methods has a much stronger sensitivity to spatial smoothing than to temporal smoothing. The sensitivity to acceleration noise (temporal smoothing) is mitigated when identifying $G_{13}$ from stress–strain curves since stress is calculated from a spatial average of acceleration over the surface, whereas strain is only averaged over a line (spatial smoothing). In the other identification routines, averaging identifications over multiple time steps similarly reduces the sensitivity to temporal smoothing. Typically, spatial smoothing would undercut the strain amplitude and cause the systematic error to rise. However, in this case, it acts as a compensation for the artificially higher shear strains caused by grid rotation. For the special optimised and manual virtual fields the closest compensation between the two competing factors is obtained for spatial smoothing windows of 21 and 25 pixels, respectively. For these identification routines, larger smoothing windows cause $e_{T}$ to rise quickly as the smoothing bias exceeds that due to grid rotation. This is also a consequence of an increase in the amount of data reconstructed along the vertical and top edges, and a reduction in measurement points used for the identification (recall one grid pitch plus one smoothing window is discarded along the bottom edge of the field of view).

The total error map for identifications from stress–strain curves has a different contour to the other routines as a result of a noise-induced bias. This is shown by comparing the systematic error maps with and without noise applied to the synthetic images (Fig. 16). For noise-free images with no smoothing applied (Fig. 16a) the systematic error deduced from Fig. 13 is recovered ($e_{S}$ = 2.9%). When 0.3% grey level noise is applied the systematic error rises drastically to 12.6%. The bias is amplified by the low signal-to-noise ratio associated with strains used in the identification under a grid rotation threshold. This is also a likely explanation for the greater sensitivity of total error to spatial smoothing compared to the other identification routines. As expected, the noise-induced bias is not as prominent for the special optimised and manual virtual fields since the identifications are based on strain fields measured later in the test (recall from Sect. 5.3, Fig. 13) where strains are larger in magnitude. Therefore, to reduce the noise-induced bias on identifications from stress–strain curves means relaxing the grid rotation threshold, which, in turn, causes the systematic error to rise (recall Fig. 13). In this study we opt to keep a tight threshold on grid rotation for stress–strain curve identifications at the expense of a lower signal-to-noise ratio rather than rely on smoothing to manage the complex, heterogeneous, artificial effects from grid rotation.

Fig. 16

Normalised systematic error maps for image deformation sweeps for identifications from stress–strain curves (SG) for: a no grey-level noise and, b 0.3% grey level noise added to the images. Note that the colour scale is different for each plot

To reduce computational expense, it is desired to perform the identifications on the same set of smoothed strain and acceleration fields (i.e., using a single set of smoothing parameters). Based on the presented parametric smoothing sweeps for the special optimised and manual virtual fields, where the identifications are more robust, we select a spatial smoothing window of 25 pixels and a temporal smoothing window of 5 frames. While these parameters do not represent the ideal set for identifications from stress–strain curves, Fig. 15a shows that large amounts of smoothing (window of 69 pixels) is required to minimise the total error to a comparable level ($e_{T}$ = 0.6%). For this level of smoothing approximately 40% of the field of view would be influenced by edge effects from the Gaussian filter. Therefore we opt to use the same smoothing parameters as the special optimised and manual virtual fields. This results in an increase in $e_{T}$ to 5.1%, but at the benefit of drastically reducing smoothing edge effects to approximately 15% of the field of view. For the selected smoothing parameters the estimated total error for identifications from special optimised virtual fields, manual virtual fields and stress–strain curves is 1.1%, 0.5% and 5.1% respectively. The typical measurement performance for experimental images processed with these smoothing parameters is listed in Table A2 in Supplementary Material.

Materials and Experimental Setup

Quasi-static Test Setup

The MTM45-1/AS4-145 material selected for this study has been extensively characterised in [39]. While the in-plane shear modulus is reported in [39] the interlaminar shear modulus is not. Therefore, to assess the strain rate sensitivity the quasi-static shear modulus was measured in-house using the quasi-static Iosipescu (or V-notch shear) test [46]. Five samples were cut from the 1-3 interlaminar plane using a diamond coated cutting wheel. The nominal dimensions were 76.2 mm $\times$ 18.3 mm (length $\times$ width) and the thickness of the samples ranged from 2.2 mm to 3.3 mm. The notches were waterjet cut according to the dimensions in Fig. 17.

Fig. 17

Schematic of Iosipescu specimens

All samples were instrumented on both sides with a Tokyo Measuring Instruments Lab (TML) FCA-1-23-120 0/90 strain rosette mounted at $45^{\circ }$ in the centre of the notched region. The position and orientation of the gauge was checked by analysing images of the gauge taken with a microscope to ensure tolerances were within that used in [47]. The gauges were oriented within $45^{\circ }\pm 0.6^{\circ }$, and within ± 0.3 mm from the centre in the horizontal and vertical directions. The quasi-static stiffness was measured by loading the samples in displacement control at a rate of 0.5 mm/min using the rig shown in Fig. 18.

Fig. 18

Rig (from [48]) used to perform Iosipescu shear tests with specimen installed

Specimens were susceptible to through-thickness strain heterogeneity as described in [49] since the loading was applied on the as-manufactured top and bottom surfaces of the laminate. Therefore, great care was taken when clamping the specimens in the fixture to mitigate this effect. Additionally, the specimens were loaded and unloaded several times to check the consistency of strain measurements. The specimen was taken out and re-installed when through-thickness effects were evident (opposite polarity of strain measurements on the front and back face upon loading). This was repeated to eliminate slack in the fixture. Back-to-back strain measurements were used to account for the through-thickness heterogeneity, with the modulus taken from average stress–strain curves. A correction factor of 0.923 was applied to the measured modulus values according to [47] to account for strain non-uniformity over the gauge section. Representative examples of average shear stress ($\overline{\sigma _{xy}} = F/A_{notch}$) plotted against engineering shear strain measured on each face and using back-to-back averaging are shown in Fig. 19a from [47].

Fig. 19

Results from Iosipescu shear tests for quasi-static characterisation of specimen #5: a stress–strain curves measured on front and back faces, and with back-to-back averaging, b evolution of tangent modulus with shear strain to determine shear modulus for the test. Note that a non-uniformity correction was applied to strains according to [47]

The strain threshold for identification of the shear modulus was determined by calculating the tangent modulus over a sliding strain window of $200\,{\upmu}{\text{m}}\,{\text{m}}^{-1}$. At the onset of non-linearity a notable decrease in tangent modulus was observed as shown in Fig. 19b. The shear modulus for the test was taken as the average value up to strains where the tangent modulus decreased by more than 5% (between 1 and $2\,{\upmu}{\text{m}}\,{\text{m}}^{-1}$ for specimen #5 in Fig. 19). Table 4 summarises the measured shear modulus from all samples.

Table 4 Interlaminar shear modulus for MTM45-1/AS4-145 under quasi-static loading (after applying 0.923 correction factor)

High Strain Rate Test Setup

All experiments were performed using the purpose-built gas gun and general experimental procedure described in [40]. The reservoir pressure was set for a nominal impact speed of $35\,{\text{m}}\,{\text{s}}^{-1}$. The waveguide support stand was aligned to within 0.20 mm and $0.20^{\circ }$ for position and angular alignments respectively, using the procedure outlined in [40]. Samples were cut as thin strips (nominally 2.5 mm in thickness), 57 mm in length from the 1–3 interlaminar plane of an 18 mm thick MTM45-1/AS4-145 laminate. Cuts were made with a Streurs E0D15 diamond saw with the automated stage set to a low feed rate of $0.1\,{\text{mm}}\,{\text{s}}^{-1}$ to reduce the likelihood of inducing machining defects. A thin coat of white paint (typ. $20\,{\upmu}{\text{m}}$ thick) was first applied to the samples followed by black grids deposited onto the painted surface using a Canon Océ Arizona 1260 XT flat bed printer. The grids had an average pitch spacing of 0.337 mm. More information of the grid printing process can be found in [40]. Samples were bonded to a 45 mm diameter aluminium 7075-T6 waveguide using cyanoacrylate glue with a set square used for alignment during bonding. The bottom edge of the sample was aligned with the bottom of the waveguide.

A Shimadzu HPV-X camera with a Sigma 105 mm lens was used to image the region on the sample which extended above the top of the waveguide at a frame rate of 5 MHz. Lighting was provided by a Bowens Gemini 1000Pro flash triggered using the light gates as described in [40]. The camera stand-off was adjusted iteratively using a series of static images such that the grid (pitch = 0.337 mm) was sampled by exactly 7 pixels/period. To minimise the fill-factor effect the images were intentionally blurred as in [26, 27, 40]. Blurring was considered sufficient when no significant fringe patterns were visible in the strain fields calculated using a static image of the grid in the reference position, and an image with the camera displaced 1 mm out-of-plane. The optical setup and a specimen mounted on the support stand in the capture chamber are shown in Fig. 20.

Fig. 20

Experimental setup used for all interlaminar tests: a camera and flash arrangement around the test chamber, and b mounted specimen supported on a test stand in the test chamber

Experimental Validation

Measured Kinematic Fields

This section presents full-field maps of acceleration (Fig. 21) and strain (Fig. 22) for a typical specimen at three time steps. The $\epsilon _{yy}$ fields are not included as the strains are below the noise floor due to the high lateral stiffness of the fibres. Raw images and maps of all displacement, strain and acceleration components are provided in the University of Southampton data repository associated with this article.

Fig. 21

Experimental acceleration fields ($a_{x}$, $a_{y}$) for specimen #1 measured at three time steps

Fig. 22

Experimental strain fields ($\epsilon _{xx}$, $\gamma _{xy}$) for specimen #1 measured at three time steps

Unlike the edge-on impact of a rectangular sample in [26], the pulse is not as distinguishable in the accelerations as the wave disperses into the part of the sample overhanging the waveguide. As the axial wave is applied to the material the shear loading is introduced beginning at the concentration at the top of the waveguide ($t = 8\,{\upmu}{\text{s}}$). As the axial pulse reflects from the free-edge, the shear loading begins to increase and the acceleration fields become highly heterogeneous ($t = 13\,{\upmu}{\text{s}}$). The shear pulse lags behind the axial pulse due to the lower shear wave speed, resulting in a gradual build up of shear strain. The axial pulse traverses the specimen width approximately twice prior to reaching maximum shear strain, which is shown in the fields at $16.4\,{\upmu}{\text{s}}$.

The rotation maps ($\omega _{xy}$) for specimen #1, based on un-smoothed displacements, are shown in Fig. 23 for the same three time steps. A qualitative comparison of the image deformation and the experimental maps shows that the simulations appear to be a good representation of the physical behaviour. At $8\,{\upmu}{\text{s}}$ (Fig. 23a) grid rotation is contained to the region closest to the loading before eventually increasing over the entire field of view (Fig. 23b, c). At $t = 18\,{\upmu}{\text{s}}$ (Fig. 23c) the rotation reaches over $1^{\circ }$ at the loading edge with similar magnitude and profile to that predicted by the simulation (Fig. 11c).

Fig. 23

Experimental rotation fields ($\omega _{xy}$) for specimen #1 measured at three time steps

The acceleration maps highlight the inertial effects present in the test, with values reaching almost $10^{7}\ {\text{m}}\,{\text{s}}^{-2}$. While such inertial effects would be problematic with existing test methods, the use of full-field measurements and the VFM allows one to identify the shear modulus directly from heterogeneous fields, as demonstrated in the following section.

Reconstructed Stress–Strain Curves

Shear stress–strain curves reconstructed using the stress-gauge equation (Eq. 4) and width-averaged shear strains ($\overline{\gamma _{xy}}^{x}$) are shown at four cross-sections for specimen #1 and #4 in Fig. 23. From impact speed of approximately $35\,{\text{m}}\,{\text{s}}^{-1}$ it was possible to consistently generate up to 60 MPa of width-average shear stress in the sample. The effect of grid rotation in the stress–strain response is most notable at $y/H = 0.72$ and 0.90, where the response artificially softens beyond $3-4\,{\text{mm}}\,{\text{m}}^{-1}$. While it is not possible to reliably characterise the full material behaviour (because of spurious effects from grid rotation), the measured stress–strain response does provide some indication that onset of non-linear material behaviour is delayed at high strain rates. For example, a linear behaviour is measured up to $4\,{\text{mm}}\,{\text{m}}^{-1}$ at y/H = 0.90 for specimen #1 (Fig. 24d), whereas non-linearity was measured in the quasi-static tests beyond $2\,{\text{mm}}\,{\text{m}}^{-1}$ (Fig. 19). Using a grid rotation threshold described in Sect. 5.2, it is possible to characterise the initial linear elastic behaviour of the material from the stress–strain curves as described in the following section. Identification of the shear modulus with the manual and special optimised virtual fields are also presented.

Fig. 24

Stress–strain curves for specimen #1 (a–d) and #4 (e–h) reconstructed from measured strain and acceleration fields at different positions along the length of the sample

Stiffness Identification

The shear modulus is identified from the stress–strain response measured at each cross-section using the slope of a linear regression fit for data within the $0.10^{\circ }$ width-averaged grid rotation threshold. The spatial distribution of the shear modulus along the length of each sample is shown in Fig. 25a. Note that data is excluded within one spatial smoothing kernel at the free edge and impact edge. The identification monotonically increases towards y/H = 1, as shown by the image deformation simulations in Fig. 13. As previously discussed, the value for each test was taken as the average value over y/H = 0.50–0.85 to mitigate the bias from grid rotation. All identifications listed in Table 5 were corrected using the estimated systematic error ($e_{s}$) of 4.3% from the image deformation simulations (Fig. 16b) for the smoothing parameters listed in Table A2 in Supplementary Material. The spatial identification of the shear modulus is remarkably consistent across all five samples with an average value of 5.69 GPa and a coefficient of variation (COV) = 3.7%. This is a dramatic improvement compared to reported measurements in the literature at similar strain rates. For example, in [5, 11, 12] the range of values reported varied by up to 10–30% relative to the mean shear modulus over all tests.

The shear modulus was also identified from the manual and special optimised virtual fields. The temporal identifications from each of these approaches are shown in Fig. 25b, c. Note that both methods were used to identify the shear modulus using spatial smoothing of 25 pixels and temporal smoothing of 5 frames and that data at the start of the test is excluded where the signal-to-noise ratio is low. Moreover, the shear modulus value for each test was taken as the average temporal identification over $t = 14{-}20\,{\upmu}{\text{s}}$ where the identification was most stable. Similar to the stress–strain curves identifications, the temporal evolution of the shear modulus with each set of virtual fields are very consistent. Over all samples an average shear modulus of 5.82 GPa (COV = 3.1%) and 5.51 GPa (COV = 2.9%) was identified from the manual and special optimised virtual fields, respectively. Interestingly, there appears to be an offset between the identifications that was not observed using image deformation. Adjusting these values using $e_{S}$ from image deformation simulations results in average identifications of 5.85 GPa and 5.67 GPa, respectively, which agree well with the corrected identification from stress–strain curves. A summary of the measured shear modulus on all six samples corrected for the systematic bias predicted from image deformation is provided in Table 5.

The shear strain–strain rate space populated by the test is shown in Fig. 26 between $t = 10{-}25\,{\upmu}{\text{s}}$ when the signal is highest. This test specimen primarily populates strain up to $5\,{\text{mm}}\,{\text{m}}^{-1}$ and strain rates up to 1500 s$^{-1}$; however strains up to $12\,{\text{mm}}\,{\text{m}}^{-1}$ and strain rates up to $3500\,{\text{s}}^{-1}$ are measured. The range of strain rates seen by the material makes it challenging to assign a single strain rate value to the measurements of shear modulus presented here. Therefore, two metrics are provided as effective strain rates for the measurements: (1) a shear-strain weighted strain rate ($|\overline{\dot{\gamma _{xy}}}^{W}|$, Eq. (9)) and and (2) the peak width-averaged shear strain rate ($\hat{\overline{\dot{\gamma _{xy}}}^{x}}$). The weighted average is believed to be a more representative measure of the effective strain rate since more emphasis is given to the areas with higher strain magnitude, which contribute most to the identification of the shear modulus. Both strain rate values reported in Table 5 represent the maximum of each metric over $t\le 20\,{\upmu}{\text{s}}$ (threshold for manual and optimised virtual fields identifications), excluding data from within one smoothing kernel of the edges of the field of view.

$$\begin{aligned} \overline{\dot{\gamma _{xy}}(t)}^{W}= \frac{\sum ^{S}\gamma _{xy}(t)\cdot \dot{\gamma _{xy}(t)}}{\sum ^{S} \gamma _{xy}(t)} \end{aligned}$$

(9)

Fig. 25

Identification of the interlaminar shear modulus, $G_{13}$: a fitting stress–strain curves using a width-average rotation threshold of 0.$10^\circ$, b manual virtual fields (Eq. 6), and b special optimised virtual fields (Eq. 8)

Fig. 26

Histogram of shear strain-strain rate space populated by specimen #1, excluding one smoothing kernel plus one pitch from the edges, between $t = 10{-}25\,{\upmu}{\text{s}}$ where the signal is highest. The colour map denotes number of occurrences. Note that strain rate on average over the field reaches $1000\,{\text{s}}^{-1}$ and locally up to $3500\,{\text{s}}^{-1}$

Table 5 High-strain-rate interlaminar shear modulus for MTM45-1/AS4-145

Since the spatial and temporal smoothing parameters were selected to minimise the error on the special optimised and manual virtual fields identification, these values are used to comment on the effect of strain rate on the shear modulus. The measured averaged stiffness ranged between 5.67 and 5.85 GPa at an average strain rate on the order of 1600 s$^{-1}$. This represents a 16–19% increase compared to the quasi-static modulus of 4.9 GPa (see Table 4). While care must be taken in data processing to mitigate the effects of grid rotation, these experiments demonstrate the potential of the IBII test principle for high-strain-rate interlaminar shear testing. Here we leverage the heterogeneity in the response caused by inertial effects and can measure the shear modulus with impressive consistency at strain rates that would otherwise be problematic for existing test methods [8]. The measured strain rate sensitivity is difficult to compare with the literature as, to the authors’ knowledge, no interlaminar high-strain-rate data are available for AS4-145/MTM45-1. Moreover, the limited studies in the literature using the SHPB can only report an ‘apparent modulus’ since it is necessary to assume the loading is pure shear. The strain rate sensitivity measured here does fall within the range reported for unidirectional composites for in-plane [9] and interlaminar planes [8, 9]. However, the data is highly scattered in these studies (sensitivity between − 14% and + 33%) and does not offer a meaningful comparison. The measured values of $G_{13}$ from the three VFM approaches fall within 5% of each other. This comparison can be considered as a type of self-validation of the measurements reported here. However, results from previous longitudinal IBII tests [36], presented in the next section, provide an extra validation of the shear moduli.

Alternative Test Configuration for Shear Modulus Identification

It was recently observed that the interlaminar shear modulus can also be identified from the standard edge-on impact configuration [26, 36] when there is slight pitch misalignment between the projectile and waveguide (angle $\alpha$ in Fig. 27). Previously the intention was to mitigate the misalignment of the impactor with the waveguide as much as possible. However, due to inherent variability in positioning the waveguide on the support stand, some pitch misalignment remained for some samples. Although unintentional, this misalignment is advantageous as the shear behaviour of the material was sufficiently activated to enable the interlaminar shear modulus to be identified. Note that for the purposes of an initial proof-of-concept, the smoothing parameters were not changed from those selected based on optimal identification of the interlaminar Young’s modulus [26], at least, optimal in the sense of minimal total error. In the future a full parametric sweep could be performed, although previous experience suggests that identifications of stiffness parameters are not overly sensitive to smoothing so long as sensible parameters are selected [25, 26].

Examples of the measured shear strain fields at three time steps for specimen R6 from [36] are shown in Fig. 28. To mitigate the effect on the identification caused by smoothing edge effects, the strains within one pitch plus one smoothing kernel of the top and bottom edges have been replaced using the approach described in Sect. 5.2.

Fig. 27

Adapted from [36]

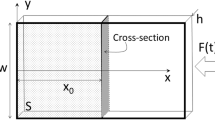
Schematic of standard IBII test configuration used previously to measure the interlaminar Young’s modulus and tensile failure stress. When the projectile and waveguide have a slight relative pitch misalignment (about the z axis) an in-plane shear wave is generated in the sample which can be used to identify $G_{13}$.

Fig. 28

Shear strain fields for specimen R6 from [36] measured at three time steps

Similar to the derivation of Eq. (4), we use a rigid-body virtual field in the y direction ($u_{x}^{*}$ = 0, $u_{y}^{*}$ = 1) to reconstruct the average shear stress along any vertical cross-section (at $x_{o}$) from the $a_{y}$ fields as follows:

$$\begin{aligned} \overline{\sigma _{xy}}^{y} = \rho x_{o}\overline{a_{y}}^{S} \end{aligned}$$

(10)

Combining the average shear stress with width-averaged shear strain ($\overline{\gamma _{xy}}^{y}$) provides direct access to the shear stress–strain response at any cross-section on the sample. Examples of reconstructed stress–strain curves at four locations along the length of specimen R6 from [36] are shown in Fig. 29. Using a linear regression to the stress–strain response provides a spatial identification of the shear modulus along the length of the sample (excluding regions at the impact and free edge where smoothing edge effects are present) as shown in Fig. 30. Note that four of the eight samples tested in [36] are not shown since, in those cases, the misalignment was negligible (as intended) and insufficient shear was generated to reliably identify the stress–strain behaviour. Even in the cases where some misalignment was present, the shear activation was low (e.g., $< 5\,{\text{mm}}\,{\text{m}}^{-1}$ as shown in Fig. 29). This explains the higher noise in reconstructed shear stress–strain curves and the spatial identification of $G_{13}$ in Fig. 30. In the future, intentional misalignment could be leveraged to activate the response more.

Fig. 29

Stress–strain curves for specimen R6 from [36] reconstructed from measured strain and acceleration fields (Eq. 10) at different positions along the length of the sample

Fig. 30

Identification of the interlaminar shear modulus, $G_{13}$ from interlaminar tension/compression specimens [36] using a linear regression fitting to the stress–strain curves

Taking the average of identifications from cross-sections over the middle 50% of the sample provides a single value for the shear modulus, which is listed in Table 6 along with the strain-weighted strain rate defined in Eq. (9). The average identified value of 5.6 GPa is in good agreement with the values measured from the IBII shear test, serving as a validation for the measurements presented in Table 5. This simple test geometry enables both interlaminar shear and Young’s moduli to be identified simultaneously and demonstrates the potential of the IBII test methodology to reduce the number of tests required for full characterisation of a fibre-reinforced polymer composites at high strain rates.

Table 6 High-strain-rate interlaminar shear modulus for MTM45-1/AS4-145

Limitations of the IBII Interlaminar Shear Test and Future Work

The results from this study demonstrate the potential of the IBII test for interlaminar shear characterisation at strain rates on the order of 1600 s$^{-1}$ where existing test methods are unreliable due to inertial effects. Two different test configurations were considered: (i) a new test configuration where a portion of the sample is overhanging the waveguide, and (ii) the standard, edge-on test configuration from [26, 36] where pitch misalignment between the projectile and waveguide created a in-plane shear wave. This work has identified some important limitations of the overhanging shear test configuration, which are described first. Following this, there is a discussion on prospective ideas for developing the IBII tests for improved activation of multiple stiffness components and more comprehensive material characterisation.

Grid Rotation

Grid rotation in the current configuration created increasing artificial shear strains as the test progressed and introduced a bias in the identification of the shear modulus with all virtual fields approaches. For small strains and linear material characterisation the bias was successfully mitigated through compensation with spatial smoothing and grid rotation thresholds, however, reducing these effects will be critical for efforts to characterise the non-linear behaviour at high strain rates. One potential approach is to intentionally misalign the grid as was done by Sur et al. [50], or use a Gaussian window, rather than a bi-triangular window in the grid method. While these options may extend the upper limit of strain that can be reliably measured with this configuration, it is unlikely to eliminate the problem and alternative test configurations need to considered. For example, it may be possible to modify the specimen geometry or waveguide to introduce sufficient shear in a more symmetric way to reduce rotation of the grid.

In this work, and previous studies using the IBII test [25, 26], the grid method was chosen over digital image correlation (DIC) due to the better trade-off between spatial and measurement resolution. However, DIC suffers less from in-plane rotation and in this case, it may be worth-while to sacrifice spatial resolution in order to reliably measure the non-linear behaviour of the material. Image deformation would serve as a useful tool for evaluating this trade-off as well as the effect of other image correlation parameters (e.g., subset size, step, shape function, interpolation, matching criterion and image pre-smoothing) similar to the model presented in [51]. This is especially relevant for the development of future tests where stress concentrations may be used to activate more deformation heterogeneity and spatial resolution becomes more critical.

Identification of Multiple Interlaminar Stiffness Parameters from a Single Test

The main objective going forward is to design tests that provide the high-strain-rate interlaminar elastic and shear moduli from a single test. The first potential configuration is the interlaminar IBII tensile sample [26] that is intentionally impacted with the impactor misaligned on the pitch axis. Section 8 showed that slight, unintentional misalignment of the impactor was enough to create a shear wave and identify the shear modulus (albeit with only small peak shear strains). In the future, a deliberate misalignment could be implemented for stronger activation of the shear behaviour and potentially more stable identification of the shear modulus. It may also be possible to use the same sample [26] but impacted over half of the height to introduce combined axial and shear loading. The VFM (including stress-gauge based stress–strain curves) can then be used to identify the activated stiffness parameters from the heterogeneous deformation fields as in [24]. This concept may also be combined with notches, holes, etc. to enhance the activation of multiple stiffness parameters.

Characterising Non-linear Material Behaviour

An additional objective would be to characterise the non-linearity in shear at high strain rates. By assuming a model for the non-linear material behaviour, it should be possible to identify the parameters of the model using the VFM as in [52] for instance. This idea was suggested in [23, 53] and other works have also explored the application of the VFM for rate sensitivity of plasticity in [54, 55]. Image deformation will be instrumental in selecting new test configurations which sufficiently activate the non-linear response for reliable identification with the VFM, and quantifying errors introduced by the camera and full-field measurement technique.

Characterising a Strain Rate Sensitivity Law from a Single Test

The loading introduced with the proposed configuration was found to populate a vast range of strains and strain rates (strains up to $12\,{\text{mm}}\,{\text{m}}^{-1}$, strain rates up to $3500\,{\text{s}}^{-1}$), Fig. 26. For materials that exhibit a stronger strain rate sensitivity (e.g., composite systems with a thermoplastic matrix) the wealth of combinations of strain and strain rate seen by the material may provide opportunity to identify a strain rate sensitivity law over a few decades of strain rates from a single test. One approach is to formulate the unknown stiffness parameters as a function of strain rate in the optimised virtual fields routine, or with the recently developed sensitivity based virtual fields [56, 57]. The potential of this approach can be explored using finite element modelling with a prescribed strain rate dependent material model, combined with synthetic image deformation routines to validate the identification of the model coefficients with the VFM.

Extension to Failure Stress Measurements

It would also be of interest to pursue test configurations for failure stress measurement under predominant shear states of stress for the purpose of populating failure envelopes. Since pure shear is very difficult to achieve, it may be reasonable to design tests which provide fracture under combined compression/shear, and tension/shear to infer the shear strength of the material after fitting a failure model. With full-field measurements and the VFM it should be possible to quantify the combined stress at failure rather than assuming pure shear stress as is required with existing test methods. This may require more advanced stress reconstructions such as the numerical approach proposed in Seghir et al. [58] who showed that under certain conditions, it may be possible to reconstruct quasi ‘full-field’ stress maps from acceleration fields, though this has yet to be implemented on experimental data.

Conclusions

This work has presented the design and experimental validation of a new IBII test to measure the interlaminar shear modulus at strain rates on the order of 1600 s$^{-1}$. This represents an important first step in establishing a new set of IBII tests aimed at interlaminar stiffness identification at high strain rates. The key results from this study are summarised below:

• A simple short-beam shear configuration was used to activate the interlaminar shear behaviour and measure the shear modulus at high strain rates.

• Explicit dynamic simulations were used to perform a design study to identify the optimal test configuration based on available waveguide and projectiles.

• Pulse duration was found to have a large influence on the amount of shear introduced into the sample. A longer pulse delayed the onset of tensile axial loading, allowing more shear to build up in the sample.

• A new set of special optimised virtual fields was developed and successfully validated for the direct identification of the interlaminar shear modulus.

• An image deformation framework was presented to quantify the effects of grid rotation, spatial resolution and smoothing on the identification of the shear modulus using three different virtual fields method routines.

• The proposed test configuration was experimentally validated. An average shear modulus of 5.5–5.8 GPa (COV = 2.9–3.7%) across all three identification routines was measured at strain rates on the order of 1600 s$^{-1}$, which represents an increase of 12% compared to the quasi-static modulus.

• The interlaminar shear modulus was also identified from standard IBII interlaminar tension/compression samples tested previously from a shear wave generated by slight pitch misalignment of the impactor. The average shear modulus of 5.6 GPa (COV = 5.3%) identified from reconstructed stress–strain curves validates the measured values from the presented IBII shear test. This highlights the versatility of the IBII test principle whereby full-field measurements and the VFM enable simultaneous identification of the interlaminar shear and Young’s moduli from a simple test configuration.