Image-Based Inertial Impact Test for Composite Interlaminar Tensile Properties

Abstract

In this work an image-based inertial impact test is proposed to measure the interlaminar tensile stiffness and strength of fibre-reinforced polymer composite materials at high strain rates. The principle is to combine ultra-high-speed imaging and full-field measurements to capture the dynamic kinematic fields and exploit the inertial effects generated under high strain rate loading. The kinematic fields are processed using the virtual fields method to reconstruct stress averages from maps of acceleration. In this way, the specimen acts like a dynamic load cell, with no gripping or external force measurement required. Stress averages are combined with strain measurements to construct stress–strain curves and identify the interlaminar stiffness and tensile strength. Special optimised virtual fields are also implemented to identify interlaminar stiffness parameters from complete maps of strain and acceleration. Interlaminar stiffness and tensile strength are successfully identified at average, peak strain rates on the order 3500 s$^{-1}$ and 5000 s$^{-1}$, respectively. Results show an increase in stiffness between 30 and 35%, and an increase in strength of 125% compared to quasi-static values.

Introduction

There are many engineering applications where fibre-reinforced polymer (FRP) composite structures are subjected to dynamic loading (e.g., impact, blast, crash, etc.). In order to develop useful numerical simulations for composite structures subjected to these loading cases, a thorough understanding of the constitutive behaviour over a wide range of strain rates must first be established. Since interlaminar properties are matrix-dominated, literature suggests that the interlaminar stiffness and strength should exhibit a strain rate dependency [1, 2]. However, the number of studies attempting to measure high strain rate properties in the interlaminar direction are relatively scarce and inconsistent [2].

Studies on the strain rate dependency of interlaminar tensile properties are comparatively fewer compared to compression and shear. The effect of strain rate is not well understood, as exemplified by highly scattered measurements in available studies [2]. For example, measured changes in stiffness for glass/epoxy woven composites range from + 10% at 125 s$^{-1}$ [3], to + 500% at 400 s$^{-1}$ [4], and − 15% at 950 s$^{-1}$ [5], compared to quasi-static values. A similar situation exists for tensile strength measurements at high strain rates. Most studies report moderate increases in strength of around 30% compared to quasi-static values [3, 5], while others report much more significant increases of up to several hundred percent [6,7,8]. Therefore, much ambiguity remains regarding the effect of strain rate on interlaminar stiffness and tensile strength. Some of the inconsistency in the literature stems from variations in material composition (fibre and matrix materials, fibre volume fraction, reinforcement architecture). Additionally, scatter is likely amplified by other factors complicating tensile tests, such as gripping, alignment and geometry (stress concentrations).

Limitations of the Split-Hopkinson pressure bar (SHPB) technique are thought to be the primary source of inconsistency in measurements above 200–300 s$^{-1}$. At such strain rates, inertial effects violate the necessary assumption that the specimen is in a state of quasi-static equilibrium. As a result, measurements of strain on the input and output bars cannot be used to directly infer the stress–state in the material until specimen acceleration dampens out. The low wave speed and small ultimate strain typical of composite materials in the through-thickness direction means that a state of quasi-static equilibrium may not be achieved before failure occurs. The lower wave speed also tends to reduce the signal-to-noise ratio of the material response transmitted to the output bar [1, 9]. Even if inertial effects dampen out prior to failure, it is generally agreed that the SHPB cannot produce reliable measures of the material stiffness [10,11,12,13].

More recently, full-field measurement techniques, combined with ultra-high-speed imaging, have shown to be a promising alternative for high strain rate testing. Ultra-high-speed imaging refers to framing rates upwards of 1 Mfps, according to [14]. Having access to dynamic full-field measurements of displacement alleviates some of the fundamental assumptions attached to test methods such as the SHPB. Specifically, the Virtual Fields Method (VFM) can be used to process dynamic maps of acceleration to exploit the inertial, heterogeneous deformation and reconstruct stress-averages in the material. Moulart et al. [15] showed that acceleration could be used in practice to identify stiffness parameters at high strain rates. The ‘Image-Based Inertial Impact’ (IBII) test first emerged from the study by Pierron and Forquin [16], and was later formalised in [17]. The concept of using acceleration to reconstruct stress-averages and identify constitutive material properties has since been successfully demonstrated in a number of experimental studies [16,17,18,19,20,21,22,23,24,25].

This work presents an extension of the IBII test method to measure the interlaminar stiffness and tensile strength of a unidirectional, carbon/epoxy composite. Both interlaminar material planes are considered (1–3 and 2–3). The IBII test is advantageous as it eliminates the need to grip the specimen or measure force externally; both of which are particularly problematic for testing interlaminar specimens in tension. This paper will begin by describing the test concept and design approach in Sect. 2. A parametric finite element model is used to design the experimental parameters (e.g., projectile length and impact velocity) in Sect. 3. In Sect. 4 the displacement fields from the finite element model are used to synthetically deform images. These images are used to systematically optimise the post-processing parameters and estimate the error on identified stiffness parameters. A description of the experimental setup is presented in Sect. 5. Experimental results are presented and discussed in Sect. 6. Finally, the limitations of the proposed test, and future developments for the work are discussed in Sect. 7.

Image-Based Inertial Impact (IBII) Test Concept and Design

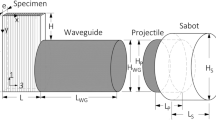
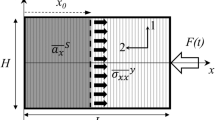
In the IBII test, the specimen is loaded dynamically by impacting one side of the specimen (represented by F(t) in Fig. 1a). The impact induces a compressive wave, which travels through the specimen towards the free edge. When the wave reaches the free edge, it reflects back towards the impact edge as a tensile pulse. The idea is to tailor the experimental parameters to ensure that the reflected tensile pulse is sufficient to cause specimen failure. Ultra-high-speed imaging is combined with the grid method to capture dynamic full-field displacements. The underlying constitutive properties are encoded in these maps, and are extracted using the VFM. The initial compressive loading is used to identify the elastic modulus, and the ‘linear stress-gauge’ equation [20] is used to estimate the tensile strength of the specimen.

Fig. 1

a Schematic of an impacted interlaminar specimen. Fibres are either, b parallel to the y axis (1–3 interlaminar plane) or c parallel to the z axis (2–3 interlaminar plane)

The Virtual Fields Method (VFM)

The VFM is used to directly identify constitutive properties from full-field measurements of strain and acceleration. The specific application of the VFM to the IBII test is outlined in [20] and therefore, only the specific aspects that apply to the interlaminar test are included here. The reader is referred to [26] for a comprehensive description of the VFM.

The principle of virtual work is satisfied by any virtual displacement fields that are continuous and piecewise differentiable. In this work, the following additional assumptions are made: (1) constant density, thickness and stiffness in space; (2) kinematic fields are uniform in the thickness dimension of the sample; and (3) the specimen can be considered to be in a state of plane stress. Under these conditions, the principle of virtual work takes the following form:

$$\begin{aligned} -\int _S {\varvec{\sigma}}:{\varvec{\epsilon ^{*}}} dS + \int _{\delta l} \overline{\varvec{T}}\cdot {\varvec{u^{*}}}dl = \rho \int _S {\varvec{a}}\cdot {\varvec{u^{*}}} dS \end{aligned}$$

(1)

where S denotes the surface of the region of interest, $\overline{\varvec{T}}$ is the Cauchy stress vector, which is applied to the in-plane boundaries denoted by l, ${\varvec{u^{*}}}$ is the virtual displacement field, ${\varvec{\epsilon^{*}}}$ the virtual strain field and ${\varvec{\sigma}}$ the Cauchy stress tensor. Note that $:$ and $\cdot$ denote the dot product in matrix and vector forms, respectively. The left hand side of Eq. (1) represent the internal and external virtual work, respectively. The term on the right hand side of the equation represents the virtual work of inertial forces. In order to use Eq. (1), it is necessary to define a constitutive model. Here, a linear elastic, orthotropic constitutive model is used. The material response in the 1–3 plane is very similar to the interlaminar response considered in [20]. For that case, using a uniaxial virtual strain field, and neglecting transverse strains from the very small Poisson effect, the VFM equation is reduced to:

$$\begin{aligned} -E_{33}\int _S \epsilon _{xx}^{*}\epsilon _{xx} dS + \int _{\delta l} T_{x} u_{x}^{*}dl = \rho \int _S a_{x} u_{x}^{*} dS \end{aligned}$$

(2)

In the case of the 2–3 interlaminar plane, an isotropic constitutive model is more appropriate, where $Q_{33}$ and $Q_{23}$ are directly identified. Therefore, Eq. (1) becomes:

$$\begin{aligned}&- Q_{33}\int _S (\epsilon _{xx}\epsilon ^{*}_{xx} + \epsilon _{yy}\epsilon ^{*}_{yy} +\frac{1}{2} \epsilon _{xy}\epsilon ^{*}_{xy}) dS \nonumber \\&-Q_{23}\int _S (\epsilon _{xx}\epsilon ^{*}_{yy} + \epsilon _{yy}\epsilon ^{*}_{xx} -\frac{1}{2} \epsilon _{xy}\epsilon ^{*}_{xy}) dS \nonumber \\&+\int _{\delta l} (T_{x}u^{*}_{x} + T_{y}u^{*}_{y}) dS = \rho \int _S (a_{x}u^{*}_{x} + a_{y}u^{*}_{y}) dS \end{aligned}$$

(3)

In both cases, virtual displacements at the impact edge are set to zero to exclude the virtual work of the unknown stress distribution along the boundary.

Stiffness Identification

Special Optimised Virtual Fields An infinite number of virtual kinematic fields can be selected to use Eqs. (2) and (3). If strain and acceleration fields are exact, all virtual fields will provide the same identification. In practice, measurements inevitably contain noise and therefore, each set of virtual fields will provide different identifications. If one selects the virtual fields intuitively, it is impossible to ensure that the chosen ones are optimal. Special optimised virtual fields are adopted here, as developed in [27]. This procedure automates the selection of virtual fields for direct identification of stiffness parameters, such that the sensitivity to strain noise is minimised. For the 1–3 plane, the uniaxial virtual displacement field results in the direct identification of $E_{33}$. For the 2–3 plane, the isotropic, special optimised virtual field procedure is used to directly identify $Q_{33}$ and $Q_{23}$ [17]. From the identified stiffness parameters, one can calculate $\nu _{23}$ ($\nu _{23} = Q_{23}/Q_{33}$) and $E_{33}$ ($E_{33} = Q_{33}(1-\nu _{23}^{2})$). This is performed at each time step over the whole field. Full details on the implementation of special optimised virtual fields are described in [26].

Stress-Gauge Equation Following from Fletcher et al. [20], the ‘stress-gauge’ (SG) equation is derived using the following rigid-body virtual field: $u_{x}^{*}=1$, $u_{y}^{*}=0$. Approximating integrals with discrete sums, one obtains a direct relationship between acceleration and average stress:

$$\begin{aligned} \overline{\sigma _{xx}}^{y} = \rho x_{o}\overline{a_{x}}^{S} \end{aligned}$$

(4)

where superscript y coupled with an overline denotes the width average at $x_{o}$, and superscript S coupled with an overline denotes the surface average between the free edge and $x_{o}$ (see Fig. 1a). The stress-gauge equation is used to plot $\overline{\sigma _{xx}}^{y}$ as a function of the average axial strain at each cross-section. This is used to verify the linearity of the response and spatial uniformity of the stiffness. The slope of the line provides a measure for $E_{33}$ (1–3 plane) or $Q_{33}$ (2–3 plane). For 2–3 plane specimens, $E_{33}$ is calculated using $\nu _{23}$ from the special optimised identification routine.

Strength Identification

By considering additional rigid body virtual fields ($u^{*}_{x}=0, u^{*}_{y} = 1; u^{*}_{x} = y$, $u^{*}_{y} = - x$), a linear approximation of the stress distribution may be reconstructed across the width of the specimen. This is referred to as the ‘linear stress-gauge’ (LSG) equation (Eq. 5),

$$\begin{aligned} \sigma _{xx}(LSG) = \rho x_{o}\overline{a_{x}}^{S} + \frac{12\rho x_o y}{H^2}(\overline{a_{x} y}^{S} - \overline{a_{y} x}^{S} + x_{o}\overline{a_{y}}^{S}) \end{aligned}$$

(5)

where H denotes the total specimen width (Fig. 1a). The full derivation of Eq. (5) is detailed in [20]. It is important to highlight that the stress-gauge equations are valid regardless of the constitutive behaviour. However, the linear stress-gauge equation only provides the first moment of stress, and does not fully resolve $\sigma _{xx}$ across the width of the specimen. This means that the stress-gauge only provides an estimate of the stress at the crack location. In this work, the linear stress-gauge equation is used for estimating interlaminar tensile strength because it accounts for possible asymmetry in the stress field (two-dimensional wave propagation).

An additional, post-hoc way to reconstruct stress is to use the identified stiffness parameters to convert strain maps to stress maps. Divergence of the different stress measures (from acceleration and from strain) provides information about the damage process, indicating when the assumptions of the constitutive law break down (i.e., plasticity, damage, failure, etc.). This can also be used to validate the constant and linear approximations for the stress field as reconstructed with the stress-gauge equations.

Numerical Design and Optimisation

The following section describes the implementation of the numerical simulations and parametric design sweeps to select test parameters.

Model Configuration and Parametric Design Sweep

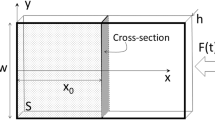
The IBII test configuration for a generic interlaminar specimen is shown in Fig. 2. Fibres are either parallel to the y-axis (1–3 plane), or parallel to the z-axis (2–3 plane), as shown in Fig. 1b and c, respectively. It is desirable to tailor the experimental parameters such that the reflected tensile stress is sufficiently high to cause failure. It is also desirable to maximise the ratio of reflected tensile stress to input compressive stress. This reduces the risk of damage during compressive loading. Numerical simulations are used to establish a design envelope such that both requirements are satisfied.

Fig. 2

Schematic of the IBII test configuration for interlaminar specimens

There are some important differences between the test design for interlaminar and in-plane properties. For direct imaging of the specimen, the geometry of an interlaminar test specimen is dependent on the thickness of the laminate. In this work, a thicker laminate (18 mm) is considered for practical reasons. Specifically, this enables plate-like specimen to be machined and accurate grids to be deposited for full-field measurement purposes. To maximise measurement spatial resolution, a smaller grid pitch is required (on the order of 0.3 mm compared to 0.9 mm in [20]). With a smaller length compared to the transverse tension specimens, the wave transit time is also shortened. This requires a higher framing rate to ensure sufficient temporal resolution of the kinematic fields (the Shimadzu HPV-X camera allows for frame rates up to 5 Mfps at full resolution).

Separate design sweeps were performed for each interlaminar plane. The length of specimens from both material planes was fixed at the nominal plate thickness of 18 mm. A height of 12 mm was selected to maximise the spatial resolution of the camera (Shimadzu HPV-X, 400 $\times$ 250 pixels), including approximately 2 mm at the free edge of the specimen to account for rigid body motion. The material used in this study is a unidirectional carbon/epoxy composite, AS4-145/MTM45-1. The properties of this material were characterised by the National Center for Advanced Material Performance (NCAMP) as summarised in [28]. Unfortunately, only quasi-static interlaminar tensile strength was measured in that campaign ($\sigma _{T}^{ult}$ = 50.4 MPa). Therefore, for test design it was assumed that reported values for the in-plane transverse Young’s modulus, shear modulus, and Poisson’s ratio were representative of that for the interlaminar planes. The quasi-static, in-plane transverse compressive strength ($\sigma _{C}^{ult} \approx$ 290 MPa) was assumed as a conservative limit for allowable compressive stress. To the authors’ knowledge, the high strain rate properties for this material have not been measured. Therefore, it was also assumed that the material strength will exhibit a similar strain rate sensitivity to that reported in [20] measured using the same IBII test (+ 57% increase in strength at strain rates on the order of 2000 s$^{-1}$). Even though reference [20] focussed on the in-plane transverse properties, the reported strain rate sensitivity was expected to be reasonably representative of the interlaminar behaviour as a matrix dominated property. Therefore, the interlaminar tensile strength at high strain rates is estimated to be 80 MPa. For the IBII interlaminar test the design space is defined by the tensile and compressive strengths as: − 290 MPa $< \overline{\sigma _{xx}}^{y}<$ 80 MPa.

The design sweep in [20] showed that the experimental parameters that primarily influence the stress state in the material are projectile length and impact velocity. Therefore, these are the only parameters considered in the design sweep of the IBII test here. In the design sweep the height of the waveguide, $H_{WG}$, and projectile, $H_P$, were fixed at 25 mm. Having a larger projectile and waveguide improves contact alignment and stability of the sample on the test stand. This also prevents the sabot from striking the alignment stand. A separate simulation study showed that the impactor height has little influence on the test provided that it does not exceed three times the specimen width. The height of the sabot is also fixed at the barrel diameter of the purpose-built gas gun (50 mm). The projectile length and projectile speed were selected using a parametric design sweep. The range of simulated values for these variables are listed in Table 1.

Table 1 Summary of simulated values used in parametric sweep for test design

The sabot length was variable such that the total length of projectile-sabot assembly was a constant 50 mm. A maximum projectile length of 20 mm was set to avoid creating an input pulse length that exceeds the specimen length. This would result in a superposition of the input and reflected waves, reducing the maximum tensile stress in the specimen. Since the waveguide and projectile are made of the same material, the waveguide length must be at least twice the length of the projectile to avoid clipping the pulse. Therefore, the waveguide length, $L_{WG}$, is fixed at 50 mm.

Finite Element Implementation

All simulations were performed in ABAQUS/Explicit. Plane stress CPS4R elements (2D, 4 node, reduced integration) were used in all simulations. The mesh size, and stiffness-proportional damping coefficient, $\beta$, were first selected using a separate parametric sweep. Some numerical damping is required to control the artificial high frequency oscillations that occur in the explicit dynamic simulations. The criterion for selection was minimisation of the error between the reconstructed stress averages, using the stress-gauge equation (Eq. 4), and simulated stress averages, over an entire wave reflection. This sweep resulted in a mesh size of 0.1 mm and $\beta$ coefficient of 7 $\times$ 10$^{-7}$ ms. For the remaining components in the simulation a mesh size of 0.2 mm was used to maintain a similar mesh density. The time step incrementation was not fixed, however, the data output step was set to match that of the camera used for the experiments (0.2 $\upmu$s inter-frame time). Isotropic linear elasticity was assumed for the projectile, waveguide, sabot and 2–3 plane interlaminar specimens. For 1–3 plane specimens a transverse isotropic, linear elastic material model was used. The simulated geometries and material properties for the interlaminar IBII test are listed in Table 2.

Table 2 Simulation parameters and material properties for the interlaminar tension IBII test

Parametric Sweep Results

The results from the parametric sweep for 1–3 and 2–3 plane specimens are shown in Fig. 3a and b, respectively. Based on the design space defined in Sect. 3.1, it is possible to select a range of experimental parameters that satisfy the design requirements. For both specimens, the design envelope that satisfies the requirements is given by: projectile length [10 mm $< L_{P}<$ 20 mm] and impact velocity [$V_{P}>$ 40 $\hbox {m}\,\hbox {s}^{-1}$]. From this, the test configuration selected for both experiments is as follows: $L_{WG} = 50$ mm, $L_P = 10$ mm, and $V_P = 50\,\hbox {m}\,\hbox {s}^{-1}$. Based on simulated stress fields, the design strength of 80 MPa is expected to be reached at approximately $x = 10$ mm from the free edge.

Fig. 3

Maximum reflected tensile stress, $\overline{\sigma _{xx,max}}^{y}$ for interlaminar IBII specimens as a function of projectile length and velocity: a 1–3 plane specimens, b 2–3 plane specimens

Material and Experimental Setup

Specimen Manufacturing

Material properties of AS4-145/MTM45-1 are provided in Table 2. The density of the plate was measured using a micro balance and water immersion to be 1605 ± 20 ${\text{kg}}\,{\text{m}}^{-3}$. The plate had an average measured cured thickness of 17.9 mm (est. 128 layers, 0.14 mm cured ply thickness [28]). Twenty interlaminar specimens were cut (10 $\times$ 1–3 material plane and 10 $\times$ 2–3 material plane). The specimens were first rough cut from the plate using a large tile saw with a diamond cutting wheel. The specimen faces were then cut using a Streurs E0D15 diamond saw. The automated stage was set to a low feed rate of 0.1 m${\text{m}}\,{\text{s}}^{-1}$ to reduce the likelihood of inducing machining defects. For the 1–3 plane, specimen dimensions (L$\times$H$\times$e) were measured to be 17.9 mm $\times$ 12.1 mm $\times$ 2.6 mm (SD ±0.2 mm, ±0.2 mm, ±0.6 mm). Similarly, 2–3 plane specimen dimensions were measured to be 18.2 mm $\times$ 12.0 mm $\times$ 2.6 mm (SD ±0.1 mm, ±0.3 mm, ±0.4 mm). Note that reported thickness measurements include the grid deposited on the surface.

Grid Deposition Techniques

Grids with a pitch p of 0.3 mm were bonded to ten specimens (5 for each interlaminar plane), using the process outlined in [29]. The epoxy layer had a typical thickness of approximately 225 $\upmu$m. While this deposition procedure worked quite well in [20] for in-plane specimens, the smaller specimens in this study were more susceptible to grid defects from air bubbles in the underlying resin layer. Since grid defects are detrimental to the inverse identification procedures, a second grid deposition process was explored for the remaining ten specimens (5 for each interlaminar plane). A thin coat of white rubber paint (Rust-Oleum Peel Coat) was first applied to the specimen. The paint layer had a typical thickness of approximately 20 $\upmu$m. A series of black squares were then printed onto the painted surface with a Canon Océ Arizona 1260 XT flat bed printer. This formed a white grid with an average pitch of 0.337 mm. Trial prints of uniform grids were found to contain periodic defects every 80 mm in the horizontal direction. This was used to define the true print resolution and adjust the grid pitch when printing on specimens. As grids were defined according to a constant ‘points-per-pitch’ ratio (6:7 (x:y) closely matches that of the true resolution), the actual pitch in the vertical and horizontal directions is 0.338 mm and 0.336 mm, respectively. More information is available online [30, 31]. This required processing of the grid images using the iterative procedure described in [32]. The limited printer resolution reduces the spatial resolution compared to the bonded grids. However, this was a manageable compromise given the simplicity of the deposition process and significant reduction in grid defects.

Specimen Naming Convention

Specimens will be referred here by specimen number followed by a dash and a letter specifying the grid type; ‘P’ denotes a printed grid (p = 0.337 mm), and ‘B’ denotes a bonded grid (p = 0.3 mm), respectively. The interlaminar plane is specified in square brackets. For example, specimen #1 from the 1–3 plane with a 0.337 mm printed grid pitch is referred to as: ‘#1-P[1–3]’.

Experimental Setup

All tests were performed using the compressed air impact rig described in [20]. The gas gun reservoir pressure was set for a nominal impact velocity between 50 and 55 ${\text{m}}\,{\text{s}}^{-1}$. Each specimen was bonded to the back of a 6061-T6 aluminium waveguide (50 mm length, 25 mm diameter) using a thin layer of cyanoacrylate glue. A copper contact trigger on the front of the waveguide was used to trigger the camera. A 10 $\upmu$s delay was programmed between the trigger event and image capture to account for the traverse time of the wave through the waveguide. All images were captured using the Shimadzu HPV-X camera (frame rate = 5 Mfps) with a Sigma 105 macro lens. The optical setup and a mounted specimen are shown in Fig. 4a and b, respectively. Further details about the optical measurement system are provided in Table 3. The low fill factor of the Shimadzu HPV-X required intentional blurring of the images to avoid aliasing of the grid and parasitic fringes in the strain maps [33]. An out-of-plane movement test (2 mm) was performed prior to each test to minimise the strain fringes (below the noise threshold) and thus, ensure that the images were sufficiently blurred. The camera stand-off distance was adjusted according to the grid being imaged. To maximise the spatial resolution of the Shimadzu HPV-X camera, the 0.3 mm grids were sampled at 6 pixels per pitch, whereas the 0.337 mm grids were sampled at 7 pixels per pitch.

Fig. 4

Experimental setup used for all interlaminar tests: a camera and flash arrangement around the test chamber, and b a mounted specimen supported on a test stand in the test chamber

Table 3 Imaging and measurement performance for the IBII tests with the grid method

Image Processing and Identification of Material Properties

The full image processing procedure is described in the following sections to explain how material properties can be extracted from deformed images of a specimen with a grid on its surface. The key steps are summarised in a flow chart shown in Fig. 5.

Fig. 5

Flow chart of processing procedure to identify material stiffness parameters from deformed grid images. Note that the exact same procedure is used for processing the experimental data and the image deformation simulations

Obtaining Displacement Fields from Deformed Grid Images

The Shimadzu HPV-X camera is used to collect a set of deformed grid images. These grid images are processed using the grid method to obtain phase maps, using a windowed discrete Fourier transform. For the bonded grids only, the phase maps were corrected for air bubble defects using a three-step procedure. (1) Each $\phi _{x}$ phase map was fitted with a mesh of linear finite elements (8 $\times$ 5 elements (x,y)) to capture gradients in the phase fields. The phase values at the nodal positions were determined using a least-squares regression fit and linear shape functions were used to interpolate the phase within each element. The regression plane fit was then subtracted from the raw phase field to obtain a map of residuals. Grid defects were first characterised by regions with phases values exceeding a 2$\sigma$ threshold on the residual. (2) A second linear regression plane fitting was performed to the phase maps, with the defects identified in (1) removed. The full extent of the defect was characterised by again using a 2$\sigma$ threshold. These defect maps were then used to remove defects in the $\phi _{y}$ maps. (3) A sliding square window of seven pitches in length was used to linearly interpolate the phase information over the defective regions identified in (2). The displacement fields were then computed from the ‘corrected’ phase maps using the iterative approach described in [32]. The iterative approach accounts for initial phase modulations in the grid (e.g., remaining small grid defects, slight grid spacing irregularities). The phase maps contain discontinuous jumps when the grid displaces more than one pitch. These jumps were corrected using spatial and temporal unwrapping. Spatial unwrapping was performed using the procedure described in [34]. Temporal unwrapping was performed using an in-house MATLAB routine. In this procedure, the spatial mean of the unwrapped phase is plotted against time and the 2$\pi$ mean phase jumps in time are corrected to obtain a monotonic increase of the longitudinal displacement representative of the rigid body translation in the impact direction.

Obtaining Strain and Acceleration Fields

One pitch of information is corrupted on the border of the phase maps due to edge effects from the windowed Fourier transform. Rather than discarding this data, previous studies have shown that identifications using the virtual fields method were drastically improved when this data was recovered using some sort of extrapolation [35, 36]. In this work, the corrupted displacement data was replaced using a linear regression fitting based on the data over one pitch (6 pixels (0.3 mm grids) or 7 pixels (0.337 mm grids)) inwards from the corrupted region. The extrapolation was performed independently for each row of pixels ($u_{x}$ fields), or column of pixels ($u_{y}$ fields). This approach was found to be better at rejecting noise compared to the approach in [20], where data was recovered using a linear extrapolation based on two points inward from the corrupted region. The displacement maps were then processed in two ways to obtain acceleration and strain fields (Fig. 5). Displacement maps were smoothed temporally using a third order Savitsky–Golay filter, and then differentiated twice in time to obtain acceleration maps. Displacement fields were padded in time by one half of the kernel size (in frames) to minimise edge effects from the filter. Raw displacement maps were also smoothed spatially, using a Gaussian filter, before differentiating to obtain strain maps. Both temporal and spatial differentiations were computed using a central difference. Strain rate maps were computed from the smoothed strain maps using a central difference, except for computing strain rate at fracture, which was performed using a backward difference based on the raw strain maps to avoid temporal leakage from unrealistic strains computed after crack initiation. To reduce edge effects from spatial smoothing, the displacement fields were first padded out by 3 smoothing kernels using a linear extrapolation. The fields were smoothed and then cropped back to the original size. The details of the corrections and smoothing can be consulted in the Matlab program provided as supplementary material with this article.

Identifying Material Properties from Kinematic Fields

The special optimised virtual fields methods presented in Sect. 2.1 were used to process acceleration and strain fields to identify stiffness parameters. Material properties were identified from acceleration and strain maps using two VFM approaches: (1) using special optimised virtual fields, and (2) using reconstructed stress averages to compute stress–strain curves at each position along the specimen length.

Special Optimised Virtual Fields The special optimised virtual fields approach provides an identification of each stiffness parameter for each time step. For 1–3 plane specimens, the reduced approach was used to process $a_{x}$ and $\epsilon _{xx}$ fields to directly identify $E_{33}$. For 2–3 plane specimens, the $a_{y}$, $\epsilon _{yy}$ and $\epsilon _{xy}$ fields were also included in the general isotropic formulation of the special optimised virtual fields approach. In this case, $Q_{33}$ and $Q_{23}$ were identified, from which $E_{33}$ and $\nu _{23}$ were determined. The value of each identified stiffness parameter for the test was taken as the average over all time steps where the identification is stable. The identification is generally poor during the first few frames of the test due to low strains as the wave enters the specimen. Stability is also challenged as the wave reflects from the free-edge, as the incoming and reflected waves superimpose, resulting in temporary low strain and acceleration signal. When the material cracks in tension, non-physical strains corrupt the identification. Therefore, optimal conditions for identification (high strain and acceleration signal) generally occurs during the first compressive loading after the stress wave has entered the specimen, but before it reflects at the free edge. The optimized virtual fields were expanded using a basis of piecewise functions (finite elements), as proposed initially in [37]. A virtual mesh refinement study was performed on the image deformation data (described in Sect. 5) and the results showed that the identification converged at a virtual mesh of 5 $\times$ 1 elements (x,y) and 5 $\times$ 4 elements (x,y) for the reduced and isotropic special optimised routines, respectively. Data is discarded within one pitch plus one spatial smoothing kernel at the impact edge to reduce smoothing filter edge effects on the identification.

Reconstructed Stress–Strain Curves Here, the stress-gauge equation (Eq. 4) was used to calculate stress averages ($\overline{\sigma _{xx}}^{y}$) from $a_{x}$ fields for all specimens. Using these stress averages, combined with axial strain ($\overline{\epsilon _{xx}}^{y}$ for 1–3 plane specimens, and $\overline{\epsilon _{xx}+\nu _{23}\epsilon _{yy}}^{y}$ for 2–3 plane specimens), stress–strain curves were generated along the length of the specimen. For the case of 2–3 plane specimens, the identified value of $\nu _{23}$ from the special optimised virtual fields procedure was used. The interlaminar stiffness ($E_{33}$ for 1–3 plane specimens, and $Q_{33}$ for 2–3 plane specimens) was identified using a linear regression fit to the stress–strain curve up to the maximum compressive stress. This is henceforth referred to as the ‘stress–strain curve’ approach. $E_{33}$ was calculated for 2–3 plane specimens using the identified value of $\nu _{23}$ from the special optimised virtual fields approach. The identification of $E_{33}$ tends to be poor near the free and impact edges due to extrapolated data at the edges of the specimen, and edge effects from spatial smoothing. Therefore, the value of $E_{33}$ for the test was taken as the average of identified values over the middle 50% of the specimen. The stress-average reconstructed at the first crack location using linear-stress gauge equation was used to estimate the interlaminar tensile strength.

Clearly, the selection of spatial and temporal smoothing parameters will influence the identification procedures. The smoothing parameters were selected using an image deformation simulation procedure similar to [36, 38, 39], as described in the following section.

Smoothing Parameter Selection and Error Quantification

Generating Synthetic Images

The purpose of this section is to select optimal smoothing parameters to be used for the experiments and estimate the experimental error using an image deformation procedure. The general concepts are described here, but the reader is referred to [36, 38, 39] for further details. A sequence of ‘static’ synthetic images were generated for both types of grids used in the experiments using an analytical function to describe the light intensity, s(x, y). For the white-on-black grids, with a 0.3 mm pitch, the intensity at any position was described as:

$$\begin{aligned} s(x,y) = A+\gamma \cdot \Big (1 + \frac{1}{2}\big (1+\cos (2\pi x/p)\big )\cdot \big (1+\cos (2\pi y/p)\big )\Big ) \end{aligned}$$

(6)

while the intensity at any position for the black-on-white grids, with a 0.337 mm pitch, was defined as:

$$\begin{aligned} s(x,y) = A+\gamma \cdot \Big (1 - \frac{1}{2}\big (1+\cos (2\pi x/p)\big )\cdot \big (1+\cos (2\pi y/p)\big )\Big ) \end{aligned}$$

(7)

where A is the average grey level illumination, $\gamma$ is the pattern contrast amplitude (between 0 and 1), and p is the grid pitch. Displacement fields from finite element simulations were used to create a set of deformed images using super-sampling interpolation. Up-sampled images were generated, and then sub-sampled by pixel averaging to simulate the resolution of the Shimadzu HPV-X camera (400 $\times$ 250 pixels). Specifically, synthetic images were generated for the bonded, 0.3 mm, white-on-black grids, and the printed, 0.337 mm, black-on-white grids, using contrast values measured from experimental static images. The parameters used to generate each set of synthetic images are listed in Table 4. Magnified views of the synthetic grid images are compared with experimental grids in Fig. 6. The lighting gradient along the specimen length is more pronounced on the black-on-white grids. Therefore, the synthetic image is based on average intensity and contrast of the experimental grids over the length of the specimen. This explains the slight differences in contrast between synthetic and experimental 0.337 mm pitch grids.

Table 4 Summary of parameters used to generate synthetic images for processing parameter optimisation

Fig. 6

Magnified views of grid images: a 0.3 mm synthetic grid (6 pixels/period), b 0.3 mm experimental grid (6 pixels/period), c 0.337 mm synthetic grid (7 pixels/period), and d 0.337 mm synthetic grid (7 pixels/period)

The deformed synthetic images were then processed using the same procedure as the experimental images (Sect. 4.5). Different combinations of spatial and temporal smoothing were used to quantify the effect of processing parameters on the identification of stiffness parameters.

Identification Sensitivity to Smoothing Parameters

Each combination of smoothing kernels was used to process synthetic images with 30 copies of noise. Gaussian white noise with a uniform standard deviation was used to approximate experimental noise. In reality, noise is dependent on grey level intensity, which could be accounted for in the future. The standard deviation was set to that measured from a series of static grid images captured with the Shimadzu HPV-X camera (Table 4). The sensitivity to smoothing parameters was assessed using the maximum total error ($e_{T}$) between the reference stiffness value and the value identified from the processed synthetic images. The total error was defined as the absolute value of the systematic error $e_{S}$, plus or minus two times the random error, $e_{R}$ ($e_{T}$ = $|e_{S} \pm 2e_{R}|$). The systematic error ($e_{S}$) was considered as the difference between the mean identified stiffness parameter and the reference stiffness, normalised by the reference stiffness as,

$$\begin{aligned} e_{S,ij}= & {} \frac{1}{Q_{FE,ij}}\bigg (\frac{1}{N}\sum _{k = 1}^{N}Q_{ID,ij}^{k}-Q_{FE,ij}\bigg )\nonumber \\&\quad {\text{for}}\quad i = 2,3, j = 3 \end{aligned}$$

(8)

where $Q_{ID,ij}^k$ is the identified stiffness parameter from the image deformation simulations for noise iteration k, N is the number of noise copies (N = 30), and $Q_{FE,ij}$ is the reference stiffness value used to generate the simulated displacement fields and deformed images. Random error ($e_{R}$) was defined as the standard deviation of the identified stiffness over the 30 copies of noise normalised by the reference stiffness as,

$$\begin{aligned} e_{R,ij}= & {} \frac{1}{Q_{FE,ij}}\sqrt{\frac{\sum _{k = 1}^{N}(Q_{ID,ij}^{k}-\overline{Q_{ID,ij}})^{2}}{N}}\nonumber \\&\quad {\text{for}} \quad i = 2,3; j = 3 \end{aligned}$$

(9)

where $\overline{Q_{ID,ij}}$ is the mean identified stiffness parameter from the image deformation simulations over all copies of noise. The reader is encouraged to recall Sect. 4.5.3 for a description of the identification procedures.

For each combination of smoothing kernels, the systematic, random and total error were calculated. Examples of systematic and random error maps for the identification of $E_{33}$ [1–3] with 0.3 mm grid, using the reduced special optimised virtual fields approach are shown in Fig. 7a, b, respectively. The error maps were very similar for identifications using the stress-gauge approach and therefore, only maps for the optimised VFM will be presented. The systematic and random errors follow similar trends as shown in previous works for quasi-static tests [38], with minimum systematic error and high random error when no smoothing is applied. The band of low systematic error represents a consistent trade-off between bias from smoothing acceleration fields (temporal smoothing), and strain fields (spatial smoothing), such that the reference stiffness is most accurately identified. The magnitude of random error is low since the identification is derived from the average over several temporal frames. The random error is more strongly influenced by temporal smoothing (noise in acceleration signal) since the optimised virtual field routine are optimised to minimise strain noise, and not acceleration noise, and there is a double differentiation in time compared to a single differentiation in space.

Fig. 7

Simulated identification error for $E_{33}$ as a function of spatial and temporal smoothing kernel size using the reduced special optimised routine (1–3 plane specimen, 0.3 mm grid, 6 pixels per period sampling): a normalised systematic error, and b normalised random error

For the 1–3 interlaminar plane specimen, the total error maps are shown in Fig. 8a (0.3 mm grid, 6 pixels/period) and b (0.337 mm, 7 pixels/period). The total error maps for 6 and 7 pixels/period are very similar in shape and magnitude. This implies that grid sampling has only a small influence on the identification in the present case. These maps suggest that optimal levels of smoothing correspond to a spatial kernel of 41 pixels, and a temporal kernel of 11 frames. For these parameters the estimated error on $E_{33}$ is approximately 0.5%.

Fig. 8

Maximum, simulated identification error for $E_{33}$ as a function of spatial and temporal smoothing kernel size using the reduced special optimised routine (1–3 plane specimen): a normalised total error for 0.3 mm grid (6 pixels/period sampling), and b normalised total error for 0.337 mm grid (7 pixels/period sampling). Minimum error indicated by white circle

The total error maps for $Q_{33}$ and $Q_{23}$, for 2–3 plane specimens with 0.3 mm (6 pixels/period) and 0.337 mm (7 pixels/period) grids are shown in Figs. 9 and 10, respectively. The higher total error at low smoothing indicates a higher sensitivity to random error. This is to be expected as $\epsilon _{yy}$ and $a_{y}$ have a lower signal-to-noise ratio. The inclusion of these fields into the identification increases the sensitivity to noise of both $Q_{33}$ and $Q_{23}$, which are identified simultaneously. Nevertheless, the minimum total error is not significantly increased compared to the 1–3 plane identification, with the minimum occurring around a 41 pixels spatial smoothing kernel, and 11 frames for the temporal smoothing kernel. These parameters have an associated error on the identification of $Q_{33}$ and $Q_{23}$ of approximately 0.5% and 2–3%, respectively.

Fig. 9

Maximum, simulated identification error for $Q_{33}$ and $Q_{23}$ as a function of spatial and temporal smoothing kernel size using the reduced special optimised routine (2–3 plane specimen, 0.3 mm grid, 6 pixels/period sampling): a normalised total error for $Q_{33}$, and b normalised total error for $Q_{23}$. Minimum error indicated by white circle

Fig. 10

Maximum, simulated identification error for $Q_{33}$ and $Q_{23}$ as a function of spatial and temporal smoothing kernel size using the reduced special optimised routine (2–3 plane specimen, 0.337 mm grid, 7 pixels/period sampling): a normalised total error for $Q_{33}$, and b normalised total error for $Q_{23}$. Minimum error indicated by white circle

The total error maps are extremely useful for selecting the optimal smoothing parameters in a rational way and provide an estimate of the total error associated with the experimental identifications. The optimal smoothing parameters selected for processing experimental images are listed in Table 5. Also included are the corresponding error estimates and measurement resolution (standard deviation of field) from static experimental images processed with the selected smoothing parameters. Image deformation simulations indicate that the predicted errors are very low, despite having limited spatial resolution. Simulations also suggest that this configuration is highly robust to spatial and temporal smoothing, so long as the user does not select extreme smoothing parameters. This is a key advantage of this IBII test configuration. The user can quickly establish reasonable limits on the bounds of smoothing for a given grid pitch assuming a rough knowledge of the material in question. For example, looking at the contour maps, the temporal smoothing is the parameter that mostly influences the error. The total error sharply rises when the temporal smoothing kernel approaches the time for the wave pulse to traverse across the specimen. Therefore, so long as the user can estimate the wave speed in the material with reasonable accuracy, an upper bound on temporal smoothing can be quickly established. Likewise, simulations suggest that spatial smoothing does not significantly effect the identification so long as the total kernel is less than 10 grid pitches.

Table 5 Selected smoothing parameters for processing experimental images and corresponding measurement performance

Experimental Results and Discussion

Full-Field Measurement Results

In this section typical experimental kinematic fields are presented for two time steps for a 1–3 plane and 2–3 plane interlaminar specimen. Since it is difficult to get a true appreciation for the dynamic nature of an impact test through still images, videos of all kinematic field for all specimens, as well as the raw grey level images can be found in the data repository detailed at the end of the manuscript.

Full-field maps of $u_x$ and $u_{y}$ are shown for specimen #2-P[1–3] in Fig. 11 for two time steps; the first time step corresponds to a state where the initial compressive pulse is well within the specimen (t = 7 $\upmu$s), and the second corresponds to a time after the pulse has reflected but before tensile failure (t = 17 $\upmu$s). Similar maps for specimen #6-B[2–3] are provided in Fig. 12. Note that the mean $u_{x}$ displacement has been subtracted to remove the rigid-body displacement and show the deformation. Due to the high lateral stiffness from the fibre reinforcement for specimen #2-P[1–3], the magnitude of $u_{y}$ is much smaller and the signal to noise ratio is much poorer compared to $u_{x}$. In the case of specimen #6-B[2–3], $u_{y}$ is approximately one order of magnitude larger. The corresponding acceleration fields for the two specimens are shown in Figs. 13 and 14. The edges of the pulse are most clearly identified in $a_x$ maps, which show that local accelerations are on the order of 10$^{7}{\text{m}}\,{\text{s}}^{-2}$. This corresponds to average axial forces on the order of 4 kN, or axial stress on the order of 100 MPa (Fig. 15). Defects are difficult to remove from acceleration fields since no temporal information is considered in the correction procedure. While this provides a reasonable reconstruction in the majority of cases, the defective region is still identifiable in some frames, as shown in Fig. 14d. While defects cannot be completely removed, providing some compensation for defects is beneficial as it acts as an outlier removal. This is particularly beneficial for identifications from stress–strain curves, which rely on local strain values.

Fig. 11

Experimental displacement fields; a, b$u_{x}$ ($\upmu$m), and c, d$u_{y}$ ($\upmu$m), for specimen #2-P[1–3] at 7 $\upmu$s, and 17 $\upmu$s. Note that the mean $u_{x}$ displacement has been subtracted to remove the rigid-body displacement

Fig. 12

Experimental displacement fields; a, b$u_{x}$ ($\upmu$m), and c, d$u_{y}$ ($\upmu$m), for specimen #6-B[2–3] at 8 $\upmu$s, and 18 $\upmu$s. Note that the mean $u_{x}$ displacement has been subtracted to remove the rigid-body displacement

Fig. 13

Experimental acceleration fields; a, b$a_{x}$ (${\text{m}}\,{{\text{s}}}^{-2}$), and c, d$a_{y}$ (${\text{m}} \, {\text{s}}^{-2}$), for specimen #2-P[1–3] at 7 $\upmu$s, and 17 $\upmu$s

Fig. 14

Experimental acceleration fields; a, b$a_{x}$ (${\text{m}}\,{\text{s}}^{-2}$), and c, d$a_{y}$ (${\text{m}}\,{\text{s}}^{-2}$), for specimen #6-B[2–3] at 8 $\upmu$s, and 18 $\upmu$s

Fig. 15

Average axial force and average axial stress profiles for specimens #2-P[1–3] and #6-B[2–3]

Fig. 16

Experimental strain fields; a, b$\epsilon _{xx}$ (mm m$^{-1}$); c, d$\epsilon _{yy}$ (mm m$^{-1}$), and e, f$\epsilon _{xy}$ (mm m$^{-1}$) for specimen #2-P[1–3] at 7 $\upmu$s, and 17 $\upmu$s

Fig. 17

Experimental strain fields; a, b$\epsilon _{xx}$ (mm m$^{-1}$); c, d$\epsilon _{yy}$ (mm m$^{-1}$), and e, f$\epsilon _{xy}$ (mm m$^{-1}$) for specimen #6-B[2–3] at 8 $\upmu$s, and 18 $\upmu$s

Fig. 18

Experimental strain rate fields; a, b$\dot{\epsilon _{xx}}$ (s$^{-1}$) for specimen #2-P[1–3] at 7 $\upmu$s, and 17 $\upmu$s

Fig. 19

Experimental strain rate fields; a, b$\dot{\epsilon _{xx}}$ (s$^{-1}$) for specimen #6-B[2–3] at 8 $\upmu$s, and 18 $\upmu$s

The $\epsilon _{xx}$, $\epsilon _{yy}$ and $\epsilon _{xy}$ strain maps for the two specimens, at the same two time steps, are shown in Figs. 16 and 17. The experimental strain maps for the 1–3 interlaminar specimen confirm that the $\epsilon _{yy}$ strains are much lower than for the $\epsilon _{xx}$ strains. Significant $\epsilon _{yy}$ strains are measured in the case of the 2–3 plane interlaminar specimen, however, the signal-to-noise ratio remains less favourable than the $\epsilon _{xx}$ strains. As a result, the edge data extrapolation procedure does not perform as well, creating some localised regions of high artificial strain. As mentioned previously, despite having high signal in the $\epsilon _{xx}$ fields, the lower signal in the $\epsilon _{yy}$ and $\epsilon _{xy}$ fields will act to reduce the identification stability since these strains are used to simultaneously identify $Q_{33}$ and $Q_{23}$. Strain rate maps ($\dot{\epsilon _{xx}}$) are shown in Figs. 18 and 19 for specimen #2-P[1–3] and specimen #6-B[2–3], respectively. Local $\dot{\epsilon _{xx}}$ strain rates are on the order of 4000 s$^{-1}$ to 7000 s$^{-1}$. For specimen #6-B[2–3], $\dot{\epsilon _{yy}}$ were measured on the order of 3000 s$^{-1}$. Strain rates in the experiments are slightly lower than that predicted from processed synthetic images based on simulated fields (peak compressive strain rates on the order of 14,000 s$^{-1}$ and peak tensile strain rates on the order of 10,000 s$^{-1}$). As previously explained, this is expected since the simulation assumes perfect, hard contact at waveguide interfaces between the projectile and specimen. Some ‘pulse-shaping’ is expected in the experiments from the thin layer of tape on the front face of the waveguide for the camera trigger, and the thin layer of glue between the waveguide and specimen.

Interlaminar properties were identified from the acceleration and strain fields using the methods presented in Sect. 2 and Sect. 4.5.3. The identification of interlaminar stiffness parameters are presented in Sect. 6.2 and the identification of interlaminar tensile strength are presented in Sect. 6.3.

Stiffness Identification

Experimental measurements of interlaminar stiffness parameters are presented separately for each of the identification techniques. The identifications using the special optimised virtual fields methods are presented first in Sect. 6.2.1 followed by the stiffness identifications with the stress–strain curve approach in Sect. 6.2.2.

Special Optimised Virtual Fields Approach

Identifications of $E_{33}$ with the reduced optimised virtual fields method for all specimens are shown in Fig. 20. Similarly, identifications of $Q_{33}$ and $Q_{23}$ are shown in Figs. 21 and 22, respectively. From identifications of $Q_{33}$ and $Q_{23}$, $\nu _{23}$ and $E_{33}$ can be determined (not shown). The identified value for all parameters was taken as the average over the time frames that $Q_{33}$ was stable. Note that identifications are stopped just prior to the wave reflection from the free edge (approx. $t = 10\,\upmu$s). The identifications do not recover beyond this due to data reconstruction errors at the free edge, low strains as the wave reflects, and the formation of macro cracks shortly after. A summary of identified interlaminar stiffness parameters for 1–3 plane specimens and 2–3 plane specimens is provided in Tables 6 and 7, respectively. In the case of specimens #6-B[1–3], #7-B[1–3], #3-P[2–3], #5-P[2–3] and #10-B[2–3], the trigger delay was too long and a true static reference was not captured, as the wave had partially propagated into the specimen in the first image. To determine how far the pulse had propagated into the specimen when image capture began, a reference image taken before the test was correlated with the first image captured during the test. The region where $\epsilon _{xx}$ exceeded the noise floor was used to locate the pulse front. Images were then reprocessed with this region excluded (these specimens marked with a superscript ‘r’ in Table 6 and Table 7). Note that this does not affect interlaminar strength measurements as the test was designed so that failure occurs in the middle of the specimen, where a reference grid was maintained.

Fig. 20

Interlaminar Young’s modulus, $E_{33}$, identified for all 1–3 plane specimens using the reduced special optimised virtual fields method. Identification from image deformation simulation processed with the same smoothing parameters is provided for comparison

Fig. 21

Interlaminar $Q_{33}$ stiffness identified for all 2–3 plane specimens using the isotropic formulation of the special optimised virtual fields method. Identification from image deformation simulation processed with the same smoothing parameters is provided for comparison

Fig. 22

Interlaminar $Q_{23}$ stiffness identified for all 2–3 plane specimens using the isotropic formulation of the special optimised virtual fields method. Identification from image deformation simulation processed with the same smoothing parameters is provided for comparison

The random error associated with identifications for 2–3 plane specimens is higher compared to the 1–3 plane. A possible explanation for this is the inclusion of $a_y$, $\epsilon _{yy}$ and $\epsilon _{xy}$ fields in the identification procedure, which have a lower-to-noise ratio. The optimised virtual fields method is formulated such that each set of virtual fields results in the direct identification of each stiffness parameter. Since these parameters are identified simultaneously, the identification of a weakly activated material parameter will influence the identification of the other parameters.

The minimisation based on strain noise also makes the identifications sensitive to defects, which have a high signal-to-noise ratio, particularly in the case where the activated strain fields have low signal-to noise-ratio. This is particularly problematic when defects occur around the edges of the specimen and interact with the edge extrapolation procedures. This will inevitably influence the identification routines and may account for the higher inter-specimen scatter in identified values for 2–3 plane specimens. To some extent, grid defects and their interaction with low signal to noise $\epsilon _{yy}$ strains will also influence the identification of $Q_{33}$ using stress–strain curves (presented in Sect. 6.2.2). However, this is thought to be minimal since strains generated from the Poisson effect are small compared to the axial strains. The interaction of the virtual fields with defects may also explain the low-frequency oscillations in the identification of $E_{33}$ from some 1–3 plane specimens (e.g., #1-P[1–3]), however further investigation is required to confirm this.

Table 6 Measured high strain rate interlaminar elastic modulus for AS4-145/MTM45-1 (1–3 plane specimens)

Table 7 Measured high strain rate interlaminar stiffness for AS4-145/MTM45-1 (2–3 plane specimens)

Table 8 Peak compressive width-average strain rate ($\overline{\dot{\epsilon _{xx}}}^{y}$)

The average value for $E_{33}$[1–3] was 10.9 GPa with a coefficient of variation (COV) of 3.5 %. This level of scatter is quite low and comparable to that for quasi-static testing of this material (COV = 3.6 %) [28]. $E_{33}$ [2–3] is identified from $Q_{33}$ and $\nu _{23}$ with an average value of 10.4 GPa, and a COV of 6.1%. The slightly higher scatter in $E_{33}$ [2–3] is likely caused by the inclusion of fields with low signal-to-noise ratios into the identification routine as described previously. Therefore, the stiffness measured on the 1–3 plane specimens is thought to be more reliable. The measured interlaminar modulus of 10.9 GPa represents an increase of 38% compared to quasi-static values [28].

Overall, the measurements are quite promising considering this is the first implementation of the IBII test to obtain interlaminar properties at such high strain rates. Regarding strain rate, it is difficult to assign a single strain rate value to the measurements due to the heterogeneity of the fields. However, when axial strain is high, so too is strain rate (see Figs. 16, 17, 18, 19). Therefore, the peak, width-average strain rate ($\overline{\dot{\epsilon _{xx}}}^{y}$) achieved during the compressive loading sequence can be considered as the limiting case for an ‘effective’ strain rate for these measurements (Table 8). It is part of future work to derive an effective strain rate using the virtual fields and the virtual strain rate fields to be able to quote a well-defined value. However, the strain rate sensitivity of this material is low enough so that this is not a critical issue and a mean or peak value is a good estimate. For most specimens, the peak compressive strain rate is on the order of 3500 s$^{-1}$. Obtaining stiffness measurements at such strain rates with the SHPB test is challenging and generally unreliable. Identifications using reconstructed stress–strain curves are presented next.

Stress–Strain Curve Approach

The stress-gauge equation is used to reconstruct $\overline{\sigma _{xx}}^{y}$ at each cross-section. This can be drawn as a function of $\overline{\epsilon _{xx}}^{y}$ (1–3 plane) or $\overline{\epsilon _{xx}+\nu _{23}\epsilon _{yy}}^{y}$ (2–3 plane) to generate stress–strain curves at each cross-section. Examples of stress–strain curves generated at a cross-section near the middle of the sample are shown for specimens #2-P[1–3], #7-B[1–3], #2-P[2–3], and #6-B[2–3] in Fig. 23. The linearity of the stress–strain responses is quite remarkable considering the high strain rates at which these measurements are made. A linear regression fitting to the compressive loading region of the curve was used to identify the interlaminar stiffness at each cross-section.

Fig. 23

Stress–strain curves generated near the middle of the sample using the stress-gauge equation for: a specimens #2-P[1–3] and #7-B[1–3] and b specimens #2-P[2–3] and #6-B[2–3]. Note that all stress–strain curves begin near the origin but have been offset by 3 $\hbox {mm}\,\hbox {m}^{-1}$ for clarity

The spatial identification of $E_{33}$ is presented for all 1–3 plane specimens in Fig. 24, and for all 2–3 plane specimens in Fig. 25. Note that in the case of 2–3 plane specimens, the identified value of $\nu _{23}$ from the special optimised virtual fields procedure is used for determining $Q_{33}$. Also note that one pitch, plus one smoothing kernel is excluded from the free edge and impact edge. The identification is unreliable in these regions due to smoothing edge effects and low spatial averaging near the free edge.

Fig. 24

Interlaminar Young’s modulus, $E_{33}$, for all 1–3 plane specimens identified using the stress-gauge approach. Identification from image deformation simulation processed with the same smoothing parameters is provided for comparison. Note that the extrapolated data at the edges of the specimen has been removed

Fig. 25

Interlaminar stiffness, $Q_{33}$, for all 2–3 plane specimens identified using the stress-gauge approach. Identification from image deformation simulation processed with the same smoothing parameters is provided for comparison. Note that the extrapolated data at the edges of the specimen has been removed

In general, the identifications from reconstructed stress–strain curves are quite consistent and stable over the middle portion of the specimen. A slightly lower stiffness is measured near the free edge on some samples with bonded 0.3 mm grids, particularly specimens #6-B[1–3], #8-B[1–3], and #9-B[1–3]. Since this is not observed on specimens with printed, 0.337 mm grids, this is thought to be a result of a slight rotation of the grid with respect to the specimen. This could also be a result of some missing data at the edge from trimming the overflow epoxy during the grid de-bonding process. Both have the effect of increasing the amount of missing data at the free edge, and thus the error on reconstructed stress. This highlights another key advantage of using printed grids, as alignment is easily and consistently controlled, and no additional steps are required to clean up the edges of the specimen following grid application. The identification of $E_{33}$ [1–3] and $E_{33}$ [2–3] was measured to have an average value of 10.4 GPa, and 10.2 GPa, respectively. The coefficient of variation for both types of specimens is low ranging between 3 and 6%. Between 1–3 and 2–3 plane specimens, this represents a 30% increase in stiffness compared to quasi-static transverse stiffness measurements ($E_{33}$ = 7.9 GPa) [28].

Figures 24 and 25 show that the identifications of $E_{33}$ and $Q_{33}$ fluctuate periodically along the length of the specimen by approximately 0.5 GPa from the mean. This pattern was also observed in the identifications from synthetic images, although with a lower magnitude (0.2 GPa). Image deformation simulations suggest that this oscillation is primarily attributed to fluctuating error on reconstructed acceleration and strain as the pulse moves through the extrapolation region at the free edge (one pitch). Extrapolation errors are highest as the high signal information within the pulse travels through the extrapolated region. It is thought that the experimental images are more sensitive to this since the pulse is smoother compared to the simulated pulse (i.e., extrapolation errors affect high signal information for a longer period of time). The effect is more pronounced on the 0.337 mm grids due to lower measurement resolution and a larger extrapolation region at the free edge.

To the authors’ knowledge, no interlaminar high strain rate data are available for AS4-145/MTM45-1. Furthermore, existing studies are limited to reporting an ‘apparent’ modulus, and scatter is so large that strain rate effects cannot be reliably extracted [2]. Therefore, it is difficult to make direct comparisons with other studies. This preliminary study shows that a consistent measurement of $E_{33}$ can be obtained by processing measured strain and acceleration fields in two different ways. Both approaches are suitable for identifying a global stiffness value in this study since material properties do not vary in space or time. Therefore, a comparison of the two methods provides a kind of validation of the measured values. The use of image deformation also shows that both routines can identify the reference $E_{33}$ within 1% when smoothing parameters are chosen appropriately. However, when material properties vary in space and time preference might be given to a single identification method depending on the information desired. For example, the stress–strain curve method might be preferred in cases where a spatial variation in stiffness is of interest, since it provides a stiffness measurement for each transverse slice along the length of the specimen. Alternatively, the special optimised virtual fields might be more useful if one was interested in resolving time-dependent behaviours, as it gives a single stiffness value for each point in time. This level of information and versatility is not available with existing test methods and highlights the potential of image-based test methods for high strain rate testing.

Strength Identification

The linear stress-gauge equation (Eq. 5) is used to estimate the tensile strength of the material, as in [20]. A comparison of the stress fields reconstructed using the identified constitutive model and the linear stress-gauge equation are shown at a frame before fracture (t = 15.0 $\upmu$s) in Fig. 26a and b, respectively. The agreement is excellent apart from the region close to the impact, demonstrating that for such a test, the linear representation in Eq. 6 provides a reasonable actual approximation of the stress field. Fracture initiation is identified using the raw, un-smoothed maps of $\epsilon _{xx}$. A crack becomes clearly visible in the $\epsilon _{xx}$ field as a concentrated region of high (artificial) strain, as shown in Fig. 26c. The temporal variations of local stress, computed with the linear stress-gauge equation, was extracted from a 2 pitch $\times$ 4 pitch (2p$\times$ 4p) virtual gauge region centred on the identified crack initiation site (as shown in Fig. 26c). The corresponding stress maps, and stress–strain curve over the virtual gauge region are shown in sub figures d, e and f. While not clearly shown in the strain map in Fig. 26d a second crack had started to form at x = 9.5 mm, but did not crack the paint. The crack clearly appears three frames later. At the fracture frame shown, the acceleration fields are strongly influenced by these two cracks, explaining the discrepancy between the stress field in Fig. 26d and the reconstructed field using the linear stress-gauge shown in Fig. 26e.

The interlaminar tensile strength is taken as the maximum stress over time within the gauge region. A summary of measured tensile strength using the stress-gauge and linear stress-gauge is provided in Table 9. The tensile average strain rates from within the virtual gauge region ($\overline{\dot{\epsilon _{xx}}}^{VG}$) just prior to failure are also provided in Table 9. Some specimens fractured but the initiation of a crack was not clearly identifiable within the kinematic maps. This suggests that either a crack initiated on the back face, or the specimen fractured from impact with the back of the test chamber. For these cases, the peak stress average is reported in Table 9 for comparison, but is excluded from the calculation of strength statistics (identified by a superscript ‘x’ in Table 9). Note that strain rate maps were computed using a backward differentiation scheme to avoid temporal leakage from non-physical forward strains caused by the crack. Strain rate at fracture was estimated by extrapolating from a regression fitting to $\overline{\dot{\epsilon _{xx}}}^{VG}$ over five frames prior to fracture. For specimens where a macro crack was not visible, the peak value of $\overline{\dot{\epsilon _{xx}}}^{VG}$ is listed (identified by a superscript ‘$+$’ in Table 9).

Fig. 26

Strength identification diagnostics for specimen #2-P[1–3]. Diagnostic figures before fracture ($t = 15.0\,\upmu$s): a stress field (MPa) constructed from $\epsilon _{xx}$ using identified $E_{33}$ ($\sigma _{xx}(\epsilon _{xx})$), and b stress field (MPa) constructed using the linear stress-gauge equation ($\sigma _{xx}(LSG)$). Diagnostic figures for a time just after the identified fracture time ($t = 19.0\,\upmu$s): c raw, un-smoothed $\epsilon _{xx}$ strain field (mm m$^{-1}$), d$\sigma _{xx}(\epsilon _{xx})$ (MPa), e$\sigma _{xx}(LSG)$ (MPa), and f stress–strain curve generated using average $\sigma _{xx} (LSG)$ and $\epsilon _{xx}$ within the virtual gauge region. In (c), (d) and (e) the virtual gauge is shown as the black rectangle. In (f) the dashed circle indicates the point of fracture and extracted strength using the linear stress-gauge equation

Table 9 Measured high strain rate interlaminar tensile strength for AS4-145/MTM45-1 and peak tensile strain rate ($\overline{\dot{\epsilon _{xx}}}^{VG}$) within virtual gauge at fracture location

The results in Table 9 suggest that strain rate has a significant influence on the interlaminar tensile strength. The interlaminar strength with the linear stress-gauge equation was measured to be 115 MPa (COV = 21%) for the [1–3] specimens and 112 MPa (COV = 21%) for the [2–3] specimens. Combining the two interlaminar planes results in an average strength of 114 MPa, with a COV = 20%. This represents an increase in strength of 125% compared to the quasi-static value of 50.4 MPa (COV = 13%) in [28]. Since the strain rate is generally high when the strain is high, the peak width-averaged strain rate at the plane of fracture offers an ‘effective’ strain rate for the measurements. This is generally on the order of 5000 s$^{-1}$. It is worth noting that comparisons to quasi-static values need to be interpreted with some caution because quasi-static interlaminar tensile tests are quite sensitive to experimental factors such as misalignment, gripping and volume effect. Typical scatter in the literature for quasi-static strength measurements ranges from 10 to 50% [6, 7, 40, 41]. Therefore, the reported coefficient of variation for quasi-static interlaminar strength of this material is comparatively low. The level of scatter in the current measurements at high strain rates is promising, with scatter comparable to well controlled quasi-static tests.

The time histories of stress averages at the fracture location are shown in Fig. 27 for four specimens (2 from each interlaminar plane). Also shown for comparison is the average stress in the gauge region as reconstructed using the stress-gauge equation (Eq. 4) and the constitutive model. In the latter, the interlaminar stiffness is taken as the average values identified from stress–strain curves and the special optimised virtual fields routine. However, this stress is not used as a measure of strength due to the uncertainty in determining when strains become non-physical and contamination from grid defects as explained later. Figure 27 shows the initial compressive loading, where all three stress measures agree well. Two of the presented specimens (Fig. 27a, b) show good agreement during the unloading, until a marked drop in average stress (stress-gauge and linear stress-gauge equations) is observed between t = 15.5–19 $\upmu$s. Specimen #2-P[1–3] shows a small offset and low-amplitude oscillation in stress averages at the start of the unloading phase. It is suspected that some through-thickness wave dispersion may have occurred as the wave reflects due to a non-square free edge cut. This effect is observed over a very short duration, and is unlikely to influence strength measurements.

In some cases an offset in stress arises between the stress reconstructed from acceleration and stress computed using the constitutive model (#3-P[1–3]; 2-P[2–3], 3-P[2–3], #6-B[2–3], 7-B[2–3], 8-B[2–3] and 9-B[2–3]), as exemplified in Fig. 27c and d. This is a result of fracture occurring near a grid defect (within one smoothing kernel). Artificial strains caused by the defect biases the strain at the fracture location. The offset increases during the unloading phase when the wave reflects from the free edge. This suggests that the quality of grid defect corrections diminish as the test progresses and the kinematic fields become more complex. This is more problematic for specimens with bonded grids, which suffer from high numbers of defects caused by missing grid or bubbles in the resin layer as discussed in Sect. 4.2. The number of defects are significantly reduced when grids are printed, making it the preferred grid deposition technique. This also supports the use of the stress-gauge equations for estimating tensile strength. The stress-gauge equations provide a much more robust estimate of strength since acceleration fields are not smoothed spatially, and because of the spatial averaging procedure used to reconstruct stress.

Fig. 27

Comparison of the temporal variations in average stress within the virtual gauge area at the location of fracture as reconstructed using the stress-gauge approach ($\overline{\sigma _{xx}}^{VG}$(SG)), linear stress-gauge ($\overline{\sigma _{xx}}^{VG}$(LSG)) and strain ($\overline{\sigma _{xx}(\epsilon )}^{VG}$) for a specimen #2-P[1–3], b specimen #7-B[1–3], c specimen #2-P[2–3], and d specimen #6-B[2–3]. Note that the location of failure is included in the header of each sub figure and the red dashed line indicates the time at which a macro-crack is clearly visible in the un-smoothed strain maps

As previously mentioned, no high strain rate studies have been reported on AS4-145/MTM45-1, thus, no direct comparisons can be made. However, indirect comparisons can be made with studies on the high strain rate through-thickness properties of other composite systems. Comparison of the current measurements to those in other studies shows the robustness of the IBII test for measuring interlaminar strength. For example, a similar strain rate sensitivity was measured by Nakai & Yokoyama (+ 77%) [6, 7]. However, the scatter on measured strength was significantly higher (39% COV), and measurements were made at much lower strain rates (50 s$^{-1}$). This amount of scatter is typical of most studies reporting tensile strength measurements using a SHPB at high strain rate such as [4, 8, 42]. Govender et al. [43] used pulse time-shifting to avoid the assumption of quasi-static equilibrium, and produced strength measurements of similar consistency to the current study. However, their approach relied on predicted stresses based on 1-D wave theory and no quasi-static values were provided to quantify the strain rate sensitivity. By using ultra-high speed imaging and full-field measurements, many of the assumptions tied to existing techniques are removed. The measurements reported here exemplify the potential for such techniques to be applied to obtain remarkably consistent strength measurements.

Future Work and Limitations

While further work is still required to refine the IBII test, the preliminary results are promising. This study exemplifies the potential of test methods developed around full-field imaging to expand the range of strain rates where composite interlaminar properties can be reliably characterised. Based on this initial study, the following points describe some limitations of the test method. This is followed by a summary of possible future investigations to better understand the preliminary results proposed here, improve the test method, and possible extensions for more comprehensive material characterisation.

Assumptions for Processing the Data with the Virtual Fields Method Since only surface deformations are measured, the following assumptions are required here: (1) the specimen is in a state of plane stress, and (2) the mechanical fields need to be uniform through the thickness. Compared to the in-plane specimens in the study by Fletcher et al. [20], the specimen dimensions are less favourable here for ensuring a state of plane stress is achieved. Based on the current specimen manufacturing technique, the smallest thickness that could be achieved, while maintaining good dimensional consistency, was approximately 2 mm. Non-uniformity through the thickness may arise following wave reflection from an angled free edge, which would violate assumption (2). Further work is required to better understand the effect of specimen geometry (e.g., thickness variation and free edge perpendicularity) on the identifications of stiffness and strength. This will be explored as part of future work using three-dimensional finite element simulations and simultaneous imaging on the front and back surfaces of the specimens during experiments. Image deformation simulations will be required to quantify the effect of these geometric ‘defects’ and other experimental factors not accounted for in the current simulation. This will assist in identifying the source of discrepancies between identifications from simulated and experimental images and establish tolerances for specimen geometry and the experimental setup.

Reconstruction of Edge Data Oscillations in the stiffness identified from the stress–strain curves was primarily attributed to reconstruction errors as the pulse moves through the extrapolated data region at the free edge. This occurs since data is inferred for a temporal phenomenon, based solely on spatial information. This effect is amplified for the 0.337 mm printed grids compared to the 0.3 mm grids due to a larger reconstructed data region. A simple way to reduce extrapolation errors is to reduce the grid pitch to enable a lower grid sampling to be used (5 pixels per pitch). It is thought that the effect of reconstructed data on stiffness identifications may also depend on the pulse. A simple way to study this is to use image deformation simulations by systematically varying the pulse characteristics (e.g., rise time, duration and amplitude). The necessity to reconstruct edge data with the grid method will unavoidably introduce errors. Fortunately, this issue will become less problematic as the spatial resolution of ultra-high-speed cameras improves.

Grid Defects The results from this study suggest that grid defects have a significant influence on the identification of stiffness parameters using the isotropic special optimised virtual fields routine. Artificial signal with high signal-to-noise ratio is thought to cause bias in the optimisation of the virtual fields, due to the low signal associated with the underlying material response. The effect is amplified when defects occur near the edges of the specimen and interact with the data extrapolation procedures. Identifications of $Q_{33}$ and $Q_{23}$ have higher scatter and are less stable compared to the image deformation simulations, which do not take into account grid defects. There are several other factors that are also not considered in the simulations and therefore, future work is required to isolate and quantify the effect of defects on the identifications. Image deformation simulations serve as a useful tool for conducting such investigations. Systematic studies on defect position, size and density can be performed by corrupting grey-levels of synthetic images based on defect profiles from real grid images. The corrupted synthetic images may then be processed using the same procedure as experimental images to quantify the influence on identified stiffness parameters.

Considering these limitations, the following summarises possible directions of future work to develop the interlaminar IBII test.

Identification of a Strain Rate Sensitive Constitutive Law Assigning a single strain rate to the measured properties is difficult due to the heterogeneous nature of the fields. This is unavoidable when testing at high strain rates in the wave regime. While this is also problematic for existing techniques, full-field measurements create the potential to exploit the heterogeneity in strain rate fields. One approach is to formulate the unknown stiffness parameters as a function of strain rate in the optimised virtual fields routine. Provided the material is subjected to a range of strain rates, the coefficients of the model could be identified from each set of kinematic fields. The potential of this approach could be explored using a user-defined material sub-routine in ABAQUS combined with the synthetic image deformation methodology. Another approach is to use the virtual fields and the virtual strain rate fields to identify a well-defined value for the effective strain rate. This will be investigated in the future.

Extension to Thinner Specimens The drawback with the current configuration is that thick plates are required, which are expensive and may not be representative of thinner panels. It will be of particular interest in the future to see how small in length we could go, and beyond this, whether a thinner specimen sandwiched between two tabs would be feasible.

Error Quantification for Interlaminar Tensile Strength This work has demonstrated the usefulness of image deformation simulations for selecting optimal smoothing parameters and estimating the total error on stiffness identifications. The ideal extension of this is an image deformation routine that provides an estimate on the error for interlaminar tensile strength. This requires finite element modelling with cohesive elements to simulate the formation of the crack. Displacements from these simulations can then be used to generate a set of deformed images. This will provide valuable insights into the effect of temporal and spatial smoothing on the current strength identification procedures. This could also extend the work to crack propagation and toughness measurements.

Combined Tension–Shear Testing Work is currently under way to explore the extension of the IBII concept to develop a test for obtaining interlaminar shear, and combined tension–shear properties. This would enable more complete failure envelopes to be populated at high strain rates. This information is not currently available and would be invaluable for improved high strain rate modelling of composite materials.

Conclusions

This work presented the design and experimental validation of the IBII test to measure interlaminar tensile properties at high strain rates. By combining ultra-high-speed imaging with the grid method, full-field maps of displacement, strain and acceleration are obtained. The virtual fields method is used to identify interlaminar stiffness and tensile strength from the measured kinematic fields. The key results from this study are summarised as follows:

• Despite limited spatial resolution, the current study demonstrates that measurement quality of current ultra-high speed cameras is sufficient to identify interlaminar stiffness and tensile strength from the same test.

• Stiffness and strength were found to exhibit a substantial sensitivity to strain rate. An average interlaminar elastic modulus of 10.3 GPa was identified across all 1–3 plane specimens using reconstructed stress–strain curves. For the same specimens, the reduced special optimised virtual fields approach identified an average modulus of 10.7 GPa. Stiffness measurements were made at peak average strain rates on the order 3500 s$^{-1}$. This represents an increase between 30 and 35% compared to quasi-static values.

• Tensile strength was found to have a higher strain rate sensitivity than stiffness. The average tensile strength over all specimens was measured to be 114 MPa at peak average strain rates on the order 4500 s$^{-1}$. This corresponds to an increase of approximately 125%, compared to quasi-static values.

• Image deformation simulations are a powerful diagnostic tool for characterising the errors arising from measurement resolution and noise. This enables one to robustly select optimal smoothing parameters. It is also a useful diagnostic tool for studying the effect of post-processing operations (e.g., effect of data extrapolation at the edges) and experimental factors (e.g., grid size, specimen geometry, grid contrast) on the identification of stiffness parameters.

• The use of printed grids has proven to be effective for significantly reducing the number of grid defects. Therefore, this approach is recommended for interlaminar testing where higher magnification is required. However, the current technology is limited to grid periods on the order of 0.3 mm, which will not be enough either for higher spatial resolution cameras or for higher magnification (smaller specimens). Other deposition routes like the one recently proposed by Brodnik et al. [44] could be pursued.

This work shows that new test methods based on full-field measurements are very promising for measuring interlaminar properties at high strain rates. This enables data to be collected at strain rates where current techniques are unreliable. The capability of full-field measurements will only increase as ultra-high-speed camera technology improves. This will create additional opportunities for the development of advanced tests, and a more complete characterisation of composite materials at high strain rates.