Design Optimization of a Composite Rail Vehicle Anchor Bracket

Abstract

The rail transportation sector is currently seeking to decrease greenhouse gas emissions by incorporating composite materials that can reduce the mass of vehicles. During early adoption of composites in the rail transportation industry, these materials have predominantly been applied to simple design geometries and lightly loaded structures, have been optimized only through modification of composite thickness and composite layer shape, and have only been constrained with respect to a single mechanical performance metric. This study investigates the use of finite element analysis software in the simulation of fiber-reinforced composite materials applied to, and optimized for, a complex and heavily loaded rail vehicle anchor bracket. The research assesses the applicability of optimization methodologies to a complex and heavily loaded structure and advances established practices by constraining the solution with respect to multiple design requirements: manufacturing, compliance, and failure criterion. The optimization process successfully developed a composite structure with a predicted mass reduction of 33% compared to an existing steel design, and simultaneously met compliance, manufacturing, and failure criteria constraints.

1 Introduction

The rail transportation industry is currently seeking to reduce greenhouse gas emissions by reducing energy use. An effective method to decrease energy use is to reduce the weight of vehicles. Fiber-reinforced composite materials, often referred to as fiber-reinforced plastics (FRP), offer unique benefits in vehicle design due to low weight and high specific stiffness [1].

Composites also offer the advantage of increased geometric flexibility when molded and fabricated into shapes that would either not be possible or would be difficult to manufacture from conventional metallic materials [2]. During composite manufacturing, the material can be tailored into complex shapes and layered to create complex geometries that satisfy structural requirements. This geometric flexibility allows the potential for structures to be designed with improved load paths and enhanced component integration, further reducing weight.

Applying these advantages over metals, vehicle designers have successfully reduced the weight of airplanes, cars, and ships by implementing composite materials [3]. Aircraft manufacturers, for example, have produced mid-sized airliners with 50% or more of the vehicle weight constructed from composites which has resulted in vehicles that are 21% more fuel efficient than their metallic-only predecessor models [4].

While rail vehicle designers have become interested in the application of composite materials in recent years, these materials have not been implemented in a large scale within the industry [5]. However, current conceptual rail vehicle designs, utilizing composites, are estimated to reduce greenhouse gas emissions by 26% by lowering vehicle weight [6]. Due to the inexperience of the rail industry with respect to composite materials, many early applications have directly replaced metals with composites in existing design geometries [7]. Further, to satisfy mechanical performance requirements, composites are often thickened uniformly. Unfortunately, this practice fails to recognize many important potential benefits of composite materials, and as a result, has slowed the adoption of these materials by the industry.

More recently, vehicle designers have begun utilizing optimization techniques to alter design geometries to better utilize the composite materials [1, 8,9,10,11,12,13,14,15]. The most common optimization technique currently used by vehicle designers is a software-simulated form of topology optimization (TO) which alters the structural geometry to optimize the weight of the design [16]. TO takes advantage of the benefit that composites offer over metallic materials: that each layer of the material can be easily altered to a unique geometry to provide an optimal structure. During TO, software simulates the process of individual layers of the composite being altered to build up or reduce the structure in areas high or low stress to reduce weight while still satisfying structural requirements. The optimized solutions are achievable through manufacturing because the process emulates how composite structures are typically produced through “laying up” discrete layers of material in a mold to develop the desired geometry profile.

So far, most applications of TO in mass transit vehicle design have been applied to relatively simple structural components such as body and floor panels which are lightly loaded [8, 17,18,19,20,21]. Body and floor panels that have been studied are considered simple because they are primarily two-dimensional flat geometries and do not involve the intersection of multiple structural sections. The intersection of multiple structural sections in more complex three-dimensional geometries increases the intricacy of the composite design process and has not been studied as frequently. Furthermore, these same studies have typically applied simple constraints to the optimization process to meet a single mechanical performance requirement while minimizing mass. Wennberg et al., for example, conducted a TO study on a rail vehicle wall panel which had a simple flat geometry, was lightly loaded, and was only constrained with respect to stiffness [17,18,19]. Mallikarjun et al. completed a TO study on a mass transit vehicle’s flat floor panel, but constrained the process only with respect to stress, and selected a simple design geometry with low loading requirements [20]. While early applications of TO by rail vehicle designers have developed designs that reduce mass, neglecting the other multiple constraints, usually considered during vehicle design, such as manufacturability and application-specific failure criterion, can lead to design solutions that are neither feasible for production nor operation. Furthermore, without applying the TO process to complicated multi-section structural geometries that are heavily loaded, it is uncertain whether the process would have applicability to all parts of a vehicle structure.

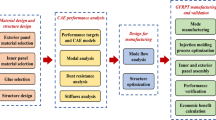
This study targets the potential gains available for the vehicle industry by applying TO methodology to a relatively complex and heavily loaded, existing vehicle structural geometry. This study includes the novel step of simultaneously applying mechanical and failure criteria as constraints in the optimization process. This study also adds a step by conducting a second optimization iteration for manufacturing to assess the feasibility of producing and implementing the design solution on a rail vehicle. Figure 1 demonstrates the difference between the optimization process used in previous studies and the one used in this current work.

Fig. 1

Previous optimization process compared with the one used in this study

It is anticipated that this study will provide evidence for vehicle designers that while the application of composites, and associated optimization methodology, to existing geometries designed for structures currently manufactured from steel will predict weight savings, ultimately, the real weight savings will be limited without a composite-specific geometry redesign. It is the development of an approach to extend current TO to enable composite-specific geometry optimization, which can most efficiently take advantage of the composite materials and incorporate manufacturing optimization, that is the long-term goal of the current work.

2 Materials and Methods

2.1 Steel Model Design

This study focuses on a common rail vehicle structure, which is complex in geometry and heavily loaded, to assess the feasibility of composites as a direct replacement for typical steel construction. During rail vehicle operation, significant forces are applied to the bogie structure during propulsion and braking. To distribute these forces, common rail vehicle designs transmit them out of the bogie frame via a traction rod, through an anchor bracket and into car body side sill. From experience, anchor brackets are only designed to support longitudinal forces, and are not designed around lateral or vertical loads. The European rail vehicle design standard, EN13749, provides Eq. 1 for determining the specific longitudinal loading values for structures such as anchor brackets [22]:

$$F_{{{\text{XC}}}} = m_{1} \cdot a_{{{\text{xc}}}},$$

(1)

where F_xc is the longitudinal force, m₁ is the mass of the vehicle, excluding the bogies, and a_xc is the longitudinal acceleration of the vehicle. A typical rail vehicle, excluding the bogies, has a mass (m₁) of 44,000 kg [23]. The European standard states that longitudinal acceleration, a_xc, is equal to the deceleration rate during emergency braking, which is typically 1.40 m/s² [24]. Inserting these mass and acceleration values into Eq. 1 results in an F_xc value of 61 kN. There are four anchor brackets that must support this load, so the 61 kN is divided over those structures for an individual bracket load of approximately 15 kN. A safety factor of 2.0 was applied to the calculated load in this study to ensure an appropriately conservative design was developed, resulting in a design load for each bracket of 30 kN. While other loading conditions could be considered, the load developed for this study is consistent with the industry standard and represents the most conservative condition the structure would experience during service. EN13749 identifies emergency braking deceleration as the event that will result in the highest loading condition and states that it is more extreme than vehicle acceleration or other typical service loads. Designing a structure against other loads associated with other service conditions would result in a structure that is not suitable for the most extreme service condition that is being used in this study.

Figure 2 illustrates that the anchor bracket is a complex, heavily loaded structural component, very different from simple, lightly loaded car body structures which have formed the basis for past research that has explored the application of composite materials.

Fig. 2

Example anchor bracket arrangement on a rail vehicle

The anchor bracket structure from a rail vehicle, as shown in Fig. 2, was modeled using finite element analysis (FEA) software. First, the existing steel anchor bracket was modeled to develop a baseline mechanical performance metric for the study. In the existing design, the main body of the bracket structure is a hollow welded fabrication, manufactured from 6.35-mm-thick ASTM A36 steel, having a mass of 25.46 kg. The main body of the bracket has weld shelves to accommodate fillet weld connections between the pieces of steel. The main structure was modeled using 2D shell elements. A solid 80-mm-thick ASTM A36 steel machined block at the base of the anchor bracket accepts forces from the traction rod through two bolts. This machined block was modeled using 3D hexahedral elements. The connection between the 2D elements and the 3D elements in the steel model were modeled using multi-point constraint equations to simulate a weld and were constrained against three degrees of freedom, but rotational degrees of freedom were free. The modeling of the 2D and 3D element connection is common practice used in the simulation of welded joints [25]. The total anchor bracket structure is 506 mm tall and 335 mm wide. The anchor bracket is affixed to the side sill structure with six mounting bolts. Figure 3 depicts how the model was constrained at the top bolting plate of the structure to represent the fixity associated with the mounting arrangement on the vehicle’s side sill. Table 1 provides details for the steel structure that was modeled.

Fig. 3

Steel anchor bracket model geometry, boundary condition, and force application

Table 1 Steel anchor bracket model details

The functional requirement of the anchor bracket is to transmit forces between the traction rod and the side sill, suggesting that a reduction in structural flexibility improves the efficiency of this force transfer. Therefore, the flexibility of the existing steel structure was modeled for use as a benchmark parameter for the proposed composite design. Compliance, $C,$ is the flexibility of a structure and is the inverse of stiffness ($k$) and is given by Eq. 2 [27]:

$$C = \frac{1}{k}.$$

(2)

Stiffness ($k$) is the amount in which a structure resists elastic deflection when force is applied, and is given by Eq. 3:

$$k = \frac{F}{\delta }{ },$$

(3)

where $F$ is the force applied, and $\delta$ is the resulting displacement in the structure. The FEA model was used to calculate an overall structural compliance of 3.82E-09 mm/N for the steel design. This compliance value will be used as a constraint during the composite optimization process.

2.2 Design Model for the Composite Structure

The same steel geometry was next modeled replacing the steel material with fiber-reinforced plastics (FRPs). FRPs consist of a matrix and a reinforcement. It is important to note that, unlike the steel structure where a material of known properties is selected, in the design of the composite structure, the composite material (the laminate) is being designed in parallel. The reinforcement is typically made from glass (GFRP) or carbon fibers (CFRP) that are manufactured into layers of oriented fibers that are each referred to as a “ply.” The polymer matrix material for heavily loaded structures is usually an epoxy resin which binds the fibers together. Fiber plies are different from the metallic materials currently used to construct anchor brackets due to their anisotropic behavior. Anisotropic materials have varying properties depending on the direction that load is applied. FRPs can, however, be manufactured or constructed to provide more consistent performance in various direction by the use of fabrics which weave fibers at various angles or by assembling “laminates” which stack multiple unidirectional plies in varying directions, thus enabling tailoring of material properties within the plane. Laminates with unidirectional plies are structurally more efficient, can be less expensive, are commonly used, and were therefore selected as the FRP construction to simulate in this study. Typical unidirectional ply angles used in composite laminates are 0°, −45°, 45°, and 90°, but varying the relative number of each orientation, or moving away from strictly these angles, allows the designer flexibility to optimize the structure.

To accurately model and optimize the anisotropic properties of composite materials, Altair’s Hyperworks FEA software was selected for this study. Hexcel 8852 AS4 carbon fiber and Scotch 1002 E-Glass were selected as representative unidirectional epoxy FRP materials. Material properties relevant to this study, for the two composite materials, were obtained from the National Center for Advanced Performance (NCAMP) and PC-LAMINATE material testing reports, and the relevant data are provided in Table 2. The anisotropic properties of the composites are evident in Table 2 through the varying moduli and strength values in different directions. For the purpose of this study, individual laminates were assumed to be joined with material that had properties matching the composites. This approach was taken in an attempt to retain a geometry consistent with the steel bracket and to verify that a performance gain could be made, through the introduction of composites, even with this severe constraint.

Table 2 Composite material properties

Figure 4 depicts how the geometries of the eight steel plates making up the hollow main body of the anchor bracket were used to create areas that could be considered for manufacture as individual composite laminates. Figure 5 shows that the solid machined block which interfaces with the traction rods remained modeled as steel to improve the comparison with the baseline steel structure, as this geometry would be difficult to manufacture from composites without a comprehensive redesign of the complete anchor bracket. The connection between the steel machined block and the composite structure was modeled as a multi-point constrain equation that allows for six degrees of freedom to simulate an adhesive joint. The modeling of the connection is consistent with the approach used in the design joints between metal and composite structures in transit vehicles [30].

Fig. 4

Anchor bracket geometry divided into eight manufacturable composite laminates

Fig. 5

Composite anchor bracket model geometry, boundary condition, and force application

As a starting point for the simulation and optimization, each laminate was modelled as eight plies oriented in the following directions: 0°, 45°, −45°, 90°, 90°, −45°, 45°, and 0°. This type of laminate is referred to as “quasi-isotropic,” and was selected as a baseline construction because it provides similar in-plane characteristics to the isotropic materials typically used in rail vehicle structures. Quasi-isotropic laminates create similar mechanical performance to isotropic materials within the plane of the plate by stacking plies symmetrically at varying angles [31].

A uniform thickness model (UTM) was developed where all plies were modeled with identical thickness and shape within each laminate, as shown in Figs. 6 and 7. As stated previously and shown in Fig. 5, the shape of the eight laminates in the UTM model matched the shape of the eight steel plates that made up the hollow main structure of the original steel model. Initially the UTM included ply thicknesses of 0.794 mm, chosen only for convenience, so that the resulting eight-ply laminate had a thickness of 6.35 mm, equal to the thickness of the original steel structure. During a preliminary check of the simulation, both carbon and glass fiber models failed to meet the compliance requirement when the UTM laminates were 6.35 mm thick. For the optimization approach to function within Hyperworks, it is necessary to begin with a structure that is thick enough to at least meet the compliance requirements. Thus, the thickness of all plies within each laminate in the UTM models were iteratively increased by 1 mm per iteration until the model achieved the required compliance. The carbon fiber model met the compliance requirement when the initial laminate thickness was set to 24 mm (~3.8 times thicker than the 25.46-kg steel structure) with a corresponding mass of 27.01 kg. The glass fiber model met compliance when the thickness was set to 96 mm (~14.8 times thicker than the steel structure) with a corresponding structural mass of 111.57 kg. Clearly, the resulting eight plies making up these thicknesses, whether the carbon fiber or glass fiber composite is considered, are unrealistically thick but were initially modeled this way for efficiency. The adjustment of the thickness and incorporation of ply thicknesses matching common practice are the subject of the following sections.

Fig. 6

UTM laminate design with 2D element thicknesses visualized to show dimensions in 3D

Fig. 7

UTM structure with 2D element thicknesses visualized to show dimensions in 3D

2.3 Topology Optimization Methodology

Optimization of composites is a complex process, due to the materials’ anisotropic nature. With advances in analysis tools and added experience related to fiber-reinforced composites, vehicle designers have developed optimization techniques to alter design geometries to better utilize these anisotropic materials [1, 8,9,10,11,12,13,14,15]. The most common optimization technique currently used by vehicle designers is termed topology optimization (TO) [16]. TO, both globally and locally, is used to alter the number of plies, ply thickness, and ply shape to reduce the weight of the design. The TO process is consistent with composite material forms and manufacturing techniques common to the aerospace industry, where the standard material utilized is in the form of prepreg (pre-impregnated reinforcement material) which can be easily cut into unique geometries, and be layered in a mold as part of the manufacturing process. This approach enables the development of structures that provide increased thickness and strength in areas of high stress while reducing thickness in low-stress areas to reduce mass. Cutting the plies into smaller geometries can cause discontinuity of the ply fibers, and as a result discontinuity of structural load paths, but the TO process can balance those negative effects against the benefit of reduced mass and still meet the structural requirements.

The optimization function for TO of each laminate is given by Eqs. 4–8:

$${\text{minimize }}f\left( x \right)$$

(4)

subject to

$$g_{a} \left( x \right) \le C$$

(5)

$${ }F \le 1$$

(6)

$$x_{i} \le x_{U} \quad i = 1, \ldots , n$$

(7)

$$\sum x \le 1 \;{\text{mm}},$$

(8)

where f(x) is the objective function, g_a(x) defines the constraint equations for C, F is the composite failure criterion, x_i is the thickness of elements within the plies following optimization, and n is the number of plies [19]. The maximum element thickness within each ply, ${x}_{U}$, is the UTM ply thickness. Minimum ply thickness was not defined, meaning areas of plies could be eliminated if the structure did not require them to meet the optimization constraints. The software requires that element thickness within each ply be uniform, so TO alters ply shape by reducing individual element sizes to zero. During the process, the original ply thickness is divided into multiple new plies to create different ply shapes that satisfy the compliance constraint, but allow the mass of the structure to be reduced. Plies of 45° and −45° were coupled, and 0° and 90° plies were also coupled to reduce complexity and provide a conservative structure, forcing their thicknesses to be modified symmetrically during the TO operation.

The TO operation had three constraints applied to it: minimum laminate thickness, compliance, and failure criterion. To preserve the original part geometry for the purpose of proper interface with the traction rod and side sill, laminate thickness (Sx) was constrained so that it would not reduce below 1 mm. For compliance, C, the overall value (3.820E-09 mm/N) obtained from the steel model was used as the constraint.

Because of the anisotropic nature of the material, analyzing failure in composite structures is different from the process used to assess the metallic structures that are common in the rail vehicle industry. There are several failure theories that are used within the composites industry, including: max. strain, max. stress, Tsai–Hill, Tsai–Wu, and Hoffman [32]. Each theory has been developed, and validated, to predict different types of composite failures. Hoffman failure criteria were specifically developed for the assessment of unidirectional composites, like those used in this study, and thus was selected as the failure theory to be applied as a constraint to the model. Hoffman’s theory simultaneously predicts failures in both the fiber and matrix of a composite laminate structure. The Hoffman failure criterion, F, is stated in Eq. 9:

$$F = \frac{{\sigma_{1}^{2} }}{{X_{t} \left| {X_{c} } \right|}} + \frac{{\sigma_{1} \sigma_{2} }}{{X_{t} X_{c} }} + \frac{{\sigma_{2}^{2} }}{{Y_{t} \left| {Y_{C} } \right|}} + \left( {\frac{1}{{X_{t} }} + \frac{1}{{X_{c} }}} \right)\sigma_{1} + \left( {\frac{1}{{Y_{t} }} + \frac{1}{{Y_{c} }}} \right)\sigma_{2} + \frac{{\tau_{2}^{2} }}{{S^{2} }} \le 1,$$

(9)

where σ₁ and σ₂ are composite stresses in longitudinal and transverse directions, and τ is the shear stress. X_t and X_c are tensile and compressive strengths parallel to the fiber direction, respectively, Y_t and Y_c are the transverse tensile and compressive strengths normal to the fiber, respectively, and S is the shear strength. The FEA software calculates allowable values of σ_1, σ_2, and τ based on material properties listed in Table 3. X_t, X_c, Y_t, Y_c, and S which were obtained from the NCAMP and PC-LAMINATE material testing reports and are listed in Table 2. Composite failure is assessed within the model on an element-by-element basis. An element failure criterion value exceeding 1 predicts that a failure would occur under the loading condition applied. Therefore, in order for the TO operation to converge on a feasible design solution, no elements can fail. As a safety factor of 2.0 was already applied to the loading condition in this study, no safety factor was applied to the failure constraint.

Table 3 Composite model properties

It is important to note that topology optimization is nonlinear, and each solution is unique to the boundary conditions, loading, and constraints applied to the process. Applying different loads or constraining the optimization process in a different way would result in unique ply geometries and thicknesses. Furthermore, altering the boundary condition, or changing the direction that forces are applied, would result in the quantity and thickness of plies of each angle to change to efficiently transfer the loads.

3 Results and Discussion

3.1 Topology Optimization Results

In this study, the objective of the optimization was to reduce mass, while meeting both compliance and the failure criteria. The results of the TO modeling is a reduction in the mass of the carbon fiber model to 14.96 kg and the glass fiber-reinforced composite model to 48.73 kg, while meeting all constraints. Figure 8 shows the overall geometry of the carbon fiber structure following the TO operation. Figure 9 shows the thickness of the carbon fiber structure following the TO operation. The resulting composite structures maintained the original laminate thickness in the connecting areas where laminates intersect, while most other areas were thinned to values ranging from 1–17 mm. This is logical, as the geometry that the composites were applied to has sharp angles in the connection areas between where laminates were applied that were designed to allow for welding of metallic plates. In the composite model, these sharp angles cause stress concentrations and then result in increasing thickness in these areas in the TO operations to satisfy failure criteria. In a composite-specific geometry, the transitions from surface to surface would be much less severe, and the overall geometry would take on more biologically inspired contours. Yet, given the current constraints, to accommodate the more complex topology of the structure, the number of plies was increased from 64 uniform-thickness plies to 236 plies of varying thickness for the carbon fiber model, and 243 plies of varying thickness for the glass fiber model. Table 3 provides details of the TO model results.

Fig. 8

Carbon fiber TO geometry

Fig. 9

Thickness contour plot of carbon fiber TO anchor bracket

As an example of how TO altered each ply geometry, Fig. 10 shows the modification of two 0° and 90° plies within laminate 8 of the carbon fiber structure. The ply shape is altered to remove area without allowing the overall compliance of the structure to fall below the constraint value. The ply thickness was also altered from the UTM value of 3 mm to 0.965 mm to reduce mass. As 0° and 90° plies were coupled within the simulation, the geometry and thickness of the two plies remain matched following the TO operation as shown in Fig. 11. Plies of 45° and −45° were also coupled, resulting in matching plies that were also thinned and modified in geometry, as shown in Fig. 12. The number of plies within the laminate increased from eight to 30 following TO, but overall thickness of the laminate decreased in many areas as each individual ply was thinned.

Fig. 10

Original carbon UTM fiber ply geometry (left) and TO results for laminate #8, [0/90] plies (right)

Fig. 11

Original UTM carbon fiber geometry and thickness (top) and TO results for laminate #8, 45° (left) and −45° (right) plies

Fig. 12

Carbon fiber TO Hoffman failure criterion results

During the TO process, composite failure is assessed on an element-by-element basis using the Hoffman criterion. The Hoffman failure criterion values for the structure following TO show maximum composite failure values of less than one for both the carbon and glass structures, predicting that no failure would occur. Figure 11 shows the locations of the maximum Hoffman failure criterion values for all plies within the carbon fiber structure following TO. Predictably, the areas with the highest failure values are on the front face and at areas where laminates connect due to the high longitudinal load that has been applied to the structure.

3.2 Manufacturing Optimization Results

The carbon fiber model was able to satisfy all constraints at a lower mass than the glass fiber composite model, which is no surprise given the lower modulus of the glass fibers. Given this substantially lower mass, 14.96 kg for carbon fiber and 48.73 kg for glass fiber, only the carbon fiber-reinforced composite is considered further for manufacturing optimization. One deficiency of the TO process is that it allows for composite plies to be modified to any thickness. In this study, the TO solver allowed for many plies to have thicknesses below 0.05 mm. This deficiency, which has not been addressed in previous studies, can lead to plies which are either too thick or too thin to be manufactured [17,18,19,20]. Therefore, an additional step was taken in this study to define manufacturing optimization (MO) constraints to be applied in the model. Manufacturing constraints were set so that each ply was required to be divisible by 0.188 mm, the manufactured thickness of a cured ply, as used in NCAMP’s material test. Application of the MO process to the TO model increased the total number of plies in the component from 236 plies of variable thickness to 738 plies with uniform thickness. Figure 13 shows the change in laminate composition following the MO operation. The thicker plies of up to 2 mm were divided into multiple plies that were 0.188 mm, while thinner plies were thickened to meet the manufacturing requirement. Due to the thickening of some thinner plies, the MO model increased in mass by 2.020 kg compared to the TO model. This structure continued to meet the compliance and failure criterion constraints that had been previously applied.

Fig. 13

Example TO ply profile (left) and MO (right) in Laminate #8

3.3 Discussion of the Methodology

This study demonstrates that composites can be applied to complicated and heavily loaded rail vehicle structural components with the potential to provide weight savings over steel designs even without geometry optimization specific to the use of composite materials. Figure 14 demonstrates how the sequence of composite material application and optimization resulted in variations in weight, with large potential reductions.

Fig. 14

Optimization geometry and mass iterations

Past composite research has included simply constrained optimization routines with the goal of minimizing mass while meeting a single mechanical performance metric [17,18,19,20]. This study advances current methodologies by incorporating manufacturing and failure criteria that would be required of the component for production and operation, and the model successfully met these requirements. The 33% mass reduction predicted in this study was comparable to weight savings in other designs accomplished in previous studies [19, 20].

If a physical model were to be created from this design, however, it would be difficult to actually achieve the 33% mass reduction that was predicted in this analysis, as the design would need to be further refined to improve manufacturability and fully integrate the eight individual laminates of this study. The final design included numerous complex ply shapes that would also make the construction of the final composite structure a time-consuming and expensive process. Constraining the optimization to limit the complexity of individual plies should result in a more manufacturable solution, but at the expense of mass.

The resulting design could also be adjusted to optimize the overall geometry for composite materials, rather than transferring the metal design directly to composites. The composite adaptation of the model included eight laminate panels, replicating the number of steel plates included in the existing design. One of the advantages of composites, when compared to steel, is the ability to remove joints and reduce the number of parts within a structure. As previously mentioned, topology optimization and manufacturing optimization are restricted to only optimize within the geometry of the original laminate and do not take advantage of the composite material's geometric flexibility to remove joints and merge geometries.

To achieve the constraints applied, the optimization process maintained 24-mm thickness in areas near laminate connections (corners of the structure), further emphasizing a potential opportunity to improve the structure by removing those joints and merging multiple laminate geometries together into a single, molded part. These thick areas also caused the number of plies required to manufacture the solution to be 744, reducing the feasibility of the design. A manufactured version of the current part geometry would likely be even more complex, however, as this model made the assumption that joints between laminates possessed the same strength as the composite material. To achieve the strength assumed in this study, still more plies would likely need to be added to the joint area to create a stronger connection between laminates. Finally, the machined block which interfaces with the traction rod was excluded from the optimization design space due to its complex geometry and solid structure. Integrating the machined block geometry into the structure would add further complexity to the design, but would be the most likely scenario for an actual composite replacement component.

Another issue with the final design is the number of plies with matching fiber orientation stacked consecutively. Stacking numerous plies of the same orientation is not considered a best practice within the composites community, as it can result in high interlaminar shear stresses and early failures [17]. While interlaminar shear was accounted for in this model, the design was tested under a static load condition in this study. In the dynamic environment of operation on an actual rail vehicle, this design may experience failure due to the consecutive stacking of multiple plies with the same fiber orientation. There is another method of optimization that has been applied following TO referred to as “shuffling optimization” that disperses plies of each orientation within the laminate to reduce the chance of interlaminar shear failure [19]. This method was not incorporated in this study because the design was already deemed to be infeasible for manufacture, and shuffling optimization would increase the complexity of manufacturing the part.

While these optimization deficiencies were anticipated, the analysis carried out using TO and multiple concurrent optimization parameters serves to demonstrate the potential for this approach and the relevance to composite material insertion into application areas traditionally reserved for metallic structure. Even in cases where the geometry is constrained to that designed for manufacture from conventional materials, such as steel, a significant weight savings is predicted. However, clearly a greater benefit is to be gained when geometry can be adapted to better utilize composite materials. New geometries should be developed to specifically gain the structural performance and manufacturing advantages that composites offer over metallic materials. Developing geometries specific to the composite application, however, is not part of common design practices currently used in the rail vehicle design industry [5].

A method to develop composite geometries is to optimize a model in three dimensions. Optimizing geometry in three dimensions promises to eliminate the need to predefine two-dimensional shell laminate geometry before establishing an optimal topology for the structure. This concept has been considered for application in rail vehicle structural parts, but, thus far, has not accounted for the anisotropic behavior of composites [14]. Research in this area is currently being initiated to develop such tools and methodologies. Figure 15 provides a preliminary design of the bracket geometry that incorporates the refinements discussed above to better take advantage of composite materials. This design, which is the starting point for a future study, removes most of the joints and connections from the original geometry, includes a composite block for interface with the traction rod, and is designed to be more composite manufacturing-friendly.

Fig. 15

Preliminary design of anchor bracket geometry redesigned for composite materials

4 Conclusions

Optimization of an existing rail vehicle steel anchor bracket geometry converted to the use of fiber-reinforced composites was undertaken. Using FEA modeling techniques, an iterative optimization was conducted following topology optimization and manufacturing optimization methodologies with the objective of minimizing mass while meeting manufacturability, failure, and compliance constraints. The final model successfully reduced the mass of the part by 33% compared to the baseline steel structure while satisfying the applied manufacturing, failure, and compliance constraints. This study represents an important step for the rail vehicle design industry by indicating the potential gains available through the application of composite materials to a complex and heavily loaded vehicle geometry. Further, the study advances composite optimization methodologies by incorporating multiple, parallel constraints into the design solution rather than applying each constraint sequentially. Ultimately, the results of this effort suggest that applying similar methodology, in conjunction with geometry optimization, for composite materials holds potential for substantial component part weight savings, even in highly loaded structural components.