1 Introduction

In India, rapid urbanization and motorization post independence have led to increased travel demand, triggering a transport crisis that includes congestion, pollution, and other environmental externalities. Mitigation of this transport crisis has become a challenging task in the transport industry. Development of public transport has been identified as a sustainable solution for all major transport problems. Moreover, public transport is the primary and only means of transport for a large section of society in India. The Working Group of Urban Transport [1] has suggested a desirable share of public transport of 60% of motorized trips to reduce energy needs and address the transport crisis. Public transport undertakings are striving to provide efficient and convenient travel. However, they are not providing better travel options due to various challenges in the public transport industry, such as financial instability, incompetence, and unreliability. Excessive operating cost, overstaffing, low productivity, and imprudent use of financial resources are a few of the institutional issues, while inadequate frequency, increased travel time, poor service quality, and overcrowding are a few of the reasons why users are shifting away from public transport. The declining share of public transport has caused the public transport industry to become loss-making.

While the government has a complete monopoly over the rail transport sector, there are many competing players in the road transport industry. In this fiercely competitive environment, state-owned public transport industry cannot operate sustainably, showing mediocre performance. In this respect, a crucial question is to identify which operating practices and administrative regulations could improve the public transport industry. Meanwhile, inefficiencies, bottlenecks, and the potential of public transport should be determined by evaluating the performance in the current scenario. Moreover, to improve the performance and efficiency in the face of reduced budgets, high political expectations, and competition between operators, the performance of the industry must be improved by optimizing the available resources.

In recent years, performance evaluation has become a focus of attention in the public transport industry, as it is viewed as a method to assess the outcomes of the system, which can be further analyzed to decide upon improvement strategies. Since public transport involves multiple stakeholders, optimization procedures must be performed rather than just evaluation. Unfortunately, performance optimization is a largely unexplored area, even though it facilitates efficient and effective use of technological, financial, material, and human resources. According to Perez et al. [2], a truly optimal solution exists only if a single criterion is considered. However, in practical scenarios, several issues must be addressed in the optimization procedure. Firstly, there are multiple decision variables, structured in multilevel hierarchies [3]; For instance, passenger transport assessment solely based on economic criteria may be too narrow, as the final decision-making depends on various types of factors other than monetary ones [4]. Secondly, some level of subjective judgement is involved in the assessment of decision variables, which can result in the use of incorrect information. Finally, the stakeholders in the public transport industry include the users, operators, and community at large [5].

The rationale for this paper is based on the following arguments: Studies on Indian SRTUs have tended to focus on performance evaluation, whereas the area of performance optimization has been left largely unexplored. While the performance evaluation process can acknowledge or assess the outcomes of any system for further analysis to decide upon improvement strategies, performance optimization can be viewed as a process of utilizing technological, financial, material, and human resources efficiently and effectively. This study proposes a performance optimization methodology integrating the analytical hierarchy process (AHP) and goal programming (GP), considering both operators’ and users’ perceptions. The analytical hierarchy process, a multicriteria decision-making tool, is used to evaluate the decision variables and calculate their weights for use as penalties in goal programming.

The objectives of this study are: (1) to identify the decision variables to be used for performance optimization, (2) to calculate their weights using the AHP, and (3) optimize the performance of the Kerala State Road Transport Corporation (KSRTC) considering both users’ and operators’ perceptions by using analytical hierarchy process and goal programming. The remainder of this manuscript is organized as follows: Section 2 reviews a few existing methodologies for performance evaluation and optimization techniques. Section 3 explains the methodology used in the study. Section 4 describes the current scenario of the KSRTC and the application of the methodology for optimization of its performance, followed by concluding remarks in Sect. 5.

2 Review of Literature

As mentioned above, performance evaluation of public transport is one of the widely investigated areas within the transit industry, whereas performance optimization is largely unexplored. According to Gleason and Barnum [6], in some instances, the terms “productivity,” “efficiency,” and “effectiveness” are synonymous with performance in the public transport industry, while in other cases “efficiency” and “effectiveness” are considered as different aspects of “productivity.” Many authors have concentrated on the development of models for performance evaluation using parametric, nonparametric, deterministic, stochastic, or soft computing techniques [7, 8].

Gleason and Barnum [6] examined various performance measures for efficiency and effectiveness and pointed out that there is a lack of understanding of system analysis concepts related to the selection of criteria. Guidelines for bus transit performance evaluation in Washington State were given by Kelley and Rutherford [9], considering both efficiency and effectiveness. He et al. [10] developed a systematic network operations management system incorporating various performance assessments of urban rail transit networks. The study analyzed various features of operation, changes in travel demand, availability of urban mass transit, and operational service quality. Thus, a technique for information system-based operational planning and performance evaluation using network operations management was developed. Various researchers [11,12,13,14,15] have used data envelopment analysis (DEA), a common nonparametric approach, for performance evaluation of the transit industry by estimating efficiency scores. Karlaftis [12] employed the DEA approach to evaluate the efficiency and effectiveness of urban transit systems using data from 256 US transit systems over a 5-year period. Nineteen public transport systems were analyzed using DEA by Sampaio et al. [14] to determine the service efficiency based on three basic inputs: labor, fuel, and capital. In the study by Lao and Liu [16], the combined application of DEA and a geographic information system (GIS) was used for performance evaluation of bus lines, considering both the operations and operating environment. In that study, the GIS was used to create demographic profiles within the service corridors, then DEA was applied to compute the operational efficiency and spatial effectiveness for comparison of operational and spatial aspects of the bus lines. Vaidya [17] evaluated the relative performance of 26 public transport undertakings in India based on 19 criteria, grouped into operations, finance, and accident categories, then evaluated their importance using the AHP. Furthermore, DEA was used to evaluate the public transport undertakings using various criteria within each group. Finally, to quantify the overall performance, a transportation efficiency number (TEN) was developed. Short- and long-run cost-efficiency analysis of Indian public bus companies was carried out using DEA by Venkatesh and Kushwaha [15]. Tsai et al. [18] used a two-stage DEA model to identify and measure the factors which determine the technical aspects, allocation, and cost-efficiency of 20 international urban rail systems.

Yeh et al. [19] examined the use of the fuzzy multicriteria approach for performance evaluation. The concept of optimality of each alternative with respect to each criterion was used to develop a fuzzy singleton matrix from a weighted fuzzy performance matrix. Finally, an overall performance index was calculated for each alternative by incorporating the decision-maker’s attitude towards risk. Sun et al. [20] used a multiagent-based simulation method to quantify performance improvement options for urban rail transit systems using a physical internet. The study examined the changes in the performance indicators before and after implementation of the physical internet. Rail transit line performance was measured using a hierarchical customer satisfaction framework in Istanbul [21]. The framework for the transit line performance evaluation used statistical analysis, the fuzzy analytic hierarchy process, fuzzy sets, and Choquet integrals to analyze customer satisfaction. This methodology is a multicriteria decision-making process that can be applied when the decision-making problem is complex with uncertain, subjective, and vague information.

The evidence described in the previous paragraph indicates that performance evaluation mainly deals only with the operational, financial, and technical characteristics of the public transport industry. Assessing public transport performance by merely using the operator’s data is an unfair practice, as the stakeholders involved in the public transport industry include operators, users, and society as a whole. Therefore, performance optimization must be carried out considering the various stakeholders. Optimization is a process of maximizing or minimizing an objective function by systematically choosing inputs from a set of input values. According to Wey and Wu [22], mathematical programming is an optimization approach using different models such as linear programming, integer programming, goal programming, dynamic programming, and game theory. Goal programming is a multiobjective optimization technique capable of handling multicriteria decision-making (MCDM) problems with multiple and conflicting goals. However, when goal programming is used as a decision-making tool, the goals correspond to diverse and conflicting criteria [23]. The performance optimization of a public transport undertaking by Murugesan and Ramamurthy [5] used the goal programming methodology, integrating users’ and operators’ perceptions. The methodology involved the identification of multiple objectives, their prioritization based on expert opinion, and determination of the optimal solution. To optimize the real-life situation more effectively, various techniques must be combined, and goal programming has been used as a part of such mixed modeling approaches. Integration of goal programming and the AHP has been applied in a variety of areas, including supplier selection [24], resource planning [25], project selection [26], transportation resource allocation [22], and location selection problems [27]. Saaty [28] illustrated the different uses of the multicriteria decision process using the AHP in the field of transportation, including route selection hierarchy, the best route mix to Pittsburgh Airport, a benefits/costs hierarchy to choose a mode, a planning hierarchy for the transportation system, and a simple dependence with a feedback cycle to choose a car. Wu et al. [3] used the AHP to identify the weights for indicators for an underground rail transit station area. The AHP was selected after comparing the rationality of different weight indicator scales.

Based on the above review of literature, we identified the following gaps: very few studies have tried to improve the performance of the public industry by optimizing the resources. However, researchers have carried out performance evaluation procedures. Moreover, to optimize real-life situations more effectively, various techniques such as goal programming and the AHP must be integrated. Also, users’ perceptions are not considered in literature to a desirable extent, even more so in the Indian context. We address these gaps herein by applying an integrated AHP–GP optimization procedure, taking into account both users’ and operators’ perceptions. The methodology adopted in this study is outlined in the next section.

3 Methodology

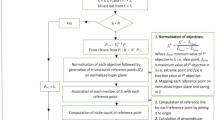
In the integrated AHP–GP model, the priorities of the decision variables are established using the AHP in the form of weighted deviations. The proposed model requires the evaluation of the decision variables with regard to how much they will affect the performance of public transport. Figure 1 presents the methodology proposed in this paper for performance optimization of public transport undertakings using the integrated AHP–GP method.

Fig. 1
figure 1

Performance optimization methodology integrating users’ and operators’ perceptions

Full size image

The methodology starts with the selection of various performance indicators, considering both operators’ and users’ perceptions. The decision variables are then categorized as user or operator oriented. The analytical hierarchy process (AHP) is used to evaluate these parameters and calculate their weights. The AHP is a multicriteria decision-making approach that can hierarchize a system involving multiple objectives, criteria, or factors. Saaty [29] provided a theoretical formulation for the AHP, which explains it as a decision support tool for solving complex decision problems. The AHP breaks down the decision problem into simpler elements based on their characteristics and organizes them into a hierarchy to incorporate significant quantities of information. The uppermost level of the hierarchy is the “goal” of the problem, intermediate levels are the criteria and subcriteria, while the lowest level is the decision variables. After this process of hierarchization, the AHP proceeds to priority setting. This involves pairwise comparison of elements at each level of the hierarchy and assigning a weight to each element to denote the priority based on its importance, as described by Saaty [29]. The judgement matrix describing the pairwise comparison of the decision variables on the AHP rating scale was collected from experts associated with bus transportation and academia using a designed pro forma.

The priorities of these elements can be estimated by determining the principal eigenvector ω of the judgement matrix A using Eq. (1)

$$A \cdot \omega = \lambda_{ \hbox{max} } \cdot \omega,$$
(1)

where A is the judgement matrix, \(\omega\) is the principal eigenvector, and \(\lambda_{ \hbox{max} }\) is the largest eigenvalue of the matrix A.

The normalized vector ω gives the vector of priorities of elements with respect to the other elements. In the final step of the AHP, logical consistency is checked, as the pairwise comparisons are based on subjective judgement. To test the consistency of the judgements systematically, first, the consistency index (CI) needs to be estimated using Eq. (2).

$${\text{CI}} = \left( {\lambda_{ \hbox{max} } - n} \right)/\left( {n - 1} \right),$$
(2)

where \({\text{CI}}\) is the consistency index, \(\lambda_{ \hbox{max} }\) is the largest eigenvalue of the matrix A, and n is the order of the matrix. Then, the consistency ratio (CR) is obtained by dividing the consistency index value by the random index (RI) values given in Table 1.

Table 1 Random index value
Full size table

The pairwise comparisons in a judgement matrix are considered to be satisfactorily consistent if the corresponding consistency ratio (CR) is less than 0.1. Considering the overall weighting of the operator and user, the final weighting for all the decision variables is obtained. These weights are given as penalties for the decision variables in the mathematical model using the goal programming (GP) methodology developed for performance optimization.

Goal programming is a multiobjective optimization technique used for multicriteria decision-making processes. This optimization technique is used to handle multiple objectives that are conflicting in nature. The GP methodology establishes a specific numeric goal for each objective which is to be achieved, assigns weights (obtained from the AHP) to these goals based on their relative importance, and finds a solution that minimizes the weighted sum of deviations from the goals. The general form of the weighted GP model is given in Eq. (3), having m goals, n decision variables, and p system constraints.

$${\text{Minimize}}{:}\;Z = \mathop \sum \limits_{i = 1}^{n} w_{i} \left( {p_{i} + n_{i} } \right),$$
(3)

subject to

$${\text{Constraints}}{:}\; \mathop \sum \limits_{j = 1}^{n} a_{ij} x_{j} - p_{i} + n_{i} = b_{i} , \quad \forall i = 1, \ldots ,m,$$
(4)
$$p_{i} , n_{i} ,x_{j} \ge 0, \quad \forall i = i, \ldots ,m;\quad j = 1, \ldots n,$$
(5)

where \(Z\) is the objective function (the sum of all the weighted deviations), \(w_{i}\) is the weight assigned to the \(i{\text{th}}\) goal constraint, \(a_{ij}\) is the coefficient of variable \(j\) in the \(i{\text{th}}\) goal, \(x_{j}\) is the \(j{\text{th}}\) decision variable, \(b_{i}\) is the associated right-hand side value, \(p_{i}\) is the positive deviation (overachievement), and \(n_{i}\) is the negative deviation (underachievement).

4 Case Study of Kerala State Road Transport Corporation

The data required for the performance optimization using the integrated AHP–GP method were obtained from the annual audit reports from 2014–2015 and 2015–2016 of the KSRTC [30, 31] and the Economic Review of Kerala [32]. The KSRTC is the single largest public-sector undertaking in Kerala, a southern state of India, carrying out passenger transport operations in the state. With 28 main depots and 45 subdepots spread across the 14 districts of Kerala State, the KSRTC caters for the transport of passengers. KSRTC owns a total of 5677 buses, with the greatest share, i.e., 3725, being ordinary city buses. According to 2016 data, 1095 buses were 10 years old or more. The KSRTC runs 7548 routes with a total length of 458,615 km, carrying about 1013.776 million passengers in the year 2015–2016. The gross distance operated is 587.011 million kilometers, with 530.989 million effective kilometers. The gross revenue earned by the KSRTC during 2015–2016 was ₹21,651.6 million INR. The gross revenue expenditure was ₹27,783 million INR, resulting in an operating loss of ₹6131.4 million INR. Table 2 presents the major indicators showing its operational efficiency.

Table 2 Major indicators showing the operational efficiency of the KSRTC [32]
Full size table

The staff per bus ratio is about 7.2, with staff productivity of 37.01 km/staff/day, and the number of breakdowns per million kilometers is 60, much higher than the national average. The heavy operating loss of the KSRTC is due to its operational inefficiency, high staff to bus ratio, operation on uneconomical routes, granting concessional rates, interest repayments, and pension commitments. Given this performance, the KSRTC cannot continue operating for long unless some reforms are applied to control the rising operating cost, utilize the funds effectively, and attract people to use public buses and thus increase the productivity. In this respect, improvements to the performance of the KSRTC can only be achieved by optimizing the available resources, considering both the operator and users.

Application of the integrated AHP–GP methodology requires the solution of two problems: the AHP and the linear goal program. The main goal of this study is to optimize the performance of the KSRTC by considering both stakeholders, viz. the operator and the users. The problem consists of first prioritizing the operator and users, then prioritizing the decision variables using the AHP. Applying the AHP involves setting the hierarchy of the decision process as shown in Fig. 2.

Fig. 2
figure 2

Hierarchy of performance optimization process

Full size image

The elements (users and operator) are further broken down into various factors or decision variables. Twelve decision variables are identified, taking into account both user and operator perceptions: controllable costs (X1), noncontrollable costs (X2), taxes (X3), staff per bus ratio (fleet operated) (X4), safety (X5), accessibility (X6), regularity (X7), load factor (X8), fleet utilization (X9), percentage of dead kilometers to effective kilometers (X10), journey speed (X11), and percentage of cancelled kilometers to scheduled kilometers (X12). Safety, accessibility, reliability, and journey speed are user perceptions, while all the other factors are operator oriented. Once the hierarchy has been established, pairwise comparison in each level was performed to determine the weights to be used in the objective function of the goal program. The comparison matrices are:

  • Level 1 Goal of the study: optimize the performance of the KSRTC

  • Level 2 The stakeholders of the public transport industry (KSRTC), viz. users and operator, a 2 × 2 matrix

  • Level 3 Decision variables: 7 × 7 matrix for the operator and 4 × 4 matrix for the users

The judgement matrix of pairwise comparison of level 2 elements (the stakeholders of the KSRTC) based on the AHP rating scale was provided by experts associated with bus transportation and academia using a designed pro forma. Table 3 presents the pairwise comparison of the two elements, viz. operator and users.

Table 3 Pairwise comparison matrix of the stakeholders
Full size table

Further, the decision variables, divided into user oriented and operator oriented, were analyzed to determine their priorities. Tables 4 and 5 present a sample pairwise comparison matrix of the operator- and user-oriented decision variables, respectively.

Table 4 Pairwise comparison matrix of operator-oriented decision variables
Full size table
Table 5 Pairwise comparison matrix of user-oriented decision variables
Full size table

Taking the overall weighting for the operator as 67% and for the users as 33%, the final weights for the decision variables are presented in Table 6.

Table 6 Final weights of decision variables
Full size table

The AHP results indicate that the operator cost and staff per schedule were the most important variables for the operator. This is in accordance with the findings in the socioeconomic review published by the state planning board of Kerala that losses incurred in the KSRTC are mainly because of the high bus staff ratio and inefficiency in operations. Among the user perceptions, safety of travel had the highest weighting. In this regard, note that Kerala recorded a total of 39,137 accidents in the year 2016, representing 3850 accidents per million vehicles registered in the state [32].

Having obtained the weights for the decision variables using the AHP method, the optimization process can continue using goal programming. The threshold values for the decision variables for GP optimization were obtained from the annual performance report of the KSRTC. The values (both actual and goal) given in Table 7 are considered for the performance optimization using the proposed methodology.

Table 7 Threshold values for decision variables
Full size table

The mathematical model for the weighted goal programming problem is explained in the methodology above. The aim is to minimize the sum of deviations such that the values obtained from the optimization are close to the goal values. Decision variables with higher weight reach their goal value before variables with lower weight. The objective is to minimize the deviations. The set of constraints formulated takes into account the higher and lower bounds of the decision variables, in the form of inequality constraints that are converted to standard equality constraints by assigning positive and negative deviations. The problem was solved using the software LINGO 17.0, a product of LINDO Systems INC, which is optimization modeling software for linear and nonlinear integer programming. The formulated GP model is as follows:

Objective function:

$$\begin{aligned} & {\text{Min }}27.39n_{1} + 27.39p_{1} + 27.39n_{2} + 27.39p_{2} + 27.39n_{3} + 27.39n_{4} + 21.22n_{5} + 21.22p_{5} + 16.77n_{6} \\ & \quad + 16.77p_{6} + 10.32n_{7} + 10.32p_{7} + 9.8n_{8} + 9.8p_{8} + 9.66n_{9} + 9.66p_{9} + 7.85n_{10} + 7.85p_{10} + 6.84n_{11} \\ & \quad + 6.84p_{11} + 5.9n_{12} + 5.9p_{12} + 4.65n_{13} + 4.65p_{13} + 4.37n_{14} + 4.37p_{14} + 4.34n_{15} + 4.34p_{15} + 3.87n_{16} \\ & \quad + 3.87p_{16} + 3.64n_{17} + 3.64p_{17} + 3.41n_{18} + 3.41p_{18} + 2.94n_{19} + 2.94p_{19} \\ \end{aligned}$$
(6)

Constraints:

Priority 1 Optimize the financial resources adequately

$$X_{1} + X_{2} + X_{3} - n_{1} = 419.044$$
(7)
$$X_{1} + X_{2} + X_{3} + p_{1} = 421.4$$
(8)
$$X_{1} - n_{2} = 337.7$$
(9)
$$X_{1} + p_{2} = 340.0$$
(10)
$$X_{2} - n_{3} = 65.442$$
(11)
$$X_{3} - n_{4} = 15.902$$
(12)

Priority 2 Maximize the safety of the users

$$X_{5} - n_{5} = 99$$
(13)
$$X_{5} + p_{5} = 99.99$$
(14)

Priority 3 Reduce the staff per bus ratio

$$X_{4} - n_{6} = 4.5$$
(15)
$$X_{4} + p_{6} = 5$$
(16)

Priority 4 Maximize the productivity by decreasing the staff per bus ratio and increasing the fleet utilization

$$X_{4} + X_{9} - n_{7} = 94.5$$
(17)
$$X_{4} + X_{9} + p_{7} = 100$$
(18)

Priority 5 Maximize the utilization of public transport by increasing the load factor

$$X_{8} - n_{8} = 115$$
(19)
$$X_{8} + p_{8} = 125$$
(20)

Priority 6 Improve safety, accessibility, and regularity

$$0.33X_{5} + 0.33X_{6} + 0.33X_{7} - n_{9} = 83$$
(21)
$$0.33X_{5} + 0.33X_{6} + 0.33X_{7} + p_{9} = 90$$
(22)

Priority 7 Increase the load factor and reduce the % of cancelled kilometers to scheduled kilometers

$$X_{8} + X_{12} - n_{10} = 120$$
(23)
$$X_{8} + X_{12} + p_{10} = 133$$
(24)

Priority 8 Increase the load factor and fleet utilization

$$X_{8} + X_{9} - n_{11} = 205$$
(25)
$$X_{8} + X_{9} + p_{11} = 220$$
(26)

Priority 9 Improve regularity by reducing the % of cancelled kilometers to scheduled kilometers

$$X_{7} + X_{12} - n_{12} = 95$$
(27)
$$X_{7} + X_{12} + p_{12} = 103$$
(28)

Priority 10 Reduce the % of cancelled kilometers to scheduled kilometers

$$X_{12} - n_{13} = 5$$
(29)
$$X_{12} + p_{13} = 8$$
(30)

Priority 11 Improve journey speed

$$X_{11} - n_{14} = 30$$
(31)
$$X_{11} + p_{14} = 35$$
(32)

Priority 12 Increase accessibility

$$X_{6} - n_{15} = 60$$
(33)
$$X_{6} + p_{15} = 75$$
(34)

Priority 13 Maximize fleet utilization

$$X_{9} - n_{16} = 90$$
(35)
$$X_{9} + p_{16} = 95$$
(36)

Priority 14 Improve accessibility and reduce the % of dead kilometers to effective kilometers

$$X_{6} + X_{10} - n_{17} = 64$$
(37)
$$X_{6} + X_{10} + p_{17} = 80$$
(38)

Priority 15 Improve regularity

$$X_{7} - n_{18} = 90$$
(39)
$$X_{7} + p_{18} = 95$$
(40)

Priority 16 Minimize the % of dead to effective kilometers

$$X_{10} - n_{19} = 4$$
(41)
$$X_{10} + p_{19} = 5$$
(42)

where X1, X2, …, X12 are the various decision variables considered, and n and p are the negative and positive deviations, respectively.

4.1 Optimal Solution and Sensitivity Analysis

To obtain the optimal values, the linear weighted integrated AHP–GP problem was solved using LINGO 17.2. The optimal values of the decision variables along with the actual values are presented in Table 8.

Table 8 Optimal and actual values for decision variables
Full size table

The optimal solution indicates that decision variables such as operator cost, staff per schedule, and safety, having higher penalties, tend more towards the goal values than variables such as the % of dead kilometers to effective kilometers, journey speed, etc. that have low penalties. For intracity bus services, an increase of 43.59% of the load factor along with an increase of 11.12% in fleet utilization and a reduction of 42.03% in the percentage of dead kilometers to effective kilometers will help to achieve the goal values with the optimal value for the objective function. Reducing the controllable costs by 15%, the staff per bus ratio by 49.15%, and the percentage of cancelled kilometers to scheduled kilometers by 75.82% would improve the optimal value of the objective function. The model solution suggests that decreasing the staff per bus would further reduce the staff cost and hence the operating cost. This can be achieved by implementing a single duty system, i.e., 8-h duty in a single shift. Thus, only one driver and conductor are required in an intracity bus. Also, the report of the subgroup on the SRTUs [33] suggests that SRTUs should employ both mechanical and operational staff on a contractual basis to reduce the staff cost. The bus to staff ratio can be reduced by introducing technological improvements such as an intelligent transport system (ITS), computerized staff scheduling, passenger information system, electronic ticketing machines (ETMs), global positioning system (GPS)-based ETM, and automated ticketing systems. In terms of the users, increasing the accessibility by 44.76%, safety by 24.85%, and regularity by 11.80% would attract passengers to the public transport, in turn improving the load factor and thus enhancing the performance of the KSRTC.

The data used for the goal programming may be subject to change, thus it is essential to check the sensitivity of the optimal solution to variations in the data. Sensitivity analysis can identify the impact that variations in the decision variables will have on the performance of the system. The values of the optimal solution and degree of goal attainment under different input combinations are listed in Table 9. Based on these values, the best condition is achieved with controllable costs of ₹340 million INR, noncontrollable costs of ₹65.442 million INR, taxes of ₹15.902 million INR, staff per bus ratio (fleet operated) of 4.5, safety of 99%, accessibility of 60%, regularity of 95%, load factor of 115%, fleet utilization of 90%, percentage of dead kilometers to effective kilometers of 4, journey speed of 35 kmph, and percentage of cancelled kilometers to scheduled kilometers of 5%. The worst condition is with controllable costs of ₹337.7 million INR, noncontrollable costs of ₹65.442 million INR, taxes of ₹15.902 million INR, staff per bus ratio (fleet operated) of 4.5, safety of 95%, accessibility of 61.525%, regularity of 95%, load factor of 115%, fleet utilization of 95%, percentage of dead kilometers to effective kilometers of 4, journey speed of 30 kmph, and percentage of cancelled kilometers to scheduled kilometers of 5.

Table 9 Sensitivity analysis
Full size table

5 Conclusions

A weighted goal programming methodology integrated with the analytical hierarchy process for performance optimization of public transport undertakings is presented, which includes users’ and operators’ perceptions. The identification of key decision variables for pairwise comparison was essential, since use of comparable and closely related parameters subjected to qualitative rating resulting in inconsistent judgements cannot be used in further analysis. These decision variables were prioritized using the AHP and modeled as a goal program. The integration of users’ and operators’ perspectives ensures that the optimization of the public transport industry can be achieved while safeguarding the interests of both passengers and operators.

As a case study, the performance optimization of the KSRTC was undertaken. Twelve decision variables were identified by taking into account both user and operator perceptions. Furthermore, the perceived importance of each of the decisive factors from the point of view of both the users and operator were obtained from experts and was prioritized using the AHP. The integrated AHP–GP model was then used to determine the optimal solution while taking multiple conflicting objectives into consideration by using penalty values, with higher penalty values for more important decision variables. The findings of this study are as follows:

  1. 1.

    The operator cost and staff per schedule were the most important variables for the operator, whereas among the user perceptions, safety of travel had the highest weighting.

  2. 2.

    The optimal solution indicates that increasing the accessibility, safety, and regularity will attract passengers to public transport, which in turn will improve the load factor and influence the operators to maximize fleet utilization and reduce the cancellation of schedules.

  3. 3.

    The proposed model solution suggests that decreasing the staff per bus will further reduce the staff cost and hence the operating cost.

The proposed method can be adopted for solving performance optimization problems of public transport undertakings. Using the AHP, planners can consistently integrate the opinions of all decision-makers and effectively evaluate scenarios and optimize resources. Further work will include the application of the proposed methodology to various other fields of public transport, such as urban rail transit, metro rail, and integrated public transport systems.