Design of Passenger Aerial Ropeway for Urban Environment

Abstract

Aerial ropeway is an effective alternative to the conventional modes of land public transport in metropolitan areas and cities. Construction of passenger aerial ropeways in urban environment is a very costly enterprise in terms of engineering and economics, and requires significant financial resources. This article is aimed at the development of the design method of the passenger aerial ropeway, ensuring the reduction in its construction cost. For this purpose, the individual components of the construction cost are considered, and the approximate calculation dependencies are proposed. It is shown that the cost of the aerial ropeway is mainly influenced by the installation step, height of intermediate towers and carrying rope tension. The task of the conditional nonlinear optimization of the given parameters is formulated and solved in the research. This task ensures the minimum cost of the aerial ropeway. The optimization task is done by taking into account possible limitations on the ropeway laying in the severely urbanized environment (the terrain, urban infrastructure arrangement, altitude performance of the urban development, technical characteristics of the carrying rope, etc.). Implementing the solution findings of the given optimization task makes it possible to significantly reduce the construction cost of aerial ropeways in urban environment.

1 Introduction

Aerial ropeways are widely used as continuous transport for organization of passenger and cargo carriage in many countries worldwide [1, 2]. Passenger aerial ropeways are mostly used for rapid and convenient movement of people to the sports, tourist, ecological and health-improving facilities within nature areas with difficult terrain which are difficult to access [3, 4]. Cargo ropeways are used in many sectors of economics for transportation of different cargos. The industries where one can see the use of cargo ropeways are mining, coal, chemical, metallurgical, power, timber and agricultural [5,6,7,8]. According to the data of the comparative techno-economic study [2, 9,10,11], aerial ropeways are more economically and environmentally beneficial than land transport (road, conveyor and rail), especially in cases when the terrain, high density of the housing and industrial development and various urban planning restrictions impede the development of the ground traffic.

The theory of passenger and cargo aerial ropeways was actively developed in the middle of the 20th century. At the same time, the studies in the area were conducted in England, Austria, Germany, Italy, Russia and other countries [1, 2, 5].

As it is shown in the related literatures [2, 6, 9, 11, 12], aerial ropeways are an effective alternative to the conventional modes of land public transport in metropolitan areas and cities. Aerial ropeways may be labeled as high-speed urban transport. The average speed of the passenger cabins may be from 18 to 40 km/h [9, 10, 13]. This value is higher than an average travel speed of the conventional land transport in straitened urban conditions. In addition, the problem of transport accessibility is becoming increasingly important when evaluating projects for the modernization of transport infrastructure in major urban centers [14]. This indicator is an apparent advantage of aerial ropeways as well.

A detailed review of exploitation of aerial ropeways in different cities is given in [2, 13, 15]. In the urbanized environment, aerial ropeways have begun to play an active role in the last 10~15 years [16]. Therefore, due to the lack of theoretical studies and scientific publications on the topic, at present a lot of specific questions related to designing, calculation and modeling of operational processes in aerial ropeways should be considered specifically for the urbanized environment. Among the early publications on the issue is the research presented in [17]. Questions related to the productivity, cost and possibility of applying of cable-propelled systems in the urban environment are considered in the article. A number of papers addressed the issues of the effect of climatic factors (wind and air temperature difference) on the dynamics of passenger cabins and the cable system of aerial ropeways [18, 19]; calculation of strength and tension of carrying ropes [20,21,22]; safety of passenger transportation [2, 3].

The research problem of passenger aerial ropeways not only includes the technical aspect. For example, [4] deals with the questions of social and economic impact of aerial ropeway construction on the development of adjacent areas; [23] addresses the issues of acquiring rights to the air space in urban environments for ropeways. To date, the economic aspects of the construction of ropeways have not been sufficiently discussed in previously published articles. However, it is these aspects that determine the prospects and economic feasibility of modernizing the urban transport infrastructure on the basis of passenger aerial ropeways.

2 Statement of the Research Task

Construction of the passenger aerial ropeway in the severely urbanized environment is a very costly enterprise in terms of engineering and economics [2, 24, 25]. The construction cost includes the costs of development effort, design and survey works, construction and assembling operations, purchase of the necessary mechanical equipment, creating an automated traffic management system, etc. A significant component of the total cost is the cost of construction of boarding stations, construction and erection of intermediate towers along the aerial ropeway, procurement of hauling and carrying steel cables. The costs directly depend on the number of intermediate towers along the line of the ropeway, i.e., dependent on the step of their installation. The installation step and the height of intermediate towers are related. With increasing step, it is needed to increase the height in order to ensure the minimum permissible height of proximity of passenger cabins to the ground. Therefore, reduction of the installation step of towers will result in the growth of their total cost due to the increase in the number of the towers. However, the unit cost will decline due to the decrease in its height. With increasing step, the unit cost of the tower and the cost of the cables will grow, although the number of the intermediate towers along the line of the ropeway will decrease. The influence of the step and height on cost of the ropeway is shown in Fig. 1. At low height values of the intermediate towers, an essential element of the ropeway cost is the cost of the boarding stations (buildings and installed equipment). Therefore, the influence of the step installation (i.e., the number of the towers along the line) is barely visible. With increasing height of the intermediate towers, a percentage of their cost in the total cost of the ropeway line rises rapidly, and the influence of the tower step becomes significant.

Fig. 1

The influence of the step and height of intermediate towers on the cost of ropeway line

It is clear that the arrangement of the intermediate towers of the ropeway is the task of technical and economic optimization. The aim of optimization is to provide the minimum cost of the erection of boarding stations, intermediate towers, procurement of hauling and carrying cables and the set of technological equipment installed on the tower [24]. Statement and solving of the optimization problem make it possible to substantially reduce the costs of construction of passenger aerial ropeways in the urbanized environment [2, 25].

3 Mathematical Model of Passenger Aerial Ropeway Line

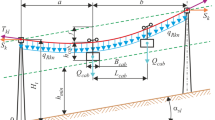
A design diagram of the section of an aerial ropeway line between two neighboring boarding stations (stations A and B) is shown in Fig. 2. In this figure, there are $v_{0} (u)$—the earth surface profile along the aerial ropeway line; $v(u)$—carrying ropes sagging line; $v_{\hbox{min} } (u)$—the line of permissible minimum proximity of the passenger cabin to the ground; $v_{fact} (u)$—the line of factual proximity of the passenger cabin to the ground.

Fig. 2

A design diagram of the optimized aerial ropeway section line between two neighboring boarding stations (A and B)

The construction costs of this section C comprise several components:

• the cost of the buildings of boarding stations A and B;

• the cost of the technological equipment mounted inside A and B stations;

• the cost of the metal structures of the intermediate towers and the foundation under them;

• the cost of the technological equipment mounted on the towers;

• the cost of the hauling and carrying ropes.

The cost value C is calculated as follows:

$$\begin{aligned} C & = C_{A} + C_{B} + C_{eA} + C_{eB} + \sum\limits_{i = 1}^{{i = I_{t} }} {\left( {C_{ti} + C_{fi} + C_{ei} } \right)} \\ & \quad + \left( {C_{kt} + n_{kn} C_{kn} } \right)\sum\limits_{m = 1}^{{m = I_{t} + 1}} {l_{km} } . \\ \end{aligned}$$

(1)

The construction cost of boarding stations may vary considerably, depending on their architecture versions. At the initial stage of aerial ropeway designing, the construction cost of boarding stations C_A and C_B may be determined as follows:

$$C_{A(B)} = \left( {C_{sA(B)} S_{fA(B)} /h_{fA(B)} } \right){\kern 1pt} H_{A(B)} .$$

The cost of the intermediate tower C_t depends on its structure and height H_t. The cost may be approximated by the power regression expression [24, 25]

$$C_{t} = C_{t0} H_{t}^{{a_{t} }} ,$$

(2)

where $C_{t0}$ and $a_{t}$—the empirical coefficients. For example, in [24, 25], they were obtained by the statistical data manipulation of the cost of metal towers having the same structure and different heights, which are produced by the industry for aerial ropeways.

Due to the need for the tension of hauling and carrying ropes, it is required to reinforce the structure of towers, thus increasing their mass and manufacturing cost. It is convenient to consider this fact by increasing the design height of towers, compared to their physical height $H_{tg}$, in proportion to the accepted tension of the carrying ropes S_k. Therefore, in Eq. (2), it is necessary to use the design height of the intermediate tower:

$$H_{t} = H_{tg} \left( {1 + \psi [n]_{k} S_{k} /R_{kn} } \right)$$

The performance specification and cost of hauling and carrying ropes for aerial ropeways are dependent of their diameter d_k. As it is shown in [25], they may be determined using the approximate regression dependences:

• dead weight of the 1 running meter of the rope length

$$q_{k} = q_{k0} d_{k}^{2} ;$$

• aggregate strength of the rope (breaking tension)

$$R_{k} = r_{k0} + r_{k1} d_{k} + r_{k2} d_{k}^{2} ;$$

• cost of 1 running meter of the rope length

$$C_{k} = c_{k0} + c_{k1} d_{k} + c_{k2} d_{k}^{2} ,$$

where $q_{k0} ,r_{k0} ,r_{k1} ,r_{k2} ,c_{k0} ,c_{k1} ,c_{k2}$—the empirical coefficients, obtained from the statistical manipulation of the data on the dead weight, aggregate strength and cost of the ropes of different diameters (using the method of least squares). For example, these coefficients for the ropes employed in the Russian Federation are given in [2, 24, 25].

A design diagram of the section of the aerial ropeway line between the neighboring intermediate towers is shown in Fig. 3. The sagging of the carrying rope is formed under several forces:

Fig. 3

The design diagram of the section of the aerial ropeway line between the neighboring intermediate towers

• vertical uniformly distributed load of the dead weight of the rope with intensity $q_{kn}$;

• vertical concentrated load of the weight of passenger cabins $Q_{cab}$;

• horizontal longitudinal tension force of the rope S_k;

• horizontal transverse statistic component of the wind pressure on the passenger cabin $p_{cab}$;

• horizontal transverse statistic component of the wind pressure on the carrying ropes $p_{kn}$.

It is convenient to replace concentrated loads $Q_{cab}$ with distributed ones with intensity

$$q_{cab} = Q_{cab} /n_{kn} L_{cab} .$$

The resultant of the transverse distributed load on the m-th carrying rope is determined as follows [24, 26]:

$$\begin{aligned} q_{Rknm} & = \sqrt {(q_{cabm} + q_{kn} )^{2} + (p_{cab} + p_{knm} )^{2} } \\ & = \left[ {\left( {q_{kn0} d_{kn}^{2} + \mu_{m} \frac{{Q_{cab} }}{{n_{kn} L_{cab} }}} \right)^{2} } \right. \\ & \quad + w_{0}^{2} \left. {\left( {\eta_{m} C_{wkn} k_{wkn} d_{kn} + \mu_{wm} C_{wcab} k_{wcab} \frac{{A_{cab} }}{{n_{kn} L_{cab} }}} \right)^{2} } \right]^{0.5} . \\ \end{aligned}$$

The carrying ropes also undergo dynamic stresses from the swaying of passenger cabins during their movement and swaying of the ropes themselves under the wind pressure. To take into account these dynamic effects, the dynamic coefficient $\psi_{d} > 1$ is used.

Depending on the ratio of the horizontal tension of the carrying rope S_k, length of the (i + 1)-th span between the neighboring i-th and (i + 1)-th towers $L_{ti + 1}$ and the difference of the elevation marks of the rope fastenings on these towers

$$\Delta v_{i + 1} = (v_{0i + 1} + H_{tgi + 1} ) - (v_{0i} + H_{tgi} ),$$

various shapes of the carrying rope sagging are possible [20]:

• shape I (the section of the maximum sagging is within the span, between the intermediate towers, shown in Fig. 3);

• shape II (the section of the maximum sagging is outside the span);

• shape III (the section of the maximum sagging coincides with one of the towers).

The sagging shape of the carrying ropes is determined by the criterion K_f [2, 25]

$$K_{f} = \frac{{q_{Rkn} L_{ti + 1}^{2} }}{{2S_{k} \Delta v_{i + 1} }} = \frac{{q_{Rkn} L_{ti + 1}^{2} }}{{2S_{k} [(v_{0i + 1} + H_{tgi + 1} ) - (v_{0i} + H_{tgi} )]}}.$$

When $K_{f} \notin ( - 1;\; + 1)$, shape I of the sagging is implemented; when $K_{f} \in ( - 1;\; + 1)$, shape II is implemented; when $K_{f} = \pm 1$, shape III is implemented.

The criterion K_f is convenient for determining the level difference value of the attachment point arrangements of the carrying rope on the neighboring intermediate towers, when the possible sagging shapes are implemented. If

$$\Delta v_{i + 1} < q_{Rkn} L_{ti + 1}^{2} /2S_{k} ,$$

then shape I of the sagging will be implemented; otherwise, shape II will be implemented; under conditions of equality, shape III will be implemented.

In Fig. 4, the surface configuration of the criterion K_f = 1 is shown, when there are the intervals of characteristic changes S_k, $L_{ti}$ and $q_{Rkn} = const$, specific for the aerial ropeway lines. The locus of points below the surface corresponds to shape I of the carrying rope sagging; the locus of points above the surface corresponds to shape II of the carrying rope sagging; the locus of points immediately on the surface corresponds to shape III of the carrying rope sagging. For the values $q_{Rkn}$ which are different from the value $q_{Rkn}$ = 200 N/m, accepted for the graph construction, the surface of the criterion K_f = 1 will shift along the axis $\Delta v_{i}$ in direct proportion.

Fig. 4

The criterion surface K_f = 1 when $q_{Rkn}$ = 200 N/m

When the relative value of the rope bending deflection is $f_{i} /L_{ti}$ < 0.1 (specific to aerial ropeways), with an error lower than 1.3% [7], the geometrical line of the carrying rope sagging in shape I in the (i + 1)-th span between the neighboring i-the and (i + 1)-the towers in the coordinate system $x0y$ (Fig. 3) may be expressed with the parabolic equation

$$\begin{aligned} & v_{kn} (u_{i} \le u \le u_{i + 1} ) \\ & \quad = \left\{ {\begin{array}{*{20}c} {v_{0i} + H_{tgi} - \psi_{d} \frac{{q_{Rkn} (u - u_{i} )^{2} }}{{2S_{k} }},\quad u_{i} \le u \le u_{i} + a_{i + 1} } \\ {v_{0i + 1} + H_{tgi + 1} - \psi_{d} \frac{{q_{Rkn} (L_{ti} - u)^{2} }}{{2S_{k} }},u_{i} + a_{i + 1} \le u \le u_{i} + L_{ti} } \\ \end{array} } \right. \\ \end{aligned}$$

(3)

The maximum rope sag $f_{i + 1}$ is

$$f_{i + 1} = a_{i + 1} \left[ {\psi_{d} \frac{{q_{Rkn} \,a_{i + 1} }}{{2S_{k} }} + \frac{{(v_{0i + 1} + H_{tgi + 1} ) - (v_{0i} + H_{tgi} )}}{{u_{i + 1} - u_{i} }}} \right]$$

(4)

and it is situated in the section at a distance of $a_{i + 1}$ and $b_{i + 1}$ from the adjacent towers i and i + 1 (Fig. 3):

$$a_{i + 1} = \frac{1}{2}\left\{ {L_{ti + 1} - \frac{{2S_{k} }}{{q_{Rkn} \,L_{ti + 1} }}\left[ {(v_{0i + 1} + H_{tgi + 1} ) - (v_{0i} + H_{tgi} )} \right]} \right\},$$

(5)

$$b_{i + 1} = \frac{1}{2}\left\{ {L_{ti + 1} + \frac{{2S_{k} }}{{q_{Rkn} \,L_{ti + 1} }}\left[ {(v_{0i + 1} + H_{tgi + 1} ) - (v_{0i} + H_{tgi} )} \right]} \right\}.$$

(6)

The length of the carrying rope in the span between the towers i and i + 1 will be approximately

$$l_{ki + 1} \approx a_{i + 1} \left( {1 + \psi_{d}^{2} \frac{{q_{Rkn}^{2} a_{i + 1}^{2} }}{{24S_{k}^{2} }}} \right) + b_{i + 1} \left( {1 + \psi_{d}^{2} \frac{{q_{Rkn}^{2} b_{i + 1}^{2} }}{{24S_{k}^{2} }}} \right)$$

and its maximum diameter, determined from the condition of the aggregate strength, can be found as the maximum value of two values:

$$d_{kn} = 0.5\left[ {\sqrt {r_{k1}^{2} - 4r_{k2} (r_{k0} - [n]_{k} T_{ki} )} - r_{k1} } \right]/r_{k2} ,$$

(7)

$$d_{kn} = 0.5\left[ {\sqrt {r_{k1}^{2} - 4r_{k2} (r_{k0} - [n]_{k} T_{ki + 1} )} - r_{k1} } \right]/r_{k2} .$$

(8)

The axial tension forces of the carrying rope $T_{ki} \,,\;T_{ki + 1}$ on the towers i and i + 1 equal

$$\begin{aligned} T_{ki} & = S_{k} /\cos \left[ {arctg(\psi_{d} \,q_{Rkn} \,a_{i + 1} /S_{k} )} \right], \\ T_{ki + 1} & = S_{k} /\cos \left[ {arctg(\psi_{d} \,q_{Rkn} \,b_{i + 1} /S_{k} )} \right]. \\ \end{aligned}$$

Taking into account the required values of the minimum diameter of the carrying rope for every $I_{t} + 1$ bay of the aerial ropeway line, completely its minimum diameter is selected to be equal to the maximum diameter determined from Eqs. (7) and (8).

Passenger aerial ropeways can be exploited in the environment conditions which have significant fluctuations in air temperatures during the year or over the years. Exploitation of the aerial ropeway at temperatures t, different from the accepted design value t₀, results in changes of the carrying rope length between the intermediate towers in proportion to the thermal elongation coefficient of the carrying rope $\alpha_{Tnk}$:

$$l_{ki + 1} (t) = l_{ki + 1} (t_{0} ) + \alpha_{Tnk} (t - t_{0} )L_{ti} .$$

Thermal length change of the carrying ropes under the constant tension value $S_{k} (t_{0} ) = S_{k} (t) = const$ may be expressed as the change in the tension force $S_{k} (t) \ne S_{k} (t_{0} )$ under the constant temperature equal to the design value $t = t_{0} = const$. From the condition of the change equivalence of the rope length in both cases, tension $S_{k} (t)$ for shape I of the carrying rope sagging is determined by solving the nonlinear equation:

$$\begin{aligned} & a_{i + 1} (t)\left( {1 + \psi_{d}^{2} \frac{{q_{Rkn}^{2} a_{i + 1}^{2} (t)}}{{24S_{k}^{2} (t)}}} \right) + b_{i + 1} (t)\left( {1 + \psi_{d}^{2} \frac{{q_{Rkn}^{2} b_{i + 1}^{2} (t)}}{{24S_{k}^{2} (t)}}} \right) \\ & \quad - \left[ {a_{i + 1} \left( {1 + \psi_{d}^{2} \frac{{q_{Rkn}^{2} a_{i + 1}^{2} }}{{24S_{k}^{2} }}} \right) + b_{i + 1} \left( {1 + \psi_{d}^{2} \frac{{q_{Rkn}^{2} b_{i + 1}^{2} }}{{24S_{k}^{2} }}} \right)} \right] \\ & \quad - \alpha_{Tkn} (t - t_{0} )L_{ti} = 0. \\ \end{aligned}$$

(9)

In this equation, the distances $a_{i + 1} (t)$ and $b_{i + 1} (t)$ are the functions of the sought quantity $S_{k} (t)$ according to Eqs. (5) and (6).

The geometrical line of the carrying rope sagging in the (i + 1)-th span and maximum rope sag $f_{i + 1}$ at unconditioned temperature t will be determined by Eqs. (3) and (4) or (9) when substituting the adjusted values $S_{k} (t)$ and $a_{i + 1} (t)$ for the corresponding members in these equations.

4 Problem Statement of Optimization of Aerial Ropeway Line

The task of optimization of the aerial ropeway line is based on the criterion of minimizing the construction cost. Therefore, the objective function of the task is based on Eq. (1). As variable characteristics of the task, the following characteristics which affect the value of the objective function should be used:

• number of the intermediate towers I_t;

• point data of the intermediate i-th tower arrangement along the aerial ropeway line $u_{i} \;(i \in [1\,;\;I_{t} ])$;

• heights of the intermediate towers $H_{tgi} \;(i \in [1\,;\;I_{t} ])$ and heights of the boarding stations $H_{A} = H_{tgi = 0}$ and $H_{B} = H_{{tgi = I_{t} + 1}}$;

• tension forces of the carrying ropes S_k.

The vector of controlled characteristics is formed from them:

$$\begin{aligned} & \{ x\}^{T} = \{ x_{1} \;x_{2} \; \ldots \;x_{n} \; \ldots \;x_{N} \} \\ & \quad = \{ H_{A} \;H_{B} \;S_{k} \;u_{1} \;u_{2} \; \ldots \;u_{{I_{t} }} \;H_{tg1} \;H_{tg2} \; \ldots \;H_{{tgI_{t} }} \} . \\ \end{aligned}$$

The number of the vector components is $N = 2I_{t} + 3$. When the distances (specific to aerial ropeways) between the neighboring boarding stations are L_AB from 3 to 5 km, the number of variables in the optimization task will be N, whose values is within 20 to 100.

The task of optimization of the aerial ropeway line between the neighboring boarding stations, taking into account the surface relief and characteristics of the urban development, ultimately comes to minimizing the objective function (the total cost of construction) when the number of the intermediate towers is fixed $I_{t} = const$. Taking into Eq. (1), the objective function is determined as follows:

$$\begin{aligned} & \left. {O(\{ x\} )} \right|_{{I_{t} = const}} = \left( {\frac{{C_{sA} S_{fA} }}{{h_{fA} }}} \right)x_{1} + \left( {\frac{{C_{sB} S_{fB} }}{{h_{fB} }}} \right)x_{2} + C_{eA} + C_{eB} \\ & \quad +\sum\limits_{i = 1}^{{i = I_{t} }} {\left( {C_{t\,0i} x_{{i + I_{t} + 3}}^{{a_{ti} }} + C_{f\,0i} x_{{i + I_{t} + 3}}^{{a_{fi} }} + C_{ei} } \right) + } (C_{kt} + n_{kn} C_{kn} ) \\ & \quad \times \sum\limits_{m = 1}^{{m = I_{t} + 1}} {\left[ {a_{m} (x_{{m + I_{t} + 2}} ;\,x_{{m + I_{t} + 3}} ;\,x_{{m + 2I_{t} + 2}} ;\,x_{{m + 2I_{t} + 3}} )\left( {1 + \frac{{\psi_{d}^{2} q_{Rkn}^{2} \,a_{m}^{2} }}{{6x_{3}^{2} }}} \right)} \right.} \\ & \quad + \left. {b_{m} (x_{{m + I_{t} + 2}} ;\,x_{{m + I_{t} + 3}} ;\,x_{{m + 2I_{t} + 2}} ;\,x_{{m + 2I_{t} + 3}} )\left( {1 + \frac{{\psi_{d}^{2} q_{Rkn}^{2} \,b_{m}^{2} }}{{6x_{3}^{2} }}} \right)} \right] \to \hbox{min} . \\ \end{aligned}$$

(10)

The algorithm of the optimal design of the aerial ropeway line includes multiple sequential minimization of the objective function (10) when the characteristic I_t takes various values. The absolute minimum will determine the characteristics of the optimal option for the projected line.

When determining the minimum of the objective function (10), the following limitations in the form of inequations should be implemented:

(1) to the mutual arrangement of the neighboring intermediate towers along the aerial ropeway line

$$\begin{aligned} u_{1} \ge 0; \hfill \\ u_{i + 1} - u_{i} ,\quad i \in [1;I_{t} - 1]; \hfill \\ L_{AB} - u_{{I_{t} }} \ge 0, \hfill \\ \end{aligned}$$

(2) to the position of the intermediate towers outside the exclusion zones (elimination of the possibility of installing them within the exclusion zones, such as rivers, ravines, water bodies, stadiums and motorways)

$$\left| {u_{i} - \bar{u}_{dj} } \right| - \Delta u_{dj} \ge 0,i \in [1;I_{t} ],j \in [1;J_{d} ];$$

(3) to the permissible variation range of the mounting step size of the neighboring towers

$$\begin{aligned} & L_{t\hbox{max} } - u_{1} \ge 0; \\ & L_{t\hbox{max} } - (u_{i + 1} - u_{i} ) \ge 0\,,\;i \in [1;\;I_{t} - 1]; \\ & L_{t\hbox{max} } - (L_{AB} - u_{{I_{t} }} ) \ge 0; \\ & u_{1} - L_{t\hbox{min} } \ge 0; \\ & (u_{i + 1} - u_{i} ) - L_{t\hbox{min} } \ge 0\,,\;i \in [1;\;I_{t} - 1]; \\ & (L_{AB} - u_{{I_{t} }} ) - L_{t\hbox{min} } \ge 0 \\ \end{aligned}$$

(4) to the maximum height of the intermediate tower

$$H_{t\;\hbox{max} } - H_{tgi} \ge 0,i \in [1;I_{t} ];$$

(5) to the permissible slope angle of the carrying ropes when the cabin is moving between the neighboring intermediate towers at the maximum air temperature

• when the rope sagging takes shape I

$$\begin{aligned} & \left[ \beta \right] - \left| {arctg(\psi_{d} q_{Rkn} a_{i + 1} (t_{\hbox{max} } )/S_{k} (t_{\hbox{max} } )} \right| \ge 0, \\ & \left[ \beta \right] - \left| {arctg(\psi_{d} q_{Rkn} b_{i + 1} (t_{\hbox{max} } )/S_{k} (t_{\hbox{max} } )} \right| \ge 0,\quad i \in [1;I_{t} + 1]; \\ \end{aligned}$$

• when the rope sagging takes shape II and III

$$\begin{aligned} & \left[ \beta \right] - \left| {arctg\left( {\frac{{(v_{0i + 1} + H_{tgi + 1} ) - (v_{0i} + H_{tgi} )}}{{L_{ti} }} - \frac{{\psi_{d} q_{Rkn} L_{ti} }}{{2S_{k} (t_{\hbox{max} } )}}} \right)} \right| \ge 0, \\ & \left[ \beta \right] - \left| {arctg\left( {\frac{{(v_{0i + 1} + H_{tgi + 1} ) - (v_{0i} + H_{tgi} )}}{{L_{ti} }} + \frac{{\psi_{d} q_{Rkn} L_{ti} }}{{2S_{k} (t_{\hbox{max} } )}}} \right)} \right| \ge 0,\quad i \in [1;I_{t} + 1]; \\ \end{aligned}$$

(6) to the permissible relative positions of the high-altitude arrangement of the fastener assemblies of the carrying rope on the neighboring intermediate towers

$$[i_{t} ] - \left| {\frac{{(v_{0i + 1} + H_{tgi + 1} ) - (v_{0i} + H_{tgi} )}}{{L_{ti} }}} \right| \ge 0,i \in [1;I_{t} + 1];$$

(7) to the permissible high-altitude arrangement of the passenger cabins when they are moving along the ropeway path at the maximum air temperature

$$\begin{aligned} & \left. {v_{kn} (u_{i} \le u \le u_{i + 1} )} \right|_{{npu\;t_{\hbox{max} } }} - h_{cab} - h_{\hbox{min} } (u_{i} \le u \le u_{i + 1} ) \\ & \quad - v_{0} (u_{i} \le u \le u_{i + 1} ) \ge 0,\quad i \in [1;I_{t} + 1]; \\ \end{aligned}$$

(8) to the acceptable variation range of the diameter of the hauling and carrying ropes

$$\begin{aligned} & d_{kt\;\hbox{max} } - d_{kt} \ge 0; \\ & d_{kt} - d_{kt\;\hbox{min} } \ge 0; \\ & d_{kn\;\hbox{max} } - d_{kn} \ge 0; \\ & d_{kn} - d_{kn\;\hbox{min} } \ge 0 \\ \end{aligned}$$

(9) to the permissible maximum rope sag of the carrying rope between the intermediate towers at the maximum air temperature

• when the rope sagging takes shape I

$$\begin{aligned} & \psi_{f} (u_{i + 1} - u_{i} ) - a_{i + 1} (t_{\hbox{max} } )\left[ {\frac{{\psi_{d} q_{Rkn} a_{i + 1} (t_{\hbox{max} } )}}{{2S_{k} (t_{\hbox{max} } )}}} \right. \\ & \quad \left. { + \frac{{\left( {v_{i + 1} - v_{i} } \right) + \left( {H_{tgi + 1} - H_{tgi} } \right)}}{{u_{i + 1} - u_{i} }}} \right] \ge 0,i \in [1;I_{t} + 1], \\ \end{aligned}$$

• when the rope sagging takes shape II or III

$$\psi_{f} (u_{i + 1} - u_{i} ) - \psi_{d} q_{Rkn} L_{ti} /8S_{k} (t_{\hbox{max} } ) \ge 0,\;i \in [1;\;I_{t} + 1];$$

(10) to the minimum carrying rope tension force according to the safety specification [2]

$$S_{k} - 10n_{cab} \psi_{d} Q_{cab} /n_{kn} \ge 0;$$

(11) to the maximum axial tension forces of the carrying rope, based on its maximum possible aggregate strength

• when the rope sagging takes shape I

$$\begin{aligned} & \frac{{R_{kn} (d_{kn\,\hbox{max} } )}}{{[n]_{k} }} - \frac{{S_{k} }}{{\cos \left[ {arctg\left( {\frac{{\psi_{d} q_{Rkn} a_{i + 1} }}{{S_{k} }}} \right)} \right]}} \ge 0, \\ & \frac{{R_{kn} (d_{kn\,\hbox{max} } )}}{{[n]_{k} }} - \frac{{S_{k} }}{{\cos \left[ {arctg\left( {\frac{{\psi_{d} q_{Rkn} b_{i + 1} }}{{S_{k} }}} \right)} \right]}} \ge 0,\quad i \in [1;I_{t} ]; \\ \end{aligned}$$

• when the rope sagging takes shape II or III

$$\frac{{R_{kn} (d_{kn\hbox{max} } )}}{{[n]_{k} }} - \frac{{S_{k} }}{{\cos \left[ {arctg\left( {\frac{{(v_{0i + 1} + H_{tgi + 1} ) - (v_{0i} + H_{tgi} )}}{{L_{ti} }} - \frac{{\psi_{d} q_{Rkn} L_{ti} }}{{2S_{k} }}} \right)} \right]}} \ge 0,\quad i \in [1;I_{t} ].$$

To determine the minimum of the objective function (10) taking into account the acceptable limitations, it is necessary to use one of the direct methods of the conditional optimization [28], based on the immediate calculation of the objective function value $O(\{ x\} )$.

5 Solutions Findings of the Optimization Task and Their Analysis

The task of the optimal design of aerial passenger ropeway for the conditions of a highly urbanized environment and high irregularity of the earth’s surface is a very complex mathematical task. Indeed, with the distances between neighboring stations for boarding passengers, which are characteristic of ropeway lines, the number of variable parameters in the optimization problem can reach up to 100 unknown values. The number of these unknown quantities determines the dimension of the optimization problem. At the same time, it is also necessary to take into account 11 types of various structural, strength and operational constraints, which should be imposed on variables during the solution of the optimization problem. These constraints are expressed using 99 mathematical dependencies in the form of inequalities. Thus, the practical implementation of the proposed mathematical model and the problem of minimizing the objective function (Eq. 1) are possible only through the use of numerical mathematical methods and computer equipment.

To this end, the authors developed a computer program “RopewayOptimization.” The original text of the program was protected by the Patent Office of the Russian Federation [29]. As a mathematical method of optimization, the method of the Hooke-Jeeves type was used [27]. The need to take into account a large number of constraints in the form of inequalities complicates the form of the domain of possible solutions of the optimization problem in the N-dimensional space of variables. Also, the presence of a large number of unknown variables leads to the fact that the objective function $\left. {O(\{ x\} )} \right|_{{I_{t} = const}}$ (Eq. 10) has several local minima within the domain of possible solutions. When optimizing for test and real conditions of designing ropeways, the authors recorded from 3 to 7 local minima of the objective function. Obviously, only one of these local minima can be considered the best solution to the optimization problem (global minimum). However, some of the local minima have objective function values that are quite close in magnitude to the value of the objective function in the global minimum. Therefore, when developing a real project of a ropeway, it is also advisable to consider such local minima. Perhaps an additional consideration of any other considerations (for example, political, legal or property reasons) will lead to the need to use the solution of the optimization problem not at the global minimum point of the objective function, but at a point of the near local minimum. Thus, it is important to correctly set the initial optimization point (i.e., the initial combination of the values of all N variables). The starting point must satisfy 1) all 99 constraints and 2) ensure that the global minimum of the objective function is found. In the RopewayOptimization program, the optimization start point was set using the repeated iteration algorithm for possible combinations of two variables—the height of intermediate towers H_t (it is assumed the same for all supports) and the horizontal longitudinal tension force of the rope S_k. Parameters H_t and S_k change with step $\Delta H_{t}$ and $\Delta S_{k}$ within the intervals of their possible change ($H_{t} \le H_{t\;\hbox{max} }$ and $S_{k} < R_{kn} (d_{kn\;\hbox{max} } )/[n]_{k}$). The experience of carrying out test calculations showed that the recommended values of these steps are $\Delta H_{t}$ ~ 10 m, $\Delta S_{k}$ ~ 40 kN. If a possible combination of parameters H_t and S_k satisfies the requirements for choosing the starting point, then the optimization problem is solved and the local minimum point of the objective function $\left. {O(\{ x\} )} \right|_{{I_{t} = const}}$ (Eq. 10) is determined. As a result, one point is selected from the set of points of local minima thus obtained, which has the lowest value of the objective function. This point is the global minimum point and, accordingly, the solution to the optimization problem.

The efficiency of the computer program “RopewayOptimization” was tested by solving several test tasks. The test tasks had a different dimension (the number of variables in the optimization problem varied within 10 to 400), various quantitative parameters of the shape of the earth’s surface and the location of exclusion zones. Regular and irregular forms of the earth’s surface along the ropeway line were considered. The regular shape was modeled by rectilinear (horizontal and oblique with a slope of up to 60 degrees) and sinusoidal functions. To simulate the irregular shape of the earth’s surface, real topographic maps of the large cities of Rostov-on-Don and Bryansk (Russian Federation) were used. At the same time, the real maps of these cities were used to specify the location and size of the exclusion areas, and thus, the actual location of the street infrastructure objects was taken into account. On the basis of the calculated data, proposals were formulated for the development of promising projects for the construction of passenger aerial ropeways in these cities [2, 11].

To evaluate the capabilities of the developed mathematical model and the optimization task when using them for designing aerial ropeway lines, the calculations of the aerial ropeway model were performed. The terrain was modeled in the form of the sinusoid with various numbers of the half-waves n along the length of the aerial ropeway line and at their different height $V_{\hbox{max} }$:

$$v(u) = V_{\hbox{max} } \sin (2\pi {\kern 1pt} n{\kern 1pt} u/L_{AB} ).$$

(11)

The further calculation results of the aerial ropeway cost are expressed in conventional units (C.U.). As a conventional unit, the Russian rouble was used when setting the cost indicators. When conducting cost optimization in other countries, the summands in Eq. (1) should be expressed in the national currency. At the same time, the mathematical model and calculation dependencies of the optimization task do not change.

The construction cost of the passenger aerial ropeway line is very sensible to the number of intermediate towers and geometrical diversity of the terrain (Fig. 5). When the number of intermediate towers is small ($I_{t} \le 7$), with reducing I_t, the cost of the line rises sharply, up to two times, from ~ 140 million of C.U. to ~ 280 million of C.U. This is a result of rapid growth of the towers height H_t due to the need to balance the increase in maximum rope sag of carrying ropes with the growth of the distance between the neighboring towers. When $I_{t} \in \left[8,14\right]$, the line cost is minimum and virtually the same, accounting for ~ 140 million of C.U. Then, it starts to rise since the tower height reaches its minimum under the condition of height of proximity of passenger cabins to the ground. A further increase in the number of towers and consequently the decrease in the distances between them lead to cost growth of the installing structurally unnecessary towers.

Fig. 5

The influence of the terrain on the cost of the aerial ropeway line when the surface shape is sinusoidal: (a) height (1—V_max = 50 m; 2—25 m; 3—0 m); (b) longitudinal variation (I—the odd number of the sinusoid half-waves; II—the even number of the sinusoid half-waves; 1—I_t = 9 pcs; 2—I_t = 12 pcs.; 3—I_t = 15 pcs)

The graphs in Fig. 5 a show the influence of the terrain diversity on the aerial ropeway line. (The terrain diversity grows with increasing the number of half-waves n.) When the terrain is slightly uneven (n < 3), the line cost is minimum and virtually the same for the different number of properties. However, when the terrain is considerably uneven (n > 4), an increasing number has a positive impact on the cost due to the possibility of installing the towers in the elevated areas. This leads to reducing the tower height and reducing their total cost despite the large number.

In Fig. 6, one can see the ground arrangement and height of the intermediate towers (I_t = 15) for the optimal options of the aerial ropeway with the length L_AB = 3000 m, depending on the even number of the half-waves n of the sinusoid (11) with V_max = 50 m. Regardless of the degree of the terrain diversity (the number of the half-waves n), the optimal arrangement of the intermediate towers barely deviates from the uniform distribution with the step $L_{ti} = L_{AB} /(I_{t} + 1)$ = 187.5 m. However, their optimal height and total cost of the aerial ropeway are sensible to the terrain diversity. Nonetheless, when the step of the towers L_ti is significantly lower than the step of the terrain waviness (Fig. 6a, b), the height of the towers $H_{tgi}$ and total cost of construction C are minimum. There is very little difference in the heights of the intermediate towers along the ropeway line L_AB, and the construction cost is not very different when the values n are the nearest. This fact can be seen through the correlation $L_{ti} < L_{AB} /2n$. In circumstances where the installation step of the intermediate towers L_ti becomes equivalent to the degree of the terrain diversity, it is necessary to provide an increased tower height. This leads to a sharp rise in the construction cost of the aerial ropeway.

Fig. 6

The influence of the terrain diversity on the optimal arrangement and height of the intermediate towers of the aerial ropeway: (a) when the number of the half-waves is n = 2; (b) n = 4; (c) n = 8; (d) n = 12; (e) n = 16

6 Conclusion

The proposed mathematical model and optimization problem should be used at the initial stage of designing passenger aerial ropeways to analyze the influence of a substantial number of cost factors, as well as construction and geometric factors on the optimal placement, height and number of intermediate towers and the tension force of the supporting ropes.

The optimal method put forward in this article would be helpful in determining the most cost-effective construction option in aerial ropeway in the given conditions, taking into account the terrain, urban infrastructure arrangement, altitude performance of the urban development, technical characteristics of the carrying rope, etc.

Implementing the solution findings of the given optimization task makes it possible to significantly reduce the construction cost of aerial ropeways in the urban environment.

A promising direction for the further improvement in the technology for designing cost-effective aerial passenger ropeways for the urban environment is to expand the functionality of the optimization mathematical model presented in this article. To do this, it is necessary to conduct research and solve the following scientific problems:

• 1. consideration of important physical processes that may affect the reliability, safety and cost of ropeways (in particular, dynamic processes during the movement of passenger cabins, increased negative environmental effects, possible deviations from normal operation, etc.);

• 2. the use of multi-criteria objective functions to determine the best options for aerial ropeways, not only taking into account the cost of construction, but also taking into account capacity, operational safety, maintenance costs, etc.