Width Design of Urban Rail Transit Station Walkway: A Novel Simulation-Based Optimization Approach

Abstract

The optimal design of the walkway at an urban rail transit station is a vital issue. The Transit Capacity and Quality of Service Manual (TCQSM) TCRP-100 report for the design of urban rail transit station walkway and the existing design models neglect the important factors such as randomness in the passenger arrival rate, randomness and state-dependent service time of the walkway and blocking phenomenon when the passenger flow demand exceeds the walkway capacity. There obviously exists a need to develop a design approach that overcomes these shortcomings. For this purpose, this paper details a simulation-based optimization approach that provides width design through automatic reconfiguration of walkway width during the simulation–optimization process based on phase-type (PH) distribution. The integrated PH/PH(n)/C/C discrete-event simulation (DES) model and optimization method that uses the genetic algorithm (GA) work together concurrently to obtain optimized (design) widths for different passenger flow and level of service (LOS) The numerical experiments are conducted to compare the proposed model with the existing design methods. It reveals that: (1) The width obtained by our proposed model is higher than the existing width design models; (2) when squared coefficient of variation of passenger arrival interval increases, the walkway width increases more for our proposed model than the existing design models; (3) when the arrival rate increases, the walkway width of our proposed model increases faster than the existing design models; (4) the increase in the length of walkway has no significant effect on the walkway width.

1 Introduction

1.1 Motivation

Building a new urban rail transit station involves a considerable amount of resource investment in a project. The design phase of the urban rail transit station project is of critical importance. It is arduous as well as costly to redesign the urban rail transit stations if there is a need to correct the flaws or other issues. The improper design of the urban rail transit station service facilities causes high-level congestion, longer travel time of passengers between service facilities, inefficient space utilization, resource wastage and increase in the waiting time of passengers. However, at the same time the urban rail transit station service facilities are obliged to hold the level of service (LOS) specified by the codes and design manuals.

The Transit Capacity and Quality of Service Manual (TCQSM) TCRP-100 report [1] presents the analysis and width design procedure of urban rail transit station walkways. The procedure involves computation of the walkway width based on a desirable LOS. The LOS of the walkway is based on the mean passenger space. The assessment of walkways LOS uses the calculation of the area occupied per passenger (m²/ped) as the basis for LOS classification as shown in Table 1. According to TCQSM, the walkway width is obtained by using passenger arrival rate divided by walkway service rate per unit width under a given LOS. However, it ignores the important factors and has several flaws:

Table 1 Passengers level of service (LOS) on the walkway [1]

• It does not take into account the randomness in passenger arrival rate [2].

• It does not take into account the variation and state-dependent service time of the walkway (in reality, the walking/travel time of passengers on the walkway depends on the walking speed of passengers as well as on the number of passengers on the walkway).

• It does not consider the blocking of passengers from the entrance to the walkway when the passenger traffic demand approximates to or exceeds the capacity of the walkway.

As a result, the walkways designed by the TCQSM always show poor performance and experience heavy congestion even during the off-peak periods because of the variation in passenger traffic demand.

Thus, there exists an urgent need to establish a new approach for the width design of urban rail transit station that overcomes these shortcomings.

1.2 Literature Review

Substantial work has been done in the past to put forward the new design approaches for the walkways in urban rail transit stations as a well as in other buildings. Due to the inherent characteristics of walkways such as relations between the passengers and walkway facility (customers and server) and the randomness in passenger flow, many researchers described the walkway facility as a queuing system, based on which both the analytical and simulation models are developed as shown in Fig. 1.

Fig. 1

Facilities analysis and design references

Many researchers have conducted their studies to evaluate and design the pedestrian facilities at urban rail transit station and in other buildings by analytical queuing models. For example, the G/M/1 queuing model by Jiang et al. [3] and the state-dependent M/G(n)/C/C queuing models by Yuhaski et al. [4], Cheah and Smith [5], Mitchell et al. [6], Chen et al. [7], Weiss et al. [8], Xu et al. [9] and the PH/PH(n)/C/C state-dependent queuing model by Hu et al. [10]. These researches showed that the queuing theory can properly illustrate and assess the pedestrian facility at urban rain transit station and other buildings. But the major drawback of all these models is fitting the exponential distribution to the passenger arrival process which is appropriate only when there is a free flow. The squared coefficient of variation ($c^{2}$) of the exponential distribution is equal to 1 which means that randomness in the arrival process is ignored but in reality there exist randomness and therefore do not depict the actual conditions. The analytical PH/PH(n)/C/C model captures the randomness in passenger’s arrival rate as well as service time (passenger travel time in the walkway facility) using the phase-type (PH) distribution. The PH distribution is a probability distribution that can fit any positive random variable with various squared coefficient of variation while keeping the Markov characteristics. Thus, it has replaced the exponential distribution in several domains such as manufacturing and communication systems (Alfa et al. [11]; Miyazawa et al. [12]; Krishnamoorthy et al. [13]; Jiang et al. [14]). The existing analytical PH/PH(n)/C/C model takes the state dependence into account. However, this model is difficult to solve because it is based on the Quasi-Birth-Death process (QBS) and Matrix Analytical Scheme (MAS) [10] that involves a large number of matrix operations and iterative in nature. The complexity becomes larger when the system state n increase as it requires huge computer storage capacity. In addition to that, the analytical PH/PH(n)/C/C model cannot control the blocking probability during the width design process.

To take the advantage of queuing system for facility design and at same time eliminate the need to solve the large matrices and equation systems, many researchers established the simulation models for the facility analysis and design, for example, the G/M/1 queuing network simulation model by Lovas [15], the M/G(n)/C/C state-dependent simulation model by Cruz et al. [16], and Khalid et al. [17], the G/G(n)/C/C simulation model by Jiang et al. [18] and so on. In these researches, the queuing systems are translated into the Discrete-Event Simulation (DES) models. Based on the DES models, the facilities are evaluated and performance measures are estimated. However, facility description still needs to be improved in the above researches. In addition, blocking probability is not controlled during the design process in all these previous researches.

Besides the DES, another well-known category of simulation is microscopic simulations. Microscopic simulation models are elaborate as they depict individual characteristics and behaviors of the pedestrians given by Teknomoet al [19] and Kaakai et al. [20]. However, they require extensive calibration work and larger computation time at the same time. On the contrary, DES does not require the specific physical environment and passenger entity, making it more efficient and easier to calibrate than microscopic simulation models. Therefore, DES is taken as an efficient and accurate simulation approach with a wide range of application. Another advantage of the DES is that simulation-based optimization can be carried out conveniently based on DES models due to its universality and efficiency.

Recently, simulation-based optimization has become a popular and efficient tool in many domains (Banks [21], Hagendorf et al. [22] and Figueira et al. [23]).It involves the optimization of model inputs by using simulation for the computation of parameters. Therefore, it is not necessary to provide an explicit analytical expression of the objective or constraint functions for optimization as in the case of analytical approach (Swisher et al. [24]; Fu [25]; Cassandras and Lafortune [26]). This is especially useful in some practical situations where the explicit analytical formulae are too complex to be deduced. In urban rail transit station domain, researchers used simulation-based optimization technique to evaluate and design different service facilities (Jiang et al. [18]; Jiang and Lin [27]; Hassannayebi et al. [28]).

To find the optimal width for the urban rail transit station walkway by a simulation-based optimization approach and overcome all the shortcomings, we need to develop a PH-based DES model of walkway in the SimEvents ^® Software. The genetic algorithm (GA) is chosen in this paper as an optimization approach and implemented in the MATLAB^® Scientific Computing Environment. The SimEvents ^® and MATLAB^® have been used in serval researches as DES modeling and optimization tool, respectively [29–33]. The MATLAB^® offers a computational infrastructure for optimizing a hybrid, discrete-event and the time-based models, which allows for a great deal of flexibility in scripting and modifying the optimization objective function, while also making it easier to tie together parallel discrete simulation and optimization without the pain of the context switching into multiple software environments.

Moreover, there are several reasons for applying a GA rather than any other traditional optimization methods. One of the important reasons is its implicit parallelism (Swisher et al. [24]; Hubscher-Younger et al. [33]; Messac [34]. The GA searches parallel from a population of points. As GA has multiple offspring, it can explore the solution in different directions at a time giving it greater chance to find the optimal solution, while other traditional methods search from a single point and may trap in local optimal solution.

Based on the above analysis, we aim to propose a new simulation-based optimization approach for the width design of urban rail transit station walkway in this paper. The contribution of this paper falls into two aspects. First, we establish a PH/PH(n)/C/C DES model to describe the walkway as a queuing system in the urban rail transit station. The PH-based DES model captures the general randomness in passengers’ arrival and walkway service time. It also takes the state-dependence of service time into consideration. Therefore, it can be used to accurately evaluate the performance of the walkways. Besides, it also serves as an important tool to validate the PH/PH(n)/C/C analytical model developed in Hu et al. [10]. Second, we design a simulation-based optimization approach by implementing the PH-based DES model and the GA to work concurrently. The simulation-based optimization approach determines the optimal widths for the walkways considering the requirements on both LOS and blocking probability. Therefore, the walkway designed by it enjoys higher service quality and less congestion.

1.3 Outline of the Paper

The rest of the paper is organized as follows. First, we describe the urban rail transit station walkway as a PH/PH(n)/C/C state-dependent queuing system in Sect. 2. Then the simulation-based optimization framework for the width design is established in the Sect. 3. The computational experiments between our proposed approach and other existing approaches are presented in Sect. 4. Finally Sect. 5 concludes the paper.

2 Modeling of Walkway as a Queuing System

In this section, the necessary notations and assumptions used in this paper are discussed first. Then we describe the PH/PH(n)/C/C state-dependent queuing system for the urban rail transit station walkways. Method for calibrating the PH arrival interval and PH service time is also presented.

2.1 Notations

This section presents almost all the notations we need for this paper.

Notation	Description
$\alpha$	Initial probability vector
D	Transient generator matrix
L	Length of the walkway (m)
W	Effective width of the walkway (m)
C	Capacity of the walkway
n	Number of passengers (system state)
$\lambda$	Passenger arrival rate (ped/h)
$c_{a}^{2}$	Squared coefficient of variation of arrival interval
q	Peak-hour volume
$\varepsilon$	Peak-hour factor
h	Mean headway between the trains (s)
$c_{h}^{2}$	Squared coefficient of variation of headway
$\mu_{n}$	State-dependent service rate
$T_{n}$	State-dependent service time of walkway
$V_{n}$	State-dependent walkway speed of passengers
$c_{s,n}^{2}$	State-dependent squared coefficient of variation of walkway service time
P c	Blocking probability
ES	Mean area occupied per passenger
f	Degree of Erlang distribution
U	Uniformly distributed random number

2.2 Assumptions

There are a few basic assumptions that should be presented before going further:

• The walkways are rectangular in shape with length (L) and width (W). The width W is the effective width of walkway facility. According to TCQSM, the total width is obtained by adding a buffer of 0.50 m on each side to the effective width.

• The passengers are uniformly distributed on the walkway. This phenomenon is quite rare from a practical point of view. But this assumption is used in many relevant studies such as [10, 18] which is important for queuing analysis.

• The queueing system to describe the walkway facility has a ‘loss queue’ which means that when the number of passengers equal to capacity of walkway then newly arrived passengers are lost or blocked. Therefore; we take into account blocking probability P _c and design the walkway by keeping the P _c below a certain value.

• The alighting passenger flow from the train is considered. Nevertheless, the proposed approach can also deal with the flow of passengers toward the walkway from entrance gate of the urban rail transit station.

• The assessment of LOS uses the mean area occupied per passenger (m²/ped) as the basis for classification (see Exhibit 7-3 in Ref. [1]). It reflects proximity to other passengers and is therefore considered as an indicator of the passenger level of comfort and freedom to maneuver without conflict. It is generally desirable for the walkway of urban rail transit station to operate at LOS ‘C’ or above. In this paper, we design the walkways under the LOS ‘B’, ‘C’ and ‘D’. The LOS values for walkways are given in Table 1.

2.3 Description of Walkway Queuing System

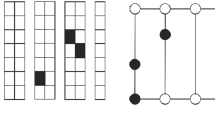
The urban rail transit station walkway and flow of passengers comprise a kind of unique finite capacity queuing system with the diversified arrival rate distribution (with no fixed squared coefficient of variation) and varying service time distribution (where the service time depends on the number of passengers). When the passengers enter into the walkway, they occupy the spaces (squares) (see Fig. 2). Each available space on the walkway acts like a server (service desk). The passengers spend some time (walking time) on the walkway and then exit. The passenger flow on the walkway can be viewed as a queuing system with passengers as customers, the spaces on the walkway facility as servers and the process of walking on the walkway as a service process.

Fig. 2

Transformation of walkway to a single-server queuing system

The number of passengers ‘n’ changes on the walkway over the time. As the number of passengers on the walkway increases, the slower passengers block faster passengers. Thus, higher passenger densities reduce the individual passenger walking speed. The speed is reduced to 0 when the number of passengers ‘n’ reaches to the capacity of walkway ‘$C = 5LW$’. The passenger flow on the walkway can be viewed as stopped when the density of passengers is 5 ped/m². [35]. The walking speed variation phenomenon with an increase or decrease in the number of passenger ‘n’ on the walkway is known as state dependence. Hence, the walkway can be described as a state-dependent queuing system with passenger arrival rate represented by A, state-dependent service rate of the walkway by B( n ) and the number of servers (available positions/spaces) C to accommodate the maximum C number of passengers, i.e., A/B(n)/C/C queuing system.

Since the value of C is generally very high in hundreds and even thousands. The queuing systems with a high value of C are difficult to simulate and cause serious problems in optimization such as low optimization efficiency. Therefore, it is necessary to simplify the A/B(n)/C/C queuing system. We use the idea of transformation which is also used in relevant researches ([10, 18]). The transformation works as follows. A virtual line and a virtual server are set at the exit of the walkway, as shown in Fig. 3. When two sequential passengers pass through the virtual line, the time interval $T_{n}$ is recorded. If the time at which the previous passenger leaves the circulation facility is viewed as the time the next passenger begins to be served, then the time interval between these two sequential passengers passing through the virtual line is equal to the service time of the virtual server. In this way, the A/B(n)/C/C queuing system with C parallel–serial servers can be transformed equivalently to an A/B^′(n)/1/C queuing system with a single server. Note, the service time of the virtual server B′(n) = B(n)/n. Now how to calibrate the parameters for the PH arrival rate and service time will be discussed in the next subsection.

Fig. 3

Simulation-based optimization for the walkway width design

2.4 PH Arrival Rate and Walkway Service Time

The Phase-Type (PH) distribution was first introduced by Neuts [36] as the generalization of exponential distribution. It is constructed by the convolution of exponential distribution. A nonnegative random variable X has a PH distribution if its distribution function is given by;

$$f(x) = \alpha e^{{{\textbf{D}}x}} d$$

(1)

$${\textbf{F(x)}} = 1 - \alpha e^{{{\textbf{D}}x}} {\textbf{1}}$$

(2)

Eqs. (1) and (2) are the probability density function (PDF) and cumulative distribution function (CDF) of PH distribution

Here; $e$: is the column vector with all the elements being 1. $\alpha$: a sub-stochastic vector $\alpha = \left( {\alpha_{1} , \ldots \alpha_{n} } \right)$ of order n, i.e., $\alpha$ is a row vector, all elements of $\alpha$ are nonnegative and $\alpha e < 1$, where n is a positive integer. D: a sub-generator of order m, i.e., D is an n × n matrix such that (1) all the diagonal elements are negative; (2) all the off-diagonal elements are nonnegative; (3) all row sums are non-positive given as ${\textbf{ D}} = \left( {\begin{array}{*{20}c} {d_{11} } & \ldots & {d_{1n} } \\ \vdots & \ddots & \vdots \\ {d_{n1} } & \cdots & {d_{nn} } \\ \end{array} } \right)$ $d$: $d = {\textbf{D}}. 1$ and 1 is a column vector of one’s of the appropriate size.

The 2-tuple ($\alpha$, D) is called a phase-type representative (PH representative) of order n for the PH distribution. There are four conditions given for fitting PH distribution (Sadre and Haverkort [37], Sadre [38]) based on the squared coefficient of variation $c^{2}$

• If the $c^{2}$ for both the arrival and service processes is <1, a hypo-exponential distribution is used to fit the arrival and service processes with the number of phases given by $m = \frac{1}{{c^{2} }}$, the initial probability vector is $\alpha = (1,0, \ldots ,0)$ and the matrix D is expressed by:

  ${\mathbf{D}} = \left( {\begin{array}{*{20}c} { - d_{0} } & {d_{0} } & {} & {} & {} \\ {} & { d_{1} } & {-d_{1} } & {} & {} \\ {} & {} & {..} & {..} & {} \\ {} & {} & {} & { - d_{m - 2} } & {d_{m - 2} } \\ {} & {} & {} & {} & { - d_{m - 1} } \\ \end{array} } \right)$,

  where

  $d_{j} = \frac{m}{E[X]}$ for $0 \le j < m - 2;$

  $d_{m - 1} = \frac{{2m\left[ {1 + \sqrt {\frac{1}{2}m(mc^{2} - 1)} } \right]}}{{E[X](m + 2 - m^{2} c^{2} )}};$

  $d_{m - 2} = \frac{{m\lambda_{m - 1} }}{{2\lambda_{m - 1} E[X] - m}}.$

• If the $c^{2}$ is greater than 1 for both the arrival and service process, a hyper-exponential distribution is used for fitting with the number of phases $m{ = 2}$, the initial probability vector is $\alpha = ({\text{g}},1 - g)$ and the matrix D is given by:

  $${\text{D }} = \, \left( {\begin{array}{*{20}c} {\frac{ - 2g}{E[X]}} & 0 \\ 0 & {\frac{ - 2(1 - \, g)}{E[X]}} \\ \end{array} } \right)\;\text{and}\;g{ = }\frac{\text{1}}{\text{2}}{ + }\frac{\text{1}}{2}\sqrt {\frac{{c^{ 2} - 1}}{{c^{ 2} { + }1}}}$$

• If $c^{2}$ is equal to 1, then the approximation corresponds to an exponential distribution.

• If $c^{2}$ is very small, i.e., $c^{2} \le 1/30$, then the PH distribution with a large number of states is obtained and its approximation corresponds to an Erlang-30 distribution or deterministic distribution.

Jiang et al. [14] and Hu et al. [10] have achieved a good fitting effect for the passenger arrival interval from the train as well state-dependent service time of circulation facilities by using a PH distribution with any $c^{2}$. The four conditions show that we can determine the PH representation for the arrival rate and service time based on $\lambda , \, c_{a}^{2} , { }\mu_{n} \,$ and $c_{s,n}^{2}$. Note that E[X] is the mean arrival interval and inverse of the arrival rate $\lambda$ and the service rate $\mu_{n}$. Therefore, the following content is about how to obtain these parameters.

The passenger arrival process to the urban rail transit station walkway is specified by the first and second moment of the inter-arrival interval. More specifically, the arrival rate $\lambda$ and $c_{\text{a}}^{2}$ are the traffic descriptors that describe the passenger traffic flow. During the planning and design phase of urban rail transit stations, $\lambda$ and $c_{a}^{2}$ can be deduced from peak-hour volume ($q$), peak-hour factor ($\varepsilon$), mean headway (${\text{h}}$) between trains and squared coefficient of variation of the headway ($c_{\text{h}}^{2}$).

The passenger arrival rate can be obtained by using Eq. (3).

$$\lambda = \frac{q}{3600\varepsilon }$$

(3)

The value of ${c}_{a}^{ 2}$ of arrival rate can be calculated from Eq. (4) [10] and (5) [39]:

$$c_{a}^{2} = \frac{{e^{6.819\varepsilon } \left( {\varepsilon - 1} \right)^{2} }}{4\varepsilon - 1}$$

(4)

$${c}_{a}^{ 2} = e^{{0.503c_{h}^{2} }} \left[ {\left( {\frac{{qh}}{3600\varepsilon }} \right) - 1} \right]$$

(5)

We obtain this equation as follows: The peak-hour factor can be calculated by $\varepsilon = \frac{q}{{4q_{15} }}$. The q ₁₅ is the maximum flow rate in one quarter of the peak hour. The passengers’ arrival intervals in the peak-15 min are divided into two parts.

• (1) One is the time interval between passenger batches that are generated by the arriving trains that is known as headway ‘h’, and the data in this part account for $(900/{h})/q_{15} = 3600\varepsilon /(q{h})$ of the entire arrival interval data in peak-15 min.

• (2) The other is the time interval between the passengers in batches from the same train. This interval is close to 0 as the alighting passengers arrive in a single batch from the same, and the data account for $1 - 3600\varepsilon /(qh)$ of the entire arrival interval in peak-15 min. If the arrival intervals between the trains on all the lines are the same, then the $c_{a}^{2}$ is equal to variance/(mean)², i.e.,

  $$c_{a}^{2} = \frac{{(3600\varepsilon /q{h})({h} - 3600\varepsilon /q)^{2} + (1 - 3600\varepsilon /q{h})(0 - 3600\varepsilon /q)^{2} }}{{(3600\varepsilon /q)^{2} }}\quad c_{a}^{2} = \left( {q{h}/3600\varepsilon } \right) - 1$$

The correction factor $(e^{{0.503c_{h}^{2} }} )$ is used in the above equation that is obtained by fitting the data by regression analysis that are obtained from field survey of stations in Beijing and Chengdu (North Railway Station on Line 1 and Tianfu Square Station which is transfer station at Line 1 and Line 2 in Chengdu and Chongwenmen Station of Beijing which is hub of Line 2 and Line 5). The reason to choose these urban rail transit stations is due to heavy passenger volume at these stations. The final equation that we get is:

$${c}_{a}^{ 2} = e^{{0.503c_{h}^{2} }} \left[ {\left( {\frac{qh}{3600\varepsilon }} \right) - 1} \right]$$

According to TCQSM [1] and traffic flow theory, the passengers flow rate ($\mu$) is given by Eq. (6):

$$\mu = kV$$

(6)

here k is the density of passengers and V is the passengers walking speed on the walkway. In case of urban rail transit station walkway, the passenger flow rate is the number of passengers passing through the walkway per unit time. The reciprocal of flow rate $1/\mu$ is referred as the time interval of the passengers leaving the walkway which is also the state-dependent service time of walkway ${T}_{n}$. Therefore, the state-dependent service time of walkway can also be expressed as Eq. (7):

$$T_{n} = 1/\mu = L/nV_{n}$$

(7)

The state-dependent service rate of walkway can be written as Eq. (8):

$$\mu_{n} = 1/T_{n} = nV_{n} /L$$

(8)

here $L$ is the length and $V_{n}$ is the state-dependent walking speed of passengers passing through the walkway. Yuhaski and Smith [4] developed an exponential model to describe the state-dependent walking speed in the corridors (walkways), shown by Eq. (9).

$${\textit{V}}_{\textit{n}} {\textit{ = V}}_{ 1} \exp \left[ {{ - }\left( {\frac{{{\textit{n - }}1}}{\omega }} \right)} \right]^{\gamma }$$

(9)

where

$$\gamma { = }\left[ {\frac{{\ln \left( {\frac{{{{v}}_{{a}} }}{{{{v}}_{1} }}} \right)}}{{\ln \left( {\frac{{{{v}}_{{b}} }}{{{{v}}_{1} }}} \right)}}{ - }\ln \left( {\frac{{{{a - }}1}}{{{{b - }}1}}} \right)} \right]\quad \omega\,=\,\left( {{{a - }}1} \right)\left[ {\ln \left( {\frac{{{{v}}_{1} }}{{{{v}}_{{a}} }}} \right)} \right]^{1 /\gamma } .$$

Thus, Eq. (9) can now be written as:

$$\mu_{n} = nV_{1} \exp \left[ { - \left( {\frac{n - 1}{{\omega_{i} }}} \right)} \right]^{\gamma } /L$$

(10)

In order to consider the randomness as well as state-dependent service rate of the walkway, the squared coefficient of variation ($c_{s,n}^{2}$) of service rate should be taken into account. The state-dependent $c_{s,n}^{2}$ of service rate of the walkway is given by Eq. (11) [10].

$${c}_{s,n}^{ 2} { = }\left[ {\left( {\frac{{\delta_{1} }}{{{v}_{1} }}} \right)\exp \left( {\left( {\frac{{{n - }1}}{\omega }} \right)^{\gamma } - \left( {\frac{{{n - }1}}{{\omega^{{\prime }} }}} \right)^{{\gamma^{{\prime }} }} } \right)} \right]^{2}$$

(11)

where

$$\gamma^{{\prime }} = \left[ {\frac{{{ \ln }\left( {\frac{{\delta_{a} }}{{\delta_{1} }}} \right)}}{{{ \ln }\left( {\frac{{\delta_{b} }}{{\delta_{1} }}} \right)}} - { \ln }\left( {\frac{a - 1}{b - 1}} \right)} \right]\quad \omega^{{\prime }} = (a - 1)\left[ {{ \ln }\left( {\frac{{\delta_{1} }}{{\delta_{a} }}} \right)} \right]^{1/\gamma }$$

${\textbf{v}}_{1}$ mean walking speed when there is only one passenger on the walkway; $\delta_{1}$ standard deviation of walking speed when there is only one passenger on the walkway; ${\textbf{v}}_{\text{a}}$ mean walking speed when there are $a = 2LW$ passengers on the walkway; $\delta_{a}$ standard deviation of walking speed when there are $a = 2LW$ passengers on the walkway; ${\textbf{v}}_{b}$ mean walking speed when there are $b = 4LW$ passengers on the walkway; $\delta_{b}$ standard deviation of walking speed when there are $b = 4LW$ passengers on the walkway.

After fitting the PH distribution, the passenger arrival process can be described by the initial probability vector $\alpha$ and the transient generator matrix ${\textbf{D}}$ as:

$$A \sim {\textbf{PH}}(\alpha ,{\textbf{D}}),$$

The state-dependent service process of the walkway can be described by the initial probability vector $\beta_{n}$ and the transient generator matrix ${\textbf{H}}_{\text{n}}$ as:

$$B(n) \sim {\textbf{PH}}(\beta_{n} ,{\textbf{H}}_{n} ),\quad n = 1,2 \ldots C$$

The initial probability vectors and the transient generator matrix are used for the generation the PH random variates in PH/PH(n)/C/C DES model of urban rail transit station walkway.

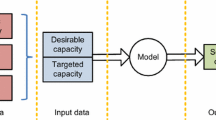
3 Simulation-based Optimization Approach for the Width Design

The simulation-based optimization approach proposed in this paper performs the optimization by genetic algorithm (GA) using PH/PH(n)/C/C DES model as representative of the urban rail transit station walkway. A PH/PH(n)/C/C DES model of walkway is developed in the SimEvents ^® to estimate the necessary performance measures (blocking probabilities ‘$P_{c}$’ and mean area occupied per passenger ‘ES’) of walkway while the optimization method that uses the genetic algorithm (GA) is implemented in the MATLAB ^® programming environment. The proposed simulation-based optimization approach blends both the PH/PH(n)/C/C DES and GA to work together concurrently and find the best model parameters (optimized width of the walkway) by minimizing an objective function of the performance measure (mean area occupied per passenger ‘ES’) while keeping the LOS and blocking probability $P_{c}$ in certain limits specified by TCQSM [1] and Hu et al. [10], respectively. The general flowchart of the simulation-based optimization for the urban rail transit station walkway width design is shown in Fig. 3. One of the main advantages of simulation-based optimization is that it not necessary to provide analytical expression of objective and constraints function as in the case of mathematical optimization. The first key ingredient of PH/PH(n)/C/C DES model is the efficient generation of PH random variates. Neuts [36] developed a ‘Count Procedure’ for the efficient generation of PH random variates.

3.1 Generation of Phase-Type (PH) Random Variates

PH distribution is proposed in this study to simulate the passenger arrival rate and state-dependent service rate of the walkway. The Neut’s procedure relies on generating an Erlang-distributed sample with degree $f$ and parameter $\lambda$ given as:

$${\text{Erl(}}f ,\,\lambda ) = - \frac{1}{\lambda }\ln \left( {\prod\limits_{j = 1}^{f} {U_{j} } } \right)$$

where U is uniformly distributed random number [0, 1]. Let $b_{j}$ represent the row vector with 1 at the position $j$. A pseudo-codes description of the PH random variates used in this work follows:

3.2 PH/PH(n)/C/C Discrete-Event Simulation Model Architecture

In contrast to PH/PH(n)/C/C analytical queuing model [3], PH/PH(n)/C/C DES model eliminates the need to solve large matrices and equations systems to estimate the performance measures. A PH/PH (n)/C/C DES model of the urban rail transit station walkway is built in the SimEvents ^®. The walkway facility is described as a PH/PH(n)/C/C queueing system. An overview of the key components of the walkway facility is presented in Fig. 4.

Fig. 4

PH/PH(n)/C/C discrete-event simulation model architecture

The key components are FIFO_Queue blocks that represent the passenger queueing space, Single-Server block that stores the entities for certain period of time, (entities in our case are passengers), Start and Read Timers that report the time associated with the arriving passengers and the Level-2 MATLAB ^® S-function blocks that compute and update different parameters in the PH/PH (n)/C/C DES model. The Event to Timed Signal blocks and Timed to Event Signal blocks convert event-based signals to time-based signals and vice versa. Constant blocks are used to input different parameters values in the DES model while Display blocks show the performance measure (output). The SimOut blocks export the values of performance measures from SimEvents ^® simulation to MATLAB ^® programming environment.

3.2.1 Passengers Generation Phase

In our PH/PH/(n)/C/C DES model as shown in Fig. 4a, the passengers are first generated at the entrance of the walkway facilities. The PH random variates are programmed in Level-2 MATLAB ^® S-function blocks (designated as S4) at passenger generation phase using ‘Count Procedure’ given in Ref. [37]. The two input parameters for the computation of PH random variates are $\lambda$ and $c_{a}^{2}$ which can be calculated by Eqs. (3), (4) and (5), respectively.

3.2.2 State-dependent Service Phase

After the generation of passengers in first phase, it must guarantee that the number of passengers that enter the walkway does not overcome its overall capacity $C = 5LW$. The passengers arriving at the entrance of the walkway facility form a queue and have to wait for free spaces (servers). At the same time, they reduce the free spaces on the walkway and affect the walking speed of passengers crossing the facility. To implement this condition, the generated passengers are stored in the FIFO_Queue block before being delayed by the Single_Server block and subsequently being sent to the successor facility.

Four Level-2 MATLAB ^® S-function blocks are used in this phase to calculate the state-dependent service rates based on PH random variates, mean area occupied per passengers ‘ES’, blocking probability $P_{c}$ and judging the number of passengers to prevent them from entry when maximum capacity $C = 5LW$ is reached as shown in Fig. 3b. The state-dependent service rate calculation depends on congestion of walkway area. The service rate calculation block takes capacity $C = 5LW$ and number of passengers (#n) from the FIFO_Queue block as input to compute the $\mu_{n}$ and $c_{s,n}^{2}$ using Eqs. (10) and (11), respectively.

The service rate calculation block dynamically updates the service rates as a function of number of passengers (#n) in the walkway. Similarly, mean area occupied per passenger ‘ES’ is calculated by using area of the walkway $A = LW$ divided by mean queue length (len) obtained by FIFO_Queue block. When the capacity $C = \, 5LW$ has been reached in the walkway, i.e., $\# n = C$ the passengers are blocked to enter the FIFO_Queue block. At the same time, the second entity port (OUT2) of Output Switch block activates and registers the blocked passengers. The blocking probability $P_{c}$ is calculated by using number of passengers departed via second entity port of Output Switch divided by total number of passengers departed via both first (OUT 1) and second ports (OUT 2).

3.2.3 PH/PH(n)/C/C DES Model Verification

Before developing the simulation-based optimization approach, we first verify the accuracy of our PH/PH(n)/C/C DES model. For this purpose, the simulation tests with different passenger arrival rate and squared coefficient of variation are performed and compared to the PH/PH(n)/C/C analytical model [10] The peak passengers arrival rate $\lambda$ are taken as 0.21, 0.34, 0.4 0.67 1.25, 1.79 (ped/s) with squared coefficient of variation of arrival interval ($c_{a}^{2}$) 3.24, 4.29, 2.36 1.82 2.05, 2.91, respectively, that are according to actual conditions of urban rail transit station. A 30 × 2 m² horizontal urban rail transit station walkway is considered for all the experiments. The three representative points for the walking speed on the walkway are given as $\left( {\nu_{1} = 1.50,\;\delta_{1} = 0.50} \right)$, $\left( {\nu_{\text{a}} = 0.64,\;\delta_{a} = 0.21} \right)$ and $\left( {\nu_{\text{b}} = 0.25,\;\delta_{b} = 0.08} \right)$, respectively [3]. The three performance measures of the walkway such as mean number of passengers on walkway E[N], mean area per passenger ‘ES’ and mean time spent by passenger on the walkway E[T] are calculated. The results of PH/PH(n)/C/C DES model are obtained after 10 replications with the simulation time of 20,000 time units. The PH/PH(n)/C/C DES model results are compared to the PH/PH(n)/C/C analytical queuing model. It is observed that the difference between PH/PH(n)/C/C DES model and PH/PH(n)/C/C analytical model is very small. The mean relative error of PH/PH(n)/C/C DES model is 2.1% for mean number of passenger on the walkway E [N], 2.9% for the mean area occupied per passenger ES and 3.2% for mean time spent by passenger on walkway E[T]. The small mean relative error indicates that PH/PH(n)/C/C DES model can be used with good accuracy in performance evaluation of urban rail transit station walkways.

The value of the mean number of passenger on walkway E[N] increases with the increase in arrival rate $\lambda$ as shown in Fig. 5. Similarly; the mean area occupied per passenger ES decreases with increase in arrival rate. It is because of the fact that when more passengers occupy the spaces on the walkway, the relative distance between them reduces. The mean time spent by passenger on walkway E[T] increases with increase in arrival rate. It is quite obvious that increase in the number of passengers due to high arrival rate causes reduction in the walking speed of the passengers and thus passengers spend more time on the walkway.

Fig. 5

Verification of the PH/PH(n)/C/C DES model

3.3 Parallel Implementation of PH/PH(n)/C/C DES Model and GA

Based on the PH/PH(n)/C/C DES model, we develop a simulation-based optimization approach for the width design of urban rail transit station walkway, The GA is used as an optimization method in conjunction with PH/PH(n)/C/C DES model to determine the optimal width of the urban rail transit station walkway. The proposed simulation-based optimization based on PH/PH(n)/C/C DES model and GA is described as follow:

• The width $W$ of the walkway is to be optimized under the LOS ‘B’, ‘C’ and ‘D; for which the blocking probability $P_{c}$ does not exceed the specified threshold $p$.

• The blocking probability.

• According to the TCQSM [1], the LOS of the walkway is reflected by the mean area occupied per passenger ES, which means that the ES on the walkway for a given LOS must fall within the range [LOS_UB, LOS_LB] where LOS_UB and LOS_LB are the upper and lower bounds of mean area occupied per passenger for the given LOS.

• The search space S for the optimal width $W_{\text{opt}}$ is defined by the upper and lower bounds of the width.

  $$S = [W_{\text{UB}} ,W_{\text{LB}} ]$$
  $$W_{\text{opt}} \in S$$

• The performance measures (outputs) ES and $P_{c}$ are estimated by running PH/PH (n)/C/C DES model of urban rail transit station walkway (see Fig. 4b).

• Mean area occupied per passenger ES on the walkway is $ES = LW/n$, from which we can see that mean area occupied per passenger will vary with the walkway width $W$. Therefore, the mean area occupied per passenger on the walkway can be expressed as a function of $W$, that is, $ES(W) = LW/n$.

• The wider the walkway width, the bigger will be the area occupied per passenger. So, the problem of finding the minimum (optimal) width $W_{\text{opt}}$ is equivalently converted to find $W_{\text{opt}}$ that makes the $ES(W) - LOS_{\text{LB}} = 0$. Therefore, the objective function (fitness function) Z for the GA is established from output ES and the lower bound of the walkway LOS,

  $Z = (ES(W) - LOS_{\text{LB}} ) \to \Re +$.

• Similarly, the constraint function is established from blocking probability (output)$P_{c}$,

  $P_{c} (W) \le p$.

• The GA search the search space S to find the parameter $W_{\text{opt}} \in S$ with

  $Z(ES(W_{\text{opt}} ) - LOS_{\text{LB}} ) \le Z(ES(W_{i} ) - LOS_{\text{LB}} )\quad \forall W_{i} \in S$

The MATLAB ^® programming environment is used for programming the constrained GA optimization script. The MATLAB ^® offers a computational infrastructure for optimizing the SimEvents ^® DES model as the SimEvents^® is embedded in it. Moreover, MATLAB ^® offers parallel DES and optimization without the pain of context switching into multiple softwares. In Table 2, the parameters setting for the GA can be observed.

Table 2 Options set for the genetic algorithm

At first, the interval containing upper and lower bounds of walkway width $U = [W_{\text{UB}} ,\,W_{\text{LB}} ]$ is defined which is supposed to contain the optimal width $W_{\text{opt}}$ of the walkway. We determine the upper and lower bounds of width by using the flow per unit width values for LOS ‘B’, ‘C’ and ‘D” that are given in Exhibit 7-3 and Table 1 of the TCQSM [1]. It should be noted that this is the rough estimation of walkway width for setting the initial range. The PH/PH(n)/C/C DES model run initiates with an arbitrary value from the defined interval to simulate the performance of the walkway and obtain the necessary performance measure such as mean area occupied per passenger ES and blocking probability $P_{c}$ when the simulation system reaches the steady state condition, i.e., (at 20,000 time units). Then the genetic algorithm (GA) that is programmed in MATLAB ^® adjusts the width $W$ according to the value of fitness function $Z = ES(W)) - LOS_{\text{LB}}$ and the constraint function $P_{c} (W) \le p$ until the optimal width $W_{\text{opt}}$ is found. It is inefficient to find the exact value of $W$ that makes the function $ES(W)) - LOS_{\text{LB}} = 0$; therefore, a function tolerance $\eta$ is defined. If the relative change in the best fitness function value is less than or equal to the $\eta$, then the corresponding $W$ can be approximately considered as the optimal width $W_{\text{opt}}$. If the difference is larger than $\eta$, the GA will replace $W$ from the defined interval $[W_{\text{UB}} ,\;W_{\text{LB}} ]$ and set the new width value $W$ in the PH/PH(n)/C/C DES model for the next iteration to obtain the ES and $P_{c}$ by same means. The iterations continue until the relative change in the best fitness function value is less than or equal to $\eta$ and the corresponding width W is the optimal width $W_{\text{opt}}$.

4 Computational Experiments

In this section, first we verify the accuracy of our PH/PH(n)/C/C simulation-based optimization approach for the width design of urban rail transit station walkway by comparing with the analytical model (Hu et al. [10]). Then, we use different LOS, arrival rates and peak-hour factors to compare our model with the existing design models.

4.1 Verification of PH/PH(n)/C/C Simulation-Based Optimization Approach

Tables 3, 4 and 5 show the comparison of widths obtained by our proposed PH/PH(n)/C/C simulation-based optimization approach and PH/PH(n)/C/C analytical model. Two different lengths of walkways, i.e., L = 10 and  30 m are considered for all the experiments under the LOS ‘B’, ‘C’ and ‘D’ requirements. The passenger arrival rate of 5,000 and 10,000 ped/h with the peak-hour factors of 0.9, 0.6 and 0.3 are considered. It should be noted that these parameters are only for illustration purposes and can be altered for different conditions. The results have shown clear consistency, and therefore our proposed PH/PH(n)/C/C simulation-based optimization approach can be used for the width design of urban rail transit stations.

Table 3 Comparison of simulation-based optimization with analytical approach under LOS ‘B’

Table 4 Comparison of simulation-based optimization with analytical approach under LOS ‘C’

Table 5 Comparison of simulation-based optimization with analytical approach under LOS ‘D’

4.2 Comparison with the Existing Design Approaches and Effect of Different Factors

The optimal (design) widths of the urban rail transit station walkway obtained by our proposed simulation-based optimization approach using PH/PH(n)/C/C DES model and GA are compared to the design widths obtained by existing M/G(n)/C/C ([5, 6, 17]) and D/D/1/C [1] analytical approaches. In TCQSM [1], the walkway width design is based on the fixed-length distribution. It means that the design procedure in TCQSM uses fixed arrival rate and a fixed service time which is similar to D/D/1/C analytical queuing model [10]. The squared coefficient t of variation $c^{2}$ is equal to 1/30 (0.03) as it neglect randomness and state dependence. We use the D/D/1/C queuing model to represent the width design procedure of TCQSM for the walkway facility. The required input parameters for the width design such as passenger arrival rate $\lambda$, peak-hour volume (q), headway between the trains (h), three representative points for the walking speed on the walkway [10] are predetermined. The $c_{a}^{2}$ is calculated by using Eq. (5) as we are dealing with the alighting passengers from the train. We consider mean headway (h) between the train as 90 s and $c_{h}^{2}$ as 0.1. The corresponding $c_{a}^{2}$ for the peak-hour factors 0.9, 0.6 and 0.3 are 140, 210 and 417, respectively. The width designed by the three approaches, PH/PH(n)/C/C simulation-based optimization, M/G(n)/C/C and D/D1/C, are presented in Fig. 6. The figures reveal some interesting and important findings:

Fig. 6

Comparitive analysis of different design approaches

• It has been observed that the width design by our PH/PH(n)/C/C simulation-based optimization is greater than the existing for all the LOS, arrival rates and squared coefficient of variation $c_{a}^{2} .$

• For all the peak-hour factors, when our proposed PH/PH(n)/C/C simulation-based optimization approach is compared with the existing M/G(n)/C/C model, it has been observed that there is an average increase of 2.44 m in width for LOS B, 2.22 m for LOS C and 2.21 m for LOS D. Similarly, the average increase in width while comparing M/G(n)/C/C and D/D/1/C model is 0.12, 0.19 and 0.7 m for LOS B, LOS C and LOS D, respectively.

• For all the three design approaches, the width of the walkway increases with increase in passenger arrival rate even when squared coefficient of variation remains the same. It is expected because of the fact that these design approaches are sensitive to arrival rate. When the arrival rate increases from 5000 to 10,000 ped/h, for all the LOS, the average increase in our proposed PH/PH(n)/C/C simulation-based optimization model and M/G(n)/C/C is 2.45 m for $\varepsilon = 0.3$, 1.97 m for $\varepsilon = 0.6$ and 1.78 m for $\varepsilon = 0.9$. Similarly; for M/G(n)/C/C and D/D/1/C, the average increase is 0.45 m for $\varepsilon = 0.3$, 0.37 m for $\varepsilon = 0.6$ and 0.24 m for $\varepsilon = 0.9$. It reveals that the growth of width is higher for low peak-hour factors that eventually results in higher values of squared coefficient of variations (by using Eq. 5). The squared coefficient of variations accounts for the randomness in passenger arrival process as well as in service process of the walkway. The existing M/G(n)/C/C model and D/D/1/C model ignore this factor and result in underestimation of width. Therefore, the design methods based on M/G(n)/C/C and D/D/1/C models are not applicable in practical system where the squared coefficient of variation is very high. On the contrary, the width of our proposed model is sensitive to squared coefficient of variation.

• The increase in passenger arrival rate from 5000 to 10,000 ped/h results in almost doubling the design width for all the peak-hour factors and LOS. The increase in width value is quite obvious because the higher arrival rates cause high density of passengers on the walkway resulting in the slow movement of passengers and congestion. Therefore, in order to avoid the congestion and the blocking, the walkway width should be more for higher arrival rates to provide safe passage for the passengers to travel.

• The design width very slightly decreases, which is almost negligible when the length of the walkway is increased from L = 10 to 30 m. For all the LOS, the average width decrease of 0.03 m for $\varepsilon = 0.3$, 0.027 m for $\varepsilon = 0.6$ and 0.02 m for $\varepsilon = 0.9$ is observed when the length increases from L = 10 to 30 m and passenger’s arrival rate from 5000 to 10,000 ped/h. It is observed that an increase in the length L has two opposing influences on the mean area occupied per passenger ES. The increase in the length means the increase in the capacity of the walkway. The ES increases with the increase in L since the area of the walkway increases; however, this advantage is adversely affected by the fact that increasing the length gives the passengers a longer distance to travel in the walkway from one end to another. Hu et al. [10] observed that due to these opposing influences, there is a threshold value of the L; when L is larger than that threshold value, the effect of the passengers having to travel a longer distance has a stronger overall effect on the congestion. If the value of L is smaller than the threshold value, then there is no significant effect.

5 Conclusion and Future Work

This paper proposes a simulation-based optimization approach using PH/PH (n)/C/C DES model and GA algorithm for the width design of urban rail transit station walkway. To reproduce the reality, the walkway is abstracted as a finite capacity queuing system. The corresponding PH/PH(n)/C/C model is developed in the SimEvents ^® software. Unlike the existing design codes (D/D/1/C) and M/G(n)/C/C model that ignore the randomness and state dependence, the proposed PH/PH(n)/C/C DES model considers the randomness and state dependence and overcomes these shortcomings. Then the GA algorithm, integrated with the PH/PH(n)/C/C DES model, determines the optimal width of the walkway with blocking probability control under the different LOS and passenger flow conditions.

The comparative experiments show that the walkway designed by our proposed model has larger widths compared with the designed by existing models. The width of the proposed model increases more with increase in $c_{a}^{2}$ of arrival interval compared to the widths of the design methods based on the M/G (n)/C/C and D/D/1/C models. The width of the proposed method increases faster than the other two methods when the arrival rate increases. The length of walkway has no significant effect on design width.

This new proposed simulation-based optimization approach, integrating DES and optimization, can help the planners and designers of urban rail transit station to make decisions regarding urban rail transit station design. The coefficient of variation ($c_{a}^{2}$) of arrival interval should be paid more attention during the design process of the walkway. To apply the proposed method, we only need the length of walkway and passenger forecast data, such as peak-hour factor ($\varepsilon$), passenger peak-hour volume (q), mean headway between the trains (h) and the $c_{h}^{2}$ of the arrival interval between the train.

Besides urban rail transit station walkway, the proposed method can also be applied to the stairs facilities in urban rail transit stations as well as corridors and stairs in other buildings such as shopping malls, stadiums and hospitals. The proposed method can be easily extended to a queuing network to design different service facilities such as a network of walkways and stairs. The alighting passenger flow from the train is considered. Nevertheless, the proposed approach can also deal with the flow of passengers toward the walkway from entrance gate of the urban rail transit station.

This paper considers rectangular walkway for evaluation and design purpose according to the TCQSM. More complicated facilities that are not rectangular can be divided into several rectangular facilities can be evaluated in similar manner. The principle procedure of transformation of walkway into a single-server finite capacity queuing system remains the same. In this research, we only consider the walkway facility. The escalator, platform and ticket facilities are not discussed in this research. These facilities can also be designed by abstracting into a queuing system. Moreover, the state-dependent arrival rate can also be considered in addition to state-dependent service rate in future research work.