3D Suspension Characterization of a Rapid Transit Vehicle Using a Multi-Body Dynamic Model

Abstract

In this work, suspension characterization of a rapid transit vehicle is performed with a multi-body dynamic model that represents full degrees of freedom of a rapid transit vehicle. The effects of lateral suspension properties on passenger ride comfort and stability are investigated by variation of critical suspension parameters using design of experiment method. The critical suspension properties are obtained for the best values of car body lateral acceleration and car body lateral stroke. The tangent track time response of the car body verified the negligible effect of both lateral viscous dampers at primary suspensions and longitudinal anti-yaw dampers at secondary suspensions on the passenger ride comfort and stability of a rapid transit vehicle.

Introduction

The suspension design of rail vehicles has been extensively studied considering all possible suspension elements for a rail vehicle [1]. Dynamic modeling of suspension components is well described in the reference [2]. However, depending on the speeds and axle load properties of the rail vehicle, some of the suspension elements may not be functional. Therefore, a special treatment shall be present for the selection of suspension elements that depends on the type or application use of the rail vehicle. Minimum possible number of suspension elements shall be used for a rail vehicle, in order to minimize the manufacturing and maintenance costs. Therefore, practically some of the suspension elements like vertical and lateral viscous dampers at primary suspension and longitudinal anti-yaw viscous dampers at secondary suspension are avoided in rapid transit vehicles. There are only a few recent works on dynamics of rapid transit vehicles that explain these specific details concerning selection of suspension components [3, 4].

Analytical dynamic models are essential tools to determine the suspension properties of rail vehicles [5]. Commercial simulation packages offer user friendly methods to obtain dynamic responses of rail vehicles [6]. However, analytical rail vehicle dynamic models are very useful tools to understand and establish relationships between suspension properties and dynamic vehicle response, stability and passenger ride comfort, etc. Therefore, even though the analytical multi-body dynamic models are simple tools to design suspensions, they form the backbone of commercial simulation software packages. It also important to note that with dynamic models exact simulation results could only be obtained with very accurate track input models [7].

The lateral stability of rail vehicles, namely wheel hunting, has been a great concern in rail vehicle suspension design [8–11]. Wheel hunting occurs after the wheel-set reaches to a critical speed at which the wheel-set motion becomes unstable which may cause derailment by the loss of lateral stability of rail vehicles. An important goal of suspension design is to obtain the suspension parameters of rail vehicles so that the resulting motion of the wheel-sets is laterally stable [12].

Wheel–track interaction is actually a very complicated phenomenon and several methods have been used to compute the normal and friction forces on wheels in the literature [13, 14]. Kalker’s linear creep theory offers an easy solution to incorporate creep forces into the rail vehicle model as a function of the speed of the rail vehicle. Therefore, Kalker’s theory is an essential ingredient of many of dynamic rail vehicle models in the present literature. Comparison of different wheel–track interaction models has been well studied; however, most of the models ignore the fact that wheel slip phenomena had been reduced significantly with the recent improvements in traction and brake technologies. Therefore, wheel slip can be observed for modern rapid transit rail vehicles depending on the wheel–track adhesion conditions, but at normal conditions wheel slide protection systems avoid wheel slide during acceleration and braking.

Rapid transit vehicles are used to rapidly transport passengers inside cities and rapid transit vehicles are mainly classified according to the axle load. In over-crowded cities, heavy rapid transit vehicles may have axle loads ranging between 15–17 tonnes at AW-8 loading conditions (8 persons per square meter). The axle load also depends on the car body material, whether car body is made of aluminum or stainless steel. The trip time for rapid transit vehicles could take longer than an hour for large cities, and hence, passenger ride comfort is an important fact and it shall be considered during the design of suspension systems. Human body is most sensitive to accelerations in lateral direction; hence, lateral acceleration can be used as a good and simple indicator of passenger ride comfort in rail vehicles.

In this work, the suspension properties for a rapid transit rail vehicle are characterized with multi-body dynamic model of 31 degrees of freedom (dof). The model accounts for all suspension elements and their degrees of freedom of a rapid transit vehicle. The lateral acceleration is used as the measure for the passenger ride comfort throughout this work. Lateral viscous dampers at primary suspensions and the longitudinal anti-yaw dampers at secondary suspension had negligible effect on the passenger ride quality, and hence, these two suspension elements are neglected in the final model. The remaining secondary lateral suspension properties are estimated by varying the suspension parameters while keeping the remaining other parameters the same and by simulating of responses of lateral stroke and lateral acceleration of the car body. Finally, the selected suspension parameters are checked against stability with the use of a 3D multi-body dynamic model and the acceleration response of a rapid transit vehicle is obtained for the optimized suspension properties.

Multi-Body Dynamic Model

In the present model, car body, bogie, and wheel-set are all assumed to be rigid. Mass and inertia properties needed to be identified before the dynamic analysis; hence, car body, bogie, and wheel-set were designed before dynamic analysis. The designs of the car body, bogie, and wheel-set designs that were performed within scope of this work are shown in Fig. 1. The car body design was according to static and fatigue requirements that are mentioned in EN 12663. The first mode of vibration of car body occurred at 13.4 Hz which is acceptable. It is a general rule that selected first mode of vibration to be over 10 Hz since human body is sensitive to the frequencies below. Similarly, bogie design was performed in accordance with EN 13749. Several different standards were considered during the design of wheel-set: EN 13103, EN 13104, EN 13260, EN 13261, and EN 13262. The inertia and mass properties of the car body, bogie, and wheel-set of the metro vehicle are shown in Table 4.

Fig. 1

Design of the rapid transit vehicle has been performed before the dynamic analysis: a. car body design according to EN 12663, b. wheel-set design according to EN 13103, EN 13104, EN 13260, EN 13261, and EN 13262, c. bogie design according to EN 13749

Basic Equations

Newton’s Second Law is used to formulate all of the dynamic models. ${\mathbf {M}}$, ${\mathbf {K}}$, ${\mathbf {C}}$, and ${\mathbf {q}}$ represent mass matrix, stiffness matrix, damping matrix, and variable vector, respectively. ${\mathbf {R}}$ is the matrix of rail stiffness and damping, while ${\mathbf {u_r}}$ is the vector containing input rail displacements. Note that input forcing term, ${\mathbf {u_r}}$, is zero for the stability analysis.

$$\begin{aligned} {\mathbf {M}} \; \ddot{\mathbf {q}} \;+\; {\mathbf {C}} \; \dot{\mathbf {q}} \;+\; {\mathbf {K}} \; {\mathbf {q}} \;=\; {\mathbf {R}} \;{\mathbf {u_r}} \end{aligned}.$$

(1)

The equation of motion is given in as shown in Eq. (2) and the ordinary differential equation is solved using ode45 function of MatLab. Please note that the variable ${\mathbf {q}}$ is rearranged as the vector ${\mathbf {q}}'$ in order to use ode45 solver.

$$\begin{aligned} \dot{\mathbf {q}}' \;=\; {\mathbf {A}} \; {\mathbf {q}}' \;+\; {\mathbf {B}} \; {\mathbf {u_r}} \end{aligned},$$

(2)

where ${\mathbf {A}}$ and ${\mathbf {B}}$ are defined as

$$\begin{aligned}{}[{\mathbf {A}}] \,=\left[ { \begin{array}{cc} {\mathbf {0}} &{} {\mathbf {I}} \\ \quad-{\mathbf {M}}^{-1}\,{\mathbf {K}} &{} \quad-{\mathbf {M}}^{-1}\,{\mathbf {C}} \end{array} }\right] \end{aligned}$$

$$\begin{aligned} {\mathbf {B}} \,=\left[ \begin{array}{c} {\mathbf {0}} \\ \quad{\mathbf {M}}^{-1} \, {\mathbf {R}} \end{array} \right] \end{aligned}.$$

Stability of the dynamic system is determined by examination of the eigenvalues of ${\mathbf {A}}$ matrix. If all the real parts of the eigenvalues have negative value, then the system is said to be stable.

Random Track Input Generation

In the following, the methodology that is used to generate random track inputs is explained. The same method is used to generate both lateral and vertical track inputs for time response analysis similar to the reference [17].

A random track profile has to be generated as the input. For this purpose, the track profile is represented with a standard 2 slope power spectral density (PSD). In Eq. 3, V, $N_{d2}$, $a_k$ , and $\phi _k$ are car velocity, number of defect functions, Gaussian random variable with expectation zero, and variance $\sigma _k$, a random variable with uniform distribution between $0-2\pi$ range, respectively.

$$\begin{aligned} u(x)\,=\,\sum _{k=1}^{N_{d2}} a_k\,\sin (\omega _k\,\dfrac{V}{x}\,+\,\phi _k) \end{aligned}.$$

(3)

The method requires a range of pulsations; hence, $\omega _u$ and $\omega _l$ have to be defined and increment of pulsation has to be calculated.

$$\begin{aligned} \Delta \omega \,=\, \dfrac{\omega _u\,-\,\omega _l}{N_{d2}\,-\,1} \end{aligned}.$$

(4)

The PSD of track is represented with a constant frequency ($\omega _c$) and track condition identifier ($A_V$) as a function of frequency ($\omega$). The coefficients of $A_V$ and $\omega _c$ are selected according to American Railway standards and, as shown in Table 1 according to the grade of the track.

Table 1 Coefficients for $A_V$ and $\omega _c$ from American Railway standard

The relation for PSD (S) is

$$\begin{aligned} S(\omega )= \dfrac{0.25\,A_V\,\omega _c^2}{(\omega ^2\,+\,\omega _c^2)\,\omega ^2} \end{aligned}.$$

(5)

The variance, $\sigma _k$, of the amplitude $a_k$ is calculated from

$$\begin{aligned} \sigma _k\,=\,4 \,S(\omega _k)\,\Delta \omega \end{aligned}.$$

(6)

Power spectral density of the track generated for grade 6 type of track which corresponds to the track displacements is shown in Fig. 2. The track condition is selected to be worse in order to test suspension capabilities with the highest available amplitude of inputs.

Fig. 2

a Power spectral density (PSD) of the track generated for grade 6 track and b corresponding vertical track displacements as the input for the dynamic analysis

Figure 3 shows the vertical track displacements of a grade 6 track for three different travel speeds: 15, 30, and 90 km/h. The frequency of track input is set by the velocity of vehicle. The vertical and the lateral track inputs are different, and a different random input is generated for each. However, the same track input for the rear and front wheel-sets with a spacing of wheelbase since all the wheels run on the same track obviously. The wheelbase and bogie spacing and the corresponding differences in the track input displacement is taken into account during assignment of inputs to each wheel-set.

Fig. 3

Amplitudes of track displacements of a grade 6 track for three different travel speeds: 15, 30, and 90 km/h

3d Vehicle Model: 31 dof

Rapid transit vehicle suspension system is characterized by 31 number of dof (Table 2).

Table 2 31 Degrees of freedoms of the metro car

The notations used for the directions and rotations are shown in Fig. 4. Table 2 shows the complete set of degrees of freedom of a metro vehicle.

Fig. 4

General notation used for directions and angular rotations

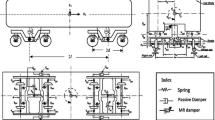
Figure 5 shows the suspension components that are used in this model. Several suspension components of a rail vehicle is not used in the model: lateral and vertical dampers at primary suspension, longitudinal anti-yaw dampers at secondary suspension.

Fig. 5

Suspension components of the metro car model. $K_p$ primary suspension stiffness, $K_s$ secondary suspension stiffness, $C_{py}$ primary suspension damping coeff. along lateral direction, $C_{pz}$ primary suspension damping coeff. along vertical direction, $C_{sz}$ secondary suspension damping coeff. along vertical direction, $C_{sy}$ secondary suspension lateral damping coeff., $K_{s\varphi }$ secondary suspension anti-roll bar stiffness

Car body equation of motions are obtained by force and moment balances as in the following. Nomenclature section contains all of the variables used in the model; hence, the variables used will not explain here again in order to avoid repetition.

• car body lateral direction ($y_c$)

  $$\begin{aligned} m_c \; \ddot{y_c} \;=\; (2\,K_{sy}\,+\,K_{cpy})\,(y_{b1}\,+\,y_{b2}\,-\,2\,y_c \,-\, 2\,h_{cs} \,\varphi _c \,+\, h_{bs}\,\varphi _{b1} \,+\, h_{bs} \,\varphi _{b2})\,+ \\ \,2\,C_{sy}\,(\dot{y}_{b1}\,+\,\dot{y}_{b2}\,-\,2\,\dot{y}_c \,-\, 2\,h_{cs} \,\dot{\varphi }_c \,+\, h_{bs}\,\dot{\varphi }_{b1} \,+\,h_{bs}\,\dot{\varphi }_{b2})\\ \,+\,m_c\,g\,\varphi _c .\end{aligned}$$

  (7)

• car body vertical direction ($z_c$)

  $$\begin{aligned} m_c \, \ddot{z_c} \;=\; 2\,K_{sz}\,(z_{b1}\,+\,z_{b2}-2\,z_{c}) \,+ \\ 2\,C_{sz}\,(\dot{z}_{b1}\,+\,\dot{z}_{b2}-2\,\dot{z}_{c}). \end{aligned}$$

  (8)

• car body pitch ($\theta _c$)

  $$\begin{aligned} I_{cy} \, \ddot{\theta _c} \;=\; -2\,l_s\,[K_{sz}\,(z_{b1}\,-\,z_{b2})\,+ \,C_{sz}\,(\dot{z}_{b1}\,-\,\dot{z}_{b2})] \\ \,-\,4\,l_s^2\,K_{sz}\,\theta _c\,-\,4\,l_s^2\,C_{sz}\,\dot{\theta }_c \end{aligned}$$

  (9)

• car body roll ($\varphi _c$)

  $$\begin{aligned} I_{cx} \, \ddot{\varphi _c} \;=\; 2\,h_{cs}\,[\,K_{sy}\,(\,y_{b1}\,+\,y_{b2}\,-\,2\,y_{c})\,+\,C_{sy}\,(\,\dot{y}_{b1}\,+\,\dot{y}_{b2}\,-\,2\,\dot{y}_{c}\,)]\,+ \\ 2\,d_{s}^2\,[\,K_{sz}\,(\,\varphi _{b1}\,+\,\varphi _{b2}\,-\,2\,\varphi _{c})\,+\,C_{sz}\,(\,\dot{\varphi }_{b1}\,+\,\dot{\varphi }_{b2}\,-\,2\,\dot{\varphi }_{c}\,)] \\ \,-\,2\,h_{cs}\,[\,K_{sy}\,(h_{bs}\,\varphi _{b1}\,+\,h_{bs}\,\varphi _{b2}\,+\,2\,h_{cs}\,\varphi _{c})\,+ \,C_{sy}\,(h_{bs}\,\dot{\varphi }_{b1}\,+\,h_{bs}\,\dot{\varphi }_{b2}\,+\,2\,h_{cs}\,\dot{\varphi }_{c})\,] \\ \,+\,2\,K_{s\varphi }\,(\varphi _{b1}\,+\,\varphi _{b2}\,-\,2\,\varphi _c) \\ \,+\,h_{cs}\,m_c\,g\,\varphi _c .\end{aligned}$$

  (10)

• car body yaw ($\psi _c$)

  $$\begin{aligned} I_{cz} \, \ddot{\psi _c} \;=\,2\,K_{sy}\,l_s\,(\,y_{b1}\,-\,y_{b2}\,)\,+\,2\,C_{sy}\,l_s\,(\,\dot{y}_{b1}\,-\,\dot{y}_{b2}\,) \\ -2\,K_{sx}\,d_s^2\,(2\,\psi _c-\psi _{b1}-\psi _{b2}) \\ -4\,l_s^2\,(\,K_{sy}\,\psi _c\,+\,C_{sy}\,\dot{\psi _c}) \\ -2\,l_s\,[\,K_{sy}\,(2\,h_{cs}\,\varphi _c\,-\,h_{bs}\,\varphi _{b1}\,-\,h_{bs}\,\varphi _{b2}\,)\,+\,C_{sy}\,(2\,h_{cs}\,\dot{\varphi }_c\,-\,h_{bs}\,\dot{\varphi }_{b1}\,-\,h_{bs}\,\dot{\varphi }_{b2}\,)\,] \\ -K_{s\psi }\,(2\,\psi _c-\psi _{b1}-\psi _{b2}) .\end{aligned}$$

  (11)

Bogie equation of motions are obtained by force and moment balances as in the following:

• bogie lateral direction ($y_b$) The last term in Eq. 12, the sign is ‘$+$’ for the front bogie and ‘−’ of rear bogie.

  $$\begin{aligned} m_b\,\ddot{y_b}\,=\, -[K_{cpy}\,+\,2\,(4\,K_{py}\,+\,K_{sy})]\,y_b\,-2\,(2\,C_{py}\,+\,C_{sy})\,\dot{y}_b \\ +\,(K_{cpy}\,+\,2\,K_{sy})\,y_c\,+\,2\,C_{sy}\,\dot{y}_c \\ +\,2\,[2\,K_{py}\,(\,y_{w1}\,+\,y_{w2})\,+\,C_{py}\,(\dot{y}_{w1}\,+\,\dot{y}_{w2})] \\ -\,4\,[C_{py}\,h_{bp}\,\dot{\varphi }_b\,+\,2\,K_{py}\,h_{bp}\,\varphi _b] \\ +\,2\,C_{sy}\,h_{bs}\,\dot{\varphi }_b\,+\,2\,K_{sy}\,h_{bs}\,\varphi _b \\ +\,2\,C_{sy}\,h_{cs}\,\dot{\varphi }_c\,+\,2\,K_{sy}\,h_{cs}\,\varphi _c \\ \pm \,2\,l_s\,(C_{sy}\,\dot{\psi }_c\,+\,K_{sy}\,\psi _c) \\ \,-\,\left(\dfrac{m_c}{2}\,+\,m_b\right)\,g\,\varphi _b .\end{aligned}$$

  (12)

• bogie vertical direction ($z_b$) The last term in Eq. 12, the sign is ‘$+$' for the rear bogie and ‘−' of front bogie.

  $$\begin{aligned} m_b\,\ddot{z_b}\,=-\,2\,(4\,K_{pz}\,+\,K_{sz})\,z_b\,-2\,(2\,C_{pz}\,+\,C_{sz})\,\dot{z}_b \\ +\,2\,K_{sz}\,z_c\,+\,2\,C_{sz}\,\dot{z}_c \\ +\,4\,(K_{pz}\,(z_{w1}\,+\,z_{w2})\,+\,2\,C_{pz}\,(\dot{z}_{w1}\,+\,\dot{z}_{w2}) \\ \pm \,2\,K_{sz}\,l_s\,\theta _c\pm \,2\,C_{sz}\,l_s\,\dot{\theta }_c .\end{aligned}$$

  (13)

• bogie pitch ($\theta _b$)

  $$\begin{aligned} I_{by}\,\ddot{\theta _b}\,=\, -2\,l_p\,[2\,K_{pz}\,(z_{w1}-z_{w2})\,+\,C_{pz}\,(\dot{z}_{w1}-\dot{z}_{w2})] \\ -4\,l_p^2\,(2\,K_{pz}\,\theta _b\,+\,C_{pz}\,\dot{\theta }_b). \end{aligned}$$

  (14)

• bogie roll ($\varphi _b$) The last term in Eq. 12, the sign is ’$+$’ for the front bogie and ’−’ of rear bogie.

  $$\begin{aligned} I_{bx}\,\ddot{\varphi _b}\,=\, 2\,d_s^2\,[K_{sz}\,(\varphi _c\,-\,\varphi _b)\,+\,C_{sz}\,(\dot{\varphi }_c\,-\,\dot{\varphi }_b)] \\ +\,2\,d_p^2\,[2\,K_{pz}\,(\varphi _{w1}\,+\,\varphi _{w2}\,-\,2\,\varphi _{b})\,+\,C_{pz}\,(\dot{\varphi }_{w1}\,+\,\dot{\varphi }_{w2}\,-\,2\,\dot{\varphi }_{b})] \\ +\,K_{s\varphi }\,(\varphi _c\,-\,\varphi _b) \\ -\,2\,h_{bs}\,[K_{sy}\,(y_c\,-\,y_b)\,+\,C_{sy}(\dot{y}_c\,-\,\dot{y}_b)] \\ +\,2\,h_{bp}[2\,K_{py}(y_{w1}\,+\,y_{w2}\,-\,2\,y_b)\,+\,C_{py}(\dot{y}_{w1}\,+\,\dot{y}_{w2}\,-\,2\,\dot{y}_b)] \\ \pm \,2\, l_s\, h_{bs}(K_{sy}\,\varphi _c\,+\,C_{sy}\,\dot{\varphi }_c) .\end{aligned}$$

  (15)

• bogie yaw ($\varphi _b$)

  $$\begin{aligned} I_{bz}\,\ddot{\psi _b}\,=\, +\,2\,K_{sx}\,d_s^2\,(\psi _c\,-\,\psi _b) \\ +\,4\,d_p^2\,K_{px}\,(\psi _{w1}\,+\,\psi _{w2}\,-\,2\,\psi _{b}) \\ +\,2\,l_p\,[2\,K_{py}\,(y_{w1}\,-\,y_{w2})\,+\,C_{py}\,(\dot{y}_{w1}\,-\,\dot{y}_{w2})] \\ -\,4\,l_p\,d_p\,[2\,K_{py}\,\psi _b\,+\,C_{py}\dot{\psi }_b] \\ +\,K_{s\psi }\,(\psi _c\,-\,\psi _b). \end{aligned}$$

  (16)

The rail displacements along lateral $y_r$ and vertical $z_r$ directions are the input forcing terms arising from rail damping and stiffness. Linear Kalker theory is used to find the creep forces on the wheels [15]. Wheel-set equations that define lateral, vertical, roll, and yaw wheel-set motions are obtained by force and moment balances as in the following:

• wheel-set lateral direction ($y_w$) The first term in Eq. 17, the sign is ‘$+$’ for the front wheel-set and ‘−’ of rear wheel-set.

  $$\begin{aligned} m_w\,\ddot{y}_w\,=\, 2\,[2\,K_{py}\,(y_b\,\pm \,l_p\,\psi _b\,+\,h_{bp}\,\varphi _b)\,+\,C_{py}\,(\dot{y}_b\,\pm \,l_p\,\dot{\psi }_b\,+\,h_{bp}\,\dot{\varphi }_b) \\ -\,4\,K_{py}\,y_w -\,2\,C_{py}\,\dot{y}_w \\ -\,\dfrac{2\,f_{11}}{V}\,\dot{y}_w\,-\,\dfrac{2\,f_{11}\,r_0}{V}\,\dot{\varphi }_w\,-\,\dfrac{2\,f_{12}}{V}\,\dot{\psi }_w\,+\,2\,f_{11}\psi _w \\ +\,F_r \,-\,\Bigg(\dfrac{m_c}{4}+\dfrac{m_b}{2}+m_w\Bigg)\,g\,\varphi _w \\ +\,C_{ry}\,\dot{y}_r\,+\,K_{ry}\,y_r, \end{aligned}$$

  (17)

  where $F_r$ is the flange contact force of the wheel and rail;

  $$ F_r = {\left\{ \begin{array}{ll} -K_{ry}\,(y_w-\delta ) &{} {\text {if }}\quad y_w \,>\, \delta ; \\ 0 &{} {\text {if}}\quad -\delta \,\le \, y_w \,\le \, \delta ; \\ -K_{ry}\,(y_w+\delta ) &{} {\text {if }}\quad y_w \,<\, -\delta . \\ \end{array}\right. } $$

  (18)

• wheel-set vertical direction ($z_w$) The last term in Eq. 19, the sign is ‘$+$’ for the rear wheel-set and ‘−’ of front wheel-set.

  $$\begin{aligned} m_w\,\ddot{z}_w\,=\, 4\,K_{pz}\,z_b\,+\,2\,C_{pz}\,\dot{z}_b \\ -\,4\,K_{pz}\,z_w\,-\,2\,C_{pz}\,\dot{z}_w \\ \pm \,4\,K_{pz}\,l_p\,\theta _b\,\pm \,2\,C_{pz}\,l_p\,\dot{\theta }_b \\ +\,C_{rz}\,\dot{z}_r\,+\,K_{rz}\,z_r. \end{aligned}$$

  (19)

• wheel-set roll ($\varphi _w$)

  $$\begin{aligned} I_{wx}\,\ddot{\varphi }_w\,=\, 2\,d_p^2\,(C_{pz}\,\dot{\varphi }_b\,+\,2\,K_{pz}\,\varphi _b) \\ -\,2\,d_p^2\,(C_{pz}\,\dot{\varphi }_w\,+\,2\,K_{pz}\,\varphi _w) \\ -\,\dfrac{2\,f_{11}\,(r_0\,+\,a\,\lambda )}{V}\,\dot{y}_w\,+\,\dfrac{2\,f_{12}\,\lambda ^2}{r_0} y_w \\ -\,\left[\dfrac{2\,f_{12}\,(r_0\,+\,a\,\lambda )}{V}\,-\,\dfrac{I_{wy}\,V}{r_0}\right]\,\dot{\psi }_w \\ +\,\left[2\,f_{11}\,(r_0\,+\,a\,\lambda )\,+\,\dfrac{2\,f_{22}\,\lambda ^2}{r_0}\right]\,\psi _w \\ -\,\dfrac{2\,f_{11}\,r_0}{V}\,(r_0\,+\,a\,\lambda )\,\dot{\varphi }_w\,+\,\dfrac{2\,f_{12}\,a\,\lambda }{r_0}\varphi _w \\ +\,a\,\lambda \,\left(\dfrac{m_c}{4}+\dfrac{m_b}{2}+m_w\right)\,g\,\varphi _w. \end{aligned}$$

  (20)

• wheel-set yaw ($\psi _w$)

  $$\begin{aligned} I_{wz}\,\ddot{\psi }_w\,=\, -\,2\,f_{12}\,\psi _w \\ -\,2\,\left(\dfrac{f_{22}\,+\,a^2\,f_{33}}{V}\right)\,\dot{\psi }_w \\ +\,\dfrac{2\,f_{12}}{V}\,\dot{y}_w\,-\,\dfrac{2\,f_{33}\,a\,\lambda }{r_0}\,y_w \\ +\,4\,d_p^2\,K_{px}\,(\psi _b\,-\,\psi _w). \end{aligned}$$

  (21)

Each wheel-set has 4 dof ignoring the pitch motion and four wheel-sets add up to 16 dof. Each bogie and car body has 5 dof individually. The motion in longitudinal direction (x direction) is irrelevant for both the stability and time response analysis. Therefore, a rapid transit vehicle suspension in this work is fully characterized with a vector containing a total number of 31 dof. The variable in vectorized form is indicated with ${\mathbf {q}}$ as shown in Appendix.

Results

In this work, suspension parameters are characterized by using full 3D multi-body dynamic model with 31 dof of rail vehicle. Initial findings of this study using different models with various dof were published in reference [19]. The main difference in this work is that the best suspension properties are searched with the use of design of experiment method in conjunction with the full degrees of the freedom of the rail vehicle. The use of different models does not yield comparable results with each other. Therefore, the best suspension properties can only be determined with a model which takes into account the full dof of a rail vehicle since the motion of wheel-sets, bogies, and car body is kinematically coupled to each other.

The primary suspension damping of a rapid transit vehicle has viscous dampers along vertical direction only. The lateral damping of primary suspension has little or no effect on the tangent track response of car body lateral acceleration. This is tested by adding a lateral viscous damper to the primary suspension and comparing the simulation results with zero damping coefficient for the same suspension element. The lateral damper at the primary suspension had no influence on the dynamic response of the vehicle at all speed levels 15, 50, and 90 km/hr, and hence it is neglected in the presented model.

Longitudinal suspension damping at secondary suspensions had a negligible effect on the tangent track response of the car body of a rapid transit vehicle. This suspension element is also neglected in the final model. Similarly, the effect of longitudinal suspension damping is tested by adding a viscous damper to the longitudinal secondary suspension and then by comparing simulation results for zero and non-zero damping values. The yaw motion between bogie and car body remains in a very small range of angular motion ($\approx 10^{-3} rad$), Fig. 7. The amplitudes of yaw motion are very small meaning that motion itself remains very small during tangent track analysis which leads to negligible effect of the longitudinal secondary suspension dampers on car body yaw motion.

The use of the aforementioned two suspension elements, lateral dampers at primary suspension and longitudinal suspension dampers at the secondary suspension (anti-yaw dampers), results in higher manufacturing and assembly costs of the rail vehicle in addition to the additional maintenance and operation costs. Therefore, the two viscous dampers, lateral suspension damper of the primary suspension and longitudinal anti-yaw dampers of secondary suspension, are not used in the suspension system of the rapid transit vehicle.

The important suspension elements that have essential influence on the passenger comfort and lateral stability are (i) secondary suspension damping along lateral direction, $C_{sy}$, secondary suspension stiffness along lateral direction of (ii) air springs, $K_{sy},$ and (iii) lateral stiffness of center pivot, $K_{cpy}$. These three main suspension elements define lateral stability of a rail vehicle during tangent track analysis. Therefore, the effect of only the three suspension parameters on the rail vehicle performance is investigated by design of experiment (doe) method [18]. Table 3 shows the values of suspension elements that are used in doe analysis for the three suspension elements.

Table 3 Test matrix that is used in the design of experiment analysis

The optimum suspension properties could also be calculated by a full optimization method. However, this requires a lot of computation times because of the nature of long random track input. That is the main reason of using doe method in this study. The division of time to very small increments by ode45 function causes long calculation times. Therefore, it was impossible to do all the calculations for all of the suspension combinations with the 31 dof model. For this reason, variation of only the three important suspension parameters is investigated in this work, while keeping the remaining other suspension parameters as constants. Accordingly, the optimization problem is simplified dramatically using doe method instead.

Figure 6 shows the relative effects of the suspension components on (i) passenger comfort which is indicated by the standard deviation of car body lateral acceleration, std($\ddot{y_c}$) and (ii) vehicle stability which is indicated by the standard deviation of car body lateral stroke that is indicated with std($y_c$). In the current analysis, the standard deviation is used as an indicator since the inputs are random in nature.

Fig. 6

Results of the design of experiments analysis: a standard deviation of car body lateral acceleration, b standard deviation of lateral car body stroke per suspension properties of $C_{sy}$, $K_{sy},$ and $K_{cpy}$

The suspension elements are directly proportional with the standard deviation of car body lateral acceleration and inversely proportional with the standard deviation of the car body lateral stroke. Lateral suspension stiffness elements of secondary air suspensions, $K_{sy},$ and secondary center pivot suspension, $K_{cpy}$, have both significant impact on the lateral response of the rail vehicle in comparison to the effect of the viscous lateral damper, $C_{sy}$. Secondary air suspension stiffness along lateral direction, $K_{sy}$, has the most significant effect on the passenger comfort, since its effect is doubled by the existence of two number of secondary air suspensions in comparison to single-center pivot suspension. The selection of softer lateral suspension stiffness provides better ride quality resulting in lower lateral car body accelerations but greater lateral car body displacements.

The lateral suspension stiffness of the secondary air suspensions, $K_{sy}$, is found to be relatively higher than the practical limits of an air suspension. However, the center pivot¹ lateral suspension stiffness, $K_{cpy}$, provides the required lateral stiffness and it is used to support the weak lateral stiffness of secondary air suspensions. Therefore, the lateral stiffness of center pivot provides the necessary additional stiffness to the secondary air suspensions.

The use of bi-level doe analysis allows relative comparison of outputs in a reliable way. This tool was very helpful to see how much effect of a change in a suspension parameter influences lateral car body acceleration and lateral car body displacement (outputs). Besides, doe method allows observation of relative effects of different parameters on the outputs. In this study, the doe design variables are limited to secondary lateral damping and stiffness only. For example, in this analysis mass and inertia properties of the vehicle as well as the other remaining suspension properties are assumed to be constant. However, in a general doe analysis these constants can be assumed as variables to be included to the parameter study. Therefore, doe method allows us to perform parameter studies that could be consisting of multiple variables. For the reasons above, the doe method is extended to be used at rail vehicle suspension design in this work.

Table 4 shows the complete set of model constants used in the dynamic models. All of the suspension properties are selected to be in agreement with the manufacturer catalog values based on the axle load. Therefore, practical physical values are used for the suspension stiffness and damping values.

Table 4 Values of dynamic model constants used in the simulations

The complete 3D response of a rapid transit rail vehicle is obtained with the use of a full 3D dynamic model after the application of doe method. Figure 7 shows the results of lateral displacement (y), vertical displacement (z), and yaw angle ($\psi$) of wheel-set, bogie, and car body of 31 dof dynamic model for the given random lateral and vertical track inputs.

Fig. 7

Results of 31 dof dynamic model: a lateral displacement (y) at 15 km/h speed, b lateral displacement (y) at 50 km/h, c lateral displacement (y) at 90 km/h speed, d yaw angle ($\psi$) at 15 km/h speed, e yaw angle ($\psi$) at 50 km/h speed and f yaw angle ($\psi$) at 90 km/h speed, g vertical displacement (z) at 15 km/h speed, h vertical displacement (z) at 50 km/h, i vertical displacement (z) at 90 km/h speed of wheel-sets, bogies, and car body

The displacement responses, Fig. 7, are less than the input displacements, Fig. 3, which indicates a properly damped system. Random vertical and lateral track input displacements with the worst possible track grade (grade 6 in Table 1) are used as the track inputs, Fig. 2. The standard deviation of lateral acceleration and the standard deviation of stoke of the car body have maximum values of 0.5366 m/s$^2$ and 0.0061 m, respectively, for the selected suspension properties at 90 km/hr traveling speed. The suspension properties are selected such that all real parts of the eigenvalues of ${\mathbf {A}}$ are negative, and hence, the selected suspension properties reveal an overall stable response, Fig. 7.

The results of the analysis reveal relatively smooth car body displacements when compared to track input displacements. Figure 7 can be used to give insights about the transmission of track vibrations to the car body. The car body displacements relative to the track inputs indicate effective absorption of shocks and vibrations that stem from the rail irregularities by the designed damping and stiffness elements. Therefore, the selected suspension coefficients provide decent passenger ride comfort with significantly reduced amplitude of vibrations of car body. The rail irregularities range in between ±15 mm (Fig. 3), which can be considered to be very high for rapid transit tracks. However, the tangent track response of the car body is within much lower and reasonable limits even though the worst track case is used, Fig 7.

The sensitivities of doe analysis show that an increase in the stiffness or damping has a direct effect on car body acceleration, while it has an opposite/inverse effect on car body displacement. This is an expected result for any dynamic system: as stiffness and/or damping increase, the corresponding forces and hence accelerations also increase. In the standard specification, limits for car body acceleration can be found (UIC 513, UIC 518, BS EN 12299, and ISO 2631). However, car body displacement is a function of characteristic features of the rail vehicle such as suspension properties, masses, and inertia. Therefore, the standard specifications do not really define the limits for displacements. For this reason, the suspension designer shall check and determine the bounds for displacements of rail vehicle components by considering real constraints on displacements.

Conclusions

A multi-body suspension model is designed specially for a rapid transit vehicle in order to determine the stiffness and damping properties of all of the suspension elements. The important conclusions are as follows:

• The proposed dynamic model for rapid transit vehicles does not contain all of the generic suspension elements of a rail vehicle such as lateral suspension dampers at the primary suspensions and longitudinal suspension dampers at the secondary suspensions.

• Tangent track response of the rapid transit vehicle is simulated for a randomly generated lateral and vertical track input of grade 6. This provides simulation of as close as possible to real situation for the worst possible track grades.

• Design of experiments (doe) method is used to find secondary suspension lateral stiffness and damping properties by examining standard deviations of lateral acceleration and lateral stroke of car body responses. The doe method allows selection of the best values for the three secondary suspension elements within reasonable computation times.

• A stable and reasonable time response for a rapid transit rail vehicle is obtained and the suspension properties are determined.

• The existing standard specifications (UIC 513, UIC 518, BS EN 12299, and ISO 2631) define limits for car body accelerations for passenger comfort. However, the limits for displacements of rail vehicle components shall be checked and determined by the designer according to practical constraints.

The dynamic model could be improved by having more physical representations of suspension elements: non-linearity that is associated with the air suspension characteristics, stop dampers on bogie along lateral direction, non-linear force-displacement behavior of conical primary suspensions, effect of leveling valves on secondary air suspension stiffness, etc. The same model and methodology could also be easily extended to investigate the curving performance of rail vehicles.

Appendix

The dynamic variables in vectorized form are given below:

$$\begin{aligned} {\mathbf {q}} =\left\{ { \begin{array}{c} y_{w1} \\ z_{w1}\\ \varphi _{w1}\\ \psi _{w1}\\ y_{w2} \\ z_{w2}\\ \varphi _{w2}\\ \psi _{w2}\\ y_{w3} \\ z_{w3}\\ \varphi _{w3}\\ \psi _{w3}\\ y_{w4} \\ z_{w4}\\ \varphi _{w4}\\ \psi _{w4}\\ y_{b1} \\ z_{b1}\\ \varphi _{b1}\\ \theta _{b1}\\ \psi _{b1}\\ y_{b2} \\ z_{b2}\\ \varphi _{b2}\\ \theta _{b2}\\ \psi _{b2}\\ y_{c} \\ z_{c}\\ \varphi _{c}\\ \theta _{c}\\ \psi _{c} \end{array}} \right\} \end{aligned}.$$

The mass matrix, ${\mathbf {M}}$, of 3D model with 31 dof is given below. Please note that the same ordering as of variable vector, ${\mathbf {q}},$ is used.

$$\begin{aligned} {\mathbf {M}}\,=\left[ { \begin{array}{ccccccccccccccccccccccccccccccc} m_w &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} m_w &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} I_{wx} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} I_{wz} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} m_w &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} m_w &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} I_{wx} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} I_{wz} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} m_w &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} m_w &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} I_{wx} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} I_{wz} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} m_w &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} m_w &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} I_{wx} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} I_{wz} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} m_b &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} m_b &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} I_{bx} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} I_{by} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} I_{bz} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} m_b &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} m_b &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} I_{bx} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} I_{by} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} I_{bz} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} m_c &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} m_c &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} I_{cx} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} I_{cy} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} I_{cz} \\ \end{array} }\right] \end{aligned}.$$

The stiffness matrix, ${\mathbf {K}}$, of the 3d model with 31 dof:

$$\begin{aligned}{}[{\mathbf {K}}]\,=\left[ { \begin{array}{ccccccccccccccccccccccccccccccc} -4 K_{py}-2 K_{ry} &{} 0 &{} -\left(\dfrac{m_c}{4}+\dfrac{m_b}{2}+m_w\right)g &{} 2 f_{11} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} -4 K_{pz}-2 K_{rz} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \dfrac{2\,f_{12}\,\lambda ^2}{r_0} &{} 0 &{} -4 K_{pz} d_p^2 \,+\,\dfrac{2\,f_{12}\,a\,\lambda }{r_0} \,+\, a\,\lambda \,\left(\dfrac{m_c}{4}+\dfrac{m_b}{2}+m_w\right)\,g &{} \left[2\,f_{11}\,(r_0\,+\,a\,\lambda )\,+\,\dfrac{2\,f_{22}\,\lambda ^2}{r_0}\right] &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ -\dfrac{2\,f_{33}\,a\,\lambda }{r_0} &{} 0 &{} 0 &{} -2 f_{12} \,-\, 4 K_{px} d_p^2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} -4 K_{py}-2 K_{ry} &{} 0 &{} -\Big(\dfrac{m_c}{4}+\dfrac{m_b}{2}+m_w\Big)g &{} 2f_{11} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -4 K_{pz}-2 K_{rz} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \dfrac{2\,f_{12}\,\lambda ^2}{r_0} &{} 0 &{} -4 K_{pz} d_p^2 \,+\,\dfrac{2\,f_{12}\,a\,\lambda }{r_0} \,+\, a\,\lambda \,\Big(\dfrac{m_c}{4}+\dfrac{m_b}{2}+m_w\Big)\,g &{} \Big[2\,f_{11}\,(r_0\,+\,a\,\lambda )\,+\,\dfrac{2\,f_{22}\,\lambda ^2}{r_0}\Big] &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} -\dfrac{2\,f_{33}\,a\,\lambda }{r_0} &{} 0 &{} 0 &{} -2 f_{12} \,-\, 4 K_{px} d_p^2 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -4 K_{py}-2 K_{ry} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \dfrac{2\,f_{12}\,\lambda ^2}{r_0} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -\dfrac{2\,f_{33}\,a\,\lambda }{r_0} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 4 K_{py}&{} 0 &{} 0 &{} 0 &{} 4 K_{py} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 4 K_{pz} &{} 0 &{} 0 &{} 0 &{} 4 K_{pz} &{} 0 &{} 0 &{} 0 \\ 4 h_{bp} K_{py} &{} 0 &{} 4 d_{p}^2 K_{pz} &{} 0 &{} 4 h_{bp} K_{py} &{} 0 &{} 4 d_{p}^2 K_{pz} &{} 0 &{} 0 \\ 0 &{} -4 l_p K_{pz} &{} 0 &{} 0 &{} 0 &{} 4 l_p K_{pz} &{} 0 &{} 0 &{} 0 \\ 4 l_{p} K_{py} &{} 0 &{} 0 &{} 4 d_p^2 K_{px} &{} -4 l_p K_{py} &{} 0 &{} 0 &{} 4 d_p^2 K_{px} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 4 K_{py}\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 4 h_{bp} K_{py} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 4 l_{p} K_{py} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \end{array} }\right. \end{aligned}.$$

The stiffness matrix, ${\mathbf {K}}$, cont’d:

$$\begin{aligned} \left. { \begin{array}{ccccccccccccccccccccccccccccccc} -4 K_{py}-2 K_{ry} &{} 0 &{} -\left(\dfrac{m_c}{4}+\dfrac{m_b}{2}+m_w\right)g &{} 2 f_{11} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} -4 K_{pz}-2 K_{rz} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \dfrac{2\,f_{12}\,\lambda ^2}{r_0} &{} 0 &{} -4 K_{pz} d_p^2 \,+\,\dfrac{2\,f_{12}\,a\,\lambda }{r_0} \,+\, a\,\lambda \,\left(\dfrac{m_c}{4}+\dfrac{m_b}{2}+m_w\right)\,g &{} \left[2\,f_{11}\,(r_0\,+\,a\,\lambda )\,+\,\dfrac{2\,f_{22}\,\lambda ^2}{r_0}\right] &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ -\dfrac{2\,f_{33}\,a\,\lambda }{r_0} &{} 0 &{} 0 &{} -2 f_{12} \,-\, 4 K_{px} d_p^2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} -4 K_{py}-2 K_{ry} &{} 0 &{} -\Big(\dfrac{m_c}{4}+\dfrac{m_b}{2}+m_w\Big)g &{} 2f_{11} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -4 K_{pz}-2 K_{rz} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \dfrac{2\,f_{12}\,\lambda ^2}{r_0} &{} 0 &{} -4 K_{pz} d_p^2 \,+\,\dfrac{2\,f_{12}\,a\,\lambda }{r_0} \,+\, a\,\lambda \,\Big(\dfrac{m_c}{4}+\dfrac{m_b}{2}+m_w\Big)\,g &{} \Big[2\,f_{11}\,(r_0\,+\,a\,\lambda )\,+\,\dfrac{2\,f_{22}\,\lambda ^2}{r_0}\Big] &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} -\dfrac{2\,f_{33}\,a\,\lambda }{r_0} &{} 0 &{} 0 &{} -2 f_{12} \,-\, 4 K_{px} d_p^2 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -4 K_{py}-2 K_{ry} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \dfrac{2\,f_{12}\,\lambda ^2}{r_0} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -\dfrac{2\,f_{33}\,a\,\lambda }{r_0} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 4 K_{py}&{} 0 &{} 0 &{} 0 &{} 4 K_{py} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 4 K_{pz} &{} 0 &{} 0 &{} 0 &{} 4 K_{pz} &{} 0 &{} 0 &{} 0 \\ 4 h_{bp} K_{py} &{} 0 &{} 4 d_{p}^2 K_{pz} &{} 0 &{} 4 h_{bp} K_{py} &{} 0 &{} 4 d_{p}^2 K_{pz} &{} 0 &{} 0 \\ 0 &{} -4 l_p K_{pz} &{} 0 &{} 0 &{} 0 &{} 4 l_p K_{pz} &{} 0 &{} 0 &{} 0 \\ 4 l_{p} K_{py} &{} 0 &{} 0 &{} 4 d_p^2 K_{px} &{} -4 l_p K_{py} &{} 0 &{} 0 &{} 4 d_p^2 K_{px} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 4 K_{py}\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 4 h_{bp} K_{py} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 4 l_{p} K_{py} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \end{array} }\right] \end{aligned}.$$

The damping matrix, ${\mathbf {C}}$, of the 3d model with 31 dof:

$$\begin{aligned}{}[{\mathbf {C}}]\,=\left[ { \begin{array}{ccccccccccccccccccccccccccccccc} -2 C_{py}\,-\,\dfrac{2 f_{11}}{V}\,-\,2 C_{ry} &{} 0 &{} -\dfrac{2 f_{11} r_0}{V} &{} -\dfrac{2 f_{12}}{V} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} -2 C_{pz}\,-\,2 C_{rz} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ -\dfrac{2\,f_{11}\,(r_0\,+\,a \lambda )}{V} &{} 0 &{} -2 C_{pz} d_p^2 \,-\,\dfrac{2\,f_{11}\,r_0}{V}(r_0\,+\,a \lambda ) &{} -\dfrac{2\,f_{12}\,(r_0\,+\,a\,\lambda )}{V},+\,\dfrac{I_{wy}\,V}{r_0} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ -\dfrac{2\,f_{12}}{V} &{} 0 &{} 0 &{} -2 \dfrac{f_{22}\,+\,a^2 f_{33}}{V} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} -2 C_{py}\,-\,\dfrac{2 f_{11}}{V}\,-\,2 C_{ry} &{} 0 &{} -\dfrac{2 f_{11} r_0}{V} &{} -\dfrac{2 f_{12}}{V} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -2 C_{pz}\,-\,2 C_{rz} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} -\dfrac{2\,f_{11}\,(r_0\,+\,a \lambda )}{V} &{} 0 &{} -2 C_{pz} d_p^2 \,-\,\dfrac{2\,f_{11}\,r_0}{V}(r_0\,+\,a \lambda ) &{} -\dfrac{2\,f_{12}\,(r_0\,+\,a\,\lambda )}{V},+\,\dfrac{I_{wy}\,V}{r_0} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} -\dfrac{2\,f_{12}}{V} &{} 0 &{} 0 &{} -2 \dfrac{f_{22}\,+\,a^2 f_{33}}{V} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -2 C_{py}\,-\,\dfrac{2 f_{11}}{V}\,-\,2 C_{ry} &{} 0 &{} -\dfrac{2 f_{11} r_0}{V} &{} -\dfrac{2 f_{12}}{V} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -2 C_{pz}\,-\,2 C_{rz} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -\dfrac{2\,f_{11}\,(r_0\,+\,a \lambda )}{V} &{} 0 &{} -2 C_{pz} d_p^2 \,-\,\dfrac{2\,f_{11}\,r_0}{V}(r_0\,+\,a \lambda ) &{} -\dfrac{2\,f_{12}\,(r_0\,+\,a\,\lambda )}{V},+\,\dfrac{I_{wy}\,V}{r_0} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -\dfrac{2\,f_{12}}{V} &{} 0 &{} 0 &{} -2 \dfrac{f_{22}\,+\,a^2 f_{33}}{V} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 2 C_{py} &{} 0 &{} 0 &{} 0 &{} 2 C_{py} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 2 C_{pz} &{} 0 &{} 0 &{} 0 &{} 2 C_{pz} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} -2 l_p C_{pz} &{} 0 &{} 0 &{} 0 &{} 2 l_p C_{pz} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 2 h_{bp} C_{py} &{} 0 &{} 2 d_{p}^2 C_{pz} &{} 0 &{} 2 h_{bp} C_{py} &{} 0 &{} 2 d_{p}^2 C_{pz} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 2 l_{p} C_{py} &{} 0 &{} 0 &{} 0 &{} -2 l_p C_{py} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 C_{py}&{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 C_{pz} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -2 l_p C_{pz} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 h_{bp} C_{py} &{} 0 &{} 2 d_{p}^2 C_{pz} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 l_{p} C_{py} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} }\right. \end{aligned}.$$

The damping matrix, ${\mathbf {C}}$, cont’d:

$$\begin{aligned} \left. { \begin{array}{ccccccccccccccccccccccccccccccc} 0 &{} 0 &{} 0 &{} 0 &{} 2 C_{py} &{} 0 &{} 2 C_{py} h_{bp} &{} 0 &{} 2 C_{py} l_p &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 C_{pz} &{} 0 &{} -2 C_{pz} l_p &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 C_{pz} d_p^2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 2 C_{py} &{} 0 &{} 2 C_{py} h_{bp} &{} 0 &{} -2 C_{py} l_p &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 C_{pz} &{} 0 &{} 2 C_{pz} l_p &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 C_{pz} d_p^2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 C_{py} &{} 0 &{} 2 C_{py} h_{bp} &{} 0 &{} 2 C_{py} l_p &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 C_{pz} &{} 0 &{} -2 C_{pz} l_p &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 C_{pz} d_p^2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ -2 C_{py}\,-\,\dfrac{2 f_{11}}{V}\,-\,2 C_{ry} &{} 0 &{} -\dfrac{2 f_{11} r_0}{V} &{} -\dfrac{2 f_{12}}{V} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 C_{py} &{} 0 &{} 2 C_{py} h_{bp} &{} 0 &{} -2 C_{py} l_p &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} -2 C_{pz}\,-\,2 C_{rz} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 C_{pz} &{} 0 &{} 2 C_{pz} l_p &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ -\dfrac{2\,f_{11}\,(r_0\,+\,a \lambda )}{V} &{} 0 &{} -2 C_{pz} d_p^2 \,-\,\dfrac{2\,f_{11}\,r_0}{V}(r_0\,+\,a \lambda ) &{} -\dfrac{2\,f_{12}\,(r_0\,+\,a\,\lambda )}{V},+\,\dfrac{I_{wy}\,V}{r_0}&{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 C_{pz} d_p^2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ -\dfrac{2\,f_{12}}{V} &{} 0 &{} 0 &{} -2 \dfrac{f_{22}\,+\,a^2 f_{33}}{V} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} -4 C_{py}\,-\,2 C_{sy} &{} 0 &{} -4 C_{py} h_{bp}\,+\,2 C_{sy} h_{bs} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 C_{sy} &{} 0 &{} 2 C_{sy} h_{cs} &{} 0 &{} 2 l_s C_{sy} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -4 C_{pz}\,-\, 2 C_{sz} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 C_{sz} &{} 0 &{} -2 C_{sz} l_{s} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -4 l_p^2 C_{pz} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 2 h_{bp} C_{py} &{} 0 &{} 2 d_{p}^2 C_{pz} &{} 0 &{} 2 h_{bp} C_{py} &{} 0 &{} 2 d_{p}^2 C_{pz} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -4 l_p d_p C_{py} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 2 C_{py} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -4 C_{py}\,-\,2 C_{sy} &{} 0 &{} -4 C_{py} h_{bp}\,+\,2 C_{sy} h_{bs} &{} 0 &{} 0 &{} 2 C_{sy} &{} 0 &{} 2 C_{sy} h_{cs} &{} 0 &{} -2 l_s C_{sy} \\ 0 &{} 2 C_{pz} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -4 C_{pz}\,-\, 2 C_{sz} &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 C_{sz} &{} 0 &{} 2 C_{sz} l_{s} &{} 0 \\ 0 &{} 2 l_p C_{pz} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -4 l_p^2 C_{pz} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 2 h_{bp} C_{py} &{} 0 &{} 2 d_{p}^2 C_{pz} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 h_{bs} C_{sy} \,-\,2 h_{bp} C_{py} &{} 0 &{} -4 d_p^2 C_{pz}\,-\,2 d_s^2 C_{sz} &{} 0 &{} 0 &{} -2 h_{bs} C_{sy} &{} 0 &{} 2 d_s^2 C_{sz} \,-\, 2 h_{bs} h_{cs} C_{sy} &{} 0 &{} 2 l_s h_{bs} C_{sy} \\ -2 l_p C_{py} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -4 l_p d_p C_{py} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 2 C_{sy} &{} 0 &{} 2 h_{bs} C_{sy} &{} 0 &{} 0 &{} 2 C_{sy} &{} 0 &{} 2 h_{bs} C_{sy} &{} 0 &{} 0 &{} -4 C_{sy} &{} 0 &{} -4 h_{cs} C_{sy} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 C_{sz} &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 C_{sz} &{} 0 &{} 0 &{} 0 &{} 0 &{} -4 C_{sz} &{} 0 &{} -4 l_s C_{sz} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 l_s C_{sz} &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 l_s C_{sz} &{} 0 &{} 0 &{} 0 &{} 0 &{} -4 l_s C_{sz} &{} 0 &{} -4 l_s^2 C_{sz} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 2 h_{cs} C_{sy} &{} 0 &{} 2 d_s^2 C_{sz}\,-\,2 h_{cs} C_{sy} h_{bs} &{} 0 &{} 0 &{} 2 h_{cs} C_{sy} &{} 0 &{} 2 d_s^2 C_{sz}\,-\,2 h_{cs} C_{sy} h_{bs} &{} 0 &{} 0 &{} -4 h_{cs} C_{sy} &{} 0 &{} -4 d_s^2 C_{sz}\,-\,4 h_{cs}^2 C_{sy} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 2 C_{sy} l_s &{} 0 &{} 2 l_s h_{bs} C_{sy} &{} 0 &{} 0 &{} -2 C_{sy} l_s &{} 0 &{} 2 l_s h_{bs} C_{sy} &{} 0 &{} 0 &{} 0 &{} 0 &{} -4 l_s C_{sy} h_{cs} &{} 0 &{} -4 l_s^2 C_{sy} \\ \end{array} }\right] \end{aligned}.$$