1 Introduction

The defense against global warming necessitates an energy efficient and pollution-free transport system in modern era. There is no doubt that MAGLEV transportation system, to a great extent will help to lessen the ill effect of global warming as no fuel is burnt in the operation of such type of transport. In general, magnetic levitation (MAGLEV) refers to any transportation system in which vehicles are suspended, guided and propelled by non-contact electromagnetic forces in lieu of conventional engines. The expense of guideway construction alone involves about 60 % ~ 70 % of the total cost in the entire venture of the system which makes it important to study the vibration of the guideway and make it optimized from the perspective of vibration [1]. To control the guideway response and to achieve satisfactory ride comfort, it is important to understand the interaction between the vehicle–guideway system.

The guideway is a slender structure having a very large span compared to its cross-sectional dimensions. As such, it resists the moving force primarily due to bending. The model of guideway has been treated as simply supported Euler–Bernoulli beam by several authors as found in the articles published by Cai et al. [2], Ren et al. [3], Wang et al. [4], Zhao and Zhai [5] and Zheng et al. [6]. Teng et al. [7] investigated the response of two-span continuous guideway for high-speed magnetic levitation system using moving distributed load without considering the effect of MAGLEV suspension systems.

In comparison to high-speed train, MAGLEV trains are more compatible with the environment. They occupy less space and consume less energy. Different authors have used different vehicle models to study guideway–vehicle interaction. A single moving load or a series of moving loads representing a high-speed train was used by Yang et al. [8] and Savin [9] to identify the condition of resonance in the bridges. Two degrees-of-freedom car model with primary and secondary suspension system have been adopted by Cai et al. [10] and Cai and Chen [11] to study only vertical motion of the vehicle. They commented that this type of vehicle model is appropriate when vertical acceleration of car body is <0.05 g (g is the acceleration due to gravity) and unsprung mass inertia force is low compared to vehicle weight. Five degrees-of-freedom (DOF) vehicle models considering angular rotation of the car body have been considered to conduct parametric study on the dynamics of urban transit MAGLEV vehicle on flexible guideway [12]. The wavelength of track irregularities has great influence on vehicle vibration specially at higher speed. Due to oscillation of vehicle, the guideway is subject to dynamic load composed of different frequencies. Dai [13], Shi et al. [14], Zhao et al. [15]. and Zeng et al. [16] modelled guideway surface irregularity as the realization of random process represented by a power spectral density function (PSD). The PSD function for subway line in Beijing has been found by Lu et al. [17], where they pointed out that it would be useful to detect track problem in order to improve safety of urban rail transit system.

In a high-speed transport system, ride quality is of great concern and thus there is a need for optimized vehicle–guideway system design. The ride quality of a vehicle is generally indicated by the magnitude of car-body acceleration. The root mean square of car-body acceleration is taken into consideration to define the objective function for optimization scheme to improve the ride quality. The optimization of suspension system has been studied using genetic algorithm by Baumal et al. [18] and Shirahatti et al. [19] where they found improvement of ride quality after using optimized value of suspension parameters in simulation studies.

Simplified analytical/numerical models that require less effort of computation but yield engineering solutions are still in demand in urban rail transit system. Although various studies on MAGLEV-guideway behaviour have been reported in literatures based on various theoretical methods, the solution in a block diagram environment has not been attempted for increased ride quality by optimization of the suspension parameters. Moreover, most of the earlier in this field considered single-span guideway. However, for practical reason double-span/multi-span continuous guideways are also adopted.

It may be worth mentioned that simulation- and model-based approach is now a part and parcel of the design of transportation infrastructures. Due to availability of updated version of MATLAB software, block diagram approach in SIMULINK can be easily adopted in design practice. ‘SIMULINK’-a block diagram-based approach that provides a graphical editor, customizable block libraries and solvers has been used in modelling and simulating MAGLEV vehicle–guideway system with an aim to find out optimized suspension parameters. The present study is a vivid example that how a complicated system can be modelled and simulated considering unfavourable conditions of guideway in a block diagram environment using widely used MATLAB SIMULINK tool box in a systematic manner. The present study will help the analyst to adopt an integrated approach consisting of modelling guideway–vehicle-coupled system, solution for dynamic response and optimization of suspension parameters to achieve satisfactory performance of the system. The parametric studies have been conducted to examine the effect of vehicle speed and guideway irregularity on the response of the system. Dynamic amplification factor for the deflection in single- and two-span guideway has been compared with that found in existing design standard. Suspension parameters have been optimized to examine the improvement of ride comfort and guideway deflection.

2 The Vehicle–Guideway System

2.1 The Guideway Model

The guideway is modelled as a double-span continuous beam rather than as plates since span-to-width ratio is generally large [20]. The beam is simply supported at both the ends and continuous over intermediate support (Fig. 1). The transverse displacement of the guideway at any point along its length is denoted by y(x,t) where x is the distance measured from a reference station and t is time instant. The cross section and material properties are uniform along the length. It is assumed that beam is initially at rest.

Fig. 1
figure 1

A two-span guideway beam

Full size image

The differential equation of motion for the transverse displacement of the beam [20] is given by

$$ {\text{EI}}\frac{{\partial^{4} y(x,t)}}{{\partial x^{4} }} + c\frac{\partial y(x,t)}{\partial t} + m\frac{{\partial^{2} y(x,t)}}{{\partial t^{2} }} = F(x,t) $$
(1)

where EI is the flexural rigidity, c is damping and m is the mass per unit length of the guideway. F(x,t) is the term representing electromagnetic force on the guideway which varies with time and space due to movement of the vehicle. The spatial coordinate x can be related to time coordinate via the vehicle forward speed, which is assumed constant in the present study as

$$ x = Vt $$
(2)

where V is the vehicle speed and t is the time.

Using modal superposition technique [21] the displacement of the beam is expressed as

$$ y(x,t) = \sum\limits_{k = 1}^{\infty } {\phi_{k} } (x)q_{k} (t) $$
(3)

where ϕ k (x) denotes the mode shape function of the beam, q k (t) the generalized coordinate corresponding to the kth mode.

The mode shape function of double-span continuous beam can be divided into two categories: odd modes which are anti-symmetric and even modes which are symmetric [1].

For k = 1, 3, 5… and x ∈ [0, 2L], the mode shape function is expressed as

$$ \phi_{k} (x) = \sin (\lambda_{k} x) $$
(4)

For k = 2, 4, 6…, and for x ∈ [0, L], the mode shape function will be

$$ \phi_{k} (x) = \frac{{\sin (\lambda_{k} x)}}{{\sin (\lambda_{k} x)}} - \frac{{\sinh (\lambda_{k} x)}}{{\sinh (\lambda_{k} x)}} ; $$
(5)

whereas for x ∈ [L, 2L], the mode shape function can be written as

$$ \phi_{k} (x) = \cos \{ \lambda_{k} (x - L)\} - \cosh \{ \lambda_{k} (x - L)\} - \cot (\lambda_{k} L)[\sin \{ \lambda_{k} (x - L)\} - \sinh \{ \lambda_{k} (x - L)\} ] $$
(6)

in which,

$$ \begin{array}{*{20}c} {\lambda_{k} = \left( {\frac{k + 1}{2L}} \right)\pi ;} & \forall k = 1,3,5, \ldots \\ {\lambda_{k} = \left( {\frac{2k + 1}{4L}} \right)\pi } & {\forall k = 2,4,6, \ldots } \\ \end{array} $$
(7)

The natural frequency of the kth mode of guideway can be expressed as [21]

$$ \omega_{k} = \lambda_{k}^{2} \sqrt {\frac{\text{EI}}{m}}. $$
(8)

The final expression for the governing dynamic equation in the generalized modal coordinate after application of beam orthogonality function [21] can be written as

$$ \frac{{d^{2} q_{k} (t)}}{{dt^{2} }} + 2\xi_{k} \omega_{k} \frac{{dq_{k} (t)}}{dt} + \omega_{k}^{2} q_{k} (t) = Q_{k} (t) $$
(9)

where ξ k is the modal damping ratio, Q k (t) is the generalized interaction force between vehicle and the guideway in kth mode which is given by

$$ Q_{k} (t) = \frac{1}{{M_{k} }}\int\limits_{0}^{2L} {F(x,t)} \varphi_{k} (x)dx. $$
(10)

In Eq. (10), M k is the generalized mass in the kth mode of the double-span beam which is given as

$$ M_{k} = \int\limits_{0}^{2L} m \varphi_{k}^{2} (x)dx. $$
(11)

The Guideway surface irregularity is approximated as a stationary random process in the spatial domain, which has been modelled as the response of a first-order linear ODE filter to a stationary white excitation [13]. This is given by

$$ \frac{1}{{r_{f} }}\frac{dh(x)}{dx} + h(x) = W(x) $$
(12)

where h(x) is the guideway surface irregularity in spatial domain; r f is a parameter that depends on the type of surface and has dimension rad/m in spatial domain; W(x) is a Gaussian white noise with zero mean and specific strength. The guideway surface irregularity can be defined by a power spectral density (PSD) function as [11, 22]

$$ S(\varOmega ) = A/\varOmega^{w} $$
(13)

where S(Ω) is the PSD of the guideway surface in m3/rad; A is the roughness amplitude (in m); Ω is the roughness wave number and has unit in rad/m. This is equal to 2π/λ where λ is the wavelength of irregularity, w is the waviness or the roughness exponent assumed to be 1.5 for shorter wavelength (up to 5 m). For longer wave length (up to 100 m), w is taken as 2.5, whereas for medium-to-long wavelengths the exponent w = 2 [11].

2.2 The Vehicle Model

In the present study, a single-car MAGLEV vehicle model has been adopted in two-dimensional analysis. For this kind of vehicle model, each car has rigid body vertical translation and pitch rotation. Moreover, there are four levitation frames each of which has vertical translation only. Thus each car body has six degrees of freedom which is commonly adopted by the researchers [23]. If more car bodies are connected, the number of degrees of freedom will be multiple of six, in which case, the present procedure will have to be repeated for required number of times.

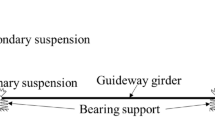
Figure 2 shows the six-DOF vehicle model. The coupling effect of vehicle–guideway is taken into account. The primary suspension couples the levitation frame with the guideway by an interacting force to be determined from the relative displacement and velocity between the levitation frame and guideway. The secondary suspension connects levitation frame with car body, thereby transferring the force to the car body depending on the relative displacement and velocity between the levitation frame and car body.

Fig. 2
figure 2

Vehicle model and its components

Full size image

Let the vertical displacements of each of the levitation frames be z f,1, z f,2, z f,3 and z f,4. The carriage body has two DOF, viz. the vertical displacement z v and pitching θ v. The equations of motion of each sub-system can be obtained using Newton’s law of motion. Let m v and m f be the car body and levitation frame masses, respectively. The electromagnetic force is linearized and is characterized by magnetic stiffness k p and magnetic damping c p which form the primary suspension system. The secondary suspension is characterized by spring stiffness k s and damping c s. The small clearance between guideway surface and supporting magnet in levitated vehicle is termed as ‘air gap’ and is denoted by s 1, s 2, s 3 and s 4 at the location of corresponding levitation frame. Zhao and Zhai [5] have opined that air gap has to be taken into consideration for determining the electromagnetic force on the guideway. In order to prevent physical contact in levitated vehicle, a nominal air gap 8–10 mm is recommended for the electromagnetic suspension [24].

The equations of motion of the first, second, third and fourth levitation frame for vertical bounce can be written as

$$ m_{\text{f}} \ddot{z}_{{{\text{f}},1}} + c_{\text{p}} \{ \dot{z}_{{{\text{f}},1}} - \dot{y}(x_{1} ,t) - \dot{s}_{1} \} + k_{\text{p}} \{ z_{{{\text{f}},1}} - y(x_{1} ,t) - s_{1} \} - c_{\text{s}} \left\{ \dot{z}_{\text{v}} + \frac{3}{8}L_{\text{v}} \dot{\theta }{\text{v}} - \dot{z}_{{{\text{f}},1}} \right\} - k_{\text{s}} \left\{ z_{\text{v}} + \frac{3}{8}L_{\text{v}} \theta_{\text{v}} - z_{{{\text{f}},1}} \right\} = 0 $$
(14)
$$ m_{\text{f}} \ddot{z}_{{{\text{f}},2}} + c_{\text{p}} \{ \dot{z}_{{{\text{f}},2}} - \dot{y}(x_{2} ,t) - \dot{s}_{2} \} + k_{\text{p}} \{ z_{{{\text{f}},2}} - y(x_{2} ,t) - s_{2} \} - c_{s} \left\{ \dot{z}{\text{v}} + \frac{1}{8}L_{\text{v}} \dot{\theta }_{\text{v}} - \dot{z}_{{{\text{f}},2}} \right\} - k_{\text{s}} \left\{ z_{\text{v}} + \frac{1}{8}L_{\text{v}} \theta_{\text{v}} - z_{{{\text{f}},2}} \right\} = 0 $$
(15)
$$ m_{\text{f}} {\ddot{z}}_{{{\text{f}},3}} + c_{\text{p}} \{ \dot{z}_{{{\text{f}},3}} - \dot{y}(x_{3} ,t) - \dot{s}_{3} \} + k_{\text{p}} \{ z_{{{\text{f}},3}} - y(x_{3} ,t) - s_{3} \} - c_{s} \left\{ \dot{z}_{v} - \frac{1}{8}L_{\text{v}} \dot{\theta }_{\text{v}} - \dot{z}_{{{\text{f}},3}} \right\} - k_{\text{s}} \left\{ z_{\text{v}} - \frac{1}{8}L_{\text{v}} \theta_{\text{v}} - z_{{{\text{f}},3}} \right\} = 0 $$
(16)
$$ m_{\text{f}} \ddot{z}_{{{\text{f}},4}} + c_{\text{p}} \{ \dot{z}_{{{\text{f}},4}} - \dot{y}(x_{4} ,t) - \dot{s}_{4} \} + k_{\text{p}} \{ z_{{{\text{f}},4}} - y(x_{4} ,t) - s_{4} \} - c_{\text{s}} \left\{ \dot{z}_{\text{v}} - \frac{3}{8}L_{\text{v}} \dot{\theta }{\text{v}} - \dot{z}_{{{\text{f}},4}} \right\} - k_{\text{s}} \left\{ z_{\text{v}} - \frac{3}{8}L_{v} \theta_{v} - z_{{{\text{f}},4}} \right\} = 0. $$
(17)

The car-body equations of motion in bounce can be obtained as

$$ m_{\text{v}} \ddot{z}_{\text{v}} - c_{\text{s}} (\dot{z}_{{{\text{f}},1}} + \dot{z}_{{{\text{f}},2}} + \dot{z}_{{{\text{f}},3}} + \dot{z}_{{{\text{f}},4}} - 4\dot{z}_{\text{v}} ) - k_{\text{s}} (\dot{z}_{{{\text{f}},1}} + \dot{z}_{{{\text{f}},2}} + \dot{z}_{{{\text{f}},3}} + \dot{z}_{{{\text{f}},4}} - 4z{\text{v}}) = 0. $$
(18)

The pitching motion of the car body is given by

$$ I_{v} \ddot{\theta }_{v} + c_{\text{s}} \left( - \frac{3}{8}L_{v} \dot{z}_{{{\text{f}},1}} - \frac{1}{8}L_{\text{v}} \dot{z}_{{{\text{f}},2}} + \frac{1}{8}L_{\text{v}} \dot{z}_{{{\text{f}},3}} + \frac{3}{8}L_{\text{v}} \dot{z}_{{{\text{f}},4}} + \frac{5}{16}L^{2}_{\text{v}} \dot{\theta }_{\text{v}} \right) - k_{\text{s}} \left( - \frac{3}{8}L_{\text{v}} z_{{{\text{f}},1}} - \frac{1}{8}L_{\text{v}} z_{{{\text{f}},2}} + \frac{1}{8}L_{\text{v}} z_{{{\text{f}},3}} + \frac{3}{8}L_{\text{v}} z_{{{\text{f}},4}} + \frac{5}{16}L^{2}_{\text{v}} \theta_{\text{v}} \right) = 0. $$
(19)

The equations of motion of the levitation frames and the car body now can be written in matrix form as

$$ [M]\{ {\ddot{Y}}(t)\} + [G]\{ \dot{Y}(t)\} + [K]\{ Y(t)\} = \{ F(t)\} $$
(20)

in which [ M], [G] and [K] denote mass, damping and stiffness matrix of the coupled system. The displacement vector {Y} contains the heave and pitch of the car body, and the vertical displacements of each of the four levitation frames. This is given as

$$ \{ Y\} = \left[ {\begin{array}{*{20}c} {z_{{{\text{f}},1}} } & {z_{{{\text{f}},2}} } & {z_{{{\text{f}},3}} } & {z_{{{\text{f}},4}} } & {z_{\text{v}} } & {\theta_{\text{v}} } \\ \end{array} } \right]^{\text{T}}. $$
(21)

{F} is the force vector whose elements are the forces corresponding to each degrees of freedom. The system matrices of Eq. (20) are given in “Appendix”.

The State-space approach is used to model the vehicle system in MATLAB-SIMULINK. Hence, we write the two state-space equations as [21]

$$ \begin{aligned} \{ \dot{x}\} = [A]\{ x\} + [B]\{ u\} \hfill \\ \{ y\} = [C]\{ x\} + [D](u\} \hfill \\ \end{aligned} $$
(22)

where {x} denotes the state variables, {u} denotes the input variables and {y} denotes the output variables. The state vector is given by

$$ \{ x\} = [\begin{array}{*{20}c} {\{ Y\} } & {\{ \dot{Y}\} ]^{{}} } \\ \end{array}^{T}. $$
(23)

Now, the input vector is the Force vector {F}, i.e. {u} = {F}. The output vectors are the same as the state variables, i.e.{y} = {x}. The state-space matrices can be rearranged as

$$ \begin{aligned} [A] = \left[ {\begin{array}{*{20}c} {[0]} & {[I]} \\ { - [M]^{ - 1} [K]} & { - [M]^{ - 1} [G]} \\ \end{array} } \right]^{{}}_{{}} \hfill \\ \hfill \\ \end{aligned} $$
(24)
$$ [B] = \left[ {\begin{array}{*{20}c} {[0]} & {[M]^{ - 1} } \\ \end{array} } \right]^{\text{T}} $$
(25)
$$ [C] = \left[ {\begin{array}{*{20}c} {[I]} & {[0]} \\ {[0]} & {[I]} \\ \end{array} } \right] $$
(26)
$$ [D] = \left[ {\begin{array}{*{20}c} {\left[ 0 \right]} & {\left[ 0 \right]} \\ \end{array} } \right]^{\text{T}} $$
(27)

where [0] is the null matrix and [I] is the unit matrix. The guideway equation of motion (9) now can be expanded incorporating the term for the generalized force as

$$ \begin{array}{*{20}c} {\frac{{{\text{d}}^{2} q_{k} (t)}}{{{\text{d}}t^{2} }} + 2\xi_{k} \omega_{k} \frac{{{\text{d}}q_{k} (t)}}{{{\text{d}}t}} + \omega_{k}^{2} q_{k} (t) = \frac{1}{{M_{k} }}\sum\limits_{i = 1}^{4} {\left[ {(m_{v} + m_{\text{f}} )\frac{g}{4} + c_{\text{p}} \{ \dot{z}_{{{\text{f}},i}} - \dot{y}(x_{i} ,t) - \dot{s}_{i} \} \quad + k_{\text{p}} \{ z_{{{\text{f}},i}} - y(x_{i} ,t) - s_{i} \} } \right]} \varphi_{k} (x_{i} )} &\quad {\left( {k = 1, 2, \ldots n} \right)} \\ \end{array} $$
(28)

where n being the number of significant beam modes of vibration for the guideway, g is the acceleration due to gravity.

The position of the i th force is given by

$$ x_{i} = V\left[ {t - (i - 1)\frac{{L_{\text{v}} }}{4V}} \right] $$
(29)

where x i denotes location of the ith force. Finally, the displacement of the guideway at mid-span can be obtained from Eq. (3) using superimposition of beam modes. It may be mentioned that theoretically infinite number of modes exist, however, for practical purpose the mode sequence need to be truncated to a finite size.

3 Block Diagram Approach for Determining Dynamic Response

The SIMULINK model comprises three sub-systems: the carriage body, the levitation frame and the guideway. The carriage body has actions from the levitation frame and in return gives reaction to it. The levitation frame has actions from both the carriage body and the guideway. These are provided as input to the levitation frame sub-system. The output reactions from the levitation frame sub-system are provided to the carriage body and guideway sub-system, completing the cycle and thus forming a coupled system as illustrated in Fig. 3. The SIMULINK State-space block has an automatically generated algorithm that accepts input {u} and provides output {y} for a defined set of state-space matrices. The expansion of the sub-system ‘Vehicle model (state-space)’ is shown in Fig. 4. In this figure, the parameters A, B, C, D shown are to be obtained from Eqs. (24)–(27).

Fig. 3
figure 3

A general block diagram for simulation

Full size image
Fig. 4
figure 4

Vehicle model (state-space) sub-system in SIMULINK

Full size image

Figure 5 shows the expansion of the guideway sub-system in SIMULINK. The guideway receives actions from the primary suspensions, and gives back reactions to the primary suspensions. Since, there is multiple wheel input, the time delay of the input excitation is also to be modelled, depending on the wheel spacing and constant forward velocity of the vehicle. This has been illustrated as ‘transport delay’ in a separate block diagram in Fig. 6. It may be noted that odd number of inputs are associated with spring action and even ones are activated by dashpot actions of the primary suspensions. Since, the guideway profile has in general irregular and unavoidable air gap fluctuation in levitated vehicle, the guideway unevenness acts as an additional input as the relative movement of the suspension system is modified on account of these factors. The guideway roughness model has been adopted as output of a first-order linear ordinary differential equation to ideal white noise as per Eq. (12). The block diagram for this is shown in Fig. 7.

Fig. 5
figure 5

Guideway sub-system in SIMULINK

Full size image
Fig. 6
figure 6

Transport delay sub-system

Full size image
Fig. 7
figure 7

Guideway roughness block diagram in SIMULINK

Full size image

4 Optimization of Suspension Parameters

For a high-speed vehicle such as MAGLEV, the ride quality is of utmost significance since the extremely high operating speeds may result in discomfort to the passengers. The suspension of such a vehicle must be designed not only to perform the role of guidance and support but also to isolate the vehicle from any disturbances arising from track irregularities. The carriage body acceleration magnitude is an indication of vehicle ride quality. The ride performance index [19] based on RMS acceleration of the car body including the effect of pitch can be defined as

$$ f_{\text{R}} = \frac{{\sum\nolimits_{1}^{n} {\{ RMS[\ddot{z}_{{{\text{v}},n}} ] + \left| {} \right.l_{n} \left. {} \right|RMS[\ddot{\theta }_{{{\text{v}},n}} ]\} } }}{{n^{2} }} $$
(30)

where n is the number of measurement points for carriage body acceleration; \( {\text{RMS}}[{\ddot{z}}_{c,n} ] \) and \( {\text{RMS}}[\ddot{\theta }_{c,n} ] \) represent the root mean square value of vertical acceleration and pitching motion of the car body, respectively; l n represents the distance between the centroid of car body and the nth suspension system; f R is the performance index or objective function taken in optimization process. The optimization method has been implemented in a direct search algorithm. Direct search is an optimization technique that does not require any data about the gradient of the objective function. MATLAB/SIMULINK Global Optimization Toolbox functions incorporate various direct search algorithms which are all fundamentally pattern-search algorithms that compute a series of points that advance towards an optimal point [25]. The pattern-search algorithm examines a set of points around the current point, seeking a point where the estimation of the objective function is less than the value at the current point.

5 Results and Discussions

In the present work, we first studied the dynamic response of guideway and car body using SIMULINK block diagram approach and then attempt to optimize the suspension parameters and to reuse these in SIMULINK to obtain comparative response behaviour. The guideway and vehicle parameters that have been used in the current study are shown in Tables 1 and 2, respectively. The data have been adopted from the literature [3, 26].

Table 1 Guideway parameters
Full size table
Table 2 Vehicle parameters
Full size table

5.1 Vehicle–Guideway Response on Smooth Guideway

The dynamic response of the guideway without considering surface irregularity has been first obtained for double-span guideway with the six-DOF vehicle loading. The velocity of the vehicle is increased from 50 to 150 m/s in increment of 50 m/s. Figures 8 and 9 show the two-span continuous guideway displacement at x = 0.5L and x = 1.5L respectively, with vehicle speeds of 50, 100 and 150 m/s. It is observed that the guideway displacement shows a trend of increasing magnitude with the increase in vehicle speed. Peak displacement in two spans does not differ much. It is seen that peak magnitude of guideway displacement is increased by 30 % when the vehicle speed increases from 50 to 150 m/s. As soon as the moving force leaves the guideway, the beam is set to free vibration and this ‘residual vibration’ of guideway at its own frequency continues for some time. The residual displacements are insignificant to cause any undesirable stresses.

Fig. 8
figure 8

Two-span continuous guideway displacement at x = 0.5L

Full size image
Fig. 9
figure 9

Two-span continuous guideway displacement at x = 1.5L

Full size image

Figure 10 presents the comparison of the maximum mid-span displacement for single-span and two-span guideway. The guideway displacement is again found to increase with the increase of vehicle speed. It can be seen that the response of two-span continuous guideway is lower than that of single span for all vehicle velocities. It is nearly 30 % lower at the highest velocity considered. The reduction of guideway displacement for two-span continuous guideway is due to redistribution of mid-span moment towards interior support. This shows that continuous guideway construction is a favourable choice for longer span when satisfactory deflection limit is to be achieved for safety and ride comfort.

Fig. 10
figure 10

Magnitude of maximum mid-span guideway displacement

Full size image

Due to guideway deflection and unavoidable air gap fluctuation, the car body as well as levitation frame is set to oscillation. The car-body vertical and angular accelerations are obtained for varying vehicle speeds as shown in Figs. 11 and 12, respectively, for the vehicle moving on two-span continuous guideway. The car-body response is seen to increase with increasing vehicle velocity. As seen from the result, peak acceleration on smooth guideway may attain a value of 0.03 g (g is the acceleration due to gravity). At lower speed, the oscillation is found to be influenced by a combination of guideway transverse mode and vehicle bounce mode. However, single frequency oscillation is apparent in the response curve at higher speed.

Fig. 11
figure 11

Car-body vertical acceleration

Full size image
Fig. 12
figure 12

Car-body angular acceleration

Full size image

In MAGLEV vehicle system, oscillation of levitation frame is significant as its vibration causes fatigue stresses in primary suspension systems. Figure 13 shows the displacement of first levitation frame (out of four in the present model) for three different velocities. It may be noted that however at lower speed acceleration of levitation frame is small, but at 150 m/s speed, vertical acceleration may reach up to 0.7 g (g is the acceleration due to gravity). However, due to existence of secondary suspension system between the car body and levitation frame, the car body experiences lower acceleration (see Fig. 11). Thus in a high-speed transportation system, optimum suspension system is necessary to increase ride comfort level. This has been further studied in the present work (see Sect. 4) and the results are separately presented in the Sect. 5.3.

Fig. 13
figure 13

Vertical acceleration of first levitation frame

Full size image

5.2 Effect of Guideway Surface Irregularity

The surface irregularity of the guideway has been simulated and used in SIMULINK. Figure 14 shows the generated surface roughness profile, whereas Fig. 15 gives a comparison between PSD of the generated profile using Welch method [27] and target PSD. The graph is shown in logarithmic scale. The generated PSD matches reasonably well in the domain of wave number (spatial frequency) considered in the study. The generated guideway irregularity used as input in the SIMULINK to obtain the response of the vehicle–guideway system on rough guideway and thereafter the response time history has been compared with that obtained on smooth guideway.

Fig. 14
figure 14

Guideway surface roughness profile

Full size image
Fig. 15
figure 15

PSD of guideway surface roughness

Full size image

The guideway displacement at x = 0.5L for vehicle speed 150 m/s has been shown in Fig. 16. It can be seen that the response of the guideway is not significantly affected by the guideway irregularity.

Fig. 16
figure 16

Guideway displacement at x = 0.5L at vehicle speed 150 m/s

Full size image

Figures 17 and 18 show the car-body vertical and angular acceleration, respectively, for the vehicle moving on rough two-span continuous guideway with vehicle speed 150 m/s. It is observed that the effect of guideway surface irregularity is quite significant and predominantly felt on the car-body response. Moreover, due to random nature of input, the car-body vertical and angular accelerations do not reveal any definite pattern of oscillation.

Fig. 17
figure 17

Comparison of car-body vertical acceleration over smooth and rough guideway

Full size image
Fig. 18
figure 18

Comparison of car-body angular acceleration over smooth and rough guideway

Full size image

5.3 Dynamic Amplification Factor (DAF)

The dynamic amplification factor is an important parameter that can be utilized by the designer in the absence of detail dynamic analysis, simply by magnifying static deflection using a DAF as a multiplier. In the present study, DAF is defined as

$$ {\text{DAF}} = \frac{{\Delta_{\text{s}} + \Delta_{\text{d}} }}{{\Delta_{\text{s}} }} $$
(31)

where Δs and Δd refer to the maximum static and dynamic deflection of guideway. Since vehicle speed has significant effect on guideway dynamic response, the DAF values for guideway displacements of single and two-span continuous guideways have been obtained and shown in Fig. 19. It is seen that the DAF slowly increases up to a speed of around 80 m/s. Beyond this speed, DAF for single-span guideway is higher than the double-span guideway up to maximum operating speed 150 m/s. The peak showing the resonance is hypothetical which will never occur due to practical limitation of ground vehicle speed. The Dynamic Amplification Factor for the design of transrapid guideway has been provided in German guideline [26] up to maximum speed of 142.75 m/s as reported by Ren et al. [3]. DAF in the operating range of speed 25–140 m/s for single- and double-span guideway has been compared with the existing standard [26] in Table 3. It can be seen that values in existing standard show a conservative estimate in the speed range 100–140 m/s compared to that obtained in the present analysis.

Fig. 19
figure 19

Dynamic amplification factors for guideway displacement

Full size image
Table 3 Comparison of DAF of guideway deflection with existing standard
Full size table

5.4 Optimized Suspension Parameters

The optimization is performed for two-span continuous guideway with six-DOF vehicle running at a speed of 150 m/s since it produces the highest magnitude of vehicle–guideway response. The vertical acceleration of the car body at the front/rear end is taken into consideration since it would be higher in magnitude than the acceleration at the centre of gravity due to angular rotation. The upper and lower bounds of the suspension parameters assumed are shown in Table 4. The objective function has been evaluated at each stage of iteration, which is shown in Fig. 20.

Table 4 Upper and lower bounds of suspension parameters
Full size table
Fig. 20
figure 20

Objective function at each stage of iteration

Full size image

It is found that convergence has been achieved after 16 iterations. The optimized values of suspension parameters are shown in Table 5. It can be observed that there are reductions of about 23–25 % in the values of suspension parameters. The vertical acceleration of the end of the car body with optimized suspension parameters is shown in Fig. 21 and compared with the response obtained initially using the suspension parameters given in Ref. [3]. The response with assumed value of suspension parameters is termed as “Normal response” in the figure. Comparison of optimized and normal response shows that there is a reduction of 60 % in magnitude of the car-body acceleration. Figure 22 shows the change in guideway deflection when optimized suspension parameters of MAGLEV system are used. Here 25 % reduction of magnitude of the peak deflection can be observed.

Table 5 Optimized values of suspension parameters
Full size table
Fig. 21
figure 21

Vertical acceleration of the end of the car body with optimized suspension parameters

Full size image
Fig. 22
figure 22

Guideway displacement with optimized suspension parameters

Full size image

To check the level of improvement in ride quality, the urban tracked air cushion vehicle (UTACV) criterion reported by Smith [28] has been utilized. The UTACV criterion has been proposed by the United States Department of Transportation for high-speed vehicles. The power spectral density (PSD) curve of the car-body vertical acceleration obtained by using initial suspension parameters has been compared with UTACV criteria in Fig. 23. It may be noted for very low frequency input, the ride quality may be deteriorated, as vertical acceleration may exceed at some point or very close to prescribed limit. Figure 24 shows the comparison of PSD of car-body vertical acceleration using optimized suspension parameters with the UTACV comfort criteria. It is evident that the use of optimized suspension system makes the car-body acceleration to remain well below the threshold curve of UTACV guidelines.

Fig. 23
figure 23

Comparison of PSD of car-body vertical acceleration (normal values) with UTACV [28] criteria

Full size image
Fig. 24
figure 24

Comparison of PSD of car-body vertical acceleration (optimized values) with UTACV [28] criteria

Full size image

6 Conclusions

An integrated approach has been laid out in block diagram environment to model and to solve the high-speed MAGLEV vehicle/guideway interaction dynamics along with optimization of vehicle suspension parameters to achieve greater ride comfort and reduction of guideway deflection. A car model with six degrees of freedom and a two-span continuous beam model for the guideway have been adopted. The method is general and multiple number of car bodies as required by the designer can be easily adopted by the mere repetition of the process. The guideway irregularity has been assumed to be a realization of random field. The present study shows how a physical system governed by coupled fourth-order partial differential equation and second-order ordinary differential equation can be easily simulated and analysed using SIMULINK of MATLAB tool box in real time. The study shows that this approach is user friendly which provides ample scope to the designer to ensure safety and economy in single platform. The major conclusions drawn from the study are given below:

  • The vehicle operating speed is the primary criteria that govern the magnitude of response of the guideway as well as of the vehicle. the dynamic amplification factor shows that the guideway displacement does not increase monotonically for vehicle speeds up to 80 m/s but increase monotonically beyond that.

  • The present model showed close agreement on DAF with the existing standard up to a speed of 80 m/s. However, at higher speed (up to 140 m/s), codal values of DAF are conservative.

  • As regards to guideway displacement, a two-span continuous guideway performs better than a single-span guideway because of redistribution of sagging moment to the interior support.

  • The guideway irregularity has greater impact on the car-body response than on the guideway response.

  • The optimization of suspension parameters results in significant improvement in vehicle ride quality as indicated by the UTACV criterion. The guideway response reduces as well, due to the reduction in the magnitude of the interaction forces. Overall, 60 % reduction of car-body vertical acceleration and 25 % reduction in guideway deflection can be achieved using the present optimized parameters.