Abstract
We construct a double null coordinate system \((u,v,\theta _\star ,\phi _\star )\) for Kerr–Newman–de Sitter black hole interior spacetimes and prove that the two dimensional spheres given by the intersection of the hypersurfaces \(u=\hbox {constant}\) and \(v=\hbox {constant}\) are \(C^\infty\) in Boyer–Lindquist coordinates (including at the “poles"). The null coordinates allow one to immediately extend some results previously proven for Kerr. As an example, we illustrate how Sbierski’s result in (On the initial value problem in general relativity and wave propagation in black-hole spacetimes. Doctoral thesis, 2014. https://doi.org/10.17863/CAM.16140), for the wave equation on the black hole interior, for Reissner–Nordström and Kerr spacetimes, applies to Kerr–Newman–de Sitter spacetimes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Kerr–Newman–de Sitter (KNdS) metric is a solution of the Einstein–Maxwell equations with a positive cosmological constant \(\Lambda\):
Here \(R_{\mu \nu }\) are the components of the Ricci tensor of the spacetime metric g, R is the scalar curvature, \(\star\) is the Hodge star operator, and \(F_{\mu \nu }\) is the Faraday electromagnetic 2-form. So, the KNdS metric is an electrovacuum solution of the Einstein field equations, i.e. it is a solution in which the only nongravitational mass-energy present is an electromagnetic field. The spacetime is the four-dimensional manifold \({{\mathbb {R}}}^2\times {{\mathbb {S}}}^2\) with metric given by
in Boyer–Lindquist coordinates, where
\(\theta\) is the colatitude, with
and \(\phi\) is the longitude, with
(see Carter [6], and Akcay and Matzner [1] and Kraniotis [23], for example). Here \(M>0\) and \(a\ne 0\) are mass and angular momentum parameters, respectively, and e is a charge parameter (which may be zero). Without loss of generality, we assume that the magnetic charge is zero and a is positive. This metric is supposed to represent a rotating black hole, with charge, in a universe which is expanding at an accelerated rate (as ours is). We refer to "Appendix C", where we calculate Komar integrals over the event horizon, for the relation between these parameters and the physical quantities of the black hole. We wish to consider subextremal metrics, meaning that \(\Delta _r\) has four distinct real roots
The event horizon \(\mathcal{H}\) corresponds to the hypersurface where \(r=r_+\), the Cauchy horizon \(\mathcal{C}\mathcal{H}\) corresponds to the hypersurface where \(r=r_-\), and the cosmological horizon corresponds to the hypersurface \(r=r_c\). We are interested in studying solutions of the wave equation in the black hole region, \(r_-<r<r_+\), and we wish to construct double null coordinates and understand their relation with Boyer–Lindquist coordinates. The coordinate t takes values in \(\mathbb {R}\).
This article follows closely the strategy and tools developed in [9]. Double null coordinate systems were constructed by Pretorius and Israel [28] for Kerr spacetimes, by Balushi and Mann [3] for Kerr–(anti) de Sitter spacetimes, and by Imseis, Balushi and Mann [19] for Kerr–Newman–(anti) de Sitter spacetimes. In [3] and [19] the authors also study the formation of caustics. In Sect. 2 we construct a double null coordinate system for Kerr–Newman–de Sitter spacetimes. This construction only differs from the one in [3] and [19] (that we were unaware of until the completion of this work) in the choice of \(\lambda\) (our choice \(\lambda =\sin ^2\theta _\star\) is identical to the one in [9] and [28]). Consider the transformation \((t,r,\theta ,\phi )\mapsto (t,r_\star ,\theta _\star ,\phi )\) in the black hole region \(r_-<r<r_+\), where \(\Delta _r<0\). The coordinate \(\theta _{\star }\) is defined implicitly as the solution of \(F(r,\theta ,\theta _{\star })=0\), where F is given by
The coordinate \(r_\star\) is defined by \(r_\star =\varrho (r,\theta ,\sin ^2\theta _{\star }(r,\theta ))\), where \(\varrho\) is given by
for some fixed \(r_0\in (r_-,r_+)\), and where f is the function which satisfies \(f(0)=0\) and
(note the difference, \(\varrho\) versus \(\rho\) in (1)).
The regularity of transformation of coordinates \((r_\star ,\theta _\star )\mapsto (r,\theta )\) for Kerr spacetimes, namely at \(\theta _\star =0\), was shown by Dafermos and Luk [9]. We adapt their work to the setting of Kerr–Newman–de Sitter spacetimes. We check that \(\theta _{\star }\) is well defined and continuous at \(\theta =0\) and \(\theta =\frac{\pi }{2}\) with
The proof of (2) requires that we use conditions characterizing subextremal black holes which are deduced in "Appendix B". Namely, we use
where the function l is given by (138). This implies the inequality
which in turn implies (2). We use the fact that \(\Lambda\) is nonnegative so that our computations are not immediately applicable to the setting of Kerr–AdS.
We also show that r and \(\theta\) are smooth functions of \(r_\star\) and \(\theta _{\star }\). When the cosmological constant is equal to zero and \(e=0\), \(\Delta _{\theta }\) is equal to 1 and our formulas reduce to the ones for the Kerr spacetime in [9]. The trigonometric identity
for \(D(\theta ,\theta _{\star })=\sin ^2\theta _{\star }\Delta _{\theta }-\sin ^2\theta\) is the key to the calculation of \(\partial _r\theta _\star\) and \(\partial _\theta \theta _\star\), as well as the successful completion of some new identities, such as (54) and (59), which we need in order to calculate the derivatives of r and \(\theta\) with respect to \(r_\star\) and \(\theta _\star\). We would like to emphasize that our calculations are successful because the dependence of \(\Delta _{\theta }\) on \(\theta\) occurs through \(\sin ^2\theta\), and not through \(\sin \theta\), or on any other non-smooth function of \(\sin ^2\theta\). (This is a reflection of the fact that the Kerr–Newman–de Sitter metric is regular on a manifold diffeomorphic to \(\mathbb {R}^2\times \mathbb {S}^2_{\theta ,\phi }\), i.e. it is regular on the full Boyer–Lindquist spheres of constant time coordinate t and radial coordinate r.) We also obtain bounds on the derivatives of r and \(\theta\) which we need later on. These bounds parallel the ones in [9].
Using
the final transformation
with h given by
allows one to bring the metric to the double null form
which one can use to carry out energy estimates.
Neither the Boyer–Lindquist coordinate system \((t,r,\theta ,\phi )\) nor the double null coordinate system \((u,v,\theta _\star ,\phi _\star )\) cover the axis \(\theta _\star =0\), obviously. But they can be naturally extended to an atlas that does cover \(\theta _\star =0\) using
In Sect. 2.2.6, we prove that the two atlases \(\mathcal{A}_{\tiny \hbox {BL}}=\{(t,r,\theta ,\phi ),(t,r,\tilde{x},\tilde{y})\}\) and \(\mathcal{A}_{\tiny \hbox { DN}}=\{(u,v,\theta _\star ,\phi _\star ),(u,v,x,y)\}\) are compatible (which would be clear if we were to exclude the points where \(\theta =\theta _\star =0\) and \(\theta =\theta _\star =\pi\) from our manifold). This implies that the two-spheres given by the intersection of the hypersurfaces \(u=\hbox {constant}\) and \(v=\hbox {constant}\) are \(C^\infty\) with respect to \(\mathcal{A}_{\tiny \hbox { BL}}\) (see Theorem 2.23).
Following [9], we analyze the decay of \(\Omega ^2\) at the future event and Cauchy horizons, \(\mathcal{H}^+\) and \(\mathcal{C}\mathcal{H}^+\). Finally, we give regular coordinates at \(\mathcal{H}^+\) and \(\mathcal{C}\mathcal{H}^+\). The Christoffel symbols of g in the double null coordinates \((u,v,\theta _\star ,\phi _\star )\) are given in "Appendix A", along with some covariant derivatives that are needed to carry out energy estimates.
In Sect. 3, using the vector field method, we study, in the black hole interior, the energy of solutions of the wave equation which have compact support on \(\mathcal{H}^+\). We apply the form (4) of the metric to construct certain blue-shift and red-shift vector fields and to calculate their covariant derivatives. We obtain the usual inequalities relating the vector and scalar currents associated to these vector fields. This allows us to illustrate how Sbierski’s result in [29] applies to Kerr–Newman–de Sitter spacetimes.
This work is a first step of our broader project to generalize the results of [7], which provides a sufficient condition, in terms of surface gravities and a parameter for an exponential decaying Price Law, for energy of waves to remain bounded up to \(\mathcal{C}\mathcal{H}^+\). The work [7] used the fact that the generators of spherical symmetry are three Killing vector fields, which is not true in the context of Kerr–Newman–de Sitter spacetimes. We expect to address this in a forthcoming paper.
An alternative approach towards extending the results of [7] to the Kerr–Newman–de Sitter setting would be to work in Boyer–Lindquist coordinates as is done in the work [25] on Kerr black hole interiors. However, as an example, the double null coordinates allow one to immediately extend the results in [14] to KNdS.
In "Appendix B", we characterize subextremal Kerr–Newman–de Sitter black holes in terms of \((r_-, r_+,\Lambda a^2,\Lambda e^2)\), proving (3), in particular, as mentioned above. The subset of \({{\mathbb {R}}}^3\) where one can choose \(\left( \frac{r_+}{r_-},\Lambda a^2,\Lambda e^2\right)\) is sketched in Fig. 2 on page 43. We make additional remarks concerning alternative choices of parameters, namely \(\left( \Lambda ,\frac{r_+}{r_-},a,e\right)\) or \((\Lambda ,M,a,e)\). Related characterizations of the parameters of subextremal Kerr–de Sitter solutions, for the case when there is no charge, can be found in Lake and Zannias [24] and Borthwick [4].
Hintz and Vasy give a uniform analysis of linear waves up to the Cauchy horizon using methods from scattering theory and microlocal analysis in [18]. Moreover, Hintz proves non-linear stability of the Kerr–Newman–de Sitter family of charged black holes in [17].
2 A double null coordinate system
2.1 Construction of the double null coordinate system
2.1.1 The coordinates \(r_\star\) and \(\theta _{\star }\)
Given the manifold \(\mathbb {R}^2\times \mathbb {S}^2\), with metric (1), we look for a function \(r_\star\) such that the axisymmetric hypersurface,
(ingoing when the plus sign is chosen, and outgoing when when the minus sign is chosen), is lightlike. Then, the function v must satisfy the eikonal equation
We follow [28] and construct particular separable solutions of the eikonal equation. We define P and Q by
Note that
and so the eikonal equation becomes
As P is independent of r, and Q is independent of \(\theta\), we look for special solutions \(r_\star\) of this equation, where
so that
Both P and Q depend on (what is so far the parameter) \(\theta _\star\), which arises because of the degree of freedom one has in breaking up the left-hand side of (5) to a sum. Indeed, to the left-hand side of (5) we subtracted and added the quantity \(a^2\sin ^2\theta _{\star }\) (which is independent of both r and \(\theta\)) and then we decomposed the resulting expression into a sum of a function depending solely on r and a function depending solely on \(\theta\). We integrate (7) and obtain
where the function f accounts for an integration constant. Thus we have
\(\varrho :(r_-,r_+)\times [0,\pi ]\times [0,1]\rightarrow \mathbb {R}\), with
for some fixed \(r_0\in (r_-,r_+)\), and
The expression for \(\varrho\) is written so that the second integral converges. Here
so that \(\hat{P}(\theta ,\lambda )= P\bigl (\theta ,\arcsin \sqrt{\lambda }\bigr ) =P(\theta ,\theta _{\star })\) and \(\hat{Q}(r,\lambda )= Q\bigl (r,\arcsin \sqrt{\lambda }\bigr )=Q(r,\theta _{\star })\).
For each fixed \(\lambda\), (8) is a solution of (7). We now proceed to obtain another solution of (7). Calculating the differential of \(\varrho\), we obtain
where
Define the function
Note that the function f is still free. We choose \(f:[0,1]\rightarrow \mathbb {R}\) to be the function which satisfies \(f(0)=0\) and
The function f is bounded. Then the expression for F becomes
Adapting the construction of [9] to our case, for \(r\in [r_-,r_+]\) and \(\theta \in (0, \frac{\pi }{2})\), we define \(\theta _{\star }\in [\theta , \frac{\pi }{2})\) implicitly to be the solution of
(see Lemma 2.4). Also, let
and
Then, the function
is another solution of (7). The functions
are solutions of the eikonal equation. Just as in the case of Kerr, it turns out that \(\theta _{\star }\) is an appropriate angle coordinate. This can be understood starting with the construction of [28]: when \(\Lambda =M=a=e=0\) (so that we are reduced to the Minkowski spacetime), \(\theta _{\star }\) is the spherical polar angle. Moreover, for r close to \(r_+\), \(\theta _{\star }\) is close to \(\theta\) (see (9) and (10)). The function \(\theta _\star\) is interpreted as the spherical polar angle and the hypersurfaces where u and v are constant are called quasi-spherical light cones. From
(recall that \(\Delta _r<0\)), a hypersurface where \(r_{\star }\) equals a constant is spacelike.
Remark 2.1
Note that \(r_{\star }\) ranges between \(-\infty\) and \(+\infty\), as r ranges between \(r_+\) and \(r_-\). More precisely, given \(L>0\), there exists \(\delta >0\) such that \(r_\star (r,\theta )>L\) for all \((r,\theta )\in (r_-,r_-+\delta )\times [0,\pi ]\). Moreover, given \(\delta >0\), there exists \(L>0\) such that \(r_\star (r,\theta )>L\) implies that \(r\in (r_-,r_-+\delta )\). In Lemma 2.9 we will prove that \((r,\theta )\mapsto (r_\star ,\theta _\star )\) is invertible. So, we are observing that \(\lim _{r\searrow r_-}r_\star (r,\theta )=+\infty\) and that \(\lim _{r_\star \nearrow +\infty }r(r_\star ,\theta _\star )=r_-\), and that these limits are uniform in \(\theta\) and in \(\theta _\star\), respectively, for \(\theta\) and \(\theta _\star\) in \([0,\pi ]\). Analogous statements can be made for the other endpoint.
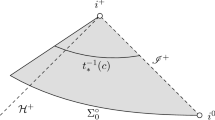
The behavior of the coordinates u and v is sketched in Fig. 1.
Remark 2.2
Because of the symmetry in (11), our statements about \(\theta\) and \(\theta _\star\) will refer to the interval \(\left( 0,\frac{\pi }{2}\right)\) and it is understood that corresponding statements will hold in \(\left( \frac{\pi }{2},\pi \right)\).
2.1.2 The metric in \((t,r_\star ,\theta _{\star },\phi )\) coordinates
Denote
and
Differentiating both sides of (9) with respect to r and \(\theta\) yields
Since
the differentials of r and \(\theta\) are given by
To write the metric in \((t,r_{\star },\theta _{\star },\phi )\) coordinates one uses (16) and (17) in (1) and obtains
with
2.1.3 Definition of \(\phi _{\star }\) and the metric in double null coordinates \((u,v,\theta _{\star },\phi _{\star })\)
From (12), one gets
Now introduce a new coordinate \(\phi _{\star }\), defined by
where
For a general function f, one has
where \(\hat{f}\) is the function f written in the \((\hat{u},\hat{v},\hat{\theta }_\star ,\phi )\) coordinate system and \(\hat{u}=u\), \(\hat{v}=v\), \(\hat{\theta }_\star =\theta _\star\). So, it follows that
These equations help us with the geometric interpretation of the change of coordinates operated by passing from \(\phi\) to \(\phi _\star\). Of course, for functions f that do not depend on \(\phi\), like the coefficients of our metric, \(\partial _uf=\partial _{\hat{u}}f\), \(\partial _vf=\partial _{\hat{v}}f\) and \(\partial _{\theta _\star }f=\partial _{\hat{\theta }_\star }f\). Defining
the expression for the metric becomes
For each pair (u, v), \({g \hspace{-4.83322pt}/}\) is a metric defined on a two-sphere. The calculation above shows that the coefficients of this metric are
The determinants of the metrics \({g \hspace{-4.83322pt}/}\) and g are
and
and the inverse of the metric g is
with coefficients given by
2.1.4 Normals to hypersurfaces and volume elements
We finish this subsection by writing down the volume elements of hypersurfaces
of our spacetime, corresponding to constant \(r_\star\), v and u. As
recalling (25) for the determinant of \({g \hspace{-4.83322pt}/}\), the volume element for \(\Sigma _{r_\star }\) is
Our choice for the normals to constant v and u hypersurfaces are
We have that
and so, since the volume element associated to the metric g is
the volume elements associated to constant v and u hypersurfaces are
and
As \(r_\star =u+v\), the tangent space to a hypersurface \(\Sigma _{r_\star }\), where \(r_\star\) is constant, is spanned by \(\partial _v-\partial _u\), \(\partial _{\theta _{\star }}\) and \(\partial _{\phi _{\star }}\), and
Remark 2.3
\(\partial _{\phi _\star }\) is equal to zero when \(\theta _\star\) is either 0 or \(\pi\).
Indeed, the vector field \(\partial _{\phi _\star }\) is tangent to the spheres \(u=\hbox {constant}\) and \(v=\hbox {constant}\) which are contained in the spacelike hypersurfaces \(r_\star =\hbox {constant}\) and
2.2 Regularity of the change of coordinates
The regularity of transformation of coordinates \((r_\star ,\theta _\star )\mapsto (r,\theta )\) for Kerr spacetimes, namely at \(\theta _\star =0\) and \(\theta _\star =\frac{\pi }{2}\), was shown by Dafermos and Luk [9]. In this subsection we adapt their work to the setting of Kerr–Newman–de Sitter spacetimes.
2.2.1 The coordinate \(\theta _{\star }\) is well defined and continuous
Lemma 2.4
\(\theta _{\star }\) is well defined.
Proof
Clearly
Moreover
which implies that
The continuity of F implies that for each pair \((r,\theta )\), with \(\theta \in \bigl (0,\frac{\pi }{2}\bigr )\), there exists \(\theta _{\star }=\theta _{\star }(r,\theta )\in \bigl (\theta ,\frac{\pi }{2}\bigr )\) such that \(F(r,\theta ,\theta _{\star })=0\).
The function F is decreasing in \(\theta _{\star }\). This follows from the fact that
is strictly increasing. Indeed, suppose \(\theta _{\star }<\tilde{\theta }_{\star }\). Setting \(\sin \tilde{\theta }'=\frac{\sin \tilde{\theta }_\star }{\sin \theta _{\star }}\sin \theta '\), as \(\theta '<\tilde{\theta }'\), we have \(\Delta _{\theta '}>\Delta _{\tilde{\theta }'}\) and
\(\square\)
Lemma 2.5
\(\theta _{\star }\) is continuous at \(\theta =0\) and \(\theta =\frac{\pi }{2}\) with
Proof
The second integral in (9) is bounded above by
for some positive \(c_{\Lambda ,M,a,e}\). On the other hand, using the substitution \(\sin \theta '=\sin \theta _{\star }\sin \tilde{\theta }\) we see that the negative of the first integral in (9) is bounded below by
Since \(F(r,\theta ,\theta _{\star })\) is equal zero, we obtain the estimate
provided the right-hand side is positive, i.e.
For fixed \(r_-\) and \(r_+\), the minimum of the last expression is attained when \(a=\sqrt{r_-r_+}\). So the last inequality is implied by the stronger restriction
According to Lemma B.1, for all subextremal black holes, we have
where l is given by (138), so that
We claim that
for all \(\alpha\) greater than 1. To show this, we define the function
which we wish to check is always greater than one. By direct computation one may check that
Indeed,
Since both sides of the last inequality are positive, the inequality holds if and only if the square of the right-hand side minus the square of the left-hand side is nonnegative. Calculating this difference, one finds out that the terms in \(\alpha ^8\), \(\alpha ^7\) and \(\alpha ^6\) cancel out. One is left with the polynomial
whose coefficients are all positive. Hence, this polynomial is positive (for \(\alpha >1\)). So,
The claim is proven.
The previous paragraph implies that (33) is satisfied, and so the right-hand side of (31) is positive. Then, we have
If we use the substitution \(\cos \theta '=\cos \theta _{\star }\sec \tilde{\theta }\) in (30) we get
If \(\frac{\cos \theta }{\cos \theta _{\star }}\le \sqrt{2}\), we are done. Otherwise, as
and \(\sin ^2\theta _{\star }\le 1\), we have that
The result follows since (29) implies that the last expression is bounded above. \(\square\)
2.2.2 The derivative of the function defining \(\theta _\star\)
Remark 2.6
Let us define
so that \(D(\theta ,\theta _{\star })=P^2(\theta ,\theta _{\star })/a^2\). Clearly,
holds. The trigonometric equality
allows us to conclude that
We will have to use the identity (35) repeatedly in our calculations.
Lemma 2.7
For \(\theta _{\star }\in \left( 0,\frac{\pi }{2}\right)\), we have that
Proof
We start from the definition of F in (9). Since \(\theta _{\star }\in \left( 0,\frac{\pi }{2}\right)\), for \(\theta '\in [\theta ,\theta _{\star }]\), we get \(\Delta _{\theta '}\ge 1+\frac{\Lambda }{3}a^2\cos ^2\theta _{\star }\), and so \(P(\theta ',\theta _{\star })\ge \sqrt{\frac{\Lambda }{3}}\frac{a^2}{2}\sin {(2\theta _{\star })}>0\). So, we do not have to worry about vanishing denominators. The result follows from the calculation
For the second equality we used (35). \(\square\)
The expression for G and the definition of L in (14) yield
Lemma 2.8
We have the following estimate for G:
for some constant \(C_{\Lambda ,M,a,e}>0\) depending on \(\Lambda , M, a\) and e.
Proof
We use expression (36). Note that
For \(\theta _{\star }\) close to zero, the right-hand side is bounded above by
whereas for \(\theta _{\star }\) close to \(\frac{\pi }{2}\), the right-hand side is bounded above by
Recalling (28), we conclude that the second term on the right-hand side of (36) is uniformly bounded below by a negative constant. Clearly, the same is true for the third term on the right-hand side of (36). Since both terms are negative, \(\csc (2\theta _{\star })\sin (2\theta )\) is bounded, and \(1/\sqrt{\sin ^2\theta _{\star }\Delta _{\theta }-\sin ^2\theta }\) is bounded below by a positive constant, we obtain (38). \(\square\)
2.2.3 The coordinates r and \(\theta\) as functions of \(r_\star\) and \(\theta _\star\)
Lemma 2.9
The mapping \((r,\theta )\rightarrow (r_\star ,\theta _\star )\), from \((r_-,r_+)\times \left[ 0,\frac{\pi }{2}\right]\) to \((-\infty ,+\infty )\times \left[ 0,\frac{\pi }{2}\right]\), is globally invertible.
Proof
Fix \((r_\star )_0\in {{\mathbb {R}}}\). For each fixed \(\theta \in \bigl (0,\frac{\pi }{2}\bigr )\), let \(r(\theta )\) be the unique (because \(\partial _rr_\star <0\)) value of \(r\in (r_-,r_+)\) such that
The Implicit Function Theorem guarantees that \((r(\,\cdot \,),\,\cdot \,)\) is a \(C^1\) curve and that
To see how \(\theta _\star\) varies along this curve we calculate
So, \(\theta _\star\) is strictly increasing along the curve \((r(\,\cdot \,),\,\cdot \,)\). Moreover, (28) shows that \(\lim _{\theta \searrow 0}\theta _\star (r(\theta ),\theta )=0\) and \(\lim _{\theta \nearrow \frac{\pi }{2}}\theta _\star (r(\theta ),\theta )=\frac{\pi }{2}\). Thus, given \(((r_\star )_0,(\theta _\star )_0)\in (-\infty ,+\infty )\times \left[ 0,\frac{\pi }{2}\right]\) there exists one and only one \((r,\theta )\) such that \((r_\star (r,\theta ),\theta _\star (r,\theta ))= ((r_\star )_0,(\theta _\star )_0)\). We conclude that the mapping
is one-to-one and onto. \(\square\)
2.2.4 First partial derivatives
Lemma 2.10
The partial derivatives of \((r, {\theta })\) with respect to \((r_{\star }, \theta _{\star })\) are given by
In the region \(r_-<r<r_+\), we have
Proof
We start from (16) and (17). We use (36) to obtain (40) and (42). The estimates for the derivatives of r and \(\theta\) follow from the estimates
which together imply that
\(\square\)
2.2.5 Higher order derivatives
Lemma 2.11
The functions r and \(\frac{\partial \theta }{\partial \theta _{\star }}\) are \(C^\infty\). For every \(k\ge 2\), we have that
Moreover, the derivatives of the function L given in (14) are bounded as follows:
Remark 2.12
We say that a function depending on \(r_\star\) and \(\theta _\star\) is \(C^\infty\) if it has derivatives of all orders with respect of \(\partial _{r_\star }\) and \(\frac{1}{\sin (2\theta _\star )}\partial _{\theta _\star }\). Refer to Remarks (2.19), (2.20) and (2.21) for an explanation about the reason for introducing the factor \(\frac{1}{\sin (2\theta _\star )}\) behind \(\partial _{\theta _\star }\). The function \(\sin ^2\theta\) is \(C^\infty\).
To prove Lemma 2.11 we need to know the derivatives of
Note that the dependence of \(\frac{\partial r}{\partial r_{\star }}\), \(\frac{1}{\sin (2\theta _{\star })}\frac{\partial r}{\partial \theta _{\star }}\), \(\frac{\partial \theta }{\partial \theta _{\star }}\) and L on \(\theta\) and \(\theta _{\star }\) is done through \(\sin ^2\theta\), \(\sin ^2\theta _{\star }\), \(\Delta _\theta\) (which is a function of \(\sin ^2\theta\), and this is crucial for our argument to work), \(\sin ^2(2\theta _{\star })\), and \(R_1\) to \(R_4\). The same is true for \(\frac{\partial \theta }{\partial r_{\star }}\), which however also has a factor \(\sin (2\theta _{\star })\). Moreover, note that
or, alternatively, \(\cos (2\theta )=1-2\sin ^2\theta\). If the factor \(\sin (2\theta )\) were to appear by itself in our formulas, or if the factor \(\sin (2\theta _{\star })\) were to appear by itself, then our argument would not go through because the derivatives \(\frac{1}{\sin (2\theta _{\star })}\partial _{\theta _{\star }}\) of each of these are not bounded. The structure of our problem is such that when one of these factors is present, then the other one is also present, and their product has derivatives of all orders with respect to \(\partial _{r_{\star }}\) and \(\frac{1}{\sin (2\theta _{\star })}\partial _{\theta _{\star }}\) which are bounded. Furthermore, as we will see below, the derivatives of \(R_1\) to \(R_4\) are sums whose summands are products of factors that are either \(R_1\), \(R_2\), \(R_3\), \(R_4\), or, when this is not the case, others that are clearly smooth (since the denominators that will appear do not vanish for \(r_-\le r\le r_+\)). Hence, it turns out that to prove that r and \(\theta\) are smooth, we just have to check that \(R_1\) to \(R_4\) are \(C^1\) and that their first derivatives have the aforementioned property. Next we calculate the first derivatives of \(R_1\) to \(R_4\).
As a small note, let \(\theta _{\star }\in \bigl (0,\frac{\pi }{2}\bigr )\). Consider the function
This is clearly bounded for \(\theta _{\star }\) close to zero. It is also bouded for \({\theta _{\star }}\) close to \(\frac{\pi }{2}\). Indeed, in this situation, we have
because \(\frac{\cos \theta }{\cos \theta _{\star }}\) is bounded ((28)). So the function is bounded for \(\theta _{\star }\in \bigl (0,\frac{\pi }{2}\bigr )\).
Remark 2.13
The reader will notice, using the expressions below, that
for each \(i\in \{1,2,3,4\}\).
Derivatives of \(R_1\). For any integer \(n\ge 1\), the following identities hold:
Proof
The proof of (53) is immediate using (41), as
By differentiation we obtain
We keep the two first integrals unchanged and use (35) on the integral marked (55) to obtain
Integrating the last integral by parts and using the fact that
we obtain
From equality (42), it follows that
Using the last equality in (56) and dividing by \(\sin (2\theta _{\star })\), we obtain (54). \(\square\)
Derivatives of \(R_2\). The following identities hold:
Proof
From (41), we get (58). To start the proof of (59), note that
For any A, the last expression is equal to
because the terms with A cancel out and the terms with \(\sin ^2(2\theta )\) cancel out. The value of A will be chosen taking (42) into account, that is we choose \(A=\Delta _{\theta }\frac{(r^2+a^2)^2 -a^2 \sin ^2\theta _{\star } \Delta _r}{(r^2+a^2)^2 \Delta _{\theta }-a^2 \sin ^2\theta \Delta _r}\). The reason we made a term with \(A-1\) appear is that such a term is proportional to \(\Delta _r\). In fact,
According to (35), we have that
Hence, the expression above is equal to
The final expression (59) is obtained using (42). \(\square\)
Derivatives of \(R_3\). The following identities hold:
Proof
From (41), we get (60). Arguing as in the proof of (59), we obtain
One concludes by once again applying (42). \(\square\)
Derivatives of \(R_4\). The following identities hold:
Proof
From (41), we immediately get (61). Moreover
Equality (62) is obtained using (57). \(\square\)
Proof of Lemma 2.11
Proof of (44). We have seen in (43) that \(\left| \frac{\partial r}{\partial {r_{\star }}}\right| \lesssim |\Delta _r|\) (this is (44) with \(k_1=1\) and \(k_2=0\)) and that \(\left| \frac{1}{\sin (2\theta _{\star })}\frac{\partial r}{\partial {\theta _{\star }}}\right| \lesssim |\Delta _r|\) (this is (44) with \(k_1=0\) and \(k_2=1\)). Thus, inequalities (44) follow from
-
(i)
(51) holds,
-
(ii)
(52) holds,
-
(iii)
\(\left| \frac{\partial r}{\partial {r_{\star }}}\right| \lesssim |\Delta _r|\), which in particular implies that \(\left| \frac{\partial \Delta _r}{\partial {r_{\star }}}\right| \lesssim |\Delta _r|\),
-
(iv)
\(\left| \frac{1}{\sin (2\theta _{\star })}\frac{\partial r}{\partial {\theta _{\star }}}\right| \lesssim |\Delta _r|\), which in particular implies that \(\left| \frac{1}{\sin (2\theta _{\star })}\frac{\partial \Delta _r}{\partial {\theta _{\star }}}\right| \lesssim |\Delta _r|\),
-
(v)
\(\left| \frac{\partial \theta }{\partial {r_{\star }}}\right| \lesssim |\Delta _r|\sin (2\theta _{\star })\lesssim |\Delta _r|\lesssim 1\),
-
(vi)
\(\left| \frac{1}{\sin (2\theta _{\star })}\frac{\partial (\sin ^2\theta )}{\partial \theta _{\star }}\right| \lesssim 1\), \(\left| \frac{1}{\sin (2\theta _{\star })}\frac{\partial (\sin (2\theta )\sin (2\theta _{\star }))}{\partial \theta _{\star }}\right| \lesssim 1\), \(\left| \frac{1}{\sin (2\theta _{\star })}\frac{\partial (\cos (2\theta ))}{\partial \theta _{\star }}\right| \lesssim 1\). \(\left| \frac{1}{\sin (2\theta _{\star })}\frac{\partial (\sin ^2\theta _{\star })}{\partial \theta _{\star }}\right| =1\), \(\left| \frac{1}{\sin (2\theta _{\star })}\frac{\partial (\sin ^2(2\theta _{\star }))}{\partial \theta _{\star }}\right| \lesssim 1\), \(\left| \frac{1}{\sin (2\theta _{\star })}\frac{\partial (\cos (2\theta _{\star }))}{\partial \theta _{\star }}\right| =2\).
\(\square\)
Proof of (45). It was shown in (43) that \(\left| \frac{\partial \theta }{\partial {r_{\star }}}\right| \lesssim |\Delta _r|\sin (2\theta _{\star })\) (this is (45) with \(k_1=1\)). Hence, inequalities (45) follow from (i), (iii) and (v) (with the bound 1). \(\square\)
Proof of (46). We have seen in (43) that \(\left| \frac{\partial \theta }{\partial {\theta _{\star }}}\right| \lesssim 1\) (this is (46) with \(k_1=0\)). Thus, inequalities (46) are a consequence of (ii), (iv) and (vi). \(\square\)
Proof of (47). Inequalities (47) result from (46), (i), (iii) and (v) (with the bound \(|\Delta _r|\)). \(\square\)
Proof of (48) and (49). These inequalities ensue from (37), (44) to (47) and (50). \(\square\)
This completes the proof of Lemma 2.11.
Remark 2.14
Note that (48) and (49) hold for any smooth function of \(r_\star\) and \(\sin ^2\theta _{\star }\).
Lemma 2.15
The functions \(\frac{1}{\sin (2\theta _{\star })}\partial _{\theta _{\star }}h\), \(b^{\phi _{\star }}\), \({g \hspace{-4.83322pt}/}_{\theta _{\star },\theta _{\star }}\), \(\frac{{g \hspace{-4.83322pt}/}_{\theta _{\star }\phi _{\star }}}{\sin ^2\theta _{\star }\sin (2\theta _\star )}\), \(\frac{{g \hspace{-4.83322pt}/}_{\phi _{\star }\phi _{\star }}}{\sin ^2\theta _{\star }}\) and \(\frac{1}{\sin ^2\theta _{\star }}\left( {g \hspace{-4.83322pt}/}_{\theta _{\star }\theta _{\star }} -\,\frac{{g \hspace{-4.83322pt}/}_{\phi _{\star }\phi _{\star }}}{\sin ^2(\theta _{\star })}\right)\) are smooth.
Proof
Since \(h(0,\theta _{\star })=0\), we have that \(\partial _{\theta _{\star }}h(0,\theta _{\star })=0\). So, as \(\partial _{r_{\star }}h=-B\), it follows that
Recall from (40) that \(\partial _{\theta _{\star }}r\) has a factor \(\Delta _r\sin (2\theta _{\star })\) and observe that
This shows that \(\frac{1}{\sin (2\theta _{\star })}\partial _{\theta _{\star }}h\) has derivatives of all orders with respect to \(\partial _{r_{\star }}\) and \(\frac{1}{\sin (2\theta _{\star })}\partial _{\theta _{\star }}\). Moreover, as \(b^{\phi _{\star }}=2B\), we obtain
and \({g \hspace{-4.83322pt}/}_{\theta _{\star }\theta _{\star }}\) is smooth.
Note that \(\frac{\sin ^2\theta }{\sin ^2\theta _{\star }}\) has derivatives of all orders with respect to \(r_\star\) and \(\sin ^2\theta _{\star }\). Indeed, we have
As \(\frac{\partial \theta }{\partial r_\star }\) has a factor \(\sin (2\theta _\star )\), the right-hand side has a factor \(\sin (2\theta )\sin (2\theta _\star )\). Taking (50) into account, differentiability at \(\theta _{\star }\) equal to \(\frac{\pi }{2}\) is not a problem. Neither is there a problem at \(\theta _{\star }\) equal to zero because
Differentiability with respect to \(\sin ^2\theta _{\star }\) holds at \(\theta _{\star }\) equal to zero because
and differentiability holds at \(\theta _{\star }\) equal to \(\frac{\pi }{2}\) because
So, we see that
are smooth. Using (13) and (37), we get
The expression inside the square parenthesis is a polynomial p in \(\alpha :=\sin ^2\theta\) and \(\beta :=\sin ^2\theta _{\star }\) satisfying \(p(0,0)=0\). So, \(p(\alpha ,\beta )=D_1p(0,0)\alpha +D_2p(0,0)\beta +\) higher order terms. Thus, it is clear that \(\frac{p(\sin ^2\theta ,\sin ^2\theta _{\star })}{\sin ^2\theta _{\star }}\) is smooth, and so it is clear that (63) is smooth at zero. Differentiability at \(\frac{\pi }{2}\) is not an issue since
\(\square\)
Remark 2.16
The Christoffel symbols of the metric \({g \hspace{-4.83322pt}/}\) are bounded with the exception of \({\Gamma \hspace{-6.66656pt}/ \,}^{\phi _{\star }}_{\theta _{\star }\phi _{\star }}\) which blows up precisely like \(\frac{1}{\sin \theta _{\star }}\).
Proof
Because \({g \hspace{-4.83322pt}/}\) behaves like the round metric on \({{\mathbb {S}}}^2\), \({g \hspace{-4.83322pt}/}^{-1}\) behaves like the inverse of the round metric on \({{\mathbb {S}}}^2\), in that \({g \hspace{-4.83322pt}/}^{\phi _{\star }\phi _{\star }}\) blows up at \(\theta _{\star }=0\) like \(\frac{1}{\sin ^2\theta _{\star }}\). Hence, the Christoffel symbols of the metric \({g \hspace{-4.83322pt}/}\) also behave like the ones of the round metric on \({{\mathbb {S}}}^2\), namely, they are all smooth with the exception of \({\Gamma \hspace{-6.66656pt}/ \,}^{\phi _{\star }}_{\theta _{\star }\phi _{\star }}\),
which blows up precisely like \(\frac{1}{\sin \theta _{\star }}\). \(\square\)
2.2.6 Regularity at \(\theta _\star =0\) and \(\theta _\star =\pi\)
Note that the coordinates that are constructed are not just locally defined but are well-defined globally on a manifold diffeomorphic to \(\mathbb {R}^2\times \mathbb {S}^2\).
Regularity of the metric.
We check the regularity of the metric at \(\theta _\star =0\) using coordinates
Lemma 2.17
The metric is smooth at \(\theta _\star =0\) and
Proof
The relations
imply that
Using (13), (22), (24) and (37), we have
As, by (23),
we obtain
The trigonometric functions of \(\phi _\star\), which would make the metric discontinuous at \(\theta _\star =0\), have disappeared. Moreover, since
and
we conclude that (65) holds. This shows that the metric is continuous at \(\theta _\star =0\). Lemma 2.15 implies that the extension of the metric is smooth. \(\square\)
Calculation of \(\partial _{\theta _\star }\theta (r_\star ,0)\).
Lemma 2.18
We have that
Proof
Using the definition of F in (9), the equation \(F(r,\theta ,\theta _\star (r,\theta ))=0\) can be written as
We will take the limit of both sides of (67) as \(\theta\) goes to 0. As \(\lim _{\theta \rightarrow 0}\theta _\star (r,\theta )=0\), uniformly in r,
Using the substitution \(s=\frac{\sin \theta '}{\sin \theta _\star }\),
with \(\cos \theta '=\sqrt{1-s^2\sin ^2\theta _\star }\). The last integrand converges uniformly to
as \(\theta\) goes to zero. Thus, we get
So, from (67) we conclude that
We know that the right-hand side of this equality is positive because we guaranteed that (32) holds. And the right-hand side is obviously smaller than \(\frac{\pi }{2}\). Therefore, we have
This is strictly greater than 1 (and goes to 1 as \(r\nearrow r_+\)). According to (6) and (15), the derivative of the map \((r,\theta )\mapsto (r_\star ,\theta _\star )\) at (r, 0) is represented by the matrix
Equality (66) follows. \(\square\)
Regularity of functions at the poles. Using the change of coordinates (64), the variable \(\theta _\star\) is written in terms of x and y as
Given a function f that transforms pairs \((r_\star ,\theta _\star )\), we want to study the differentiability of
Remark 2.19
Let \(f:(-\infty ,+\infty )\times \left[ 0,\pi \right] \rightarrow {{\mathbb {R}}}\) be \(C^1\) such that \(\frac{1}{\sin (2\theta _\star )}\left( \partial _{\theta _\star }f\right)\) has a limit when \(\theta _\star =0\). Then \(\hat{f}\) is \(C^1\).
Proof
The derivative of \(\hat{f}\) with respect to x is
We observe that, although the map \((x,y)\mapsto \sqrt{x^2+y^2}\) is not differentiable at the origin, when \(x=y=0\) the quotient \(\frac{x}{\sqrt{x^2+y^2}}\) in (68) is \(+1\) or \(-1\), according to the calculation of a right or a left derivative. If we assume that \(\frac{1}{\sin (2\theta _\star )}\left( \partial _{\theta _\star }f\right)\) has a limit at \(((r_\star )_0,0)\), then \(\partial _{\theta _\star }f((r_\star )_0,0)=0\), so there is no indetermination in (68), and
The function \(\hat{f}\) has continuous partial derivatives with respect to \(r_\star\), x and y in a neighborhood of each point \(((r_\star )_0,0,0)\), and so it is differentiable. \(\square\)
Note that we can write (68) as
(This is the derivative of f with respect to \(\sin ^2\theta _\star =x^2+y^2\) multiplied by the derivative of \(\sin ^2\theta _\star\) with respect to x.) Expression (69) shows that if the quotient \(\frac{1}{\sin (2\theta _\star )}\left( \partial _{\theta _\star }f\right)\) were unbounded, then one might have problems with the differentiability when \((x,y)=(0,0)\). For example, if this quotient were to behave like \(\frac{1}{\sin \theta _\star }\) around \(((r_\star )_0,0)\), then \(\partial _x\hat{f}\) would behave like \(\cos \phi _\star\), so that \(\partial _x\hat{f}((r_\star )_0,0,0)\) would not exist.
Remark 2.20
Let \(f:(-\infty ,+\infty )\times \left[ 0,\pi \right] \rightarrow {{\mathbb {R}}}\) be \(C^\infty\) in the sense of Remark 2.12. Then \(\hat{f}\) is \(C^\infty\).
Proof
It is clear that \(\partial _{r_\star }^2\hat{f}\), \(\partial _x\partial _{r_\star }\hat{f}\) and \(\partial _y\partial _{r_\star }\hat{f}\) are continuous. The continuity of \(\partial _x^2\hat{f}\) is a consequence of
The continuity of \(\partial _x\partial _y\hat{f}\) and \(\partial _y^2\hat{f}\) follow in the same way. So \(\hat{f}\) is \(C^2\). One proves by induction that \(\hat{f}\) is \(C^\infty\). \(\square\)
Remark 2.21
A differentiable function such that \(f(r_\star ,\theta _\star ) =f(r_\star ,\pi -\theta _\star )\) satisfies \(\partial _{\theta _\star }f\left( r_\star ,\frac{\pi }{2}\right) =0\). The quotient \(\frac{1}{\sin (2\theta _\star )}\partial _{\theta _\star }f\) has a finite limit at \(\left( r_\star ,\frac{\pi }{2}\right)\), provided that the numerator is analytic.
Indeed, both the numerator and the denominator vanish at \(\left( r_\star ,\frac{\pi }{2}\right)\) and the denominator has a first order zero there.
Remark 2.22
Suppose that \(f:(-\infty ,+\infty )\times [0,\pi ]\times S^1\rightarrow {{\mathbb {R}}}\) is smooth and define
where \(\phi _\star =\arg (x+iy)=\arctan \frac{y}{x}\) for \(x>0\), and otherwise \(\arg (x+iy)\) is \(\arctan \frac{y}{x}\) with an appropriate constant added. Then
Regularity of the change of coordinates \((t,r,\theta ,\phi )\mapsto (t,r_\star ,\theta _\star ,\phi )\). Define
-
(i)
The map \((t,r_\star ,\hat{x},\hat{y})\mapsto (t,r,\tilde{x},\tilde{y})\) is smooth. The derivative \(\partial _{r_\star }r\) is given by (39). Moreover, using (69), we get
$$\begin{aligned} \partial _{\hat{x}} r& = 2{\hat{x}} \frac{1}{\sin (2\hat{\theta }_\star )} \partial _{\theta _\star }r\quad (\hbox {see}~(40)\ \hbox {for}\ \partial _{\theta _\star }r),\\ \partial _{\hat{y}} r& = 2{\hat{y}} \frac{1}{\sin (2\hat{\theta }_\star )} \partial _{\theta _\star }r,\\ \partial _{r_\star }\sin \theta& = \cos \theta \frac{\partial \theta }{\partial r_\star }\ =\ 2\frac{\sin (2\hat{\theta }_\star )}{\sin (2\theta )}\sin \theta \cos ^2\theta \left( \frac{1}{\sin (2\hat{\theta }_\star )}\partial _{r_\star }\theta \right) \quad (\hbox {see}~(41)\ \hbox {for}\ \partial _{r_\star }\theta ). \end{aligned}$$Applying Remark 2.22, we obtain
$$\begin{aligned} \partial _{\hat{x}}\tilde{x}& = \frac{\cos \theta }{\cos \theta _\star }\cos ^2\phi \, \partial _{\theta _\star }\theta +\frac{\sin \theta }{\sin \theta _\star }\sin ^2\phi ,\\ \partial _{\hat{y}}\tilde{x}& = \frac{\cos \theta }{\cos \theta _\star }\sin \phi \cos \phi \, \partial _{\theta _\star }\theta -\, \frac{\sin \theta }{\sin \theta _\star }\sin \phi \cos \phi ,\\ \partial _{\hat{x}}\tilde{y}& = \frac{\cos \theta }{\cos \theta _\star }\sin \phi \cos \phi \, \partial _{\theta _\star }\theta -\, \frac{\sin \theta }{\sin \theta _\star }\sin \phi \cos \phi ,\\ \partial _{\hat{y}}\tilde{y}& = \frac{\cos \theta }{\cos \theta _\star }\sin ^2\phi \, \partial _{\theta _\star }\theta + \frac{\sin \theta }{\sin \theta _\star }\cos ^2\phi . \end{aligned}$$Notice that when \(\theta =0\), we have
$$\begin{aligned} \partial _{\hat{x}}\tilde{x}& = \partial _{\theta _\star }\theta ,\\ \partial _{\hat{y}}\tilde{x}& = 0,\\ \partial _{\hat{x}}\tilde{y}& = 0,\\ \partial _{\hat{y}}\tilde{y}& = \partial _{\theta _\star }\theta . \end{aligned}$$The quotient \(\frac{\cos \theta }{\cos \theta _\star }\) is smooth because
$$\begin{aligned} \frac{1}{\sin (2\theta _\star )}\partial _{\theta _\star }\left( \frac{\cos \theta }{\cos \theta _\star }\right) = -\,\frac{1}{2}\frac{\sin (2\theta )}{\sin (2\theta _\star )} \frac{\cos \theta _\star }{\cos \theta }\frac{\partial \theta }{\partial \theta _\star } +\frac{1}{2}\frac{\cos \theta }{\cos \theta _\star }\frac{1}{\cos ^2\theta _\star }. \end{aligned}$$(70)The quotient \(\frac{\sin \theta }{\sin \theta _\star }\) is smooth because
$$\begin{aligned} \frac{\sin \theta }{\sin \theta _\star }=\frac{\sin (2\theta )}{\sin (2\theta _\star )} \frac{\cos \theta _\star }{\cos \theta }. \end{aligned}$$Thus r, \(\tilde{x}\) and \(\tilde{y}\) are \(C^\infty\) functions of \(r_\star\), \(\hat{x}\) and \(\hat{y}\).
-
(ii)
The map \((t,r,\tilde{x},\tilde{y})\mapsto (t,r_\star ,\hat{x},\hat{y})\) is smooth. Recall that \(\partial _rr_\star\) is given in (6), and
$$\begin{aligned} \partial _r\sin \theta _\star =\cos \theta _\star \partial _r\theta _\star =\cos \theta _\star \frac{1}{GQ}= 2\frac{\sin (2\theta )}{\sin (2\theta _\star )}\sin \theta _\star \cos ^2\theta _\star \left( \frac{1}{\sin (2\theta )}\frac{1}{GQ} \right) , \end{aligned}$$as \(\partial _r\theta _\star\) is given in (15). Inequalities (38) yield
$$\begin{aligned} \lim _{\theta \rightarrow 0}\frac{1}{G(r,\theta ,\theta _\star (r,\theta ))}=0. \end{aligned}$$One other consequence of (6) and (15) is
$$\begin{aligned} \partial _{\tilde{x}}r_\star& = 2\tilde{x}\frac{1}{\sin (2\theta )}\partial _\theta r_\star \ =\ 2a\tilde{x}\frac{\sqrt{\sin ^2\theta _\star \Delta _\theta -\sin ^2\theta }}{\Delta _\theta \sin (2\theta )},\\ \partial _{\tilde{y}}r_\star& = 2\tilde{y}\frac{1}{\sin (2\theta )}\partial _\theta r_\star \ =\ 2a\tilde{y}\frac{\sqrt{\sin ^2\theta _\star \Delta _\theta -\sin ^2\theta }}{\Delta _\theta \sin (2\theta )}. \end{aligned}$$The formulas for \(\partial _{\tilde{x}}\hat{x}\), \(\partial _{\tilde{y}}\hat{x}\), \(\partial _{\tilde{x}}\hat{y}\) and \(\partial _{\tilde{y}}\hat{y}\), are similar to the ones for \(\partial _{\hat{x}}\tilde{x}\), \(\partial _{\hat{y}}\tilde{x}\), \(\partial _{\hat{x}}\tilde{y}\) and \(\partial _{\hat{y}}\tilde{y}\) (interchange \(\theta\) and \(\theta _\star\)). Recall that \(\partial _\theta \theta _\star =-\,\frac{1}{GP}\). It follows that \(r_\star\), \(\hat{x}\) and \(\hat{y}\) are \(C^\infty\) functions of r, \(\tilde{x}\) and \(\tilde{y}\).
Regularity of the change of coordinates \((t,r_\star ,\theta _\star ,\phi )\mapsto (t,r_\star ,\theta _\star ,\phi _\star )\). Recall that
The fact that both \((t,r_\star ,\theta _\star ,\phi )\mapsto (t,r_\star ,\theta _\star ,\phi _\star )\) and \((t,r_\star ,\theta _\star ,\phi _\star )\mapsto (t,r_\star ,\theta _\star ,\phi )\) are \(C^\infty\) is a simple consequence of (18), which gives \(\partial _{r_\star }h\), and Lemma 2.15, which gives \(\frac{1}{\sin (2\theta _\star )}\partial _{\theta _\star }h\).
We remark that
Hence, the differentiability of \((t,r_\star ,x,y)\mapsto (t,r_\star ,\hat{x},\hat{y})\) follows from
Note that these are smooth functions and that at \(\theta _\star =0\) they are independent of \(\phi\) and \(\phi _\star\). The differentiability of \((t,r_\star ,\hat{x},\hat{y})\mapsto (t,r_\star ,x,y)\) follows in a similar way.
Regularity of the spheres given by the intersection of hypersurfaces \(u=\hbox {constant}\) and \(v=\hbox {constant}\).
It is obvious that the two atlases \(\{(t,r_\star ,\theta _\star ,\phi _\star ),(t,r_\star ,x,y)\}\) and \(\mathcal{A}_{\tiny \hbox { DN}}=\{(u,v,\theta _\star ,\phi _\star ),(u,v,x,y)\}\) are compatible. So, combining the conclusions of the previous paragraphs, the two atlases \(\mathcal{A}_{\tiny \hbox { BL}}=\{(t,r,\theta ,\phi ),(t,r,\tilde{x},\tilde{y})\}\) and \(\mathcal{A}_{\tiny \hbox { DN}}\) are compatible. The spheres given by the intersection of hypersurfaces \(u=\hbox {constant}\) and \(v=\hbox {constant}\) are smooth in the atlas \(\mathcal{A}_{\tiny \hbox { DN}}\) by definition. Therefore, they are smooth in the atlas \(\mathcal{A}_{\tiny \hbox { BL}}\). This proves
Theorem 2.23
The topological two-spheres given by the intersection of hypersurfaces \(u=\hbox {constant}\) and \(v=\hbox {constant}\) are \(C^\infty\) in the Boyer–Lindquist coordinates.
2.3 Coordinates at the horizons
2.3.1 The decay of \(\Omega ^2\) at the horizons
Recall that the surface gravities of the horizons are given by
(confirm the formula for \(\kappa _-\) with Example A.3).
Lemma 2.24
Given \(C_R\in {{\mathbb {R}}}\), there exist \(c,C>0\) such that
Proof
The formula
shows that \(\frac{\partial r}{\partial r_{\star }}(r=r_-,\theta )=0\). To write the linear approximation for this function, we start by calculating
Hence, we get
According to Remark 2.1, there exists \(C > 0\) and \((r_\star )_0\) such that for \(r_\star \ge (r_\star )_0\) we have
So, for \(r\ge (r_\star )_0\) we obtain
Remembering that \(\kappa _-<0\), it follows that
Integrating from \((r_{\star })_0\) to \(r_\star\) yields
These inequalities can be rearranged to
This shows that there exists \(D > 0\) and \((r_\star )_0\) such that
for \(r_\star \ge (r_\star )_0\). Thus, there exist \(c,C>0\), such that \(r_\star \ge (r_\star )_0\) implies
Let \(C_R\) be a real number. Decreasing c and increasing C if necessary, one sees that
for \(C_R\le r_\star \le (r_\star )_0\). Combining the previous two inequalities, they hold for \(r_\star \ge C_R\). Moreover, in this region,
for other appropriate constants \(c,C>0\). Hence, given \(C_R\in {{\mathbb {R}}}\), there exist \(c,C>0\) such that
for \(r_\star \ge C_R\). As \(\Omega ^2\) is comparable to \(|\Delta _r|\), we conclude that \(\Omega ^2\) is comparable to \(e^{2\kappa _-r_\star }\) in the region \(r_\star \ge C_R\). This proves (74). The proof of (75) is analogous. \(\square\)
Remark 2.25
The function \(\Omega ^2\) given in (19) is obviously smooth on the spheres where u and v are simultaneously constant.
2.3.2 Coordinates at the Cauchy horizon
Let us recall how one may define coordinates to cover the Cauchy horizon. We consider a new smooth coordinate \(v_{{\tiny \mathcal{C}\mathcal{H}^+}}(v)\), with positive derivative, equal to v for \(v\le -1\), satisfying \(v_{{\tiny \mathcal{C}\mathcal{H}^+}}\rightarrow 0\) as \(v\rightarrow +\infty\), and satisfying
for \(v\ge 0\). Moreover, we define
Remark 2.26
\(v_{{\tiny \mathcal{C}\mathcal{H}^+}}\) is also a smooth function of v, and so the change of coordinates \((v,\phi _{\star })\leftrightarrow (v_{{\tiny \mathcal{C}\mathcal{H}^+}},\phi _{\star ,\mathcal{C}\mathcal{H}^+})\) is smooth.
From (20), we see that
For \(v\ge 0\), the differentials of \(\phi _\star\) and \(\phi _{\star ,\mathcal{C}\mathcal{H}^+}\) are related by
For \(v\ge 0\), the expression of the metric (21) in the new coordinates is
with
Henceforth we will assume that we are working in the region \(v\ge 0\), our formulas will always refer to this region. To estimate \(b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\) we calculate
Using (12) and (76), we estimate
for \(u+v\ge C_R\). Thus, inequalities (74) implies the following bounds for \(\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}\) and \(b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\), when \(u+v\ge C_R\):
For a general function f, we have
where \(\tilde{f}\) is the function f written in the coordinates \((u,\tilde{v},\theta _{\star },\phi _{\star ,\mathcal{C}\mathcal{H}^+})\) and \({\tilde{v}}=v\). So
We define
This, (77) and \(\partial _{\phi _{\star }}=\partial _{\phi _{\star ,\mathcal{C}\mathcal{H}^+}}\) imply that
We can write the vector field \(\partial _t\) using the coordinates at the Cauchy horizon as
The vector field \(\partial _t\) is not null on the Cauchy horizon. A Killing vector field which is null on the Cauchy horizon is
2.3.3 Coordinates at the event horizon
We consider a new smooth coordinate \(u_{\mathcal{H}^+}(u)\), with positive derivative, equal to u for \(u\ge 1\), satisfying \(u_{\mathcal{H}^+}\rightarrow 0\) as \(u\rightarrow -\infty\), and satisfying
for \(u\le 0\). Moreover, we define \(v_{\mathcal{H}^+}=v\) and
Remark 2.27
\(u_{\mathcal{H}^+}\) is also a smooth function of u, and the change of coordinates \((v,\phi _{\star })\leftrightarrow (v_{\mathcal{H}^+},\phi _{\star ,\mathcal{H}^+})\) is smooth.
Note that
For \(u\le 0\), we may write the metric as
with
Henceforth we will assume that we are working in the region \(u\le 0\), our formulas will always refer to this region. For a general function f, we have
where \(\tilde{f}\) is the function f written in the coordinates \((u_{\mathcal{H}^+},v_{\mathcal{H}^+},\theta _{\star },\phi _{\star ,\mathcal{H}^+})\). So, defining
we get
This, (77) and \(\partial _{\phi _{\star }}=\partial _{\phi _{\star ,\mathcal{H}^+}}\) imply that
A Killing vector field which is null on the event horizon is
The value
is the angular velocity \(\Omega _H\) on the event horizon.
3 The energy of the solutions of the wave equation
We will use the vector field method to study the energy of solutions of the wave equation which have compact support on \(\mathcal{H}^+\). As is well known, the method, used by Morawetz [26], John [20], Klainerman [21, 22], Dafermos [8,9,10,11,12] and Rodnianski [11, 22], among many others, consists in applying the Divergence Theorem to some currents obtained by contracting the energy-momentum tensor \(T_{\mu \nu }\) with appropriate vector field multipliers constructed specifically according to each region of spacetime.
We refer to the region close to the Cauchy horizon as the blue-shift region, and the region close to the event horizon as the red-shift region. We call the intermediate region the no-shift region. A very general construction of red-shift vector fields on general spacetimes which contain Killing horizons with positive surface gravity is carried out in the lecture notes [11]. Here we perform the computations explicitly in double null coordinates.
The blue-shift vector field (85) is constructed using the vector field Y in Lemma 3.1, and the red-shift vector field (96) is constructed using the vector field V in Lemma 3.2. We go on to calculate the covariant derivative of Y, \(\nabla ^\mu Y^\nu\), and the scalar current associated to Y, \(T_{\mu \nu }\nabla ^\mu Y^\nu\). We obtain the usual inequalities for the currents associated to the blue-shift vector field, and for the currents associated to the red-shift vector field. We finish with Theorem 3.5, which is Sbierski’s result, for the Reissner–Nordström and Kerr spacetimes, applied to Kerr–Newman–de Sitter spacetimes.
3.1 The blue-shift and red-shift vector fields
3.1.1 Construction
Here the blue-shift vector field is defined to be
where Y is given in
Lemma 3.1
Let \(\iota \in {{\mathbb {R}}}^+\) be given. The initial value problem
(Z as in (81)) has a unique time invariant solution, Y, defined in a neighborhood of the Cauchy horizon, i.e. defined for \(r_\star\) sufficiently large.
Proof
- (a):
-
(Y time invariant.) The vector field \({\textstyle \frac{1}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}} \left( \partial _{v_{{\tiny \mathcal{C}\mathcal{H}^+}}}\!\!+b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\partial _{\phi _\star }\right)\) commutes with \(\partial _t\). In fact, we have
$$\begin{aligned} \left[ \partial _t,\frac{1}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}\partial _{v_{{\tiny \mathcal{C}\mathcal{H}^+}}}\right] = \left[ \partial _t,\frac{1}{\Omega ^2}\partial _{\tilde{v}}\right] =\frac{1}{\Omega ^2}\left[ \frac{1}{2}\partial _v-\,\frac{1}{2}\partial _u, \left( \partial _v+b^{\phi _{\star }}|_{r=r_-}\partial _{\phi _\star }\right) \right] =0 \end{aligned}$$and
$$\begin{aligned} \frac{b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}=\frac{b^{\phi _{\star }}-b^{\phi _{\star }}|_{r=r_-}}{\Omega ^2} \ \Rightarrow \ \left[ \partial _t,\frac{b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}\partial _{\phi _\star }\right] =0. \end{aligned}$$So, any Y of the form
$$\begin{aligned} Y& = \tilde{f}\partial _u+\tilde{g}{\textstyle \frac{1}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}} \left( \partial _{v_{{\tiny \mathcal{C}\mathcal{H}^+}}}\!\!+b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\partial _{\phi _\star }\right) +\tilde{h}\partial _{\theta _\star }+\tilde{{\jmath }}\partial _{\phi _\star }, \end{aligned}$$with
$$\begin{aligned} \tilde{f}=\tilde{f}(r,\theta ),\ \tilde{g}=\tilde{g}(r,\theta ),\ \tilde{h}=\tilde{h}(r,\theta ),\ \tilde{{\jmath }}=\tilde{{\jmath }}(r,\theta ), \end{aligned}$$commutes with \(\partial _t\).
- (b):
-
(The differential equation.) Expanding the left-hand side of (86), we get
$$\begin{aligned} \nabla _YY& = \tilde{f}\partial _{r_\star }\tilde{f}\partial _u+\tilde{f}\partial _{r_\star }\tilde{g}{\textstyle \frac{1}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}} \left( \partial _{v_{{\tiny \mathcal{C}\mathcal{H}^+}}}\!\!+b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\partial _{\phi _\star }\right) +\tilde{f}\partial _{r_\star }\tilde{h}\partial _{\theta _\star }+\tilde{f}\partial _{r_\star }\tilde{{\jmath }}\partial _{\phi _\star }\\{} & {} +\tilde{f}^2\nabla _{\partial _u}\partial _u+\tilde{f}\tilde{g}\nabla _{\partial _u}{\textstyle \frac{1}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}} \left( \partial _{v_{{\tiny \mathcal{C}\mathcal{H}^+}}}\!\!+b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\partial _{\phi _\star }\right) +\tilde{f}\tilde{h}\nabla _{\partial _u}\partial _{\theta _\star }+\tilde{f}\tilde{{\jmath }}\nabla _{\partial _u}\partial _{\phi _\star }\\{} & {} +\tilde{g}\frac{\sigma }{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}\partial _{r_\star }\tilde{f}\partial _u+\tilde{g}\frac{\sigma }{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}\partial _{r_\star }\tilde{g}{\textstyle \frac{1}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}} \left( \partial _{v_{{\tiny \mathcal{C}\mathcal{H}^+}}}\!\!+b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\partial _{\phi _\star }\right) +\tilde{g}\frac{\sigma }{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}\partial _{r_\star }\tilde{h}\partial _{\theta _\star }\\{} & {} +\tilde{g}\frac{\sigma }{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}\partial _{r_\star }\tilde{{\jmath }}\partial _{\phi _\star }\\{} & {} +\tilde{f}\tilde{g}\nabla _{{\textstyle \frac{1}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}} \left( \partial _{v_{{\tiny \mathcal{C}\mathcal{H}^+}}}\!\!+b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\partial _{\phi _\star }\right) }\partial _u+\tilde{g}\tilde{h}\nabla _{{\textstyle \frac{1}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}} \left( \partial _{v_{{\tiny \mathcal{C}\mathcal{H}^+}}}\!\!+b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\partial _{\phi _\star }\right) }\partial _{\theta _\star }\\{} & {} +\tilde{g}\tilde{{\jmath }}\nabla _{{\textstyle \frac{1}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}} \left( \partial _{v_{{\tiny \mathcal{C}\mathcal{H}^+}}}\!\!+b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\partial _{\phi _\star }\right) }\partial _{\phi _\star }\\{} & {} +\tilde{h}\partial _{\theta _\star }\tilde{f}\partial _u+\tilde{h}\partial _{\theta _\star }\tilde{g}{\textstyle \frac{1}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}} \left( \partial _{v_{{\tiny \mathcal{C}\mathcal{H}^+}}}\!\!+b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\partial _{\phi _\star }\right) +\tilde{h}\partial _{\theta _\star }\tilde{h}\partial _{\theta _\star }+\tilde{h}\partial _{\theta _\star }\tilde{{\jmath }}\partial _{\phi _\star }\\{} & {} +\tilde{f}\tilde{h}\nabla _{\partial _{\theta _\star }}\partial _u+\tilde{g}\tilde{h}\nabla _{\partial _{\theta _\star }}{\textstyle \frac{1}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}} \left( \partial _{v_{{\tiny \mathcal{C}\mathcal{H}^+}}}\!\!+b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\partial _{\phi _\star }\right) +\tilde{h}^2\nabla _{\partial _{\theta _\star }}\partial _{\theta _\star }+\tilde{h}\tilde{{\jmath }}\nabla _{\partial _{\theta _\star }}\partial _{\phi _\star }\\{} & {} +\tilde{f}\tilde{{\jmath }}\nabla _{\partial _{\phi _\star }}\partial _u+\tilde{g}\tilde{{\jmath }}\nabla _{\partial _{\phi _\star }}{\textstyle \frac{1}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}} \left( \partial _{v_{{\tiny \mathcal{C}\mathcal{H}^+}}}\!\!+b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\partial _{\phi _\star }\right) +\tilde{h}\tilde{{\jmath }}\nabla _{\partial _{\phi _\star }}\partial _{\theta _\star }+\tilde{{\jmath }}^2\nabla _{\partial _{\phi _\star }}\partial _{\phi _\star }. \end{aligned}$$We used (109) to eliminate the term in \(\tilde{g}^2\). This initial value problem (86), (87) is equivalent to a system of four equations, for the \(\partial _u\), \({\textstyle \frac{1}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}} \left( \partial _{v_{{\tiny \mathcal{C}\mathcal{H}^+}}}\!\!+b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\partial _{\phi _\star }\right)\), \(\partial _{\theta _\star }\) and \(\partial _{\phi _\star }\) components of each side, for the four unknowns \(\tilde{f}\), \(\tilde{g}\), \(\tilde{h}\) and \(\tilde{{\jmath }}\), with
$$\begin{aligned} \tilde{f}(r_-,\theta )=0,\quad \tilde{g}(r_-,\theta )=1,\quad \tilde{h}(r_-,\theta )=0,\quad \tilde{{\jmath }}(r_-,\theta )=0. \end{aligned}$$(88)The system reads
$$\begin{aligned} \tilde{f}\partial _{r_\star }\tilde{f}+\tilde{g}\frac{\sigma }{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}\partial _{r_\star }\tilde{f}+\tilde{h}\partial _{\theta _\star }\tilde{f}& = \ldots ,\\ \tilde{f}\partial _{r_\star }\tilde{g}+\tilde{g}\frac{\sigma }{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}\partial _{r_\star }\tilde{g}+\tilde{h}\partial _{\theta _\star }\tilde{g}& = \ldots ,\\ \tilde{f}\partial _{r_\star }\tilde{h}+\tilde{g}\frac{\sigma }{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}\partial _{r_\star }\tilde{h}+\tilde{h}\partial _{\theta _\star }\tilde{h}& = \ldots ,\\ \tilde{f}\partial _{r_\star }\tilde{{\jmath }}+\tilde{g}\frac{\sigma }{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}\partial _{r_\star }\tilde{{\jmath }}+\tilde{h}\partial _{\theta _\star }\tilde{{\jmath }}& = \ldots , \end{aligned}$$where the right-hand sides involve the Christoffel symbols of the metric, \(\partial _{r_\star }b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\), \(\partial _{\theta _\star }b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\), and \(\tilde{f}\), \(\tilde{g}\), \(\tilde{h}\) and \(\tilde{{\jmath }}\), but do not involve any derivatives of these last four functions. The system may be written as
$$\begin{aligned} \mathcal{V}\cdot \tilde{f}& = \ldots ,\end{aligned}$$(89)$$\begin{aligned} \mathcal{V}\cdot \tilde{g}& = \ldots ,\end{aligned}$$(90)$$\begin{aligned} \mathcal{V}\cdot \tilde{h}& = \ldots ,\end{aligned}$$(91)$$\begin{aligned} \mathcal{V}\cdot \,\tilde{{\jmath }}& = \ldots , \end{aligned}$$(92)where
$$\begin{aligned}{} & {} \mathcal{V}= \left( \left( \frac{1}{\Delta _r}\frac{\partial r}{\partial r_\star }\right) \left( \tilde{f}\Delta _r+\tilde{g}\left( -\,\frac{\Upsilon }{\rho ^2\Delta _\theta }\right) \right) +\tilde{h}\frac{\partial r}{\partial \theta _\star }\right) \frac{\partial }{\partial r}+\\{} & {} \quad \left( \left( \frac{1}{\Delta _r}\frac{\partial \theta }{\partial r_\star }\right) \left( \tilde{f}\Delta _r+\tilde{g}\left( -\,\frac{\Upsilon }{\rho ^2\Delta _\theta }\right) \right) +\tilde{h}\frac{\partial \theta }{\partial \theta _\star }\right) \frac{\partial }{\partial \theta }. \end{aligned}$$We used
$$\begin{aligned} \frac{\sigma \Delta _r}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}=-\,\frac{\Upsilon }{\rho ^2\Delta _\theta }, \end{aligned}$$ - (c):
-
(An auxiliary calculation.) In the next step we will use the following identity. We mention that it implies that \(\tilde{h}\) is not identically equal to zero. Using (111) and (112), we have
$$\begin{aligned}{} & {} {\,\textrm{d}}\theta _\star \left( \nabla _{\partial _u}{\textstyle \frac{1}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}} \left( \partial _{v_{{\tiny \mathcal{C}\mathcal{H}^+}}}\!\!+b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\partial _{\phi _\star }\right) +\nabla _{{\textstyle \frac{1}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}} \left( \partial _{v_{{\tiny \mathcal{C}\mathcal{H}^+}}}\!\!+b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\partial _{\phi _\star }\right) }\partial _u\right) =2{g \hspace{-4.83322pt}/}^{\theta _\star \theta _\star }\frac{\partial _{\theta _\star }(\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}})}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}. \end{aligned}$$(93) - (d):
-
(The characteristics do not cross the boundary.) We now check that
$$\begin{aligned} \tilde{h}(r,0)=0\qquad \hbox {and}\qquad \tilde{h}\left( r,\frac{\pi }{2}\right) =0. \end{aligned}$$(94)This implies
$$\begin{aligned} \mathcal{V}^\theta (r,0)=0\qquad \hbox {and}\qquad \mathcal{V}^\theta \left( r,\frac{\pi }{2}\right) =0, \end{aligned}$$(95)and guarantees that the characteristics of our differential equations do not leave the region, \([r_-,r_+]\times \left[ 0,\frac{\pi }{2}\right]\), where we want to solve our system. It also guarantees that Y is well defined when \(\theta =0\), notwithstanding \(\partial _{\theta _\star }\) not being well defined when \(\theta =0\). The vanishing of \(\tilde{h}\) at \(\theta =\frac{\pi }{2}\) can also be seen as a consequence of the symmetry of our problem under the reflection \(\theta \mapsto \pi -\theta\), which implies that Y should not have any component in the \(\partial _{\theta _\star }\) direction at the equators of the spheres where u and v are both constant. The right hand side of (91) consists of a sum of terms which we divide into two parts. The first part consists of sum of the eight summands that have \(\tilde{h}\) as a factor. The term
$$\begin{aligned} {\,\textrm{d}}\theta _\star (-\iota (Y+Z))=-\iota {\,\textrm{d}}\theta _\star (Y) =-\iota \tilde{h} \end{aligned}$$is proportional to \(\tilde{h}\). The second part consists of the sum of the remaining eight summands, which are \({\,\textrm{d}}\theta _\star\) applied to
$$\begin{aligned}{} & {} -\tilde{f}^2\nabla _{\partial _u}\partial _u-\tilde{f}\tilde{g}\nabla _{\partial _u}{\textstyle \frac{1}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}} \left( \partial _{v_{{\tiny \mathcal{C}\mathcal{H}^+}}}\!\!+b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\partial _{\phi _\star }\right) -2\tilde{f}\tilde{{\jmath }}\nabla _{\partial _u}\partial _{\phi _\star }\\{} & {} -\tilde{f}\tilde{g}\nabla _{{\textstyle \frac{1}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}} \left( \partial _{v_{{\tiny \mathcal{C}\mathcal{H}^+}}}\!\!+b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\partial _{\phi _\star }\right) }\partial _u-2\tilde{g}\tilde{{\jmath }}\nabla _{{\textstyle \frac{1}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}} \left( \partial _{v_{{\tiny \mathcal{C}\mathcal{H}^+}}}\!\!+b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\partial _{\phi _\star }\right) }\partial _{\phi _\star }-\tilde{{\jmath }}^2\nabla _{\partial _{\phi _\star }}\partial _{\phi _\star }. \end{aligned}$$Taking into account (93), the second part is
$$\begin{aligned}{} & {} -\tilde{f}^2\Gamma _{uu}^{\theta _\star }-4\tilde{f}\tilde{g}\frac{{g \hspace{-4.83322pt}/}^{\theta _\star \theta _\star }}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}}\partial _{\theta _\star }(\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}})-2\tilde{f}\tilde{{\jmath }}\Gamma _{u\phi _{\star ,\mathcal{C}\mathcal{H}^+}}^{\theta _\star }\\{} & {} -2\tilde{g}\tilde{{\jmath }}\frac{1}{\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}} \left( \Gamma _{v_{{\tiny \mathcal{C}\mathcal{H}^+}}\phi _{\star ,\mathcal{C}\mathcal{H}^+}}^{\theta _\star }+b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\Gamma _{\phi _{\star ,\mathcal{C}\mathcal{H}^+}\phi _{\star ,\mathcal{C}\mathcal{H}^+}}^{\theta _\star }\right) -\tilde{{\jmath }}^2\Gamma _{\phi _{\star ,\mathcal{C}\mathcal{H}^+}\phi _{\star ,\mathcal{C}\mathcal{H}^+}}^{\theta _\star }. \end{aligned}$$At \(\theta _\star =0\) and at \(\theta _\star =\frac{\pi }{2}\) this sum is zero because each of the terms is equal to zero. Indeed, all terms are a product of a differentiable function by \(\sin (2\theta _\star )\). This is easy to check. Let us exemplify this assertion with one of the less immediate terms to analyze, the one which contains
$$\begin{aligned} \Gamma _{u\phi _{\star ,\mathcal{C}\mathcal{H}^+}}^{\theta _\star }= \frac{{g \hspace{-4.83322pt}/}^{\theta _\star \theta _\star }}{2} \partial _{r_\star }{g \hspace{-4.83322pt}/}_{\theta _\star \phi _\star } +\frac{{g \hspace{-4.83322pt}/}^{\theta _\star \phi _\star }}{2} \partial _{r_\star }{g \hspace{-4.83322pt}/}_{\phi _\star \phi _\star } \end{aligned}$$(see (106)). Since both \({g \hspace{-4.83322pt}/}_{\theta _\star \phi _\star }\) and \({g \hspace{-4.83322pt}/}^{\theta _\star \phi _\star }\) contain \(\sin (2\theta _\star )\), so does this Christoffel symbol. Let us examine in more detail (91) for points (r, 0) and \(\left( r,\frac{\pi }{2}\right)\). Since \(\partial _{r_\star }\theta\) also contains a factor \(\sin (2\theta _\star )\), over these two segments, \([r_-,r_+)\times \{0\}\) and \([r_-,r_+)\times \{\frac{\pi }{2}\}\), (91) reads
$$\begin{aligned} \mathcal{V}^r\partial _r\tilde{h}=-\tilde{h}\frac{\partial \theta }{\partial \theta _\star }\frac{\partial \tilde{h}}{\partial \theta }+\tilde{h}\times \hbox {smooth function}=\tilde{h}\times \hbox {smooth function}. \end{aligned}$$As
$$\begin{aligned} \tilde{h}(r_-,0)=0\qquad \hbox {and}\qquad \tilde{h}\left( r_-,\frac{\pi }{2}\right) =0 \end{aligned}$$and \(\mathcal{V}^r\) is not zero (at least initially at \(r_-\), see below), we conclude that, if there exists a solution to our initial value problem, then it must satisfy (94). Using the fact that \(\partial _{r_\star }\theta\) contains a factor \(\sin (2\theta _\star )\) once again, we obtain (95).
- (e):
-
(Existence and uniqueness of solution.) Using (13) and (39), we have
$$\begin{aligned} \mathcal{V}^r(r_-,\theta )=\left( \frac{1}{\Delta _r}\frac{\partial r}{\partial r_\star }\right) \left( -\,\frac{\Upsilon }{\rho ^2\Delta _\theta }\right) =\frac{1}{(r_-^2+a^2)} \left( -\,\frac{(r_-^2+a^2)^2}{\rho ^2}\right) =-\,\frac{(r_-^2+a^2)}{r_-^2+a^2\cos ^2\theta }. \end{aligned}$$This shows that the segment \(\{r_-\}\times \left[ 0,\frac{\pi }{2}\right]\) is noncharacteristic for our system of four first-order quasilinear partial differential equations. We observe that when the Christoffel symbols \(\Gamma _{v\theta _\star }^{\phi _\star }\) and \(\Gamma _{\theta _\star \phi _\star }^{\phi _\star }\), which blow up at \(\theta _\star =0\) like \(\frac{1}{\sin \theta _\star }\) (see Corollary A.2), appear in the system above, then they appear multiplied by \(\tilde{h}\), which has to vanish to first order at (r, 0). So that the summands where these Christoffel appear are continuous functions. By a standard existence and uniqueness theorem for non characteristic first order quasilinear partial differential equations, we know that our initial value problem has a solution for \((r,\theta )\in [r_-,r_-+\delta ]\times [0,\pi ]\), for some positive \(\delta\). Recall that constructing the solution involves solving the system of ordinary differential equations
$$\begin{aligned} \left\{ \begin{array}{rcl} \dot{r}&{}=&{}\mathcal{V}^r\\ \dot{\theta }&{}=&{}\mathcal{V}^{\theta }\\ \dot{\tilde{f}}&{}=&{}\hbox {right-hand side of}\ (89)\\ \dot{\tilde{g}}&{}=&{}\hbox {right-hand side of}\ (90)\\ \dot{\tilde{h}}&{}=&{}\hbox {right-hand side of}\ (91)\\ \dot{\tilde{{\jmath }}}&{}=&{}\hbox {right-hand side of}\ (92) \end{array} \right. \qquad \hbox {with}\qquad \left\{ \begin{array}{rcl} r(0)&{}=&{}r_-\\ \theta (0)&{}=&{}\theta _0\\ \tilde{f}(0)&{}=&{}0\\ \tilde{g}(0)&{}=&{}1\\ h(0)&{}=&{}0\\ \tilde{{\jmath }}(0)&{}=&{}0 \end{array} \right. . \end{aligned}$$We know from Remark 2.1 that, for \(r_\star\) sufficiently large, r is close to \(r_-\). So we have the existence of a solution for large \(r_\star\).
\(\square\)
Here the red-shift vector field is defined to be
where V is given in
Lemma 3.2
Let \(\iota \in {{\mathbb {R}}}^+\) be given. The initial value problem
(W as in (83)) has a unique time invariant solution, V, defined in a neighborhood of the event horizon, i.e. defined for \(r_\star\) sufficiently negative (i.e. for \(r_\star <-C\) with C sufficiently large).
Proof
Choose V of the form
with
\(\square\)
3.1.2 Covariant derivative
One could consider working in the frame \((Z,Y,\partial _{\theta _\star },\partial _{\phi _\star })\) but this is not a good choice because the energy-momentum tensor does not have a simple expression in this frame. So, instead, we define
and work in the frame
We see that
The dual frame is
Calculation of the covariant derivative of Y.
The covariant derivative of Y is
One readily checks that the metric dual basis to \((\omega _{{\tiny \overline{\texttt {T}}}},\omega _{{\tiny \overline{\texttt {Y}}}},\omega _{\theta _\star },\omega _{\phi _\star })\) is
Using the fact that \(2\overline{T}=\partial _u=\partial _{r_\star }= (\partial _{r_\star }r)\partial _r+(\partial _{r_\star }\theta )\partial _\theta\), (88) and (112), we obtain
where
The values of \(a^{\theta _\star }\) and \(a^{\phi _\star }\) can be read off from (112). Using (86) and the formulas in "Appendix A", we get
where
The factor \(\frac{1}{\sin \theta }\) in front of \(\partial _{\phi _\star }\) in the last summand arises from \(\Gamma _{v\theta _\star }^{\phi _\star }\) and \(\Gamma _{\theta _\star \phi _\star }^{\phi _\star }\). Using the fact that \(\partial _{\theta _\star }= (\partial _{\theta _\star }r)\partial _r +(\partial _{\theta _\star }\theta )\partial _\theta\) and (113), we obtain
The values of \(h^{\ \ \theta _\star }_{\theta _\star }\) and \(h^{\ \ \phi _\star }_{\theta _\star }\) can be read off from (113). Finally, we have
The values of \(h^{\ \ \theta _\star }_{\phi _\star }\) and \(h^{\ \ \phi _\star }_{\phi _\star }\) can be read off from (114). Here
Note that although \(\Gamma _{\theta _\star \phi _\star }^{\phi _\star }\) does contain the factor \(\frac{1}{\sin \theta }\), in the last calculation this Christoffel symbol appears multiplied by \(\tilde{h}\) which vanishes to first order at \(\theta _\star =0\) and \(\theta _\star =\pi\). So, the last equality is a consequence of Lemma A.1 and of the fact that \(\tilde{f}\), \(\tilde{g}\), \(\tilde{h}\) and \(\tilde{{\jmath }}\) do not depend on \(\phi _\star\). Indeed, the components of \(\nabla _{\partial _{\phi _\star }}X_\dagger\) in \(\overline{T}\), \(\overline{Y}\) and \(\partial _{\theta _\star }\) all contain the factor \(\sin \theta\), for \(\dagger \,\in \,\{{ \overline{\texttt {T}}},{ \overline{\texttt {Y}}},\theta _\star ,\phi _\star \}\). The expressions (97)–(100) above correspond to [11, (19)–(22)]. Combining the previous results, we can write the covariant derivative of Y as
We may write the error term as
because \(\omega _{\phi _\star }^\sharp =\partial ^{\phi _\star }\) behaves like \({g \hspace{-4.83322pt}/}^{\phi _\star \phi _\star }\partial _{\phi _\star }\), which in turn behaves like \(\frac{1}{\sin ^2\theta }\partial _{\phi _\star }\).
3.1.3 Currents
3.1.3.1 The energy momentum tensor of a massless scalar field and the vector current
The energy momentum tensor is given by
and one readily checks that
The energy-momentum tensor is written as
The vector currents associated to the blue-shift and red-shift vector fields are
respectively.
3.1.3.2 The scalar current associated to the blue-shift vector field
The scalar current associated to \(N_b\) is \(K^{N_b}=T_{\mu \nu }\nabla ^\mu N_b^\nu\). Since Z is a Killing vector field this is equal to \(K^Y\), which is
We estimate \(K^Y\). Suppose we are given \(\delta \in \bigl (0,\frac{1}{3}\bigr )\). Let \(\overline{c}=2(-\kappa _-)\delta\). Choose \(\iota =c+\overline{c}+1\), where \(c=c_\delta\) is the constant below (which is independent of Y). There exists \(r_0>r_-\) such that \(r\in (r_-,r_0)\) implies that
We have used the fact that
3.1.3.3 Inequalities relating the currents
The blue-shift vector field satisfies
Lemma 3.3
Let \(0<\delta <\frac{1}{3}\). If \((r_\star )_0\) is chosen sufficiently large (see Remark 2.1), then
Proof
Using (27) and (101), we obtain
Using (26), we see that
For each \(0<\delta <\frac{1}{3}\), there exists \(r_0>r_-\) such that \(r\in (r_-,r_0)\) implies that
Multiplying both sides by \(2\kappa _-(1+\delta )/(1-\delta )\), we get
This implies (102) because \(\frac{1+\delta }{1-\delta }<1+3\delta\) and \(-2\kappa _-\delta \frac{1+\delta }{1-\delta }<-4\kappa _-\delta =2\overline{c}\). \(\square\)
Similarly to (102), the red-shift vector field satisfies
Lemma 3.4
Let \(\delta >0\). For \((r_\star )_0\) sufficiently negative (see Remark 2.1), we have
Proof
Work in the frame \((\overline{V},\underline{T},\partial _{\theta _\star },\partial _{\phi _\star })\), with
\(\square\)
3.2 Energy estimates
We are interested in solutions of the wave equation which are regular up to, and including, \(\mathcal{H}^+\), and which have compact support on \(\mathcal{H}^+\), i.e. we are interested in functions belonging to the space
The following theorem, established by Sbierski in his thesis [29] for Reissner–Nordström and Kerr black holes, applies to Kerr–Newman–de Sitter black holes.
Theorem 3.5
Let \(2\kappa _+>-\kappa _-\) and \(\psi \in \mathcal{F}\). Then, for any \(u_0\), \(v_0\in {{\mathbb {R}}}\), we have
Proof
We sketch the proof and refer to [29] for further details.
(a) Estimates in the red-shift region. For \(\kappa <\kappa _+\), define \(\underline{N}_r=e^{2\kappa v}N_r\). Choose the \(\delta\) in (103) such that \(\kappa <\kappa _+(1-\delta )\). Since \(K^{\underline{N}_r}\ge 0\), the Divergence Theorem implies that we have
The left-hand side can be bounded below by
where \(u(u_{\mathcal{H}^+})\) denotes the u corresponding to \(u_{\mathcal{H}^+}\). As \(\psi\) is a regular function on \(\mathcal{H}^+\), we have
We conclude that
(b) Estimates in the no-shift region. We recall [29, Lemma 4.5.6]: Given \((r_\star )_1>(r_\star )_0\) and a smooth future directed timelike time invariant vector field N, there exists a constant \(C>0\) such that
holds for all solutions of the wave equation.
(c) Estimates in the blue-shift region. We also recall [7, Lemma 4.5]: Let \(f:[t_0,\infty [\rightarrow {{\mathbb {R}}}\) and assume that for some \(\alpha _1, C>0\), and for all \(t\ge t_0\),
Then, for all \(0<\alpha _2<\alpha _1\) and \(t\ge t_0\), we have
By assumption \(2\kappa _+>-\kappa _-\). If we choose \(\kappa <\kappa _+\) sufficiently close to \(\kappa _+\) and and \(\overline{\kappa }<\kappa _-\) sufficiently close to \(\kappa _-\), then \(2\kappa >-\overline{\kappa }\). Using (104), (105) and the fact that
are comparable, we conclude that
Define \(\underline{N}_b=e^{-2\overline{\kappa }u}N_b\). Choose the \(\delta\) in (102) such that \(\overline{\kappa }<\kappa _-(1+3\delta )\). Since \(K^{\underline{N}_b}\ge 0\), the Divergence Theorem implies that
This finishes the proof. \(\square\)
This theorem shows that for KNdS black holes, with surface gravities satisfying \(2\kappa _+>-\kappa _-\), the energy of a wave with compact support on \(\mathcal{H}^+\) has finite energy along a null hypersurface intersecting the Cauchy horizon. This suggests that there exists a set of of black hole parameters for which compactly supported perturbations do not lead to mass inflation and to instability of the Cauchy horizon. It is one more step towards understanding the conjectured instability of black hole interiors in the context of KNdS spacetimes.
References
Akcay, S., Matzner, R.A.: The Kerr-de Sitter universe. Class. Quantum Gravity 28(8), 085012 (2011)
Ballik, W., Lake, K.: Vector volume and black holes. Phys. Rev. D 88(10), 104038 (2013)
Balushi, A.A., Mann, R.B.: Null hypersurfaces in Kerr-(A)dS spacetimes. Class. Quantum Gravity 36, 245017 (2019)
Borthwick, J.: Maximal Kerr-de Sitter spacetimes. Class. Quantum Gravity 35(21), 215006 (2018)
Caldarelli, M.M., Cognola, G., Klemm, D.: Thermodynamics of Kerr–Newman–AdS black holes and conformal field theories. Class. Quantum Gravity 17(2), 399–420 (2000)
Carter, B.: Black hole equilibrium states. Black holes/Les astres occlus (École d’Été Phys. Théor., Les Houches, 1972), pp. 57–214. Gordon and Breach, New York (1973)
Costa, J.L., Franzen, A.T.: Bounded energy waves on the black hole interior of Reissner–Nordström-de Sitter. Ann. Henri Poincaré 18(10), 3371–3398 (2017)
Dafermos, M., Holzegel, G., Rodnianski., I.: A scattering theory construction of dynamical vacuum black holes. arXiv:1306.5364 (2013)
Dafermos, M., Luk, J.: The interior of dynamical vacuum black holes I: The \(C^0\)-stability of the Kerr Cauchy horizon (2017). arXiv:1710.01722
Dafermos, M., Rodnianski, I.: The red-shift effect and radiation decay on black hole spacetimes. Commun. Pure Appl. Math. 62(7), 859–919 (2009)
Dafermos, M., Rodnianski, I.: Lectures on black holes and linear waves. Clay Math. Proc. 17, 97–205 (2013)
Dafermos, M., Shlapentokh-Rothman, Y.: Rough initial data and the strength of the blue-shift instability on cosmological black holes with \(\Lambda >0\). Class. Quantum Gravity 35(19), 195010 (2018)
Dolan, B.P., Kastor, D., Kubizňák, D., Mann, R.B., Traschenk, J.: Thermodynamic volumes and isoperimetric inequalities for de Sitter black holes. Phys. Rev. D 87, 104017 (2013)
Franzen, A.T.: Boundedness of massless scalar waves on Kerr interior backgrounds. Ann. Henri Poincaré 21(4), 1045–1111 (2020)
Gibbons, G.W., Yi Pang, Y., Pope, C.N.: Thermodynamics of magnetized Kerr–Newman black holes. Phys. Rev. D 89, 044029 (2014)
Gibbons, G.W., Perry, M.J., Pope, C.N.: The first law of thermodynamics for Kerr-anti-de Sitter black holes. Class. Quantum Gravity 22(9), 1503–1526 (2005)
Hintz, P.: Non-linear stability of the Kerr–Newman–de Sitter family of charged black holes. Ann. PDE 4(1), paper no. 11 (2018)
Hintz, P., Vasy, A.: Analysis of linear waves near the Cauchy horizon of cosmological black holes. J. Math. Phys. 58(8), 081509 (2017)
Imseis, M.T.N., Balushi, A.A., Mann, R.B.: Null hypersurfaces in Kerr–Newman–AdS Black hole and super-entropic black hole spacetimes. Class. Quantum Gravity 38, 045018 (2021)
John, F.: Lower bounds for the life span of solutions of nonlinear wave equations in three dimensions. Commun. Pure Appl. Math. 36(1), 1–35 (1983)
Klainerman, S.: Uniform decay estimates and the Lorentz invariance of the classical wave equation. Commun. Pure Appl. Math. 38(3), 321–332 (1985)
Klainerman, S., Rodnianski, I.: Rough solutions of the Einstein-vacuum equations. Ann. Math. (2) 161(3), 1143–1193 (2005)
Kraniotis, G.V.: Precise relativistic orbits in Kerr and Kerr-(anti) de Sitter spacetimes. Class. Quantum Gravity 21(19), 4743–4769 (2004)
Lake, K., Zannias, T.: Global structure of Kerr-de Sitter spacetimes. Phys. Rev. D 92(8), 084003 (2015)
Luk, J., Sbierski, J.: Instability results for the wave equation in the interior of Kerr black holes. J. Funct. Anal. 271(7), 1948–1995 (2016)
Morawetz, C.S.: The limiting amplitude principle. Commun. Pure Appl. Math. 15, 349–361 (1962)
Parikh, M.K.: Volume of black holes. Phys. Rev. D (3) 73(12), 124021 (2006)
Pretorius, F., Israel, W.: Quasi-spherical light cones of the Kerr geometry. Class. Quantum Gravity 15(8), 2289–2301 (1998)
Sbierski, J.: On the initial value problem in general relativity and wave propagation in black-hole spacetimes. Doctoral thesis. https://doi.org/10.17863/CAM.16140 (2014)
Acknowledgements
The authors were both partially supported by FCT/Portugal through UID/MAT/04459/2019. A.T. Franzen was also supported by SFRH/BPD/115959/2016.
Funding
Open access funding provided by FCT|FCCN (b-on).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no Conflict of interest.
Additional information
Communicated by Carlos Rocha
Dedicated to Giorgio Fusco.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A. The Christoffel symbols
1.1 A.1. \(\boldsymbol{(u,v,\theta _\star ,\phi _\star )}\) coordinates
Using the notation
we write the Christoffel symbols of the metric g. If we use coordinates \((u,v,\theta _\star ,\phi _\star )\), the values of both \(\sigma\) and \(\varsigma\) are equal to 1. We have that
Recall that \({g \hspace{-4.83322pt}/}^{\phi _\star \phi _\star }\) behaves like \(\frac{1}{\sin ^2\theta _\star }\). In the Christoffel symbols above, this metric coefficient appears multiplied by
Lemma A.1
The derivatives \(\partial _{r_\star }b_{\phi _\star }\), \(\partial _{r_\star }{g \hspace{-4.83322pt}/}_{\theta _\star \phi _\star }\), \(\partial _{\theta _\star }{g \hspace{-4.83322pt}/}_{\theta _\star \phi _\star }\), \(\partial _{r_\star }{g \hspace{-4.83322pt}/}_{\phi _\star \phi _\star }\) behave like \(\sin ^2\theta _\star\), and the derivatives \(\partial _{\theta _\star }b_{\phi _\star }\) and \(\partial _{\theta _\star }{g \hspace{-4.83322pt}/}_{\phi _\star \phi _\star }\) behave like \(\sin (2\theta _\star )\).
Lemma A.1 implies
Corollary A.2
The Christoffel symbols of the metric g are all bounded, except for
which blow up like \(\frac{1}{\sin \theta _\star }\).
In the formulas above, the terms that blow up appear in (107) and (108).
Proof of Lemma A.1
Using (24), \({g \hspace{-4.83322pt}/}_{\phi _\star \phi _\star }\), and thus \(b_{\phi _\star }\), is of the form \(\mathcal{A}\sin ^2\theta\) for a regular function \(\mathcal{A}\). We have
Using (41), we see that \(\frac{\partial \theta }{\partial r_\star }\) contains a factor \(\sin (2\theta _\star )\). Moreover,
We recall that, according to (43), \(\frac{\partial \theta }{\partial \theta _\star }\) is bounded. Thus, recalling (28), \(\partial _{r_\star }(\mathcal{A}\sin ^2\theta )\) behaves like \(\sin ^2\theta _\star\) and \(\partial _{\theta _\star }(\mathcal{A}\sin ^2\theta )\) behaves like \(\sin (2\theta _\star )\). On the other hand, according to Lemma 2.15, \({g \hspace{-4.83322pt}/}_{\theta _\star \phi _\star }=\mathcal{A}\sin ^2\theta _\star \sin (2\theta _\star )\), for another smooth function \(\mathcal{A}\). Therefore, \(\partial _{\theta _\star }{g \hspace{-4.83322pt}/}_{\theta _\star \phi _\star }\) behaves like \(\sin ^2\theta _\star\). \(\square\)
Note that the vector fields \(\frac{\partial _u}{\Omega ^2}\) and \({\textstyle \frac{1}{\Omega ^2}} \left( \partial _{v}+b^{\phi _{\star }}\partial _{\phi _\star }\right)\) are geodesic:
Since we work in the frame
it is also convenient to have the following covariant derivatives:
1.2 A.2. \(\boldsymbol{(u,v_{{\tiny \mathcal{C}\mathcal{H}^+}},\theta _\star ,\phi _{\star ,\mathcal{C}\mathcal{H}^+})}\) coordinates
If we use coordinates \((u,v_{{\tiny \mathcal{C}\mathcal{H}^+}},\theta _\star ,\phi _{\star ,\mathcal{C}\mathcal{H}^+})\) then, in the formulas above, the value of \(\varsigma\) continues to be 1, but one has to replace \(\Omega ^2\) by \(\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}\), \(b^{\phi _{\star }}\) by \(b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\), and the value of \(\sigma\) has to be as in (80). Indeed, the expressions \(\sigma \partial _{r_\star }\) arise when taking derivatives with respect to \(v_{{\tiny \mathcal{C}\mathcal{H}^+}}\). Now, using (77) and (79), we have
But the coefficients of the metric do not depend either on \(\phi _\star\) or on t. So, when computing the Christoffel symbols, and differentiating functions that depend exclusively on r and \(\theta\), the derivative \(\partial _{v_{{\tiny \mathcal{C}\mathcal{H}^+}}}\) may be replaced by
The expressions for the innermost parenthesis are obtained from (39) and (41). Note that they are well defined on the Cauchy horizon, notwithstanding the coordinate \(r_\star\) not being defined there. The factor \(e^{-2\kappa _-v}\Delta _r\) is bounded above and below according to (76). So, given \(C_R\in {{\mathbb {R}}}\), there exist constants \(c,C>0\) such that
for \(u+v\ge C_R\). Special care has to be taken when differentiating \(b_{{\tiny \mathcal{C}\mathcal{H}^+}}^{\phi _\star }\) and \(\Omega ^2_{{\tiny \mathcal{C}\mathcal{H}^+}}\) with respect to \(v_{{\tiny \mathcal{C}\mathcal{H}^+}}\) because these functions also depend on v. This occurs when calculating \(\Gamma _{v_{{\tiny \mathcal{C}\mathcal{H}^+}}v_{{\tiny \mathcal{C}\mathcal{H}^+}}}^*\):
Notice that all terms are bounded except the last two summands of \(\Gamma _{v_{{\tiny \mathcal{C}\mathcal{H}^+}}v_{{\tiny \mathcal{C}\mathcal{H}^+}}}^{\phi _\star }\) that add up to
We remark that no terms that blow up at the Cauchy horizon appear when calculating \(\nabla _{X_\dagger }X_\ddagger\), for \(X_\dagger\) and \(X_\ddagger\) elements of the frame (110). For example, we have that
Example A.3
As a simple example, we calculate directly the surface gravity of the Cauchy horizon. Recall that the surface gravity \(\kappa _-\) is given by
where Z is the Killing vector field given by (81). On the Cauchy horizon \(\nabla _{\partial _u}\partial _{\phi _\star }=\nabla _{\partial _{\phi _\star }}\partial _u=0\) apply, because \(\Gamma _{u\phi _{\star ,\mathcal{C}\mathcal{H}^+}}^u=\Gamma _{u\phi _{\star ,\mathcal{C}\mathcal{H}^+}}^{\theta _\star }= \Gamma _{u\phi _{\star ,\mathcal{C}\mathcal{H}^+}}^{\phi _{\star ,\mathcal{C}\mathcal{H}^+}}=0\) on the Cauchy horizon, and \(\Gamma _{u\phi _{\star ,\mathcal{C}\mathcal{H}^+}}^v\) is identically zero. Obviously,
hold because the vector fields \(\partial _u\) and \(\partial _{\phi _\star }\) are tangent to the Cauchy horizon. Moreover, we know that
So, we conclude that
We used (78), then (19) and finally (39). This shows that
which is equality (73).
1.3 A.3. \({(u_{\mathcal{H}^+},v_{\mathcal{H}^+},\theta _\star ,\phi _{\star ,\mathcal{H}^+})}\) coordinates
If we use coordinates \((u_{\mathcal{H}^+},v_{\mathcal{H}^+},\theta _\star ,\phi _{\star ,\mathcal{H}^+})\) then, in the formulas above, the value of \(\sigma\) is 1, but one has to replace \(\Omega ^2\) by \(\Omega ^2_{{\tiny \mathcal{H}^+}}\), \(b^{\phi _{\star }}\) by \(b_{{\tiny \mathcal{H}^+}}^{\phi _\star }\), and the value of \(\varsigma\) has to be as in (82). Special care has to be taken when calculating \(\Gamma _{u_{\mathcal{H}^+}u_{\mathcal{H}^+}}^*\) because in this case one has to differentiate \(\Omega ^2_{{\tiny \mathcal{H}^+}}\) with respect to u:
B. Characterization of the parameters of subextremal KNdS spacetimes
The main result of this appendix is summarized in Lemma B.1, which characterizes subextremal Kerr–Newman–de Sitter black holes in terms of \((r_-, r_+,\Lambda a^2,\Lambda e^2)\). In Remarks B.2 and B.3, we consider alternative choices of parameters, namely \(\left( \Lambda ,\frac{r_+}{r_-},a,e\right)\) or \((\Lambda ,M,a,e)\). As mentioned in the Introduction, in the case that \(e=0\), related results can be found in Lake and Zannias [24] and Borthwick [4].
Lemma B.1
Each Kerr–Newman–de Sitter subextremal solution is determined by a quadruple \((r_-, r_+,\Lambda a^2,\Lambda e^2)\) satisfying \(0<r_-<r_+\),
and
with
where l is the function given by (138). The graph of l is sketched in Fig. 2.
The graphs of \(l(\,\cdot ,\Lambda e^2)\) for several values of \(\Lambda e^2\in \left[ 0,\frac{1}{4}\right)\) are sketched in Fig. 3.
For a choice of parameters on the graph of l we have \(r_+=r_c\) (see Fig. 4).
The value of \(\Lambda\) is given by
and the value of M is given by
with \(r_c\) given by
Alternative formulas for the mass are
Remark B.2
We can write (116) in the form
This formula is useful if we start with a parameter set
(see Remark B.6 for a clarification of the meaning of \(l^{-1}\)). Fixing \(\Lambda\), e and a, consider the function \(r_-(\Lambda ,\,\cdot ,a,e)\). We have
Note that the functions \(\sqrt{\Lambda }r_\#\) depend solely on \((\alpha ,\Lambda a^2,\Lambda e^2)\). In Fig. 5, we sketch their graphs for \(\Lambda e^2=\gamma =1/8\) and \(\Lambda a^2=\epsilon =(21-6\sqrt{12+\gamma })/2\). (See (141) for a formula for \(l^{-1}(\Lambda a^2,\Lambda e^2)\)). This implies that the mass M (whose expression is given in (117), (119) and (120)) satisfies
The function \(M(\Lambda ,\,\cdot ,a,e)\) is strictly increasing in the interval \([1,l^{-1}(\Lambda a^2,\Lambda e^2)]\). The function \(\sqrt{\Lambda }M\) also depends solely on \((\alpha ,\Lambda a^2,\Lambda e^2)\). In Fig. 6, we sketch the graph of \(\sqrt{\Lambda }M\) for \(\Lambda e^2=1/8\) (recall that \(\Lambda e^2\in [0,\frac{1}{4})\)).
We can use \(\partial _\alpha r_-(\Lambda ,l^{-1}(\Lambda a^2,\Lambda e^2),a,e)=0\) to show that \(\partial _\alpha M(\Lambda ,l^{-1}(\Lambda a^2,\Lambda e^2),a,e)=0\); this together with (117) allows us to deduce that \(\partial _\alpha r_c(\Lambda ,l^{-1}(\Lambda a^2,\Lambda e^2),a,e)=- \partial _\alpha r_+(\Lambda ,l^{-1}(\Lambda a^2,\Lambda e^2),a,e)\). The other assertions follow by direct calculation.
Remark B.3
In Lemma B.1 we can think that our subextremal solution is characterized by \((r_-,\alpha ,\Lambda a^2,\Lambda e^2)\) and in Remark B.2 we can think that our subextremal solution is characterized by \((\Lambda ,\alpha ,\Lambda a^2,\Lambda e^2)\). Formula (121) relates \(r_-\) with \(\Lambda\). In this paper, the preferred viewpoint is that each spacetime is characterized by the three parameters \((\alpha ,\epsilon ,\gamma )=\left( \frac{\sqrt{\Lambda }r_+}{\sqrt{\Lambda }r_-},(\sqrt{\Lambda }a)^2,(\sqrt{\Lambda }e)^2\right)\). These determine the other quantities, like \(\sqrt{\Lambda }r_-\) or \(\sqrt{\Lambda }M\). In this sense, the cosmological constant appears as a scale parameter.
Remark B.4
The reader interested in the characterization of Kerr–de Sitter spacetimes in terms of the parameters \((\Lambda ,M,a)\) (which is physically more natural, although not what we need in Sect. 2) should consult Borthwick [4], where extreme and fast Kerr–de Sitter are also considered.
Remark B.5
In summary, the region where the parameters \((\alpha ,\epsilon ,\gamma )\) can vary (which is sketched in Fig. 2) is defined by
where E is given in (137) and l is given in (138); alternatively, by
where \(\Gamma\) is given in (139); or still by
where \(l^{-1}\) is given in (141).
Proof of Lemma B.1
(1) (\(\Delta _r\)) The relationship between \((M, \Lambda , a,e)\) and \((r_-, r_+,\Lambda a^2,\Lambda e^2)\) is obtained via the polynomial \(\Delta _r\). On the one hand this polynomial is given by
and on the other hand it is given by
\(\square\)
since, according to our subextremal hypothesis, \(\Delta _r\) has one negative root \(r_n\), and three positive roots \(r_-<r_+<r_c\). Expanding the last expression yields
We will now compare the coefficients of \(\Delta _r\) in \(r^0\), \(r^1\), \(r^2\) and \(r^3\); the coefficient in \(r^4\) is already matched.
(1a) (Coefficient in \(\varvec{r^3)}\)) We start with the coefficient of \(\Delta _r\) in \(r^3\). As it is equal to 0, we have
(1b) (Coefficient in \(\varvec{r^0)}\) Equating the coefficients of \(\Delta _r\) in \(r^0\), we get, using (122),
We regard this as a quadratic equation for \(r_c\), which will be satisfied by choosing an appropriate \(r_c\). Defining
(123) can be rewritten as
(1c) (Coefficient in \(\varvec{r^1)}\) Equating the coefficients of \(\Delta _r\) in \(r^1\) we arrive at the value of M given in (117). The expression (119) is obtained from (117) using \(r_+=\alpha r_-\) and (118) (deduced below). The formula (120) is the statement that \(r_-\) is a root of \(\Delta _r\). Of course, in (120) we may replace \(r_-\) by \(r_+\) or by \(r_c\).
(1d) (Coefficient in \(\varvec{r^2)}\) Finally, we compare the coefficients of \(\Delta _r\) in \(r^2\). Using again (122), leads to
Defining
and using (124), Eq. (126) is equivalent to
or
This is a quadratic equation which will determine \(\Lambda\).
(2) \(\varvec{(\Lambda )}\) As we are considering de Sitter black holes, \(\Lambda\) is positive, and therefore \(\epsilon\) is positive and \(\gamma\) is nonnegative. So, the product of the roots of (127) is positive, and the two roots have the same sign. Since \(\Lambda\) is positive, we must have
Solving (127), we get
We denote these values of \(\Lambda\) by \(\Lambda _0\) and \(\Lambda _1\). \(\Lambda _0\) and \(\Lambda _1\) will have the minus sign and the plus sign in front of the square root, respectively, so that \(\Lambda _0\le \Lambda _1\). We will see below that only the value of \(\Lambda _0\) is admissible.
(2a) (\(\Lambda\) real) Define
so that
The discriminant in (129) should be nonnegative, that is
Since \(\epsilon\) is positive, we see that \(\gamma\) has to satisfy
This is not our final restriction on \(\epsilon\) though. By requiring that \(r_c>r_+\) a further restriction on \(\epsilon\) will arise, as well as the requirement that \(\Lambda =\Lambda _0\).
(3) \(\varvec{(r_c)}\) To obtain \(r_c\), we rewrite (125) as
Hence,
This is (118). The condition \(r_c>r_+\) is equivalent to
or
Using the definition of x in (124), this is the same as
or
Now we use the definition of \(\epsilon\) and the assumption that \(\Lambda\) is positive which, as we have seen, implies \(0<\epsilon <3\). For \(\epsilon\) in this range, (132) is equivalent to
where, for the last equality, we used the quadratic equation (127) for \(\Lambda\). Our last task is to guarantee (133).
(3a) \(\varvec{(\Lambda =\Lambda _0)}\) First we take \(\Lambda =\Lambda _0\) in (133). Then
which can be rewritten as
We need to examine the sign of the right-hand side of (134). This can be written as
Above we guaranteed (130). Since we have that
the right-hand side of (134) is nonnegative. Therefore, (134) is equivalent to
Let us define
Then, expanding the left-hand side of (135), we get
or
because
is positive. Substituting c and d by their expressions in terms of \(\alpha\), we obtain
The inequality (136) has solutions for \(\epsilon\) positive if and only if
This inequality for \(\gamma\) is more restrictive than (131). We remark that
(this function is 1 at \(\alpha =1\) and grows to \(\frac{9}{8}\) as \(\alpha\) goes to \(+\infty\)). Therefore, all solutions of (136) are solutions of (130). The inequality (136) is equivalent to
where
and \(\tilde{r}(\alpha ,\gamma )\) is defined by the same expression, with the minus sign replaced by a plus sign. The function \(\tilde{r}\) satisfies
So, the inequality \(\epsilon >\tilde{r}(\alpha ,\gamma )\) is incompatible with (128). Fix a \(\gamma\) belonging to the interval \(\left[ 0,\frac{1}{4}\right)\). The function \(l(\,\cdot ,\gamma )\) is strictly decreasing and satisfies
In Fig. 3, we sketch the graphs of \(l(\,\cdot ,0)\), \(l(\,\cdot ,0.05)\), \(l(\,\cdot ,0.1)\), \(l(\,\cdot ,0.15)\), \(l(\,\cdot \,,0.20)\) and \(l(\,\cdot \,,0.24)\). The function \(l(\,\cdot ,\gamma )\) is nonnegative for \(\alpha \in \left( 1, \Gamma (\gamma ) \right)\), and
where \(\Gamma (\gamma )\) is the inverse of the function E in (137), i.e. is the solution greater than one of
namely
for \(\gamma \in \left( 0,\frac{1}{4}\right)\), \(\Gamma (0)=+\infty\) (in which case \(\alpha \in (1,+\infty )\)). Note that
The graph of \(\Gamma\) is sketched in Fig. 7. We remark that
In summary, for \(\Lambda =\Lambda _0\) inequality (133) is satisfied for
(3b) \(\varvec{(\Lambda =\Lambda _1)}\) Now we take \(\Lambda =\Lambda _1\) in (133). Then, instead of (134), we obtain
Note that the left-hand side of (140) is the symmetric of the right-hand side of (134). We have shown above that the right-hand side of (134) is nonnegative. Hence, inequality (140) never holds.
We conclude that we must choose \(\Lambda =\Lambda _0\) in (129). This establishes expression (116) of Lemma B.1.
Define
Remark B.6
The inverse of the function l, in the sense that
is
for \(0\le \gamma <\frac{1}{4}\) and \(\epsilon \in \,]0,21-6\sqrt{12+\gamma }]\). In particular, \(l^{-1}(21-6\sqrt{12+\gamma },\gamma )= l^{-1}(l(1,\gamma ),\gamma )=1\).
Remark B.7
If we start with a parameter set \((\Lambda ,M,a,e)\), we can regard (116) and (119) as a system for \(r_-\) and \(\alpha\). In this case, it is natural to consider the quantities
In terms of these quantities, (116) and (119) can be written as
The Eq. (142) can be solved for A, yielding
The system (143)−(144) allows us to determine A and R from \(\sqrt{\Lambda }M\), \(\Lambda a^2\) and \(\Lambda e^2\). Of course, another way to do this would be by calculating the roots of the polynomial \(\Delta _r\).
C. Komar integrals
The purpose of this appendix is to obtain expression (149), for the mass of the black hole at the event horizon. Besides the expected term \(\frac{M}{\Xi ^2}\), the mass has one correction term which is a constant multiple of the product of the cosmological constant by the Parikh volume of the black hole, and has another term which reflects the energy due to the electric field. In this way we recall the physical interpretation of the parameters of our metric. Let \({\tilde{K}}:=\partial _{\phi _\star }\). Consider the 2-dimensional surface on the event horizon \(\mathcal{S}=\{(u_{\mathcal{H}^+},v_{\mathcal{H}^+},\theta _\star ,\phi _{\star ,\mathcal{H}^+}):u_{\mathcal{H}^+}=0,\ v_{\mathcal{H}^+}=(v_{\mathcal{H}^+})_0\}\), where \(v_{\mathcal{H}^+}=(v_{\mathcal{H}^+})_0\), for some fixed \((v_{\mathcal{H}^+})_0\). Let us calculate the Komar integral
(JQ is not the angular momentum if \(e\ne 0\). See [15, Subsection III.B] for the definition of the angular momentum.)
Remark C.1
In the calculation below we use the coordinates \((u,v,\theta _\star ,\phi _\star )\) of Sect.2.1.3, notwithstanding the fact that \(\mathcal{S}\) is contained in the event horizon, where these coordinates are not defined. Our computations may be easily justified by considering a sequence \(\mathcal{S}_n\) of surfaces which approximate \(\mathcal{S}\) from within the black hole, which is covered by the coordinates, computing the integrals over \(\mathcal{S}_n\), and then passing to the limit.
We have that
and
As the vectors on the tangent space of \(\mathcal{S}\) do not have neither components in \(\partial _u\) nor components in \(\partial _v\), only the components \(({\textrm{d}}{\tilde{K}}_\flat )^{uv}\) and \(({\textrm{d}}{\tilde{K}}_\flat )^{vu}\) are relevant for the calculation of JQ. On the other hand, as
the terms \(({\textrm{d}}{\tilde{K}}_\flat )_{\theta _\star *}\) and \(({\textrm{d}}{\tilde{K}}_\flat )_{*\theta _\star }\) do not contribute to JQ. Notice that \(({\textrm{d}}{\tilde{K}}_\flat )_{v\phi _\star }\) and \(({\textrm{d}}{\tilde{K}}_\flat )_{\phi _\star v}\) do not enter into the calculation of \(({\textrm{d}}{\tilde{K}}_\flat )^{uv}\) and \(({\textrm{d}}{\tilde{K}}_\flat )^{vu}\) either. Thus, we write
and
Remembering that \(b^{\phi _{\star }}\) is constant on the event horizon, we have
on the event horizon, because \(\Upsilon =4(r^2+a^2)^2\Delta _\theta\) there. Since
and
it follows that
because \(L=(r^2+a^2)\partial _{\theta _\star }\theta\) on the event horizon. Now, we have
Taking into account that
and
we arrive at
Here
an expression that makes clear the behavior of the function \(\textrm{BT}\), as the first two terms of the Taylor expansion of \(x\mapsto \arctan x\) around zero are \(x-\,\frac{x^3}{3}\). In particular, the function \(\textrm{BT}\) is strictly increasing, satisfies \(\textrm{BT}(0)=0\), \(\textrm{BT}(0)=\frac{8}{3}\), and \(\lim _{x\rightarrow +\infty } \left( \textrm{BT}\,(x)/ \left( \frac{\pi }{2}x^2\right) \right) =1\). This finally yields
with
the total charge (see [5, (19)] and [17, beginning of Subsection 3.2 on p. 32]).
Now we consider K to be \(K=\frac{\partial _t}{\Xi }\) and we turn to the calculation of the Komar integral
This is the mass calculated at the event horizon. To justify this choice of K we refer to [16, (2.12) and Subsection 2.2] (see also [5, (18)]). As \(\partial _t=\frac{1}{2}\partial _v-\,\frac{1}{2}\partial _u\), we have that
and
Using (115), (145), (146) and (147), this yields
with
Remark C.2
The quantity
is the Parikh [27, (10)] volume of the black hole (see also [2, (91)]).
Of course, (148) is Smarr’s formula (recall (84))
(see, for example, [5, (9)] for the value of \(\mathcal{A}\), and see [13] for much more on Smarr’s formula).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Franzen, A.T., Girão, P.M. Regularity of a double null coordinate system for Kerr–Newman–de Sitter spacetimes. São Paulo J. Math. Sci. (2024). https://doi.org/10.1007/s40863-024-00421-y
Accepted:
Published:
DOI: https://doi.org/10.1007/s40863-024-00421-y