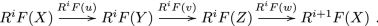This is a contributed paper to the proceedings of the 2nd Workshop of the São Paulo Journal of Mathematical Sciences: “Jean-Louis Koszul in São Paulo, His Work and Legacy.” Institute of Mathematics and Statistics, University of São Paulo, Brazil, November 13-14, 2019
Abstract
We study some spectral sequences associated with a locally free \({{\mathscr {O}}}_X\)-module \({{\mathscr {A}}}\) which has a Lie algebroid structure. Here X is either a complex manifold or a regular scheme over an algebraically closed field k. One spectral sequence can be associated with \({{\mathscr {A}}}\) by choosing a global section V of \({{\mathscr {A}}}\), and considering a Koszul complex with a differential given by inner product by V. This spectral sequence is shown to degenerate at the second page by using Deligne’s degeneracy criterion. Another spectral sequence we study arises when considering the Atiyah algebroid \({{{\mathscr {D}}}_{{{\mathscr {E}}}}}\) of a holomolorphic vector bundle \({{\mathscr {E}}}\) on a complex manifold. If V is a differential operator on \({{\mathscr {E}}}\) with scalar symbol, i.e, a global section of \({{{\mathscr {D}}}_{{{\mathscr {E}}}}}\), we associate with the pair \(({{\mathscr {E}}},V)\) a twisted Koszul complex. The first spectral sequence associated with this complex is known to degenerate at the first page in the untwisted (\({{\mathscr {E}}}=0\)) case.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we consider some spectral sequences that one can attach to a Lie algebroid. To be more precise, if X is a complex manifold, or a regular noetherian scheme over an algebraically closed field k of characteristic zero, we consider a locally free \({{\mathscr {O}}}_X\)-module \({{\mathscr {A}}}\) having a Lie algebroid structure (definitions will be given in the next Section). One can introduce a complex \(\Omega _{{\mathscr {A}}}^\bullet =\Lambda ^\bullet {{\mathscr {A}}}^*\) which is a generalization of the (holomorphic) de Rham complex \(\Omega _X^\bullet\). Now a Lie algebroid \({{\mathscr {A}}}\) comes with a morphism of sheaves of Lie k-algebras (the anchor morphism) to the tangent sheaf \(\Theta _X\), and the kernel of the anchor is a sheaf of ideals of \({{\mathscr {A}}}\) (and a sheaf of Lie \({{\mathscr {O}}}_X\)-algebras); this allows one to introduce, in analogy with the Hochschild-Serre spectral sequence [14], a filtration leading to a spectral sequence which converges to the hypercohomology \({\mathbb {H}}(X,\Omega _{{\mathscr {A}}}^\bullet )\). This was already considered in [3] in the \(C^\infty\) case; moreover, [16, 17] describe this spectral sequence in the case of the Atiyah algebroid of a vector bundle. In [4] and [5] this and other spectral sequences were studied in detail. Lie-Rinehart algebras can be regarded as special cases of Lie algebroids, so that we get a spectral sequence for Lie-Rinehart algebras: this generalizes the Hochschild-Serre spectral sequence for ideals in Lie algebras [14].
Other spectral sequences arise when we fix a section V of \({{\mathscr {A}}}\); this yields a complex of the Koszul type, which we call a Lie-Koszul complex. Then the general machinery of homological algebra [13, 18] produces two spectral sequences. In Sect. 2, by using Deligne’s degeneracy criterion [11], we show that the second spectral sequence degenerates. The fact that this spectral sequence satisfies the condition of Deligne’s criterion means that the Lie-Koszul complex of a (holomorphic) Lie algebroid is formal (it is isomorphic, in the derived category of coherent sheaves, with the complex formed by its cohomology sheaves).
To study the first spectral sequence of a Lie-Koszul complex, we specialize to the case when \({{\mathscr {A}}}\) is the Atiyah algebroid of a holomorphic vector bundle \({{\mathscr {E}}}\) on a complex manifold X (Sect. 3). Let us recall that \({{{\mathscr {D}}}_{{{\mathscr {E}}}}}\) is the bundle of first order differential operators on \({{\mathscr {E}}}\) with scalar symbol. \({{{\mathscr {D}}}_{{{\mathscr {E}}}}}\) sits in an exact sequence of sheaves of \({{\mathscr {O}}}_X\)-modules
where \(\sigma\) is the symbol map. This spectral sequence relates to the twisted holomorphic equivariant cohomology we introduced in [6]. For \({{\mathscr {E}}}=0\) (i.e, in the case of the de Rham complex) this spectral sequence was studied by Carrell and Lieberman [8] and Bismut [2] when X is Kähler manifold. In that case the spectral sequence degenerates at the first page.
2 Formality of the Lie-Koszul complexes
We consider a (holomorphic) Lie algebroid \({{\mathscr {A}}}\), over X, the latter being a complex manifold, or a regular noetherian scheme over an algebraically closed field k. We choose a global section V of \({{\mathscr {A}}}\) and consider the morphism (inner product) \(i_V:{\mathscr {K}}_{{\mathscr {A}}}^\bullet \rightarrow {\mathscr {K}}_{{\mathscr {A}}}^{\bullet +1}\), where \({\mathscr {K}}_{{\mathscr {A}}}^p = \Omega _{{\mathscr {A}}}^{-p}\), \(p\le 0\). We shall call \(({\mathscr {K}}_{{\mathscr {A}}}^\bullet ,i_V)\) the Lie-Koszul complex associated with the pair \(({{\mathscr {A}}},V)\). This generalizes the Koszul complex \((\Omega _X^{-\bullet },i_V)\) associated with the complex of differential forms on X with the differential given by the inner product by a (holomorphic) vector field V on X. This will be called the de Rham-Koszul complex associated with the vector field V.
By general principles [13, 18] we can associate two spectral sequences with this complex, both converging to the hypecohomology \({\mathbb {H}}({\mathscr {K}}_{{\mathscr {A}}}^\bullet ,i_V)\). In general, if \({\mathfrak {A}}\), \({\mathfrak {B}}\) are Abelian categories, denote by \(D^+({\mathfrak {A}})\) the derived category of complexes of objects in \({\mathfrak {A}}\) bounded from below, and let \(F:D^+({\mathfrak {A}}) \rightarrow {\mathfrak {B}}\) a cohomological functor.Footnote 1 Let \({\mathscr {K}}\) be an object in \(D^+({\mathfrak {A}})\). We recall from [13, 18] that with these data one can associate two spectral sequences, both functorial in \({\mathscr {K}}\), and both converging to \(R^{\bullet }F({\mathscr {K}})\). The first two pages of the first spectral sequence are
and the differential \(d_1\) coincides (perhaps up to a sign, depending on conventions) with the differential of the complex \({\mathscr {K}}\). The second page of the second spectral sequence is
The degeneration of the the second spectral sequence may be studied by means of Deligne’s degeneracy criterion [11]. Let us state it in generality. We shall replace the derived category \(D^+({\mathfrak {A}})\) by the bounded derived category \(D^b({\mathfrak {A}})\).
Theorem 2.1
(Deligne) The following two conditions are equivalent:
-
(i)
the spectral sequence \(I\! I_\bullet\) degenerates at its second page for every choice of the functor F;
-
(ii)
\({\mathscr {K}}^\bullet\) is isomorphic to \(\oplus _i H^i({\mathscr {K}}^\bullet )[-i]\) in \(D^b({\mathfrak {A}})\).
(In the language of homological algebra, the second condition is called formality of the complex \({\mathscr {K}}^\bullet\).)
To apply Deligne’s criterion to our case we take \({\mathscr {A}} = Coh(X)\), \({\mathscr {B}} = {{\mathbf {K}}}({\text{ Ab}})\) (the category of complexes of Abelian groups) and for F we take the global section functor \(\Gamma\). The object we fix in \(D^b(X)\) is the Lie-Koszul complex \(({\mathscr {K}}_{{\mathscr {A}}}^\bullet ,i_{ V})\). We denote by \({\mathscr {H}}_{{\mathscr {A}}}^\bullet\) the cohomology sheaves of the complex \(({\mathscr {K}}_{{\mathscr {A}}}^\bullet ,i_{ V})\), and by Y the scheme of zeroes of V. It is a closed, possibly nonreduced, subscheme (analytical subspace) of X. The sheaves \({\mathscr {H}}_{{\mathscr {A}}}^\bullet\) are supported on Y. Let \(j :Y \rightarrow X\) be the scheme-theoretic inclusion, or the inclusion as a morphism in the category of analytic spaces (a closed immersion). The functor \(j_*\) is right adjoint to \(j^*\), so that there are morphisms \(j^\star :{\mathscr {F}}\rightarrow j_*j^*{\mathscr {F}}\) for every coherent sheaf \({\mathscr {F}}\) on X. There is a commutative diagram

i.e., \(j^\star\) is a morphism of complexes if we equip \(j_*j^*{\mathscr {K}}_{{\mathscr {A}}}^\bullet\) with the zero morphisms. Finally, \({\mathscr {H}}_{{\mathscr {A}}}^\bullet \simeq j_*j^*{\mathscr {K}}_{{\mathscr {A}}}^\bullet\). Now we have:
Proposition 2.2
The morphism of complexes \(j^\star :({\mathscr {K}}_{{\mathscr {A}}}^{\bullet }, i_{V}) \rightarrow (j_*j^*{\mathscr {K}}_{{\mathscr {A}}}^{\bullet },0)\) is a quasi-isomorphism.
As a consequence, the objects \(({\mathscr {K}}_{{\mathscr {A}}}^{\bullet }, i_{V})\) and \(\bigoplus _i {\mathscr {H}}_{{\mathscr {A}}}^i[-i]\) are isomorphic in the derived category \(D^b(X)\). By Deligne’s degeneracy criterion, we obtain that the spectral sequence \(I\! I_\bullet\) degenerates at the second page.
We can also say something about the hypercohomology \({\mathbb {H}}^\bullet ({\mathscr {K}}_{{\mathscr {A}}})\). Let us denote by \(\dim Y\) the dimension of the highest-dimensional component of Y. The proof of the following result goes as in the case of the de Rham-Koszul complex treated in [8], p. 306.
Proposition 2.3
\({\mathbb {H}}^m({\mathscr {K}}_{{\mathscr {A}}}^\bullet ,i_V)=0\) for \(m>\dim Y\).
Proof
Where \(V\ne 0\) the Lie-Koszul complex is exact, so that the supports of the cohomology sheaves \({\mathscr {H}}_{{\mathscr {A}}}^q\) are contained in Y; hence \(I\! I_2^{p,q}=0\) for \(p>\dim Y\). Moreover, \({\mathscr {H}}_{{\mathscr {A}}}^q=0\) for \(q>0\). Thus \(I\! I_2^{p,q}=0\) for \(p+q>\dim Y\). By standard homological arguments we get the thesis. \(\square\)
If \(\dim Y=0,1\), this gives an easy proof of the degeneration of the second spectral sequence at the second page, since \(d_2:I\! I_2^{p,q} \rightarrow I\! I_2^{p+2,q-1}\) vanishes in that case. One also has
When \(\dim Y=0\), the second page of the spectral sequence is such that \(I\! I_2^{p,q} =0\) if \(p\ne 0\).
3 A spectral sequence associated with Atiyah algebroids
In this section we study the spectral sequence \(I_\bullet\) in the special case when the Lie algebroid \({{\mathscr {A}}}\) is the Atiyah algebroid \({{{\mathscr {D}}}_{{{\mathscr {E}}}}}\) of a holomorphic vector bundle \({{\mathscr {E}}}\) on a complex manifold X (as in eq. (1)).
We fix once and for all a section V in \(\Gamma ({{{\mathscr {D}}}_{{{\mathscr {E}}}}})\). The pair \(({{\mathscr {E}}},V)\) is called an equivariant holomorphic vector bundle. (“Equivariant” refers to the fact that V covers the infinitesimal action of the vector field \(\sigma (V)\) on X.) We consider the associated Lie-Koszul complex, i.e., the complex \(({\mathscr {K}}_{{\mathscr {E}}}^\bullet ,i_{V})\) where \({\mathscr {K}}_{{\mathscr {E}}}^{p} = \Lambda ^{-p}{{{\mathscr {D}}}_{{\mathscr {E}}}^*}\) for \(p\le 0\), and \({\mathscr {K}}_{{\mathscr {E}}}^{p}=0\) for \(p>0\). This twisted Koszul complex, or, to be more precise, its Dolbeault resolution, is a building block of a “twisted holomorphic equivariant cohomology” that we introduced in [6] and for which we proved a localization formula that generalizes Carrell-Lieberman’s [7, 9], Feng-Ma’s [12] and Baum-Bott’s [1] formulas.
The spectral sequence \(I_\bullet\) relates in this case to the double complex we introduced in [6]. For \({{\mathscr {E}}}=0\) this spectral sequence was studied by Carrell and Lieberman [8] (see also Bismut [2]) and in turn relates to K. Liu’s “untwisted” holomorphic equivariant cohomology [15].
We denote by \(\Omega _X^{p,q}\) the sheaf of differential forms of type (p, q) on X, and consider the complex
with the differential \({\bar{\partial }}_{{{\mathscr {E}}},V}={\bar{\partial }}_{{\mathscr {E}}}+ i_{V}\), where by \({\bar{\partial }}_{{\mathscr {E}}}\) we collectively denote the Cauchy-Riemann operators of the bundles \(\Lambda ^{p}{{{\mathscr {D}}}_{{\mathscr {E}}}^*}\). We denote by \(H^\bullet _{V}(X,{{\mathscr {E}}})\) the cohomology of this complex. For \({{\mathscr {E}}}=0\) this reduces to the cohomology introduced by K. Liu [15] (see also Carrell and Lieberman [8] and Bismut [2].)
Remark 3.1
If \(V=0\) then \(H^k_{V}(X,{{\mathscr {E}}})=\bigoplus _{q-p=k} H^q(X,{\Lambda ^{p}{{{\mathscr {D}}}_{{\mathscr {E}}}^*}})\).
Proposition 3.2
The cohomology \(H^\bullet _{V}(X,{{\mathscr {E}}})\) is isomorphic to the hypercohomology \({\mathbb {H}}^\bullet ({\mathscr {K}}_{{\mathscr {E}}}^\bullet )\) of the complex \(({\mathscr {K}}_{{\mathscr {E}}}^\bullet ,i_{V})\).
Proof
The double complex \(\Lambda ^{-\bullet }{{{\mathscr {D}}}_{{\mathscr {E}}}^*}\otimes _{{{\mathscr {O}}}_X}\Omega ^{0,\bullet }_X\) is an acyclic resolution of the complex \({\mathscr {K}}_{{\mathscr {E}}}^\bullet\), and the total complex of \((\Lambda ^{-\bullet }{{{\mathscr {D}}}_{{\mathscr {E}}}^*}\otimes _{{{\mathscr {O}}}_X}\Omega ^{0,\bullet }_X,i_V,{\bar{\partial }}_{{\mathscr {E}}})\) coincides with \(({\Lambda ^{\bullet }{{{\mathscr {D}}}_{{\mathscr {E}}}^*}},{\bar{\partial }}_{{{\mathscr {E}}},V})\). (This resolution is not made by coherent sheaves, but the argument works anyway, just going into the category of sheaves of Abelian groups.) \(\square\)
We denote
with \(p\le 0\), so that \(G_\bullet ^q\) is a descending filtration of \(Q^q_{{\mathscr {E}}}(X)\). Note that
This filtration of the complex \((Q_{{\mathscr {E}}}^{(\bullet )}(X) ,{\bar{\partial }}_{{{\mathscr {E}}},V})\) defines a spectral sequence whose zeroth page is
The spectral sequence converges to the cohomology \(H^\bullet _{V}(X,{{\mathscr {E}}})\). The differential \(d_0\) coincides with \({\bar{\partial }}_{{\mathscr {E}}}\), as one easily checks. Therefore,
It is now easy to check that this spectral sequence coincides with \(I_\bullet\).
Henceforth we assume that the zero locus Y of V is a complex submanifold of X. Therefore it makes sense to consider the complex (3) on Y; after letting \({\tilde{{{\mathscr {E}}}}}={{\mathscr {E}}}_{\vert Y}\), we denote this new complex \(Q^\bullet _{{\tilde{{{\mathscr {E}}}}}}(Y)\). Denoting by \(j:{{\tilde{Y}}}\rightarrow X\) the embedding, we have the restriction morphism \(j^*:Q^ \bullet _{{{\mathscr {E}}}} (X)\rightarrow Q^\bullet _{{\tilde{{{\mathscr {E}}}}}}( Y)\), which is a morphism of filtered complexes. We are going to show that, under some conditions, this is a quasi-isomorphism.
Note that there is an exact sequence
where \(N_{Y/X}\) is the normal bundle to Y. Since V is zero on Y, the commutator \({\mathbb {L}}_{V}(u) = [V,u]\) is well defined if \(u\in {{{\mathscr {D}}}_{{{\mathscr {E}}}}}_{\vert Y}\). This operator vanishes on \({\mathscr {D}}_{{\tilde{{{\mathscr {E}}}}}}\), so it is well defined on \(N_{Y/X}\). If it is injective, by composing with the projection \({{{\mathscr {D}}}_{{{\mathscr {E}}}}}_{\vert Y} \rightarrow N_{Y/X}\) it yields an isomorphism, thus splitting the sequence (4).
For clarity, we stress what we are assuming:
Assumption 3.3
The zero locus Y of V is a complex submanifold on X, and the morphism \({\mathbb {L}}_{V}:N_{Y/X} \rightarrow {{{\mathscr {D}}}_{{{\mathscr {E}}}}}_{\vert Y}\) is injective.
This implies the following preliminary result. Let \(\tilde{{\mathscr {K}}}^\bullet _{\tilde{{{\mathscr {E}}}}}\) be the complex of sheaves on Y
with the zero differential.
Lemma 3.4
\(j^*{\mathscr {H}}^p_{{\mathscr {E}}}\simeq \tilde{{\mathscr {K}}}^p_{\tilde{{{\mathscr {E}}}}}\). In particular, \({\mathscr {H}}^p_{{\mathscr {E}}}=0\) if \(-p>\dim Y\).
Proof
There is a naturally defined morphism \(j^*{\mathscr {H}}^p_{{\mathscr {E}}}\rightarrow \tilde{{\mathscr {K}}}^p_{\tilde{{{\mathscr {E}}}}}\). We need to show that this gives an isomorphism between the stalks of the two sheaves. Considering the exact sequence (1) restricted to the stalks at a point \(y\in Y\), it splits, and one has
Let \({{\tilde{V}}}\) be the vector field \({{\tilde{V}}}=\sigma (V)\). It vanishes on Y. Then one knows that the cohomology of the complex \((\Omega ^{-\bullet }_X,i_{{{\tilde{V}}}})\) restricted to Y is isomorphic to the cohomology of the complex \((\Omega ^{-\bullet }_Y,0)\) [2]. This, together with the Künneth theorem, implies the result. \(\square\)
The following result generalizes to the twisted case Theorem 5.1 in [2]. The proof goes as in [2], but for clarity we report it here, adapted to the present situation, and with some more details.
Theorem 3.5
Under the Assumption 3.3,the restriction morphism \(j^*:Q^ \bullet _{{{\mathscr {E}}}} (X)\rightarrow Q^\bullet _{{\tilde{{{\mathscr {E}}}}}}(Y)\) is a quasi-isomorphism.
Proof
Let \({\mathfrak {U}}\) be an open cover of X, and consider the Čech-Koszul complex
with differential \({\tilde{\delta }}=\delta +i_V\), where \(\delta\) is the usual Čech differential. We define the descending filtration
so that \(F_{q+1}^p\subset F_q^p\),
and
Let \((E_\bullet (X),d_\bullet )\) be the ensuing spectral sequence. The \(d_0\) differential acting on the 0-th page coincides with \(i_V\), so that the first page of the spectral sequence is
The differential \(d_1\) acting on this complex is the Čech differential. By Lemma 3.4, we also have
where \(\tilde{{\mathfrak {U}}}\) is the open cover of Y obtained by restricting the open sets of \({\mathfrak {U}}\) to Y.
Consider now the complex
The resulting spectral sequence \(E_\bullet (Y)\) has a vanishing \(d_0\) differential, hence \(E_1(Y)\) coincides with the \(E_0\) page. The restriction morphism \(j^*\) induces a morphism \(j^*:E_1(X) \rightarrow E_1(Y)\). By the commutativity of the diagram (2), this is an isomorphism and commutes with the respective differentials (which are the Čech differentials of the respective Čech complexes). By [10, Ch. XV, Thm. 3.2] the successive pages of the two spectral sequences are isomorphic, and the spectral sequences converge to the same group. Therefore, the complexes \(C^{(\bullet )}(X)\) and \(C^{(\bullet )}(Y)\) are quasi-isomorphic.
Via the standard Čech-Dolbeault spectral sequence, the cohomology of the complex \(C^{(\bullet )}(Y)\) is, after taking a direct limit on the covers \({\mathfrak {U}}\), isomorphic to the cohomology of \((Q^{\bullet }_{\tilde{{{\mathscr {E}}}}}(Y),{\bar{\partial }}_{{\tilde{{{\mathscr {E}}}}}})\). In the same way, the cohomology of \(C^{(\bullet )}(X)\) is isomorphic, after taking a direct limit, to the cohomology of \((Q_{{\mathscr {E}}}^{\bullet }(X),{\bar{\partial }}_{{{\mathscr {E}}},V})\). This concludes the proof.\(\square\)
Corollary 3.6
\(H^k_{V}(X,{{\mathscr {E}}})\simeq \bigoplus _{q-p=k}H^q( Y,\Lambda ^p{\mathscr {D}}_{{\tilde{{{\mathscr {E}}}}}}^*)\).
(Compare with Remark 3.1.)
Proof
Since \(V=0\) on Y this follows from Remark 3.1.\(\square\)
Let us eventually consider the first spectral sequence \(I_\bullet\). Its first page is
In the untwisted (\({{\mathscr {E}}}=0\)) case, and assuming that X is compact and Kähler, Carrell and Lieberman [8], by an argument inspired by Deligne’s degeneracy criterion, show that \(d_1=0\), so that this spectral sequence degenerates at the first page.
Notes
F is said to be a cohomological functor if it maps every distinguished triangle

to a long exact sequence
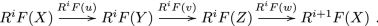
References
Baum, P., Bott, R.: On the zeroes of meromorphic vector fields, in Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), pp. 29–47. Springer, New York (1970)
Bismut, J.-M.: Holomorphic and de Rham torsion. Compos. Math. 140, 1302–1356 (2004)
Bressler, P., Kapranov, M.,Tsygan, B.,Vasserot, E.:Riemann-Roch for real varieties, in Algebra, arithmetic, and geometry: in honor of Yu. I. Manin. Vol. I, vol. 269 of Progr. Math. Birkhäuser Boston Inc., Boston, MA, 2009, pp. 125–164
Bruzzo, U.: Lie algebroid cohomology as a derived functor. J. Algebra 483, 245–261 (2017)
Bruzzo, U., Mencattini, I., Rubtsov, V., Tortella, P.: Nonabelian Lie algebroid extensions. Int. J. Math. 26, 1550040 (2015)
Bruzzo, U., Rubtsov, V.: On localization in holomorphic equivariant cohomology. Cent. Eur. J. Math. 10, 1442–1454 (2012)
Carrell, J.B.: Vector fields, residues and cohomology, in Parameter spaces Warsaw: vol. 36 of Banach Center Publ. Polish Acad. Sci. Warsaw. 1996: 51–59 (1994)
Carrell, J.B., Lieberman, D.I.: Holomorphic vector fields and Kaehler manifolds. Invent. Math. 21, 303–309 (1973)
Carrell, J.B., Lieberman, D.I.: Vector fields and Chern numbers. Math. Ann. 225, 263–273 (1977)
Cartan, H., Eilenberg, S.: Homological algebra, Princeton Landmarks in Mathematics. Princeton University Press, Princeton (1999)
Deligne, P.: Théorème de Lefschetz et critères de dégénerescence des suites spectrales, Institut des Hautes Études Scientifiques. Publ. Math. 35, 107–126 (1968)
Feng, H., Ma, X.: Transversal holomorphic sections and localization of analytic torsions. Pacific J. Math. 219, 255–270 (2005)
Grothendieck, A.: Éléments de géométrie algébrique. III. Étude cohomologique des faisceaux cohérents. I, Inst. Hautes Études Sci. Publ. Math. 11:1–167 (1961)
Hochschild, G., Serre, J.-P.: Cohomology of Lie algebras. Ann. Math. 57, 591–603 (1953)
Liu, K.: Holomorphic equivariant cohomology. Math. Ann. 303, 125–148 (1995)
Rubtsov, V.N.: Cohomology of Der-complex. Russian Math. Surv. 35(4), 190–191 (1980)
Rubtsov, V.N.: On the cohomology of the derivation complex of a vector bundle. (Russian), Ph.D. thesis, Minsk, Bielorussian State University, (1983)
Verdier, J.-L.: Des catégories dérivées des catégories abéliennes. Astérisque 239, (1996)
Acknowledgements
We thank Paul Bressler, Tony Pantev, Jean-Claude Thomas and Pietro Tortella for useful discussions. U.B. thanks the organizers of the “Jean-Louis Koszul in São Paulo, His Work and Legacy” workshop for their kind invitation.
Funding
Open access funding provided by Scuola Internazionale Superiore di Studi Avanzati - SISSA within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Claudio Gorodski.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors gratefully acknowledge financial support and hospitality during visits to Université d’Angers and sissa. Support for this work was provided by prin “Geometria delle varietà algebriche,” the infn project gast “Gauge and string theories”, the einstein Italo-Russian project “Integrability in topological string and field theory,’ and the DEFIMATH-Angers-sissa project “Generalized Lie algebroid strucures.” VR was partially supported by the Russian Foundation for Basic Research under the Grants RFBR 18-01-00461.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bruzzo, U., Rubtsov, V.N. Koszul complexes and spectral sequences associated with Lie algebroids. São Paulo J. Math. Sci. 15, 495–504 (2021). https://doi.org/10.1007/s40863-020-00199-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40863-020-00199-9