Derivation rings of Lie rings

Abstract

We establish some connections between Lie rings, their derivation rings and generalized derivations rings.

1 Introduction

Let A be a Lie ring (with addition “$+$” and multiplication “$[-,-]$”). An additive mapping $d:A\rightarrow A$ is called a derivation of A if

$$\begin{aligned} d([x,y])=[d(x),y]+[x,d(y)] \end{aligned}$$

for any $x,y\in A$. By ${\mathrm{Der}} A$ we denote the set of all derivations of A. It is well known that ${\mathrm{Der}} A$ is a Lie ring with respect to operations of the point-wise addition “$+$” and the point-wise Lie multiplication “$[-,-]$” defined by rules

$$\begin{aligned} (d+\delta )(r)=d(r)+\delta (r)\ \text{ and }\ \ [d,\delta ](r)=d(\delta (r))-\delta (d(r)) \end{aligned}$$

for all $r\in A$ and $d,\delta \in {\mathrm{Der}} A$ [11]. The mapping

$$\begin{aligned} {\mathrm{ad}}_a:A\ni x\mapsto [a,x]\in A \end{aligned}$$

determines a derivation ${\mathrm{ad}}_a$ of A (so-called inner derivation of A induced by $a\in A$). The set

$$\begin{aligned} {\mathrm{ad}} A=\{ {\mathrm{ad}}_a \mid a\in A\} \end{aligned}$$

of all inner derivations of A is an ideal in ${\mathrm{Der}} A$.

Let N be the set of positive integers,

$$\begin{aligned}{}[a_1,\ldots ,a_n,a_{n+1}]:=[[a_1,\ldots ,a_n],a_{n+1}] \end{aligned}$$

for any $n\in \text{ N }$ and $a_1,\ldots ,a_n, a_{n+1}\in A$. If $A_i\subseteq A$, then $[A_1,\ldots ,A_n]$ is a subgroup of the additive group $A^+$ of A generated by all $[a_1,\ldots ,a_n]$, where $a_i\in A_i$$(i=1,\ldots ,n)$. A Lie ring A is called:

• solvable if there exists $n\in \text{ N }$ such that $A^{(n)}=0$, where $A^{(1)}:=[A,A]=A'$, $A^{(2)}:=[A',A']=A''$ and $A^{(k+1)}=[A^{(k)},A^{(k)}]$ for any $k\in \text{ N }$,

• abelian if $A'=0$,

• perfect if $A'=A$,

• complete if its derivations are inner and the center $Z(A)=0$ is zero (i.e. A is centerless) [13].

Many authors have been investigated the structure of derivation algebra ${\mathrm{Der}} L$ and its relations with the structure of a (finite or infinite dimensional) Lie algebra L (see e.g. [6, 7, 9, 12, 23,24,25,26, 28, 30, 31] and others). In this way Leger [16] has investigated Lie algebras L over a field of characteristic 0 such that ${\mathrm{Der}} L={\mathrm{ad}} L$. Luks [20] has constructed an example of a Lie algebra over a field of characteristic zero with only inner derivations which is not complete. Su and Zhu [27, Theorem 1.1] have proved that the Lie algebra of all derivations of a centerless perfect Lie algebra (over any field) is complete. Augolopoulos [1] has constructed a class of complete Lie algebras over the complex numbers field that are not semisimple. Interesting results about complete Lie algebras were obtained by Meng and Wang (see [21], where further references can be found).

An additive mapping $F:A\rightarrow A$ is called a generalized derivation ofAassociated with a derivation$\delta \in {\mathrm{Der}} A$ (in the sence of Brešar [4]) if

$$\begin{aligned} F([x,y])=[F(x),y]+[x,\delta (y)] \end{aligned}$$

for any $x,y\in A$. The set of all generalized derivations of a Lie ring A we denote by

$$\begin{aligned} {\mathrm{GDer}} A. \end{aligned}$$

We will write$(F, \delta )\in {\mathrm{GDer}} A$if and only ifFis a generalized derivation ofAassociated with$\delta \in {\mathrm{Der}} A$. Since $(\delta ,\delta )\in {\mathrm{GDer}} A$ for any $\delta \in {\mathrm{Der}} A$, we conclude that

$$\begin{aligned} {\mathrm{ad}} A\subseteq {\mathrm{Der}} A\subseteq {\mathrm{GDer}} A. \end{aligned}$$

A generalized derivation F of A associated with an inner derivation ${\mathrm{ad}}_a\in {\mathrm{ad}} A$ is called a generalized inner derivation of A. By

$$\begin{aligned} {\mathrm{IGDer}} A \end{aligned}$$

we denote the set of all generalized inner derivations of A. Another types of generalized derivations was introduced in [8,9,10, 17, 29, 32] and others.

We shall use the following notation. Let$D={\mathrm{Der}} A$, $G={\mathrm{GDer}} A$, $\varDelta$be a nonempty subset ofD (respectively G). If $I\subseteq A$ and $\delta (I)\subseteq I$ for all $\delta \in \varDelta$, then we say that I is $\varDelta$-closed in A. If I is a $\varDelta$-closed ideal of A, then it is called a $\varDelta$-ideal of A. Moreover, $Z(A):=\{z\in A\mid za=az\ \text{ for } \text{ all }\ a\in A\}$ is the center of A.

Let $X\in \{0, \varDelta \}$. By a 0-ideal of R we mean an ideal of R. An ideal Y of a Lie ring A is called:

• X-semiprime if, for any X-ideal B of A, the condition $[B,B]\subseteq Y$ implies that $B\subseteq Y$ ,

• X-prime if, for any X-ideals B, C of A, the condition $[B,C]\subseteq Y$ implies that $B\subseteq Y$ or $C\subseteq Y$,

• X-simple if $[A,A]\nsubseteq Y$ and, for any proper X-ideal B of A, it is true that $B\subseteq Y$,

• X-primary if, for any X-ideals B, C of A, the condition $[B,C]\subseteq Y$ implies that $B\subseteq Y$ or

  

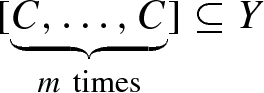  (1)

  for some $m\in \text{ N }$.

In particular, if the zero ideal 0 of A is a X-simple (respectively X-prime, X-semiprime or X-primary) Lie ring and $X=0$, then A is called simple (respectively prime, semiprime or primary). Moreover, A / Y is semiprime (respectively prime, simple or primary) if so is Y. Every $\varDelta$-prime Lie ring is $\varDelta$-semiprime and every $\varDelta$-simple Lie ring is $\varDelta$-prime.

The purpose of this paper is to study relationships between Lie rings A, their derivation rings ${\mathrm{Der}} A$ (in particular, inner derivation rings ${\mathrm{IDer}} A$) and generalized derivation rings ${\mathrm{GDer}} A$. In many cases every derivation of a simple Lie algebra is inner (see e.g. [11, 24, 34, 35] and others). Our first result is the following

Proposition 1

Let A be a Lie ring. Then we have:

• (1) if D is a simple Lie ring, then one of the following holds:

  • (a) A is abelian,

  • (b) $D={\mathrm{ad}} A$, A / Z(A) is a simple Lie ring and either

    • (i) $A=A'$ is simple, or

    • (ii) $A=A'+Z(A)$ and $A'$ is the smallest noncentral ideal of A,

• (2) if A is a D-simple Lie ring, then $A=A'$, $Z(A)=0$ and D is complete.

We say that a subring S is of finite index in A if its additive subgroup $S^+$ has finite index $|A:S|:=|A^+:S^+|$ in $A^+$. By analogy with group theory [22], we will say that a Lie ring A is a LieFC-ring if, for any $a\in A$, the centralizer

$$\begin{aligned} C_A(a)=\{ z\in A\mid [z,a]=0\} \end{aligned}$$

is of finite index in A. If A is FC, then for every $a\in A$ there exists an ideal $I_a$ of A such that $[a,I_a]=0$ (Corollary 4). In the proof of this result we use the following

Proposition 2

Let A be a Lie ring. If S is its subring of finite index, then there exists an ideal I of A such that $I\le S$ and $|A:I|<\infty$.

Since an inner derivation ${\mathrm{ad}}_a:A^+\rightarrow A^+$ is an endomorphism of the additive group $A^+$ for any $a\in A$,

$$\begin{aligned}{}[A,a]\ni [x,a]\mapsto x+C_A(a)\in A/C_A(a) \end{aligned}$$

is an additive group isomorphism and the kernel ${\mathrm{Ker}} \ {\mathrm{ad}}_a=C_A(a)$, we conclude that A is FC if and only if the image ${\mathrm{Im}} \ {\mathrm{ad}}_a$ is finite for any $a\in A$. If the set ${\mathrm{IDer}} A$ is finite (or equivalently $|A:Z(A)|<\infty$ by Proposition 3), then A is FC (Lemma 6), the commutator ideal $A'$ is finite and there exists a solvable ideal S of A such that $S\le A'$, $A'=A''+S$ and $A'/S$ is a direct summand of A / S (Corollary 6).

Derivations are very important in the study of structures of Lie algebras. Lie algebras with semisimple (in particular, simple) derivation algebras have been discussed by Hochschild [9], Block [3], de Ruiter [5], Elduque and Montaner [7], Walcher [34] and others. For example, it was proved in [9, Theorem 4.4] that a finite dimensional Lie algebra L over a field of characteristic 0 is semisimple if and only if its derivation algebra ${\mathrm{Der}} L$ is semisimple. In this way we prove the next result.

Theorem 1

Let A be a Lie ring. If A is a D-prime (respectively D-semiprime) Lie ring, then D is prime (respectively semiprime).

An additive mapping $T:A\rightarrow A$ is called a multiplier of A if

$$\begin{aligned} T([x,y])=[T(x),y] \end{aligned}$$

for all $x,y\in A$. Then we have

$$\begin{aligned} T([x,y])=T(-[y,x])=-[T(y),x]=[x,T(y)]. \end{aligned}$$

The set of all multipliers of A we denote by

$$\begin{aligned} {\mathrm{M}} (A). \end{aligned}$$

Obviously, for any $T\in {\mathrm{M}} (A)$, $(T,0)\in {\mathrm{GDer}} A$ and so

$$\begin{aligned} {\mathrm{M}} (A)\subseteq {\mathrm{IGDer}} A. \end{aligned}$$

We obtain the following

Theorem 2

Let A be a Lie ring. If ${\mathrm{GDer}} A/{\mathrm{M}} (A)$ is a prime (respectively semiprime, simple or primary) Lie ring, then Z(A) is a G-prime (respectively G-semiprime, G-simple or G-primary) ideal of A.

Any unexplained terminology is standard as in [13,14,15, 22, 33].

2 Inner derivations

We first give some information about inner derivation rings.

Lemma 1

Let A be a Lie ring. Then we have:

• (i) if $\varDelta$ is a subring of ${\mathrm{Der}} A$, S is a $\varDelta$-closed additive subgroup of A and ${\mathrm{ad}}_SA=\{ {\mathrm{ad}}_t \mid t\in S\}$, then $[{\mathrm{ad}}_SA,\varDelta ]\subseteq {\mathrm{ad}}_SA$ (where ${\mathrm{ad}}_AA={\mathrm{ad}} A$),

• (ii) if K is an ideal of A, then ${\mathrm{ad}}_K A$ is an ideal of ${\mathrm{ad}} A$,

• (iii) if $\varPhi$ is an ideal of ${\mathrm{Der}} A$, then

  $$\begin{aligned} \nabla _\varPhi =\{x\in A\mid {\mathrm{ad}}_x\in \varPhi \} \end{aligned}$$

  is a D-ideal of A,

• (iv) if $\varPhi$ is an ideal of $\mathrm{ad}A$, then $\nabla _\varPhi$ is an ideal of A,

Proof

(i):

If $s\in S$ and $\delta \in \varDelta$, then $\delta (s)\in S$ and so

$$\begin{aligned}{}[\delta ,{\mathrm{ad}}_s]={\mathrm{ad}}_{\delta (s)}\in \mathrm{ad}_SA. \end{aligned}$$

(ii):

Since K is an $({\mathrm{ad}} A)$-closed additive subgroup of A, the result follows from part (i).

(iii):

If $x,y\in \nabla _\varPhi$, $a\in A$ and $\delta \in D$, then ${\mathrm{ad}}_{x-y}={\mathrm{ad}}_x-{\mathrm{ad}}_y,\ {\mathrm{ad}}_{[a,x]}=[{\mathrm{ad}}_a,{\mathrm{ad}}_x],\ {\mathrm{ad}}_{\delta (x)}=[\delta ,{\mathrm{ad}}_x]\in \varPhi$ and consequently $x-y,\ [a,x],\ \delta (x)\in \nabla _\varPhi$.

(iv):

By the same argument as in part (iii).

$\square$

Lemma 2

Let A be a Lie ring and $\varDelta$ a subring of ${\mathrm{Der}} A$. Then we have:

• (i) if B is a $\varDelta$-ideal of A, then $\{ \delta \in \varDelta \mid \delta (A)\subseteq B\}$ is an ideal of $\varDelta$,

• (ii) if B is an ideal of A, then $\{ \delta \in {\mathrm{ad}} A\mid \delta (A)\subseteq B\}$ is an ideal of ${\mathrm{ad}} A$,

• (iii) if $\varPhi$ is an ideal of ${\mathrm{ad}} A$, then $\{ a\in A\mid \delta (a)=0\ \text{ for } \text{ all }\ \delta \in \varPhi \}$ is an ideal of A,

• (iv) if B is a $\varDelta$-ideal of A, then $\{ x\in A\mid {\mathrm{ad}}_x(A)\subseteq B\}$ is a $\varDelta$-ideal of A,

• (v) if B is a $\varDelta$-ideal of A, then the centralizer $C_A(B)=\{ x\in A\mid {\mathrm{ad}}_x(B)=0\}$ of B in A is a $\varDelta$-ideal of A,

• (vi) [19, Proposition 2.2] there exists the Lie ring isomorphism

  $$\begin{aligned} {\mathrm{ad}} A\ni {\mathrm{ad}}_a\mapsto a+Z(A)\in A/Z(A), \end{aligned}$$

• (vii) if B is a $\varDelta$-ideal of A, then the center Z(B) is a $\varDelta$-ideal of A.

Proof

By routine calculations. $\square$

Lemma 3

Let A be a $\varDelta$-semiprime Lie ring, B its nonzero $\varDelta$-ideal, where $\emptyset \ne \varDelta \subseteq D$. Then the following are true:

• (i) A is nonabelian,

• (ii) $Z(A)=0$, i.e. A is centerless,

• (iii) $B\cap C_A(B)=0$,

• (iv) $Z(B)=0$,

• (v) $C_A(A')=0$,

• (vi) if A is $\varDelta$-prime, then $C_A(B)=0$.

Proof

(i)–(ii) Evident.

(iii) Inasmuch as $B\cap C_A(B)$ is a $\varDelta$-ideal of A in view of Lemma 3 (v) and

$$\begin{aligned} \left[ B\bigcap C_A(B),B\bigcap C_A(B)\right] =0, \end{aligned}$$

we deduce that $B\cap C_A(B)=0$.

(iv) In view of Lemma 2 (vii), [A, Z(B)] is a $\varDelta$-ideal of A and $[A,Z(B)]\subseteq Z(B)$. However,

$$\begin{aligned}{}[[A,Z(B)],[A,Z(B)]]=0 \end{aligned}$$

and therefore $[A,Z(B)]=0$. Then we find that $Z(B)\subseteq Z(A)=0$.

(v) It is easy to see that $A'$ is nonzero,

$$\begin{aligned}{}[z,A]\subseteq A'\bigcap C_A(A')=0 \end{aligned}$$

for any $z\in C_A(A')$ and so $z\in Z(A)$. Hence $z=0$ by (ii).

(vi) It holds in view of Lemma 2 (v). $\square$

Corollary 1

Let A be a Lie ring. Then we have:

• (i) if A is simple, then ${\mathrm{ad}} A$ is a simple Lie ring,

• (ii) if ${\mathrm{ad}} A$ is simple, then A / Z(A) is a simple Lie ring and

  $$\begin{aligned} A=A'+Z(A) \end{aligned}$$

  (2)

  (and then $A'$ is the smallest noncentral ideal of A),

• (iii) if A is a prime (respectively semiprime) Lie ring, then so is ${\mathrm{ad}} A$,

• (iv) if A / Z(A) is a primary Lie ring, then so is ${\mathrm{ad}} A$,

• (v) if ${\mathrm{ad}} A$ is prime (respectively semiprime or primary), then so is A / Z(A).

Proof

(i) and (iii)–(v) It follows in view of Lemma 2 (vi).

(ii) Obviously that A is nonabelian and therefore $A'\ne 0$. Lemma 2 (vi) implies that the quotient Lie ring A / Z(A) is simple. Using the fact that

$$\begin{aligned} {\mathrm{ad}}_{A'}A=[{\mathrm{ad}} A,{\mathrm{ad}} A]={\mathrm{ad}} A \end{aligned}$$

(3)

and $A'\nsubseteq Z(A)$ we deduce that A satisfies Eq. (2). $\square$

Corollary 2

Let A be a semiprime Lie ring. Then ${\mathrm{ad}} A$ is simple if and only if so is A.

Let p be a prime,

$$\begin{aligned} F(A):=\{ a\in A\mid a \ \text{ is } \text{ of } \text{ finite } \text{ order } \text{ in } \text{ the } \text{ additive } \text{ group }\ A^+\} \end{aligned}$$

the torsion part and

$$\begin{aligned} F_p(A):=\{ a\in F(A)\mid p^na=0\ \text{ for } \text{ some } \text{ nonnegative } \text{ integer }\ n\} \end{aligned}$$

the torsion p-part of a Lie ring A.

Remark 1

If A is a $\varDelta$-prime Lie ring, then one of the following holds:

(i):

$F(A)=0$,

(ii):

$pA=0$ for some prime p.

Indeed, if F(A) is nonzero, then $F_p(A)\ne 0$ for some prime p. From $pA\ne 0$ it follows that

$$\begin{aligned} \varOmega _1:=\{ a\in F_p(A)\mid pa=0\}\ne 0 \end{aligned}$$

and $[pA,\varOmega _1]=0$, a contradiction. Hence $pA=0$.

Lemma 4

Let A be a centerless Lie ring. If $\varPhi$ is an ideal of ${\mathrm{Der}} A$, then

$$\begin{aligned} \varPhi \bigcap {\mathrm{ad}} A=0 \Leftrightarrow \varPhi =0. \end{aligned}$$

Proof

In fact, if $\varPhi \cap {\mathrm{ad}} A=0$, then $0=[d,{\mathrm{ad}}_a]={\mathrm{ad}}_{d(a)}$ and therefore $d(a)\in Z(A)$ for any $d\in \varPhi$ and $a\in A$. Consequently $d=0$. $\square$

Lemma 5

If A is a D-simple Lie ring, then

$$\begin{aligned} \mathrm{ad}A=[{\mathrm{ad}} A,{\mathrm{ad}} A] \end{aligned}$$

(4)

is the smallest nonzero ideal of D (and so A is perfect).

Proof

It is easy to see that $A'$ is a nonzero D-ideal of A, $Z(A)=0$ and therefore $A'=A$ by Corollary 1. Let $\varPhi$ be a nonzero ideal of D. By Lemma 4,

$$\begin{aligned} \varPhi _1:=\varPhi \bigcap {\mathrm{ad}} A\ne 0. \end{aligned}$$

Then $\nabla _{\varPhi _1}\ne 0$ is a D-ideal of A by Lemma 1(iii) and consequently $\nabla _{\varPhi _1}=A$. Then ${\mathrm{ad}} A\subseteq \varPhi$, Eqs. (4) and (3) are true and ${\mathrm{ad}} A$ is the smallest nonzero ideal of D. $\square$

Corollary 3

Let A be a Lie ring. Then the following hold:

• (1) $[{\mathrm{ad}} A,{\mathrm{ad}} A]$ is a simple (respectively semiprime, prime or primary) Lie ring if and only if so is

  $$\begin{aligned} A'\Big /\left( A'\bigcap Z(A)\right) , \end{aligned}$$

• (2) if A is semiprime and $[{\mathrm{ad}} A,{\mathrm{ad}} A]$ is a simple Lie ring, then $A'$ is the smallest nonzero ideal of A.

Proof

• (1) If $a,b\in A$, then the rule

  $$\begin{aligned}{}[{\mathrm{ad}} A,{\mathrm{ad}} A]\ni [{\mathrm{ad}}_a,{\mathrm{ad}}_b]\mapsto [a,b]+\left( A'\bigcap Z(A)\right) \in A'\Big /\left( A'\bigcap Z(A)\right) \end{aligned}$$

  induces a Lie ring isomorphism.

• (2) Let I be a nonzero ideal of A. Then $0\ne [I,I]\subseteq A'$. Since ${\mathrm{ad}}_IA$ is a nonzero ideal of the Lie ring ${\mathrm{ad}} A$, we deduce that

  $$\begin{aligned} {\mathrm{ad}}_{[I,I]}A=[{\mathrm{ad}}_IA,{\mathrm{ad}}_IA]=[{\mathrm{ad}} A,{\mathrm{ad}} A]={\mathrm{ad}}_{A'}A. \end{aligned}$$

  Moreover, $Z(A)=0$ and therefore $A'=[I,I]\subseteq I$. Hence $A'$ is the smallest nonzero ideal of A.

$\square$

3 Lie FC-rings

Proposition 2 is analogous with the Lewin result [18, Lemma 1].

Proof of Proposition 2

Since every Lie ring is a Leibniz ring, Proposition 2 follows from [2, Proposition 5.2]. We prove it here in order to have the paper more self-contained. Suppose that $|A:S|=n$ for some $n\in \text{ N }$ and the quotient group

$$\begin{aligned} A^+/S^+=\{ a_1+S^+,\ldots ,a_n+S^+\} \end{aligned}$$

for some elements $a_1,\ldots ,a_n\in A$. Let $s\in S$. The rule

$$\begin{aligned} g_s:A^+/S^+\ni a+S^+\mapsto [a,s]+S^+\in A^+/S^+ \end{aligned}$$

determines an endomorphism $g_s$ of the additive group $A^+/S^+$. Since $A^+/S^+$ is finite, its endomorphism ring ${\mathrm{End}} (A^+/S^+)$ is the ones. Then the group homomorphism

$$\begin{aligned} g:S^+\ni s \mapsto g_s\in {\mathrm{End}} (A^+/S^+) \end{aligned}$$

has the kernel $K_g:=\{ s\in S\mid [A,s]\subseteq S\}$ of finite index in S. The rule

$$\begin{aligned} \varphi _{(i_1,\ldots ,i_k)}:K_g\ni w\mapsto \varphi _{(w,i_1,\ldots ,i_k)}\in {\mathrm{End}} (A^+/S^+), \end{aligned}$$

where $k\in \text{ N }$, $(i_1,\ldots ,i_k)\in {\text{ N }}^k$ and

$$\begin{aligned} \varphi _{(w,i_1,\ldots ,i_k)}:A^+/S^+\ni r+S^+\mapsto [[\ldots [[w,a_{j_{i_1}}],a_{j_{i_2}}],\ldots ,a_{j_{i_k}}],r]+S^+\in A^+/S^+ \end{aligned}$$

is an endomorphism of $A^+/S^+$, determines a group homomorphism. Then the set

$$\begin{aligned} \{ \varphi _{(w,i_1,\ldots ,i_k)}\mid w\in K_g,\ k\in {\text{ N }}\ \text{ and }\ \ (i_1,\ldots ,i_k)\in {\text{ N }}^k\} \end{aligned}$$

is finite, every kernel ${\mathrm{Ker}}\ \varphi _{(w,i_1,\ldots ,i_k)}$ is of finite index in $K_g$ and therefore we deduce that

$$\begin{aligned} I:=\bigcap _{\begin{array}{c}w\in K_g\\ (i_1,\ldots ,i_k)\in {\text{ N }}^k\end{array}}{\mathrm{Ker}}\ \varphi _{(w,i_1,\ldots ,i_k)} \end{aligned}$$

is of finite index in $K_g$ (and consequently in A). Moreover, $I\le S$ and

for any $k\in {\mathbf{N}}$. Hence

is an ideal of finite index in A such that $I_0\le S$. $\square$

Corollary 4

If A is a Lie FC-ring, then, for every $a\in A$, there exists an ideal $I_a$ of finite index in A such that $[a,I_a]=0$.

The next proposition is an analogue of [2, Theorem 5.2].

Proposition 3

Let A be a Lie ring. Then the set ${\mathrm{IDer}} A$ is finite if and only if $|A:Z(A)|<\infty$.

Proof

$(\Rightarrow )$ Suppose that ${\mathrm{IDer}} A= \{ {\mathrm{ad}}_{u_i}\mid i=1,\ldots ,m\}$ for some $m\in {\text{ N }}$ and $u_1,\ldots ,u_m\in A$. If $x\in A$, then there exists $s=s(x)\in {\text{ N }}$ such that $1\le s\le m$ and ${\mathrm{ad}}_x={\mathrm{ad}}_{u_s}$. Hence $x\in u_s+Z(A)$ and $A/Z(A)=\{u_i+Z(A)\mid i=1,\ldots ,m\}$ is finite.

$(\Leftarrow )$ Since

$$\begin{aligned} A/Z(A)=\{ a_1+Z(A),\ldots ,a_n+Z(A)\} \end{aligned}$$

(5)

for some $n\in {\text{ N }}$ and $a_1,\ldots ,a_n\in A$ and, for every $x\in A$, there exists $i=i(x)$$(1\le i\le n)$ such that $x\in a_i+Z(A)$, we see that ${\mathrm{ad}}_{x}={\mathrm{ad}}_{a_i}$. Thus

$$\begin{aligned} {\mathrm{IDer}} A=\{ {\mathrm{ad}}_x\mid x\in A\}= \{ {\mathrm{ad}}_{a_i}\mid i=1,\ldots ,n\} \end{aligned}$$

is finite. $\square$

Corollary 5

Let A be a Lie ring. Then the following hold:

• (1) if $|A:Z(A)|<\infty$, then the commutator ideal $A'$ is finite,

• (2) if ${\mathrm{IDer}} A$ is finite, then the commutator ideal $A'$ is finite.

Proof

For a proof, see [2, Lemma 5.12]. $\square$

Lemma 6

Let A be a Lie ring. Then the following hold:

• (1) if $A'$ is finite, then A is FC,

• (2) if ${\mathrm{IDer}} A$ is finite, then A is FC.

Proof

(1) Let $a\in A$. Since ${\mathrm{ad}}_a$ is an endomorphism of $A^+$ and $Z(A)\le C_A(x)={\mathrm{Ker}}\ {\mathrm{ad}}_a$, we conclude that

$$\begin{aligned} A/C_A(a)=A/{\mathrm{Ker}}\ {\mathrm{ad}}_a\cong [A,a]\le A' \end{aligned}$$

is finite for any $a\in A$. Hence A is FC.

(2) follows immediately from part (1). $\square$

Lemma 7

If A is a finitely generated Lie FC-ring, then its commutator ideal $A'$ is finite.

Proof

Suppose that A is generated by some elements $x_1,\ldots ,x_n\in A$. Inasmuch as $|A:C_A(x_i)|<\infty$ for $i=1,\ldots ,n$ and

$$\begin{aligned} Z(A)=\bigcap _{i=1}^n C_A(x_i), \end{aligned}$$

we have that Z(A) is of finite index in A and, by Corollary 5, $A'$ is finite. $\square$

Lemma 8

If F is a finite ideal of a Lie ring A, then $|A:C_A(F)|<\infty$.

Proof

Suppose that $F=\{x_1,\ldots ,x_n\}$. Then

$$\begin{aligned}{}[x_i,A]\cong A/C_A(x_i) \end{aligned}$$

for any $x_i\in F$ what implies that

$$\begin{aligned} \bigcap _{i=1}^nC_A(x_i)\le C_A(F) \end{aligned}$$

and the result follows. $\square$

Recall that M is a minimal ideal of a Lie ring A if $M\ne 0$ and, for any ideal I of A, the implication

$$\begin{aligned} 0\le I\le M\Rightarrow I=0\ \text{ or }\ I=M \end{aligned}$$

holds. If M is a minimal nonzero ideal of A, then $[M,M]=M$ (i.e. M is perfect) or $[M,M]=0$.

Lemma 9

If M is a perfect minimal ideal of a Lie ring A, then the quotient Lie ring $A/C_A(M)$ is prime.

Proof

If B, C are ideals of A such that $[B,M]\ne 0$ and $[C,M]\ne 0$, then $[B,M]=M=[C,M]$ and $M\le [B,C]$. This yields that $[[B,C],M]\ne 0$ and so $A/C_A(M)$ is prime. $\square$

Lemma 10

If F is a finite ideal of a Lie ring A, then the following hold:

• (1) if F is a perfect minimal ideal, then $A=F\oplus C_A(F)$ is a direct sum of ideals,

• (2) if F does not contain nonzero nonabelian ideal of A, then there exist perfect minimal ideals $B_1,\ldots ,B_k$ of A such that $B_i\le F$$(i=1,\ldots k)$, $A=B_1\oplus \cdots \oplus B_k\oplus C$ is a direct sum of ideals and $F\cap C$ is solvable,

• (3) F contains a solvable ideal S of A such that $F=F'+S$ and the quotient Lie ring $A/S=(F/S)\oplus K$ is a direct sum for some its ideal K.

Proof

• (1) By Lemmas 9 and 8, $K:=A/C_A(F)$ is a finite prime (and therefore simple) Lie ring. Since K is perfect and $F\nsubseteq C_A(F)$, we deduce that

  $$\begin{aligned} (F+C_A(F))/C_A(F)=A/C_A(F) \end{aligned}$$

  and the result follows.

• (2) It is easy to see that F contains a minimal ideal $B_1$ of A and $B_1$ is nonabelian. By part (1), $A=B_1\oplus C_A(B_1)$ is a direct sum of ideals. Since F is finite, we obtain the assertion by finite number of steps.

• (3) Suppose that S is an ideal generated by all solvable ideals of A that are contained in F. Then F / S is a finite semiprime Lie ring (and consequently it is a direct sum of finitely many nonabelian minimal ideals of A / S) in view of part (1). This gives that $F=F'+S$. The rest it follows from part (2).

$\square$

Corollary 6

Let A be a Lie ring. If ${\mathrm{IDer}} A$ is finite, then the commutator ideal $A'$ is finite and there exists a solvable ideal S of A such that $S\le A'$, $A'=A''+S$ and $A/S=(A'/S)\oplus K$ is a direct sum of ideals for some abelian ideal K.

Proof

By Proposition 3 and Corollary 5, $A'$ is finite and so the result holds by Lemma 10. $\square$

4 Generalized derivations

Let

$$\begin{aligned} {\mathrm{CDer}} A:=\{ h\in {\mathrm{Der}} A\mid h(A)\subseteq Z(A)\} \end{aligned}$$

be the set of all central derivations of A. The structural properties of a Lie algebra L with central inner derivations (i.e. $\mathrm{ad}L\subseteq {\mathrm{CDer}} L$) was studied by Tôgô [30].

Lemma 11

Let A be a Lie ring. Then:

• (i) ${\mathrm{GDer}} A$ is a Lie ring,

• (ii) $F(Z(A))\subseteq Z(A)$ for any $F\in {\mathrm{GDer}} A$,

• (iii) ${\mathrm{CDer}} A$ is an ideal of ${\mathrm{GDer}} A$,

• (iv) ${\mathrm{GDer}} A={\mathrm{M}} (A)+{\mathrm{Der}} A$, where ${\mathrm{M}} (A)$ is an ideal of ${\mathrm{GDer}} A$, and

  $$\begin{aligned} {\mathrm{M}} (A)\bigcap {\mathrm{Der}} A\subseteq {\mathrm{CDer}} A, \end{aligned}$$

• (v) ${\mathrm{IGDer}} A={\mathrm{M}} (A)+{\mathrm{ad}} A$, where ${\mathrm{M}} (A)$ is an ideal of ${\mathrm{IGDer}} A$, and

  $$\begin{aligned} {\mathrm{M}} (A)\bigcap {\mathrm{ad}} A\subseteq {\mathrm{CDer}} A, \end{aligned}$$

• (vi) if B is a D-closed ideal of A, then

  $$\begin{aligned} {\mathrm{I_BGDer}} A:=\{ F\in {\mathrm{GDer}} A\mid F\ \text{ is } \text{ associated } \text{ with } \text{ some } {\mathrm{ad}}_a\text{, } \text{ where }\ a\in B\} \end{aligned}$$

  (in particular, ${\mathrm{M}} (A)={\mathrm{I_OGDer}} A={\mathrm{I_{Z(A)}GDer}} A\subseteq {\mathrm{IGDer}} A:={\mathrm{I_AGDer}} A$) is an ideal of ${\mathrm{GDer}} A$,

• (vii) $C(A):=\{ k\in \mathrm{M}(A)\mid k(A)\subseteq Z(A)\}$ is an ideal of ${\mathrm{GDer}} A$,

• (viii) if $(F, \delta ), (F,\mu )\in {\mathrm{GDer}} A$, then $\delta +{\mathrm{CDer}} A=\mu +{\mathrm{CDer}} A$,

• (ix) if $(F, {\mathrm{ad}}_a), (F,{\mathrm{ad}}_b)\in {\mathrm{GDer}} A$ for some $a,b\in A$, then $[a-b,A]\subseteq Z(A)$.

Proof

Assume that $(F,\delta ),(H,d)\in G$, $T\in {\mathrm{M}} (A)$, $h\in {\mathrm{CDer}} A$ and $x,y\in A$.

(i):

We see that $(F-H,\delta -d)\in G$,

$$\begin{aligned} \begin{array}{c} [F,H]([x,y])=F([H(x),y]+[x,d(y)])-H([F(x),y]+[x,\delta (y)])\\ =[[F,H](x),y]+[x,[\delta ,d](y)]\end{array} \end{aligned}$$

and so $([F,H],[\delta , d])\in G$.

(ii):

Evident.

(iii):

Since $h(A)\subseteq Z(A)$ for $h\in {\mathrm{CDer}} A$, we have that $[F,h](A)\subseteq Z(A)$, i.e. $[F,h]\in {\mathrm{CDer}} A$.

(iv):

The equality

$$\begin{aligned}{}[F,T]([x,y])=[[F,T](x),y] \end{aligned}$$

implies that $[F,T]\in {\mathrm{M}} (A)$ and so ${\mathrm{M}} (A)$ is an ideal of G. Moreover,

$$\begin{aligned} (\delta - F)([x,y])=[\delta (x),y]+[x,\delta (y)]-[F(x),y]-[x,\delta (y)]=[(\delta -F)(x),y] \end{aligned}$$

and thus $\delta -F\in {\mathrm{M}} (A)$. If $h\in D\cap {\mathrm{M}} (A)$, then

$$\begin{aligned}{}[h(x),y]=h([x,y])=[h(x),y]+[x,h(y)]. \end{aligned}$$

From this it follows $[x,h(y)]=0$ and therefore $h(A)\subseteq Z(A)$.

(v):

By the same argument as in (iv).

(vi):

If $(K,{\mathrm{ad}}_a),(M,{\mathrm{ad}}_b)\in {\mathrm{I_BGDer}} A$, then $(K-M,{\mathrm{ad}}_{a-b})\in {\mathrm{I_BGDer}} A$ and

$$\begin{aligned}{}[F,K]([x,y])= & {} F([K(x),y]+[x,\mathrm{ad}_a(y)])-K([F(x),y]+[x,\delta (y)])=\nonumber \\= & {} [[F,K](x),y]+[x,{\mathrm{ad}}_{\delta (a)}(y)] \end{aligned}$$

(6)

that is $([F,K], {\mathrm{ad}}_{\delta (a)})\in {\mathrm{I_BGDer}} A$.

(vii):

If $k\in C(A)$, then

$$\begin{aligned}{}[F,k]([x,y])=[[F,k](x),y]=0 \end{aligned}$$

and consequently $[F,k]\in C(A)$.

(viii)–(ix):

If $(F,\delta ),(F,\mu )\in G$ for some $\delta ,\mu \in D$, then

$$\begin{aligned}{}[x, \delta (y)]=[x,\mu (y)] \end{aligned}$$

and therefore $[x,(\delta -\mu )(y)]=0$. This means that $(\delta -\mu )(A)\subseteq Z(A)$ and the result follows.

$\square$

Corollary 7

Let A be a Lie ring. Then the following hold:

• (1) if $Z(A)=0$, then

  $$\begin{aligned} {\mathrm{GDer}} A={\mathrm{M}} (A)+{\mathrm{Der}} A,\ {\mathrm{IGDer}} A={\mathrm{M}} (A)+{\mathrm{ad}} A\ \text{ and }\ {\mathrm{M}}(A)\bigcap {\mathrm{Der}} A=0, \end{aligned}$$

• (2) if A is a simple (respectively semiprime or prime) ring, then the Lie rings ${\mathrm{GDer}} A/{\mathrm{M}} (A)$ and ${\mathrm{Der}} A$ are isomorphic.

Proof

• (1) If $Z(A)=0$, then ${\mathrm{CDer}} A=0$ and the result holds by Lemma 11 (iv) and (v).

• (2) Since Z(A) is an ideal of A, we deduce that $Z(A)=0$. The rest follows in view of part (1).

$\square$

Let $\varPhi \subseteq {\mathrm{GDer}} A$, $\varGamma \subseteq {\mathrm{Der}} A$,

$$\begin{aligned} T_{\varPhi }= & {} \{ d\in {\mathrm{Der}} A\mid \ \text { there is }H\in \varPhi \text { that is associated with }d\in {\mathrm{Der}} A\},\\ U_{\varGamma }= & {} \{ H\in {\mathrm{GDer}} A\mid H\ \text{ is } \text{ associated } \text{ with } \text{ some }\ \ d\in \varGamma \} \end{aligned}$$

and

$$\begin{aligned} \varSigma _\varPhi =\{ a\in A\mid \ \text { there exists }H\in \varPhi \text { that is associated with }\ {\mathrm{ad}}_a\}. \end{aligned}$$

Lemma 12

Let A be a Lie ring. Then the following hold:

• (i) if $\varPhi$ is an ideal of ${\mathrm{GDer}} A$, then $T_{\varPhi }$ is an ideal of ${\mathrm{Der}} A$,

• (ii) if $\varGamma$ is an ideal of ${\mathrm{Der}} A$, $U_{\varGamma }$ is a nonzero ideal of ${\mathrm{GDer}} A$ (in particular, $U_0={\mathrm{M}} (A)$),

• (iii) if $\varPhi$ is an ideal of ${\mathrm{IGDer}} A$ (respectively ${\mathrm{GDer}} A$), then $\varSigma _{\varPhi }$ is an ideal (respectively a D-ideal) of A.

Proof

For a proof, see [2, Lemma 5.7]. $\square$

Lie algebras L with abelian derivation algebras ${\mathrm{Der}} L$ was studied, in particular, in [29].

Lemma 13

Let A be a Lie ring and $(F,d)\in {\mathrm{GDer}} A$. Then we have:

• (i) if $F=0$, then $d(A)\subseteq Z(A)$,

• (ii) if $d(A)\subseteq Z(A)$, then $F\in {\mathrm{M}} (A)$,

• (iii) if ${\mathrm{GDer}} A$ is an abelian Lie ring, then ${\mathrm{Der}} A$ is abelian,

• (iv) if $A\ne 0$, then ${\mathrm{M}}(A)\ne 0$.

Proof

For a proof, see [2, Lemma 5.4]. $\square$

Lemma 14

Let A be a Lie ring and $(M,{\mathrm{ad}}_a)\in {\mathrm{IGDer}} A$. Then the following hold:

• (i) if $M=0$, then $[a,A]\subseteq Z(A)$,

• (ii) if $[a,A]\subseteq Z(A)$, then $M\in {\mathrm{M}} (A)$,

• (iii) if ${\mathrm{IGDer}} A$ is an abelian Lie ring, then ${\mathrm{ad}} A$ is abelian,

• (iv) if A is abelian, then ${\mathrm{IGDer}} A={\mathrm{M}} (A)$.

Proof

For a proof, see [2, Lemmas 5.4 and 5.5]. $\square$

Lemma 15

Let A be a Lie ring, B its ideal. Then:

• (i) if $\varPhi$ is an ideal of ${\mathrm{GDer}} A$, then $\varPhi \cap {\mathrm{IGDer}} A=0$ implies that $[\delta (A),A]\subseteq Z(A)$ for any $\delta \in T_{\varPhi }$,

• (ii) the following conditions are equivalent:

  • (a) ${\mathrm{I_BGDer}} A \subseteq {\mathrm{M}} (A)$,

  • (b) $B\subseteq Z(A)$,

  • (c) ${\mathrm{ad}}_BA=0$,

• (iii) there exist Lie ring isomorphisms:

  • (d)
    $$\begin{aligned} {\mathrm{Der}} A/{\mathrm{CDer}} A\ni \delta +{\mathrm{CDer}} A\mapsto \delta +{\mathrm{M}} (A)\in {\mathrm{GDer}} A/{\mathrm{M}} (A), \end{aligned}$$
  • (e)
    $$\begin{aligned}&{\mathrm{ad}} A\big /\left( {\mathrm{ad}} A\bigcap {\mathrm{CDer}} A\right) \ni {\mathrm{ad}}_a+\left( {\mathrm{ad}} A\bigcap {\mathrm{CDer}} A\right) \mapsto {\mathrm{ad}}_a \\&\quad +\,{\mathrm{M}} (A)\in {\mathrm{IGDer}} A/{\mathrm{M}} (A). \end{aligned}$$

Proof

(i) If $(F,\delta )\in \varPhi$ and $(H,{\mathrm{ad}}_a)\in \mathrm{IGDer}A$, then $([F,H],{\mathrm{ad}}_{\delta (a)})\in {\mathrm{IGDer}} A$ and so ${\mathrm{ad}}_{\delta (a)}\in {\mathrm{CDer}} A$ by Lemma 14 (i).

(ii)–(iii) are evident. $\square$

Corollary 8

Let A be a Lie ring. If ${\mathrm{ad}} A$ is a semiprime (respectively prime or simple) Lie ring, then ${\mathrm{IGDer}} A/ {\mathrm{M}} (A)$ is a semiprime (respectively prime, or simple) Lie ring.

Proof

If $a\in A$ and ${\mathrm{ad}}_b\in {\mathrm{CDer}} A \cap {\mathrm{ad}} A$, then $[a,b]\in Z(A)$ and $[{\mathrm{ad}}_a,{\mathrm{ad}}_b]={\mathrm{ad}}_{[a,b]}=0$. Then ${\mathrm{CDer}} A \cap {\mathrm{ad}} A=0$ because ${\mathrm{ad}} A$ is semiprime (respectively prime or simple) and so ${\mathrm{ad}} A$ is isomorphic to ${\mathrm{IGDer}} A/{\mathrm{M}}(A)$ by Lemma 15 (iii). $\square$

Lemma 16

Let A be a nonnilpotent Lie ring. If A is primary, then the quotient Lie ring so is ${\mathrm{IGDer}} A/{\mathrm{M}} (A)$.

Proof

Assume that $\varPhi , \varLambda$ are ideals of ${\mathrm{IGDer}} A$ such that $[\varPhi ,\varLambda ]=0$. By Lemma 14 (i), $[[\varSigma _\varPhi , \varSigma _\varLambda ],A]\subseteq Z(A)$. Since A is nonnilpotent primary (and therefore $Z(A)=0$), we deduce that $[\varSigma _\varPhi ,\varSigma _\varLambda ]=0$. This implies that $\varSigma _\varPhi =0$ (and then $\varPhi \subseteq {\mathrm{M}} (A)$) or

(and consequently

for some positive integer m. Hence ${\mathrm{IGDer}} A/{\mathrm{M}} (A)$ is a primary Lie ring. $\square$

5 Proofs

Proof of Proposition 1

(1) Let D be a simple Lie ring. Then D and A are nonzero. Since ${\mathrm{ad}} A$ is an ideal of D, we deduce that ${\mathrm{ad}} A=0$ (and then A is abelian) or ${\mathrm{ad}} A=D$. Assume that ${\mathrm{ad}} A=D$ and K is arbitrary noncentral ideal of A. Then

$$\begin{aligned} 0\ne {\mathrm{ad}}_KA={\mathrm{ad}} A \end{aligned}$$

by Lemma 1 (ii) and so $A=K+Z(A)$. This means that $\overline{A}:=A/Z(A)\cong {\mathrm{ad}} A$ is a simple Lie ring. Then it is nonabelian and therefore $\overline{A}'\ne \overline{0}$. Consequently $\overline{A}'=\overline{A}$ and $A=A'$ is simple or Eq. (2) follows.

(2) Let A be a D-simple Lie ring. Then $0\ne A'=A$ and $Z(A)=0$. By the same argument, as in the proof of Theorem 1.1 (i) from [27], $D={\mathrm{ad}} A$ is complete. $\square$

Proof of Theorem 1

(a) Let A be a D-prime Lie ring. Then $Z(A)=0$. Assume that $\varPhi ,\varLambda$ are nonzero ideals of D such that $[\varPhi , \varLambda ]=0$. By Lemma 4,

$$\begin{aligned} \varPhi _1:=\varPhi \bigcap {\mathrm{ad}} A\ne 0\ \text{ and }\ \varLambda _1:= \varLambda \bigcap {\mathrm{ad}} A\ne 0 \end{aligned}$$

and $\nabla _{\varPhi _1},\nabla _{\varLambda _1}$ are nonzero. Since

$$\begin{aligned} {\mathrm{ad}}_{[\nabla _{\varPhi _1},\nabla _{\varLambda _1}]}A=[{\mathrm{ad}}_{\nabla _{\varPhi _1}}A, {\mathrm{ad}}_{\nabla _{\varLambda _1}}A]=[\varPhi _1,\varLambda _1]=0, \end{aligned}$$

we see that

$$\begin{aligned} {[}\nabla _{\varPhi _1},\nabla _{\varLambda _1}{]}\subseteq Z(A)=0. \end{aligned}$$

By Lemma 1 (iii), $\nabla _{\varPhi _1}$ and $\nabla _{\varLambda _1}$ are D-ideals of A and we obtain a contradiction. Hence D is prime.

(b) If A is a D-semiprime Lie ring, then we can obtain that D is semiprime by the same argument as in part (a). $\square$

Proof of Theorem 2

(a) Assume that $G/{\mathrm{M}} (A)$ is a prime Lie ring and B, C are G-ideals of A such that

$$\begin{aligned}{}[B,C]\subseteq Z(A). \end{aligned}$$

(7)

Then ${\mathrm{I_BGDer}} A$, ${\mathrm{I_CGDer}} A$ are ideals of G by Lemma 11 (vi) and

$$\begin{aligned}{}[{\mathrm{I_BGDer}} A, {\mathrm{I_CGDer}} A]\subseteq {\mathrm{M}} (A) \end{aligned}$$

(8)

in view of Eq. (6). Then, by the primeness of $G/{\mathrm{M}}(A)$, ${\mathrm{I_BGDer}} A\subseteq {\mathrm{M}} (A)$ or ${\mathrm{I_CGDer}} A\subseteq {\mathrm{M}} (A)$ what implies that $B\subseteq Z(A)$ or $C\subseteq Z(A)$ by Lemma 15 (iii), and hence Z(A) is G-prime.

(b) If $G/{\mathrm{M}} (A)$ is a semiprime Lie ring, then we can prove by the same argument as in case (a).

(c) Assume that $G/{\mathrm{M}} (A)$ is a simple Lie ring and B is a G-ideal of A. Then ${\mathrm{I_BGDer}} A$ is an ideal of G and consequently

$$\begin{aligned} {\mathrm{I_BGDer}} A\subseteq {\mathrm{M}} (A) \end{aligned}$$

(and so $B\subseteq Z(A)$ by Lemma 15 (ii)) or

$$\begin{aligned} G/{\mathrm{M}} (A)={\mathrm{I_BGDer}} A/{\mathrm{M}} (A). \end{aligned}$$

In the second case we have ${\mathrm{M}}(A)\ne {\mathrm{I_BGDer}} A={\mathrm{IGDer}} A={\mathrm{GDer}} A$. Then ${\mathrm{ad}}_BA={\mathrm{ad}} A$ what gives that $A=B+Z(A)$. This means that Z(A) is G-simple.

(d) Let $G/{\mathrm{M}} (A)$ be a primary Lie ring and B, C be G-ideals of A such that Eq. (7) is true. Then Eq. (8) is true (and so ${\mathrm{I_BGDer}} A\subseteq {\mathrm{M}} (A))$ or

for some positive integer m). Then $B\subseteq Z(A)$ or

and consequently Z(A) is a G-primary ideal of A. $\square$