Abstract
Purpose
To determine the best kinetic model to be applied on dynamic brain [18 F]FDG PET images by characterizing the regional brain glucose metabolism of normal Göttingen minipigs.
Methods
Nine Göttingen minipigs were scanned with a clinical PET/CT tomograph, starting from the injection of an intravenous bolus of [18 F]FDG, for about 25 min. Dynamic images were reconstructed and nine brain regions of interest (ROI), plus a vascular region, were defined and time-activity curves (TAC) were determined.
Three kinetic models were considered for fitting with experimental TACs: one-tissue compartment model 1TC, two-tissue irreversible compartment model 2TCi and two-tissue reversible model 2TC. Akaike Information Criterion was considered to evaluate the goodness of each model fitting. Regional and global kinetic parameter values were evaluated, in addition to the partition coefficient, net influx rate and retention index (RI).
Results
Both 2TCi and 2TC models turned out to be good choices for the next analysis. Parameter values were very similar between the different brain regions, with similar values to when the brain as a whole is considered (kinetic parameters mean values, from 2TCi model: K1 = 1.0 ml/g/min, k2 = 0.49 min− 1, k3 = 0.034 min− 1, K1/k2 = 2.14ml/g, Ki =0.069 ml/g/min; from 2TC model: K1 = 1.10 ml/g/min, k2 = 0.54 min− 1, k3 = 0.058 min− 1, k4 = 0.039 min− 1, K1/k2 = 2.18 ml/g, Ki = 0.10 ml/g/min; RI mean ± sd: 0.147 ± 0.037 min− 1), with the exception of the cerebellum (mean values from the 2TCi model: K1 = 0.52 ml/g/min, k2 = 0.56 min− 1, k3 = 0.025 min− 1, K1/k2 = 0.98ml/g, Ki=0.022 ml/g/min; from 2TC model: K1 = 0.54 ml/g/min, k2 = 0.61 min− 1, k3 = 0.044 min− 1, k4 = 0.038 min− 1, K1/k2 = 0.95ml/g, Ki=0.032 ml/g/min; RI mean ± sd: 0.071 ± 0.018 min− 1).
Conclusion
The two-tissue model is able to describe the regional brain metabolism in Göttingen minipigs. Compared to the 2TCi model, in the 2TC model the k4 micro-parameter was also evaluated. This led to adjustments of the other microparameters, especially k3 and consequently the net influx rate Ki. For healthy minipigs, the glucose metabolism was similar in all of the brain regions analyzed, with the exception of the cerebellum, where the FDG uptake was lower.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The study of neurodegenerative diseases has increasingly required the use of larger animal models with more human-like brains. Although minipigs have been used for numerous biomedical applications and research [1, 2], they have recently been proposed for the study of neurodegenerative diseases because of certain neuroanatomical and neurophysiological similarities to humans [3]. Therefore, there is an increasing demand for in vivo non-invasive characterization of brain structure, function or metabolism over time using clinically relevant imaging tools.
The most suitable modalities for large animals in vivo imaging applications are also based on nuclear medicine techniques. In fact, the use of clinical scanners for positron emission tomography (PET) imaging on large animals such as minipigs, is regarded as the gold standard approach, especially to characterize organ-specific phenotypes in response to age, injury and novel treatments as preliminary studies, before being applied to humans [4, 5].
PET imaging can add value to longitudinal preclinical studies by enabling dynamic evaluations on the same animal in a clinically relevant manner. Therefore, the improvement in high-resolution in vivo PET imaging technologies provides a unique opportunity to better study the organ phenotype heterogeneity in real time, in a quantitative way and at the molecular level.
Brain dynamic PET images after injection of 2-[18 F]fluoro2-deoxyglucose ([ 18F]FDG) enable mapping of the cerebral glucose uptake (the brain’s main energy supply) using kinetic models from which it is possible to evaluate micro- or macro- kinetic parameters that describe the dynamics of the metabolism [6, 7].
In order to assess the extent of a pathology and, in the case of ongoing therapies, its follow-up, it is good to have reference values of the parameters under study in normal subjects.
To the best of our knowledge, no studies in the literature have evaluated the best kinetic model to be applied on dynamic brain [18 F]FDG PET images and provided kinetic parameters as reference values for normal Göttingen minipigs.
The aims of our study were: (a) to determine the kinetic model characterizing the brain glucose metabolism of normal Göttingen minipigs; (b) given the kinetic model, to establish micro-parameter kinetic values for normal brains; (c) to evaluate to what extent the values of the kinetic parameters change in different brain regions of interest.
2 Materials and Methods
2.1 Animal Preparation and Treatment
Nine overnight fasting male young Göttingen minipigs (4 to 6 months of age) were lightly sedated with a cocktail of tiletamine hydrochloride and zolazepam hydrochloride (3.5-5 mg kg− 1 i.m, depending on the animal’s response to sedation) and azaperonum (3–4 mg kg− 1 i.m, depending on the animal’s response to sedation). Deeper sedation was subsequently maintained with propofol intravenous infusion (2–3 mg kg− 1 h− 1) in spontaneously breathing animals during monitoring of glycaemia, heart rate and blood pressure. The entire scanning procedure lasted approximately 45 min. Upon completion of the PET scan, sedated pigs were transferred back to their home cage to recover. The physiological parameters of the minipigs are listed in Table 1 .
[18F]FDG dynamic images acquisition and Time-activity-curve generation.
The minipigs were scanned with a clinical PET/CT scanner (Discovery RX VCT 64-slice tomography - GE Healthcare, Milwaukee, WI, USA) in dorsal recumbency (supine) position.
Low-dose computed tomography (CT) (tube current 30 mA, tube voltage 120 kV) was firstly performed through the brain for attenuation correction for an effective dose of 1 mSv. A 3-dimensional (3D) list-mode dynamic PET acquisition was then performed for about 25 min. The PET dynamic acquisition started at the same time as the injection of an intravenous bolus of [18 F]FDG using a fully automated PET infusion system (MEDRAD® Intego; 148 MBq at a flow rate of 0.5 mL/sec) followed by a saline flush of 10 mL. Dynamic images were reconstructed from the list-mode data using 24 frames with different timings:10 × 5, 10 × 30, 4 × 300 s., for a total of approximately 26 min (precisely: 25 min. and 50 s.). Ordered-subset expectation maximization (OSEM) iterative algorithm was used for reconstruction, with three iterations and 21 subsets; a 128 × 128 × 47 pixel 3D matrix was obtained for each time frame.
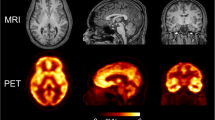
Figure 1 shows 3-plane view of PET/CT reconstructed images from the nine minipigs ; PET images are relevant to the last temporal point from dynamic images.
Reconstructed dynamic 3D PET images were then exported to a remote PC for the analysis. Emission values were converted to standardized uptake values (SUV)s, defined as the mean voxel intensity within the volumetric region of interest (ROI) normalized by the whole-body concentration of the injected radioactivity and multiplied by body mass.
Different brain regions of interest (ROI) were manually drawn by an expert from the 3D dynamic images. The regions selected were: right and left occipital, right and left temporal, right and left parietal, right and left frontal and cerebellum, plus a vascular ROI. For each ROI, a time-activity curve (TAC) was then determined by evaluating the mean SUV value inside the ROI at each time.
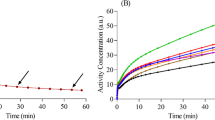
Figure 2 shows representative dynamic images with selected ROIs, and relevant TACs .
2.2 Kinetic Models and Data Analysis
Kinetic analysis of TAC curves was performed using the non-linear tissue-compartment models. Linear models are often preferred because of their higher computational efficiency. However, nonlinear kinetic models provide a more detailed description of the biochemical properties of different tissues [7, 8]. Most non-linear models are built exploiting the compartmental model theory, in order to describe the temporal behavior of the tracer within the tissue. The parameters of the model to be estimated are constant transfer rates, related to the movement of the tracer among different compartments. The total tracer concentration of a tissue region in time can be modeled as [8, 9]:
where \({f}_{v}\) is the fractional volume of blood in the tissue, \({c}_{p}\left(t\right)\)is the measured tracer concentration in the plasma, \({c}_{n}\left(t\right)\) is the impulse response function (IRF) for the n-th tissue compartment, \(d\) is the radioactive decay constant of the tracer that for [ 18F]FDG is equal to \(\text{ln}\left(2\right)/109.8{min}^{-1}\), and \({c}_{b}\left(t\right)\) is the measured whole blood concentration.
The kinetics of the tracer within the compartments can be described by a set of ordinary differential equations:
where c\(\left(t\right)=\left[{c}_{1}\left(t\right),\dots .,{c}_{N}\left(t\right)\right]\text{'}\), \(u\left(t\right)\) is the system input; \(K\) and \(I\) are the kinetic parameters matrices from which we can define the vector of the tracer’s rate constants: \(\text{P}=\left[{K}_{1},{k}_{2},\dots {k}_{nk},{f}_{v}\right]\text{'}\) i.e. the parameters to be estimated during the fitting.
The fitting operation between the model in Eq. (1) and experimental data, was performed by the analytic fitting method described in [9]. Experimental data consist in the TAC from a ROI covering a vessel (TACv) and to ROIs relevant to the following tissue regions: TACro, TAClo (right and left occipital), TACrt ,TAClt (right and left temporal), TACrf, TAClf (right and left frontal), TACrp, TAClp (right and left parietal), and TACc (cerebellum). For each brain region, the kinetic parameters were assessed, according to the model fitting.
We considered three different models: (i) a one-tissue compartment model 1TC (i.e. with N = 1 and nk = 2 in Eqs. (1) and (2)); (ii) a two-tissue irreversible compartment model 2TCi (with N = 2 and nk = 3), and (iii) a two-tissue reversible model 2TC (with N = 2 and nk = 4).
In [ 18F]FDG kinetic modelling, each rate constant (K1-k4) has a physiological and biological significance, indicating the transport of FDG forward (K1) and backward (k2) from plasma to tissue and FDG phosphorylation (k3), and dephosphorylation (k4).
In order to reduce the dependence of the parameter \({K}_{1}\) on the animal’s hemodynamic status, a normalization of the estimated \({K}_{1}\) was performed with the rate-pressure product, which is closely linked to the flow at rest.
Among the macro-parameters, the partition coefficient K1/k2 was estimated. In addition, the net influx rate macro-parameter \({K}_{i}={K}_{1}{k}_{3}/({k}_{2}+{k}_{3})\) was also evaluated from the 2TCi and 2TC estimated microparameters. The net influx rate macro-parameter is analogous to the one evaluated by the graphical Patlak method.
To assess the goodness of each model fitting with the experimental TACs [10], the Akaike Information Criterion coefficient, corrected for small sample sizes, (AICc) [11] was considered.
This was evaluated as:
where \({w}_{t}\) is the weight applied to the residual of t-th acquisition; and k is the number of parameters to be estimated in the fitting.
2.3 Retention Index
The retention index is often used when more than one image is acquired, at different times [12]. With the dynamic images available, we determined the retention value of the tracer over time points, [13, 14] which was evaluated as the mean SUV values between approximately 11 and 25 min (last four time points) after the tracer injection, divided by the integral of the blood pool SUV between 0 and about 25 min (all time points of the TAC covering the vessel):
2.4 Statistical Analyses
Continuous variables were expressed as mean ± standard deviation or median and range, as appropriate. The parametric hypothesis test of normality of the variables was evaluated according to the Shapiro-Willis normality test. When the indices evaluated followed a normal distribution, the ANOVA (one- or two-ways, depending on the groups) test was used for comparison between group samples; otherwise, the Kruskal-Wallis test was used. A 2-tailed P-value < 0.05 was considered significant.
ROI selection, TAC generation extraction and kinetic data fitting were implemented in MATLAB TM v. 2021b (The MathWorks, Inc., Natick Massachusetts, United States). Statistical analysis was performed using MATLAB Statistics and Machine Learning Toolbox TM.
3 Results
3.1 Evaluation of the Best Kinetic Model
By applying the analytical fitting with the models 1TC, 2TCi and 2TC, the relevant tracer’s rate constants \(\text{P}=\left[{f}_{v}{K}_{1},{k}_{2},\dots {k}_{nk}\right]\text{'}\) were determined, with nk = 2 for 1TC, nk = 3 for 2TCi and nk = 4 for 2TC. Fitting operations were performed on each ROI covering the various brain regions.
Table 2 shows the AICc mean values (sd) obtained from each model fitting and evaluated on all the anatomical ROIs of all the minipigs.
The two-way ANOVA analysis and pairwise comparison between the three models showed that 1CT model produced worse results than the other two models. On the other hand, coefficients from 2TCi and 2TC models were not significantly different. The difference values between regions were not significant for any of the kinetics models analyzed.
Accordingly, both 2TCi and 2TC kinetic models were considered in the following analysis.
3.2 Kinetic Parameters Estimated by 2TCi Model Fitting
Table 3 shows the estimated kinetic micro-parameters (K1,k2,k3,fv,) and the macro-parameters K1/k2 and Ki, for each brain ROI. Parameters were evaluated from individual regions, and from a global region that covers all the higher metabolic areas as a whole. The low metabolic region, i.e. the cerebellum, was considered separately.
Figure 3 shows boxplots of the estimated kinetic micro-parameters and K1/k2 and Ki macro-parameters, for each brain ROI.
The Kruskal-Wallis test showed that none of the values of the estimated parameters were significantly different between the brain regions, with the exception of the cerebellum. Thus the corresponding parameter K1 was significantly different compared to the occipital and frontal regions (both left and right), and the net influx rate macro-parameter Ki was significantly different from the frontal regions (both left and right).
3.3 Kinetic Parameters Estimated by 2TC Model Fitting
Table 4 shows the estimated kinetic micro-parameters (K1,k2,k3,k4,fv,) and the macro-parameters K1/k2 and Ki, for each brain ROI.
Figure 4 shows boxplots of the estimated kinetic micro-parameters and K1/k2 and Ki macro-parameters, for each brain ROI.
The Kruskal-Wallis test showed that none of the values of the estimated parameters were significantly different between the brain regions, with the exception of the cerebellum. In particular: (i) the parameter K1 in cerebellum ROI was significantly different compared to the occipital and frontal regions (both left and right); (ii) the partition coefficient K1/k2 in cerebellum was different from the right occipital, left parietal and left and right frontal regions; and (iii) the net influx rate macro-parameter Ki was significantly different from the frontal regions (both left and right).
4 Retention Index
5 Discussion
The noninvasive characterization of the brain metabolic phenotype in healthy minipigs can be used to detect reference values underlying homeostasis and to carefully assess early temporospatial changes over time due to injury or genetic alterations.
The relationship between cerebral glucose metabolism and glucose transporter expression can be investigated by analyzing dynamic PET images after the administration of the [ 18F]FDG tracer. This analysis includes fitting the experimental data with specific kinetic models.
For what we believe is the first time, we assessed the most appropriate kinetic model to characterize the glucose metabolism of minipig brains using [ 18F]FDG dynamic PET images. In fact, the results establish the kinetic microparameters of the brain regions of healthy minipigs. Our analysis defines reliable reference values of the parameters in normal Göttingen minipig brains which will be helpful in detecting early changes in cerebral viability during the onset of neurological diseases.
Although [ 18F]FDG PET scans are considered the gold standard for evaluating glucose use and cell viability in brain regions of humans [15], rodents [16], piglets [17], dogs [18], and non-human primates [19], the use of dynamic [18 F]FDG to explore changes in cerebral glucose metabolism in young Göttingen minipigs remains a desirable goal since they are a breed of small swine increasingly used to study cognitive and behavioral disorders ([20,21,22]).
To date, the cerebral glucose metabolism has been studied in piglets [17], Danish Yorkshire land pigs [23], and domestic pigs, [24]. In all these studies, however, only the net influx rate macro-parameter was evaluated, and the corresponding cerebral metabolic rate of glucose (CMRgl) was shown.
Considering the value of the lumped constant equal to 0.44 as in [17], our CMRgl results are slightly lower than those obtained in [17]: 21.2 (± 7.9) mmol/min per 100 g of tissue in [17], compared to 13.10 (± 5.49) from 2TCi model and 17.63 (± 8.42) from 2TC model.
In [23], the net influx rate was evaluated by both multilinear regression and graphical analysis from [ 18F]FDG dynamic brain PET images. The cerebral net influx rate macro-parameter Ki values were of the same order of magnitude as our results, although our minipigs showed slightly higher values i.e. about 0.017 ml/g/min in[23] compared to 0.069 ml/g/min as mean value in the global region from 2TCi model. From the 2TC model, fitting the Ki value was higher both than the 2TCi model and the values presented in [23]. Another study showing results on the [ 18F]FDG uptake is described in [24], in domestic pigs, which investigates infectious lesion regions and focuses mainly on the evaluation of the net uptake rate Ki. However, in [24] osteomyelitic and soft tissue lesions, not including the brain, were considered.
It should also be highlighted that we used a different breed of small pigs from that used in [17, 23, 24].
As for the choice of the model that best fits the experimental data, according to the AICc coefficient values shown in Table 2, the difference in coefficients between the 2TCi and 2TC models was not significant, thus we considered both models in the analysis. Compared to the 2TCi model, the 2TC model requires the estimation of the additional parameter k4 which represents the reverse hydrolysis reaction that converts FDG-6P into FDG in tissues.
Tables 3 and 4 show the quantitative estimates of the parameters and enable us to more accurately evaluate the ability of the method to characterize the cerebral metabolism of the deeply sedated Göttingen minipig.
The analysis showed that the parameter values were not significantly different between the regions, with similar values when considering the brain as a whole (penultimate row of Tables 3 and 4). In terms of the data obtained from both models, the only region with parameter values that differed from the global one is the cerebellum which has above all the K1, and consequently, the K1/k2 and Ki, lower than for the other regions. This is also confirmed by the shape of the TAC curve obtained from the cerebellum ROIs (see TACc curve in Fig. 2) which has a different shape to the other curves, especially in the initial ascent phase of the TAC, which most influences the value of K1.
Our data are in accordance with a previous study showing that PET radioligand activity cleared over time much faster in the cerebellum compared to other brain regions in propofol-sedated Gottingen minipigs [25]. Although propofol leads to a 35% decrease in the cerebral metabolic rate of oxygen and a 39% decrease in cerebral blood flow [26], the administration of ketamine and xylazine, which are known to result in a lower uptake of FDG, led to a lower cerebellar uptake compared to other brain regions [27].
For this reason, to set normal values for the pig brain as a whole (i.e. as a single large region of interest), it is preferable to consider only the regions with a higher metabolism, therefore excluding the cerebellum, as shown in Tables 3 and 4. In fact, the Retention Index (RI) values, which show the best relation with biological and clinical parameters, were also very similar between different regions of interest, except for the cerebellum which showed a 51% lower RI than the mean value of the other regions (seeTable 5).
The comparison of the results obtained from the estimation using the 2TCi model and the 2TC model (Tables 3 and 4, respectively) shows that the average parameter values are almost all very similar, with the exception of K3 and consequently Ki. The estimated value of K3 (and therefore Ki) from the 2TCi model is lower than that estimated from the 2TC model. This may be due to the fact that in the 2TC model, the k4 is not null; this means that part of the FDG-6P is transformed into FDG, but always keeping the same amount of FDG-6P in the tissue. However, the low values obtained of k4 (see Table 4) suggest that the cerebral metabolism is predominantly irreversible, although a small fraction of the tracer converted to FDG seems present. The high values of standard deviation from the k4 estimation suggest that to obtain a more precise evaluation of this parameter, more experimental data need to be evaluated, possibly with a higher time sampling, and with less noise.
A qualitative view of the resulting parameter values from the two models (Figs. 3 and 4) shows whether there are large variations in the estimated values.
In Figs. 3 and 4, the plus symbols (+) represent outliers, i.e. 1.5 * IQR (interquartile range) away from the top or bottom of the box. The number of outliers is not very high; most concern the parameter K1, for the left occipital, left temporal, left parietal, right and left frontal regions, and are shown in the results of both the 2TCi and 2TC models and regard the results of minipigs 5 and 6. Also, for k3 there are some outliers, mainly in the 2TCi model which are related to minipigs 5 and 6. These outliers are again present in the Ki values from the 2TC model in all regions except for the right occipital and cerebellum. Again, these outliers concern minipig 5 which is evidently the most anomalous in the estimation of micro and macro-parameters. However, we included this pig in the analysis, to take into account the possible variability in the measured data.
The variability in the estimated parameters (see standard deviation values in Tables 3, 4 and 5 and dimensions of boxplots in Figs. 3 and 4), in addition to the experimental variability, is due to various causes related to both data acquisition and analysis. For example, the spillover effect in the PET images, due to the limited spatial resolution, leads to an error in the evaluation of the correct emission in the region of interest and therefore in the estimation of the parameters, which is most noticeable for small ROIs. Furthermore, the noise in the images, and therefore in the TAC curves, makes the correct estimate of the parameters more complex, leading to a variability in the results, which is even more evident for those parameters that are mostly influenced by the last part of the curve, such as k3, k4 and, consequently, Ki.
On the other hand, the variability in the RI index due to noise is much lower (see sd values in Table 5), since integrals of the TAC curves are made for its estimate (Eq. (4)).
Unfortunately, it is not possible to perform a PET scan in awake fasted Gottingen minipigs and the use of anesthetic drugs is the limitation of our in vivo study which should be considered in designing protocol including dynamic [ 18F]FDG PET to analyze regional brain activity. Similarly, anesthetics impede myocardial FDG uptake in mice [28], and pigs [29], however the magnitude of effects depends on the type of anesthetics used. Therefore, the selection of anesthetic agents should be seriously taken into account when minipigs undergo PET imaging with [18 F]FDG. Besides these methodological aspects, the present study shows normality values of the brain metabolic dynamic parameters in minipigs using kinetic models applied to a PET scanner for a hospital setting.
6 Conclusion
We assessed the normality values of the kinetic parameters characterizing glucose metabolism in the brain of fasted male Göttingen minipigs.
The results obtained suggest that both the 2TCi and 2TC model were able to describe the regional brain metabolism in minipigs. Although in the few studies available in the literature, metabolism has been modeled according to the irreversible model, the 2TC model seems to more fully describe the behavior of the glucose metabolism in the brain, also taking into account the reversibility of the phenomenon.
For healthy minipigs, glucose metabolism was similar in all the brain regions analyzed, with the exception of the cerebellum where the FDG uptake was very low.
References
Lionetti, V., Guiducci, L., Simioniuc, A., et al. (2007). Mismatch between uniform increase in cardiac glucose uptake and regional contractile dysfunction in pacing-induced heart failure. American Journal Of Physiology Heart And Circulatory Physiology, 293, 2747–2756. https://doi.org/10.1152/ajpheart.00592.2007
Aquaro, G. D., Frijia, F., Positano, V., et al. (2013). 3D CMR mapping of metabolism by hyperpolarized 13 C-pyruvate in ischemia-reperfusion. JACC: Cardiovascular Imaging, 6, 743–744
Hoffe, B., & Holahan, M. R. (2019). The Use of Pigs as a Translational Model for Studying Neurodegenerative Diseases.Frontiers in Physiology10
Rozkot, M., Václavková, E., & Bělková, J. (2015). Minipigs As Laboratory Animals-Review.Research in Pig Breeding, 9(2)
Vodička, P., Smetana, K., Dvořánková, B., et al. (2005). The miniature pig as an animal model in biomedical research. Annals of the New York Academy of Sciences (pp. 161–171). New York Academy of Sciences
Carson, R. E. (2003). 6 Tracer Kinetic Modeling in PET *. Positron Emission Tomography: Basic Science and Clinical Practice 147–179. https://doi.org/10.1016/j.cpet.2007.08.003
Bentourkia, M., & Zaidi, H. (2007). Tracer Kinetic Modeling in PET. PET Clinics, 2, 267–277. https://doi.org/10.1016/j.cpet.2007.08.003
Gunn, R. N., Gunn, S. R., & Cunningham, J. (2001). Positron Emission Tomography Compartmental Models. Journal of Cerebral Blood Flow and Metabolism, 21, 635–652
Scipioni, M., Giorgetti, A., della Latta, D., et al. (2018). Accelerated PET kinetic maps estimation by analytic fitting method. Computers in Biology and Medicine, 99, 221–235. https://doi.org/10.1016/j.compbiomed.2018.06.015
Santarelli, M. F., Genovesi, D., Scipioni, M., et al. (2021). Cardiac amyloidosis characterization by kinetic model fitting on [18F]florbetaben PET images. Journal of Nuclear Cardiology. https://doi.org/10.1007/s12350-021-02608-8
Golla, S. S. V., Adriaanse, S. M., Yaqub, M., et al. (2017). Model selection criteria for dynamic brain PET studies. EJNMMI Physics, 4, 30. https://doi.org/10.1186/s40658-017-0197-0
Bochev, P. H., Klisarova, A., & Kaprelyan, A. G. (2013). Delayed FDG-PET/CT Images in Patients With Brain Tumors - Impact On Visual And Semiquantitative Assessment. Journal of IMAB - Annual Proceeding (Scientific Papers) 19:367–371. https://doi.org/10.5272/jimab.2013191.367
Antoni, G., Lubberink, M., Estrada, S., et al. (2013). In vivo visualization of amyloid deposits in the heart with 11 C-PIB and PET. Journal of Nuclear Medicine, 54, 213–220. https://doi.org/10.2967/jnumed.111.102053
Santarelli, M. F., Genovesi, D., Positano, V., et al. (2020). Cardiac amyloidosis detection by early bisphosphonate (99mTc-HMDP) scintigraphy. Journal of Nuclear Cardiology. https://doi.org/10.1007/s12350-020-02239-5
Chiaravalloti, A., Micarelli, A., Ricci, M., et al. (2019). Evaluation of Task-Related Brain Activity: Is There a Role for 18F FDG-PET Imaging? BioMed Research International 2019
O’Brien, T. J., & Jupp, B. (2009). In-vivo imaging with small animal FDG-PET: A tool to unlock the secrets of epileptogenesis? Experimental Neurology, 220, 1–4
de Lange, C., Malinen, E., Qu, H., et al. (2012). Dynamic FDG PET for assessing early effects of cerebral hypoxia and resuscitation in new-born pigs. European Journal of Nuclear Medicine and Molecular Imaging, 39, 792–799. https://doi.org/10.1007/s00259-011-2055-y
Li, Y. Q., Liao, X. X., Lu, J. H., et al. (2015). Assessing the early changes of cerebral glucose metabolism via dynamic 18FDG-PET/CT during cardiac arrest. Metabolic Brain Disease, 30, 969–977. https://doi.org/10.1007/s11011-015-9658-0
Chen, X., Zhang, S., Zhang, J., et al. (2021). Noninvasive quantification of nonhuman primate dynamic 18F-FDG PET imaging. Physics in Medicine & Biology, 66, 064005. https://doi.org/10.1088/1361-6560/abe83b
Haagensen, A. M. J., Klein, A. B., Ettrup, A., et al. (2013). Cognitive Performance of Göttingen Minipigs Is Affected by Diet in a Spatial Hole-Board Discrimination Test. Plos One, 8, e79429. https://doi.org/10.1371/journal.pone.0079429
Gieling, E., Wehkamp, W., Willigenburg, R., et al. (2013). Performance of conventional pigs and Göttingen miniature pigs in a spatial holeboard task: effects of the putative muscarinic cognition impairer Biperiden. Behavioral and Brain Functions, 9, 4. https://doi.org/10.1186/1744-9081-9-4
Steinmüller, J. B., Bjarkam, C. R., Orlowski, D., et al. (2021). Anterograde Tracing From the Göttingen Minipig Motor and Prefrontal Cortex Displays a Topographic Subthalamic and Striatal Axonal Termination Pattern Comparable to Previous Findings in Primates. Frontiers in Neural Circuits, 15, https://doi.org/10.3389/fncir.2021.716145
Poulsen, P. H., Smith, D. F., Østergaard, L., et al. (1997). In vivo estimation of cerebral blood flow, oxygen consumption and glucose metabolism in the pig by [ 15 O]water injection, [ 15 O]oxygen inhalation and dual injections of [ 18 F]fluorodeoxyglucose. Journal of Neuroscience Methods, 77, 199–209
Jødal, L., Jensen, S. B., Nielsen, O. L., et al. (2017). Kinetic modelling of infection tracers [18F]FDG, [68Ga]Ga-citrate, [11 C] methionine, and [11 C] donepezil in a porcine osteomyelitis model. Contrast Media and Molecular Imaging 2017:. https://doi.org/10.1155/2017/9256858
Alstrup, A. K. O., Landau, A. M., Holden, J. E., et al. (2013). Effects of Anesthesia and Species on the Uptake or Binding of Radioligands In Vivo in the Göttingen Minipig. BioMed Research International, 2013, 1–9. https://doi.org/10.1155/2013/808713
Lagerkranser, M., Stånge, K., & Sollevi, A. (1997). Effects of Propofol on Cerebral Blood Flow, Metabolism and Cerebral Autoregulation in the Anesthetized Pig. Journal of Neurosurgical Anesthesiology, 9, 188–193. https://doi.org/10.1097/00008506-199704000-00015
Sokoloff, L., Reivich, M., Kennedy, C., et al. (1977). THE [ 14 C]Deoxyglucose Method For The Measurement Of Local Cerebral Glucose Utilization: Theory, Procedure, And Normal Values In The Conscious And Anesthetized Albino Rat. Journal of Neurochemistry, 28, 897–916. https://doi.org/10.1111/j.1471-4159.1977.tb10649.x
Toyama, H., Ichise, M., Liow, J. S., et al. (2004). Evaluation of anesthesia effects on [18F]FDG uptake in mouse brain and heart using small animal PET. Nuclear Medicine and Biology, 31, 251–256. https://doi.org/10.1016/S0969-8051(03)00124-0
Lee, Y. A., Kim, J. I., Lee, J. W., et al. (2012). Effects of various anesthetic protocols on 18F-flurodeoxyglucose uptake into the brains and hearts of normal miniature pigs (Sus scrofa domestica). Journal Of The American Association For Laboratory Animal Science, 51, 246–252
Funding
This work was in part funded by ETHERNA project (Prog. n. 161/16, Fondazione Pisa, Italy) (VL) and in part by institutional funds from Fondazione Toscana “G.Monasterio”, Pisa, Italy (AG).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
Authors have no conflicts of interest to declare.
Ethical Approval
All animal procedures were approved by the Italian Ministry of Health and conducted in conformity with the guidelines from Legislative Decree n°26/2014 of Italian Ministry of Health and Directive 2010/63/EU of the European Parliament, and with the guidelines for the Care and Use of Laboratory Animals (NIH publication No. 85–23) on the protection of animals used for scientific purposes.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic Supplementary Material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Filomena, S.M., Elena, P., Carlotta, B. et al. Regional Characterization of the Gottingen Minipig Brain by [18 F]FDG Dynamic Pet Modeling. J. Med. Biol. Eng. 42, 692–702 (2022). https://doi.org/10.1007/s40846-022-00739-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40846-022-00739-y