Abstract
Purpose
Three-dimensional (3D) gallbladder (GB) geometrical models are essential to GB motor function evaluation and GB wall biomechanical property identification by employing finite element analysis (FEA) in GB disease diagnosis with ultrasound systems. Methods for establishing such 3D geometrical models based on static two-dimensional (2D) ultrasound images scanned along the long-axis/sagittal and short-axis/transverse cross-sections in routine GB disease diagnosis at the beginning of emptying phase have not been documented in the literature so far.
Methods
Based on two custom MATLAB codes composed, two images were segmented manually to secure two sets of the scattered points for the long- and short-axis GB cross-section edges; and the points were best fitted with a piecewise cubic spline function, and the short-axis cross-section edges were lofted along the long-axis to yield a 3D geometrical model, then GB volume of the model was figured out. The model was read into SolidWorks for real surface generation and involved in ABAQUS for FEA.
Results
3D geometrical models of seven typical GB samples were established. Their GB volumes are with 15.5% and − 4.4% mean errors in comparison with those estimated with the ellipsoid model and sum-of-cylinders method but can be correlated to the latter very well. The maximum first principal in-plane stress in the 3D models is higher than in the ellipsoid model by a factor of 1.76.
Conclusions
A numerical method was put forward here to create 3D GB geometrical models and can be applied to GB disease diagnosis and GB shape analysis with principal component method potentially in the future.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Acalculous biliary pain (ABP), which has been a variety of names such as right upper quadrant pain, functional gallbladder (GB) disorder, biliary dyskinesia, GB dysmotility and ampullary stenosis, is a common clinical problem [1]. The frequency of ABP has been shown to be 7.6% in men and 20.7% in women [2]. Since 1990′s, laparoscopic cholecystectomy (LC) has been performed on patients with ABP after cholescintigraphy or ultrasound scans with cholecystokinin (CCK) infusion [3,4,5,6,7,8,9,10]. Unfortunately, the patients with persistent symptom still can be as many as 20% after LC [2]. More recently, clinical trials have been carried out in [10,11,12,13,14,15,16,17,18,19,20,21,22,23]. It was shown that the majority of ABP patients can have resolution of painful symptom, but the GB bile ejection fraction (EF) determined in cholescintigraphy or ultrasound scans doesn’t predict outcome and the patients with normal GB EF are subject to a less benefit form LC.
A few meta-analyses on the existing outcome after LC based on CCK-cholescintigraphy or ultrasound scans for ABP patients were performed [24,25,26,27], and it was indicated that the use of EF to select patient with suspected ABP is not supported, even though the symptom is more significantly relived than nonoperative therapy; consequently, randomized clinical trials are on demand [24, 25, 28, 29]. To standardize the trials and make the outcomes of different trials comparable, a protocol was recommended based on 0.02 µg/kg sincalide over 60 min with normal EF specified ≥ 38% [30]. A pilot randomized controlled trial of LC was launched in [31] based on that protocol for 30 ABP patients.
ABP can involve biomechanical factors. For instance, GB smooth muscle is subject to an impaired contractile capacity in response to CCK [32], and the smooth muscle to fibrosis layer thickness ratio might be associated with abnormal EF [33]. These two factors can alter the bile pressure in a GB and the stress level in the GB wall. Bearing this fact in mind, the total (active plus passive) peak stress was estimated at the beginning of GB emptying phase during a CCK-ultrasound scan examination based on an ellipsoid model in [34, 35]. It turned out that the peak stress can correlate to the ABP symptom well. Even though the ellipsoid model can be easily applied in clinical trials, it likely underestimates the stress level in the GB wall based on the stress in the sheep GB wall predicted by finite element analysis (FEA) in terms of a thin-walled membrane mechanical model [36]. Since the stress level in a GB wall is related to GB pain threshold application and pain prediction outcome, further validations on the stress level are desirable based on real GB shapes.
Actually, ultrasound/ultrasonography has been proven to be a sensitive non-invasive and simple screening tool in the diagnosis of biliary tract and GB disorders since 1970′s. Significant contributions in this issue can be found in [37,38,39,40,41,42,43,44,45,46,47,48,49,50] to name a few. Simultaneously, ultrasound was applied to investigate GB motor function or motility by determining its real-time volume during the emptying/contraction phase to help surgeons in the diagnosis of GB diseases [51,52,53,54,55,56,57,58,59,60].
Even though three-dimensional (3D) ultrasound can measure GB real-time volume accurately, it has been difficult yet in obtaining 3D GB geometrical models for FEA so far [58,59,60,61,62]. To extract real-time GB geometrical models from ultrasound images, image registration is required. Because of artifacts and speckle in ultrasound images, automatic registration of GB ultrasound image in 3D ultrasound systems remains to be an unsolved problem right now [62].
Automatic segmentation methods have been proposed for two-dimensional (2D) ultrasound static long-axis/sagittal view images of GB based on pixel grey level [63,64,65] or brightness [66] or intensity [67]. However, in these interesting studies, there are not any 3D GB geometrical models produced.
In this article, a method for generating human GB 3D geometrical models was developed based on two static ultrasound 2D images of human GBs scanned in the long-axis/sagittal and short-axis/transverse directions, respectively. The GB bile volumes of the 3D geometrical models were calculated and compared with those from the ellipsoid model and sum-of-cylinders method in [51, 52, 58]. The geometrical models were meshed in ABAQUS and FEA on them was performed based on a homogenous, isotropic, thin shell mechanical model. Additionally, the peak stress was compared with that in the ellipsoid model in [35]. A mean peak stress level ratio from the FEA was obtained against the GB ellipsoid model and the peak stress underestimation extent of the ellipsoid model was validated.
2 Images and Numerical Method
2.1 Ultrasound Images of Human GB
A series of two ultrasound static 2D images of human GB scanned in the long-axis/sagittal and short-axis/transverse directions has been obtained from a teaching hospital for seven patients. The images at the beginning of emptying phase are shown in Fig. 1 to reflect a variety of GB shapes. These images were taken when the patients were routinely inspected for GB diseases with an ordinary clinical ultrasound system. The hospital did not provide us with system parameter settings and patient information when the images were scanned. Such information seems to be unimportant here because the method for generating GB 3D geometrical models was concerned only in the paper.
2.2 Numerical Method
In the images shown in Fig. 1, there are two views only: one is in the long-axis plane where one longitudinal GB cross-section is presented; the other is in the short-axis/transverse plane where one cross-section with the maximum cross-sectional area is specified. The two images in these two views must be utilized to generate 3D GB geometrical models. There are three steps in the method, as demonstrated in Fig. 2.
In the first step, GB ultrasound images are segmented manually in MATLAB with a custom program to decide scattered points of GB wall edges. Then, two edges are generated by fitting the points with the piecewise cubic spline function in MATLAB. The closed short-axis cross-section is lofted and the GB volume is calculated. Finally, the data files of short-axis cross-sections and guide lines are made for SolidWorks.
In the second step, GB short-axis cross-sections and guide line profiles are established in SolidWorks, and a surface is lofted with these profiles, the surface is enclosed with a small sphere cap in the apex of GB fundus. Geometrical model information exchange files in the initial graphics exchange specification (IGES) and Parasolid formats are prepared for ABAQUS or ADINA to perform FEA under a specific bile pressure and boundary condition.
In the third step, a geometrical model information exchange file is read into ABAQUS or ADINA. A mesh is created and a FEA is conducted by means of homogenous isotropic thin shell solid mechanics model with a certain thickness and a specific internal bile pressure load as well as a boundary condition.
Figure 3 illustrates the scattered points of GB 36 wall edges, fitted short-axis and long-axis cross-sections, surface of the GB wall, GB surface presentation and a quadrilateral mesh for FEA in ABAQUS.
In the second step, GB cross-section curve fitting, lofting and volume calculation are the essential in 3D GB geometrical model generation. The details of the MATLAB code for accomplishing these functions are as follows:
- (1)
Determine image scales based on marks and number figures in the images in Fig. 1;
- (2)
Read data files of two edges scattered points are made in the previous segmentation;
- (3)
Calculate the geometrical centre coordinates of the short-axis/transverse cross-sectional curve (xc, yc), determine the polar-coordinate system (θ, r), and perform the curve fitting with the MATLAB spline function r = csape(θ, r,’periodic’), which is cubic spline interpolation with end conditions, the coordinates of the edge are (xc + r cosθ, yc + r sinθ);
- (4)
Locate the middle point of GB neck (yfneck, zfneck) and specify it as the reference point of the long-axis/sagittal cross-section edge scattered points, determine the other reference point (\(y_{b\hbox{max} }\), \(z_{b\hbox{max} }\)) at which the maximum length is achieved from the middle point (yfneck, zfneck), rotate the cross-section edge points in an angle of \(- \tan ^{{ - 1}} \left[ {\left( {y_{{{\text{bmax}}}} - y_{{{\text{fneck}}}} } \right)/\left( {z_{{{\text{bmax}}}} - z_{{{\text{fneck}}}} } \right)} \right]\) to allow the cross-section to be laid horizontally in the new coordinates (\(y_{rot}\), \(z_{rot}\)), compute the arc length \(s\) of the scattered points from the first one to the last one in the neck, define the MATLAB spline function z = csape(\(s\), \(z_{\text{rot}}\), \(q\)), y = csape(\(s\), \(z_{\text{rot}}\), \(q\)), and \(q = {1 \mathord{\left/ {\vphantom {1 {\left[ {1 + {{\left( {z_{\text{rot2}} - z_{\text{rot1}} } \right)^{3} } \mathord{\left/ {\vphantom {{\left( {z_{\text{rot2}} - z_{\text{rot1}} } \right)^{3} } 6}} \right. \kern-0pt} 6}} \right]}}} \right. \kern-0pt} {\left[ {1 + {{\left( {z_{\text{rot2}} - z_{\text{rot1}} } \right)^{3} } \mathord{\left/ {\vphantom {{\left( {z_{\text{rot2}} - z_{\text{rot1}} } \right)^{3} } 6}} \right. \kern-0pt} 6}} \right]}}\) is the end condition parameter, \(z_{\text{rot1}}\) and \(z_{\text{rot2}}\) are the horizontal coordinates of the first and second scattered points after rotation, then the rotated scattered points are interpolated, the reference point (\(y_{b\hbox{max} }\), \(z_{b\hbox{max} }\)) is searched again, and the angle of rotation is updated, and the points are rotated accordingly, the MATLAB spline function is redefined, and a subsequent interpolation is launched once more; such a cycle is repeated for five times until the sagittal cross-section is horizontal exactly;
- (5)
Interpolate more dense scattered points with the functions defined in (4), divide the whole long-axis cross-section edge into two parts: i.e. upper and lower parts, determine the location where the maximum height in the long-axis cross-section occurs, rescale the existing short-axis cross-section height and insert this cross-section into the long-axis cross-section orthogonally;
- (6)
Specify the short-axis cross-section at the GB neck and the short-axis cross-section near the GB fundus apex are a circle, and then loft the rest short-axis cross-sections from three existing short-axis cross-sections based on the ratio of a local short-axis cross-section height to the maximum short-axis cross-section height;
- (7)
Calculate the volume of GB by summarizing the volumes of each truncated cone formed by two neighbouring short-axis cross-sections, this method is slightly more complex than the sum-of-cylinders method [51, 52, 58];
- (8)
Write the Cartesian coordinates (\(x_{surf}\), \(y_{surf}\), \(z_{surf}\)) of all short-axis cross-section edges (lofted plus existing) into separate data files for SolidWorks, and the Cartesian coordinates of the long-axis cross-section edges in the horizontal and vertical planes are also written into data files for SolidWorks as guide lines.
3 GB Shape, Volume and FEA
3.1 GB Shape
GB wall surfaces of the rest six GB samples, which were generated by means of the method mentioned above, are illustrated in Fig. 4. It is shown that GB 1 and 17 present a pear shape, while GB 9, 30 and 36 in Fig. 3 exhibit a slender structure, but GB 19 and 37 are in an odd shape.
3.2 GB Bile Volume
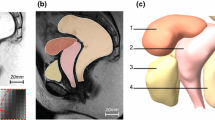
The bile volumes of seven GB samples have been calculated based on the ellipsoid model with three major axis lengths measured in each 3D model dimensions from the image and the 3D model itself, respectively. The ellipsoid model [35] and its original 3D model for the image of GB 36 are illustrated in Fig. 5a, b as an example. The GB volume was estimated by means of the sum-of-cylinders method [51] and presented in the figure, too. The ellipsoid model volume is calculated by the expression \(V_{el} = {{\pi d_{1} d_{2} d_{3} } \mathord{\left/ {\vphantom {{\pi d_{1} d_{2} d_{3} } 6}} \right. \kern-0pt} 6}\) [52, 58], the formula of the sum-of-cylinders method for GB volume can be found in [51, 52, 58]. The GB volume of 3D model is due to the method in Sect. 2.2. A comparison of GB volume is made between three methods in Fig. 5c and Table 1.
GB 3D model from the image of GB 36 (a), its corresponding ellipsoid model with three major axis lengths such as d1, d2 and d3 (b), GB volumes based on ellipsoid model, sum-of-cylinders method and 3D model from the images of seven GB samples (c), and regressed relationships of V3D to Vel and Vsc, respectively (d)
The GB volumes from 3D models, \(V_{{ 3 {\text{D}}}}\), are consistently larger than those from the simple ellipsoid model, \(V_{\text{el}}\), across all the GB samples with an error in the range of (0.8–29.2) % and the mean of 20.1%, which is basically close to a similar value of 15.0% in [58]. The GB volumes from the tedious sum-of-cylinders method, \(V_{\text{sc}}\), are basically smaller than those from 3D models with an error in (− 8.9 to 0.4)% and the mean of − 4.4%. Even though there is a noticed difference in GB volume across three methods, the GB volumes from 3D models can correlate to the volumes predicted with the sum-of-cylinders and ellipsoid models very well, respectively, as shown in Fig. 5d.
This fact suggests that the method for generating 3D GB geometrical model from 2D ultrasound images proposed in the article is meaningful and reliable. Since GB volume from the ellipsoid model or sum-of-cylinders method is always higher or smaller than that from the 3D model, the ellipsoid method still can be used clinically due to its simplicity. Specially, one can use the correlations in Fig. 5d to predict a nearly true GB volume based on either \(V_{\text{el}}\) or \(V_{\text{sc}}\).
3.3 FEA
Seven 3D GB geometrical models were put into ABAQUS 6.11 standard to carry out a linear FEA with an aim to identify whether the geometrical models can be applicable in FEA and what the stress pattern and level are different from those based on the analytical solution of an ellipsoid GB geometrical model in [35]. The material property constants and the model parameter setting in FEA are presented in Table 2.
The Young’s modulus is 500 kPa approximately based on the experimental data summarized in [68], and the Poisson’s ratio 0.49 is chosen for incompressible GB wall. The GB wall thickness was assumed to be 2.5 mm uniform [35]. Thin shell elements used in the FEA are included by choosing type S3 (3-node triangular general-purpose shell) and S4 (4-node quadrilateral general-purpose shell) elements. The pressure load was applied on the GB inside surface, and the load magnitudes are patient-specific and referred to [35]. The boundary condition was imposed in the GB neck inlet by fixing six degrees of freedom. The convergence tolerance is the default value of \(1 \times 10^{ - 5}\) in displacements in ABAQUS. The independence of mesh size and effects of Young’s modulus are demonstrated in Appendix. The results achieved with mesh1 in Table 5 are shown the following sections.
The ratio of the maximum first principal in-plane stress in a 3D GB geometrical model to the counterpart in its ellipsoid model, i.e. \(S = {{\sigma_{1,3D} } \mathord{\left/ {\vphantom {{\sigma_{1,3D} } {\sigma_{1,e} }}} \right. \kern-0pt} {\sigma_{1,e} }}\), is shown in Fig. 6 to quantity the difference in stress level between two geometrical models. The first principal in-plane stress in the ellipsoid model was calculated based on the method in [35]. Clearly, under the same loading condition and material property constants, the stress level in the 3D geometrical model is higher than that in the ellipsoid model across the samples. The mean ratio is 1.76 with 0.11 standard deviation.
The first principal in-plane stress ratio of seven GB samples, it is defined as the ratio of the maximum first principal in-plane stress in a GB 3D geometrical model, \(\sigma_{1,3D}\), to the counterpart in its ellipsoid model, \(\sigma_{1,e}\), \(S = {{\sigma_{1,3D} } \mathord{\left/ {\vphantom {{\sigma_{1,3D} } {\sigma_{1,e} }}} \right. \kern-0pt} {\sigma_{1,e} }}\)
The contours of the first principal in-plane stress across seven 3D GB geometrical models are illustrated in Fig. 7. Further, the location for the maximum stress is coincident with the location for the largest strain, as shown in Fig. 8.
Since the curvature of the cross-sectional edge changes significantly in the short-axis/transverse plane, see Fig. 3b, the stress exhibits a bumpy variation, particularly with compression (negative) stress. In the contour of the first principal stress given by the analytical method based on the ellipsoid model in [35] demonstrates a bumpy characteristic as well, but in a different pattern and without compression stress, see Fig. 9 for GB 36.
Contour of the first principal in-plane stress in GB36 due to ellipsoid model and analytical method in [35]
These facts suggest that the GB ellipsoid model provides us with a simple clinical biomechanical model, however, its volume and stress level estimated can be lower by a certain factor than those based on 3D GB geometrical models from ultrasound images. Note that the contour of the first principal in-plane stress from the more realistic 3D GB models can differ from the pattern produced based on the ellipsoid model and analytical method.
4 Discussions
In the paper, a numerical method was proposed to establish human 3D GB geometrical models from static ultrasound 2D images in the long-axis/sagittal and short-axis/transverse cross-sections in routine biliary disease diagnosis at the beginning of emptying phase in hospital. The extracted 3D models were adopted to estimate GB volume in MATLAB, stress level and distribution in ABAQUS and the corresponding results were compared with those due to the existing ellipsoid model and analytical method [35]. The idea and work are original, and have not been indicated in the literature, and can be meaningful in biomedical engineering and ABP diagnosis.
The cubic spline function in MATLAB was chosen to fit the scattered points in the long-axis/sagittal and short-axis/transverse cross-sections for the edges. The function can represent the complex edge shape of human GB wall. In [69], the Fourier series with five terms was utilized to fit the scattered points in the short-axis/transverse cross-section. Initially, this method was employed to perform the fitting task. However, the fitted curve is unable to pass through the scattered points picked up from the image simultaneously, as seen Fig. 10 for GB 36. However, the fitted curve generated by the cubic spline function passes through the points and can preserve the edge geometrical feature. Thus, the cubic spline function in MATLAB was favoured in the paper.
A comparison of fitting curves established by Fourier series [69], circle and cubic spline function in MATLAB for the scattered points in the short-axis/transverse cross-section of GB 36
In Figs. 3 and 4, seven human GB samples exhibit a variety of shapes. Fortunately, these GB shapes can be observed in GB 3D volumes rendered computed tomography (CT) cholangiographic images shown in Fig. 11 [48]. Among these shapes, GB 1 has a similar shape to the GB in Fig. 11a to some degree, so does GB 17 to the GB in Fig. 11b, GB30 to the GB in Fig. 11c, GB 36 to the GB in Fig. 11d, GB 19 to the GB in Fig. 11e and GB 37 to the GB in Fig. 11f. This information suggests that the method proposed in the paper is sensitive to GB shape.
GB 3D volumes rendered computed tomography (CT) cholangiographic images at the beginning of emptying phase, a–g GB pictures are after [48]
Honestly, the paper is subject to a few limitations. Firstly, the method was not validated directly by using a balloon filled by liquid or 3D ultrasound data or magnetic resonance imaging (MRI) images of GB, because these kinds of data are lack in open source databases presently. However, an indirect validation has been made in Sect. 3.2 in terms of GB bile volume. The mean errors in GB bile volume calculated by the ellipsoid model and the sum-of-cylinders method are 20.1% and − 4.4% against the 3D GB geometrical model, respectively, in the paper. In [58], the corresponding mean errors of the ellipsoid model and the sum-of-cylinders method are 15.0% and 2.7% against the GB bile volume determined by 3D ultrasound system. Thus, the bile volume based on the 3D GB geometrical model in the paper seems to be reasonable and its accuracy in GB volume estimations can be considered at least equivalent to those of the ellipsoid model and the sum-of-cylinders method.
Secondly, human GB wall can exhibit both anisotropic and nonlinear behavior in biomechanical property shown by in vivo computational biomechanics approach [36, 70, 71] and by in vitro uniaxial tensile test [72, 73]. However, in the paper, GB wall property has been considered isotropic and linear, even though the geometrical nonlinearity was involved when the biomechanical model being set up in ABAQUS. During the emptying phase of human GB, there are both active and passive tensions. The passive tension and anisotropic property can be modelled by using the numerical approach and fibre structure presented in [71]. The method for modelling the active tension developed in human GB in the emptying phase has been unavailable at all so far.
Thirdly, in a linear numerical GB biomechanical analysis, the reference configuration can be the same as the current configuration. However, the reference configuration should be different from the current configuration because the strain can be quite large in a nonlinear numerical GB biomechanical analysis. Accordingly, a reference configuration must be known in advance in the nonlinear analysis. How to determine the reference configuration for a GB based on in vivo ultrasound images remains unknown currently. Nonetheless, active tension modelling and reference configuration determination will be two key issues in nonlinear human GB biomechanics during the emptying phase.
Based on GB volume predicted, the method proposed herein is equivalent to the ellipsoid model or sum-of-cylinders method in accuracy based on two-view ultrasound images. However, the method in the paper can produce a more realistic GB shape in terms of the comaprison with the existing GB volumes rendered from CT images. Consequently, the stress and strain levels and patterns in terms of such a shape may more likely close to the true values and patterns than those based on the existing GB ellipsoid model. These 3D GB shapes potentially can be applied to GB shape analysis by using principal component analysis (PCA) method to correlate the shape features to GB pain score in the future. Note that the method is preliminary and further validations performed by radiologists or other experts are on demand.
5 Conclusions
A numerical approach was proposed to establish 3D GB geometrical models from existing static 2D long-axis/sagittal and short-axis/transverse cross-sectional ultrasound images scanned in routine GB disease diagnosis practice in hospital at the beginning of emptying phase. GB volumes of the geometrical models were extracted and compared with those estimated with well-known ellipsoid model and sum-of-cylinders method. The models were read into SolidWorks for surface generation and then involved in ABAQUS for FEA analysis based on homogenous isotropic linear material and thin shell mechanical model. The results were discussed against those of the ellipsoid model. The approach developed in the article can create a satisfactory 3D geometrical model from the ultrasound images of human GB. The GB volumes from 3D geometrical models are different from those estimated by using the ellipsoid model and sum-of-cylinders method with 15.5% and − 4.4% mean errors, respectively, but can correlate positively to the latter with a correlation coefficient as large as 0.99. The first principal stress level in the 3D geometrical models can be higher than that in the ellipsoid model by a factor of 1.0–2.63 with the mean of 1.76. The bumpy stress pattern in the 3D geometrical models is significantly deviated from that in the ellipsoid model. The method proposed potentially can be applicable in clinical diagnosis of GB disease and GB shape analysis in terms of principal component method in the future. The forthcoming work includes generating 3D GB geometrical models in the whole emptying phase, determining GB reference configuration, identifying anisotropic nonlinear material properties of GB wall in passive state, and modelling active behavior of GB wall in the emptying phase based on the generated 3D models.
References
Cotton, P. B., Elta, G. H., Carter, C. R., et al. (2016). Gallbladder and sphincter of Oddi disorders. Gastroenterology,150(6), 1420–1429.
Wald, A. (2005). Functional biliary-type pain. Journal of Clinical Gastroenterology,39(S3), S217–S222.
Misra, D. C., Blosssom, G. B., Fink-Bennett, D., et al. (1991). Results of surgical therapy for biliary dyskinesia. Achieve of Surgery,126(8), 957–960.
Yap, L., Wycherly, A. G., Morphett, A. D., et al. (1991). Acalculous biliary pain: Cholecystectomy alleviates symptoms in patients with abnormal cholescintigraphy. Gastroenterology,101(3), 786–793.
Halverson, J. D., Garner, B. A., Siegel, B. A., et al. (1992). The use of hepatobiliary scintigraphy in patients with acalculous biliary colic. Achieve Internal Medicine,152(6), 1305–1307.
Kloiber, R., Molnar, C. P., & Shaffer, E. A. (1992). Chronic biliary-type pain in the absence of gallstones: The values of cholecystokinin cholescintigraphy. American Journal of Roentgenology,159(3), 509–513.
Sorenson, M. K., Fancher, S., Lang, N. P., et al. (1993). Abnormal gallbladder nuclear ejection fraction prediction success of cholecystectomy in patients with biliary dyskinesia. American Journal of Surgery,166(6), 672–675.
Smythe, A., Majeed, A., Fitzhebry, M., et al. (1998). A requiem for the cholecystokinin provocation test? Gut,43(4), 571–574.
Canfield, A. J., Hetz, S. P., Schriver, J. P., et al. (1998). Biliary dyskinesia: A study of more than 2000 patients and review of the literature. Journal of Gastrointestinal Surgery,2(5), 443–448.
Yost, F., Margenthalaer, J., Presti, M., et al. (1999). Cholecystokinin is an effective treatment for biliary dyskinesia. American Journal of Surgery,178(6), 462–465.
Fuller, R. A., Kuhn, J. A., Fisher, T. L., et al. (2000). Laparoscopic cholecystectomy for acalculous gallbladder disease. Baylor University Medical Center Proceedings,13(4), 331–333.
Skipper, K., Sligh, S., Dunn, E., et al. (2000). Laparoscopic cholecystectomy for an abnormal hepato-iminodiacetic acid scan: A worthwhile procedure. American Surgeon,66(1), 30–32.
Chen, P. F. M., Mimeri, A., Pham, Q. H. T., et al. (2001). The clinical diagnosis of chronic acalculous cholecystitis. Surgery,130(4), 578–583.
Gall, C. A., & Chambers, K. J. (2002). Cholecystectomy for gallbladder dyskinesia: Symptom resolution and satisfaction in a rural surgeries practice. ANZ Journal of Surgery,72(10), 731–734.
Ozden, N., & DiBaise, J. K. (2003). Gallbladder ejection fraction and symptom outcome in patients with acalculous biliary-like pain. Digestive Diseases and Sciences,48(5), 890–897.
Bingener, J., Richards, M. L., Schwesinger, W. H., et al. (2004). Laparoscopic cholecystectomy for biliary dyskinesia. Surgical Endoscopy,18(5), 802–806.
Patel, N. A., Lamb, J. J., Hogle, N. J., et al. (2004). Therapeutic efficacy of laparoscopic cholecystectomy in the treatment of biliary dyskinesia. American Journal of Surgery,187(2), 209–212.
Riyad, K., Chalmers, C. R., Aldouri, A., et al. (2007). The role of 99mtechnerium-labelled hepato imino diacetic acid (HIDA) scan in the management of biliary pain. HPB,9(3), 219–224.
Sabbaghian, M. S., Rich, B. S., Rothberger, G. D., et al. (2008). Evaluation of surgical outcome and gallbladder characteristics in patients in biliary dyskinesia. Journal of Gastrointestinal Surgery,12(8), 1323–1330.
Wybourn, C. A., Kitsis, R. M., & Baker, T. A. (2013). Laparoscopic cholecystectomy for biliary dyskinesia: Which patients have long term benefit. Surgery,154(4), 761–768.
Jones, A., Shahtahmassebi, G., & Stell, D. (2015). Gallbladder ejection fraction declines with age in patients undergoing cholecystectomy for acalculous biliary symptoms but has low accuracy in the prediction of gallbladder pathology. Digestive Surgery,32(1), 68–72.
Edwards, M. A., Mullenbach, B., & Chamberlain, S. M. (2014). Pain provocation and low gallbladder ejection fraction with CCK cholescintigraphy are not predictive of chronic acalculous gallbladder disease symptom relief after cholecystectomy. Digestive Diseases and Sciences,59(11), 2773–2778.
Pihl, K. D., Jones, M. W., Deppen, J. G., et al. (2018). Effects of laparoscopic cholecystectomy in normokinetic biliary dyskinesia. American Journal of Surgery,215(1), 116–119.
Delgado-Aros, S., Cremonini, F., Bredenoord, A. J., et al. (2003). Systematic review and meta-analysis: Does gall-bladder ejection fraction on cholecystokinin cholescintigraphy predict outcome after cholecystectomy in suspected functional biliary pain? Alimentary Pharmacology & Therapeutics,18(2), 167–174.
DiBaise, J. K., & Oleynikov, D. (2003). Does gallbladder ejection fraction predict outcome after cholecystectomy for suspected chronic acalculous gallbladder dysfunction? A systematic review. American Journal of Gastroenterology,98(12), 2605–2611.
Ponsky, T. A., DeSafun, R., & Brody, F. (2005). Surgical therapy for biliary dyskinesia: A meta-analysis and review of the literature. Journal of Laparoendoscopic & Advanced Surgical Techniques,15(5), 438–442.
Mahid, S. S., Jafri, N. S., Brangers, B. C., et al. (2009). Meta-analysis of cholecystectomy in symptomatic patients with positive hepatobiliary iminodiacetic acid scan results without gallstones. Archives of Surgery,14(2), 180–187.
Richmond, B. K., DiBaise, J., & Ziessman, H. (2013). Utilization of cholecystokinin cholescintigraphy in clinical practice. Journal of American College of Surgeons,217(2), 317–323.
Goussous, N., Kowdley, G. C., Sardana, N., et al. (2014). Gallbladder dysfunction: How much longer will it be controversial? Digestion,90(3), 147–154.
DuBaise, J. K., Richmond, B. K., Ziessman, H. H., et al. (2011). Cholecystokinin-cholescintigraphy in Adults: Consensus recommendations of an interdisciplinary panel. Clinical Gastroenterology and Hepatology,9(5), 376–384.
Richmond, B. K., Grodman, C., Walker, J., et al. (2016). Pilot randomized controlled trial of laparoscopic cholecystectomy vs active nonoperative therapy for the treatment of biliary dyskinesia. Journal of American College of Surgeons,222(6), 1156–1163.
Merg, A. R., Kalinowski, S. E., Hinkhous, M. M., et al. (2002). Mechanisms of impaired gallbladder contractile response in chronic acalculous cholecystitis. Journal of Gastrointestinal Surgery,6(3), 432–437.
Lim, J. U., Joo, K. R., Won, K. Y., et al. (2017). Predictor of abnormal gallbladder ejection fraction in patients with atypical biliary pain: Histopathological point of view. Medicine (Baltimore),96(51), e9269.
Li, W. G., Luo, X. Y., Hill, N. A., et al. (2008). Correlation of mechanical factors and gallbladder pain. Computational & Mathematical Methods in Medicine,9(1), 27–45.
Li, W. G., Luo, X. Y., Hill, N. A., et al. (2011). A mechanical model for CCK-induced acalculous gallstone pain. Annals of Biomedical Engineering,39(2), 786–800.
Li, W. G., Bird, N., & Luo, X. Y. (2017). A Pointwise method for identifying biomechanical heterogeneity of the human gallbladder. Frontiers in Physiology. https://doi.org/10.3389/fphys.2017.00176.
Bartrum, R. J., Crow, H. C., & Foote, S. R. (1977). Ultrasonic and radiographic cholecystography. The New England Journal of Medicine,296(10), 538–541.
Kappelman, N. B., & Sanders, R. C. (1978). Ultrasound in the investigation of gallbladder disease. JAMA,239(14), 1426–1428.
Clair, M. R., Rosenberg, E. R., Ram, P. C., et al. (1982). Comparison of real-time and static-mode gray-scale ultrasonography in the diagnosis of cholelithiasis. Journal of Ultrasound in Medicine,1(5), 201–203.
Kishk, S. M. A., Darweesh, R. M. A., Dodds, W. J., et al. (1987). Sonographic evaluation of resting gallbladder volume and postprandial emptying in patients with gallstones. American Journal of Roentgenology,148(5), 875–879.
Fitzgerald, E. J., & Toi, A. (1987). Pitfalls in the ultrasonographic diagnosis of gallbladder diseases. Postgraduate Medical Journal,63(741), 525–532.
Sakijan, A. S., & Atan, M. (1987). Choledocholithiasis: Diagnosis by ultrasound. Medical Journal of Malaysia,42(2), 115–118.
Nelson, T. R., & Pretorius, D. H. (1998). Three-dimensional ultrasound imaging. Ultrasound in Medicine and Biology,24(9), 1243–1270.
Portincsa, P., Moschetta, A., Colecchia, A., et al. (2003). Measurements of gallbladder motor function by ultrasonography: Towards standardization. Digestive and Liver Disease,35(Supplement 3), S56–S61.
Xu, H. X., Yin, X. Y., Lu, M. D., et al. (2003). Three- and two-dimensional sonography in gallbladder diseases. Journal of Ultrasound in Medicine,22(2), 181–191.
Irshad, A., Ackerman, S. J., Spicer, K., et al. (2011). Ultrasound evaluation of gallbladder dyskinesia: Comparison of scintigraphy and dynamic 3D and 4D ultrasound techniques. American Journal of Roentgenology,197(5), 1103–1110.
Thind, G., & Rudralingam, V. (2011). Ultrasound imaging of the gallbladder. RAD Magazine,37(436), 16–18.
Fider, J. L., Knudsen, J. M., & Collins, D. A. (2013). Prospective assessment of dynamic CT and MR cholangiography in functional biliary pain. American Journal of Roentgenology,201(12), W271–W282.
Frank, S. J., & Kurian, J. (2016). Three-dimensional sonography of biliary tract disorders. Journal of Ultrasound in Medicine,35(4), 791–804.
Serra, C., Pallotti, F., Bortolotti, M., et al. (2016). A new reliable method for evaluating gallbladder dynamics. Journal of Ultrasound in Medicine,35(2), 297–304.
Everson, G. Y., Braverman, D. Z., Johnson, M. L., et al. (1980). A critical evaluation of real-time ultrasonography for the study of gallbladder volume and contraction. Gastroenterology,79(1), 40–46.
Dodds, W. J., Groh, W. J., Darwesh, R. M. A., et al. (1982). Sonographic measurement of gallbladder volume. American Journal of Roentgenology,145(5), 1009–1011.
Hopman, W. P. M., Brouwer, W. F. M., Rosenbusch, G., et al. (1985). A computerized method for rapid quantification of gallbladder volume from real-time sonograms. Radiology,154(1), 236–237.
Stolk, M. F. J., van Erpecum, K. J., van Berge, Henegouwen G. P., et al. (1990). Gallbladder volume and contraction measured by sum-of-cylinders methods compared with ellipsoid and area-length methods. Acta Radiology,31(6), 591–596.
Wedmann, B., Schmidt, G., Wegener, M., et al. (1991). Sonographic evaluation of gallbladder kinetics: in vitro and in vivo comparison of different methods to assess gallbladder emptying. Journal of Clinical Ultrasound,19(6), 341–349.
Andersen, I. B., Monrad, H., Gronvall, S., et al. (1993). In vitro and in vivo accuracy of sonographic gallbladder volume determinations. Journal of Clinical Ultrasound,21(3), 157–162.
Hurrell, M. A., Chapman, B. A., & Wilson, I. R. (1994). Variation in the estimation of gallbladder volume using the sum-of cylinders method. Investigative Radiology,29(5), 536–539.
Pauletzki, J., Sackman, M., Holl, J., et al. (1996). Evaluation of gallbladder volume and emptying with a novel three-dimensional ultrasound system: Comparison with the sum-of-cylinders and the ellipsoid methods. Journal of Clinical Ultrasound,24(6), 277–285.
Hashimoto, S., Goto, H., Hirooka, Y., et al. (1999). An evaluation of three-dimensional ultrasonography for the measurement of gallbladder volume. American Journal of Gastroenterology,94(12), 3492–3496.
Stads, S., Venneman, N. G., Scheffer, R. C. H., et al. (2007). Evaluation of gallbladder motility: comparison of two-dimensional and three-dimensional ultrasonography. Annals of Hepatology,6(3), 164–169.
Yoon, H. J., Kim, P. N., Kim, A. Y., et al. (2005). Three-dimensional sonographic evaluation of gallbladder contractility: Comparison with cholescintigraphy. Journal of Clinical Ultrasound,34(3), 123–127.
Rohling, R. N., Gee, A. H., & Berman, L. (1998). Automatic registration of 3-D ultrasound images. Ultrasound in Medicine and Biology,24(6), 841–854.
Bodzioch, S., & Ogiela, M. R. (2009). Effective filtration techniques for gallbladder ultrasound images with variable contrast. Journal of Signal Processing Systems,54(1–3), 127–144.
Bodzioch, S., & Ogiela, M. R. (2009). New approach to gallbladder ultrasonic images analysis and lesions recognition. Computerized Medical Imaging and Graphics,33(2), 154–170.
Ogiela, M. R., & Bodzioch, S. (2011). Computer analysis of gallbladder ultrasonic images towards recognition of pathological lesions. Opto-Electronics,19(2), 155–168.
Ciecholewski, M., & Chocholowicz, J. (2013). Gallbladder shape extraction from ultrasound images using active contour models. Computers in Biology and Medicine,43(12), 2238–2255.
Lian, J., Ma, Y., Shi, B., et al. (2017). Automatic gallbladder and gallstone regions segmentation in ultrasound image. International Journal of Computer Assisted Radiology and Surgery,12(4), 553–568.
Li, W. G. (2019). Constitutive law of gallbladder walls in passive state with damage effect. Biomedical Engineering Letters, 9(2), 189–201.
Liao, D. H., Duch, B. U., Stodkilde-Jorgensen, H., et al. (2004). Tension and stress calculations in a 3-D Fourier model of gall bladder geometry obtained from MR images. Annals of Biomedical Engineering,32(5), 744–755.
Li, W. G., Luo, X. Y., Hill, N. A., et al. (2012). A quasi-nonlinear analysis on anisotropic behaviour of human gallbladder wall. Journal of Biomechanical Engineering,134, 0101009.
Li, W. G., Hill, N. A., Ogden, R. W., et al. (2013). Anistropic behaviour of human gallbldder walls. Journal of the Mechanical Behavior of Biomedical Materials,20, 363–375.
Xiong, L., Chui, C. K., & Teo, C. L. (2013). Reality based modelling and simulation of gallbladder shape deformation using variational methods. International Journal of Computer Assisted Radiology and Surgery,8, 857–865.
Karimi, A., Shojaei, A., & Tehrani, P. (2017). Measurement of the mechanical properties of the human gallbladder. Journal of Medical Engineering & Technology,41(7), 541–545.
Funding
None
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
All authors declare that they have no conflict of interest.
Appendix Independence of Mesh Size and Effects of Young’s Modulus
Appendix Independence of Mesh Size and Effects of Young’s Modulus
Quadrilateral and triangle elements were utilized to discretize GB walls in the paper. Table 3 illustrates the element shape selection criteria limits in ABAQUS for those two kinds of elements. For triangle elements the shape factor of an element is defined as the ratio of the element area to the optimal element area, which is the area of an equilateral triangle with the same circumradius as the element.
To identify the independence of mesh size in FEA of seven GBs, three meshes, namely mesh1, mesh2 and mesh3 were created with different mesh sizes, i.e. the edge lengths used in the discretization of element. The mesh quality parameters and number of elements in these meshes are summarized in Table 4. The mesh quality parameters include mean minimum, maximum and worst face corner angles, mean and worst aspect ratios and shape factor (for triangle elements only). In these meshes, each mesh quality parameter varies in a consistent range from mesh1 to mesh3 and is not beyond the limits specified in Table 3 at all, suggesting a better mesh quality.
Based on these meshes, the independence of mesh size was examined with mesh1, mesh2 and mesh3 in terms of the material property constants and loading conditions presented in Table 2. The maximum first principal stresses were extracted and are tabulated in Table 5. When the mesh is changed from mesh1 to mesh2 and mesh3, the errors in the stress vary in the range of − 3.05% and + 2.76%, depending on GB samples themselves. This fact suggests that the stress with mesh1 can be considered mesh size-independent. Thus, the stress and strain at mesh1 are used in the paper.
The stress level may be influenced by Young’s modulus. Based on mesh1 and the loading conditions in Table 2, a series of FEA was performed when the Young’s modulus varied − 20% (− 100 kPa) and + 20% (+ 100 kPa), respectively from the Young’s modulus E = 500 kPa. It is shown in Table 6 that the stress level rises with increasing Young’s modulus or declines with decreasing Young’s modulus. A 20% change in Young’s modulus can result in a variation ranged from − 4.59% to + 7.03% in the maximum first principal stress, depending on GB samples, especially for GBs 9, 19 and 36 which are subject to a longer longitudinal axis. This implies that the Young’s modulus of GB walls may be patient-specific. A constant Young’s modulus assigned to all the GB sample can lead to a variation in the stress level in the range of − 2.57% and + 2.92% in average.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Li, WG. Ultrasound Image Based Human Gallbladder 3D Modelling along with Volume and Stress Level Assessment. J. Med. Biol. Eng. 40, 112–127 (2020). https://doi.org/10.1007/s40846-019-00493-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40846-019-00493-8