Abstract
Population density that indicates a critical point in population growth is able to estimate from the relationship between population density and population movement. In the case of adopting usual definition of population density, the critical point depends on how to divide the space into unit of measurement. We find proper definition of population density. There are both inhabitable and uninhabitable areas. For population density adjusted by the size of the inhabitable area without agricultural land, the critical population density does not depend on the unit of measurement. We observe this statistical characteristic from detailed Japanese census data and land use data.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Population is one of the most basic indices for estimating human statistics. The relationship between population density and various values has been investigated by several researchers. The correlation between population density and GDP was reported in Sutton et al. (2007) and Pan et al. (2013). The relationship between urban density and transport-related energy consumption was reported in Newman and Kenworthy (1988); Lefèvre (2009). The correlation between population density and crime was investigated in Hanley et al. (2016). A model of urban productivity with the agglomeration effect of population density was estimated in Abel et al. (2012). Models that demonstrate a negative correlation between population density and human fertility has been proposed (Lutz et al. 2007).
The concept of density is effective when dealing with an object that has a simple internal structure. By estimating the density of a region, we regard the region as having uniform density. However, it is necessary to be careful when dealing with complex social phenomena. Population density is normally obtained by dividing population by land area. However, the area inhabited by people is not the entire land area. We introduce definition for three types of land area to compare differences in population density.
We focus on population movement as it is easy to observe the effects on population density. Each person moves for various reasons, such as proceeding to the next stage of education, finding employment, or marriage. Regardless of reason, it is considered that the majority of people move from low population density places to high population density places. The result of these movements is the phenomenon of population agglomeration. Agglomeration effects have been modeled in several papers (Fujita and Ogawa 1982; Berliant and Konishi 2000; Ciccone 2002). This effect is related to various problems in modern society, such as population explosion in developing countries, aging in developed countries, and immigration issues. It is important to establish a method of analyzing agglomeration effects from empirical data.
In this study, we propose a method of analyzing agglomeration effects by observing relationship between population density and population increase or decrease. The data used for the analysis is census data and land use data for Japan. Population growth can be regarded as a function in terms of population density. We are then able to cleanly observe the phenomenon using integrated function because fluctuations in the original function are cancelled during integration.
When aggregating a population and an area, it is necessary to determine regional units for aggregation. Regional units can be determined using various methods of spatial division. The division method usually occurs at the administrative level, such as borders of prefectures. However, using administrative divisions is not optimal for reasons such as historical factors. For these reasons, various spatial division methods were proposed in Holmes and Lee (2009), Rozenfeld et al. (2011) and Fujimoto et al. (2015). We analyze agglomeration effects under both administrative spatial division and square block spatial division. The results obtained do not depend on the method of spatial division. A key point in obtaining the results is definition of land area for evaluating population density.
2 Details of the data
The Statistics Bureau of the Japanese Ministry of Internal Affairs and Communications conducts a census every 5 years. Much of this census data can be obtained in a mesh data format from http://www.e-stat.go.jp/, including population data from 2005 and 2010. The mesh data are raster data obtained by equal division of latitude and longitude. The highest accuracy mesh size for the population data is estimated as 500\(\times\)500 m\(^2\). Mesh codes are assigned to each bit of data, and we can specify the corresponding position on the map from this code. Furthermore, we obtained 5-year interval age class population mesh data. Figure 1 shows population pyramids for Japan in 2005 and 2010. Unnatural reduction rates can be observed in the younger generation. These are considered to be errors because of the difficulty of the questionnaire survey. The non-response rates for the survey were 4.4% in 2005 and 8.8% in 2010 (http://www.stat.go.jp/info/kenkyu/kokusei/houdou2.htm). When questionnaires were not returned, the enumerators contacted neighbors to obtain basic information on absent households.
Japanese population pyramids for 2005 and 2010.The horizontal axis for 2010 is shifted 5 years relative to 2005. The black squares are the populations in each 5-year age class in 2005. The gray circles are the populations in 2010. The black triangles are the reduction rates from 2005 to 2010 in each age class
The Japanese Ministry of Land, Infrastructure, Transport and Tourism provides land use data on its website (http://nlftp.mlit.go.jp/ksj/). The land use data are also provided in a mesh data format. A mesh of about 100\(\times\)100 m\(^2\) provides the highest accuracy for land use. In this data, a land use code (see Table 1) is assigned to each cell.
We estimated three types of area by combining areas whose land use codes are checked in Table 1. Type I land is all land. This type is estimated by the land use codes 1, 2, 5, 6, 7, 9, A, B, E and G.
Type II land is inhabitable land. An inhabitable place is defined as any place that is fit for humans to live. Inhabitable land area can be estimated by subtracting such uninhabitable land as forests and lakes from the total land area. This type is estimated by land use codes 1, 2, 7, 9, A and G. Only about 33% of Japan’s land area is inhabitable because there is much mountainous area. This percentage is smaller than for European countries. For example, the percentages of inhabitable area in Germany, France, and the United Kingdom are 68, 71, and 88%, respectively (Fujimoto et al. 2015).
Type III land is land where people are living. This area is obtained by subtracting the area where people are not living such as agricultural land, from type II. This type is estimated by the land use codes 7, 9 and A.
3 Dividing the spatial region
To measure population and land area, it is necessary to determine how the measurement region is to be divided. There are several methods of dividing the land area of Japan into measurement regions. In this paper, we compare the results obtained using various spatial division methods.
The first spatial division uses the following eight regions based on traditional ways of combining several prefectures: Hokkaido, Tohoku, Kanto, Chubu, Kinki, Chugoku, Shikoku, and Kyushu. The average land area of these eight regions is about 47,246 km\(^2\).
The second spatial division uses the borders of the 47 prefectures. The average land area of the prefectures is about 8,041 km\(^2\).
The third spatial division uses the Shi-Ku-Cho-Son borders. Shi-Ku-Cho-Son are municipal units incorporated for local self-government. The closest English words to Shi, Ku, Cho and Son are city, ward, town and village, respectively. These borders have sometimes changed, such as in municipal mergers. We use the borders in 2010. The numbers of Shi, Ku, Cho and Son in 2010 were 767, 23, 757 and 184, respectively. The land area distribution of Shi-Ku-Cho-Son roughly obeys an exponential distribution. The average land area of Shi-Ku-Cho-Son is about 218 km\(^2\).
The fourth spatial division is into square blocks. In this case, we can control the scale of the spatial division by changing the size of the squares.
4 Correlation between population movement and population density
Let us introduce some variables for analyzing population movement.
The population in each region in 2005 is given by
where (i) indicates the region.
The total type I land area in region (i) is given by
The population aged 15–19 years in region (i) in 2005 is given by
The population aged 20–24 years in region (i) in 2010 is given by
Ignoring reductions due to deaths, movements involving foreign countries, and survey errors, the values \(\sum _{(i)}\tilde{n}_{2005}^{(i)}\) and \(\sum _{(i)}\tilde{n}_{2010}^{(i)}\) are equal, where the sums over the index (i) give totals for all of Japan. However, the reduction rate in this age group is about 2% (see Fig. 1). To reduce the influence of this reduction, we introduce normalized populations:
The logarithmic population density in region (i) is given by
The logarithmic growth ratio of the normalized population in region (i) is given by
The left figures in Fig. 2 shows scatter plots of \(x^{(i)}\) versus \(y^{(i)}\). The black circles in the top left figure in Fig. 2 indicate the eight traditional regions used as the spatial division method; the crosses indicate the prefectures used as the spatial division method; the gray dots indicate Shi-Ku-Cho-Son used as the spatial division method.
We perform the same analysis using square blocks. The gray dots in the bottom left figure in Fig. 2 indicate 15\(\times\)15 km\(^2\) square blocks used as the spatial division method; the crosses indicate 90\(\times\)90 km\(^2\) square blocks used as the spatial division method; the black circles indicate 200\(\times\)200 km\(^2\) square blocks used as the spatial division method. Note that the area of a 15\(\times\)15 km\(^2\) square is approximately the average area of a Shi-Ku-Cho-Son unit, the area of a 90\(\times\)90 km\(^2\) square is approximately the average area of a prefecture, and the area of a 200\(\times\)200 km\(^2\) square is approximately the average area of the traditional eight regions.
There are two important quantities that should be determined from the left figures in Fig. 2. The first is the whole slope, which represents the strength of the force moving 15–19 year-olds from low population density areas to high population density areas. The second quantity is the value of x where y is equal to zero (x-intercept). This value represents the boundary between population increase and population decrease.
We assumed constant parameters a and b with respect to y-intercept and whole slope. We tried regression analysis by
where \(e^{(i)}\) is fluctuation of \(y^{(i)}\). Table 2 shows the results of the regression analysis. In particular, under the case of square blocks spatial division, fluctuations of \(y^{(i)}\) are very large in low x region. For this reason, regression analysis do not work well.
To extract the values of the slope and the x-intercept not using regression analysis, we introduce the concept of integration. The relationship between a function f(x) acting at position x and integrated function F(x) is
where \(x_0\) means referential point. We apply this relationship to the scatter plots in the left figures in Fig. 2. We regard the horizontal axis x as position and the vertical axis y as a function, \(y=f(x)\). We implement the integration of Eq. (9) on the discrete scatter plot data as follows:
-
1.
Sort the data in ascending order of x:
$$\begin{aligned} \cdots , (x^{(i)},y^{(i)}), (x^{(i+1)},y^{(i+1)}), \cdots \quad x^{(i)}<x^{(i+1)}. \end{aligned}$$(10) -
2.
Evaluate the integrated function \(F(x^{(i)})\) using
$$\begin{aligned} F(x^{(i)})=-\sum _{j=2}^i y^{(j)}(x^{(j-1)}-x^{(j)}). \end{aligned}$$(11)
Assuming \(y^{(i)}=f(x^{(i)})+e^{(i)}\) with random noise \(e^{(i)}\), the cumulative sum of the second step has the effect of canceling the fluctuation \(e^{(i)}\).
The solid curve in the top right figure in Fig. 2 shows the integrated evaluated from the black circles in the top left figure. For easy comparison with results under other conditions, the maximum value of the integrated function is set to zero. The whole slope of the top left figure is expressed by the curvature of the curve. The position of x where \(y=0\) in the top left figure corresponds to the peak of the curve.
The solid gray curve in the top right figure in Fig. 2 shows the integrated function evaluation from the crosses in the top left figure. The dashed curve in the top right figure in Fig. 2 shows the integrated function evaluated from the gray dots in the top left figure. The dotted curve in the top right figure in Fig. 2 shows the integrated function evaluated using a 40\(\times\)40 km\(^2\) square block spatial division method for comparison.
The bottom right figure in Fig. 2 shows the same analysis as the top right figure for the square block spatial division method. The solid gray curve in the bottom right figure shows the integrated function evaluated from the gray dots in the bottom left figure; the dashed curve in the bottom right figure shows the integrated function evaluated from the crosses in the bottom left figure; the solid curve in the bottom right figure shows the integrated function evaluated from the black circles in the bottom left figure. Although the smoothness of the curve is lost, the results are almost same as for the administrative spatial division methods.
Let us now focus on the differences in the results for the different spatial division methods. The positions of the peaks move to right as the spatial division becomes finer. In the next section, we modify the definition of the population density on the horizontal axis to change the scale dependence of the horizontal axis. We find that the differences between the peaks for different spatial division methods become smaller.
Type I area is used to evaluate population density. The left figures are scatter plots of the logarithmic population density \(x^{(i)}\) versus the logarithmic growth ratio of the population \(y^{(i)}\). The right figures are population movement integrated functions measured by population density. The top figures are comparisons among the results using eight regions, 47 prefectures, or Shi-Ku-Cho-Son. The bottom figures are comparisons among the results using 200\(\times\)200 km\(^2\), 90\(\times\)90 km\(^2\), or 15\(\times\)15 km\(^2\) square blocks
5 Comparison among the three types of definition of population density
The population density is obtained by dividing the population in a certain region by the land area of the region. It does not make sense to include uninhabitable land in the land area, where inhabitable places are defined as any place fit for humans to live. The total inhabitable area is calculated as the total type II area in Table 1.
Figure 3 and Table 2 shows the results using the same analysis as in previous section, with the population density evaluated using type II land area rather than type I land area. Let us compare Figs. 3 and 2. The curvatures of the curves in Fig. 3 are sharper than those in Fig. 2. The differences between the peaks of the curves in Fig. 3 are smaller than the differences in Fig. 2. The results depend less on the spatial division method when using type II land area instead of type I land area.
Type II area is used to evaluate population density. The left figures are scatter plots of the logarithmic population density \(x^{(i)}\) versus the logarithmic growth ratio of the population \(y^{(i)}\). The right figures are population movement integrated functions measured by population density. The top figures are comparison among the results using eight regions, 47 prefectures, or Shi-Ku-Cho-Son. The bottom figures are comparisons among the results using 200\(\times\)200 km\(^2\), 90\(\times\)90 km\(^2\), or 15\(\times\)15 km\(^2\) square blocks
Let us further reconsider population density. It appears that regions with land uses such as agriculture are unrelated to the movement of 15–19 years old. Type III land in Table 1 removes codes such as agriculture from type II land.
Figure 4 and Table 2 show the results using the same analysis as in the previous section, with the population density evaluated using type III land area rather than type I land area. Let us compare Figs. 4 and 3. The curvatures of the curves in Fig. 4 are sharper than those in Fig. 3. The differences between the peaks of the curves in Fig. 4 are smaller than the differences in Fig. 4. The results depend less on the spatial division method when using type III land area instead of type II land area. The population density at the peaks are \(10^{3.623}, 10^{3.726}\) and \(10^{3.782}\), when we use the spatial division 8-regions, prefectures and Shi-Ku-Cho-Son with respectively. The population density at the peaks are \(10^{3.682}, 10^{3.748}\) and \(10^{3.787}\), when we use the spatial division 200\(\times\)200, 90\(\times\)90 and 15\(\times\)15 \(\mathrm{km}^2\) squares with respectively. The population density at the peak is approximately \(10^{3.6}\)–\(10^{3.8}\sim\) 4,000–6,000\(/\mathrm{km}^2\).
Table 3 shows the list of logarithmic population density of capital cities of every prefecture. Many cities which have closely critical population density distributed over Japan. For this reason, it is required to estimate the critical point accurately. Our result is estimated under the assumptions of cancellation of the fluctuation. To discuss precision of the result, it is necessary to investigate the fluctuation of the various regions of x. It is considered the fluctuation closely around the critical point is important.
Type III area is used to evaluate population density. The left figures are scatter plots of the logarithmic population density \(x^{(i)}\) versus the logarithmic growth ratio of the population \(y^{(i)}\). The right figures are population movement integrated functions measured by population density. The top figures are comparisons among the results using eight regions, 47 prefectures, or Shi-Ku-Cho-Son. The bottom figures are comparisons among the results using 200\(\times\)200 km\(^2\), 90\(\times\)90 km\(^2\), or 15\(\times\)15 km\(^2\) square blocks
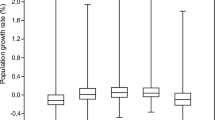
In addition, let us confirm relationship between the statistics of population and area. Figure 5 shows five numbers summaries of three types of area and population. It is observed that interquartile ranges of logarithmic population distributions and logarithmic type III area distributions are almost overlaping each other by shifting the scale about 3.5. This property is considered to be one of the reasons that the peaks in Fig. 4 is not dependent on the method of spatial division. The difference of the interquartile ranges of logarithmic population distributions and logarithmic area distributions are considered to be one of the reasons that the difference of peaks in Fig. 2 and Fig. 3.
Five numbers summaries of area distributions and population distributions. The cross marks are the average of of each distribution. The top left boxplots are comparisons among the type I area distributions. The third quartile value, median and maximum value are the same in the case of \(15\times 15\) squares spatial division. The bottom left boxplots are comparisons among the type II area distributions. The top right boxplots are comparisons among the type III area distributions. The bottom right boxplots are comparisons among the population distributions. Here, the scale on the horizontal axis is shifted 3.5
6 Analysis of various age classes
We investigate the integrated function for other age classes using the same analysis as in previous sections. There are 18 classes at all. The breakdown is ages 0–4 in 2005 (ages 5–9 in 2010), ages 5–9 in 2005 (ages 10–14 in 2010), \(\ldots\), ages 70–74 in 2005 (ages 75–79 in 2010), and ages 75–79 in 2005 (ages 80–84 in 2010). Figure 6 shows the integrated functions for every class. Shi-Ku-Cho-Son borders are used for the spatial division. The type III land area is used to evaluate population density. The results are shown as curves in different shades of gray from black (young age class) to white (old age class). The thick solid curve shows the integrated function for ages 10–14 in 2005. The thick dashed curve shows the integrated function for ages 15–19 in 2005. Clean peaks are available for the 10–14 and 15–19 classes. The positions of the two peaks are almost the same. The curvature for the 15–19 class is sharper than the curvature for the 10–14 class. Many people in these classes experienced their March high school graduation event at 18 years old during the 5-year period. Around 50% of people continue to college or university in Japan (see “Enrollment and Advancement Rate” in http://www.mext.go.jp/english/statistics/) The difference in these curvatures is considered to be due to the proportions of 18 year olds in these classes.
Clean peaks are not observed in the other classes. There is not much correlation between the logarithmic population density and the growth ratio of the population. For example, we show a scatter plot (see Fig. 7) of these two values for ages 20–24 in 2005.
7 Conclusion
We analyze the relationship between the population density and the growth ratio of the population. The relationship is clear for ages 10–14 in 2005 (ages 15–19 in 2010) and ages 15–19 in 2005 (ages 20–24 in 2010). This shows the agglomeration effect that people gather in more densely populated regions. The value of the population density that indicates a critical point in population growth is important. We evaluate this value using the concepts of integration. It is necessary to decide how to divide the land area when the population and the area are combined. We found that the results do not depend on how the area is divided when evaluating population density using the inhabitable area without agricultural land. It is concluded that around 4,000–6,000 /km\(^2\) population density is the critical point. Although the curve of integrated function is considered to be universal curve throughout Japan, the fluctuations from the curve depend on how to divide the land area.
We do not observe clear correlations between population density and population growth in the other age classes. Nevertheless, it is difficult to assume that people in these classes move randomly. It is possible that a stratified analysis using life events would be more useful than an analysis based on age group. Various life events, such as entering school, starting work, changing jobs, getting married, getting divorced, and recuperating can affect population movement. We would like to find quantities that relate to population movement independently of population density. For getting a job, we guess that per capita GDP density is more important than population density. For recuperation, we guess that the density of hospitals is more important than population density.
References
Abel JR, Dey I, Gabe TM (2012) Productivity and the density of human capital. J Reg Sci 52:562
Berliant M, Konishi H (2000) The endogenous formation of a city: population agglomeration and marketplaces in a location-specific production economy. Reg Sci Urban Econ 30:289
Ciccone A (2002) Agglomeration effects in Europe. Eur Econ Rev 46:213
Fujita M, Ogawa H (1982) Multiple equilibria and structural transition of non-monocentric urban configurations. Reg Sci Urban Econ 12:161
Fujimoto S, Mizuno T, Ohnishi T, Shimizu C, Watanabe T (2015) Geographic dependency of population distribution. In: Takayasu H, Ito N, Noda I, Takayasu M (eds) Proceedings of the International Conference on Social Modeling and Simulation, plus Econophysics Colloquium 2014. Springer International Publishing, pp 151–162
Hanley QS, Lewis D, Ribeiro HV (2016) Rural to urban population density scaling of crime and property transactions in english and welsh parliamentary constituencies. PLoS One 11:e0149546
Holmes TJ, Lee S (2009) Cities as six-by-six mile squares: Zip'f law? In: Glaeser E (ed) The economics of agglomerations. University of Chicago Press, pp 105–131
Lefèvre B (2009) Urban transport energy consumption: determinants and strategies for its reduction. S.A.P.I.EN.S 2(3). http://sapiens.revues.org/914. Accessed 14 Dec 2016
Lutz W, Testa MR, Penn DJ (2007) Population density is a key factor in declining human fertility. Popul Environ 28:69
Mext: Statistics. http://www.mext.go.jp/english/statistics/
Newman P, Kenworthy J (1988) The transport energy trade-off: fuel-efficient traffic versus fuel-efficient cities. Transp Res 22A:163
National land numerical information download service. http://nlftp.mlit.go.jp/ksj/
Pan W, Ghoshal G, Krumme C, Cebrian M, Pentland A (2013) Urban characteristics attributable to density-driven tie formation. Nat Commun 4:1961
Portal site of official statistics of japan. http://www.e-stat.go.jp/
Press material by ministry of internal affairs and communications in japanese. http://www.stat.go.jp/info/kenkyu/kokusei/houdou2.htm
Rozenfeld HD, Rybski D, Gabaix X, Makse HA (2011) The area and population of cities: new insights from a different perspective on cities. Am Econ Rev 101(5):2205
Sutton PC, Elvidge CD, Ghosh T (2007) Estimation of gross domestic product at sub-national scales using nighttime satellite imagery. Int J Ecol Econ Stat 8(S07):5
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Fujimoto, S., Mizuno, T., Ohnishi, T. et al. Relationship between population density and population movement in inhabitable lands. Evolut Inst Econ Rev 14, 117–130 (2017). https://doi.org/10.1007/s40844-016-0064-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40844-016-0064-z