Edge General Position Sets in Fibonacci and Lucas Cubes

Abstract

A set of edges $X\subseteq E(G)$ of a graph G is an edge general position set if no three edges from X lie on a common shortest path in G. The cardinality of a largest edge general position set of G is the edge general position number of G. In this paper, edge general position sets are investigated in partial cubes. In particular, it is proved that the union of two largest $\Theta$-classes of a Fibonacci cube or a Lucas cube is a maximal edge general position set.

1 Introduction

A set of vertices $S\subseteq V(G)$ of a graph $G = (V(G), E(G))$ is a general position set if no three vertices from S lie on a common shortest path of G. Similarly, a set of edges $X\subseteq E(G)$ of G is an edge general position set if no three edges from X lie on a common shortest path. The cardinality of a largest general position set (resp. edge general position set) of G is the general position number (resp. edge general position number) and denoted by $\textrm{gp}(G)$ (resp. $\mathrm{gp_{e}}(G)$).

General position sets in graphs have already received a lot of attention. They were introduced in [16, 28], and we refer to [1, 12, 21, 27, 31] for a selection of further developments. On the other hand, the edge version of this concept has been introduced only recently in [17]. In this paper, we continue this line of the research.

To determine the general position, the number of hypercubes turns out to be a very difficult problem, cf. [15]. On the other hand, a closed formula for the edge general position number of hypercubes has been determined in [17]. Combining the facts that the edge general position number is doable on hypercubes and that hypercubes form the cornerstone of the class of partial cubes, we focus in this paper on the edge general position number of two important and interesting families of partial cubes, Fibonacci cubes and Lucas cubes. The first of these two classes of graphs was introduced in [8] as a model for interconnection networks. In due course, these graphs have found numerous applications elsewhere and are also extremely interesting in their own right. Lucas cubes, introduced in [20], form a class of graphs which naturally symmetrises the Fibonacci cubes and also have many interesting properties. The state of research up to 2013 on these classes of graphs (and some additional related ones) is summarised in the survey paper [11]; the following list of papers is a selection from subsequent research [4,5,6, 9, 18, 19, 22,23,24,25, 29].

The rest of this paper is organised as follows. In the next section, we define the concepts discussed in this paper, introduce the required notation, and recall a known result. In Sect. 3, we discuss partial cubes and the interdependence of their edge general position sets and $\Theta$-classes. In Sect. 4, we prove that the union of two largest $\Theta$-classes of a Fibonacci cube or a Lucas cube is always a maximal edge general position set. We conjecture that for Fibonacci cubes these sets are also maximum general position sets and show that this is not the case for Lucas cubes.

2 Preliminaries

Unless stated otherwise, graphs considered in this paper are connected. The path of order n is denoted by $P_n$. The Cartesian product $G\,\square \,H$ of graphs G and H has vertices $V(G)\times V(H)$ and edges $(g,h)(g',h')$, where either $g=g'$ and $hh'\in E(H)$, or $h=h'$ and $gg'\in E(G)$. The r-dimensional hypercube $Q_r$, $r\ge 1$, is a graph with $V(Q_r) = \{0, 1\}^r$, and there is an edge between two vertices if and only if they differ in exactly one coordinate. That is, if $x = (x_1, \ldots , x_r)$ and $y = (y_1, \ldots , y_r)$ are vertices of $Q_r$, then $xy\in E(Q_r)$ if and only if there exists $j\in [r] = \{1,\ldots , r\}$ such that $x_j \ne y_j$ and $x_i = y_i$ for every $i\ne j$. $Q_r$, $r\ge 2$, can also be described as the Cartesian product $Q_{r-1}\,\square \,P_2$.

The distance $d_G(u, v)$ between vertices u and v of a graph $G = (V(G), E(G))$ is the number of edges on a shortest u, v-path. A subgraph H of a graph G is isometric if $d_H(x, y) = d_G(x, y)$ holds for every pair of vertices x, y of H. We also say that H is isometrically embedded into G. Isometric subgraphs of hypercubes are known as partial cubes.

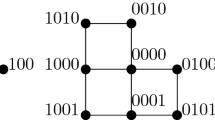
A Fibonacci string of length $n\ge 1$ is a binary string that contains no consecutive 1 s. The Fibonacci cube $\Gamma _n$, $n\ge 1$, is the graph whose vertices are all Fibonacci strings of length n, two vertices being adjacent if they differ in a single coordinate. $\Gamma _n$ can be equivalently defined as an induced subgraph of $Q_n$ obtained from $Q_n$ by removing all the vertices that contain at least one pair of consecutive 1 s. Further, the Lucas cube $\Lambda _n$, $n\ge 1$, is obtained from $\Gamma _n$ by removing the vertices that start and end with 1. See Fig. 1 for $\Gamma _5$ and $\Lambda _5$ and note that the latter is obtained from the former by removing the vertices 10001 and 10101.

Fig. 1

$\Gamma _5$ and $\Lambda _5$

It is well known that the order of $\Gamma _{n}$ is $F_{n+2}$, where $F_n$ are the Fibonacci numbers defined by the recurrence $F_{n+2} = F_{n+1} + F_{n}$, $n\ge 0$, with the initial terms $F_0 = 0$ and $F_1 = 1$. Also, the order of $\Lambda _{n}$ is $L_n$, where $L_n$ are the Lucas numbers defined by the same recurrence relation with the initial terms $L_0 = 2$ and $L_1 = 1$.

To complete the preliminaries, we recall the following inequality on Fibonacci numbers.

Lemma 2.1

[2, Corollary] If n is a positive integer and $0 \le i\le \lfloor n/2\rfloor$, then $F_{n}\ge F_{i}F_{n-i+1}$.

3 On Edge General Position Sets in Partial Cubes

In this section, we recall several results on the edge general position sets in partial cubes from [17] and derive some new results. This will motivate us to consider edge general position sets in Fibonacci cubes and in Lucas cubes in the next section.

Let G be a graph. Then, we say that edges xy and uv of G are in the Djoković–Winkler relation $\Theta$ if $d_G(x,u)\,+\, d_G(y,v) \not = d_G(x,v)\,+\,d_G(y,u)$ [3, 30]. A connected graph G is a partial cube if and only if G is bipartite and $\Theta$ is transitive [30]. It follows that $\Theta$ partitions the edge set of a partial cube into $\Theta$-classes. Moreover, if G is a partial cube isometrically embedded into $Q_n$ such that for each $i\in [n]$ there exits an edge $xy\in E(G)\subseteq E(Q_n)$ with $x_i\ne y_i$, then G contains exactly n $\Theta$-classes. We will denote them by $\Theta _1(G), \ldots , \Theta _n(G)$, where $\Theta _i(G)$, $i\in [n]$, consists of the edges of G which differ in coordinate i.

We first recall the following result.

Lemma 3.1

[17, Lemma 3.1] If G is a partial cube embedded into $Q_n$, then $\Theta _i(G) \cup \Theta _j(G)$ is an edge general position set of G.

Using Lemma 3.1, it was proved in [17] that $\mathrm{gp_{e}}(Q_r) = 2^r$. It was also proved that $\mathrm{gp_{e}}(P_r\,\square \,P_r) = 4r - 8$ for $r\ge 4$, see [17, Theorem 4.1]. Note, however, that $|\Theta _i(P_r\,\square \,P_r)| = r$ for each $i\in [2r-2]$. Hence, Lemma 3.1 only yields $\mathrm{gp_{e}}(P_r\,\square \,P_r) \ge 2r$ which is arbitrary away from the optimal value. Moreover, if $r\ge 5$, then by [17, Theorem 4.2] a largest edge general position set of $P_r\,\square \,P_r$ is unique and is not a union of some $\Theta$-classes. On the other hand, we can have large edge general position sets which are the union of many $\Theta$-classes as the following result asserts, where by an end block of a graph G we mean a block of G which contains exactly one cut vertex.

To prove the next proposition, we recall the following auxiliary result.

Lemma 3.2

[14, Lemma 6.4] Let H be an isometric subgraph of G, and let e and f be edges from different blocks of H. Then, e is not in relation $\Theta$ with f in G.

Proposition 3.3

Let $B_1,\ldots , B_k$ be the end blocks of a partial cube G and for $i\in [k]$ let $\Theta ^{i}(G)$ be an arbitrary $\Theta$-class of G with an edge in $B_i$. Then, $\bigcup _{i\in [k]} \Theta ^{i}(G)$ is an edge general position set of G.

Proof

By Lemma 3.2, $\Theta ^{i}(G) \subseteq E(B_i)$, and thus, $\Theta ^{i}(G)$ also forms a $\Theta$-class of $B_i$. Consider now an arbitrary shortest path P of G and suppose it contains an edge $e_i$ of some $\Theta ^{i}(G)$. Then, by the above, $e_i$ is the only edge of P from $\Theta ^{i}(G)$. If P contains an edge $e_j$ from some other $\Theta ^{j}(G)$, then also $e_j$ is the only edge of P from $\Theta ^{j}(G)$. Moreover, in this case, $E(P) \cap \bigcup _{i\in [k]} \Theta ^{i}(G) = \{e_i, e_j\}$ because all the edges of P which do not lie in $B_i \cup B_j$ are from blocks which are not end blocks. $\square$

Note that Proposition 3.3 implies that the set of leaves of a tree T forms an edge general position set. For another example of an edge general position which is the union of many $\Theta$-classes, see Fig. 2.

Fig. 2

An edge general position set

To finish this section, consider the partial cube G from Fig. 3. In the left figure, the union of its two largest $\Theta$-classes forms an edge general position set of cardinality 8. In the middle figure, the union of four $\Theta$-classes also forms an edge general position set of G of cardinality 8. Finally, since we can cover the edges of G by four shortest paths as shown in the right figure, we have $\mathrm{gp_{e}}(G)\le 8$ which means that both indicated sets are largest edge general position sets.

Fig. 3

Two largest edge general position sets of a partial cube and a cover of it by shortest paths

4 On Edge General Position Sets in Fibonacci and Lucas Cubes

Fibonacci cubes and Lucas cubes are partial cubes [10]. Thus, all the results and comments of the previous section can be applied to them. The cardinality of the $\Theta$-classes of Fibonacci cubes was independently determined in [13, 26] and the cardinality of the $\Theta$-classes of Lucas cubes in [13]. These results read as follows.

Proposition 4.1

• (i) If $n\ge 1$ and $i\in [n]$, then $|\Theta _i(\Gamma _n)| = F_{i}F_{n-i+1}$.

• (ii) If $n\ge 1$ and $i\in [n]$, then $|\Theta _i(\Lambda _n)| = F_{n-1}$.

To find large edge general position sets in $\Gamma _n$, we can apply Lemma 3.1. For this sake, we first answer the question for which i and j the value $|\Theta _i(\Gamma _n) \cup \Theta _j(\Gamma _n)|$ is maximum.

Proposition 4.2

If $n\ge 2$, then

$$\begin{aligned} 2F_n = \max \{|\Theta _i(\Gamma _n)| + |\Theta _j(\Gamma _n)|:\ i, j\in [n], i\ne j\}. \end{aligned}$$

Proof

Set $M = \max \{|\Theta _i(\Gamma _n)| + |\Theta _j(\Gamma _n)|:\ i, j\in [n], i\ne j\}$. Using Proposition 4.1 and Lemma 2.1, we can then estimate as follows:

$$\begin{aligned} M&= \max \{|\Theta _i(\Gamma _n)| + |\Theta _j(\Gamma _n)|:\ i, j\in [n], i\ne j\} \\&= \max \{F_iF_{n-i+1} + F_jF_{n-j+1}:\ i, j\in [n], i\ne j\} \\&\le \max \{F_n + F_n:\ i, j\in [n], i\ne j\} \\&= 2F_n\,. \end{aligned}$$

On the other hand, $|\Theta _1(\Gamma _n)| + |\Theta _n(\Gamma _n)| = F_n + F_n$; hence, we can conclude that $M = 2F_n$. $\square$

Theorem 4.3

If $n\ge 2$, then $\Theta _1(\Gamma _n) \cup \Theta _n(\Gamma _n)$ is a maximal edge general position set of $\Gamma _n$. Moreover, $\mathrm{gp_{e}}(\Gamma _n)\ge 2F_n$.

Proof

To prove the first assertion, we will use the fact that a shortest path can contain at most one edge from $\Theta _1(\Gamma _n)$ and at most one edge from $\Theta _n(\Gamma _n)$, cf. [7, Lemma 11.1]. Hence, we only need to prove that no edge can be added to $\Theta _1(\Gamma _n) \cup \Theta _n(\Gamma _n)$ in order to keep the edge general position property.

The statement of the theorem clearly holds for $\Gamma _2$ and can be easily verified for $\Gamma _3$ and $\Gamma _4$. In the rest, we may thus assume that $n\ge 5$. Consider an arbitrary edge $e = uv\in \Theta _i(\Gamma _n)$, where $2\le i\le n-1$. We may without loss of generality assume that $u_i = 0$ and $v_i = 1$. We need to show that e lies on some shortest path that contains one edge from $\Theta _1(\Gamma _n)$ and one edge from $\Theta _n(\Gamma _n)$. We distinguish the following two cases.

Case 1: $i \in \{2, n-1\}$. Suppose first that $i = 2$. In this case, $u = 000 \ldots$ and $v = 010\ldots$ If $u_n = v_n = 1$, then the following path

$$\begin{aligned} y&= 1\,0\,0\, \ldots \, 0\,0 \\ x&= 0\,0\,0\, \ldots \, 0\,0 \\ u&= 0\,0\,0\, \ldots \, 0\,1 \\ v&= 0\,1\,0\, \ldots \, 0\,1 \end{aligned}$$

is a shortest x, y-path in $\Gamma _n$ that contains $yx\in \Theta _1(\Gamma _n)$ and $xu\in \Theta _n(\Gamma _n)$. If $u_n = v_n = 0$, then we consider two subcases. In the first one, $u = 000 \ldots 00$ and $v = 010\ldots 00$. Then, the following shortest path

$$\begin{aligned} x&= 1\,0\,0\, \ldots \, 0\,0 \\ u&= 0\,0\,0\, \ldots \, 0\,0 \\ v&= 0\,1\,0\, \ldots \, 0\,0 \\ y&= 0\,1\,0\, \ldots \, 0\,1 \end{aligned}$$

contains $xu\in \Theta _1(\Gamma _n)$ and $vy\in \Theta _n(\Gamma _n)$. In the second subcase, we consider $u = 000 \ldots 10$ and $v = 010\ldots 10$, in which case we have $u = 000 \ldots 010$ and $v = 010\ldots 010$. Then, the path

$$\begin{aligned} x&= 1\,0\,0\, \ldots \, 0\,1\,0 \\ u&= 0\,0\,0\, \ldots \, 0\,1\,0 \\ v&= 0\,1\,0\, \ldots \, 0\,1\,0 \\ y&= 0\,1\,0\, \ldots \, 0\,0\,0 \\ z&= 0\,1\,0\, \ldots \, 0\,0\,1 \end{aligned}$$

is a shortest path in $\Gamma _n$ and contains $xu\in \Theta _1(\Gamma _n)$ and $yz\in \Theta _n(\Gamma _n)$. For instance, if $n=5$, then the path constructed is: $x=10010$, $u=00010$, $v=01010$, $y=01000$, $z=01001$.

We have thus considered all the subcases when $i = 2$. By the symmetry of Fibonacci strings, the case $i = n-1$ can be done analogously.

Case 2: $2< i < n-1$. In this case, we have $u = \ldots 000 \ldots$ and $v = \ldots 010 \ldots$ Assume first that $u_1= v_1 = 1$ and $u_n = v_n = 1$, so that $u = 10 \ldots 010\ldots 01$ and $v = 10 \ldots 000 \ldots 01$. Then, the path

$$\begin{aligned} x&= 0\,0\, \ldots \, 0\,1\,0 \ldots 0\, 1\\ v&= 1\,0\, \ldots \, 0\,1\,0 \ldots 0\, 1\\ u&= 1\,0\, \ldots \, 0\,0\,0 \ldots 0\, 1\\ y&= 1\,0\, \ldots \, 0\,0\,0 \ldots 0\, 0 \end{aligned}$$

is a shortest path in $\Gamma _n$ and contains edges $xv\in \Theta _1(\Gamma _n)$ and $uy\in \Theta _n(\Gamma _n)$. For instance, if $n=5$, then the path constructed is: $x=00101$, $v=10101$, $u=10001$, $y=10000$.

If u and v start and end by 00, we simply change the first and the last bit to construct a required shortest path. Assume next that $u = 01 \ldots 000\ldots 10$ and $v = 01 \ldots 010 \ldots 10$. Because v starts and ends with 0 and contains at least three 1s, in this case we have $n\ge 7$. Then, the path

$$\begin{aligned} x&= 1\,0\, \ldots \, 0\,1\,0 \ldots 1\, 0\\ x'&= 0\,0\, \ldots \, 0\,1\,0 \ldots 1\, 0\\ v&= 0\,1\, \ldots \, 0\,1\,0 \ldots 1\, 0\\ u&= 0\,1\, \ldots \, 0\,0\,0 \ldots 1\, 0\\ y&= 0\,1\, \ldots \, 0\,0\,0 \ldots 0\, 0\\ y'&= 0\,1\, \ldots \, 0\,0\,0 \ldots 0\, 1 \end{aligned}$$

is a shortest path in $\Gamma _n$ which contains $xx'\in \Theta _1(\Gamma _n)$ and $yy'\in \Theta _n(\Gamma _n)$. The final cases when u and v begin by 0 and end by 1 (or the other way around) are done by combining the above paths.

By Proposition 4.1(i), $|\Theta _1(\Gamma _n)| = |\Theta _n(\Gamma _n)| = F_n$; hence, $\mathrm{gp_{e}}(\Gamma _n)\ge |\Theta _1(\Gamma _n)| + |\Theta _n(\Gamma _n)| = 2F_n$. $\square$

With a lot of effort, we can further prove that for any i and j, the set $\Theta _i(\Gamma _n)\cup \Theta _j(\Gamma _n)$ is a maximal edge general position set. However, since $\Theta _1(\Gamma _n)\cup \Theta _n(\Gamma _n)$ is a largest such a set, we omit the long case analysis here.

Based on Theorem 4.3, we wonder whether $\Theta _1(\Gamma _n) \cup \Theta _n(\Gamma _n)$ is not only a maximal edge general position set of $\Gamma _n$ but also a maximum edge general position set. While we have no answer in general, we next show that this is true up to dimension $n\le 5$. For $n\le 4$, this can be easily checked, and for $n=5$ we have the following.

Proposition 4.4

$\mathrm{gp_{e}}(\Gamma _5) = 10$.

Proof

By Theorem 4.3, we have $\mathrm{gp_{e}}(\Gamma _5) \ge 10$. Consider now the four paths in $\Gamma _5$ as indicated in Fig. 4, and note that each of them is a shortest path. The only edges not contained in one of these four paths are e, $e'$, and $e''$, see Fig. 4 again.

Fig. 4

Four shortest paths in $\Gamma _5$

Let X be an arbitrary edge general position set of $\Gamma _5$. Since each of the four paths from Fig. 4 is a shortest path, each of them can contain at most two edges from X and thus $|X| \le 4\cdot 2 + 3 = 11$. Supposing that $|X| = 11$, we must have $e, e', e''\in X$. However, by inspection we can now infer that if $e, e', e''\in X$, then there are only 5 more additional edges that could possibly lie in X; hence if $e, e', e''\in X$, then actually $|X| \le 8$ holds. $\square$

Based on Theorem 4.3 and Proposition 4.4, we pose:

Conjecture 4.5

If $n\ge 2$, then $\mathrm{gp_{e}}(\Gamma _n) = 2F_n$.

For the Lucas cubes, we have the following result parallel to Theorem 4.3.

Theorem 4.6

If $n\ge 4$, then $\Theta _1(\Lambda _n) \cup \Theta _n(\Lambda _n)$ is a maximal edge general position set of $\Lambda _n$. Moreover, $\mathrm{gp_{e}}(\Lambda _n)\ge 2F_{n-1}$.

Proof

We proceed parallel with the proof of Theorem 4.3. More precisely, we need to show that no edge can be added to $\Theta _1(\Lambda _n) \cup \Theta _n(\Lambda _n)$ in order to keep the edge general position property. Then, all the paths constructed in the proof of Theorem 4.3 contain no vertex which would start and end with 1; hence, the same paths are suitable also for the present proof. The only exception appears to be the path as constructed in the first subcase of Case 2. However, this subcase is not relevant in the present proof because the vertices u and v are not vertices of $\Lambda _n$, and hence, we need not consider them here. Finally, by Proposition 4.1(ii), $|\Theta _1(\Lambda _n)| = |\Theta _n(\Lambda _n)| = F_{n-1}$; hence, $\mathrm{gp_{e}}(\Lambda _n)\ge |\Theta _1(\Lambda _n)| + |\Theta _n(\Lambda _n)| = 2F_{n-1}$. $\square$

By Theorem 4.6, $\mathrm{gp_{e}}(\Lambda _5)\ge 6$. The following result then comes as a surprise.

Proposition 4.7

$\mathrm{gp_{e}}(\Lambda _5) = 7$.

Proof

Let X be an arbitrary edge general position set of $\Lambda _{5}$ and let $u=00000$. Let $F = \left\{ e_{1},e_{2},e_{3},e_{4},e_{5}\right\}$ be the set of the edges incident to u, where $e_{1}=\{u,10000\}$, $e_{2} = \{u,01000\}$, $e_{3} = \{u, 00100\}$, $e_{4} = \{u, 00010\}$, and $e_{5} = \{u, 00001\}$. See Fig. 5.

Fig. 5

$\Lambda _5$ and its largest edge general position set

Since F is an edge general position set, we consider the following cases.

Case 1: $\left| X\cap F\right| =5$. In this case, no edge from $E(\Lambda _{5})\backslash F$ can be added to X, so $|X| = 5$.

Case 2: $\left| X\cap F\right| =4$. We may without loss of generality assume that $F=\{e_1, e_3, e_5, e_2\}$. Then, only the edges $\{01010, 00010\}$ and $\{10010, 00010\}$ can be added to X; hence, in this case we have $|X|\le 6$.

Case 3: $\left| X\cap F\right| =3$. By the symmetry of $\Lambda _5$, it suffices to distinguish the following two subcases.

(i) X contains three consecutive edges, say $X\cap F=\left\{ e_{1},e_{3},e_{5}\right\}$. Then, at most two edges of $E(\Lambda _{5})\backslash F$ can be added to X.

(ii) X does not contain three consecutive edges, say $X\cap F=\left\{ e_{1},e_{2},e_{3}\right\}$. Then, four edges of $E(\Lambda _{5})\backslash F$ can be added to X as shown in the right-hand side of Fig. 5. So in this case $|X| = 7$.

Case 4: $\left| X\cap F\right| =2$. In this case, no matter whether the edges from $X\cap F$ are consecutive or not, we can easily check that at most four edges of $E(\Lambda _{5})\backslash F$ can be added to X.

Case 5: $\left| X\cap F\right| =1$. We may assume that $F = \{e_1\}$. Then, considering the three subcases based on whether $\{10000, 10010\}$ and $\{10000, 10100\}$ lie in X, we get that in every case $|X| \le 6$.

Case 6: $\left| X\cap F\right| =0$. In this case, we observe that at most every second edge from the outer 10-cycle can lie in X; hence, $|X|\le 5$.

Note that the proof of Proposition 4.7 also implies that a largest edge general position set of $\Lambda _5$ is unique up to symmetry.