1 Introduction

Prediction models for clinical outcomes can greatly aid clinicians with early diagnosis, cost-effective management and primary prevention of many medical conditions. Clinical prediction models typically estimate risk scores of outcome of interest based on various factors such as age, sex, ethnicity, body mass index (BMI), smoking habit and genetic history [1]. A well-known example is the QRISK®risk calculator, which is a well-established cardiovascular disease (CVD) risk assessment tool in context of the UK population [2]. This estimates the risk of developing CVD over the next 10 years based on current measures of age, sex, ethnicity, smoking status, cholesterol, blood pressure levels etc. Although these prediction models have been tremendously useful for day-to-day clinical practice, most conventional risk models make use of predictors measured at a single time point, e.g. at baseline or at the most recent hospital visit or follow-up [3]. Predictors measured at a single time point do not reflect the changes in longitudinal predictor profiles and the way these changes influence the risk of an event. This is counter-intuitive to the way health professionals assess their patients’ health states by progressively updating a prognosis based on total history of available information. Also, conventional prediction models are not well placed in terms of exploiting the full potential of patient level longitudinal data available from modern electronic health records systems.

Dynamic prediction has recently emerged as an alternative and more appealing prediction technique that can fully utilise the longitudinal changes in prediction variables [3]. Dynamic prediction in time-to-event analysis is the computation of predictive distribution at a certain moment in time, given the history of event(s) and covariates [4]. The predictions can be updated as additional information gets collected from further follow-up or visits and the access to updated risks may be very useful for making clinical decisions such as may enable clinicians to gain better understanding of the disease dynamics, and help making most optimal decision at the specific time point.

There are two approaches that are commonly used for dynamic prediction based on longitudinally measured biomarkers [5]. They are: (i) joint models for longitudinal and time-to-event data [6, 7], and (ii) landmarking in time-to-event analysis [8]. The use of joint models for dynamic prediction is based on a formal and theoretically rigorous statistical framework that jointly characterises the evolution of the longitudinal biomarkers and the time-to-event processes. The predictions using correctly specified joint models are expected to be efficient [5], although their implementation generally is computationally demanding, and requires specialised software [9, 10], that has not yet been incorporated within the mainstream standard statistical software packages.

The landmarking approach of dynamic prediction does not specify a formal statistical model for the longitudinal markers and therefore is based on a pragmatic rather than a formal statistical model of the joint distribution of longitudinal markers and the time-to-event process [4, 8]. Due to not providing a model-based continuum of the predicted longitudinal markers, landmarking approach is generally less efficient than joint modelling, and prediction can often be somewhat biased for intermittently observed longitudinal markers resulting from relying on last observation carried forward to impute unobserved values of the longitudinal biomarkers. The method is, however, still popular due to ease of implementation as dynamic prediction based on landmarking can be obtained using commonly used standard statistical software.

Comparison of predictive performance of joint modelling and landmarking approaches has been recently explored in the statistical literature. Using various functional forms of the association structure between a longitudinal marker and time-to-event processes, Rizopoulos et al. [1] demonstrated that prediction accuracy of the joint model is better than the landmarking approach. Suresh et al. [11] compared joint modelling and landmarking approaches in context of a binary longitudinal marker (representing an illness-death model). The paper did not lead to a conclusion of whether prediction by one approach is more accurate than the other, but, suggests that joint modelling is likely to perform better when the stochastic process of the longitudinal markers can be well characterised from the available data. When this is harder (e.g. in case of sparse longitudinal data), or if there are many longitudinal markers, prediction by landmarking may provide a good enough approximation.

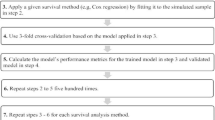
Most of the comparisons in the literature are mainly based on model based data simulations, meaning data are simulated according to specific statistical models. This poses no problems for predictions based on joint models as they completely specify a data generation mechanism. However, this may be problematic for the landmarking approach as the method does not provide a complete data generation mechanisms for the longitudinal process. Therefore, data generated according to joint models are likely to be more favourable to prediction using joint models than that using landmarking approach. To overcome this issue, and to facilitate a fairer comparison of the two methods, we consider real data for performance comparison using bootstrap simulation. We use bootstrap simulation to correct for any potential “optimism” which often results from evaluating model performance on the same data that are used to train the model. The main motivation for bootstrap simulation-based comparison is to ensure that the data generation mechanism does not depend on either of the underlying statistical models, so that the comparison is impartial to predictions based on both joint modelling and landmarking approaches.

2 Methods

2.1 Dynamic Prediction via Joint Modelling

The basic principle of joint modelling for time-to-event and longitudinal data is to couple a survival model for the time-to-event process with a suitable model for the longitudinal process that will account for any interdependence between the two processes [7]. Joint modelling fully specifies the joint distribution that characterises and links the two models for the longitudinal marker process Y(t), and the time-to-event process T by a statistical framework involving shared parameters to model the interdependence [6, 7, 12]. Using notations similar to [7], we denote the observed value of the longitudinal marker for subject i (\(i=1,\ldots , n\)) at time point t by \(y_{i}(t)\), and more specifically, the observed longitudinal marker for subject i at a specific occasion \(t_{ij}\) by \(y_i(t_{ij})\). The observed longitudinal marker process therefore is denoted by \(y_{ij}=\left\{ y_i(t_{ij}), j=1,\ldots ,n_i\right\} \). The longitudinal sub-model can be written as [1],

$$\begin{aligned} y_{i}(t)= & {} \mu _{i}(t)+\epsilon _{i}(t) \nonumber \\= & {} \varvec{x}_{i}'(t) \varvec{\beta } +\varvec{z}_{i}'(t)\varvec{b}_{i} + \epsilon _{i}(t), \end{aligned}$$
(1)

where \(\varvec{x}_{i}(t)\) and \(\varvec{z}_{i}(t)\) are the corresponding design vectors for the fixed-effects \(\varvec{\beta }\) and random effects \(\varvec{b}_i\), respectively, with \(\varvec{b}_i \sim N(\varvec{0}, \varvec{D})\). The corresponding random error terms, \(\epsilon _{i}(t)\), are assumed to be independent of the random effects with \(\epsilon _{i}(t) \sim N(0, \sigma ^2)\) and \(\mathrm{cov}[(\epsilon _{i}(t), \epsilon _{i}(\tilde{t})]=0\) for \(\tilde{t} \ne t\).

To formulate the survival sub-model, we denote the true event time for the ith subject by \(T_i\) and the corresponding observed event time by \( T_{i}^{*}=\min (T_i, C_i)\) where \(C_i\) is the potential censoring time and \(\delta _i=1(T_{i}\le C_i)\) is the event indicator. The time-to-event sub-model relates \(\mu _{i}(t)\) with event time \(T_{i}\) via

$$\begin{aligned} \lambda _{i} \left\{ t|\mathcal {M}_i(t), w_i\right\}= & {} \mathrm{lim}_{\Delta t \downarrow 0}\mathrm{Pr}\left\{ t<T_{i} \le t+\Delta t| T_{i}>t,\mathcal {M}_{i}(t), w_i\right\} /\Delta t \nonumber \\= & {} \lambda _{0}(t)\exp \left\{ \varvec{\gamma }'w_{i}+\alpha \mu _{i}(t) \right\} , \end{aligned}$$
(2)

where \(\mathcal {M}_i(t)=\{ \mu _i(s), 0 \le s < t \}\) represents the accumulated history of the true unobserved longitudinal marker up to the time point t, \(w_i\) is a vector of baseline covariates and \(\lambda _{0}(\cdot )\) is the baseline hazard function. The vector of regression coefficients \(\varvec{\gamma }\) represents the effects of the baseline covariates, and the parameter \(\alpha \) quantifies the effect of the underlying longitudinal marker.

Although the survival sub-model (2) looks similar to an extended Cox regression, and the risk for an event at time t appears to depend only on the current value of the longitudinal marker \(\mu _i(t)\), the estimation of joint models depends on the whole history of the longitudinal marker, \(\mathcal {M}_i(t)\). This is evident from the definition of survival function for model (2) which can be expressed as

$$\begin{aligned} S_{i} \left\{ t|\mathcal {M}_i(t), w_i\right\}= & {} \mathrm{Pr} (T_{i} > t| \mathcal {M}_{i}(t), w_i) \nonumber \\= & {} \exp \left( - \int _{0}^{t} \lambda _{0}(s)\exp \left\{ \gamma ' w_{i}+\alpha \mu _{i}(t) \right\} \mathrm{d}s \right) , \end{aligned}$$
(3)

and the fact that the survival function (3) is a part of the likelihood function for the joint models [7].

The dynamic predictions of survival probabilities can be obtained after fitting a joint model on a training sample \(D_{n}=\left\{ T_{i}^{*}, \delta _{i}, w_i,y_{i} ; i=1,\ldots ,n\right\} \). The probability of survival of a person i at least up to a horizon, \(t_{\mathrm{hor}}\), given alive at \(t_{s}\) (\(t_{\mathrm{hor}}>t_{s}\)) is estimated by [7]

$$\begin{aligned} \hat{\pi }_{i}(t_{\mathrm{hor}}|t_{s})=\mathrm{Pr}(T_{i}>t_{\mathrm{hor}}|T_{i}>t_{s}, \mathcal {Y}_{i}(t_{s}),w_{i},D_{n};\hat{\theta }), \end{aligned}$$
(4)

where \(w_i\) is a vector of baseline predictors, \(\hat{\theta }\) is the vector of estimated parameters of the joint model, and \(\mathcal {Y}_{i}(t_s)=\left\{ y_{i}(u):0\le u<t_{s} \right\} \) is the observed accumulated history of the longitudinal marker.

Various methods have been suggested for estimation of the parameters of the joint model in the literature. We use the maximum likelihood approach suggested by Rizopoulos [7], which is based on the conditional independence assumption, i.e. given the random effects (\(b_i\)), the time-to-event process and the longitudinal marker process are independent of each other. More precisely, this implies that the random effects account for the covariance between the longitudinal and time-to-event processes as well as the pairwise correlation between the repeated measurements of the longitudinal marker. More detailed expressions for the likelihood function and the formula for dynamic prediction given in Eq. (4) can be found in Rizopoulos [7].

2.2 Dynamic Prediction via Landmarking

Although joint modelling is a natural framework and one of most rigorous methods for dynamic prediction, its implementation often involves hard computational procedures, e.g. the likelihood construction requires numerical integration over multiple dimensions, which can often be computationally intensive or even infeasible for more than one longitudinal predictors. Dynamic prediction by landmarking is considered as a more flexible and easier alternative. The idea of landmarking approach, introduced by van Houwelingen [4], is to fit standard survival models on the subsample of subjects at risk at the landmark time \(t_s\) , and use this as a basis for dynamic prediction.

The dynamic prediction via landmarking can be obtained by preselecting a landmark time \(t_{s}\) and subjects risk at \(t_{s}\) from the original sample \(\mathcal {D}_n\), i.e. construct the adjusted risk set at \(t_{s}\): \(\mathcal {R}(t_{s})=\left\{ i: T_i>t_s \right\} \), and then use standard survival model to predict probability of survival up to a horizon, \(t_{\mathrm{hor}}>t_{s}\). Typically, the standard Cox regression models are used and can be written as

$$\begin{aligned} \lambda _{i}(t)=\lambda _{0}(t)\exp \left\{ \gamma 'w_{i}+\alpha \tilde{y}_{i}(t_s) \right\} ;\quad t_s\le t\le t_{\mathrm{hor}}, \end{aligned}$$
(5)

where \(\tilde{y}_i(t_s)\) is the last observed value of the longitudinal marker, \(w_{i}\) is the vector of baseline covariates and the time origin is reset at the landmark: \(t-t_{s}\). Based on the Cox regression model, the estimation of \(\pi _{i}(t_{\mathrm{hor}}|t_{s})\) by landmark analysis can be obtained as

$$\begin{aligned} \hat{\pi }_{i}^{LM}(t_{\mathrm{hor}}|t_{s})= \exp \left[ -\hat{\Lambda }_{0}(t_{\mathrm{hor}})\exp \left\{ \hat{\gamma }'w_{i}+\hat{\alpha }\tilde{y}_{i}(t_s) \right\} \right] , \end{aligned}$$
(6)

where \(\hat{\Lambda }_{0}(t_{\mathrm{hor}})\) is the estimate of baseline cumulative hazard. A commonly used choice for the estimate of baseline cumulative hazard is the Breslow estimator given by

$$\begin{aligned} \hat{\Lambda }_{0}(t_{\mathrm{hor}})=\sum _{i \in \mathcal {R}(t_{s})} \frac{I(T_i \le t_{\mathrm{hor}}) \delta _{i}}{\sum _{l \in \mathcal {R}(t_{\mathrm{hor}})} \exp \left\{ \hat{\gamma }'w_{l}+\hat{\alpha }\tilde{y}_{l}(t_s) \right\} }. \end{aligned}$$
(7)

2.3 Criteria for Comparison of Prediction Performance

As recommended for clinical prediction models [13], we assessed the performance of both approaches for dynamic prediction in terms of discrimination and calibration. We use their extended definitions in the context of dynamic prediction [1]. The estimation of joint models, calculation of dynamic predictions, discrimination and calibration were implemented using the R packages JM [9] and JMbayes [10].

2.3.1 Discrimination

Discrimination measures the ability of a prediction model to distinguish between subjects with positive and negative outcomes (e.g. the presence and absence of dementia) [13,14,15]. Discrimination measures for dynamic predictions are typically based on an extended definition of the area under the receiver operating characteristic curve, termed dynamic AUC (dynAUC). We use the definition of dynAUC based on the principle that, at any given point, one would like a prediction tool that gives higher predicted risk of event for subjects who are more likely to experience the event than for subjects who are less likely to experience it [1, 16].

2.3.2 Calibration

Calibration measures the agreement between observed and predicted outcomes [17, 18]. Calibration assessment for time-to-event outcomes, typically based on comparison of observed Kaplan–Meier survival probabilities with average predictions across groups of patients, does not directly carry over to dynamic predictions from joint models as the aim and nature of predictions are different in the latter context. For dynamic predictions from joint models, it is of interest to predict subject-specific conditional risk of events at landmark times \(t_s\) for a prediction window given survival and history of longitudinal marker up to the landmark time \(t_s\) [19]. Rizopoulos [1] proposed an estimator of this calibration measure, termed expected prediction error (PE), which is implemented in the R package JMbayes [10].

2.4 The ADNI Data

Data used in the preparation of this article were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (http://adni.loni.usc.edu). The ADNI was launched in 2003 as a public–private partnership, led by Principal Investigator Michael W. Weiner, MD. We used the longitudinal Mini-Mental State Examination (MMSE) data from ADNI to conduct the bootstrap simulation study. In total 863 MCI (mild cognitive impairment) participants aged 55–90 years at baseline were included. The frequency and interval of follow-up visits varied over the course of the study, but overall, participants were initially assessed every 6 months for the first two years (i.e. at baseline, 6, 12, 18 and 24 months) and then on a yearly basis. The version of the dataset we used has up to 12 follow-up visits and a maximum follow-up duration of 9 years. Of the 863 MCI subjects, 295 (34%) progressed to Alzheimer’s disease (AD) during the follow-up period. The survival outcome of interest is the time to conversion to AD from the MCI state, and the repeat MMSE scores are considered as the time-varying exposure variable (or the longitudinal outcome in context the of joint models). The analyses using both joint models and Cox regression considered several baseline covariates including demographic (age, sex, education), behavioural (smoking status, alcohol abuse), medical history (family history, body mass index (BMI), blood pressure) and genetic marker (APOE4 genotype) for Alzheimer’s disease.

2.5 Results

The MMSE profiles of the participants (converters and non-converters) of ADNI analysis sample are shown in Fig. 1. The plot has been stratified by the event status—the right hand side panel shows the MMSE profiles of the participants who have converted to AD, and the left hand side panel shows that of participants who have not developed AD before the end of follow-up or death.

Fig. 1
figure 1

MMSE profiles of the ADNI sample stratified by event status

Full size image

As can expected, the profile plot of MMSE scores suggests that, on average, the participants who went on developing AD experienced deterioration of cognitive performance at a much faster rate than those who did not convert to AD by the end of the follow-up period or by the date of censoring (i.e. by the date of death or date lost to follow-up).

The predicted survival probabilities based on Cox regression model at several given MMSE levels are displayed in Fig. 2.

Fig. 2
figure 2

Predicted survival probabilities based on Cox regression model

Full size image

The plot of survival probabilities by MMSE levels (Fig. 2) clearly indicates that the global cognitive performance measured by MMSE scores has a substantial impact on the development of AD. People with smaller MMSE scores (poorer cognitive performance) appear more susceptible to develop AD. The evidence shown in Figs. 1 and 2 along with the statistically significant association observed (\(\hat{\alpha }=-0.19\), \(p<0.001\), 95%CI: \(-0.22\) to \(-0.17\)) between the longitudinal MMSE scores and development of AD from the estimated joint model (full results given in “Appendix”) indicate that repeat cognitive performance measured by MMSE scale plays an important role in predicting the risk of developing Alzheimer’s disease.

2.6 Optimism Corrected Performance Estimates

As we explained in Introduction section, the main motivation of this study is to compare performance of dynamic prediction via joint models and landmarking using bootstrap simulation as model-based simulation of data is likely to favour predictions based on joint models. We use bootstrap simulation to ensure that the data generation mechanism does not depend on either of the underlying statistical models, so that the comparison is impartial to predictions based on both joint models and landmarking approaches. As is typically done for evaluating prediction models, we compare the methods in terms of discrimination and calibration, but using extended definitions of these criteria suitable for dynamic predictions, namely dynAUC and PE, respectively. We generate \(B=500\) bootstrap samples from the ADNI sample described earlier in the methods section. A total of 500 bootstrap replications estimated the relevant parameters with reasonably high precision. For example, the standard deviations of the dynAUC estimates over the 500 replicates for the joint modelling and landmarking approaches were very small (0.017 and 0.018) which were 50 and 45 folds smaller than the corresponding means, respectively. We then use optimism corrected estimates of dynAUC and PE to account for any potential “optimism” which often results from evaluating model performance on the same data that are used to fit the model.

We estimated the optimism corrected dynAUC and PE by following the the algorithm suggested in Steyerberg [20]. Specifically, steps for estimating dynAUC are given below.

  1. (a)

    calculate dynAUC on original data, dynAUC\(_{\mathrm{orig}}\)

  2. (b)

    take B bootstrap samples and then calculate dynAUC\(_{b, \mathrm{boot}}; b=1,\ldots , B\).

  3. (c)

    calculate dynAUC\(_{b, \mathrm{orig}}; b=1,\ldots , B\):

    1. (i)

      by fitting models to each bootstrap sample, and

    2. (ii)

      using them to calculate performance on the original data

  4. (d)

    calculate the estimate of optimism:

    $$\begin{aligned} O =(1/B) \sum _{b=1}^{B}\left\{ \text{ dynAUC}_{b,\mathrm{boot}}-\text{ dynAUC}_{b,\mathrm{orig}} \right\} \end{aligned}$$
  5. (e)

    calculate the optimism corrected estimate of dynAUC as: \(\text{ dynAUC}_{\mathrm{orig}} -O\).

The same steps apply to calculation of optimism corrected PE.

We summarised simulation results obtained from 500 bootstrap samples from the ADNI data in Table 1 and Fig. 3. The dynAUC and PE were compared at landmarks \( t_{s}=1.0, 1.5, 2.0\,\text{ and }\,2.5\) and within a 2-year window from the landmark time points, i.e. the time horizon corresponding to each landmark time point was set at \( t_{\mathrm{hor}}=t_{s}+2\). The results from Table 1 and Fig. 3 imply that the values of dynAUC for joint modelling approach are slightly higher than that of landmarking. In terms of discrimination (dynAUC), the performance of joint model has been found to be 1.26, 3.22, 2.76 and 0.12% better at the four landmark time points 1.0, 1.5, 2.0 and 2.5 years, respectively. Apart from the final landmark point (at 2.5 years), dynamic prediction based on joint models has also performed somewhat better in terms of calibration. The expected prediction errors (PE) for joint models were 0.70, 2.56 and 2.04% lower at the first three landmark time points 1.0, 1.5 and 2.0 years, respectively, compared to the landmarking approach.

Table 1 Optimism corrected estimates of performance measures in terms of discrimination (dynAUC) and calibration (expected prediction error, PE) for dynamic prediction using joint modelling and landmarking
Full size table
Fig. 3
figure 3

The dynAUC and PE for joint modelling and landmarking at different landmark time points

Full size image

Overall, it appears the joint modelling approach has performed slightly better than landmarking in terms of both discrimination and calibration in context of dynamic prediction, although the magnitude of difference was very small.

3 Discussion and Conclusion

With the advent of richer patient level longitudinal biomarker data available from modern electronic health records systems, dynamic risk prediction of clinical outcomes has recently emerged as an appealing prediction technique due to its ability to utilise the full history as well as the temporal changes in prediction variables. The prediction is dynamic in the sense that the predicted risk can be updated as additional information become available from further follow-up visits which may help healthcare professionals making most optimal decision at the specific point in time.

In this article, we have compared prediction performance of two well-known approaches for dynamic prediction, namely joint modelling and landmarking, of survival probabilities using bootstrap simulation. Unlike other comparative studies of the two methods in the literature, we focused on real data-based bootstrap simulation using the ADNI data in an attempt to be as impartial as possible to both methods. This is motivated by the fact that while joint model is based on a proper statistical framework and provides a complete data generation mechanism, landmarking is a pragmatic approach which does not specify a statistical model for the distribution of longitudinal markers, and therefore, any comparison based on model based data simulation may potentially be more advantageous to joint modelling approach.

Based on optimism corrected estimates of prediction performance in terms of discrimination (dynAUC) and calibration (expected prediction error, PE) in predicting Alzheimer’s disease, in general, joint modelling approach has been found to have performed better than the landmarking approach. Although this finding is consistent with previous comparative studies in the literature e.g. [1], the margin of gain in performance by using joint models over landmarking was relatively small (highest gains in dynAUC and PE were 3.2% and 2.6%, respectively). Overall, the findings from our analysis suggest that joint modelling have performed little better, but landmarking approach was close enough, despite not having a precise statistical model characterising the evolution of the longitudinal markers.

The above conclusion echoes that from another comparative study by Suresh et al. [11] in context of a binary longitudinal marker suggesting that joint modelling is likely to perform better when the evolution of the longitudinal markers can be well characterised statistically. When model misspecification is a concern, prediction by landmarking may provide a good enough approximation.

In the current work, we have considered only the standard form of joint models and the landmarking approach. In the joint model, a quadratic function of time was used to characterise the longitudinal MMSE scores within a linear mixed model, and for the landmarking approach any missing MMSE scores corresponding to the time points of interest were approximated via last observation carried forward (LOCF) which is often considered as the main source of bias in landmarking approach. Several extensions of landmarking have been considered in the literature which may potentially improve prediction performance [8]. It may be sensible for future comparative studies to consider extended landmarking approaches as well recent extensions of joint models [21] which may overcome some of the limitations of standard methods.