A Novel Lomax Extension with Statistical Properties, Copulas, Different Estimation Methods and Applications

Abstract

A new compound Lomax model is proposed and analyzed. The novel distribution is derived based on compounding the zero truncated Poisson distribution and the exponentiated exponential Lomax distribution. The new density can be “monotonically left skewed,” “monotonically right skewed” and “symmetric” with various useful shapes. The new hazard rate can be “upside down bathtub-increasing,” “bathtub (U-shape),” “monotonically decreasing,” “increasing-constant” and “monotonically increasing.” Relevant statistical properties are derived. We briefly describe different estimation methods, namely the maximum likelihood, Cramér-von-Mises, ordinary least squares, weighted least square, Anderson–Darling, right tail Anderson–Darling and left tail Anderson–Darling. Monte Carlo simulation experiments are performed for comparing the performances of the proposed methods of estimation for both small and large samples. For facilitating the mathematical modeling of the bivariate real data sets, we derive some new corresponding bivariate distributions. Graphical simulation study is performed for assessing the finite sample behavior of the estimators using the maximum likelihood method. Two applications are provided for illustrating the applicability of the new model.

1 Introduction

Lomax [33] presented a new distribution for modeling business failure data, and this model is called the Lomax distribution also named as Pareto type-II (PII) distribution. A special attention is paid to the Lomax distribution and its generalizations in applied statistics and related fields such as instance models, biological studies, wealth inequality, income, engineering, medicine, engineering, and reliability. The Lomax model is applied in modeling income and wealth data (see Harris [25] and Asgharzadeh and Valiollahi [10]), progressively type-II censored competing risks data [18], firm size data (see Corbellini et al. [16]), engineering, reliability and economic data sets (see Elgohari and Yousof [19]), failure times data (see Chesneau and Yousof [15]), among others. Furthermore, many other Lomax extensions can be cited such as exponentiated Lomax [24], gamma Lomax [17], transmuted Topp–Leone Lomax [43], Kumaraswamy Lomax [32], Burr-Hatke Lomax [41], beta Lomax [32], odd log-logistic Lomax [19], Poisson Burr X generalized Lomax model [28], proportional reversed hazard rate Lomax [19], special generalized mixture Lomax [15], the Burr X exponentiated Lomax distribution and the Marshall–Olkin Lehmann Lomax distribution [2]. However, other related Lomax models with different applications under censored and uncensored data can be found in Aboraya and Butt [3], Goual and Yousof [21], Ibrahim et al. [27], Ibrahim [26] and Mansour et al. [36].

A random variable (RV) is said to have the Lomax distribution if its cumulative distribution function (CDF) is given by

$$ F_{\theta } \left( z \right) = 1 - \left( {1 + z} \right)^{ - \theta } |_{z \ge 0} , $$

where $\theta > 0$ refers to the shape parameter. The above CDF is a special case from the Burr type XII (BXII) model. So, many useful details about the Lomax model along with its relationship with other related models can be found in Burr [11,12,13], Lomax [33], Burr and Cislak [14], Harris [25], Rodriguez [34], Tadikamalla [35] and Yadav et al. [44]. In this paper, we propose and study a new compound version Lomax (L) distribution using zero truncated Poisson (ZTP) distribution. Suppose that a system has $N$ (a discrete random variable) subsystems functioning independently at a given time where $N$ has ZTP distribution with parameter $a$ and the failure time of ith component $Y_{i} |i = 1,2, \ldots$ (say), independent of $N$. It is the conditional probability distribution of a Poisson-distributed random variable (RV), given that the value of the RV is not zero. The probability mass function (PMF) of $N$ is given by

$$ P_{a} \left( {N = n} \right) = \frac{{a^{n} \exp ( - a)}}{{{{\varvec{\Gamma}}}\left( {1 + n} \right)\left[ {1 - \exp \left( { - a} \right)} \right]}}|_{{a \in {\mathbb{R}}^{ + } }} . $$

Note that for ZTP RV, the expected value ${\mathbf{E}}(N|a)$ and variance ${\mathbf{V}}(N|a)$ are, respectively, given by

$$ {\mathbf{E}}(N|a) = a/\left[ {1 - \exp \left( { - a} \right)} \right] $$

and

$$ {\mathbf{V}}(N|a) = \frac{{a\left( {1 + a} \right)}}{{1 - \exp \left( { - a} \right)}} - \frac{{a^{2} }}{{\left[ {1 - \exp \left( { - a} \right)} \right]^{2} }}. $$

Suppose that for each sub-device, the failure time (i.e., ith sub-device) has the exponentiated exponential Lomax (EEL) and having the following CDF

$$ G_{b,\theta } \left( z \right) = \left( {1 - \exp \left\{ { - \left[ {\left( {1 + z} \right)^{\theta } - 1} \right]} \right\}} \right)^{b} |_{{z \in {\mathbb{R}}^{ + } }} , $$

(1)

where $b > 0$ is the shape parameter. For $b = 1$, the exponentiated exponential Lomax model reduces to exponential Lomax model. For $\theta = 1$, the exponentiated exponential Lomax model reduces to exponentiated exponential model. For $b = \theta = 1$, the exponentiated exponential Lomax model reduces to exponential model. Let $Y_{i}$ denotes the failure time of the ith subsystem and let $Z = \min \left\{ {Y_{1} ,Y_{2} , \ldots ,Y_{N} } \right\}.$ Then, the conditional CDF of $Z$ given N is

$$ F\left( {z|N} \right) = 1 - {\text{Pr}}\left( {Z > z|N} \right) = 1 - \left[ {1 - \left( {1 - \exp \left\{ { - \left[ {\left( {1 + z} \right)^{\theta } - 1} \right]} \right\}} \right)^{b} } \right]^{N} . $$

Therefore, the unconditional CDF of X, as described in Aryal and Yousof [5], Korkmaz et al. [31], Alizadeh et al. [6], can be expressed as

$$ F_{a,b,\theta } \left( z \right) {=} \frac{1}{{1 - \exp \left( { - a} \right)}}\left( {1 - \exp \left\{ { - a\left( {1 {-} \exp \left\{ { - \left[ {\left( {1 + z} \right)^{\theta } - 1} \right]} \right\}} \right)^{b} } \right\}} \right)|_{{a \in {\mathbb{R}} {-} \left\{ 0 \right\},z \in {\mathbb{R}}^{ + } }} . $$

(2)

The CDF in (2) is called the Poisson exponentiated exponential Lomax (PEEL) model. The corresponding probability density function (PDF) can be derived as

$$ \begin{aligned} f_{a,b,\theta } \left( z \right) & = \frac{{ab\theta \left( {1 + z} \right)^{\theta - 1} \exp \left\{ { - \left[ {\left( {1 + z} \right)^{\theta } - 1} \right]} \right\}}}{{\left[ {1 - \exp \left( { - a} \right)} \right]\left( {1 - \exp \left\{ { - \left[ {\left( {1 + z} \right)^{\theta } - 1} \right]} \right\}} \right)^{1 - b} }} \\ & \quad \times \underbrace {{\exp \left\{ { - a\left( {1 - \exp \left\{ { - \left[ {\left( {1 + z} \right)^{\theta } - 1} \right]} \right\}} \right)^{b} } \right\}}}_{{{\mathcal{A}}_{a,b,} \left( z \right)}}|_{{a \in {\mathbb{R}} - \left\{ 0 \right\},z \in {\mathbb{R}}^{ + } }} . \\ \end{aligned} $$

(3)

A RV $Z$ having PDF (3) will be denoted by $Z$ ~ PEEL $\left( {a,b,\theta } \right)$. The PDF in (3) is said to be “concave PDF” if for any $Z_{1} \sim {\text{PEEL }}\left( {a_{1} ,b_{1} ,\theta_{1} } \right) \;{\text{and }}\;Z_{2} \sim {\text{PEEL }}\left( {a_{2} ,b_{2} ,\theta_{2} } \right)$ the PDF satisfies

$$ f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right) \ge {\varvec{\varepsilon}}f_{{{\mathbf{\underline {V} }}_{1} }} \left( {z_{1} } \right) + \overline{\user2{\varepsilon }}f_{{{\mathbf{\underline {V} }}_{2} }} \left( {z_{2} } \right)|_{{0 \le {\varvec{\varepsilon}} \le 1{ }\;{\text{and }}\; \overline{\user2{\varepsilon }} = 1 - {\varvec{\varepsilon}}}} . $$

If the function $f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)$ is twice differentiable, then if $f^{//} \left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right) < 0, \forall Z \in {\mathbb{R}}^{ + }$, then $f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)$ is “strictly convex.” If $f^{//} \left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right) \le 0, \forall Z \in {\mathbb{R}}^{ + }$, then $f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)$ is “convex.”

The PDF in (3) is said to be “convex PDF” if for any $Z_{1} \sim {\text{PEEL }}\left( {a_{1} ,b_{1} ,\theta_{1} } \right) \;{\text{and}}\; Z_{2} \sim {\text{PEEL }}\left( {a_{2} ,b_{2} ,\theta_{2} } \right)$, the PDF satisfies

$$ f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right) \le {\varvec{\varepsilon}}f_{{{\mathbf{\underline {V} }}_{1} }} \left( {z_{1} } \right) + \overline{\user2{\varepsilon }}f_{{{\mathbf{\underline {V} }}_{2} }} \left( {z_{2} } \right)|_{{0 \le {\varvec{\varepsilon}} \le 1{ }\;{\text{and }} \; \overline{\user2{\varepsilon }} = 1 - {\varvec{\varepsilon}}}} . $$

If the function $f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)$ is twice differentiable, then if $f^{//} \left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right) > 0, \forall Z \in {\mathbb{R}}^{ + }$, then $f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)$ is “strictly convex PDF.” If $f^{//} \left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right) \ge 0, \forall Z \in {\mathbb{R}}^{ + }$, then $f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)$ is “convex.” If $f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)$ is “convex PDF” and $\psi$ is a constant, then the function $\psi f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)$ is “convex.” If $f\left( {\varepsilon z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)$ is “convex PDF,” then $\left[ {\psi f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)} \right]$ is convex for every $\psi > 0$. If $f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)$ and $g\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)$ are “convex PDF,” then $\left[ {f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right) + g\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)} \right]$ is also “convex PDF.” If $f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)$ and $g\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)$ are “convex PDF,” then $\left[ {f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right) \cdot g\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)} \right]$ is also “convex PDF.” If the function $- f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)$ is “convex PDF,” then the function $f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)$ is “convex PDF.” If $f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)$ is “concave PDF,” then $1/f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)$ is “convex PDF” if $f\left( z \right) > 0$. If $f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)$ is “concave PDF,” $1/f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)$ is “convex PDF” if $f\left( z \right) < 0$. If $f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)$ is “concave PDF,” $1/f\left( {{\varvec{\varepsilon}}z_{1} + \overline{\user2{\varepsilon }}z_{2} } \right)$ is “convex PDF.”

Staying in (3), for $a = 1$, the Poisson exponentiated exponential Lomax reduces to quasi-Poisson exponentiated exponential Lomax (QPEEL) model. For $b = 1$, the Poisson exponentiated exponential Lomax model reduces to Poisson exponential Lomax model. For $\theta = 1$, the Poisson exponentiated exponential Lomax model reduces to Poisson exponentiated exponential model. For $b = \theta = 1$, the Poisson exponentiated exponential Lomax model reduces to Poisson exponential model. For $a = b = 1$, the Poisson exponentiated exponential Lomax model reduces to quasi-Poisson exponential Lomax model. For $a = \theta = 1$, the Poisson exponentiated exponential Lomax model reduces to quasi-Poisson exponentiated exponential model. For $a = b = \theta = 1$, the Poisson exponentiated exponential Lomax model reduces to quasi-Poisson exponential model.

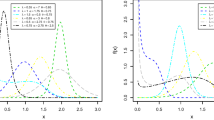
The hazard rate function (HRF) can be derived from $f_{a,b,\theta } \left( z \right)/\left[ {1 - F_{a,b,\theta } \left( z \right)} \right]$. Figure 1 (left plot) gives some plots of the PEEL PDF. Figure 1 (right plot) gives some plots of the PEEL HRF for some selected values of the parameters. Based on Fig. 1 (left plot), it is noted that the PDF of the PEEL can be “monotonically left skewed,” “monotonically right skewed” and “symmetric” with various useful shapes. Based on Fig. 1 (right plot), it is noted that the HRF of the PEEL can be “upside down bathtub-increasing,” “bathtub (U-shape),” “monotonically decreasing,” “increasing-constant” and “monotonically increasing.” The PEEL model could be useful in modeling the “asymmetric monotonically increasing HRF” real data sets as illustrated in Sect. 6 (Figs. 3, 4 (bottom left plots)); the real datasets which have no outliers as shown in Sect. 6 (Figs. 3, 4 (bottom right plots)) and the real data sets which its Kernel density is bimodal and semi-symmetric as given in Sect. 6 (Figs. 3, 4 (top left plots)).

Fig. 1

Plots of the PEEL PDF (left) and plots of the PEEL HRF (right)

First, for facilitating the mathematical modeling of the bivariate RVs, we derive some new bivariate PEEL (BPEEL) type distributions using “Farlie–Gumbel-Morgenstern copula” (FGMCp) Morgenstern [37], Farlie [20], Gumbel [22], Gumbel [23], Johnson [29] and Johnson [30], modified FGMCp which contains four internal types, “ Clayton copula (CCp)” (see Nelsen [39] for details), “Renyi's entropy copula (RECp)” (Pougaza and Djafari [40] and “Ali-Mikhail-Haq copula (AMHCp)” [4]. The multivariate PEEL (MPEEL) type can be easily derived based on the Clayton copula. However, future works may be allocated to study these new models. Additionally, we briefly describe different estimation methods, namely the maximum likelihood, Cramér-von-Mises, ordinary least square, weighted least square, Anderson–Darling, right tail Anderson–Darling and left tail Anderson–Darling. Monte Carlo simulation experiments are performed for comparing the performances of the proposed methods of estimation for both small and large samples. The above-mentioned estimation methods are compared also using two real data sets.

Second, we briefly considered and then described different estimation methods, namely the maximum likelihood estimation (MLE) method, Cramér-von-Mises estimation (CVM) method, ordinary least square estimation (OLS) method, weighted least square estimation (WLSE) method, Anderson–Darling estimation (ADE) method, right tail Anderson–Darling estimation (RTADE) method, left tail Anderson–Darling estimation (LTADE) method. These methods are used in estimation process of the unknown parameters.

Generally, in statistical modeling of the failure times of the aircraft windshield data, the PEEL model is compared with many common Lomax extensions such as the special generalized mixture Lomax, the odd log-logistic Lomax, the Burr-Hatke Lomax, the transmuted Topp–Leone Lomax, the Gamma Lomax, the Kumaraswamy Lomax, the McDonald Lomax, the exponentiated Lomax and the proportional reversed hazard rate Lomax under the Akaike information criteria, consistent-information criteria, Bayesian information criteria and Hannan–Quinn information criteria. The PEEL model provided better fits in modeling failure times of the aircraft windshield data. In statistical modeling of the service times of the aircraft windshield, the PEEL model is compared with many common Lomax extensions such as the special generalized mixture Lomax, the odd log-logistic Lomax, the Burr-Hatke Lomax, the transmuted Topp–Leone Lomax, the Gamma Lomax, the Kumaraswamy Lomax, the McDonald Lomax, the exponentiated Lomax and the proportional reversed hazard rate Lomax under the Akaike information criteria, consistent-information criteria, Bayesian information criteria and Hannan–Quinn information criteria. The PEEL model provided better fits in modeling service times of the aircraft windshield data.

In this paper, after studying the main statistical properties and presenting some bivariate type extensions, we briefly considered and then described different estimations. Monte Carlo simulation experiments are performed for comparing the performances of the proposed methods of estimation for both small and large samples.

2 Properties

2.1 Expanding the New Density

We present a simple useful expansion for the new PDF given on (3) in terms of the exponentiated Lx (exp-L) model. Using the obtained expansion, we derive the main mathematical properties of the new PDF of the PEE model. Note thatThen, the PDF in (4) can be expressed as

$$ {\mathcal{A}}_{a,b,} \left( z \right) = \mathop \sum \limits_{h = 0}^{ + \infty } \frac{1}{h!}\left( { - a} \right)^{h} \left( {1 - \exp \left\{ { - \left[ {\left( {1 + z} \right)^{\theta } - 1} \right]} \right\}} \right)^{bh} . $$

$$ \begin{aligned}f_{a,b,\theta } \left( z \right) &= \frac{b\theta }{{1 - \exp \left( { - a} \right)}}\mathop \sum \limits_{h = 0}^{ + \infty } \frac{{\left( { - 1} \right)^{h} a^{1 + h} \left( {1 + z} \right)^{\theta - 1} }}{{l!\exp \left\{ { - \left[ {\left( {1 + z} \right)^{\theta } - 1} \right]} \right\}}}\\& \quad\underbrace {{\left( {1 - \exp \left\{ { - \left[ {\left( {1 + z} \right)^{\theta } - 1} \right]} \right\}} \right)^{{b\left( {h + 1} \right) - 1}} }}_{{B_{{b\left( {h + 1} \right),}} \left( z \right)}}. \end{aligned}$$

(4)

Considering the power series

$$ \left( {1 - \frac{{c_{1} }}{{c_{2} }}} \right)^{{c_{3} + 1}} = \mathop \sum \limits_{l = 0}^{ + \infty } \frac{{\left( { - 1} \right)^{l} {{\varvec{\Gamma}}}\left( {2 + c_{3} } \right)}}{{l!{{\varvec{\Gamma}}}\left( {2 + c_{3} - l} \right)}}\left( {\frac{{c_{1} }}{{c_{2} }}} \right)^{l} ,\left| {\frac{{c_{1} }}{{c_{2} }}} \right|\left\langle {1{ }\;{\text{and }}\;c_{3} } \right\rangle 0, $$

(5)

and applying (5) to the quantity $B_{{b\left( {h + 1} \right),}} \left( z \right)$ in (4), we get

$$ B_{{b\left( {h + 1} \right),}} \left( z \right) = \mathop \sum \limits_{l = 0}^{ + \infty } \frac{{\left( { - 1} \right)^{l} {{\varvec{\Gamma}}}\left( {b\left( {h + 1} \right)} \right)}}{{l!h!{{\varvec{\Gamma}}}\left( {b\left( {h + 1} \right) - l} \right)}}\exp \left\{ { - l\left[ {\left( {1 + z} \right)^{\theta } - 1} \right]} \right\}. $$

Inserting the expansion of the quantity $B_{{b\left( {h + 1} \right),}} \left( z \right)$ into (4), then, the PDF of the PEEL can be expressed as

$$ f_{a,b,\theta } \left( z \right) = \frac{b\theta }{{1 - \exp \left( { - a} \right)}}\left( {1 + z} \right)^{\theta - 1} \mathop \sum \limits_{{h,{\varvec{l}} = 0}}^{ + \infty } a^{{1 + {\mathbf{h}}}} \frac{{\left( { - 1} \right)^{h + l} {{\varvec{\Gamma}}}\left( {b\left( {h + 1} \right)} \right)}}{{l!h!{{\varvec{\Gamma}}}\left( {b\left( {h + 1} \right) - i} \right)}}C_{{\left( {l + 1} \right)}} \left( z \right). $$

(6)

Expanding the quantity $C_{{\left( {l + 1} \right)}} \left( z \right)$, we can write

$$ C_{{\left( {l + 1} \right)}} \left( z \right) = \exp \left[ { - \left( {l + 1} \right)\left[ {\left( {1 + z} \right)^{\theta } - 1} \right]} \right] = \mathop \sum \limits_{{{\varvec{\tau}} = 0}}^{ + \infty } \left( { - 1} \right)^{{\varvec{\tau}}} \left( {l + 1} \right)^{{\varvec{\tau}}} \frac{{\left[ {1 - \left( {1 + z} \right)^{ - \theta } } \right]^{{\varvec{\tau}}} }}{{{\varvec{\tau}}!\left( {1 + z} \right)^{{ - \theta {\varvec{\tau}}}} }}. $$

(7)

Inserting the result of (7) into (6), the PEEL density can be reduced to

$$ \begin{aligned}f_{a,b,\theta } \left( z \right) &= \frac{{b\theta \left( {1 + z} \right)^{ - \theta - 1} }}{{1 - \exp \left( { - a} \right)}}\mathop \sum \limits_{{h,{\varvec{l}},{\varvec{\tau}} = 0}}^{ + \infty } a^{1 + h} \frac{{\left( { - 1} \right)^{{h + {\varvec{\tau}} + {\varvec{l}}}} {{\varvec{\Gamma}}}\left( {b\left( {h + 1} \right)} \right)\left( {l + 1} \right)^{{\varvec{\tau}}} }}{{h!l!{\varvec{\tau}}!{{\varvec{\Gamma}}}\left( {b\left( {h + 1} \right) - l} \right)}}\\& \quad \frac{{\left[ {1 - \left( {1 + z} \right)^{ - \theta } } \right]^{{\varvec{\tau}}} }}{{\left( {1 + z} \right)^{{{\varvec{\tau}} + 2}} }}.\end{aligned} $$

(8)

Expanding $\left( {1 + z} \right)^{{ - {\varvec{\tau}} - 2}}$ via generalized binomial expansion, we get

$$ \left( {1 + z} \right)^{{ - {\varvec{\tau}} - 2}} = \mathop \sum \limits_{d = 0}^{ + \infty } \frac{{{{\varvec{\Gamma}}}\left( {\tau + d + 2} \right)}}{{{\text{k}}!{{\varvec{\Gamma}}}\left( {{\varvec{\tau}} + 2} \right)}}\left[ {1 - \left( {1 + z} \right)^{ - \theta } } \right]^{d} . $$

(9)

Inserting (9) in (8), the PDF of the PEEL can be summarized as

$$ f_{a,b,\theta } \left( z \right) = \mathop \sum \limits_{{{\varvec{\tau}},d = 0}}^{ + \infty } \varepsilon_{{{\varvec{\tau}},d}} h_{{{\varvec{\tau}} + d + 1}} \left( {z;\theta } \right)|_{{\left( {\tau + d + 1} \right) > 0}} , $$

(10)

where

$$ h_{{{\varvec{\tau}} + d + 1}} \left( {z;\theta } \right) = \theta \left( {\tau + d + 1} \right)\left( {1 + z} \right)^{ - \theta - 1} \left[ {1 - \left( {1 + z} \right)^{ - \theta } } \right]^{{{\varvec{\tau}} + d}} $$

(11)

is the PDF of the exp-L model with power $\tau + d + 1$ and $\varepsilon_{{{\varvec{\tau}},d}}$ is a constant where

$$ \varepsilon_{{{\varvec{\tau}},{\varvec{d}}}} = \frac{b}{{\left[ {1 - \exp \left( { - a} \right)} \right]{\varvec{\tau}}!d!}}\mathop \sum \limits_{{h,{\varvec{l}} = 0}}^{ + \infty } a^{1 + h} \frac{{\left( { - 1} \right)^{{h + {\varvec{\tau}} + {\varvec{l}}}} \left( {l + 1} \right)^{{\varvec{\tau}}} {{\varvec{\Gamma}}}\left( {b\left( {h + 1} \right)} \right){{\varvec{\Gamma}}}\left( {\tau + d + 2} \right)}}{{h!l!\left( {{\varvec{\tau}} + d + 1} \right){{\varvec{\Gamma}}}\left( {b\left( {h + 1} \right) - l} \right){{\varvec{\Gamma}}}\left( {{\varvec{\tau}} + 2} \right)}}. $$

Similarly, the CDF of the PEEL model can also be expressed as

$$ F_{a,b,\theta } \left( z \right) = \mathop \sum \limits_{{{\varvec{\tau}},d = 0}}^{ + \infty } \varepsilon_{{{\varvec{\tau}},d}} H_{{{\varvec{\tau}} + d + 1}} \left( {z;\theta } \right)|_{{\left( {\tau + d + 1} \right) > 0}} , $$

(12)

where $H_{{{\varvec{\tau}} + d + 1}} \left( {z;\theta } \right) = \left[ {1 - \left( {1 + z} \right)^{ - \theta } } \right]^{{{\varvec{\tau}} + d + 1}}$ is the CDF of the exp-L family with power $\tau + d + 1$.

2.2 Moments

The calculations of this subsection involve several special functions, including the complete beta function $B\left( {l_{1} ,l_{2} } \right) = \mathop \smallint \limits_{0}^{1} u^{{l_{1} - 1}} \left( {1 - u} \right)^{{l_{2} - 1}} {\text{d}}u$, the incomplete beta function $B_{{l_{3} }} \left( {l_{1} ,l_{2} } \right) = \mathop \smallint \limits_{0}^{{l_{3} }} u^{{l_{1} - 1}} \left( {1 - u} \right)^{{l_{2} - 1}} {\text{d}}u$, the complete gamma function

$$ {{\varvec{\Gamma}}}\left( {1 + l_{1} } \right) = \mathop \smallint \limits_{0}^{ + \infty } y^{{l_{1} }} \exp \left( { - y} \right)dy = l_{1} ! = \mathop \prod \limits_{{l_{2} = 0}}^{{l_{1} - 1}} \left( {l_{1} - l_{2} } \right), $$

the lower incomplete gamma function

$\gamma \left( {l_{1} ,l_{2} } \right) = \mathop \smallint \limits_{0}^{{l_{2} }} y^{{l_{1} - 1}} \exp \left( { - y} \right)dy = \mathop \sum \limits_{{l_{3} = 0}}^{ + \infty } \frac{{\left( { - 1} \right)^{{l_{3} }} l_{2}^{{l_{1} + l_{3} }} }}{{{{\varvec{\Gamma}}}\left( {1 + l_{3} } \right)\left( {l_{1} + l_{3} } \right)}},$ and the upper incomplete gamma function. Noting that

$$ {{\varvec{\Gamma}}}\left( {l_{1} } \right) = {{\varvec{\Gamma}}}\left( {l_{1} ,l_{2} } \right) + \gamma \left( {l_{1} ,l_{2} } \right). $$

Let $Z$ be a RV having the PEEL $\left( {a,b,\theta } \right)$ model. Then, the $p$th moment of the RV $Z$ is

$$ \mu_{{p,{\text{Z}}}}^{^{\prime}} {=} {\mathbb{E}}\left( {Z^{p} } \right) = \mathop \sum \limits_{\tau ,d = 0}^{ + \infty } \mathop \sum \limits_{l = 0}^{p} \varepsilon_{\tau ,d} \left( {{\varvec{\tau}} + {\varvec{d}} + 1} \right)\left( { - 1} \right)^{l} \left( {\begin{array}{*{20}c} p \\ l \\ \end{array} } \right)B\left( {{\varvec{\tau}} {+} {\varvec{d}} + 1,1 {+} \frac{l - p}{\theta }} \right)|_{\theta > p} . $$

2.3 Moment Generating Function (MGF)

Clearly, the MGF can be derived from Eq. (10) as

$$ M_{Z} \left( t \right) = \mathop \sum \limits_{\tau ,d,p = 0}^{ + \infty } \mathop \sum \limits_{l = 0}^{p} \frac{{t^{p} }}{p!}\varepsilon_{\tau ,d} \left( {{\varvec{\tau}} + {\varvec{d}} + 1} \right)\left( { - 1} \right)^{l} \left( {\begin{array}{*{20}c} p \\ l \\ \end{array} } \right)B\left( {{\varvec{\tau}} + {\varvec{d}} + 1,1 + \frac{l - p}{\theta }} \right)|_{\theta > p} . $$

2.4 Incomplete Moments

The pth incomplete moments, say ${\mathbf{I}}_{p,Z} \left( t \right)$, of the RV $Z$ can be obtained from (10) as

$$ {\mathbf{I}}_{p,Z} \left( t \right) = \mathop \sum \limits_{\tau ,d = 0}^{n} \varepsilon_{{{\varvec{\tau}},{\varvec{d}}}} {\mathbf{I}}_{{p,{\varvec{\tau}} + {\varvec{d}} + 1}}^{ - \infty ,t} \left( t \right), $$

where ${\mathbf{I}}_{{p,{\varvec{\tau}} + {\varvec{d}} + 1}}^{ - \infty ,t} \left( t \right) = \mathop \smallint \limits_{ - \infty }^{t} z^{p} h_{{{\varvec{\tau}} + {\varvec{d}} + 1}} \left( z \right){\text{d}}z$. Then, the pth incomplete moments can be written as

$$ {\mathbf{I}}_{p,Z} \left( t \right) = \mathop \sum \limits_{\tau ,d = 0}^{ + \infty } \mathop \sum \limits_{l = 0}^{p} \varepsilon_{\tau ,d} \left( {{\varvec{\tau}} + {\varvec{d}} + 1} \right)\left( { - 1} \right)^{l} \left( {\begin{array}{*{20}c} p \\ l \\ \end{array} } \right)B_{t} \left( {{\varvec{\tau}} + {\varvec{d}} + 1,1 + \frac{l - p}{\theta }} \right)|_{\theta > p} , $$

the 1st incomplete moments can be written as

$$ {\mathbf{I}}_{1,Z} \left( t \right) = \mathop \sum \limits_{\tau ,d = 0}^{ + \infty } \mathop \sum \limits_{l = 0}^{p} \varepsilon_{\tau ,d} \left( {{\varvec{\tau}} + {\varvec{d}} + 1} \right)\left( { - 1} \right)^{l} \left( {\begin{array}{*{20}c} 1 \\ l \\ \end{array} } \right)B_{t} \left( {{\varvec{\tau}} + {\varvec{d}} + 1,1 + \frac{l - 1}{\theta }} \right)\left| \theta \right\rangle 1. $$

The mean deviations (MDs) about the $\mu_{{1,{\text{Z}}}}^{^{\prime}}$ are ${\mathbb{E}}\left( {\left| {Z - \mu_{{1,{\text{Z}}}}^{^{\prime}} } \right|} \right) = m_{1} \left( {\mu_{{1,{\text{Z}}}}^{^{\prime}} } \right)$ and the MDs about the median (D) are ${\mathbb{E}}\left( {\left| {Z - {\text{D}}} \right|} \right) = m_{2,Z} \left( {\text{D}} \right)$ of the RV $Z$ are given by $m_{1,Z} \left( {\mu_{{1,{\text{Z}}}}^{^{\prime}} } \right) = 2\mu_{{1,{\text{Z}}}}^{^{\prime}} F\left( {\mu_{{1,{\text{Z}}}}^{^{\prime}} } \right) - 2{\mathbf{I}}_{1,Z} \left( {\mu_{{1,{\text{Z}}}}^{^{\prime}} } \right)$ and $m_{2,Z} \left( {\text{D}} \right) = \mu_{{1,{\text{Z}}}}^{^{\prime}} - 2{\mathbf{I}}_{1,Z} \left( {\text{D}} \right)$, respectively, where $\mu_{{1,{\text{Z}}}}^{^{\prime}} = {\mathbb{E}}\left( Z \right) \;{\text{is}}\;{\text{ the}}\;{\text{ arithmetic }}\;{\text{mean }}\;{\text{of }}\;{\text{the }}\;{\text{RV}}\;{ }Z$, ${\text{D}} = Q\left( \frac{1}{2} \right)$ is the median of the RV $Z$, and ${\mathbf{I}}_{1,Z} \left( t \right)$ is the first incomplete moment is given by ${\mathbf{I}}_{1,Z} \left( t \right)$. These results for ${\mathbf{I}}_{1,Z} \left( t \right)$ can be directly applied for calculating the Bonferroni (${\mathcal{B}}on\left( {\Delta } \right)$) and Lorenz (${\mathcal{L}}or\left( {\Delta } \right)$) curves defined, for a certain given probability, say ${\Delta }$, by ${\mathcal{B}}on\left( {\Delta } \right) = {\mathbf{I}}_{1,Z} \left( {Q\left( {\Delta } \right)} \right)/\left( {{\Delta }\mu_{{1,{\text{Z}}}}^{^{\prime}} } \right)$ and ${\mathcal{L}}or\left( {\Delta } \right) = {\mathbf{I}}_{1,Z} \left( {Q\left( {\Delta } \right)} \right)/\mu_{{1,{\text{Z}}}}^{^{\prime}}$, respectively.

2.5 Residual Life (RL) and Reversed Residual Life (RRL)

The jth moment of the RL of the RV $Z$ can be obtained from $w_{{{{j}},Z}} \left( t \right) = {\mathbb{E}}[( Z - t)^{j} ]|_{{Z > t\;{\text{and}}\;j \in {\mathbb{N}}}}$ or from

$$ w_{j,Z} \left( t \right) = \frac{1}{{1 - F_{a,b,\theta } \left( t \right)}}{ }\mathop \smallint \limits_{t}^{\infty } (z - t)^{j} f_{a,b,\theta } \left( z \right){\text{d}}z, $$

which can also be written as

$$ w_{j,Z} \left( t \right) = \frac{1}{{1 - F_{a,b,\theta } \left( t \right)}}\mathop \sum \limits_{{{\varvec{\tau}},d = 0}}^{ + \infty } \mathop \sum \limits_{i = 0}^{j} \varepsilon_{{{\varvec{\tau}},d}} \left( {\begin{array}{*{20}l} j \hfill \\ i \hfill \\ \end{array} } \right)\left( { - t} \right)^{j - i} {\mathbf{I}}_{{{{j}},{\varvec{\tau}} + d + 1}}^{t, + \infty } \left( t \right). $$

Then,

$$\begin{aligned} w_{j,Z} \left( t \right) &= \frac{1}{{1 - F_{a,b,\theta } \left( t \right)}}\mathop \sum \limits_{\tau ,d = 0}^{ + \infty } \mathop \sum \limits_{l = 0}^{j} \varepsilon_{\tau ,d,l} \left( {w,j} \right)\left( {{\varvec{\tau}} + {\varvec{d}} + 1} \right)\left( { - 1} \right)^{l} \left( {\begin{array}{*{20}c} j \\ l \\ \end{array} } \right)\\ & \quad B_{t} \left( {{\varvec{\tau}} + {\varvec{d}} + 1,1 + \frac{l - j}{\theta }} \right)|_{{t > 0,j \in {\mathbb{N}},\theta > j}} ,\end{aligned} $$

where $\varepsilon_{\tau ,d,l} \left( {w,j} \right) = \varepsilon_{\tau ,d} \mathop \sum \limits_{i = 0}^{j} \left( {\begin{array}{*{20}l} j \hfill \\ i \hfill \\ \end{array} } \right)\left( { - t} \right)^{j - i} .$. For $j = 1,$ we obtain the mean of the residual life (MRL) which can be derived from $w_{1,Z} \left( t \right) = {\mathbb{E}}\left[ {\left( {Z - t} \right)} \right]|_{{Z > t\;{\text{and}}\;j \in {\mathbb{N}}}}$ as

$$\begin{aligned} w_{1,Z} \left( t \right) &= \frac{1}{{1 - F_{a,b,\theta } \left( t \right)}}\mathop \sum \limits_{\tau ,d = 0}^{ + \infty } \mathop \sum \limits_{l = 0}^{1} \varepsilon_{\tau ,d,l} \left( {w,1} \right)\left( {\tau + d + 1} \right)\left( { - 1} \right)^{l} \left( {\begin{array}{*{20}c} 1 \\ l \\ \end{array} } \right)\\ & \quad B_{t} \left( {\tau + d + 1,1 + \frac{l - 1}{\theta }} \right)|_{t > 0,j = 1,\theta > j} , \end{aligned}$$

where $\varepsilon_{\tau ,d,l} \left( {w,1} \right) = \varepsilon_{\tau ,d} \mathop \sum \limits_{i = 0}^{1} \left( {\begin{array}{*{20}l} 1 \hfill \\ i \hfill \\ \end{array} } \right)\left( { - t} \right)^{1 - i} .$ On the other hand, the jth moment of the RRL is ${\mathbf{\mathcal{W}}}_{j,Z} \left( t \right) = {\mathbb{E}}\left[ {(t - Z)^{j} } \right]|_{{Z \le t,{ }t > 0\;{\text{ and}}\;j \in {\mathbb{N}}}}$ or

$$ {\mathbf{\mathcal{W}}}_{j,Z} \left( t \right) = \frac{1}{{F_{a,b,\theta } \left( t \right)}}\mathop \smallint \limits_{0}^{t} (t - z)^{j} f_{a,b,\theta } \left( z \right){\text{d}}z $$

which can also be expressed as

$$ {\mathbf{\mathcal{W}}}_{j,Z} \left( t \right) = \frac{1}{{F_{a,b,\theta } \left( t \right)}}\mathop \sum \limits_{{{\varvec{\tau}},d = 0}}^{ + \infty } \mathop \sum \limits_{i = 0}^{j} \varepsilon_{{{\varvec{\tau}},{\varvec{d}}}} \left( { - 1} \right)^{i} \left( {\begin{array}{*{20}l} j \hfill \\ i \hfill \\ \end{array} } \right)t^{j - i} {\mathbf{I}}_{{j,{\varvec{\tau}} + {\varvec{d}} + 1}}^{ - \infty ,t} \left( t \right). $$

Then,

$$\begin{aligned} {\mathbf{\mathcal{W}}}_{j,Z} \left( t \right) &= \frac{1}{{F_{{\underline {V} }} \left( t \right)}}\mathop \sum \limits_{\tau ,d = 0}^{ + \infty } \mathop \sum \limits_{l = 0}^{{{j}}} \varepsilon_{\tau ,d,l} \left( {{\mathbf{\mathcal{W}}},j} \right)\left( {\tau + d + 1} \right)\left( { - 1} \right)^{l} \left( {\begin{array}{*{20}c} j \\ l \\ \end{array} } \right)\\ & \quad B_{t} \left( {\tau + d + 1,1 + \frac{l - j}{\theta }} \right)|_{{t > 0,j \in {\mathbb{N}},\theta > j}} , \end{aligned}$$

where $\varepsilon_{\tau ,d,l} \left( {{\mathbf{\mathcal{W}}},j} \right) = \varepsilon_{\tau ,d} \mathop \sum \limits_{i = 0}^{j} \left( { - 1} \right)^{i} \left( {\begin{array}{*{20}l} j \hfill \\ i \hfill \\ \end{array} } \right)t^{j - i} .$ For $j = 1,$ we obtain the mean waiting time (MWT) which also called the mean inactivity time (MIT) which can be derived from ${\mathbf{\mathcal{W}}}_{1,Z} \left( t \right) = {\mathbb{E}}\left[ {\left( {t - Z} \right)} \right]|_{{Z \le t,{ }t > 0{ }\;{\text{and}}\;j = 1}}$.

$$ \begin{aligned}{\mathbf{\mathcal{W}}}_{1,Z} \left( t \right) &= \frac{1}{{F_{a,b,\theta } \left( t \right)}}\mathop \sum \limits_{\tau ,d = 0}^{ + \infty } \mathop \sum \limits_{l = 0}^{1} \varepsilon_{\tau ,d,l} \left( {{\mathbf{\mathcal{W}}},1} \right)\left( {\tau + d + 1} \right)\left( { - 1} \right)^{l} \left( {\begin{array}{*{20}c} 1 \\ l \\ \end{array} } \right)\\ & \quad B_{t} \left( {\tau + d + 1,1 + \frac{l - 1}{\theta }} \right)|_{t > 0,j = 1,\theta > j} . \end{aligned}$$

where $\varepsilon_{\tau ,d,l} \left( {{\mathbf{\mathcal{W}}},1} \right) = \varepsilon_{\tau ,d} \mathop \sum \limits_{i = 0}^{1} {(} - 1{)}^{i} \left( {\begin{array}{*{20}l} 1 \hfill \\ i \hfill \\ \end{array} } \right)t^{1 - i} .$

2.6 Numerical Analysis for Some Measures

Table 1 gives some numerical calculations for the mean (${\mathbb{E}}\left( Z \right)$), variance (V$\left( Z \right)$), skewness (S$\left( Z \right)$) and kurtosis (K$\left( Z \right)$) for PEEL distribution. Based on results listed in Table 1, it is noted that S$\left( Z \right) \in \left( {0.{9},{173}0.{1}} \right)$ and K$\left( Z \right)$ ranging from 3.525878 to 3,332,135.

Table 1 ${\mathbb{E}}\left( Z \right)$, V$\left( Z \right)$, (S$\left( Z \right)$ and kurtosis K$\left( Z \right)$ for PEEL model

3 Copula

3.1 BPEEL Type via CCp

Let us assume that $X_{1} \sim {\text{PEEL}}\left( {a_{1} ,b_{1} ,\theta_{1} } \right)$ and $X_{2} \sim {\text{PEEL}}\left( {a_{2} ,b_{2} ,\theta_{2} } \right)$. The CCp depending on the continuous marginal functions ${\overline{\mathcal{U}}} = 1 - {\mathcal{U}}$ and ${\overline{\mathcal{V}}} = 1 - {\mathcal{V}}$ can be considered as

(13)

Let ${\overline{\mathcal{U}}} = 1 - F_{{a_{1} ,b_{1} ,\theta_{1} }} \left( {z_{1} } \right)|_{{a_{1} ,b_{1} ,\theta_{1} }}$, ${\overline{\mathcal{V}}} = 1 - F_{{a_{2} ,b_{2} ,\theta_{2} }} \left( {z_{2} } \right)|_{{a_{2} ,b_{2} ,\theta_{2} }} .$ Then, the BPEEL type distribution can be obtained from (5). A straightforward multivariate PEEL (m-dimensional extension) via CCp can be easily derived analogously. The m-dimensional extension via CCp which is function operating in $\left[ {0,1} \right]^{m}$, and in that case, $z_{i}$ is not a value in $\left[ {0,1} \right]$ necessarily.

3.2 BPEEL type via RECp

Following Pougaza and Djafari [40], the RECp can be derived as $C\left( {{\mathcal{U}},{\mathcal{V}}} \right) = z_{2} {\mathcal{U}} + z_{1} {\mathcal{V}} - z_{1} z_{2} ,$ with the continuous marginal functions ${\mathcal{U}} = 1 - {\overline{\mathcal{U}}} = F_{{{\mathbf{\underline {V} }}_{1} }} \left( {z_{1} } \right) \in \left( {0,1} \right)$ and ${\mathcal{V}} = 1 - {\overline{\mathcal{V}}} = F_{{{\mathbf{\underline {V} }}_{1} }} \left( {z_{2} } \right) \in \left( {0,1} \right)$, where the values $z_{1}$ and $z_{2}$ are in order to guarantee that $C\left( {{\mathcal{U}},{\mathcal{V}}} \right)$ is a copula. Then, the associated CDF of the BPEEL will be

$$ F\left( {z_{1} ,z_{2} } \right) = C\left( {F_{{a_{1} ,b_{1} ,\theta_{1} }} \left( {z_{1} } \right),F_{{a_{2} ,b_{2} ,\theta_{2} }} \left( {z_{2} } \right)} \right), $$

where $F_{{a_{1} ,b_{1} ,\theta_{1} }} \left( {z_{1} } \right)$ and $F_{{a_{2} ,b_{2} ,\theta_{2} }} \left( {z_{2} } \right)$ are defined above. It is worth mentioning that in [18], the authors emphasize that this copula does not show a closed form and numerical approaches become necessary.

3.3 BPEEL type via FGMCp

Considering the FGMCp (see ([10,11,12,13,14,15]), the joint CDF can be written as

where the continuous marginal function ${\mathcal{U}} \in \left( {0,1} \right)$, ${\mathcal{V}} \in \left( {0,1} \right)$ and where which is "grounded minimum condition" and and which is "grounded maximum condition ." The grounded minimum/maximum conditions are valid for any copula. Setting ${\overline{\mathcal{U}}} = {\overline{\mathcal{U}}}_{{{\mathbf{\underline {V} }}_{1} }} |_{{{\mathbf{\underline {V} }}_{1} > 0}}$ and ${\overline{\mathcal{V}}} = {\overline{\mathcal{V}}}_{{{\mathbf{\underline {V} }}_{2} }} |_{{{\mathbf{\underline {V} }}_{2} > 0}} ,$ then, we have

The joint PDF can be derived from

or from

where the two function and are densities corresponding to the joint CDFs and .

3.4 BPEEL type via modified FGMCp

The modified formula of the modified FGMCp can be written as

with ${\mathbf{O}}\left( {\mathcal{U}} \right)^{ \bullet } = {\mathcal{U}}\overline{{{\mathbf{O}}\left( {\mathcal{U}} \right)}}$ and ${\mathbf{\mathcal{K}}}\left( {\mathcal{V}} \right)^{ \bullet } = {\mathcal{V}}\overline{{{\mathbf{\mathcal{K}}}\left( {\mathcal{V}} \right)}}$ where ${\mathbf{O}}\left( {\mathcal{U}} \right) \in \left( {0,1} \right)$ and ${\mathbf{\mathcal{K}}}\left( {\mathcal{V}} \right) \in \left( {0,1} \right)$ are two continuous functions where ${\mathbf{O}}\left( {{\mathcal{U}} = 0} \right) = {\mathbf{O}}\left( {{\mathcal{U}} = 1} \right) = {\mathbf{\mathcal{K}}}\left( {{\mathcal{V}} = 0} \right) = {\mathbf{\mathcal{K}}}\left( {{\mathcal{V}} = 1} \right) = 0.$ The following four types can be derived and considered:

• Type I modified FGMCp

Consider ${\mathbf{O}}\left( {\mathcal{U}} \right)^{ \bullet } = {\mathcal{U}}\overline{{{\mathbf{O}}\left( {\mathcal{U}} \right)}}$ and ${\mathbf{\mathcal{K}}}\left( {\mathcal{V}} \right)^{ \bullet } = {\mathcal{V}}\overline{{{\mathbf{\mathcal{K}}}\left( {\mathcal{V}} \right)}}$ where ${\mathbf{O}}\left( {\mathcal{U}} \right) \in \left( {0,1} \right)$ and ${{\mathcal{K}}}\left( {\mathcal{V}} \right) \in \left( {0,1} \right)$ are two continuous functions where ${\mathbf{O}}\left( {{\mathcal{U}} = 0} \right) = {\mathbf{O}}\left( {{\mathcal{U}} = 1} \right) = {\mathbf{\mathcal{K}}}\left( {{\mathcal{V}} = 0} \right) = {\mathbf{\mathcal{K}}}\left( {{\mathcal{V}} = 1} \right) = 0$ which satisfy the above conditions. Then, new bivariate version via modified FGMCp type I can be directly obtained from

• Type II modified FGMCp

Consider and which satisfy the above conditions where . Then, the corresponding bivariate version (modified FGMCp Type II) can be derived from

• Type III modified FGMCp

Let $\widetilde{{{\mathbf{\mathcal{A}}}\left( {\mathcal{U}} \right)}} = {\mathcal{U}}\left[ {\log \left( {1 + {\overline{\mathcal{U}}}} \right)} \right]|_{{\left( {{\overline{\mathcal{U}}} = 1 - {\mathcal{U}}} \right)}} { }\;{\text{and}}\;{ }\widetilde{{{\mathbf{\mathcal{Z}}}\left( {\mathcal{V}} \right)}} = {\mathcal{V}}\left[ {\log \left( {1 + {\overline{\mathcal{V}}}} \right)} \right]|_{{\left( {{\overline{\mathcal{V}}} = 1 - {\mathcal{V}}} \right)}} .$ Then, the associated CDF of the BPEEL-FGM (modified FGMCp type III) is

• Type IV modified FGMCp

Using the quantile concept, the CDF of the BPEEL-FGM (modified FGMCp type IV) model can be obtained using

$$ C\left( {{\mathcal{U}},{\mathcal{V}}} \right) = {\mathcal{U}}F^{ - 1} \left( {\mathcal{U}} \right) - F^{ - 1} \left( {\mathcal{U}} \right)F^{ - 1} \left( {\mathcal{V}} \right) + {\mathcal{V}}F^{ - 1} \left( {\mathcal{V}} \right) $$

where $F^{ - 1} \left( {\mathcal{U}} \right) = Q\left( {\mathcal{U}} \right)$ and $F^{ - 1} \left( {\mathcal{V}} \right) = Q\left( {\mathcal{V}} \right).$

3.5 BPEEL type via AMHCp

Under the “stronger Lipschitz condition,” the joint CDF of the Archimedean AMHCp can be written as

the corresponding joint PDF of the Archimedean AMHCp can be expressed as

Then, for any ${\overline{\mathcal{U}}} = 1 - F_{{a_{1} ,b_{1} ,\theta_{1} }} \left( {z_{1} } \right) = |_{{\left[ {{\overline{\mathcal{U}}} = \left( {1 - {\mathcal{U}}} \right) \in \left( {0,1} \right)} \right]}}$ and ${\overline{\mathcal{V}}} = 1 - F_{{a_{2} ,b_{2} ,\theta_{2} }} \left( {z_{2} } \right)|_{{\left[ {{\overline{\mathcal{V}}} = \left( {1 - {\mathcal{V}}} \right) \in \left( {0,1} \right)} \right]}}$,we have

and

4 Estimation Methods

In this Section, we briefly describe and consider different classical estimation methods, namely the MLE method, CVM method, OLS method, WLSE method, ADE method, RTADE method, left tail LTADE. All these methods are discussed in the statistical literature with more details. In this work, we may ignore some of its derivation details for avoiding repetition.

4.1 The ML Method

Let $Z_{1} ,Z_{2} , \ldots ,Z_{m}$ be any observed random sample (RS) from the PEEL model. Then, the log-likelihood function ($l_{a,b,\theta }$) is given by $l_{a,b,\theta } = \log \left[ {\mathop \prod \limits_{i = 1}^{m} f_{a,b,\theta } \left( {z_{i,m} } \right)} \right]$ and can be maximized directly using many common software packages such as the R software (using the “optim function”) or, in some cases, by solving the system of the nonlinear equations of the likelihood derivatives from differentiating $l_{a,b,\theta }$ with respect to $a,b,\theta$. The score vector components ${\mathbf{U}}_{a,m} = \frac{\partial }{\partial a}l_{a,b,\theta } ,{\mathbf{U}}_{b,m} = \frac{\partial }{\partial b}l_{a,b,\theta }$ and ${\mathbf{U}}_{\theta ,m} = \frac{\partial }{\partial \theta }l_{a,b,\theta }$ can be easily derived from the nonlinear system ${\mathbf{U}}_{a,m} = {\mathbf{U}}_{b,m} = {\mathbf{U}}_{\theta ,m} = 0$ and then solving them simultaneously for getting the maximum likelihood estimates (MLE) of $a,b,\theta$. This system can only be solved numerically for the complicated models using some common iterative algorithms such as the “Newton–Raphson” algorithm.

4.2 The CVM Method

The CVM estimates (CVMEs) of the parameters $a, b$ and $\;\theta$ are obtained via minimizing the following expression with respect to the parameters $a, b$ and $\;\theta$, respectively, where

$$ {\text{CVME}}_{{\left( {a,b,\theta } \right)}} = \frac{1}{12}m^{ - 1} + \mathop \sum \limits_{i = 1}^{m} \left[ {F_{a,b,\theta } \left( {z_{{\left[ {i,m} \right]}} } \right) - c_{{\left( {i,m} \right)}} } \right]^{2} , $$

and $c_{{\left( {i,m} \right)}} = \left[ {\left( {2i - 1} \right)/2m} \right]$ and

$$\begin{aligned} {\text{CVME}}_{{\left( {a,b,\theta } \right)}} &= \mathop \sum \limits_{i = 1}^{m} \left( {\frac{1}{{1 - \exp \left( { - a} \right)}}\left( {1 - \exp \left\{ { - a\left( {1 - \exp \left\{ { - \left[ {\left( {1 + z_{{\left[ {i,m} \right]}} } \right)^{\theta } - 1} \right]} \right\}} \right)^{b} } \right\}} \right) }\right. \\ & \quad \left.{\vphantom{\frac{1}{1 - \exp \left( - a \right)}}- c_{{\left( {i,m} \right)}} } \right)^{2} .\end{aligned} $$

The CVME of the parameters $a, b$ and $\;\theta$ is obtained by solving the following nonlinear equations

$$ \begin{aligned} 0 &= \mathop \sum \limits_{{{{i}} = 1}}^{m} \left[ {{\mathcal{Q}}\left( a \right)\left( {1 - \exp \left\{ { - a\left( {1 - \exp \left\{ { - \left[ {\left( {1 + z_{{\left[ {i,m} \right]}} } \right)^{\theta } - 1} \right]} \right\}} \right)^{b} } \right\}} \right) - c_{{\left( {i,m} \right)}} } \right]\\ & \quad \nabla_{\left( a \right)} \left( {z_{{\left[ {i,m} \right]}} ;a,b,\theta } \right), \\ 0 &= \mathop \sum \limits_{{{{i}} = 1}}^{m} \left[ {{\mathcal{Q}}\left( a \right)\left( {1 - \exp \left\{ { - a\left( {1 - \exp \left\{ { - \left[ {\left( {1 + z_{{\left[ {i,m} \right]}} } \right)^{\theta } - 1} \right]} \right\}} \right)^{b} } \right\}} \right) - c_{{\left( {i,m} \right)}} } \right]\\& \quad \nabla_{\left( b \right)} \left( {z_{{\left[ {i,m} \right]}} ;a,b,\theta } \right), \\ \end{aligned} $$

and

$$ \begin{aligned}0 &= \mathop \sum \limits_{i = 1}^{m} \left[ {{\mathcal{Q}}\left( a \right)\left( {1 - \exp \left\{ { - a\left( {1 - \exp \left\{ { - \left[ {\left( {1 + z_{{\left[ {i,m} \right]}} } \right)^{\theta } - 1} \right]} \right\}} \right)^{b} } \right\}} \right) - c_{{\left( {i,m} \right)}} } \right]\\ & \quad \nabla_{\left( \theta \right)} \left( {z_{{\left[ {i,m} \right]}} ;a,b,\theta } \right),\end{aligned} $$

where

$$\begin{aligned} {\mathcal{Q}}\left( a \right)& = \frac{1}{{1 - \exp \left( { - a} \right)}},\nabla_{\left( a \right)} \left( {z_{{\left[ {i,m} \right]}} ;a,b,\theta } \right) = \partial F_{a,b,\theta } \left( {z_{{\left[ {i,m} \right]}} } \right)/\partial a,\\ & \quad \nabla_{\left( b \right)} \left( {z_{{\left[ {i,m} \right]}} ;a,b,\theta } \right) = \partial F_{a,b,\theta } \left( {z_{{\left[ {i,m} \right]}} } \right)/\partial b,\end{aligned} $$

and

$$ \nabla_{\left( \theta \right)} \left( {z_{{\left[ {i,m} \right]}} ;a,b,\theta } \right) = \partial F_{a,b,\theta } \left( {z_{{\left[ {i,m} \right]}} } \right)/\partial \theta . $$

4.3 The OLS Method

Let $F_{a,b,\theta } \left( {z_{{\left[ {i,m} \right]}} } \right)$ denote the CDF of PEEL model and let $z_{1} < z_{2} < \cdots < z_{m}$ be the $m$ ordered random sample. The OLS estimates (OLSEs) are obtained upon minimizing

$$ {\text{OLSE}}\left( {a,b,\theta } \right) = \mathop \sum \limits_{i = 1}^{m} \left[ {F_{a,b,\theta } \left( {z_{{\left[ {i,m} \right]}} } \right) - b_{{\left( {i,m} \right)}} } \right]^{2} . $$

and equivalently

$$ {\text{OLSE}}\left( {a,b,\theta } \right) = \mathop \sum \limits_{{{{i}} = 1}}^{m} \left[ {{\mathcal{Q}}\left( a \right)\left( {1 - \exp \left\{ { - a\left( {1 - \exp \left\{ { - \left[ {\left( {1 + z_{{\left[ {i,m} \right]}} } \right)^{\theta } - 1} \right]} \right\}} \right)^{b} } \right\}} \right) - b_{{\left( {i,m} \right)}} } \right]^{2} , $$

where $b_{{\left( {i,m} \right)}} = \frac{i}{m + 1}$. The OLSEs are obtained via solving the following nonlinear equations

$$\begin{aligned} 0 &= \mathop \sum \limits_{{{{i}} = 1}}^{m} \left[ {{\mathcal{Q}}\left( a \right)\left( {1 - \exp \left\{ { - a\left( {1 - \exp \left\{ { - \left[ {\left( {1 +_{{\left[ {{{i}},m} \right]}} } \right)^{\theta } - 1} \right]} \right\}} \right)^{b} } \right\}} \right) - b_{{\left( {{{i}},m} \right)}} } \right]\\ & \quad \nabla_{\left( a \right)} \left( {_{{\left[ {{{i}},m} \right]}} ;a,b,\theta } \right),\end{aligned} $$

$$ \begin{aligned}0 &= \mathop \sum \limits_{{{{i}} = 1}}^{m} \left[ {{\mathcal{Q}}\left( a \right)\left( {1 - \exp \left\{ { - a\left( {1 - \exp \left\{ { - \left[ {\left( {1 +_{{\left[ {{{i}},m} \right]}} } \right)^{\theta } - 1} \right]} \right\}} \right)^{b} } \right\}} \right) - b_{{\left( {{{i}},m} \right)}} } \right]\\& \quad \nabla_{\left( b \right)} \left( {_{{\left[ {{{i}},m} \right]}} ;a,b,\theta } \right), \end{aligned}$$

and

$$ \begin{aligned}0 &= \mathop \sum \limits_{i = 1}^{m} \left[ {{\mathcal{Q}}\left( a \right)\left( {1 - \exp \left\{ { - a\left( {1 - \exp \left\{ { - \left[ {\left( {1 + z_{{\left[ {i,m} \right]}} } \right)^{\theta } - 1} \right]} \right\}} \right)^{b} } \right\}} \right) - b_{{\left( {i,m} \right)}} } \right]\\ & \quad \nabla_{\left( \theta \right)} \left( {z_{{\left[ {i,m} \right]}} ;a,b,\theta } \right), \end{aligned}$$

where $\nabla_{\left( a \right)} \left( {z_{{\left[ {i,m} \right]}} ;a,b,\theta } \right),$ $\nabla_{\left( b \right)} \left( {z_{{\left[ {i,m} \right]}} ;a,b,\theta } \right)$ and $\nabla_{\left( \theta \right)} \left( {z_{{\left[ {i,m} \right]}} ;a,b,\theta } \right)$ are defined before.

4.4 The WLS Method

The WLS estimates (WLSEs) are obtained by minimizing the function WLSE $\left( {a,b,\theta } \right)$ with respect to $a, b$ and $\;\theta$ where

$$ {\text{WLSE}}\left( {a,b,\theta } \right) = \mathop \sum \limits_{i = 1}^{m} \omega_{{\left( {i,m} \right)}} \left[ {F_{a,b,\theta } \left( {z_{{\left[ {i,m} \right]}} } \right) - b_{{\left( {i,m} \right)}} } \right]^{2} , $$

and $\omega_{{\left( {i,m} \right)}} = \left[ {(1 + m)^{2} \left( {2 + m} \right)} \right]/\left[ {i\left( {1 + m - i} \right)} \right].$ The WLSEs are obtained by solving

$$ \begin{aligned} 0 &= \mathop \sum \limits_{i = 1}^{m} \left[ {{\mathcal{Q}}\left( a \right)\left( {1 - \exp \left\{ { - a\left( {1 - \exp \left\{ { - \left[ {\left( {1 + z_{{\left[ {i,m} \right]}} } \right)^{\theta } - 1} \right]} \right\}} \right)^{b} } \right\}} \right) - b_{{\left( {i,m} \right)}} } \right]\omega_{{\left( {i,m} \right)}} \\& \quad \nabla_{\left( a \right)} \left( {z_{{\left[ {i,m} \right]}} ;a,b,\theta } \right), \\ 0 &= \mathop \sum \limits_{i = 1}^{m} \omega_{{\left( {i,m} \right)}} \left[ {{\mathcal{Q}}\left( a \right)\left( {1 - \exp \left\{ { - a\left( {1 - \exp \left\{ { - \left[ {\left( {1 + z_{{\left[ {i,m} \right]}} } \right)^{\theta } - 1} \right]} \right\}} \right)^{b} } \right\}} \right) - b_{{\left( {i,m} \right)}} } \right]\\& \quad \nabla_{\left( b \right)} \left( {z_{{\left[ {i,m} \right]}} ;a,b,\theta } \right), \\ \end{aligned} $$

and

$$ \begin{aligned}0 &= \mathop \sum \limits_{i = 1}^{m} \omega_{{\left( {i,m} \right)}} \left[ {{\mathcal{Q}}\left( a \right)\left( {1 - \exp \left\{ { - a\left( {1 - \exp \left\{ { - \left[ {\left( {1 + z_{{\left[ {i,m} \right]}} } \right)^{\theta } - 1} \right]} \right\}} \right)^{b} } \right\}} \right) - b_{{\left( {i,m} \right)}} } \right]\\ & \quad \nabla_{\left( \theta \right)} \left( {z_{{\left[ {i,m} \right]}} ;a,b,\theta } \right).\end{aligned} $$

4.5 The AD Method

The AD estimates (ADEs) of $a, b$ and $\;\theta$ are obtained by minimizing the function

$$ {\text{ADE}}_{{\left( {z_{{\left[ {{{i}},m} \right]}} ,z_{{\left[ { - {{i}} + 1 + m:m} \right]}} } \right)}} \left( {a,b,\theta } \right) = - m - m^{ - 1} \mathop \sum \limits_{i = 1}^{m} \left( {2i - 1} \right)\left\{ {\begin{array}{*{20}c} {\log F_{a,b,\theta } \left( {z_{{\left[ {i,m} \right]}} } \right)} \\ { + \log \left[ {1 - F_{a,b,\theta } \left( {z_{{\left[ {1 + m - i:m} \right]}} } \right)} \right]} \\ \end{array} } \right\}. $$

The parameter estimates of $a, b$ and $\;\theta$ follow by solving the nonlinear equations

$$ 0 = \partial \left[ {{\text{ADE}}_{{\left( {z_{{\left[ {i,m} \right]}} ,z_{{\left[ {1 + m - i:m} \right]}} } \right)}} \left( {a,b,\theta } \right)} \right]/\partial a,0 = \partial \left[ {{\text{ADE}}_{{\left( {z_{{\left[ {i,m} \right]}} ,z_{{\left[ {1 + m - i:m} \right]}} } \right)}} \left( {a,b,\theta } \right)} \right]/\partial b, $$

and

$$ 0 = \partial \left[ {{\text{ADE}}_{{\left( {z_{{\left[ {i,m} \right]}} ,z_{{\left[ {1 + m - i:m} \right]}} } \right)}} \left( {a,b,\theta } \right)} \right]/\partial \theta . $$

4.6 The RTAD Method

The RTAD estimates (RTADEs) of $a, b$ and $\;\theta$ are obtained by minimizing

$$ \begin{aligned}{\text{RTADE}}_{{\left( {z_{{\left[ {i,m} \right]}} ,z_{{\left[ {1 + m - i:m} \right]}} } \right)}} \left( {a,b,\theta } \right)& = \frac{1}{2}m - 2\mathop \sum \limits_{{{{i}} = 1}}^{m} F_{a,b,\theta } \left( {z_{{\left[ {i,m} \right]}} } \right)\\& - \frac{1}{m}\mathop \sum \limits_{i = 1}^{m} \left( {2i - 1} \right)\left\{ {\log \left[ {1 - F_{{\left( {a,b,\theta } \right)}} \left( {z_{{\left[ {1 + m - i:m} \right]}} } \right)} \right]} \right\}. \end{aligned}$$

The estimates of $a, b$ and $\;\theta$ are obtained by solving the nonlinear equations

$$ 0 = \partial \left[ {{\text{RTADE}}_{{\left( {z_{{\left[ {i,m} \right]}} ,z_{{\left[ {1 + m - i:m} \right]}} } \right)}} \left( {a,b,\theta } \right)} \right]/\partial a,0 = \partial \left[ {{\text{RTADE}}_{{\left( {z_{{\left[ {i,m} \right]}} ,z_{{\left[ {1 + m - i:m} \right]}} } \right)}} \left( {a,b,\theta } \right)} \right]/\partial b, $$

and

$$ 0 = \partial \left[ {{\text{RTADE}}_{{\left( {z_{{\left[ {i,m} \right]}} ,z_{{\left[ {1 + m - i:m} \right]}} } \right)}} \left( {a,b,\theta } \right)} \right]/\partial \theta . $$

4.7 The LTAD Method

The LTAD estimates (LTADEs) of $a, b$ and $\;\theta$ are obtained by minimizing

$$ {\text{LTADE}}_{{\left( {z_{{\left[ {i,m} \right]}} } \right)}} \left( \theta \right) = - \frac{3}{2}m + 2\mathop \sum \limits_{{{{i}} = 1}}^{m} F_{a,b,\theta } \left( {z_{{\left[ {i,m} \right]}} } \right) - \frac{1}{m}\mathop \sum \limits_{i = 1}^{m} \left( {2i - 1} \right)\log F_{a,b,\theta } \left( {z_{{\left[ {i,m} \right]}} } \right). $$

The parameter estimates of $\delta ,\theta$ and $\beta$ are obtained by solving the nonlinear equations

$$ 0 = \partial \left[ {{\text{LTADE}}_{{\left( {z_{{\left[ {i,m} \right]}} } \right)}} \left( {a,b,\theta } \right)} \right]/\partial a,0 = \partial \left[ {{\text{LTADE}}_{{\left( {z_{{\left[ {i,m} \right]}} } \right)}} \left( {a,b,\theta } \right)} \right]/\partial b, $$

and

$$ 0 = \partial \left[ {{\text{LTADE}}_{{\left( {z_{{\left[ {i,m} \right]}} } \right)}} \left( {a,b,\theta } \right)} \right]/\partial \theta . $$

5 Simulations for Comparing Methods

A numerical simulation is performed in to compare the classical estimation methods. The simulation study is based on $N = 1000$ generated data sets from the PEEL version where $m = 50, 100, 150\;$ and $300$ and

	$a$	$b$	$\theta$
I	0.8	0.8	0.8
II	0.5	1.2	0.9
III	2	0.9	1.5

The estimates are compared in terms of their bias and the root mean-standard error (RMSE). The mean of the absolute difference between the theoretical and the estimates (D-abs) and the maximum absolute difference between the true parameters and estimates (D-max) are also reported. Tables 2, 3 and 4 give the simulation results. From Tables 2, 3 and 4, we note that the RMSE $\left( {\underline {\Theta } } \right)$ tends to zero when $m$ increases which means incidence of consistency property.

Table 2 Simulation results for parameters $a = 0.8,b = 0.8,\theta = 0.8$

Table 3 Simulation results for parameters $a = 0.5,b = 1.2,\theta = 0.9$

Table 4 Simulation results for parameters $a = 2,b = 0.9,\theta = 1.5$

6 Comparing Methods

Two applications to real data sets are considered for comparing the estimation methods. The data set I represents the data on failure times of 84 aircraft windshields. The data set II represents the data on service times of 63 aircraft windshields. The two real data sets were reported by Murthy et al. [38]. The required computations are carried out using the MATHCAD software. In order to compare the estimation methods, we consider the Cramér-von Mises (CVM) and the Anderson–Darling (AD) statistics. These two statistics are widely used to determine how closely a specific CDF fits the empirical distribution of a given data set. The results are given in Tables 5 and 6. From Table 5, we conclude that the ML method is the best method with CVM* = 0.06444 and AD* = 0.64651. From Table 6, we conclude that the RTAD method is the best method with CVM* = 0.10075 and AD* = 0.61025. However, all other methods performed well.

Table 5 Comparing estimation methods via data set I

Table 6 Comparing estimation methods via data set II

7 Applications

In this Section, we consider the same two real data sets of Murthy et al. [38] for applications to show the flexibility and the importance of the family presented under the L case. The fits of the PEEL are compared with many common Lomax extensions shown such as:

• I. Special generalized mixture Lomax (SGML).

• II. Odd log-logistic Lomax (OLLL).

• III. Reduced OLL Lomax (ROLLL).

• IV. Reduced Burr-Hatke Lomax (RBHL).

• V. Transmuted Topp–Leone Lomax (TTLL).

• VI. Reduced TTL Lomax (RTTLL).

• VII. Gamma Lomax (GL).

• VIII. Kumaraswamy Lomax (KL).

• IX. Beta Lomax (BL).

• X. Exponentiated Lomax (Exp-L).

• XI. Lomax (L) Lomax [33].

• XII. Proportional reversed hazard rate Lomax (PRHRL).

These two data sets are considered by matching their properties and the shapes of the PDF of the new model (see Fig. 1 (right plot)). By examining Fig. 1 (the right panel), it is noted that the new PDF can be “symmetric” and also “asymmetric right skewed function” with variable shapes. Additionally, by examining the initial density shapes of the two real data sets, it is seen that the initial densities are “semi symmetric” PDFs. Furthermore, the HRF of the new family can be “upside down bathtub-increasing,” “bathtub (U-shape),” monotonically decreasing, “increasing-constant” and “monotonically increasing” (see Fig. 1 (left plot)). Many other symmetric and asymmetric useful data sets can be found in Yousof et al. [41], Aryal et al. [9], Altun et al. [7].

For model comparison, some competitive models using a certain real data set (sets), we first need to explore the data. Exploring real data set can be used either numerically or graphically or with both techniques. In this section, we will consider many graphical techniques such as the skewness-kurtosis plot (or the Cullen and Frey plot) for exploring initial fit to the theoretical distributions such as normal, uniform, exponential, logistic, beta, lognormal and Weibull distributions (see Fig. 2 top left (1st data) and Fig. 2 top right (2nd data)). Bootstrapping is applied and plotted for more accuracy. Cullen and Frey plot just compares distributions in terms of squared skewness and kurtosis. This is a good summary but still only a summary of the properties of a distribution. The scattergram plots are also given in Fig. 2 middle left and bottom left for the 1st data and Fig. 2 middle right and bottom right for the 2nd data.

Fig. 2

Cullen–Frey and scattergram plots for the two real data sets

The “normality” of the two real data sets is checked using the “Quantile–Quantile” (Q-Q) plot (Figs. 3, 4 (top right plots)). The initial HRFs shape is explored by using the “total time in test (TTT)” tool (Figs. 3, 4 (bottom left plots)). The “nonparametric Kernel density estimation (NKDE)” tool is used for exploring the initial PDF shape (Figs. 3, 4 (top left plots)). The outliers are checked by the “box plot” (Figs. 3, 4 (bottom right plots)). Based on Figs. 3 and 4 (top left plots), it is seen that the NKDE is bimodal and semi-symmetric functions. Based on Figs. 3, 4 (top right plots), it is seen that the “normality” nearly exists for the two data sets (bottom left plots). It is shown that the HRF is " monotonically increasing HRF" for the two data sets. From Figs. 3 and 4 (bottom right plots), it is observed that no extreme values were spotted.

Fig. 3

NKDE, Q-Q, TTT, box plot for the 1st data

Fig. 4

NKDE, Q-Q, TTT, box plot for the 2nd data

The following goodness-of-fit (GOF) statistics are used for comparing competitive models:

• I. The “Akaike information” (AICr).

• II. The “consistent-AIC” (CAICr).

• III. The “Bayesian-IC” (BICr).

• IV. The “Hannan-Quinn-IC” (HQICr).

Tables 7 and 9 give the MLEs and the corresponding SEs for the two data sets, respectively. Tables 8 and 10 give the four GOF tests for the two data sets, respectively. Figures 5 and 6 give fitted PDFs, the Probability– Probability (P-P) plots, Kaplan–Meier Survival (KMS) plot and estimated HRF (E-HRF) plot for the two data sets, respectively. Based on Tables 3 and 5, it is noted that the PEEL model gives the lowest values for all GOF statistics with AICr = 267.836, CAICr = 268.136, BICr = 275.1288 and HQICr = 270.768 for the 1st data, and AICr = 207.087, CAICr = 207.494, BICr = 213.517 and HQICr = 209.616 for the 2nd data among all fitted competitive models. So, it could be selected as the best model under these GOF criteria.

Table 7 MLEs and SEs for 1st data

Table 8 GOF statistics for 1st data

Table 9 MLEs and SEs for 2nd data

Table 10 GOF statistics for 2nd data

Fig. 5

EPDF, EHRF, P-P, KMS plots for the 1st data set

Fig. 6

EPDF, EHRF, P-P, KMS plots for the 2nd data set

8 Conclusions

In this work, a new compound Lomax model called the Poisson exponentiated exponential Lomax distribution is proposed and analyzed. The Poisson exponentiated exponential Lomax distribution is derived based on compounding the zero truncated Poisson distribution and the exponentiated exponential Lomax distribution. The new density can be “monotonically left skewed,” “monotonically right skewed” and “symmetric” with various useful shapes. The new hazard rate can be “upside down bathtub-increasing,” “bathtub (U-shape),” “monotonically decreasing,” “increasing-constant” and “monotonically increasing.” Relevant statistical properties such as ordinary moments, incomplete moments, moments of residual life, moments of the reversed residual life and mean deviation are derived. For facilitating the mathematical modeling of the bivariate real data sets, we derive some new bivariate Poisson exponentiated exponential Lomax distributions using “Farlie–Gumbel–Morgenstern copula, modified Farlie–Gumbel–Morgenstern copula which contains four internal types,” Clayton copula,” “Renyi's entropy copula (RECp)” and “Ali-Mikhail-Haq copula.” However, future works may be allocated to study these new models.

After studying the main statistical properties and presenting some bivariate type extensions, we briefly considered and then described different estimation methods, namely the maximum likelihood, Cramér-von-Mises estimation, ordinary least square, weighted least square, Anderson–Darling, right tail Anderson–Darling and left tail Anderson–Darling. These methods are used in estimation process of the unknown parameters. Monte Carlo simulation experiments are performed for comparing the performances of the proposed methods of estimation for both small and large samples. Furthermore, two applications are provided for illustrating the applicability of the Poisson exponentiated exponential Lomax model. The Kernel density plot, the “Quantile–Quantile plot, the total time in test plot and box plot are provided and analyzed. Based on two real data sets, the Poisson exponentiated exponential Lomax model gives the lowest statistic test AICr = 267.836, CAICr = 268.136, BICr = 275.1288 and HQICr = 270.768 for the failure times data and AICr = 207.087, CAICr = 207.494, BICr = 213.517 and HQICr = 209.616 for the service times data.