Introduction

The production of pure or high-grade chromite ore is challenging since chromium occurs in complex mineralogy due to its association with a variety of other elements such as iron (Fe), magnesium (Mg), silicon (Si) and aluminium (Al). This challenge is exceptionally more pronounced when it concerns magmatic deposits, as is the case of South African ores found in the Bushveld Igneous Complex (BIC). During mining and processing operations, large amounts of fines are generated. These fines present problems regarding their handling and storage that inevitably lead to substantial environmental concerns. According to Murthy et al. [1], more than 25% of the mineral value is lost as slime during the processing of many ores. The economic, environmental, financial, and political pressures undergoing most South African industries owning such tailings facilities have drawn their attention to focus on the retreatment of old and new chromite tailings [2].

According to Blake [3], some mining companies are looking into the possibilities of exploring old tailings facilities to reduce the cost involved in deep-level mining activities. Considering this option will contribute to raising revenue since it will be zero-cost mining. In the last decade, several mining companies operating in plants where significant amounts of chromite are disposed of as tailings have considered focusing on those tailings as alternative potential chromium-bearing mineral reserves. The necessity of recovering chromite values from these rejected tailings has motivated numerous research and development (R&D) organizations to concentrate on this task [1]. Hence, projects are initiated to propose a sustainable process route to reprocess these tailings to recover chromite and address environmental regulations by generating alternative tailing management options. Numerous methods for recovering chromite values using conventional beneficiation methods such as gravity separations, magnetic separations, flotation, have been proposed and reported during the past 20 years in the form of technical studies, papers and reviews [4,5,6,7,8]. Several challenges were raised, showing the limitations of using conventional beneficiation methods, leading to the loss of important amounts of chromite values to the tailings as a sign of non-optimized process routes. On the other hand, since most plants are optimized for a specific size fraction (≥ 75 µm) and the tailings of chromite plants are generally characterized by fine particles, a recurring problem associated with fines revealed that poor performances due to the entrainment of huge quantities of silicate in the concentrate indicate the beneficiation of such ores. Consequently, this reduces the final concentrate grade and recovery due to the loss of chromite to the tailings as a result of poor separation efficiency in the beneficiation process [9].

A more adaptable and sustainable process should be designed to address the challenges and limitations encountered during the beneficiation of such minerals. However, due to the size fraction of the ore (fines), a cost-effective and low-energy consumption process that does not involve milling and generates hazardous wastes was adopted. Implementing the beneficiation approach, considering challenges and limitations, will promote the shift towards greener metallurgy, minimize the industry’s ecological footprint, and promote the choice of an efficient process. To adopt sustainability and create a more environmentally friendly future, a creative and comprehensive strategy must maximize the recovery of valuable material while attending to environmental issues. Developing and implementing eco-efficient metallurgical processes that reduce waste production, energy use, and environmental impact while enhancing operational performance and cost-effectiveness are critical to the sustainability strategy. One flexible separation method that was suggested to overcome the technical and environmental challenges was the shaking table. By modifying the operational parameter values, the effectiveness of the shaking table can increase separation efficiency and result in ideal separation conditions [10].

Consequently, to comprehend and manage the separation process, it is necessary to carefully set various operating parameters to consider their impact on the process. In practice, assessing the parameters’ effect independently at all levels is time-consuming and expensive. Therefore, a well-designed experimental test program is required to determine the response of the separation process to each factor. Nowadays, factorial designs have been successfully used in several design experiments to develop empirical models [11].

Response surface methodology (RSM), available in MINITAB and other proprietary software, is a collection of statistical and mathematical techniques useful for developing, improving, and optimizing processes. It is a critical and very robust tool for manipulating and analyzing research data to obtain a quality result or improvement [12]. Recently, the RSM has found more applications in mineral processing to assist in the obtention of appropriate process variables and conditions, leading to optimum results during the beneficiation of ores. However, several experimental designs have been performed for different objectives. For instance, Alsan [13] revealed that the Central Composite Design (CCD) was used to optimize independent variables while cleaning coal using a multi-gravity separator. Furthermore, Sen [14] showed that the three-level and three-factor full factorial experimental design was used to investigate the impact of different independent parameters while using the Knelson separator. Finally, Panda et al. [15] demonstrated that the Box Behnken experimental design can be used to investigate the significance of different operating parameters on the beneficiation of ultrafine chromite through selective flocculation.

The current study proposes and optimizes a beneficiation procedure to recover chromite from South African Middle Group chromite plant tailings using a Wilfley shaking table. The effects of the processing parameters (tilt angle (°), water flow rate (L/h), vibration frequency (Hz), particle size (µm), feed rate (g/min)) on chromite recovery, grade, Cr/Fe ratio and separation efficiency were studied simultaneously using CCD of RSM. The statistical models developed were used for the prediction and optimization of the developed procedure.

Materials and Methods

Sample Preparation

200 kg of chromite plant tailings were collected from one of the Middle Group seam chromite beneficiation plants in the Northwest Province, South Africa. The bulk sample was made up of fine material (100% passing 500 µm) and 10% moisture. The sample was split into representative sub-samples using the laboratory rotative splitter after blending. About 500 g of the sample were collected and fed into the small rotative splitter to collect a representative sample for characterization using X-ray fluorescence (XRF), X-ray diffraction (XRD) and scanning electron microscopy with energy dispersive X-ray spectroscopy (SEM/EDX). About 300 g of the head sample were subjected to wet screening analysis for the particle size distribution (PSD) using 500, 425, 300, 212, 150, 106, 75, and 53 µm screens.

Analytical Methods

The chemical composition of the raw sample was assessed through XRF analysis. The Rigaku ZSX Primus II instrument, equipped with SQX analysis software, was utilized for conducting the XRF analysis. Additionally, the mineralogical composition was determined using XRD analysis. The Rigaku Ultima IV instrument was employed for the XRD analysis, where X-rays are generated in a cathode ray tube by heating a filament to produce electrons, accelerating the electrons by applying a voltage of 20 to 45 kV, and bombarding the CuKα radiation target material with electrons. Furthermore, a TESCAN SEM/EDX instrument, coupled with EDX analysis software for elemental analysis performance in nanospace, which resolves a picture in high vacuum mode SEO (3.0 nm at 30 kV), medium vacuum mode, and low vacuum mode BSE (3.5 nm at 30 kV), was employed for the SEM analysis. The QEMSCAN was operated using an accelerating voltage of 200 V to 3 kV with a scanning speed of 20 ns to 10 ms per pixel, adjustable in steps or continuously.

Experimental Procedure

The experiments consisted of gravity separation of the South African Middle Group chromite plant tailings to concentrate the chromite using a laboratory-type Wilfley shaking table. The shaking table used had a fiberglass deck characterized by a rectangular working area of 2 feet (60.96 cm) length by 4 feet (121.92 cm) width with an easily adjustable angle ranging from 0 to 10°. The water was supplied in the working area from two different sources, which were placed on the deck in the feeding zone and on the perpendicular side as washing water. To promote the separation, the vibrations were kept at a frequency ranging from 0 to 50 Hz, while the shaking table could receive a maximum optimized sample feed rate of 50 kg/h. 1 kg of samples were fed at a controlled flow rate while parameters such as water flow rate, deck tilt angle and vibration were adjusted at different running conditions according to the design of experiments (DoE) on different size fractions. Throughout the experiments, the products were collected into different buckets as follows: tailings, middlings, and concentrate. Each product was filtered, dried, and weighed prior to the analysis. The XRF analysis was performed on each fraction to evaluate the separation efficiency.

Grade and recovery are the most widely accepted process noneconomical indices, which are used in mineral processing to evaluate the efficiency of concentration processes [16]. The recovery was calculated using Eq. 1.

$$R = \frac{Cc}{{Ff}} \times 100$$
(1)

where R is the recovery, C and F are the dry weights of the concentrate and the feed, respectively, while c and f are grades of Cr2O3 values in the concentrated tailings and feed expressed in %.

Separation efficiency (SE) is one of the critical indices used in mineral processing to evaluate the performance of the concentration process because of the selectivity based on the grade of the concentrated mineral or element. It is calculated according to Eq. 2.

$$SE = \left( {\frac{Cc}{{Ff}} - \frac{{C\left( {1 - c} \right)}}{{F\left( {1 - f} \right)}}} \right) \times 100$$
(2)

The validation test from the Wilfley shaking table was done to verify the accuracy of the predicted results from the RSM and the experimental data. The errors between the average of the experimental and predicted values were calculated using Eq. 3.

$$Error{ }\left( {\text{\% }} \right) = \left( {\frac{{Experimental\,Data - RSM{ }optimal\,Prediction}}{{Experimental\,Data}}} \right) \times 100$$
(3)

The flowsheet of the experimental procedure is shown in Fig. 1.

Fig. 1
figure 1

The flowsheet of the experimental procedure

Full size image

Statistical Analysis

The effect of independent variables such as deck tilt angle (°), sample feed rate (g/min), table vibration (Hz), water flow rate (L/h), and particle size range (µm) were investigated, while recovery (%), grade (%), the Cr/Fe ratio and separation efficiency were determined as response variables using RSM utilizing the Central Composite Design (CCD) as summarized in Table 1.

Table 1 Factors and responses, along with levels considered for the statistical analysis of the Wilfley shaking table
Full size table

A total of 54 experimental runs were designed and conducted using the mathematical software package Minitab. The statistical analysis of each of the experiments used is presented in Table 2. These runs were carefully planned and executed to investigate the various combinations of factors and their effects on the response variables.

Table 2 Statistical analysis of experiments
Full size table

Results and Discussion

Chemical Composition of the Sample

According to the data presented in Table 3, the as-received sample contains a substantial proportion of silicate, constituting approximately 15.72% of silicon. Among the elements present in the ore, chromium exhibits the highest concentration, accounting for 13.59% of the sample, followed closely by iron at 12.68% with a Cr/Fe ratio of 1.07. The grade of chromite found in the sample is deemed sufficient for further exploitation through mineral processing using any appropriate technique.

Table 3 The chemical composition of the chromite plant tailings sample
Full size table

Based on the results, it can be inferred that the sample can be classified as ferruginous due to the significant amount of iron present. Furthermore, the presence of iron signifies the need for specific processing techniques tailored to address the ferruginous nature of the sample. Additionally, the specific gravity of the sample was measured to be 3.5, which aided in determining the optimal strategies for separation and concentration of chromite during the processing stage.

Mineralogy of the as-Received Sample

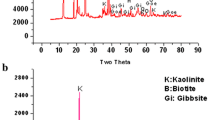
The main compound identified was chromite, and it corresponded to the generic Magnesiochromite (Cr2, Mg) O4 and chromite phase (Cr2FeO4), where almost all of the iron is Fe (II) in Magnesioferrite (Al, Fe, Mg)O4, Fayalite (Fe2O4·SiO2), and Magnetite (Fe3O4). Figure 2 shows that the sample contains other mineral phases that are considered gangue minerals, such as A-Catena silicate, B-Spinel, C-Magnesioferrite, E-Fayalite, F-Lime, G-Quartz, and H-Magnetite. These results are very similar to results obtained by Maruli and Nheta [17].

Fig. 2
figure 2

X-ray Diffraction pattern of chromite sample

Full size image

Mineral Distribution of the Raw Sample

According to Fig. 3, it is apparent that it is a low-grade sample showing a relatively low concentration of the desired elements. The figure exhibits three distinct contrasts: bright, grey, and light grey. These contrasts correspond to different phases or components within the sample. Specifically, the bright contrast observed in the figure corresponds to chromite grains. These grains are characterized by compact crystals, which can be visually distinguished from the surrounding components based on their unique appearance and brightness. The grey and light grey contrasts represent additional phases or mineral constituents present in the sample, offering further insights into the mineralogical composition and heterogeneity of the sample [18, 19]. The analysis of the SEM images also revealed that chromite is well-liberated from silicate minerals.

Fig. 3
figure 3

Scanning electron microscopy micrograph of the as-received sample

Full size image

The EDS results displayed in Table 4 reveals the presence of various gangue minerals within the sample, including catena silicate, magnesioferrite, fayalite, lime, quartz, and magnetite. These minerals contribute to the overall composition and structure of the sample, providing valuable insights into its geological characteristics.

Table 4 Spectrums and elements of the as-received sample
Full size table

Interestingly, when examining the chromium content within the sample, relatively high values are detected in spectra 2, 5, and 6. These phases correspond to chromite spinels and magnesiochromite, with chromium concentrations of 32.75, 26.08, and 26.87%, respectively. The presence of these chromium-rich phases signifies the potential for valuable extraction and utilization of chromium within the sample [20]. Spectrum 1 is represented by magnesioferrite, a chromite grain containing a combination of magnesium, aluminum, and iron. This phase further contributes to the overall mineralogical composition of the sample, highlighting its diverse nature. Specifically, spectra 2 and 8 in the analysis correspond to quartz and magnesioferrite, or spinel, respectively. These findings contribute to a better understanding of the mineral assemblage, highlighting the presence of different phases with distinct chemical compositions and properties.

Particle Size Distribution (PSD) of the as-Received Sample

To determine the particle-size distribution (PSD) of the as-received sample, a particle-size measurement was conducted using a wet screen shaker. The obtained data from this analysis are presented in Fig. 4. It is evident that the PSD of the sample is characterized as fine. This is consistent with the typical PSDs of most PGM tailings found in the Bushveld Complex (BC) of South Africa [21].

Fig. 4
figure 4

Particle size distribution of the as-received sample

Full size image

According to Wills and Finch [16], the sample is suitable for recovering chromite using the gravity separation method due to the particle size distribution. One notable observation is that the sample has a P80 of 106 µm. This particular size range indicates optimal liberation of particles, suggesting that the sample exhibits favorable characteristics for subsequent processing.

Further examination of the results revealed that 26.21% of the particles fall within the coarse range, ranging from [− 500 + 150 µm]. Additionally, 57.9% of the particles fall within the fine range, ranging from [− 106 + 75 µm]. This range represents a significant portion of the sample, indicating the presence of finely dispersed particles. Furthermore, the analysis identifies that 15.89% of the particles are classified as ultrafine, dispersed below the size of − 53 µm. These ultrafine particles represent a fraction of the sample with smaller sizes and potentially different characteristics compared to the coarser and finer fractions. A similar trend was observed by Ross et al. [8], whilst working with UG2 plant tailings.

Optimization Process

The recovery of chromite was optimized using RSM under CCD. Throughout the investigation, to show the correlation between independent variables and corresponding responses, the following was investigated:

Goodness-of-Fit

The summary of the model presented in Table 5 reveals that the fitted values for the recovery, grade, Cr/Fe ratio, and separation efficiency exhibit R-squared (R-sq), adjusted R-squared (Adj-R-sq), and predicted R-squared (R-sq (pred)) values. These values provide insights into how well the model fits the data and explain the variation in the target variables. The results indicate that the second-order model can adequately explain the variation in recovery, grade, Cr/Fe ratio, and separation efficiency. Specifically, the R-squared values obtained for these variables are 71.40, 81.19, 77.99, and 63.51%, respectively. These values indicate that the model accounts for a significant proportion of the variability in the target variables, demonstrating a relatively good fit. These results are similar to those of Ross et al.[8].

Table 5 Model summary of the response variables
Full size table

However, it is important to note that the R-squared (pred) value of 0.00% suggests that the model may be overfitting the data [22]. Overfitting occurs when a model becomes too complex and fits the training data too closely, resulting in poor generalization to new data. In this case, the model’s predictive ability may be limited, and caution should be exercised when extrapolating or making predictions based on the model. To assess the adequacy of the developed mathematical models for the recovery, grade, Cr/Fe ratio, and separation efficiency, additional measures such as R-squared (R-sq) and Adjusted R-squared (Adj-R-sq) values were used. These values provide a more robust evaluation of the model’s fit and account for the number of predictors in the model. By considering these metrics, researchers can determine whether the models adequately capture the relationships between the input variables and the target variables [9, 11, 22].

Analysis of Variance (ANOVA)

The ANOVA analysis table for the second-order model, as presented in Table 6, provides valuable information regarding the statistical significance of the model for recovery, grade, ratio, and separation efficiency. It is evident that the p-values associated with the model are less than 0.05, indicating statistical significance [23]. This implies that the proposed model is meaningful and has a significant impact on the response variables.

Table 6 Analysis of variance of recovery, grade, Cr/Fe ratio and SE
Full size table

Furthermore, the model’s lack-of-fit error is assessed to determine its accuracy in predicting the response variables. The analysis reveals that the lack-of-fit error is found to be insignificant. This result suggests that the fitted model adequately captures the relationships between the input variables and the response variables, demonstrating its accuracy in predicting the desired outcomes. The significance of the model, as indicated by the low p-values, further supports the reliability and effectiveness of the proposed second-order model. Researchers can have confidence in the model’s ability to explain the variation in recovery, grade, ratio, and separation efficiency.

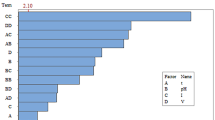
Pareto Chart and Mathematical Models

The pareto chart for the recovery, grade, Cr/Fe ratio, and separation efficiency of chromite in concentrate, as depicted in Fig. 5, provides valuable insights into the effects of various factors and their interactions on the response variables. The factors considered in the analysis are denoted as A, B, C, D, and E, representing tilt angle (°), feed rate (g/min), vibration (Hz), water flow rate (L/H), and size (µm), respectively. Additionally, the interactions between these factors are also investigated, including AA (Angle*Angle), BB (Feed rate*Feed rate), CC (Vibration*Vibration), DD (Water flow*Water flow), EE (Size*Size), AB (Angle*Feed rate), AC (Angle*Vibration), AD (Angle*Water flow), AE (Angle*Size), BC (Feed rate*Vibration), BD (Feed rate*Water flow), BE (Feed rate*Size), CD (Vibration*Water flow), CE (Vibration*Size), and DE (Water flow*Size). The examination of ANOVA analysis shows that the p-value associated with the model is less than 0.05, indicating statistical significance. This suggests that the model is meaningful and has a significant impact on the recovery, grade, Cr/Fe ratio, and separation efficiency of chromite in the concentrate.

Fig. 5
figure 5

Pareto chart of the effect of various factors on the recovery, grade, Cr/Fe ratio, and separation efficiency (SE) of chromite

Full size image

In the recovery model, the analysis reveals that factors A, E and EE exhibit significant effects. This suggests that the recovery of chromite is more influenced by the particle size (µm) compared to the tilt angle (°). The size of the particles has a greater impact on the recovery process, and the generated model provided by Minitab software is presented in Eq. 4. However, studies by Tripathy et al. [7] revealed that the chromite recovery is affected more by the variation of the deck tilt angle.

$$Recovery{ }\left( {\text{\% }} \right) = - 26 + 6.46A + 0.246E - 0.00401EE$$
(4)

For the grade model, significant factors are A, E, AC, CE, and EE. This indicates that the grade of the chromite concentrate is more sensitive to the particle size (µm) compared to the tilt angle (°) and vibration (Hz). Equation 5 presents the generated model for grade.

$$Grade{ }\left( {\text{\% }} \right) = - 24.7 + 5.85A - 0.0630E - 0.0894{ }AC + 0.00229CE - 0.001684EE$$
(5)

The particle size plays a more crucial role in determining the grade of the concentrate, while both the tilt angle and vibration also contribute significantly to the grade. In the Cr/Fe ratio model, the significant factors are E and EE, implying that the ratio of chromium to iron in the concentrate is more influenced by the particle size (µm). The particle size plays a key role in determining the Cr/Fe ratio, and the model generated is presented in Eq. 6.

$$Ratio\frac{Cr}{{Fe}} = 0.85 + 0.00042E - 0.000056EE$$
(6)

For the separation efficiency model, the significant factors are A and CC. This indicates that the separation efficiency is more sensitive to vibration (Hz) compared to the tilt angle (°). Vibration has a greater impact on the efficiency of the separation process, while the tilt angle also plays a significant role. The proposed mathematical model presented in Eq. 7 offers a quantitative representation of the relationship between the factors and the response variables.

$$SE = - 156.2 + 6.67A - 0.0918CC$$
(7)

Residuals Versus Order Plot

The normal probability plots of residuals for the response variables, including recovery, grade, Cr/Fe ratio, and separation efficiency, have been generated and plotted on Fig. 6. These plots serve as a tool for assessing the validity of the assumption that the residuals follow a normal distribution.

Fig. 6
figure 6

Probability plots of residuals for the response variables a recovery, b grade, c Cr/Fe ratio, and c separation efficiency

Full size image

In visualizing the normal probability plots, if the data points on the plot align closely to a straight line, it indicates that the residuals conform to a normal distribution, thus validating the assumption by Myers et al. [24]. Conversely, if the data points deviate significantly from a straight line, it suggests potential issues with the assumption. However, if deviations from the expected pattern are observed, further investigation may be necessary to identify and address potential problems with the assumption.

In Fig. 6, it can be observed that the residuals align closely with a straight line, indicating that the errors associated with recovery, grade, Cr/Fe ratio, and separation efficiency are normally distributed. This suggests that the empirical models developed accurately represent the process. Consequently, these models can be utilized for optimizing the process parameters, allowing for improved efficiency and effectiveness.

Main and Interaction Effects Plot

Based on the existing literature, the presence of parallel lines in interaction plots indicates the absence of interactions in the model [25]. Consequently, only the lines that are not parallel hold significance in influencing the relationship between the predictors and the response variable. In the provided interaction plots, it can be observed that some lines are parallel while others are not, implying that certain predictors have a significant impact on the relationship while others do not exhibit any interaction effects. This analysis helps in identifying the key predictors that play a crucial role in explaining the variations observed in the response variable. The interaction effect plots for the recovery response variables are presented in Fig. 7.

Fig. 7
figure 7

Plots of the effects of the main parameters and their interactions for chromite recovery

Full size image

Based on the observations from Fig. 7, three interaction plots are identified in the response of recovery, specifically the interaction plots for vibration-tilt angle, vibration-feed rate, and water flow rate-tilt angle. These interaction effects demonstrate the relationship between the recovery and the factors influenced by the tilt angle, vibration, and feed rate. The non-parallel nature of these interaction plots indicates that the combined influence of these factors on the recovery is not simply additive or independent. Instead, the interaction between these factors plays a significant role in shaping the overall recovery outcome.

On Fig. 8, it is evident that there are four interaction plots in the grade response that do not exhibit parallel lines. These interaction plots include the feed rate-tilt angle interaction plot, the vibration-tilt angle interaction plot, the water flow rate-tilt angle interaction plot, and the water flow rate-vibration interaction plot. The non-parallel nature of these plots indicates that the relationship between the grade and the respective factors (angle, vibration, feed rate, and the water flow rate) is not solely determined by the individual effects of these factors. Instead, the combined influence of these factors, as represented by the interaction plots, significantly impacts the grade of the material. Understanding and considering these interaction effects are crucial for accurately predicting and optimizing the grade response, as they reveal the intricate interplay between the factors involved.

Fig. 8
figure 8

Plots of the effects of the main parameters and their interactions on concentrate chromite grade

Full size image

From the examined data presented in Fig. 9, it is observed that there is only one interaction plot in the Cr/Fe ratio response that is not parallel, specifically the interaction plot for feed rate-tilt angle. This interaction plot indicates that the relationship between the Cr/Fe ratio and the factors of feed rate and tilt angle is influenced by their combined effect. The results also clearly demonstrated that all independent parameters were essential; however, Feed rate*Angle had positive effects on Cr/Fe when considered individually. The non-parallel nature of this interaction plot suggests that the impact of these factors on the Cr/Fe ratio is not solely determined by their individual effects but is influenced by their interaction.

Fig. 9
figure 9

Plots of the effects of the main parameters and their interactions on concentrate Cr/Fe ratio

Full size image

Based on the analysis of Fig. 10, three interaction plots are identified for the separation efficiency response. These plots include the water flow rate-tilt angle plot, the water flow rate-vibration plot, and the size-vibration plot. These interaction plots highlight the interplay between the factors of water flow rate, tilt angle, vibration, and size in relation to the separation efficiency. The non-parallel nature of these interaction plots indicates that the combined influence of these factors significantly affects the separation efficiency. Through the analysis of these interaction effects, researchers can acquire valuable insights into the ideal conditions necessary to achieve enhanced separation efficiency. These findings emphasize the importance of considering the interactions between multiple factors when aiming to enhance the overall efficiency of the separation process.

Fig. 10
figure 10

Plots of the effects of the main parameters and their interactions on separation efficiency chromite

Full size image

Contour and Surface Plot of Affecting Parameters

To illustrate the impact of the independent variables on the recovery, grade, Cr/Fe ratio, and separation efficiency, contour plots of the quadratic polynomial model were created. These plots depict the relationship between two selected variables while keeping the other two variables constant at their central values within the experimental range. By visually examining these contour plots, researchers can better understand how changes in the selected variables influence the respective responses [15]. This visualization aids in identifying optimal parameter settings and determining the sensitivity of the responses to specific variable combinations.

To enhance comprehension of the findings, response surface plots have been generated utilizing a second-order quadratic equation. These plots provide a visual representation of the interactional effects of process variables on the recovery, grade, Cr/Fe ratio, and separation efficiency within the concentrate fraction of the shaking table. By examining these response surface plots, researchers can gain valuable insights into how changes in the process variables impact the targeted responses. This graphical representation allows for a deeper understanding of the relationships and interactions between the variables, aiding in the optimization of process parameters for achieving desired outcomes in terms of recovery, grade, Cr/Fe ratio, and separation efficiency.

Recovery

Figure 11 illustrates the influence of process parameters on the recovery of the concentrate fraction in the shaking table.

Fig. 11
figure 11

Contour plots of the effects of various parameters a table vibration and tilt angle; b table vibration and feed rate; and c water flow rate and tilt angle on chromite recovery

Full size image

From Fig. 11a, it can be observed that the optimal results are achieved within the range of 67.5 to 70% recovery. Notably, an increase in the tilt angle from 4 to 7° corresponds to improved recovery within the vibration range of 35 to 47.5 Hz. However, beyond an angle of 7° and a vibration frequency of 47.5 Hz, the effect on recovery becomes insignificant. These findings suggest that a specific combination of tilt angle and vibration frequency is critical for achieving optimal recovery results, while extreme values outside the identified ranges may have a limited impact on the recovery process.

Figure 11b provides a visual representation of the effects of vibration and feed rate on recovery. It is evident from the figure that the highest recovery rates (˃ 72%) are observed at both the lowest feed rate ( < 50 g/min) and the highest feed rate (˃ 150 g/min) when combined with the highest vibration frequency of 50 Hz. However, as the feed rate increases beyond the optimal range, the recovery rate starts to decrease. This suggests that there exists an optimal combination of vibration frequency and feed rate that maximizes the recovery process. The results indicate that excessively high or low feed rates can have a negative impact on recovery, highlighting the importance of selecting an appropriate feed rate to achieve the desired recovery levels.

Figure 11c illustrates the effects of water flow rate and tilt angle on recovery. The plot shows that the highest recovery rates (˃ 70%) are achieved within the water flow rate range of 350 to 475 L/H and the tilt angle range of 5 to 7°, while Tripathy et al. [7] found that water flow rate is of higher value (> 5 Liter per min) compared to the other variables (deck tilt angle and feed rate). However, as both the angle and water flow rate increase simultaneously, there is a decrease in recovery. This phenomenon can be attributed to the concentration of valuable minerals, such as chromite, in the tailings due to the steep inclination of the shaking table and the increased water flow rates. The concentration of these minerals in the tailings reduces their recovery in the concentrate fraction, leading to a decline in overall recovery [8, 20, 21].

Grade Cr2O3

Figure 12 provides insights into the impact of process parameters on the grade of the concentrate fraction in the shaking table. Figure 12a presents 2D contour plots depicting the effects of feed rate and tilt angle on the grade of chromite. The highest grade (41% Cr2O3) is achieved within two distinct ranges: Firstly, when the tilt angle ranges from 5 to 8° and the feed rate is below 50 g/min. Secondly, when the tilt angle ranges from 4 to 7° and the feed rate is up to 160 g/min. These ranges indicate the optimal conditions for obtaining the desired grade of chromite in the concentrate fraction. By carefully controlling the feed rate and tilt angle within these ranges, it is possible to enhance the grade of chromite concentrate.

Fig. 12
figure 12

Contour plots of the effects of various parameters a feed rate and tilt angle; b table vibration and tilt angle; c water flow rate and tilt angle and d water flow rate and table vibration on concentrate chromite grade

Full size image

Figure 12b presents the plots showcasing the impact of the angle and vibration on the grade of the concentrate fraction. The optimal grade of chromite (above 34% Cr2O3) is observed within the range of 4 to 6˚ for a vibration range of 43 to 48 Hz. It is evident from the figure that as the tilt angle increases beyond 7 to 10°, the grade of the concentrate fraction decreases significantly (below 34% Cr2O3). In Fig. 12c, the influence of the water flow rate and angle on the grade of chromite concentrate is illustrated. The 2D contour plot reveals a range where the response (grade) becomes less significant, with values below 36% Cr2O3. This range is obtained at angles as high as 8°. The highest grade of chromite is achieved when the water flow rate exceeds 500 L/H in the tilt angle range below 7°. These findings demonstrate the importance of controlling the water flow rate and angle within the specified ranges to achieve the desired grade of chromite in the concentrate fraction. Figure 12d depicts the impact of both water flow rate and vibration on the chromite concentrate grade. The contour plot distinctly reveals a zone where the response (grade) is negligible, registering values below 36% Cr2O3. This interval is observed at frequencies below 37.5 Hz. Optimal chromite grades are evident within the frequency range of 42.5 to 50 Hz, particularly with water flow rates exceeding 475 L/H.

The influence of feed rate and tilt angle on the Cr/Fe ratio of the concentrate fraction is depicted in Fig. 13. It is evident from the figure that the feed rate has a negative impact on the Cr/Fe ratio. At lower feed rates (less than 150 g/min), the Cr/Fe ratio is relatively low. However, as the feed rate is increased to 170 g/min, the response shows an improvement within the tilt angle range of 4 to 7°. This suggests that optimizing the feed rate within this specific range can contribute to achieving a higher Cr/Fe ratio in the concentrate fraction.

Fig. 13
figure 13

Contour plots of the effects of feed rate and tilt angle on the Cr/Fe ratio of the concentrate

Full size image
Separation Efficiency

The separation efficiency contour plots for effects of water flow rate and angle, water flow and vibration, and size and vibration are presented in Fig. 14.

Fig. 14
figure 14

Contour plots of the effects of various parameters a water flow rate and tilt angle; b water flow rate and table vibration and c particle size and table vibration on separation efficiency

Full size image

The highest separation efficiency was observed in the ranges of 4 to 6° of tilt angle, with a flow rate over 450 L/H for the water flow and angle plot. On the contour plot of water flow and vibration, a range of highest separation efficiency was observed between 40 and 50 Hz of vibration. Lastly, the contour plot of size and vibration shows a range where the size of the particle shows an effect on the separation efficiency. From the plot, the highest area of separation efficiency was seen in the range of particle size between 0 and 75 µm and the vibration of 42 to 48 Hz. It was not possible to get good results under 40 Hz of vibration because the response becomes insignificant.

Overlaid

The overlaid graphical approach presented in Fig. 15 facilitated the determination of the region where the responses met the specified expectations, aiding in the optimization of the experimental conditions. The white region within the Design Space optimization, referred to as the “optimized formulation region”, represents the area where the desired outcomes are achieved through feasible formulations. This region takes into account multidimensional variations and interactions of the responses, including recovery, grade, Cr/Fe ratio, and separation efficiency. The criteria within this region align with the strategic goals of the organization and serve as indicators of successful process optimization [26].

Fig. 15
figure 15

Contour plots of the effect of table vibration and particle sizes on SE, Cr/Fe, grade, and recovery

Full size image

In the plot, the response variables of recovery, grade, Cr/Fe ratio, and separation efficiency are represented. The x-axis corresponds to the particle size (µm), while the y-axis represents the vibration frequency (Hz). The white area on the plot indicates the range of size and vibration values that result in satisfactory fitted values for all four response variables. Thus, any combination of size and vibration settings within this region is expected to yield a product with an acceptable mean response across the considered variables. This information is valuable for determining the optimal parameter values to achieve the desired outcomes for the process.

It is evident that the response area is bound by an outer limit of 120 µm and an inner limit of 70 µm for the size parameter. Additionally, the vibration range is restricted to 30–60 Hz. Furthermore, within this region, the maximum recovery achievable is 77.99%. The grade of the product is limited to a maximum value of 40.15% Cr2O3, and the feed rate should be at least 103 g/min. These constraints ensure that the response variables remain within their desired ranges and provide guidance for optimizing the process parameters.

Desirability to Define the Optimum Operating Condition for Optimum Responses

The desirable optimum condition leading to the optimum responses at the rougher stage is presented in the desirability diagram in Fig. 16.

Fig. 16
figure 16

Desirable optimum conditions for the optimum grade, Cr/Fe ratio, recovery, and separation efficiency of the shaking table

Full size image

The response optimal prediction presented in Table 7 and Fig. 16 showed that the optimal working conditions outlined the operating conditions of a tilt angle of 5.88°, feed rate of 175 g/min, vibration frequency of 44.55 Hz, water flow rate of 366.16 L/H, and size fraction of − 106 + 53 µm led to optimal recovery of 71.59% chromite with a grade of 36.97% Cr2O3, a Cr/Fe ratio of 1.52, and separation efficiency of 30%. It was important to note that these working conditions fell within the feasible range where all responses met the desired criteria according to the designed space.

Table 7 Response prediction
Full size table

Optimization and Verification Using RSM

Results displayed in Table 8 revealed that the outcomes obtained from experimental measurements agreed with the values predicted from the RSM models, since the calculated errors between the actual and predicted values are in absolute value lower than 9% [24, 25]. These findings demonstrate that CCD is a useful and reliable method for optimizing the beneficiation of chromite from the South African Middle Group chromite seams plant tailings with the desired performance.

Table 8 Experimental and model results for the validation of RSM models
Full size table

Furthermore, the standard deviation was also determined to see how far the experimental results are from the predicted results using RSM, and the outcomes are presented in Table 8 and Fig. 17. The results conform to a very slight deviation. Therefore, the grade was 34.65 ± 1.62 (%), the recovery was 74,648 ± 2.76 (%), the Cr/Fe ratio was 1,216 ± 0.12 and the SE was 31.15 ± 1.96 (%), respectively. These results also verified the conformity between the RSM predictions and the experimental data [24, 26].

Fig. 17
figure 17

Experimental and model results for the validation of RSM models

Full size image

Conclusion

The detailed characterization and gravity concentration studies carried out on chromite plant tailings from South African Middle Group seams show that chromite can be recovered from the tailings. Response Surface Methodology with a central composite design was successfully employed in studying the effects of various operating parameters and optimizing of chromite recovery from plant tailings using a shaking table. The optimum chromite recovery, grade, Cr/Fe ratio, and separation efficiency of 71.59%, 36.97%, 1.52, and 30%, respectively, were achieved. They were obtained under optimum operating conditions of a tilt angle of approximately 5.88°, a feed rate of 175 g/min, a vibration frequency of 44.55 Hz, a water flow rate of 366.16 L/H, and a size fraction of − 106 + 53 µm. The response variables recovery, grade, Cr/Fe ratio and SE are affected more by the effects of deck tilt angle and particle size for recovery and separation efficiency, deck tilt angle, particle size and vibration for grade and particle size for Cr/Fe ratio. The grade and Cr/Fe ratio can be improved by further processing the concentrate using a magnetic separation process.