Introduction

Gallium is a rare and valuable metal which has found significant applications in the semiconductor industry. It is classified as a strategic metal due to its relative scarcity and increasing use. Additionally, it has no minerals of its own so it must be recovered as a byproduct from other metallurgical processes, mostly associated with ores of zinc and aluminum [1]. These previous facts, together with the increasing demand of this metal, have led to a strong interest in the recovery of gallium from wastes. Among them, it is important to mention that gallium and its compounds have been found in wastewater discharged from semiconductor plants and may be a threat for humans [2]. However, due to the rapid growth in use of gallium, knowledge of its toxicity and human exposure has been overlooked due to its use, and there is no standard limit for gallium exposure in humans. Nevertheless, gallium is shown to accumulate in inflammatory tissue and at concentrations higher than 50 µg/mL induces cytotoxic effects and immune cells’ apoptosis [3, 4]. Therefore, the removal of gallium from aqueous solutions has become an important objective.

The recovery of gallium can be performed by different processes, but most of the studies are related to solvent extraction [5,6,7]. This method has an important disadvantage because of the environmental contamination associated with the use of chemical solvents. An alternative to this technique is adsorption. Adsorption/ion exchange is considered a good option due to its metal removal efficiency from aqueous effluents. However, the benefits of this technique are offset against the rising cost of adsorbents [8, 9]. Therefore, the necessity of a widely affordable adsorbent has motivated researchers to focus on naturally available adsorbents like zeolites.

Clinoptilolite, the most common natural zeolite, is an aluminosilicate with the following general chemical formula: (Na,K,Ca)4Al6Si30O72·24H2O. It has a silicon-to-aluminum ratio between 4.2 and 5.2 and a high thermal stability (600–800 °C). It also has a net negative charge, due to the replacement of Si4+ by Al3+, which has to be balanced by cations like Na+, K+, Ca2+, and Mg2+, and its crystal morphology shows a structure formed by open channels of 8- to 10-membered rings [10].

Two main mechanisms are attributed to heavy metal removal by clinoptilolite: ion exchange due to extra-framework cations which are movable and easily exchanged with cation solutions, and adsorption on active sites as surface crystal faces, surface imperfections, broken bonds as well as hydroxyl groups [11]. These characteristics make the clinoptilolite particularly suitable for adsorption of metals from wastewater. Many researchers have previously used this material to treat aqueous systems polluted with different metals in batch mode, such as Zn2+, Cu2+, Pb2+, or Cd2+, among others [12,13,14,15,16]. However, the utilization of clinoptilolite in fixed bed has not been widely used, only to remove metals like Mn2+, Cr3+, Cd2+, and Zn2+ [17, 18] and, more specifically, the use of clinoptilolite to remove gallium has not been extensively studied. In fact, the number of contributions regarding gallium adsorption is much lower than for other metals. Suryavanshi and Shukla employed oxidized coir to adsorb Ga3+ [19]. Employing this material, the percentage of removal at pH 3 was 71%. Roosen et al. used a chitosan–silica matrix impregnated with 8-hydroxyquinoline and 8-hydroxyquinaldine, as adsorbent for the selective recovery of Ga3+ from a synthetic Bayer liquor solution, reaching equilibria in 8 h with an adsorption capacity of 26.49 mg/g [20]. Zhang et al. proposed carboxyl-functionalized materials based on natural corn stalk to be used to remove gallium, with a maximum gallium adsorption capacity of approximately 140 mg/g [21]. Vollprecht et al. employed zero-valent iron to remove critical metals, including gallium and indium, reaching a removal percentage of 90% [22]

The aim of this paper was to study the batch and continuous removal of gallium from aqueous solutions by adsorption onto a low-cost zeolite. Clinoptilolite was selected as adsorbent rather than other zeolites, thanks to its high availability and consequently reduced cost, which is a crucial aspect for water treatment, as well as its relatively high Si/Al ratio (higher than 4), giving it greater chemical stability for acid treatment [23]. With this zeolite, initially the effect of the main parameters was analyzed in a batch process (adsorbent dosage, temperature, adsorbent particle size, competition between gallium and other cations); secondly, to approach to the operation way at industrial scale, sorption experiments in a fixed-bed column were performed, in which the effect of particle size, mass of clinoptilolite, and solution flow rate on breakthrough curve were investigated.

Materials and Methods

Zeolite Source, Conditioning, and Characterization

The zeolite employed in this study was supplied by Zeocat Soluciones Ecológicas S.L.U (Barcelona, Spain). It consists of 82–86% clinoptilolite, the remaining constituents mainly being the feldspars, quartz, illite, and cristobalite. Regarding the chemical composition of zeolite sample, the results provided by the supplier are as follows (wt.%): SiO2: 68.15; Al2O3: 12.30; K2O: 2.80; CaO: 3.95; Na2O: 0.75, MgO: 0.90; Fe2O3: 1.30; TiO2: 0.20.

Before being used as adsorbent, clinoptilolite (CPL) was washed with deionized water to remove its turbidity, dried at 373 K for 24 h, and further calcined at 623 K for 3.5 h. The calcined zeolite was sieved to obtain different particle size fractions: 0.1, 0.9, and 1.8 mm for batch experiments and 1.1, 1.4, and 1.8 mm for continuous experiments. Finally, each CLP fraction was further treated with HCl (H-CPL) to obtain the protonated form. The protonation was carried out by disposing the zeolite (1 g) on a filter and adding the acid (50 mL of HCl 2 M) step by step over the zeolite. This technique has been successfully used in the research group by Gómez et al. to exchange sodium by potassium in FAU zeolite [24]. Additionally, although the contact time between zeolite and HCl is not too long, just sufficient enough to get the clinoptilolite protonated, the acid can be reused to treat more zeolite, thus reducing the cost. Afterward, clinoptilolite was washed with deionized water until no Cl− was detected in the washing water. Finally, the samples were dried at 373 K for 24 h. This treatment improves the removal of Ga3+ ions and assures an acidic medium that avoids gallium precipitation (it precipitates as hydroxide if the pH value is above 3.6 [25]).

To characterize the modified clinoptilolite, several techniques were employed. The crystal structure was examined by X-ray-diffraction (XRD) using a PANalytical X’Pert MPD equipment with CuKα radiation in the range of 5°–70° with a step size of 0.1°. The chemical composition was determined by X-ray-fluorescence (XRF) using an Aχios PANalytical. The textural properties were measured by means of nitrogen adsorption–desorption isotherms at 77 K, using a Micromeritics ASAP-2020 adsorption apparatus. The specific surface area (SBET) was determined employing the standard Brunauer–Emmet–Teller (BET) method. Finally, the clinoptilolite and the Ga(NO3)3·xH2O surface charge were analyzed by zeta potential measurements, employing a MALVERN Zetasizer Nano Z-apparatus.

Adsorption Experiments

Batch Experiments

The batch sorption studies were carried out in flasks filled with known concentration of gallium ion (prepared by dissolving Ga(NO3)3·xH2O in deionized water) and the proper adsorbent dosage. Typically, 10 g/L of adsorbent dosage and 40 mg/L of gallium ions were used for all the experiments, except for adsorbent dosage study, in which this value was increased from 2 to 14 g/L, and temperature study where the gallium concentration employed was increased from 10 to 200 mg/L in order to obtain the isotherm. The flasks were agitated in a multi-position magnetic stirrer (P. Selecta Multimatic-9PS) at a constant rate (approximately 250 r.p.m) and temperature, and it was controlled using a thermostat water bath (P. SelectaTectro 200) until equilibrium was attained. The stirring rate was fast enough to assure an effective mass transfer. This point was confirmed in a previous work [26]. The pH was kept free (the one provided by the gallium solution with H-clinoptilolite) ensuring that it was below 3.6 to avoid the precipitation of metal ions. Typically, the pH for the experiments was 2.8 initially and 2.5 at the end. The samples were initially taken every 15 min up to the first 90 min, after which they were taken every 60 min. When the equilibrium was close to be attained, samples were taken day by day until the concentration of samples in consecutive days were same or very similar. The total volume extracted was less than 15% of the total sample volume. After being taken, the samples were passed through a 0.2-µm filter to separate the sorbent. The concentration of the metal ion remaining in the solution was determined by atomic absorption spectroscopy (Shimadzu AA-7000). The amount of gallium ions removed by clinoptilolite was calculated using Eqs. (1) and (2):

$$ q \left( {{{{\text{mg}}} \mathord{\left/ {\vphantom {{{\text{mg}}} {\text{g}}}} \right. \kern-\nulldelimiterspace} {\text{g}}}} \right) = \frac{{\left( {C_{0} - C_{{\text{t}}} } \right) \cdot V}}{m} $$
(1)
$$ {\text{Removal}}\;\left( \% \right) = \frac{{\left( {C_{0} - C_{{\text{t}}} } \right)}}{{C_{0} }}, $$
(2)

where q is the amount of Ga3+ sorbed per gram (mg/g); C0 is the initial gallium concentration (mg/L); Ct is the gallium concentration after time t (mg/L); V is the solution volume (L); and m is the mass of the adsorbent (g).

The batch procedure was used to determine the effect of the operation variables such as adsorbent dosage (ranging from 2 to 14 g/L), salt addition (KCl, NaCl, and CaCl2 were added to aqueous solutions) and zeolite particle size (ranging from 0.1 to 1.8 mm) in the adsorption kinetics, and temperature (ranging from 303 to 333 K), to evaluate its influence in the adsorption equilibrium and the thermodynamic process. These values will be very useful for the subsequent fixed-bed experiments. The percentage of associated error was expressed as the ratio between the 95% confidence interval and the average value of the repeated sample measurements (5–6 times). This error was estimated in 5%.

Fixed-Bed Experiments

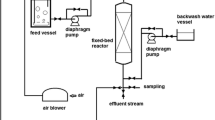
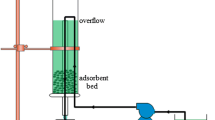
Fixed-bed experiments were carried out in a 1.8-cm internal diameter and 30-cm total length glass column filled with CLP. Packed clinoptilolite bed (1.4 mm size fraction) had a porosity of 0.54 and bulk density of 1.06 g/mL, values determined by means of Hg porosimeter. To carry out each experiment, a 40 mg/L gallium solution was fed in the column at a constant volumetric flow rate, employing a peristaltic pump in an up-flow mode to assure complete wetting of the zeolite particles and a good liquid distribution [27]. Liquid samples were withdrawn at the exit of the bed at specific time intervals, depending on the flow rate and bed length. The sample treatment was analogous to the one described for the discontinuous experiments and analyzed by AAS. By plotting the outlet metal concentration vs. time, the breakthrough curves can be obtained. Fixed-bed experiments were conducted to determine the influence of different variables such as volumetric flow rate, from 7 to 15 BV/h (9.0–17.4 mL/min) (where BV is a volume of liquid equal to the volume of empty bed), zeolite particle size, from 1.1 to 1.8 mm and bed length (for zeolite mas between 21 and 63 g).

In the present study, the breakpoint is set at 5% of the initial concentration and the total volume of the treated solution until this point (VBR) is used as a measure of the removal efficiency of the operation, and can be calculated using Eq. (3):

$$ V_{{{\text{BR}}}} = \frac{{{\text{Volume of the solution treated until breakpoint}}}}{{{\text{Volume of the adsorbent bed}}}} $$
(3)

Additionally, adsorption capacities at breakpoint (qR) and at C/C0 = 0.5 (q0.5) are calculated using Eqs. (4) and (5):

$$ q_{{\text{R}}} = \frac{{C_{0} \cdot Q \cdot \mathop \smallint \nolimits_{0}^{{t_{{\text{R}}} }} \left( {1 - \frac{C}{{C_{0} }}} \right) \cdot dt - V_{{\text{M}}} \cdot C_{0} }}{m} $$
(4)
$$ q_{0.5} = \frac{{C_{0} \cdot Q \cdot \mathop \smallint \nolimits_{0}^{{t_{0.5} }} \left( {1 - \frac{C}{{C_{0} }}} \right) \cdot dt - V_{{\text{M}}} \cdot C_{0} }}{m}, $$
(5)

where C0 is the concentration (mg/L); Q is the flow rate (L/min); tR breakpoint time (min); t0.5 time to reach C/C0 = 0.5 (min); m is the weight of adsorbent in the column (g); and VM is the dead volume (L), calculated using an inert material with characteristics similar to clinoptilolite.

Lastly, the mass transfer zone (MTZ) is a function of hydraulic loading rate and defined as the length of the fixed bed (Z) where adsorption of solute takes places. It can be calculated using Eq. (6):

$$ {\text{MTZ}} = Z \cdot \left( {1 - \frac{{q_{{\text{R}}} }}{{q_{0.5} }} } \right). $$
(6)

Results and Discussion

Characterization

Figure 1 displays the XRD spectra of raw and acid-treated clinoptilolite. The XRD characterization analysis shows a typical mineralogical diffraction pattern of a clinoptilolite [28] with impurities as reported by supplier, indicating that the acid treatment did not affect the structure. In Fig. 1, the peaks pointed out with an asterisk in the raw clinoptilolite curve refer to the characteristic peaks of zeolite-type clinoptilolite. These peaks are also observed in the clinoptilolite treated with acid. Regarding the peak intensity of both zeolites, it is very similar, so it can be assumed that the acid treatment has not produced a dealumination. To verify this affirmation, the lattice parameters were calculated from XRD data, considering that clinoptilolite has monoclinic morphology. For this kind of morphology, the lattice parameters are different from each other (a ≠ b ≠ c) while the angles α (angle between b and c) and γ (angle between a and b) are 90° and β (angle between a and c) is different to 90°. In Eq (7) is shown the interplanar spacing as a function of the lattice parameters, for the monoclinic crystal system [29].

$$ \frac{1}{{d_{{{\text{hkl}}}}^{2} }} = \frac{{h^{2} }}{{a^{2} \cdot {\text{sin}}^{2} \beta }} + \frac{{k^{2} }}{{b^{2} }} + \frac{{l^{2} }}{{c^{2} \cdot {\text{sin}}^{2} \beta }} + \frac{{2 \cdot h \cdot l \cdot {\text{cos}}\beta }}{{a \cdot c \cdot {\text{sin}}^{2} \beta }}, $$
(7)

where dhkl is the interplanar spacing (Å); h,k,l are the Miller indices; a,b,c the lattice parameters (Å); and β is the angle between a and c (°). The planes employed in the calculation, with their corresponding distances, are shown in Table 1.

Fig. 1
figure 1

XRD pattern of CPL and H-CPL

Full size image
Table 1 Planes and their corresponding distances to estimate the lattice parameters
Full size table

The lattice parameters obtained were a = 17.1 Å; b = 17.8 Å; c = 7.2 Å; and β = 113.6° for CPL and a = 17.2 Å; b = 17.8 Å; c = 7.2 Å; and β = 113.6° for H-CPL. As can be observed, the values are practically identical for both zeolites confirming that the acid treatment has not modified the zeolite structure. The theoretical values for a clinoptilolite zeolite are a = 17.6 Å; b = 17.9 Å; c = 7.4 Å; and β = 116.5° [28], very close to the values calculated from the XRD patterns of the studied solids.

In relation to the XRF analysis, the initial clinoptilolite showed an estimated Si/Al ratio of 5.3 without any dominant cation but with large amounts of K+ and Ca2+. After the acid treatment, the Si/Al ratio increased until 5.7 and the protonation percentage was increased from 5 to 17%. The protonation percentage is calculated as the difference between 1 and the cations to aluminum ratio because, theoretically, the cations present in the zeolite balance the negative charge of the cations, so it can be assumed that the difference between both values is due to the hydronium ions exchange. So, the modification of the zeolite was stronger enough to increase the quantity of protons but without causing dealumination, as predicted by the XRD results.

Figure 2 shows the zeta potential measurements corresponding to unmodified and modified zeolite.

Fig. 2
figure 2

Zeta potential results for H-CPL and CPL

Full size image

As it can be observed in Fig. 2, CPL and H-CPL do not present isoelectric point in the studied pH range. This can be due to the large number of Al3+ substitutions, and thus the high positive charge deficiency, as well as to the impurities. As a result, the negatively charged surface of clinoptilolite, even at very acidic pH values, is an advantage for inorganic cations electrostatic interactions induction (gallium has small radius so a greater positive charge and electronegative upper than 1.8) or adsorption [30]. Regarding the acid treatment, H-CPL shows more negative values of Z potential than CPL specially at acid pHs. Wang et al. [31] studied this effect and determined that if the acid treatment was not too aggressive, a break in the Si–O bond was produced, giving the zeolite a more electronegative nature.

Finally, Fig. 3 shows the nitrogen sorption isotherms of CPL and H-CPL, while Table 2 shows the values of the main parameters obtained from the analysis of the isotherms: specific surface area (SBET), external surface area (SEXT), and micropore area (SMICRO), calculated using t-plot method.

Fig. 3
figure 3

Nitrogen sorption isotherms at 77 K on CPL and H-CPL

Full size image
Table 2 Surface values of CPL and H-CPL
Full size table

The isotherms of CPL and H-CPL are IUPAC type IV (a) with H3 hysteresis loop, which is in agreement with the literature [32]. As it can be observed in Table 2, the SBET values are relatively low and close to SEXT especially in the case of CPL. When clinoptilolite is treated with HCl, the specific surface area is increased. This is a consequence of the fact that cations, such as sodium, calcium, and potassium, are located along the channels of clinoptilolite, hindering the motion/diffusion of N2 molecules into them. However, with the acid treatment, the zeolite suffered loss of cations (the protonation percentage was increased from 5 to 17%) improving the mobility of N2 molecules into the channels. This effect can be also observed in the micropore area increase. This phenomenon will be studied in more detail analyzing the pore size distribution calculated by Barrett–Joyner–Halenda (BJH) method (Fig. 4).

Fig. 4
figure 4

Pore size distribution of CPL and H-CPL a adsorption branch b desorption branch

Full size image

To determine the pore size distribution, adsorption, and desorption, branches of BJH method will be used. From the adsorption branches, it can be observed that both clinoptilolites show pores in the range of mesoporosity, according to IUPAC classification. The micropore contribution is practically zero for CPL and slightly higher for H-CPL due to acid treatment. Natural zeolites are characterized by two types of porosity: primary or microporosity, which is given by the structure and properties of natural zeolite, and secondary or mesoporosity, which is present due to the impurities that contain the material [33]. However, the crystalline structure of clinoptilolite does not promote the formation of micropores so its contribution is low [33]. Regarding desorption branch, there is a wide distribution with a relative maximum pore diameter around (2–4) nm. This maximum is related to fluid to crystalline phase transition of nitrogen [34, 35]. This phenomenon usually occurs at a relative pressure of 0.4.

Batch Sorption Results

H-Clinoptilolite Dosage Influence

The effect of H-clinoptilolite dosage on the adsorption of Ga3+ was studied using different adsorbent doses, in the range from 2 to 14 g/L, for an initial gallium concentration of 40 mg/L. Figure 5 shows the adsorption equilibrium capacity and the Ga3+ removal (%) for each dosage.

Fig. 5
figure 5

Effect of H-clinoptilolite dosage on adsorption of Ga3+ at free pH (initial pH 2.8), 298 K, 0.9 mm, 250 r.p.m, and 40 mg/L of initial concentration

Full size image

As it can be expected, Fig. 5, the adsorption process depends on H-CPL dosage. The removal percentage increases with the adsorbent dosage up to a value of 10 g/L where a maximum value of removal percentage (92%) is reached. From this point, the removal values decreased due to a partial aggregation of clinoptilolite, as observed by other authors. Javanbakht et al. [36] studied the removal of Pb2+ using chitosan/clinoptilolite/magnetite nanocomposite and detected that when a high dosage of material was used, the removal of Pb2+ was lower due to the aggregation of the adsorbent. The opposite situation occurs with the adsorption capacity (q), because when the H-CPL dosage is increased there is an increase in the number of active adsorption sites, but the concentration of ions remains the same; therefore, the adsorbed quantity per weight unit decreases. For this reason, the optimum dosage of H-CPL selected to carry out the successive studies is 10 g/L, with which an adsorption capacity of 3.1 mg/g and a removal percentage of 92% are reached.

Particle Size Influence

The effect of the sorbent particle size on the adsorption capacity was analyzed using three different sieved fractions: 0.1, 0.9, and 1.8 mm. The results obtained are shown in Fig. 6.

Fig. 6
figure 6

Effect of particle size on adsorption of Ga3+ at 298 K, 10 g/L H-CPL dosage, 250 r.p.m., free pH (initial pH 2.8), and 40 mg/L of initial concentration

Full size image

As it can be observed in Fig. 6, the particle size has a significant influence in adsorption capacity. The removal percentages reached were 96, 92, and 87% for 0.1, 0.9, and 1.8 mm particle sizes, respectively. An exchange or and adsorption site is characterized by its availability and its accessibility with respect to the incoming ion. In 0.1 mm particles, the availability of adsorption sites is almost the same to the larger particles because the zeolite has practically the same active sites concentration, while accessibility is easier since the diffusion paths become shorter. Availability is related to equilibrium while accessibility is related to the kinetic behavior of the adsorption process. So, for a similar specific surface area, the equilibrium adsorption capacity should be independent of particle size. This phenomenon is observed for the smallest particles, while for the biggest ones, the adsorption capacity reached is 9% lower. Table 3 shows the results of adsorption capacity, specific and external surface area, percentage of protonation, and Si/Al ratio for each particle size.

Table 3 Values of adsorption capacity, specific and external surface area, percentage of protonation, and Si/Al ratio for each particle size
Full size table

As it can be observed in Table 3, the specific surface area as well as the difference between this value and the external specific surface area value increase when the particle size decreases. In the case of the largest particle size, the protonation percentage is the lowest which means that the voluminous cations (such as Na, Ca, K) are blocking the channels making both, total and external surface area, very similar. So, although the availability of the adsorption sites should be like the one of the smaller particle sizes, accessibility is not the same. Consequently, the measured adsorption capacity is lower. On the other hand, the smallest particle size presents the highest protonation percentage and the highest difference between total and external surface area; this results in the highest adsorption capacity. With the aim of studying the influence of particle size on adsorption kinetics, the experimental data were adjusted to different kinetic (pseudo-first order, pseudo-second order, Elovich) and intraparticular diffusion (Webber–Morris) models. These equations are summarized in Table 4:

Table 4 Equations of several kinetic and intraparticular diffusion models
Full size table

By fitting the experimental data to the corresponding equation (Fig. 7), the values of kinetic parameters were obtained and are listed in Table 5.

Fig. 7
figure 7

Experimental data fitted at different kinetic and intraparticle diffusion models

Full size image
Table 5 Parameters estimated from experimental data fitted at different models
Full size table

As it can be appreciated in Table 5, the pseudo-second-order equation appears to be the best-fitting model among the three kinetic models—pseudo-first order, pseudo-second order, and Elovich (the correlation coefficient is almost 1 for the pseudo-second-order equation). The agreement of the experimental data with the pseudo-second-order kinetic model indicates that the adsorption of the gallium onto H-CPL is controlled by chemisorption, involving valence forces through electron sharing or electron exchange between adsorbate and adsorbent [40, 41]. For pseudo-second-order equation, qe was treated as an adjustable parameter with the aim to compare the values obtained with the fitting with the experimental ones to verify the goodness of the model. As can be observed in Table 5, the pseudo-second-order model can determine with accurate precision the adsorption capacity at the equilibrium (3.1 mg/g for 0.1 mm, 2.9 mg/g for 0.9 mm, and 2.6 mg/g for 1.8 mm) being these values close to those obtained experimentally. In addition, this model allows the calculation of the initial adsorption rate and t1/2 which shows that the kinetics takes place faster for the smaller particle size, as expected (25 min for the smallest particle size and 101 min for the largest particle size), and as can also be observed with the rate constant.

The Webber and Morris model is employed to determine the main rate-limiting step in the overall adsorption mechanism. As it can be observed, the plots q vs. t0.5 presented in Fig. 7 are multilinear. The time interval of each region is shown in Table 5 where tI is the time interval for the first region, tII is the time interval for the second region, and tIII is the time interval for the third interval. The first region describes the external resistance to mass transfer, while the second region indicates a predominance of the intraparticle diffusion. For the smallest particle size, there is a third step which describes the decrease of Ga3+ concentration in the aqueous phase, as well as the decrease of the active sites available for adsorption. For this reason, it is the slowest step (Table 5). Based on the results presented in Fig. 7 and Table 5, it can be concluded that the adsorption process is controlled by external diffusion, intraparticle diffusion, and chemisorption in the adsorption of Ga3+ onto the H-CPL. All the steps significatively contribute to the global process rate as they have similar slow rates. Observing the kII values, the highest value of this parameter corresponds to the smallest particle size, because it has shorter and less tortuous paths so intraparticle diffusion is not so impeded. For successive studies, the particle size selected was 0.9 mm due to its easier handling and similar adsorption capability, as compared with 0.1 mm particle size.

Competitive Cations Addition Influence

To investigate the competitive adsorption of Ga3+ and other cations, a known concentration of different salts was added to the media. The adsorption media in these experiments were constituted by a concentration of 25 mM of added salts (NaCl, CaCl2, and KCl) combined with 40 mg/L (0.5 mM) of Ga3+. The concentration of the added salts was studied in a previous work [42]. The results obtained are shown in Fig. 8.

Fig. 8
figure 8

Effect of competitive cations on adsorption of Ga3+ at 298 K, 10 g/L H-CPL dosage, 250 r.p.m., free pH (initial pH: 2.8 for only Ga (III) and 3.0 for the rest), 0.9 mm of particle size, and 40 mg/L of initial concentration

Full size image

As it can be observed in Fig. 8, when salt is added to the solution, a competition between gallium ions and other metal ions is produced, involving a decrease in the Ga adsorption capacity of the H-CPL. This decrease is 5% when CaCl2 is added, 13% for NaCl, and 20% for KCl. Therefore, the gallium adsorption capacity depends on the cations present in the solution. Gómez et al. [43] studied the ionic strength influence concluding that the adsorption capacity is less affected by the ionic strength at high equilibrium concentrations. The higher the metal ion adsorption onto clinoptilolite is, the lower the dehydration energy, the lower the hydration radius, and the higher the electronegativity. Table 6 shows the features for each metal ion.

Table 6 Characteristics for each metal
Full size table

According to Fig. 8, K+ is the ion which most affects the adsorption of gallium due to either its lower dehydration energy and hydration radius or the higher affinity of clinoptilolite for this metal [45, 46]. A similar situation occurs with sodium due to similar reasons. However, Ca2+ follows a different trend because despite its lower hydration radius and dehydration energy, under its presence, the gallium adsorption capacity is maintained. This can be explained because H-CPL has a high affinity for gallium due to its high electronegativity, which shields Ca2+ ions as it is a large cation and cannot penetrate the channels. This is not the case of Na+ and K+ because of their lower hydrated radius. However, it is important to note that even though there is a decrease in gallium adsorption capacity, it is not very significant when considering each ion concentration.

Temperature Influence

The influence of temperature on gallium adsorption on H-CPL was studied varying the temperature from 303 to 333 K. Up to this point, the results previously shown have been related to kinetics, but the effect of temperature has been studied at equilibrium conditions by means of isotherms obtained for gallium initial concentrations ranging from 10 to 200 mg/L. Figure 9 shows the adsorption isotherms at each temperature.

Fig. 9
figure 9

Effect of the temperature of Ga3+. 250 r.p.m, free pH (initial values of pH were ranged from 2.8 to 1.4 for the lowest and highest concentration, respectively), 10 g/L of dosage, 0.9 mm particle size

Full size image

The previous graph indicates that the gallium adsorption is larger when the temperature increases. The saturation adsorption capacity rises from 5.0 mg/g at 303 K to 17.1 mg/g for 333 K. So, in the first instance, it can be considered that the adsorption is an endothermic process which implies that not only physisorption but also chemisorption is taking place. Nevertheless, the endothermicity of the process will be studied with more detail following the adjustment of isotherms. This increase with the temperature can be produced for different reasons: (i) change in the zeolite and its adsorption sites and activity; (ii) like adsorption of gallium on H-CPL occurs with a chemisorption, a rise in the temperature implies an increase in the rate of chemical reaction. Regarding the shape of the isotherms, according to Giles classification they can be classified as L2 for 303 and 313 K temperatures, H2 for 323 K, and H1 for 333 K. In all cases, an increase of gallium concentration does not imply saturation of the adsorbent [47]. H isotherm is a particular case of L isotherm, where the initial slope is very sharp because the compound exhibits a high affinity for the solid [48]. The change in the shape of the isotherm is produced because high temperatures improve the mobility of metal ions encouraging the adsorption process.

To describe the equilibrium sorption of Ga3+ ions onto the H-CPL, several theoretical isotherm models have been selected taking in consideration the isotherm types [49]. The employed isotherm model equations are summarized in Table 7. The experimental data were fitted to the models (Fig. 10) by means of non-linear regression. The isotherms at 303, 313, and 323 K were adjusted at Langmuir and Sips models because they were classified as L2 while 333 K isotherm was fitted at Freundlich model for being classified as H1. The obtained isotherm parameters are listed in Table 8. The analysis of the fitting goodness was performed by considering the values of correlation coefficient (R2) and root mean squared error (RMSE).

Table 7 Equations of several theoretical isotherm models used to describe the equilibrium sorption of Ga3+ onto clinoptilolite at different temperatures
Full size table
Fig. 10
figure 10

Isotherm model fitted

Full size image
Table 8 Isotherm parameter values calculated by non-linear regression
Full size table

As it can be observed, the high R2 and the low RMSE values indicate that Sips and Freundlich are the best-fitting models for describing the Ga3+ adsorption onto clinoptilolite at different temperatures. The maximum theoretical sorption capacities resulted from the Sips model have a 19% deviation from the experimental values despite the high correlation obtained. In fact, the best estimation of maximum sorption capacities is the one obtained by Langmuir model. Regarding nS parameter, its value at 303, 313, and 323 K point outs for the system heterogeneity. On the other hand, the Freundlich equation can be successfully applied to the highest temperature experimental data, obtaining a 1/nF value of 0.4, which also indicates the system heterogeneity.

To understand the effect of temperature increasing on the Ga3+ adsorption onto clinoptilolite, three thermodynamic parameters were studied: Gibbs free energy (ΔG0), enthalpy change (ΔH0), and entropy change (ΔS0) which are calculated in Eqs. (8) and (9):

$$ \Delta G^{0} = - {\text{R}} \cdot T \cdot {\text{ln}}\,K $$
(8)
$$ {\text{ln}} K = \frac{{\Delta S^{0} }}{{\text{R}}} - \frac{{\Delta H^{0} }}{{\text{R}}} \cdot \frac{1}{T}, $$
(9)

where T is the temperature (K), R is the universal gas constant (8.314·10−3 kJ/mol), and K is the equilibrium constant. This constant was evaluated using the Khan and Singh method (Eq. 10) [53]:

$$ K = \frac{{a_{{\text{s}}} }}{{a_{{\text{e}}} }} = \frac{{\upsilon_{{\text{s}}} \cdot q_{{\text{s}}} }}{{\upsilon_{{\text{e}}} \cdot C_{{\text{e}}} }}, $$
(10)

where as is the activity of the adsorbed gallium, ae is the activity of the adsorbed gallium at equilibrium, υs represents the activity of the adsorbed gallium, and υe corresponds to the activity coefficient of the gallium in the equilibrium solution.

Table 9 shows the summary of the obtained thermodynamic parameters. As it can be observed, the enthalpy value obtained is coherent because it is positive, so it is an endothermic process: an increment in temperature produces an increase in gallium removal. This agrees with the negative values of ΔG0 at higher temperatures, indicating that the adsorption of Ga3+ is spontaneous in the experimental temperature range. The positive value of ΔS0 indicates the randomness at the solid/solution interface which is associated with the affinity of the clinoptilolite for Ga3+ ions. Generally, the values of ΔH0 are (2.1 ~ 20.9) kJ/mol and (80 ~ 200) kJ/mol related to physical adsorption and chemical adsorption, respectively [54]. The value of ΔH0 in Table 9 is higher than 20.9 kJ/mol indicating that the adsorption of Ga3+ on H-CPL is chemical adsorption, with a great influence of physical adsorption, in well agreement with ΔG0.

Table 9 Thermodynamic parameters for adsorption of gallium on H-CPL
Full size table

Fixed-Bed Sorption Results

Bed Height Influence

The influence of bed height was studied increasing the mass of adsorbent from 21 g (corresponding to L/D of 5) to 63 g (L/D of 15). The results obtained are shown in Fig. 11, while Table 10 displays a summary of the calculated column performance parameters.

Fig. 11
figure 11

Effect of bed mass on breakthrough curves. Free pH (initial pH 2.8), 298 K, Flow rate 9.03 mL/min, and initial concentration 40 mg/L

Full size image
Table 10 Summary of fixed-bed columns parameters for Ga3+ ions adsorption on H-CPL
Full size table

As it can be observed, the breakthrough curves illustrated in Fig. 11 show a concave profile at initial times, linear profile in the center, and convex profile at long times, so, these breakthrough curves do not follow a step function produced in an ideal adsorption system. To estimate the deviation from ideality, MTZ parameter has been calculated from C/C0 = 0.05 to C/C0 = 0.5. These results are shown in Table 10 (the value for 63 g is not available as the curve does not reach the value of C/C0 0.5). So, as it can be observed, the breakthrough curves are far from ideal as no MTZ values are close to 0, indicating the presence of diffusion phenomena such as axial dispersion, external film resistance as well as intraparticle diffusion resistance. Nevertheless, the value of MTZ seems to improve when the amount of bed mass is increased, as it can be seen in MTZ/Z parameter. These phenomena were also observed by other authors [55]. Regarding tR (Table 10), this parameter is increased drastically when the bed mass is increased due to the higher number of binding sites as well as a major adsorbent–adsorbate contact time. Hence, greater adsorbent mass could treat larger amount of Ga3+ up to breakpoint. In fact, attending to adsorption capacity values shown in Table 10 (qR and q0.5), it can be appreciated that an increase in the bed mass improves the adsorption capacity; therefore the amount of gallium adsorbed increases to a greater extent than the increase of the bed mass. It is important to point out that if the bed mass continued being augmented, it would be possible that this adsorption capacity might decrease. Therefore, for the following experiments, a bed mass of 42 g will be employed.

Flow Rate Influence

The influence of flow rate on breakthrough curves was conducted at different values of the flow rate between 14 BV/h (9.0 mL/min) and 30 BV/h (17.4 mL/min). The results obtained are shown in Fig. 12:

Fig. 12
figure 12

Effect of flow rate on breakthrough curves. Free pH, (initial pH 2.8) 298 K, Bed mass 42 g, and initial concentration 40 mg/L

Full size image

As it can be observed in Fig. 12 and Table 10, the removal efficiency is favored by lower volumetric flow rates in the region of (14–30) BV/h. The volume of the treated solution until breakpoint is 22 BV, 16 BV, and 10 BV for 14 BV/h, 20 BV/h, and 30 BV/h, respectively. This is because the higher the flow is, the shorter the sorbent—Ga3+ contact time. When the flow rate is increased, more Ga3+ is supplied and this raises competition for the limited adsorption sites; as a result, the bed becomes saturated faster. Regarding the adsorption capacities values (Table 10), a similar trend can be observed than the one observed when varying the bed mass. The q0.5 is reduced approximately by 63% when the flow rate is increased from 14 BV/h to 30 BV/h. As far as MTZ is considered, the values of Table 10 show that higher flow rates imply higher MTZ values, so the process is more inefficient. This effect was observed by several authors in literature, who attributed it to the fact that the residence time of the pollutant in the column is not enough to reach equilibrium, as well as a weak distribution of the liquid inside the column which leads to a lower diffusivity of the solute among the particles of the adsorbent [56, 57]. All these result in an MTZ that is not fully established. For the following experiments, 14 BV/h will be selected because it is a more efficient process and allows treating more quantity of Ga3+ solution.

Particle Size Influence

The influence of particle size on breakthrough curves was examined varying the size from (1.00–1.19) to (1.68–2.00) mm, keeping a bed mass of 21 g. In this study, the mass was reduced to maintain the pressure drop produced by smallest particle size in reasonable values. The results are shown in Fig. 13:

Fig. 13
figure 13

Effect of particle size on breakthrough curves. Free pH (initial pH 2.8), 298 K, bed mass 21 g, and initial concentration 40 mg/L

Full size image

When the particle size lowers from (1.19–1.68) to (1.00–1.19) mm, tR and VBR are increased by a factor near to 2.4 (Table 10), while if the particle size decreases from (1.68–2.00) to (1.19–1.68) mm, tR and VBR are only increased by a factor near to 1.1. Similar conclusions are reached if qR and q0.5 values are observed (Table 10). So, there is a strong influence of particle size on breakthrough curves only when the particle size is reduced from (1.19–1.68) to (1.00–1.19) mm. This dependence leads to the conclusion that diffusion (either particle or film) is the rate-limiting step. This phenomenon was also observed by other authors. Inglezakis and Grigoropoulou [58] concluded that the exchange rate is proportional to D*/dp (where D* is the diffusion coefficient and dp particle diameter). In addition, particle size is independent of either the equilibrium state or the diffusion coefficient (Eq. 11) of a specific cation; so higher rates should be observed for smaller particles considering neglected structural problems or pore clogging. Consequently, when comparing rates for particles with dp1 and dp2 (dp1 < dp2), smaller particle size might result in higher kinetics only if Eq. (12) is satisfied:

$$ D_{{{\text{AB}}}} = \frac{{{\text{R}} \cdot T}}{{6 \cdot \pi \cdot \mu_{B} \cdot r_{A} }} $$
(11)
$$ \frac{{D*_{1} }}{{d_{{{\text{p}}1}}^{2} }} > \frac{{D*_{2} }}{{d_{{{\text{p}}2}}^{2} }} \Leftrightarrow \frac{{D*_{1} }}{{D*_{2} }}\cdot\left( {\frac{{d_{{{\text{p}}2}} }}{{d_{{{\text{p}}1}} }}} \right)^{2} > 1 $$
(12)

According to the experimental data, the particle diffusion is the controlling step so, the exchange rate is increased when moving from (1.68–2.00) to (1.00–1.19) mm. Consequently, the breakpoint time and volume treated up to breakpoint are increased (Table 10). However, small particle sizes result in high flow resistance of the column and should be avoided. Regarding MTZ values, Table 10 shows that, when the particle size (1.00–1.19) mm is employed, the MTZ values are lower, indicating a more efficient process due to a better contact between adsorbent and adsorbate as well as a decrease in intraparticle diffusion.

As it was previously done in batch mode when studying the particle size effect, the breakthrough curves have been fitted to different models, to analyze the differences between the particle sizes studied. The employed models are as follows:

  • - Adams–Bohart model: it assumes that the adsorption rate is proportional to both the residual capacity of the adsorbate and the concentration of the solute species, which is suitable for predicting the initial part of the breakthrough curve. The Adams–Bohart model is expressed as shown in Eq. (13) [59]:

    $$ \frac{C}{{C_{0} }} = \frac{{e^{{\left( {K_{{{\text{AB}}}} \cdot C_{0} \cdot t} \right)}} }}{{e^{{\left( {K_{{{\text{AB}}}} \cdot q_{0} \cdot Z/V_{{\text{L}}} } \right)}} - 1 + e^{{\left( {K_{{{\text{AB}}}} \cdot C_{0} \cdot t} \right)}} }}, $$
    (13)

    where KAB is the kinetic constant in the Adams–Bohart model (L/mg·min); VL is the linear velocity (m/min); q0 is the adsorption capacity predicted (mg/L); Z is bed height (m). Equation (13) could be reduced to Eq. (14) because the exponential term \(e^{{\left( {K_{{{\text{AB}}}} \cdot q_{0} \cdot Z/V_{{\text{L}}} } \right)}}\) is expected to be much larger than unity:

    $$ \frac{C}{{C_{0} }} = \frac{{e^{{\left( {K_{{{\text{AB}}}} \cdot C_{0} \cdot t} \right)}} }}{{e^{{\left( {K_{{{\text{AB}}}} \cdot q_{0} \cdot Z/V_{{\text{L}}} } \right)}} + e^{{\left( {K_{{{\text{AB}}}} \cdot C_{0} \cdot t} \right)}} }}. $$
    (14)

Equation (14) may be simplified and rewritten as

$$ \frac{C}{{C_{0} }} = \frac{1}{{1 + e^{{\left( {a - b \cdot t} \right)}} }}, $$
(15)

where a and b can be calculated with Eqs. (16) and (17):

$$ a = K_{{{\text{AB}}}} \cdot q_{0} \cdot Z/V_{{\text{L}}} $$
(16)
$$ b = K_{{{\text{AB}}}} \cdot C_{0}. $$
(17)

Chu [60] studied the analysis of breakthrough curves by simplistic models of fixed-bed adsorption and demonstrated that equation (15) could be used to describe small breakthrough curves (C/C0 < 0.5) with better overall fit.

Additionally, when Adams–Bohart model is applied to describe the initial part of the breakthrough curve (C/C0 < 0.15), it is reduce to Eq. (18):

$$ \frac{C}{{C_{0} }} = e^{{\left( {K_{{{\text{AB}}}} \cdot C_{0} \cdot t - K_{{{\text{AB}}}} \cdot q_{0} \cdot Z/V_{{\text{L}}} } \right)}} $$
(18)

  • - Yoon–Nelson model: this model was developed by Yoon–Nelson in 1984 and it is a relatively simple model to describe the adsorption and breakthrough curves of gases in activated charcoal [61]. It assumes that the decrease in the probability of each adsorbate to be adsorbed is proportional to the probability of its adsorption and breakthrough on the adsorbent (Eq. 19).

    $$ \frac{C}{{C_{0} }} = \frac{1}{{e^{{\left( {K_{{{\text{YN}}}} \cdot \left( {\tau - t} \right)} \right)}} + 1}}, $$
    (19)

where KYN is the kinetic constant in the Yoon–Nelson model (min−1); \(\tau \) is the time required for 50% adsorbate breakthrough time (min).

Figure 14 shows the experimental breakthrough curves along with the fittings to the previously mentioned models, while Table 11 displays the parameters obtained from adjustments.

Fig. 14
figure 14

Fitted breakthrough curves at Adams–Bohart and Yoon–Nelson models

Full size image
Table 11 Parameter values calculated by non-linear regression
Full size table

As can be observed in Fig. 14, Adams–Bohart simplified model fits to initial part of breakthrough curves for three particle sizes. This fact is confirmed by the high R2 (> 0.90) and the low RMSE values (Table 11). Attending to the kinetic constant values (kAB), predicted by this model, it can be appreciated that they decrease as the particle size increases, indicating that the overall adsorption process is faster when smaller particle sizes are employed, in agreement with previously discussed. In relation to q0 value, it rises when the particle size is smaller, as was also observed with the experimental parameters (Table 10). Comparing these results (experimental parameters) with the ones obtained by Eq. 14 (calculated), the calculated values of q0 are such greater because they are obtained considering a major part of breakthrough curve. However, the goodness of fit for this equation is lower (R2 < 0.90). Regarding Yoon–Nelson equation, this model is not capable of predicting the behavior of the adsorption system because it considers the diffusion phenomena negligible, and they are evident inside the column.

Conclusion

Gallium (III) ions adsorption using H-CPL was investigated in this study in batch and fixed-bed modes. It can be concluded that the acid treatment of clinoptilolite plays a fundamental role in the adsorption of Ga (III), because it allows working without changing the pH. The batch experiments allow concluding that the adsorption of gallium onto H-CPL is an endothermic and spontaneous process in the studied temperature range, and that protonated clinoptilolite presents a high affinity for gallium, as experiments of competitive adsorption reveal (the Ga adsorption capacity only drops by 20%, in the presence of other salts like NaCl or KCl, although the initial concentration of the competitive ions in the solution is 50 times higher than gallium concentration). The adjustment of experimental data to several kinetic models indicates that the pseudo-second-order model is the one which best describes the adsorption kinetics, suggesting that chemisorption is the rate-limiting step in the adsorption process, but with high influence of external and intraparticle diffusion. The variables to reach the maximum adsorption capacity for the removal Ga (III) onto clinoptilolite are 60 °C, 12 g/L of adsorbent dosage, 0.9 mm of particle size, and without other salts in the aqueous media, though if there were any, it would not reduce the adsorption capacity too much.

In relation to the fixed-bed column continuous experiments, the influence of several variables on the breakthrough curves as well as on several operational parameters was studied. The study indicates that a decrease of the flow rate and size particle resulted in an increase of the removal efficiency (higher values of tR, VBR, and q). However, because it is necessary to balance these variables with the fact of avoiding high pressure drops, the optimum values were found to be 7BV/h of flow rate, 42 g of bed mass, and (1.19–1.68) mm of particle size. Finally, the initial zone of the breakthrough curves was successfully modeled with the Adams–Bohart model simplified. This confirms the influence of particle size on adsorption kinetics, obtaining higher kinetic constants for smaller sizes.