Motivation

The key idea of any phase field approach is to replace sharp interfaces between several phases by a diffuse interface formulation, thus avoiding the need of embedding and tracking such spatial discontinuities, but also ensuring the differentiability of field variables at the interface. In the phase field description, the two-dimensional sharp interface is smeared out (spatially regularized) over a three-dimensional region whose spatial extension correlates with an internal length-scale. To this end, smooth order parameter fields are introduced as additional degrees of freedom into the continuum description, which interpolate phase related properties, cf. [1,2,3,4]. The conceptual differences of these approaches are illustrated in Fig. 1.

Fig. 1
figure 1

Sharp vs. diffuse interface formulations. Shown are schematic representations, each depicting a three-dimensional, dual-phase continuum body, with sub-scale sketches attached to a representative material point at the respective interface. Left: physical interface \(\Gamma \) with local oscillations; middle: idealized sharp interface \(\overline{\Gamma }\); right: diffuse interface \(\widetilde{\Gamma }\), described by the order parameter (phase) field \(\eta (\varvec{X})\). In each case, a single interface splitting the body into two parts was chosen for visualization simplicity. In general, a network of interfaces with complex topology will have to be considered

Full size image

An additional key point—often overlooked in this modeling procedure—, is the origin of the resulting interface energy, whose definition is crucial in terms of microstructural evolution mechanisms. To further elucidate this aspect, consider a general dual-phase material body \(\mathcal {B}\), whose thermodynamic state is entirely defined by its Helmholtz potential (free energy) \(\psi (\varvec{X}, \varvec{\varepsilon }(\varvec{X}), \theta (\varvec{X}))\). Here, \(\varvec{\varepsilon }\) denotes choices of common strain measures and \(\theta \) the current temperature state, evaluated at material points \(\varvec{X} \in \mathcal {B}\). In general, inelastic effects can easily be included through the concept of internal state variables, i.e., \(\psi (\varvec{X}, \varvec{\varepsilon }(\varvec{X}), \theta (\varvec{X}), \varvec{{\mathcal {I}}}(\varvec{X}))\), but will be omitted in this discussion for the sake of conciseness. In this work the local temperature \(\theta \) is—without loss of generality on the homogenization framework to be addressed—assumed to be constant and thus characterizes a material type parameter instead of an actual degree of freedom, i.e., \(\theta (\varvec{X}) = \theta \).

The prescribed transition from the sharp to the diffuse interface formulation may then be based on the averaged energetic response. To this end, and referring back to the schematics of Fig. 1, one may assign energy to an idealized sharp interface \(\overline{\psi }^{\,\Gamma }\) in order to equivalently represent the average energy \(\langle \psi \rangle _{\mathcal {B}} \) stored in the physical continuum body, in which the interface \(\Gamma \) is energy-free, but associated with local oscillations of the relevant field variables on the underlying scale, i.e.,

$$\langle \psi \rangle _{{\mathcal{B}}} = \langle \psi \rangle _{{{\mathcal{B}}\backslash \Gamma }} = \langle \overline{\psi }^{\;\!\mathrm{B}} \rangle _{{\overline{{\mathcal{B}}} \backslash \overline{\Gamma }}} + \overline{\psi }^{{\,\Gamma }} .$$
(1)

Here, \(\overline{\psi }^{\!\;\mathrm{B}}\) represents the energy in the bulk material. The interface energy is commonly assumed to scale with the corresponding interface area, i.e., \(\overline{\psi }^{\!\;\Gamma } \approx \overline{\psi }^{\!\;\Gamma }_{0}A(\overline{\Gamma })/V(\overline{\mathcal {B}})\). By further introducing the order parameter field \(\eta (\varvec{X})\), the energetic state at a material point \(\varvec{X} \in \widetilde{\mathcal {B}}\) in the phase field description is defined by

$$\begin{aligned}&\widetilde{\psi }(\varvec{\varepsilon }(\varvec{X}), \eta (\varvec{X}), \varvec{\nabla }\eta (\varvec{X})) := \widetilde{\psi }^{\!\;B}(\varvec{\varepsilon }(\varvec{X}), \eta (\varvec{X})) + \widetilde{\psi }^{\,\Gamma }(\eta (\varvec{X}), \varvec{\nabla }\eta (\varvec{X})) \ . \end{aligned}$$
(2)

This decomposition implies a volumetrically weighted average of the bulk and interface contributions \(\widetilde{\psi }^{\!\;\mathrm{B}}\) and an interface part \(\widetilde{\psi }^{\,\Gamma }\)

$$\begin{aligned} \langle \widetilde{\psi } \rangle _{\widetilde{\mathcal {B}}} \approx \frac{V(\widetilde{\mathcal {B}}/\widetilde{\Gamma })}{V(\widetilde{\mathcal {B}})}\, \langle \widetilde{\psi }^{\!\;\mathrm{B}} \rangle _{\widetilde{\mathcal {B}}/\widetilde{\Gamma }} + \frac{V(\widetilde{\Gamma })}{V(\widetilde{\mathcal {B}})}\,\langle \widetilde{\psi }^{\!\;\mathrm{B}} + \widetilde{\psi }^{\,\Gamma } \rangle _{\widetilde{\Gamma }} \,. \end{aligned}$$
(3)

Consequently, the set of points comprising the interface \(\widetilde{\Gamma }\) is captured by a volumetric measure within the diffuse configuration \(\widetilde{\mathcal {B}}\). This represents a key difference compared to the sharp interface approach, in which the interface \(\overline{\Gamma }\) can only be measured by an associated area. Since phase field modeling is performed on the diffuse configuration, the interface is henceforth referred to as a volumetrically measurable set in this work. Furthermore, the notation \(\widetilde{\mathcal {B}}\) will be used for diffuse bodies to strictly differentiate it from its sharp interface representation \(\overline{\mathcal {B}}\) and the original description of finely resolved, physical continuum bodies \(\mathcal {B}\).

The bulk energy itself is usually split up into a mechanical part and a temperature-dependent chemical contribution, i.e., \(\widetilde{\psi }^{\!\;\mathrm{B}}(\varvec{\varepsilon }, \theta , \eta ) = \widetilde{\psi }^{\!\;\mathrm {m}}(\varvec{\varepsilon }, \eta ) + \widetilde{\psi }^{\!\;\mathrm {ch}}(\theta ,\eta )\). Note further that only within the phase field approach does the bulk energy contribute to the (volumetric) average over the interface. The fact that another approximation is usually made in \(\langle \widetilde{\psi } \rangle _{\widetilde{\mathcal {B}}} \approx \langle \overline{\psi }^{\!\;\mathrm{B}} \rangle _{\overline{\mathcal {B}}\backslash \overline{\Gamma }} + \overline{\psi }^{\!\;\Gamma }\) is discussed in Remark 2 in “Fundamentals of Phase Field Modeling” section. It should also be pointed out that this whole line of argumentation is in some sense opposite to that of \(\Gamma \)-convergence, see [5, 6], where the diffuse interface formulation is considered as the starting point and the sharp interface description results as the limit of vanishing interface thickness.

The central aspect addressed in this work is the question of how to appropriately define consistent volumetric averages of all relevant field quantities—and consequently effective material properties—within the transition regions between the single-phase parts of the continuum body, where \(\eta \in (0,1)\). For the general framework proposed here, this involves notions of phase interpolation functions and weighted averaging operators, in which established (variationally consistent) homogenization assumptions of phase field modeling are contained as special cases.

This paper is structured as follows: In “Fundamentals of Phase Field Modeling” section fundamental aspects of phase field modeling are briefly reviewed and inconsistencies between phase property interpolation function approaches and classical volume average-based homogenization schemes are pointed out. “Mathematical Considerations on Weighted Averaging Operators” section introduces the notion of weighted averaging operators, as the mathematical basis for the generalized homogenization framework for phase field modeling that represents the core contribution of this work. “Conventional Unweighted Homogenization of Elastic Properties and Equally Weighted Homogenization of Elastic Properties” sections then compare applications of unweighted and weighted homogenization schemes in the computation of effective elastic properties within the diffuse interface region. Finally, “Conclusion and Outlook” section summarizes the key conclusions and presents an outlook on possible future extensions of the proposed concept.

Fundamentals of Phase Field Modeling

The origin of phase field methods was set by the pioneering works of Cahn and Hilliard [7], who incorporated interface energy contributions to characterize the total free energy of a non-uniform system. Based on the concept of local energy minimization Allen and Cahn [8] then proposed a model predicting antiphase boundary motion in a diffuse approximation of the underlying sharp interface problem. Therein, the current material phase is mathematically described by a spatially distributed order parameter, whose local evolution is governed by a partial differential equation in space and time. Embedding of the established Cahn-Hilliard and Allen-Cahn models within a thermodynamically consistent framework is given, for instance, in Gurtin [9], Provatas and Elder [10], or Choudhury and Nestler [11], just to mention a few. Due to the underlying continuum structure, the phase field approach offers a wide range of applications within multiphysical modeling problems, e.g., general continuum mechanics (see Bartels and Mosler [2] or Levitas et al. [12,13,14,15]) and chemo-mechanics (see Svendsen et al. [16] or Bai et al. [17]).

The link between conventional homogenization methods (cf. Eringen [18], Nemat-Nasser and Hori [19], or Hütter [20]) and an effective property description within diffuse interface regions has, for instance, been summarized in Forest et al. [21], in terms of conventional Taylor–Voigt and Reuss–Sachs assumptions and extended toward Hashin-Shtrikman bounds for multi-phase systems by Liu [22]. Recent research developments accounting for consistent mechanical jump conditions (see Schneider et al. [4, 23]) and rank-one convexification (see Mosler et al. [24]) demonstrate the differences in resulting thermodynamic driving forces between various variationally consistent homogenization approaches, particularly in terms of microstructure prediction and numerical convergence rates (see Kiefer, Furlan, and Mosler [1]). This brief review of the literature underlines the fact that—from a conceptual standpoint—, there is no unique way of selecting suitable homogenization assumptions and the resulting phase field model may therefore vary in terms of the respective constitutive relations and, in general, even in the governing system of partial differential equations.

In order to make it more tangible, we base our discussion on the thermodynamically consistent, and thermo-mechanically coupled Allen-Cahn-type phase field framework summarized in Table 1, that will be used as reference throughout this work. The subsequently proposed methodology for homogenization in the context of phase field modeling is, however, general and therefore equally applicable to Cahn-Hilliard formulations.

Table 1 General, thermodynamically consistent phase field modeling framework based on Ginzburg–Landau type partial differential equations derived from a micro-force balance, as outlined by Gurtin [9]
Full size table

In the phase field framework outlined in Table 1, two constitutive functions play a key role, namely the energy storage function \(\widetilde{\psi } = {\hat{\psi }}(\varvec{\varepsilon }, \eta , \varvec{\nabla }\eta , \dot{\eta }, \varvec{\nabla }\dot{\eta })\) and the dissipation potential \(\phi = \hat{\phi }(\varvec{\varepsilon }, \eta , \varvec{\nabla }\eta , \dot{\eta }, \varvec{\nabla }\dot{\eta })\). A central question that then naturally arises is how to determine the effective free energy in the diffuse interface region, within which a phase mixture exists at every material point, see Fig. 1. If, for the sake of simplicity, we momentarily restrict our discussion to a dual-phase (dp) system, with linear elastic properties of the individual phases, the mechanical free energy contribution in the bulk material is commonly described as

$$\begin{aligned} \widetilde{\psi }^\mathrm {\;\!m}(\varvec{\varepsilon }, \eta )&= \frac{1}{2}\,[\varvec{\varepsilon } - \varvec{\varepsilon }^\mathrm {\;\!tr}(\eta )]:\varvec{C}(\eta ):[\varvec{\varepsilon } - \varvec{\varepsilon }^\mathrm {\;\!tr}(\eta )]\ , \end{aligned}$$
(4)

which can equivalently be expressed in terms of the free enthalpy (Gibbs potential)

$$\begin{aligned} \widetilde{g}^{\,\mathrm {m}}(\varvec{\sigma }, \eta )&= -\,\frac{1}{2}\,\varvec{\sigma }:\varvec{S}(\eta ):\varvec{\sigma } -\varvec{\sigma }:\varvec{\varepsilon }^{\;\!\mathrm {tr}}(\eta ) \ , \end{aligned}$$
(5)

in case (5) is consistently derived from (4) through a Legendre transformation—see also Remark 1 below. Here, \(\varvec{\varepsilon }^\mathrm {tr}(\eta )\) denotes the effective inelastic strain tensor related to transformation (Bain) strains of the different phases. Usually, this interpolation is performed via a nonlinear function \(\varphi (\eta )\) in the following way

$$\begin{aligned} \varvec{\varepsilon }^{\;\!\mathrm {tr}}(\eta ) = \varphi (\eta )\,\varvec{\varepsilon }^{\;\!\mathrm {tr}\!\;\textcircled{2}} + [1-\varphi (\eta )]\,\varvec{\varepsilon }^{\;\!\mathrm {tr}\!\;\textcircled{1}}\ . \end{aligned}$$
(6)

Analogously, \(\varvec{C}(\eta )\) and \(\varvec{S}(\eta )\) in (4) and (5) represent effective elastic properties interpolated between pure phase states in stiffness or compliance representation. The former

$$\begin{aligned} \varvec{C}_{\scriptscriptstyle \mathrm {C}}(\eta )&= \varphi (\eta )\,\varvec{C}^{\textcircled{2}} + [1-\varphi (\eta )]\,\varvec{C}^{\textcircled{1}} \nonumber \\&\ne \left[ \varphi (\eta )\,\varvec{S}^{\textcircled{2}} + [1-\varphi (\eta )]\,\varvec{S}^{\textcircled{1}} \right] ^{-1} =\varvec{S}^{\!\,-1}_{\scriptscriptstyle \mathrm {S}}(\eta ) \end{aligned}$$
(7)

is interpretable as the classical Taylor–Voigt upper energetic bound and the latter

$$\begin{aligned} \varvec{S}_{\scriptscriptstyle \mathrm {S}}(\eta )&= \varphi (\eta )\,\varvec{S}^{\textcircled{2}} + [1-\varphi (\eta )]\,\varvec{S}^{\textcircled{1}} \nonumber \\&\ne \left[ \varphi (\eta )\,\varvec{C}^{\textcircled{2}} + [1-\varphi (\eta )]\,\varvec{C}^{\textcircled{1}} \right] ^{-1} =\varvec{C}^{\!\,-1}_{\scriptscriptstyle \mathrm {C}}(\eta ) \ \end{aligned}$$
(8)

as the Reuss–Sachs lower bound, cf. [21, 24]. The additional labels \((\cdot )_{\scriptscriptstyle \mathrm {C}}\) and \((\cdot )_{\scriptscriptstyle \mathrm {S}}\) were introduced to distinguish cases in which the stiffness or, respectively, the compliance interpolations are taken as the basis of the elastic energy expression. It is clear from (7) and (8) that, when using identical interpolation functions \(\varphi (\eta )\), the effective elastic property tensors are not mutual inverses in general—they consequently represent different constitutive models. A common example in which \( \varvec{C}_{\scriptscriptstyle \mathrm {C}}(\eta ) \ne \varvec{S}^{\!\,-1}_{\scriptscriptstyle \mathrm {S}}(\eta )\) is when the individual phases exhibit different types of elastic anisotropy.

It is further noteworthy that (7) and (8) are by far not the only two possible interpolation schemes, as we will discuss later. At this point they suffice to demonstrate the differences in the resulting driving forces for the evolution of the phase field.

Fig. 2
figure 2

Energy landscapes for stiffness- and compliance-based interpolation with identical \(\varphi (\eta )\). Left: Helmholtz potentials \(\widetilde{\psi }^{\;\!\mathrm{m}}(\varvec{C}_{\scriptscriptstyle\mathrm {C}}(\eta ))\) and \(\widetilde{\psi }^{\;\!\mathrm{m}}(\varvec{S}^{\!\,-1}_{\scriptscriptstyle \mathrm {S}}(\eta ))\); right: Gibbs potentials \(\widetilde{g}^{\;\!\mathrm {m}}( \varvec{S}_{\scriptscriptstyle \mathrm {S}}(\eta ))\) and \(\widetilde{g}^{\;\!\mathrm {m}}(\varvec{C}^{\!\,-1}_{\scriptscriptstyle \mathrm {C}}(\eta ))\). Example based on the parameters of a phase field model for phase transformation in \(\text {$\mathrm{Zr\;\!O}$}_{2}\), cf. [25]. Plotted landscapes correspond to the fixed bi-axial strain state \(\varvec{\varepsilon } = 0.08\,[\varvec{e}_{1}\otimes \varvec{e}_{1} - \varvec{e}_{2}\otimes \varvec{e}_{2}]\), chosen to trigger anisotropic behavior. The underlying interpolation function is of the symmetric nonlinear type specified in Fig. 4

Full size image

The choice of the interpolation scheme therefore determines the respective energy landscape, (7) or (8), which in turn governs the microstructures predicted by the phase field model. Representative results of a numerical study for a phase transforming ceramic material that reflect this are shown in Fig. 2 in terms of energy landscapes. The corresponding simulated stationary martensitic microstructures are presented in Fig. 3.

Fig. 3
figure 3

Finite element computations of stationary martensitic microstructures in \(\text {$\mathrm{Zr\;\!O}$}_{2}\) at different undercooling levels. These simulations are based on the stiffness and compliance interpolations and resulting Helmholtz free energy landscapes of Fig. 2, see also [25]

Full size image

Note that stationary values for \(\eta \) are typically constrained to a specific interval in \(\mathbb {R}\), e.g., Fig. 3 represents a range of \(\eta \in [-1,1]\). In fact, several phase field models use different ranges for each order parameter which do not coincide with the conventionally used interval \(\eta \in [0,1]\). Furthermore, the commonly chosen interval \(\eta \in [0,1]\) is associated with an actual phase volume fraction only within the special case of unweighted averaging operators. Clearly, this states an immense restriction on how to define order parameters in general. To naturally (without numerical effort) arrive at a stationary phase distribution within an arbitrary interval, the prescribed unconstrained modeling framework must provide locally stationary points within the energetic landscapes at which thermodynamic equilibrium is obtained, i.e., \(\delta _{\eta }\hat{\psi } = 0\). According to the Landau-Ginzburg equation given in Table 1, the transformation rate \(\dot{\eta }\)—in the case of homogeneously distributed order parameter fields (\(\varvec{\nabla }\eta =\varvec{0}\)) without local, chemical sources (\(\gamma =0\))—is proportionally determined by the negative slope of the corresponding energy landscape, i.e., \(\dot{\eta } \propto -\partial _{\eta }\hat{\psi }|_{\varvec{\varepsilon }}\). Since the order parameter enters the respective potential only indirectly via the interpolation function, it follows that \(\dot{\eta } \propto -\partial _{\varphi }\hat{\psi }|_{\varvec{\varepsilon }}\,\partial _{\eta }{\varphi }\). Consequently, the structure of \(\varphi (\eta )\) is often subject to stationary conditions in order to remain pure phase properties and prevent transformations within homogeneously distributed single-phase states. Considering for example the commonly used restriction \(\eta \in [0, 1]\), the necessary constraints for suitable nonlinear interpolation functions read

$$\begin{aligned} \quad \quad \varphi (0)=0, \quad \quad \varphi (1)=1 \quad \text {and}\quad \partial _{\eta }\varphi \big |_{\eta \in \{0,\,1\}} = 0\,. \end{aligned}$$
(9)

Consequently, \(\eta \) might be interpreted as a volume fraction with a range of \(\eta \in [0,1]\), whereas the associated interpolation function \(\varphi (\eta )\)—which is unbounded in general—defines the effect of a current phase state, since it determines the corresponding driving force entering the underlying evolution law. In addition, several other conditions could potentially be applied—e.g., instability constraints and energetic barrier conditions, cf. [13, 14]—that are omitted at this point for sake of simplicity and without loss of generality on the nonlinear structure of \(\varphi (\eta )\). The definition of an appropriate interpolation is therefore not unique, see Fig. 4.

Fig. 4
figure 4

Commonly used types of interpolation functions \(\varphi (\eta )\) and their corresponding derivatives \(\partial _{\eta }\varphi \) representing associated mechanical driving forces. Only a nonlinear interpolation involves stationary points as seen by continuous intersections with \(\eta \)-axis in the associated driving force graphs. In terms of linear interpolation, respective limits for the order parameter, e.g., \(\eta \in [0,1]\), have to be ensured numerically

Full size image

Remark 1

Switching between Helmholtz and Gibbs representations of interface energetics requires the definition of an appropriate involutive transformation, to carry all thermodynamic information in both formulations. Since only sufficiently differentiable potentials are discussed in this work, the partial Legendre transformation is commonly used and defined in the following way, cf. [26]: Given \({\varvec{q}}(\varvec{\varepsilon }, \eta ):=\partial _{\varvec{\varepsilon }}\widetilde{\psi }^{\!\;\mathrm {m}}(\varvec{\varepsilon} , \eta )\) and its continuous inverse \(\varvec{p}(\varvec{\sigma }, \eta )\), i.e., \(\varvec{p}(\varvec{q}(\varvec{\varepsilon },\eta ),\eta ) = \varvec{\varepsilon }\) and \(\varvec{q}(\varvec{p}(\varvec{\sigma }, \eta ), \eta ) = \varvec{\sigma }\), the mechanical part of the Helmholtz free energy \(\widetilde{\psi }^{\!\;\mathrm {m}}(\varvec{\varepsilon }, \eta )\) is said to have a partial Legendre transformation, namely the mechanical Gibbs free enthalpy \(\widetilde{g}^{\;\!\mathrm {m}}(\varvec{\sigma }, \eta )\), defined by

$$\begin{aligned} \widetilde{g}^{\;\!\mathrm {m}}(\varvec{\sigma }, \eta ) := \widetilde{\psi }^{\!\;\mathrm {m}}(\varvec{p}(\varvec{\sigma }, \eta ), \eta ) - \varvec{\sigma }:\varvec{p}(\varvec{\sigma }, \eta ) \end{aligned}$$
(10)

and it follows, that \(\varvec{p}(\varvec{\sigma }, \eta ) = -\partial _{\varvec{\sigma }}\widetilde{g}^{\;\!\mathrm {m}}(\varvec{\sigma }, \eta )\). Inversely, the Helmholtz free energy could also be obtained by a partial Legendre transformation of Gibbs free enthalpy, i.e.,

$$\begin{aligned} \widetilde{\psi }^{\!\;\mathrm {m}}(\varvec{\varepsilon }, \eta ) = \widetilde{g}^{\;\!\mathrm {m}}(\varvec{q}(\varvec{\varepsilon }, \eta ), \eta ) - \varvec{\varepsilon }:\varvec{q}(\varvec{\varepsilon }, \eta )\,. \end{aligned}$$
(11)

Note that the outlined definition slightly differs from the one given in [26] by the sign, in order to obtain equal thermodynamic driving forces in both Helmholtz and Gibbs formulations, i.e.,

$$\begin{aligned} \partial _{\eta }\widetilde{g}^{\;\!\mathrm {m}}(\varvec{\sigma }, \eta ) = \partial _{\eta }\widetilde{\psi }^{\!\;\mathrm {m}}(\varvec{p}(\varvec{\sigma }, \eta ), \eta ) \quad \text {and}\quad \partial _{\eta }\widetilde{\psi }^{\!\;\mathrm {m}}(\varvec{\varepsilon }, \eta ) = \partial _{\eta }\widetilde{g}^{\;\!\mathrm {m}}(\varvec{q}(\varvec{\varepsilon }, \eta ), \eta )\,. \end{aligned}$$
(12)

Remark 2

Note that differences in resulting stationary microstructures could be reduced by calibrating parameters corresponding to the interface energy \(\widetilde{\psi }^{\,\Gamma }\), but only for one specific loading scenario. Therefore, consider

$$\begin{aligned} \widetilde{\psi }^{\,\Gamma } := \varvec{\beta }:\varvec{\nabla }\otimes \varvec{\nabla }\eta \end{aligned}$$
(13)

with the positive definite interface scale parameter tensor \(\varvec{\beta }\). Clearly, in order to fulfill (1) by (3) a calibration with the sharp interface approach gives

$$\begin{aligned} \varvec{\beta } = \arg \left\{ \;\inf \limits _{\varvec{\beta }^{\star }}\;\big | \langle \widetilde{\psi }^{\!\;\mathrm{B}} \rangle _{\widetilde{\mathcal {B}}} + \varvec{\beta }^{\star }:\langle \varvec{\nabla }\otimes \varvec{\nabla }\eta \rangle _{\widetilde{\mathcal {B}}} -\langle \overline{\psi }^{\;\!\mathrm{B}} \rangle _{\overline{\mathcal {B}}\backslash \overline{\Gamma }} - \overline{\psi }^{\!\;\Gamma } \big | \right\} \end{aligned}$$
(14)

evaluated at the stationary state, i.e., \(\dot{\eta }\approx 0\) \(\forall \varvec{X}\in \widetilde{\mathcal {B}}\). Despite the fact, that this formulation does not necessarily lead to a unique solution, it strictly depends on the topology of \(\widetilde{\mathcal {B}}\) and its loading path history, since only the stationary system is evaluated. Consequently, even a calibration of interface related phase field parameters in an averaged manner will potentially lead to differing microstructural evolution mechanisms for different types of mechanical property interpolation!

Mathematical Considerations on Weighted Averaging Operators

It is convenient to identify certain field variables on a macroscopic scale with their spatially averaged microscopic counterparts, as outlined in “Motivation” section in terms of interface energetics. More specifically, macroscopic relations between several quantities may only result under certain assumptions on the associated microscale, that dramatically restrict the space of possible microscopic fluctuation fields of those quantities, in general. To this end, suitable averaging operators have to be defined—acting on a theoretically infinitesimal region \(\Delta V \subset \mathbb {R}^{n}\) within a macroscopic point \(\varvec{X}\)—, so that the problem of finding suitable constraints on microscopic fields could be relaxed by introducing specific weighting functions in the following way.

Let \(\mathcal {Q}_{\Delta V}\) be the set of physical field quantities of arbitrary order

$$\begin{aligned} \mathcal {Q}_{\Delta V} \ni \varvec{\alpha } :\; \Delta V&\rightarrow \mathbb {R}^{n}\otimes\;\!...\otimes \mathbb {R}^{n} \nonumber \\ \varvec{x}&\mapsto \varvec{\alpha }(\varvec{x}) \end{aligned}$$
(15)

and \(\mathcal {W}_{\Delta V}\) the set of corresponding weighting functions on a specific scale (domain) \(\Delta V\), such that

$$\begin{aligned} \mathcal {W}_{\Delta V} \ni \varvec{\Phi }_{\varvec{\alpha }} :\; \Delta V \times \mathcal {Q}_{\Delta V}&\rightarrow \mathbb {R}^{n}\otimes\;\!... \otimes \mathbb {R}^{n} \nonumber \\ (\varvec{x}, \varvec{\beta })&\mapsto \varvec{\Phi }_{\varvec{\alpha }}(\varvec{x}, \varvec{\beta }(\varvec{x})) {=}{:}\varvec{\Phi }_{\varvec{\alpha }}^{\varvec{\beta }}(\varvec{x}) \;. \end{aligned}$$
(16)

A so called weighted averaging operator—transforming physical quantities between \(\Delta V\) and the next larger scale—may thus be defined as a mapping

$$\begin{aligned} \langle \quad \rangle _{\Delta V} :\; \mathcal {Q}_{\Delta V} \times \mathcal {W}_{\Delta V}&\rightarrow \mathbb {R}^{n}\otimes \;\!... \otimes \mathbb {R}^{n} \nonumber \\ (\varvec{\beta }, \varvec{\Phi }_{\varvec{\alpha }})&\mapsto \langle (\varvec{\beta }, \varvec{\Phi }_{\varvec{\alpha }}) \rangle _{\Delta V} {=}{:}\langle \varvec{\Phi }_{\varvec{\alpha }}^{\varvec{\beta }} \rangle _{\Delta V} \end{aligned}$$
(17)

with the respective transition rule

$$\begin{aligned} \langle \varvec{\Phi }_{\varvec{\alpha }}^{\varvec{\beta }} \rangle _{\Delta V} {:}{=}\frac{1}{\Delta V}\int _{\Delta V} \!\! \varvec{\Phi }_{\varvec{\alpha }}^{\varvec{\beta }}(\varvec{x}) \, \mathrm {d}V \;. \end{aligned}$$
(18)

Hence, it is assumed, that for each \(\varvec{\alpha }\) there exists a corresponding—in general nonlinear—weighting function \(\varvec{\Phi }_{\varvec{\alpha }}\), for which reason especially the reflexive micro-macro transitions \(\langle \varvec{\Phi }_{\varvec{\alpha }}^{\varvec{\alpha }} \rangle _{\Delta V}\) will be of interest due to physical interpretability.

Moreover, the special case of linear weighting functions leads to a simplified definition

$$\begin{aligned} \varvec{\Phi }_{\varvec{\alpha }}^{\varvec{\beta }}(\varvec{x}) {:}{=}\varvec{\Phi }_{\varvec{\alpha }}(\varvec{x}) \;\!\varvec{\bullet }\;\!\varvec{\beta }(\varvec{x}) \in \mathbb {R}^{n}\otimes \;\!... \otimes \mathbb {R}^{n} \end{aligned}$$
(19)

in which \(\varvec{\bullet }\) characterizes a generalized dot-product. By using the identity tensor \(\varvec{1}\) of arbitrary order, conventional (non-weighted) volumetric averaging operators may thus be rewritten in weighted formulation

$$\begin{aligned} \langle \varvec{\alpha } \rangle _{\Delta V} {:}{=}\langle \varvec{1} \varvec{\bullet}\;\!\varvec{\alpha } \rangle _{\Delta V} \,. \end{aligned}$$
(20)

Note that for nonlinear weighting functions \(\varvec{1}\) simply generalizes toward the identity map on \(\mathcal {Q}_{\Delta V}\), i.e., \(\langle \varvec{\Phi }(\varvec{\alpha }) \rangle _{\Delta V} := \langle \,\mathrm {id}_{\mathcal {Q}_{\Delta V}}(\varvec{\alpha }) \rangle _{\Delta V} = \langle \varvec{\alpha } \rangle _{\Delta V}\).

Remark 3

Even though the described definitions may imply a free choice for \(\varvec{\Phi }_{\varvec{\alpha }}\), realistic physical interpretations of respective micro-macro transitions are related to several constraints that have to be considered within the space of suitable weighting functions \(\mathcal {W}_{\Delta V}\). The reader is furthermore referred to the fact, that weighting functions not only correspond to specific physical quantities on their own, but also to a certain microscopic scale, so that \(\mathcal {W}_{\Delta V} \ne \mathcal {W}_{\Delta V_{\mathrm {i}}}\) for \(\Delta V_{\mathrm {i}} \subset \Delta V\), which will be discussed in terms of domain relations.

Explicit and implicit macroscopic links

Consider explicit physical relations of different microscopic quantities, e.g., stress and strain, i.e., \(\varvec{\alpha }= \varvec{f}(\varvec{\beta })\). Then, \(\varvec{\alpha }\) and \(\varvec{\beta }\) are called explicitly, macroscopically linked if there also exists an explicit relation of their macroscopic counterparts, i.e.,

$$\begin{aligned} \langle \varvec{\Phi }_{\varvec{\alpha }}^{\varvec{\alpha }} \rangle _{\Delta V} = \varvec{\mathcal {F}}(\langle \varvec{\Phi }_{\varvec{\beta }}^{\varvec{\beta }} \rangle _{\Delta V})\,. \end{aligned}$$
(21)

Furthermore, consider implicit physical relations of different quantities, i.e., \(\varvec{f}(\varvec{\alpha }, \varvec{\beta }) = \varvec{0}\). Then, \(\varvec{\alpha }\) and \(\varvec{\beta }\) are called implicitly, macroscopically linked if there also exists an implicit relation of their macroscopic counterparts, i.e.,

$$\begin{aligned} \varvec{\mathcal {F}}(\langle \varvec{\Phi }_{\varvec{\alpha }}^{\varvec{\alpha }} \rangle _{\Delta V}, \langle \varvec{\Phi }_{\varvec{\beta }}^{\varvec{\beta }} \rangle _{\Delta V}) = \varvec{0} \,. \end{aligned}$$
(22)

Clearly, explicit, macroscopic links imply implicit, macroscopic links. Note, that the prescribed definitions do not include any types of differential operators, since there is no consistent and mathematically rigorous micro-macro transition of differential operators in terms of averaging operators known to the authors knowledge. Proposed derivations of macroscopic gradients, cf. [18, 20], lean on the fact of defining macroscopic normal vectors used to apply a macroscopic divergence theorem to end up with a definition for homogenized differential operators. Unfortunately, existence and actual derivation of such normal vectors have not been shown yet, to the authors knowledge.

An example for non-unique, conventionally averaged macroscopic links

As discussed, conventional unweighted averaging operators, in general, do not yield unique macroscopic relations of averaged microscopically related quantities without additional constraints on the corresponding microscopic field distributions. More specifically, the only reasonable constraints should be given by partial differential equations determining the respective field distributions naturally. To demonstrate this, consider a one-dimensional body (rod) \(\widetilde{\mathcal {B}}\), whose thermodynamic state is fully characterized by an order parameter distribution \(\eta (x,t)\), a homogeneous temperature field \(\theta \) and an associated Helmholtz free energy \(\widetilde{\psi }(\eta , \partial _{x}\eta , \theta ) = \widetilde{\psi }^{\,\mathrm {ch}}(\eta , \theta ) + {\widetilde{\psi }}^{\,\Gamma }(\partial _{x}\eta )\), decomposed into chemical and interface contributions, cf. [13, 14], given by

$$\begin{aligned} \widetilde{\psi }^{\,\mathrm {ch}}(\eta , \theta )&= \frac{1}{2}\,A(\theta )\,\eta ^{2} + [3\,\Delta G(\theta ) - A(\theta )]\,\eta ^{4} + \frac{1}{2}\,[A(\theta ) - 4\,\Delta G(\theta )]\,\eta ^{6} \end{aligned}$$
(23)
$$\begin{aligned} \widetilde{\psi }^{\,\Gamma }(\partial _{x}\eta )&= \beta \,[\partial _{x}\eta ]^{2} \ , \end{aligned}$$
(24)

wherein, \(A(\theta ) = A_{0}\,[\theta - \theta _{\mathrm {c}}]\) and \(\Delta G(\theta ) = z\,[\theta - \theta _{\mathrm {e}}]\). Corresponding material parameters are given based on measurements of microstructure formation in \(\mathrm{Zr\;\!O}_{2}\) as outlined in [25], as \(A_{0} = 0.55\,\mathrm {MPa/K}\), \(\theta _{c} = 1187\,\mathrm {K}\), \(z = 0.185\,\mathrm {MPa/K}\) and \(\theta _{\mathrm {e}} = 1299\,\mathrm {K}\). Following the Allen-Cahn based phase field modeling approach outlined in Table 1, the associated evolution law

$$\begin{aligned} M\dot{\eta } = -\partial _{\eta }\widetilde{\psi }^{\,\mathrm {ch}} + \partial _{\partial _{x}\eta }\widetilde{\psi }^{\,\Gamma } \end{aligned}$$
(25)

guarantees the existence of any order distribution within the initial state \(\eta (x) := \eta (x,0)\) that is twice differentiable in \(\widetilde{\mathcal {B}}\). For demonstration purposes, three such fields with the same unweighted mean value of \(\langle \eta \rangle _{\widetilde{B}} = 0.5\) are plotted in Fig. 5. The question arises, if there exists a unique macroscopic link between the unweighted, averaged quantities, in the sense

$$\begin{aligned} \widetilde{\psi } = f(\eta , \partial _{x}\eta , \theta ) {\mathop {\implies }\limits ^{?}} \langle \widetilde{\psi } \rangle _{\widetilde{\mathcal {B}}} = \mathcal {F}(\langle \eta \rangle _{\widetilde{\mathcal {B}}}, \langle \partial _{x}\eta \rangle _{\widetilde{\mathcal {B}}}, \langle \theta \rangle _{\widetilde{\mathcal {B}}}) \, . \end{aligned}$$
(26)

Since \(\langle \widetilde{\psi } \rangle _{\widetilde{\mathcal {B}}} = \langle \widetilde{\psi }^{\,\mathrm {ch}} \rangle _{\widetilde{\mathcal {B}}} + \langle \widetilde{\psi }^{\,\Gamma } \rangle _{\widetilde{\mathcal {B}}}\) and \(\widetilde{\psi }^{\,\Gamma }\) is only a function of \(\partial _{x}\eta \), it is sufficient to analyze the functional dependencies of \(\langle \widetilde{\psi }^{\,\mathrm {ch}} \rangle _{\widetilde{\mathcal {B}}}\). Therefore, as shown in Fig. 5, there exist no unique relation (function) of the type \(\langle \widetilde{\psi }^{\,\mathrm {ch}} \rangle _{\widetilde{\mathcal {B}}} = \mathcal {F}^{\;\!\mathrm {ch}}(\langle \eta \rangle _{\widetilde{\mathcal {B}}}, \langle \theta \rangle _{\widetilde{\mathcal {B}}})\), since multiple effective energies are assigned to the same mean order parameter \(\langle \eta \rangle _{\widetilde{\mathcal {B}}}\) and temperature state \(\langle \theta \rangle _{\widetilde{\mathcal {B}}} = \theta \). The macroscopic energetic state of the body \(\widetilde{\mathcal {B}}\) is thus not uniquely characterized.

Fig. 5
figure 5

One-dimensional body \(\mathcal {B}\) with three different order parameter distributions \(\eta (x)\) (left plot) and its effective chemical energy contributions \(\langle \widetilde{\psi }^{\mathrm {ch}} \rangle _{\widetilde{\mathcal {B}}}\) (right plot) for varying homogeneous temperature states \(\theta \). Despite possessing identical unweighted mean values of \(\langle \eta \rangle _{\widetilde{\mathcal {B}}}=0.5\), the considered order parameter distributions result in different macroscopic energy states

Full size image

Domain relations

Again, let \(\mathcal {Q}_{\Delta V}\) and \(\mathcal {W}_{\Delta V}\) be sets of physical quantities and corresponding weighting functions on \(\Delta V\). Considering an arbitrary domain decomposition \(\Delta V = \bigcup _{i} \Delta V_{i}\) with respective sets of \(subdomain\,\;\!weighting\,\;\!functions\)

$$\begin{aligned} \overline{\mathcal {W}}^{\,\varvec{\alpha }}_{\!\Delta V}&= \{{{}_{\textcircled{1}}}\!\overline{\varvec{\Phi }}_{\varvec{\alpha }}, ..., {{}_{\textcircled{i}}}\!\overline{\varvec{\Phi }}_{\varvec{\alpha }}, ...\} \ , \end{aligned}$$
(27)
$$\begin{aligned} \widetilde{\mathcal {W}}^{\,\varvec{\alpha }}_{\!\Delta V}&= \{{{}_{\textcircled{1}}}\!\widetilde{\varvec{\Phi }}_{\varvec{\alpha }}, ..., {{}_{\textcircled{i}}}\!\widetilde{\varvec{\Phi }}_{\varvec{\alpha }}, ...\} \ , \end{aligned}$$
(28)

the triple \((\mathcal {W}_{\Delta V}, \overline{\mathcal {W}}^{\,\varvec{\alpha }}_{\!\Delta V}, \widetilde{\mathcal {W}}^{\,\varvec{\alpha }}_{\!\Delta V})\) is called to provide a domain relation on \(\Delta V\), if for all possible fields \(\varvec{\alpha }(\varvec{x}) \in \mathcal {Q}_{\Delta V}\)

$$\begin{aligned} \langle \varvec{\Phi }^{\varvec{\alpha }}_{\varvec{\alpha }} \rangle _{\Delta V} = \sum _{i} \big \langle {{}_{\textcircled{i}}}\!\overline{\varvec{\Phi }}_{\varvec{\alpha }}\big (\langle {{}_{\textcircled{i}}}\!\widetilde{\varvec{\Phi }}^{\varvec{\alpha }}_{\varvec{\alpha }} \rangle _{\Delta V_{i}}\big )\big \rangle _{\Delta V_{i}} \ . \end{aligned}$$
(29)

In this case, the weighted sum of a subdomain averaged quantity \(\varvec{\alpha }\) is equal to its total domain average, with respective weighting functions (see Fig. 6).

Fig. 6
figure 6

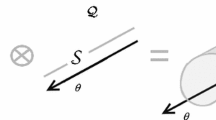
Schematic visualization of a domain relation for an arbitrary field distribution \(\varvec{\alpha }(\varvec{x}) \in \mathcal {Q}_{\Delta V}\) consisting of spatially dependent subdomain weights \(\overline{\varvec{\Phi }}_{\varvec{\alpha }}^{\varvec{\alpha }}(\varvec{x}) = \overline{\varvec{\Phi }}_{\varvec{\alpha }}(\varvec{x}, \varvec{\alpha }(\varvec{x}))\) and \(\widetilde{\varvec{\Phi }}_{\varvec{\alpha }}^{\varvec{\alpha }}(\varvec{x}) = \widetilde{\varvec{\Phi }}_{\varvec{\alpha }}(\varvec{x}, \varvec{\alpha }(\varvec{x}))\). The microscopic domain \(\Delta V\) is decomposed into a finite number of subdomains \(\Delta V =\bigcup _{i}\Delta V_{i}\). The continuous field \(\varvec{\alpha }(\varvec{x})\) (left circle) is then non-linearly mapped onto spatially constant distributions \(\langle {}{}_{\textcircled{i}}\widetilde{\varvec{\Phi }}^{\varvec{\alpha }}_{\varvec{\alpha }} \rangle _{\Delta V_{i}}\) within each subdomain \(\Delta V_{i}\) (middle circle). Afterward, an additional mapping toward piecewise continuous distributions—that may be discontinuous over their respective boundaries—is performed again via nonlinear subdomain weights, so that the resulting sum of subdomain averages \(\sum _{i}\langle {}{}_{\textcircled{i}}\overline{\varvec{\Phi }}_{\varvec{\alpha }}(\langle {}{}_{\textcircled{i}}\widetilde{\varvec{\Phi }}^{\varvec{\alpha }}_{\varvec{\alpha }} \rangle _{\Delta V_{i}}) \rangle _{\Delta V_{i}}\) (right circle) equals the total, weighted average \(\langle \varvec{\Phi }^{\varvec{\alpha }}_{\varvec{\alpha }} \rangle _{\Delta V}\)

Full size image

Consequently, definitions for \({{}_{\textcircled{i}}}\!\overline{\varvec{\Phi }}_{\varvec{\alpha }}\) as well as \({{}_{\textcircled{i}}}\!\widetilde{\varvec{\Phi }}_{\varvec{\alpha }}\) are identical to (16), whereby the spatial dependency is subject to the actual subdomain. In case of linear weighting functions, a domain relation is automatically achieved by elements of \((\mathcal {W}_{\Delta V}, \overline{\mathcal {W}}^{\,\varvec{\alpha }}_{\!\Delta V}, \widetilde{\mathcal {W}}^{\,\varvec{\alpha }}_{\!\Delta V})\), if

$$\begin{aligned} \quad \quad \varvec{\Phi }_{\varvec{\alpha }}(\varvec{x}) = \dfrac{\Delta V}{\Delta V_{i}} \, {{}_{\textcircled{i}}} \! \overline{\varvec{\Phi }}_{\varvec{\alpha }} \varvec{\cdot }{{}_{\textcircled{i}}} \! \widetilde{\varvec{\Phi }}_{\varvec{\alpha }}(\varvec{x}) \quad \quad \forall \varvec{x} \in \Delta V_{i} \;. \end{aligned}$$
(30)

Basic constraints

Regarding spatially independent quantities \(\varvec{\beta }(\varvec{x}) = \mathrm {const.}|_{\varvec{x}} = \overline{\varvec{\beta }}\) within \(\Delta V\), macroscopic identity conditions can be formulated as basic constraints for all types of weighting functions, such that

$$\begin{aligned} \quad \quad \langle \varvec{\Phi }_{\varvec{\alpha }}^{\overline{\varvec{\beta }}} \rangle _{\Delta V} = \frac{1}{\Delta V} \int _{\Delta V} \!\! \varvec{\Phi }_{\varvec{\alpha }}(\varvec{x}, \overline{\varvec{\beta }}) \, \mathrm {d}V \equiv \overline{\varvec{\beta }} \quad \quad \forall \overline{\varvec{\beta }} \in \mathbb {R}^{n} \otimes\;\!... \otimes \mathbb {R}^{n} \;. \end{aligned}$$
(31)

In terms of linear weighting functions, this constraint yields

$$\begin{aligned} \frac{1}{\Delta V} \int _{\Delta V} \!\! \varvec{\Phi }_{\varvec{\alpha }}(\varvec{x}) \, \mathrm {d}V \equiv \varvec{\mathrm {1}} \;. \end{aligned}$$
(32)

Considering linear domain relations, these conditions must also be fulfilled by elements of \(\overline{\mathcal {W}}^{\,\varvec{\alpha }}_{\!\Delta V}\) and \(\widetilde{\mathcal {W}}^{\,\varvec{\alpha }}_{\!\Delta V}\), i.e.,

$$\begin{aligned} \sum _{i} \langle {{}_{\textcircled{i}}}\!\overline{\varvec{\Phi }}_{\varvec{\alpha }}\varvec{\cdot }\langle {}{}_{\textcircled{i}}\widetilde{\varvec{\Phi }}_{\varvec{\alpha }} \rangle _{\Delta V_{i}} \rangle _{\Delta V_{i}}\equiv \varvec{\mathrm {1}} \;. \end{aligned}$$
(33)

Note, that identity conditions could also be applied either for all elements of \(\overline{\mathcal {W}}^{\,\varvec{\alpha }}_{\!\Delta V}\) or \(\widetilde{\mathcal {W}}^{\,\varvec{\alpha }}_{\!\Delta V}\) on their respective subdomains, so that (in the linear case)

$$\begin{aligned} \sum _{i}\langle {}{}_{\textcircled{i}}\widetilde{\varvec{\Phi }}_{\alpha } \rangle _{\Delta V_{i}} = \varvec{1} \quad \text {or} \quad \sum _{i}\langle {}{}_{\textcircled{i}}\overline{\varvec{\Phi }}_{\alpha } \rangle _{\Delta V_{i}} = \varvec{1} \,, \end{aligned}$$
(34)

but not for both simultaneously! In addition, objectivity has to remain during homogenization which also limits the space of suitable weighting functions. Note that also multiple other constraints could potentially be formulated when the underlying homogenization scheme requires finite scale separations and access for generalized continua, which is not discussed in this work.

Conventional unweighted homogenization of elastic properties

Applying the phase field approach to multi-phase mixtures, cf. [14, 16], the amount of a single phase i is mathematically characterized by individual order parameters \(\eta _{\mathrm {i}} \in \mathbb {R}\). Since transitions are assumed to happen between parent and product phases, each order parameter typically lies in between a closed interval \(\eta _{i} \in [0,1]\) or \(\eta _{i} \in [-1,1]\), such that \(\eta =0\) identifies the parent and \(\eta _{i} \in \{-1,\,1\}\) the product phase of different variants. Consequently, a physical interpretation of \(\eta _{i} = {\Delta V_{i}}/{\Delta V}\) as volume fractions between phase and reference volume may only be suitable for positive order parameters.

Applying the non-weighted averaging operator defined in relation (20) over a microscopic domain \(\Delta V\) leads to

$$\begin{aligned} \langle \varvec{\varepsilon }_{e} \rangle _{\Delta V}&= \frac{1}{\Delta V}\, \sum _{i} \int _{\Delta V_{i}} \!\! \varvec{\varepsilon }_{e} \, \mathrm {d}V \;\!{\mathop {=}\limits ^{(\mathrm {dp})}}\;\! \eta \, \varvec{\varepsilon }_{e}^{\textcircled{2}} + \left[ 1-\eta \right] \varvec{\varepsilon }_{e}^{\textcircled{1}} \;, \end{aligned}$$
(35)
$$\begin{aligned} \langle \varvec{\sigma } \rangle _{\Delta V}&= \frac{1}{\Delta V}\, \sum _{i} \! \int _{\Delta V_{i}} \!\! \varvec{\sigma } \, \mathrm {d}V \;\!{\mathop {=}\limits ^{(\mathrm {dp})}}\;\! \eta \, \varvec{\sigma }^{\textcircled{2}} + \left[ 1-\eta \right] \varvec{\sigma }^{\textcircled{1}} \;, \end{aligned}$$
(36)

with single-phase elastic strains \(\varvec{\varepsilon }_{e}^{\textcircled{i}} = \langle \varvec{\varepsilon }_{e} \rangle _{\Delta V_{\mathrm {i}}}\), stresses \(\varvec{\sigma }^{\textcircled{i}} = \langle \varvec{\sigma } \rangle _{\Delta V_{i}}\) and an order parameter \(\eta := {\Delta V_{2}}/{\Delta V}\) related to the volume fraction of phase \(\textcircled{2}\). Furthermore, assuming linear elastic, microscopic material relations in terms of single-phase compliance \(\varvec{S}^{\textcircled{i}}\) and stiffness \(\varvec{C}^{\textcircled{i}} = {\varvec{S}^{\textcircled{i}}}^{-1}\) tensors, i.e.,

$$\begin{aligned} \varvec{\varepsilon }_{e}^{\textcircled{i}} = \varvec{S}^{\textcircled{i}} : \varvec{\sigma }^{\textcircled{i}} \quad \mathrm {and} \quad \varvec{\sigma }^{\textcircled{i}} = {\varvec{S}^{\textcircled{i}}}^{-1} : \varvec{\varepsilon }_{e}^{\textcircled{i}} \,, \end{aligned}$$
(37)

the question arises, how to derive respective macroscopic relations including effective elastic properties, such like

$$\begin{aligned} \;\, \langle \varvec{\varepsilon }_{e} \rangle _{\Delta V} = \varvec{S}^{\star } : \langle \varvec{\sigma } \rangle _{\Delta V} \quad \mathrm {or} \quad \langle \varvec{\sigma } \rangle _{\Delta V} = \varvec{C}^{\star } : \langle \varvec{\varepsilon }_{e} \rangle _{\Delta V} \;. \end{aligned}$$
(38)

Taylor–Voigt homogenization

In Taylor–Voigt homogenization formats the total strains within the underlying microstructure are assumed to be spatially and therefore phase-independent, i.e.,

$$\begin{aligned} \varvec{\varepsilon }^{\textcircled{1}} = \varvec{\varepsilon }^{\textcircled{2}} \equiv \varvec{\varepsilon } = \langle \varvec{\varepsilon } \rangle _{\Delta V} \;. \end{aligned}$$
(39)

Using relations (35) - (38), the macroscopic stress-strain-relation with an effective material stiffness tensor \(\varvec{C}_{\mathrm {TV}}^{\star }\) reads

$$\begin{aligned} \langle \varvec{\sigma } \rangle _{\Delta V} = \varvec{C}_{\mathrm {TV}}^{\star } : \varvec{\varepsilon }_{e}^{\star } = \left[ \eta \, {\varvec{C}^{\textcircled{2}}} + \left[ 1-\eta \right] \varvec{C}^{\textcircled{1}} \right] : \left[ \langle \varvec{\varepsilon } \rangle _{\Delta V} - \varvec{\varepsilon }_{tr}^{\star } \right] \;. \end{aligned}$$
(40)

Despite kinematic compatibility of total strains, the resulting stresses inescapably result in static incompatibility for varying elastic properties between different phases. It follows for the effective inelastic eigenstrains, that

$$\begin{aligned} \varvec{\varepsilon }_{\mathrm {tr}}^{\star } = {\varvec{C}_{\mathrm {TV}}^{\star }}^{-1} : \left[ \eta \,\varvec{C}^{\textcircled{2}} \! : \varvec{\varepsilon }_{\mathrm {tr}}^{\textcircled{2}} + \left[ 1 - \eta \right] \,\varvec{C}^{\textcircled{1}} \! : \varvec{\varepsilon }_{\mathrm {tr}}^{\textcircled{1}}\right] \ne \langle \varvec{\varepsilon }_{\mathrm {tr}} \rangle _{\Delta V} \end{aligned}$$
(41)

and consequently \(\varvec{\varepsilon }_{\mathrm {e}}\) and \(\varvec{\sigma }\) are not macroscopically linked, since

$$\begin{aligned} \varvec{\varepsilon }_{\mathrm {e}}^{\star } \ne \langle \varvec{\varepsilon }_{\mathrm {e}} \rangle _{\Delta V} \;. \end{aligned}$$
(42)

Reuss–Sachs homogenization

In Reuss–Sachs homogenization formats the microscopic stresses are assumed to be spatially and therefore phase-independent, i.e.,

$$\begin{aligned} \varvec{\sigma }^{\textcircled{1}} = \varvec{\sigma }^{\textcircled{2}} \equiv \varvec{\sigma } = \langle \varvec{\sigma } \rangle _{\Delta V} \;. \end{aligned}$$
(43)

which a priori fulfills static compatibility at costs of kinematic incompatibility. In contrast to the Taylor–Voigt approach the homogenized material response is now obtained by interpolating the elastic properties of the single phases in terms of an effective compliance tensor \(\varvec{S}_{\mathrm {RS}}^{\star }\) generating an explicit, macroscopic link between \(\varvec{\varepsilon }_{\mathrm {e}}\) and \(\varvec{\sigma }\), i.e.,

$$\begin{aligned} \langle \varvec{\varepsilon }_{\mathrm {e}} \rangle _{\Delta V} = \varvec{S}_{\mathrm {RS}}^{\star } : \varvec{\sigma } = \left[ \eta \, \varvec{S}^{\textcircled{2}} + \left[ 1 - \eta \right] \varvec{S}^{\textcircled{1}} \right] : \varvec{\sigma } \;. \end{aligned}$$
(44)

Partial rank-one homogenization

The prescribed models can be generalized within a variational framework, in which the jump of deformation gradient

$$\begin{aligned} \llbracket \varvec{F}\rrbracket _{\Delta V} := \langle \varvec{F} \rangle _{\Delta V_{2}} - \langle \varvec{F} \rangle _{\Delta V_{1}} \equiv \varvec{a}\otimes \varvec{N} \end{aligned}$$
(45)

is subject to the Hadamard jump condition (kinematic compatibility) on the subdomain averaged interface with normal vector \(\varvec{N}\). Assuming explicit, macroscopic links on subdomain averages of the Helmholtz potential, i.e.,

$$\begin{aligned} \langle \widetilde{\psi }(\varvec{F}) \rangle _{\Delta V_{i}} = \langle \widetilde{\psi } \rangle _{\Delta V_{i}}(\langle \varvec{F} \rangle _{\Delta V_{i}})\,, \end{aligned}$$
(46)

yields its macroscopic counterpart

$$\begin{aligned} \langle \widetilde{\psi } \rangle _{\Delta V} = \eta \,\widetilde{\psi }^{\textcircled{2}}(\langle \varvec{F} \rangle _{\Delta V} + [1-\eta ]\,\llbracket \varvec{F}\rrbracket _{\Delta V}) + [1-\eta ]\,\widetilde{\psi }^{\textcircled{1}}(\langle \varvec{F} \rangle _{\Delta V} - \eta \,\llbracket \varvec{F}\rrbracket _{\Delta V}) \,. \end{aligned}$$
(47)

It can be shown, cf. [2, 24], that minimization of this macroscopic potential w.r.t. the jump vector \(\varvec{a}\) leads to static compatibility on the subdomain averaged interface and therefore, the relaxed potential entering the macroscopic continuum reads

$$\begin{aligned} \langle \widetilde{\psi } \rangle _{\Delta V}^{\mathrm {rel}} = \inf _{\varvec{a}}\;\langle \widetilde{\psi } \rangle _{\Delta V}(\langle \varvec{F} \rangle _{\Delta V}, \eta , \varvec{a}\otimes \varvec{N}) = \mathcal {F}(\langle \varvec{F} \rangle _{\Delta V}, \eta , \varvec{N}) \,. \end{aligned}$$
(48)

Note that this minimization framework also includes the prescribed Taylor–Voigt or Reuss–Sachs procedures by either assuming \(\llbracket \varvec{F}\rrbracket _{\Delta V} \in \emptyset \) or \(\llbracket \varvec{F}\rrbracket _{\Delta V} \in \mathbb {R}^{n}\otimes \mathbb {R}^{n}\), respectively.

Equally weighted homogenization of elastic properties

To address the concept of vanishing thermodynamic driving forces within homogeneously distributed single-phase states, a physically equal weighting function \(\varvec{\Phi } = \Phi (\eta , \varvec{x}) \, \varvec{1}\) is introduced, such that the weighted volumetric means (18) of elastic strains and stresses read

$$\begin{aligned} \langle \varvec{\Phi }^{\varvec{\varepsilon }_{\mathrm {e}}} \rangle _{\Delta V}&= \frac{1}{\Delta V} \sum _{i} \! \int _{\Delta V_{i}} \!\! \Phi (\eta , \varvec{x}) \, \varvec{\varepsilon }_{\mathrm {e}} \, \mathrm {d}V {\mathop {=}\limits ^{(\mathrm {dp})}} \varphi (\eta ) \, \varvec{\varepsilon }_{\mathrm {e}}^{\textcircled{2}} + \left[ 1-\varphi (\eta )\right] \varvec{\varepsilon }_{\mathrm {e}}^{\textcircled{1}} \ , \end{aligned}$$
(49)
$$\begin{aligned} \langle \varvec{\Phi }^{\varvec{\sigma }} \rangle _{\Delta V}&= \frac{1}{\Delta V} \sum _{i} \! \int _{\Delta V_{i}} \!\! \Phi (\eta , \varvec{x}) \, \varvec{\sigma } \, \mathrm {d}V {\mathop {=}\limits ^{(\mathrm {dp})}} \varphi (\eta ) \, \varvec{\sigma }^{\textcircled{2}} + \left[ 1-\varphi (\eta )\right] \varvec{\sigma }^{\textcircled{1}} \ . \end{aligned}$$
(50)

Regarding (29), there exists a domain relation for both quantities on \(\Delta V\), if the weighted sums over their single-phase domain means \(\varvec{\varepsilon }_{\mathrm {e}}^{\textcircled{i}} = \langle {{}_{\textcircled{i}}}\!\widetilde{\varvec{\Phi }}^{\varvec{\varepsilon }_{\mathrm {e}}} \rangle _{\Delta V_{i}}\) and \(\varvec{\sigma }^{\textcircled{i}} = \langle {{}_{\textcircled{i}}}\!\widetilde{\varvec{\Phi }}^{\varvec{\sigma }} \rangle _{\Delta V_{i}}\) are equal to their total volume average. This can be ensured by factorization of the corresponding scalar valued weighting function \(\Phi (\eta , \varvec{x})\) within the specific subdomains (see Fig. 7), leading to

$$\begin{aligned} \Phi (\eta , \varvec{x}) = {\left\{ \begin{array}{ll} \dfrac{1}{1-\eta } \, {}{}_{\textcircled{1}}\overline{\Phi }(\eta ) \, {}{}_{\textcircled{1}}\widetilde{\Phi }(\varvec{x}) = \dfrac{1-\varphi (\eta )}{1-\eta } \, {}{}_{\textcircled{1}}\widetilde{\Phi }(\varvec{x}) \quad &{}\forall \varvec{x} \in \Delta V_{1} \\ \\ \quad \;\, \; \dfrac{1}{\eta } \, {}{}_{\textcircled{2}}\overline{\Phi }(\eta )\,{}{}_{\textcircled{2}}\widetilde{\Phi }(\varvec{x}) = \dfrac{\varphi (\eta )}{\eta } \, {}{}_{\textcircled{2}}\widetilde{\Phi }(\varvec{x}) \quad &{}\forall \varvec{x} \in \Delta V_{2} \end{array}\right. } \;. \end{aligned}$$
(51)

Since the macroscopic identity conditions are directly fulfilled for the sum of subdomain weights \({}{}_{\textcircled{i}}\overline{\Phi }(\eta )\), only the choice of suitable \({}{}_{\textcircled{i}}\widetilde{\Phi }(\varvec{x})\) is restricted to previously discussed basic constraints, i.e.,

$$\begin{aligned} \sum _{i} {}{}_{\textcircled{i}}\overline{\Phi }(\eta ) = 1 \quad \text {and} \quad \frac{1}{\Delta V_{i}}\int _{\Delta V_{i}}\!\! {}{}_{\textcircled{i}}\widetilde{\Phi }(\varvec{x}) \, \mathrm {d}V \equiv 1 \ . \end{aligned}$$
(52)

Note that the definition of associated subdomains is related to the actual phase morphology and consequently not dependent on the underlying field distributions for \(\varvec{\varepsilon }_{\mathrm {e}}\) or \(\varvec{\sigma }\). Consequently, actual values of macroscopic quantities are invariant to any rotations of the microscopic domain \(\Delta V\), which preserves objectivity within constitutive, macroscopic relations.

Fig. 7
figure 7

Schematic visualization of an equally and linearly weighted domain relation for an arbitrary field distribution \(\varvec{\alpha }(\varvec{x}) \in \mathcal {Q}_{\Delta V}\) with piecewise constant subdomain weights \({}{}_{\textcircled{i}}\overline{\Phi }=\mathrm {const.}|_{\varvec{x}}\) (\(\forall \varvec{x}\in \Delta V_{i}\)). The microscopic domain \(\Delta V\) is decomposed into two subdomains that are related to pure phase regions within a dual-phase system. The continuous field \(\varvec{\alpha }(\varvec{x})\) (left circle) is then mapped onto constant distributions within each single-phase domain by the linearly weighted operation \(\langle {}{}_{\textcircled{i}}\widetilde{\Phi }\,\varvec{\alpha } \rangle _{\Delta V_{i}}\) (middle circle). Afterward, an additional scaling within each subdomain \(\Delta V_{i}\) is performed by associated linear subdomain weights (right circle), i.e., \({}{}_{\textcircled{i}}\overline{\Phi }\,\langle {}{}_{\textcircled{i}}\widetilde{\Phi }\,\varvec{\alpha } \rangle _{\Delta V_{i}}\), whose sum over all subdomains states a domain relation according to (30)

Full size image

Equally weighted Taylor–Voigt homogenization

Applying the Taylor–Voigt isostrain model, which is described in terms of macroscopic identity conditions for suitable weighting functions by

$$\begin{aligned} \varvec{\varepsilon }^{\textcircled{1}} = \varvec{\varepsilon }^{\textcircled{2}} \equiv \langle \varvec{\Phi }^{\varvec{\varepsilon }} \rangle _{\Delta V} = \varvec{\varepsilon } \ , \end{aligned}$$
(53)

the effective (\(\ne \) macroscopically linked) elastic material law reads

$$\begin{aligned} \langle \varvec{\Phi }^{\varvec{\sigma }} \rangle _{\Delta V} = \varvec{C}_{\mathrm {TV}}^{\star } : \varvec{\varepsilon }_{\mathrm {e}}^{\star } = \left[ \varphi (\eta ) \, \varvec{C}^{\textcircled{2}} + \left[ 1-\varphi (\eta )\right] \varvec{C}^{\textcircled{1}} \right] : \left[ \varvec{\varepsilon } - \varvec{\varepsilon }_{\mathrm {tr}}^{\star } \right] \ . \end{aligned}$$
(54)

It follows, that the coefficients of an effective fourth order elastic stiffness tensor are non-linearly interpolated between the respective single-phase ones and the effective transformation strains are derived by

$$\begin{aligned} \varvec{\varepsilon }_{\mathrm {tr}}^{\star } = {\varvec{C}_{\mathrm {TV}}^{\star }}^{-1} : \left[ \varphi (\eta )\, \varvec{C}^{\textcircled{2}} : \varvec{\varepsilon }_{\mathrm {tr}}^{\textcircled{2}} + \left[ 1 - \varphi (\eta )\right] \varvec{C}^{\textcircled{1}} : \varvec{\varepsilon }_{\mathrm {tr}}^{\textcircled{1}}\right] \ne \langle \varvec{\Phi }^{\varvec{\varepsilon }_{\mathrm {tr}}} \rangle _{\Delta V} \ . \end{aligned}$$
(55)

Equally weighted Reuss–Sachs homogenization

Assuming a spatially independent stress distribution on microscale within Reuss–Sachs homogenization formats

$$\begin{aligned} \varvec{\sigma }^{\textcircled{1}} = \varvec{\sigma }^{\textcircled{2}} \equiv \langle \varvec{\Phi }^{\varvec{\sigma }} \rangle _{\Delta V} = \varvec{\sigma } \ , \end{aligned}$$
(56)

an effective (\(=\) macroscopically linked) material law in terms of equal and linear weighting functions, i.e., \(\langle \varvec{\Phi }^{\varvec{\varepsilon }_{\mathrm {e}}} \rangle _{\Delta V} = \langle \varvec{\Phi }^{\varvec{S}} \rangle _{\Delta V} : \langle \varvec{\Phi }^{\varvec{\sigma }} \rangle _{\Delta V}\), is obtained by interpolating the single-phase elastic compliance tensors, such that

$$\begin{aligned} \langle \varvec{\Phi }^{\varvec{\varepsilon }_{\mathrm {e}}} \rangle _{\Delta V} = \varvec{S}_{\mathrm {RS}}^{\star } : \varvec{\sigma } = \left[ \varphi (\eta )\,\varvec{S}^{\textcircled{2}} + \left[ 1 - \varphi (\eta ) \right] \varvec{S}^{\textcircled{1}} \right] : \varvec{\sigma } \ . \end{aligned}$$
(57)

Equally weighted partial rank-one homogenization

In case of equally weighted homogenization, the jump of deformation gradient

$$\begin{aligned} \llbracket \varvec{F}\rrbracket _{\Delta V} := \langle \varvec{\Phi }^{\varvec{F}} \rangle _{\Delta V_{2}} - \langle \varvec{\Phi }^{\varvec{F}} \rangle _{\Delta V_{1}} \equiv \varvec{a}\otimes \varvec{N} \end{aligned}$$
(58)

is again subjected to the Hadamard jump condition (kinematic compatibility) on the weighted subdomain averaged interface with normal vector \(\varvec{N}\). Consequently, assuming explicit, macroscopic links on weighted subdomain averages of the Helmholtz potential, i.e.,

$$\begin{aligned} \langle \Phi ^{\widetilde{\psi }}(\varvec{F}) \rangle _{\Delta V_{i}} = \langle \Phi ^{\widetilde{\psi }} \rangle _{\Delta V_{i}}(\langle \varvec{\Phi }^{\varvec{F}} \rangle _{\Delta V_{i}}) =: \widetilde{\psi }^{\textcircled{i}}(\langle \varvec{\Phi }^{\varvec{F}} \rangle _{\Delta V_{i}})\,, \end{aligned}$$
(59)

yields its macroscopic counterpart

$$\begin{aligned} \langle \Phi ^{\widetilde{\psi }} \rangle _{\Delta V} = \;&\varphi (\eta )\,\widetilde{\psi }^{\textcircled{2}}(\langle \varvec{\Phi }^{\varvec{F}} \rangle _{\Delta V} + [1-\varphi (\eta )]\,\llbracket \varvec{F}\rrbracket _{\Delta V}) \nonumber \\&\quad + [1-\varphi (\eta )]\,\widetilde{\psi }^{\textcircled{1}}(\langle \varvec{\Phi }^{\varvec{F}} \rangle _{\Delta V} - \varphi (\eta )\,\llbracket \varvec{F}\rrbracket _{\Delta V}) \,. \end{aligned}$$
(60)

Again, minimization w.r.t. the jump vector \(\varvec{a}\) leads to static compatibility on the weighted subdomain averaged interface and therefore the relaxed potential entering the macroscopic continuum reads

$$\begin{aligned} \langle \Phi ^{\widetilde{\psi }} \rangle _{\Delta V}^{\mathrm {rel}} = \inf _{\varvec{a}}\left\{ \langle \Phi ^{\widetilde{\psi }} \rangle _{\Delta V}(\langle \varvec{\Phi }^{\varvec{F}} \rangle _{\Delta V}, \eta , \varvec{a}\otimes \varvec{N})\right\} = \mathcal {F}(\langle \varvec{\Phi }^{\varvec{F}} \rangle _{\Delta V}, \eta , \varvec{N}) \,. \end{aligned}$$
(61)

Conclusion and Outlook

In summary, all of the presented homogenization schemes—Taylor–Voigt, Reuss–Sachs and rank-one convexification—include the previously described definitions for macroscopic links, domain relations and macroscopic identity conditions at least at some point within their specific frameworks, even in the case of equally weighted averaging operators. The justification of these assumptions are typically based on specific restrictions for microstructural distributions of physical field quantities, e.g., jump conditions, spatial homogeneity within subdomains, specific boundary conditions, etc., or on topological assumptions on the microstructure itself, e.g., definition and existence of an interface normal vector \(\varvec{N}\) or specific phase distributions within the interface. A physical interpretation of these assumptions may only be given partially or even omitted in order to obtain premeditated results. In conclusion, the problem of making reasonable assumptions within the underlying microscopic, representative volume element may be shifted toward the definition of appropriate weighting functions.

To this end, the following question arises: Let \(\varvec{\varvec{A}}_{0} = \varvec{\mathcal {F}}(\varvec{A}_{1}, \varvec{A}_{2}, ..., \varvec{A}_{n})\) be a given explicit macroscopic relation between \(n+1\) quantities. Do there exist respective weighting functions \(\varvec{\Phi }_{\varvec{\alpha }_{i}}\) corresponding to microscopic quantities \(\varvec{\alpha }_{i}\) (\(i\in \{0,1, ..., n\}\))—subject to microscopic relations \(\varvec{\alpha }_{0} = \varvec{f}(\varvec{\alpha }_{1}, \varvec{\alpha }_{2}, ..., \varvec{\alpha }_{n})\), macroscopic links, domain relations and identity conditions, only justified by specific assumptions on the microstructural level without including additional information from the macroscopic continuum—so that \(\varvec{A}_{i} = \langle \varvec{\Phi }^{\varvec{\alpha }_{i}}_{\varvec{\alpha }_{i}} \rangle _{\Delta V}\)?

To further justify the investigation of unequally and non-linearly weighted averaging operators, consider the following argument based on propositional logic: If for a given set of microscopic constraints \(\mathcal {C}\)

$$\begin{aligned} \mathbb {A} :\Longleftrightarrow \,\Big [\,&\exists _{1}\,\varvec{f}^{\star }:\;\, \forall \,\varvec{\alpha }_{i} \;\,\text {subject to}\;\,\mathcal {C}: \nonumber \\&\quad \quad \quad \langle \varvec{\alpha }_{0} \rangle _{\Delta V} = \varvec{f}^{\star }\big ( \langle \varvec{\alpha }_{1} \rangle _{\Delta V}, \langle \varvec{\alpha }_{2} \rangle _{\Delta V}, ..., \langle \varvec{\alpha }_{n} \rangle _{\Delta V}\big ) \Big ] \nonumber \\&\quad \Longrightarrow \nonumber \\ \Big [\,&\exists\, (\varvec{\Phi }_{\varvec{\alpha }_{0}},\,\varvec{\Phi }_{\varvec{\alpha }_{1}},\,\varvec{\Phi }_{\varvec{\alpha }_{2}}, ...,\,\varvec{\Phi }_{\varvec{\alpha }_{n}},\,\varvec{\mathcal {F}}): \;\, \forall \,\varvec{\alpha }_{i} \;\,\text {subject to}\;\,\mathcal {C}: \nonumber \\&\quad \langle \varvec{\Phi }_{\varvec{\alpha }_{0}}^{\varvec{\alpha }_{0}} \rangle _{\Delta V} = \varvec{\mathcal {F}} \big ( \langle \varvec{\Phi }_{\varvec{\alpha }_{1}}^{\varvec{\alpha }_{1}} \rangle _{\Delta V}, \langle \varvec{\Phi }_{\varvec{\alpha }_{2}}^{\varvec{\alpha }_{2}} \rangle _{\Delta V}, ..., \langle \varvec{\Phi }_{\varvec{\alpha }_{n}}^{\varvec{\alpha }_{n}} \rangle _{\Delta V}\big ) \Big ] \Longleftrightarrow : \mathbb {B} \end{aligned}$$
(62)

and consequently

$$\begin{aligned} \lnot \, \mathbb {B} \;\Longrightarrow \; \lnot \, \mathbb {A} \,. \end{aligned}$$
(63)

To put this implication into words, if there exists no macroscopic relation to be derived based on unequally and non-linearly weighted averaging operators—neglecting trivial solutions, e.g., \((\varvec{\Phi }_{\varvec{\alpha }_{0}},\,\varvec{\Phi }_{\varvec{\alpha }_{1}},\,\varvec{\Phi }_{\varvec{\alpha }_{2}}, ...,\,\varvec{\Phi }_{\varvec{\alpha }_{n}},\,\varvec{\mathcal {F}}) = \varvec{0}\) and similar expressions—, there can also be no solution within the conventional, unweighted homogenization approach. The specific derivation of such averaging operators, however, is the subject of on-going work.

Despite these considerations, an additional—and possibly the most crucial—problem in terms of homogenization assumptions within phase field modeling should be outlined carefully. Whereas microscopic relations are usually of the type \(\varvec{\alpha }_{0} = \varvec{f}(\varvec{\alpha }_{1}, \varvec{\alpha }_{2}, ..., \varvec{\alpha }_{n})\), macroscopic continuum models instead—especially within Allen-Cahn frameworks—are typically characterized by relations involving the rate of additional degrees of freedom, e.g., order parameters, so that \(\dot{\varvec{A}}_{n+1} = \varvec{\mathcal {G}}(\varvec{A}_{0}, \varvec{A}_{1}, ..., \varvec{A}_{n})\). However, it does not exist a notion of homogenization based on a microscopic problem formulated without time derivatives toward a rate dependent model on the macroscale. All efforts regarding consistent homogenization assumptions within phase field modeling thus propose a staggered structure decomposed into a transient and a stationary problem, i.e., \(\dot{\varvec{A}}_{n+1} = \varvec{\mathcal {G}}(\varvec{A}_{0})\) and \(\varvec{A}_{0} = \varvec{\mathcal {F}}(\varvec{A}_{1}, \varvec{A}_{2}, ..., \varvec{A}_{n})\). Consequently, even if the stationary part could be derived by appropriate homogenization methods, the transient part represents an additional modeling step on the macroscale. A recently investigated, alternative procedure, that directly results in a macroscopic relation with associated rates of homogenized quantities, could eventually be derived by prescribing evolution equations on the microscale itself and applying the concept of multiscale convergence, as outlined in [27, 28] for partial differential equations including the Landau-Ginzburg relations as a special case. Such an approach involves multiple spatial and temporal scales so that not only effective interpolation rules between single-phase properties but also long-term evolution and stationary microstructure prediction could potentially be obtained in a mathematically rigorous fashion. We will aim to address this important aspect in future work on general theoretical considerations regarding homogenization assumptions in phase field modeling of multi-phase solids.