Introduction

Nickel titanium (Ni–Ti, or nitinol) has become the material of choice for numerous medical applications, including peripheral vascular and venous stents, endovascular aneurysm repair grafts, heart valve frames, and filters [1, 2]. The unique superelastic properties of nitinol have enabled many of these interventional procedures, as no other biocompatible material is capable of recovering its shape after delivery through minimally invasive access ports and sheaths. Superelastic recovery strains of over 10% can be realized by the reversion of stress-induced monoclinic B19’ martensite (M) to a simple cubic B2 austenite parent phase (A). We will use “AMA” to describe this traditional view of nitinol superelasticity: stress inducing M directly from A and reverting directly back to A.

In many instances, however, a third phase called the R-phase (R) competes with the M and A phases. The R-phase is trigonal, intermediate to A and R in terms of entropy, and is very similar to A from a transformational strain perspective. This three-phase competition is akin to the vapor–liquid–ice system of water in that the three phases create a triple point in stress (or pressure)–temperature space. The structure and thermodynamics of these three phases have been studied extensively [3,4,5,6,7], but here we need only concern ourselves with two concepts that dominate this three-phase competition for stability:

  1. 1.

    The kinetic barriers between the A and R-phase are far smaller than between either A and M or between R and M. This results in a much smaller hysteresis (typically 0–3 °C compared to 30–60 °C between A and M or R and M). This, in turn, creates an asymmetry, making the R-phase far more prevalent in cooling than heating. In fact, it is common that R enjoys a wide temperature range of stability upon cooling, while M reverts directly to A upon heating.

  2. 2.

    The strain differences between M variants are 5–10 times greater than between R variants, greatly diminishing the effect of stress on the stability of R though the Clausius–Clapeyron relationship. Thus, it is easy to form R through cooling, but much less common to stress induce R, simply because stress has so little effect on the stability of R.

Often, it has been erroneously suggested that superelasticity only occurs when Af (the Austenite finish temperature) is below ambient temperature (see, for example, [8]). Superelasticity, however, relies on the stress-induced formation of M and the reversion of M upon unloading. Because R and A are nearly identical from a strain perspective, R can equally well serve as the parent in a superelastic transaction. In such a case, R is the direct parent of M during loading and unloading. We will use “RMR” to describe this variation of nitinol superelasticity: stress inducing M directly from R and reverting directly back to R.

One reason that R is often ignored as a suitable parent to M is that it requires the triple point to be above ambient temperature, which is unusual for a medical device operating at 37 °C. To achieve this, one must stabilize R with respect to both A and M. It has recently been shown, however, that one can obtain excellent RMR superelasticity at body temperature by aging in the 100–300 °C range [9]. As shown in Reference [9], these low-temperature aging treatments cause clustering of nickel atoms, as well as fine coherent precipitation of Ni4Ti3, though the details of why nickel clustering stabilized R require further investigation. Recognizing now that either R or A can be the direct parent to stress-induced M, it begs to be asked whether there are advantages to having R as the parent in a medical implant. And to answer that, we turn our attention now to fatigue.

Once delivered to the anatomical site of therapy, nitinol implants must endure complex and demanding fatigue loads related to the pulsatile cycle of the circulatory system, in addition to other cyclic biomechanical forces such as respiration, gait, or Valsalva. In applications such as these, fatigue durability is often the most demanding design constraint [10, 11]. For these reasons, the industrial community has extensively researched the mechanisms that govern fatigue and fracture in nitinol material. We know, for example, that fatigue cracks almost invariably nucleate at microstructural discontinuities at or near surfaces, most notably at non-metallic inclusions and related voids [12, 13]. To address this, industry has invested considerable resources to develop high-purity nitinol alloys, with fewer and smaller inclusions. These high-purity materials have less than 100 wppm oxygen and carbon, and are becoming the standard for the most demanding durability-constrained medical applications [14,15,16].

Nucleation, however, is only part of the story: once nucleated, cracks grow through the accumulation of a small amount of microstructural damage with each cycle [17,18,19], expressed by the area encompassed by the cyclic stress–strain curve (Fig. 1). It has been suggested by at least one investigator [20] that decreasing the cyclic modulus and/or increasing the stress hysteresis should reduce the cyclic damage by increasing the strain that can be accommodated elastically.

Fig. 1
figure 1

Tensile results for straight wire specimens with conventional (AMA) heat treatment, and an R-phase stabilizing heat treatment (RMR) demonstrate an increase in compliance when R is the parent of M (dashed red) versus when A is the parent (solid blue) (Color figure online)

Full size image

It has also been observed that the transformation to and from M is imperfectly accommodated, creating local stress heterogeneities, plasticity, and residual islands of non-transformed material at the phase boundary [21]. In this view, the damage ultimately resulting in crack nucleation and growth is thought to be related to the volume of material affected by the B19’ martensitic transformation in each fatigue cycle [22].

Following these suggestions, Shamimi et al. [9] pointed out that since the R-phase is more compliant than is austenite, it should allow more strain to be elastically accommodated, decreasing that circumscribed area of the stress–strain duty cycle shown in Fig. 1. Furthermore, with R-phase accommodating more of the deformation elastically, the relative volume of material transforming to and from B19’ martensite may be favorably reduced. It was therefore suggested that RMR cycling should slow the accumulation of plasticity and improve fatigue lifetime as compared to AMA cycling.

This study is intended to test the hypothesis that one obtains better fatigue life when R is the superelastic parent of M due to an increased cyclic compliance. As with all fatigue studies, proving this is difficult for a host of reasons, and literature baseline data are of little relevance: fatigue life is highly sensitive to the details of the experiment, so one must conduct careful side-by-side studies of two populations, with both arms made from the same raw material, carefully tuned to the same upper and lower plateaus, as well as UTS values.

Two completely independent side-by-side comparative studies are reported below, using two different source materials and two different test methods. The first battery of tests was conducted on conventional source wire using tension–tension samples. While such tests can be tedious to run, this configuration samples the largest amount of material and thus tends to produce the most consistent results. Unfortunately, it is not representative of most medical devices which primarily employ bending, exposing nitinol’s inherent tension/compression asymmetry [23, 24]. The second battery of tests was thus intended to focus on bending. Both arms of this second test battery also employed a high-purity material. Of course since the high strain areas are much more localized, one expects a longer lifetime regardless of the starting material [22].

Materials and Methods

Differential scanning calorimetry (DSC) was performed using a TA Instruments Q100 according to ASTM F2004 [25]. Tensile testing was conducted using an Instron load frame equipped with a temperature control chamber and a video extensometer. All tensile testing was conducted at 37 °C, according to ASTM F2516 [26]. Fatigue tests were performed in displacement control using an Instron E3000 test frame, provisioned to test and monitor five individual specimens per test. Samples were submerged in deionized water held at 37 °C for the duration of the test.

Experiment 1: Straight Wire Tension–Tension Fatigue

Tension–tension fatigue specimens were fabricated from 0.280-mm-diameter nickel titanium wire, Ni50.8Ti49.2. Composition and related material properties are detailed in Table 1. The oxygen + nitrogen and carbon levels by mass were 0.08% and 0.03%, respectively. The source material was received in an as-drawn state, with 40% cold work by area reduction in the final draw step, and wire segments were subsequently straightened under 5.5 MPa tension at 530 °C for 4.5 min. All specimens were masked and electropolished to achieve a 0.228-mm-diameter gauge section, 37.0 mm in length. Prior to electropolishing, the specimens were heat treated using two different processes. The AMA group was aged at 530 °C for 4.5 min in a salt bath (in a stress-free state) then immediately quenched. The RMR group received the same 4.5-min aging at 530 °C, then was subsequently aged at 250 °C for 15 h (also stress free) and quenched.

Table 1 Straight wire specimens subjected to 107 cycles of tension–tension fatigue
Full size table

Fatigue testing itself employed a total of 148 fatigue wire specimens cycled to 10 million cycles (or fracture) at mean strains ranging from 0.5 to 5.8%, and strain amplitudes ranging from 0.15 to 0.45%. Prior to cycling, all specimens were first loaded to 6% tensile strain (also described as “pre-strain,” which is recognized to influence durability performance [27]), then allowed to recover, before calibrating the load and displacement at each station. Testing included a total of 101 AMA specimens and 47 RMR specimens. Samples that failed at the grips, outside the gauge section, were excluded from the test population.

Experiment 2: Formed Wire Bending Fatigue

Formed wire bending samples were fabricated from 0.406-mm-diameter, high-purity superelastic wire, Ni50.8Ti49.2, received in an “as-drawn” condition, with 40% cold work in the final draw step. Composition and related material properties are detailed in Table 2. The oxygen + nitrogen and carbon levels by mass were < 0.006% and < 0.002%, respectively. AMA samples were heat treated under tension on a forming mandrel at 525 °C for 3 min, then electropolished to a nominal wire diameter of 0.381 mm. The RMR samples were subjected to a second 250 °C stress-free heat treatment for 15 h, then electropolished identically.

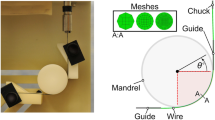
Table 2 Formed wire specimens subjected to 106 cycles of bending fatigue
Full size table

Figure 2 depicts the sample geometry used for the formed wire bending fatigue tests, using a similar approach as described by [28]. The design was intended to represent a portion of a simple stent-like structure, of the type often used to support endografts for treatment of abdominal aortic aneurysms (AAA) or thoracic aortic aneurysms (TAA). This specimen is formed from high-purity nitinol material, as now commonly specified for durability-critical medical applications. The component is formed by wrapping "as-drawn" wire in tension around pins on a mandrel, and heat treating to set the desired shape. For these experiments, sections of the formed structure were fixed in grips as shown in the left panel of Fig. 2. Finite element analysis (FEA) was used to model the strain levels in the nitinol component corresponding to vertical displacement of the grips. An iterative series of FEA simulations were completed to determine crosshead positions necessary to achieve desired levels of maximum mean strain and strain amplitude in the component. For this experiment, the most critical strains were confirmed to localize at the central apex, as represented by the red area in the central panel of Fig. 2. All fractures were observed to occur at this location.

Fig. 2
figure 2

Formed wire specimen positioned in grips (left), strain localization during cycling (middle), and deformation during cycling (right)

Full size image

Results

Experiment 1: Straight Wire Tension–Tension Fatigue

DSC results in Fig. 3 illustrate the temperatures of the forward and reverse stress-free phase transitions for the two heat treatment conditions.Footnote 1 Note that the temperature at which martensite reverts on warming, indicated by M*p, is equivalent for both groups. For the AMA condition, austenite finish temperature (Af) is significantly below body temperature at 15 °C. For the RMR condition, Af is above body temperature of 37 °C.

Fig. 3
figure 3

DSC results for straight wire specimens with conventional (AMA) heat treatment, and an R-phase stabilizing heat treatment (RMR)

Full size image

Tensile test results of the two conditions are shown in Fig. 1. These results confirm that the upper plateau stress (UPS) and lower plateau stress (LPS) are equivalent for both groups, at 500 MPa and 300 MPa, respectively. The inflection in the loading curves of the RMR condition confirms that whatever austenite that might have been present before loading has transformed to R well before stress inducing M. With a duty cycle operating between LPS and the UPS, the AMA material cycles between A and M, while the RMR material cycles strictly between R and M with no appearance of A.

Figure 4 summarizes all tension–tension fatigue tests, with AMA results at the left and RMR at the right. The color of the symbols represents the probability of fracture at each mean strain and strain amplitude. The size of the symbol represents the number of samples at each strain level, with the smallest representing N = 1 and the largest N = 5. Dashed lines estimate the threshold for 50% probability of fracture, and solid lines estimate the threshold for 0% probability of fracture. Note the discontinuity in the RMR 0% probability threshold, a consequence of insufficient results at the 3.5% mean strain level. While the population size and strain distributions are different between the AMA and RMR groups, the RMR process appears to show a fatigue durability advantage.

Fig. 4
figure 4

Fatigue testing results for AMA (left) and RMR (right) processes, in the form of a strain limit diagram

Full size image

Figure 5 is another view of the fatigue results, representing the cycles to failure on a logarithmic scale vs. strain amplitude, with AMA results the left and RMR at the right. Runouts are represented by > symbols. Here, we see a clear durability advantage for the RMR process. For the non-runout samples, the strain amplitude at fracture was 0.29% (95% CI 0.26–0.32%) for the AMA group, compared with 0.38% (95% CI 0.35–0.42%) for the RMR group. This suggests that the RMR treatment confers a 0.1% strain amplitude advantage relative to the AMA treatment.

Fig. 5
figure 5

ε–N diagram for straight wire tension–tension fatigue testing results

Full size image

Table 1 summarizes the results for both groups. To eliminate a possible bias related to differences in population size and strain levels between the groups, a strain-matched subset of data was selected and is similarly detailed in this table. The subset includes 22 samples from each group selected to match the distributions of mean strain and strain amplitude as closely as possible.

Figure 6 is a Kaplan–Meier plot comparing the probability of 10 million cycle survival for both subsets. The shaded bands represent 95% simultaneous confidence intervals for each trace. In this subset, the AMA group includes 13 failures and nine runouts (41% survival). The RMR group includes 5 failures and 17 runouts (77% survival). With a relatively small sample size, and overlapping confidence bands, these results are not statistically definitive. However, this analysis also supports a durability advantage for the RMR process. Differentiation between the groups is evident by 100,000 cycles, and the advantage of the RMR process increases for the duration of the 10 million cycle test.

Fig. 6
figure 6

Kaplan–Meier survival plot for a strain-matched subset of 22 AMA and 22 RMR straight wire samples

Full size image

Experiment 2: Formed Wire in Bending Fatigue

As with the first experiment, the second heat treatment in the RMR group was intended to influence only the R-phase transition, while minimizing the influence on reversion of M and thus minimizing differences in mechanical properties. Figure 7 shows phase transition temperatures measured by DSC. Here, we see that the low-temperature aging treatment increased the R-phase reversion temperature (Af) by 35 °C, from 0 to + 35 °C, while the martensite reversion peak increases by only 6 °C from − 11 to − 5 °C.

Fig. 7
figure 7

DSC results for formed wire specimens with conventional (AMA) heat treatment, and an R-phase stabilizing heat treatment (RMR)

Full size image

Figure 8 shows the tensile test results of straight wires heat treated identically to the formed AMA and RMR specimens. The plateau stresses are again nearly equal for both groups, with a UPS of 500 MPa and an LPS of 300 MPa, and the R-phase transition for the RMR material is evident at about 250 MPa. This confirms that when this material is cycled between lower and upper plateau stresses, it is cycling between R and M. Note that in this case, the lower Af value results in a small superelastic response as R reverts to A during unloading, while in the previous case the deformed R variants remained after unloading.

Fig. 8
figure 8

Tensile results of formed wire specimens with conventional (AMA) heat treatment, and an R-phase stabilizing heat treatment (RMR), tested at 37 °C

Full size image

A total of 46 formed wire specimens were cycled for up to 1 million cycles in displacement controlled cyclic fatigue, at a mean strain of 1.2%. The AMA group included strain amplitudes ranging from 0.72 to 1.42% (N = 28, μ = 1.02%, σ = 0.15%). The RMR group included strain amplitudes ranging from 0.91 to 1.42% (N = 18, μ = 1.16%,  σ =  0.23%). In this testing, the AMA group included two runouts and 16 fractures, and the RMR group included 12 runouts and 6 fractures. Table 2 summarizes results for the formed wire bending fatigue experiment.

Figure 9 illustrates results for all 46 formed wire samples, plotting cycles to failure on a logarithmic scale vs. strain amplitude. Fractured specimens are represented by filled symbols, diamonds for AMA, and circles for RMR. Runouts are represented by unfilled symbols, + for AMA, and > for RMR. Solid and dashed lines represent a first-order least squares fit of the AMA and RMR data, respectively. Here, again with formed wire specimens, we see a durability advantage for the RMR process. Of the N = 28 AMA specimens, 24 fractured before reaching 1 million cycles, at a mean strain amplitude of 1.03% (95% CI 0.95–1.09%). Of the N = 18 RMR specimens, 6 fractured before reaching 1 million cycles, at a mean strain amplitude of 1.35% (95% CI 1.20–1.50%). In summary, in this experiment, the probability of survival for RMR was 67% compared with 14% for AMA, and fractured RMR specimens tolerated average strain amplitudes 0.3% greater than those of the AMA group.

Fig. 9
figure 9

ε–N diagram for formed wire bend fatigue testing results

Full size image

Figure 10 is a Kaplan–Meier survival plot comparing the probability of 1 million cycle survival for the RMR group vs. a subset of the AMA group having and equal sample size (N = 18 each), matching strain amplitude levels as closely as possible. The AMA subgroup included strain amplitudes ranging from 0.72% to 1.42% (N = 18, μ = 1.03%, σ = 0.16%), and the RMR group included the same population as described above. 11.1% of the AMA subgroup survived 1 million cycles, compared with 66.6% survival for the RMR group. Again, the small sample size results in overlapping confidence bands, but there is a clear trend differentiating performance of the two groups. The durability advantage of RMR is apparent by 20,000 cycles under these conditions.

Fig. 10
figure 10

Kaplan–Meier survival plot for a strain-matched subset of 18 AMA and 18 RMR formed wire samples

Full size image

Conclusions

Two carefully controlled batteries of fatigue tests confirm the hypothesis that fatigue damage is reduced when R rather than A is the superelastic parent phase to M. This improvement appears to result from an increased cyclic compliance (see Fig. 11) that increases the proportion of cyclic strain accommodated elastically, thereby reducing the rate at which transformation-related plasticity is accumulated. The durability benefit was demonstrated in tension–tension fatigue testing of straight wire specimens, and bend fatigue testing of formed wire specimens representative of many medical components. The benefit was demonstrated in standard purity and high-purity material, confirming that this approach can be used to further increase the known durability benefit of high-purity material. Testing demonstrates that the benefit in terms of strain amplitude threshold may be as much a 0.1% to 0.3%, and the probability of fracture-free survival may be doubled or more for up to 10 million cycles.

Fig. 11
figure 11

Magnified view of the 2% mean strain 0.3% strain amplitude cyclic loop from Fig. 1, showing the decreased cyclic compliance and reduced enclosed area (energy) of the RMR vs. AMA specimen, and the increased proportion of cyclic strain accommodated by elasticity for the RMR treatment (εelRMR)

Full size image

RMR superelasticity is accomplished by aging at a low temperature, which increases the Af temperature and triple point without affecting the stress at which martensite forms (related to the M peak) and the stress at which it reverts (related to the M* peak).

It should be noted that changing the parent to the R-phase does come at a cost, even if small. One must assume that the 0.2–0.5% strain typically recovered as R reverts to A may not be recovered superelastically at body temperature. This strain is small and can usually easily be accommodated during the design phase by adjusting the as-manufactured shape. The result is a slight loss in superelastic strain.

Finally, we note that while these two tests support the hypothesis in two testing modes and using two material purities, more testing would be most helpful. For example, one expects the differences to be most pronounced at low mean strains and least pronounced at high mean strains when the compliance becomes dominated by the martensite phase.