Introduction

Superelastic NiTi shape memory alloy wires were developed 30 years ago for applications in medical devices, particularly to cardiovascular stents [1]. Since that time, they have been spreading into other engineering areas such as e.g., seismic protection in civil engineering, actuation in robotics, or wide range of novel applications in automotive and aerospace sectors [2]. The wires show excellent superelasticity at body temperature 37 °C [1, 3,4,5,6] for which they were developed but this does not warrant same performance at different temperatures. Once the test temperature exceeds 50 °C [4], the cyclic superelastic stress–strain responses of the commercially available superelastic NiTi wires gradually change and become unstable.

Commercial medical grade NiTi wires commonly possess a nanograin microstructure [5] resulting from unique combination of cold work and heat treatment applied in their production. This microstructure, however, changes when the wire is deformed plastically and/or heated to temperature higher than that applied during the production heat treatment. As a result, the functional properties of the wire, including the stability of its cyclic superelastic response, change. In fact, this frequently happens during the shape setting of already superelastic wires [7, 8].

Since superelasticity and actuation are primarily of interest in the SMA research, cyclic stress–strain tests at constant temperature and/or cyclic strain-temperature tests at constant stress have been typically focused in the literature. The tensile stress–strain tests until rupture were systematically performed 30 years ago when the superelastic NiTi technology was being developed [1], but these tests seem to be currently out of interest.

However, the superelastic NiTi wires exhibit instability of cyclic stress–strain response and related functional and structural fatigue, which represents serious problems for many promising engineering applications. It was linked to the transformation—plasticity coupling in the literature [3,4,5,6,7,8,9,10,11]. In this respect, tensile tests until rupture on NiTi wires have become of interest again. Motivated by this, we have performed systematic tensile tests until rupture on superelastic NiTi wires having various microstructures in a wide temperature range from − 100 to + 200 °C and for selected microstructures and test temperatures we carried out also 20 superelastic cycles to characterize their instability in cyclic superelastic loads. The results were complemented by the investigation of lattice defects created by superelastic cycling by transmission electron microscopy/TEM/. The work complements our earlier research focusing functional property setting of superelastic NiTi wires by electropulse heat treatment [3, 5, 6, 12].

Materials and Methods

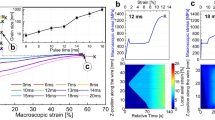
The experiments were performed on a commercial superelastic NiTi wire produced by Fort Wayne Metals, FWM #1 (Ti–50.9 at.%Ni, degree of cold work 42.1%, 0.1 mm in diameter). The ends of the NiTi wire were crimped by two steel capillaries (outer diameter 1.6 mm), while it was subjected to electropulse treatments and tensile testing. The wire was heat treated by an electropulse method [12] using the MITTER apparatus (Fig. 1). A controlled pulse of electric power was applied to the pre-strained cold worked NiTi wire (50 or 30 mm long) at room temperature 20 °C applying electric power density of 160 W/mm3 for pulse times 0–20 ms (Fig. 2a). When such short time electric power pulse is applied, temperature sharply increases until the end of the pulse time and then decreases with a much slower cooling rate [12]. Application of pulse times longer than 22 ms with power density 160 W/mm3 causes rapid oxidation, even at short millisecond times, which severely damages the wire. Hence, 20 ms was set as the maximum pulse length in present research. Evolution of the wire temperature during the electropulse treatment is calculated by heat equation as described in [12]. Controlling the electric power in time during the electropulse heating is essential for repetitiveness of the results on different wires, since the electric resistance of the heated wire changes in time quite substantially (Fig. 2a). In heat treatments with pulse times shorter than 20 ms, the heating stopped at pulse times denoted in Fig. 2a by dashed lines. Lower maximum temperatures were thus reached in shorter heat treatments [12]. In addition to the temperature evolving during the fast heating, Fig. 2a shows also electric resistance of the wire and tensile stress, which provide time resolved information about the recovery and recrystallization processes during the constrained heating [8, 12].

Fig. 1
figure 1

Thermomechanical tester MITTER with highlighted key components featuring 450 N load cell, stepper motor, position encoder, environmental chamber, electrically conductive grips, and closed-loop LabView based control system

Full size image
Fig. 2
figure 2

a Electropulse heat treatment of a cold worked NiTi wire. Variation of the temperature T, tensile stress σ and electric resistance R of the wire preloaded to 200 MPa during the application of a pulse of constant electric power P = 37.8 W for pulse time t = 20 ms to 30 mm long wire. b Microstructures observed by TEM in selected NiTi wires heat treated by electric power pulses of various times. The noise on the electric resistance signal appears when prior and after the power pulse since only 3 mA current is applied out of the pulse in order not to heat the wire

Full size image

Figure 2b shows examples of microstructures observed by TEM in NiTi wires heat treated by selected pulse times. Microstructure of the cold worked wire (0 ms) consists of a mixture of austenite, amorphous phase, residual martensite, and localized deformation bands consisting of austenite twins (inset) [5]. As the degree of the recovery and recrystallization increases with increasing pulse time, martensite and internal stress gradually disappear, density of defects decreases and size of the recrystallized grains increases from ~ 10 nm (10 ms wire) up to more than 6 μm (20 ms wire) [12]. The power density and pulse time used in the heat treatment thus result in a specific microstructure and related functional properties of the heat treated wire. See Refs. [5, 6, 8, 12] for further details on the microstructure and functional property setting of superelastic NiTi wires via electropulse heat treatment. Since power density is constant in present experiments, we use the pulse time to denote wires with specific microstructures. An alternative approach, consisting in keeping constant pulse time and varying electric power density, is equally possible and was employed e.g., in Ref. [6].

The MITTER apparatus (Fig. 1) was used for electropulse heat treatments as well as tensile testing. It consists of an environmental chamber, two electrical conductive grips, a 450 N load cell, a linear actuator, a position sensor and closed-loop Labview control system. The environmental chamber (Peltier elements, resistive elements and liquid nitrogen vapors) enables to maintain homogeneous temperature around the thin wire. The conductive grips enable the application of electric pulse to the prestressed wire as well as the evaluation of the electric resistance of the thermomechanically processed wire. The control of temperature, stress, or strain is implemented by the close-loop Labview control system. The 30 mm long wires were used in tensile tests until rupture (to keep the 50% deformed wires inside the environmental chamber) and the 50 mm long ones for both cyclic superelastic tests and tensile tests until rupture (on wires which fracture at ~ 15% strain).

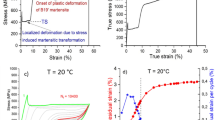
Stress–strain-electric resistance responses of heat treated NiTi wires determined from tensile tests until rupture and cyclic superelastic tests were characterized by a set of material parameters introduced in Fig. 3. Besides the commonly used material parameters (Young’s modulus of austenite EA, Young’s modulus of stress induced martensite EM, upper plateau stress σ UPP and lower plateau stress σ LOP , upper plateau strain ε UPP , and lower plateau strain ε LOP , unrecovered strain in a single cycle εUS, accumulated unrecovered strain ε accUS ), additional material parameters characterizing plastic deformation beyond the end of the stress plateau (yield stress σY, yield strain εY, maximum stress σmax, and maximum strain εmax) are introduced in this work.

Fig. 3
figure 3

Definition of material parameters evaluated from: a engineering stress–strain curves recorded in tensile tests till rupture, b cyclic stress–strain curves upon tensile cycling at constant temperature (1st curve—blue, 20th curve—red). The material parameters are: Young’s modulus of austenite EA, Young’s modulus of martensite EM, upper plateau stress σ UPP , upper plateau strain ε UPP , lower plateau stress σ LOP , lower plateau strain ε LOP , yield stress σY, yield strain εY, maximum tensile stress (strength) σmax, maximum tensile strain (ductility) εmax, unrecovered strain in one cycle εUS, accumulated unrecovered strain in 20 cycles ε accUS (Color figure online)

Full size image

Since the analysis of experimental results relies on the comparison of the results measured on different wire samples at different temperatures, repeatability of the results of heat treatments as well as tensile tests is absolutely crucial. Two essential measures were adopted to warrant repetitiveness. Samples were taken from a single spool containing 1800 m long cold worked NiTi filament. Environmental furnace was used to control the test temperature and to prevent air flow around the thin wire sample during both Joule heating and tensile testing. This is essential since the heated and/or deformed wires transform martensitically and exchange latent heat with the environment. In tensile tests, upper plateau stress value scatters ~ 10 MPa, tensile strength ~ 20 MPa, upper plateau strain ~ 0.1% strain and ductility ~ 1% strain, which is similar to the scatters measured on straight annealed commercially produced FWM #1 NiTi wires.

The cooling/heating dilatometry experiments were performed using thermal/mechanical analyser LINSEIS TMA PT1600) under 100 mN force (13 MPa tensile stress). Samples for TEM observation of lattice defects in microstructures of deformed wires were prepared by FIB-SEM technique in a form of lamellas using FEI Quanta 3D electron microscope. The TEM observations were carried out by FEI Tecnai F20 field emission gun microscope operated at 200 kV with a double tilt specimen holder.

Experimental Results

Before presenting the results of tensile tests, let us briefly explain what we mean by the term “microstructure”. Generally, the starting microstructure of NiTi wire refers to its grain size, density of lattice defects, texture, precipitates, inclusions, internal stress etc. As we use a single cold worked NiTi wire in all heat treatments, we prepare wire samples having a range of microstructures that are highly predetermined by the cold worked material state (same hot/cold work, texture, precipitates, inclusions etc.) and differ due to the different degree of recovery and recrystallization that occurred during the fast electropulse heating [12]. The maximum temperature reached during the short pulse heating (Fig. 2a) depends on the length and diameter of the wire, parameters of the electric pulse (mainly electric power and pulse time) as well as on the environmental conditions (heat transfer to the environment) controlled by the environmental furnace. While keeping the supplied electric power density constant, the varying pulse time can thus be linked to the various maximum temperatures which results in specific microstructure and properties of the heat treated wire (Fig. 2b). Hence, since we used the power density 160 W/mm3 in all heat treatments, we use the pulse time to denote the NiTi wire with specific microstructure to be studied in tensile experiments. For example, the “16 ms wire” means the cold worked NiTi FWM #1 wire heat treated by controlled pulse of electric power density 160 W/mm3 for 16 ms (Fig. 2). In fact, the pulse time “quantifies” the microstructure it produced—i.e., the microstructure denoted as “16 ms” can be associated with specific electric resistance, grains size, texture, transformation temperatures, internal stress, density of lattice defects, etc., which allows for evaluating microstructure dependence of parameters determined from tensile tests. Since the previous hot processing and cold work applied to the wire have a very significant impact on the wire microstructure, it shall be pointed out that the above established link between pulse time and microstructure applies only to the cold worked wire taken from the same spool (same hot processing and cold work).

Transformation temperatures of the wire (Rs, Ms, Mf, Af) were evaluated by cooling/heating dilatometry experiments (Fig. 4). Transformation temperatures of the alloy in the fully annealed state (20 ms wire) were determined as Ms = − 25 °C, Mf = − 38 °C and Af = − 10 °C. Cold work and short pulse annealing (below 11 ms) shifts the Ms temperature below the dilatometer’s temperature range limit − 150 °C. The Ms temperature gradually increases with increasing pulse time up to − 25 °C for 20 ms wire (Fig. 4b). R-phase appears in 8–16 ms wires and the Rs temperature decreases linearly with increasing pulse time until it reaches the Ms temperature and does not appear anymore. It is interesting to note that the 12–16 ms wires develop significant tensile strain upon cooling under 13 MPa stress. This strain appears when the B2 austenite transforms to the R-phase as well as while it is being cooled within the R-phase state. It sums up with the tensile strain due to the R-B19′ transformation. We assume that this deformation appearing spontaneously under very low stress is due to an internal stress persisting in the microstructure of 0–17 ms wires in combination with the R-phase appearing in 12–16 ms wires (Fig. 4b). The dilatometry experiments thus, in addition to the determination of the phase transformation temperatures, bring additional information on the microstructure (internal stress) of heat treated wires. However, these phenomena were not further investigated in this work.

Fig. 4
figure 4

Transformation temperatures of NiTi wires determined from dilatometry experiments: a strain–temperature responses recorded upon cooling/heating of denoted NiTi wires under 13 MPa constant stress, b transformation temperatures Rs, Ms, Mf, Af and dilatometer strain due to phase transformation εDIL in dependence on wire microstructure (pulse time). Transformation temperatures were determined from the thermal expansion—temperature response upon cooling/heating, B2-R and R-B19′ can be well distinguished upon cooling, upon heating only Af temperature was evaluated (Color figure online)

Full size image

It shall be also mentioned that the microstructures obtained by the short electropulse treatment slightly differ from those obtained by heat treating in a furnace. Heat treatment of cold worked NiTi is being typically performed at 400–500 °C, slightly below the recrystallization temperature [13]. Following such long time heat treatments, lattice defects and internal stress partially remain in the microstructure. In case of short time electropulse treatments, on the other hand, much higher maximum temperature is reached for a very short time. The short pulse treatment promotes recrystallization [12] over recovery of defects. Degree of the recovery and growth of recrystallized grains in early stages can be precisely controlled by selecting proper pulse time [12]. Unique microstructures with small grains (20–100 nm) free of lattice defects can be achieved. No precipitation/precipitate dissolution takes place during the short pulse.

Finally, it shall be pointed out that the effects of grain size, density of lattice defects, texture, precipitates, inclusions, and internal stresses characterizing the microstructure of a specific NiTi wire on mechanical and functional properties of the wire are interrelated. One can investigate effect of one of the characteristics provided that the other remains constant. Since this is not the case in present experiments (Fig. 2b), we prefer to characterize wire microstructures by the pulse times and not by e.g., grain size, as frequently reported in the literature.

Tensile Tests Until Rupture at Room Temperature

Results of tensile tests until rupture at room temperature on heat treated NiTi wires having various microstructures (pulse time 0–22 ms) are presented as engineering stress-engineering strain curves (Fig. 5a) and true stress-true strain curves (Fig. 5b). Stress–strain curves of wires selected for systematic tensile testing in wide temperature range are in bold and colored (pulse times (8, 10, 12, 14, 15, 16, 18, 20) ms). It is well known, that tensile deformation of NiTi wires in the plateau range is localized in macroscopic interfaces—martensite band fronts propagating at constant force along the wire and converting the austenitic microstructure into the presumably martensitic microstructure within the martensite band [14]. It is much less known that these wires fail by strain localization in necks. The necking was observed in tensile tests to precede the fracture of the wire at ~ 13% strains (pulse times < 14 ms) as well as at ~ 50% strain (pulse times > 5 ms) (Fig. 5). To demonstrate the necking deformation preceding the fracture of the wires, SEM pictures of the 14 ms wire fractured at 12.8% strain were inserted into Fig. 5b.

Fig. 5
figure 5

Tensile tests on NiTi wires having various microstructures until rupture at room temperature: a engineering stress–strain curves, b true stress–true strain curves. Stress–strain curves corresponding to wire samples investigated in tests at various temperatures are in bold. SEM picture of 14 ms NiTi wire fractured at 12.8% strain is included in b to demonstrate the failure of this wire via strain localization and necking (Color figure online)

Full size image

Figure 5a shows variation of the engineering stress–strain curves at room temperature measured on NiTi wires having various microstructures (pulse time). In the range 0–8 ms, the inelastic deformation due to stress induced martensitic transformation gradually develops from linear stress–strain response of cold worked wire (0 ms) to plateau type superelastic curve with 3.7% plateau strain of the 8 ms wire, the wire strength (maximum tensile stress) remains approximately constant (~ 2 GPa) and ductility (maximum tensile strain) increases from ~ 4 up to ~ 14%. In the range 8–14.3 ms, upper plateau stress decreases, upper plateau strain increases and yield stress decreases with increasing pulse time. The ductility remains around ~ 14%. Above 14.3 ms pulse time (Fig. 6b), the wire suddenly starts to deform plastically beyond the 14% strain (from 14.3 to 14.5 ms the ductility increases from 14 up to 35%). In the 14.5–20 ms range, the yield stress and upper plateau stress further decrease and the upper plateau strain further increases with pulse time. The ductility reaches 64% in the case of the 20 ms wire.

Fig. 6
figure 6

Stress–strain curves recorded in tensile tests until rupture at various test temperatures on NiTi wires with different microstructures denoted by pulse times (8, 10, 12, 14, 15, 16, 18, 20) ms (Color figure online)

Full size image

As concerns the true stress-true strain curves (Fig. 5b), they are meaningless within the plateau range, where the deformation is localized in martensite band fronts. Beyond the yield strain, however, these curves inform correctly the stresses and strains in tensioned wires and provide correct information on the strain-hardening rate for various microstructures and temperatures. Note that the wires, which do not suffer from necking around the yield strain, are those which show remarkable strain-hardening rate upon further loading. The 8–14 ms wires fractured at ~ 13% true strain because the strain-hardening rate beyond the yield strain is not large enough to prevent strain localization in neck. Whether the strain localization in a neck will occur at ~ 13% strain is controlled by the Considére criterion (Eq. 1) for the stability of tensile deformation [15]. This criterion relates the magnitude of the true stress σT with the strain hardening at given true strain εT.

$$\frac{{\partial \sigma_{\text{T}} }}{{\partial \varepsilon_{\text{T}} }} = \sigma_{\text{T}}$$
(1)

The strain-hardening rate increases with increasing pulse time from 14.3 to 20 ms because the microstructure of the wires treated with longer pulses is less resistant against dislocation slip. The 15–20 ms wires fractured via strain localization and necking at ~ 45% true strain when they reach ~ 1600 MPa true stress, at which the criterion (1) does not support homogeneous tensile deformation anymore. Knowledge of the strain-hardening rate is very important when studying the mechanism and stability of homogeneous tensile deformation of NiTi wires in dependence on the strain, temperature, and wire microstructure. As this is, however, beyond the scope of this work, we will show further on only engineering stress–strain curves, which are more common in the SMA field.

Tensile Tests Until Rupture at Various Test Temperatures

Stress–strain curves recorded in tensile tests until rupture on various NiTi wires (pulse times (8, 10, 12, 14, 15, 16, 18, 20) ms) in temperature range from − 100 up to 200 °C are shown in Fig. 6. Material parameters determined from those stress–strain curves are presented in Figs. 7 and 8 in dependence on the test temperature and wire microstructure (pulse time). Elastic deformation of austenite is homogeneous, deformation within the upper plateau range due to the stress induced martensitic transformation is localized within martensite band fronts, further deformation beyond the end of the stress plateau is homogeneous until the strain localizes into neck and wire fractures either at ~ 13 or ~ 45% true strain.

Fig. 7
figure 7

Temperature and microstructure (pulse time) dependence of material parameters determined from tensile tests until rupture: yield stress (a, b), upper plateau stress (c, d), upper plateau strain (e, f) and maximum tensile strain (g, h)

Full size image
Fig. 8
figure 8

Temperature dependence of material parameters (upper plateau stress σ UPP , yield stress σY and upper plateau strain ε UPP ) determined from tensile tests until rupture on NiTi wires having different microstructures [denoted by pulse times (8, 10, 12, 14, 15, 16, 18, 20) ms]. Individual graphs represent stress-temperature diagrams of particular NiTi wires complemented with upper plateau strain. The black lines represent the forward B2-B19′ transformation lines. Transformation lines for B2-R transformation (green) and martensite reorientation (orange) are added for completeness (Color figure online)

Full size image

Figure 7 provides comprehensive information on the temperature and microstructure (pulse time) dependencies of material parameters determined from tensile tests in Fig. 6. The upper plateau stress, yield stress, upper plateau strain, and maximum tensile strain vary significantly with the test temperature (left column figures) as well as with the wire microstructure (right column figures). Let us mention only the most important results. The yield stress does not depend much on the test temperature but varies strongly with the microstructure (decreases with increasing pulse time). While the upper plateau stress linearly increases with increasing temperature in case of 8–13 ms wires, for 15–20 ms wires, these dependencies deviate from the linearity at temperatures characteristic for each microstructure. Interestingly, these deviations coincide with the pronounced maxima of upper plateau strains, as denoted by vertical dashed lines (Fig. 7a, c, e). The maxima of upper plateau strains thus appear for pulse times, at which the upper plateau stress approaches the yield stress (Fig. 7b, d, f), as denoted by the vertical dashed lines in right figures. The ductility increases sharply with increasing pulse time in the range 14–16 ms (Fig. 7h). The sharp change of ductility is observed at any test temperature in the range −90 to 100 °C, it is less sharp at 150 °C. The ductility of all wires decreases with temperature increasing above 100 °C.

Figure 8 presents those results in a form of stress-temperature diagrams with superimposed upper plateau strains for all studied microstructures. From those diagrams, it becomes very clear that the temperature dependencies of the upper plateau strains show pronounced maxima at temperatures, at which the increasing upper plateau stress reaches the yield stress. Since this tends to happen at lower temperatures in wires heat treated with longer pulse times, the plateau strain maxima occur at ~ 160 °C in case of 14 ms wire but at 60 °C in case of 20 ms wire.

Cyclic Superelastic Tests

There is no information on the strain reversibility, hysteresis and cyclic stability of superelastic responses in Figs. 5, 6, 7, and 8, which is of main interest for engineering applications of superelastic NiTi wires. To present relevant experimental evidence on that, we have performed cyclic superelastic tensile tests on selected NiTi wires (pulse times (7, 8, 10, 12, 14, 15, 16, 18, 20) ms) at room temperature (Figs. 9, 10, 11, 12) and on the 12 ms wire at various temperatures (Figs. 13, 14, 15). The wires were deformed up to the end of the stress plateau determined in the tensile tests until rupture.

Fig. 9
figure 9

Cyclic superelastic tensile tests (20 cycles) at room temperature 20 °C on NiTi wires with different microstructures denoted by pulse times (7, 8, 10, 12, 14, 15, 16, 19, 20) ms

Full size image
Fig. 10
figure 10

Evolution of material parameters determined from cyclic superelastic tests at room temperature (Fig. 9) with number of cycles: a upper plateau stress, b upper plateau strain, c lower plateau stress, d unrecovered strains in one cycle

Full size image
Fig. 11
figure 11

Material parameters determined in the 1st and 20th superelastic cycle on NiTi wires with various microstructures (pulse times) shown in Fig. 9: a upper plateau stress, b upper plateau strain, c lower plateau stress, d accumulated unrecovered strain in 20 cycles

Full size image
Fig. 12
figure 12

TEM micrographs of lattice defects created by cyclic superelastic deformation of 16 ms NiTi wire at 20 °C temperature after 1, 2, 5, 20 cycles

Full size image
Fig. 13
figure 13

Cyclic superelastic tests on 12 ms NiTi wire (20 cycles) performed at various test temperatures (0, 20, 40, 60, 80, 100)  °C

Full size image
Fig. 14
figure 14

Evolution of material parameters determined from cyclic superelastic tests on 12 ms NiTi wire at various temperatures (Fig. 13) with number of cycles: a upper plateau stress, b upper plateau strain, c lower plateau stress, d unrecovered strain in one cycle

Full size image

Figure 9 shows cyclic stress–strain curves evolving in 20 tensile cycles at room temperature for wires having different microstructures. Figure 10 shows how material parameters (upper plateau stress, upper plateau strain, lower plateau stress, and unrecovered strain) evolve with cycle numbers while Fig. 11 shows how these parameters (accumulated unrecovered strain instead of unrecovered strain) depend on the microstructure (pulse time). Except for the 7 ms wire, which deforms homogeneously from the 1st to the 20th cycle, all tested wires exhibit superelastic plateau in the 1st cycle due to localized superelastic deformation. However, the 16–20 ms wires maintain this type of behavior only in the first few cycles.

The cyclic superelastic responses of 7–12 ms wires (Fig. 9) are relatively stable. The magnitude of the upper plateau strain and area of the hysteretic loop increase with increasing pulse time due to gradually increasing involvement of the stress induced martensitic transformation upon cycling. In the 14–20 ms wires, the plateau strain further increases with increasing pulse time but the cyclic stress–strain response becomes gradually unstable so that the area of the hysteretic loop and transformation strain decreases upon cycling.

Figure 10 shows the evolution of material parameters upon cycling. The upper plateau stress slightly decreases upon cycling in all wires (Fig. 10a). The lower plateau stress (Fig. 10c) practically does not change upon cycling in case of 7–12 ms wires but increases with increasing pulse time in the early cycles of 14–20 ms NiTi wires. The upper plateau strain remains constant in 7–12 ms wires but decreases with number of cycles in case of 14–20 ms wires. The unrecovered strain in a superelastic cycle also decreases with number of cycles in 14–20 ms wires, but surprisingly, maximum unrecovered strain is not observed in the first cycle but in the second or third cycle (Fig. 10d). The stability of cyclic superelastic deformation of various NiTi wires can be assessed by comparing the parameters characterizing the cyclic stress–strain responses in the 1st and 20th cycle in Fig. 11. Clearly, the cyclic stability of superelastic responses of 7–12 and 14–20 ms wires is rather different (Fig. 11b, d).

In order to investigate the origin of the instability of cyclic deformation, lattice defects created during the cyclic superelastic deformation of one selected 16 ms wire at room temperature were observed by TEM on thin lamellas prepared from cycled wires (Fig. 12). The rationale behind selecting the 16 ms wire is that the grains are sufficiently large and free of lattice defects from previous cold work, which enables TEM analysis of lattice defects created by the cyclic superelastic deformation. The cyclic instability of the 16 ms wire in the first 20 cycles at room temperature (Fig. 9g) allows for linking the TEM results to the cyclic instability. The results are presented in a form of microstructures observed in wires deformed by 1, 2, 5, 20 cycles in Fig. 12. Let us point out that, according to our in situ X-ray diffraction experiments on the 16 ms wire [16], this wire transforms at room temperature almost completely to the martensite phase in the first cycle. This means that the crystal lattice was completely martensitic at the end of the stress plateau in the first cycle (Fig. 9g). All stress induced martensite retransformed back to the austenite upon unloading and we could only observe isolated slip dislocations left within the microstructure after the first cycle (Fig. 12—1st cycle). This corresponds to the experimental observations that almost all strain was recovered in the first cycle. However, significantly higher dislocation density was observed after the second and fifth cycles. This corresponds to the fact that maximal unrecovered strains were observed in the 2nd and 3rd cycle (Fig. 10d). After the 5th cycle, the observed density of dislocations became considerably higher and even isolated {114} austenite twins were occasionally found (see [4, 7, 8] for identification and analysis of the {114} austenite twins in deformed microstructures). After the 20th cycle, when the accumulated unrecovered strain approached nearly 7%, {114} austenite twins became common defects in the microstructure of cyclically deformed 16 ms wire.

The stability of cyclic superelastic response depends not only on the wire microstructure but also on the test temperature. Figure 13 shows cyclic superelastic stress–strain response of 12 ms wire at (0, 20, 40, 60, 80, 100)  °C test temperatures. The 12 ms wire has a nano-grained microstructure (Fig. 2b) almost identical to the microstructure of the commercial straight annealed FWM #1 wire [5]. Note that, while the superelastic stress–strain response of the 12 ms wire is relatively stable in the narrow temperature range 0–20 °C, it gradually becomes unstable at elevated temperatures 40–100 °C. While the upper plateau stress decreases upon cycling, the lower plateau stress remains constant (Fig. 14). The upper plateau strain and unrecovered strain became unstable and evolve upon cycling, particularly at elevated temperatures above 40 °C. Figure 15 assesses the cyclic stability of the 12 ms wire at various temperatures by comparing the parameters characterizing the cyclic stress–strain responses in the 1st and 20th cycle. It shows that the cyclic instability starts to develop at temperatures just above the body temperature.

Fig. 15
figure 15

Material parameters determined in the 1st and 20th superelastic cycle on 12 ms NiTi wire at various temperatures (Fig. 13): a upper plateau stress, b upper plateau strain, c lower plateau stress, d accumulated unrecovered strain in 20 cycles

Full size image

Discussion

Temperature and Microstructure Dependence of Tensile Deformation

Since the superelastic functional properties of NiTi wires are affected by the microstructure and test temperature, one needs to investigate both (or at least to be sure that starting microstructure of the wire does not change when investigating the effect of test temperature and vice versa). Such results are, however, very rare in the literature. Taking advantage of the electropulse treatment, we prepared set of NiTi wires with very different microstructures and performed systematic tensile tests until rupture (Figs. 4, 5, 6, 7, 8) and cyclic superelastic tests (Figs. 9, 10, 11, 12, 13, 14, 15). As far as we are aware of, this is the first ever dataset of this kind published in the literature.

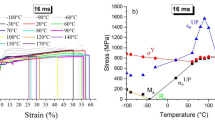
Figure 16 shows material parameters characterizing superelastic functional behavior at room temperature shown in Fig. 5 in dependence on the wire microstructure evolving with increasing pulse time. When the cold worked wire is electropulse treated with pulse time 0–8 ms (relatively low maximum temperatures reached during the electropulse heating), recovery of lattice defects, disappearance of internal stresses and residual martensite from the cold worked microstructure [12] mainly take place, as evidenced by the electric resistance decreasing with increasing temperature (Fig. 2a). The electric resistivity of the heat treated wire measured later prior the tensile test at room temperature (Fig. 16a) decreases with increasing pulse time in the range pulse times 4–8 ms. The microstructure changes occurring from the 4 to the 8 ms allow for the stress induced martensitic transformation to gradually take place in subsequent tensile tests. As a result of the increasing involvement of stress induced martensitic transformation with increasing pulse time, stresses required to generate inelastic strains (in the range 800–2000 MPa) decrease significantly with increasing pulse time so that first superelastic plateau with localized deformation appears on the stress–strain curve of the 8 ms wire (Fig. 5a). Surprisingly, yield stress and strength of the wire are not affected by the heat treatments in the range 0–8 ms, where the stress–strain behavior develops from the elastic to the plateau type superelastic.

Fig. 16
figure 16

a Material parameters characterizing the microstructure of NiTi wires: electric resistivity of the wire ρ measured at room temperature (scales mainly with the density of lattice defects, internal stress and residual martensite fraction in the initial mainly austenitic microstructure) and grain size dgr, b Material parameters determined from tensile tests at room temperature characterizing the functional behavior of the wires with different microstructures: yield stress σY, upper plateau stress σ UPP , upper plateau strain ε UPP and accumulated unrecovered strain in 20 cycles ε accUS . The electric resistivity ρ is presented only for 0–8 ms wires, since it is affected by the presence of the R-phase at room temperature in case of 8–12 ms wires

Full size image

When heating the wire up to higher maximum temperatures with pulse times 8–12 ms, the upper plateau stress decreases with increasing pulse time (Fig. 16b) due to the upward shift of the Ms temperature with pulse time (Fig. 4b). This is reflected by the shift of transformation lines describing the increase of upper plateau stress with increasing temperature in the stress-temperature space (Fig. 7c). The upper plateau strain increases up to 6% at 12 ms (Fig. 16b), the yield stress slightly decreases but still remains quite high (above 1400 MPa). When heating the wire to even higher maximum temperatures with pulse times 12–20 ms, plateau stress remains nearly constant, yield stress sharply decreases and upper plateau strain further increases up to 9%. Small recrystallized grains (~ 50 nm) that start to appear in the microstructure of 12 ms wire grow with increasing pulse time up to ~ 6 μm of the 20 ms wire (Fig. 2b). The superelasticity of the 12 ms wires is fully developed. With increasing pulse time or test temperature, the cyclic stress–strain response becomes gradually unstable (Figs. 9, 13, 16b). The 12 ms wire thus exhibits optimum stable superelasticity at room temperature. Generally, however, wires with specific microstructures show best superelastic properties at characteristic specific temperatures (Fig. 7).

Although it is generally accepted that functional properties of NiTi depend on the microstructure and test temperature, it is rather difficult to explain how, since the effects of microstructure and temperature are cross related as mentioned above. Taking advantage of having a dataset obtained from large number of tensile tests (Figs. 6, 7, 8), we have interpolated the experimentally measured temperature and pulse time dependencies of material parameters (yield stress, upper plateau stress, upper plateau strain, maximum strain, and accumulated unrecovered strain) and plotted the results in Fig. 17, which thus serves as a useful guide to the superelasticity of the electropulse treated FWM #1 wires. It shows how the yield stress, upper plateau stress and ductility depend on the pulse time and test temperature. It clearly denotes the pulse time—temperature conditions for which the long plateaus are observed in tensile tests and how the cyclic superelasticity becomes gradually unstable with increasing pulse time and temperature.

Fig. 17
figure 17

Temperature—microstructure (pulse time) interpolated maps of parameters characterizing superelasticity of FWM #1 NiTi wires (yield stress, upper plateau stress, upper plateau strain, maximum tensile strain, and accumulated unrecovered strain). White crosses denote the [microstructure, temperature].points, in which tensile tests till rupture (a–e) and cyclic superelastic tests (f) were performed (Color figure online)

Full size image

There is a question up to which extent are these results relevant generally, particularly, whether the conclusions (i–v) apply for NiTi wires heat treated in a furnace. Due to the lack of systematic experiments on NiTi wires with defined microstructures in the literature, this is difficult to assess. Our limited data on NiTi FWM #1 wires heat treated in a furnace at various temperature/time suggest that the conclusions (i–v) approximately hold.

Large Deformation Beyond the Yield Strain

As ordered intermetallics, most of shape memory alloys suffer from poor ductility. In a contrast, NiTi alloys can be relatively easily cold worked [13, 17]. Although the stresses applied during the cold deformation tend to be high, very large deformations can be reached without introducing cracks not only by cold drawing or cold rolling, but also by severe plastic deformation processing [18, 19]. TEM investigations of lattice defects in heavily deformed NiTi revealed deformation bands composed of austenite twins, among which {114} austenite twins were reported most frequently [20,21,22]. Some authors [18, 22] suggested that those austenite twins were produced by deformation twinning in heavily plastically deformed B19’ martensite and inherited into the austenite phase during the reverse transformation. The {114} austenite twins were, however, observed also in the microstructures of NiTi polycrystals subjected to tensile or compressive deformation just beyond the yield strain [23, 24] or created upon heating the oriented martensite under tensile stress [7, 8, 25]. Nevertheless, in spite of this experimental evidence, deformation mechanisms activated in tensile tests beyond the yield strain in wide temperature range are usually referred to as a plastic deformation of martensite in the NiTi literature without specifying how it actually proceeds.

The ductility of the NiTi wire in tensile tests, as shown in this work, depends mainly on its initial microstructure and much less on the test temperature (Figs. 5, 6, 17d). The effect of microstructure on the malleability of NiTi is characterized by the decrease of the yield stress and increase of the strain-hardening rate with increasing pulse time (Figs. 7b, 16b, 17a). Conventionally, the decrease of the yield stress with increasing pulse time would be ascribed to the enhanced dislocation slip in recovered and recrystallized microstructures (Fig. 2). However, several intriguing questions appear when considering this more closely (Fig. 6e–h). First of all, dislocation slip in austenite can be safely excluded since the stress induced martensitic transformation always precedes the second yielding (the wire is always in oriented martensite phase when the applied stress approaches the yield stress) and very little is known about the dislocation slip in oriented martensite phase. So how the plastic deformation occurs then if not via dislocation slip? Why the yield stress practically does not depend on the test temperature (Figs. 7a, 17a)? Why the ductility changes stepwise with the microstructure (Figs. 5, 7h, 17d)? These questions can hardly be answered assuming dislocation slip in stress induced martensite as the dominating deformation mechanism. Yes, dislocation slip definitely proceeds in the wire deformed beyond the yield strain but is it the key deformation mechanism at the yield strain? Previous in situ studies of martensite deformation of NiTi by TEM [26] and neutron diffraction [27, 28] support the activity of deformation twinning in the oriented martensite [23, 29, 30] beyond the yield strain level. However, as far as we are aware of, Figs. 5, 6, 7, and 8 present first ever systematic experimental data in the literature on the microstructure and temperature dependence of the yield stress, strain hardening and ductility of NiTi wires deformed beyond the yield strain level. Further research by ex situ TEM, in situ electric resistance, in situ synchrotron X-ray diffraction [30] is currently underway to explore this deformation mechanism in detail.

Let us assume that deformation twinning in the stress induced martensite plays a significant role in the deformation beyond the yield strain [28, 30]. We know that all tested wires failed by strain localization and necking (Fig. 5) either at ~ 14% strain (7–14.3 ms wires) or at ~ 50% strain (14.5–20 ms wires). Assuming that the key deformation mechanism around the yield strain is the deformation twinning in oriented martensite, whether the strain will localize in a neck or not at ~ 14% strain, depends on the true stress and strain-hardening rate associated with deformation twinning. If strain hardening rate due to deformation twinning is large enough, the wire deforms homogeneously, if not, strain localization takes place via necking and wire fractures according to the Considere’s criterion (Eq. 1) [15]. The experimentally observed microstructure and temperature dependence of the yield stress (Figs. 7a, b, 16b, 17a) thus has to be related to the microstructure and temperature dependence of deformation twinning not dislocation slip. The key question is then why the yield stress drops from 1800 to 400 MPa with increasing pulse time (Fig. 5a). It shall be due to the microstructure effect on deformation twinning in the range of grain sizes 10 nm–6 μm. Indeed, a pronounced size effect on deformation twinning has been recently observed in compression experiments on Ti single crystal nanopillars [31]. Assuming that the yield stress for deformation twinning in oriented martensite decreases with increasing grain size in accord with the size effect on deformation twinning reported in [31], the experimentally observed microstructure and temperature dependence of the yield stress (Figs. 7a, b, 16b, 17a) can be explained. The yield stress would strongly decrease with pulse time and would not depend much on the test temperature. On the other hand, care has to be taken since our TEM observations clearly show that dislocation activity accompanying the deformation twinning also increases with increasing temperature [30]. In the same range of pulse times and tests temperatures, the yield stress slightly decreases with increasing temperature (Fig. 8a).

Instability of Cyclic Superelastic Deformation

Finally, let us discuss the microstructure and temperature dependence of the instability in cyclic superelastic loading of NiTi wires. Considering the results in Figs. 9, 10, 11, 12, 13, 14, 15, and 16, one can conclude that the instability worsens with increasing pulse time and test temperature, which can be possibly explained by the increasing involvement of dislocation slip with increasing pulse time and test temperature. The dislocation slip is most likely responsible for generating small unrecovered strains when the plateau type response is retained upon cycling (Figs. 9a–f, 13a–d). We have recently rationalized these small unrecovered strains and dislocation defects created upon superelastic cycling by incremental dislocation slip taking place during the forward as well as during the reverse martensitic transformation [4]. It was revealed that the unrecovered strain is generated only if the transformation proceeds under external stress and that its magnitude increases with increasing temperature and stress at which the transformation proceeds. When the temperature, however, increased beyond ~ 100 °C, the unrecovered strain was found to increase even more dramatically [7], which was explained by the activation of the stress induced B2 ⇒ B19′ ⇒ B2T martensitic transformation [7, 8, 32] serving as a plastic deformation mechanism of NiTi at elevated temperatures.

The present results show how the cyclic superelastic response of NiTi wire depends not only on the test temperature (Fig. 13) but also on the wire microstructure (Fig. 9). The cyclic instability appears due to the combined effect of temperature and microstructure. At room temperature, the 12 ms NiTi wire is an ideal superelastic wire (Fig. 9) showing large plateau strain and stable superelasticity. However, this wire gradually develops cyclic instability with increasing temperature above 40 °C (Fig. 13). It appears that 8–10 ms NiTi wires would be more appropriate for stable superelastic functionality at elevated temperatures above 50 °C (Figs. 11, 17).

Lattice defects created by cyclic superelastic deformation of 16 ms wires were found to be mainly dislocations (Fig. 12). Note that, in spite of the large 8.5% plateau strain in the 1st cycle, the unrecovered strain is quite small (0.25%), which corresponds to the fact that only isolated dislocations were found in the deformed microstructure by TEM. However, large unrecovered strains (~ 1%) were observed from the 2nd to the 5th cycle (Fig. 10d), in which the observed dislocation density significantly increases (Fig. 12). Slip dislocations observed after the 10th superelastic cycle on the 16 ms wire were analyzed in detail in our earlier work [3] and associated with the 〈100〉/{011} austenite slip systems.

New surprising result reported in this work is the frequent appearance of {114} austenite twins in the microstructure of the 16 ms wire after the 5th and the 20th cycles. The {114} austenite twins were identified as the dominant lattice defects in the microstructure of wires deformed beyond the yield strain level at any test temperature [30] or within the microstructure of wires deformed in the temperature range, in which the long plateaus appear [32]. In particular, the {114} austenite twins were found in the 16 ms wire deformed at 90 °C but never at room temperature in a single loading unloading cycle below yield stress/strain. It was surprising to see gradual introduction of the {114} austenite twins into the microstructure by cyclic loading (starting from the 5th cycle).

The occurrence of the {114} austenite twins in the microstructure of superelastically deformed NiTi wire was ascribed in [7, 8, 32] to the activity of the stress induced B2 ⇒ B19′ ⇒ B2T martensitic transformation at elevated temperatures and stresses. Let us assume that this transformation becomes activated in superelastic tests at temperatures, at which the upper plateau stress approaches the yield stress (systematic experimental evidence for this claim is reported in [32]). The observation of {114} austenite twins in the microstructure of 16 ms wire cycled at room temperature suggests that the B2 ⇒ B19′ ⇒ B2T martensitic transformation takes place upon cyclic loading at lower temperature. The trends in Figs. 9 and 13, however, suggest that the cyclic instability dramatically increases when the upper plateau stress approaches the yield stress (Figs. 8, 17). In other words, it seems that the cyclic deformation promotes the activity of the B2 ⇒ B19′ ⇒ B2T martensitic transformation even under conditions, at which it has never been observed in the first cycle [32]. Considering this, we suggest that the instability of cyclic superelastic deformation shall also be linked to the onset of the activity of the B2 ⇒ B19′ ⇒ B2T transformation. This would explain why the instability is inversely related to the difference between the upper plateau stress and yield stress. The difference between the yield stress and upper plateau stress plot shown in Fig. 17 can be compared with the accumulated unrecovered strain. This proposition is somehow similar to the concept for the origin of functional fatigue of NiTi proposed recently by Gao et al. [33] who claimed that cyclically deformed NiTi displays irreversible changes of atomic configurations (called a symmetry-dictated non-phase-transformation pathway). This proposition does not disregard the role of dislocation slip in cyclic instability, as articulated in Ref. [4].

Conclusions

Superelastic NiTi wires were prepared from a single cold worked wire by various electropulse heat treatments. Wire samples having a wide range of virgin microstructures were subjected to tensile tests until rupture in a wide temperature range and cyclic superelastic tensile were performed for selected microstructures and test temperatures. Lattice defects created by superelastic cycling up to 1, 2, 5, 20 cycles at room temperature were analyzed by TEM.

Following key results were obtained.

  • The yield stress depends mainly on the wire microstructure (decreases with increasing pulse time) but varies only slightly with the test temperature;

  • The upper plateau stress depends on microstructure (decreases with increasing pulse time) due to the increase of the Ms temperature with increasing pulse time;

  • The upper plateau stress increases linearly with increasing test temperature in accord with the Clausius–Clapeyron equation only up to a certain temperature, at which it reaches the yield stress and becomes temperature independent at higher test temperatures;

  • Unusually long upper stress plateaus (12–18%) were observed at test temperatures and microstructures (pulse times), where the upper plateau stress reaches the yield stress (stresses driving the stress induced transformation and deformation twinning in the stress induced martensite become comparable);

  • The upper plateau strain maxima were explained by the activation of the stress induced B2 ⇒ B19′ ⇒ B2T martensitic transformation under specific [microstructure, temperature] conditions;

  • The instability of cyclic superelastic deformation increases as the upper plateau stress approaches the yield stress with increasing temperature and/or pulse time;

  • Cyclic superelastic deformation gradually introduces dislocation slip into the microstructure and promotes formation of {114} austenite twins upon later cycling;

  • The instability of cyclic superelastic deformation was linked to the dislocation slip accompanying martensitic transformation under stress at low temperatures and to the stress induced B2 ⇒ B19′ ⇒ B2T martensitic transformation at elevated temperatures;

  • The ductility changed stepwise with changing microstructure (increased from ~ 13% in case of 14 ms wire up to ~ 55% in case of 15 ms wire) and gradually decreased with temperature increasing above 100 °C.

The data presented in Figs. 5, 6, 9, and 13 can be downloaded from http://ofm.fzu.cz/special-topics.