Introduction

In shape-memory alloy research and technology, binary NiTi is still the most used alloy. Many recent research activities have concentrated on high-temperature shape-memory alloys, ternary or even quarternary systems, and novel Ta- or Ti-based alloy systems. The majority of fundamental studies even today are carried out using poly- or single-crystalline bulk materials, typically produced by melting processes. Complementing this traditional production route, a growing scientific community fabricates thin NiTi films via different gas-phase processes, such as chemical vapor deposition or physical vapor deposition. Those gas-phase thin film fabrication routes in principle offer several advantages, like the possibility of bypassing time- and energy-consuming thermo-mechanical treatments that typically need to be performed after the melting procedures. Especially medical applications require high-purity materials and typically small, tailor-made dimensions, ideally without the need of additional fabrication steps [1–3]. Gas-phase-based fabrication is a very efficient approach to meet these demands.

Gas-phase-based techniques also provide possibilities to create functional composite (layered) materials. For instance, much interest exists in materials where a substrate is combined with a functional material to create additional sensor capabilities. An even more ambitious, prospective idea is to design “self-healing” components based on shape-memory polymers or composite materials. To fully implement these novel ideas, it will be necessary to not only provide the composite materials but also to produce the materials in large dimensions and/or in forms like functional foils. Usually free-standing NiTi films are produced by wet-chemical processing [4]. The production of free-standing films without the need of complex chemical processes is another substantial challenge. One promising way to obtain free-standing NiTi films without post-deposition wet-chemical processing is the use of substrates that show a reduced wetting behavior for NiTi. Melting of NiTi is often performed using carbon crucibles. This serves as motivation to investigate if carbon-based substrates can also be used for gas-phase-based thin film deposition, and to study particularly if it is possible to deposit films with sufficient quality, and by what parameters the properties of the deposited films can be modified.

At present, graphene sheets are the best carbon-based substrate materials for basic research experiments: They are characterized by a nearly perfect, defect-free microstructure and they are readily commercially available. One common way to influence the adhesion between a substrate and NiTi is to insert thin metal layers in-between. In the present study, we use copper to form such an interlayer to improve the deposition of NiTi on graphene. We present microstructural details of the NiTi top layer that were unexpected and that have not been reported in the literature before. We then use complementary DFT calculations to rationalize our experimental observations. Recently, many first-principle investigations within the DFT framework on the details of interfaces between graphene and different metals have been performed [5–7]. But to the best of our knowledge, there are yet no studies that investigate NiTi-graphene and NiTi–copper interfaces, and our novel results therefore are also interesting from a theoretical point of view.

Materials and Experiments

Functional NiTi layers were deposited on graphene layer sheets on top of silicon substrates. The substrates were obtained from EMfutur, Spain. The physical vapor deposition (PVD) of the NiTi and additional copper (Cu) layers were performed by Acquandas (Germany). The produced NiTi thin films have a thickness of 2 μm and the Cu layer was a few nanometers. The deposition was carried out at room temperature, resulting in an amorphous microstructure. For crystallization, the thin films were subsequently heat-treated at 450 °C for a few minutes in order to obtain a cubic B2 structure in the NiTi layer with a composition of 50.6 at.% Ni. More details about the deposition process are described elsewhere [8]. In this study, we investigate two different types of stacked layers: a first series of samples consists of a NiTi layer directly deposited on top of the graphene sheet. In a second series of samples, a thin Cu layer (with a thickness of a few nanometers) was inserted between the graphene sheet and the NiTi layer on top.

The microstructures of both sample types were investigated by electron backscatter diffraction (EBSD) in order to characterize grain size and grain orientations in a Zeiss NEON40EsB scanning electron microscope (SEM). Bright field images were taken in a Hitachi H8100 (200 kV) type transmission electron microscope (TEM) in order to evaluate grain sizes on the nanometer scale. For the EBSD investigations, sample surfaces were polished in a VibroMet2 vibratory polisher (polishing time 24 h, in a MasterMet 2 solution by Buehler). The chemical composition was determined by energy-dispersive X-ray spectroscopy (EDX) carried out in the SEM and was confirmed to be 50.6 at.% Ni. The TEM samples were prepared by ion beam thinning in a precision ion polishing system (GATAN).

All computational investigations discussed in this article were carried out within the DFT framework. We used a recent version (0.91) of the GPAW DFT program package [9]. This program uses real-space uniform grids and multigrid methods to represent the Kohn–Sham orbitals and DFT potentials. We utilized atom-centered basis-functions together with the reasonably large double-zeta-polarized basis set. The functional suggested by Perdew and Wang (PW92) [10] within the local density approximation (LDA) was used in all calculations to approximate exchange and correlation energies. For the investigations considering the graphene layers, we included semi-empirical dispersion correction according to the Grimme DFT-D3 method [11].

The model systems were created based on structural data obtained from the Inorganic Crystal Structure Database (ICSD) [12] for graphene, Cu, and cubic NiTi. We used the Virtual Nano Lab software package [13] to construct supercells that represent different interfaces based on the bulk structures. We studied different orientations of the topmost NiTi layer: (100), (111), and (101). As a starting point of our calculations (prior to relaxation), the NiTi slab was rotated around the corresponding surface normal such that lattice mismatch between NiTi and the substrate was minimized (initial lattice strains in all cases considered further were below 3%). In all models, we considered at least five subsequent layers of NiTi on top (z-axis) of either five layers of Cu(111) or graphene (see also Fig. 2). We used periodic boundary conditions only in the x- and y-directions to account for the periodic structure of the surfaces. We used 36 (\(6 \times 6 \times 1\)) Monkhorst–Pack sampling k-points for Brillouin zone integration and we added 10 Å of vacuum above and below each interface slab. These settings were verified to lead to a total energy convergence (less than 2 meV/atom). We expect that the supercell approach utilized here gives a reasonable description of the energetics of the interface structures.

We started the geometry optimization by fixing the atoms of the graphene and copper layers and optimizing the positions of the atoms in the NiTi layer until the forces on the individual atoms were all below 0.025 eV/Å. In a subsequent step, we further relaxed all atoms until the forces were all below the selected threshold. We checked the stability of the obtained structures by calculating the vibrational spectra of the relaxed models and made sure that no negative frequencies are present. These final structures were used for the subsequent analysis.

Fig. 1
figure 1

Microstructural observations by experimental SEM and TEM techniques (viewing direction is top down on NiTi layer; parallel to the substrate material): a the inverse pole figure map of NiTi deposited on graphene sheet obtained by EBSD shows randomly oriented polycrystalline grains. Globular grain size is in the range of about 5–15 μm. b The inverse pole figure map of NiTi deposited on Cu-layer-graphene-sheet, obtained by EBSD, shows a prominent (101) fiber texture confirmed by the pole figure plot on the right side. The microstructure is polycrystalline and the grains are smaller than 1 micron. c The TEM image of NiTi deposited on Cu-layer-graphene-sheet confirms a small grain size in the range of about 20–100 nm.

Full size image

Effect of Graphene Layer on Preferential NiTi Grain Orientation

In all investigations discussed in this paper, we used the sample arrangement as described in the experimental section. Our main interest was to study the influence of the graphene on the growth and crystallization behavior of NiTi. An important observation in our deposition experiments was that, in case of a direct deposition of a functional NiTi layer on top of the graphene-covered substrate, the NiTi layer was only very weakly bonded. In this case, the NiTi thin films can be easily removed from the graphene substrates, and thus free-standing functional NiTi films can be produced. We also found that a Cu interlayer (with a thickness of a few nanometers) can be used to adjust the adhesion between graphene and NiTi and to improve the adhesion conditions in general. Comparing our samples to recent results obtained from experiments using silicon substrates [8, 14] together with Ni, Ti, and Cu interlayers, we did not expect to observe any influence on the NiTi grain orientation and grain size. However, after introducing the additional Cu layer between graphene and NiTi, we observed a quite different behavior, as discussed below.

We first discuss the direct deposition of NiTi on graphene (i.e., without an additional Cu interlayer). Representative results from a direct deposition experiment are shown in Fig. 1. A random grain orientation of NiTi is observed (see Fig. 1a). This is expected because the process conditions, with respect to temperature and substrate material, do not lead to epitaxial growth. It is well known that NiTi thin films deposited on silicon substrates exhibit a random grain orientation fully in line with our observations as shown in Fig. 1a [14]. Such a randomly oriented microstructure is typically characterized by globular grains with grain sizes that are in the range of about 5–15 μm. Analyzing the experimentally determined inverse pole figure maps, we did not observe a prominent fiber texture in deposition direction. Similar deposition experiments, but using the additional Cu interlayer between NiTi and graphene, did result in a very different microstructure. An example of a typical EBSD measurement is shown in Fig. 1b, indicating a prominent (101) fiber texture. In contrast, in Fig. 1a, we only observed very small areas (in the range of a few nanometers) of the NiTi thin film that show random orientations. The inverse pole figure map of the NiTi layer on top of graphene with an additional Cu interlayer is shown next to Fig. 1b. One can clearly see that this type of sample, apart from some small areas, exhibits a continuous (101) orientation in the direction of deposition. Based on the measured pole figure (next to Fig. 1b), we conclude that the grains represented in the map are rotated randomly in-plane. Furthermore, the grains are about one order of magnitude smaller in comparison to the grains resulting from the direct NiTi-graphene deposition (see Fig. 1a).

We emphasize that, since both sample types were heat-treated in the same way, our observations of strongly differing grain sizes and grain orientations are highly unusual. The EBSD results on the NiTi–Cu–graphene sample point out a grain size below one micron, but the data are limited by the spatial resolution of the EBSD technique. Our TEM investigations actually show grain sizes in the range of 20–100 nm as shown in Fig. 1c. Another interesting observation is that, even at high magnifications in the TEM, the samples containing additional Cu do not show Ni-rich precipitates (which one would expect in bulk NiTi after the heat-treatment used in this study [15, 16]). Considering the chemical composition, determined as 50.6 at.% Ni, one usually observes Ni-rich precipitates smaller than 100 nm. These microstructural effects in terms of grain orientation and size in thin NiTi films have not been reported before. Typically, the use of Si substrates in combination with thin Cu interlayers results in randomly oriented grains with no fiber texture of the topmost NiTi layer [1, 4, 8]. Obviously, our microstructural observations must be directly related to the novel combination of graphene and the Cu interlayer. We therefore calculated the interface conditions (e.g., binding energies and stacking geometries) for both interface types, with the aim of a more detailed analysis of the atomistic details; the corresponding theoretical results are discussed in the remainder of this paper.

Binding Energies from DFT Calculations

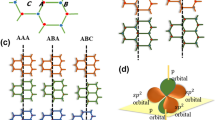
In Fig. 2, we show a summary of the DFT calculations. While DFT modeling of binding properties of interfaces between different metals is straight-forward, the hybrid system containing the metal alloy NiTi and graphene is more challenging [17]. It is already known that the pure metals can be divided into those with strong and those with weak interactions with graphene [18, 19]. While a strong metal–graphene interaction leads to a disturbed (doped) electronic structure of the graphene [5] and in low binding distances around 2 Å, weak bonding is only governed by the Van-der-Waals interactions [20] and hardly changes the electronic structure of graphene. Figure 2a shows sections of the relaxed model systems for different NiTi orientations on top of graphene, and Fig. 2b shows the corresponding results for the different NiTi orientations on top of Cu(111). The schematic figures show top and side views of the structures. For better visualization, particularly of the relative positions of the NiTi atoms compared to the substrate, we only show the first complete NiTi layer in the top views. The binding energies per atom as obtained from these calculations are listed in Table 1.

Fig. 2
figure 2

Model systems as obtained from the DFT calculations: a geometries of the graphene/NiTi interfaces for the (001), (111), and (101) planes of NiTi on top of the graphene substrate. The view from the bottom shows how the relaxation arranges the Ni and Ti atoms relative to the carbon atoms of the graphene. b Geometries of the different Cu(111)–NiTi interfaces for the different NiTi orientations. The Cu(111)–NiTi(101) interface was found to be the lowest energy structure. (Additional top/bottom layers that were used in the calculations have been removed for better presentation; black straight lines in the drawings represent the borders of the unit cells used for the calculations.)

Full size image

To quantitatively characterize the properties of the different interfaces, the binding energy between the graphene sheets and the metal is calculated as \(E_{\rm b} = E_{\rm C-M} - (E_{\rm C} + E_{\rm M})\), where \(E_{\rm C-M},\;E_{\rm C}\) and \(E_{\rm M}\) are the energies of the hybrid system, of isolated graphene, and of the metal, respectively.

Graphene–NiTi Interface

We start our discussion with the results of the graphene–NiTi interface. Figure 2a shows the optimized atomic structure of the graphene–NiTi interfaces. In experiments, a metal substrate is usually much thicker than the graphene layer. This represents a simplification to reduce the numerical effort in the DFT calculations. A larger number of metal layers in the DFT simulations do not change the results.

Table 1 Collection of the obtained binding energies from the DFT calculations together with the interface distances (db)
Full size table

From the obtained values for the binding energies, it is evident that the NiTi(111) surface has the largest binding energy of 0.35 eV/atom. However, this value is only slightly above the values obtained for the other two surface orientations, with 0.30 eV/atom for the (101) and 0.31 eV/atom for the (001) surface, respectively. During relaxation of the model systems, we observed a rather strong binding effect between graphene sheet and NiTi. In all configurations, the Ni and Ti atoms in the two layers closest to the graphene sheet tend to move towards positions as close as possible to the center of the carbon 6-rings of graphene. The Ti atoms moved into a distance of about 1.95 Å (111), 1.98 Å (001), and 2.03 Å (101) above the graphene sheet. These binding distances are in reasonable agreement with the experimental (2.1 Å) and DFT-calculated (2.08 Å) binding distances calculated for pure Ni on graphene [20]. We can therefore conclude that NiTi has a comparable bond strength to graphene quite similar to pure Ni. Moreover, the small differences between the calculated binding energies and binding distances for the different orientations of NiTi do not let us expect a preferred orientation for the samples with a direct NiTi–graphene interface; this agrees well with our experimental observations.

Fig. 3
figure 3

Calculated charge-density difference integrated over the x–y plane for the interface between a NiTi(111) and graphene, and b NiTi(111) and Cu. Positive values mean a gain of electron density, negative values correspond to a loss. The dashed line marks the middle between the NiTi surface and the substrate. The insets show the relation between the z-axis of the plot and the corresponding model systems. Different NiTi orientations only have a minor impact on the charge-density differences

Full size image

A more detailed insight into the origin of the NiTi–graphene interaction can be obtained by analyzing the charge transfer at the interface of the hybrid system. When two materials with different chemical potentials are combined, the alignment of the Fermi energy of the two materials results in a charge redistribution at the interface. The electron density is shifted towards the material with the lower chemical potential. The resulting partial charges at the interface generate an attractive Coulomb force that supports the binding. By the use of DFT calculations, one can estimate the magnitude of this effect. The difference between the ground state density of the relaxed graphene–metal hybrid system \(\rho _{\rm C-M}\) and of the sum of the density of the graphene \(\rho _{\rm C}\) and NiTi \(\rho _{\rm M}\) part \(\Updelta \rho = \rho _{\rm C-M} - (\rho _{\rm C} + \rho _{\rm M})\) gives an estimate about the magnitude of the redistributed electron density [21]. In Fig. 3a, we show \(\Updelta \rho\) along the z-direction perpendicular to the interface and integrated over the x–y plane to equalize local modulations of the density. One clearly sees that a distinct amount of charge is transferred from the metal to the graphene layer. As a result, the graphene layer gets partially negatively charged, the first two NiTi layers gain a positive charge and an interface dipole is formed. This electrostatic interaction within this configuration is mainly responsible for the binding. The charge transfer occurs mainly between the occupied metal d-states and unoccupied states in graphene. As a direct result, the carbon–carbon binding distance in the model structures increases by about 15% compared to the binding distance in the free graphene sheet.

Copper–NiTi Interface

The details of the binding between the two metals Cu(111) and NiTi are fundamentally different compared to the graphene–NiTi interface. Due to the metallic character of the bonding, only a small portion of charge is transferred through the interface. A typical representation of such a small charge transfer between NiTi(111) on Cu(111) is shown in Fig. 3b.

For the different orientations of NiTi on Cu, we obtain a much broader range of binding energies, with the highest binding energy of 0.23 eV/atom for the (101) orientation of NiTi. The binding energies for (111) and (001) are calculated to be 0.06 and 0.14 eV/atom, respectively. Unlike in the graphene–NiTi system, we observe a significant spread in binding energies between the different NiTi orientations. This numerical result also explains the more pronounced differences in the relaxed structures of the interfaces as shown in Fig. 2. From the three considered NiTi surfaces, the (101) surface matches best onto the Cu(111) surface. The Ni and Ti atoms almost perfectly fit into the position between the Cu atoms. This results in a very short binding distance of 2.05 Å , and the NiTi and Cu layers in direct contact are mostly undisturbed. In case of the NiTi(111) interface, after geometry optimization the Ni atoms acquire positions directly on top of the nearest Cu atoms. The small binding energy is reflected in the large binding distance of 2.95 Å  and also in a significant distortion of the first two NiTi layers compared to the NiTi(101) model structure. The results for the NiTi(001) surface are a mixture of the previous observations: The Ni and Ti atoms try to acquire hollow and on-top positions with the copper atoms. Due to the lattice mismatch, this also results in a notably higher distortion of the Cu surface compared to the (111) and (101) orientations. The binding distance of 2.52 Å  is in between the values for NiTi(111) and (101).

The DFT results discussed above qualitatively support the experimental findings: NiTi on graphene exhibits a strong interaction governed by a significant charge transfer from NiTi to graphene. Because this charge transfer is very similar for each of the different orientations studied here, we do not expect a preference for a specific NiTi surface orientation to bind to graphene, and this is directly reflected in our experiments. In contrast, the binding between the metals NiTi and Cu is influenced mainly by the geometric fitting of the corresponding surfaces. The NiTi(101)–Cu(111) interface induces the lowest distortions and has therefore the highest binding energy. This effect likely strongly contributes to our novel experimental finding, where the NiTi(101) direction is massively preferred in the Cu–graphene samples. We note in closing that there are some general concerns regarding the validity of DFT with the LDA for a hybrid metal–graphene system as considered here.

However, the inclusion of semi-empirical dispersion correction in the calculations is known to be a reliable method to obtain rather accurate binding distances for pure Ni–graphene interfaces [19]. It seems therefore a reasonable approach to apply the same methodology also to investigate NiTi–graphene interfaces, particularly in light of the good agreement between our microstructural observations and the DFT results. Nevertheless, in subsequent studies direct experimental measurements should be used to characterize the interfacial properties in detail and to further validate these theoretical results.

Summary

We have briefly presented a new approach for the fabrication of free-standing NiTi thin films by the use of a graphene substrate. The austenitic microstructure (observed by EBSD) of the NiTi-graphene sample shows randomly oriented grains in normal direction. The observed grain sizes range from 5 to 15 microns. Supporting DFT calculations yield low binding energies that do not favor a particular NiTi orientation on top of graphene. This is in good agreement with the experimental data and also explains why graphene provides an easy way to produce free-standing films. Most importantly, we could show that the addition of a very thin copper interlayer leads to an improved adhesion between the functional NiTi layer and the graphene substrate. The microstructure of the NiTi top layer is also austenitic, but, quite surprisingly, it is characterized by a pronounced fiber texture in (101) direction out of plane and a reduction of NiTi grain size by approx. one order of magnitude compared to the NiTi-graphene without Cu interlayer. This experimental result can also be rationalized theoretically: considering that the deposited Cu interlayer is oriented in (111) direction, the DFT calculations confirm that the NiTi(101) orientation is energetically preferred compared to NiTi(001) and NiTi(111) orientations. This study shows that the proper combination of graphene substrate, metallic interlayer, and functional NiTi top layer can be used to produce tailor-made microstructures that may well be further optimized by using different metals as interlayer.