Introduction

Shape memory alloys (SMA) are capable of sustaining large mechanical strains in a reversible way. This property makes SMA very interesting for various industrial applications, e.g., for medical devices as stents. Furthermore, shape memory alloys can be used as “all-in-one” actuators: they fulfill inherently the task of sensors, controlling devices, and engines. If SMA are loaded at low temperatures, they show an apparently permanent deformation. However, if the construction part is heated, it transforms back to its original configuration as soon as a certain transformation temperature is exceeded (to be precise, there exists a material-dependent temperature interval during which the process of back deformation takes place). The forces which are provided during the back deformation are large as compared to piezo actuators, for instance.

The physical reason for these two material characteristics is hidden in the metallic crystal of shape memory alloys. At high temperatures, the atoms are in the austenite state which is cubic. At low temperatures, the crystal is martensitic which results from the austenite crystal by shear and shuffle. In contrast to other metals, the transformation strains which describe the transformation from austenite to martensite are (nearly) volume conserving. This special property allows also for reversible mechanically induced phase transformations which is a unique skill.

At high temperatures the initial austenite crystal transforms to a composition of martensitic variants when a certain transformation stress has been reached. During the transformation, stress remains constant and increases not until the transformation is complete. Thereby, the elastic constants of austenite and martensite differ. During unloading, the material shows again a constant stress plateau when the back transformation from martensite to austenite takes place. This plateau stress is lower than the one during loading. Consequently, the material shows a hysteresis in the stress/strain diagram which is also a hint that the phase transformations are dissipative. Due to the (nearly) complete recovery of the initial state of deformation, this property is called pseudoelasticity.

At lower temperatures, the material is martensitic. Normally, this state has been reached through a cooling of the austenite. If the material deforms unbounded, there is no preferred direction and all martensitic variants are uniformly distributed. This state is referred to as twinned martensite. During mechanical loads, the martensite detwinns which means that orientation-dependently some variants will transform to other ones which are more favorable for the specific load. The transformation stress which is observed during this transformation is much lower than the transformation stresses discussed above. When the material is unloaded until no force is applied, an apparently permanent deformation remains in the material since a recovery of the twinned state is energetically not favorable. Consequently, the detwinned state only unloads in an elastic manner. If the prescribed deformation is reduced further, stresses become negative and at the same absolute value as for the transformation during loading: the material transforms into a different detwinned martensitic composition during which the stress is constant again. Due to the similarity to plasticity, this behavior is referred to as pseudoplasticity. However, if the material is heated, the caloric driving force becomes more pronounced and the martensitic state transforms to an austenitic composition. This effect is accompanied by a reduction of the previous deformation if the material was unbounded. If the displacements are fixed, however, large forces result from the transformation from martensite to austenite. If the free material is cooled afterwards, the original twinned configuration is reestablished and the process could start again. This behavior is termed as the one-way effect.

Detailed information on martensitic transformations and the related theory can be found in e.g., [1] or [2].

It is obvious that the entire material behavior is strongly thermo-mechanically coupled. Although the material characteristics are highly appreciated, the complex processes which are the origin for the demanded material behavior are simultaneously a great obstacle for engineering products made of SMA. One promising tool for solving this problem is numerical simulation which predicts the material behavior and allows for digital material and product design. There exists already a large number of models. To mention the most prominent ones, we refer to the model of Auricchio and Taylor [3] which has also been implemented to the commercial finite element programs ABAQUS and ANSYS. A different model was formulated by Govindjee and Hall [4] while Lagoudas discusses also the engineering applications using modeling approaches [5]. A model considering finite deformations was published by Reese and Christ [6]. Other models were proposed by Stebner and Brinson [7] and Stupiekwicz and Petryk [8].

All models share the property that they can be implemented in a finite element framework which allows for the modeling of entire construction parts. Then, for each integration point the material model is solved and the microstructural state, which is described in a model-dependent manner in terms of varying internal variables (e.g., volume fractions or transformation strains), is updated. Our work group contributed to the modeling of SMA with various works. However, the intention of this publication is the synthesis of the work in [9], which is based on the model in [10], and the work in [11]. Furthermore, we lay a special focus on the numerical implementation of the model into a finite element framework and show some examples how material models and simulations may influence the engineering process in a positive way.

Material Model

The material model was originally published in [10] and simplified further in [11]. The key idea is an energy-based description of the material and a subsequent variational analysis of the Helmholtz free energy and the dissipation function. Evaluation of the stationary point results in the evolution equations for the internal variables and a Legendre–Fenchel transformation closes the system of equations by an associated yield function. The entire model automatically accounts for constraints, e.g., mass conservation, and there is no need for a direct postulation of a yield function which may be quite challenging. As demonstrated by Hall and Govindjee (see [12]), the shape of a yield function even for an isothermal setting is complex (see Fig. 1). The application of so-called variational approaches, in contrast, results without any further assumptions in a closed model formulation.

The fundamental idea of variational concepts is the Hamilton principle which is well known for the description of rigid body systems. The identification of the kinetic and potential energy is sufficient to end at the equations of motion by application of the Lagrange equation. The Lagrange equation itself is nothing but the necessary condition for the action to be minimal. In an analogous way, Hamilton’s principle can be expanded such that dissipative effects can be taken into account and a formal extension of the principle for continuous bodies reads

$$\delta {\mathcal {G}} + \int _\Omega \frac{\partial {\mathcal {D}}}{\partial {\dot{\varvec{\upsilon }}}}\cdot \delta {\varvec{\upsilon }}\ {\rm d}V = 0 \ , \quad \forall \delta {\varvec{u}}, \delta {\varvec{\upsilon }}$$
(1)

Here \({\mathcal {G}}\) is the Gibbs energy, \({\mathcal {D}}\) denotes the dissipation function, \({\Omega }\) is the body’s volume, \({\varvec{u}}\) are the displacements, and \({\varvec{\upsilon }}\) is the generalized internal variable which has to be specified for each material. This principle can also be applied to inverse problems as demonstrated for the problem of topology optimization in [13, 14].

Fig. 1
figure 1

Shape of the yield function for CuAlNi published by Hall and Govindjee [12]

Full size image

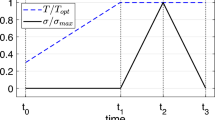
The model for shape memory alloys in [10, 11] uses two internal variables: the volume fractions for austenite and a varying number of martensitic variants which are collected in the vectorial quantity \({\varvec{\lambda }}\), and the three Euler angles which are collected in \({\varvec{\alpha}}\). The inclusion of Euler angles allows for the modeling of polycrystalline SMAs. A schematic plot of the material behavior which shall be modeled is depicted in Fig. 2.

Fig. 2
figure 2

Schematic plot of the material behavior. The volume fraction of phases \({\varvec{\lambda }}\) is changing along with the orientation distribution function of phase-transforming grains \({\varvec{\alpha }}\)

Full size image

In a real polycrystalline ensemble, phase transformations take place in grains which possess an orientation that is favorable in terms of the applied external load (direction). While phase transformation is proceeding, other grains may become active until (nearly) the entire material has transformed. However, implementation of such a model into a finite element code reveals that such a model is very time consuming and thus not appropriate for an industrial use (see [15]). Therefore, the polycrystalline character is condensed to a modeling approach in which a dynamically evolving orientation distribution function is considered and parameterized by Euler angles. The Helmholtz free energy was derived for such a modeling approach in [10] and reads

$$\Psi = \frac{1}{2} \left({\varvec{\varepsilon}}- {\varvec{Q}}^T\cdot {\bar{\varvec{\eta }}}\cdot {\varvec{Q}}\right) : {\bar{\mathbb{C}}} : \left({\varvec{\varepsilon}}- {\varvec{Q}}^T\cdot {\bar{\varvec{\eta}}}\cdot {\varvec{Q}}\right) + {\bar{c}}$$
(2)

with the effective quantities for transformation strain \({\bar{\varvec{\eta}}}\), elastic constants \({\bar{\mathbb {C}}}\), and caloric parts \({\bar{c}}\)

$${\bar{\varvec{\eta}}} = \sum _{i=0}^n \lambda _i{\varvec{\eta}}_i, \quad {\bar{\mathbb{C}}} = \left[ \sum _{i=0}^n \lambda _i \left( {\mathbb {C}}_i\right) ^{-1}\right] ^{-1}, \quad {\bar{c}} = \sum _{i=0}^n \lambda _i c_i$$
(3)

The quantity n is the number of martensitic variants that are considered. The Euler angles enter the rotation matrix \({\varvec{Q}}\). More details are given in [10].

Hamilton’s principle in Eq. 1 furthermore demands the dissipation function to be defined. In [10] a rate-independent approach has been presented while a rate-dependent approach was suggested in [11]. Both approaches yield reasonable results. However, the rate-dependent approach is more stable in a numerical context. Thus, the dissipation function is chosen to be

$${\mathcal {D}}= r_1 |{\dot{\varvec{\lambda}}}| + \frac{r_2}{2} |{\dot{\varvec{\lambda}}}|^2 + \frac{r_\alpha }{2(1-\cos ^2{\vartheta})} ||{\varvec{\Omega}}||^2$$
(4)

with the skew-symmetric matrix of angular velocities \({\varvec{\Omega}} = {\dot{\varvec{Q}}}\cdot {\varvec{Q}}^{-1}\), see also [11]. The parameters \(r_1\), \(r_2\), and \(r_\alpha\) are material dependent and termed dissipation parameters. Application of Hamilton’s principle results in the evolution equations for the volume fractions and the Euler angles. They are given as

$${\dot{\varvec{\lambda}}} = \frac{1}{r_2} \left(|{\rm dev}_{\mathcal{A}}\, {\varvec{p}}_\lambda | - r_1 \right) _{+} {\rm sgn}\left( {\rm dev}_\mathcal {A}\, {\varvec{p}}_\lambda \right)$$
(5)

with the active deviator \({\rm dev}_{\mathcal{A}}{\varvec{p}}_\lambda := {\varvec{p}}_\lambda - \frac{1}{n_{\mathcal{A}}} \sum _{j\in {\mathcal{A}}} p_{\lambda ,j}\) (the active set is defined as \({\mathcal {A}}= \{ i |\lambda _i\not =0\} \cup \{i|\lambda _i=0 \wedge {\dot{\lambda}}_i>0 \}\)) and

$${\dot{\varphi}} = \frac{1}{\sqrt{2}\, r_\alpha }\, \left( p_\varphi - p_\omega \cos \vartheta \right)$$
(6)
$${\dot{\vartheta}} = \frac{1}{\sqrt{2}\, r_\alpha }\, p_\vartheta \, (1-\cos ^2 \vartheta )$$
(7)
$${\dot{\omega}} = \frac{1}{\sqrt{2}\, r_\alpha }\, \left( p_\omega - p_\varphi \cos \vartheta \right)$$
(8)

The quantities \({\varvec{p}}_\lambda :=-\partial \Psi /\partial {\varvec{\lambda}}\), \(p_\varphi :=-\partial \Psi /\partial \varphi\), \(p_\vartheta :=-\partial \Psi /\partial \vartheta\), and \(p_\omega := -\partial \Psi /\partial \omega\) are the driving forces for the volume fractions and the Euler angles \(\varphi\), \(\vartheta\), and \(\omega\), respectively. More details can be found in [11].

Numerical Implementation

In a finite element setting, both the stresses and its tangent to the strains is required. The stress is given as

$${\varvec{\sigma}}({\varvec{\varepsilon}},{\varvec{\lambda}}, {\varvec{\alpha}}) = {\bar{\mathbb {C}}}({\varvec{\lambda}}):\left[{\varvec{\varepsilon }}-{\varvec{Q}}^T({\varvec{\alpha}})\cdot {\bar{\varvec{\eta}}}({\varvec{\lambda}})\cdot {\varvec{Q}}({\varvec{\alpha}})\right]$$
(9)

which is linearized as follows

$$\begin{aligned}{\varvec{\sigma}}^{k+1} & = {\varvec{\sigma}}^k + \left. \frac{\partial {\varvec{\sigma }}}{\partial {\varvec{\varepsilon}}}\right| _k : \Delta {\varvec{\varepsilon}}+ \left. \frac{\partial {\varvec{\sigma }}}{\partial {\varvec{\lambda}}}\right| _k \cdot \Delta {\varvec{\lambda}}+ \left. \frac{\partial {\varvec{\sigma }}}{\partial {\varvec{\alpha}}}\right| _k \cdot \Delta {\varvec{\alpha}}\\ &=\varvec{\sigma }^k + \left. \frac{\partial \varvec{\sigma }}{\partial \varvec{\varepsilon }}\right| _k : (\varvec{\varepsilon }^{k+1}-\varvec{\varepsilon }^k) + \left. \frac{\partial \varvec{\sigma }}{\partial \varvec{\lambda }}\right| _k\cdot (\varvec{\lambda }^{k+1} - \varvec{\lambda }^k) + \left. \frac{\partial \varvec{\sigma }}{\partial \varvec{\alpha }}\right| _k \cdot (\varvec{\alpha }^{k+1} - \varvec{\alpha }^k) \end{aligned}$$
(10)

which allows the direct calculation of the tangent as

$$\frac{{\rm d}{\varvec{\sigma}}^{k+1}}{ {\rm d}{\varvec{\varepsilon}}^{n+1}} = \left. \frac{\partial {\varvec{\sigma}}}{\partial {\varvec{\varepsilon}}}\right| _k + \left. \frac{\partial {\varvec{\sigma}}}{\partial {\varvec{\lambda}}}\right| _k \cdot \frac{\partial {\varvec{\lambda}}^{k+1}}{\partial {\varvec{\varepsilon }}^{k+1}} + \left. \frac{\partial {\varvec{\sigma}}}{\partial {\varvec{\alpha}}}\right| _k \cdot \frac{\partial {\varvec{\alpha}}^{k+1}}{\partial {\varvec{\varepsilon }}^{k+1}},$$
(11)

where \(k+1\) is the current load step. The evolution equations in (5) and (6-7) are discretized in an explicit Euler integration scheme. They thus read

$${\varvec{\lambda}}^{k+1} = {\varvec{\lambda}}^k + \frac{\Delta t}{r_2} \Phi _+({\varvec{\varepsilon }}^{k+1}, {\varvec{\lambda}}^k,{\varvec{\alpha}}^k) \frac{{\rm dev}_{\mathcal{A}}\, {\varvec{p}}_\lambda ({\varvec{\varepsilon}}^{k+1}, {\varvec{\lambda }}^k, {\varvec{\alpha}}^k)}{|{\rm dev}_{\mathcal {A}}\, {\varvec{p}}_\lambda ({\varvec{\varepsilon }}^{k+1}, {\varvec{\lambda}}^k, {\varvec{\alpha}}^k)|}$$
(12)
$${\varvec{\alpha}}^{k+1} = {\varvec{\alpha}}^k + \frac{\Delta t}{r_\alpha } \ {\rm obj}\, \varvec{p}_\alpha ({\varvec{\varepsilon}}^{k+1}, {\varvec{\lambda}}^k,{\varvec{\alpha}}^k)$$
(13)

with the objectivity operator

$${\text{obj}}\,{\varvec{p}}_\alpha = \left(\begin{array}{l} p_\varphi - p_\omega \cos \vartheta \\ p_\vartheta \, (1-\cos ^2 \vartheta )\\ p_\omega - p_\varphi \cos \vartheta \end{array}\right)$$
(14)

The yield function \(\Phi\) is defined as

$$\Phi := |{\rm dev}_{\mathcal {A}}\, {\varvec{p}}_\lambda | - r_1$$
(15)

and for \(\Phi >0\), the derivative of \({\varvec{\lambda}}^{k+1}\) with respect to the current strains can be reformulated to

$$\frac{\partial {\varvec{\lambda}}^{k+1}}{\partial {\varvec{\varepsilon}}^{k+1}} = \Delta t \frac{\partial }{\partial {\varvec{\varepsilon}}^{k+1}} \left[ {\rm dev}{\varvec{p}}({\varvec{\varepsilon }}^{k+1},{\varvec{\lambda}}^k,{\varvec{\alpha}}^k) - r_1 \frac{{\rm dev} {\varvec{p}}({\varvec{\varepsilon }}^{k+1}, {\varvec{\lambda}}^k, {\varvec{\alpha}}^k)}{|{\rm dev} {\varvec{p}}({\varvec{\varepsilon}}^{k+1}, {\varvec{\lambda}}^k, {\varvec{\alpha}}^k)|} \right]$$
(16)

The driving forces are specified to

$$p_{\lambda ,i}({\varvec{\varepsilon}},{\varvec{\lambda }},{\varvec{\alpha}}) = {\varvec{Q}}^T({\varvec{\alpha}}) \cdot {\varvec{\eta}}_i \cdot {\varvec{Q}}({\varvec{\alpha }}): {\varvec{\sigma}}({\varvec{\varepsilon }}, {\varvec{\lambda}}, {\varvec{\alpha}}) + \frac{1}{2}{\varvec{\sigma}}({\varvec{\varepsilon }},{\varvec{\lambda}},{\varvec{\alpha}}) : \mathbb {C}^{-1}_i : {\varvec{\sigma}}({\varvec{\varepsilon }},{\varvec{\lambda}},{\varvec{\alpha}}) - c_i$$
(17)
$${\varvec{p}}_\alpha ({\varvec{\varepsilon }},{\varvec{\lambda}},{\varvec{\alpha}}) = 2\, {\bar{\varvec{\eta}}} \cdot {\varvec{Q}}({\varvec{\alpha}}) \cdot {\varvec{\sigma}}({\varvec{\varepsilon }},{\varvec{\lambda}},{\varvec{\alpha}}): \frac{\partial {\varvec{Q}}({\varvec{\alpha}})}{\partial {\varvec{\alpha}}}$$
(18)

in which the last derivative depends on the chosen representation of the rotation matrix \({\varvec{Q}}\). More details may be found in [10].

Now, all derivatives can be calculated which are needed for the tangent given in Eq. (11); precisely, the derivatives of the stress are given as

$$\left. \frac{\partial {\varvec{\sigma}}}{\partial {\varvec{\varepsilon}}}\right| _k = {\bar{\mathbb {C}}}({\varvec{\lambda}}^k)$$
(19)
$$\left. \frac{\partial {\varvec{\sigma}}}{\partial \lambda _i}\right| _k = \left. -\frac{\partial p_{\lambda ,i}}{\partial {\varvec{\varepsilon}}}\right| _k = - \left[{\varvec{Q}}^T({\varvec{\alpha}}^k) \cdot {\varvec{\eta}}_i \cdot {\varvec{Q}}({\varvec{\alpha}}^k) + {\mathbb {C}}_i^{-1}: {\varvec{\sigma }}({\varvec{\varepsilon}}^k, {\varvec{\lambda }}^k, {\varvec{\alpha}}^k) \right] : {\bar{\mathbb {C}}}({\varvec{\lambda}}^k)$$
(20)
$$\left. \frac{\partial {\varvec{\sigma}}_6}{\partial {\varvec{\alpha}}}\right| _k = - \left. \frac{\partial {\varvec{p}}_\alpha }{\partial {\varvec{\varepsilon }}_6}\right| _k = - {\bar{\mathbb {C}}}_6({\varvec{\lambda }}) \cdot {\bar{\varvec{\eta}}}_{6} \ \cdot \left. \frac{\partial {\varvec{Q}}_6}{\partial {\varvec{\alpha}}}\right| _k$$
(21)

The subscript \((\cdot )_6\) indicates the notation according to Mehrabadi and Cowin (see [16]).

The missing derivatives of the internal variables and the driving force of the volume fractions are calculated as

$$\frac{\partial {\varvec{\lambda}}^{k+1}}{\partial {\varvec{\varepsilon}}^{k+1}}= \frac{\Delta t}{r_2} \left[ {\rm dev}\frac{\partial {\varvec{p}}_\lambda ^{k+1}}{\partial {\varvec{\varepsilon}}^{k+1}} - \frac{r_1}{|{\rm dev}{\varvec{p}}_\lambda ^{n+1}|} \left({\mathbb {I}}_4 - \frac{{\rm dev}{\varvec{p}}_\lambda ^{k+1}\otimes {\rm dev}{\varvec{p}}_\lambda ^{k+1}}{|{\rm dev}{\varvec{p}}_\lambda ^{k+1}|^2} \right) \cdot {\rm dev}\frac{\partial {\varvec{p}}_\lambda ^{k+1}}{\partial {\varvec{\varepsilon }}^{k+1}} \right]$$
(22)
$$\begin{aligned} {\rm dev}\frac{\partial p_{\lambda ,i}^{k+1}}{\partial {\varvec{\varepsilon}}^{k+1}}& =\, {\rm dev}\left\{ \left[{\varvec{Q}}^T({\varvec{\alpha}}^k) \cdot {\varvec{\eta}}_i \cdot {\varvec{Q}}({\varvec{\alpha}}^k) \right. \right. \\&\left. \left.\quad +\, {\mathbb {C}}_i^{-1}:{\bar{\mathbb {C}}}({\varvec{\lambda}}^k):\left( {\varvec{\varepsilon}}^{k+1} - {\varvec{Q}}^T({\varvec{\alpha}}^k) \cdot {\bar{\varvec{\eta}}}({\varvec{\lambda}}^k) \cdot {\varvec{Q}}({\varvec{\alpha}}^k)\right) \right] : {\bar{\mathbb {C}}}({\varvec{\lambda}}^k) \right\}\end{aligned}$$
(23)
$$\frac{\partial {\varvec{\alpha}}^{k+1}}{\partial {\varvec{\varepsilon}}^{k+1}}= {\rm obj}\left\{ 2 \, \frac{\Delta t}{r_\alpha } \, {\bar{\varvec{\eta}}} \cdot {\varvec{Q}}({\varvec{\alpha}}^k) \cdot \left({\bar{\mathbb {C}}}({\varvec{\lambda}}^k) : \left. \frac{\partial {\varvec{Q}}({\varvec{\alpha}})}{\partial {\varvec{\alpha }}}\right| _k\right) ^T \right\}$$
(24)

Inserting the derivatives in Eqs. (19–20) and (22–23) into Eqs. (17–18) yields the consistent tangent operator to the linearized stress in Eq. (16) which ensures a good convergence.

Model Calibration

The model uses several material parameters. The elastic constants for austenite and martensite \({\mathbb {C}}_i\) as well as the transformation strains \({\varvec{\eta}}_i\) can be found experimentally, e.g., using a tensile test. Same holds true for the caloric part of the Helmholtz free energy \(c_i\) which can be found using a DSC experiment (digital scattering calorimetry). The dissipation parameters, however, are less “intuitive” to be found. In [9] a formula was derived for the dissipation parameter \(r_1\) which controls when transformation sets in (\(r_2\) and \(r_\alpha\) are the viscous parameters which have to be adjusted such that the evolution is “fast enough”). The formula reads

$$r_1 = \sqrt{\frac{n}{n+1}} |\Delta c(\theta _E)| ,$$
(25)

where \(\theta _E:=(M_{\rm p}+A_{\rm p})/2\) is the equilibrium temperature (the peak temperatures are denoted by \(M_{\rm p}\) and \(A_{\rm p}\), respectively). It is thus obvious that the material model can be calibrated by means of thermal experiments. However, it is formulated both for thermal and mechanical loads. Therefore, the model was calibrated thermally for Ni51.0Ti49.0 and no further fitting parameters were needed. Afterwards, the model was evaluated in a finite element setting for tensile tests at varying ambient temperature. The results are presented in Fig. 3.

Fig. 3
figure 3

Finite element results for different geometries at 295.15, 232.15, and 333.15 K (from left to right, see [9]). Experiments after [17] (295.15 K) and [18] (232.15 and 333.15 K)

Full size image

Without knowing the plateau stresses or the shape of the hysteresis, the model is capable of predicting the correct material reaction. The only small mismatch is present at the beginning of the plateau at 293.15 K: at this low temperature, the austenite transforms first into the so-called R-phase before this phase transforms to martensite. The R-phase is not included yet into the material model. Thus, this material behavior cannot be simulated. However, theses results demonstrate impressively that a proper material model is able to predictively analyze the complex material behavior of shape memory alloys which supports product engineering to a great degree. Since the model was solely calibrated on thermal experiments and it was still able to predict the material behavior, it possesses a rather universal applicability while the results are reliable and accurate.

Sometimes it is more convenient to calibrate the model directly on tensile tests. Therefore, calibration formulas for both for the dissipation parameter \(r_1\) and the caloric energy (for one specific temperature) were derived in [11]. They read

$$r_1 = \frac{1}{\sqrt{2}} \left( \frac{\sigma _{\rm u} - \sigma _{\rm l}}{2} \, {\hat{\eta}} - \frac{\sigma _{\rm u}^2 - \sigma _{\rm l}^2}{4} \left( \frac{1}{G_{\rm A}} - \frac{1}{G_{\rm M}} \right) \right)$$
(26)

and

$$\Delta c = - \frac{\sigma _{\rm u} + \sigma _{\rm l}}{2} \, {\hat{\eta}} + \frac{\sigma_{\rm u}^2 + \sigma _{\rm l}^2}{4} \left( \frac{1}{G_{\rm A}} - \frac{1}{G_{\rm M}} \right),$$
(27)

where \(G_{\rm A}\) and \(G_{\rm M}\) denote the shear moduli of austenite and martensite, respectively, and \({\hat{\eta}}\) is the transformation strain which can be determined from the Maxwell stress \(\sigma _{\rm Maxwell}:=(\sigma _{\rm u}-\sigma _{\rm l})/2\) (\(\sigma _{\rm u}\) is the upper plateau stress and \(\sigma _{\rm l}\) is the lower one). The numerical results for this calibration are presented in Fig. 4. We also emphasize that the material model works properly no matter whether the austenite or the martensite phase possesses the stronger elastic modulus.

Fig. 4
figure 4

Finite element results for different geometries at 295.15, 232.15, and 333.15 K (from left to right, see [11]). Experiments in dashed lines after [17] (295.15 K) and [18] (232.15 and 333.15 K). The red line stops at maximum experimental strain, the blue one shows the simulated material behavior for a maximum strain of 0.08 (Color figure online)

Full size image

As a last example, we show a scratch test for a martensitic bar which thus reacts pseudoplastically (Fig. 5). For this setting, the caloric energy is set to the (arbitrary but positive) value of \(\Delta c = 10\) MPa—all other model parameters are kept constant. This example was computed using the commercial software ABAQUS (whereas the previous results were obtained using the software FEAP). The model was implemented via a umat.f interface.

Fig. 5
figure 5

Pseudoplastic NiTi bar subjected to a steel indenter scratching at the surface. Distribution of one martensitic variant at the end of the second loading step. Full geometry as simulated (top) and clip as used in Fig. 6

Full size image

The scratch test was realized by a bar consisting of 10 \(\times\) 10\(\times\) 100 hexahedra elements and employing full integration. The indenter was chosen to be steel which thus was fully deformable. During a first loading step, the indenter was pressed into the shape memory bar and subsequently scratched into the longitudinal direction of the bar during the second load step. The resulting distribution of one martensitic variant at various time steps is presented in Fig. 6.

Fig. 6
figure 6

Pseudoplastic NiTi bar subjected to a steel indenter scratching at the surface. Distribution of one martensitic variant at various loading steps. Bottom: deformed configuration at the end of the second loading step scaled by a factor of four (indenter is not shown)

Full size image

Conclusions

We presented a synthesis of a material model that is based on Hamilton’s principle and thus purely energy based. It has been demonstrated that a direct formulation of yield functions may be too complicated for the complex material shape memory alloy. Furthermore, a detailed instruction how to implement the model into a finite element routine has been given. Afterwards, two different possibilities have been shown on how the model can be calibrated: one possibility used only thermal data as input whereas the second one allowed for a calibration directly related to tensile tests. Since the model is able to predict the mechanical material behavior based on thermal calibration data, it was empirically proven that the model is of rather universal applicability and that the results are accurate and reliable.

In conclusion, a fast, stable, and accurate material model as the one presented can be advantageous in the context of SMA product engineering since the complex thermo-mechanically coupled material behavior can be studied at low costs in a virtual way. Implementations of the model into commercial finite element software are feasible and increase the applicability of the model by e.g., the inclusion of sophisticated contact boundary conditions.