Abstract
Catalysed diesel particulate filters (c-DPF) have been described as multifunctional reactor systems. Integration of selective catalytic reduction (SCR) functionality in the DPF enhances filter performance to achieve nitrous oxides (NOx) treatment along with particulate matter (PM) collection. The physical and chemical aspects of the integrated SCR-filter make modelling difficult. The goal of this work is to develop a low-complexity model of the SCR-filter system with good fidelity. The first part of our work—presented in this paper—lays out the structure of the SCR-filter model and highlights a new approach to implement faster than real-time solution to the “full-order” or “high-complexity” model. The validated model was applied to evaluate the impact of diffusion on deNOx functionality of the SCR-filter system in a simulated characterisation exercise for the SCR-filter unit. We found that internal (pore) diffusion (effective diffusivity coefficient) and external channel to wall diffusion (mass transfer coefficient) orthogonal to the channel direction are significant for accurate characterisation of the deNOx performance of the SCR-coated filter system. System modelling can be used to select the geometric properties of the monolith (length and density of the SCR-coated filter system) and micro-properties of the washcoat (catalyst loading and zoning) to optimise the influence of diffusion on the system performance. The main contribution of this paper is the presentation of a different approach to implementing the solution to the cDPF model and in enough detail so that it can be easily replicated.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Diesel engines offer superior performance in fuel economy compared to gasoline engines [1], but the simultaneous control of soot/particulates (PM) and nitrogen oxides (NOx) is challenging. Integration of the selective catalytic reduction (SCR) catalyst within a diesel particulate filter (DPF) monolith is an emerging technology for simultaneous control of soot and NOx emissions.
The integration of urea-SCR catalyst in a catalysed diesel particulate filter (cDPF) block (SCR-coated filterFootnote 1) will yield a more compact component of the diesel exhaust after-treatment system (EATS). OEMs must combine multiple EATS components together to meet the increasingly stringent emission limits. A compact, integrated unit is expected to save cost as total package weight/volume is reduced; and with less total thermal mass, it can be heated up much faster than the conventional system, thus potentially improving cold start performance [2,3,4,5,6].
To demonstrate the effectiveness of the technology and facilitate wider industry development, representative system model needs to be developed. Modelling of the SCR-coated filter system is, however, complicated. The main challenge is how to best capture the complexity of the physical and chemical phenomena—e.g., the competition of soot oxidation and SCR reaction for available NO2, the interaction of washcoat loading on deNOx performance, PM filtration efficiency and system pressure drop—in a simplified but adequate representation [7]. This work is focused on the development of an SCR-in-DPF model which achieves the right balance between adequacy and complexity and which can form the basis of a control algorithm that can be implemented within an engine control unit (ECU).
A model of the SCR-coated filter system has been developed and validated. This model is based on the catalysed DPF model [8,9,10,11,12]. It is developed from first principles and includes the main system dynamics: specie transport in the channels and wall layer and surface ammonia and soot dynamics. Our model closely follows Premchand et al.’s model [13,14,15] but deviates in two fundamental ways: we implement the SCR reactions on the filter wall and implement a different model solution approach. Premchand’s approach for the solution of the wall layer specie material balance applied a linear tri-diagonal finite difference scheme to the specie wall balance partial differential equation (PDE). The PDE is however nonlinear and implicit in specie concentrations because of the rate of reaction source term which is also a function of the unknown specie concentrations. In our opinion this method of solution of the resulting matrix of algebraic equation is potentially not applicable or, at best, results in non-unique specie concentrations.
We developed a different approach to the solution of the cDPF model which addresses the weakness of the Premchand’s approach. We explicitly describe the coupling between the channel and wall specie equations. We describe how we developed these into a large system of nonlinear PDEs with coupled boundary conditions. We highlight the complication in the model with the coupling of many specie equations over multiple axes. We introduce the MATLAB routine bvp4c employed to tackle the implicit two-point boundary value problem and describe how we tackled the coupled channel specie equation with a Euler ODE scheme. We provide the details of our approach to the cDPF model solution so that it can be easily replicated.
The objective this work is twofold:
- 1.
To offer a new approach to the solution of the cDPF model
- 2.
To use the developed cDPF model as foundation for model order reduction in our follow-on paper
For completeness, our validated model is applied in a SCR-filter characterisation simulation. Our model was used to evaluate the impact of internal and external diffusion on the deNOx functionality of a SCR-coated filter. In this work, internal diffusion is the diffusion of species in the inter-crystalline voids (pores) within the washcoat, and external diffusion is the diffusion of species from the gas phase to the surface of washcoat [16].
We found that internal diffusion (effective diffusivity coefficient) and external diffusion (mass transfer coefficient) orthogonal to the channel direction are significant for accurate characterisation of the deNOx performance of the SCR-coated filter system. System modelling can be used to select the geometric properties of the monolith (length and density of the SCR-coated filter system) and micro-properties of the washcoat (catalyst loading and zoning) to optimise the influence of diffusion on the system performance.
The rest of the paper is organised as follows. Some aspects of the model are presented in the next section; this is followed by a report of the model validation exercise. The model is then applied to investigate the effect of diffusion on SCR-filter deNOx performance on its own and when compounded with other system parameters like temperature, space velocity and monolith geometry. A summary of our findings is presented in a concluding section.
2 Model Development
2.1 Filter Model
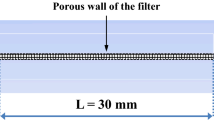
The SCR-filter model is based on the catalysed DPF model [17]. The model comprises continuity, momentum and energy conservation equations for the representative inlet and outlet channels in the axial direction and transverse flow through the filter wall (Fig. 1). The wall surface dynamics included in the model are ammonia surface coverage on the filter wall and soot deposition and oxidation dynamics.
An outline of the 1D + 1D SCR-in-DPF model is presented in [18,19,20]. Some aspects of the model of interest are presented here with comments on our considerations. As per Fig. 1, z is the axial dimension along the catalyst length, and x is the dimension perpendicular to the wall surface. The figure is not to scale: the size of the channel is in the order of millimetres, while the length of the channel is in the hundreds of millimetres.
2.1.1 Species Continuity Balance in the Channel
The species continuity balance in the inlet and outlet channels are given by Eqs. 1 and 2, respectively.
where y1, j, y2, j are the jth species concentration (in mole fraction) in the inlet and outlet channel, y1s, j, y2s, j are the jth species concentration (in mole fraction) in the inlet channel to top wall interface layer and the outlet channel to bottom wall interface layer and k1m, j, k2m, j are the inlet and outlet channel jth specie mass transfer coefficients.
The species continuity balance implies that component material transport is due partly to advection, which is a function of the bulk wall flow velocity, and external diffusion, which is the function of the specie mass transfer coefficient. From a numerical perspective, the mass transfer coefficient is about two orders of magnitude larger than the wall velocity, so the second term on the right in Eqs. 1 and 2 can be dominant depending on the value of the interphase transport between the bulk and the wall surface.
The channel bulk to wall surface concentration difference is also impacted by the reaction within the wall layer. Local consumption or production of species due to reactions within the wall layer can create interface concentration difference. Therefore, the species continuity balance in the channel is coupled with the specie continuity balance within the wall.
The specie concentration at the inlet to the SCR-filter is assumed to be known, and this forms the boundary condition for Eq. 1. The nature of Eq. 2 merely requires that the specie concentration at the inlet edge of the outlet channel be finite [21]; this serves as the boundary condition for Eq. 2.
2.1.2 Filter Wall Layer
The specie conservation within the wall layer is given by a plug flow reactor design equation with axial dispersion [22] in Eq. 3.
The boundary conditions are Eq. 4 at the inlet channel to wall layer interface and Eq. 5 at the wall layer to outlet channel interface.
where ∑Rj is the net rate of reaction of specie j, Dj is the effective diffusivity of specie j and fx is a channel width shrink factor given by
The transport of species through the filter wall is driven partly by advection (the first term on LHS in Eq. 3), internal or pore diffusion (second term on LHS in Eq. 3) and reaction (RHS term in Eq. 3). Quasi-steady state is assumed in the gas-phase specie transport equation because of fast dynamics relative to the substrate-phase dynamics.
It has been shown for the length scale in the catalysed DPF system that internal (or pore) diffusion is a strong component of the species transport in the wall layer [23]. It has been shown, for example, that back-diffusion of NO2 from wall layer to surface cake soot layer is essential in accurate modelling of the passive soot regeneration dynamics [17]. Therefore, to adequately characterise the wall layer gas-phase specie transport, the internal diffusion term must be included in Eq. 3.
The reaction term can be significant in the local specie transport within the wall [22]. The relative influence of diffusion and reaction to specie transport within the wall layer will be highlighted in later sections.
Retaining the internal diffusion term (in Eq. 3) complicates the solution of the SCR-filter model in two ways. Firstly, the specie transport can no longer be solved unidirectionally (top to bottom across the wall) because of the second-order derivative. This means an implicit solver must be deployed to handle the coupled equation. This is significantly more computationally demanding.
Secondly, the channels and wall layer specie transport equations are coupled. The nature of the problem is such that the coupling is over two different dimensions and length scales: the long channel axis and the short wall axis. The solution of the coupled equations is a large system of equations that comprise the entire channel and wall axes. These can quickly blow up to a very large system of nonlinear equations if enough grid refinement is desired in the channel and wall axes. This contributes to the computational burden of solving the system model.
The boundary Eqs. 4 and 5 ensure that material is conserved across the channel-wall interface. At the top wall interface, the internal diffusion within the wall is balanced by advection flow and mass transfer from the channel bulk to the wall surface (external diffusion). At the bottom layer, advection is driven by the outlet wall concentration, therefore cancelling out both sides of outlet interface so that diffusion out of the wall is balanced by mass transfer from the wall surface to the outlet channel bulk [19]. This specification of the boundary conditions make Eq. 3 a two-point boundary value problem (BVP), which is typically more problematic to solve compared to initial value differential equation problem (IVP) [24].
2.1.3 Chemical Reactions
The catalysed DPF model is adapted for SCR-filter dynamics by incorporating the SCR reaction. Soot oxidation also occurs on the surface of the filter wall. Passive soot oxidation with NO2 occurs at low temperature [25], leading to competition between the SCR reactions and soot oxidation for available NO2. The reaction schemes implemented in this model are presented in Table 1 for the SCR reaction and in Table 2 for the soot oxidation reactions.
The SCR reaction kinetics parameters are calibrated in this work against published experimental data in Schrade et al. [6]. The soot oxidation kinetics parameters are obtained from the work of Premchand et al. [13].
2.2 Model Solution
2.2.1 Overview
The solution domain is discretised in the axial (channel) and transverse (wall) directions as depicted in Fig. 2.
There are N-units in the channel direction and w-units in the wall direction. A method of lines approach is applied in each dimension and time to convert the PDEs to ODEs which can be further discretised to algebraic equations as described in Sect. 2.2.2. The gas velocity field is solved using the analytical approach of [9]. The inlet channel, wall layer and outlet channel equations are solved simultaneously with a boundary value problem solver (bvp4c) coupled with an Euler ODE scheme. A fourth-order Runge-Kutta method is applied to solve the first-order ammonia surface coverage, soot mass balance and wall temperature equations in time. MATLAB is the solution environment.
The numerical method of the bvp4c solver is a method of collocation utilising a continuously differentiable cubic polynomial function to approximate the problem within the solution domain. The Simpson’s method is implemented for evaluating the interpolating function at the collocation points, and the residual is used to control mesh size, implementation efficiency and solution accuracy [26]. The implementation is handled internally within the MATLAB environment, and the performance of the bvp4c is shown to be superior to another BVP solver, MIRKDC, which also uses residual control in its implementation [26]. We use MATLAB as our environment for bvp4c for convenience. There are other software environments that implement the bvp4c method, e.g. py_bvp in Python [27].
An overview of the model solution approach is presented in Fig. 3.
2.2.2 Coupled Channel-Wall Equations
The inlet channel specie balance of Eq. 1 becomes Eq. 8 when the differential term is expanded by an upwind finite difference scheme.
This equation holds for j-species over the N-discrete units in the channel axis, with boundary conditions y1, j|i = 1 = y1, j − in.
The outlet channel specie balance equation can be written in a similar way.
The boundary condition assumed for the outlet channel specie balance is y2, j|i = 1 = ϕsy1, j − in where ϕsϵ[0 1] is a “slip” parameter to indicate how much of the inlet exhaust gas mixture permeates through the plugged inlet side of outlet channel.
The wall layer Eq. 3 can be expanded in the same finite difference scheme to become equation
Equation 10 holds for each j-specie in the jx = 2 to jx = w − 1 units of the wall layer. The rate of reaction source term (RHS) is a function of concentration of the different species, i.e. Rj = f(yj = 1, yj = 2, …, yj = c) according to the SCR and soot reactions. The top and bottom boundary conditions Eqs. 4 and 5 complete the w-equations in the wall layer.
The top boundary conditions expanded in a similar finite difference scheme to yield Eq. 11
Equation 11 shows the coupling between the inlet channel-wall interface concentration (first term in Eq. 11), the concentration in the second unit of the wall layer (second term in Eq. 11) and the bulk inlet channel concentration (the RHS of Eq. 11).
The bottom boundary condition is expanded to yield
Equation 12 shows the coupling between the outlet channel-wall interface concentration (first term in Eq. 12), the concentration in the penultimate unit of the wall layer (second term in Eq. 12) and the bulk outlet channel concentration (the RHS of Eq. 12).
For each j-specie, the channel-wall coupled equations make up (2 + w) differential algebraic equations with two-point boundary value type second-order differential equations and implicit nonlinear terms due to the chemical reaction source terms.
These equations are solved in step 4 of the algorithm in Fig. 3 with the bvp4c MATLAB routine coupled with an Euler ODE scheme. To reduce the number of equations, the specie equations are only solved for the trace components (CO, CO2, NOx and NH3).
2.2.3 Time-Explicit First-Order ODEs
The filter surface dynamics are slow compared with the gas phase dynamics which therefore have time-explicit components in their conservation equations. The ammonia surface coverage, mass of soot retained in the wall and cake layer and the filter wall temperature are all first-order differential equations in time [18, 20]. These time-explicit variables form the state of the system.
The filter wall temperature equation is solved with ode45, and the ammonia surface coverage is solved with ode15s, both in the MATLAB environment. ode45 proved acceptable for the lumped parameter filter temperature dynamics; while the option of JPattern [28] in the ode15s routine enabled fast simulation of the surface coverage equation.
2.2.4 Difference from Other Methods
Our model builds on the work of many brilliant researchers in the cDPF modelling community [10, 13, 14, 18,19,20, 29,30,31]. Our general model approach closely follows that of Premchand et al. [13,14,15]. In contrast we implement the SCR reaction in the catalysed filter wall and approach the model solution differently. We identified a weakness in the implementation of the Premchand et al.’s model. A major point which was unaddressed in Premchand’s thesis or their papers is the way in which they applied a linear tri-diagonal finite difference scheme to the PDE specie wall balance equation which is, by definition, nonlinear and implicit in specie concentrations because of the rate of reaction source term. For example, in Eqs. D.12a–D.16d in reference [15], both the LHS and RHS contain unknown specie concentration. The solution of the resulting matrix of algebraic equations as described in [15] is potentially non-unique as the method of solution is generally not applicable to this system of implicit nonlinear equations.
We did not quantify the errors introduced by this approximation in the results published in Premchand et al.’s work because of insufficient information in their publication. We however note a fundamental mismatch of solution technique vs. the problem context which was unaddressed in the publications. In this work, more chemical reactions are implemented in our SCR and soot oxidation reaction system within the catalysed wall layer compared to the reactions implemented in Premchand et al.’s model [20]. We suspect that an attempt to implement Premchand et al.’s approach in our context would have been problematic.
The other difference in our work is that our model implementation is described in detail so that it can be replicated. Other published models provide only general overviews of implementation approach to protect proprietary/commercial interests. Our complete model is available on request.
3 Model Validation
Two model validation activities are reported in this section. Firstly, the model is validated against a subset of the problem which has an analytical solution. Secondly, the model is validated against experimental data published in the literature.
3.1 Analytical Validation
Konstandopoulos and Kostoglou [21] presented the analytical solution to a simplified version of the catalysed DPF model. They assumed uniform wall velocity along filter channel, isothermal conditions and first-order reaction kinetics with only one component and negligible mass transfer in the outlet channel. These simplifying assumptions enabled the derivation of closed-form solutions for the specie concentration profile in the channels and filter wall.
Our numerical model was adapted for the case described in [21] by taking the same simplifying assumptions. This was to validate the theoretical basis of the numerical method.
Numerical model validation against analytical result is a common approach in engineering and is the preferred approach if an analytical closed-form solution exists to the problem under consideration.
This approach has been used in published works in catalysed filter modelling [23, 32]. The sensitivity of model performance to kinetic parameters—which need to be identified from experimental data—makes this approach convenient for EATS modelling.
3.1.1 Analytical Model and Solution
A key difference in our model and the analytical model in [21] is the assumption of negligible mass transfer in the outlet channel. This assumption essentially replaces Eq. 5 with Eq. 13.
This simplifying assumption ignores potential back-diffusion from the outlet channel to the wall layer. In our experience, there is considerable component mass slip from the inlet to the outlet channel at the inlet end of the filter. As this slipped component moves toward the outlet end, the concentration difference can force back-diffusion of species. Consequently, the outlet channel exit concentration can be affected.
The analytical solutions for the specie concentration profile in the inlet/outlet channels and wall layer for the simplified catalysed DPF case in [21] are presented in Eqs. 14–16.
The independent variables z and x are distance along the channel and wall, respectively.
The constants of the equations are derived from system properties: Peclet number, Damköhler number and a dimensionless flow velocity. The Peclet number Pe = vwws/De denotes the ratio of the advection to diffusion contributions to the transport in the porous wall. The Damköhler number Da = kws/vw is the ratio of the reaction rate to the advection transfer in the porous wall. Readers are referred to [21] for additional details.
3.1.2 Results
In the results presented here, the Peclet (Pe) and Damköhler (Da) numbers are manipulated to simulate different relative contributions of diffusion, reaction and advection to specie mass transport. NO was the specie/component in our system.
As base case, Fig. 4 presents the concentration profile in the inlet and outlet channels (left) and the wall layer at the front, mid and tail sections of the filter (right) as a function of location. The Pe number is 5.89 and the Da number is 6.73 for this base case.
The concentration profile shows good agreement between the analytical (“ref”) and numerical simulation (“sim”) results. This combination of Pe and Da numbers indicates that reaction is dominant in specie material transport with considerable diffusion contribution. Strong reaction transport is evident in significant specie concentration reduction through the filter wall at the front section (z = 0, ca 90%), middle section (z = 0.5, ca 55%) and end section (z = 1, ca 15%) of the filter. Diffusion is considerable but not limiting in this scenario as the concentration profiles across the wall are similar from the front to the back of the filter. The specie concentration in the outlet channel is low and relatively flat with overall conversionFootnote 2 of approximately 95%.
Figure 5 and Fig. 6 show model validation results for other combinations of Da and Pe numbers. The relative contribution of diffusion and reaction influences the specie concentration profiles and conversions achieved. Overall, the results show good agreement between the analytic and numerical modelsFootnote 3.
3.2 Validation with Published Data
The second attempt at model validation was against data in published literature. Schrade et al. [6] published an important work on modelling of integrated SCR on DPF system. They report data from synthetic gas bench (SGB) experiment for ammonia temperature programmed desorption (TPD) and steady-state NOx conversion carried out on a given sample of the SCR-filter core. The publication provided enough information about the experiments carried out and data obtained to be useful for our validation.
We have followed the approach of Gamma Technologies who use the same data for validating the SCR-filter component of the GT-suite after-treatment modelling software [33].
3.2.1 Schrade Data
Data from two of the experiments carried out in [6] are used for our model validation: (a) ammonia TPD and (b) steady-state NOx conversion. Table 3 presents the specification of the SCR-filter sample, and the parameters of the SGB tests are provided in Table 4.
The TPD experiment is conducted as follows. First the system is stabilised at the given temperature with feed gas containing H2O and N2. The filter is then exposed to 250 ppm of NH3 until the inlet concentration equals the outlet concentration (equilibrium). The NH3 dosing is then switched off, and the temperature is increased at 15 °C/min until no more NH3 is detected at the outlet. Data for system temperature at 150 °C is used for model validation.
The steady-state NOx conversion SGB test is conducted as follows. The system is stabilised at the required temperature with feed gas containing H2O, O2 and N2. Feed gas containing NOx at 200 ppm and NH3 at 250 ppm is then introduced until steady-state conversion is established. Thereafter, NO2/NOx ratio is varied between 0 and 1 in steps, and a new steady-state conversion is reached at each step. The experiment is repeated at various system temperatures and space velocities. Data at 200 °C system temperature and 20 k/h space velocity is used for our validation.
3.2.2 Ammonia TPD Results
Figure 7 presents the performance of the system in the ammonia TPD simulation at 150 °C.
The results show good agreement between simulation and the published experimental results [6]. Predicted outlet NH3 follows the experimental results closely in the adsorption phase. A similar bimodal peak structure in the experimental data is predicted by the numerical simulation during the desorption phase. This is expected of two active sites on the catalyst with different desorption activation energies. The predicted total ammonia storage capacity (area between in and out ammonia curves) is within 10% of the estimate from the experimental data, 0.75 g/l.
Further attempts to improve the simulation prediction with respect to the experiment data have not been conducted. The activation parameters used in the SCR reactions were taken from [33] without further optimisation. The reasonably good alignment of our simulation results with the experimental result demonstrated in Fig. 7 meets the objective of model validation.
3.2.3 Steady-State NOx Results
The steady-state NOx conversion simulation results are presented in this section. The inlet concentration is presented in Fig. 8, and Fig. 9 shows the model simulation results compared with the experimental data.
The results show good agreement between the numerical simulation and the experiment which further validates our model.
The results also align with established SCR system performance. For example, the fast SCR reaction (R3 in Table 1) occurs when NO and NO2 exist in equimolar concentration. This is obvious from the lowest outlet NH3 concentration (i.e. largest consumption of NH3) in this operating regime.
Our model performs better in predicting NOx concentration compared to NH3 because NOx SCR parameters were further optimised in this assessment from the reference points in [33]. No further attempt was conducted to improve NH3 outlet concentration model prediction. The results as presented in Fig. 9 further demonstrate the validity of our numerical model.
4 Model Application
The model was applied to evaluate the impact of diffusion on the deNOx functionality of the SCR-coated filter system. The relative impact of changes in internal and external diffusion to the SCR-coated filter NOx conversion is explored. Internal diffusion is varied via the effective diffusivity coefficient, Dw, j, and external diffusion is varied via the mass transfer coefficient, kim. Each variable is varied in turn by an increase or decrease of one order of magnitude.
The effect of internal and external diffusion is compounded by changes in temperature, space velocity and monolith geometry to investigate how those factors further influence the changes in diffusion.
The system properties are retained from [6] for this characterisation simulation. Table 5 shows the parameter matrix for the simulations carried out.
4.1 Internal vs. External Diffusion
Figure 10 shows how the specie conversionFootnote 4 varies with changes in internal and external diffusion. The results show that for this system, internal diffusion is not limiting as the change in effective diffusivity coefficient (EDC) has marginal effect on NOx and NH3 conversion. The impact of external diffusion is however more significant as specie conversion is worsened at the low mass transfer coefficient (MTC). There is weaker transport of the species from the bulk channel to the wall surface where the conversion reactions occur at lower MTC. Thus, overall conversion deteriorates when external diffusion in relatively restricted by low mass transfer coefficient.
The timescales of the external diffusion, internal diffusion and reaction transport terms are estimated versus the system residence time to further illuminate the system-controlling dynamics. The assessment follows the approach of [34]. The results are presented in Table 6.
The results show that (a) in the base case, the system is surface reaction controlled; (b) internal diffusion transport is faster than the reaction and system residence timescales for all the cases considered; therefore, the impact of changing the effective diffusivity coefficient on the specie conversion is minimal; and (c) the timescale for external diffusion in the low case is of similar magnitude as the timescale for reaction and the system residence time; therefore, the impact of low external mass transfer coefficient is apparent in the specie conversion trends as shown in Fig. 10.
The performance of NOx and NH3 species in the channel and wall of the SCR-coated filter was further investigated in region where NO2/NOx ratio is 0.5 as this is where the largest deviation in specie conversion due to variation in internal and external diffusion is observed (see Table 7).
Figure 11 shows the contour of NOx concentration profiles in the inlet channel, wall layer and outlet channel at NO2/NOx ratio of 0.5 for the base and low casesFootnote 5. In the plot, the inlet channel width is represented as negative dimension. The wall layer begins at zero with its thickness highlighted with black lines. The outlet channel width is represented as positive dimension. It is assumed that there is no radial axis variation; therefore, the channel concentration varies only along the axial length.
The NOx contour shows a few differences for the internal vs. external diffusion low cases (bottom plots): (a) there is more specie concentration spread in the inlet channel of the external diffusion case due to restricted transverse transport through the wall at low MTC, and (b) there is more slip into the wall region for the internal diffusion case. This supports earlier comment about relatively weaker transport of specie from the bulk phase to the wall layer at lower MTC, leading to deterioration in the specie conversion at the low external diffusion case.
The overall behaviour of the system to changes in internal and external diffusion is summarized in Fig. 12.
The results show that (a) specie conversion is enhanced when the diffusive component of transport is increased; this is true for internal and external diffusion; (b) specie conversion deteriorates when the diffusive component of transport is reduced; this is true for internal and external diffusion; and (c) the impact of external diffusion is more significant on the specie conversion compared to internal diffusion.
Internal pore diffusion (EDC) and external channel to wall diffusion (MTC) are significant for accurate characterisation of the deNOx performance of the SCR-coated filter system. The length and density of the SCR-coated filter system, as well as the catalyst loading and zoning, can be selected to optimise the influence of diffusion on the system performance.
4.2 Compound Effects
The effects of compounding the change in internal and external diffusion with changes in temperature, space velocity and monolith geometry are reported in this section.
4.2.1 Temperature
Figure 13 shows the change in NOx conversion when temperature and diffusion are compounded.
Temperature improves NOx and NH3 conversion in this system. The NOx conversion approaches 100% for all NO2/NOx conditions, for high and low internal and external diffusion. The reaction rate is enhanced at higher temperature as per the Arrhenius equation. Increased reactivity results in increased specie conversion. As shown in Table 6, the system is surface reaction controlled at the base case (200 °C). This explains the rise in specie conversions observed when the system temperature increased to 300 °C.
The NOx and NH3 conversion when NO2/NOx ratio is 0.5 is presented in Table 8 with the compound effect of variation in diffusion highlighted. Percentage variation in parenthesis in Table 8 is evaluated as follows: the impact of the compound factor on the base case scenario is given, followed by the incremental impact of compounding with internal or external diffusion.
Temperature increases the base case NOx conversion by about 30% and the NH3 conversion by about 52%, but only marginal variation is achieved by changing MTC and diffusivity coefficient at high temperature. Temperature increases overall specie conversion, but in this application, temperature does not significantly enhance or hinder the effect of diffusion on system deNOx performance.
4.2.2 Space Velocity
Figure 14 shows the change in NOx and NH3 conversion when space velocity and diffusion are compounded.
Higher space velocity results in poorer specie conversion [35]. At higher space velocity, there is less residence time in the system for reaction. Reduction in reaction rates leads to poorer system conversion.
Figure 15 shows the relative impact of internal and external diffusion on NOx and NH3 conversion (at NO2/NOx ratio of 0.5) when compounded with space velocity. The results show that space velocity marginally amplifies the impact of diffusion on specie conversion, with the effect on external diffusion relatively more pronounced.
The impact of high diffusion is enlarged when compounded by space velocity, and the impact of low diffusion is somewhat limited when compounded with space velocity for both internal and external diffusion simulations. This is due to the coupling effect of advection and diffusion in the specie transport balance equations. Higher space velocity increases the advection component of material transport (by increase in the wall velocity). On coupling with high diffusion, the combined effect is enhanced; while coupling with the low diffusion case dampens the combined effect. These effects are marginal in this application.
Increase in space velocity results in poorer specie conversion. The influence of external diffusion is more significant on specie conversion compared to internal diffusion when compounded with space velocity. Space velocity marginally amplifies the effect of internal and external diffusion on species conversion in the high case and marginally limits the effect of internal and external diffusion in the low case.
4.2.3 Monolith Geometry
The impact of diffusion on the SCR-filter deNOx functionality when compounded with change in monolith geometry is evaluated. For this consideration, the monolith volume is fixed with the length shortened by 50% and diameter extended by the same factor. The wall thickness is also increased by 50%.
The results of NOx and NH3 conversions are presented in Fig. 16. In the plots, “L” and “WT” refer to the substrate monolith length and wall thickness, respectively.
The results show that shortening the monolith brick and making the walls thicker improved the species conversion for all NO2/NOx ratios. This result is contrary to findings about flow-through monoliths where better specie conversion was predicted for shorter and thinner monoliths [36]. Our results however align with expectation of a wall flow system: the conversion reactions occur as flow travels through the walls; therefore, for fixed washcoat loading per substrate volume, active site density will increase in the wall layer when length is reduced and wall thickness increased, consequently promoting more reaction and specie conversion.
When diffusion is compounded with monolith geometry, the impact is similar to that observed for space velocity for the low case. The effect of diffusion on specie conversion is limited when compounded with monolith geometry (see Fig. 17).
For high diffusion, the effects of compounding monolith geometry with internal and external diffusion are different. In the former case, specie conversion is marginally improved, while in the latter case, specie conversion is marginally muted. As the internal diffusion primarily occurs in the wall layer, it is expected that an increase in the wall thickness will improve conversion at high effective diffusivity coefficient.
A shorter and thicker-walled monolith with the same washcoat loading improves specie conversion. The change in monolith geometry limits the impact of diffusion except at high internal diffusion case. It is believed that the increase in wall thickness supports the stronger diffusive transport in this case.
5 Conclusions
The model of a SCR-coated filter has been developed and validated against analytic solution and published data. This is the first step in our objective of reducing the complexity of the SCR-filter model for an online model-based control application in a vehicle ECU. In this work, a different approach to the solution of the SCR-coated filter model is presented. The model solution implementation is presented in sufficient detail that it can be replicated.
The validated model was applied to evaluate the effect of internal and external diffusion on the deNOx functionality of a SCR-coated filter in a steady-state characterisation simulation. It was found that:
- 1.
Specie conversion was enhanced when the diffusive component of transport is increased; this is true for internal and external diffusion;
- 2.
Specie conversion deteriorated when the diffusive component of transport was reduced; this is true for internal and external diffusion;
- 3.
The impact of external diffusion was more significant on the specie conversion compared to internal diffusion.
The effect of compounding the variation in internal and external diffusion with changes in temperature, space velocity and the monolith geometry was also evaluated. It was found that:
Overall specie conversion is improved at higher temperature due to the system being reaction kinetics controlled. Temperature did not, however, significantly enhance or hinder the effect of diffusion on system deNOx performance.
Overall specie conversion deteriorated at higher space velocity, due to the reduced residence time for reactions. The influence of external diffusion was more significant on specie conversion compared to internal diffusion when compounded with space velocity. Space velocity marginally amplified the effect of internal and external diffusion on species conversion in the high case, and marginally limited the effect of internal and external diffusion in the low case.
A shorter and thicker-walled monolith with the same washcoat loading improved specie conversion. The change in monolith geometry limited the impact of diffusion except for the high internal diffusion case. It is believed that the increase in wall thickness supports the stronger diffusive transport in this case.
Internal (pore) diffusion and external channel (bulk to wall-surface) diffusion are significant for accurate characterisation of the deNOx performance of the SCR-coated filter system. The length and density of the SCR-coated filter system, as well as the catalyst loading and zoning, should be selected to optimise the influence of diffusion on the system performance.
Notes
SCR-coated filter also referred to as SCRF, SDPF and SCR-in-DPF
Conversion is 1 − y2(z = 1).
A deviation is noticed in the simulation results vs. the analytical results at the outlet boundary of the system. This deviation narrows as the number of grid points in the solution domain increases. This is believed to be an artefact of the approximation of the analytical solution over a finite-spaced numerical grid. A similar observation is noted in [32]. We have selected the number of grid points to minimise this deviation without incurring excessive computational overhead.
Specie conversion is defined as \( 1-\frac{y_i}{y_{i-\mathrm{in}}} \). NH3 conversion is used instead of NH3 slip because NH3 was supplied in excess in this system.
The high diffusion case is similar to the base case, thus not shown in the plot.
References
Fleming, R.D.: Fuel economy of light-duty diesel vehicles (1976). https://doi.org/10.4271/760592
Tang, W., Youngren, D., SantaMaria, M., Kumar, S.: On-engine investigation of SCR on filters (SCRoF) for HDD passive applications. SAE Int. J. Engines. 6(2), 862–872 (2013). https://doi.org/10.4271/2013-01-1066
Bush P, Iretskaya S, Tadrous T. "SCR coated DPF: continuous soot oxidation and NOx reduction". 16th Glob Powertrain Congr . 2010.
Tan, J., Solbrig, C., Schmieg, S.J.: The development of advanced 2-way SCR/DPF systems to meet future heavy-duty diesel emissions (2011). https://doi.org/10.4271/2011-01-1140
He, Y., Brown, D.B., Lu, S., Paratore, M.J., Li, J.: Opportunities and challenges for blended 2-way SCR/DPF aftertreatment technologies (2009). https://doi.org/10.4271/2009-01-0274
Schrade, F., Brammer, M., Schaeffner, J., Langeheinecke, K., Kraemer, L.: Physico-chemical modeling of an integrated SCR on DPF (SCR/DPF) system. SAE Int. J. Engines. 5(3), 958–974 (2012). https://doi.org/10.4271/2012-01-1083
Olowojebutu S, Steffen T. "A review of the literature on modelling of integrated SCR-in-DPF systems". SAE Tech Pap. 2017. https://doi.org/10.4271/2017-01-0976.
Bissett, E.J.: Mathematical model of the thermal regeneration of a wall-flow monolith diesel particulate filter. Chem. Eng. Sci.39(7), 1233–1244 (1984)
Konstandopoulos, A.G., Johnson, J.H.: Wall-flow diesel particulate filters—their pressure drop and collection efficiency (1989). https://doi.org/10.4271/890405
Konstandopoulos, A.G., Kostoglou, M., Skaperdas, E., Papaioannou, E., Zarvalis, D., Kladopoulou, E.: Fundamental studies of diesel particulate filters: transient loading, regeneration and aging (2000). https://doi.org/10.4271/2000-01-1016
Koltsakis, G.C., Stamatelos, A.M.: Modeling thermal regeneration of wall-flow diesel particulate traps. AIChE J. 42(6), 1662–1672 (1996)
Kandylas, I.P., Koltsakis, G.C.: NO2-assisted regeneration of diesel particulate filters: a modeling study. Ind. Eng. Chem. Res.41(9), 2115–2123 (2002). https://doi.org/10.1021/ie010842m
Premchand, K.C., Surenahalli, H., Johnson, J.H.: Particulate matter and nitrogen oxides kinetics based on engine experimental data for a catalyzed diesel particulate filter (2014). https://doi.org/10.4271/2014-01-1553
Surenhalli, H.S., Premchand, K., Johnson, J.H., Parker, G.: Modeling study of active regeneration of a catalyzed particulate filter using one-dimensional DOC and CPF models (2011). https://doi.org/10.4271/2011-01-1242
Premchand KC. "Development of a 1-D catalyzed diesel particulate filter model for simulation of the performance and the oxidation of particulate matter and nitrogen oxides using passive oxidation and active regeneration engine experimental data". 2013.
Olsson, L., Sjövall, H., Blint, R.J.: A kinetic model for ammonia selective catalytic reduction over Cu-ZSM-5. Appl. Catal. B Environ.81(3), 203–217 (2008)
Koltsakis, G., Haralampous, O., Depcik, C., Ragone, J.C.: Catalyzed diesel particulate filter modeling. Rev. Chem. Eng.29(1), 1 (2013). https://doi.org/10.1515/revce-2012-0008
Tronconi, E., Nova, I., Marchitti, F., Koltsakis, G., Karamitros, D., Maletic, B., Markert, N., Chatterjee, D., Hehle, M.: Interaction of NO x reduction and soot oxidation in a DPF with Cu-zeolite SCR coating. Emiss Control Sci Technol. 1(2), 134–151 (2015). https://doi.org/10.1007/s40825-015-0014-y
Haralampous OA, Koltsakis GC, Samaras ZC, et al. "Reaction and diffusion phenomena in catalyzed diesel particulate filters". SAE Technical Paper; 2004. doi:https://doi.org/10.4271/2004-01-0696.
Premchand, K.C., Johnson, J.H., Yang, S.-L.: Development of a 1-D catalyzed diesel particulate filter model for simulation of the oxidation of particulate matter and gaseous species during passive oxidation and active regeneration (2013). https://doi.org/10.4271/2013-01-1574
Konstandopoulos AG, Kostoglou M. "Computationally fast implementations of convection, diffusion and chemical reaction phenomena in diesel particulate filters". 2010. https://doi.org/10.4271/2010-01-0890.
Fogler HS. "Essentials of Chemical Reaction Engineering". Pearson Education; 2010.
Wurzenberger, J.C., Triebl, C., Kutschi, S.: Diffusion supporting passive filter regeneration- a modeling contribution on coated filters (2018). https://doi.org/10.4271/2018-01-0957
De Iaco Veris A. "Practical Methods for Ordinary Differential Equations". Aracne; 2008. https://books.google.co.uk/books?id = EKgKngEACAAJ.
York APE, Ahmadinejad M, Watling TC, et al. "Modeling of the catalyzed continuously regenerating diesel particulate filter (CCR-DPF) system: model development and passive regeneration studies". 2007. https://doi.org/10.4271/2007-01-0043.
Shampine, L., Kierzenka, J.: A BVP solver based on residual control and the MATLAB PSE. ACM Trans. Math. Softw.27, 299–315 (2001)
Boisvert JJ, Muir PH, Spiteri RJ. "py_bvp: a universal Python interface for BVP codes". In: Proceedings of the 2010 Spring Simulation Multiconference. Society for Computer Simulation International; 2010:95.
MathWorks. "ode15s". https://uk.mathworks.com/help/matlab/ref/ode15s.html. Accessed June 15, 2018.
Konstandopoulos, A.G., Kostoglou, M.: Periodically reversed flow regeneration of diesel particulate traps (1999). https://doi.org/10.4271/1999-01-0469
Konstandopoulos, A.G., Kostoglou, M., Lorentzou, S.: Wall-scale reaction models in diesel particulate filters (2007). https://doi.org/10.4271/2007-01-1130
Koltsakis, G.C., Bollerhoff, T., Samaras, Z., Markomanolakis, I.: Modeling the interactions of soot and SCR reactions in advanced DPF technologies with non-homogeneous wall structure (2012). https://doi.org/10.4271/2012-01-1298
Wurzenberger, J.C., Bardubitzki, S., Kutschi, S., Fairbrother, R., Poetsch, C.: Modeling of catalyzed particulate filters - concept phase simulation and real-time plant modeling on HiL. SAE Int. J. Engines. 9(3), 1720–1734 (2016). https://doi.org/10.4271/2016-01-0969
Gamma Technologies. "SCR coated DPF, SCR-F example model demonstrating NH3 storage and NOx reduction over a diesel particulate filter". 2016.
Park, S.Y., Rutland, C.J., Narayanaswamy, K., Schmieg, S.J., He, Y.S., Brown, D.B.: Development and validation of a model for wall-flow type selective catalytic reduction system. Proc Inst Mech Eng Part D J Automob Eng. 225(12), 1641–1659 (2011)
Yang, Y., Cho, G., Rutland, C.: Model based study of DeNOx characteristics for integrated DPF/SCR System over Cu-Zeolite (2015). https://doi.org/10.4271/2015-01-1060
Gong, J., Cai, L., Peng, W., et al.: Analysis to the impact of monolith geometric parameters on emission conversion performance based on an improved three-way catalytic converter simulation model (2006). https://doi.org/10.4271/2006-32-0089
Acknowledgements
The authors would like to acknowledge the support of the Engineering and Physical Sciences Research Council (EPSRC) and Eminox Ltd. for the funding for this research.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This is the first of two papers on the model order reduction of integrated SCR filter systems.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Olowojebutu, S., Steffen, T. & Bush, P. SCR-Filter Model Order Reduction (1): Development and Validation of the Base “High-Fidelity” Model. Emiss. Control Sci. Technol. 6, 58–74 (2020). https://doi.org/10.1007/s40825-019-00150-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40825-019-00150-1