Defining Landscapes and Scales to Model Landscape–Organism Interactions

Abstract

Purpose of Review

We review and provide comment on issues of scale in ecological studies in the context of two paradigms used to define landscapes: the patch-mosaic and gradient models. Our intent is to offer guidance for structuring habitat-selection models with examples of how scale, autocorrelation, measurement error, and choice of patch-mosaic or gradient models, analysis methods, and covariates by the researcher can influence inferences regarding landscape–organism interactions.

Recent Findings

Methods that allow the organism or data to define the grain and extent of scale of the study offer promise by reducing subjectivity in choices of scale. Ultimately, we recommend that the ecological phenomenon of interest should shape the selection of models defining landscape–organism interaction; however, the choice of model remains with the researcher and is dependent on the research question and the availability of data. Clearly, both the patch-mosaic and gradient models can provide reasonable frameworks for study, and multiple scales that draw from both paradigms often may be most appropriate.

Summary

Scale has been identified as a crucial feature of landscape ecology, yet scale as a paradigm has offered little direction for ecologists. Likewise, debate contrasting gradient models and patch-mosaic models offers few new insights on how ecologists might decide on an appropriate scale for analysis of organism distribution or habitat selection. Various ecological processes influence organisms at different scales and modeling approaches need to be able to accommodate multiple scales simultaneously, which may vary by landscape structure and movement ecology. The continuum of scales and combinations of both gradient and patch-mosaic landscapes provides the necessary array of structures that can be used to construct combinations of landscape covariates that coincide with the ecology of the organism across scales.

Introduction

Several of the foundations of spatial ecology were conceptualized and modeled for a landscape consisting of patches. These included the ideal free distribution [1], metapopulations [2], and foraging theory such as the marginal value theorem [3]. The patch concept made the mathematical theory simple and tractable, although this approach reduced and simplified much of the spatial variation. Landscape ecologists have continued the reliance on concepts of the patch with the patch-mosaic model (PMM) [4, 5]. Users of the PMM assumed that the distribution of organisms can be explained adequately by discrete patches, or polygons, with aggregated and homogenous characteristics. For example, one might use aerial photographs to delineate discrete patches of vegetation type for use in habitat-selection analyses. The early formation of the PMM might have been as much based on adherence to the patch concept as on the limited availability and irrelevancy of fine-grained spatial data (both telemetry and environmental) for analyses. The shortcoming of the PMM was that in many circumstances it did not capture the environmental complexity inherent in patches and ecological systems. Critics claimed that delineation of patches for the PMM often could be subjective and that it oversimplified systems by offering an organism being modeled only a binary choice of whether they use or do not use a patch.

To remedy these deficiencies, McGarigal and Cushman [6, 7] proposed a gradient model (GM) of landscape structure. Instead of representing landscapes as patches of a particular type, the GM represented environmental conditions along a continuous scale. Whereas the practitioner of the PMM decides the cut-off values and therefore spatial extent of patches, the GM eliminates this burden and lessens the bias in analysis by allowing the organism to delineate the extent of patches through observed use. One might suppose that the advent of highly accurate and precise global positioning system (GPS) radiotelemetry at fine temporal scales, combined with remote-sensing technology [8], reinforced the relevance of the GM paradigm for asking more fine-grained questions. Technological advances allowed researchers to estimate variables such as greenness [9] or vegetation height and cover [10] continuously and over large areas, thereby facilitating a more dynamic characterization of habitats suitable for organisms.

Despite these advances, both the PMM and GM remain relevant conceptual frameworks for the analysis and characterization of landscape–organism interactions. Both provide context-specific advantages that depend on the nature of the landscape of interest and environmental covariates available. For example, although organizing a landscape into patches or a classified map can erode information that exists at finer spatial scales, or create discontinuities at larger scales, vegetation patches truly exist even though mapping of vegetation communities might simplify the actual spatial heterogeneity [11]. Patches often make sense for characterizing patterns of vegetation or landscape heterogeneity, and these patches can be important for characterizing how organisms are distributed on landscapes [12]. In a practical sense, the PMM also provides for an intuitive understanding of landscape variation, and lends itself well to visualization. This can be of great importance for application, e.g., foresters map forest stands of similar composition that are then managed as a unit. However, patches make less sense when considering those environmental covariates that are best measured with continuous metrics such as elevation, distance to certain features, or predation-risk values [7, 8].

Here, we organize what we believe to be key considerations for building models of landscape–organism interactions and suggest that the appropriate framework rests along a continuum and often requires analysis involving multiple scales and a mix of the GM and PMM. Deciding on the appropriate model structure to investigate a given ecological question requires thoughtful consideration of several aspects of a study. We do not believe that it is possible to prescribe a priori the necessary components of an effective spatial model of landscape–organism interactions but we know that the following components can have major influence and warrant attention: landscape organization, autocorrelation, measurement error, and the influence of decisions made by the researcher.

How Do We Organize and Define Landscapes to Study Organisms?

Our perception of landscape–organism interactions harks back to early definitions of ecology, i.e., seeking an understanding of the distribution and abundance of organisms [13]. For animals, movement and habitat selection (space use) are fundamental mechanisms that result in patterns of distribution [14]. Various environmental variables that contribute to space use can be relevant at different spatial scales, which in turn requires flexible characterization of habitats [15, 16•, 17•]. Models of habitat selection, such as resource selection functions [18], can readily accommodate predictor covariates measured at a variety of scales drawing from either the PMM or GM.

Many methods exist for characterizing landscapes and the choice of scale can substantially influence results [19•]. Complex landscape–organism interactions frame the relevant ecological scale, but, even more importantly, also the ecological phenomenon of interest. The onus of determining what level of information loss is acceptable rests with the researcher, and begins with the proper formulation of the research question.

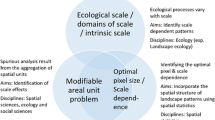
We suggest that both the PMM and GM have similar shortcomings resulting in a loss of information. Indeed, any spatial characterization of an environment will impart some level of homogenization, and an important consideration for the researcher is what degree of loss of heterogeneity is acceptable. Aggregating spatial information into homogeneous patches under the PMM results in a greater loss of information regarding landscape heterogeneity than under a GM framework, although loss of information under a GM framework also occurs. Depending on scale and sampling capability, researchers aggregate information in the GM based on the grid resolution for maps (i.e., cell or pixel size), sampling intensity, and observation limits [11]. Therefore, in many cases the application of GM is essentially a finer-resolution use of the PMM, and we reiterate that the appropriate framework rests along this continuum and often features multi-scale analysis [16•, 20].

The potential ramifications from the aggregation of spatial information extend beyond more commonplace consequences such as the reduction of vegetation classes in a patch. Simplifying a landscape into the PMM destroys some structural attributes of the landscape. For example, although a researcher can measure the distance of an organism to the edge of a homogenous patch, there is a loss of information about the gradient of environmental heterogeneity leading to the edge [21]. A nice example is from the northern spotted owl (Strix occidentalis caurina), which avoids ‘hard’ edges such as those created by timber harvest but selects ‘feathered’ edges created by natural processes such as fire [22]. In context of estimating a habitat-selection model such as a resource-selection function for owls, it might be best to use fine-grained spatial data (GM) that facilitates characterization of edge conditions. Yet, patch structure remains useful for defining old growth stands that are essential components of spotted owl habitats and necessary for forest management.

In other instances, aggregation into patches at a fine scale is defensible to identify foraging patches. In elk (Cervus elaphus), foraging occurs in small patches of vegetation followed by larger movements between foraging patches within the home range [23]. However, seasonal ranges are shaped at much larger scales. Elk move many kilometers between summer and winter ranges, across which gradients of road density influence habitat selection [24, 25]. Likewise, aggregation into patches can be useful for modeling anthropogenic disturbances (e.g., forestry cutblocks) and habitat management regimes of landscapes. For example, the use of patches by caribou (Rangifer tarandus) has been linked to both the intrinsic characteristics of a patch and those of the surrounding matrix [26]. In this case, the use of the PMM incorporates analysis at different scales, which is important for species that respond to disturbance at multiple scales [27]. The PMM also provides results (e.g., patch sizes necessary for habitat use) that can be directly applied to land and resource management.

Organizing and defining landscapes involves aggregating spatial data into bins or zones. This can trigger the modifiable areal unit problem (MAUP), which remains an unresolved problem in landscape ecology. In short, MAUP occurs when the interpretation of results varies according to scale [28, 29]. For example, a response variable can show a negative relationship with a predictor variable at a fine scale and a positive relationship at coarser scales [30]. This is not only an issue for spatial scale, but for temporal scales as well (Modifiable Temporal Unit Problem [MTUP]) [31]. We suspect that the MAUP is more prevalent in most map classifications, such as the PMM [32]; however, to date this has not been tested. One potential solution to the MAUP is to incorporate random effects of space into a mixed-effects model, especially if the factors leading to spatial heterogeneity are unknown [30]. However, this is not a one-size-fits-all solution, because the number and size of areas represented by random effects still requires careful consideration, and this solution would not apply to the MTUP [30].

To recap, organizing and defining landscapes, e.g., creating maps, invariably requires choices of scale and these choices influence our ability to characterize the spatial ecology of organisms. To avoid the MAUP we believe that the safest scales will be those anchored with some form of biological motivation, e.g., estimating movement-constrained habitat selection models [25], or within the bounds of the animal’s home range [18]. Yet, political boundaries or other management constraints often impose scales or patches that compromise our ability to study spatial patterns driven by ecological processes.

Autocorrelation

Finer-resolution data across spatiotemporal scales are now widely available thanks to ever-increasing technological advancements [33], but these data often are correlated in space and time, violating statistical inference assumptions [29]. Landscapes by their very nature are autocorrelated. After all, when we plot the spatial autocorrelogram, we can estimate patch size at the spatial lag where the autocorrelation goes to zero [34], thus the autocorrelation function of a GM landscape can be used as an objective method for creating a map of PMM. Important landscape structure can be discerned from the range of the autocorrelation of environmental covariates [35, 36]. The PMM will always increase spatial autocorrelation above that of the GM by aggregating spatial units into patches [11]. In context of habitat modeling, spatial autocorrelation will result in variances being underestimated even though the estimated models might be unbiased [37]. This creates potential problems for statistical inference, although this problem tends to be lessened in landscape ecology because the statistical paradigm is usually one of developing weight of evidence instead of Popperian hypothesis testing. Comparing alternative models using information-theoretic metrics such as the Akaike Information Criteria has become more common than trying to estimate P-values. Nevertheless, we still need some way to evaluate whether our models have utility for prediction or at least explaining variability. Whether using GM or PMM, we might measure a model’s predictive ability by cross validation [38], and several alternative approaches are available. We could, for instance, estimate a model for habitat selection that is based on autocorrelated landscape attributes and then examine residuals from this model. If these landscape attributes were the source of the autocorrelation, the residuals should lack spatial autocorrelation and we can conclude that the autocorrelation simply reflects the underlying landscape pattern [39]. Alternatively, we might be interested in the magnitude of model coefficients to evaluate the existence of selection for or against a landscape attribute. Because of autocorrelation, our estimates of variance associated with these coefficient estimates will be underestimated [11] and this will be more serious for PMM than for GM. Thus, we could expect that confidence intervals for those coefficients might not overlap zero even though in reality there is no significant effect, i.e., a type I error. Variance inflation methods exist, such as sandwich estimators or Newey-West estimators, which can be used to fix this problem [40, 41], or modeling approaches can include autocorrelation structures [42]. Thus autocorrelation remains a consideration when building effective models of landscape–organisms interactions, but seldom is it likely to be a major constraint.

Measurement Error

While landscape ecologists have become cognizant of potential issues arising from autocorrelation, problems stemming from measurement error can be less obvious. Measurement error adds noise, uncertainty, can influence effect size [43], and might contribute to the MAUP [28]. With small sample sizes in particular, measurement error can increase the magnitude of the observed effect resulting in a significant relationship (type I error), whereas with larger samples the effect size would have been much smaller [43]. Measurement error is present in any remotely collected data, including data commonly used to evaluate species–habitat relationships such as GPS radiotelemetry data and habitat variables commonly derived in a geographic information system (GIS; e.g., landcover type, digital-elevations models, normalized difference vegetation index, etc.). Measurement error can affect both precision and accuracy [29]. Researchers often assume that poor precision should not inherently lead to bias; however, past research illustrates that this assumption is not always true [44]. Indeed, poor precision itself can result in attenuation bias, which can lead to incorrect conclusions [44, 45]. That said, in the case of radiotelemetry, measurement error associated with fix success is often predictable, and consequently tools exist to overcome this bias in habitat selection modeling using statistical corrections [33, 46,47,48,49].

Higher-resolution data often used in the GM approach, e.g., from remote sensing, are not necessarily precise, and there can be substantial measurement error associated with such data layers [50]. Misclassification of habitats can significantly affect results using both the GM and PMM, with selection coefficients in species–habitat models providing an example [50, 51]. These types of errors may be compounded in the PMM, where aggregation into larger homogenous patches can incorporate multiple errors or misclassifications [52]. In general, rare habitats are more subject to type II error (false negatives), while common habitat types are more subject to type I errors (false positives) [48]. Again, these errors can be exacerbated by broader homogenization in the PMM. Linear features such as roads, trails, and power lines can be particularly problematic when coupled with radiotelemetry relocation data; linear features might be quite common on the landscape, but animal use of these features might be grossly underrepresented because of measurement error [53, 54].

Although the homogenization of the PMM can in some cases compound issues of measurement error [52], awareness of these shortcomings by the researcher could help to mitigate adverse effects. In contrast, the finer resolution of the GM could lead users to, knowingly or not, ignore measurement error associated with covariates. For example, we may consider a satellite imagery land-cover classification with accuracy above 80% adequate to use in our analysis, but might not consider what error this introduces into results [55]. Habitat-selection models drawing from multiple attributes of the landscape actually modulate these errors so that extrapolations to population dynamics may not be unreliable [56].

Choices Made When Building Models

Aside from errors that may be inherent in remotely sensed data from measurement error, the researcher can further introduce biases in data layers through selection of resolution (grain) and domain (extent). The grain and extent of the data used will affect the perceived animal response to human-imposed landscape change [57], and so we should seek to minimize these effects. Often, researchers choose grain and extent subjectively, complicating comparisons between ecological studies [15]. The scale of spatial layers should match the data or processes of interest [58, 59], and movement ecology can help us to identify those scales [28, 60]. For example, researchers should not couple imprecise Argos satellite data with fine-scale habitat characteristics in a habitat-selection model [44]—similarly, the decision to use the PMM or GM should depend on the question at hand.

In the case of animals, movement across scales is non-arbitrary, reinforcing that habitat selection requires consideration of multiple scales [61]. When studying animal behavior, it is often useful or necessary for appropriate inference to capture the perception of the landscape by the organism [16•]. In habitat-selection models, space use of an animal is contrasted with what is available [40, 62]. For the most part, the grain, or resolution, of availability influences the adequacy of sampling landscape variation, while the extent dictates which behaviors are captured and missed [62]. The resolution of habitat attributes can shape the observed pattern in selection with variation in what is deemed available (termed the functional response in habitat selection); specifically, smaller grain sizes show a stronger signal for a relationship between selection and availability [63] and this is true for either GM or PMM. Further, changing the extent of the area sampled to characterize availability can alter observed patterns of selection even though the resolution of availability and the used domain remain constant [17•]. Availability extent can be delineated using observed movement behavior [60]. Movement and selection response to a habitat feature, (e.g., human disturbance) can be modeled together, corresponding to the reality of an organism responding to their environment [25, 42]. The researcher invariably must attempt to think like the study animal; for example, does the animal perceive a clearcut itself (PMM) or does the animal perceive the cover afforded by the dense vegetation associated with the clearcut that could be measured on a gradient? When inferring selection behavior, the pivotal decision is what the animals perceive to be available [64]. However, instead of being viewed as solely a challenge or caution, the flexibility in availability domains provides freedom for researchers to study wildlife behavior that acts simultaneously across scales [16•].

This notion is important because wildlife behavior at one scale is not isolated from its behavior at a different scale. Observed behavioral responses at different scales are inextricably linked and occurring simultaneously as animals move through space and time. For example, the strategies of prey in response to predation risk (natural and human) include coarse and fine-scale variation in the use of the landscape, from seasonal migrations to movements into cover within hours [17•, 25, 65, 66]. Whether the multiple components that influence the ecology of scale are best tied to PMM or GM depends more on the structure of the landscape than the process of habitat selection or movement.

The scale of behavior might occur within a hierarchy, with coarser scales regulating behavior at finer scales and factors most limiting to animal fitness enacting their influence at the coarsest scales [67, 68]. The scale-dependent hierarchy of landscape–organism interaction has been documented in light of predation risk and human disturbance [27, 69]. Conversely, the scaling-up hypothesis suggests that fine-scale drivers are linked to the observations occurring at coarse scales [70]. A scaling up, or scale-independent, pattern in selection behavior has been observed in recent literature that employ a multi-scale comparative approach when studying risk avoidance and resource selection [17•, 71], indicating that this concept is deserving of further exploration. Likewise, mixing PMM and GM approaches to characterize the landscape can allow better conceptualization of how animals perceive their environment.

Conclusion

How ecological patterns and processes relate to the scale at which we study them has long been of interest to ecologists [72]. More recently, authors have advocated for multi-scale research and methods that emphasize or allow for the behavior of an organism to identify biologically relevant scales. Observing the variation in the behavior of an organism at multiple scales, and with different resources availability, provides opportunity for the data to inform the influence of a landscape feature [73,74,75]. Likewise, characterizing landscapes with a mix of variables drawn from both GM and PMM gives us the flexibility to accommodate the complexity of spatial ecology. Despite the longstanding discussion of scale [76], a review conducted by McGarigal et al. [16•] highlights the paucity of multi-scale research in habitat-selection studies. Further, the decision of scale might be perpetually discretionary due the complexity of the issue. Given this, researchers should clearly present the rationale regarding selection of scale [16•]. However, only 29% of all studies (45% of mammal studies) provide biological reasons for the choice [77].

We emphasize that in many cases the ‘appropriate scale’ for ecological studies is in fact a range of scales. A recent study tested variation in models of cougar (Puma concolor) habitat selection by creating 2500 models with variables defined at different grains, from different sources, and as either continuous (GM) or categorical (PMM). The best performing models tended to have a mix of patches and gradients and used finer grain, although more studies will be necessary to determine if the same effects are found in other model types and ecosystems [19•]. Habitat selection during dispersal often demonstrates a mix of scales [78, 79] or optimization at intermediate scales [80, 81].

Though it is appealing to search for general methods to define ‘appropriate scales’, environmental complexity and the influence of the research interest on appropriate scale render generalities elusive. We argue that the selection of scale should be driven primarily by a well-defined question [82]. The choice of an appropriate landscape framework will then depend on this question and the format of covariates.