Numerical Analysis WSGD Scheme for One- and Two-Dimensional Distributed Order Fractional Reaction–Diffusion Equation with Collocation Method via Fractional B-Spline

Abstract

The main propose of this paper is presenting an efficient numerical scheme to solve WSGD scheme for one- and two-dimensional distributed order fractional reaction–diffusion equation. The proposed method is based on fractional B-spline basics in collocation method which involve Caputo-type fractional derivatives for $0 < \alpha < 1$. The most significant privilege of proposed method is efficient and quite accurate and it requires relatively less computational work. The solution of consideration problem is transmute to the solution of the linear system of algebraic equations which can be solved by a suitable numerical method. The finally, several numerical WSGD Scheme for one- and two-dimensional distributed order fractional reaction–diffusion equation.

Introduction

Over the past few decades, fractional differential equation (FDM) models have become an increasingly important tool for physics, finance, materials, control, viscoelasticity, chaos, bioengineering and engineering to understand and make predictions about how phenomena functions evolve through time and space [1,2,3,4]. In [5] Baleanu and et. al. studied an iteration scheme based on the local fractional Laplace variation iteration method (LFLVIM) and too developed an iterative scheme for the exact solutions of local fractional wave equations (LFWEs). In [6] Khan and et. al. presented numerical solutions of fractional differential equations the fractional-order Brusselator and used of Bernstein polynomials.

These models often consist of Fractional differential equations (FDEs) that are discretized with a numerical method and solved on a computer [7]. The most commonly used discretization methods are the finite difference method (FDM) [8], the finite volume method [9], the finite element method (FEM) [10, 11], the discrete element method, the boundary element method, meshless method or combination of these methods [12, 13]. In theory, each method provides the same solution to the original PDEs. However, in practice, certain methods are better suited to certain problems than others. Often, one method dominates within any given discipline and in the sciences, the (FDM) is the most prevalent, due to its simplicity.

In Some papers describing the existence of solutions for fractional order models based on the Caputo’s fractional derivative and some analytical solutions for the fractional differential equations such as in [14] that Baleanu et. al. investigated conditions for the existence and unique solutions of a hybrid differential hybrid equation (HDEs) system and in [15] to studied the existence and uniqueness of mild solution (EUMS) of coupled system of hybrid fractional differential equations (HFDEs). They also referred to the article in [16] a fractional differential equation of order $\delta_{1}$ that $3 < \delta_{1} \le 4$ with initial and boundary conditions addressing the existence of a positive solution (EPS), where the fractional derivatives $D^{{\delta_{1} }}$, $D^{{\alpha_{1} }}$ are in the Riemanne-Liouville sense of the order $\alpha_{1}$, $\delta_{1}$. They established an equivalent integral form of the problem with the help of a Green’s function. For example, an abnormal release phenomenon is often a concern of many mathematicians in transportation processes through complex systems or disordered systems, including fractal media [17] and time-fractional diffusion equations. There are significant benefits to the development of numerical schemes for solving distributed differential equations, however, the current research is very interesting in this regard. According to researchers, only a small number of numerical solution algorithms for such equations are proposed, and most of these numerical schemes are distributed with ordinary differential equations (see for example [18,19,20,21]) and one-dimensional differential equations of the distributed order (see for example [22,23,24]). They did not find any reports on the OSC method to solve the problem. Based on WSGD approximation in time, they establish discrete-time OSC method. One of the approaches for modeling of such processes is to employ time-fractional diffusion equations of distributed order. Langlands [25] used Laplace transform to reduce the resulting equation to an ordinary algebraic equation. Gafiychuk [26] studied a fractional reaction–diffusion system with two types of variables: activator and inhibitor. Interactions between components were modeled by cubical nonlinearity. Luchko [27, 28] considered the maximum principle and some uniqueness and existence results too Zhunang et. al. [29] considered a variable-order fractional advection–diffusion equation with a nonlinear source term on a finite domain. Explicit and implicit Euler approximations for the equation are proposed. Stability and convergence of the methods are discussed.

In recent years, several numerical methods have been applied for the solution of fractional distributed order partial differential equations too in process physic and engineering was focused on the multi-term fractional equation, scientists and engineers seeking for new perspective to describe some phonomania which is more effective than the single term fractional problems. Luchko and Yamamoto [30,31,32,33] studied subsequently the asymptotic behaviors of solutions. Guang and Sun [34] the Grünwald formula is used to approximate the involved fractional derivatives. Based on the error asymptotic expansion of this formula, two effective extrapolation methods are presented to improve the numerical accuracy in time and strict error analysis for the extrapolation methods is also given in $H^{1}$ norm in 2015. In [35] Lischke, Zayernouri and Karniadikis have presented a Laguerre Petrov–Galerkin spectral method for solving multi-term fractional initial value problems on the half line with linear complexity, which is a significant reduction from the cubic complexity required for existing spectral methods in 2017. Gao et al. [36] a special point is found for the interpolation approximation of the linear combination of multi-term fractional derivatives. The derived numerical differentiation formula can achieve at least second order accuracy. Then the formula is used to numerically solve the time multi-term and distributed-order fractional sub-diffusion equations in 2017. They proved that the schemes are unconditionally stable and convergent with the convergence orders ${\mathcal{O}}\left( {\tau + h_{1}^{2} + h_{2}^{2} + \Delta \upalpha ^{2} } \right)$ and ${\mathcal{O}}\left( {\tau + h_{1}^{4} + h_{2}^{4} + \Delta \upalpha ^{4} } \right)$ in $H^{1}$ norm, respectively, where $\tau$, $h_{1}$, $h_{2}$ and $\Delta$ are the step sizes in time, space in x- and y-direction, and distributed order. Yang et al. [37] had developed an effective WSGD-OSC scheme for the two dimensional distributed order time fractional reaction diffusion equation in 2018. A detailed analysis shows that the proposed scheme is unconditionally stable and convergent with the convergence order ${\mathcal{O}}\left( {\tau^{2} + \Delta^{2} + h^{r + 1} } \right)$, where $\tau$, $\Delta$, $h$ and $r$ are, respectively the time step size, step size in distributed-order variable, space step size, and polynomial degree of space.

We consider the following distributed order time fractional reaction diffusion equation:

$$ \left\{ {\begin{array}{*{20}l} {{\mathcal{D}}_{t}^{\omega } {\mathcal{U}}\left( {X,t} \right) - \Delta {\mathcal{U}}\left( {X,t} \right) = {\mathbb{F}}\left( {X,t} \right),} \hfill & {\left( {X,t} \right) \in \Omega \times \left( {0,T} \right],} \hfill \\ {{\mathcal{U}}\left( {X,0} \right) = \psi_{1} \left( X \right),} \hfill & {X \in \Omega ,} \hfill \\ {{\mathcal{U}}\left( {X,t} \right) = \Phi \left( {X,t} \right),} \hfill & {X \in \partial \Omega ,} \hfill \\ \end{array} } \right. $$

(1)

where ${\mathbb{F}}$ is the source term, subject to the compatible initial condition $\psi_{1}$ and boundary condition $\Phi$ are given functions on $\Omega$ and ${\mathcal{D}}_{t}^{\omega }$ denotes the distributed order fractional derivative of ${\mathcal{U}}$ in time t, given by

$$ {\mathcal{D}}_{t}^{\omega } {\mathcal{U}}\left( {X,t} \right) = \mathop \int \limits_{0}^{t} \omega \left( \upalpha \right){\mathcal{D}}_{t} {\mathcal{U}}\left( {X,t} \right)d, $$

(2)

here $\omega \left( \upalpha \right)$ is a continuous non-negative weight function, such that the conditions:

$$ \omega \left( \alpha \right) \ge 0;\;\omega \ne 0;\; \in \left[ {0,1} \right];\;\omega \left( \upalpha \right) = \mathop \int \limits_{0}^{t} \omega \left( \upalpha \right)d = c_{0} > 0, $$

(3)

hold true, where $c_{0}$ is a positive constant. $D_{t}^{\alpha } {\mathcal{U}}\left( {X,t} \right)$ is the th order time Caputo fractional derivative defined by $\upalpha _{i} \in \left( {0,1} \right)$

$$ D_{t}^{\alpha } {\mathcal{U}}\left( t \right) = \left\{ {\begin{array}{*{20}l} {\frac{1}{{\Gamma \left( {k - } \right)}}\mathop \int \limits_{0}^{t} (t - \xi )^{k - \alpha - 1} {\mathcal{U}}^{k} \left( \xi \right)d\xi } \hfill & {k - 1 < \alpha \left\langle {k, t} \right\rangle 0,} \hfill \\ {{\mathcal{U}}^{k} \left( t \right) } \hfill & {\upalpha = k.} \hfill \\ \end{array} } \right. $$

(4)

where ${\Gamma }\left( . \right)$ is a usual Gamma function.

Several numerical techniques are available to find approximate solutions to differential equations of mathematical models of engineering problems [38, 39]. One of the techniques available is collocation technique. A collocation method involves satisfying a differential equation to some tolerance at a finite number of points, called collocation points.

The main superiority of this technique is its simplicity and hence low cost of computation. However the level of accuracy as provided by this technique is not high which limits its applicability to a relatively narrow area. Collocation technique using B-spline basis functions is increasingly used to solve engineering problems. The idea is to connect the smoothness of fractional B-spline basis functions with the low computational cost of collocation. It has been shown that this technique can be efficient and at par to other established techniques of Finite Element analysis and Finite Difference technique. The fractional B-spline collocation method has a few distinct advantages over the Finite Element and Finite Difference Methods. An advantage of B-spline collocation methods over the Finite Element Method is that the former procedure is simpler and easy to apply to many problems involving differential equations.

In this paper our aim is to explore the implementation of collocation method using fractional B-spline basis function to solve Eq. (1). We have used the collocation method with fractional B-spline basis functions to find numerical solutions of some multi-term time fractional differential equations.

The paper is organized in the following way, in "Fractional B-Spline" section, we recall some basic definitions and theorems of fractional B-splines and its properties. "Distributed Order Time Fractional Reaction Diffusion Equation" section is devoted to the solution of WSGD Scheme for one- and two-dimensional distributed order fractional reaction–diffusion equation with fractional B-spline basics and we present the exist answer theorem for this problem. Finally, some numerical examples are given in "Numerical Results and Discussions" section to demonstrate the effectiveness of the proposed method with the help of forms and error tables.

Fractional B-Spline

It has been shown in [40,41,42,43,44,45] that spline functions in signal processing, mathematics and computer graphics are very efficient and useful. In this section we will state some definition and theorem without prove of [46]. We’ll use the following theorems and definitions.

Definition 2.1

A polynomial spline of order $n + 1$ (or degree n) is a piecewise polynomial function of degree n that is constrained on $\left[ {a,b} \right]$ in following:

• (1) The $a = t_{1} \le t_{2} \le t_{3} \le \cdots \le t_{d} = b$ are knots for interpolation and in between every $\left[ {t_{i} ,t_{{\left( {i + 1} \right)}} } \right]$ is one polynomials of degree n too connected to other polynomials on interval $\left[ {t_{{\left( {i + 1} \right)}} ,t_{{\left( {i + 2} \right)}} } \right]$:

  $$ S^{n} \left( t \right) = \left\{ {\begin{array}{*{20}l} {s_{1} \left( t \right);} \hfill & {t_{1} \le t \le t_{2} ,} \hfill \\ {s_{2} \left( t \right);} \hfill & {t_{2} \le t \le t_{3} ,} \hfill \\ \vdots \hfill & {} \hfill \\ {s_{{\left( {d - 1} \right)}} \left( t \right)} \hfill & {t_{{\left( {d - 1} \right)}} \le t \le t_{d} } \hfill \\ \end{array} } \right. $$

  (5)

  The $S^{n} \left( t \right)$ is spline of degree n and $s_{i} \left( t \right),i = 1,2, \ldots ,d - 1$ are polynomials on every interval.

• (2) Thus, its nth derivative which is bounded, exhibits some isolated discontinuities at the knots which are the joining points between the polynomial segments or Everyone of $s_{i} \left( t \right),i = 1,2, \ldots ,d - 1$ have derivatives continues of order $n - 1$ on $\left[ {t_{i} ,t_{{\left( {i + 1} \right)}} } \right]$.

Schoenberg [47, 48] were introduced polynomial splines with uniform knots in his 1946 landmark paper which sets the theoretical foundations for the subject. He had organized of terms B-splines The basic functions in following:

$$ S^{n} \left( t \right) = \mathop \sum \limits_{{j \in {\mathbb{Z}}}} c_{j} \beta^{n} \left( {t - j} \right), $$

(6)

$$ \beta^{n} \left( t \right) = \frac{1}{n!}\mathop \sum \limits_{j = 0}^{n + 1} ( - 1)^{j} \left( {\begin{array}{*{20}c} {n + 1} \\ j \\ \end{array} } \right)(t - j)_{ + }^{n} $$

(7)

where

$$ (t - j)_{ + }^{n} = \left\{ {\begin{array}{*{20}l} {(t - j)^{n} } \hfill & {t > j,} \hfill \\ 0 \hfill & {t \le j.} \hfill \\ \end{array} } \right. $$

(8)

We presented some figures of B-splines with different powers:

In Fig. 1, B-spline $\beta^{0} \left( t \right)$ with power 0 of constant function Fig. 2, $\beta^{1} \left( t \right)$ of linear function called Hat function Fig. 3, $\beta^{2} \left( t \right)$ of order two function and Fig. 4, $\beta^{3} \left( t \right)$ of order tree function and called bell function. These functions now does the basic work in approximation theory and numerical analysis. They have a number of favorable properties that make them useful in a variety of applications [49,50,51,52].

Fig. 1

The B-spline function diagram of the zero degree is actually $\beta^{0} \left( t \right)$

Fig. 2

The B-spline function diagram of the one degree is actually $\beta^{1} \left( t \right)$

Fig. 3

The B-spline function diagram of the two degree is actually $\beta^{2} \left( t \right)$

Fig. 4

The B-spline function diagram of the tree degree is actually $\beta^{3} \left( t \right)$

In [53], Blu and Unser gave an extension of B-splines to fractional orders. They showed that all the desirable properties of B-splines carry over to the fractional case.

Definition 2.2

The representation of the fractional B-spine of the fractional $\beta^{{\upalpha }} \left( t \right)$ is:

$$ \beta^{{\upalpha }} \left( t \right) = \frac{1}{{\Gamma \left( {{\upalpha } + 1} \right)}}\mathop \sum \limits_{k \le 0} ( - 1)^{k} \left( {\begin{array}{*{20}l} {\alpha + 1} \hfill \\ k \hfill \\ \end{array} } \right)(t - k)_{ + }^{\alpha } $$

(9)

this equation is valid point wise for all $t \in {\mathbb{R}}$ and also in the $L^{2} \left( {\mathbb{R}} \right)$.

Some examples of fractional B-splines are shown in Figs. 5, 6, 7 and 8, while they seem to be decaying reasonably rapidly, they are not compactly supported unless is an integer, in which case we recover the classical B-splines. In general, they do not have an axis of symmetry either.

Fig. 5

The fractional B-spline function diagram of the 0.1 degree is actually $\beta^{0.1} \left( t \right)$

Fig. 6

The fractional B-spline function diagram of the 0.3 degree is actually $\beta^{0.3} \left( t \right)$

Fig. 7

The fractional B-spline function diagram of the 0.3 degree is actually $\beta^{0.7} \left( t \right)$

Fig. 8

The fractional B-spline function diagram of the 1.3 degree is actually $\beta^{1.3} \left( t \right)$

The fractional B-spline can approximate the functions with fractional power very good or every continuous parameter $\alpha > - 1$. This family interpolates the normal splines which match to the special case where $\alpha$ is an integer. First, they considered a more constrained setting univariate with equally spaced knots which allows us to be much more explicit; the uniform grid in particular is required for constructing multiresolution wavelet bases. Second, their method returns a larger class of splines than is possible with a purely variational formulation.

The fractional splines share virtually all the properties of the conventional polynomial splines except that the support of the B-splines for nonintegral $\alpha$ is no longer compact. In particular, they satisfy a two-scale relation and yield multiresolution analysis that are dense in $L^{2}$ as soon as $\alpha > \frac{ - 1}{2}$.

Now we define the fractional B-spline spaces at scale $a$:

$$ S_{a}^{\alpha } = \left\{ {s_{a} :\exists c \in l^{2} ,s_{a} \left( x \right) = \mathop \sum \limits_{{k \in {\mathbb{Z}}}} c_{k} \beta^{\alpha } \left( {\frac{x}{a} - k} \right)} \right\} $$

(10)

Then given an arbitrary function $f \in L^{2} \left( {\mathbb{R}} \right)$, we determine its least squares approximation in $S_{a}^{\alpha }$.

Theorem 2.3

The fractional splines have a fractional order of approximation $\alpha + 1$ . Specifically, the least-squares approximation error is bounded by

$$ \forall f \in W_{2}^{\alpha + 1} ,\parallel f - P_{a} f\parallel_{{L^{2} }} \le a^{\alpha + 1} \parallel {\mathcal{D}}^{\alpha + 1} f\parallel_{{L^{2} }} \frac{{\sqrt {2\xi \left( {\alpha + 2} \right) - \frac{1}{2}} }}{{\Pi^{ + 1} }};a \to 0. $$

(11)

Proof

The proofs in ([53], Theorem 4.1).

In Theorem 2.3, $P_{a} f$ is an interpolation function of f. The fractional B-splines generate valid multiresolution analysis of $L^{2}$ for $\alpha > - \frac{1}{2}$. The fractional splines can be designed to have an arbitrary order of smoothness. They generate multiresolution analysis for signal analysis.

The fractional B-splines generate a sequence of space flowing:

$$ 0 \subset \cdots \subset {\mathcal{X}}_{ - 1} \subset {\mathcal{X}}_{0} \subset {\mathcal{X}}_{1} \subset \cdots \subset L^{2} \left( {\mathbb{R}} \right). $$

(12)

With the following properties: (a) $\bigcap\nolimits_{{i \in {\mathbb{Z}}}} {{\mathcal{X}}_{i} } = 0$ and $\overline{{\bigcup\nolimits_{{i \in {\mathbb{Z}}}} {{\mathcal{X}}_{i} } }} = L^{2} \left( {\mathbb{R}} \right)$, (b) $f\left( {*} \right) \in {\mathcal{X}}_{i}$ if and only if $f\left( {2^{ - i} {*}} \right) \in {\mathcal{X}}_{0}$, (c) $f\left( {*} \right) \in {\mathcal{X}}_{0}$ if and only if $f\left( {{*} - k} \right) \in {\mathcal{X}}_{0}$ for all $k \in {\mathbb{Z}}$ and there exists a function $\varphi \in {\mathcal{X}}_{0}$, called a scaling function, such that $\varphi (* - k)_{{k \in {\mathbb{Z}}}}$ forms an orthonormal basis of ${\mathcal{X}}_{0}$. The ${\mathcal{X}}_{n}$ are spaces fractional B-spline of order $\alpha \in {\mathbb{R}}$ with knot points $k \times 2^{n} ,k \in {\mathbb{Z}}$ Then the spaces:

$$ {\mathcal{X}}_{n} = \overline{{span\left\{ {\beta^{\alpha } \left( {\frac{{x - 2^{n} k}}{{2^{n} }}} \right)^{{L^{2} \left( {\mathbb{R}} \right)}} } \right\}}} ;\;\alpha \ge - \frac{1}{2},n \in {\mathbb{Z}}. $$

(13)

To prove that $\beta^{\alpha }$ generates a multiresolution analysis. Let’s assume $a = 2^{i}$ then Some example of multiresolution and shift fractional B-spline $\beta^{\alpha }$ as shown by the following:

Figure 9 some shift $\beta^{1} \left( {t - k} \right)$, Fig. 10, some shift $\beta^{2} \left( t \right)$, Fig. 11, some shift $\beta^{1} \left( {2t} \right)$ and Fig. 12, $\beta^{2} \left( {2t} \right)$ this functions are basics function for methods in numerical analysis.

Fig. 9

The B-spline function diagram of the one degree are with $i = 0$ i.e. $a = 1$ and some different k of Eq. (10) actually $\beta^{1} \left( t \right)$, $\beta^{1} \left( {t - 1} \right)$, $\beta^{1} \left( {t + 1} \right)$, $\beta^{1} \left( {t + 2} \right)$

Fig. 10

The B-spline function diagram of the two degree are with $i = 0$ i.e. $a = 1$ and some different k of Eq. (10) actually $\beta^{2} \left( t \right)$, $\beta^{2} \left( {t - 1} \right)$, $\beta^{2} \left( {t + 1} \right)$

Fig. 11

The B-spline function diagram of the one degree are with $i = - 1$ i.e. $a = \frac{1}{2}$ and some different k of Eq. (10) actually $\beta^{1} \left( {2t} \right)$, $\beta^{1} \left( {2t - 1} \right)$, $\beta^{1} \left( {2t + 1} \right)$, $\beta^{1} \left( {2t + 2} \right)$, $\beta^{2} \left( {2t} \right)$

Fig. 12

The B-spline function diagram of the two degree are with $i = - 1$ i.e. $a = \frac{1}{2}$ and some different k of Eq. (10) actually $\beta^{2} \left( {2t - 2} \right)$, $\beta^{2} \left( {2t - 1} \right)$, $\beta^{2} \left( {2t + 1} \right)$

In Figs. 13 and 14 some shift fractional B-spline of the ${\upalpha } = 0.3$ degree are with $a = 1$ and $a = \frac{1}{2}$ and some different k of according to Eq. (10) in fact $\beta^{0.3} \left( t \right)$ and $\beta^{0.3} \left( {2t} \right)$.

Fig. 13

The fractional B-spline function diagram of the $= 0.3$ degree are with $i = 0$ i.e. $a = 1$ and some different k of Eq. (10) actually $\beta^{0.3} \left( t \right)$, $\beta^{0.3} \left( {t - 1} \right)$., $\beta^{0.3} \left( {t - 2} \right)$, $\beta^{0.3} \left( {t - 3} \right)$

Fig. 14

The fractional B-spline function diagram of the $= 0.3$ degree are with $i = - 1$ i.e. $a = \frac{1}{2}$ and some different k of Eq. (10) actually $\beta^{0.3} \left( {2t} \right)$, $\beta^{0.3} \left( {2t - 1} \right)$, $\beta^{0.3} \left( {2t + 1} \right)$, $\beta^{0.3} \left( {2t - 2} \right)$

Distributed Order Time Fractional Reaction Diffusion Equation

We introduce the composite midpoint formula that will be frequently used in the discretization of the distributed order time derivative. Divide the interval [0,1] into $\hbar$ subintervals with $\Delta \upalpha = \hbar$ that $\upalpha _{\iota } ,\iota = 0, \ldots ,{\mathfrak{n}}$ and $h = \frac{1}{{\mathfrak{n}}}$.

Theorem 3.1

([54]) Let $S\left( {\upalpha } \right) \in C^{2} \left[ {0,1} \right]$, then we have

$$ \mathop \int \limits_{0}^{1} s\left( \upalpha \right)d = \Delta \upalpha \mathop \sum \limits_{\iota = 1}^{n} s\left( {\frac{{\upalpha _{\iota } + \upalpha _{\iota - 1} }}{2}} \right) - \frac{{\Delta^{2} s^{\prime \prime } \left( \zeta \right)}}{24},\;\zeta \in \left[ {0,1} \right]. $$

(14)

We considering:

$$ \mathop \int \limits_{0}^{1} s\left( \upalpha \right)d \simeq \Delta \upalpha \mathop \sum \limits_{\iota = 1}^{n} s\left( {\frac{{\upalpha _{\iota } + \upalpha _{\iota - 1} }}{2}} \right). $$

(15)

We solve Eq. (1) with help Eq. (15). There have been a lot of work developments in the distributed order time fractional reaction diffusion equation. We are applying a collocation method base on fractional B-spline approximation. In this paper, we consider Caputo’s time derivatives 1D (one dimension), 2D (two dimension) on convex domain $\Omega$ with initial condition and boundary condition. We consider the following distributed order time reaction diffusion equation:

$$ \left\{ {\begin{array}{*{20}l} {\hbar \mathop \sum \limits_{\iota = 1}^{{\mathfrak{n}}} \omega \left( {\frac{{\upalpha _{\iota } + \upalpha _{\iota - 1} }}{2}} \right){\mathcal{D}}_{t}^{{\frac{{\upalpha _{\iota } + \upalpha _{\iota - 1} }}{2}}} \left( {\overline{X},t} \right) - \Delta {\mathcal{U}}\left( {\overline{X},t} \right) = {\mathbb{F}}\left( {\overline{X},t} \right) \left( {\overline{X},t} \right) \in \Omega \times \left( {0,T} \right],} \hfill \\ {{\mathcal{U}}\left( {\overline{X},0} \right) = \psi_{1} \left( {\overline{X}} \right),\quad \overline{X} \in \Omega } \hfill \\ {{\mathcal{U}}\left( {\overline{X},t} \right) = \Phi \left( {\overline{X},t} \right),\quad \overline{X} \in \partial \Omega .} \hfill \\ \end{array} } \right. $$

(16)

The Fractional B-Spline Collocation Method for One Dimension

In the one dimension case, Let consider the in Eq. (16), we assume that K is compact on a Banach space ${\mathcal{X}}$ to ${\mathcal{X}}$. We choose a finite dimensional family of functions $\tilde{\mathcal{U}}_{N} \left( {{\overline{\mathbf{X}}},t} \right)$ which is close to the exact solution ${\mathcal{U}}_{N} \left( {{\overline{\mathbf{X}}},t} \right)$. ${\overline{\mathbf{X}}}$ be one dimension so we can be written as follows:

$$ {\mathcal{U}}_{N} \left( {{\overline{\mathbf{X}}},t} \right) = {\mathcal{U}}_{N} \left( {x,t} \right)\quad x \in {\mathbb{R}} $$

and

$$ {\mathbb{F}}\left( {{\overline{\mathbf{X}}},t} \right) = {\mathbb{F}}\left( {x,t} \right)\quad x \in {\mathbb{R}} $$

then we choose a sequence of dimensional subspace ${\mathcal{X}}_{N} \subset {\mathcal{X}};N \ge 0$ that ${\mathcal{X}}_{N}$ have a basis $\beta^{r} \left( {\frac{{x - 2^{N} k}}{{2^{N} }}} \right)$ and $\beta^{p} \left( {\frac{{t - 2^{N} l}}{{2^{N} }}} \right)$. We seek a function $\tilde{\mathcal{U}}_{N} \left( {x,t} \right) \in {\mathcal{X}}_{N} \times {\mathcal{X}}_{N}$ that it can be written as:

$$ \tilde{\mathcal{U}}_{N} \left( {x,t} \right) = \sum\limits_{k = 1}^{d} {\sum\limits_{l = 1}^{d} {c_{kl} \beta^{r} \left( {\frac{{x - 2^{N} k}}{{2^{N} }}} \right)\beta^{p} \left( {\frac{{t - 2^{N} l}}{{2^{N} }}} \right)} } . $$

(17)

Then we replace $\tilde{\mathcal{U}}_{N} \left( {x,t} \right)$ with ${\mathcal{U}}_{N} \left( {x,t} \right)$ in the Eq. (16) and solve it. After that, let’s consider $\left( {x,t} \right) \in \left[ {a,b} \right] \times \left[ {c,d} \right]$, which by this $k,l$ in Eq. (17) is limited on $\left[ {a,b} \right]$. Now we seek points $\left( {x_{1} ,t_{1} } \right)$, $\left( {x_{2} ,t_{2} } \right)$, $\left( {x_{3} ,t_{3} } \right)$, …, $\left( {x_{d} ,t_{d} } \right)$ where $\left( {x,t} \right) \in \left[ {a,b} \right] \times \left[ {c,d} \right]$ and $c_{11} , \ldots ,c_{dd}$ are determinant by solve linear system below:

$$ \begin{aligned} R_{N} \left( {x_{i} ,t_{j} } \right) & = \hbar \mathop \sum \limits_{\iota = 1}^{{\mathfrak{n}}} \omega \left( {\frac{{ \upalpha _{\iota } + \upalpha _{\iota - 1} }}{2}} \right){\mathcal{D}}_{t}^{{\frac{{\upalpha _{\iota } + \upalpha _{\iota - 1} }}{2}}} \mathop \sum \limits_{k = 1}^{d} \mathop \sum \limits_{l = 1}^{d} c_{kl} \beta^{r} \left( {\frac{{x_{i} - 2^{N} k}}{{2^{N} }}} \right)\beta^{p} \left( {\frac{{t_{j} - 2^{N} l}}{{2^{N} }}} \right) \\ & \quad - \;\sum\limits_{k = 1}^{d} {\sum\limits_{l = 1}^{d} {c_{kl} \Delta \beta^{r} \left( {\frac{{x_{i} - 2^{N} k}}{{2^{N} }}} \right)\beta^{p} \left( {\frac{{t_{j} - 2^{N} l}}{{2^{N} }}} \right)} } \\ & \quad - \;\mathop \sum \limits_{j = 1}^{d} \mathop \sum \limits_{i = 1}^{d} {\mathbb{F}}\left( {x_{i} ,t_{j} } \right) = 0,\quad i,j = 0,1, \ldots ,d - 1. \\ \end{aligned} $$

(18)

Then we use of Eq. (9) in the above equation, which we will have:

$$ \begin{aligned} R_{N} \left( {x_{i} ,t_{j} } \right) & = \mathop \sum \limits_{k = 1}^{d} \mathop \sum \limits_{l = 1}^{d} c_{kl} \left( {\mathop \sum \limits_{s \ge 0} ( - 1)^{s} \left( {\begin{array}{*{20}c} {r + 1} \\ s \\ \end{array} } \right)\frac{{\left( {\frac{{x_{i} - 2^{N} k}}{{2^{N} }} - s} \right)_{t}^{r} }}{{\Gamma \left( {r + 1} \right)}}} \right) \\ & \quad \times \;\left( {\hbar \mathop \sum \limits_{\iota = 1}^{{\mathfrak{n}}} \omega \left( {\frac{{\upalpha _{\iota } + \upalpha _{\iota - 1} }}{2}} \right){\mathcal{D}}_{t}^{{\frac{{\upalpha _{\iota } + \upalpha _{\iota - 1} }}{2}}} \mathop \sum \limits_{h \ge 0} ( - 1)^{h} \left( {\begin{array}{*{20}c} {p + 1} \\ h \\ \end{array} } \right)\frac{{\left( {\frac{{t_{j} - 2^{N} l}}{{2^{N} }} - s} \right)_{t}^{p} }}{{\Gamma \left( {p + 1} \right)}}} \right) \\ & \quad - \;\mathop \sum \limits_{k = 1}^{d} \mathop \sum \limits_{l = 1}^{d} c_{kl} \Delta \left( {\mathop \sum \limits_{s \ge 0} ( - 1)^{s} \left( {\begin{array}{*{20}c} {r + 1} \\ s \\ \end{array} } \right)\frac{{\left( {\frac{{x_{i} - 2^{N} k}}{{2^{N} }} - s} \right)_{t}^{r} }}{{\Gamma \left( {r + 1} \right)}}} \right) \\ &\quad \left( {\mathop \sum \limits_{h \ge 0} ( - 1)^{h} \left( {\begin{array}{*{20}c} {p + 1} \\ h \\ \end{array} } \right)\frac{{\left( {\frac{{t_{j} - 2^{N} l}}{{2^{N} }} - s} \right)_{t}^{p} }}{{\Gamma \left( {p + 1} \right)}}} \right) \\ & = \mathop \sum \limits_{k = 1}^{d} \mathop \sum \limits_{l = 1}^{d} {\mathbb{F}}\left( {x_{i} ,t_{j} } \right),\quad i,j = 0, \ldots ,d - 1. \\ \end{aligned} $$

(19)

We can show Eq. (18) to matrix hence we define:

$$ B_{k,l} \left( {x,t} \right) = \beta^{r} \left( {\frac{{x - 2^{N} k}}{{2^{N} }}} \right)\beta^{p} \left( {\frac{{t - 2^{N} l}}{{2^{N} }}} \right),\quad k,l = 1, \ldots ,d $$

and

$$ F_{k,l} \left( {x_{i} ,t_{j} } \right) = \mathop \sum \limits_{k = 1}^{d} \mathop \sum \limits_{l = 1}^{d} {\mathbb{F}}\left( {x_{i} ,t_{j} } \right) $$

and

$$ DB_{k,l}^{\alpha } \left( {x,t} \right) = {\mathcal{D}}_{t}^{{\frac{{\upalpha _{\iota } + \upalpha _{\iota - 1} }}{2}}} \mathop \sum \limits_{k = 1}^{d} \mathop \sum \limits_{l = 1}^{d} c_{kl} B_{k,l} \left( {x,t} \right) $$

then we have

$$ A^{\alpha } = \left[ {DB_{k,l}^{\alpha } \left( {x_{i} ,t_{j} } \right)} \right]_{k,l = 1,1}^{d,d} $$

and

$$ \Delta A = \left[ {\Delta B_{k,l} \left( {x_{i} ,t_{j} } \right)} \right]_{k,l = 1,1}^{d,d} $$

and

$$ C = \left[ {c_{1,1} ,c_{1,2} ,c_{1,3} , \ldots ,c_{1,l} ,c_{2,1} ,c_{2,2} , \ldots .,c_{2,l} , \ldots ,c_{k,1} ,c_{k,2} , \ldots ,c_{k,l} } \right] $$

and then

$$ \begin{aligned} b & = \left[ F_{k,l} \left( {x_{1} ,t_{1} } \right),F_{k,l} \left( {x_{1} ,t_{2} } \right), \ldots ,F_{k,l} \left( {x_{1} ,t_{l} } \right),F_{k,l} \left( {x_{2} ,t_{1} } \right),F_{k,l} \left( {x_{2} ,t_{2} } \right), \ldots , \right. \\ &\quad \left. F_{k,l} \left( {x_{2} ,t_{l} } \right),F_{k,l} \left( {x_{k} ,t_{1} } \right),F_{k,l} \left( {x_{k} ,t_{2} } \right),F_{k,l} \left( {x_{k} ,t_{l} } \right) \right] \end{aligned} $$

and

$$ AA = \left[ {\hbar \mathop \sum \limits_{\iota = 1}^{{\mathfrak{n}}} \omega \left( {\frac{{\upalpha _{\iota } + \upalpha _{\iota - 1} }}{2}} \right)A^{\alpha } } \right] - \left[ {\Delta A} \right]. $$

At end

$$ AA \times [C]^{T} = \left[ b \right] $$

that

$$ [C]^{T} = AA^{ - 1} \times \left[ b \right]. $$

At in relation above $k,l = 1, \ldots ,d$ and $i,j = 0,1, \ldots ,d - 1$.

The Fractional B-Spline Collocation Method for Two Dimension

In the two dimension case, we are consider ${\overline{\mathbf{X}}} \in {\mathbb{R}}^{2}$ i.e., ${\mathbb{F}}\left( {{\overline{\mathbf{X}}},t} \right) = {\mathbb{F}}\left( {x,y,t} \right)$; then we choose a sequence of dimensional subspace ${\mathcal{X}}_{N} \subset {\mathcal{X}};N \ge 0$ that ${\mathcal{X}}_{N}$ have a basis $\beta^{r} \left( {\frac{{x - 2^{N} i}}{{2^{N} }}} \right),\beta^{q} \left( {\frac{{y - 2^{N} j}}{{2^{N} }}} \right)$ and $\beta^{p} \left( {\frac{{t - 2^{N} k}}{{2^{N} }}} \right)$. We seek a function $\tilde{\mathcal{U}}_{N} \left( {x,y,t} \right) \in {\mathcal{X}}_{N} \times {\mathcal{X}}_{N} \times {\mathcal{X}}_{N}$ that it can be written as:

$$ \tilde{\mathcal{U}}_{N} \left( {x,t} \right) = \mathop \sum \limits_{{i \in {\mathbb{N}}}} \mathop \sum \limits_{{j \in {\mathbb{N}}}} \mathop \sum \limits_{{k \in {\mathbb{N}}}} c_{ijk} \beta^{r} \left( {\frac{{x - 2^{N} i}}{{2^{N} }}} \right)\beta^{q} \left( {\frac{{y - 2^{N} j}}{{2^{N} }}} \right)\beta^{p} \left( {\frac{{t - 2^{N} k}}{{2^{N} }}} \right). $$

(20)

Then we replace $\tilde{\mathcal{U}}_{N} \left( {x,y,t} \right)$ with ${\mathcal{U}}\left( {x,y,t} \right)$ in the Eq. (16) and solve it. After that, let’s consider $\left( {x,y,t} \right) \in \left[ {c,d} \right] \times \left[ {e,f} \right] \times \left[ {a,b} \right]$, which by this $i,j,k$ in Eq. (20) is limited on $\left[ {a,b} \right]$.

Now we seek points $\left( {x_{1} ,y_{1} ,t_{1} } \right)$, $\left( {x_{2} ,y_{1} ,t_{1} } \right)$, $\left( {x_{3} ,y_{1} ,t_{1} } \right)$, …, $\left( {x_{d} ,y_{d} ,t_{d} } \right)$ where $\left( {x,y,t} \right) \in \left[ {a,b} \right] \times \left[ {c,d} \right] \times \left[ {e,f} \right]$ and $c_{111}$, $c_{211}$, …, $c_{ddd}$ are determinant by solve linear system below:

$$ \begin{aligned} R_{N} \left( {x_{w} ,y_{v} ,t_{z} } \right) & = \hbar \mathop \sum \limits_{\iota = 1}^{{\mathfrak{n}}} \omega \left( {\frac{{\upalpha _{\iota } + \upalpha _{\iota - 1} }}{2}} \right){\mathcal{D}}_{t}^{{\frac{{\upalpha _{\iota } + \upalpha _{\iota - 1} }}{2}}} \mathop \sum \limits_{i = 1}^{d} \mathop \sum \limits_{j = 1}^{d} \mathop \sum \limits_{k = 1}^{d} c_{ijk} \beta^{r} \left( {\frac{{x_{w} - 2^{N} i}}{{2^{N} }}} \right) \\ &\quad \beta^{p} \left( {\frac{{y_{v} - 2^{N} j}}{{2^{N} }}} \right) \beta^{q} \left( {\frac{{t_{z} - 2^{N} k}}{{2^{N} }}} \right) \\ & \quad - \;\Delta \mathop \sum \limits_{i = 1}^{d} \mathop \sum \limits_{j = 1}^{d} \mathop \sum \limits_{k = 1}^{d} c_{ijk} \beta^{r} \left( {\frac{{x_{w} - 2^{N} i}}{{2^{N} }}} \right)\beta^{p} \left( {\frac{{y_{v} - 2^{N} j}}{{2^{N} }}} \right)\beta^{q} \left( {\frac{{t_{z} - 2^{N} k}}{{2^{N} }}} \right) \\ & \quad - \;\mathop \sum \limits_{i = 1}^{d} \mathop \sum \limits_{j = 1}^{d} \mathop \sum \limits_{k = 1}^{d} {\mathbb{F}}\left( {x_{w} ,y_{v} ,t_{z} } \right) = 0,w,v,z = 0, \ldots ,d - 1. \\ \end{aligned} $$

(21)

Like the one-dimensional state, putting Eq. (9) can find the unknown coefficients.

We can show Eq. (18) to matrix hence we define:

$$ B_{i,j,k} \left( {x,y,t} \right) = \beta^{r} \left( {\frac{{x - 2^{N} i}}{{2^{N} }}} \right)\beta^{q} \left( {\frac{{y - 2^{N} j}}{{2^{N} }}} \right)\beta^{p} \left( {\frac{{t - 2^{N} k}}{{2^{N} }}} \right) $$

and

$$ F_{i,j,k} \left( {x_{w} ,y_{v} ,t_{z} } \right) = \mathop \sum \limits_{i = 1}^{d} \mathop \sum \limits_{j = 1}^{d} \mathop \sum \limits_{k = 1}^{d} {\mathbb{F}}\left( {x_{w} ,y_{v} ,t_{z} } \right), $$

and

$$ DB_{i,j,k}^{\alpha } \left( {x,y,t} \right) = \hbar \mathop \sum \limits_{\iota = 1}^{{\mathfrak{n}}} \omega \left( {\frac{{\upalpha _{\iota } + \upalpha _{\iota - 1} }}{2}} \right){\mathcal{D}}_{t}^{{\frac{{\upalpha _{\iota } + \upalpha _{\iota - 1} }}{2}}} \mathop \sum \limits_{i = 1}^{d} \mathop \sum \limits_{j = 1}^{d} \mathop \sum \limits_{k = 1}^{d} c_{ijk} B_{i,j,k} \left( {x,y,t} \right) $$

then we have

$$ A^{\alpha } = \left[ {DB_{i,j,k}^{\alpha } \left( {x_{w} ,y_{v} ,t_{z} } \right)} \right]_{i,j,k = 1,1,1}^{d,d,d} $$

and

$$ \Delta A = \left[ {\Delta B_{i,j,k} \left( {x_{w} ,y_{v} ,t_{z} } \right)} \right]_{i,j,k = 1,1,1}^{d,d,d} $$

and

$$ C = \left[ {c_{i,j,k} } \right]_{i,j,k = 1,1,1}^{d,d,d} $$

and then

$$ b = \left[ {F_{i,j,k} \left( {x_{w} ,y_{v} ,t_{z} } \right)} \right]_{i,j,k = 1,1,1}^{d,d,d} $$

and

$$ AA = \left[ {\mathop \sum \limits_{ii = 1}^{m} r_{ii} A^{\alpha } \left[ {\Delta A} \right]} \right],\quad ii = 1,2, \ldots ,m. $$

and

$$ AA \times [C]^{T} = \left[ b \right] $$

that

$$ [C]^{T} = AA^{ - 1} \times \left[ b \right]. $$

In the relation above

$$ w,v,z = 1, \ldots ,d\;and\;i,j,k = 0,1, \ldots ,d - 1. $$

In the case of one-dimensional and two-dimensional matrix is formed by placing the two nodes. We know that the integral equation with a weakly kernel is the same as the Caputos time derivatives equation. Equation (16) can be solved with collocation method by using fractional B-spline basis. If we introduce Eq. (17) and Eq. (20) to projection operator $P_{n}$ that maps ${\mathcal{X}}$ onto ${\mathcal{X}}_{n}$, define $P_{n} {\mathcal{U}}\left( {{\overline{\mathbf{x}}},t} \right)$ to be that element of ${\mathcal{X}}_{n}$ that interpolates ${\mathcal{X}}$ at the nodes used in one and two dimension. This means writing

$$ P_{n} {\mathcal{U}}\left( {{\overline{\mathbf{X}}},t} \right) = \tilde{\mathcal{U}}_{N} \left( {{\overline{\mathbf{X}}},t} \right) $$

with the coefficients $c_{ij}$ in one dimension and $c_{ijk}$ in two dimension determined by solving the linear system (19) and (9). Then this linear system has a unique solution if

$$ det\left( {R_{N} \left( {x_{i} ,t_{j} } \right)} \right) \ne 0 $$

or

$$ det\left( {R_{N} \left( {x_{w} ,y_{v} ,t_{z} } \right)} \right) \ne 0. $$

From Theorem 2.3. fractional B-spline basis belong to $L^{2} \left( {\mathbb{R}} \right)$ and with the help Eq. (13), this method is convergent.

Numerical Results and Discussions

In this section, we show the results obtained for four examples using the collocation method with fractional b-spline for WSGD-OSC Scheme for one- and two-dimensional distributed order fractionl Reaction–Diffusion equation. described in previous sections. In all examples, we show the accuracy of the methods and also for comparing with the proposed technique two kinds of error measures, maximum absolute error $\varepsilon_{\infty }$ and relative error $\varepsilon_{R}$:

$$ Error = \parallel \tilde{\mathcal{U}}_{N} \left( {\overline{X}_{i} ,t} \right) - {\mathcal{U}}\left( {\overline{X}_{i} ,t} \right)\parallel_{\infty } ,\quad 0 \le t \le T $$

(22)

$$ RMS_{j}^{{\text{N}}} = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\tilde{\mathcal{U}}_{N} \left( {\overline{X}_{i} ,t} \right) - {\mathcal{U}}\left( {\overline{X}_{i} ,t} \right)} \right)^{2} }}{n}} , $$

(23)

are used, where ${\mathcal{U}}\left( {\overline{X}_{i} ,t} \right)$, $\tilde{\mathcal{U}}_{N} \left( {\overline{X}_{i} ,t} \right)$ denote exact and approximate solutions, $N$ dimension of fractional B-spline space and $n$ is number points for draw figure and calculate relative error exact and approximate solutions, respectively. In all problems the regular node distribution is used then with solution system Eq. (18) or (19) and find $c_{kl}$ or $c_{ijk}$ for approximate solution Eq. (17) and Eq. (20) then dividing the domain of the answer to the $n$ of the equal part and calculating the error using the formula Eq. (22) to plot it. Error Eq. (23) in fact relative error for different dimension of fractional B-spline and $\alpha$ with attention example.

Example 1

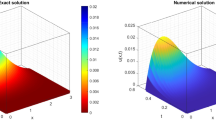
(One dimensional) In this test example, we consider the Eq. (16) with various $\hbar$, and $\Delta t^{i} = t^{i} - t^{i - 1} = 0.01$ in regular domain $\Omega = \left[ {0,1} \right]$ and $t \in \left[ {0,1} \right]$. The initial and exact solution is supposed to be

$$ {\mathcal{U}}\left( {x,t} \right) = x^{2} e^{t} $$

so the boundary conditions are defined accordingly ${\mathbb{F}}\left( {x,t} \right) = - 2e^{t}$ and

$$ \omega \left( \upalpha \right) = \Gamma \left( {1 - \alpha } \right)e^{2i\pi } . $$

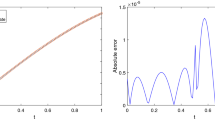
In Table 1, we present RMS of Eq. (23) for different $\hbar$’s. RMS solutions in is much less than $10^{ - 5}$. Table 1 with $\hbar = 0.2$ that ${\mathfrak{n}} = 5$, $\hbar = 0.166$ that ${\mathfrak{n}} = 6$ and $\hbar = 0.142$ that ${\mathfrak{n}} = 7$ illustrates the RMS obtained using for $n = 500$ and different values of ${\Delta }t$. In Figs. 15, 16 and 17, when the N increases, the error is decreasing with relatively small speed and increasing the error by increasing the X with a small amount small increase.

Table 1 Example of Eq. (16) and error Eq. (23) and in this table t, x, n

Fig. 15

Example of Eq. (16) and error Eq. (22) and in diagram error for $\hbar = 0.2$

Fig. 16

Example of Eq. (16) and error Eq. (22) and in diagram error with $\hbar = 0.166$

Fig. 17

Example of Eq. (16) and error Eq. (22) and in diagram error with $\hbar = 0.142$

Figures 15, 16 and 17 are shows the Error of Eq. (22) that approximate solutions with $\hbar = 0.2$, $\hbar = 0.166$ and $\hbar = 0.142$, the N is dimensions of fractional B-splines. We see in the Figs. 15, 16 and 17, Error in direction X is increase until $10^{ - 1}$ by attention to that in $N = 2$ it is $10^{ - 2}$, this is proceeding is slow but its speed decrease is observable.

Example 2

(One dimensional) In this test example, we consider the Eq. (16) with various $\hbar$, and $\vartriangle t^{i} = t^{i} - t^{i - 1} = 0.01$ in regular domain $\Omega = \left[ {0,1} \right]$ and $t \in \left[ {0,1} \right]$. The initial and exact solution is supposed to be

$$ {\mathcal{U}}\left( {x,t} \right) = sin\left( {\pi x} \right)e^{2t} $$

so the boundary conditions are defined accordingly and ${\mathbb{F}}\left( {x,t} \right) = \pi^{2} sin\left( {\pi x} \right)e^{2t}$ and

$$ \omega \left( \upalpha \right) = \Gamma \left( {1 - \alpha } \right)e^{2i\pi } 2^{1 - \alpha } . $$

In Table 2 we present RMS of Eq. (23) for different $\hbar$’s. RMS solutions in is much less than $10^{ - 4}$. illustrates the RMS obtained using for $n = 500$ and different values of and $\Delta t$. In Figs. 18, 19 and 20, when the N increases, the error is decreasing with relatively small speed and increasing the error by increasing the X with a small amount small increase.

Table 2 Example of Eq. (16) and error Eq. (23) and in this table y is constant and t, x, n are variable

Fig. 18

Example of Eq. (16) and error Eq. (22) and in diagram of absolute error of $u\left( {x,t} \right)$ with $\Delta t = 0.01$ and $n = 500$ with $\hbar = 0.2$

Fig. 19

Example of Eq. (16) and error Eq. (22) and in diagram of absolute error of $u\left( {x,t} \right)$ with $\Delta t = 0.01$ and $n = 500$ with $\hbar = 0.166$

Fig. 20

Example of Eq. (16) and error Eq. (22) and in diagram of absolute error of $u\left( {x,t} \right)$ with $\Delta t = 0.01$ and $n = 500$ with $\hbar = 0.142$

Figures 18, 19 and 20 are shows the Error of Eq. (22) that approximate solutions with $\hbar = 0.2$, $\hbar = 0.166$ and $\hbar = 0.142$, the N is dimensions of fractional B-splines. We see in the Figs. 18, 19 and 20, Error in direction X is increase by attention to that, this is proceeding is slow but its speed decrease is observable.

Example 3

In this test example, we consider the Eq. (16) with various values for and $\vartriangle t = t^{i} - t^{i - 1} = 0.01$ in regular domain ${\Omega } = \left[ {0,0.5\left] \times \right[0,0.5} \right]$ and $t \in \left[ {0,1} \right]$. The initial and exact solution is supposed to be

$$ {\mathcal{U}}\left( {x,y,t} \right) = sin\left( {\pi x} \right)y^{2} e^{t} $$

so the boundary conditions are defined accordingly ${\mathbb{F}}\left( {x,t} \right) = - 2sin\left( {\pi x} \right)e^{t} + \pi^{2} y^{2} sin\left( {\pi x} \right)e^{t}$ and

$$ \omega \left( {\upalpha } \right) = {\Gamma }\left( {1 - \alpha } \right)e^{i\pi } . $$

In this test for draw the $Error$ of approximate solutions for values of fractional order we should constant one of variable $X$ or $Y$ and the RMS relative error in tables that we calculate. We consider values constant farther than point early. Again the $N$ is dimension of Fractional B-splines and the $N$ is increase Error is decrease. This is here solutions at different time levels for $\hbar$ have been shown in Figs. 21, 22, 23, 24, 25 and 26.

Fig. 21

Example of Eq. (16) and error Eq. (22) and in diagram of absolute error of $u\left( {x,0.5,t} \right)$ at with $\Delta t = 0.01$ and $n = 500$, with $\hbar = 0.2$ that ${\mathfrak{n}} = 5$

Fig. 22

Example of Eq. (16) and error Eq. (22) and in diagram of absolute error of $u\left( {x,0.5,t} \right)$ at with $\Delta t = 0.01$ and $n = 500$, with $\hbar = 0.166$ that ${\mathfrak{n}} = 6$

Fig. 23

Example of Eq. (16) and error Eq. (22) and in diagram of absolute error of $u\left( {x,0.5,t} \right)$ at with $\Delta t = 0.01$ and $n = 500$, with $\hbar = 0.142$ that ${\mathfrak{n}} = 7$

Fig. 24

Example of Eq. (16) and error Eq. (22) and in diagram of absolute error of $u\left( {0.5,y,t} \right)$ at with $\Delta t = 0.01$ and $n = 500$, with $\hbar = 0.2$ that ${\mathfrak{n}} = 5$

Fig. 25

Example of Eq. (16) and error Eq. (22) and in diagram of absolute error of $u\left( {0.5,y,t} \right)$ at with $\Delta t = 0.01$ and $n = 500$, with $\hbar = 0.166$ that ${\mathfrak{n}} = 6$

Fig. 26

Example of Eq. (16) and error Eq. (22) and in diagram of absolute error of $u\left( {0.5,y,t} \right)$ at with $\Delta t = 0.01$ and $n = 500$, with $\hbar = 0.142$ that ${\mathfrak{n}} = 7$

Tables 3 and 4, we present RMS of Eq. (23) for different $\hbar$’s. RMS solutions in is much less than $10^{ - 5}$. In Table 3 is illustrates the RMS obtained using for $n = 1000$ and different values of $\hbar$ and ${\Delta }t$ with $y = 0.5$, we see RMS is started of $10^{ - 4}$ and it is have to $10^{ - 6}$ that the numerical results and the exact solution are in sufficient agreement and even the time step size at has nearly no influence if it is small enough. In Table 4 that $x = 0.5$ is constant, RMS are between $10^{ - 5}$ and $10^{ - 7}$ and RMS is better than Table 3.

Table 3 Example of Eq. (16) and error Eq. (23) and in this table y is constant and t, x, n are variable with $\hbar$

Table 4 Example of Eq. (16) and error Eq. (23) and in this is table x is constant and t, x, n are variable with $\hbar$

Figure 21, 22 and 23 shows the $Error$ of Eq. (22) that approximate solutions with $y = 0.5$ in Fig. 21, we have $\hbar = 0.2$ that ${\mathfrak{n}} = 5$, in Fig. 22, that $\hbar = 0.166$ that ${\mathfrak{n}} = 6$ and in Fig. 23, that $\hbar = 0.142$ that ${\mathfrak{n}} = 7$, the $N$ is dimensions of fractional B-splines. We see the figures $Error$ in direction $X$ are increase until $10^{ - 3}$ by attention to that in $N = 2$ it is $10^{ - 4}$, this is proceeding is slow but its speed decrease is observable.

Figure 24, 25 and 26 shows the $Error$ of Eq. (22) that approximate solutions with $x = 0.5$ in Fig. 24, we have $\hbar = 0.2$ that ${\mathfrak{n}} = 5$, in Fig. 25, that $\hbar = 0.166$ that ${\mathfrak{n}} = 6$ and in Fig. 26, that $\hbar = 0.142$ that ${\mathfrak{n}} = 7$,, the $N$ is dimensions of fractional B-splines. We see the figures $Error$ in direction $X$ are increase until $10^{ - 3}$ by attention to that in $N = 2$ it is $10^{ - 4}$, this is proceeding is slow but its speed decrease is observable.

Example 4

In this test example, we consider the Eq. (16) with various values for and $\vartriangle t = t^{i} - t^{i - 1} = 0.01$ in regular domain ${\Omega } = \left[ {0,0.5\left] \times \right[0,0.5} \right]$ and $t \in \left[ {0,1} \right]$. The initial and exact solution is supposed to be

$$ {\mathcal{U}}\left( {x,y,t} \right) = sin\left( {\frac{\pi }{2}x} \right)cos\left( {\frac{\pi }{2}y} \right)e^{t} $$

so the boundary conditions are defined accordingly ${\mathbb{F}}\left( {x,y,t} \right) = \frac{1}{2}sin\left( {\frac{\pi }{2}x} \right)cos\left( {\frac{\pi }{2}x} \right)\pi^{2} e^{t}$ and

$$ \omega \left( {\upalpha } \right) = {\Gamma }\left( {1 - \alpha } \right)e^{i\pi } . $$

In this test, we have one $sin\left( {\frac{\pi }{2}x} \right)$ function and one $cos\left( {\frac{\pi }{2}x} \right)$ function for draw the Error of approximate solutions for values of fractional order we should constant one of variable X or Y and RMS relative error in tables that we calculate. We select values constant farther than point early. Again the N is dimension of fractional B-splines and the N is increase Error is decrease. The RMS solutions at different time levels for have been shown in Figs. 27, 28, 29, 30, 31 and 32.

Fig. 27

Example of Eq. (16) and error Eq. (22) and in diagram of absolute error of $u\left( {x,0.5,t} \right)$ at with $\Delta t = 0.01$ and $n = 500$, with $\hbar = 0.2$ that ${\mathfrak{n}} = 5$

Fig. 28

Example of Eq. (16) and error Eq. (22) and in diagram of absolute error of $u\left( {x,0.5,t} \right)$ at with $\Delta t = 0.01$ and $n = 500$, with $\hbar = 0.166$ that ${\mathfrak{n}} = 6$

Fig. 29

Example of Eq. (16) and error Eq. (22) and in diagram of absolute error of $u\left( {x,0.5,t} \right)$ at with $\Delta t = 0.01$ and $n = 500$, with $\hbar = 0.142$ that ${\mathfrak{n}} = 7$

Fig. 30

Example of Eq. (16) and error Eq. (22) and in diagram of absolute error of $u\left( {0.5,y,t} \right)$ at with $\Delta t = 0.01$ and $n = 500$, with $\hbar = 0.2$ that ${\mathfrak{n}} = 5$

Fig. 31

Example of Eq. (16) and error Eq. (22) and in diagram of absolute error of $u\left( {0.5,y,t} \right)$ at with $\Delta t = 0.01$ and $n = 500$, with $\hbar = 0.166$ that ${\mathfrak{n}} = 6$

Fig. 32

Example of Eq. (16) and error Eq. (22) and in diagram of absolute error of $u\left( {0.5,y,t} \right)$ at with $\Delta t = 0.01$ and $n = 500$, with $\hbar = 0.142$ that ${\mathfrak{n}} = 7$

In Table 5, we present RMS of Eq. (23) for different’s. RMS solutions in is much less than $10^{ - 2}$. In Table 6 is illustrates the RMS obtained using for $n = 1000$ and different values of $\hbar$ and $\Delta t$ with $y = 0.5$, we see RMS is started of $10^{ - 2}$ and it is have to $10^{ - 5}$ that the numerical results and the exact solution are in adequate agreement and even the time step size at has nearly no influence if it is small enough. In Table 6 that $x = 0.5$ is constant, RMS are between $10^{ - 4}$ and $10^{ - 5}$ and RMS is similar in the kind Table 5.

Table 5 Example of Eq. (16) and error Eq. (23) and in this table y is constant and t, x, n are variable with $\hbar$

Table 6 Example of Eq. (16) and error Eq. (23) and in this is table x is constant and t, x, n are variable with $\hbar$

Figures 27, 28 and 29 shows the Error of Eq. (22) that approximate solutions with $y = 0.5$ in Fig. 27, we have $\hbar = 0.2$ that ${\mathfrak{n}} = 5$, in Fig. 28, that $\hbar = 0.166$ that ${\mathfrak{n}} = 6$ and in Fig. 29, that $\hbar = 0.142$ that ${\mathfrak{n}} = 7$, the N is dimensions of fractional B-splines. We see in every two figures Error in direction X is increase until $10^{ - 2}$ by attention to that in $N = 2$ it is $10^{ - 3}$, this is proceeding is slow but its speed decrease is observable.

Figures 27 and 28 shows the Error of Eq. (22) that approximate solutions with $x = 0.5$ in Fig. 30, we have $\hbar = 0.2$ that ${\mathfrak{n}} = 5$, in Fig. 31 that $\hbar = 0.166$ that ${\mathfrak{n}} = 6$ and in Fig. 32, that $\hbar = 0.142$ that ${\mathfrak{n}} = 7$, the $N$ is dimensions of fractional B-splines. We see the figures Error in direction X are increase until $10^{ - 3}$ by attention to that in $N = 2$ it is $10^{ - 4}$, this is proceeding is slow but its speed decrease is observable.

Conclusions

In this investigation, we have employed the Collocation Method for the solution of WSGD Scheme for one- and two-dimensional distributed order fractional reaction–diffusion equation. The time fractional derivative has been defined by Caputo sense for ($0 < \upalpha < 1$). We have considered an arbitrary one- and two-dimentional. We have used fractional B-spline bases collocation technique.

We followed two topics here, the first was to thoroughly document the fractional B-spline Collocation Method in a very simple and easy to follow format. The second objective was to apply the fractional B-spline Collocation Method to solve a multi term time fractional differential equation.

The provided numerical results and figures demonstrate the effectiveness and high accuracy of the proposed numerical approximate scheme. For testing the accurateness of the scheme, we give four numerical experiments have been presented and satisfactory agreements with the exact solutions. The numerical simulations were carried out using Mathlab.