Complex Dynamics and Optimal Treatment of an Epidemic Model with Two Infectious Diseases

Abstract

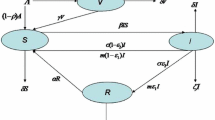
In this paper, we have proposed and formulated an epidemic model with two types of diseases-one is comparative weaker and the other is comparatively stronger with the assumption that both the diseases are active simultaneously in the system. The dynamical behavior of the model; equilibrium analyses with their existence criteria and local stability criteria have been discussed rigorously. With the help of second generation matrix method, we evaluate basic reproduction number of the proposed model. We propose an optimal control problem considering treatment as control parameter and solve it in order to minimize the compound loss due to the presence of infection. All the theoretical results are verified with some appropriate computer simulation works.

Appendix A

The characteristic equation of the system (1) at the unique endemic equilibrium $E^*$ is given by:

$$\begin{aligned} \lambda ^4+N_1\lambda ^3+N_2\lambda ^2 +N_3\lambda +N_4=0 \end{aligned}$$

(16)

where, $N_1=-A_1-B_2-C_3-D_4$, $N_2=-A_2 B_1+A_1 B_2-A_3 C_1+A_1 C_3+A_1 D_4-B_3 C_2+B_2 C_3+B_2 D_4+C_3 D_4$, $N_3=A_3 B_2 C_1-A_2 B_3 C_1-A_3 B_1 C_2+A_1 B_3 C_2+A_2 B_1 C_3-A_1 B_2 C_3-A_4 B_1 D_2+A_2 B_1 D_4-A_1 B_2 D_4-A_4 C_1 D_3+A_3 C_1 D_4-A_1 C_3 D_4+B_3 C_2 D_4-B_2 C_3 D_4$, $N_4=-A_4 B_3 C_1 D_2+A_4 B_1 C_3 D_2+A_4 B_2 C_1 D_3-A_4 B_1 C_2 D_3-A_3 B_2 C_1 D_4+A_2 B_3 C_1 D_4+A_3 B_1 C_2 D_4-A_1 B_3 C_2 D_4-A_2 B_1 C_3 D_4+A_1 B_2 C_3 D_4$ and $A_1=-d-\alpha I^*_1-\frac{\beta I^*_2}{1+\eta I^*_2}$, $A_2=-\alpha S^*$, $A_3=-\frac{\beta S^*}{(1+\eta I^*_{2})^2}$, $A_4=\sigma$, $B_1=\alpha I^*_1$, $B_2=\alpha S^*-\rho I^*_2-(d+m)$, $B_3=-\rho I^*_1$, $C_1=\frac{\beta I^*_2}{1+\eta I^*_2}$, $C_2=\rho I^*_2$, $C_3=\frac{\beta S^*}{(1+\eta I^*_2)^2}-(d+\delta +\gamma +bu)+\rho I^*_1$, $D_2=m$, $D_3=bu+\gamma$, $D_4=-(d+\sigma ).$

Now

(i) $N_1>0,\;\;$ if $A_2+A_3+B_1+B_3+\text {bu}+\gamma +C_1+C_2+4 d+2 \delta +m>0,$

(ii) $N_2>0,\;\;$ if$6d^2+\sigma (3d+bu)+(3d+\delta +\gamma +\sigma +bu)(C_1+C_2+B_1+A_2+m)+(3d+m+\sigma +A_2)(B_3+A_3)+(\sigma +3d)(\gamma +\delta +bu)+(B_3+C_2)(C_1+B_1)+A_3(B_1+C_2)+A_2C_3+B_1 m>0,$

(iii) $N_3>0,\;\;$ if $(2d+\gamma +\delta +\sigma +bu)(A_2C_1+B_1C_2+C_1C_2+C_1m)+(2d+m+\sigma )(B_3C_1+B_1B_3+A_3B_1+B_1bu)+(C_1+C_2)(3d^2+2\gamma d+2 \delta d+ 2 d \sigma +\delta \sigma +2bud)+(2d+\sigma )(A_3C_2+B_1 \gamma +B_1 \delta +A_2 \delta +\gamma m+\delta m +bum+A_2 \gamma +A_2 bu+A_2 A_3+A_3m+A_2B_3)+2d(m+ \sigma )(B_1+B_3)+(B_1m+2 d \sigma )(\gamma +\delta )+3d^2(A_2+A_3+B_1+B_3+\gamma +\delta +m+\sigma +bu)+2d(A_2 \delta +A_3 \sigma +bum+2d+m \sigma )+\sigma (B_3 m+bu C_2+ \gamma C_2)>0,$

(iv) $N_4>0,\;\;$ if $d^2(B_1+C_1+d)(d+\gamma +\delta +\sigma +bu+m)+d(B_1C_2+A_2C_1+C_1C_2)(d+\gamma +\delta +\sigma +bu)+d(A_3d+B_1B_3+A_3C_2+A_2bu+C_2bu+bum)(d+\delta )+d(A_2 \sigma +d \sigma +m \sigma +C_1m+C_2 \sigma )(\gamma +\delta )+d^2(d+\gamma +\delta +\sigma )(A_2+C_2)+B_1d(\gamma \sigma +\delta \sigma +\gamma m+\delta m)+d^2m(\gamma +\delta +\sigma ) +\delta \sigma (A_2C_1+B_1C_2+C_1C_2+C_1d+B_1bud(m+\sigma )+C_1m \sigma (d+\delta )+bud^2 \sigma +B_3dm \sigma +buC_1dm+A_3dm \sigma +B_1\delta dm >0,$

$(v)\;\;N_1N_2-N_3>0$ if $A_1 (A_2 B_1 + A_3 C_1) + A_2 (B_1 B_2 + B_3 C_1) + A_3 B_1 C_2 + B_2 B_3 C_2 + A_3 C_1 C_3 + B_3 C_2 C_3 + A_4 B_1 D_2 + A_4 C_1 D_3 \;\;>\;\; (B_2 + C_3) (B_2 + D_4) (C_3 + D_4) + A_1^2(B_2+C_3+D_4) + A_1 (B_2 + C_3 + D_4)^2.$

According to the Routh-Hurwitz criterion, all the roots of (16) have negative real parts if all the above (i)–(v) hold and $N_3(N_1N_2-N_3)>N_4$ also holds good and then the system (1) is locally asymptotically stable around its unique endemic equilibrium point $E^*$.