Abstract
This paper establishes a mathematical proof of the blue-shift instability at the sub-extremal Kerr Cauchy horizon for the linearised vacuum Einstein equations. More precisely, we exhibit conditions on the \(s=+2\) Teukolsky field, consisting of suitable integrated upper and lower bounds on the decay along the event horizon, that ensure that the Teukolsky field, with respect to a frame that is regular at the Cauchy horizon, becomes singular. The conditions are in particular satisfied by solutions of the Teukolsky equation arising from generic and compactly supported initial data by the recent work [51] of Ma and Zhang for slowly rotating Kerr.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The sub-extremal Kerr solution of the vacuum Einstein equations
models a stationary and rotating black hole, devoid of any gravitational radiation. While we expect that the exterior is stable if small gravitational radiation is taken into account,Footnote 1 heuristics going back to Penrose [55] indicate that the interior is subject to a blue-shift instability: gravitational radiation entering the black hole builds up at the Cauchy horizon \(\mathcal{C}\mathcal{H}^+\) and leads to the formation of a singularity.
Although the full resolution of this conjecture is still open, a large body of research concerning simplified models has since lent support to the validity of this scenario. The first class of simplified models we would like to mention here concerns non-linear spherically symmetric perturbations of the sub-extremal Reissner-Nordström black hole, which also possesses a Cauchy horizon in its interior that is subject to a blue-shift instability. The works by Hiscock [34], Poisson-Israel [57, 58], and Ori [54] investigate and prove this blue-shift instability for the spherically symmetric Einstein-Maxwell-null dust system and the works of Dafermos [12, 13] and of Luk-Oh [46, 47]Footnote 2 do so for the spherically symmetric Einstein-Maxwell-scalar field system. The second class of simplified models are linear models on a Kerr background – and in particular the linear scalar wave equation which serves as a “poor man’s linearisatio” of the vacuum Einstein equations. The study was initiated by McNamara [52], who indeed also considers gravitational perturbations. Results of a similar nature for the scalar wave equation were proven by Dafermos-Shlapentokh–Rothman [20] and in [60]. These results all have in common that they only ensure the abstract existence of solutions that become singular at the Cauchy horizon, but they do not provide explicit criteria that ensure that a particular solution becomes singular. This gap was filled for the scalar wave equation in collaboration with Luk in [49], which shows that under the assumption of suitable upper and lower bounds on the decay along the event horizon, the energy of the scalar field becomes unbounded at the Cauchy horizon. (The wave itself remains bounded [24, 31].) It was later shown by Hintz [32] and Angelopoulos-Aretakis-Gajic [2] that the assumed bounds on the event horizon are generically satisfied.
The present work makes the step from the scalar wave equation to linearised gravitational perturbations in the form of the Teukolsky field [67]. Analogously to [49] we exhibit conditions on the Teukolsky field along the event horizon, consisting of integrated upper and lower bounds on the decay, which ensure the blow-up of the Teukolsky field at the Cauchy horizon. More precisely, we show
Theorem 1.1
Assume \(\psi \) satisfies the Teukolsky equation with \(s=+2\) and, along the event horizon \({\mathcal {H}}^+\),
-
assume that there exists \(p \in {\mathbb {N}}\) s.t. \(\int _{{\mathcal {H}}^+\cap \{v_+ \geqslant 1\}} v_+^{2p} |\psi |^2 \, \textrm{vol}_{{\mathbb {S}}^2}dv_+ = \infty .\) Let \(p_0\) be the smallest such integer and assume \(p_0 \geqslant 2\),
-
\(\int _{{\mathcal {H}}^+\cap \{v_+ \geqslant 1\}} v_+^{2p_0} |\psi _{S(m_0l_0)}|^2 \, dv_+ = \infty \) for some \(m_0 \in {\mathbb {Z}}\), \(l_0 \geqslant \max \{2, |m_0|\}\), where \(\psi _{S(ml)}\) denotes the projection of \(\psi \) on the (m, l) spin 2-weighted spherical harmonic,
-
\(\int _{{\mathcal {H}}^+\cap \{v_+ \geqslant 1\}} v_+^{2p_0} | \partial _{v_+} \psi |^2 \, \textrm{vol}_{{\mathbb {S}}^2}dv_+ < \infty \),
-
\(\int _{{\mathcal {H}}^+\cap \{v_+ \geqslant 1\}} v_+^{q_r} |\partial ^k \psi |^2 \, \textrm{vol}_{{\mathbb {S}}^2}dv_+ < \infty \) for some \(2< q_r < 2p_0\) with \(q_r \in {\mathbb {R}}\) and for all \(k = 0, 1, \ldots , 7\).Footnote 3
It then follows that
where \(\Sigma \) is a hypersurface transversal to \(\mathcal{C}\mathcal{H}^+\) as in Figure 2.
The statement of Theorem 1.1
Here, \(v_+ = t + r^*\) and \(\partial _{v_+}\) is the Killing vector field which is a time-translation at spatial infinity, see also Section 2.1. We also refer the reader to Theorem 3.9 in Section 3 for the precise statement of Theorem 1.1.
We would like to bring to the reader’s attention that the coordinate \(v_+\) is not regular at the Cauchy horizon. There, \(V^+_{r_-} = - e^{\kappa _- v_+}\) is a regular boundary defining function with \(\{V^+_{r_-} = 0\}\) being the Cauchy horizon. The constant \(\kappa _- <0\) is the surface gravity of \(\mathcal{C}\mathcal{H}^+\). Moreover, the regular Teukolsky field \({\hat{\psi }}\) at \(\mathcal{C}\mathcal{H}^+\), i.e., the linearisation of the Teukolsky \(s=+2\) curvature component with respect to a regular frame at \(\mathcal{C}\mathcal{H}^+\), is given by \(e^{-2 \kappa _- v_+} \psi = \frac{1}{(V^+_{r_-})^2} \psi \), modulo a regular factor which remains bounded away from zero (and infinity) at \(\mathcal{C}\mathcal{H}^+\). We thus obtain that the conclusion (1.2) of Theorem 1.1 with respect to regular quantities at \(\mathcal{C}\mathcal{H}^+\) reads
which makes manifest the blow-up of the Teukolsky field with respect to a regular frame at the Cauchy horizon.
Moreover, we note that in the slowly rotating case the assumptions made in Theorem 1.1 were recently shown to be satisfied generically ([51] and [15, 50]) for solutions arising from compactly supported initial data on a global Cauchy hypersurface \(\Sigma _0\) as in Figure 1 with \(p_0 = 7\), \(l_0 =2\) and \(m_0 \in \{-2,-1,1,2\}\). The parameter \(q_r\) can be chosen to be anything strictly less than 13. See also Remark 3.11 for further discussion.
Let us also remark that we expect Theorem 1.1 to be an important ingredient in the analysis of the blue-shift instability at the Cauchy horizon for the full non-linear vacuum Einstein equations.
1.1 The Case of the Full Non-linear Einstein Equations
Standard energy estimates entail that solutions of linear equations arising from regular initial Cauchy data can at most become singular at the (null) boundary of the black hole interior, i.e., at the Cauchy horizon of Kerr – but not earlier inside the black hole. For the vacuum Einstein equations, however, which are non-linear, it is a priori conceivable that the non-linearities amplify the blow-up and lead to the formation of a singularity in the black hole interior which is everywhere spacelike. Whether this happens or not has been contentious for a long time.
For the spherically symmetric Einstein-Maxwell-scalar field system numerical evidence was presented in [5] which indicated that the non-linearities do not amplify the blow-up in the sense that one always has a piece of a null singularity emanating from timelike infinity in the Penrose diagram.Footnote 4 This scenario in spherical symmetry was later rigorously confirmed in the works [12, 13, 46, 47]. Indeed, if one only considers sufficiently small perturbations of two-ended sub-extremal Reissner-Nordström initial data, then the singularity only occurs along the bifurcate Cauchy horizon, i.e., there is no piece of the singularity which is spacelike, see [14].
The statement of Theorem 1.4
Concerning the vacuum Einstein equations Dafermos and Luk established the following seminal result:
Theorem 1.4
(Dafermos-Luk, [17]) Consider a suitable spacelike hypersurface \(\Sigma \) in the interior of a sub-extremal Kerr black hole, see Figure 3, and consider small perturbations of the induced initial data which decay towards \(i^+\) with a rate that is in particular compatible with what is expected to arise dynamically from small perturbations of exact sub-extremal Kerr initial data on a global Cauchy hypersurface \(\Sigma _0\) as in Figure 1. Then the maximal globally hyperbolic development of the perturbed initial data contains a region which is \(C^0\)-close to, and the Penrose diagram of which is given by, the darker shaded region of the unperturbed sub-extremal Kerr spacetime as in Figure 3.
This result in particular entails that also for the vacuum Einstein equations, and under the assumptions of their theorem, the non-linearities do not amplify the blow-up to create a spacelike singularity emanating from timelike infinity in the Penrose diagram (cf. in Figure 4). The result is only compatible with a null singularity emanating from timelike infinity (i.e. the Cauchy horizon becoming singular) as in the spherically symmetric case. But whether the Cauchy horizon is indeed generically singular is not established in [17]. The result obtained in this paper is a first step in this direction.
Note that Theorem 1.4 also shows that the metric remains continuous up to and including the Cauchy horizon. Thus, if a singularity forms, it is not at the level of the metric itself, as is the case for example for the Schwarzschild singularity (see [61, 62]), but we expect that it is the connection which will generically become singular. This expectation is mainly based on the spherically symmetric models discussed earlier for which one also obtains that the metric extends continuously to the Cauchy horizon but the connection becomes unbounded [12, 13, 46, 47, 63]. Such singularities have been termed ‘weak null singularities’. The construction of weak null singularities in vacuum spacetimes without any symmetry was achieved in [43], where it was also shown that they propagate (for some finite time). We expect that such weak null singularities as given in [43] do generically form at the Cauchy horizon of perturbed Kerr.
1.2 Relation to the Strong Cosmic Censorship Conjecture
Going back to the result of this paper in the form of (1.3), and if one trusts the naive expectation that there is a linearised Christoffel symbol which is better than \({\hat{\psi }}\) by a power of \(V^+_{r_-}\), i.e., of order \(V^+_{r_-} {\hat{\psi }}\), then (1.3) shows that this linearised Christoffel symbol is not in \(L^2_{\textrm{loc}}\) at the Cauchy horizon with respect to the differentiable structure of the background. This makes contact with the modern formulation of the strong cosmic censorship conjecture:
Strong cosmic censorship conjecture The maximal globally hyperbolic development arising from generic asymptotically flat initial data for the vacuum Einstein equations is inextendible as a Lorentzian manifold with a continuous metric and locally square integrable Christoffel symbols.
The strong cosmic censorship conjecture was originally conceived by Penrose [56], the formulation given here in terms of the initial value problem and the conjectured breakdown of the regularity goes back to Christodoulou [10] and Chrusciel [11]. The inextendibility as a Lorentzian manifold with \(g \in C^0\) and \(\partial g \in L^2_{\textrm{loc}}\) in particular rules out the extension of the maximal globally hyperbolic development as a weak solution.Footnote 5 We note that for exact sub-extremal Kerr initial data the maximal globally hyperbolic development is given in Figure 1 and is in fact extendible in various ways across the Cauchy horizon even as a smooth solution: determinism is violated. However, as we discussed earlier, for generic small perturbations of exact sub-extremal Kerr initial data we expect the blue-shift instability to turn the Cauchy horizon into a weak null singularity and in this way preventing non-unique extensions as weak solutions. Determinism would thus be restored generically.
The result obtained in this paper can be thought of as a first step towards establishing the generic divergence of curvature at the Cauchy horizon of non-linearly perturbed sub-extremal Kerr – and thus the generic inextendibility as a Lorentzian manifold with \(g \in C^2\). And with the earlier naive expectation that there is a (linearised) Christoffel symbol of order \(V^+_{r_-} {\hat{\psi }}\) it is also a first step towards showing that the metric cannot be extended with \(g \in C^0\) and \(\partial g \in L^2_{\textrm{loc}}\) in a particular natural-looking coordinate system. However, the result does not contribute to developing methods which show that no matter what coordinate system is chosen for the extension, the metric cannot be extended in \(g \in C^0\) and \(\partial g \in L^2_{\textrm{loc}}\). This is an open problem. For recent progress in this direction we refer the reader to [63].
1.3 Related Results and Directions Concerning the Interior of Black Holes
The studies mentioned earlier on perturbations of sub-extremal Reissner Nordström under the spherically symmetric Einstein-Maxwell-scalar field system were extended in [68] to the spherically symmetric Einstein-Maxwell-massive and charged scalar field system. This matter model in particular allows for asymptotically flat one-ended spherically symmetric black hole solutions which possess a Cauchy horizon and is thus a good model to understand the contraction and breakdown of weak null singularities in the interior of black holes [69].
For the behaviour of linear waves and of axisymmetric and polarized perturbations in the interior of non-rotating (Schwarzschild) black holes see [1, 23].
Another interesting direction of research concerns the interior of extremal black holes where the blue-shift instability at the Cauchy horizon is much weaker than in the sub-extremal case. For results concerning linear waves see [25, 26] and for non-linear results in spherical symmetry see [27].
Finally, for the investigation of the blue-shift instability in the presence of a cosmological constant \(\Lambda \) we refer the reader to [6, 14, 21, 22, 33] for \(\Lambda >0\) and to [35, 36] for \(\Lambda <0\) as well as to the references given in those papers.
1.4 Outline of Proof
A good, simple, and instructive model problem for gravitational perturbations in the interior of a subextremal rotating Kerr black hole is the spherically symmetric scalar wave equation in the interior of a subextremal charged Reissner-Nordström black hole. The blue-shift instability in this scenario is well-established and various results along with various methods of proof have been developed: the methods in [20, 52] are based on the scattering map from characteristic initial data on the right even horizon \({\mathcal {H}}^+_r\) (past null infinity \({\mathcal {I}}^-\)) to the trace of the wave on the left Cauchy horizon \(\mathcal{C}\mathcal{H}^+_l\), making crucial use of the time-translation invariance of this map. See Figure 5 below for the notation. The \(C^1\)-instability results in [8, 37] are also obtained via scattering theory together with meromorphic continuation. One can also use the geometric optics (Gaussian beam) approximation together with an application of the closed graph theorem, see [60] and the introduction of [49], to capture a formulation of the blue-shift instability. In [45] a neat argument by contradiction is given, using that one can solve the linear wave equation in spherical symmetry sideways. A proof in physical space using energy estimates and at the heart of which is the conservation law associated to the spacelike Killing vector field \(\partial _t\) is presented in [49]. And finally, in [48], Luk, Oh, and Shlapentokh–Rothman give another scattering theoretic proof of the blue-shift instability at the Cauchy horizon. It is this last method of proof which is being taken up in this paper and being implemented for the Teukolsky equation on Kerr. In the following we shall first outline the argument from [48] in spherical symmetry and then discuss the main differences to the proof in this paper.
1.4.1 Spherically Symmetric Scalar Waves on Reissner-Nordström
The interior of a charged subextremal Reissner-Nordström black hole is the Lorentzian manifoldFootnote 6\(({\mathcal {M}},g)\), where \({\mathcal {M}}:= {\mathbb {R}}\times (r_-, r_+) \times {\mathbb {S}}^2\) with standard \((t,r, \theta , \varphi )\)-coordinates and \(r_\pm := M \pm \sqrt{M^2 - e^2}\), where \(0< |e| < M\) are real parameters modelling the charge and the mass of the black hole, respectively. The Lorentzian metric g is given by
with \(\Delta := r^2 - 2Mr + e^2\). The spherically symmetric scalar wave equation \(\Box _g \phi = 0\), where \(\phi : {\mathcal {M}} \rightarrow {\mathbb {C}}\) is only a function of t and r, takes in the above coordinates the form
Let \(r^*(r)\) be a function with \(\frac{dr^*}{dr} = \frac{r^2}{\Delta }\) and then introduce the null coordinates \(v:= r^* + t\) and \(u:= r^* - t\). We define \(\kappa _\pm := \frac{r_\pm - r_{\mp }}{2r_\pm ^2}\) and use those to introduce the Kruskal-like null coordinatesFootnote 7\(V_{r_+}:= e^{\kappa _+ v}\) and \(U_{r_+}:= e^{\kappa _+ u}\) in which the Lorentzian manifold \(({\mathcal {M}},g)\) extends analytically to \(r=r_+\) (r as a function of \(V_{r_+}, U_{r_+}\)) and similarly \(V_{r_-}:= -e^{\kappa _- v}\) and \(U_{r_-}:= -e^{\kappa _- u}\) in which the Lorentzian manifold extends analytically to \(r=r_-\). The boundary null hypersurface \(\{V_{r_+} = 0\} =: {\mathcal {H}}^+_l\), at which we have \(r = r_+\), is called the left event horizon, the boundary null hypersurface \(\{U_{r_+} = 0\} =: {\mathcal {H}}^+_r\), at which we also have \(r=r_+\), the right event horizon, and the boundary sphere \(\{V_{r_+} = U_{r_+} = 0\} =:{\mathbb {S}}^2_b\) is the bottom bifurcation sphere. Moreover, we call the boundary null hypersurface \(\{U_{r_-} = 0 \} =: \mathcal{C}\mathcal{H}^+_l\) the left Cauchy horizon, the boundary null hypersurface \(\{V_{r_-} = 0 \} =: \mathcal{C}\mathcal{H}^+_r\) the right Cauchy horizon, and the boundary sphere \(\{V_{r_-} = U_{r_-} = 0\} =: {\mathbb {S}}_t^2\) the top bifurcation sphere. A Penrose diagram of \(({\mathcal {M}},g)\) with the boundaries attached is given in Figure 5 below.
In [48] the following theorem is shown
Theorem 1.6
(Corollary 4.2 in [48]) Consider the region \(\big ({\mathcal {M}} \cup {\mathcal {H}}^+_r \big ) \cap \{v \geqslant v_0\} \cap \{u \leqslant u_1\}\) for some \(v_0, u_1 \geqslant 1\) and let \(\phi \) be a smooth solution of the spherically symmetric wave equation (1.5) in this region, which, moreover, satisfies
and there exists \({\mathbb {N}}\ni p_0 \geqslant 2\) such that
holds. We further assume that \(p_0\) is the smallest such integer with this property. And finally we assume
Then for any \(u_2 \leqslant u_1\) we have
This is the local statement that is the analogue of Theorem 3.7 (or 1.1) for Teukolsky. It is inferred from the following global statement, which is the analogue of Theorem 3.9 for Teukolsky, by an extension procedure of the solution.
Theorem 1.11
(Theorem 4.1 in [48]) Let \(\phi \) be a smooth solution of the spherically symmetric wave equation (1.5) on \({\mathcal {M}} \cup {\mathcal {H}}^+_r \cup {\mathcal {H}}^+_l\). Suppose that in addition to (1.7), (1.8), (1.9) (for some \(v_0 \geqslant 1\)) we also have that there exists \(v_* \in {\mathbb {R}}\) such that \(\phi |_{{\mathcal {H}}^+_r}(v) = 0\) for \(v \leqslant v_*\) and there exists \(u_* \in {\mathbb {R}}\) such that \(\phi |_{{\mathcal {H}}^+_l}(u) = 0\) for \(u \geqslant u_*\).Footnote 8 Then (1.10) holds for any \(u_2 \in {\mathbb {R}}\) (and any \(v_0 \in {\mathbb {R}}\)).
Before we discuss the structure of the proof, let us recall the formal separation of the spherically symmetric wave equation (1.5). By taking the Fourier transform

of \(\phi \) in t one obtains that formally \(\phi \) satisfies (1.5) if, and only if,  satisfiesFootnote 9
satisfiesFootnote 9

This ODE has two regular singular points at \(r= r_+\) and \(r=r_-\); for all \(\omega \ne 0\) we can find a fundamental system of solutions with asymptoticsFootnote 10
for \(r \rightarrow r_+\) and another fundamental system of solutions with asymptotics
for \(r \rightarrow r_-\), where \(r^*(r)\) is as defined earlier. Since any three solutions have to be linearly dependent, we can write
and
where \({\mathfrak {T}}_{{\mathcal {H}}^+_r}(\omega )\), \({\mathfrak {R}}_{{\mathcal {H}}^+_r}(\omega )\) and \({\mathfrak {T}}_{{\mathcal {H}}^+_l}(\omega )\), \({\mathfrak {R}}_{{\mathcal {H}}^+_l}(\omega )\) are the transmission and reflection coefficients of the right event horizon and left event horizon, respectively. A priori they are only defined for \(\omega \in {\mathbb {R}}\setminus \{0\}\), but it can be shown that they extend analytically to all of \({\mathbb {R}}\). A key ingredient needed for the proof of Theorem 1.11 is that \({\mathfrak {T}}_{{\mathcal {H}}^+_r}(0) \ne 0\), which can be shown using the \(\partial _t\)-conservation law (see for example [37, 48]) or by direct computation using special functions (see for example [29, 37]).
For \(\omega \ne 0\) we can thus expand any solution of (1.13) as  with \(a_{{\mathcal {H}}^+_r}, a_{{\mathcal {H}}^+_l}: {\mathbb {R}}{\setminus } \{0\} \rightarrow {\mathbb {C}}\) and thus, at least formally,
with \(a_{{\mathcal {H}}^+_r}, a_{{\mathcal {H}}^+_l}: {\mathbb {R}}{\setminus } \{0\} \rightarrow {\mathbb {C}}\) and thus, at least formally,
is a solution of (1.5).
We now discuss the reduction of Theorem 1.6 to Theorem 1.11. Let \(\phi : ({\mathcal {M}} \cup {\mathcal {H}}^+_r )\cap \{v \geqslant v_0\} \cap \{u \leqslant u_1\} \rightarrow {\mathbb {C}}\) be as in Theorem 1.6. One extends the induced initial data on \({\mathcal {H}}^+_r \cap \{v \geqslant v_0\}\) smoothly to all of \({\mathcal {H}}^+_r\) in such a way that \(\phi |_{{\mathcal {H}}^+_r}(v) = 0\) for \(v \leqslant v_0 -1\). Using that we are in spherical symmetry, we can now solve the wave equation sideways to extend \(\phi \) to the region \(({\mathcal {M}} \cup {\mathcal {H}}^+_r \cup {\mathcal {H}}^+_l) \cap \{u \leqslant u_1\}\). Again we extend the induced initial data on \({\mathcal {H}}^+_l \cap \{u \leqslant u_1\}\) to all of \({\mathcal {H}}^+_l\) such that \(\phi |_{{\mathcal {H}}^+_l}(u) = 0\) for \(u \geqslant u_1 +1\) and solve the wave equation forwards to get a global solution in \({\mathcal {M}} \cup {\mathcal {H}}^+_r \cup {\mathcal {H}}^+_l\) which satisfies the assumptions in Theorem 1.11. This is the reduction of Theorem 1.6 to Theorem 1.11 by extension of \(\phi \).
We now turn towards the sketch of a proof of Theorem 1.11. One first shows that the solution \(\phi \) is indeed (i.e., not just formally) given by (1.17) with
being the (inverse) Fourier transforms of the characteristic initial data. This can be established in (at least) two ways: one way is to start from the expression (1.17) with the coefficients \(a_{{\mathcal {H}}^+_r}, a_{{\mathcal {H}}^+_l}\) given by (1.18) and to show by direct computation that it solves the wave equation (1.5) and attains the prescribed initial data when \(r \rightarrow r_+\) and u or v, respectively, are fixed. By the uniqueness of the characteristic initial value problem we thus obtain that (1.17) with (1.18) is indeed the wanted solution. Another possibility, which will be implemented in this paper for Teukolsky on Kerr, is to first prove via energy estimates decay of \(\phi (t,r)\) in t for all \(r \in (r_-,r_+)\) which one uses to justify that the Fourier transform (1.12) is well-defined for all \(r \in (r_-,r_+)\) and that it satisfies (1.13). One then infers that \(\phi \) must be given by (1.17) with some \(a_{{\mathcal {H}}^+_r}\), \(a_{{\mathcal {H}}^+_l}\), which one then determines by passing the expression (1.17) to the limit \(r \rightarrow r_+\) for either fixed u or fixed v. Since, as will become clear below, we only use the frequency regime around \(\omega = 0\) of the wave to prove the blow-up, this second approach, in contrast to the first one, allows us to completely ignore the behaviour of the other frequency regimes in the separated picture. Let us also remark that since \(\phi \) vanishes at the bifurcation sphere, we do have exponential decay of \(\phi \) in v, u along \({\mathcal {H}}^+_r, {\mathcal {H}}^+_l\), respectively, when approaching the bifurcation sphere and thus \(a_{{\mathcal {H}}^+_r}\) and \(a_{{\mathcal {H}}^+_l}\) are in particular in \(L^2_\omega ({\mathbb {R}})\). If \(\phi \) did not vanish at the bifurcation sphere, the coefficients \(a_{{\mathcal {H}}^+_r}\), \(a_{{\mathcal {H}}^+_l}\) would have additional poles at zero frequency which encode the constant at the bifurcation sphere.
We now investigate the regularity of the coefficient functions (1.18) around \(\omega = 0\). First note that by (1.7) and a Hardy inequalityFootnote 11 we have  . Furthermore (1.8) and (1.9) imply
. Furthermore (1.8) and (1.9) imply



It follows from (1.19) and (1.21) that  . Together with (1.20) this now implies
. Together with (1.20) this now implies  for any \(\varepsilon >0\). By (1.18) we thus obtain for any \(\varepsilon >0\)
for any \(\varepsilon >0\). By (1.18) we thus obtain for any \(\varepsilon >0\)
Furthermore we straightforwardly obtain
We now move on to the analysis of the wave near the Cauchy horizon at \(r=r_-\). Using for example energy estimates one shows that the wave \(\phi \) extends (even continuously) to the Cauchy horizon \(\mathcal{C}\mathcal{H}^+_l\)Footnote 12 and satisfies
where \(\chi (v): {\mathbb {R}}\rightarrow (0, \infty )\) is a positive function with \(\chi (v) \simeq |v|^{2p_0}\) forFootnote 13\(v \rightarrow -\infty \) and \(\chi (v) \simeq |v|^{2(p_0 - 1)}\) for \(v \rightarrow + \infty \). In particular one can take the Fourier transform of \(\partial _v \phi |_{\mathcal{C}\mathcal{H}^+_l}\) in \(L^2\). Using the language of the transmission and reflection coefficients introduced earlier we can rewrite (1.17) as
Noticing that the Killing vector field \(\partial _t\) equals \(\partial _v\) on \(\mathcal{C}\mathcal{H}^+_l\) and using the asymptotics (1.15) of \(B_{\mathcal{C}\mathcal{H}^+_l}(r; \omega )\) and \(B_{\mathcal{C}\mathcal{H}^+_r}(r; \omega )\), we can pass (1.25) to the limit \(r \rightarrow r_-\) for fixed v to obtain

i.e., a Fourier representation of \(\partial _v \phi _{\mathcal{C}\mathcal{H}^+_l}\) in terms of the Fourier representations of the characteristic initial data and the transmission and reflection coefficients.Footnote 14 We can now investigate the decay of \(\partial _v \phi |_{\mathcal{C}\mathcal{H}^+_l}\) in v by considering the regularity of  at \(\omega = 0\):
at \(\omega = 0\):

The last two terms (the two sums) on the right hand side are in \(L^2_\omega \big ((-1,1)\big )\) by the analyticity of the transmission and reflection coefficients \({\mathfrak {T}}_{{\mathcal {H}}^+_r}(\omega ), {\mathfrak {R}}_{{\mathcal {H}}^+_r}(\omega )\) and by (1.23) and the second property in (1.22). It now follows from the first property in (1.22) together with \({\mathfrak {T}}_{{\mathcal {H}}^+_r}(0) \ne 0\) (cf. remark below (1.16)), applied to the first term on the right hand side of (1.26) that  for any \(\varepsilon >0\). Plancherel now implies
for any \(\varepsilon >0\). Plancherel now implies
This, however, does not tell us yet whether the slow decay of \(\partial _v \phi |_{\mathcal{C}\mathcal{H}^+_l}\) in v is for \(v \rightarrow + \infty \) or for \(v \rightarrow - \infty \). However, with (1.24) we can finally infer
The statement (1.10) of Theorem 1.11 then follows by propagating the singularity backwards along \(\mathcal{C}\mathcal{H}^+_r\), using energy estimates. This is a standard propagation of regularity result. We have now concluded the sketch of a proof of Theorem 1.11 and will discuss next how this method of proof changes for the Teukolsky field on Kerr.
1.4.2 Comparison to Teukolsky on Kerr
We will mainly use the \((v_+,r, \theta , \varphi _+)\)-coordinate system on Kerr, which can be thought of as the analogue of the \((v,r, \theta , \varphi )\)-coordinate system on Reissner-Nordström. However, \(v_+\) is not a null coordinate any more, but its level sets are timelike. The Teukolsky equation takes the formFootnote 15

where the Teukolsky field \(\psi \) is with respect to an algebraically special frame which is regular at the right event horizon \({\mathcal {H}}^+_r\), cf. Sections 2.2 and 2.3. For \(s=+2\), the case we are concerned with, the frame component entering the Teukolsky field degenerates near \({\mathcal {H}}^+_l\) and thus a regular Teukolsky field \(\psi \) vanishes on the left event horizon including at the bifurcation sphere.
Let us begin by discussing the differences between the energy estimates for Teukolsky and the linear wave equation. As is well-known, the spacetime geometry near the event horizons is such that localised energy of linear waves decays exponentially. This is usually referred to as the ‘red-shift effect’; it helps the analyst to close energy estimates. The name of course derives from a shift in frequency, which is also present at the event horizons. The shift in frequency and the decay of energy are not one and the same thing – indeed, they decouple for the Teukolsky equation. We give a detailed discussion in Remark 4.20. For the energy estimates it is of course the decay of localised energy which is most relevant – let us refer to this effect as the ‘red-shift effect for energy’ in order to keep in touch with standard terminology. For the Teukolsky field \(\psi \) (and for \(s = +2\)) we now have an effective blue-shift for the energy at the right event horizon \({\mathcal {H}}^+_r\). This can be seen from the dashed term in (1.27). It is effective in the sense that it turns into a red-shift for the energy after two commutations with \(\partial _r\). It is thus at this level that we close the energy estimate for the Teukolsky field near \({\mathcal {H}}^+_r\). The Teukolsky equation for \({\hat{\psi }}:= \Delta ^{-s} \psi \), which is the Teukolsky field with respect to a frame that is regular at the left event horizonFootnote 16\({\mathcal {H}}^+_l\), does still have a red-shift for energy near \({\mathcal {H}}^+_l\); so there, the energy estimates can be closed at the level of \({\hat{\psi }}\) as for the wave equation.
On the other hand, the blue-shift for energy for the wave equation near the Cauchy horizon turns into an effective red-shift for energy for the Teukolsky field \(\psi \) near the left Cauchy horizon \(\mathcal{C}\mathcal{H}^+_l\). This makes the energy estimates for (1.27) near \(r=r_-\) in a sense even easier than for the wave equation (disregarding the more technical nature of implementing the energy estimates for Teukolsky). It is again ‘effective’ in the sense that after two commutations with \(\partial _r\) we have again a blue-shift for energy.
We now discuss the formal separation. Denoting with \(Y^{[s]}_{ml}(\theta , \varphi ; \omega ) = S^{[s]}_{ml}( \cos \theta ; \omega ) e^{im \varphi } \) the spin s-weighted spheroidal harmonics (see Section 5.1; we have \({\mathbb {N}}\ni l \geqslant \max \{|s|, |m|\}\), \(m \in {\mathbb {Z}}\)), the Teukolsky transform of \(\psi \) is given by

Formally, \(\psi \) satisfies the Teukolsky equation (1.27) if, and only if,  satisfiesFootnote 17
satisfiesFootnote 17

Like (1.13), the radial ODE (1.29) has two regular singular points at \(r=r_-\) and \(r=r_+\). Let \(\omega _\pm = \frac{a}{2Mr_\pm }\) and fix \(s=+2\). For \(\omega \ne \omega _+m\) we can find a fundamental system of solutions with asymptotics
for \(r \rightarrow r_+\) and for \(\omega \ne \omega _- m\) another fundamental system of solutions with asymptotics
for \(r \rightarrow r_-\). The fact that \(A_{{\mathcal {H}}^+_r, ml}\) and \(B_{\mathcal{C}\mathcal{H}^+_l, ml}\) do not have oscillating phases as for the wave equation in (1.14) and (1.15) is due to our choice of \((v_+,r, \theta , \varphi _+)\)-coordinates. If we had used Boyer-Lindquist coordinates \((t,r,\theta , \varphi )\) for the separation, both branches would be oscillatory. Note, however, the difference in the r-weights between the two branches, which is related to \(\psi \) being regular at \({\mathcal {H}}^+_r\) and degenerate at \({\mathcal {H}}^+_l\), and similarly for the Cauchy horizons. Another important difference is that while the branches \(A_{{\mathcal {H}}^+_l, ml}\) and \(B_{\mathcal{C}\mathcal{H}^+_r, ml}\) extend analytically to \(\omega = \omega _+m\) and \(\omega = \omega _- m\), respectively, the branches \(A_{{\mathcal {H}}^+_r, ml}\) and \(B_{\mathcal{C}\mathcal{H}^+_l, ml}\) become singular at \(\omega = \omega _+m\) and \(\omega = \omega _- m\), respectively. This should be contrasted with both branches \(A_{{\mathcal {H}}^+_r}\) and \(A_{{\mathcal {H}}^+_l}\) in (1.14) for the wave equation having a regular (and indeed identical) limit \(\omega \rightarrow 0\) (similarly for the other two branches in (1.15)). This difference impacts a priori on relating the coefficients in the separated picture to the Teukolsky transform of the characteristic initial data (more about this later) and also on the regularity of the transmission and reflection coefficients: as before we can write
where the transmission and reflection coefficients are a priori only defined and analytic on \({\mathbb {R}}\setminus \{\omega _+m, \omega _-m\}\). Recall that the structure of the blow-up argument only requires information on the frequency regime near \(\omega = 0\). So for \(m \ne 0\) we know that the transmission and reflection coefficients are analytic in a neighbourhood of \(\omega = 0\). Moreover, for non-vanishing m we show by direct computation that \({\mathfrak {T}}_{{\mathcal {H}}^+_r, ml}(0) \ne 0\), where we use that for \(\omega = 0\) the radial ODE (1.29) turns into a hypergeometric equation. For \(m=0\), however, the potentially problematic frequency at \(\omega = 0\) cannot be avoided. We show that \({\mathfrak {T}}_{{\mathcal {H}}^+_l, 0\,l}, {\mathfrak {R}}_{{\mathcal {H}}^+_l,0\,l}, {\mathfrak {T}}_{{\mathcal {H}}^+_r,0\,l}\) all extend analytically to \(\omega = 0\), but for the reflection coefficient of the right event horizon we only show that \(\omega \cdot {\mathfrak {R}}_{{\mathcal {H}}^+_r, 0l}\) extends analytically to \(\omega = 0\).Footnote 18
It can also be shown by direct computation for \(m = 0\) that \({\mathfrak {T}}_{{\mathcal {H}}^+_r, 0l}(0) \ne 0\). However, this is more complicated than in the case \(m \ne 0\), because it cannot be inferred alone from the \(\omega \rightarrow 0\) limit of (1.29), which is a hypergeometric equation, but we also need to get information on the \(\omega \)-derivatives of solutions to (1.29) at \(\omega = 0\). We take this as an opportunity to implement and demonstrate a second approach to showing the non-vanishing of the transmission coefficients at \(\omega = 0\), namely by making use of the Teukolsky-Starobinsky conservation law, which can be thought of as the equivalent to using the conservation law associated to the Killing vector field \(\partial _t\) in the case of spherically symmetric waves on Reissner-Nordström mentioned in Section 1.4.1. It is for this implementation where we need that \(\omega {\mathfrak {R}}_{{\mathcal {H}}^+_r, 0l}\) extends continuously to \(\omega = 0\). Let us mention that we also show how the Teukolsky-Starobinsky conservation law can be used to obtain \({\mathfrak {T}}_{{\mathcal {H}}^+_r, ml}(0) \ne 0\) for \(m \ne 0\), but in this case, which gives the leading blow-up at the Cauchy horizon, the direct computation is much easier.
Finally, we also mention at this point that for a reason to be explained below we also need in the case \(m=0\) the vanishing of \({\mathfrak {R}}_{{\mathcal {H}}^+_l, 0l}(0)\) in order to implement the blow-up argument. Again, this is shown by direct computation.
For \(\omega \ne \omega _+m\) we can expand any solution of (1.29) as

with \(a_{{\mathcal {H}}^+_r, ml}, a_{{\mathcal {H}}^+_l, ml}: {\mathbb {R}}{\setminus } \{ \omega _+m\} \rightarrow {\mathbb {C}}\) and thus, at least formally, we obtain that
is a solution to (1.27).
In a similar way to how the local Theorem 1.6 for the spherically symmetric wave equation on Reissner-Nordström is reduced to the global Theorem 1.11, we also reduce the local Theorem 1.1 (or Theorem 3.7) for the Teukolsky field of Kerr to a global theorem, see Theorem 3.9. In spherical symmetry we extended the local solution to a global one by first solving sideways and in this way ensuring that the extended solution vanishes at the bottom bifurcation sphere. For the Teukolsky equation we can no longer solve sideways, but, by solving two initial value problems, we can still extend the local solution to a global one which is compactly supported on \({\mathcal {H}}^+_l \cup {\mathbb {S}}^2_b\). This is done in Theorem 8.6 in Section 8.2, see also Figure 9. However, we can no longer ensure that the regular Teukolsky field vanishes at the bottom bifurcation sphere, which entails that we have to deal with what is the analogue of the poles in the Fourier expansion coefficients \(a_{{\mathcal {H}}^+_r}\) and \(a_{{\mathcal {H}}^+_l}\) in the spherically symmetric case, cf. discussion above (1.19).Footnote 19
We now discuss the implementation of the proof of the global Theorem 1.11 to Teukolsky on Kerr (i.e., the proof of Theorem 3.7 in Section 3). In Sections 4.1 and 4.2 we prove the energy estimates needed to establish the representation (1.30). The coefficients \(a_{{\mathcal {H}}^+_r, ml}\) and \(a_{{\mathcal {H}}^+_l, ml}\) are being determined in Section 7. Keeping the \(v_+\) coordinate fixed one can pass to the limit \(r \rightarrow r_+\) in an analogous manner as for the wave equation to establish that

where  is the Teukolsky transform (1.28). Note that because of the exponential decay in \(v_+\) of \(\psi |_{{\mathcal {H}}^+_r}\) towards \({\mathbb {S}}_b^2\) we have that \(\psi |_{{\mathcal {H}}^+_r}\) is in particular in \(L^2_{v_+}L^2({\mathbb {S}}^2)\), so no poles are present. Because \(\psi \) vanishes on \({\mathcal {H}}^+_l\), we first go over to the quantity \(\partial _r^2 \psi \), which is regular at \({\mathcal {H}}^+_l\) due to the blow-up of \(\partial _r\) near \({\mathcal {H}}^+_l\) (see also Footnote 19). We thus take two r-derivatives of (1.30) and then pass to the limit \(r \rightarrow r_+\) with fixed \(v_-\).Footnote 20 However, it is clear from the preceding discussion that one cannot hope to establish an \(L^2\)-limit, since \(\partial _r^2 \psi \) does not vanish at \({\mathbb {S}}_b^2\). We take a limit in the sense of distributions to recover that \(a_{{\mathcal {H}}^+_l, ml}\) is related to the Teukolsky transform of \(\partial _r^2 \psi |_{{\mathcal {H}}^+_l}\) (modulo a delta distribution). The support of the Teukolsky field at \({\mathbb {S}}_b^2\) implies that \(a_{{\mathcal {H}}^+_l, ml}\) has a pole at \(\omega = \omega _+m\). For \(m \ne 0\) we can ignore this pole, since it is disjoint from a neighbourhood of \(\omega = 0\) which is important for the argument. But for \(m = 0\) the pole potentially interferes with our argument which is based on exploiting the limited regularity of the Fourier coefficients at \(\omega = 0\). It is for this reason that \({\mathfrak {R}}_{{\mathcal {H}}^+_l, 0l}(0) = 0\) is needed later, which cancels the pole.
is the Teukolsky transform (1.28). Note that because of the exponential decay in \(v_+\) of \(\psi |_{{\mathcal {H}}^+_r}\) towards \({\mathbb {S}}_b^2\) we have that \(\psi |_{{\mathcal {H}}^+_r}\) is in particular in \(L^2_{v_+}L^2({\mathbb {S}}^2)\), so no poles are present. Because \(\psi \) vanishes on \({\mathcal {H}}^+_l\), we first go over to the quantity \(\partial _r^2 \psi \), which is regular at \({\mathcal {H}}^+_l\) due to the blow-up of \(\partial _r\) near \({\mathcal {H}}^+_l\) (see also Footnote 19). We thus take two r-derivatives of (1.30) and then pass to the limit \(r \rightarrow r_+\) with fixed \(v_-\).Footnote 20 However, it is clear from the preceding discussion that one cannot hope to establish an \(L^2\)-limit, since \(\partial _r^2 \psi \) does not vanish at \({\mathbb {S}}_b^2\). We take a limit in the sense of distributions to recover that \(a_{{\mathcal {H}}^+_l, ml}\) is related to the Teukolsky transform of \(\partial _r^2 \psi |_{{\mathcal {H}}^+_l}\) (modulo a delta distribution). The support of the Teukolsky field at \({\mathbb {S}}_b^2\) implies that \(a_{{\mathcal {H}}^+_l, ml}\) has a pole at \(\omega = \omega _+m\). For \(m \ne 0\) we can ignore this pole, since it is disjoint from a neighbourhood of \(\omega = 0\) which is important for the argument. But for \(m = 0\) the pole potentially interferes with our argument which is based on exploiting the limited regularity of the Fourier coefficients at \(\omega = 0\). It is for this reason that \({\mathfrak {R}}_{{\mathcal {H}}^+_l, 0l}(0) = 0\) is needed later, which cancels the pole.
Recall how we inferred for the spherically symmetric wave the limited regularity (1.22) of \(a_{{\mathcal {H}}^+_r}\) at \(\omega = 0\) from the decay assumptions of \(\psi \) along \({\mathcal {H}}^+_r\). In spherical symmetry we only had one mode – the spherically symmetric one – for Teukolsky we want to work with the \(m_0l_0\)-mode for which we assume slow decay in Theorem 1.1 (or Theorem 3.7). Note, however, that in the assumptions the \(m_0l_0\)-mode is with respect to spin 2-weighted spherical harmonics and not spin 2-weighted spheroidal harmonics.
So we would like to obtain for any \(\varepsilon >0\)
Note that the derivation of (1.22) used at its heart that v-weights translate in the Fourier picture as \(\omega \)-derivatives. Since the spin weighted spheroidal harmonics in the Teukolsky transform (1.28) depend on \(\omega \), this correspondence does not hold true any more for Kerr.Footnote 21 Exploiting, however, that for \(\omega = 0\) the spin weighted spheroidal harmonics agree with the spin weighted spherical harmonics, we can still obtain (1.31), see Proposition 7.5.
In an analogous way as for the spherically symmetric wave equation (see (1.25)) we can now express (1.30) in terms of the fundamental solutions \(B_{\mathcal{C}\mathcal{H}^+_l, ml}\), \(B_{\mathcal{C}\mathcal{H}^+_r, ml}\) normalised at the Cauchy horizons and the transmission and reflection coefficients and prove energy estimates which allow us to pass to the limit \(r \rightarrow r_-\) with fixed \(v_+\) to obtain that

As before, and using \({\mathfrak {R}}_{{\mathcal {H}}^+_l, 0l}(0) = 0\) in the case \(m_0 = 0\), we deduce that  for any \(\varepsilon >0\). When converting this into the statement
for any \(\varepsilon >0\). When converting this into the statement
we again have to address the complication that v-weights do not exactly correspond to \(\omega \)-derivatives. This is done by proving bounds on \(\partial _\omega ^k Y^{[s]}_{ml}(\theta , \varphi _+; \omega )\), see Propositions 5.6 and 5.22. As for the spherically symmetric model we prove energy estimates in Section 4.3 to show that the infinitude of the integral in (1.32) is due to the behaviour of \(\psi \) for large positive \(v_+\) and also that we can propagate the singularity backwards. This concludes the outline of the proof.
1.5 Outline of Paper
In Section 2 we begin by introducing the interior of the Kerr black hole, then recall briefly the derivation of the Teukolsky equation, and we define spin weighted functions on the sphere as well as on spacetime. Moreover, we show that the Teukolsky field has the regularity of such a spin weighted function on spacetime and we record the form of the Teukolsky equation in various coordinate systems for later reference. Section 3 formulates the main theorems of this paper and their assumptions. The proof of the main theorems begins in Section 4 where we establish the energy estimates required and record some corollaries which are needed later for the limits \(r \rightarrow r_\pm \), the separation of the solution, the extension to the Cauchy horizon, and the backwards propagation of the singularity. In Section 5 we recall the spin weighted spheroidal harmonics, establish a couple of results which are needed for the translation of \(v_+\)-weights to \(\omega \)-derivatives, and then use the energy estimates to give the separation of the Teukolsky field. We continue in Section 6 with the analysis of the radial Teukolsky ODE, introduce the fundamental systems of solutions we work with, and prove the required properties of the transmission and reflection coefficients. Section 7 is concerned with the passing to the limit \(r \rightarrow r_+\) and the determination of the Fourier coefficients in terms of the characteristic initial data. And finally in Section 8 we conclude the proofs of the main theorems. Appendix A records the form of the Teukolsky equation in coordinates which are regular near the bottom bifurcation sphere and discusses the initial value problem for Teukolsky, which is needed for the extension procedure which reduces the local Theorem 3.7 to the global Theorem 3.9. The Appendices B, C, and D collect commutator expressions required for the energy estimates in Section 4.
2 The Interior of Sub-extremal Kerr and Gravitational Perturbations
This section presents the set-up of this paper. We first introduce the geometry of the interior of a sub-extremal Kerr black hole and then recall the derivation of the Teukolsky equation along with the notion of spin weighted functions. We also show that the geometrically arising Teukolsky field is indeed such a spin weighted function.
We also introduce the following notation: for a function f and a non-negative function g the notation \(f \lesssim g\) means that there exists a constant \(C>0\) such that \(|f(x)| \leqslant C \cdot g(x)\) holds for all points x for which both functions are defined. If we say ‘\(f \lesssim g\) on A’, where A is a subset of the domains of definition of f and g, then this means that there exists a constant \(C>0\) such that \(|f| \leqslant C \cdot g\) holds on A. Similarly, ‘\(f \lesssim g\) for \(x \rightarrow x_0\)’ means that there exists a neighbourhood A of \(x_0\) such that \(f \lesssim g\) on A. Here, \(x_0\) may also be \(\infty \). The notations ‘\(f \lesssim g\) as \(x \rightarrow x_0\)’ and ‘\(f = {\mathcal {O}}(g)\) as \(x \rightarrow x_0\)’ have the same meaning.Footnote 22 Finally, if both f and g are non-negative, then the notation \(f \simeq g\) stands for ‘\(f \lesssim g\) and \(g \lesssim f\)’, i.e., there exists a constant \(C >0\) such that \(\frac{1}{C} f \leqslant g \leqslant C \cdot g\). Again, we may specify a region or a limit in which \(f \simeq g\) is supposed to hold.
2.1 The Manifold and Metric of the Interior of Sub-extremal Kerr
We consider the standard \((t,r,\theta , \varphi )\) coordinates on the smooth manifold \({\mathcal {M}} = {\mathbb {R}}\times (r_-,r_+) \times {\mathbb {S}}^2\), where \(r_- = M - \sqrt{M^2 - a^2}\), \(r_+ =M + \sqrt{M^2 - a^2}\), and \(0< |a| < M \) are constants which later represent the angular momentum per unit mass and the mass of the black hole, respectively. A Lorentzian metric g on \({\mathcal {M}}\) is defined by
where
Note that \(r_- < r_+\) are the roots of \(\Delta \). We also compute \(\det g = -\rho ^4 \sin ^2 \theta \) for later convenience. We fix a time orientation on the Lorentzian manifold \(({\mathcal {M}},g)\) by stipulating that \(-\partial _r\) is future directed. The time oriented Lorentzian manifold \(({\mathcal {M}},g)\) is called the interior of a sub-extremal Kerr black hole and the coordinates \((t,r,\theta , \varphi )\) are called Boyer–Lindquist coordinates. Moreover, let us fix an orientation by stipulating that the Lorentzian volume form \(\textrm{vol}= \rho ^2 \sin \theta \,dt \wedge dr \wedge d\theta \wedge {d}\varphi \) is positive. A longer computation yields that \(({\mathcal {M}},g)\) is a solution to the vacuum Einstein equations \(\textrm{Ric}(g)=0\).
For later reference we note that the inverse metric \(g^{-1}\) in the Boyer–Lindquist coordinates \((t, \varphi , r, \theta )\) is given by
In the following we will attach boundaries to \({\mathcal {M}}\). Let \(r^*(r)\) be a function on \((r_-,r_+)\) satisfying \(\frac{dr^*}{dr} = \frac{r^2 + a^2}{\Delta }\) and \({\overline{r}}(r)\) a function on \((r_-,r_+)\) satisfying \(\frac{d{\overline{r}}}{dr} = \frac{a}{\Delta }\). We now define the following functions on \({\mathcal {M}}\):
It is easy to check that \((v_+, \varphi _+, r, \theta )\) and \((v_-, \varphi _-, r, \theta )\) are coordinate systems for \({\mathcal {M}}\). The metric g in these coordinates takes the following form:
A simple computation shows that those expressions define non-degenerate (and analytic) Lorentzian metrics for all positive values of r. We now set
and define the Kruskal-like coordinate functions
The Kruskal-like coordinates \((V_{r_+}^+, V_{r_+}^-, \theta , \Phi _{r_+})\) map \({\mathcal {M}}\) onto \((0, \infty ) \times (0, \infty ) \times {\mathbb {S}}^2\). It can be shown (see [53], Chapter 3.5) that the Kerr metric (2.1) extends, under this mapping, regularly to the manifold \([0, \infty ) \times [0,\infty ) \times {\mathbb {S}}^2\). We call the null hypersurface \(\{0\} \times [0, \infty ) \times {\mathbb {S}}^2 =: {\mathcal {H}}^+_\ell \) the (left) event horizon and the null hypersurface \([0, \infty ) \times \{0\} \times {\mathbb {S}}^2 =: {\mathcal {H}}^+_r\) the (right) event horizon. The sphere \(\{0\} \times \{0\} \times {\mathbb {S}}^2 = {\mathcal {H}}^+_r\cap {\mathcal {H}}^+_\ell =:{\mathbb {S}}^2_b\) is called the (bottom) bifurcation sphere.
In order to extend \({\mathcal {M}}\) to \(r = r_-\), we define another set of Kruskal-like coordinate functions by
The Kruskal-like coordinates \((V_{r_-}^+, V_{r_-}^-, \theta , \Phi _{r_-})\) map \({\mathcal {M}}\) onto \((-\infty , 0) \times (-\infty , 0) \times {\mathbb {S}}^2\) and in the same way it can be shown that the Kerr metric (2.1) extends in these coordinates regularly to \((-\infty , 0] \times (-\infty , 0] \times {\mathbb {S}}^2\). We call the null hypersurface \(\{0\} \times (-\infty , 0] \times {\mathbb {S}}^2 =: \mathcal{C}\mathcal{H}^+_r\) the (right) Cauchy horizon and the null hypersurface \((-\infty ,0] \times \{0\} \times {\mathbb {S}}^2 =: \mathcal{C}\mathcal{H}^+_l\) the (left) Cauchy horizon. The sphere \(\{0\} \times \{0\} \times {\mathbb {S}}^2 = \mathcal{C}\mathcal{H}^+_r \cap \mathcal{C}\mathcal{H}^+_l =: {\mathbb {S}}_t\) is called the (top) bifurcation sphere.
Using the two Kruskal-like coordinate systems we define the manifold with corners \(\underline{\overline{{\mathcal {M}}}}:= {\mathcal {M}} \cup {\mathcal {H}}^+_l \cup {\mathcal {H}}^+_r \cup \mathcal{C}\mathcal{H}^+_l \cup \mathcal{C}\mathcal{H}^+_r\), which is depicted in a Penrose-style diagramFootnote 23 in Figure 6. Figure 7 shows the behaviour and range of the functions \(t, r, v_-,\) and \(v_+\). We also define the manifolds with corners \(\underline{{\mathcal {M}}}:= {\mathcal {M}} \cup {\mathcal {H}}^+_l \cup {\mathcal {H}}^+_r\) and \(\overline{{\mathcal {M}}}:= {\mathcal {M}} \cup \mathcal{C}\mathcal{H}^+_l \cup \mathcal{C}\mathcal{H}^+_r\).
We also note that the coordinates \(\{v_+, \varphi _+, r, \theta \}\) cover \({\mathcal {M}} \cup ({\mathcal {H}}^+_r {\setminus } {\mathbb {S}}^2_b) \cup (\mathcal{C}\mathcal{H}^+_l {\setminus } {\mathbb {S}}^2_t)\). For later reference we express the Boyer-Lindquist coordinate vector fields (on the left) in terms of the \(\{v_+, \varphi _+, r, \theta \}\) coordinate vector fields (on the right):
We also note that the volume form in \(\{v_+, \varphi _+, r, \theta \}\)-coordinates is given by \(\textrm{vol}= \rho ^2 \sin \theta \, dv_+ \wedge dr \wedge d\theta \wedge d\varphi _+\).
Similarly we express the Boyer-Lindquist coordinate vector fields (on the left) in terms of the \(\{v_-, \varphi _-, r, \theta \}\) coordinate vector fields (on the right):
We also note that the volume form in \(\{v_-, \varphi _-, r, \theta \}\)-coordinates is given by \(\textrm{vol}= \rho ^2 \sin \theta \, dv_- \wedge dr \wedge d\theta \wedge d\varphi _-\).
Note that \(<dv_+, dv_+> = <dv_-, dv_-> = \frac{a^2 \sin ^2 \theta }{\rho ^2}\), thus showing that for \(a >0\) the level sets of \(v_+\) and \(v_-\) are timelike hypersurfaces away from the axis.
We now define the functions \(f^+:= v_+ -r + r_+\) and \(f^-:= v_- - r + r_-\). An easy computation gives
which shows that the level sets of \(f^+\) and \(f^-\) are spacelike hypersurfaces, cf. Figure 7. Moreover, it is immediate that the level sets of r are spacelike hypersurfaces.
2.1.1 Relation of \(\Phi _{r_+}\) and \(\varphi _+\) on \({\mathcal {H}}^+_r\) – and Similarly for \(\Phi _{r_+}, \varphi _-\) on \({\mathcal {H}}^+_l\)
We define \(\omega _\pm := \frac{a}{r_\pm ^2 + a^2}\) and set
This defines smooth functions for \(r \in (r_-, r_+)\). Moreover, \(\phi _+\) extends smoothly to \(r_+\) and \(\phi _-\) extends smoothly to \(r_-\): for \(\phi _+\) this follows from
where the right hand side clearly extends smoothly to \(r=r_+\). We denote \(\lim _{r \rightarrow r_+} \phi _+(r) =: \phi _+(r_+)\). Similarly for \(\phi _-\) and we denote \(\lim _{r \rightarrow r_-} \phi _-(r) =: \phi _-(r_-)\).
We will also need to relate the angular functions \(\Phi _{r_+}\) and \(\varphi _+\) (\(\varphi _-\)) on the right (left) event horizon, where they are both defined. For \(r \in (r_-, r_+)\) we have
On \({\mathcal {H}}^+_r\) we thus have
while on \({\mathcal {H}}^+_l\) we have
2.1.2 Estimates for \(r^*\) near \(r = r_\pm \)
We write \(\frac{dr^*}{dr} = \frac{r^2 + a^2}{(r - r_+)(r-r_-)} = \frac{r_+^2 + a^2}{(r-r_+)(r_+ - r_-)} + f_+(r)\) with a function \(f_+: (r_-, r_+) \rightarrow {\mathbb {R}}\) that extends regularly to \(r_+\). Integration gives
with a function \(F_+: (r_-,r_+) \rightarrow {\mathbb {R}}\) that extends regularly to \(r_+\). Recalling \(r^* = \frac{1}{2}(v_+ + v_-)\) we obtain
Similarly, we obtain
with a function \(F_-: (r_-, r_+) \rightarrow {\mathbb {R}}\) that extends regularly to \(r_{-}\).
2.2 The Principal Null Frame
For convenience we introduce the abbreviations  and
and  . Moreover, using the Boyer–Lindquist coordinates, we define
. Moreover, using the Boyer–Lindquist coordinates, we define

A principal null frame is then given by

The vector fields \({\hat{e}}_3\) and \({\hat{e}}_4\) are null and future directed and satisfy \(\langle {\hat{e}}_3,{\hat{e}}_4\rangle = -2\). Let us denote the distribution spanned by \({\hat{e}}_3\) and \({\hat{e}}_4\) by \(\Pi \) and the distribution orthogonal to \(\Pi \) by \(\Pi ^\perp \). The vector fields \(e_1\) and \(e_2\) are not defined on the axis, but where defined they form an orthonormal basis for \(\Pi ^\perp \).
Note that in \((v_-,r,\theta ,\varphi _-)\)-coordinates we haveFootnote 24
while in \((v_+, r, \theta , \varphi _+)\)-coordinates we have
Hence, the null vectors \({\hat{e}}_3\) and \({\hat{e}}_4\) are regular at the left event horizon \({\mathcal {H}}^+_l\) and at the right Cauchy horizon \(\mathcal{C}\mathcal{H}^+_r\), but not at the right event horizon \({\mathcal {H}}^+_r\) and at the left Cauchy horizon \(\mathcal{C}\mathcal{H}^+_l\). There, the vector fields
are regular.
2.3 The Teukolsky Equation and Spin-Weighted Functions
2.3.1 Gravitational Perturbations in the Newman-Penrose Formalism
In the following we recall the basic steps in the derivation of the Teukolsky equation for gravitational perturbations of Kerr, see [67]. We start by clarifying that our convention for the Riemann curvature tensor is
where \(x^\mu \) denotes a local coordinate system.
We now make contact with and follow [67] by setting
With respect to this complex principal null frame we haveFootnote 25
Let now g(s), \(s \in [0, \varepsilon )\), be a smooth family of Lorentzian metrics defined on \({\mathcal {M}} \cup {\mathcal {H}}^+_l \cup {\mathcal {H}}^+_r\) satisfying the vacuum Einstein equations \(\textrm{Ric}\big (g(s)\big ) = 0\) and such that g(0) is the metric (2.1) of sub-extremal Kerr. Moreover, let l(s), n(s), \({m_a}(s)\), \(\overline{{m_a}}(s)\) be a complex frame field (not necessarily null) such that for \(s=0\) they agree with (2.9) and define \(\Psi _i(s)\) in analogy with (2.10) for all s. It now follows from (2.10) that
i.e., \({\dot{\Psi }}_0(0)\) is in fact independent of the continuation of the complex principal null frame (2.9) for \(s>0\). Moreover, because \(\Psi _0\) is a vanishing scalar, \({\dot{\Psi }}_0(0)\) is also gauge invariant. The same observations hold for \({\dot{\Psi }}_4(0)\). In [67], Teukolsky derived the following equation, now called the Teukolsky equation,
which is satisfied for \(s = +2\) by \({\hat{\psi }}_2 = {\dot{\Psi }}_0(0)\) and for \(s=-2\) by \({\hat{\psi }}_{-2} = (r - ia \cos \theta )^4 \cdot {\dot{\Psi }}_4(0)\).
2.3.2 The Teukolsky Equation for a Regular Field Near \({\mathcal {H}}^+_r\)
We recall that \(l = -{\hat{e}}_4\) blows up at the right event horizon \({\mathcal {H}}^+_r\) and that \(\Delta l = e_4\) is regular at \({\mathcal {H}}^+_r\). Hence, the curvature component \(\alpha = R(e_4, {m_a}, e_4,{m_a}) = \Delta ^2 \Psi _0\) is regular at \({\mathcal {H}}^+_r\) (and vanishes at \({\mathcal {H}}^+_l\)) and for its linearisation \({\dot{\alpha }}\) we obtain \({\dot{\alpha }} = \Delta ^2 {\dot{\Psi }}_0\). This motivates to set \(\psi _s:= \Delta ^s {\hat{\psi }}_s\). It now follows that if \({\hat{\psi }}_s\) satisfies (2.11), then \(\psi _s\) satisfies
where we have used
In particular, the quantity we are most interested in, \({\dot{\alpha }}=\psi _2\), satisfies (2.12) for \(s=+2\).
Using the definition of the wave operator
we can rewrite (2.12) as
2.3.3 Spin s-weighted Functions on \({\mathbb {S}}^2\)
In the following we will exhibit the appropriate function space on which the Teukolsky equation (2.12) is defined – and in particular which function spaces \({\dot{\alpha }}\) and \({\dot{\Psi }}_0(0)\) belong to (it is immediate from their definition that they are not regular at \(\theta = 0, \pi \)). We begin by discussing spin s-weighted functions on the 2-sphere which arise by expressing tensors on \({\mathbb {S}}^2\) with respect to a (necessarily) non-global frame field. We consider the standard \((\theta , \varphi )\) coordinate system on \({\mathbb {S}}^2\) in which the round metric takes the form \(g_{{\mathbb {S}}^2} = d\theta ^2 + \sin ^2 \theta \, d\varphi ^2\) and choose as an orthonormal frame field \(E_1 = \partial _\theta \) and \(E_2 =\frac{1}{\sin \theta }\partial _\varphi \), which are defined away from the north pole at \(\{\theta = 0\}\) and the south pole at \(\{\theta = \pi \}\). We combine this frame field into a single complex vector
Consider now the space \(\Gamma ^\infty (S^2T^*{\mathbb {S}}^2)\) of all smooth symmetric 2-covariant tensor fields on \({\mathbb {S}}^2\) and define a map
by \(\iota _m(\alpha ) = \alpha (m, m)\).
Definition 2.15
The space of smooth spin 2-weighted functions on \({\mathbb {S}}^2\) is defined as

Remark 2.16
For \(\alpha \in S^2T^*{\mathbb {S}}^2\) we compute
where we have used the symmetry of \(\alpha \). It follows that \(g_{{\mathbb {S}}^2}(m,m) =0\) and thus the kernel of \(\iota _m\) contains \(g_{{\mathbb {S}}^2} \cdot C^\infty ({\mathbb {S}}^2)\). We now show that the kernel of \(\iota _m\) equals \(g_{{\mathbb {S}}^2} \cdot C^\infty ({\mathbb {S}}^2)\). We note that \(\nicefrac {\Gamma ^\infty (S^2T^*{\mathbb {S}}^2) }{g_{{\mathbb {S}}^2} \cdot C^\infty ({\mathbb {S}}^2)} \simeq \Gamma ^\infty (S^2_{\textrm{tf}}T^*{\mathbb {S}}^2) \), where \(\Gamma ^\infty (S^2_{\textrm{tf}}T^*{\mathbb {S}}^2) \) denotes the space of all smooth symmetric and trace-free 2-covariant tensor fields on \({\mathbb {S}}^2\). For \(\alpha \in \Gamma ^\infty (S^2_{\textrm{tf}}T^*{\mathbb {S}}^2)\) we have \(\alpha _{\theta \theta } + \frac{1}{\sin ^2 \theta } \alpha _{\varphi \varphi } = 0\) and thus
which shows that \(\alpha (m,m) \) characterises \(\alpha \) uniquely. This shows that  is an isomorphism.Footnote 26
is an isomorphism.Footnote 26
We also remark that the space of smooth spin \(-2\)-weighted functions is defined as the image of \(\Gamma ^\infty (S^2T^*{\mathbb {S}}^2)\) under \(\iota _{{\overline{m}}}\) in \(C^\infty ({\mathbb {S}}^2 {\setminus } \{\theta = 0, \pi \})\), where \({\overline{m}}\) is the complex conjugate of m. Although not needed in this paper, we also briefly remark that smooth spin (\(\pm 1)\)-weighted functions are defined as the images (under \(\iota _m\) and \(\iota _{{\overline{m}}}\)) of all smooth one-forms on \({\mathbb {S}}^2\). We also remark that it follows directly from the definition that the spaces of smooth spin weighted functions are invariant under multiplication by smooth functions on \({\mathbb {S}}^2\).
We now give an intrinsic characterisation of the spin s-weighted functions on \({\mathbb {S}}^2\). We define
These first order differential operators satisfy \([{\tilde{Z}}_1, {\tilde{Z}}_2] = {\tilde{Z}}_3\), \([{\tilde{Z}}_2, {\tilde{Z}}_3] = {\tilde{Z}}_1\), and \([{\tilde{Z}}_3, {\tilde{Z}}_1] = {\tilde{Z}}_2\).
Proposition 2.18
\(f \in C^\infty ({\mathbb {S}}^2\setminus \{\theta = 0, \pi \})\) lies in  if, and only if, \(e^{is\varphi }({\tilde{Z}}_1)^{k_1}({\tilde{Z}}_2)^{k_2}({\tilde{Z}}_3)^{k_3} f\) extends continuously to the north pole \(\theta = 0\) and \(e^{-is\varphi }({\tilde{Z}}_1)^{k_1}({\tilde{Z}}_2)^{k_2}({\tilde{Z}}_3)^{k_3} f\) extends continuously to the south pole \(\theta = \pi \) for all \(0 \leqslant k_1 + k_2 + k_3 < \infty \), \(k_i \in {\mathbb {N}}_0\).
if, and only if, \(e^{is\varphi }({\tilde{Z}}_1)^{k_1}({\tilde{Z}}_2)^{k_2}({\tilde{Z}}_3)^{k_3} f\) extends continuously to the north pole \(\theta = 0\) and \(e^{-is\varphi }({\tilde{Z}}_1)^{k_1}({\tilde{Z}}_2)^{k_2}({\tilde{Z}}_3)^{k_3} f\) extends continuously to the south pole \(\theta = \pi \) for all \(0 \leqslant k_1 + k_2 + k_3 < \infty \), \(k_i \in {\mathbb {N}}_0\).
Before we give the proof we recall that the vector fields
are smooth on \({\mathbb {S}}^2\), span \(T{\mathbb {S}}^2\) at each point of \({\mathbb {S}}^2\), and satisfy \([Z_1, Z_2] = Z_3\), \([Z_2, Z_3] = Z_1\), and \([Z_3, Z_1] = Z_2\).
Proof
We observe that
is continuous at the north pole \(\theta = 0\) and, similarly,
is continuous at the south pole \(\theta = \pi \). Moreover, we compute
For \(s = +2\) and \(\alpha \in \Gamma ^\infty (S^2T^*{\mathbb {S}}^2)\) we now compute
Iteratively, we obtain
for \(0 \leqslant k_1 + k_2 +k_3 < \infty \).
Given now  , it follows from (2.21) together with the above observations that
, it follows from (2.21) together with the above observations that
extends continuously to the north pole. The analogous computation shows the claim for the south pole.
Vice versa, let \(f \in C^\infty ({\mathbb {S}}^2\setminus \{\theta = 0, \pi \})\) satisfy the continuity properties stated in the proposition. By Remark 2.16\(\alpha (m,m):= f\) defines a smooth symmetric and trace-free two-covariant tensor field (over \({\mathbb {R}}\)) on \({\mathbb {S}}^2\setminus \{\theta = 0, \pi \})\). It now follows as before from (2.21) that this tensor field extends smoothly to the north and south pole.
The statement of the proposition for \(s = -2\) (as well as for \(s = \pm 1\)) follows analogously. \(\square \)
Now we introduce spin weighted Sobolev spaces. Some properties of those will later be needed for the energy estimates and Sobolev embeddings of spin weighted functions.
Definition 2.22
The spin s-weighted Sobolev space \(H^m_{[s]}({\mathbb {S}}^2)\) is defined by
We denote with \({\mathbb {S}}^2_+\) the (closed) northern hemisphere of \({\mathbb {S}}^2\) and with \({\mathbb {S}}^2_-\) the (closed) southern hemisphere.
Lemma 2.23
If \(f \in H^j_{[s]}({\mathbb {S}}^2)\), then \(e^{is\varphi } f \in H^j({\mathbb {S}}^2_+)\) and \(e^{-is\varphi }f \in H^j({\mathbb {S}}^2_-)\) for \(j = 1,2\).
Proof
We compute
Let us now restrict to the upper sign and to the northern hemisphere. It then follows that \(a_-(\theta ,\varphi ) = is \cos \varphi \cdot {\mathcal {O}}(\theta ) \in C^{0,1}({\mathbb {S}}^2_+)\), and similarly \(b_- \in C^{0,1}({\mathbb {S}}^2_+)\). Thus all the terms in (2.24) are in \(L^2({\mathbb {S}}^2_+)\). Moreover, it now follows easily that \(Z_i\big (Z_j( e^{is\varphi } f)\big ) \in L^2({\mathbb {S}}^2_+)\) for all \(i,j \in \{1,2,3\}\). For example we have
Similarly for the lower sign and the southern hemisphere. \(\square \)
Proposition 2.25
We have 
Proof
The inclusion “\(\subseteq \)” follows directly from Proposition 2.18. For the reverse inclusion let \(f \in \bigcap _{0 \leqslant m < \infty } H^m_{[s]}({\mathbb {S}}^2)\) and note that for \(0 \leqslant k_1 + k_2 + k_3\) we have \(({\tilde{Z}}_1)^{k_1}({\tilde{Z}}_2)^{k_2}({\tilde{Z}}_3)^{k_3} f \in H^2_{[s]}({\mathbb {S}}^2)\). It now follows from Lemma 2.23 together with the standard Sobolev embedding that \(e^{is\varphi } ({\tilde{Z}}_1)^{k_1}({\tilde{Z}}_2)^{k_2}({\tilde{Z}}_3)^{k_3} f \) is continuous at the north pole \(\theta = 0\) while \(e^{-is\varphi } ({\tilde{Z}}_1)^{k_1}({\tilde{Z}}_2)^{k_2}({\tilde{Z}}_3)^{k_3} f \) is continuous at the south pole \(\theta = \pi \). The conclusion now follows again from Proposition 2.18. \(\square \)
Let us denote the standard volume form on \({\mathbb {S}}^2\) by \(\textrm{vol}_{{\mathbb {S}}^2}= \sin \theta d\theta \wedge d\varphi \). We now derive an integration by parts formula for spin weighted functions.
Proposition 2.26
For  and \(i \in \{1,2,3\}\) we have
and \(i \in \{1,2,3\}\) we have
Proof
We give the proof for \(s = +2\), but the other cases are analogous. We begin by noticing that
where \(\varepsilon = \textrm{vol}_{{\mathbb {S}}^2}^\sharp \in \Gamma ^\infty (\Lambda ^2T^*{\mathbb {S}}^2)\) is the raised volume form. Note that \(m \otimes {\overline{m}}\) is a smooth tensor on \({\mathbb {S}}^2\). In particular, since the vector fields \(Z_i\) are Killing vector fields, we obtain
Let now \(\alpha , \beta \in \Gamma ^\infty (S^2T^*{\mathbb {S}}^2)\) with \(\alpha (m, m) = f\) and \(\beta (m,m) = h\). Using (2.20), (2.28), and the smoothness of \(m \otimes {\overline{m}}\) we compute
\(\square \)
Remark 2.29
Note that the smoothness of \(m \otimes {\overline{m}}\) implies that if  , then \(f {\overline{h}} \in C^\infty ({\mathbb {S}}^2)\). The above can now also be derived from observing \(Z_i(f {\overline{h}}) = (Z_i f) {\overline{h}} + f Z_i {\overline{h}} =({\tilde{Z}}_i f){\overline{h}} + f \overline{{\tilde{Z}}_i h}\).
, then \(f {\overline{h}} \in C^\infty ({\mathbb {S}}^2)\). The above can now also be derived from observing \(Z_i(f {\overline{h}}) = (Z_i f) {\overline{h}} + f Z_i {\overline{h}} =({\tilde{Z}}_i f){\overline{h}} + f \overline{{\tilde{Z}}_i h}\).
2.3.4 The Spin s-weighted Laplacian
The spin s-weighted Laplacian  on \({\mathbb {S}}^2\) is defined for
on \({\mathbb {S}}^2\) is defined for  in standard \((\theta , \varphi )\) coordinates byFootnote 27
in standard \((\theta , \varphi )\) coordinates byFootnote 27

We note that

such that it follows easily from Proposition 2.18 that (2.30) is a smooth operator on  .
.
It follows directly from Proposition 2.26 and (2.31) that for  we have
we have

Note that for \(s=0\) the right hand side of (2.32) is equal to \(\int _{{\mathbb {S}}^2} \big ( |\partial _\theta f|^2 + \frac{1}{\sin ^2 \theta } |\partial _\varphi f|^2\big ) \; \textrm{vol}_{{\mathbb {S}}^2}\), which gives non-degenerate control of the \(\partial _\varphi \) derivative towards the north and south pole of \({\mathbb {S}}^2\). For \(s \ne 0\), however, \(\frac{1}{\sin \theta } \partial _\varphi f\) has in general a pole in \(\theta \) at \(\theta = 0, \pi \) and thus, in particular, is not square integrable on \({\mathbb {S}}^2\). The next lemma gives the appropriate generalisation, which is needed in Sects. 4.2 and 4.3.
Lemma 2.33
For  we have
we have
and the following holds:
Proof
In order to prove (2.34) we note that by Proposition 2.18 we have
Multiplying (2.36) by \(\cos \theta \) and adding \(\frac{1}{\sin \theta } \sin ^2 \theta \cdot \partial _{\varphi } f\), which is clearly also bounded on \({\mathbb {S}}^2\), we obtain the second claim in (2.34). The proof of (2.35) is a direct computation:
\(\square \)
Lemma 2.37
For  we have
we have

where \(\underset{a.i.}{=}\) denotes equality after integration over the sphere.
Proof
Using Proposition 2.26 we compute

Moreover, using the commutation relations \([{\widetilde{Z}}_i, {\widetilde{Z}}_j] = \varepsilon _{ijk} {\widetilde{Z}}_k\), we further compute
\(\square \)
2.3.5 The Teukolsky Equation in Boyer-Lindquist Coordinates
Using (2.30) and \(\Delta ^{-s} \partial _r (\Delta ^{s+1} \partial _r \psi _s) = 2(r-M)(s+1)\partial _r\psi _s + \Delta \partial _r^2 \psi _s\) we can rewrite the Teukolsky equation (2.12) as

2.3.6 The Teukolsky Equation in \(\{v_+, \varphi _+, r,\theta \}\) Coordinates
Using (2.3) we rewrite (2.38) in terms of \(\{v_+, \varphi _+, r,\theta \}\) coordinates, which are regular at the right event horizon \({\mathcal {H}}^+_r\), to obtain

2.3.7 The Teukolsky Equation in \(\{v_-, \varphi _-, r,\theta \}\) Coordinates
We express the Teukolsky equation (2.11) for \({\hat{\psi }}_s\) (which is regular at \({\mathcal {H}}^+_l\)) in terms of \(\{v_-,\varphi _-,r,\theta \}\) coordinates (which are also regular at \({\mathcal {H}}^+_l\)), using (2.4), to obtain

2.3.8 Spin Weighted Functions on Spacetime
We consider \({\mathcal {M}}\) and observe that the vector field \(m = \frac{1}{\sqrt{2}}(\partial _\theta + \frac{i}{\sin \theta } \partial _\varphi )\), given in Boyer Lindquist coordinates, extends smoothly to \(\underline{\overline{{\mathcal {M}}}}\setminus \{\theta = 0, \pi \}\) by virtue of \(\partial _\varphi = \partial _{\Phi _{r_+}} = \partial _{\Phi _{r_-}}\). We consider the space \(\Gamma ^\infty (S^2(T^*\underline{\overline{{\mathcal {M}}}}))\) of all smooth and symmetric sections of \(T^*\underline{\overline{{\mathcal {M}}}}\otimes T^*\underline{\overline{{\mathcal {M}}}}\) and the map \(\iota _m\) which acts on an element \(\alpha \) of \(\Gamma ^\infty (S^2(T^*\underline{\overline{{\mathcal {M}}}}))\) by \(\iota _m \alpha = \alpha (m,m)\).
Definition 2.41
The space  of smooth spin 2-weighted functions on \(\underline{\overline{{\mathcal {M}}}}\) is defined as the image of \(\Gamma ^\infty (S^2(T^*\underline{\overline{{\mathcal {M}}}}))\) under \(\iota _m\), i.e.
of smooth spin 2-weighted functions on \(\underline{\overline{{\mathcal {M}}}}\) is defined as the image of \(\Gamma ^\infty (S^2(T^*\underline{\overline{{\mathcal {M}}}}))\) under \(\iota _m\), i.e.

Remark 2.42
-
1.
As before, the space of smooth spin \(-2\)-weighted functions is defined as the image of \(\Gamma ^\infty (S^2(T^*\underline{\overline{{\mathcal {M}}}}))\) under \(\iota _{{\overline{m}}}\) and the spin \(\pm 1\)-weighted functions are defined as the images of the space of smooth one-forms on \(\underline{\overline{{\mathcal {M}}}}\).
-
2.
It follows from the definition of the spin weighted spaces that they are invariant under multiplication by elements in \(C^\infty (\underline{\overline{{\mathcal {M}}}}, {\mathbb {C}})\). To see this we note that multiplication by i of a smooth spin 1-weighted function corresponds to a concatenation of the one-covector field by a rotation of \(\frac{\pi }{2}\) (with respect to the oriented frame field \(\{\partial _\theta , \frac{1}{\sin \theta }\partial _\varphi \}\)) while for smooth spin 2-weighted functions it corresponds to a concatenation of the symmetric two covector field with a rotation of \(\frac{\pi }{4}\).
Let us define the distribution \(D \subset T\underline{\overline{{\mathcal {M}}}}\) which is annihilated by \(\{dV^+_{r_+}, dV^-_{r_+}, dV^+_{r_-}, dV^-_{r_-}\}\) (where defined). Its integral manifolds in the interior of \(\underline{\overline{{\mathcal {M}}}}\) are exactly the Boyer-Lindquist spheres of constant t and r. We note that m lies in the complexification of D. Moreover, we denote the dual bundle of D by \(D^*\).
Remark 2.43
-
1.
Given a subset \(A \subseteq \underline{\overline{{\mathcal {M}}}}\) with the property that the integral manifolds of D restricted to A are complete spheres, we define the spin weighted spaces
 analogously. For example we will choose \(A = \underline{{\mathcal {M}}}\) later.
analogously. For example we will choose \(A = \underline{{\mathcal {M}}}\) later. -
2.
We define an auxiliary round metric
 on the integral manifolds of D by the symmetric part of \(m \otimes {\overline{m}}\), cf. (2.27). The kernel of the map \(\iota _m: \Gamma ^\infty (S^2(T^*\underline{\overline{{\mathcal {M}}}})) \rightarrow C^\infty (\underline{\overline{{\mathcal {M}}}}\setminus \{\theta = 0,\pi \}, {\mathbb {C}})\) is the span of all those symmetric two-tensor fields that, when restricted to D, vanish or are proportional to
on the integral manifolds of D by the symmetric part of \(m \otimes {\overline{m}}\), cf. (2.27). The kernel of the map \(\iota _m: \Gamma ^\infty (S^2(T^*\underline{\overline{{\mathcal {M}}}})) \rightarrow C^\infty (\underline{\overline{{\mathcal {M}}}}\setminus \{\theta = 0,\pi \}, {\mathbb {C}})\) is the span of all those symmetric two-tensor fields that, when restricted to D, vanish or are proportional to  . Thus, the space
. Thus, the space  of smooth spin 2-weighted functions on \(\underline{\overline{{\mathcal {M}}}}\) is isomorphic to the space \(\Gamma ^\infty \big (S^2(D^* \rightarrow \underline{\overline{{\mathcal {M}}}})\big )\), the space of all smooth, symmetric, and trace-free (with respect to
of smooth spin 2-weighted functions on \(\underline{\overline{{\mathcal {M}}}}\) is isomorphic to the space \(\Gamma ^\infty \big (S^2(D^* \rightarrow \underline{\overline{{\mathcal {M}}}})\big )\), the space of all smooth, symmetric, and trace-free (with respect to  ) sections of \(D^* \otimes D^* \rightarrow \underline{\overline{{\mathcal {M}}}}\).
) sections of \(D^* \otimes D^* \rightarrow \underline{\overline{{\mathcal {M}}}}\). -
3.
Given the above, a convenient realisation of the space
 is as all those elements in \(\Gamma ^\infty (S^2(T^*\underline{{\mathcal {M}}}))\) that
is as all those elements in \(\Gamma ^\infty (S^2(T^*\underline{{\mathcal {M}}}))\) that-
vanish if \(\partial _{V^+_{r_+}}\) is inserted in one of the slots
-
vanish if \(\partial _{V^-_{r_+}}\) is inserted in one of the slots
-
are trace-free with respect to
 .
.
We will call such an element a symmetric and trace-free \({\mathbb {S}}^2\) 2-covariant tensor field. On this subset of \(\Gamma ^\infty (S^2(T^*\underline{{\mathcal {M}}}))\), \(\iota _m\) is an isomorphism.
-
As before we can characterise the spin weighted functions on \(\underline{\overline{{\mathcal {M}}}}\) among the elements of \(C^\infty (\underline{\overline{{\mathcal {M}}}}\setminus \{\theta = 0, \pi \},{\mathbb {C}})\). We do this in regions on which we have global coordinate charts. For example on \(\underline{{\mathcal {M}}}\) we introduce the first order differential operators \({\tilde{Z}}_{i,r_+}\), \(i = 1,2,3\), which are defined as in (2.17) but with respect to the \(\{V^+_{r_+}, V^-_{r_+}, \theta , \Phi _{r_+}\}\) coordinate system, i.e., we replace \(\varphi \) in (2.17) by \(\Phi _{r_+}\). We obtain
Proposition 2.44
\(f \in C^\infty (\underline{{\mathcal {M}}}\setminus \{\theta = 0,\pi \}),{\mathbb {C}})\) lies in  if, and only if,
if, and only if,
extends continuously to \(\underline{{\mathcal {M}}}\setminus \{\theta = \pi \}\) and
extends continuously to \(\underline{{\mathcal {M}}}\setminus \{\theta =0\})\) for all \(l_1, l_2, k_1, k_2, k_3 \in {\mathbb {N}}_0\).
Proof
This is the same as the proof of Proposition 2.18, noticing that we have \(\partial _\varphi = \partial _{\Phi _{r_+}}\), \({\mathcal {L}}_{\partial _{V^+_{r_+}}} m = 0\), \({\mathcal {L}}_{\partial _{V^-_{r_+}}} m = 0\), and also the last point in Remark 2.43. \(\square \)
Similarly we choose \(\{V^+_{r_-}, V^-_{r_-}, \theta , \Phi _{r_-}\}\) coordinates on \(\overline{{\mathcal {M}}}\) and define the operators \({\tilde{Z}}_{i,r_-}\), \(i=1,2,3\), by replacing \(\varphi \) in (2.17) by \(\Phi _{r_-}\). We obtain an analogous characterisation of elements in  . Taken together, this gives a characterisation of elements in
. Taken together, this gives a characterisation of elements in  among those of \(C^\infty (\underline{\overline{{\mathcal {M}}}}{\setminus } \{\theta = 0,\pi \}),{\mathbb {C}})\).
among those of \(C^\infty (\underline{\overline{{\mathcal {M}}}}{\setminus } \{\theta = 0,\pi \}),{\mathbb {C}})\).
We will also need to define the operators \({\tilde{Z}}_{i,+}\), \(i=1,2,3\), with respect to the \(\{v_+, \varphi _+, r, \theta \}\) coordinate system, i.e., we replace \(\varphi \) in (2.17) by \(\varphi _+\). Similarly we define the operators \({\tilde{Z}}_{i,-}\), \(i=1,2,3\), with respect to the \(\{v_-, \varphi _-, r, \theta \}\) coordinate system. We obtain analogous characterisations to Proposition 2.44 in the regions covered by each of these coordinate systems.
It now follows from (2.31) (which obviously holds for any of the sets of \({\tilde{Z}}\) defined), the second part of Remark 2.42, and Proposition 2.44 that the Teukolsky operator \({\mathcal {T}}_{[s]}\), defined in (2.39), is a smooth operator on  . Similalry, the Teukolsky operator \(\hat{{\mathcal {T}}}_{[s]}\), defined in (2.40), is a smooth operator on
. Similalry, the Teukolsky operator \(\hat{{\mathcal {T}}}_{[s]}\), defined in (2.40), is a smooth operator on  .
.
2.3.9 The Spin Weighted Carter Operator
Definition 2.45
We define the spin s-weighted Carter operator \({\mathcal {Q}}_{[s]}\) by

Note that it follows directly from (2.39) and (2.40) that the spin s-weighted Carter operator commutes with the Teukolsky operator, i.e. we have \([{\mathcal {T}}_{[s]}, {\mathcal {Q}}_{[s]}] = 0 = [\hat{{\mathcal {T}}}_{[s]}, {\mathcal {Q}}_{[s]}]\).
2.3.10 The Regularity of \({\dot{\alpha }}\) as Defined in Section 2.3.1 and 2.3.2
Our following global theorem will concern spin 2-weighted functions, satisfying the Teukolsky equation, that satisfy the following smoothness properties.
Assumption 2.46
-
 .
. -
 . Note that this implies, using (2.7), that
. Note that this implies, using (2.7), that  .
. -
\(\psi \) satisfies \({\mathcal {T}}_{[2]}\psi = 0\) in \({\mathcal {M}} \cup ({\mathcal {H}}^+_r {\setminus } {\mathbb {S}}^2_b)\). Note that this implies that \({\hat{\psi }}\) satisfies \({\hat{{\mathcal {T}}}}_{[2]} {\hat{\psi }} = 0\) in \({\mathcal {M}} \cup ({\mathcal {H}}^+_l {\setminus } {\mathbb {S}}^2_b)\).
We have dropped here the subscript 2 from \(\psi \) to shorten notation. No confusion can arise, since the remainder of the paper is only concerned with spin 2-weighted functions.
We investigate what the above regularity assumptions imply for \(\partial _r \psi \) and \(\partial _r^2 \psi \), where the partial derivative is with respect to the \((v_+, r,\theta , \varphi _+)\) coordinate system. By (A.1) and (2.7) we have \(\partial _r = \frac{1}{V^+_{r_+}} f_1(r) \partial _{V^-_{r_+}} + f_2(r) \partial _{\Phi _{r_+}}\), where \(f_1(r)\) and \(f_2(r)\) are functions which extend smoothly to \(r = r_+\). It now follows from Assumption 2.46 that \(\psi \) decays at least like \((V^+_{r_+})^2\) for \(V^+_{r_+} \rightarrow 0\), \(\partial _r\psi \) at least like \(V^+_{r_+}\), and \(\partial _r^2 \psi \) does in general not decay but is a regular smooth spin 2-weighted function on \(\underline{{\mathcal {M}}}\).
We now show that \({\dot{\alpha }}\), as defined in Sections 2.3.1 and 2.3.2, satisfies the above smoothness assumptions 2.46.Footnote 28
Proposition 2.47
The quantity \(\psi :={\dot{\alpha }}\) from Section 2.3.2 satisfies the Assumptions 2.46.
Proof
Recall that \(e_4\) is a smooth vector field on \(\underline{{\mathcal {M}}}\), vanishing at \({\mathcal {H}}^+_l\). Also recall that
where we have defined \(\beta \), a smooth and symmetric tensor field on \(\underline{{\mathcal {M}}}\). By (2.9) we have
By the second point in Remark 2.42 it suffices to show that  . By definition of the spin weighted spaces we have
. By definition of the spin weighted spaces we have  and thus it remains to establish that
and thus it remains to establish that  and
and  . Let us define the smooth one-form \(\gamma := \sin \theta \, d \theta \) on \(\underline{{\mathcal {M}}}\). Then \(\gamma \otimes \gamma \) is a symmetric two-covector field with \((\gamma \otimes \gamma )(m, m) = \frac{1}{2} \sin ^2 \theta \), which lies in
. Let us define the smooth one-form \(\gamma := \sin \theta \, d \theta \) on \(\underline{{\mathcal {M}}}\). Then \(\gamma \otimes \gamma \) is a symmetric two-covector field with \((\gamma \otimes \gamma )(m, m) = \frac{1}{2} \sin ^2 \theta \), which lies in  . Similarly, defining the symmetric two-covector field \(\gamma \otimes \beta (\cdot , \partial _t) + \beta (\cdot , \partial _t) \otimes \gamma \) shows that
. Similarly, defining the symmetric two-covector field \(\gamma \otimes \beta (\cdot , \partial _t) + \beta (\cdot , \partial _t) \otimes \gamma \) shows that  . This shows the first point. The second point follows analogously recalling from Section A that \(\frac{1}{V^+_{r_+}} e_4\) is a smooth vector field on \(\underline{{\mathcal {M}}}\). The last two points were established in the previous sections. \(\square \)
. This shows the first point. The second point follows analogously recalling from Section A that \(\frac{1}{V^+_{r_+}} e_4\) is a smooth vector field on \(\underline{{\mathcal {M}}}\). The last two points were established in the previous sections. \(\square \)
3 Assumptions on the Event Horizon and the Main Theorem
In addition to the smoothness assumptions in Assumption 2.46 we make the following assumptions on \(\psi \) along the event horizons:
Along the right event horizon \({\mathcal {H}}^+_r\): Assume that there exists a \(p \in {\mathbb {N}}\) such that \(\int _{{\mathcal {H}}^+_r \cap \{v_+ \geqslant 1\}} v_+^{2p} |\psi |^2 \, \textrm{vol}_{{\mathbb {S}}^2}\,dv_+ = + \infty \). Let \(p_0\in {\mathbb {N}}\) be the smallest integer such that this holds, i.e., we have
Assume that \(p_0 \geqslant 2\). Moreover, we assume that there is \(m_0 \in {\mathbb {Z}}\) and \( {\mathbb {N}}\ni l_0 \geqslant \max \{2, |m_0|\}\) such that
where \((\psi |_{{\mathcal {H}}^+_r})_{S(ml)}(v_+) =\int _{{\mathbb {S}}^2} \psi |_{{\mathcal {H}}^+_r} (v_+, \theta , \varphi _+) \overline{Y^{[+2]}_{ml}(\theta , \varphi _+;0)} \, \textrm{vol}_{{\mathbb {S}}^2}\) denotes the projection of \(\psi |_{{\mathcal {H}}^+_r}\) onto the spin 2-weighted spherical harmonic \(Y^{[+2]}_{ml}(\theta , \varphi _+;0) \), cf. Section 5.1. We also assume that
holds and that for some \(2<q_r <2p_0\), \(q_r \in {\mathbb {R}}\), we haveFootnote 29
with \(f \in \{\partial _{v_+}^a\partial _{\varphi _+}^b\partial _r^c\psi , \partial _{v_+} \partial _{v_+}^a\partial _{\varphi _+}^b\partial _r^c\psi , {\mathcal {Q}}_{[s]} \partial _{v_+}^a\partial _{\varphi _+}^b\partial _r^c \psi , \}\), \(0 \leqslant a + b \leqslant 2\), \(c = 0,1,2\).
Along the left event horizon \({\mathcal {H}}^+_l\): Assume that
i.e., there exists a \(v_0 \in {\mathbb {R}}\) such that \({\hat{\psi }}\) vanishes in \({\mathcal {H}}^+_l \cap \{v_- \geqslant v_0\}\). However, all our results remain true if we replace (3.5) by the much weaker
with \(f \in \{\partial _{v_-}^a \partial _{\varphi _-}^b \partial _r^c {\hat{\psi }}, \partial _{v_-} \partial _{v_-}^a \partial _{\varphi _-}^b \partial _r^c {\hat{\psi }}, {\mathcal {Q}}_{[s]} \partial _{v_-}^a \partial _{\varphi _-}^b \partial _r^c {\hat{\psi }}\}\), \(0 \leqslant a+b+c \leqslant 2\), \(a,b,c \in {\mathbb {N}}_0\) and \({\mathbb {R}}\ni q_l \geqslant 2p_0\).Footnote 30 To see that (3.5) implies (3.6) for \(f = \partial _r {\hat{\psi }}\), we notice that the Teukolsky equation (2.40) reduces in the region \({\mathcal {H}}^+_l \cap \{v_- \geqslant v_0\}\), where \({\hat{\psi }}\) vanishes, to \(\big (2(r^2 + a^2) \partial _{v_-} - 2a \partial _{\varphi _-} \big ) \partial _r {\hat{\psi }}+ 2(r-M)(1+s) \partial _r {\hat{\psi }}=0\). This shows that \(\partial _r {\hat{\psi }}\) decays exponentially along \({\mathcal {H}}^+_l\) – a manifestation of the red-shift effect. Further commutations with \(\partial _r\) even improve the red-shift.
For the statements of the intermediate results in the main body of the paper we will often use the phrase ‘under the assumptions of Section 3’. Let us make explicit that by this we mean the Assumption 2.46 together with (3.1), (3.2), (3.3), (3.4), and (3.6). However, usually not all of these assumptions are required for the specific partial result proven.
With the exception of Section 6.2.4, where we briefly consider the case \(s=-2\), this paper is only concerned with the case \(s= +2\). However, we will not replace the s in the Teukolsky equation by 2 so that the reader can follow the importance of the value of s for the validity of our estimates. With the exception of Section 6.2.4 the convention in this paper is that \(s=+2\).
Theorem 3.7
Let \(\psi \) satisfy the Assumptions 2.46, (3.1), (3.2), (3.3), (3.4), and (3.6). Let \(v_2 \in {\mathbb {R}}\) and consider the spacelike hypersurface \(\Sigma := \{ f^- = v_2\}\) which is transversal to \(\mathcal{C}\mathcal{H}^+_r\). We then have
The above theorem is global in nature, it concerns solutions of the Teukolsky equation defined in all of the interior of asymptotically flat two-ended Kerr black holes. As stated, it is not a useful ingredient for treating realistic one-ended rotating black holes. In the following we give a version of Theorem 3.7 localised to a neighbourhood of timelike infinity.
Theorem 3.9
Consider a patch of \(\underline{{\mathcal {M}}}\) given by \(\underline{{\mathcal {M}}}\cap \{f_- \leqslant v_1\} \cap \{f_+ \geqslant v_0\}\) for some \(v_1, v_2 \in {\mathbb {R}}\), see also Figure 9 on page 88. Let  satisfy the Teukolsky equation \({\mathcal {T}}_{[2]}\psi = 0\) andFootnote 31 (3.1), (3.2), (3.3), and (3.4). Let \(v_2 \leqslant v_1\) and consider the spacelike hypersurface \(\Sigma := \{ f^- = v_2\}\) which is transversal to \(\mathcal{C}\mathcal{H}^+_r\). We then have
satisfy the Teukolsky equation \({\mathcal {T}}_{[2]}\psi = 0\) andFootnote 31 (3.1), (3.2), (3.3), and (3.4). Let \(v_2 \leqslant v_1\) and consider the spacelike hypersurface \(\Sigma := \{ f^- = v_2\}\) which is transversal to \(\mathcal{C}\mathcal{H}^+_r\). We then have
Remark 3.11
-
1.
The proof of Theorems 3.7 and 3.9 contains a crucial Fourier-theoretic component. To obtain the instability at the Cauchy horizon we use that there is a smallest \(p_0 \in {\mathbb {N}}\) and \(m_0 \in {\mathbb {Z}}\) and \({\mathbb {N}}\ni l_0 \geqslant \max \{2, |m_0|\}\) such that
 (3.12)
(3.12)Here
 results from \(\psi |_{{\mathcal {H}}^+_r}\) by taking the Fourier transform in \(v_+\) and subsequent projection on the \(m_0,l_0\) spin 2-weighted spheroidal harmonic, cf. Section 5.2. The physical space assumptions (3.1), (3.2), (3.3) are only used to guarantee (3.12), see Proposition 7.5. In particular the above Theorems remain true if (3.1), (3.2), (3.3) are replaced by (3.12). Note that the assumption (3.4) implies that \(2p_0 \) must be greater than \(q_r\).
results from \(\psi |_{{\mathcal {H}}^+_r}\) by taking the Fourier transform in \(v_+\) and subsequent projection on the \(m_0,l_0\) spin 2-weighted spheroidal harmonic, cf. Section 5.2. The physical space assumptions (3.1), (3.2), (3.3) are only used to guarantee (3.12), see Proposition 7.5. In particular the above Theorems remain true if (3.1), (3.2), (3.3) are replaced by (3.12). Note that the assumption (3.4) implies that \(2p_0 \) must be greater than \(q_r\). -
2.
Having dropped the subscript s from \(\psi \), we introduce the notation
$$\begin{aligned} \psi _m(v_+,r,\theta , \varphi _+):= \int _{{\mathbb {S}}^1} \psi (v_+, r, \theta , \varphi _+') \cdot e^{-im\varphi _+'} \, d \varphi _+' \cdot e^{im \varphi _+} \end{aligned}$$for the projection on the m-th azimuthal mode, \(m \in {\mathbb {Z}}\), and also \(\psi _{\ne 0}:= \psi - \psi _0\). Note that if \(\psi \) solves the Teukolsky equation then so does \(\psi _m\). We can thus apply the above theorems also to the projections \(\psi _m\) individually to obtain statements which, through the ensuing m-dependent parameter \(p_0\), depend on m.
-
3.
It was shown recently in [51] (see also [15, 50] and also [3]) that for slowly rotatingFootnote 32 sub-extremal Kerr and for compactly supported initial data for the Teukolsky equation, posed on a spacelike hypersurface connecting the event horizon with spacelike infinity, one has
$$\begin{aligned} \big | \partial _{v_+}^j \psi _{m \ne 0}|_{{\mathcal {H}}^+_r} - \sum _{m = \pm 1, \pm 2}Q_{m,2} Y^{[+2]}_{m2}(\theta , \varphi _+; 0) v_+^{-7-j} \big | \lesssim v_+^{-7-j - \varepsilon } , \end{aligned}$$where \(\varepsilon >0\) and \(Q_{m,2} \in {\mathbb {C}}\) is generically non-vanishing, and
$$\begin{aligned} \big | \partial _{v_+}^j \psi _0|_{{\mathcal {H}}^+_r} - Q_{0,2} Y^{[+2]}_{02}(\theta , \varphi _+; 0) v_+^{-8-j} \big | \lesssim v_+^{-8-j - \varepsilon } , \end{aligned}$$where again \(Q_{0,2} \in {\mathbb {C}}\) is generically non-vanishing. For \(v_+\) large enough we thus obtain for \(m = \pm 1, \pm 2\) generically \(|(\psi |_{{\mathcal {H}}^+_r})_{S(m2)}| \geqslant c v_+^{-7}\) with \(c>0\) and for \(m = 0\) generically \(|(\psi |_{{\mathcal {H}}^+_r})_{S(02)}| \geqslant c v_+^{-8}\) with \(c>0\). Hence for \(m_0 = \pm 1, \pm 2\) the assumptions made in this section are generically satisfied with \(l_0 = 2 \) and \(p_0 = 7\) and for \(m_0 = 0\) with \(l_0 = 2\) and \(p_0 = 8\). If we do not decompose into azimuthal modes the assumptions are generically satisfied with \(p_0 = 7\), \(l_0=2\) and \(m_0 \in \{-2,-1,1,2\}\). The parameter \(q_r\) can be chosen to be anything strictly less than 13.
If we do not assume the initial data to be compactly supported, but still to be smooth with respect to the conformal compactification at future null infinity, we expect the generic decay rates to be slower by a power of \(v_{+}^{-1}\), see also [2]. There is evidence that the assumption of smoothness at future null infinity is not satisfied in many physically interesting situations (see [9, 38]) and that this impacts the late time tails [39]. There is also evidence that tails arising on dynamical black hole exteriors differ from those on stationary exteriors [44].
-
4.
We rewrite (3.10) in terms of quantities that are regular at \(\mathcal{C}\mathcal{H}^+_r\): we first recall that \({\hat{\psi }} = \frac{1}{\Delta ^2} \psi \) is the linearisation of the curvature component with respect to the algebraically special frame that is regular at \(\mathcal{C}\mathcal{H}^+_r\) and that we have \(\Delta ^2 \simeq e^{2 \kappa _-(v_+ + v_-)} \simeq e^{2 \kappa _- v_+}\) along \(\Sigma \) for \(v_+ \rightarrow \infty \), where we have used (2.8). Moreover, we have \(V^{+}_{r_-} = - e^{\kappa _- v_+}\) and thus \(\log (-V^+_{r_-}) = \kappa _- v_+\) and \(dv_+ = \frac{1}{\kappa _- V^+_{r_-}}dV^+_{r_-}\). We thus find \(v_+^{2p_0} |\psi |^2 \simeq \big [\log (-V^+_{r_-})\big ]^{2p_0} (-V^+_{r_-})^4 |{\hat{\psi }}|^2 \) along \(\Sigma \) for \(v_+ \rightarrow \infty \) and hence (3.10) is equivalent to
$$\begin{aligned} \int _{\Sigma \cap \{v_+ \geqslant 1\}} \big [\log (-V^+_{r_-})\big ]^{2p_0} (-V^+_{r_-})^3 |{\hat{\psi }}|^2 \, \textrm{vol}_{{\mathbb {S}}^2}dV^+_{r_-} = \infty . \end{aligned}$$(3.13) -
5.
As a side result we also prove
$$\begin{aligned} \int \limits _{\Sigma \cap \{v_+ \geqslant 1\}} v_+^{q_r} |\psi |^2 \, \textrm{vol}_{{\mathbb {S}}^2}dv_+ < \infty , \end{aligned}$$see (4.76). Hence, the integral in (3.13) with \(2p_0\) replaced by \(q_r\) is finite. Recall that we said that in particular for compactly supported initial data \(q_r\) can be chosen to be anything strictly less that \(2p_0 - 1\).
4 Energy Estimates for the Teukolsky Equation: Upper Bounds
In this section we prove stability estimates which are being used to justify Teukolsky’s separation of variables, to pass to the limits \(r \rightarrow r_\pm \), and to propagate the singularity backwards along \(\mathcal{C}\mathcal{H}^+_r\).
4.1 Estimates Near the Event Horizons
We begin with the semi-global estimates near the left event horizon, since they are the simplest and thus the structure is easier to understand here.
Proposition 4.1
Under the assumptions of Section 3 there exists an \(r_\textrm{red}\in (r_-, r_+)\) and a \(C>0\) such that
holds for \(f \in \{\partial _{v_-}^a \partial _{\varphi _-}^b \partial _r^c {\hat{\psi }}, \partial _{v_-} \partial _{v_-}^a \partial _{\varphi _-}^b \partial _r^c {\hat{\psi }}, {\mathcal {Q}}_{[s]} \partial _{v_-}^a \partial _{\varphi _-}^b \partial _r^c {\hat{\psi }}\}\), \(0 \leqslant a+b+c \leqslant 2\), \(a,b,c \in {\mathbb {N}}_0\).Footnote 33
Here, and in the following propositions and corollaries throughout Section 4, the constant C depends in particular on the initial data of the Teukolsky field on \({\mathcal {H}}^+_l\) and \({\mathcal {H}}^+_r\), on \(q_l\) and \(q_r\), on the black hole parameters, and, in general, on the region in which the estimate holds. The exact dependency and the optimal value of the constant is, however, of no interest to this paper. We only need the qualitative statement that the quantity in question is finite.
Proof
\(\underline{{\textbf {Step 1: The multiplier.}}}\) In the following we restrict to \(v_- \geqslant 1\). We start from the following multiplier identity, where \(\lambda , \eta , \mu >0\) are constants to be chosen:
Here, for \(\lambda >0\) suitably, the vector field \( -(1 + \lambda \Delta )\partial _r + (1+ \lambda \Delta )\partial _{v_-}\) is a choice of the redshift vector field of Dafermos and Rodnianski, [18, 19], and the underbraced term is added in order to control the zeroth order terms, as will become clear in the following. After integration over the spheres, and using the form (2.40) of the Teukolsky equation, the right hand side of (4.3) is the sum of
-
1.
the sum of all the terms on the right hand sides of B.1 and B.2
-
2.
the real part of the terms

-
3.
the underbraced term in (4.3).
As will become clear later, we can derive a boundedness statement if the bulk terms (those terms which are not total derivatives) are negative. Recall that \(\partial _r \Delta (r_+) = 2(r_+ -M) >0\).
\(\underline{{\textbf {Step 2: Estimating all bulk terms that are quadratic in derivatives.}}}\)
The two dashed terms, which are the most important terms, combine to give a negative contribution for r close enough (depending on \(\lambda \)) to \(r_+\). Indeed, for \(s=0\) this is the familiar red-shift for the wave equation and we see that for \(s=+2\) we even get an improved red-shift for the energy.Footnote 34
We now investigate all the  with a wavy underline, which are all those that are leading order in \(\lambda \). The first of those terms in B.1 is negative. The second of those terms in B.1, which indeed appears again from the fourth equation in B.2, can be controlled as follows:
with a wavy underline, which are all those that are leading order in \(\lambda \). The first of those terms in B.1 is negative. The second of those terms in B.1, which indeed appears again from the fourth equation in B.2, can be controlled as follows:
Note that \(|a|< M < r_+\) so that there exists \(0< \alpha <1\) close to 1 such that \(r_+^2 + a^2 > 2 \alpha ^{-1} a^2\). Hence, (4.4) can be estimated uniformly in \(\lambda \) by the last wavily underlined term in B.1 and the one in B.2. In summary, all the wavily underlined terms and the dashed terms are estimated from above by
where \(f(r_+, \lambda )>0\) is independent of \(\lambda \). All the other bulk terms which are quadratic in derivatives of \({\hat{\psi }}\) can now be controlled in absolute value by \(-\frac{1}{2}\times \) (4.5) by choosing first \(\lambda >0\) big enough and then restricting to \(r \in [r_\textrm{red}, r_+]\), \(v_- \geqslant v_0\) with \(r_\textrm{red} < r_+\) close enough to \(r_+\) and \(v_0 >1\) large enough.Footnote 35
\(\underline{{\textbf {Step 3: Estimating boundary terms.}}}\)
We gather all the total derivatives appearing on the right hand side of (4.3). They are \(\partial _{v_-} \big (A(v_-,r,{\hat{\psi }}, \partial {\hat{\psi }})\big )\) and \(\partial _r\big ( B(v_-,r,{\hat{\psi }}, \partial {\hat{\psi }})\big )\) with
and
We begin by establishing coercivity of B for r close enough to \(r_+\). The second term in (4.6) can be absorbed by the fifth and sixth term as follows
where \(0< \alpha <1\) and we argue as in (4.4). The seventh term in (4.6) is estimated by the third and sixth term by
for \(0< \alpha < 1\), where we note that the additional \(|\Delta |\) allows us to absorb the \(|\partial _{v_-} {\hat{\psi }}|^2\) term. Finally we choose \(\mu >0\) as a function of \(\eta >0\) (to be determined later) such that \(\mu (\eta ) e^{\eta r_+} = 2(s+s^2)\). It thus follows that for \(r_\textrm{red}<r_+\) close enough to \(r_+\) we have
for \(r \in [r_\textrm{red}, r_+]\).
Next we establish the coercivity of \(B(v_-,r, {\hat{\psi }}, \partial {\hat{\psi }}) - A(v_-,r, {\hat{\psi }}, \partial {\hat{\psi }})\). We first compute
In particular completing the square for the underlined term gives
The first term is estimated in the same way as before now by the third and sixth term. Note that the fourth term vanishes at \(r= r_+\). Thus, with our choice of \(\eta \) from above we obtain
for \(r \in [r_\textrm{red}, r_+]\) with \(r_\textrm{red}\) close enough to \(r_+\).
\(\underline{{\textbf {Step 4: Estimating the remaining bulk terms:}}}\)
The last two terms in (4.3) are estimated by
We can now choose \(\eta >0\) sufficiently large such that the last term can be controlled by \(-\frac{1}{4}\times \) (4.5) and such that the first term controls the zeroth order terms arising in the bulk from (B.1) and (B.2) (those have an overall ‘bad’ positive sign and need to be controlled).
\(\underline{{\textbf {Step 5: Putting it all together:}}}\)
We thus obtain after integration over the spheres
for \(v_- \geqslant v_0\) and \(r_\textrm{red} \leqslant r \leqslant r_+\). Let \(r' \in [r_\textrm{red}, r_+)\). We integrate over the region \(\{2v_0 \leqslant f^- \leqslant v_1 \} \cap \{r' \leqslant r \leqslant r_+\}\) with respect to \(dv_-\wedge dr \wedge \textrm{vol}_{{\mathbb {S}}^2}= \frac{1}{\rho ^2} \textrm{vol}\) and use that on a level set of \(f^-\) we have \(dr = dv_-\) to obtain

where \(c>0\). Using now the lower bounds (4.7) and (4.8), the trivial upper bounds on A and B, the assumption (3.6) on \({\hat{\psi }}\) as well as the regularity Assumption 2.46 for the boundary term on \(\{f^- = 2v_0\}\), and letting \(v_1 \rightarrow \infty \) we obtain

for some \(C>0\), where, in a second step we have also taken the limit \(r' \rightarrow r_\textrm{red}\) to obtain the bulk term. Together with the regularity Assumption 2.46 used for the remaining compact spacetime region this shows (4.2) with \(f = {\hat{\psi }}\).
\(\underline{{\textbf {Step 6: Estimating higher derivatives:}}}\)
Recall that \(\partial _{v_-}\), \(\partial _{\varphi _-}\), and \({\mathcal {Q}}_{[s]}\) commute with \(\hat{{\mathcal {T}}}_{[s]}\). By our assumptions on the left event horizon (3.6) we can thus repeat the above argument now with \({\hat{\psi }}\) replaced by \({\mathcal {Q}}_{[s]}^d \partial _{v_-}^a \partial _{\varphi _-}^b {\hat{\psi }}\) to obtain (4.2) for \(f = {\mathcal {Q}}_{[s]}^d \partial _{v_-}^a \partial _{\varphi _-}^b {\hat{\psi }}\), for \(0 \leqslant a + b \leqslant 2\), \(d = 0,1\).
We now commute the Teukolsky equation with \(\partial _r\):

Of course, the principal part is unchanged. Also note that the dashed red-shift term is even improved. Thus, the same vector field multiplier (with \({\hat{\psi }}\) replaced by \(\partial _r {\hat{\psi }}\)) can be used to control all bulk terms quadratic in derivatives of \(\partial _r {\hat{\psi }}\). Also the same modification, i.e., the underbraced term in (4.3) with \({\hat{\psi }}\) replaced by \(\partial _r {\hat{\psi }}\), can be used to generate an arbitrarily large bulk term quadratic in \(\partial _r {\hat{\psi }}\) of the ‘good’ negative sign. The boundary terms are exactly of the same form with \({\hat{\psi }}\) replaced by \(\partial _r {\hat{\psi }}\). So the only qualitatively new term we need to estimate is the underlined term, which is neither \(\partial _r {\hat{\psi }}\) nor derivatives of it. This term can be estimated either by a modification similarly to the one we used above, now with \({\hat{\psi }}\) replaced by \(\partial _{v_-} {\hat{\psi }}\), or, more straightforwardly, we can use directly the bulk term in (4.2). Thus, we obtain, after possibly choosing \(r_\textrm{red}\) closer to \(r_+\)

for some \(C>0\), which is (4.2) with \(f = \partial _r {\hat{\psi }}\). Again, we can in addition commute with the Killing vector fields \(\partial _{v_-}\), \(\partial _{\varphi _-}\), as well as with \({\mathcal {Q}}_{[s]}\).
Differentiating (4.10) once more in r we obtain

The dashed red-shift term is even further improved and no qualitatively new terms compared to (4.10) (with \({\hat{\psi }}\) replaced by \(\partial _r {\hat{\psi }}\)) have appeared. This completes the proof. \(\square \)
We now continue with the red shift estimate near the right event horizon.
Proposition 4.11
Under the assumptions of Section 3 there exists an \(r_\textrm{red}\in (r_-, r_+)\) and a \(C>0\) such that
holds for \(f \in \{\partial _{v_+}^a\partial _{\varphi _+}^b\partial _r^c\psi , \partial _{v_+} \partial _{v_+}^a\partial _{\varphi _+}^b\partial _r^c\psi , {\mathcal {Q}}_{[s]} \partial _{v_+}^a\partial _{\varphi _+}^b\partial _r^c \psi , \}\), with \(0 \leqslant a + b +c \leqslant 2\).
The symmetry between left and right event horizon for the wave equation is broken for the Teukolsky equation because of a choice of frame field. Indeed, near the right event horizon \({\mathcal {H}}^+_r\) we do have a blue-shift for the energy of the Teukolsky field \(\psi \). This is the reason why in the following proof we need to commute twice with \(\partial _r\) in order to get a red-shift near \({\mathcal {H}}^+_r\).
Proof
Many elements of the proof are the same as those of the proof of Proposition 4.1. For this reason we will be more concise here and highlight the essential differences. We begin by observing that the crucial seventh term of (2.39) has a ‘bad’ sign for \(s=2\). Multiplying by \(-v_+^{q_r} (1 + \lambda \Delta ) \overline{\partial _r \psi }\) as we did before would give a bulk term in \(|\partial _r \psi |^2\) of positive sign – but we recall that for stability we needed the good negative sign. We differentiate (2.39) in r to obtain

Differentiating once more we obtain

\(\underline{{\textbf {Step 1: The multiplier:}}}\) We restrict in the following to \(v_+ \geqslant 1\). We consider the following multiplier identity, where \(\lambda , \eta , \mu >0\) are constants to be chosen:
After integration over the spheres, the right hand side of (4.14) is the sum of
-
1.
the sum of all the terms on the right hand sides of C.1 and C.2 with \(\chi (v_+) = v_+^{q_r}\) and \(\psi \) replaced by \(\partial _r^2 \psi \)
-
2.
the real part of the terms

-
3.
the underbraced terms in (4.14).
The second underbraced term in (4.14) has been added to control the double underlined term above. As before, we can derive a boundedness statement if the bulk terms are negative. We proceed as before:
\(\underline{{\textbf {Step 2: Estimating all bulk terms that are quadratic in derivatives of }}\partial _r^2 \psi .}\)
As before the two dashed terms combine to give a negative definite contribution in \(|\partial _r^3 \psi |^2\) for r close enough to \(r_+\). Next, we look at the wavily underlined terms which are all those that are leading order in \(\lambda \). Again, the first of those terms in C.1 has a good negative sign, the second can be controlled by the third one in C.1 and by the one in C.2 (as in (4.4)) for r close enough to \(r_+\) so that the wavily underlined terms and the dashed terms combined can be estimated from above by
where \(f(r_+, \lambda )>0\) is independent of \(\lambda \). Choosing now \(\lambda >0\) and \(v_0\geqslant 1\) large enough and \(r_\textrm{red}< r_+\) close enough to \(r_+\), all other bulk terms that are quadratic in derivatives of \(\partial _r^2 \psi \) can be controlled in absolute value by \(-\frac{1}{2} \times \)(4.15) in the region \(\{ r_\textrm{red}\leqslant r \leqslant r_+\} \cap \{v_+ \geqslant v_0\}\).
\(\underline{{\textbf {Step 3: Estimating boundary terms.}}}\)
We gather all the total derivatives \(\partial _{v_+} \big (A(v_+,r,\partial _r^2\psi , \partial \partial _r^2 \psi )\big )\) and \(\partial _r\big (B(v_+,r,\partial _{v_+}\partial _r \psi , \partial _r^2 \psi , \partial \partial _r^2 \psi )\big )\) appearing on the right hand side of (4.14), where we find
and
The coercivity of B and \(B - A\) for r close enough to \(r_+\) is established in the same way as in the proof of Proposition 4.1, Step 3, by choosing \(\mu (\eta )\) such that \(\mu (\eta ) e^{\eta r_+} = 2(s + s^2)\) to obtain
and
for \(r \in [r_\textrm{red}, r_+]\) with \(r_\textrm{red}\) close enough to \(r_+\).
\(\underline{{\textbf {Step 4: Estimating the remaining bulk terms.}}}\)
The last two terms of each underbraced term in (4.14) are estimated as in (4.9) of Step 4 of the proof of Proposition 4.1, where we again choose \(\eta >0\) so large that the resulting terms quadratic in derivatives of \(\partial _r^2 \psi \) are absorbed by \(\frac{1}{4}\times \) (4.15) and such that the terms \(-\frac{1}{2} v_+^{q_r} \eta \mu e^{\eta r} (|\partial _r^2 \psi |^2 + |\partial _{v_+} \partial _r \psi |^2)\) control all the remaining bulk terms.
\(\underline{{\textbf {Step 5: Putting it all together.}}}\)
We obtain from (4.14) after integration over the spheres
for \(v_+ \geqslant v_0\) and \(r_\textrm{red}\leqslant r \leqslant r_+\). Let now \(r' \in [r_\textrm{red}, r_+)\). We integrate over the region \(\{2v_0 \leqslant f^+ \leqslant v_1\} \cap \{r' \leqslant r \leqslant r_+\}\) with respect to \(dv_+ \wedge dr \wedge \textrm{vol}_{{\mathbb {S}}^2}= \frac{1}{\rho ^2} \textrm{vol}\) and use that on a level set of \(f^+\) we have \(dr = dv_+\) to obtain

where \(c>0\). Using the lower bounds (4.16) and (4.17), the trivial upper bounds on A and B, the Assumptions 2.46 and (3.4) on \(\psi \) to control the boundary terms on the right hand side, we obtain from this
for some \(C>0\). Together with Assumption 2.46 this in particular gives (4.12) with \(f = \partial _r^2 \psi \).
\(\underline{{\textbf {Step 6: Estimating higher, lower, and other derivatives.}}}\)
We can again just commute (4.13) with \(\partial _{v_+}\), \(\partial _{\varphi _+}\), and \({\mathcal {Q}}_{[s]}\) to obtain (4.12) also for \(f \in \{ \partial _{v_+}^a \partial _{\varphi _+}^b \partial _r^2\psi , \) \( \partial _{v_+} \partial _{v_+}^a \partial _{\varphi _+}^b\partial _r^2 \psi , {\mathcal {Q}}_{[s]} \partial _{v_+}^a \partial _{\varphi _+}^b \partial _r^2 \psi \}\) for \(0 \leqslant a+b \leqslant 2\).Footnote 36 The lower order terms are now estimated by integrating in r using the fundamental theorem of calculus together with Minkowski’s inequalityFootnote 37 and using the assumptions (3.4) on the right event horizon to obtain
for some \(C>0\) and \(f \in \{ \partial _{v_+}^a \partial _{\varphi _+}^b \partial _r\psi , \) \( \partial _{v_+} \partial _{v_+}^a \partial _{\varphi _+}^b\partial _r \psi , {\mathcal {Q}}_{[s]} \partial _{v_+}^a \partial _{\varphi _+}^b \partial _r \psi \}\) for \(0 \leqslant a+b \leqslant 2\). Integrating once more in this way concludes the proof of Proposition 4.11. \(\square \)
The following remark about the altered red-shift effect for the Teukolsky equation and Gaussian beams is not needed for the result of the paper but the reader might still find it instructive.
Remark 4.20
The red-shift effect along the event horizon for the scalar wave equation is by now a classic effect which has been used in various guises. To understand how it changes for the Teukolsky equation it is helpful to differentiate between the following three manifestations of the red-shift effect (one could easily consider more). We consider a family of observers with timelike velocity vector fields N which are Lie-transported along the Hawking Killing vector field \(T_{{\mathcal {H}}^+} = \partial _{v_+} + \frac{a}{r_+^2 + a^2} \partial _{\varphi _+}\) along the event horizon.
-
1.
The frequency, as measured by the family of observers, of a (Gaussian) beam propagating along the event horizon is shifted exponentially to the red. This could be seen as the original red-shift effect.
-
2.
The energy of a (Gaussian) beam propagating along the event horizon decays exponentially, see [59, 60]. Note that this is a priori independent of the change of colour of the light, but it is the most relevant manifestation of the so-called red-shift effect on energy estimates.
-
3.
Consider compactly supported initial data along the event horizon. Then the transversal derivative decays exponentially along the event horizon, see (2.39).
For the Teukolsky equation, as we will see, it no longer makes sense to refer to those three effects collectively as the ‘red-shift effect’. Dividing (2.39) by \(\rho ^2\) we obtain that the Teukolsky equation in \((v_+,r, \theta , \varphi _+)\) coordinates is of the form \(\Box _g \psi + X\psi + f \psi =0\) with
Note that in the construction of Gaussian beams for wave equations with lower order terms, the lower order terms only impinge on the amplitude, but not on the phase function, see Appendix 3.D of [59]. Thus the frequency/colour is still shifted to the red for all values of s.
We now consider the behaviour of the energy of Gaussian beams for which we refer the reader to Appendix 3.D of [59]. It follows from \(\nabla _{T_{{\mathcal {H}}^+}}T_{{\mathcal {H}}^+} = \kappa _+ T_{{\mathcal {H}}^+}\) that \(e^{-\kappa _+ v_+} T_{{\mathcal {H}}^+}\) is a null geodesic velocity vector field along the event horizon. The N-energy of a Gaussian beam for the wave equation localised along one of the integral curves thus behaves like \(e^{-\kappa _+v_+}\). Let us now choose either the integral curve at \(\theta = 0\) or \(\theta = \pi \) so that \(g(X, e^{-\kappa _+ v_+} T_{{\mathcal {H}}^+_+}) = - e^{-\kappa _+ v_+} 2\,s \kappa _+\). With the terminology from [59] we hence obtain the modulating factor \(|m_X(v_+)|^2 = e^{2s \kappa _+ v_+}\) of the amplitude of the Gaussian beam for the Teukolsky equation compared to that for the wave equation. Hence, the N-energy of such a Gaussian beam for the Teukolsky equation behaves like \(e^{(2s-1)\kappa _+ v_+}\).
In Appendix 3.E of [59] it was obtained that an integrated local energy decay statement for the Teukolsky equation cannot hold in the exterior of a Kerr black hole without the ‘loss of a derivative’ by considering Gaussian beams localised along trapped null geodesics away from the horizon. By considering a Gaussian beam along the event horizon as above it follows that not even a uniform energy boundedness statement for the Teukolsky equation for \(s=+1,+2\) can hold without the ‘loss of a derivative’.
Finally, for compactly supported initial data along the right event horizon it directly follows from (2.39) that for \(s=+1\) the transversal derivative remains constant for large \(v_+\) while for \(s=+2\) it grows in general exponentially (i.e., if it does not vanish). This shows very nicely how these three different effects decouple for the Teukolsky equation.
4.1.1 Corollaries
Let \(\chi : {\mathbb {R}}\rightarrow (0, \infty )\) be a fixed positive smooth function with \(\chi (v_+) = v_+^{q_r}\) for \(v_+ \geqslant 1\) and \(\chi (v_+) = |v_+|^{q_l}\) for \(v_+ \leqslant -1\). The next corollary will be our starting point for the estimates in the next section which are needed for the separation of the Teukolsky field. It combines the results of Proposition 4.1 and 4.11, but we can afford to discard uniformity up to the event horizons.
Corollary 4.21
Under the assumptions of Section 3 there exists an \(r_\textrm{red}\in (r_-, r_+)\) such that for any \(r_1 \in (r_\textrm{red}, r_+)\) there exists a \(C>0\) such that
holds for \(f \in \{ \partial _{v_+}^a \partial _{\varphi _+}^b(\partial _r|_+)^c \psi , \partial _{v_+}\partial _{v_+}^a \partial _{\varphi _+}^b(\partial _r|_+)^c \psi , {\mathcal {Q}}_{[s]} \partial _{v_+}^a \partial _{\varphi _+}^b(\partial _r|_+)^c \psi \}\), \(0 \leqslant a + b + c \leqslant 2\).
Here we have employed the notation \(\partial _r|_+\) to emphasise that this is a partial derivative in r with respect to the \((v_+, r, \theta , \varphi _+)\)-coordinate system.
Proof
It follows from (2.3) and (2.4) that we have \(\partial _r|_+ = 2 \frac{r^2 + a^2}{\Delta } \partial _{v_-} - 2 \frac{a}{\Delta } \partial _{\varphi _-} + \partial _r|_-\). Recalling moreover that \(\psi = \Delta ^2 {\hat{\psi }}\), we obtain
and
and \((\partial _r|_+)^3 \psi \) is a linear combination of \(\partial _{v_-}^a \partial _{\varphi _-}^b (\partial _r|_-)^c {\hat{\psi }}\) with \(0 \leqslant a + b + c \leqslant 3\), \(a,b,c, \in {\mathbb {N}}_0\). Moreover, using \(\varphi _+ = \varphi _- + 2{\overline{r}}\) we directly compute
We also observe \(\partial _{v_+} = - \partial _{v_-}\). Moreover, it follows from \(v_+ = - v_- + 2r^*\) that for \(r' \in [r_\textrm{red}, r_+)\) we have \(|v_+| \leqslant C(r') |v_-|\) for \(v_+ \leqslant -C(r')\) with the constant \(C(r')\) blowing up for \(r' \rightarrow r_+\). Now (4.22) follows directly from the Propositions 4.1 and 4.11 and the regularity Assumption 2.46. \(\square \)
Remark 4.26
The constant on the right hand side of (4.22) will in general blow up for \(r_1 \rightarrow r_+\), because of the conversion of the \(v_-\)-weights from Proposition 4.1 into \(v_+\)-weights. However, for \(f = \psi , \partial _r \psi \), we do have exponential decay in \(v_+\) for \(v_+ \rightarrow -\infty \) approaching \({\mathcal {H}}^+_l\) by the regularity Assumption 2.46, which compensates for the blow up of the constant in the conversion and (4.22) can actually be shown to hold uniformly up to \(r_+\). Since \(f = (\partial _r|_+)^2 \psi \) is in general regular and non-vanishing near the bottom bifurcation sphere \({\mathbb {S}}^2_b\) we do no longer have decay for \(v_+ \rightarrow - \infty \) approaching \({\mathcal {H}}^+_l\) and so the constant blows up for \(r_1 \rightarrow r_+\).
The next corollary is needed in Section 7 for passing to the limit \(r \rightarrow r_+\) in the separated picture, in particular for Proposition 7.4 and Proposition 7.17.
Corollary 4.27
Under the assumptions in Section 3 we have for \(r_+ > r \rightarrow r_+\)
and
for any \(v_0 \in {\mathbb {R}}\).
Proof
We begin with proving (4.28). The fundamental theorem of calculus gives \(|\psi (v_+, r, \theta , \varphi _+) - \psi (v_+, r_+, \theta , \varphi _+)| \leqslant \int _{[r,r_+]} |\partial _r \psi (v_+, r', \theta , \varphi _+) |\, dr'\). Cauchy Schwarz yields
which thus gives
It follows from (4.23) together with (4.2), from the bulk term in (4.12), as well as from the regularity Assumption 2.46 that the spacetime integral is uniformly bounded. This shows (4.28).
To prove (4.29) we compute in an analogous manner as before
Differentiating (4.24) once in \((\partial _r|_-)\) we obtain that \((\partial _r|_-)(\partial _r|_+)^2 \psi \) is a linear combination (with uniformly bounded coefficients) of the terms \(\partial _{v_-}^a \partial _{\varphi _-}^b (\partial _r|_-)^c {\hat{\psi }}\) with \(0 \leqslant a + b + c \leqslant 3\). For \(v_0 \geqslant 1\) all those terms are controlled by the bulk term in (4.2) – and for \(v_0 \leqslant 1\) we complement this bulk term by the regularity Assumption 2.46. Hence, the spacetime integral in (4.30) is uniformly bounded. This shows (4.29). \(\square \)
4.2 Estimates Away from the Event and Cauchy Horizons
Proposition 4.31
Under the assumptions of Section 3, and with \(r_\textrm{red}\) as in Corollary 4.21, we have that for any \(r_0 \in (r_-, r_\textrm{red}]\) there exists a constant \(C>0\) (depending on \(r_0\)) such that
holds for \(f \in \{\partial _r^c\psi , \partial _{v_+} \partial _r^c\psi , {\mathcal {Q}}_{[s]} \partial _r^c\psi \}\) for \(c = 0,1,2\).
Proof
We use Boyer-Lindquist coordinates for the proof. Since the region under consideration in (4.32) is bounded away from \(r_-\) and \(r_+\), we have that \(\partial _r|_+\) is a bounded linear combination of \(\partial _t, \partial _\varphi , \partial _r|_{\textrm{BL}}\). Thus, it is straightforward to see that (4.32) follows from
for \(f \in \{\partial _t^a \partial _\varphi ^b (\partial _r|_{\textrm{BL}})^c\psi , \partial _t \partial _t^a \partial _\varphi ^b (\partial _r|_{\textrm{BL}})^c\psi , {\mathcal {Q}}_{[s]} \partial _t^a \partial _\varphi ^b (\partial _r|_{\textrm{BL}})^c\psi \}\), with \(0 \leqslant a + b + c \leqslant 2\). In the following we will prove (4.33).
\(\underline{{\textbf {Step 1: The multiplier.}}}\) We start out from the following multiplier identity, where \(\lambda , \mu , \eta >0\) are constants to be chosen and \(\chi \) is as above:
After integration over the spheres, and using the form (2.38) of the Teukolsky equation, the right hand side of (4.34) equals the sum of
-
1.
the sum of all the terms on the right hand side of D.1
-
2.
the terms
$$\begin{aligned} \begin{aligned}&-\chi (t) e^{\lambda r} 2(r-M)(1-s)|\partial _r\psi |^2 - \chi (t) e^{\lambda r} 2s\frac{a(r-M)}{\Delta } \mathfrak {Re}(\partial _\varphi \psi \overline{\partial _r \psi }) \\&\quad -\chi (t)e^{\lambda r} 2s \Big [\frac{M(r^2 - a^2)}{\Delta } - r -ia \cos \theta \Big ]\mathfrak {Re}(\partial _t \psi \overline{\partial _r \psi }) + \chi (t) e^{\lambda r}2s \mathfrak {Re}(\psi \overline{\partial _r \psi }) \end{aligned} \end{aligned}$$ -
3.
the underbraced terms in (4.34).
As before, it will turn out that we can derive a boundedness statement if all the bulk terms are negative.
\(\underline{{\textbf {Step 2: Estimating all bulk terms that are quadratic in derivatives of }}\psi .}\) We collect the leading order terms in \(\lambda \) from D.1, which are the wavily underlined terms:
It turns out that in order to control the non-definite second term it is actually not sufficient just to use the \(|\partial _\varphi \psi |^2\) control of the last term. Instead, we need to use the strengthened control provided by Lemma 2.33 together with the \(a^2 \sin ^2 \theta \) contribution of the first term in (4.35). Thus, using Lemma 2.33, we rewrite (4.35) as
The underbraced terms will be treated as error terms. We show now that for \(r \in [r_0, r_\textrm{red}]\) with \(r_{0} > r_{-}\) the remaining terms (modulo zeroth order terms) are uniformly bounded from above by
for some \(c>0\) depending on \(r_-<r_0< r_\textrm{red}< r_+\). For this it is clearly sufficient to show that the non-underbraced terms in (4.36) are uniformly negative definite in \(\partial _t \psi \) and \(\frac{1}{\sin \theta } (is \cos \theta \cdot \psi + \partial _\varphi \psi )\). A straightforward computation gives
which shows the claim.
We can now choose \(\lambda >0\) large enough such that all bulk terms that are quadratic in derivatives of \(\psi \) can be controlled in absolute value by \(-\frac{1}{4}\times \)(4.37). The underbraced bulk terms in (4.36) of the form \(\mathfrak {Re}(\psi \overline{\partial \psi })\), which are also leading order in \(\lambda \), can be estimated by \(|\mathfrak {Re}(\psi \overline{\partial \psi })| \leqslant \frac{1}{2} \varepsilon |\partial \psi |^2 + \frac{1}{2} \varepsilon ^{-1} |\psi |^2\), where we choose \(\varepsilon >0\) so small that the arising first term can be bounded by \(-\frac{1}{4}\times \)(4.37). It thus only remains to estimate the zeroth order bulk terms, which will be done in Step 4.
\(\underline{{\textbf {Step 3: Estimating boundary terms.}}}\) We collect all the total derivatives appearing on the right hand side of (4.34). They are of the form \(\partial _t (A)\) and \(\partial _r(B)\), where
and
The coercivity of B,
in the region \(r_0 \leqslant r \leqslant r_\textrm{red}\) is established using the same computation as in Step 2: First, we use Lemma 2.33 and moreover replace every \(\partial _\varphi \psi \) in (4.39) by \(\frac{1}{\sin \theta }(is \cos \theta \cdot \psi + \partial _\varphi \psi )\), thus obtaining again error terms. The lower bound of B in \(\chi (t)\big (|\partial _r \psi |^2 + |\partial _t \psi |^2 + \sum _i |{\widetilde{Z}}_i \psi |^2\big )\) then follows again from (4.38) at the expense of a large zeroth order error term. We now choose \(\mu \) as a function of \(\eta \) such that the last term in (4.39), \(\chi (t)\mu e^{\eta r}|\psi |^2\), is large enough in the region \(r_0 \leqslant r \leqslant r_\textrm{red}\) to dominate this error term. This yields (4.40).
Next we establish the coercivity of \(B \pm \frac{\Delta }{2Mr} A\),
in the region \(r_0 \leqslant r \leqslant r_\textrm{red}\). It follows again from Lemma 2.33 that we have
where the underbraced terms are considered as error terms. Again, we consider the part of the above expression that is quadratic in \(\{\partial _t \psi , \frac{1}{\sin \theta }(is \cos \theta \cdot \psi + \partial _\varphi \psi ), \partial _r \psi \}\) as a quadratic form. Its associated matrix is
which we claim is positive definite in the region \(r_0 \leqslant r \leqslant r_\textrm{red}\): Obviously, the first main minor is positive, the second main minor was computed in (4.38) to be positive, and a computation gives
from which the claim follows. Now, if necessary, choosing \(\mu (\eta )\) even larger, we can control all the error terms in (4.42) to obtain (4.41).
\(\underline{{\textbf {Step 4: Estimating the remaining bulk terms.}}}\) As familiar from the proof of Propositions 4.1 and 4.11 we estimate the last two of the underbraced terms in (4.34) by
We now choose \(\eta >0\) sufficiently large so that the last term can be controlled by \(-\frac{1}{4} \times \) (4.37) and such that the first term controls all the zeroth order terms in the bulk (including those generated at the end of Step 2).
\(\underline{{\textbf {Step 5: Putting it all together.}}}\) After integration over the spheres we thus obtain from (4.34)
for \(r_0 \leqslant r \leqslant r_\textrm{red}\). Let \(r' \in [r_0, r_\textrm{red})\). Integrating (4.43) over \(\{r' \leqslant r \leqslant r_\textrm{red}\} \cap \{f^- \leqslant t_0\} \cap \{f^+ \leqslant t_0\}\) with respect to \(\frac{1}{\rho ^2} \textrm{vol}= dt \wedge dr \wedge \textrm{vol}_{{\mathbb {S}}^2}\), where \(t_0 \gg 1\), and using that on the level sets of \(f^-\) as well as on those of \(f^+\) we have \(\big |\frac{dr}{dt}\big | = \frac{|\Delta |}{2Mr}\), we obtain

where \(c>0\) is a constant depending on \(r_0\). Using (4.41) to infer the positivity of the second and third term, (4.40), and letting \(t_0 \rightarrow \infty \), we obtain

where \(C>0\) is a constant depending on \(r_0\). This, together with the trivial upper bounds on B and Corollary 4.21 (note that \(\partial _r|_{\textrm{BL}}\) is a bounded linear combination of \(\partial _{v_+}, \partial _{\varphi _+}, \partial _r|_+\)), gives (4.33) for \(f = \psi \).
\(\underline{{\textbf {Step 6: Estimating higher derivatives.}}}\) Because \(\partial _t\), \(\partial _\varphi \), \({\mathcal {Q}}_{[s]}\) commute with \({\mathcal {T}}_{[s]}\), it follows directly that (4.44) also holds with \(\psi \) replaced by \(\partial _t^a \partial _\varphi ^b \psi \), \(\partial _t \partial _t^a \partial _\varphi ^b \psi \), and \({\mathcal {Q}}_{[s]}\partial _t^a \partial _t^b \psi \) with \(0 \leqslant a + b \leqslant 2\). The conclusion of Corollary 4.21 implies that the boundary term at \(\{r = r_\textrm{red}\}\) is bounded, thus giving (4.33) with \(c =0\).
Moreover, we observe that

Thus, all the additional bulk terms in the energy estimate
after Cauchy Schwarz, have either already been controlled by the integrated (4.33) with \(c=0\) (or the bulk term in (4.44) with \(\psi \) replaced by \(\partial _t^a \partial _\varphi ^b\psi \)) or are at the level of energy for \(\partial _r \psi \) (i.e., the dotted term in (4.45)). We thus also obtain (4.44) with \(\psi \) replaced by \(\partial _r \psi \). Since \(\partial _r|_{\textrm{BL}}\) is a bounded linear combination of \(\partial _{v_+}, \partial _{\varphi _+}, \partial _r|_+\), the boundary term at \(\{r = r_\textrm{red}\}\) is bounded by Corollary 4.21. We can again commute with \(\partial _t, \partial _\varphi , {\mathcal {Q}}_{[s]}\) to obtain (4.33) for \(c = 1\).
Finally, commuting (2.38) once more with \(\partial _r\) we find that \([\partial _r^2, {\mathcal {T}}_{[s]}]\) is a bounded linear combination of the terms  . We can repeat the same energy estimate, but now for \(\partial _r^2 \psi \). The dotted term is again at the level of the energy for \(\partial _r^2\psi \) and all the other terms have already been controlled. Commutation with \(\partial _t\) and \({\mathcal {Q}}_{[s]}\) then concludes the proof. \(\square \)
. We can repeat the same energy estimate, but now for \(\partial _r^2 \psi \). The dotted term is again at the level of the energy for \(\partial _r^2\psi \) and all the other terms have already been controlled. Commutation with \(\partial _t\) and \({\mathcal {Q}}_{[s]}\) then concludes the proof. \(\square \)
4.2.1 Corollaries
The following corollary is needed for Teukolsky’s separation of variables in Theorem 5.26.
Corollary 4.46
Under the assumptions of Section 3 and for \(r_-< r_0< r_1 < r_+\) there exists a constant \(C>0\) (depending on \(r_0, r_1\)) such that for \(f \in \{ \psi , \partial _r \psi , \partial _r^2 \psi \}\)
holds and
holds for \(r \in (r_0, r_1)\) and all \((\theta , \varphi _+) \in {\mathbb {S}}^2 {\setminus } \{ \theta = 0, \pi \}\).
Proof
We begin by proving the bound (4.47); first for \(f = \psi \). Then all the terms with \(0 \leqslant i_1 + i_2 + i_3 + j \leqslant 1\) are controlled by (4.32) and (4.22) with \(f = \psi \). Using \(f = \partial _{v_+} \psi \) in (4.32) and (4.22) extends control to all terms except those with \(i_1 + i_2 + i_3 = 2\). We now use \(f = {\mathcal {Q}}_{[s]} \psi \) in (4.32) and (4.22) and use just the \(L^2\)-control. By the Definition 2.45 of the Carter operator and by the fact that we have already controlled \(\partial _{v_+}\psi \) and \(\partial _{v_+}^2 \psi \) in \(L^2\), this gives us \(L^2\)-control of  . Lemma 2.37, together with the \(L^2\)-control of the first angular derivatives already obtained, now controls the remaining terms with \(i_1 + i_2 + i_3 = 2\). The cases of \(f = \partial _r \psi , \partial _r^2 \psi \) can be treated analogously using that (4.32) and (4.22) hold for \(f \in \{\partial _r^k\psi , \partial _{v_+} \partial _r^k\psi , {\mathcal {Q}}_{[s]} \partial _r^k\psi \}\) for \(k = 0,1,2\).
. Lemma 2.37, together with the \(L^2\)-control of the first angular derivatives already obtained, now controls the remaining terms with \(i_1 + i_2 + i_3 = 2\). The cases of \(f = \partial _r \psi , \partial _r^2 \psi \) can be treated analogously using that (4.32) and (4.22) hold for \(f \in \{\partial _r^k\psi , \partial _{v_+} \partial _r^k\psi , {\mathcal {Q}}_{[s]} \partial _r^k\psi \}\) for \(k = 0,1,2\).
To prove (4.48) we observe that for \(1 \leqslant v_0 < \infty \) (4.47) implies
By Lemma 2.23 we thus have
and similarly for the southern hemisphere \({\mathbb {S}}^2_-\). A standard Sobolev inequalityFootnote 38 applied to \(e^{\pm is \varphi _+} f\) thus gives
for \(v_0 \geqslant 1\). We proceed similarly for \(v_0 \leqslant -1\) and for \(v_+ \in [-1,1], r \in [r_0, r_1]\) the field is uniformly bounded since it is regular. This shows (4.48). \(\square \)
Note that the reason for why the constant \(C>0\) in Corollary 4.46 blows up when we let \(r_1\) go to \(r_+\) is because of the conversion of the \(v_-\)-weights to \(v_+\)-weights, which becomes worse and worse when \(r_1 \rightarrow r_+\), cf. the proof of Corollary 4.21. If we restrict to the region \(v_+ \geqslant 1\) then the constant can be chosen uniformly up to \(r = r_+\):
Corollary 4.49
Under the assumptions of Section 3 and for given \(r_-< r_0 < r_+\) there exists \(C>0\) such that for \( f \in \{ \psi , \partial _r \psi , \partial _r^2 \psi \}\)
holds for all \(r \in [r_0, r_+], v_+ \geqslant 1, (\theta , \varphi ) \in {\mathbb {S}}^2{\setminus } \{ \theta = 0, \pi \}\).
Indeed, the statement is only needed for \(f= \partial _r^2 \psi \) (for Proposition 7.17).
Proof
In the same way as in the proof of (4.47) in Corollary 4.46 one obtains
from Proposition 4.11 (and Proposition 4.31) for \( f \in \{ \psi , \partial _r \psi , \partial _r^2 \psi \}\), but now with a constant which is uniform up to \(r=r_+\). As before one now proves (4.50) by Sobolev embedding. \(\square \)
4.3 Estimates Near the Cauchy Horizons
Recall that for the method of proof of Theorem 3.7 it is convenient to first establish the blow-up result (3.8) along the left Cauchy horizon and then to propagate it backwards. The estimates established in this section are used to show that 1) we can indeed extend \( \psi \) to the left Cauchy horizon (along with a convergence result); 2) the \(\chi \)-weighted \(L^2\)-bound propagates all the way to the left Cauchy horizon; 3) the singularity can be propagated backwards from the left Cauchy horizon. All this is used in Section 8.
Proposition 4.51
Under the assumptions of Section 3 there exists an \(r_{\textrm{ered}} \in (r_-, r_\textrm{red})\) and a constant \(C>0\) such that the following holds


where the function \(\chi \) is as in Corollary 4.21.
Proof
We use that for \(s=+2\) there is an effective red-shift for the energy operating close to the left Cauchy horizon. The red-shift is effective in the sense that while it persists after one commutation of \({\mathcal {T}}_{[s]} \psi = 0\) with \(\partial _r\), after two commutations with \(\partial _r\) it turns into a blue-shift for the energy, which becomes stronger with subsequent commutations. We use \(\chi _n(v_+)(1 + \lambda \Delta )(-\partial _r + \partial _{v_+} + \frac{a}{r_-^2 + a^2} \partial _{\varphi _+})\) as a multiplier. Note that, compared to the multiplier used in the proof of Proposition 4.11, the additional contribution in \(\partial _{\varphi _+}\) makes the vector field timelike near the Cauchy horizons.
\(\underline{{\textbf {Step 1: The multiplier.}}}\) We start out from the following multiplier identity, where \(\lambda <0\) and \(\eta , \mu >0\) are constants to be chosen:
Here, the function \(\chi _n: {\mathbb {R}}\rightarrow (0, \infty )\) results from locally smoothing out the corners of the function
Given \(\delta >0\) it is easy to see that one can choose \(n\geqslant 1\) large enough such that \(|\chi '_n(v_+)| \leqslant \delta \chi _n(v_+)\) holds for all \(v_+ \in {\mathbb {R}}\). The parameter n will be fixed in the next step.
After integration over the spheres, the right hand side of (4.54) consists of the sum of the following terms
-
1.
the sum of all the terms on the right hand sides of C.1, C.2, and C.3 with \(\chi (v_+) = \chi _n(v_+)\)
-
2.
the real parts of the terms

-
3.
the underbraced terms in (4.54).
Again, our desired boundedness statement requires all the bulk terms to yield a negative definite contribution. We also recall here that \((\partial _r \Delta )(r_-) = 2(r_- - M) <0\).
\(\underline{{\textbf {Step 2: Estimating all bulk terms that are quadratic in derivatives of }}\psi .}\)
We first consider all those terms that are quadratic in \(\partial _r \psi \). The leading order terms are the dashed term from 2. in Step 1 and the dashed term from C.1. Their sum at \(r=r_-\) equals
which is negative for \(s=+2\). The other two bulk terms quadratic in \(\partial _r \psi \) from C.1 and C.2 sum to
We can now choose \(n \gg 1\) large enough and \(r_- < r_{\textrm{ered}}\) close enough to \(r_-\) (\(r_{\textrm{ered}}\) depending in particular on \(\lambda \) at this point) such that (4.55) is controlled by \(-\frac{1}{2}\) times the sum of the dashed terms in \(r_- < r \leqslant r_{\textrm{ered}}\).
We next consider all those terms quadratic in \(\partial \psi \) that are leading order in \(\lambda \); these are all the wavily underlined terms from C.1, C.2, and C.3. They sum to
where we have used again Lemma 2.33 and we consider the underbraced terms again as error terms. Considering the non-underbraced terms as a quadratic form in \(\big (\partial _{v_+} \psi , \frac{1}{\sin \theta }(is \cos \theta \cdot \psi + \partial _{\varphi _+} \psi )\big )\), the corresponding matrix is \(-\chi _n(v_+) \lambda 2(r-M) Q_1\) with
The determinant of \(Q_1\) evaluated at \(r=r_-\) is easily computed to be \(\det Q_1(r_-) =\frac{1}{2(r_-^2 + a^2)} (r_-^2 + a^2 \cos ^2 \theta )^2 >0\), and hence \(Q_1\) is positive definite at \(r=r_-\). Recalling that \(\lambda <0\) and \(2(r_- - M) <0\) it now follows that for \(r_{\textrm{ered}}> r_-\) close enough to \(r_-\) there exist constants \(c>0, C>0\) such that the following holds in \(r_-< r\leqslant r_{\textrm{ered}}\):
Together with our earlier estimates for \(\partial _r \psi \) this shows that the dashed terms, the other terms quadratic in \(\partial _r \psi \), and the wavily underlined terms are bounded from above by
in the region \(r_-<r\leqslant r_{\textrm{ered}}\). We can now choose \(\lambda <0\) large enough in absolute value such that the sum of all the non-underbraced terms on the right hand side of (4.54) that are not total derivatives are estimated from above by
in a region \(r_- < r\leqslant r_{\textrm{ered}}\), where \(c>0\), \(C>0\) are (new) constants.
\(\underline{{\textbf {Step 3: Estimating boundary terms.}}}\) We now gather all the total derivatives appearing on the right hand side of (4.54). They are \(\partial _r(B)\) and \(\partial _{v_+}(A)\) with
and

where we have used Lemma 2.33. We begin by establishing the coercivity of B. We first only consider the dotted terms and in a procedure already familiar by now we complete all individual \(\partial _{\varphi _+} \psi \) terms into \(\frac{1}{\sin \theta } (is \cos \theta \cdot \psi + \partial _{\varphi _+} \psi )\) at the expense of adding error terms. We treat the arising expression (without the error terms) as a quadratic form in \((\partial _{v_+} \psi , \frac{1}{\sin \theta }(is \cos \theta \cdot \psi + \partial _{\varphi _+} \psi ), \sqrt{-\Delta } \partial _r \psi )\) (note the weight in front of the \(\partial _r\) derivative) the corresponding matrix of which is easily seen to be
The positive definiteness of this matrix in a region \(r_- < r \leqslant r_{\textrm{ered}}\) follows easily from noting that the left-upper 2-2 matrix has already been shown (below (4.57)) to be positive definite in such a region while the other off-diagonal terms vanish at \(r=r_-\). Choosing now \(\mu (\eta )\) such that \(\mu (\eta ) e^{\eta r}\) is large enough we can control all the error terms to obtain
in a region \(r_- < r \leqslant r_{\textrm{ered}}\).
We next establish the coercivity of \(B-A\). We find
Again, completing the \(\partial _{\varphi _+} \psi \) terms to \(\frac{1}{\sin \theta }(is \cos \theta \cdot \psi + \partial _{\varphi _+} \psi )\) terms by introducing error terms and considering those terms that are quadratic in \((\partial _{v_+} \psi , \frac{1}{\sin \theta }(is \cos \theta \cdot \psi + \partial _{\varphi _+} \psi ), \partial _r \psi )\) as a quadratic form (note that this time we do not include a weight in the \(\partial _r\) derivative), we need to establish the positive definiteness of the matrix
The first main minor is clearly positive, the second main minor at \(r=r_-\) is found to be
and we compute
Again, choosing \(\mu (\eta ) e^{\eta r}\) large enough we control all the error terms and conclude that
holds for \(r_- < r \leqslant r_{\textrm{ered}}\) for \(r_{\textrm{ered}}\) close enough to \(r_-\).
Finally, we need to establish the coercivity of \(B + \frac{|\Delta |}{r^2 + 2Mr + a^2} A\) for r close enough to \(r_-\). We compute
Again, we complete all isolated \(\partial _{\varphi _+} \psi \) terms into \(\frac{1}{\sin \theta }( is \cos \theta + \partial _{\varphi _+} \psi )\) by adding error terms and treat the part of the expression that is quadratic in \(\{\partial _{v_+} \psi , \frac{1}{\sin \theta } (is \cos \theta \cdot \psi + \partial _{\varphi _+} \psi ), \Delta \partial _r \psi \}\) as a quadratic form (note the weight in front of the \(\partial _r\) derivative). Its corresponding matrix at \(r=r_-\), modulo the factor \(\chi _n(v_+)\), is easily seen to be
where we have used \(2Mr_- = r_-^2 + a^2\). The left upper \(2\times 2\) matrix is already known to be positive definite. Moreover, we compute
Hence, \(Q_3\) is positive definite and after choosing \(\mu (\eta ) e^{\eta r}\) large enough we obtain
in \(r_- < r \leqslant r_{\textrm{ered}}\) for \(r_{\textrm{ered}}\) close enough to \(r_-\).
\(\underline{{\textbf {Step 4: Estimating the remaining bulk terms.}}}\) The last two terms in (4.54) are estimated by
Choosing now \(\eta >0\) large enough and recalling (4.58) we finally obtain from (4.54)
in the region \(r_- < r \leqslant r_{\textrm{ered}}\).
\(\underline{{\textbf {Step 5: Putting it all together.}}}\) Let \(r' \in (r_-, r_{\textrm{ered}})\). We integrate (4.62) over the region \(\{r' \leqslant r \leqslant r_{\textrm{ered}}\} \cap \{f^- \leqslant t_0\} \cap \{f^+ \leqslant t_0\}\), with \(t_0 \gg 1\), with respect to \( dv_+ \wedge dr \wedge \textrm{vol}_{{\mathbb {S}}^2}= \frac{1}{\rho ^2} \textrm{vol}\). Moreover, using that on a level set of \(f^+\) we have \(dr = dv_+\) and on a level set of \(f^-\) we have \(dr = \frac{\Delta }{r^2 + 2Mr + a^2} dv_+\), we obtain

where \(c>0\). Using (4.59), (4.60), and (4.61), the trivial upper bounds on B for the right hand side together with Proposition 4.31, letting \(t_0 \rightarrow \infty \) and \(r' \rightarrow r_-\), we conclude the proof of the proposition. \(\square \)
4.3.1 Extension of \(\psi \) to the Cauchy Horizon \(\mathcal{C}\mathcal{H}^+_l\)
Proposition 4.64
Under the assumptions of Section 3 the limit
exists in \(L^2({\mathbb {R}}\times {\mathbb {S}}^2)\) and satisfies
where the function \(\chi (v_+)\) is as in Proposition 4.51.
Proof
For \(r_1, r_2 > r_-\) and for \(\theta \ne 0, \pi \) by the fundamental theorem of calculus we have
Squaring and Cauchy-Schwarz gives
Integrating with respect to \(\chi (v_+) \textrm{vol}_{{\mathbb {S}}^2}dv_+\) gives
Let \(L^2_{\chi (v_+)}({\mathbb {R}}\times {\mathbb {S}}^2)\) denote the \(L^2\) space with respect to the measure \(\chi (v_+) \textrm{vol}_{{\mathbb {S}}^2}dv_+\). By (4.53) we have \(\psi (v_+, \theta , \varphi _+;r) \in L^2_{\chi (v_+)}({\mathbb {R}}\times {\mathbb {S}}^2)\) for r close enough to \(r_-\) and by (4.52) we have that the right hand side of (4.66) is bounded by \(|r_1 - r_2|\cdot C\). This shows that \(\psi (v_+, \theta , \varphi _+;r)\) is Cauchy in \(L^2_{\chi (v_+)}({\mathbb {R}}\times {\mathbb {S}}^2)\) for \(r \rightarrow r_-\), from which both claims in the proposition follow. \(\square \)
4.3.2 Backwards Propagation of the Singularity
Proposition 4.67
Under the assumptions of Section 3, and considering the hypersurface \(\Sigma := \{f^- = v_0\}\) transversal to \(\mathcal{C}\mathcal{H}^+_r\) for some \(v_0 \in {\mathbb {R}}\), there exists a constant \(C>0\) such that we have for all \(v' \gg 1\) large enough
where \(\psi (\cdot \;;r_-)\) is the \(L^2\)-limit from Proposition 4.64.Footnote 39
Proof
\(\underline{{\textbf {Step 1:}}}\) We recall that \(f^-(v_+, r) = - v_+ + 2r^* - r + r_+\). Thus, on \(\Sigma = \{f^- = v_0\}\) we have
where we have used (2.8) (recall that \(F_-(r)\) extends regularly to \(r_-\)). The right hand side of (4.68) is clearly a strictly decreasing function in r and thus the inverse function exists which we denote by \(r_\Sigma \) so to obtain \(r_\Sigma (v_+) = r\) on \(\Sigma \). It is also immediate that we have \(r_\Sigma (v_+) \rightarrow r_-\) for \(v_+ \rightarrow \infty \).
Taking the exponential, we obtain from (4.68)
on \(\Sigma \) with \(\lim _{r \rightarrow r_-} G(r) >0\). Thus, for \(v_+ \gg 1\) large enough we have
\(\underline{{\textbf {Step 2:}}}\) Let now \(r' > r_-\) be close to \(r_-\).
We now estimate, in a manner similar to the proof of Proposition 4.64, as follows (see also Figure 8):
Squaring and Cauchy-Schwarz gives
Let \(v_{\{r = r'\} \cap \Sigma } = 2r^*(r') - r' + r_+ - v_0\) be the value of \(v_+\) on \(\Sigma \) where \(r = r'\). For \(v' < v_{\{r = r'\} \cap \Sigma }\) we integrate to obtain
which gives
We now let \(r' \rightarrow r_-\) and note that this implies \(v_{\{r = r'\} \cap \Sigma } \rightarrow \infty \). Moreover, we have
where \(\mathbb {1}_A\) denotes the characteristic function of the set A. The first summand on the right hand side of (4.71) goes to zero in \(L^2({\mathbb {R}}\times {\mathbb {S}}^2)\) by Proposition 4.64 while the second goes to zero in \(L^2({\mathbb {R}}\times {\mathbb {S}}^2)\) by dominated convergence. We thus obtain from (4.70) after \(r' \rightarrow r_-\) and for \(v' \gg 1\) large enough
where we have used (4.69) and (4.52) in the last step. Since I is finite by Proposition 4.64, II is also finite. Multiplying (4.72) by \(I + II \leqslant C\) concludes the proof. \(\square \)
Lemma 4.73
Let \(f,g: [1, \infty ) \rightarrow [0, \infty )\) be positive, integrable functions that satisfy for \(v'\) sufficiently large
with \(\kappa >0\). For \(p >0\) we then have
Proof
Let us assume \(\int _{1}^\infty v^p \cdot f(v) \; dv < \infty \). By assumption we have
for all \(n \in {\mathbb {N}}\). It follows that
We then compute, using (4.74),
\(\square \)
Applying the lemma with \(f(v_+) = \int _{{\mathbb {S}}^2}|\psi (v_+,\theta , \varphi _+; r_-)|^2 \;\textrm{vol}_{{\mathbb {S}}^2}\) and \(g(v_+) = \int _{{\mathbb {S}}^2} |\psi (v_+, r_\Sigma (v_+), \theta , \varphi _+)|^2 \; \textrm{vol}_{{\mathbb {S}}^2}\) gives the following
Corollary 4.75
In the setting of Proposition 4.67 we have
where \(p>0\). It follows in particular from Proposition 4.64 that
5 Teukolsky’s Separation of Variables
In this section we use the upper bounds derived on the Teukosky field in Corollary 4.46 to establish the separation of variables. We begin by a discussion of the spin 2-weighted spheroidal harmonics, then introduce the Teukolsky transform, and prove a non-trivial result regarding the relation of physical space \(v_+\)-weights and frequency domain \(\omega \)-derivatives. We then derive the radial Teukolsky equation belonging to (2.39).
5.1 Spin 2-Weighted Spheroidal Harmonics
For \(\omega \in {\mathbb {R}}\) and  we defineFootnote 40
we defineFootnote 40

Clearly,  maps
maps  into
into  .
.
Proposition 5.2
The operator  has a complete and orthonormal (with respect to \(L^2({\mathbb {S}}^2)\)) set of eigenfunctions
has a complete and orthonormal (with respect to \(L^2({\mathbb {S}}^2)\)) set of eigenfunctions  indexed by \(m \in {\mathbb {Z}}\), \({\mathbb {N}}\ni l \geqslant \max (|m|, |s|)\) and eigenvalues \(\lambda _{ml}^{[s]}(\omega ) \in {\mathbb {R}}\) satisfying
indexed by \(m \in {\mathbb {Z}}\), \({\mathbb {N}}\ni l \geqslant \max (|m|, |s|)\) and eigenvalues \(\lambda _{ml}^{[s]}(\omega ) \in {\mathbb {R}}\) satisfying

The eigenfunctions are known as spin 2-weighted spheroidal harmonics and are of the form
where the \(S^{[s]}_{ml}(\cos \theta ; \omega )\) form a complete and orthonormal (with respect to \(L^2([-1,1], d \cos \theta )\)) set of eigenfunctions of the operator
with eigenvalues \(\lambda ^{[s]}_{ml}(\omega )\)Footnote 41
The eigenvalues \(\lambda ^{[s]}_{ml}(\omega )\) depend analytically on \(\omega \) and the eigenfunctions \(S^{[s]}_{ml}(\cos \theta ; \omega )\) are analytic in \(\omega \) and in \(x= \cos \theta \) away from \(x= \pm 1\). Near \(x = \pm 1\) we have the the following asymptotic expansions for all \(k \in {\mathbb {N}}\): Near \(x = -1\) we have
where \(a_{k}(x; \omega )\) is analytic in both arguments near \(x= -1\); and near \(x=+1\)
is valid with \(b_k(x; \omega )\) being analytic in both arguments near \(x = +1\).
Moreover, we have \(\lambda _{ml}^{[s]}(\omega ) - s = \lambda ^{[-s]}_{ml}(\omega ) + s\) and for \(\omega = 0\) the eigenvalues are given by \(\lambda _{ml}^{[s]}(0) = -(l -s)(l+s+1) = -l(l+1) + s(s+1)\).
Proof
The result is standard, see for example [67] or [15], although we do not know a reference that includes a proof. We will thus give an outline of the proof here.
Making the separation of variables ansatz \(Y_{m}(\theta , \varphi ) = S_m(\theta ) e^{im \varphi }\) we obtain

We will now find an orthonormal basis of eigenfunctions for \(L_m^{[s]}(\omega )\) using Sturm-Liouville theory. The substitution \(x = \cos \theta \) yields
We now go over to \(L_m^{[s]} - \lambda \) for \(\lambda \in {\mathbb {C}}\). The points \(x = \pm 1\) are regular singular points of the second order differential operator and, moreover, it depends analytically on \(\omega \) and \(\lambda \), even for complex \(\omega \). The Frobenius method, see for example [66], shows that there is a fundamental system of solutions of \((L_m^{[s]} - \lambda )S_m = 0\), normalised at \(x =-1\), of the form
where \(h_1\) and \(h_2\) are analytic in \([-1,1) \times {\mathbb {R}}\times {\mathbb {R}}\) and the constant c might be zero unless \(m =s\). Similarly, there is a fundamental system of solutions normalised at \(x=+1\):
where \(g_1\) and \(g_2\) are analytic in \((-1,1] \times {\mathbb {R}}\times {\mathbb {R}}\) and the constant c might be zero unless \(m = -s\). Note that \(u_1\) is regular at \(x = -1\) while \(v_1\) is regular at \(x =+1\). For \(\lambda = \lambda _0 >0\) large enough one can show that \(u_1\) and \(v_1\) are linearly independent. Using this pair of solutions one constructs the Green’s function in the same way as for a regular Sturm-Liouville problem, c.f. [66]. The above asymptotics imply that the Green’s function is in \(L^2([-1,1] \times [-1,1])\), and thus the solution operator \(K_{\lambda _0}\) is a symmetric and compact operator on \(L^2([-1,1])\). It is easy to show that the kernel vanishes and thus, by the spectral theorem, there is an orthonormal basis of eigenfunctions \(S^{[s]}_{ml}(x)\) of \(K_{\lambda _0}\) with real eigenvalues \(\mu ^{[s]}_{ml}\). Using the asymptotics of \(u_1\) and \(v_1\) in the Green’s function one shows that \(S^{[s]}_{ml}\) are continuous at \(x = \pm 1\). Moreover, they satisfy \((L_m^{[s]} - \lambda _0) (\mu ^{[s]}_{ml}S_{ml}^{[s]} ) = S^{[s]}_{ml}\) and thus
It follows that \(S^{[s]}_{ml} \sim u_1 \sim v_1\) – and thus in particular that the eigenvalues are simple.
To show the analytic dependence of the eigenvalues on \(\omega \) we notice that they are exactly the zeros of the modified Wronskian \(W(u_1, v_1)(\lambda , \omega ):= u_1(x; \lambda , \omega ) (1-x^2) v_1'(x; \lambda , \omega ) - (1-x^2) u_1'(x; \lambda , \omega ) v_1(x; \lambda , \omega )\). One now shows that the zeros of the Wronskian in \(\lambda \) are simple, i.e., \(\partial _\lambda W(u_1, v_1) (\lambda ^{[s]}_{ml}, \omega ) \ne 0\). The analytic implicit function theorem then yields that the eigenvalues \(\lambda ^{[s]}(\omega )\) depend analytically on \(\omega \). It follows that \(u_1(x; \lambda ^{[s]}_{ml}(\omega ), \omega )\) depends analytically on \(\omega \). Normalising it in \(L^2([-1,1])\) then gives \(S^{[s]}_{ml}(x; \omega )\), which shows in particular the regularity claimed in the proposition.
It is straightforward to show that \(Y^{[s]}_{lm}(\omega )\) is an orthonormal basis of \(L^2({\mathbb {S}}^2)\). To show  , we can use the asymptotics of \(S^{[s]}_{ml}(\omega )\) given by the Frobenius solutions above and tediously verify the conditions in Proposition 2.18. Alternatively, and more elegantly, we can multiply (5.3) by \(\overline{Y^{[s]}_{ml}(\omega )}\), integrate over the sphere and check that the asymptotics of \(S_{ml}^{[s]}(\omega )\) allow us to do one integration by parts to conclude that \(Y^{[s]}_{ml}(\omega ) \in H^1_{[s]}({\mathbb {S}}^2)\). We now go over the corresponding trace-free and symmetric 2-covariant tensor field \(\alpha _{ml}(\omega )\) on \({\mathbb {S}}^2\) which is smooth except possibly at the poles of the sphere. Using (2.21) we now rewrite (5.3) as a standard elliptic equation for \(\alpha _{ml}(\omega )\). It now follows from standard elliptic regularity theory that \(\alpha _{ml}(\omega )\) is smooth on all of the sphere – showing the claim.
, we can use the asymptotics of \(S^{[s]}_{ml}(\omega )\) given by the Frobenius solutions above and tediously verify the conditions in Proposition 2.18. Alternatively, and more elegantly, we can multiply (5.3) by \(\overline{Y^{[s]}_{ml}(\omega )}\), integrate over the sphere and check that the asymptotics of \(S_{ml}^{[s]}(\omega )\) allow us to do one integration by parts to conclude that \(Y^{[s]}_{ml}(\omega ) \in H^1_{[s]}({\mathbb {S}}^2)\). We now go over the corresponding trace-free and symmetric 2-covariant tensor field \(\alpha _{ml}(\omega )\) on \({\mathbb {S}}^2\) which is smooth except possibly at the poles of the sphere. Using (2.21) we now rewrite (5.3) as a standard elliptic equation for \(\alpha _{ml}(\omega )\). It now follows from standard elliptic regularity theory that \(\alpha _{ml}(\omega )\) is smooth on all of the sphere – showing the claim.
The relation \(\lambda _{ml}^{[s]}(\omega ) - s = \lambda ^{[-s]}_{ml}(\omega ) + s\) follows from the substitution \(x \rightarrow - x\) in (5.5). Finally, we refer the reader to [28] for the evaluation of the eigenvalues at \(\omega = 0\). \(\square \)
The following quantitative result on the \(\omega \)-dependence of the eigenfunctions \(Y^{[s]}_{ml}(\omega )\) is needed for the proof of Proposition 5.22.
Proposition 5.6
By Proposition 5.2 we know that \(\partial _\omega ^k S_{ml}^{[s]}( \omega ) \in L^2([-1,1])\) for all \(k \in {\mathbb {N}}\). We can thus expand in \(L^2([-1,1])\)
with \(D_{mll';k}^{[s]}(\omega ) \in {\mathbb {R}}\).
There exists \(\varepsilon >0\) such that for \(|\omega | \leqslant \varepsilon \) we have
where the constant is independent of m and \(|\omega | \leqslant \varepsilon \).
Let us remark that (5.7) is equivalent to
Proof
Differentiating (5.4) in \(\omega \) gives
Note that since \(||S^{[s]}_{ml}(\omega )||_{L^2} = 1\) for all \(\omega \), we have \(\langle S^{[s]}_{ml}(\omega ), \partial _\omega S^{[s]}_{ml}(\omega )\rangle _{L^2} = 0\). Multiplying (5.9) by \(S^{[s]}_{ml}(\omega )\) and integrating gives
We now integrate by parts in the first termFootnote 42 to obtain
This finally leaves us with
Multiplying (5.9) by \(S^{[s]}_{ml'}(\omega )\), \(l \ne l'\), and integrating over \([-1,1]\) in x gives, after the integration by parts as before,
We thus obtain for \(l \ne l'\)
For \(l = l'\) we have \(D^{[s]}_{mll;1}(\omega ) = 0\). To derive an expression for \(D^{[s]}_{mll';k}\) we first note that by the regularity of \(\partial _\omega ^iS^{[s]}_{ml}(\omega )\) from Proposition 5.2 we have that \(\langle \partial _\omega S^{[s]}_{ml}(\omega ), S^{[s]}_{ml'}(\omega )\rangle _{L^2}\) is smooth in \(\omega \). We now compute
We also need to estimate the eigenvalues for small \(|\omega |\): for \(|\omega | \leqslant 1\) it follows directly from (5.10) that
We now choose \(1>\varepsilon >0\) such that for \(|\omega | \leqslant \varepsilon \) we have
uniformly in m and l.
We now prove (5.7) by induction in k. We start with \(k = 1\) and estimate (5.11). We have \(|\langle 2a (a \omega x^2 - sx) S^{[s]}_{ml}(\omega ), S^{[s]}_{ml'}(\omega )\rangle _{L^2}| \leqslant 2a(a \varepsilon +|s|)\). We now estimate the denominator using (5.13) and \(\lambda ^{[s]}_{ml}(0) = -l(l+1) + s(s+1)\):
This proves the claim for \(k = 1\).
We now assume that (5.7) holds up to and including \(k-1\). We first show that for \(1 \leqslant j \leqslant k-1\) and \(|\omega | \leqslant \varepsilon \) we have
where the constant is independent of m, l. Let \(f^{[s]}(x; \omega ):= 2a(a \omega x^2 - sx)\). Thus \(\partial _\omega \lambda ^{[s]}_{ml}(\omega ) = \langle f^{[s]}(\omega ) S^{[s]}_{ml}(\omega ), S^{[s]}_{ml}(\omega ) \rangle _{L^2}\) and thus
Clearly, \(\partial _\omega ^{i_1} f^{[s]}(\omega )\) is bounded in \(L^\infty _x([-1,1])\) by a constant only depending on s for \(|\omega | \leqslant \varepsilon \), and \(\partial ^i_\omega S^{[s]}_{ml}(\omega )\) is bounded in \(L^2_x([-1,1])\) by a constant independent of m, l by the induction hypothesis and (5.8). This shows (5.15).
We now use (5.12) to show that \(D^{[s]}_{mll';k}(\omega )\) is bounded in \(\ell ^2(l,l')\). The induction hypothesis shows directly that the \(\ell ^2\)-norm in \(l,l'\) of the underbraced terms in (5.12) is bounded. It thus remains to show that the \(\ell ^2\)-norm of the left hand side of (5.12) is bounded. Note that for \(l = l'\) it vanishes identically. For \(l \ne l'\) we compute using (5.11)
The underbraced terms are bounded uniformly in \(m,l,l'\) and \(|\omega | \leqslant \varepsilon \) as in (5.16). Using (5.15), we can bound
where the constant is independent of \(m,l,l'\). It now follows from (5.14) that the \(\ell ^2(l,l')\) norm of the left hand side of (5.12) is bounded. This concludes the proof. \(\square \)
5.2 Teukolsky’s Expansion
For \(f(v_+, \theta , \varphi _+) \in L^1_{v_+} L^2_{{\mathbb {S}}^2}\) we define the Fourier transform  of f by
of f by

It can be easily checked that this is a map  . It gives rise in the standard way to an isometry
. It gives rise in the standard way to an isometry  which we denote again in the same way.
which we denote again in the same way.
For \(g \in L^2_\omega L^2_{{\mathbb {S}}^2}\) we define the map \((\cdot )_{ml}: L^2_\omega L^2_{{\mathbb {S}}^2} \rightarrow L^2_\omega \ell ^2_{m,l}\) by
which is also an isometry since for each \(\omega \in {\mathbb {R}}\) the \(Y^{[s]}_{ml}(\omega )\) form an orthonormal basis of \(L^2({\mathbb {S}}^2)\). The summation in \(\ell ^2_{m,l}\) is over \(m \in {\mathbb {Z}}\) and \({\mathbb {N}}\ni l \geqslant \max (|m|, |s|)\).
For \(f \in L^1_{v_+} L^2_{{\mathbb {S}}^2} \cap L^2_{v_+} L^2_{{\mathbb {S}}^2}\) the composite map  , which we call the Teukolsky transform, is given by
, which we call the Teukolsky transform, is given by

Note that by
the order of integration in (5.19) does not matter.
The inverse map of (5.18) is given by
and the inverse map of  is given by
is given by

where this can be taken literally for  and serves as notation for
and serves as notation for  in the standard way, which is then defined via approximation by functions in \(L^1_\omega L^2_{{\mathbb {S}}^2} \cap L^2_\omega L^2_{{\mathbb {S}}^2}\). In particular for
in the standard way, which is then defined via approximation by functions in \(L^1_\omega L^2_{{\mathbb {S}}^2} \cap L^2_\omega L^2_{{\mathbb {S}}^2}\). In particular for  we have
we have  and thus we have literally
and thus we have literally

as a map \(L^1_\omega \ell ^2_{m,l} \cap L^2_\omega \ell ^2_{m,l} \rightarrow L^2_{v_+} L^2_{{\mathbb {S}}^2}\).
For \(f \in L^2_{v_+} L^2_{{\mathbb {S}}^2}\) we have the Plancherel relation

We also haveFootnote 43

and

Note, however, that in general  , since the orthonormal basis functions \(Y^{[s]}_{ml}\) of \(L^2({\mathbb {S}}^2)\) in (5.18) are \(\omega \)-dependent.
, since the orthonormal basis functions \(Y^{[s]}_{ml}\) of \(L^2({\mathbb {S}}^2)\) in (5.18) are \(\omega \)-dependent.
In the following we address this point and show that under suitable assumptions we can still infer limited decay of \(f(v_+, \theta , \varphi _+)\) for \(|v_+| \rightarrow \infty \) from limited regularity of  in \(\omega \).
in \(\omega \).
5.2.1 Slow Decay in \(v_+\) of f in Terms of Limited Regularity of 
Proposition 5.22
Let \(\varepsilon >0\) be as in Proposition 5.6, let  and let \(q_0 \in {\mathbb {N}}_0\). Then
and let \(q_0 \in {\mathbb {N}}_0\). Then  , i.e.,
, i.e.,

for all \(0 \leqslant q \leqslant q_0\), \(q \in {\mathbb {N}}_0\) if, and only if,  , i.e.,
, i.e.,

for all \(0 \leqslant q \leqslant q_0\), \(q \in {\mathbb {N}}\). Here, all derivatives are weak derivatives.Footnote 44
Proof
Assume first that  has \(q_0\) weak \(\omega \)-derivatives in \(L^2_{(-\varepsilon , \varepsilon )}L^2_{{\mathbb {S}}^2}\). We then have for \(0 \leqslant q \leqslant q_0\)
has \(q_0\) weak \(\omega \)-derivatives in \(L^2_{(-\varepsilon , \varepsilon )}L^2_{{\mathbb {S}}^2}\). We then have for \(0 \leqslant q \leqslant q_0\)

where, in the second equality we have used the smoothness of the \(Y^{[s]}_{ml}\) in \(\omega \) and the product rule
which of course also holds for weak derivatives if b is smooth, in the third equality we have used that we can pull out weak derivatives from under the integralFootnote 45 and the representation of \(\partial _\omega ^{q'} Y^{[s]}_{ml}\) from Proposition (5.6), and in the fourth equation we just used that the limit in \(l'\) is an \(L^2({\mathbb {S}}^2)\) limit, so we can pull it out of the integral.
Now by (5.23) and Plancherel we have

Thus (5.24) follows if we show

for \(0 \leqslant q' \leqslant q\). By Cauchy-Schwarz, Proposition 5.6, Plancherel, and (5.23) we compute

To prove the reverse direction, we now assume that  has \(q_0\) weak \(\omega \)-derivatives satisfying (5.24). Let \(0 \leqslant q \leqslant q_0\) and \(\chi \in C^\infty _0\big ((-\varepsilon , \varepsilon ) \times {\mathbb {S}}^2\big )\). Then
has \(q_0\) weak \(\omega \)-derivatives satisfying (5.24). Let \(0 \leqslant q \leqslant q_0\) and \(\chi \in C^\infty _0\big ((-\varepsilon , \varepsilon ) \times {\mathbb {S}}^2\big )\). Then

where we introduced \(\langle \cdot , \cdot \rangle _{L^2({\mathbb {S}}^2)}\) for the standard Hermitian product on \(L^2({\mathbb {S}}^2)\) for brevity, used Plancherel in the second line, dominated convergence in the third line as well as the combinatorial formula
which can be proved easily via induction; we used that  admits \(q_0\) weak \(\omega \)-derivatives in \(L^2_{(-\varepsilon , \varepsilon )}\) in the fourth line and finally Proposition 5.6, (5.24), and dominated convergence again in the last line. Proposition 5.6 and (5.24) together now also show (5.23). \(\square \)
admits \(q_0\) weak \(\omega \)-derivatives in \(L^2_{(-\varepsilon , \varepsilon )}\) in the fourth line and finally Proposition 5.6, (5.24), and dominated convergence again in the last line. Proposition 5.6 and (5.24) together now also show (5.23). \(\square \)
5.3 Application of Teukolsky’s Separation to the Teukolsky Field \(\psi \)
Theorem 5.26
Under the assumptions of Section 3 and for every \(r \in (r_-, r_+)\) the Teukolsky transform

of the Teukolsky field \(\psi (v_+,r, \theta , \varphi _+)\) is well-defined and we have  . Moreover, for every \(r \in (r_-, r_+)\), \(m \in {\mathbb {Z}}\), and \({\mathbb {N}}\ni l \geqslant \max \{|m|, |s|\}\) we have
. Moreover, for every \(r \in (r_-, r_+)\), \(m \in {\mathbb {Z}}\), and \({\mathbb {N}}\ni l \geqslant \max \{|m|, |s|\}\) we have  .
.
For fixed \(\omega , m, l\) the Teukolsky transform  is twice continuously differentiable in \(r \in (r_-, r_+)\) and we also have
is twice continuously differentiable in \(r \in (r_-, r_+)\) and we also have  for every \(r \in (r_-, r_+)\) and m, l.Footnote 46 Moreover, the Teukolsky transform satisfies
for every \(r \in (r_-, r_+)\) and m, l.Footnote 46 Moreover, the Teukolsky transform satisfies

for all \(\omega \in {\mathbb {R}}\), \(m \in {\mathbb {Z}}\), \( {\mathbb {N}}\ni l \geqslant \max \{|m|, |s|\}\). Since we have  the representation
the representation

is valid for every \(r \in (r_-, r_+)\) in particular in \(L^2_{v_+} L^2_{{\mathbb {S}}^2}\).
Proof
Corollary 4.46 in particular states that for each \(r \in (r_-,r_+)\) we have \(\psi (v_+,r, \theta , \varphi _+)\) is in \(L^2_{v_+}L^2_{{\mathbb {S}}^2}\). It now follows from Section 5.2 that the Teukolsky transform is well-defined with  and also that (5.29) holds.
and also that (5.29) holds.
By (4.48) for \(f = \psi \), and since \(q_r > 2\), we obtain that \(\psi (v_+,r, \theta , \varphi _+) \in L^1({\mathbb {R}}\times {\mathbb {S}}^2)\). Together with the boundedness of \(Y^{[s]}_{ml}(\theta , \varphi ; \omega )\) and its continuity in \(\omega \) we obtain from (5.27) that  for fixed r, m, l. By (4.48) for \(f = \partial _r\psi , \partial _r^2 \psi \) we also obtain that we can continuously differentiate in r twice under the integral in (5.27) for fixed \(\omega , m,l\) and also the continuous dependence of the derivatives on \(\omega \) as before.
for fixed r, m, l. By (4.48) for \(f = \partial _r\psi , \partial _r^2 \psi \) we also obtain that we can continuously differentiate in r twice under the integral in (5.27) for fixed \(\omega , m,l\) and also the continuous dependence of the derivatives on \(\omega \) as before.
In order to derive (5.28) we recall the coordinate expression (2.39) of \({\mathcal {T}}_{[s]} \psi = 0\) to see that

holds for all \(r \in (r_-, r_+)\) and all \(\omega \in {\mathbb {R}}\), where we have used (4.47), which in particular impliesFootnote 47\(\partial _{v_+}^a\partial _{\varphi _+}^{b_1} \partial _r^{b_2} \psi (r) \in L^1_{v_+} L^2_{{\mathbb {S}}^2}\) for \(0 \leqslant a + b_1 + b_2 \leqslant 2\), \(a, b_1, b_2 \in {\mathbb {N}}\) which we use to do the integration by parts in \(v_+\). We assemble  from (5.1) to find
from (5.1) to find

We now use that \(\psi \) and \(Y^{[s]}_{ml}\) are smooth spin 2-weighted functions so that by Proposition 2.26 and (2.31) we can do the integration by parts to bring  over to obtain a term of the form
over to obtain a term of the form  , where we used that the eigenvalues \(\lambda ^{[s]}_{ml}(\omega )\) are real. Finally, by (4.48) for \(f = \partial _r \psi , \partial _r^2 \psi \) and the boundedness of \(Y^{[s]}_{ml}(\theta , \varphi ; \omega )\) dominated convergence allows us to pull the r-derivatives out of the integral to obtain (5.28). \(\square \)
, where we used that the eigenvalues \(\lambda ^{[s]}_{ml}(\omega )\) are real. Finally, by (4.48) for \(f = \partial _r \psi , \partial _r^2 \psi \) and the boundedness of \(Y^{[s]}_{ml}(\theta , \varphi ; \omega )\) dominated convergence allows us to pull the r-derivatives out of the integral to obtain (5.28). \(\square \)
6 Analysis of the Heun Equation and Transmission and Reflection coefficients for \(\omega = 0\)
This section analyses the radial Teukolsky equation (5.28). We show that it is of the Heun-form and that the limit \(\omega = 0\) is a hypergeometric equation. We introduce specific fundamental systems of solutions along with the corresponding transmission and reflection coefficients and investigate their regularity and their behaviour for \(\omega \rightarrow 0\).
6.1 The Heun Equation
Setting \(x:= \frac{r - r_-}{r_+ - r_-}\) in (5.28) so that we have \(x = 0\) for \(r = r_-\) and \(x = 1\) for \(r = r_+\) the equation (5.28) transforms to the Heun equation
where we have just written  for brevity and generality and where
for brevity and generality and where
and \(\omega _\pm := \frac{a}{2Mr_\pm }\).
Setting \(y:=1 - x = \frac{r_+ - r}{r_+ - r_-}\) so that we have \(y = 0\) for \(r = r_+\) and \(y= 1\) for \(r = r_-\) the equation (6.1) transforms to the Heun equation
where
6.1.1 The Hypergeometric Equation Arising as the Limit \(\omega = 0\) of the Heun Equation
We compute the values of the Greek parameters \(\alpha , \ldots , \varepsilon \) for \(\omega = 0\), where we also use \(\lambda _{ml}^{[s]}(0) = -l(l+1) + s(s+1)\) from Proposition 5.2:
A straightforward computation then shows that for \(\omega = 0\) the Heun equation (6.1) turns into the hypergeometric equation
with
Setting again \(y = 1-x\), (6.5) transforms into
with
6.2 Fundamental Systems of Solutions and Reflection and Transmission Coefficients
We now recall the Frobenius method to determine the possible asymptotics of solutions of the radial ODE (5.28) at the regular singular points \(r = r_+\) and \(r=r_-\) and to construct fundamental systems of solutions with these prescribed asymptotics. We only provide a sketch of the derivation, full details of this textbook material are found for example in Chapter 4 of [66].
We begin with the discussion of the regular singular point \(x=0\) in (6.1), which corresponds to the Cauchy horizon \(r=r_-\). The asymptotics at the event horizon, which is \(y=0\) for (6.3), then follow directly from this discussion by replacing the Greek parameters \(\alpha , \ldots , \varepsilon \) by their tilded versions.
We make the ansatz \(x^\sigma \sum _{j=0}^\infty d_j(\omega , m,l) x^j\) for a solution of (6.1). Entering this ansatz into (6.1) and comparing powers of x yields
For \(j = -1\) we obtain the indicial equation \(\sigma (\sigma - 1 + \gamma ) = 0\) which has the two solutions \(\sigma = 0\) and \(\sigma = 1 - \gamma \).
Consider first \(\sigma =1 - \gamma \) and set \(d_0 = 1\). It then follows from (6.8) with \(\sigma = 1- \gamma \) that the coefficients are recursively determined by
Note that for \(s= 2\) we have \(\gamma = -1 + i \frac{4Mr_-}{r_+ - r_-}(\omega - \omega _-m)\) and thus the denominator in (6.9) is non-vanishing for all \(j \in {\mathbb {N}}\) and for all \(\omega \in {\mathbb {R}}\). It can be shown that this power series converges absolutely for \(x \in [0,1)\). Also note that since the coefficients \(\alpha , \ldots , \varepsilon \) depend analytically on \(\omega \), so do all the \(d_j(\omega , m,l)\). The radius of convergence of the power series of \(d_j(\omega , m, l)\) in \(\omega \) is uniformly lower bounded in j (it essentially depends on the radius of convergence of the power series in \(\omega \) of \(\lambda ^{[s]}_{ml}(\omega )\) and on \(\frac{4Mr_-}{r_+ - r_-}\)). Since the convergence is uniform, we obtain that the arising power seriesFootnote 48 is also analytic in \(\omega \) for all \(\omega \in {\mathbb {R}}\). We label this solution by \(B^{[s]}_{\mathcal{C}\mathcal{H}^+_r, ml}(x; \omega ):= x^{1 - \gamma } \sum _{j = 0}^\infty d_j^{[s]}(\omega , m,l) x^j\).
To construct a second linearly independent solution we make the other choice \(\sigma = 0\), i.e., we are looking for a solution of the form \(\sum _{j=0}^\infty c_j(\omega , m,l) x^j\), which we normalise by \(c_0 =1\). From (6.8) with the \(d's\) replaced by \(c's\) we obtain the recursive relation
Since \(\gamma = \frac{4iMr_-}{r_+ - r_-} (\omega - \omega _-m) + 1-s\), the denominator vanishes for \(j=1\) and \(\omega = \omega _-m\), but for all other \(\omega \) one can show as before that the power series converges absolutely for \(x \in [0,1)\) and is analytic in \(\omega \in {\mathbb {R}}\setminus \{\omega _- m\}\). We label this solution by \(B^{[s]}_{\mathcal{C}\mathcal{H}^+_l, ml}(x; \omega ):= \sum _{j = 0}^\infty c_j^{[s]}(\omega , m, l) x^j\). From (6.10) we compute \(c_1(\omega , m, l) = - \frac{\varepsilon }{\gamma }\) and \(c_2(\omega , m, l) = \frac{1}{2(1 + \gamma )} \Big [ \frac{\varepsilon }{ \gamma } (\beta + \varepsilon ) - \delta \Big ]\) for later.
The Frobenius solutions of (6.3) normalised at \(y=0\) are obtained in the analogous way by replacing \(\alpha , \ldots , \varepsilon \) by \({\tilde{\alpha }}, \ldots , {\tilde{\varepsilon }}\). We summarise this discussion in the following
Proposition 6.11
-
1.
For \( \omega \ne \omega _- m\) equation (6.1) has a fundamental system of solutions \(\{B^{[s]}_{\mathcal{C}\mathcal{H}^+_l, ml}(x; \omega ), B^{[s]}_{\mathcal{C}\mathcal{H}^+_r, ml}(x;\omega )\}\) which are of the form
$$\begin{aligned} \begin{aligned} B^{[s]}_{\mathcal{C}\mathcal{H}^+_l, ml}(x; \omega )&= \sum _{j = 0}^\infty c_j^{[s]}(\omega , m, l) x^j \\ B^{[s]}_{\mathcal{C}\mathcal{H}^+_r, ml}(x; \omega )&= x^{1 - \gamma } \sum _{j = 0}^\infty d_j^{[s]}(\omega , m,l) x^j \end{aligned} \end{aligned}$$and are normalised by \(c_0^{[s]}(\omega , m,l) = 1\) and \(d_0^{[s]}(\omega , m,l) = 1\). The power series \(\sum _{j = 0}^\infty d_j^{[s]}(\omega , m,l) x^j\) is analytic in \([0,1) \times {\mathbb {R}}\) (and thus \(B^{[s]}_{\mathcal{C}\mathcal{H}^+_r, ml}(x; \omega )\) is in particular also a solution for \(\omega = \omega _- m\)) while the solution \(B^{[s]}_{\mathcal{C}\mathcal{H}^+_l, ml}(x; \omega )\) is only analytic and defined on \([0,1) \times ({\mathbb {R}}\setminus \{\omega _- m\})\). The coefficients are determined recursively and we find in particular \(c_1^{[s]}(\omega , m, l) = - \frac{\varepsilon }{\gamma }\) and \(c_2^{[s]}(\omega , m, l) = \frac{1}{2(1 + \gamma )} \Big [ \frac{\varepsilon }{ \gamma } (\beta + \varepsilon ) - \delta \Big ]\).Footnote 49
-
2.
For \( \omega \ne \omega _+ m\) equation (6.3) has a fundamental system of solutions \(\{ A^{[s]}_{{\mathcal {H}}^+_r, ml}(y;\omega ), A^{[s]}_{{\mathcal {H}}^+_l, ml}(y;\omega ) \}\) which are of the form
$$\begin{aligned} \begin{aligned} A^{[s]}_{{\mathcal {H}}^+_r, ml}(y;\omega )&= \sum _{j= 0}^\infty a_j^{[s]}(\omega , m,l) y^j \\ A^{[s]}_{{\mathcal {H}}^+_l, ml}(y; \omega )&= y^{1 - {\tilde{\gamma }}} \sum _{j= 0}^\infty b_j^{[s]}(\omega , m, l) y^j \end{aligned} \end{aligned}$$and are normalised by \(a_0^{[s]}(\omega , m, l) = 1 \) and \(b_0^{[s]}(\omega , m,l) = 1\). The power series \(\sum _{j= 0}^\infty b_j^{[s]}(\omega , m, l) y^j \) is analytic in \([0,1) \times {\mathbb {R}}\) (and thus \(A^{[s]}_{{\mathcal {H}}^+_l, ml}(y; \omega )\) is in particular also a solution for \(\omega = \omega _+ m\)) while the solution \(A^{[s]}_{{\mathcal {H}}^+_r, ml}(y;\omega )\) is only analytic and defined on \([0,1) \times ({\mathbb {R}}\setminus \{\omega _+ m\})\). The coefficients are determined recursively and we find in particular \(a_1^{[s]}(\omega , m, l) = - \frac{{\tilde{\varepsilon }}}{{\tilde{\gamma }}} \) and \(a_2^{[s]}(\omega , m, l ) = \frac{1}{2(1 + {\tilde{\gamma }})} \Big [ \frac{{\tilde{\varepsilon }}}{{\tilde{\gamma }}}({\tilde{\beta }} + {\tilde{\varepsilon }}) - {\tilde{\delta }}\Big ] \).Footnote 50
Our reason for labelling the solutions with \({\mathcal {H}}^+_r, {\mathcal {H}}^+_l, \mathcal{C}\mathcal{H}^+_l, \mathcal{C}\mathcal{H}^+_r\) will become apparent in Sects. 7 and 8. It follows that we can write for \(\omega \ne \omega _+ m\) the Teukolsky transform  from Theorem 5.26, with the r-coordinate replaced by the y-coordinate, as
from Theorem 5.26, with the r-coordinate replaced by the y-coordinate, as

where \(a_{{\mathcal {H}}^+_r, ml}, a_{{\mathcal {H}}^+_l, ml}: {\mathbb {R}}{\setminus } \{\omega _+m\} \rightarrow {\mathbb {C}}\) are functions which will be determined later in Section 7.
Lemma 6.13
Under the assumptions of Section 3 we have \(a_{{\mathcal {H}}^+_r, ml}, a_{{\mathcal {H}}^+_l, ml} \in C^0({\mathbb {R}}{\setminus }\{ \omega _+m\}, {\mathbb {C}})\).
Proof
Differentiating (6.12) in y we obtain for \(\omega \ne \omega _+ m\)

Fix \(y \in (0,1)\). Since \(\{ A_{{\mathcal {H}}^+_r, ml}(y; \omega ), A_{{\mathcal {H}}^+_l, ml}(y; \omega ) \}\) are linearly independent, the matrix has an inverse which is also analytic in \(\omega \) for \(\omega \ne \omega _+m\). We can thus solve for \(a_{{\mathcal {H}}^+_r, ml}(\omega ), a_{{\mathcal {H}}^+_l, ml}(\omega )\) and thus they inherit the regularity of the left hand side of (6.14), which is continuous by Theorem 5.26. \(\square \)
6.2.1 Alternative Representation of Second Frobenius Solution
Let us also recall a different way of constructing the second Frobenius solution \(B^{[s]}_{\mathcal{C}\mathcal{H}^+_l, ml}(x;\omega )\) which will be useful later on in Section 6.2.4. This is the variation of constant ansatz, see for example Chapter 4 of [66] for full details.
To obtain a second linearly independent solution we make the variation of constants ansatz
Entering this into equation (6.1) gives
Here, the prime stands for \(\frac{d}{dx}\). This is a first order equation for \(e'(x)\). Again, making a power series ansatz one can show that (6.15) has a unique solution of the form
which we normalise by \(e_0 = \gamma - 1\) and where the coefficients are determined recursively by an algebraic expression which involves \(\alpha , \beta , \gamma , e_j, d_j\). In particular, each \(e_j(\omega , m, l)\) is an analytic function of \(\omega \) for all \(\omega \in {\mathbb {R}}\).
As before let us now assume that \(\omega \ne \omega _- m\), so the parameter \(\gamma \) has an imaginary part. In particular \(e'(x)\) does not have a term proportional to \(\frac{1}{x}\). An integral of \(e'(x)\) is thus given by
The underbraced power series converges absolutely on \(x \in [0,1)\) and is analytic in \(\omega \) for \(\omega \ne \omega _-m\). Since we have chosen \(e_0 = \gamma -1\) we see that the coefficient in the power series in front of \(x^0\) is 1. Thus,
is a solution of (6.5) of the form
with \(c_0(\omega , m, l) = 1\). The coefficients \(c_j(\omega , m, l)\) can of course be computed from those of e(x) and those of \(B^{[s]}_{\mathcal{C}\mathcal{H}^+_r, ml}(x; \omega ) = x^{1 - \gamma } \sum _{j = 0}^\infty d_j(\omega , m,l) x^j\), for example we have
On the other hand it follows from the asymptotics that the solution (6.18) we have constructed here must agree with \(B^{[s]}_{\mathcal{C}\mathcal{H}^+_l, ml} (x; \omega )\) from Proposition 6.11, for which we have already obtained the explicit values of \(c_1\) and \(c_2\). We thus find
Multiplying by \((1+\gamma )\) and setting \(\omega = \omega _-m\) we obtain
Similarly, we find an alternative expression of \(A^{[s]}_{{\mathcal {H}}^+_r, ml}(y;\omega )\) as
where
with
The underbraced power series converges absolutely on \(y \in [0,1)\) and is analytic in \(\omega \) for \(\omega \ne \omega _+m\).
6.2.2 Reflection and Transmission Coefficients
Since \(\{B^{[s]}_{\mathcal{C}\mathcal{H}^+_l, ml},B^{[s]}_{\mathcal{C}\mathcal{H}^+_r, ml}\}\) forms a fundamental system of solutions, we can express each of the two solutions \(A^{[s]}_{{\mathcal {H}}^+_r, ml}, A^{[s]}_{{\mathcal {H}}^+_l, ml}\) as a linear combination thereof, i.e., we can write for each \(\omega \in {\mathbb {R}}{\setminus } \{\omega _-m, \omega _+m\}\)
with \({\mathfrak {T}}^{[s]}_{{\mathcal {H}}^+_r, ml}, {\mathfrak {R}}^{[s]}_{{\mathcal {H}}^+_r, ml}, {\mathfrak {T}}^{[s]}_{{\mathcal {H}}^+_l, ml}, {\mathfrak {R}}^{[s]}_{{\mathcal {H}}^+_l, ml}: {\mathbb {R}}{\setminus } \{\omega _-m, \omega _+m\} \rightarrow {\mathbb {C}}\), where we call \({\mathfrak {T}}^{[s]}_{{\mathcal {H}}^+_r, ml}(\omega ), {\mathfrak {T}}^{[s]}_{{\mathcal {H}}^+_l, ml}\) the transmission coefficients of the right and left even horizon, respectively, and \({\mathfrak {R}}^{[s]}_{{\mathcal {H}}^+_r, ml}, {\mathfrak {R}}^{[s]}_{{\mathcal {H}}^+_l, ml}\) the reflection coefficients of the right and left event horizon, respectively.
6.2.3 The Case \(m \ne 0\)
Proposition 6.22
Let \(m \ne 0\). Then the transmission and reflection coefficients \({\mathfrak {T}}^{[s]}_{{\mathcal {H}}^+_r, ml}(\omega ), {\mathfrak {R}}^{[s]}_{{\mathcal {H}}^+_r, ml}(\omega )\), \({\mathfrak {T}}^{[s]}_{{\mathcal {H}}^+_l, ml}(\omega ), {\mathfrak {R}}^{[s]}_{{\mathcal {H}}^+_l, ml}(\omega )\) are (defined and) analytic for \(\omega \in (-|\omega _+|, |\omega _+|)\) and we have \({\mathfrak {T}}^{[s]}_{{\mathcal {H}}^+_r, ml}(0) \ne 0\).
Proof
Note that \(0< |\omega _+| < |\omega _-|\). Hence for \(m \ne 0\) the fundamental solutions in (6.21) are defined for \(\omega \in (-|\omega _+|, |\omega _+|)\) and thus so are the transmission and reflection coefficients.
Combining the first line of (6.21) with its differentiated version in x we obtain the vector equation
Fix \(x \in (0,1)\). Note that the matrix on the right hand side is invertible (since \(B^{[s]}_{\mathcal{C}\mathcal{H}^+_l, ml}(x; \omega ) \) and \(B^{[s]}_{\mathcal{C}\mathcal{H}^+_r, ml} (x; \omega )\) are linearly independent) and analytic in \(\omega \) for \(\omega \in (-|\omega _+|, |\omega _+|)\). The left hand side is analytic for \(\omega \in (-|\omega _+|, |\omega _+|)\) as well. We can thus solve for \({\mathfrak {T}}^{[s]}_{{\mathcal {H}}^+_r, ml}(\omega ) \) and \({\mathfrak {R}}^{[s]}_{{\mathcal {H}}^+_r, ml} (\omega )\) and obtain that they are analytic in \(\omega \in (-|\omega _+|, |\omega _+|)\). Similarly one obtains that the transmission and reflection coefficients of the left event horizon are analytic in \((-|\omega _+|, |\omega _+|)\).
To show \({\mathfrak {T}}^{[s]}_{{\mathcal {H}}^+_r, ml}(0) \ne 0\) we begin by noticing that \( A^{[s]}_{{\mathcal {H}}^+_r, ml}(y; 0)\) and \(A^{[s]}_{{\mathcal {H}}^+_l, ml}(y; 0)\) solve (6.7) and \(B^{[s]}_{\mathcal{C}\mathcal{H}^+_l, ml} (x; 0)\) and \(B^{[s]}_{\mathcal{C}\mathcal{H}^+_r, ml} (x; 0)\) solve (6.5). For the hypergeometric equation there are convenient closed expressions for the Frobenius solutions, which we recall in the following, see for example Chapter 8 of [4], but they can also be verified directly.
For \(\underline{a} \in {\mathbb {C}}\) and \(n \in {\mathbb {N}}_0\) we define \((\underline{a})_n:= \underline{a}(\underline{a} +1) (\underline{a} + 2 ) \cdots (\underline{a} + n-1) = \frac{\Gamma (\underline{a} +n)}{\Gamma (\underline{a})}\), where \(\Gamma \) is the Gamma function. Then, for \(-\underline{c} \notin {\mathbb {N}}_0\)
is a solution of (6.5) with \( F(\underline{a}, \underline{b}, \underline{c}; 0) = 1\). And for \(\underline{c} -2 \notin {\mathbb {N}}_0\)
is also a solution of (6.5). Clearly, for \(\underline{c} \ne 1\) these two solutions are linearly independent. Recall from Section 6.1.1 that \(B^{[s]}_{\mathcal{C}\mathcal{H}^+_l, ml} (x; 0)\) and \(B^{[s]}_{\mathcal{C}\mathcal{H}^+_r, ml} (x; 0)\) are solutions of the hypergeometric equation (6.5) with \(\underline{c} = \gamma (\omega = 0) = -1 - \frac{2iam}{r_+ - r_-} \). For \(m \ne 0\) we thus obtain, by comparison of the asymptotics, that we must have
with \(\underline{a}\), \(\underline{b}\) and \(\underline{c}\) as in Section 6.1.1. Similarly we obtain
with \(\underline{{\tilde{c}}}\) as in Section 6.1.1.
Now note that (6.24) is a polynomial in x if, and only if, \(\underline{a}\) or \(\underline{b}\) are negative integers. Since we have \(\underline{b} = -s -l = -2 -l\) and \({\mathbb {N}}\ni l \geqslant \max (|m|, |s|)\), \(\underline{b}\) is a negative integer and thus \(B^{[s]}_{\mathcal{C}\mathcal{H}^+_l, ml} (x; 0)\) and \(A^{[s]}_{{\mathcal {H}}^+_r, ml}(1-x; 0)\) are polynomials in x. Moreover, since \(\underline{c}\) and \(\tilde{\underline{c}}\) have non-vanishing imaginary parts it is straightforward to see that \(B^{[s]}_{\mathcal{C}\mathcal{H}^+_r, ml} (x; 0) \) and \(A^{[s]}_{{\mathcal {H}}^+_l, ml} (x;0)\) are not polynomials in x. Entering with this information into (6.21) gives directly that \({\mathfrak {R}}^{[s]}_{{\mathcal {H}}^+_r, ml} (0)\) has to vanish and thus \({\mathfrak {T}}^{[s]}_{{\mathcal {H}}^+_r, ml}(0) \ne 0\). \(\square \)
Remark 6.26
Indeed, all the transmission and reflection coefficients at \(\omega = 0\) for \(m \ne 0\) can be computed explicitly using the classical theory of linear relations of solutions of the hypergeometric ODE, see for instance Chapter 8 of [4]. For example one obtains \({\mathfrak {T}}^{[s]}_{{\mathcal {H}}^+_r, ml}(0) = \frac{\Gamma (\underline{a} + \underline{b} + 1 - \underline{c}) \Gamma (1 - \underline{c})}{\Gamma (\underline{a} + 1 - \underline{c}) \Gamma (\underline{b} + 1 - \underline{c})}\). Setting \(\xi (0):= - \frac{2iam}{r_+ - r_-}\) and plugging in the exact values of the parameters for \(s=2\) from (6.6) we obtain
from which it also follows that \(|{\mathfrak {T}}^{[s]}_{{\mathcal {H}}^+_r, ml}(0)|=1\).
6.2.4 The Case \(m=0\) via the Teukolsky-Starobinsky Conservation Law
Proposition 6.27
The transmission coefficient \({\mathfrak {T}}^{[s]}_{{\mathcal {H}}^+_r, 0l}\) of the right event horizon and the reflection coefficient \({\mathfrak {R}}^{[s]}_{{\mathcal {H}}^+_l, 0l}\) of the left event horizon, as well as \(\omega \cdot {\mathfrak {R}}^{[s]}_{{\mathcal {H}}^+_r, 0l}\) (all of which are a priori not defined at \(\omega = 0\)) extend analytically to \(\omega \in {\mathbb {R}}\). Moreover, we have \({\mathfrak {R}}^{[s]}_{{\mathcal {H}}^+_l, 0\,l} (0) = 0\).
Proof
We construct a set of fundamental solutions which is regular for all \(\omega \in {\mathbb {R}}\). Recall from Proposition 6.11 that \(B^{[s]}_{\mathcal{C}\mathcal{H}^+_r, ml}(x;\omega )\) is defined for all \(\omega \in {\mathbb {R}}\). For \(\omega \ne 0\) we now use the alternative representation of the second Frobenius solution \(B^{[s]}_{\mathcal{C}\mathcal{H}^+_l, 0l}(x; \omega )\) from Section 6.2.1 and define
We thus see that \(U_{\mathcal{C}\mathcal{H}^+,0l}(x; \omega )\) extends analytically as a solutionFootnote 51 of (6.1) to \(\omega = 0\) for which we have
Hence, \(\{ B_{\mathcal{C}\mathcal{H}^+_r,0l}(x;\omega ), U_{\mathcal{C}\mathcal{H}^+,0l}(x; \omega )\}\) is a fundamental system of solutions of (6.1) for \(m = 0\) which is defined and analytic for all \(\omega \in {\mathbb {R}}\). (The linear independence of the solutions is shown below.)
Similarly we set
to obtain a fundamental system \(\{A_{{\mathcal {H}}^+_l,0\,l}(y;\omega ), U_{{\mathcal {H}}^+,0\,l}(y; \omega )\}\) of solutions of (6.3) for \(m =0\) which is defined and analytic for all \(\omega \in {\mathbb {R}}\). Moreover, \(U_{{\mathcal {H}}^+,0l}(y; 0)\) is of the form
Let us also note that it follows from (6.19), (6.20) and Section 6.1 that
for \(l \geqslant 2\) and thus the solutions (6.28) and (6.29) do indeed have \(\log \) terms and are linearly independent from \( B_{\mathcal{C}\mathcal{H}^+_r,0\,l}(x;0)\) and \(A_{{\mathcal {H}}^+_l,0\,l}(y;0)\), respectively.
We can now expand for all \(\omega \in {\mathbb {R}}\)
where \(X_{{\mathcal {H}}^+,0l}, Y_{{\mathcal {H}}^+, 0l}, X_{{\mathcal {H}}^+_l, 0l}, Y_{{\mathcal {H}}^+_l, 0l}\) are complex valued functions. It follows as in (6.23) that they are analytic on all of \({\mathbb {R}}\).
We now show that we have \(Y_{{\mathcal {H}}^+_l, 0l}(0) = 0\). Recall that for \(m=0\) and \(\omega =0\) the coefficients of the hypergeometric equations which \( \{ B_{\mathcal{C}\mathcal{H}^+_r,0l}(x;0), U_{\mathcal{C}\mathcal{H}^+,0l}(x; 0)\}\) and \(\{U_{{\mathcal {H}}^+, 0l}(y; 0), A_{{\mathcal {H}}^+_l, 0l}(y; 0)\}\) are satisfying are \(\underline{c} = \tilde{\underline{c}} = -1\), \(\underline{a} = l -1\), and \(\underline{b} = -2-l\). It thus follows that (6.25) still defines a solution to the hypergeometric equation which is clearly linearly independent to \(U_{\mathcal{C}\mathcal{H}^+,0l}(x; 0)\) (\(U_{{\mathcal {H}}^+, 0l}(y; 0)\)), since the latter contains a non-vanishing \(\log \)-term. By comparison of the leading order coefficients we thus obtain
Note that \(\underline{b} +1 - \underline{c} = \underline{b} +1 - \underline{{\tilde{c}}} =-l \in -{\mathbb {N}}\) and thus, as we observed in the proof of Proposition 6.22, \(B_{\mathcal{C}\mathcal{H}^+_r,0l}(x;0)\) and \(A_{{\mathcal {H}}^+_l, 0l}(y; 0) \) are polynomials. Since \(U_{\mathcal{C}\mathcal{H}^+,0l}(x; 0)\) is clearly not a polynomial because of the \(\log \)-term, it directly follows from (6.30) that we must have \(Y_{{\mathcal {H}}^+_l, 0\,l}(0) = 0\).
Expanding (6.30) in terms of our original systems of fundamental solutions gives
which directly shows that \({\mathfrak {R}}_{{\mathcal {H}}^+_l, 0l}(\omega )\) is analytic on \({\mathbb {R}}\) and vanishes at \(\omega = 0\), and
Since we have shown that \(Y_{{\mathcal {H}}^+_l, 0l}(0) =0\) it follows that \({\mathfrak {T}}_{{\mathcal {H}}^+_r, 0l}(\omega )\) is analytic on all of \({\mathbb {R}}\). Moreover, we have \({\mathfrak {R}}_{{\mathcal {H}}^+_r, 0\,l}(\omega ) = Y_{{\mathcal {H}}^+, 0\,l}(\omega ) + \frac{{\tilde{e}}_2(\omega , 0, l)}{{\tilde{\gamma }} + 1} X_{{\mathcal {H}}^+_l, 0\,l}(\omega ) - \frac{e_2(\omega , 0, l)}{\gamma +1} {\mathfrak {T}}_{{\mathcal {H}}^+_r, 0\,l}(\omega )\), from which it follows that \(\omega \cdot {\mathfrak {R}}_{{\mathcal {H}}^+_r, 0l}(\omega )\) extends analytically to \(\omega = 0\). \(\square \)
Note that (6.31) directly shows that our previous approach for \(m \ne 0\) of showing that \({\mathfrak {T}}_{{\mathcal {H}}^+_r, ml}(0) \ne 0\), namely by computing the transmission coefficient for the simpler hypergeometric equation, does not directly transfer to \(m =0\), since here we actually need to know the value of \(\partial _\omega Y_{{\mathcal {H}}^+_l, 0\,l}(0)\), which is a statement that goes beyond the hypergeometric equation. The omega derivative can be computed – however, it seems easier to use the Teukolsky-Starobinsky conservation law instead which has been made use of recently and developed in much detail in [64, 65]Footnote 52.
6.2.5 The Teukolsky-Starobinsky Conservation Law
What is needed of the Teukolsky-Starobinsky conservation law for this paper can be developed quite quickly, which keeps the paper self-contained. To make contact with [64, 65] we begin by noting that  satisfies (5.28) if, and only if,
satisfies (5.28) if, and only if,  satisfies
satisfies
Note that (6.32) is the radial Teukolsky equation in its most common form as it also appears for example in (150) of [15] where, however, their \(\lambda _{ml}^{[s]}\) differs from ours here by a minus sign. A direct computation, see also [15], gives furthermore that \(R_{ml}^{[s]}(r; \omega )\) satisfies (6.32) if, and only if, \(u_{ml}^{[s]}(r; \omega ):= \Delta ^{\nicefrac {s}{2}} (r^2 + a^2)^{\nicefrac {1}{2}} R_{ml}^{[s]}(r; \omega )\) satisfies
with
Note that one has \(V^{[s]}_{ml}(r; \omega ) = \overline{V^{[-s]}_{ml}(r; \omega )}\), for which we recall \(\lambda _{ml}^{[s]}(\omega ) - s = \lambda _{ml}^{[-s]}(\omega ) + s\) from Proposition 5.2. It follows that if \(u_{ml}^{[-2]}\) is a solution of (6.33) with \(s = -2\), then \(\overline{u_{ml}^{[-2]}}\) is a solution of (6.33) with \(s = +2\). Unwinding the above relations we find that if  satisfies (5.28) (or (6.1)) with \(s = -2\) then
satisfies (5.28) (or (6.1)) with \(s = -2\) then  satisfies (6.33) with \(s = +2\) and thus
satisfies (6.33) with \(s = +2\) and thus

satisfies (5.28) (or (6.1)) with \(s = +2\).
Moreover, we observe that since (6.33) does not have any first order terms, the Wronskian
is conserved in r for any two solutions \(u_{ml}^{[s]}(r^*; \omega )\) and \(w_{ml}^{[s]}(r^*; \omega )\) of (6.33). Hence, if \(v_{1, ml}^{[+2]}(x; \omega )\) and \(v_{2,ml}^{[+2]}(x; \omega )\) are two solutions of (6.1) with \(s = +2\) then
where we have used \(\frac{d}{dr^*} = \frac{\Delta }{r^2 + a^2} \frac{1}{r_+ - r_-} \frac{d}{dx}\).
The Teukolsky-Starobinsky identities allow us to produce a solution for the \(s=-2\) equation from one of the \(s=+2\) equation – and vice versa. Here, only the first direction is needed which is straightforward to establish for the radial Teukolsky equation in the form (6.1). We claim that if \(v^{[+2]}\) is a solution to (6.1) with \(s=+2\), then \(\frac{d^4}{dx^4} v^{[+2]}\) is a solution to (6.1) with \(s=-2\). To prove this we first note that (6.2) gives the following relation of the parameters of the Heun equation for \(s\pm 2\)
where we have used again \(\lambda _{ml}^{[s]}(\omega ) - s = \lambda _{ml}^{[-s]}(\omega ) + s\). Taking \(\frac{d^4}{dx^4}\) of (6.1) now gives
where we have used \(12 \alpha ^{[+2]} + 4 \delta ^{[+2]} = 0\).
We now apply this to the Frobenius solutions for \(\omega \ne \omega _+m, \omega _- m\). Recalling \(\frac{d}{dy} = - \frac{d}{dx}\) we have
With the notation from Section 2.1.1 and 2.1.2 we find near \(r = r_+\)
and near \(r=r_-\)
Note that \({\mathcal {D}}_\pm \) is regular at \(r= r_\pm \) and that we have \(|{\mathcal {D}}_{\pm }| = 1\). We also recall that \(\Delta = (r_+ - r_-)^2 (x-1)x = (r_+ - r_-)^2 (y-1)y\).
By (6.34)
is a solution of (6.1) with \(s = +2\). Comparing asymptotics we find
Similarly we have
Again by (6.34)
is a solution of (6.1) with \(s = +2\). Noting that \(\overline{\gamma ^{[+2]}} = - \gamma ^{[+2]} -2\) and comparing asymptotics we find
We now apply (6.35) to \(A_{{\mathcal {H}}^+_r, ml}^{[+2]}(x; \omega )\) and \(\Delta ^2 e^{-2im {\overline{r}}} e^{2 i \omega r^*} \overline{\frac{d^4}{dy^4} A_{{\mathcal {H}}^+_r, ml}^{[+2]} }\). Using again (6.36) and (6.38) we obtain
for \(y \rightarrow 0\), where we have used
for \(y \rightarrow 0\). We now evaluate (6.40) for \(x \rightarrow 0\). Note that it follows from differentiating
Hence, the constant from (6.40) is also given by
for \(x \rightarrow 0\), where we have used
as \(x \rightarrow 0\). From (6.40) and (6.41) we now obtain the conservation law
which is valid for \(\omega \ne \omega _+m, \omega _-m\). From now on again we will drop the superscript \(s=+2\).
We evaluate the coefficients next. We set \(\xi := \frac{4iMr_-}{r_+ -r_-}(\omega - \omega _-m)\) and \({\tilde{\xi }}:= - \frac{4iMr_+}{r_+ - r_-}(\omega - \omega _+m)\). Let us agree that \(\xi (0)\) and \({\tilde{\xi }}(0)\) refer to \(\xi (\omega = 0) = -\frac{2iam}{r_+ -r_-} = -{\tilde{\xi }}(\omega = 0)\). Then \({\tilde{\gamma }} = -1 + {\tilde{\xi }}\) and \(\gamma = -1 + \xi \). We observe that
The recursion relation (6.10) gives
and similarly for the \(a_i\), where all parameters are replaced by their tilded analogues.
We now proceed by setting \(m=0\). However, see Remark 6.49for \(m \ne 0\). For \(m=0\) (6.42) is valid for \(\omega \ne 0\). We will show that if we multiply by \(\omega \) then both sides extend analytically to \(\omega = 0\).
From (6.44) and (6.4) we obtain successively
where \(\varepsilon (0) = (l-2)(l+3) +4 >0\). Thus
and similarly
Multiplying (6.42) by \(\omega \) and using (6.43) we get
By Proposition 6.27\({\mathfrak {T}}_{{\mathcal {H}}^+_r, 0l}(\omega )\) and \(\omega {\mathfrak {R}}_{{\mathcal {H}}^+_r, 0l}(\omega )\) extend analytically to \(\omega =0\). By the above, \(\omega \cdot c_4(\omega , 0, l)\) and \(\omega \cdot a_4(\omega , 0, l)\) do as well. We may thus take the limit \(\omega \rightarrow 0\) in (6.47) to obtain
where we used (6.45) and (6.46). Brining the last term over to the left hand side this in particular implies the following
Proposition 6.48
We have \({\mathfrak {T}}^{[s]}_{{\mathcal {H}}^+_r, 0l}(0) \ne 0\).
We conclude this section with the following
Remark 6.49
For \(m \ne 0\) the conservation law (6.42) may be evaluated directly at \(\omega = 0\). A direct computation using (6.44) gives \(\overline{c_4(0,m,l)} = \frac{[\varepsilon (0)]^2 [2+ \varepsilon (0)]^2}{24} \frac{1}{|1 + \xi |^2 (2 - \xi ) \xi }\) and \(\overline{a_4(0,m,l) } = \frac{[\varepsilon (0)]^2 [2+ \varepsilon (0)]^2}{24} \frac{1}{|1 + {\tilde{\xi }}|^2 (2 - {\tilde{\xi }}) {\tilde{\xi }}}\). Plugging those values into (6.42), together with (6.43), gives
This would have been another way of showing that \({\mathfrak {T}}_{{\mathcal {H}}^+_r, ml}(0) \ne 0\) for \(m \ne 0\). However, the approach taken in Section 6.2.3 is more direct. Note that if we use the additional information that \({\mathfrak {R}}_{{\mathcal {H}}^+_r, ml}(0) = 0\), which was shown in Section 6.2.3, then we recover that \(|{\mathfrak {T}}_{{\mathcal {H}}^+_r, ml}(0)| = 1\), which is of course compatible with Remark 6.26.
7 Determination of the Coefficients \(a_{{\mathcal {H}}^+_l, ml}(\omega )\) and \(a_{{\mathcal {H}}^+_r, ml}(\omega )\) in Terms of the Initial Data on \({\mathcal {H}}^+_l\) and \({\mathcal {H}}^+_r\)
We will replace in this section the r-coordinate by the y-coordinate for convenience. Recall that \(y = \frac{r_+ - r}{r_+ - r_-}\). Also recall from Theorem 5.26 and (6.12) the representation

Note that while we know that for example \(A_{{\mathcal {H}}^+_r, ml}(y; \omega )\) has a pole at \(\omega = \omega _+ m\), we know that the terms in the linear combination conspire so that the total underbraced term is more regular, in particular continuous in \(\omega \) for \(y \in (0,1)\). In this section we will relate the coefficients \(a_{{\mathcal {H}}^+_r, ml}(\omega )\) and \(a_{{\mathcal {H}}^+_l, ml}(\omega )\) to the initial data on \({\mathcal {H}}^+_r\) and \({\mathcal {H}}^+_l\) (at least in a neighbourhood of \(\omega = 0\)).
7.1 Passing to the Limit \(r \rightarrow r_+\) in \((v_+,r, \theta , \varphi _+)\) Coordinates
We begin with the following
Lemma 7.2
Under the assumptions from Section 3 we have  .
.
Proof
Recall that

It follows from the exponential decay of \(\psi |_{{\mathcal {H}}^+_r}\) in \(v_+\) for \(v_+ \rightarrow - \infty \) (by Assumption 2.46) together with (3.4) and \(q_r\) being in particular bigger than 1 that
Together with the boundedness of \(S_{ml}^{[s]}(\cos \theta ; \omega )\) and its continuous dependence on \(\omega \) the result now follows from dominated convergence. \(\square \)
Proposition 7.4
Let \(\psi \) satisfy the assumptions from Section 3. We then have  for all \(\omega \ne \omega _+m\). In particular \(a_{{\mathcal {H}}^+_r, ml}\) extends as a \(C^0\) function to \(\omega = \omega _+m\).
for all \(\omega \ne \omega _+m\). In particular \(a_{{\mathcal {H}}^+_r, ml}\) extends as a \(C^0\) function to \(\omega = \omega _+m\).
Proof
By (4.28) of Corollary 4.27 we have \(\int _{{\mathbb {R}}\times {\mathbb {S}}^2}|\psi (v_+, y, \theta , \varphi _+) - \psi (v_+, 0, \theta , \varphi _+)|^2 \, \textrm{vol}_{{\mathbb {S}}^2}dv_+ \rightarrow 0\) for \(y \rightarrow 0\). By Plancherel (5.20) this gives

Fix m and l. It now follows that there is a sequence \(y_n \rightarrow 0\) with  for almost every \(\omega \in {\mathbb {R}}\). For \(\omega \ne \omega _+ m\) we have
for almost every \(\omega \in {\mathbb {R}}\). For \(\omega \ne \omega _+ m\) we have

as \(y_n \rightarrow 0\) by the normalisation of the Frobenius solutions – and thus we have  for a.e. \(\omega \in {\mathbb {R}}{\setminus } \{\omega _+m\}\). Since both functions are continuous on \({\mathbb {R}}{\setminus } \{\omega _+m\}\) by Lemmas 6.13 and 7.2 they agree everywhere. \(\square \)
for a.e. \(\omega \in {\mathbb {R}}{\setminus } \{\omega _+m\}\). Since both functions are continuous on \({\mathbb {R}}{\setminus } \{\omega _+m\}\) by Lemmas 6.13 and 7.2 they agree everywhere. \(\square \)
Proposition 7.5
The assumptions (3.1), (3.2), and (3.3) from Section 3, together with the regularity Assumption 2.46, imply that  for any \(0 \leqslant q < p_0\), \(q \in {\mathbb {N}}_0\) and
for any \(0 \leqslant q < p_0\), \(q \in {\mathbb {N}}_0\) and  for any \(\varepsilon >0\).
for any \(\varepsilon >0\).
Proof
We drop the \(|_{{\mathcal {H}}^+_r}\) from \(\psi |_{{\mathcal {H}}^+_r}\) here to ease the notation. We only consider \(\psi \) restricted to the event horizon. It follows from the regularity Assumption 2.46, which ensures exponential decay of \(\psi \) for \(v_+ \rightarrow -\infty \), that (3.1), (3.2), (3.3) imply
for all \(0 \leqslant q < p_0\), \(q \in {\mathbb {N}}_0\). Recall from Section 3 that

denotes the projection of the Fourier transform  of \(\psi \in L^2_{v_+}L^2_{{\mathbb {S}}^2}\) (see (5.17)) onto the spin 2-weighted spherical harmonic \(Y^{[s]}_{ml}(\theta , \varphi _+; 0)\). The map \((\cdot )_{S(ml)}\) is clearly an isometry \(L^2_\omega L^2_{{\mathbb {S}}^2} \rightarrow L^2_\omega \ell ^2_{ml}\). By Plancherel (7.6) is thus equivalent to
of \(\psi \in L^2_{v_+}L^2_{{\mathbb {S}}^2}\) (see (5.17)) onto the spin 2-weighted spherical harmonic \(Y^{[s]}_{ml}(\theta , \varphi _+; 0)\). The map \((\cdot )_{S(ml)}\) is clearly an isometry \(L^2_\omega L^2_{{\mathbb {S}}^2} \rightarrow L^2_\omega \ell ^2_{ml}\). By Plancherel (7.6) is thus equivalent to



for all \(0 \leqslant q < p_0\), \(q \in {\mathbb {N}}_0\). It follows from


Together with (7.9) this gives in particular

We relate the projection onto the spin 2-weighted spheroidal harmonics to that onto the spin 2-weighted spherical harmonics in the next step.
We expand in \(L^2([-1,1], d \cos \theta )\)
where \(E_{mll'}^{[s]}(\omega ): \ell ^2_{l'} \rightarrow \ell ^2_{l}\) is a change of orthonormal basis map for every \(\omega \in {\mathbb {R}}\) and it is also smooth in \(\omega \). We have
where, for fixed m, l, the constant can be chosen uniform on compact subsets of \(\omega \) by the smoothness of \(S^{[s]}_{ml}(\omega )\) in \(\omega \), see Proposition 5.2. We have  in \(L^2_\omega ({\mathbb {R}})\) and weak differentiation gives
in \(L^2_\omega ({\mathbb {R}})\) and weak differentiation gives

Consider first all the terms  for \({q'} \geqslant 1\). We estimate those on the compact subset \([-2,2] \subseteq {\mathbb {R}}\) using (7.7) and (7.12) as follows:
for \({q'} \geqslant 1\). We estimate those on the compact subset \([-2,2] \subseteq {\mathbb {R}}\) using (7.7) and (7.12) as follows:

Note in particular that if we replace \(p_0\) in (7.13) by \(0 \leqslant q <p_0\) then all terms can be estimated in this way. This proves the first claim in the proposition. We go back to (7.13) with \(p_0\) and consider next those terms with \({q'}=0\) and \(l \ne l_0\). We note that for \(l \ne l_0\) we have \(E^{[s]}_{m_0l_0l}(0) = 0\) and thus \(E^{[s]}_{m_0l_0l}(\omega ) = \int _0^\omega \partial _\omega E_{m_0l_0l}^{[s]}(\omega ') \, d \omega '\). Using this we estimate

We continue estimating the first factor on the right hand side for \(\omega \in [-2,2]\) using (7.12)
Using this in (7.14) together with (7.10) gives

It remains the term with \({q'}=0\) and \(l=l_0\) in (7.13), which is  . Note that we have \(E^{[s]}_{m_0l_0l_0}(0)=1\) and thus we can find \(\varepsilon '>0\) such that \(E^{[s]}_{m_0l_0l_0}(\omega ) \geqslant \frac{1}{2}\) for \(|\omega |\leqslant \varepsilon '\). It thus follows from (7.11) that this term is not in \(L_{\omega }^2(-\varepsilon , \varepsilon )\) for any \(\varepsilon >0\). Entering all this information into (7.13) concludes the proof. \(\square \)
. Note that we have \(E^{[s]}_{m_0l_0l_0}(0)=1\) and thus we can find \(\varepsilon '>0\) such that \(E^{[s]}_{m_0l_0l_0}(\omega ) \geqslant \frac{1}{2}\) for \(|\omega |\leqslant \varepsilon '\). It thus follows from (7.11) that this term is not in \(L_{\omega }^2(-\varepsilon , \varepsilon )\) for any \(\varepsilon >0\). Entering all this information into (7.13) concludes the proof. \(\square \)
Corollary 7.15
Under the assumption from Section 3 we have \(\partial _\omega ^qa_{{\mathcal {H}}^+_r, m_0l_0} \in L^2_\omega ([-2,2])\) for any \(0 \leqslant q < p_0\), \(q \in {\mathbb {N}}_0\) and \(\partial _\omega ^{p_0} a_{{\mathcal {H}}^+_r, m_0l_0}(\omega ) \notin L^2_{\omega }(-\varepsilon , \varepsilon )\) for any \(\varepsilon >0\).
Proof
This follows directly from Propositions 7.4 and 7.5. \(\square \)
7.2 Passing to the Limit \(r \rightarrow r_+\) in \((v_-,r, \theta , \varphi _-)\) Coordinates
The determination of \(a_{{\mathcal {H}}^+_l, ml}(\omega )\) is more complicated. Note that \(\psi \) vanishes on \({\mathcal {H}}^+_l\), so in order to take a non-vanishing limit we consider \((\partial _r|_+)^2 \psi = \frac{1}{(r_+ - r_-)^2} (\partial _y|_+)^2 \psi =: \frac{1}{(r_+ - r_-)^2} \partial _y^2 \psi \) instead of \(\psi \). Here, and throughout this section, we have made the convention that \(\partial _y^2 \psi \) is always with respect to the \((v_+, y, \theta , \varphi _+)\)-coordinate system, even if we otherwise use \((v_-, y, \theta , \varphi _-)\)-coordinates. This is simply to ease the amount of notation. There are now two main differences to the limiting procedure of Section 7.1. The first one is that \(\partial _y^2 \psi \) does not vanish at the bottom bifurcation sphere, so one cannot hope to take an \(L^2\)-limit \(y \rightarrow 0\) in \((v_-, y, \theta , \varphi _-)\)-coordinates. We will instead take a limit in the sense of distributions. The second difference is that the branch \(A_{{\mathcal {H}}^+_r, ml}(y; \omega )\) in (7.1) in general also gives a non-vanishing contribution under this limit (see Footnote 54) – by choosing the support of the test functions suitably though and, in the case of \(m_0 =0\), also using that the reflection coefficient of the left event horizon vanishes at \(\omega = 0\) (see Corollary 7.29 and Section 8), we can circumvent this second difficulty. We begin with introducing our test functions.
Lemma 7.16
Let \(\xi \in C^{\infty }_0({\mathbb {R}})\) and set
Then \(||v^j \partial _{v}^k \tau _{\xi , ml} ||_{L^\infty \big ({\mathbb {R}}\times (- \pi , \pi )\big )} \leqslant C(j,k) < \infty \) for all \(j,k \in {\mathbb {N}}_0\), where C(j, k) also depends on m, l and \(\xi \).
Proof
Differentiating under the integral we compute
Since \(S_{ml}^{[s]}(\cos \theta ;\omega )\) and all its \(\omega \)-derivatives are continuous on \([-1,1] \times {\mathbb {R}}\) and since \(\xi (\omega )\) is smooth and of compact support, the \(L^\infty \) norm in \( \theta \) of the integrand is absolutely integrable. \(\square \)
Proposition 7.17
Let \(\xi \in C^\infty _0({\mathbb {R}})\) and consider the assumptions in Section 3. Then as \(y \rightarrow 0\)
Proof
Let \(\varepsilon >0\) be given. Then, using Lemma 7.16 and for a \(v_0 \leqslant 0 \) to be chosen later, we estimate
where we have used Corollary 4.49 and the regularity assumption 2.46 to infer that \(\partial _y^2 \psi \) is uniformly bounded in \(\{r_0 \leqslant r \leqslant r_+\} \cap \{v_- \leqslant v_0\}\) for some \(r_-< r_0 < r_+\). By Lemma 7.16\(\tau _{\xi ,ml}\) is integrable, so we can choose \(v_0 \ll -1\) such that the last term is less than \(\frac{\varepsilon }{2}\). By (4.29) we have that for all y close enough to 0 the first summand on the right hand side is less than \(\frac{\varepsilon }{2}\). \(\square \)
We now compute both sides of (7.18). We start with the right hand side and recall the convention \(\partial _y = \partial _y|_+\). We use \((V^-_{r_+}, \theta , \Phi _{r_+})\) coordinates on \({\mathcal {H}}^+_l\) and write
We first consider the contribution of \(\Omega \) to the right hand side of (7.18). Note that we have \(\Omega (v_-, \theta , \varphi _-) = \partial _y^2 \psi |_{{\mathcal {H}}^+_l}(v_-, \theta , \varphi _-)\) for \(v_- \geqslant 0\) and also \(|\Omega (V^-_{r_+}, \theta , \Phi _{r_+})| \leqslant C \cdot V^-_{r_+}\) for \(0 \leqslant V^-_{r_+} \leqslant 1\). Since we have \(V^-_{r_+} = e^{\kappa _+ v_-}\) this gives us exponential decay in \(v_-\) towards the bottom bifurcation sphere, i.e., \(|\Omega (v_-, \theta , \varphi _-)| \leqslant C \cdot e^{\kappa _+ v_-}\) for \(v_- \leqslant 0\). By assumption (3.6) and (4.24) we can thus use Fubini (or Plancherel) to obtain

where we introduced \(\Omega ^-(v_-, \theta , \varphi _-):= \Omega (-v_-, \theta , \varphi _-)\) to account for the different sign in the phase of the Fourier transform compared to our convention (5.19).
By assumption (3.6) and (4.24) we have \(\int _{{\mathbb {R}}} \int _{{\mathbb {S}}^2} (1 + |v_-|^{q_l}) | \Omega ^-(v_-, \theta , \varphi _-)|^2 \, \textrm{vol}_{{\mathbb {S}}^2}dv_- < \infty \) and thus  for all \(0 \leqslant q \leqslant \frac{q_l}{2}\), \(q \in {\mathbb {N}}_0\). Proposition 5.22 now gives
for all \(0 \leqslant q \leqslant \frac{q_l}{2}\), \(q \in {\mathbb {N}}_0\). Proposition 5.22 now gives

for all \(0 \leqslant q \leqslant \frac{q_l}{2}\), \(q \in {\mathbb {N}}_0\), where \(\varepsilon >0\) is as in Proposition 5.22.Footnote 53
We now come to the contribution of the first term in (7.19) to (7.18). We compute
Let us note that \(\Psi _{ml}(\omega )\) is clearly smooth in \(\omega \). We now divide the domain of integration into \(|\omega - \omega _+ m| \leqslant \delta \) and its complement for some \(\delta >0\). We first compute
For the domain \(|\omega - \omega _+m| > \delta \) we compute using Riemann-Lebesgue
Clearly \(\mathring{\Psi }_{ml}(\omega )\) is smooth in \(\omega \). Combining everything and letting \(\delta \) go to zero we obtain
We now claim that we have
for all \(q \in {\mathbb {N}}_0\) for some \(\varepsilon >0\). To see this, we first recall that \(\Psi _{ml}(\omega ) = \int _{{\mathbb {S}}^2} \partial _y^2 \psi |_{{\mathcal {H}}^+_l}(0, \theta , \Phi _{r_+}) S^{[s]}_{ml}(\cos \theta ; \omega ) e^{-im \Phi _{r_+}} \, \textrm{vol}_{{\mathbb {S}}^2}\) and thus, using the notation from Proposition 5.6,
Hence, we obtain
The claim (7.22) with the sum restricted to \(m \ne 0\) then follows directly: if necessary we choose \(\varepsilon >0\) from Proposition 5.6 even smaller than \(|\omega _+|\) and then differentiate \(\mathring{\Psi }_{ml}(\omega ) = \frac{\Psi _{ml}(\omega ) - \Psi _{ml}(\omega _+m)}{\omega - \omega _+ m}\) in the region \((-\varepsilon , \varepsilon )\), which is disjoint from \(\omega = \omega _+m\), and apply (7.23) and Proposition 5.6.
To see that the contribution from \(m=0\) to the sum in (7.22) is also finite we observe that \(\mathring{\Psi }_{0\,l}(\omega ) = \frac{\int _0^\omega \partial _\omega \Psi _{0\,l}(\omega ') \, d \omega '}{\omega } = \int _0^1 \partial _\omega \Psi _{0\,l}(\tau \omega ) \, d \tau \) with \(\omega ' = \tau \omega \) and thus
Using (7.23) we continue to estimate
and for \(\omega \in (-\varepsilon , \varepsilon )\)
Note that the underbraced term is independent of \(\tau \omega \). Thus the integration in \(\tau \) is trivial and we can also trivially integrate (7.24) in \(\omega \) over \((-\varepsilon , \varepsilon )\). This finally proves the claim (7.22).
We summarise what we have shown in the following
Proposition 7.25
Under the assumptions from Section 3 and for every \(\xi \in C^\infty _0({\mathbb {R}}, {\mathbb {C}})\) we have

where \(\Omega ^-(v_-, \theta , \varphi _-) = \Omega (-v_-, \theta , \varphi _-)\) and \(\Omega \) is defined in (7.19), \(\Psi _{ml}\) is defined in (7.20), \(\mathring{\Psi }_{ml}\) is defined in (7.21), and there exists an \(\varepsilon >0\) such that  for all \(0 \leqslant q \leqslant \frac{q_l}{2}\), \(q \in {\mathbb {N}}_0\), with \(q_l\) as in Section 3.
for all \(0 \leqslant q \leqslant \frac{q_l}{2}\), \(q \in {\mathbb {N}}_0\), with \(q_l\) as in Section 3.
Let us remark that we only need the statement of this proposition for test functions \(\xi \) which are supported away from \(\omega = \omega _+m\). This would slightly shorten the proof – the delta distribution term would be absent. Moreover, we only need the statement for the mode \(m_0l_0\). We next evaluate the left hand side of (7.18).
Proposition 7.26
Under the assumptions of Section 3 and for \(\xi \in C^\infty _0({\mathbb {R}}{\setminus } \{ \omega _+m\}, {\mathbb {C}})\) we have
where \(F_+\) and \(\phi _+\) are as in Sects. 2.1.1 and 2.1.2.
It is important for the validity of the proposition as stated that one chooses the support of \(\xi \) away from \(\omega _+ m\).Footnote 54
Proof
Recall that we have \(\varphi _- = \varphi _+ - 2 {\overline{r}}\) and \(v_- = 2r^* - v_+\) and \({\overline{r}} = \omega _+ r^* - \phi _+(r)\). We thus obtain

where we have used the same kind of reasoning as in the proof of Theorem 5.26, \('\) denotes \(\frac{d}{dy}\), and we consider \(r^*\) and r as functions of y. Recall from Lemma 6.13 that \(a_{{\mathcal {H}}^+_r, ml}, a_{{\mathcal {H}}^+_l, ml} \in C^0({\mathbb {R}}{\setminus }\{ \omega _+m\}, {\mathbb {C}})\). Since we have chosen the support of \(\xi \) to be disjoint from \(\omega _+m\) it is immediate that we can evaluate the integrals of the two summands separately. We begin with the first one.
We have \(A_{{\mathcal {H}}^+_r, ml}''(y; \omega ) = \sum _{j = 0}^\infty j(j-1) a_j(\omega , m, l) y^{j -2} = 2a_2(\omega , m, l) + {\mathcal {O}}(y)\). Note that the \({\mathcal {O}}(y)\) is uniform in \(\omega \) on the support of \(\xi \); and \(a_2(\omega , m,l)\) is also uniformly bounded on \(\textrm{supp}(\xi )\). Moreover we have \(r^*(y) \rightarrow - \infty \) for \(y \rightarrow 0\). We thus obtain from Riemann-Lebesgue and direct estimation
In order to evaluate the second summand in (7.27) we first note that for \(s=2\)
Also recall that \(y = \frac{r_+ - r}{r_+ - r_-}\) and, from Section 2.1.2, \(r_+ - r= e^{2 \kappa _+ r^*} e^{- 2 \kappa _+ F_+(r)}\). This gives
Thus
\(\square \)
It now follows from Propositions 7.17, 7.25, and 7.26 that for \(\xi \in C^\infty _0({\mathbb {R}}{\setminus } \{ \omega _+m\}, {\mathbb {C}})\) we have

Note that  is continuous in \(\omega \) (this follows as in the proof of Lemma 7.2). Thus, all terms multiplying \(\overline{\xi (\omega )}\) on each side are (at least) continuous in \(\omega \) away from \(\omega _+m\). We thus conclude that for \(\omega \ne \omega _+m\)
is continuous in \(\omega \) (this follows as in the proof of Lemma 7.2). Thus, all terms multiplying \(\overline{\xi (\omega )}\) on each side are (at least) continuous in \(\omega \) away from \(\omega _+m\). We thus conclude that for \(\omega \ne \omega _+m\)

Corollary 7.29
Under the assumptions from Section 3 there exists \(\varepsilon _0 >0\) such that
-
1.
for \(m \ne 0\) we have \(\partial _\omega ^q a_{{\mathcal {H}}^+_l, ml} \in L^2_{(-\varepsilon _0, \varepsilon _0)} \ell ^2_{\begin{array}{c} m,l \\ m \ne 0 \end{array}}\) for all \(0 \leqslant q \leqslant \frac{q_l}{2}\), \(q \in {\mathbb {N}}_0\).
-
2.
for \(m = 0\) we have that \(\omega \cdot a_{{\mathcal {H}}^+_l, 0l}\) extends continuously to \(\omega =0\) and, moreover, we have \(\partial _\omega ^q (\omega a_{{\mathcal {H}}^+_l, 0\,l}) \in L^2_{(-\varepsilon _0, \varepsilon _0)} \ell ^2_{l} \) for all \(0 \leqslant q \leqslant \frac{q_l}{2}\), \(q \in {\mathbb {N}}_0\).
Proof
This is immediate from (7.28) and Proposition 7.25. \(\square \)
8 Proof of the Main Theorems
8.1 Proof of Theorem 3.7
We are now in a position to prove the main theorem.
Proof of Theorem 3.7
Recall from Proposition 4.64 that the \(L^2({\mathbb {R}}\times {\mathbb {S}}^2)\)-limit of \(\psi (v_+,r, \theta , \varphi _+)\) for \(r \rightarrow r_-\) exists and that we labelled it suggestively by \(\psi (v_+, r_-, \theta , \varphi _+)\). Taking the Teukolsky transform we have

where  is continuous in \(\omega \) by (4.65), cf. the proof of Lemma 7.2.Footnote 55 By Proposition 4.64 and Plancherel we have for \(r \rightarrow r_-\)
is continuous in \(\omega \) by (4.65), cf. the proof of Lemma 7.2.Footnote 55 By Proposition 4.64 and Plancherel we have for \(r \rightarrow r_-\)

Fix m and l. Then there exists a sequence \(r_n \rightarrow r_-\) such that  for almost all \(\omega \in {\mathbb {R}}\).
for almost all \(\omega \in {\mathbb {R}}\).
It now follows from (6.12) and (6.21) that for \(\omega \ne \omega _+m, \omega _-m\)

The asymptotics of the Frobenius solutions from Proposition 6.11 imply  for \(\omega \ne \omega _+m, \omega _-m\) and thus we obtain
for \(\omega \ne \omega _+m, \omega _-m\) and thus we obtain

for almost every \(\omega \in {\mathbb {R}}{\setminus }\{ \omega _+m, \omega _-m\} \). We claim that there is an \(\varepsilon >0\) such that the right hand side is continuous for \(\omega \in (-\varepsilon , \varepsilon )\). For \(m \ne 0\) this follows directly from Lemma 6.13 and Proposition 6.22. For \(m = 0\) Propositions 7.4 and 6.27 imply that \({\mathfrak {T}}_{{\mathcal {H}}^+_r, 0l}(\omega ) a_{{\mathcal {H}}^+_r, 0l}(\omega ) \) is continuous and, moreover, Proposition 6.27 implies that \({\mathfrak {R}}_{{\mathcal {H}}^+_l, 0l}(\omega )\) is of the form \({\mathfrak {R}}_{{\mathcal {H}}^+_l, 0\,l}(\omega ) =: \omega \cdot \widehat{{\mathfrak {R}}_{{\mathcal {H}}^+_l, 0\,l}}(\omega )\) with \(\widehat{{\mathfrak {R}}_{{\mathcal {H}}^+_l, 0l}}(\omega )\) analytic for all \(\omega \in {\mathbb {R}}\). Hence, Corollary 7.29 implies that also \({\mathfrak {R}}_{{\mathcal {H}}^+_l, 0\,l}(\omega ) a_{{\mathcal {H}}^+_l, 0\,l}(\omega ) = \widehat{{\mathfrak {R}}_{{\mathcal {H}}^+_l, 0\,l}}(\omega ) (\omega \cdot a_{{\mathcal {H}}^+_l, 0\,l}(\omega ))\) is continuous in \(\omega \). We thus obtain (8.1) for all \(\omega \in (-\varepsilon , \varepsilon )\).
We consider \(\underline{{\textbf {the case}} m_0 \ne 0}\) first and compute

The derivatives of the transmission and reflection coefficients are uniformly bounded on \((-\varepsilon , \varepsilon )\) by Proposition 6.22. It thus follows from Corollary 7.29 and Corollary 7.15 that all terms on the right hand side of (8.2), with the exception of \({\mathfrak {T}}_{{\mathcal {H}}^+_r, m_0l_0}(\omega ) \cdot \partial _\omega ^{p_0} a_{{\mathcal {H}}^+_r, m_0l_0}(\omega )\), are in \(L^2_\omega (\big (-\varepsilon _0,\varepsilon _0)\big )\) for some \(\varepsilon _0 >0\). On the other hand \({\mathfrak {T}}_{{\mathcal {H}}^+_r, m_0l_0}(\omega ) \) is strictly bounded away from 0 in a small neighbourhood of \(\omega = 0\) by Proposition 6.22. It thus follows from Corollary 7.15 that \({\mathfrak {T}}_{{\mathcal {H}}^+_r, m_0l_0}(\omega ) \cdot \partial _\omega ^{p_0} a_{{\mathcal {H}}^+_r, m_0l_0}(\omega ) \notin L^2_\omega \big ((-\varepsilon , \varepsilon )\big )\) for any \(\varepsilon >0\). Hence we obtain that  for any \(\varepsilon >0\).
for any \(\varepsilon >0\).
We proceed with \(\underline{{\textbf {the case}} m_0 = 0}\) and compute

It follows again from Corollary 7.29 and Corollary 7.15 that all terms on the right hand side of (8.3), with the exception of \({\mathfrak {T}}_{{\mathcal {H}}^+_r, 0l_0}(\omega ) \cdot \partial _\omega ^{p_0} a_{{\mathcal {H}}^+_r, 0l_0}(\omega )\), are in \(L^2_\omega (\big (-\varepsilon _0,\varepsilon _0)\big )\) for some \(\varepsilon _0 >0\). On the other hand \({\mathfrak {T}}_{{\mathcal {H}}^+_r, 0l_0}(\omega ) \) is strictly bounded away from 0 in a small neighbourhood of \(\omega = 0\) this time by Proposition 6.27. It thus follows from Corollary 7.15 that \({\mathfrak {T}}_{{\mathcal {H}}^+_r, 0l_0}(\omega ) \cdot \partial _\omega ^{p_0} a_{{\mathcal {H}}^+_r, 0l_0}(\omega ) \notin L^2_\omega \big ((-\varepsilon , \varepsilon )\big )\) for any \(\varepsilon >0\). Hence we obtain that  for any \(\varepsilon >0\).
for any \(\varepsilon >0\).
Taking the two cases together we have shown that

We claim that this implies
If (8.5) was finite then together with \(\int _{{\mathbb {R}}}\int _{{\mathbb {S}}^2} | \psi (v_+, r_-, \theta , \varphi _+)|^2 \, \textrm{vol}_{{\mathbb {S}}^2}dv_+ < \infty \) from (4.65) we would have  for all \(0 \leqslant q \leqslant p_0\). Proposition 5.22 then gives
for all \(0 \leqslant q \leqslant p_0\). Proposition 5.22 then gives  for all \(0 \leqslant q \leqslant p_0\), where \(\varepsilon >0\) is as in Proposition 5.22. This clearly contradicts (8.4) and we thus infer (8.5).
for all \(0 \leqslant q \leqslant p_0\), where \(\varepsilon >0\) is as in Proposition 5.22. This clearly contradicts (8.4) and we thus infer (8.5).
On the other hand by (4.65) we know that
since \(\frac{q_l}{2} \geqslant p_0\) and thus we must have
The theorem now follows from Corollary 4.75. \(\square \)
8.2 Extension Theorem and Proof of Theorem 3.9
Theorem 8.6
Let \(v_0, v_1 \in {\mathbb {R}}\) and let  be a solution of the Teukolsky equation \({\mathcal {T}}_{[2]} \psi = 0\) in \(\underline{{\mathcal {M}}}\cap \{f^+ \geqslant v_0\} \cap \{f^- \leqslant v_1\}\) satisfying the assumptions (3.1), (3.2), (3.3), (3.4) along the right event horizon.Footnote 56 Then there exists a
be a solution of the Teukolsky equation \({\mathcal {T}}_{[2]} \psi = 0\) in \(\underline{{\mathcal {M}}}\cap \{f^+ \geqslant v_0\} \cap \{f^- \leqslant v_1\}\) satisfying the assumptions (3.1), (3.2), (3.3), (3.4) along the right event horizon.Footnote 56 Then there exists a  which extends \(\psi \) (i.e. \(\chi |_{\underline{{\mathcal {M}}}\cap \{f^+ \geqslant v_0\} \cap \{f^- \leqslant v_1\}} = \psi \)) which moreover satisfies the Assumptions 2.46 and condition (3.5).
which extends \(\psi \) (i.e. \(\chi |_{\underline{{\mathcal {M}}}\cap \{f^+ \geqslant v_0\} \cap \{f^- \leqslant v_1\}} = \psi \)) which moreover satisfies the Assumptions 2.46 and condition (3.5).
Proof
The idea of the proof is outlined in Figure 9. Also recall that the level sets of the functions \(f^-\) and \(f^+\) are spacelike hypersurfaces.
We consider the Teukolsky equation (A.5) which is regular in \(\underline{{\mathcal {M}}}\). Recall that \({\tilde{\chi }}\) satisfies (A.5) if, and only if, \(\chi = (V^+_{r_+})^2 {\tilde{\chi }}\) satisfies (2.39). We now consider the induced initial data of \({\tilde{\psi }}:= \frac{1}{(V^+_{r_+})^2} \psi \) on \(\{f^+ = v_0\} \cap \{f^- \leqslant v_1\}\) and, moreover, extend the induced initial data on \(\{f^- = v_1\} \cap \{f^+ \geqslant v_0\}\) smoothly to \(\{f^- = v_1\} \cap \{f^+ \leqslant v_0\}\). Since \({\tilde{\psi }}\) is a solution of (A.5) in \(\{f^+ \geqslant v_0\} \cap \{f^- \leqslant v_1\}\), it is clear that this choice of initial data satisfies the appropriate corner condition. In the appendix A.2 it is shown that the initial value problem for (A.5) is well-posed. We can thus solve backwards to obtain a smooth solution \({\tilde{\chi }}\) of (A.5) in the region \(\{f^- \leqslant v_1\} \cap \{f^+ \leqslant v_0\}\) that attains the prescribed initial data.
In the second step we consider the initial value problem for (A.5) with compactly supported initial data on \({\mathcal {H}}^+_l \cap \{f^- \geqslant v_1\}\), which is a smooth extension of the induced initial data of \({\tilde{\chi }}\) on \({\mathcal {H}}^+_l \cap \{f^- \leqslant v_1\}\), and, moreover, with the induced initial data of \({\tilde{\chi }}\) on \(\{f^- = v_1\}\). Again, the corner condition is satisfied and we obtain a solution in the region \(\{f^- \geqslant v_1\}\). Patching these three solutions together proves the extension theorem. \(\square \)
Proof of Theorem 3.9
This is immediate from Theorem 8.6 and Theorem 3.7. \(\square \)
Notes
See also [45] for the linearised case.
See assumption (3.4) on page 29 for the precise statement.
The definitions of symbols made here are only valid in this section. In the rest of the paper we will use \({\mathcal {M}}, g, r_+, r_-,\) etc. to refer to objects and quantities on Kerr.
See also [30] for a more detailed discussion of the Reissner-Nordström spacetime.
The important properties here are that \(\phi \) vanishes at the bottom bifurcation sphere \({\mathbb {S}}^2_b\) and decays sufficiently fast along \({\mathcal {H}}^+_l\). The first one is not strictly necessary, but simplifies the proof.
We introduce the following notation: for \(f,g: {\mathbb {R}}\supseteq I \rightarrow {\mathbb {C}}\) the notation \(f \sim g\) for \(I \ni x \rightarrow x_0 \in {\mathbb {R}}\) stands for \(\lim _{x \rightarrow x_0} \frac{f(x)}{g(x)} = 1\). When obvious which limit point is considered, we may just write \(f \sim g\).
Recall that \(\phi |_{{\mathcal {H}}^+_r}\) has exponential decay towards the bifurcation sphere.
It also extends continuously to \(\mathcal{C}\mathcal{H}^+_r\).
For \(v \rightarrow - \infty \) one can replace \(|v|^{2p_0}\) by \(|v|^q\) for any \(q \in {\mathbb {N}}\). For the definition of the notation \(\simeq \) we refer the reader to the very beginning of Section 2.
Let us remark that a fully fledged scattering theory for the wave equation in the interior of a Reissner-Nordström black hole has been presented in [37].
Recall that \(\psi \) degenerates (vanishes) at \({\mathcal {H}}^+_l\).
Here, \(\lambda _{ml}^{[s]}(\omega )\) denotes the eigenvalue associated to the eigenfunction \(Y^{[s]}_{ml}(\cdot ; \omega )\) of the spin 2-weighted spheroidal Laplacian, see Section 5.1.
The analyticity of \({\mathfrak {T}}_{{\mathcal {H}}^+_l, 0l}\) at \(\omega = 0\) is of no relevance to this paper and has not been explicitly stated, but is also proven as a side-result in the proof of Proposition 6.27. And while we do not show that \({\mathfrak {R}}_{{\mathcal {H}}^+_r, 0l}\) has indeed a pole at \(\omega = 0\), this is what we would expect – and it can be decided by a longer and direct computation. However, this is of no relevance to this paper.
To be slightly more precise here, recall that \(\psi \) vanishes automatically at the bottom bifurcation sphere because of the degeneration of the frame chosen. The Teukolsky analogue of the vanishing of the scalar field at \({\mathbb {S}}^2_b\), which avoids poles in the Fourier expansion coefficients, is the vanishing of \(\partial _r^2 \psi \), which is non-degenerate at \({\mathbb {S}}^2_b\) due to the blow-up of \(\partial _r\) in \((v_+,r, \theta , \varphi _+)\)-coordinates at \({\mathbb {S}}^2_b\).
Being confronted with a non-trivial field at the bottom bifurcation sphere one might still entertain the following approach, which can easily be implemented for the wave equation: by decomposing the initial data, we write the solution \(\psi \) obtained by the above extension procedure as a superposition of a solution \(\psi _1\), the initial data of which is supported on \({\mathcal {H}}^+_l \cup {\mathcal {H}}^+_r\) only in a compact neighbourhood of \({\mathbb {S}}^2_b\), and another solution \(\psi _2\) that vanishes on \({\mathcal {H}}^+_l\) including at \({\mathbb {S}}^2_b\) (and agrees with \(\psi \) on \({\mathcal {H}}^+_r\) for late affine times). One can now run the desired argument for \(\psi _2\) to obtain the singularity at the Cauchy horizon and then use standard energy estimates for \(\psi _1\) to see that \(\psi _1\) is much more regular at the Cauchy horizon – and can essentially be neglected. However, one runs into difficulty when trying to implement this strategy for Teukolsky due to the effective blue-shift effect on \({\mathcal {H}}^+_r\) mentioned earlier. The reader can see directly from (1.27) that the transversal derivative \(\partial _r \psi _1\) of the solution \(\psi _1\), whose trace on \({\mathcal {H}}^+_r\) vanishes for late affine times, will in general grow exponentially along \({\mathcal {H}}^+_r\) – thus prohibiting the stability estimates. (For the wave equation, due to the red-shift effect, the transversal derivative decays exponentially.) For this reason our proof of the blow-up of the Teukolsky field at the Cauchy horizon is more global in nature than for the wave equation.
See Section 2.1 for the definition of \(v_-\). It can be thought of as the analogue of u in Reissner-Nordström.
This is not an issue arising from considering Teukolsky versus the wave equation, but already appears when considering the wave equation on Kerr.
The reason we use both notations is that we find it convenient to use the \({\mathcal {O}}\) notation within equations: an equation of the form \(f = t \cdot {\mathcal {O}}(g) + h\) has to be read as ‘\(f = t \cdot u + h\) with \(u = {\mathcal {O}}(g)\)’. The limit associated with the \({\mathcal {O}}\) notation is often understood from the context and not mentioned explicitly.
To be more precise, depicted is a slice of constant \(0<\theta < \pi \) and each point represents an \({\mathbb {S}}^1\).
In the following \(\big |_\pm \) indicates a partial derivative in the \((v_\pm , r, \theta , \varphi _\pm )\) coordinate system.
Indeed, one could have defined the space
 as the image of \(\Gamma ^\infty (S^2_{\textrm{tf}}T^*{\mathbb {S}}^2)\) under \(\iota _m\). However, for the proof of Proposition 2.47 we will need that
as the image of \(\Gamma ^\infty (S^2_{\textrm{tf}}T^*{\mathbb {S}}^2)\) under \(\iota _m\). However, for the proof of Proposition 2.47 we will need that  even if \(\alpha \) is not trace-free.
even if \(\alpha \) is not trace-free.This differs from the spin s-weighted Laplacian in [15] by an overall minus sign.
Recall that \(m_a\) differs from m by a term proportional to \(\partial _t\) – thus the claim that \({\dot{\alpha }}\) is spin 2-weighted is not trivial.
We have made no attempt in this paper to keep the number of derivatives required as low as possible, one can certainly improve on it. It is also likely that one can improve on the requirement \(2 < q_r\) and thus also on the lower bound on \(2 \leqslant p_0\). The bound \(2 <q_r\) is used in Theorem 5.26 (via Corollary 4.46 – for which we also use all the derivatives assumed) to derive the radial ODE (5.28).
The asymmetry between the number of derivatives assumed on the left and right event horizons can be traced back to the necessity to close the energy estimate near \({\mathcal {H}}^+_r\) at the level of \((\partial _r|_+)^2 \psi \) while near \({\mathcal {H}}^+_l\) we close it at the level of \({\hat{\psi }}\). The higher number of derivatives assumed on \({\mathcal {H}}^+_r\) allows us to ease the presentation of the proof of Proposition 4.11 in Step 6. However, one can certainly improve on that.
with the integration \({\mathcal {H}}^+_r \cap \{v_+ \geqslant 1\}\) replaced by \({\mathcal {H}}^+_r \cap \{v_+ \geqslant v_0\}\)
One expects that these results remain true in the full sub-extremal range, see [51].
Note that away from \(r_\pm \) we have \(\textrm{span}\{\partial _r|_+, \partial _{v_+}, \partial _{\varphi _+}\} = \textrm{span}\{\partial _r|_-, \partial _{v_-}, \partial _{\varphi _-}\} = \textrm{span}\{\partial _r, \partial _{t}, \partial _{\varphi }\}\). Since we carry out the different energy estimates in different coordinates, it is convenient to always consider this combination of derivatives.
Note that the structure for \(s=+2\) is the following: for \({\hat{\psi }}\) strong red-shift for the energy at \({\mathcal {H}}^+_l\), strong blue-shift at \(\mathcal{C}\mathcal{H}^+_r\); for \(\psi \) blue-shift at \({\mathcal {H}}^+_r\), red-shift at \(\mathcal{C}\mathcal{H}^+_l\). This is the reason why the estimate for \(\psi \) at \({\mathcal {H}}^+_r\) is slightly more complicated.
We need to choose \(v_0\) large enough to control the second term on the right hand side of the third multiplier expression computed in B.1. This one is quadratic in \(\partial _r {\hat{\psi }}\), has a positive sign, but a sub-leading \(v_-\)-weight.
This gives control over some higher derivatives which are not stated in Proposition 4.11 and which are not needed. We are wasteful here with derivatives in order to streamline the presentation. Being a bit more careful one can safe a couple of derivatives here.
Concretely, we use
$$\begin{aligned}{} & {} \Big (\mathop {\int }\limits _{\{r=r'\} \cap \{v_+ \geqslant 1\}} h^2 \textrm{vol}_{{\mathbb {S}}^2}dv_+ \Big )^\frac{1}{2} \leqslant \Big (\mathop {\int }\limits _{\{r=r_+\} \cap \{v_+ \geqslant 1\}} h^2 \textrm{vol}_{{\mathbb {S}}^2}dv_+ \Big )^\frac{1}{2} \\ {}{} & {} \quad + \int _{r'}^{r_+} \Big (\int \limits _{\{r={\tilde{r}}\} \cap \{v_+ \geqslant 1\}} (\partial _rh)^2 \textrm{vol}_{{\mathbb {S}}^2}dv_+ \Big )^\frac{1}{2} dr \end{aligned}$$for \(h \in \{ {\widetilde{Z}}^{i_1}_{1,+} {\widetilde{Z}}^{i_2}_{2,+} {\widetilde{Z}}^{i_3}_{3,+} \partial _{v_+}^j\partial _r^k (\partial _{v_+}^d {\mathcal {Q}}_{[s]}^e \partial _{v_{+}}^a \partial _{\varphi _{+}}^b \partial _r \psi )\}\), \(0 \leqslant i_1 + i_2 + i_3 + j +k \leqslant 1\), and \(0 \leqslant a + b \leqslant 2\), \(0 \leqslant d + e \leqslant 1\).
See for example 8.8 Theorem in [42]. By choosing suitable coordinates for \({\mathbb {S}}^2_+\) the domain \((v_0, \infty ) \times {\mathbb {S}}^2_+\) can be viewed as an open subset of \({\mathbb {R}}^3\) which satisfies a cone property that is uniform in \(v_0\).
Also recall that \(\kappa _- <0\).
This differs from the analogous operator defined in Section 6.2.1 in [15] by an overall minus sign.
This is the same equation as (4.10) in [67] with \(A = - \lambda _{ml}:^{[s]}(\omega )\).
Note that the arising boundary terms are
$$\begin{aligned} \Big [(1 - x^2) \frac{d}{dx} \partial _\omega S^{[s]}_{ml}(\omega ) \cdot S^{[s]}_{ml}(\omega )\Big ]^1_{-1} - \Big [ \partial _\omega S^{[s]}_{ml}(\omega ) \cdot (1- x^2) \frac{d}{dx} S^{[s]}_{ml}(\omega )\Big ]^1_{-1}, \end{aligned}$$which vanishes given the asymptotics of \(\partial _\omega ^k S^{[s]}_{ml}(\omega )\) from Proposition 5.2.
Proof as in [42] 7.9 Theorem.
For this paper only the ‘only if’ direction, i.e., ‘\(\implies \)’, is needed.
Let \(g(\theta , \varphi _+; \omega ), \partial _\omega g(\theta , \varphi _+; \omega ) \in L^2_\omega L^1_{{\mathbb {S}}^2}\) and let \(h(\omega ):= \int _{{\mathbb {S}}^2} g(\theta , \varphi _+; \omega ) \, \textrm{vol}_{{\mathbb {S}}^2}\). Then the weak derivative of h is given by \(\int _{{\mathbb {S}}^2} \partial _\omega g(\theta , \varphi _+; \omega ) \, \textrm{vol}_{{\mathbb {S}}^2}\): for \(\chi (\omega ) \in C^\infty _0({\mathbb {R}})\) we compute
$$\begin{aligned} \begin{aligned} -\int _{\mathbb {R}}h(\omega ) \partial _\omega \chi (\omega ) \, d\omega&= -\int _{\mathbb {R}}\int _{{\mathbb {S}}^2} g(\theta , \varphi _+; \omega ) \, \textrm{vol}_{{\mathbb {S}}^2}\, \partial _\omega \chi (\omega ) \, d\omega \\&= - \int _{\mathbb {R}}\int _{{\mathbb {S}}^2} g(\theta , \varphi _+; \omega ) \partial _\omega \chi (\omega ) \, \textrm{vol}_{{\mathbb {S}}^2}d \omega \\&= \int _{\mathbb {R}}\int _{{\mathbb {S}}^2} \partial _\omega g(\theta , \varphi _+; \omega ) \chi (\omega ) \textrm{vol}_{{\mathbb {S}}^2}d \omega . \end{aligned} \end{aligned}$$We only need
 (for Lemma 6.13).
(for Lemma 6.13).We use
$$\begin{aligned} \int _{\mathbb {R}}\Big ( \int _{{\mathbb {S}}^2} |\partial _{v_+}^a \partial _{\varphi _+}^b \psi (r')|^2 \textrm{vol}_{{\mathbb {S}}^2}\Big )^{\frac{1}{2}} dv_+ \leqslant \underbrace{\Big (\int _{\mathbb {R}}\frac{1}{\chi (v_+)} \, dv_+\Big )^\frac{1}{2}}_{< \infty } \Big ( \int _{{\mathbb {R}}} \int _{{\mathbb {S}}^2} \chi (v_+) | \partial _{v_+}^a \partial _{\varphi _+}^b \psi (r') |^2 \textrm{vol}_{{\mathbb {S}}^2}dv_+\Big )^\frac{1}{2} . \end{aligned}$$Note that the multiplying factor \(x^{1 - \gamma }\) is not analytic at \(x = 0\) if \(\omega \ne \omega _-m\).
Note that \(\gamma (\omega ) \rightarrow 1-s = -1\) for \(\omega \rightarrow \omega _- m\). This shows that \(B^{[s]}_{\mathcal{C}\mathcal{H}^+_l, ml} (x;\omega )\) is in general not regular for \(\omega \rightarrow \omega _- m\).
Note that \({\tilde{\gamma }}(\omega ) \rightarrow 1-s = -1\) for \(\omega \rightarrow \omega _+ m\). This shows that \(A^{[s]}_{{\mathcal {H}}^+_r, ml} (y;\omega )\) is in general not regular for \(\omega \rightarrow \omega _+ m\).
Note that the above construction corresponds to choosing as an integral of (6.16) not (6.17) but
$$\begin{aligned} x^{\gamma - 1} \Big ( \sum _{\begin{array}{c} j = 0 \\ j \ne 2 \end{array}}^\infty \frac{e_j}{\gamma - 1 + j} x^j \Big ) + e_2 \frac{x^{\gamma +1} - 1}{\gamma + 1} , \end{aligned}$$which differs from (6.17) by an \(\omega \)-dependent constant and makes it analytic for all \(\omega \in {\mathbb {R}}\).
The Teukolsky-Starobinsky conservation law also provides an alternative approach to showing that \({\mathfrak {T}}_{{\mathcal {H}}^+_r, ml}(0) \ne 0\) for \(m \ne 0\), cf. Remark 6.49
We only need this statement for the single mode \(m_0l_0\), for which we do not need to appeal to Proposition 5.22.
One can evaluate the limit also for \(\xi \) which are supported on \(\omega _+m\); one then picks up a delta distribution term at \(\omega _+ m\). With additional work it can be shown that it exactly agrees with the delta distribution term appearing in Proposition 7.25, i.e., \(a_{{\mathcal {H}}^+_l, ml}(\omega )\) does not contain a delta distribution, but only poles. This, however, is not needed for the method of proof of the main theorem chosen in this paper.
Note that
 is a priori not related in any way to
is a priori not related in any way to  for \(r \in (r_-,r_+)\). The choice of terminology is justified by hindsight. However, it should not confuse the reader into believing that there is nothing to show in the following.
for \(r \in (r_-,r_+)\). The choice of terminology is justified by hindsight. However, it should not confuse the reader into believing that there is nothing to show in the following.With \({\mathcal {H}}^+_r \cap \{v_+ \geqslant 1\}\) replaced by \({\mathcal {H}}^+\cap \{v_+ \geqslant v_0\}\) when appropriate.
Here \({\mathcal {O}}(1)\) is with respect to \(r\rightarrow r_+\) and \(c>0\).
I.e. we have \(\alpha (\partial _{V^+} \cdot ) = \alpha (\partial _{V^-}, \cdot ) =0\).
For example one can reduce it to the initial value problem for a scalar wave equation as follows: Choose a frame field \((f_1, f_2, f_3, f_4)\) for \(T\underline{{\mathcal {M}}}\) that is smooth away from \(\theta = 0\) and another one, \(({\hat{f}}_1, {\hat{f}}_2, {\hat{f}}_3, {\hat{f}}_4)\), that is smooth away from \(\theta = \pi \). Equation (A.9) yields now induced scalar equations for the components of \(\alpha \) with respect to the frame \((f_1, f_2, f_3, f_4)\), which, by putting the principal symbol back together, are manifestly wave equations with principal symbol \(g^{-1}\) on \(\underline{{\mathcal {M}}}\setminus \{\theta = 0\}\) – and analogously for the components of \(\alpha \) with respect to the hatted frame field. Given geometric initial data for (A.9) one can now solve for the components of \(\alpha \) with respect to \((f_1, f_2, f_3, f_4)\), and also with respect to the hatted frame field, in their corresponding domains of dependence (recall that \(\theta = 0\), \(\theta = \pi \) is removed from \(\underline{{\mathcal {M}}}\), respectively). By virtue of (A.9) being a geometric equation, each set of solutions transforms to solutions of the other set under the change of frame – whenever they are both defined. By uniqueness of the initial value problem, the untransformed and the transformed sets have to agree and we can now patch the two sets of solutions together to obtain a local solution \(\alpha \) of (A.9). We then iterate this procedure. Hence, the main point of this part of the appendix was to show that the Teukolsky equation (A.5) is the scalarisation of a regular geometric equation – which is not surprising at all given its derivation...
References
Alexakis, S., Fournodavlos, G.: Stable space-like singularity formation for axi-symmetric and polarized near-Schwarzschild black hole interiors. arXiv:2004.00692 (2020)
Angelopoulos, Y., Aretakis, S., Gajic, D.: Late-time tails and mode coupling of linear waves on Kerr spacetimes. arXiv:2102.11884 (2021)
Barack, L., Ori, A.: Late-time decay of gravitational and electromagnetic perturbations along the event horizon. Physical Review D 60(12), 124005 (1999)
Beals, R., Wong, R.: Special Functions. Cambridge University Press (2010)
Brady, P.R., Smith, J.D.: Black Hole Singularities: A Numerical Approach. Phys. Rev. Lett. 75, 1256–1259 (1995)
Cardoso, V., Costa, J.L., Destounis, K., Hintz, P., Jansen, A.: Quasinormal modes and strong cosmic censorship. Physical review letters 120(3), 031103 (2018)
Chandrasekhar, S.: The Mathematical Theory of Black Holes. Clarendon Press (1998)
Chandrasekhar, S., Hartle, J.: On crossing the Cauchy horizon of a Reissner-Nordström black-hole. Proc. R. Soc. Lond. A 384, 301–315 (1982)
Christodoulou, D.: The global initial value problem in general relativity. In: The Ninth Marcel Grossmann Meeting: On Recent Developments in Theoretical and Experimental General Relativity, Gravitation and Relativistic Field Theories (In 3 Volumes), World Scientific, pp. 44–54 (2002)
Christodoulou, D.: The formation of black holes in general relativity. European Mathematical Society (2009)
Chruściel, P.: On Uniqueness in the Large of Solutions of Einstein’s Equations. Proceedings of the CMA 27 (1991)
Dafermos, M.: Stability and instability of the Cauchy horizon for the spherically symmetric Einstein-Maxwell-scalar field equations. Ann. of Math. 158, 875–928 (2003)
Dafermos, M.: The interior of charged black holes and the problem of uniqueness in general relativity. Comm. Pure Appl. Math. 58, 445–504 (2005)
Dafermos, M.: Black holes without spacelike singularities. Comm. Math. Phys. 332, 729–757 (2014)
Dafermos, M., Holzegel, G., Rodnianski, I.: Boundedness and decay for the Teukolsky equation on Kerr spacetimes I: the case \(|a|\ll M\). Annals of PDE 5, 2 (2019)
Dafermos, M., Holzegel, G., Rodnianski, I., Taylor, M.: The non-linear stability of the Schwarzschild family of black holes. arXiv:2104.08222 (2021)
Dafermos, M., Luk, J.: The interior of dynamical vacuum black holes I: The \(C^0\)-stability of the Kerr Cauchy horizon. arXiv:1710.01772 (2017)
Dafermos, M., Rodnianski, I.: The redshift effect and radiation decay on black hole spacetimes. Comm. Pure Appl. Math. 52, 859–919 (2009)
Dafermos, M., Rodnianski, I.: Lectures on black holes and linear waves. Evolution equations, Clay Mathematics Proceedings, Amer. Math. Soc. 17, 97–205 (2013) (also arXiv:0811.0354)
Dafermos, M., Shlapentokh-Rothman, Y.: Time-translation invariance of scattering maps and blue-shift instabilities on kerr black hole spacetimes. Communications in Mathematical Physics 350(3), 985–1016 (2017)
Dafermos, M., Shlapentokh-Rothman, Y.: Rough initial data and the strength of the blue-shift instability on cosmological black holes with \(\Lambda > 0\). Classical and Quantum Gravity 35(19), 195010 (2018)
Dias, O.J., Eperon, F.C., Reall, H.S., Santos, J.E.: Strong cosmic censorship in de Sitter space. Physical Review D 97(10), 104060 (2018)
Fournodavlos, G., Sbierski, J.: Generic Blow-Up Results for the Wave Equation in the Interior of a Schwarzschild Black Hole. Arch. Rational Mech. Anal. 235, 927–971 (2020)
Franzen, A. T.: Boundedness of massless scalar waves on Kerr interior backgrounds. In: Annales Henri Poincaré, vol. 21, Springer, pp. 1045–1111 (2020)
Gajic, D.: Linear waves in the interior of extremal black holes I. Communications in Mathematical Physics 353(2), 717–770 (2017)
Gajic, D.: Linear waves in the interior of extremal black holes II. In: Annales Henri Poincaré, vol. 18, Springer, pp. 4005–4081 (2017)
Gajic, D., Luk, J.: The interior of dynamical extremal black holes in spherical symmetry. Pure and Applied Analysis 1(2), 263–326 (2019)
Goldberg, J.N., Macfarlane, A.J., Newman, E.T., Rohrlich, F., Sudarshan, E.C.G.: Spin-s spherical harmonics and \(\eth \). Journal of Mathematical Physics 8(11), 2155–2161 (1967)
Gürsel, Y., Novikov, I.D., Sandberg, V.D., Starobinsky, A.: Final state of the evolution of the interior of a charged black hole. Physical Review D 20(6), 1260 (1979)
Hawking, S., Ellis, G.: The large scale structure of space-time. Cambridge University Press (1973)
Hintz, P.: Boundedness and decay of scalar waves at the Cauchy horizon of the Kerr spacetime. Commentarii Mathematici Helvetici 92(4), 801–837 (2017)
Hintz, P.: A Sharp Version of Price’s Law for Wave Decay on Asymptotically Flat Spacetimes. Communications in Mathematical Physics 389(1), 491–542 (2022)
Hintz, P., Vasy, A.: Analysis of linear waves near the Cauchy horizon of cosmological black holes. Journal of Mathematical Physics 58(8), 081509 (2017)
Hiscock, W.: Evolution of the interior of a charged black hole. Phys. Rev. Lett. 83A, 110–112 (1981)
Kehle, C.: Blowup of the local energy of linear waves at the Reissner-Nordström-AdS Cauchy horizon. Classical and Quantum Gravity 38(21), 214001 (2021)
Kehle, C.: Diophantine approximation as Cosmic Censor for Kerr–AdS black holes. Inventiones mathematicae (2021)
Kehle, C., Shlapentokh-Rothman, Y.: A Scattering Theory for Linear Waves on the Interior of Reissner-Nordström Black Holes. Annales Henri Poincaré 20(5), 1583–1650 (2019)
Kehrberger, L.: The Case Against Smooth Null Infinity I: Heuristics and Counter-Examples. Annales Henri Poincaré (2021)
Kehrberger, L.: The Case Against Smooth Null Infinity II: A Logarithmically Modified Price’s Law. arXiv:2105.08084 (2021)
Klainerman, S., Szeftel, J.: Global Nonlinear Stability of Schwarzschild Spacetime under Polarized Perturbations. Princeton University Press (2020)
Klainerman, S., Szeftel, J.: Kerr stability for small angular momentum. arXiv:2104.11857 (2021)
Lieb, E., Loss, M.: Analysis. AMS (2001)
Luk, J.: Weak null singularities in general relativity. Journal of the American mathematical society 31(1), 1–63 (2018)
Luk, J., Oh, S.-J.: Late-time tails of waves on dynamic asymptotically flat spacetimes of odd space dimensions. Forthcoming
Luk, J., Oh, S.-J.: Proof of linear instability of the Reissner-Nordström Cauchy horizon under scalar perturbations. Duke Mathematical Journal 166(3), 437–493 (2017)
Luk, J., Oh, S.-J.: Strong cosmic censorship in spherical symmetry for two-ended asymptotically flat initial data I. The interior of the black hole region. Annals of Math. 190(1), 1–111 (2019)
Luk, J., Oh, S.-J.: Strong cosmic censorship in spherical symmetry for two-ended asymptotically flat initial data II. The exterior of the black hole region. Annals of PDE 5, 6 (2019)
Luk, J., Oh, S.-J., Shlapentokh-Rothman, Y.: A scattering theory approach to Cauchy horizon instability and applications to mass inflation. preprint (2022)
Luk, J., Sbierski, J.: Instability results for the wave equation in the interior of Kerr black holes. J. Funct. Anal. 271(7), 1948–1995 (2016)
Ma, S.: Uniform energy bound and Morawetz estimate for extreme components of spin fields in the exterior of a slowly rotating Kerr black hole II: linearized gravity. Communications in Mathematical Physics 377, 2489–2551 (2020)
Ma, S., Zhang, L.: Sharp decay for teukolsky equation in kerr spacetimes. arXiv:2111.04489 (2021)
McNamara, J.: Instability of black hole inner horizons. Proc. R. Soc. Lond. A 358, 499–517 (1978)
O’Neill, B.: The Geometry of Kerr Black Holes. A K Peters (1995)
Ori, A.: Inner Structure of a Charged Black Hole: An Exact Mass-Inflation Solution. Phys. Rev. Lett. 67 (1991)
Penrose, R.: ‘Structure of Space-Time’ in Battelle Rencontres. Benjamin, W. A (1968)
Penrose, R.: Singularities and time-asymmetry. In General Relativity: An Einstein Centenary Survey, pp. 581–638. Cambridge University Press (1979)
Poisson, E., Israel, W.: Inner-Horizon Instability and Mass Inflation in Black Holes. Phys. Rev. Lett. 63(16), 1663–1666 (1989)
Poisson, E., Israel, W.: Internal structure of black holes. Phys. Rev. D 41, 1796–1809 (1990)
Sbierski, J.: On the initial value problem in general relativity and wave propagation in black-hole spacetimes. PhD Thesis, University of Cambridge (2014)
Sbierski, J.: Characterisation of the Energy of Gaussian Beams on Lorentzian Manifolds: with Applications to Black Hole Spacetimes. Analysis & PDE 8, 1379–1420 (2015)
Sbierski, J.: On the proof of the \(C^0\)-inextendibility of the Schwarzschild spacetime. J. Phys. Conf. Ser. 968 (2018)
Sbierski, J.: The \(C^0\)-inextendibility of the Schwarzschild spacetime and the spacelike diameter in Lorentzian geometry. J. Diff. Geom. 108(2), 319–378 (2018)
Sbierski, J.: On holonomy singularities in general relativity and the \(C^{0,1}_{\rm loc}\)-inextendibility of spacetimes. arXiv:2007.12049, to appear in Duke Mathematical Journal (2020)
Shlapentokh-Rothman, Y., Teixeira da Costa, R.: Boundedness and decay for the Teukolsky equation on Kerr in the full subextremal range \(| a|< M \): frequency space analysis. arXiv:2007.07211 (2020)
Teixeira da Costa, R.: Mode Stability for the Teukolsky Equation on Extremal and Subextremal Kerr Spacetimes. Communications in Mathematical Physics 378(1), 705–781 (2020)
Teschl, G.: Ordinary differential equations and dynamical systems. Graduate Studies in Mathematics 140, 08854–8019 (2000)
Teukolsky, S.: Perturbations of a rotating black hole. I. Fundamental equations for gravitational, electromagnetic, and neutrino-field perturbations. Astrophys. J. 185, 635–647 (1973)
Van de Moortel, M.: Stability and Instability of the Sub-extremal Reissner-Nordström Black Hole Interior for the Einstein-Maxwell-Klein-Gordon Equations in Spherical Symmetry. Commun. Math. Phys. 360(1), 103–168 (2018)
Van de Moortel, M.: The breakdown of weak null singularities inside black holes. arXiv:1912.10890 (2019)
Acknowledgements
I would like to acknowledge that this project started out as a collaboration with Jonathan Luk which had to be discontinued because of time constraints. Several ideas in this paper have been developed together with him and I am also grateful to Jonathan for bringing the Teukolsky-Starobinsky conservation law to my attention. Moreover, I would like to thank Yakov Shlapentokh-Rothman for a helpful discussion. A large body of this work was completed while I was supported through the Sylvester Research Fellowship at the University of Oxford. I now acknowledge support through the Royal Society University Research Fellowship URF\R1\211216. There are no competing interests.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Kruskal-Like Coordinate Transformations
We express the \(\{v_+, \varphi _+, r, \theta \}\) coordinate vector fields in terms of the \(\{V^+_{r_+}, V^-_{r_+}, \theta , \Phi _{r_+}\}\) coordinate vector fields.
Note that the vector field \(\partial _{v_+}\) does not vanish at the bottom bifurcation sphere \({\mathbb {S}}^2_b\).
Using (A.1) we thus compute
It now follows from (2.7) that \(\frac{1}{V^+_{r_+}} e_4\) is a regular and non-degenerate vector field at \({\mathcal {H}}^+_r \cup {\mathcal {H}}^+_l \cup {\mathbb {S}}^2_b\). Note, however, that compared toFootnote 57\({\hat{e}}_4 = -\frac{1}{\Delta } e_4 = (\frac{c}{V^+_{r_+}V^-_{r_+}} + {\mathcal {O}}(1)) e_4\), which blows up at \({\mathbb {S}}^2_b\), \(\frac{1}{V^+_{r_+}} e_4\) grows exponentially in \(v_-\) for \(v_- \rightarrow +\infty \).
1.1 The Regular Teukolsky Equation in \(\underline{{\mathcal {M}}}\)
The above suggests that if \(\psi \) satisfies \({\mathcal {T}}_s \psi = 0\), then the quantity \({\tilde{\psi }}_s:= \frac{1}{(V^+_{r_+})^s} \psi _s\) should satisfy a regular equation in \(\underline{{\mathcal {M}}}\), thus in particular near the bottom bifurcation sphere. In order to show this claim, we start by rewriting (2.39) in \((v_+, r, \theta , \varphi _+)\) coordinates as
A straightforward computation shows that  satisfies (A.3) if, and only if, \({\tilde{\psi }}_s\) satisfies
satisfies (A.3) if, and only if, \({\tilde{\psi }}_s\) satisfies
Rewriting (A.4) in terms of \(\{V^+_{r_+}, V^-_{r_+}, \theta , \Phi _{r_+}\}\) coordinates (in the following we will drop the \(r_+\), i.e., we will only write \(\{V^+, V^-, \theta , \Phi \}\)) gives
where

Note that the dashed terms are \({\mathcal {O}}(r_+-r)\). To see this we recall that \(r_+ - r_- = 2(r_+ -M)\) and compute
Hence, we have \({\tilde{X}}_s^{V^+}, {\tilde{X}}_s^{V^-}, {\tilde{X}}_s^{\Phi }, {\tilde{f}}_s \in C^\infty (\underline{{\mathcal {M}}})\).
1.2 The Initial Value Problem for the Teukolsky Equation (A.5)
In this section we show that the initial value problem for the Teukolsky equation (A.5) is well-posed by reducing it to an initial value problem for a tensorial wave equation. In the following we restrict to \(s = +2\) and drop the subscript s from \({\tilde{\psi }}_s\). For  there exists, by Remark 2.43, a unique \(\alpha \in \Gamma ^\infty \big (S^2T^*{\mathcal {M}}\big )\) with \(\alpha (m,m) = {\tilde{\psi }}\) that is trace-free with respect to
there exists, by Remark 2.43, a unique \(\alpha \in \Gamma ^\infty \big (S^2T^*{\mathcal {M}}\big )\) with \(\alpha (m,m) = {\tilde{\psi }}\) that is trace-free with respect to  and that is an \({\mathbb {S}}^2\) tensor,Footnote 58. We rewrite (A.5) as
and that is an \({\mathbb {S}}^2\) tensor,Footnote 58. We rewrite (A.5) as
The differentials of the Kruskal-like coordinate system are
which, together with (2.2), easily yields that the components of the inverse metric in Kruskal-like coordinates satisfy
Moreover, we note that \(\Box _g \Phi = 0\) and \(\Box _g \theta = \frac{\cos \theta }{\rho ^2 \sin \theta }\) away from the axis \(\theta = 0, \pi \). Also using (2.30) we obtain from (A.6)

Using now (2.31), (2.20), \({\mathcal {L}}_{\partial _{V^+}} m = {\mathcal {L}}_{\partial _{V^-}} m = {\mathcal {L}}_{\partial _{\Phi }} m =0\), and again Remark 2.43 yields that \({\tilde{\psi }} = \alpha (m,m)\) satisfies (A.8) if, and only if, \(\alpha \) satisfies
Here, the vector fields \(Z_{i, r_+}\) are the vector fields from (2.19) with \(\varphi \) replaced by \(\Phi _{r_+}\). Note that firstly the equation (A.9) extends regularly to the axis \(\theta \in \{0, \pi \}\) and secondly it also extends regularly to all of \(\underline{{\mathcal {M}}}\) by virtue of \({\tilde{X}}_s^{V^+}, {\tilde{X}}_s^{V^-}, {\tilde{X}}_s^{\Phi }, {\tilde{f}}_s \in C^\infty (\underline{{\mathcal {M}}})\) and (A.7).
It is now easy to see that (A.9) is a tensorial wave equation with principal symbol \(g^{-1}\) and thus the initial value problem is well-posedFootnote 59. Taking the trace of (A.9) with respect to  shows that if \(\alpha \in \Gamma ^\infty (S^2T^*\underline{{\mathcal {M}}})\) satisfies (A.9), then the trace of \(\alpha \) satisfies a homogeneous wave equation. Similarly, inserting \(\partial _{V^+}\) or \(\partial _{V^-}\) into one of the components of (A.9) (and using that the Lie-bracket of coordinate vector fields vanishes) shows that \(\alpha (\partial _{V^+}, \cdot )\) and \(\alpha (\partial _{V^-}, \cdot )\) satisfy homogeneous wave equations. The same holds for the antisymmetric part of \(\alpha \). Thus, symmetric and trace-free \({\mathbb {S}}^2\) initial data (cf. Remark 2.43) for (A.9) gives rise to a symmetric and trace-free \({\mathbb {S}}^2\) solution. Finally, we recall that by Remark 2.43 initial data for \({\tilde{\psi }}\) for equation (A.5) uniquely determines geometric symmetric and trace-free \({\mathbb {S}}^2\) initial data for \(\alpha \) for (A.9). This establishes well-posedness for the Teukolsky equation (A.5) in \(\underline{{\mathcal {M}}}\).
shows that if \(\alpha \in \Gamma ^\infty (S^2T^*\underline{{\mathcal {M}}})\) satisfies (A.9), then the trace of \(\alpha \) satisfies a homogeneous wave equation. Similarly, inserting \(\partial _{V^+}\) or \(\partial _{V^-}\) into one of the components of (A.9) (and using that the Lie-bracket of coordinate vector fields vanishes) shows that \(\alpha (\partial _{V^+}, \cdot )\) and \(\alpha (\partial _{V^-}, \cdot )\) satisfy homogeneous wave equations. The same holds for the antisymmetric part of \(\alpha \). Thus, symmetric and trace-free \({\mathbb {S}}^2\) initial data (cf. Remark 2.43) for (A.9) gives rise to a symmetric and trace-free \({\mathbb {S}}^2\) solution. Finally, we recall that by Remark 2.43 initial data for \({\tilde{\psi }}\) for equation (A.5) uniquely determines geometric symmetric and trace-free \({\mathbb {S}}^2\) initial data for \(\alpha \) for (A.9). This establishes well-posedness for the Teukolsky equation (A.5) in \(\underline{{\mathcal {M}}}\).
Commutator Computations for (2.40)
The second order terms of \( \hat{{\mathcal {T}}}_{[s]}\) are

We use \(v_-^q \big (-(1+ \lambda \Delta )\partial _r + (1 + \lambda \Delta )\partial _{v_-}\big ) {\overline{{\hat{\psi }}}}\) as a multiplier and compute the commutator expressions in the following individually for the \(\partial _r\) component and the \(\partial _{v_-}\) component of the multiplier, term by term. We will use the notation \(\underset{a.i.}{=}\) to denote equality after integration over the spheres with respect to \(\textrm{vol}_{{\mathbb {S}}^2}\).
1.1 The Multiplier \(-v_-^q(1 + \lambda \Delta )\overline{\partial _r {\hat{\psi }}}\)

1.2 The Multiplier \(v_-^q(1 + \lambda \Delta )\overline{\partial _{v_-} {\hat{\psi }}}\)

Commutator Computations for (2.39)
The second order terms of \( {\mathcal {T}}_{[s]}\) in \(\{v_+, r, \theta , \varphi _+\}\) coordinates are

We use \(\chi (v_+) \big (-(1+ \lambda \Delta )\partial _r + (1 + \lambda \Delta )\partial _{v_+}\big ) {\overline{\psi }}\) as a multiplier and compute the commutator expressions in the following individually for the \(\partial _r\) component and the \(\partial _{v_+}\) component of the multiplier, term by term. Note that due to formal similarity all these expressions can be easily inferred from the computations in Appendix B (or vice versa). They are listed here nevertheless for the convenience of the reader. Again we use the notation \(\underset{a.i.}{=}\) to denote equality after integration over the spheres with respect to \(\textrm{vol}_{{\mathbb {S}}^2}\).
We also use \(\chi (v_+)(1 + \lambda \Delta )(-\partial _r + \partial _{v_+} + \frac{a}{r_-^2 + a^2} \partial _{\varphi _+}){\overline{\psi }}\) as a multiplier. The \(\partial _{\varphi _+} {\overline{\psi }}\) component is also computed here separately.
1.1 The Multiplier \(-\chi (v_+)(1 + \lambda \Delta )\overline{\partial _r \psi }\)

1.2 The Multiplier \(\chi (v_+)(1 + \lambda \Delta )\overline{\partial _{v_+} \psi }\)

1.3 The Multiplier \(\chi (v_+)(1 + \lambda \Delta )\frac{a}{r_-^2 + a^2}\overline{\partial _{\varphi _+} \psi }\)


Commutator Computations for (2.38)
The second order terms of \({\mathcal {T}}_{[s]}\) in Boyer-Lindquist coordinates are

We use \(-\chi (t) e^{\lambda r} \overline{\partial _r \psi }\) as a multiplier and compute the commutator expressions again term by term.
1.1 The Multiplier \(-\chi (t) e^{\lambda r} \overline{\partial _r \psi }\)


Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sbierski, J. Instability of the Kerr Cauchy Horizon Under Linearised Gravitational Perturbations. Ann. PDE 9, 7 (2023). https://doi.org/10.1007/s40818-023-00146-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40818-023-00146-9


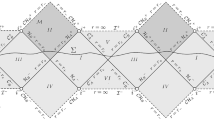
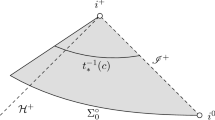
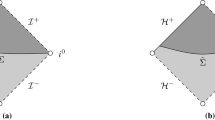







 analogously. For example we will choose
analogously. For example we will choose  on the integral manifolds of D by the symmetric part of
on the integral manifolds of D by the symmetric part of  . Thus, the space
. Thus, the space  of smooth spin 2-weighted functions on
of smooth spin 2-weighted functions on  ) sections of
) sections of  is as all those elements in
is as all those elements in  .
. .
. . Note that this implies, using (
. Note that this implies, using ( .
.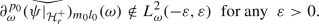
 results from
results from 





 is the spin s-weighted spherical Laplacian, see Section
is the spin s-weighted spherical Laplacian, see Section  as the image of
as the image of  even if
even if  (for Lemma
(for Lemma  is a priori not related in any way to
is a priori not related in any way to  for
for