1 Introduction

For a few decades, fuzzy logic-based systems remain a favorite tool for nonlinear regression. The main advantage of this universal approximator is the possibility to include a linguistically represented knowledge about the object and vice-versa to characterize the identified system by words and thus enhance the interpretability of the obtained model.

Unfortunately, not any prior knowledge about the system can be easily expressed in the form of If-Then rules [1]. One such knowledge that is quite often encountered in many real-world applications is the information about the monotonicity of the corresponding mapping. Such information can be of different origins. In nonlinear dynamical systems, it may result from physical laws describing their behaviour, e.g., the level of a liquid in the tank increases with the inlet. Very often monotonicity reflects natural human behaviour, e g., the price of a flat is increasing with its area. Last but not least monotonicity appears as a consequence of human observations, e.g. the risk of many diseases increases with the mass and the age of the patient.

There are many papers showing that the incorporation of prior information about monotonicity into regression or classification has some benefits. In [1, 2] it is demonstrated that preserving monotonicity suppresses the effect of the noise and prevents the model from overfitting. Using information about monotonicity may increase the generalization ability of fuzzy systems, especially in the regions where the obtained data are sparse [3]. In classification problems the results of monotonic procedures are more reasonable and better interpretable [4, 5].

Possibilities of how to include the requirement of monotonicity have been considered for most machine learning-based techniques. Monotonic support vector regression (SVR) and support vector machines (SVM) were investigated in [6, 7], respectively. Pelckmans et al [8] used the duality to include monotonicity conditions in kernel regression. Properties of monotonic classification of evolutionary algorithms are examined in [9], nearest neighbour in [10] and decision trees in [11, 12] with their fusion in [13, 14]. Basic results on the monotonicity of multilayer perceptrons were stated in [15] and [16]. The applications include nonlinear dynamic system identification and control [17, 18], credit risk rating [19, 20], consumer loan evaluation [21], predicting Alzheimer’s disease progression [22], manufacturing [23] or breast cancer prediction [24] and its detection on mammograms [25].

In the case of fuzzy systems, monotonicity was first studied in [1] where Mamdani-type fuzzy systems with piecewise linear membership functions were considered. First results on monotonic Takagi–Sugeno fuzzy systems with differentiable membership functions and membership functions that are not differentiable in a finite number of points were presented by Won et al. [26] and further discussed in [27] and applied for least square identification in [28]. Since then some more results have been achieved on different inference engines [29], fuzzy-inference methods [30], defuzzification methods [2, 31], hierarchical fuzzy systems [32], fuzzy decision trees [14] or type-2 fuzzy systems [33, 34]. Monotonicity conditions for fuzzy systems with ellipsoidal antecedents were presented in [35]. Deng et al. [36] handle monotonicity of TS fuzzy systems for classification on a set of virtual samples expressed as constraints on related optimization tasks. Applications of monotonic fuzzy systems can be found in the detection of failures [37], decision making [38], thermal comfort prediction [39], assessing material recyclability [40] and classification [9, 41, 42].

Unfortunately, there are significant drawbacks when considering Takagi–Sugeno fuzzy systems for regression with the most commonly used membership functions [43, 44]. Triangular or trapezoidal membership functions produce non-smooth output whereas monotonicity conditions for Gaussian membership functions [26] are very conservative due to unbounded support. The latter is applicable for membership functions with the same width only. Those facts lead to increasing interest in smooth membership functions with compact support if the smooth monotone output is required [35]. Advantages of smooth fuzzy models have been shown in [45, 46].

In this paper, first-order Takagi–Sugeno fuzzy systems with raised cosine membership functions are investigated. Even though not commonly used within a fuzzy community a big advantage of raised cosine functions is that they are infinitely differentiable and therefore constitute a smooth fuzzy system. The derived sufficient monotonicity conditions are quite intuitive and make it possible to use efficient and reliable numerical algorithms for solving related optimization problems. Performance of the proposed smooth monotone fuzzy system will be compared with other monotone and non-monotone artificial intelligence-based regressors on a few commonly used benchmark datasets.

2 Problem Formulation

2.1 First-Order Takagi–Sugeno Fuzzy System

Let us consider first-order Takagi–Sugeno type fuzzy system [47] where \(M_j\) fuzzy sets \(A_j^1,A_j^2\ldots ,A_j^{M_j}\) characterize each input \(x_j, j=1,\ldots ,n\). The corresponding \(M = \prod _{j=1}^n M_j\) rules covering the whole input space are in the form

$$\begin{aligned}&R_{\textbf{k}}: \quad \text{If} \,\, x_1 \,\, \text{is} \,\, A_1^{k_1} \,\, \text{and} \,\, \cdots \text{and} \,\, x_n \,\, \text{is} \,\, A_n^{k_n}&\\ {}&\text{then} \,\, \,\, y = x^{{}} Ta^{k} + a_{0}^{k} &\end{aligned},$$

where \(x = [x_1,\ldots , x_n]^\text{T} \in U = [U_1 \times U_2 \times \cdots \times U_n], U_j = [\underline{u}_j,\overline{u}_j]\) is the input vector, y is the scalar output, \(a^\textbf{k} = [a^\textbf{k}_{1},\ldots ,a^\textbf{k}_{n}]^\text{T} \in \Re ^n\) and \(a^\textbf{k}_{0} \in \Re \) are the parameters of the linear submodels and \(\textbf{k} = (k_1,k_2,\ldots ,k_n) \in K \subset N_0^n, 1 \le k_j \le M_j\) is the multi-index. Using the product inference engine and center of gravity defuzzification the total output of the fuzzy model is determined by

$$\begin{aligned} F(x)= & {} \frac{\sum _{k_1 = 1}^{M_1} \cdots \sum _{k_n = 1}^{M_n} (x^\text{T} a^\textbf{k} + a^\textbf{k}_{0}) \prod _{j=1}^n \mu _j^{k_j}(x_j)}{\sum _{k_1 = 1}^{M_1} \cdots \sum _{k_n = 1}^{M_n} \prod _{j=1}^n \mu _j^{k_j}(x_j)} \nonumber \\= & {} \frac{\sum _{\textbf{k} \in K} (x^\text{T} a^\textbf{k} + a^\textbf{k}_{0}) \prod _{j=1}^n \mu _j^{k_j}(x_j)}{\sum _{\textbf{k} \in K} \prod _{j=1}^n \mu _j^{k_j}(x_j)}\, \end{aligned},$$
(1)

where \(\mu _j^{k_j}(x_j)\) are the membership functions characterizing input fuzzy sets \(A_j^{k_j},\, j=1,\dots ,n\).

2.2 Raised Cosine Membership Function

The raised cosine membership functions investigated in this paper are defined by \(\mu _j^{k_j}(x_j)\), i. e.

$$\begin{aligned} \mu (z) = \left\{ \begin{array}{l} \frac{1}{2} (1 + \cos (z)), \quad \text{if} \,\, |z| \le \pi \\ 0, \quad \quad \quad \quad \quad \quad \, \text{if} \,\, |z| > \pi \end{array} \right. \end{aligned},$$
(2)

where \(z = \pi \frac{x_i-c}{\sigma }\), \(\sigma > 0\), see Fig. 1.

Fig. 1
figure 1

Raised cosine membership function

Full size image

2.3 Monotone Fuzzy System

For a monotone fuzzy system, its output is monotonic with respect to its input. For multi-input fuzzy systems investigated in this paper, the definition used in [26] is adopted.

Definition 1

(Monotonicity of fuzzy system, [26]). The mapping \(F: U \rightarrow \Re \) defined by (1) is said to be monotonically nondecreasing with respect to \(x_i\) if and only if \(x_i^1 < x_i^2\) implies

$$\begin{aligned} F(x_1,\ldots ,x_i^1,\ldots ,x_n) \le F(x_1,\ldots ,x_i^2,\ldots ,x_n) \end{aligned}$$
(3)

for any \([x_1,\ldots ,x_{i-1},x_{i+1},\ldots ,x_n]\) such that \([x_1,\ldots ,\) \(x_{i-1},x_i^1,x_{i+1},\ldots ,x_n]^{\text{T}}\), \([x_1,\ldots ,x_{i-1},x_i^2,x_{i+1},\ldots \), \(x_n]^{\text{T}}\) \(\in U\). A non-increasing mapping is defined adequately.

3 Monotonicity Conditions

Since the mapping (1) with membership functions defined by (2) is differentiable in any \(x \in U\) it is monotonically non-decreasing with respect to \(x_i\), \(i=1,\ldots ,n\) if and only if partial derivative \(\frac{\partial F}{\partial x_i} \ge 0\) for all \(x \in U\). The partial derivative can be expressed as

$$\begin{aligned}&\frac{\partial F}{\partial x_i} = \frac{1}{(\sum _{j=1}^{M_i}\mu _j(x_i))^2} \left\{ \sum _{p=1}^{M_i} \sum _{q=1}^{M_i} a^\textbf{p}_{i}\mu ^p_i(x_i)\mu ^q_i(x_i) + \right. \nonumber&\\&\left. \sum _{p=1}^{M_i-1} \sum _{q=p+1}^{M_i} \Big (x^\text{T} a^\textbf{p} + a^\textbf{p}_{0} - x^\text{T} a^\textbf{q} - a^\textbf{q}_{0}\Big ) \times \nonumber \right.&\\ {}&\left. \Big (\frac{d \mu ^p_i(x_i)}{d x_i} \mu ^q_i(x_i) - \frac{d \mu ^ q_i(x_i)}{d x_i} \mu ^p_i(x_i)\Big )\right\}&\end{aligned}$$
(4)

for all multi-indices \(\textbf{p} < \textbf{q}, \textbf{p}, \textbf{q} \in K,\) where the inequality \(\textbf{p} < \textbf{q}\) stands for \(\textbf{p} = [k_1,\ldots ,k_{i-1},p,k_{i+1},\ldots ,M_i]\),

\(\textbf{q} = [k_1,\ldots ,k_{i-1},q,k_{i+1},\ldots ,M_i]\) such that \(1 \le p < q \le M_i\) (i. e. for all combinations of \((k_1,\ldots ,k_{i-1},k_{i+1}\),

\(\ldots ,k_n),\) where \(k_i \in [1,M_i]\)).

Therefore the mapping (1) is non-decreasing with respect to \(x_i\) if

  1. 1.

    \(a^\textbf{k}_{i} > 0 \,\, \forall \textbf{k} \in K\),

  2. 2.

    \(x^\text{T} a^\textbf{p} + a^\textbf{p}_{0} - x^\text{T} a^\textbf{q} - a^\textbf{q}_{0} \le 0, \textbf{p} < \textbf{q}\),

  3. 3.

    \(\frac{d\mu _i^p (x_i)}{dx_i}\mu _i^q (x_i) - \frac{d\mu _i^q (x_i)}{dx_i}\mu _i^p (x_i) \le 0 \, \forall x_i \in U_i\) and \(1 \le p < q \le M_i\).

Here one can see the fundamental advantage of membership functions with compact support. The conditions 2. and 3. need to be satisfied only for those \(\textbf{p} < \textbf{q},\) where the corresponding rules fire simultaneously. Therefore they are much less restrictive than e. g. in the case of Gaussian or sigmoidal membership functions where those conditions need to be satisfied for all pairs \(\textbf{p},\textbf{q} \in K\).

Since the rules \(R_\textbf{p}\) and \(R_\textbf{q}\) are active at the same time if and only if \(c_i^q - \sigma _i^q < c_i^p + \sigma _i^p\) the condition 2. need to be met on the domain \(U^\textbf{pq} = \prod _{i=1}^{n} [c_i^q - \sigma _i^q,\,c_i^p + \sigma _i^p]\) that corresponds to \(2^n\) linear constraints on coefficients \(a^\textbf{p}, a^\textbf{q}\) for each \(\textbf{p} < \textbf{q}\) generated by all combinations of lower and upper bounds of those intervals. Denote the parameter vector

$$\begin{aligned} \theta = [a^{\textbf{k}_1}_{0},\ldots ,a^{\textbf{k}_1}_{n},\ldots ,a^{\textbf{k}_M}_{0},\ldots ,a^{\textbf{k}_M}_{n}]^\text{T}. \end{aligned}$$
(5)

Then those constraints can be expressed as

$$\begin{aligned} L \theta \le 0. \end{aligned}$$
(6)

Fulfillment of condition 3. is guaranteed by the following theorem.

Theorem 1

Membership functions (2) satisfy condition 3. if \(c_i^p - \sigma _i^p \le c_i^q - \sigma _i^q\) and \(c_i^p + \sigma _i^p \le c_i^q + \sigma _i^q\) for all \(1 \le p < q \le M_i\).

Proof

For the sake of simplicity in what follows the index i is omitted. The condition is clearly satisfied whenever \(\mu ^p(x) = 0\) or \(\mu ^q(x) = 0\) and for \(x \in [c^p,c^q],\) where \(\mu ^p(x) \le 0\) and \(\mu ^q(x) \ge 0\). In the region where both membership functions are active simultaneously \((x \in U^{pq} = (c^q - \sigma ^q,\, c^p + \sigma ^p))\) the condition 3. yields

$$\begin{aligned}{} & {} \frac{d\mu ^p (x)}{dx}\mu ^q (x) - \frac{d\mu ^q (x)}{dx}\mu ^p (x) = \frac{-\pi }{\sigma _p} (\sin (z_p)) \nonumber \\ {}{} & {} \times (1 + \cos (z_q)) + \frac{\pi }{\sigma _q} (\sin (z_q)) (1 + \cos (z_p)) \le 0 \end{aligned}$$
(7)

with \(z_p = \pi \frac{x-c^p}{\sigma ^p}\) and \(z_q = \pi \frac{x-c^q}{\sigma ^q}\).

Let us first check it for \(x \in (c^q - \sigma ^q,c^p),\) where \(z_p,\,z_q \in (-\pi ,\,0)\) and \(z_p > z_q\). In that interval inequality (7) is equivalent to

$$\begin{aligned}{} & {} \frac{1}{\sigma ^q} \frac{\sin (z_q)}{ 1 + \cos (z_q)} - \frac{1}{\sigma ^p} \frac{\sin (z_p)}{ 1 + \cos (z_p)} = \\{} & {} \frac{1}{\sigma ^q} \tan \Big (\frac{z_q}{2}\Big ) - \frac{1}{\sigma ^p} \tan \Big (\frac{z_p}{2}\Big ) \le 0 \end{aligned}$$

that can be rewritten as

$$\begin{aligned} f(x) \equiv \frac{\tan \Big (\frac{z_p}{2}\Big )}{\tan \Big (\frac{z_q}{2}\Big )} - \frac{\sigma ^p}{\sigma ^q} \le 0. \end{aligned}$$
(8)

Since \(z_p > z_q\) and function tangent is monotonically increasing for \(z_p, z_q \in (-\pi ,\,0)\) inequality (8) is satisfied whenever \(\sigma ^p \ge \sigma ^q\).

For the case \(\sigma ^p < \sigma ^q\) first let us observe that the values of the function f(x) are decreasing with increasing parameter \(c^q\) since \(z_q\) and hence \(\tan \Big (\frac{z_q}{2}\Big )\) are decreasing and negative. Hence it is sufficient to check inequality (8) for the lowest possible value of \(c^q\) which under conditions of theorem 1 happens if \(c^p - \sigma ^p = c^q - \sigma ^q\). Let us prove that in that case f(x) is a decreasing function of x. The derivative

$$\begin{aligned} f'(x) =\frac{\sigma ^q}{\sigma ^p} \frac{\cos ^2 \Big (\frac{z_q}{2}\Big )}{\cos ^2 \Big (\frac{z_p}{2}\Big )} - \frac{\sigma ^p}{\sigma ^q} \end{aligned}$$
(9)

is negative if

$$\begin{aligned} \sigma ^p \cos \Big (\frac{z_p}{2}\Big ) - \sigma ^q \cos \Big (\frac{z_q}{2}\Big ) < 0. \end{aligned}$$
(10)

Since because of \(\sigma ^q > \sigma ^p\) and \(z_p > z_q\), \(z_p,\,z_q \in (-\pi ,0)\) and thus \( \sin \big (\frac{z_q}{2}\Big ) < \sin \Big (\frac{z_p}{2}\Big )\) the derivative of left-hand side of (10) gives

$$\begin{aligned} \sigma ^q \sin \Big (\frac{z_q}{2}\Big ) - \sigma ^p \sin \Big (\frac{z_p}{2}\Big ) < 0 \end{aligned}$$
(11)

and therefore \(f'(x)\) is a decreasing function of x and achieves its maximum value at the minimum point of the admissible interval \(x = c^q - \sigma ^q\). Since that maximum value is negative due to \(z_q = -\pi \) and \(\cos \Big (\frac{z_p}{2}\Big ) < 0\) the inequality (10) holds and the first derivative \(f'(x)\) is decreasing. Therefore it is sufficient to check inequality (8) as well in the point \(x = c^q - \sigma ^q,\) where f(x) achieves its maximum value.

To obtain the maximum value of f(x) let us apply three times L’Hospital’s rule on the left term of (8) that gives

$$\begin{aligned}{} & {} \lim _{x \rightarrow c^q - \sigma ^q} \frac{\tan (\frac{z_p}{2})}{\tan (\frac{z_q}{2})} = \lim _{x \rightarrow c^q - \sigma ^q} \frac{(\tan (\frac{z_p}{2}))'''}{(\tan (\frac{z_q}{2}))'''} = \\ {}{} & {} \lim _{x \rightarrow c^q - \sigma ^q} \frac{\Big (\cos ^2 \Big (\frac{z_q}{2}\Big )\Big )''}{\Big (\cos ^2 \Big (\frac{z_p}{2}\Big )\Big )''} \frac{\sigma ^q}{\sigma ^p} = \lim _{x \rightarrow c^q - \sigma ^q} \frac{(\sin (z_q))'}{(\sin (z_p))'} = \nonumber \\ {}{} & {} \lim _{x \rightarrow c^q - \sigma ^q} \frac{\cos (z_q)}{\cos (z_p)} \frac{\sigma ^p}{\sigma ^q} = \frac{\sigma ^p}{\sigma ^q}. \end{aligned}$$

Therefore maximum of f(x) is equal to 0 and the inequality (8) holds for \(x \in (c^q - \sigma ^q,\,c^p)\).

Analogous reasoning can be used to confirm that the inequality (8) holds for \(x \in (c^q,\,c^p + \sigma ^p)\). \(\square \)

Theorem 1 actually defines the ordering of fuzzy sets. Even though such an ordering and the monotonicity conditions are quite natural (see Fig. 2) they do not guarantee monotonicity for arbitrarily shaped membership functions.

Fig. 2
figure 2

Intuitiveness of monotonicity conditions: a cosine membership functions, b linear submodels, c increasing output

Full size image

4 Monotone Fuzzy System-Based Regression

Suppose that the parameters of membership functions (2) are given such that conditions in Theorem 1 hold. Then the mapping (1) can be written as

$$\begin{aligned} F(x) = \Phi (x)\cdot \theta \end{aligned}$$
(12)

with

$$\begin{aligned} \Phi (x) = \frac{[\mu ^{\textbf{k}_1}(x),\ldots ,\mu ^{\textbf{k}_M}(x)] \otimes [1,x_1,\ldots ,x_n]}{\sum _{\textbf{k} \in K}\mu ^\textbf{k}(x)} \end{aligned}$$
(13)

and the parameter vector \(\theta, \) defined by (5) where \(\otimes \) stands for Kronecker product, \(\mu ^{\textbf{k}_j} = \prod _{i=1}^{n} \mu _i^{k_i}(x_i)\) and \(\textbf{k}_j \in K,\, j = 1,\ldots ,M\). The mapping (12) is linear with respect to the submodel parameters \(a^{\textbf{k}_j}\).

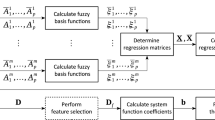
Now assume that the regressor \(\{x^l,y^l;x^l \in \Re ^n,y^l \in \Re , l = 1,\ldots ,N\}\) is available. The parameters guaranteeing monotonicity and minimizing the least squares are given by

$$\begin{aligned} \theta _{\text{opt}} = \arg \min _{\theta } ||Z\theta - \textbf{y}|| \quad \quad \text{s. \, t.} \end{aligned},$$
(14)

where \(Z = [\Phi (x^1)^{\text{T}},\ldots ,\Phi (x^N)^{\text{T}}]^{\text{T}}\), \(\textbf{y} = [y^1,\ldots ,y^N]^{\text{T}}\).

5 Methods Evaluation

Performance of a fuzzy system will beevaluated by its accuracy and goodness of fit, both on validation data \(\{x_\text{v}^k,y_\text{v}^k;x_\text{v}^k \in \Re ^n,y_\text{v}^k \in \Re , k = 1,\ldots ,N_\text{v}\}\).

The accuracy of the models will be validated by root mean square error (RMSE) between the given output \(y_\text{v}\) and the fuzzy model output \(F(x_\text{v})\) defined as

$$\begin{aligned} \text{RMSE}= & {} \sqrt{\frac{1}{N_\text{v}}\sum _{k=1}^{N_\text{v}}(y_\text{v}^k - F(x_\text{v}^k))^2}. \end{aligned}$$
(15)

The goodness of fit of the models will be measured by \(R^2\) coefficient defined as

$$\begin{aligned} R^2= & {} 1 - \frac{\sum _{k=1}^{N_\text{v}}(y_\text{v}^k - F(x_\text{v}^k))^2}{\sum _{k=1}^{N_\text{v}}(y_\text{v}^k - \bar{y})^2} \end{aligned},$$
(16)

where \(\bar{y} = \frac{1}{N_\text{v}}\sum _{k=1}^{N_\text{v}}y_\text{v}^k\) is the average of the observed data.

Monotonicity of a TS fuzzy model (1) non-decreasing with respect to a set of indices \(L,\, L \subset \{1,\dots ,n\}\) will be evaluated by monotonicity index \(I_\text{mon} \in [0,1]\) that is defined as

$$\begin{aligned} I_\text{mon} = \text{card} \Bigg (x_\text{g} \in X_\text{g}: \frac{\partial F}{\partial x_l}(x_\text{g}) \ge 0 \, \forall l \in L \Bigg ) \Bigg / \text{card}(X_\text{g})\nonumber \\ \end{aligned},$$
(17)

where \(\text{card}(\cdot )\) stands for cardinality of a set. The set \(X_\text{g}\) is usually generated by gridding the input set U.

6 Benchmark Datasets

6.1 Predicted Mean Vote (PMV) Dataset

PMV dataset is related to the prediction of the thermal comfort index [48]. The thermal comfort index in EN ISO 7730 is used and needed to evaluate the room climate. The predicted mean vote for thermal comfort is determined by the heat balance of the human being with his environment. The PMV index is a function of six variables, namely air temperature, radiant temperature, relative humidity, air velocity, human activity level, and clothing thermal resistance. The PMV index is calculated using a complex equation from [48] and it ranges between \(-3\) and 3. It increases with increasing air temperature and relative humidity, the remaining attributes are supposed to have no monotone impact. The dataset contains 567 samples reported in [49].

The achieved results will be compared with monotone zero-order TS fuzzy system identification procedure described in [49]. That procedure transforms related constrained optimization problem into a sequence of unconstrained minimization problems that are solved by David-Fletcher-Powell (DFP) algorithm. Let us note that just as the presented method the method in [49] (Stage E which gives the best results) guarantees monotonicity on the whole domain.

For each simulation the original 567 samples in 425 (75 %) is randomly split constituting a training data set and the remaining 142 (25 %) for the testing set. That step was repeated 50 times, and average values of RMSE for the testing set were compared. All the experiments are carried out on Intel core i7 5600K, 3.5GHz with 4GB of RAM and MATLAB R2016b.

At first, the original monotone data are used. Average RMSE achieved on testing sets of non-monotone zero-order TS fuzzy system (NON ZOTS, results taken from [39]), the presented monotone first-order TS fuzzy system (MON FOTS) and Stage E of the monotone zero-order TS fuzzy system proposed in [49] (MON ZOTS) for different numbers of input membership functions are compared in Table 1. Raised cosine membership functions (plotted in Fig. 3) were chosen to be similar to triangular membership functions used in [49]. One can see that the presented monotone first-order TS fuzzy system gives similar results and the results are improving for a higher number of input fuzzy sets which is not the case of method in [49]. Table 1 also shows that for noise-free data the difference between monotone and non-monotone regression is quite small. A slightly higher accuracy of the presented method is not surprising since a first-order TS fuzzy system contains more parameters compared to a zero-order TS fuzzy system. Moreover, the average computational time reported in [49] is 401.7012s whereas for the presented method it is 94.1s. The presented method is significantly faster since it relies on very efficient linearly constrained least squares algorithms.

RMSE achieved on all 567 data samples for non-monotone zero-order TS fuzzy system for \(M_1 = M_2 = 5\) is 0.0774 (reported in [39]) and for Stage E of the monotone zero-order TS fuzzy system proposed in [49] is 0.0021. RMSE on the same data samples for the proposed monotone first-order TS fuzzy system is 0.0036.

Fig. 3
figure 3

Input membership functions for PMV dataset

Full size image

Next, the original data are contaminated by noise,

$$\begin{aligned} noise = 0.5 \times rand \times data \end{aligned},$$
(18)

where rand is a normally distributed random number with a mean of 0 and variance 1. Now non-monotone data are obtained and the same identification algorithms as in the previous case are used to create fuzzy models. A comparison of RMSE is shown in Table 2. The values show that for a small number of input fuzzy sets the presented monotone TS fuzzy system is worse compared to the monotone ZO TSFS but it gets much better for a higher number of input fuzzy sets. Quite naturally, both monotone TS fuzzy systems exhibit better results compared to non-monotone ones. The average computational time for monotone FO TSFS (\(M_1 = M_2 = 5\)) was 101.5s which is almost the same as for noise-free dataset and it is considerably less than the 1903.59s reported in [49] for monotone ZO TSFS.

Table 1 Comparison of \(\text{RMSE}\) for different methods for monotone PMV dataset
Full size table
Table 2 Comparison of \(\text{RMSE}\) for non-monotone noisy PMV dataset
Full size table

In Table 3 and Table 4, the presented method using cosine membership functions was compared with triangular, Gaussian, and sigmoidal membership functions. Unfortunately, there are no conditions guaranteeing monotonicity for Gaussian and sigmoidal membership functions with different widths, therefore the same width was used for all of them. As expected, the presented method achieves better results since the conditions imposed on the linear models in the consequents are less restrictive for cosine membership functions.

Table 3 Comparison of \(\text{RMSE}\) for different membership functions for monotone PMV dataset
Full size table
Table 4 Comparison of \(\text{RMSE}\) for different membership functions for non-monotone noisy PMV dataset
Full size table

The original dependency and its approximations by non-monotone and monotone TS fuzzy systems with \(M_1 = M_2 = 5\) membership functions are shown in Fig. 4, 5 and 6, respectively.

Fig. 4
figure 4

Original PMV dataset

Full size image
Fig. 5
figure 5

PMV dataset non-monotone TS fuzzy system approximation

Full size image
Fig. 6
figure 6

PMV dataset monotone TS fuzzy system approximation

Full size image

6.2 Boston Housing Dataset

In the second case study, a commonly used dataset that contains information about different houses in Boston [50] is adopted. The dataset was developed to illustrate the issues with using housing market data to measure consumer willingness to pay for clean air. The input to this model was a dataset comprising the Boston Standard Metropolitan Statistical Area, with the nitric oxide concentration (NOX) serving as a proxy for air quality. The variables in the dataset were collected in the early 1970 s and come from a mixture of surveys, administrative records, and other research papers. The goal is to predict the price of a house based on 13 input attributes described in Table 5. The dataset contains 506 datapoints.

Table 5 Description of attributes of Boston housing dataset
Full size table

After performing a correlation analysis, the following 6 attributes are considered monotone (ordered by decreasing absolute value of correlation coefficient). The lower status of the population (LSTAT), the higher the average number of rooms per dwelling (RM), the lower the tax rate (TAX), the lower the nitric oxide concentration (NOX), the lower the distance to the center (DIST), the lower the crime level (CRIM), the higher the median value of the price.

Because of the strong correlation between the attributes TAX and RAD (positive), DIS and AGE (negative), and NOX and INDUS (negative), attributes RAD, AGE, and INDUS are not considered for prediction. Because of the weak correlation between the price and the attributes CHAS and B those two were disregarded as well. The remaining attributes PTRA and ZN are treated as non-monotone. Two raised cosine membership functions are used for each attribute.

506 datapoints were divided as 380 for the training set (75 %) and 106 for the testing set (25 %). That step is repeated 50 times and average values of RMSE and its variance and \(R^2\) are calculated. The performance is compared with monotone multilayer perceptron (MLP) (proposed in [51]) and monotone MIN-MAX network (MM, proposed in [15]). The RMSE and \(R^2\) values for those two methods and linear regression (LR) are taken from [52]. Let us note that all considered tools guarantee monotonicity.

Table 6 Comparison of \(\text{RMSE}\) and \(R^2\) for Boston housing dataset
Full size table

Table 6 shows that the best results in terms of mean RMSE and its variance were achieved for the four-layer MIN-MAX network. Nevertheless, in contrast to presented TS fuzzy systems, MIN-MAX networks do not produce smooth output. First-order TS fuzzy systems achieve better accuracy compared to monotone two-layer perceptron. As expected, all nonlinear regression approaches exhibit better predictions than linear ones.

6.3 Large Datasets

Three more benchmark datasets adopted from the machine learning repository of the University of California, Irvine (UCI) [53] were used to compare the presented algorithm with many commonly used regression models, both monotone and non-monotone. As the third tested dataset, a large Abalone dataset was used. The Abalone dataset contains the physical measurements of abalones, which are large, edible sea snails. Predicting the age of abalone from physical measurements. The age of abalone is determined by cutting the shell through the cone, staining it, and counting the number of rings through a microscope—a boring and time-consuming task. Other measurements, which are easier to obtain, are used to predict the age. Further information, such as weather patterns and location (hence food availability) may be required to solve the problem.

The dataset contains 4177 items, each of which has 7 attributes, 6 of them were handled as monotone (Length, Diameter, Height, Whole weight, Shucked weight, Viscera weight), one as a non-monotone (Shell weight).

The dataset containing 9568 data points collected from a Combined Cycle Power Plant over 6 years (2006-2011), when the power plant was set to work with full load, was used as another example. Features consist of hourly average ambient variables temperature, ambient pressure, relative humidity, and exhaust vacuum to predict the net hourly electrical energy output of the plant. The higher the temperature and the exhaust vacuum the lower the electrical energy power. Therefore the attributes temperature and exhaust vacuum were treated as monotone, the remaining ones as non-monotone. In both datasets the categorization of monotone and non-monotone attributes was taken from [52].

As the last dataset, the Auto-MPG taken from the StatLib library maintained by Carnegie Mellon University was used. The dataset contains 392 instances, each having eight attributes: number of cylinders (decreasing), displacement, horsepower, weight of the car (decreasing), acceleration, model year (increasing), and origin. The aim is to predict the city-cycle fuel consumption in miles per gallon (mpg). According to an expert who majors in automobiles and mechanical engineering fuel consumption grows with increasing model year and decreasing number of cylinders and weight of the car. The other attributes were considered to have a non-monotone impact on the predicted output.

The datasets were divided into a training set (70 % of the dataset) and a test set (remaining 30 % of the dataset). That step was repeated 50 times for different numbers of membership functions and different widths and the average results were taken. The presented monotone first-order TS fuzzy system with cosine membership functions (MonCOS ) was compared with the regression models commonly used in machine learning. As non-monotone regressors first-order TS fuzzy system with cosine (NonCOS) and Gaussian membership functions (NonGAUSS), non-monotone multilayer perceptron (NonMLP), and non-monotone support vector regression (NonSVR) are considered. Monotone first-order TS fuzzy system with Gaussian membership functions (MonGAUSS, [26]), monotone multilayer perceptron (MonMLP, [51]), monotone MIN-MAX network (MonMM, [15]) and monotone support vector regression (MonSVR, [6], does not guarantee monotonicity) were taken into account as monotone regression models.

Table 7 Comparison of RMSE, its variance, \(R^2\) and \(I_\text{mon}\) for Abalone dataset
Full size table
Table 8 Comparison of RMSE, its variance, \(R^2\) and \(I_\text{mon}\) for Combined Cycle Power Plant dataset
Full size table
Table 9 Comparison of RMSE, its variance, \(R^2\) and \(I_\text{mon}\) for Auto-MPG
Full size table

First, the results confirm the expected fact—taking into account monotonic dependency considerably improves any regression model performance. Second, when comparing monotone regressors there is no big difference among the models. Generally, neural networks (MLP, MIN-MAX) exhibit the best results, nevertheless their interpretability is very low. One can also see that there is almost no difference between non-monotone fuzzy systems with cosine and Gaussian membership functions. However, in the monotone case, cosine membership functions have better accuracy since the monotonicity conditions imposed on the consequent part are less restrictive.

7 Conclusion

The paper presents sufficient conditions guaranteeing the monotonicity of first-order Takagi–Sugeno fuzzy systems with raised cosine membership functions. The conditions are separated into antecedent and consequent parts. Whereas the former are satisfied by suitable choice of membership functions parameters the latter are expressed as linear constraints on submodels parameters. Experiments performed on benchmark datasets confirm that using knowledge about monotonicity with respect to some or all input variables improves performance of nonlinear regression analysis, especially in the presence of noise in data. The main advantage of monotone TS fuzzy systems with raised cosine membership functions over other smooth functions is that the derived monotonicity conditions are feasible for membership functions with different widths and are less conservative and therefore performance of those systems is better. When comparing the goniometric membership functions with triangular ones the former produces a smooth output and the corresponding algorithm is much faster.