1 Introduction

In 1965, Zadeh [1] put forward the concept of fuzzy sets, to represent uncertain information through membership and non-membership. After that, Torra [2] proposed the hesitant fuzzy sets (HFSs), which further enriched the theory and application of fuzzy sets. Besides, many scholars have made research on HFSs, which have been extended into hesitant fuzzy linguistic term sets [3], interval value-hesitant fuzzy sets [4], dual-hesitant fuzzy sets [5], generalized hesitant fuzzy sets [6], and hesitant triangular fuzzy sets [7] and so on in recent years.

However, HFSs assume that the probability of each element is equal, so it cannot express the preference of experts; in order to improve this problem, Zhu [8] applied probability information into HFS, firstly proposed the probability hesitant fuzzy sets(PHFSs); and due to the full use of probability information, the PHFS can not only describe decision makers’ cognition of uncertainty, but also illustrate the difference of the importance of all evaluations. Because of the perfect mathematical form, the PHFS has received wide attention of scholars, a series of achievements have been made in integration operators [9,10,11,12], preference relation theory [13, 14], and decision-making method [15,16,17]; among them, the preference relation has great application prospects because it conforms to the process of group decision making. In addition, scholars have also extended the PHFS to interval value probability hesitant fuzzy sets [18], dual probability hesitant fuzzy sets [19], and so on, which provided a great supplement to PHFS theory.

In the researches mentioned above, correlation coefficient measure is an important field to be further studied. Correlation coefficient, as a common mathematical method in data analysis, is widely used in multi-attribute decision making. Different from the distance measure [20], similarity [21], and entropy measure [22], the correlation coefficient studies the degree of linear correlation between two variables, which has the necessity and uniqueness of analysis. In this paper, we devote ourselves to the correlation coefficient of PHFS. Some scholars have studied the correlation coefficient of HFSs and obtained some remarkable achievements.

Xu [23] first defined five correlation coefficients of HFEs and applied them to medical diagnosis. On this basis, Chen [24] given some correlation coefficients of HFSs to solve the clustering problem. Guan [25] analyzed the limitations of the available correlation coefficients of HFSs and proposed a new correlation coefficient that not only satisfies statistical intuition, but does not require the same quantity of membership degrees in HFE. In addition, the team also proposed a comprehensive correlation coefficient [26] by defining the characteristics of several types of HFSs, which solved the anti-intuition phenomenon in the existing correlation coefficients. Regarding the current concerns that the existing correlation coefficients of HFS violate the statistical intuition and stochastic process, Xu [27, 28] proposed a novel correlation coefficient of HFS based on a more rigorous mathematical definition and utilized it to solve multi-sensor decision-making problems. Furthermore, Reference [29,30,31,32] also extended the correlation coefficients to dual-hesitant fuzzy set, interval value-hesitant fuzzy set, interval value dual-hesitant fuzzy set, and hesitant fuzzy linguistic term set, which were applied in fields of cluster analysis, water quality assessment, medical diagnosis, and so on. Nevertheless, compared with the HFS, the measurement theory of PHFS is much more complex [33], so there are still few researches on the correlation coefficients of PHFS at present. Farhadinia [34] proposed five correlation coefficients of PHFSs and employed them to medical diagnosis. By defining mean and variance of PHFE, Wang [35] studied the correlation coefficient of PHFEs and expanded it into weighted form. Zhu [36] defined the correlation coefficients of discrete and continuous PHFSs, and proposed a multi-attribute decision model based on them. Song [37] proposed an improved correlation coefficient of PHFS and applied it to cluster analysis.

Although the above correlation coefficients have been put to use in many fields, they all have corresponding shortcomings. The value of correlation coefficient should be positive and negative. However, the value range of correlation coefficient proposed by Farhadinia [34] is lie in [0, 1], which only reflects the positive correlation and ignores the negative correlation, which does not conform to the strict mathematical definition of correlation coefficient condition, and it is necessary to meet the condition of equal number of elements through element continuation; some correlation coefficients consider the case of negative correlation, such as reference [35, 37], but they are essentially a kind of mean correlation coefficient, that is, no matter how the membership degree in PHFE is distributed; as long as its mean value is equal, the calculation results are equal. It ignores the specific distribution and quantity of membership degree and other factors, so it may lead to counter-intuitive phenomenon and has certain limitations.

Although some literature considers the case of negative correlation, such as references [35, 37], it is essentially an average correlation coefficient,

The primary motivations and contributions of this paper are summarized as follows.

  1. (1)

    We analyzed the shortcomings of existing PHFS correlation coefficients. For example, the range of some correlation coefficients is unreasonable, that is, negative correlation cannot be characterized, in addition, some correlation coefficients are essentially a kind of mean correlation coefficient, which only measures the aggregation of PHFE, so there is one-sidedness and counter-intuitive phenomena when expressing the correlation between data;

  2. (2)

    We defined mean, variance, and length ratio three characteristics of PHFE through strict mathematical derivation, which characterized the integrity, distribution, and number of elements in PHFE, respectively. On this basis, we defined mean, variance, and length three basic correlation coefficients; then we obtained the mixed correlation coefficient by combining the three, and proved that it meets the conditions of correlation coefficient, and finally extend it to PHFS.

  3. (3)

    Based on the research emphasis of this paper, a multi-attribute decision-making model based on correlation coefficient is constructed, and the advantages of improved correlation coefficient are verified through two simulations of data association and multi-attribute decision making.

Since the main task of this paper is correlation coefficient, it is necessary to provide a clear explanation of the advantages of improving correlation coefficients as follows:

  1. (1)

    Avoid counter-intuitive phenomena and make the results more reasonable;

  2. (2)

    The mixed correlation coefficient has greater flexibility and can achieve results that better align with decision makers’ intentions by adjusting parameters;

  3. (3)

    The results of the mixed correlation coefficient are more comprehensive, and its decision making is more convincing compared to a single feature.

The chapters of this paper are arranged as follows:

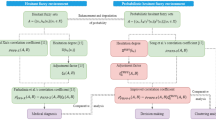
First, we summarized the current research status and achievements of PHFS in Sect. 1, and some basic concepts of PHFS are introduced in Sect. 2. In Sect. 3, we analyze the existing correlation coefficient and its deficiencies; In Sect. 4, we give the three basic concepts of mean, variance, and length ratio of PHFE, and define the corresponding three basic correlation coefficients, and then integrate the three correlation coefficients to obtain the mixed form, which is expanded to the weighted form. In Sect. 5, the validity and superiority of the proposed correlation coefficient are verified through two examples of data association analysis and multi-attribute decision making. Finally, we summarize the work done in this paper and make prospects for future research directions in Sect. 6.

2 Preliminary

The basic concept and operation rules of PHFS are briefly introduced in this section.

Definition 1

The reference domain is any nonempty set X, and the PHFS H is expressed as a probability distribution function mapping from X to the interval [0,1], which is defined as follows:

$$\begin{aligned} H = \{ \langle x,{h_x}({p_x})\rangle \vert x \in X\}, \end{aligned}$$
(1)

where h(x) represents the membership degree of X belonging to a certain set, the value is the subset on the interval [0,1]. \({p_x}\) is the corresponding probability of a membership degree in h(x), which is also a subset of [0,1]. Besides,\({h_x}({p_x})\) is known as probability hesitant fuzzy element(PHFE), which is abbreviated as h(p) and can be expressed as follows:

$$\begin{aligned} h(p) = \{ {\gamma ^\lambda }\vert {p^\lambda },\lambda = 1,2, \cdots ,\left| {h(p)} \right| \}, \end{aligned}$$
(2)

in which \(\left| {h(p)} \right|\) represents the quantity of membership degree, \({\gamma ^\lambda }\) depicts the possibility that x belongs to H, and \({p ^\lambda }\) is the corresponding occurrence probability of \({\gamma ^\lambda }\), which satisfies \(\sum \nolimits _{\lambda = 1}^{\left| {h(p)} \right| } {{p^\lambda } \le 1}\).

3 PHFS Correlation Coefficient Analysis

In this section, we summarize the existing probability hesitation fuzzy correlation coefficient, and analyze its shortcomings emphatically; then we mainly makes comparison in the subsequent simulation analysis with the correlation coefficient defined in reference [37].

3.1 Existing PHFS Correlation Coefficient

The PHFS correlation coefficient in reference [37] is described as follows.

Definition 2

Assume the reference domain \(X = \{ {x_1},{x_2}, \cdots ,{x_n}\}\),and two random PHFSs \(A = \{ \langle x,{h_{Ai}}({p_x})\rangle \vert {x_i} \in X\}\) and \(B = \{ \langle x,{h_{Bi}}({p_x})\rangle \vert {x_i} \in X\}\), where the PHFE of A is \({h_{Ai}}({p_x}) = \{ \gamma _{Ai}^\lambda \vert p_{Ai}^\lambda ,\lambda = 1,2, \cdots ,{l_{Ai}}\}\), then the average and variance of A, the covariance and correlation coefficient between A and B are respectively expressed as follows:

The average of PHFS A is defined as follows:

$$\begin{aligned} {\bar{A}} = E(A) = \frac{1}{n}\sum \limits _{i = 1}^n {{{{\bar{h}}}_{Ai}}({p_x})} = \frac{1}{n}\sum \limits _{i = 1}^n {\left[ {\sum \nolimits _{\lambda = 1}^{{l_{Ai}}} {(\gamma _{Ai}^\lambda \cdot p_{Ai}^\lambda )} } \right] }, \end{aligned}$$
(3)

where \({{\bar{h}}_{Ai}}({p_x})\) represents the average of PHFE \({h_{Ai}}({p_x})\):

$$\begin{aligned} {{\bar{h}}_{Ai}}({p_x}) = \sum \nolimits _{\lambda = 1}^{{l_{Ai}}} {(\gamma _{Ai}^\lambda \cdot p_{Ai}^\lambda )}. \end{aligned}$$
(4)

The variance of PHFS A based on the average \({\bar{A}}\) is defined as follows:

$$\begin{aligned} Var(A) = \frac{1}{n}\sum \limits _{i = 1}^n {{{\left[ {{{{\bar{h}}}_{Ai}}({p_x}) - {\bar{A}}} \right] }^2}}. \end{aligned}$$
(5)

The covariance between PHFSs A and B is expressed as follows:

$$\begin{aligned} C(A,B) = \frac{1}{n}\sum \limits _{i = 1}^n {\left[ {{{{\bar{h}}}_{Ai}}({p_x}) - {\bar{A}}} \right] \cdot \left[ {{{{\bar{h}}}_{Bi}}({p_x}) - {\bar{B}}} \right] }. \end{aligned}$$
(6)

Based on the covariance C(A, B), the correlation coefficient between PHFSs A and B is expressed as follows:

$$\begin{aligned}{} & {} \rho (A,B) = \frac{{C(A,B)}}{{{{\left[ {C(A,A) \cdot C(B,B)} \right] }^{\frac{1}{2}}}}} \nonumber \\{} & {} \quad = \frac{{\frac{1}{n}\sum \nolimits _{i = 1}^n {\left[ {{{{\bar{h}}}_{Ai}}({p_x}) - {\bar{A}}} \right] \cdot \left[ {{{{\bar{h}}}_{Bi}}({p_x}) - {\bar{B}}} \right] } }}{{{{\left[ {\frac{1}{n}\sum \nolimits _{i = 1}^n {{{\left[ {{{{\bar{h}}}_{Ai}}({p_x}) - {\bar{A}}} \right] }^2} \cdot \frac{1}{n}\sum \nolimits _{i = 1}^n {{{\left[ {{{{\bar{h}}}_{Ai}}({p_x}) - {\bar{A}}} \right] }^2}} } } \right] }^{\frac{1}{2}}}}}. \end{aligned}$$
(7)

Definition 3

If the weights of elements on X are taken into account, assuming that the weight vector on X is \({\omega _i} \in [0,1],i = 1,2, \cdots ,n\), which satisfies \(\sum \nolimits _{i = 1}^n {{\omega _i}} = 1\), then the weighted average, variance of PHFS A, as well as the weighted covariance and correlation coefficient between A and B are expressed as follows respectively.

The weighted average of PHFS A is

$$\begin{aligned} {{\bar{A}}_\omega } = \frac{1}{n}\sum \limits _{i = 1}^n {{\omega _i}{{{\bar{h}}}_{Ai}}({p_x})} = \frac{1}{n}\sum \limits _{i = 1}^n {\left[ {{\omega _i}\sum \nolimits _{\lambda = 1}^{{l_{Ai}}} {(\gamma _{Ai}^\lambda \cdot p_{Ai}^\lambda )} } \right] }. \end{aligned}$$
(8)

The weighted variance of PHFS A is

$$\begin{aligned} Va{r_\omega }(A) = \frac{1}{n}\sum \limits _{i = 1}^n {{{\left[ {{\omega _i}{{{\bar{h}}}_{Ai}}({p_x}) - {{{\bar{A}}}_\omega }} \right] }^2}}. \end{aligned}$$
(9)

The weighted covariance between PHFSs A and B is expressed as follows:

$$\begin{aligned} {C_\omega }(A,B) = \frac{1}{n}\sum \limits _{i = 1}^n {\left[ {{\omega _i}{{{\bar{h}}}_{Ai}}({p_x}) - {{{\bar{A}}}_\omega }} \right] \cdot \left[ {{\omega _i}{{{\bar{h}}}_{Bi}}({p_x}) - {{{\bar{B}}}_\omega }} \right] }. \end{aligned}$$
(10)

Based on covariance \({C_\omega }(A,B)\), the weighted correlation coefficient between PHFSs A and B is expressed as follows:

$$\begin{aligned}{} & {} {\rho _\omega }(A,B) = \frac{{{C_\omega }(A,B)}}{{{{\left[ {{C_\omega }(A,A) \cdot {C_\omega }(B,B)} \right] }^{1/2}}}} \nonumber \\{} & {} \quad = \frac{{\sum \nolimits _{i = 1}^n {\left[ {{\omega _i}{{{\bar{h}}}_{Ai}}({p_x}) - {{{\bar{A}}}_\omega }} \right] \cdot \left[ {{\omega _i}{{{\bar{h}}}_{Bi}}({p_x}) - {{{\bar{B}}}_\omega }} \right] } }}{{\sqrt{\sum \nolimits _{i = 1}^n {{{\left[ {{\omega _i}{{{\bar{h}}}_{Ai}}({p_x}) - {{{\bar{A}}}_\omega }} \right] }^2}} } \cdot \sqrt{\sum \nolimits _{i = 1}^n {{{\left[ {{\omega _i}{{{\bar{h}}}_{Bi}}({p_x}) - {{{\bar{B}}}_\omega }} \right] }^2}} }}}. \end{aligned}$$
(11)

3.2 Existing Correlation Coefficient Limitation Analysis

Example 1

Given a PHFE \(h(p) = \{ 0.8\vert 0.7,0.2\vert 0.3\}\), which means the membership degree of x belonging to H is 0.8 or 0.2, and the probability being 0.8 is 0.7, the probability being 0.2 is 0.3. When all the probability of membership degree is \(1/\left| {h(p)} \right|\), h(p) turns to \(\{ 0.8\vert 0.\mathrm{{5}},0.2\vert 0.\mathrm{{5}}\}\). At this time, it can be obtained that all membership degrees have the same probability through the probability information, in other words, decision makers do not prefer any membership degree.

Similarly, the hesitation fuzzy element (HFE) \(\{ 0.8,0.2\}\) cannot determine which membership degree decision makers prefer because it does not contain probability information. Therefore, when the probability of membership degree is equal, the information delivered by the PHFS is equivalent to that of hesitation fuzzy set(HFS), that is to say, the HFS can be understood as a special case of the PHFS. Therefore, we consider the following example.

Example 2

Considering the simplest case, given the reference domain \(X = \{ {x_1},{x_2},{x_3}\}\), three PHFSs A, B, and C are expressed as below, respectively:

$$\begin{aligned}{} & {} \begin{aligned} A&= \left\{< {x_1},\left\{ 0.3\vert \frac{1}{2},0.5\vert \frac{1}{2}\right\}>,\right. \\&< {x_2}, \left\{ 0.3\vert \frac{1}{3},0.6\vert \frac{1}{3},0.9\vert \frac{1}{3}\right\}>,\\&\left.< {x_3},\left\{ 0.1\vert \frac{1}{4},0.2\vert \frac{1}{4},0.8\vert \frac{1}{4},0.9\vert \frac{1}{4}\right\}> \right\} , \end{aligned}\\{} & {} \begin{aligned} B&= \left\{< {x_1},\left\{ 0.1\vert \frac{1}{2},0.7\vert \frac{1}{2}\right\}>,\right. \\&< {x_2},\left\{ 0.2\vert \frac{1}{3},0.7\vert \frac{1}{3},0.9\vert \frac{1}{3}\right\}>,\\&\left.< {x_3},\left\{ 0.3\vert \frac{1}{3},0.5\vert \frac{1}{3},0.7\vert \frac{1}{3}\right\}> \right\} , \end{aligned}\\{} & {} \begin{aligned} C&= \left\{< {x_1},\left\{ 0.2\vert \frac{1}{3},0.3\vert \frac{1}{3},0.7\vert \frac{1}{3}\right\}>,\right. \\&< {x_2},\left\{ 0.5\vert \frac{1}{2},0.7\vert \frac{1}{2}\right\}>,\\&\left. < {x_3},\left\{ 0.4\vert \frac{1}{3},0.5\vert \frac{1}{3},0.6\vert \frac{1}{3}\right\} > \right\} . \end{aligned} \end{aligned}$$

The correlation coefficients between A, B, and C are calculated according to definition 2, and the specific process is as follows:

The average values of PHFE in A, B, and C are

$$\begin{aligned} {{\bar{h}}_{Ai}}({p_x}) = {{\bar{h}}_{Bi}}({p_x}) = {{\bar{h}}_{Ci}}({p_x}) = \{ 0.4,0.6,0.5\}. \end{aligned}$$

The average values of PHFSs A, B, and C are

$$\begin{aligned} {\bar{A}} = {\bar{B}} = {\bar{C}} = 0.5. \end{aligned}$$

The variance of PHFSs A, B, and C is

$$\begin{aligned} Var(A) = Var(B) = Var(C) = \frac{{0.02}}{3}. \end{aligned}$$

The covariance between PHFSs A, B, and C is

$$\begin{aligned} C(A,B) = C(A,C) = C(B,C) = \frac{{0.02}}{3}. \end{aligned}$$

Then the correlation coefficients between A, B, and C are

$$\begin{aligned} \rho (A,B) = \rho (A,C) = \rho (B,C) = 1. \end{aligned}$$

Obviously, the above conclusion is counter-intuitive, because PHFSs A, B, and C are completely distinct and there is no linearity between them, so the correlation coefficient between them should not be 1, indicating that the existing method fails in this example, the reasons can be summarized as follows:

(1) The existing correlation coefficient is essentially a kind of average correlation coefficient, namely it ignores the specific distribution characteristic of membership degrees of PHFE, only calculates the average of each PHFE to reconstruct a new HFE, so we can say that no matter how the membership degrees are distributed, as long as the corresponding PHFE average is equal, the calculation result is the same.

(2) The existing correlation coefficient does not take into account the influence of quantity of membership degrees. Although it is not mandatory to have equal quantity of membership degrees but also makes this factor not play an important part during the calculation, if the number of membership degrees is inconsistent, the corresponding correlation coefficients should not be equal; therefore, the membership number of PHFS shall be as an important feature in the definition of correlation coefficient.

4 PHFS Mixed Correlation Coefficient

Mathematically, the correlation coefficient is defined as ’random variable normalization covariance.’ Therefore, this section defines a mixed correlation coefficient from the viewpoint of statistics and stochastic process to make it more mathematical. First, the definitions of variance and covariance of PHFSs are given from the aspect of statistics. Then, according to the strict mathematical definition of covariance, the new correlation coefficient is defined according to the mathematical meaning of ’random variable normalization covariance.’

According to previous analysis, the new correlation coefficient should take the entirety, specific distribution, and number of membership degrees in PHFEs into account. Therefore, on the basis of reference [38], this section uses the average value to represent the entirety of PHFE, variance to indicate its specific distribution, length ratio to reflect the number of membership degrees, which are used to construct average, variance, and length three basic correlation coefficients, respectively; finally, they are integrated to obtain the mixed correlation coefficient, and the basic definition is described below.

4.1 Basic Definition of PHFE Characteristics

Definition 4

Given the reference domain set \(X = \{ {x_1},{x_2}, \cdots ,{x_n}\}\), a random PHFS \(A = \{ \langle x,{h_{Ai}}({p_x})\rangle \vert {x_i} \in X\}\), where the PHFE is \({h_{Ai}}({p_x}) = \{ \gamma _{Ai}^\lambda \vert p_{Ai}^\lambda ,\lambda = 1,2, \cdots ,{l_{Ai}}\}\), then the average, variance, and length ratio of \({h_{Ai}}({p_x})\) are respectively defined as follows.

The average of PHFE \({h_{Ai}}({p_x})\) is

$$\begin{aligned} {{\bar{h}}_{Ai}}({p_x}) = \sum \nolimits _{\lambda = 1}^{{l_{Ai}}} {(\gamma _{Ai}^\lambda \cdot p_{Ai}^\lambda )}. \end{aligned}$$
(12)

The variance of PHFE \({h_{Ai}}({p_x})\) is

$$\begin{aligned} Var({h_{Ai}}({p_x})) = \sum \limits _{\lambda = 1}^{{l_{Ai}}} {{{\left[ {\gamma _{Ai}^\lambda - {{{\bar{h}}}_{Ai}}({p_x})} \right] }^2}p_{Ai}^\lambda }. \end{aligned}$$
(13)

The length ratio of PHFE \({h_{Ai}}({p_x})\) is

$$\begin{aligned} u\left( {{h_{Ai}}({p_x})} \right) = 1 - \frac{1}{{{l_{Ai}}}}, \end{aligned}$$
(14)

where \(u\left( {{h_{Ai}}({p_x})} \right)\) satisfies \(0 \le u\left( {{h_{Ai}}({p_x})} \right) \le 1\), when the number of membership degrees is 1, \(u\left( {{h_{Ai}}({p_x})} \right) = 0\), which indicates that the PHFE has the minimum membership degrees, when the number of membership degrees approaches infinity, \(u\left( {{h_{Ai}}({p_x})} \right) = 1\), indicates that the PHFE has the maximum membership degrees. Besides, the length ratio of PHFS A is expressed as follows:

$$\begin{aligned} u(A) = \frac{1}{n}\sum \limits _{i = 1}^n {u\left( {{h_{Ai}}({p_x})} \right) }. \end{aligned}$$
(15)

4.2 Three Basic PHFS Correlation Coefficients

According to the analysis in Sect. 4.1, the average, variance, and length three basic correlation coefficients are defined respectively as below.

Assume the reference domain \(X = \{ {x_1},{x_2}, \cdots ,{x_n}\}\), and two random PHFSs \(A = \{ \langle x,{h_{Ai}}({p_x})\rangle \vert {x_i} \in X\}\) and \(B = \{ \langle x,{h_{Bi}}({p_x})\rangle \vert {x_i} \in X\}\), where the PHFE of A and B are respectively \({h_{Ai}}({p_x}) = \{ \gamma _{Ai}^\lambda \vert p_{Ai}^\lambda ,\lambda = 1,2, \cdots ,{l_{Ai}}\}\) and \({h_{Bi}}({p_x}) = \{ \gamma _{Bi}^\lambda \vert p_{Bi}^\lambda ,\lambda = 1,2, \cdots ,{l_{Bi}}\},i = 1,2, \cdots ,n\).

4.2.1 Average Correlation Coefficient

The average correlation coefficient is actually the same as that mentioned in reference [37]. In order to unify the mathematical expression, it is briefly described as follows.

Definition 5

The average covariance between PHFSs A and B is

$$\begin{aligned} {C_M}(A,B) = \frac{1}{n}\sum \limits _{i = 1}^n {\left[ {{{{\bar{h}}}_{Ai}}({p_x}) - {\bar{A}}} \right] \left[ {{{{\bar{h}}}_{Bi}}({p_x}) - {\bar{B}}} \right] }. \end{aligned}$$
(16)

Based on \({C_M}(A,B)\), the average correlation coefficient between A and B is defined as follows:

$$\begin{aligned}{} & {} {\rho _M}(A,B) = \frac{{{C_M}(A,B)}}{{{{\left[ {{C_M}(A,A){C_M}(B,B)} \right] }^{1/2}}}} \nonumber \\{} & {} \quad = \frac{{\sum \nolimits _{i = 1}^n {\left[ {{{{\bar{h}}}_{Ai}}({p_x}) - {\bar{A}}} \right] \left[ {{{{\bar{h}}}_{Bi}}({p_x}) - {\bar{B}}} \right] } }}{{{{\left[ {\sum \nolimits _{i = 1}^n {{{\left[ {{{{\bar{h}}}_{Ai}}({p_x}) - {\bar{A}}} \right] }^2}\sum \nolimits _{i = 1}^n {{{\left[ {{{{\bar{h}}}_{Ai}}({p_x}) - {\bar{A}}} \right] }^2}} } } \right] }^{1/2}}}}. \end{aligned}$$
(17)

4.2.2 Variance Correlation Coefficient

Definition 6

The average of the variance of PHFE \({h_{Ai}}({p_x})\) is defined as follows:

$$\begin{aligned}{} & {} {{{\bar{A}}}_V} = E(Var({h_{Ai}}({p_x}))) = \frac{1}{n}\sum \limits _{i = 1}^n {Var({h_{Ai}}({p_x}))} \nonumber \\{} & {} \quad = \frac{1}{n}\sum \limits _{i = 1}^n {\left[ {\sum \limits _{\lambda = 1}^{{l_{Ai}}} {{{\left[ {\gamma _{Ai}^\lambda - {{{\bar{h}}}_{Ai}}({p_x})} \right] }^2}p_{Ai}^\lambda } } \right] }. \end{aligned}$$
(18)

The variance of the variance of PHFE \({h_{Ai}}({p_x})\) is defined as follows:

$$\begin{aligned} \begin{aligned}&Var(Var({h_{Ai}}({p_x}))) = \frac{1}{n}\sum \limits _{i = 1}^n {{{\left[ {Var({h_{Ai}}({p_x})) - {{{\bar{A}}}_V}} \right] }^2}}\\&\quad = \frac{1}{n}\sum \limits _{i = 1}^n \left[ Var({h_{Ai}}({p_x})) \right. \\&\qquad \left. - \frac{1}{n}\sum \limits _{i = 1}^n {\left[ {\sum \limits _{\lambda = 1}^{{l_{Ai}}} {{{\left[ {\gamma _{Ai}^\lambda - {{{\bar{h}}}_{Ai}}({p_x})} \right] }^2}p_{Ai}^\lambda } } \right] } \right] ^2, \end{aligned} \end{aligned}$$
(19)

On this basis, the covariance of the variance between PHFSs A and B is

$$\begin{aligned} {C_V}(A,B)= & {} \frac{1}{n}\sum \limits _{i = 1}^n \left[ {Var({h_{Ai}}({p_x})) - {{{\bar{A}}}_V}} \right] \nonumber \\{} & {} \left[ {Var({h_{Bi}}({p_x})) - {{{\bar{B}}}_V}} \right]. \end{aligned}$$
(20)

Based on \({C_V}(A,B)\), the variance correlation coefficient between A and B is expressed as follows:

$$\begin{aligned} \begin{aligned}&{\rho _V}(A,B) = \frac{{{C_V}(A,B)}}{{{{\left[ {{C_V}(A,A){C_V}(B,B)} \right] }^{1/2}}}}\\&\quad = \frac{{\sum \nolimits _{i = 1}^n {\left[ {Var({h_{Ai}}({p_x})) - {{{\bar{A}}}_V}} \right] \left[ {Var({h_{Bi}}({p_x})) - {{{\bar{B}}}_V}} \right] } }}{{{{\left[ {\sum \nolimits _{i = 1}^n {{{\left[ {Var({h_{Ai}}({p_x})) - {{{\bar{A}}}_V}} \right] }^2}\sum \nolimits _{i = 1}^n {{{\left[ {Var({h_{Bi}}({p_x})) - {{{\bar{B}}}_V}} \right] }^2}} } } \right] }^{1/2}}}}. \end{aligned} \end{aligned}$$
(21)

4.2.3 Length Correlation Coefficient

Definition 7

The average of the length ratio of PHFE \({h_{Ai}}({p_x})\) is defined as follows:

$$\begin{aligned} {{\bar{A}}_L} = E(u({h_{Ai}}({p_x}))) = \frac{1}{n}\sum \limits _{i = 1}^n {u({h_{Ai}}({p_x}))} = \frac{1}{n}\sum \limits _{i = 1}^n {\left( {1 - \frac{1}{{{l_{Ai}}}}} \right) }. \end{aligned}$$
(22)

It can be found that the above formula is consistent with equation (15).

The variance of the length ratio of PHFE \({h_{Ai}}({p_x})\) is defined as follows:

$$\begin{aligned} \begin{aligned} Var(u({h_{Ai}}({p_x})))&= \frac{1}{n}\sum \limits _{i = 1}^n {{{\left[ {u({h_{Ai}}({p_x})) - {{{\bar{A}}}_L}} \right] }^2}}\\&= \frac{1}{n}\sum \limits _{i = 1}^n {{{\left[ {u({h_{Ai}}({p_x})) - \frac{1}{n}\sum \limits _{i = 1}^n {\left( {1 - \frac{1}{{{l_{Ai}}}}} \right) } } \right] }^2}}. \end{aligned} \end{aligned}$$
(23)

On this basis, the covariance of length ratio between PHFSs A and B is expressed as follows:

$$\begin{aligned} {C_L}(A,B) = \frac{1}{n}\sum \limits _{i = 1}^n {\left[ {u({h_{Ai}}({p_x})) - {{{\bar{A}}}_L}} \right] \left[ {u({h_{Bi}}({p_x})) - {{{\bar{B}}}_L}} \right] }. \end{aligned}$$
(24)

Based on \({C_L}(A,B)\), the length correlation coefficient between A and B is expressed as follows:

$$\begin{aligned} \begin{aligned}&{\rho _L}(A,B) = \frac{{{C_L}(A,B)}}{{{{\left[ {{C_L}(A,A){C_L}(B,B)} \right] }^{1/2}}}}\\&\quad = \frac{{\sum \nolimits _{i = 1}^n {\left[ {u({h_{Ai}}({p_x})) - {{{\bar{A}}}_L}} \right] \left[ {u({h_{Bi}}({p_x})) - {{{\bar{B}}}_L}} \right] } }}{{{{\left[ {\sum \nolimits _{i = 1}^n {{{\left[ {u({h_{Ai}}({p_x})) - {{{\bar{A}}}_L}} \right] }^2}\sum \nolimits _{i = 1}^n {{{\left[ {u({h_{Bi}}({p_x})) - {{{\bar{B}}}_L}} \right] }^2}} } } \right] }^{1/2}}}}. \end{aligned} \end{aligned}$$
(25)

Besides, the correlation coefficient should meet the following three axiom theorems:

  1. (1)

    \(\rho (A,B) = \rho (B,A)\),

  2. (2)

    if \(A = B\), then \(\rho (A,B) = 1\),

  3. (3)

    \(- 1 \le \rho (A,B) \le 1\).

Therefore, we need to prove that the three basic correlation coefficients meet the theorems. We only prove the variance correlation coefficient here because of the homologous definition process, the proof of other two correlation coefficients is similar.

Since theorems (1) and (2) are clearly true, we need only prove theorem (3).

Proof of Theorem(3)

Assuming \({\rho _i} = Var({h_{Ai}}({p_x})) - {{\bar{A}}_V}\),\({\theta _i} = Var({h_{Bi}}({p_x})) - {{\bar{B}}_V}\), according to the Cauchy-Schwarz inequality:

$$\begin{aligned}{} & {} {({a_1}{b_1} + {a_2}{b_2} + \cdots + {a_n}{b_n})^2} \le ({a_1}^2 + {a_2}^2 + \cdots + {a_n}^2)\\{} & {} \qquad ({b_1}^2 + {b_2}^2 + \cdots + {b_n}^2), \end{aligned}$$

we can get

$$\begin{aligned} \left| {\sum \limits _{i = 1}^n {{\rho _i}{\theta _i}} } \right| \le {\left( {\sum \limits _{i = 1}^n {{\rho _i}^2} \sum \limits _{i = 1}^n {{\theta _i}^2} } \right) ^{1/2}}, \end{aligned}$$

that is, \(\left| {{\rho _V}(A,B)} \right| = \frac{{\left| {{C_V}(A,B)} \right| }}{{{{\left[ {{C_V}(A,A){C_V}(B,B)} \right] }^{1/2}}}} \le 1\),

so we can get \(- 1 \le {\rho _V}(A,B) \le 1\). \(\square\)

4.3 Mixed Correlation Coefficient

Based on three basic correlation coefficients of PHFSs, the mixed correlation coefficient is defined as follows:

$$\begin{aligned} {\rho _{MVL}}(A,B) = \alpha \cdot {\rho _M}(A,B) + \beta \cdot {\rho _V}(A,B) + \gamma \cdot {\rho _L}(A,B), \end{aligned}$$
(26)

where \(\alpha , \beta\) and \(\gamma\) are the weights of average, variance, and length correlation coefficients, respectively, which satisfy \(\alpha + \beta + \gamma = 1\).

The following is to prove that the mixed correlation coefficient \({\rho _{MVL}}(A,B)\) meets the three theorems of correlation coefficient.

Proof

Theorem (1) clearly holds;

With regard to theorem (2), if \(A=B\), according to the conclusion in the previous section, there is \({\rho _M}(A,B) = {\rho _V}(A,B) = {\rho _L}(A,B) = 1\), then \({\rho _{MVL}}(A,B) = \alpha + \beta + \gamma = 1\).

With respect to theorem (3), by reason of

$$\begin{aligned}{} & {} - 1 \le {\rho _M}(A,B) \le 1, - 1 \le {\rho _V}(A,B) \le 1, - 1 \\{} & {} \qquad \le {\rho _L}(A,B) \le 1, \end{aligned}$$

and \(\alpha \ge 0,\beta \ge 0,\gamma \ge 0\),

there are

$$\begin{aligned}{} & {} - \alpha \le \alpha {\rho _M}(A,B) \le \alpha , - \beta \le \beta {\rho _V}(A,B) \le \beta , - \gamma \\{} & {} \qquad \le \gamma {\rho _L}(A,B) \le \gamma . \end{aligned}$$

so

$$\begin{aligned}{} & {} - \left( {\alpha + \beta + \gamma } \right) \le \alpha {\rho _M}(A,B) + \beta {\rho _V}(A,B) \\{} & {} \qquad + \gamma {\rho _L}(A,B) \le \alpha + \beta + \gamma , \end{aligned}$$

therefore, \(- 1 \le {\rho _{MVL}}(A,B) \le 1\). \(\square\)

Example 3

The mixed correlation coefficient is applied to recalculate the correlation coefficient between PHFSs A, B, and C in example 2. Assuming that the weight of three basic correlation coefficients is 1/3 equally, the calculation process is as follows:

The variance and length ratio of each PHFE in A, B, and C is

$$\begin{aligned}{} & {} \begin{aligned}&Var({h_{A1}}({p_x})) = 0.01,Var({h_{A2}}({p_x})) = 0.06,Var({h_{A3}}({p_x})) \\&\qquad = \frac{{0.25}}{2},\\&Var({h_{B1}}({p_x})) = 0.09,Var({h_{B2}}({p_x})) = \frac{{0.26}}{3},Var({h_{B3}}({p_x})) \\&\qquad = \frac{{0.08}}{3},\\&Var({h_{C1}}({p_x})) = \frac{{0.14}}{3},Var({h_{C2}}({p_x})) = 0.01,Var({h_{C3}}({p_x})) \\&\qquad = \frac{{0.02}}{3}. \end{aligned}\\{} & {} \begin{aligned}&u({h_{A1}}({p_x})) = \frac{1}{2},u({h_{A2}}({p_x})) = \frac{2}{3},u({h_{A3}}({p_x})) = \frac{3}{4},\\&u({h_{B1}}({p_x})) = \frac{1}{2},u({h_{B2}}({p_x})) = \frac{2}{3},u({h_{B3}}({p_x})) = \frac{2}{3},\\&u({h_{C1}}({p_x})) = \frac{2}{3},u({h_{C2}}({p_x})) = \frac{1}{2},u({h_{C3}}({p_x})) = \frac{2}{3}. \end{aligned} \end{aligned}$$

Based on the variance and length ratio, the variance and length correlation coefficient between A, B, and C are respectively as follows:

$$\begin{aligned} \begin{aligned}&{\rho _V}(A,B) = - 0.915,{\rho _V}(A,C) = - 0.985,{\rho _V}(B,C) = 0.733.\\&{\rho _L}(A,B) = 0.943,{\rho _L}(A,C) = - 0.188,{\rho _L}(B,C) = - 0.503. \end{aligned} \end{aligned}$$

Therefore, according to equation (26), the mixed correlation coefficient between A, B, and C can be obtained:

$$\begin{aligned} \rho (A,B) = 0.343,\rho (A,C) = - 0.058,\rho (B,C) = 0.41. \end{aligned}$$

From above, it can be seen that the result of the mixed correlation coefficient is different from that in reference [37]. Although the average correlation coefficient is equal to 1, with the help of variance and length correlation coefficient, the mixed correlation coefficient can overcome the deficiency of reference [37], distinguish the data well, which makes the calculation result more convincing.

4.4 Weighted Mixed Correlation Coefficient

Actually, in practical problems, the weight of each element in the domain \(X = \{ {x_1},{x_2}, \cdots ,{x_n}\}\) is often different. Assuming that the weight vector of elements in X is \(\omega = {({\omega _1},{\omega _2}, \cdots ,{\omega _n})^\mathrm{{T}}}\), which satisfies \(\sum \nolimits _{i = 1}^n {{\omega _i}} = 1\), then the three weighted basic correlation coefficients are defined as follows.

Weighted average correlation coefficient:

$$\begin{aligned} {\rho _{\omega M}}(A,B) = \frac{{\sum \nolimits _{i = 1}^n {{\omega _i}\left[ {{{{\bar{h}}}_{Ai}}({p_x}) - \sum \nolimits _{i = 1}^n {{\omega _i}{{{\bar{h}}}_{Ai}}({p_x})} } \right] \left[ {{{{\bar{h}}}_{Bi}}({p_x}) - \sum \nolimits _{i = 1}^n {{\omega _i}{{{\bar{h}}}_{Bi}}({p_x})} } \right] } }}{{{{\left[ {\sum \nolimits _{i = 1}^n {{\omega _i}{{\left[ {{{{\bar{h}}}_{Ai}}({p_x}) - \sum \nolimits _{i = 1}^n {{\omega _i}{{{\bar{h}}}_{Ai}}({p_x})} } \right] }^2}\sum \nolimits _{i = 1}^n {{\omega _i}{{\left[ {{{{\bar{h}}}_{Ai}}({p_x}) - \sum \nolimits _{i = 1}^n {{\omega _i}{{{\bar{h}}}_{Bi}}({p_x})} } \right] }^2}} } } \right] }^{1/2}}}}. \end{aligned}$$
(27)

Weighted variance correlation coefficient:

$$\begin{aligned} \begin{aligned}&{\rho _{\omega V}}(A,B) = \\&\frac{{\sum \nolimits _{i = 1}^n {{\omega _i}\left[ {Var({h_{Ai}}({p_x})) - \sum \nolimits _{i = 1}^n {{\omega _i}Var({h_{Ai}}({p_x}))} } \right] \left[ {Var({h_{Bi}}({p_x})) - \sum \nolimits _{i = 1}^n {{\omega _i}Var({h_{Bi}}({p_x}))} } \right] } }}{{{{\left[ {\sum \nolimits _{i = 1}^n {{\omega _i}{{\left[ {Var({h_{Ai}}({p_x})) - \sum \nolimits _{i = 1}^n {{\omega _i}Var({h_{Ai}}({p_x}))} } \right] }^2}\sum \nolimits _{i = 1}^n {{\omega _i}{{\left[ {Var({h_{Ai}}({p_x})) - \sum \nolimits _{i = 1}^n {{\omega _i}Var({h_{Bi}}({p_x}))} } \right] }^2}} } } \right] }^{1/2}}}}. \end{aligned} \end{aligned}$$
(28)

Weighted length correlation coefficient:

$$\begin{aligned} {\rho _{\omega L}}(A,B) = \frac{{\sum \nolimits _{i = 1}^n {{\omega _i}\left[ {u({h_{Ai}}({p_x})) - \sum \nolimits _{i = 1}^n {{\omega _i}\left( {1 - \frac{1}{{{l_{Ai}}}}} \right) } } \right] \left[ {u({h_{Bi}}({p_x})) - \sum \nolimits _{i = 1}^n {{\omega _i}\left( {1 - \frac{1}{{{l_{Bi}}}}} \right) } } \right] } }}{{{{\left[ {\sum \nolimits _{i = 1}^n {{\omega _i}{{\left[ {u({h_{Ai}}({p_x})) - \sum \nolimits _{i = 1}^n {{\omega _i}\left( {1 - \frac{1}{{{l_{Ai}}}}} \right) } } \right] }^2}\sum \nolimits _{i = 1}^n {{\omega _i}{{\left[ {u({h_{Bi}}({p_x})) - \sum \nolimits _{i = 1}^n {{\omega _i}\left( {1 - \frac{1}{{{l_{Bi}}}}} \right) } } \right] }^2}} } } \right] }^{1/2}}}}. \end{aligned}$$
(29)

Then, the weighted mixed correlation coefficient is expressed as follows:

$$\begin{aligned} {\rho _{\omega MVL}}(A,B) = {\alpha _\omega }{\rho _{\omega M}}(A,B) + {\beta _\omega }{\rho _{\omega V}}(A,B) + {\gamma _\omega }{\rho _{\omega L}}(A,B), \end{aligned}$$
(30)

where \({\alpha _\omega }\),\({\beta _\omega },\) and \({\gamma _\omega }\) are the weights of weighted average, variance, and length correlation coefficients, respectively, which satisfy \({\alpha _\omega } + {\beta _\omega } + {\gamma _\omega } = 1\).

It should be noted that the weight \({\omega _i}\) in the above equations cannot be reduced like \(\frac{1}{n}\) in ordinary correlation coefficients of Sect. 4.2.

5 Simulation Applications

In this section, we apply the improved correlation coefficient to the analysis of two examples to verify its effectiveness.

5.1 Data Association Application

5.1.1 Simulation Analysis

Assuming that the reconnaissance agency detects two groups of data and reports the data to the fusion center in the form of PHFS after the primary decision. These data are shown in Table 1.

Table 1 PHFS initial decision data
Full size table

The decision-making department needs to determine whether the two sets of data belong to the same observation object. We will utilize the proposed correlation coefficient for association analysis to solve this problem.

According to the equations in Sect. 4.2, the basic average, variance, and length correlation coefficients of two groups of data are 0.9042, \(-\)0.784, and \(-\)0.5, then the mixed correlation coefficient can be represented by \(0.9042\alpha -0.784\beta -0.5\gamma\), with the restrictions of \(\alpha +\beta +\gamma =1\) and \(0 \le \alpha ,\beta ,\gamma \le 1\); as the weights vary, the calculation result of the mixed correlation coefficient is shown as figure 1.

Fig. 1
figure 1

Four-dimensional diagram of mixed correlation coefficient

Full size image

According to figure 1, when the weight value is (1,0,0), the maximum correlation coefficient is 0.9042, and when the weight value is (0,1,0), the minimum value is \(-\)0.784. When the weights are all equal to 1/3, the calculation result is \(-\)0.1266.

The above analysis shows that when only one characteristic is considered, the conclusion is strong correlation or negative correlation, which is one sided actually. Only when all three characteristics are fully considered, we conclude that there is no correlation exists, which is more practical.

5.1.2 Comparison Analysis

In order to illustrate the advantages of the mixed correlation coefficient, the correlation coefficients in reference [34, 37] are used to solve the above data association problem, and compared with the proposed correlation coefficient. We selected \(\rho _{WHFS1}\) among multiple correlation coefficients in reference [34], the calculation results are shown in Table 2.

Table 2 Calculation results of different correlation coefficients
Full size table

According to Table 2, because the negative correlation cannot be calculated in reference [34], the conclusion is 0.3188; that is, it is difficult to judge whether there is an association between the two targets; the method in reference [37] is essentially the same as basic mean correlation coefficient of this paper, so the conclusion of “strong association” is obtained, because it neglects the scatter and length of the two groups of data, while the mixed correlation coefficient takes all above factors into account, and the result is \(-\)0.1266, indicating that there is no association between the two groups of data, which is more practical. However, when the weight setting is unreasonable, the wrong conclusion will also be obtained.

Therefore, it can be concluded that the mixed correlation coefficient can obtain more reasonable and comprehensive decision results by evaluating the different characteristics of the data overall, but how to select reasonable weight parameters is significant and still worth further research.

5.2 Multi-attribute Decision Making in PHFSs

This paper focuses on the study of the new correlation coefficient, instead of the innovation of multi-attribute decision-making method, so only on the basis of existing theory, we provide a simple ideal scheme proximity-ranking method for decision making, the multi-attribute decision-making problem is described as follows.

5.2.1 Decision-Making Method

Assuming that in the multi-attribute decision-making problem, there are n alternative schemes \(A = \{ {A_1},{A_2}, \cdots ,{A_n}\}\) and m attributes \(G = \{ {G_1},{G_2}, \cdots ,{G_m}\}\), the attribute weights are unknown and independent of each other, there are t decision-making experts \(D = \{ {D_1},{D_2}, \cdots ,{D_t}\}\) in total. Assuming that the weight of each expert is equal, then the evaluation information of scheme \(A_i\) under attribute \(G_j\) by expert k is expressed as follows:

$$\begin{aligned} D_{ij}^k = \{ \gamma _{ij}^{k\lambda }\vert p_{ij}^{k\lambda },\lambda = 1,2, \cdots ,\left| {D_{ij}^k} \right| \}. \end{aligned}$$
(31)

According to the information integration method in reference [22], the evaluation information of all experts on scheme \(A_i\) under attribute \(G_j\) is expressed as follows:

$$\begin{aligned} {D_{ij}} = \{ \gamma _{ij}^\lambda \vert p_{ij}^\lambda ,\lambda = 1,2, \cdots ,\left| {{D_{ij}}} \right| \}. \end{aligned}$$
(32)

Then the evaluation information of all experts about alternative scheme \(A_i\) is obtained as follows:

$$\begin{aligned} {D_i} = \{ {D_{i1}},{D_{i2}}, \cdots ,{D_{im}}\} ,i = 1,2, \cdots ,n. \end{aligned}$$
(33)

Finally, the decision matrix D is expressed as follows:

$$\begin{aligned} D = \{ {D_{ij}}\vert i = 1,2, \cdots ,n;j = 1,2, \cdots ,m\}. \end{aligned}$$
(34)

Through the above description, the problem model is established. The following mainly introduces the steps of multi-attribute decision-making method.

Firstly, assume that all attributes are benefit attributes, the optimal ideal scheme is obtained as follows:

$$\begin{aligned} {A^*} = \max \{ {A_i}\vert \sum {\gamma _{ij}^\lambda p_{ij}^\lambda } ,i = 1,2, \cdots ,n;j = 1,2, \cdots ,m\}. \end{aligned}$$
(35)

Calculate the correlation coefficients \(\rho ({A_i},{A^*})\) between each scheme and \({A^*},\) respectively.

The higher the correlation coefficient is, the higher the similarity between the corresponding scheme and \({A^*}\) is, and the better the scheme is. On this basis, the correlation coefficient is taken as the decision-making index to determine the decision scheme with the largest correlation coefficient and output the corresponding scheme label:

$$\begin{aligned} \mathrm{{dec}}(i) = \mathrm{{output(}}\max \{ \rho ({A_i},{A^*})\} ),i = 1,2, \cdots ,n. \end{aligned}$$
(36)

The specific steps of decision-making method based on mixed correlation coefficient are described as follows:

Step 1. Obtain the evaluation information of each expert \(D_i\) presented in the form of PHFS.

Step 2. Integrate all expert evaluation information to obtain comprehensive evaluation information D;

Step 3. Calculate the optimal ideal scheme \({A^*}\);

Step 4. According to equation (26), calculate the mixed correlation coefficients \({\rho _{MVL}}({A_i},{A^*})\) of each alternative scheme with \({A^*},\) respectively, and rank the decision schemes according to the correlation coefficient. The scheme with the largest value is determined as the final decision result.

5.2.2 Simulation Analysis

In order to facilitate comparison, an example in reference [36] is used to verify the proposed method.

Four candidates apply for one doctoral supervisor for the only doctoral enrollment. In order to select the best student fairly, PHFSs are introduced. The candidates were asked to be interviewed by 4 experts, each with equal weight, the interview process was assessed on 3 attributes: computing ability \(A_1\), academic level \(A_2,\) and English ability \(A_3\).

In order to facilitate comparison and keep consistent with reference [36], attribute weight vector is set as (0.39,0.26,0.35), and all three attributes are benefit type. Assume that the weights of average, variance, and length correlation coefficients are (0.5,0.25,0.25), respectively. The specific steps of multi-attribute decision making are described as follows.

Step 1. Obtain the PHFS evaluation information of four experts under the 3 attributes(the specific data refer to reference [36]).

Step 2. The PHFS evaluation information of all experts is integrated as Table 3.

Table 3 All experts integrated evaluation information
Full size table

Step 3. Calculate the optimal ideal scheme. According to equation (35), the optimal ideal scheme is shown in Table 4.

Table 4 Optimal ideal scheme
Full size table

Step 4. Calculate the three basic correlation coefficients of each scheme with \(A^*\) respectively, as shown in Table 5.

Table 5 PHFS initial decision data
Full size table

Step 5. According to the calculation results of the mixed correlation coefficient, the ranking of all schemes is \({x_1}> {x_2}> {x_3} > {x_4}\).

Therefore, the candidate \({x_1}\) is determined to be the best choice for doctoral candidate through multi-attribute decision making. The results are consistent with those obtained by entropy measure in reference [22], which proves the effectiveness of our proposed algorithm.

In order to verify the effectiveness and comprehensiveness of the mixed correlation coefficient in this paper, only one basic correlation coefficient is adapted and the results were compared with those of the mixed correlation coefficient. The calculation results are shown in Table 5.

It can be seen that the ranking results of three basic correlation coefficients are not the same, especially the length correlation coefficient determines \(x_1\) and \(x_3\) as the best candidate, which has the biggest gap with the conclusion of the mixed correlation coefficient; the reason is that the length correlation coefficient only considered the factor of membership degree number, without considering the specific distribution of membership degrees. Therefore, it is one sided to use any basic correlation coefficient for evaluation. In practical application, three basic correlation coefficients must be considered comprehensively to obtain reasonable discriminant results.

5.2.3 Weight Sensitivity Analysis of Basic Correlation Coefficients

The influence is further analyzed brought by weight changes of different basic correlation coefficients. Assume that the weight of any basic correlation coefficient increases from 0.1 to 0.9 in step size of 0.2, the weights of others are equally divided. The calculation results are shown in figure 2.

Fig. 2
figure 2

Comparison result under different basic correlation coefficient weights

Full size image

From figure 2, we can analyze that the result changes with the weight of the basic correlation coefficient, leading to the change of ranking order. Taking figure 2 as an example, with the increase of the weight of the average correlation coefficient, the correlation coefficient of \(x_1\) slowly increases, and the correlation coefficient of \(x_2\) and \(x_4\) gradually increases, and the correlation coefficient of \(x_3\) gradually decreases, and the sorting result gradually approximates that the result of only average correlation coefficient is used \({x_1}> {x_2}> {x_4} > {x_3}\), and when the weight is around 0.45 and 0.75, the sorting result changes correspondingly;; that is, the correlation coefficient of \(x_2\) exceeds \(x_3\), and the correlation coefficient of \(x_4\) exceeds \(x_3\). Similarly, with the change of the weight of the variance correlation coefficient, the sorting result also changes twice, while with the weight varying, the length correlation coefficient always keeps the sorting result of \({x_1}> {x_3}> {x_2} > {x_4}\).

Based on the above analysis, it is shown that the mixed correlation coefficient in this paper is sensitive to the weight parameters of the basic correlation coefficient. In application, the weight value needs to be set according to the specific situation. Since only the number of membership degree is involved in the calculation process of length correlation coefficient, the average correlation coefficient should be considered as the main decision basis in practical application, and the variance and length correlation coefficient should be considered as auxiliary decision.

5.2.4 Sensitivity Analysis of Attribute Weight

In the above discussion, the attribute weight is always set as (0.39,0.26,0.35). Nevertheless in the actual decision-making process, the role of attribute weight on decision making cannot be ignored. Therefore, it is necessary to study the sensitivity of weighted correlation coefficient to the change of attribute weight. Assuming that the weight of each attribute changes from 0.1 to 0.9 in step size of 0.2, and the weights of others are equally divided, the weight of the three basic correlation coefficients is set as (0.5,0.25,0.25), and then the calculated results are shown in figure 3.

Fig. 3
figure 3

Comparison result under different attribute weights

Full size image

As can be seen from figure 3, with the change of attribute weight, the overall situation of ranking results does not change much,\(x_1\) is always the best candidate, \(x_4\) is always the worst choice, only the relative size of \(x_2\) and \(x_3\) fluctuates. With the increase of the weight of computing ability \(A_1\), the correlation coefficient of \(x_2\) increases gradually, while that of \(x_3\) decreases gradually. And the order of \(x_2\) and \(x_3\) is exchanged when it is near 0.3. With the increase of the weight of academic level \(A_2\), when the weight value is 0.5, the ordering of \(x_2\) and \(x_3\) is changed. With the increase of weight of English ability \(A_3\), the correlation coefficient difference between \(x_2\) and \(x_3\) shows a trend of decreasing.

The above analysis shows that the mixed correlation coefficient in this paper is less sensitive to attribute weight parameters, but the determination of attribute weight is always an important part of multi-attribute decision making, so scientific weight calculation method should be adopted to solve it in practical application.

5.2.5 Comparative Analysis

In this section, we conducted comparative simulations with several existing correlation coefficients with our decision algorithm and the improved TOPSIS method in reference [39], so as to confirm the universality and advantages of the mixed correlation coefficient under different methods.

First of all, in order to illustrate the advantages of the correlation coefficient proposed in this paper, strength analysis was made with the correlation coefficients in reference [34, 35] and [37]. We selected \(\rho _{WHFS1}\) among multiple correlation coefficients in reference [34], assume that the attribute weights of all methods are (0.39,0.26,0.35), and the weight of three basic correlation coefficients in this paper is (0.5,0.25,0.25). The calculation results are shown in Table 6.

Table 6 Correlation coefficient comparison of different algorithms
Full size table

As can be seen from the results in Table 6, the best candidate obtained by the mixed correlation coefficient is \(x_1\), the same as the methods in reference [34, 35, 37].

However, it can be analyzed that the methods in reference [34, 35, 37] have different defects: the correlation coefficient in reference [34] cannot reflect the true linear proximity between data because it cannot calculate negative correlation, which has certain limitations in expression. reference [35] uses the method of calculating the correlation coefficient of PHFE first, and then summing it, so it will be greater than 1, it is essentially a kind of mean correlation coefficient similar to reference [37], so the ranking results are all \({x_1}> {x_2}> {x_4} > {x_3}\). On the basis of mean correlation coefficient, this paper takes into account the overall distribution of the membership degree and the number of membership degrees in PHFSs, and determines that \(x_4\) is the worst candidate decision, which is consistent with the conclusion obtained by other measurement in reference [22], so the decision result is more comprehensive and reasonable.

Secondly, in order to verify the universality and advantages of the mixed correlation coefficient under different methods, the improved TOPSIS decision-making method in reference [39] was used for comparative simulation. Firstly, the positive and negative ideal solutions are determined as shown in Table 7, and the sorting results are shown in figure 4.

Table 7 The positive and negative ideal solutions
Full size table
Fig. 4
figure 4

Sorting results under TOPSIS method

Full size image

As can be seen from figure 4, the ranking results under different correlation coefficients are different. The ranking result is \({x_1}>{x_3}>{x_2}>{x_4}\) by referencer [34], while the results are all \({x_1}>{x_2}>{x_4}>{x_3}\) in references [35] and [37]. The ranking result through the proposed correlation coefficient is \({x_1}>{x_2}>{x_3}>{x_4}\), which is consistent with the situation obtained by the decision-making method in this paper, and verifies the universality of the method in this paper and the strong stability of proposed correlation coefficient.

Based on the above experimental analysis, the simulations in Sects. 5.2.3 and 5.2.4 show that the mixed correlation coefficient has greater flexibility and can obtain more subjective results by adjusting parameters according to the decision maker’s intention. The comparative simulation in Sect. 5.2.5 validates the universality of the proposed algorithm, and compared with existing correlation coefficients, due to the consideration of multiple features, more comprehensive decision results can be obtained.

6 Conclusion

We consider the integrity, scatter, and length of PHFEs comprehensively in this paper, then define average, variance, and length the three basic correlation coefficients, and propose a brand-new mixed correlation coefficient, and the corresponding weighted form is also extended. Then, we utilize the proposed correlation coefficient to some practical applications, such as correlation analysis and multi-attribute decision making. Compared with the existing correlation coefficients, the mixed correlation coefficient has several advantages: on the one hand, by taking into account the number and the specific distribution of membership degrees, the proposed correlation coefficient can avoid the occurrence of counter-intuitive phenomena and obtain more comprehensive results; on the other hand, the weight of attributes and basic correlation coefficients can be determined according to the needs of practical problems, which has better flexibility. The comparison results show that the proposed correlation coefficient is superior and effective.

Next, we will introduce the proposed correlation coefficient to the fields of machine learning and pattern recognition. In addition, we will pay close attention to how to improve the existing multi-attribute decision-making methods to improve the computational efficiency and accuracy.