An Application of Fully Intuitionistic Fuzzy Multi-objective Linear Fractional Programming Problem in E-education System

Abstract

This article addresses a special class of non-linear programming problems, viz., linear fractional programming problems having multiple objectives. In solving the real-life linear fractional optimization problems, the ambiguity and hesitation in the decision are inherent and ever-present, therefore, it is perfectly viable to formulate and solve these optimization models using the intuitionistic fuzzy environment. The purpose of this study is to propose a simple and computationally efficient approach to obtain the solution of multiple objective linear fractional programming problems having all the decision variables and parameters expressed in terms of triangular intuitionistic fuzzy numbers. The proposed solution algorithm is primarily based on the goal programming approach, fuzzy-based linearization technique, and a membership function strategy. The original linear fractional programming problem is first converted to its equivalent deterministic/crisp multi-objective linear fractional optimization problem using the weighted goal programming methodology along with the linear membership technique to resolve the intuitionistic fuzzy constraints into the crisp one. Finally, the variable transformation technique for the under- and over-deviational variables of the goal programming model is employed to linearize all the fractions involved in the problem so as to convert the original problem to an equivalent linear optimization problem. Further, this linear programming problem can be solved using any available commercial packages. Moreover, a numerical illustration is provided to demonstrate the steps of the proposed technique followed by the analysis and solution of an E-education set-up problem. The discussion and comparisons of the practical case establish the relevancy and usefulness of the proposed model.

1 Introduction

In real-world decision-making processes, it is more relevant to optimize the ratios of physical quantities rather than optimizing the bi-linear functions involved in the problem. Such problems involving optimization of the ratio of linear functions are called LFP problems. The extensive applications of the fractional programming problems can be observed in production planning, economics, engineering, resource allocation, finance, health care, transportation, and investment return. The fractional programming problems are used very often in situations which require optimizing several relative physical and/or economical quantities such as inventory/sales, debt/equity, profit/investment, output/employee, nurses/patients, student/teacher, placement/admission, customer/staff along-with some set of constraints. Due to the wide practical applicability of LFP models, several researchers [1, 2] studied these optimization problems and devised different approaches to solve them. A comprehensive review of LFP problems can be seen in Bajalinov [3]. An LFP can be solved either by converting it into a linear optimization problem, employing the technique of variable transformation developed by Charnes and Cooper [4], or using the updated objective function method given by Bitran and Novaes [5]. Later, Tantawy [6] considered an LFP model having inequality constraints and introduced an iterative scheme using the conjugate gradient projection approach. After that, Tantawy [7] elaborated the concept of duality for LFP problems. Recently, a very interesting deterministic annealing neural network-based methodology was developed by Wu et al. [8, 9] to solve various optimization problems.

The techniques discussed in [3,4,5,6,7] are developed to solve the LFP models having single objective. However, while dealing with many practical situations such as in the field of the finance sector, transportation, supply chain, etc., the model requires optimizing more than one objective simultaneously under the same set of constraints. Such problems are described to be multi-objective optimization problems. The mathematical model of a multi-objective programming problem can be presented as follows:

$$\begin{aligned}&{\mathbf {(P)}}\max Z(x)=\left\{ Z_{1}(x),Z_{2}(x), \dots , Z_{K}(x) \right\} \\&\text {subject to}_j (x) \le 0, \, j \in J=\{1,2, \dots , m\} \end{aligned}$$

where X is a non-empty subset of ${\mathbb {R}}^n$ and for $j \in J,k=1,2,\dots , K;$ $Z_k,h_j: X \rightarrow {\mathbb {R}}$ are real-valued functions. Due to the involvement of conflicting multiple objectives in (P), the best approximation to the optimal values of individual objectives involved in the problem can be obtained using the concept of efficient solution. Broadly, there are two techniques to handle such problems, namely, goal programming and fuzzy programming methodologies. The LFP problem having multiple objectives is called a MOLFP problem. Luhandjula [10] developed a fuzzy linguistic variable technique to solve the MOLFP problems. A further modification to Luhandjula’s approach [10] was given by Dutta et al. [11]. Later on, Chakraborty and Gupta [12] proposed a fuzzy-based methodology for solving MOLFP problems by employing the variable transformation technique. The goal programming approach is a very effective and computationally simple technique to solve multi-objective optimization problems. Pal et al. [13] devised a fuzzy-based goal programming approach using the variable transformations for the linearization process to handle the MOLFP problems. A Taylor-series method was also developed to solve such problems by Guzel and Sivri [14]. Recently, Chang [15] introduced a fuzzy linearization strategy for MOLFP problems with binary utility functions and discussed the E-learning system topology for a university.

The numerical data of a problem is often decided by the DM based on his past experiences or judgements. However, due to many uncontrollable realistic factors such as errors in measurement, time period, financial up/down in the market, climate factors, and many others, the data or the parameters of a problem may not be available as crisp numbers. There may involve certain ambiguity or vagueness in the parameters. Fuzzy sets are highly suitable to incorporate this imprecision in the formulation of a problem. Bellman and Zadeh [16] developed the fuzzy decision-making theory and then several researchers applied it to solve various fuzzy optimization problems. Abo-Sinna and Baky [17] proposed a fuzzy goal programming technique to solve the bi-level MOLFP problems. A model of the LFP/MOLFP problem having the cost coefficients, resources, or technological coefficients expressed in terms of fuzzy numbers is described as a fuzzy LFP/MOLFP problem. Li and Chen [18] introduced a fuzzy-based approach to solve fuzzy LFP models. Pop and Stancu-Minasian [19] considered a fully fuzzy LFP problem in which the variables are also taken to be fuzzy quantities and devised a scheme to optimize such problems by transforming the LFP model into an equivalent deterministic multi-objective linear programming problem. After that, Veeramani and Sumathi [20] developed a numerical approach to obtain the optimal solution of LFP problems in a fuzzy environment. Further, Ebrahimnejad et al. [21] showed a limitation in the method of Veeramani and Sumathi [20] and extended their approach to find a non-negative fuzzy solution of the fully fuzzy LFP problems. Arya et al. [22] introduced a fuzzy-based branch-and-bound technique to handle a deterministic MOLFP model. Next, Arya et al. [23] worked upon the modelling and optimization of a fully fuzzy MOLFP problem and hence, solved the problem of establishing distance learning centres of some higher education institutions. Additionally, Luo et al. [24] and Ju et al. [25] addressed and solved the problem of heterogeneous vehicle platoons under uncertainty. Recently, Singh and Yadav [26] developed a scalarization-based technique to handle the fuzzy MOLFP model with its application in an integrated production-transportation problem. Motivated by the Zadeh’s extension principle, Stanojević [27] proposed a Monte Carlo simulation algorithm based technique to solve the fully fuzzy MOLFP problems. Thereafter, Borza and Rambely [28] employed the concept of $\alpha$-cuts and max–min technique to devise an approach for linear fractional problems with fuzzy coefficients. Stanojević and Stanojević [29] provided an empirical $(\alpha ,\beta )$-acceptable optimal solutions following the extension principle and the aggregation of fuzzy quantities for a class of fully fuzzy LFP problems.

It is evident that while assigning the numerical values to the parameters of a realistic problem in different areas such as hospitals, bank branches, education sector, court administration, air force maintenance units, stock market, etc., there may involve certain hesitation along-with the ambiguity in the decision-making process. The IF theory fits better to handle such a scenario. The modelling of an LFP problem by assigning the parameters of the problem as IF numbers gave rise to an IF-LFP problem. Furthermore, if all the parameters and the decision variables of an LFP are expressed as IF numbers then the problem is said to be a fully IF-LFP problem. Jayalakshmi [30] proposed the separation and bound method to solve a fully IF-LFP model. Singh and Yadav [31] used fuzzy programming based approach to handle the IF-LFP problem by converting it first to a multi-objective LFP model and then used the variable transformation technique to linearize the problem. Later on, Amer [32] developed an interactive fuzzy algorithm to deal with the IF non-linear fractional programming problem. Another application of IF theory in LFP can be seen in the work of Bharati [33] who has incorporated the IF theory to solve a fractional transportation problem. Thereafter, Ali et al. [34] introduced the fuzzy goal programming approach for solving a multi-objective linear fractional inventory problem under the IF environment. Then, El Sayed and Abo-Sinna [35] extended Zimmermann’s approach to deal with the IF multi-objective fractional transportation problems. Sahoo et al. [36] introduced Zimmermann’s technique to optimize the multi-objective LFP problems using the pentagonal IF numbers. Further, several recent studies on fuzzy, IF and interval-valued fuzzy theory along-with their practical applications can be seen in [37,38,39,40,41].

A brief outlook on some of the existing studies to solve the fuzzy/IF LFP problems along with the contribution of present study is given in Table 1.

Many times, the DM often fails to provide the data of a problem with preciseness. In such cases, the modelling of an optimization problem in an IF environment best reflects mathematically the impact of various factors on the parameters of a realistic problem. Since, an IF set considers the acceptance as well as the rejection degrees of each element of the set, therefore, formulation of an optimization problem by expressing the parameters and decision variables of the problem using IF numbers is more viable. To the best of our knowledge, no methodology exists in the literature to solve a fully IF-MO-LFP problem which has a number of significant applications in various fields. Therefore, motivated by the Zimmermann’s technique used by Pal et al. [13], description of goal programming by Mohamed [42], we have devised a fuzzy weighted goal programming approach in conjunction with the linearization technique to handle the IF-MO-LFP problems. The main contributions of the present study can be summarized as follows:

(i):

A new fuzzy-based goal programming approach is proposed to obtain an efficient solution of a fully IF-MO-LFP problem.

(ii):

The proposed approach is also computationally efficient since it involves the linearization of fractions associated with the objective functions. This is further supported by giving a valid mathematical explanation of the involved linearization process.

(iii):

The developed algorithm takes care of the DM preferences by allotting suitable weights and assigning aspiration levels to different objectives.

(iv):

The steps of the proposed technique are illustrated in detail by solving a numerical example.

(v):

An application of the proposed algorithm is presented in the E-education system and comparisons are carried out with the related existing methods.

The rest of the paper is organized as follows: In Sect. 2, we revisit some preliminaries related to IF theory. In Sect. 3, we have presented the mathematical formulation of a fully IF-MO-LFP problem followed by describing the proposed algorithm, goal programming formulation, and linearization strategy of the problem. A brief description of the proposed approach is summarized in Sect. 4. The advantages of the proposed approach over the existing studies are discussed in Sect. 5. The developed approach is illustrated by a numerical example in Sect. 6. In Sect. 7, a practical application in an E-education system is framed and solved along with the analysis and comparison of the obtained results. Finally, conclusions with some future directions are drawn in the last section.

Table 1 Literature review on fuzzy/IF LFP problems and contribution of the present study

2 Preliminaries

This section presents the basic concepts related to the IF set theory used in the paper.

2.1 Basic Definitions

Definition 1

[35] An IF set ${\tilde{A}}^{I}$ in a non-empty universe X is a set of ordered triples ${\tilde{A}}^I =\{ (x, \mu _{{\tilde{A}}^I}(x), \nu _{{\tilde{A}}^I}(x)): x \in X \}$, where $\mu _{{\tilde{A}}^I}(x) : X \rightarrow [0,1]$ and $\nu _{{\tilde{A}}^I}(x) : X \rightarrow [0,1]$ represent the degree of membership and degree of non-membership of the element $x \in X$ being in ${\tilde{A}}^{I}$, respectively, such that $\forall ~ x \in X,~ 0 \le \mu _{{\tilde{A}}^I}(x)+\nu _{{\tilde{A}}^I}(x) \le 1$. The value $h_{{\tilde{A}}^{I}}(x)=1-\mu _{{\tilde{A}}^I}(x)-\nu _{{\tilde{A}}^I}(x)$ represents the degree of hesitation for the element $x \in X$ being in ${\tilde{A}}^I$.

An IF set ${\tilde{A}}^I =\{ (x, \mu _{{\tilde{A}}^I}(x), \nu _{{\tilde{A}}^I}(x)): x \in X \}$ in X

• is normal if there exists $x_{0},~ x_{1} \in X$ such that $\mu _{{\tilde{A}}^I}(x_{0})=1$ and $\nu _{{\tilde{A}}^I}(x_{1})=1$.

• is convex if $\forall ~x_1,x_2 \in X,~0 \le \lambda \le 1,$

  $$\begin{aligned} \mu _{{\tilde{A}}^I}(\lambda x_1+(1-\lambda ) x_2) \ge \min \{ \mu _{{\tilde{A}}^I}(x_1), \mu _{{\tilde{A}}^I}(x_2)\}~\text {and} \\ \nu _{{\tilde{A}}^I}(\lambda x_1+(1-\lambda ) x_2) \le \max \{\nu _{{\tilde{A}}^I}(x_1), \nu _{{\tilde{A}}^I}(x_2)\}.~~~~~ \end{aligned}$$

Definition 2

[31] An IF set ${\tilde{A}}^I =\{ (x, \mu _{{\tilde{A}}^I}(x), \nu _{{\tilde{A}}^I}(x)): x \in {\mathbb {R}} \}$ is called an IFN if

(i):

${\tilde{A}}^I$ is a normal IF set,

(ii):

${\tilde{A}}^I$ is a convex IF set, and

(iii):

$\mu _{{\tilde{A}}^I}$ and $\nu _{{\tilde{A}}^I}$ are piecewise continuous functions from ${\mathbb {R}}$ to the closed interval [0, 1] such that $0 \le \mu _{{\tilde{A}}^I}(x)+\nu _{{\tilde{A}}^I}(x) \le 1~~\forall ~ x \in {\mathbb {R}}$.

Therefore, the membership function $\mu _{{\tilde{A}}^I}$ and non- membership function $\nu _{{\tilde{A}}^I}$ of an IFN ${\tilde{A}}^I$ can be expressed mathematically in the following form:

$$\ \begin{gathered} \mu _{{\tilde{A}^{I} }} (x) = \left\{ \begin{gathered} m_{1} (x),\quad m - l < x < m, \hfill \\ 1,\quad x = m, \hfill \\ m_{2} (x),\quad m < x < m + r, \hfill \\ 0,\quad {\text{otherwise}} \hfill \\ \end{gathered} \right.{\text{ and }} \hfill \\ \nu _{{\tilde{A}^{I} }} (x) = \left\{ \begin{gathered} n_{1} (x),\quad m - l^{\prime} < x < m, \hfill \\ 0,\quad x = m, \hfill \\ n_{2} (x),\quad m < x < m + r^{\prime}, \hfill \\ 1,\quad {\text{otherwise}} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$

where $m_1(x),n_2(x)$ are piecewise continuous and increasing functions in $(m-l,m),(m,m+r^{\prime })$, respectively while $m_2(x),n_1(x)$ are piecewise continuous and decreasing functions in $(m,m+r),(m-l^{\prime },m)$, respectively such that $0 \le m_1(x)+n_1(x) \le 1$ and $0 \le m_2(x)+n_2(x) \le 1$ holds for all $x \in {\mathbb {R}}$. Here, l, r are called the left, right spreads of $\mu _{{\tilde{A}}^{I}}$ and $l^{\prime },r^{\prime }$ are the left, right spreads of $\nu _{{\tilde{A}}^{I}}$. A general IFN ${\tilde{A}}^I$ is denoted by $(m;l,r;l^{\prime },r^{\prime })$ and graphically represented by Fig. 1.

Fig. 1

General intuitionistic fuzzy number

Definition 3

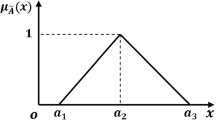
[34] A triangular intuitionistic fuzzy number (TIFN, Fig. 2) ${\tilde{A}}^I$ is an IFN having the membership and non-membership function defined by

$$\begin{aligned} \mu _{{\tilde{A}^{I} }} (x) & = \left\{ \begin{gathered} \frac{{x - a_{1} }}{{a_{2} - a_{1} }},\quad {\text{if }}~~a_{1} < x \le a_{2} , \hfill \\ \frac{{a_{3} - x}}{{a_{3} - a_{2} }},\quad {\text{if }}~~a_{2} < x \le a_{3} , \hfill \\ 0,\quad {\text{otherwise}} \hfill \\ \end{gathered} \right.{\text{ and}} \\ \nu _{{\tilde{A}^{I} }} (x) & = \left\{ \begin{gathered} \frac{{a_{2} - x}}{{a_{2} - a^{\prime}_{1} }},\quad {\text{if }}~~a^{\prime}_{1} < x \le a_{2} , \hfill \\ \frac{{x - a_{2} }}{{a^{\prime}_{3} - a_{2} }},\quad {\text{if }}~~a_{2} < x \le a^{\prime}_{3} , \hfill \\ 1,\quad {\text{otherwise}} \hfill \\ \end{gathered} \right. \\ \end{aligned}$$

where $a^{\prime }_1 \le a_1 \le a_2 \le a_3 \le a^{\prime }_3.$ The TIFN ${\tilde{A}}^I$ is denoted by $(a_1,a_2,a_3;a_1^{\prime },a_2,a_3^{\prime }).$

Fig. 2

Triangular intuitionistic fuzzy number

Definition 4

A TIFN ${\tilde{A}}^I =(a_1,a_2,a_3; a^{\prime }_1,a_2,a^{\prime }_3)$ is said to be

• non-negative $(\succeq 0)$ if and only if $a^{\prime }_1\ge 0$.

• positive $(\succ 0)$ if and only if $a^{\prime }_1 > 0$.

• non-positive $(\preceq 0)$ if and only if $a^{\prime }_3 \le 0$.

• negative $(\prec 0)$ if and only if $a^{\prime }_3 < 0$.

• equal to a TIFN ${\tilde{B}}^I =(b_1,b_2,b_3; b^{\prime }_1,b_2,b^{\prime }_3)$ if and only if $a_1=b_1,~a_2=b_2,~a_3=b_3,a^{\prime }_1=b^{\prime }_1~\text{ and }~a^{\prime }_3=b^{\prime }_3$.

Definition 5

[35] Let ${\tilde{A}}^I =(a_1,a_2,a_3; a^{\prime }_1,a_2,a^{\prime }_3)$ be a TIFN. Then, the accuracy function of ${\tilde{A}}^I$ is denoted by ${\mathfrak {R}}\left( {\tilde{A}}^I \right)$ and is given by the expression:

$$\begin{aligned} {\mathfrak {R}}\left( {\tilde{A}}^I \right) =\dfrac{a_1+a_3+4a_2+ a^{\prime }_1+a^{\prime }_3}{8}. \end{aligned}$$

Furthermore, if $a^{\prime }_1=a_1$ and $a^{\prime }_3=a_3$, then the TIFN ${\tilde{A}}^I$ reduces to a triangular fuzzy number ${\tilde{A}}=(a_1,a_2,a_3).$

Definition 6

[23] A feasible point ${\bar{x}}$ is said to be an efficient or Pareto optimal solution of the problem (P) if there does not exist any feasible x such that $Z_{k}(x) \ge Z_{k}({\bar{x}}) ~\forall ~k$ and $Z_{k}(x) > Z_{k}({\bar{x}})$ for at least one k.

2.2 Fundamental Arithmetic Operations on TIFNs

Let ${\tilde{A}}^I =(a_1,a_2,a_3; a^{\prime }_1,a_2,a^{\prime }_3)$ and ${\tilde{B}}^I =(b_1,b_2,b_3; b^{\prime }_1,b_2,b^{\prime }_3)$ be two TIFNs and $\lambda$ be a real number. Then

(i):

${\tilde{A}}^I \oplus {\tilde{B}}^I=(a_1+b_1,a_2+b_2,a_3+b_3;~ a^{\prime }_1+b^{\prime }_1,a_2+b_2,a^{\prime }_3+b^{\prime }_3)$.

(ii):

${\tilde{A}}^I \ominus {\tilde{B}}^I=(a_1-b_3,a_2-b_2,a_3-b_1;~ a^{\prime }_1-b^{\prime }_3,a_2-b_2,a^{\prime }_3-b^{\prime }_1)$.

(iii):

$\lambda {\tilde{A}}^I={\left\{ \begin{array}{ll} (\lambda a_1,\lambda a_2,\lambda a_3; \lambda a^{\prime }_1,\lambda a_2,\lambda a^{\prime }_3), &{} \text{ if } \; \lambda \ge 0,\\ (\lambda a_3,\lambda a_2,\lambda a_1; \lambda a^{\prime }_3,\lambda a_2,\lambda a^{\prime }_1), &{} \text{ if }\; \lambda < 0. \end{array}\right. }$

(iv):

${\tilde{A}}^I\otimes {\tilde{B}}^I \simeq (c_1,c_2,c_3; c^{\prime }_1,c_2,c^{\prime }_3)~~$ where $c_1=\text{ min }\{a_1b_1,a_1b_3,a_3b_1,a_3b_3\},$ $c_2=a_2b_2,$ $c_3=\text{ max }\{a_1b_1,a_1b_3,a_3b_1,a_3b_3\},$ $c^{\prime }_1=\text{ min }\{a^{\prime }_1b^{\prime }_1,a^{\prime }_1b^{\prime }_3,a^{\prime }_3b^{\prime }_1,a^{\prime }_3b^{\prime }_3\}~~\text{ and }$ $c^{\prime }_3=\text{ max }\{a^{\prime }_1b^{\prime }_1,a^{\prime }_1b^{\prime }_3,a^{\prime }_3b^{\prime }_1,a^{\prime }_3b^{\prime }_3\}.$

(v):

The reciprocal of ${\tilde{A}}^I$ is defined by

$$\begin{aligned} \dfrac{1}{{\tilde{A}}^I} \simeq \Bigg (\dfrac{1}{a_3},\dfrac{1}{a_2},\dfrac{1}{a_1};\dfrac{1}{a_3^{\prime }}, \dfrac{1}{a_2},\dfrac{1}{a_1^{\prime }} \Bigg ), \end{aligned}$$

$\text{ provided }~a_1^{\prime } >0~\text{ or }~a_3^{\prime }<0.$

(vi):

If $b_1^{\prime }>0$ or $b_3^{\prime }<0$, then the division of ${\tilde{A}}$ and ${\tilde{B}}$ is given by

$$\begin{aligned} \dfrac{{\tilde{A}}^I}{{\tilde{B}}^I} \simeq (d_1,d_2,d_3; d_1^{\prime },d_2,d_3^{\prime }) \end{aligned}$$

where $d_1=\text{ min }\left\{ \dfrac{a_1}{b_1},\dfrac{a_1}{b_3},\dfrac{a_3}{b_1},\dfrac{a_3}{b_3} \right\} ,~~d_2=\dfrac{a_2}{b_2},$ $d_3=\text{ max }\left\{ \dfrac{a_1}{b_1},\dfrac{a_1}{b_3},\dfrac{a_3}{b_1},\dfrac{a_3}{b_3} \right\} ,$ $d^{\prime }_1=\text{ min }\left\{ \dfrac{a^{\prime }_1}{b^{\prime }_1},\dfrac{a^{\prime }_1}{b^{\prime }_3},\dfrac{a^{\prime }_3}{b^{\prime }_1},\dfrac{a^{\prime }_3}{b^{\prime }_3} \right\} ,~~\text{ and }$ $d^{\prime }_3=\text{ max }\left\{ \dfrac{a^{\prime }_1}{b^{\prime }_1},\dfrac{a^{\prime }_1}{b^{\prime }_3},\dfrac{a^{\prime }_3}{b^{\prime }_1},\dfrac{a^{\prime }_3}{b^{\prime }_3} \right\} .$

2.3 Ordering of TIFNs [31]

Let ${\tilde{A}}^I =(a_1,a_2,a_3; a^{\prime }_1,a_2,a^{\prime }_3)$ and ${\tilde{B}}^I =(b_1,b_2,b_3; b^{\prime }_1,b_2,b^{\prime }_3)$ be two TIFNs. Then, the ordering based on their components is defined as follows:

(i):

${\tilde{A}}^I \succeq {\tilde{B}}^I~\text {if and only if}~a_1 \ge b_1,a_2 \ge b_2,a_3 \ge b_3;a_1^{\prime } \ge b_1^{\prime },a_2 \ge b_2,~\text {and}~a_3^{\prime } \ge b_3^{\prime }$,

(ii):

${\tilde{A}}^I \preceq {\tilde{B}}^I~\text {if and only if}~a_1 \le b_1,a_2 \le b_2,a_3 \le b_3;a_1^{\prime } \le b_1^{\prime },a_2 \le b_2,~\text {and}~a_3^{\prime } \le b_3^{\prime }$,

(iii):

$\min ({\tilde{A}}^I, {\tilde{B}}^I)={\tilde{A}}^I~\text {if and only if}~{\tilde{A}}^I \preceq {\tilde{B}}^I$,

(iv):

$\max ({\tilde{A}}^I, {\tilde{B}}^I)={\tilde{A}}^I~\text {if and only if}~{\tilde{A}}^I \succeq {\tilde{B}}^I$.

3 Problem Formulation

The multiple objective linear fractional optimization problems have significant applications while dealing with real-world problems of various sectors. However, due to various factors such as errors in measurement, judgement, recording of the data, and many others, a DM fails to provide the values of the parameters of the problem with full certainty. Under these circumstances, there may involve some vagueness as well as indeterminacy in the available data. In such conditions, the formulation of the fractional problem in an intuitionistic fuzzy environment having all the parameters and decision variables expressed by IFNs is proved to be more relevant and promising. The general format of a fully intuitionistic fuzzy multiple objective linear fractional programming problem can be presented as:

${\textbf {(P1)}}~~\text{ Max }~~{\tilde{Z}}({\tilde{x}})=\{{\tilde{Z}}_1({\tilde{x}}),{\tilde{Z}}_2({\tilde{x}}), \dots , {\tilde{Z}}_K({\tilde{x}})\}$

$\text{ where }~~~{\tilde{Z}}_k({\tilde{x}})=\frac{{\tilde{F}}_k({\tilde{x}})}{{\tilde{G}}_k({\tilde{x}})}=\frac{ \sum ^{n} _{j=1}({\tilde{c}}_j^k \otimes {\tilde{x}}_j)\oplus \tilde{\alpha }_k}{ \sum_{j=1}^{n}({\tilde{d}}_j^k \otimes {\tilde{x}}_j) \oplus \tilde{\beta }_k},$

$\quad ~~~~~~~~~~~~~~~~k=1,2, \dots, K$

$\quad ~~~~~~\text{ s.t. }~~\sum _{j=1}^{n}{\tilde{a}}_{ij} \otimes {\tilde{x}}_j \preceq {\tilde{b}}_i,~~i=1,2,\dots ,m,$ $\quad {\tilde{x}}_j \succeq 0,~~~j=1,2,\dots , n~~$

where the parameters and variables of the problem (P1) are taken to be in the form of TIFNs, as follows:

${\tilde{c}}_j^k=(c_{j1}^k,c_{j2}^k,c_{j3}^k;c_{j1}^{\prime k},c_{j2}^{k},c_{j3}^{\prime k}),$

$\tilde{\alpha }_k=(p_{1}^k,p_{2}^k,p_{3}^k;p_{1}^{\prime k},p_{2}^{k},p_{3}^{\prime k}),$

${\tilde{d}}_j^k=(d_{j1}^k,d_{j2}^k,d_{j3}^k;d_{j1}^{\prime k},d_{j2}^{k},d_{j3}^{\prime k}),$

$\tilde{\beta }_k=(q_{1}^k,q_{2}^k,q_{3}^k;q_{1}^{\prime k},q_{2}^{k},q_{3}^{\prime k}),~~~~~k=1,2,\dots , K,$

${\tilde{a}}_{ij}=(a_{ij1},a_{ij2},a_{ij3};a_{ij1}^{\prime },a_{ij2},a_{ij3}^{\prime }),$

${\tilde{b}}_i=(b_{i1},b_{i2},b_{i3};b_{i1}^{\prime },b_{i2},b_{i3}^{\prime }),$

${\tilde{x}}_j=(x_{j1},x_{j2},x_{j3};x_{j1}^{\prime },x_{j2},x_{j3}^{\prime }),$

$i=1,2,\dots ,m;~~j=1,2,\dots ,n.$

Let S denote the set of all feasible solutions of (P1). Further, assume that ${\tilde{G}}_k({\tilde{x}}) \succ 0~\forall ~ {\tilde{x}} \in S.$ Substituting the cost vector parameters, constraints coefficients and variables of the problem in the form of TIFNs, the model (P1) becomes:

${\textbf {(P2)}}~\text{ Max }~{\tilde{Z}}({\tilde{x}})=\{{\tilde{Z}}_1({\tilde{x}}),{\tilde{Z}}_2({\tilde{x}}), \dots , {\tilde{Z}}_K({\tilde{x}})\}$

$\quad ~~~~~~\text{s.t.}~~ \sum _{j=1}^{n} (l_{ij1},l_{ij2},l_{ij3};l_{ij1}^{\prime },l_{ij2},l_{ij3}^{\prime })$

$\quad ~~~~~~~~~~~~\preceq (b_{i1},b_{i2},b_{i3};b_{i1}^{\prime },b_{i2},b_{i3}^{\prime }),$

$\quad ~~~~~~~~~~~~~(x_{j1},x_{j2},x_{j3};x_{j1}^{\prime },x_{j2},x_{j3}^{\prime }) \succeq 0,$

$\quad ~~~~~~~~~~~~~i=1,2,\dots ,m,~~~j=1,2,\dots , n$

$\quad ~\text{ where }~{\tilde{Z}}_k({\tilde{x}})=\dfrac{{\tilde{F}}_k({\tilde{x}})}{{\tilde{G}}_k({\tilde{x}})},~~k=1,2, \dots , K,$

$\quad ~~~~~~~~~~~~~{\tilde{F}}_k({\tilde{x}})= \sum _{j=1}^n(c_{j1}^k,c_{j2}^k,c_{j3}^k;c_{j1}^{\prime k},c_{j2}^{k},c_{j3}^{\prime k})$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~\otimes (x_{j1},x_{j2},x_{j3};x_{j1}^{\prime },x_{j2},x_{j3}^{\prime })$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~\oplus (p_{1}^k,p_{2}^k,p_{3}^k;p_{1}^{\prime k},p_{2}^{k},p_{3}^{\prime k}),$

$\quad ~~~~~~~~~~~~~{\tilde{G}}_k({\tilde{x}})= \sum _{j=1}^n (d_{j1}^k,d_{j2}^k,d_{j3}^k;d_{j1}^{\prime k},d_{j2}^{k},d_{j3}^{\prime k})$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~\otimes (x_{j1},x_{j2},x_{j3};x_{j1}^{\prime },x_{j2},x_{j3}^{\prime })$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~\oplus (q_{1}^k,q_{2}^k,q_{3}^k;q_{1}^{\prime k},q_{2}^{k},q_{3}^{\prime k}),$

$\quad ~~~~~~~~~~~~~\text {and}$

$\quad ~~~~~~~~~~~~~(l_{ij1},l_{ij2},l_{ij3};l_{ij1}^{\prime },l_{ij2},l_{ij3}^{\prime })$

$\quad ~~~~~~~~~~~~~~~=(a_{ij1},a_{ij2},a_{ij3};a_{ij1}^{\prime },a_{ij2},a_{ij3}^{\prime })$

$\quad ~~~~~~~~~~~~~~~~~~~\otimes (x_{j1},x_{j2},x_{j3};x_{j1}^{\prime },x_{j2},x_{j3}^{\prime }).$

Applying the basic arithmetic operations (Sect. 2.2), the model (P2) can be recast into

${\textbf {(P3)}}~\text{ Max }~{\tilde{Z}}({\tilde{x}})=\{{\tilde{Z}}_1({\tilde{x}}),{\tilde{Z}}_2({\tilde{x}}), \dots , {\tilde{Z}}_K({\tilde{x}})\}$

$\quad ~~~~~~~\text{s.t.}~ \sum _{j=1}^{n} (l_{ij1},l_{ij2},l_{ij3};l_{ij1}^{\prime },l_{ij2},l_{ij3}^{\prime })$

$\quad ~~~~~~~~~~~~~\preceq (b_{i1},b_{i2},b_{i3};b_{i1}^{\prime },b_{i2},b_{i3}^{\prime }),$

$\quad ~~~~~~~~~~~~~~(x_{j1},x_{j2},x_{j3};x_{j1}^{\prime },x_{j2},x_{j3}^{\prime }) \succeq 0,$

$\quad ~~~~~~~~~~~~~~i=1,2,\dots ,m,\quad j=1,2,\dots , n$

$\quad \text{ where }~~{\tilde{Z}}_k({\tilde{x}})=(Z_{k1},Z_{k2},Z_{k3};Z_{k1}^{'},Z_{k2},Z_{k3}^{'}),$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~k=1,2, \dots , K,$

$\quad ~~~~~~~~~~~~~~Z_{k1}=\dfrac{\sum _{j=1}^n c_{j1}^k x_{j1}+p_{1}^k}{\sum _{j=1}^n d_{j3}^k x_{j3}+q_{3}^k},$

$\quad ~~~~~~~~~~~~~~Z_{k2}=\dfrac{\sum _{j=1}^n c_{j2}^k x_{j2}+p_{2}^k}{\sum _{j=1}^n d_{j2}^k x_{j2}+q_{2}^k},$

$\quad ~~~~~~~~~~~~~~Z_{k3}=\dfrac{ \sum _{j=1}^n c_{j3}^k x_{j3}+p_{3}^k}{\sum _{j=1}^n d_{j1}^k x_{j1}+q_{1}^k},$

$\quad ~~~~~~~~~~~~~~Z_{k1}^{\prime }=\frac{\sum_{j=1}^n c_{j1}^{\prime k} x_{j1}^{\prime } +p_{1}^{\prime k}}{\sum _{j=1}^n d_{j3}^{\prime k} x_{j3}^{\prime } +q_{3}^{\prime k}},$

$\quad ~~~~~~~~~~~~~~Z_{k3}^{\prime }=\dfrac{\sum _{j=1}^n c_{j3}^{\prime k} x_{j3}^{\prime } +p_{3}^{\prime k}}{\sum _{j=1}^n d_{j1}^{\prime k} x_{j1}^{\prime } +q_{1}^{\prime k}},$

$\quad ~~~~~~~~~~~~~~(l_{ij1},l_{ij2},l_{ij3};l_{ij1}^{\prime },l_{ij2},l_{ij3}^{\prime })=(a_{ij1}x_{j1},$

$\quad ~~~~~~~~~~~~~~~a_{ij2}x_{j2},a_{ij3}x_{j3}; a_{ij1}^{\prime }x_{j1}^{\prime }, a_{ij2}x_{j2},a_{ij3}^{\prime }x_{j3}^{\prime }).$ Further, using the ordering technique as defined in Sect. 2.3 over the set of constraints and maintaining the form of TIFNs, the equivalent problem for (P3) can be expressed as:

$${\textbf {(P4)}}~\text{ Max }~{\tilde{Z}}({\tilde{x}})=\{{\tilde{Z}}_1({\tilde{x}}),{\tilde{Z}}_2({\tilde{x}}), \dots , {\tilde{Z}}_K({\tilde{x}})\}$$

$\quad \text{ where }~{\tilde{Z}}_k({\tilde{x}})=(Z_{k1},Z_{k2},Z_{k3};Z_{k1}^{'},Z_{k2},Z_{k3}^{'}),$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~k=1,2, \dots , K$

$\quad ~~~~~~\text{s.t.}~ \sum _{j=1}^{n} a_{ij1}x_{j1} \le b_{i1},~~~\sum _{j=1}^{n} a_{ij2}x_{j2} \le b_{i2},$

$\quad ~~~~~~~~~~~~\sum _{j=1}^{n} a_{ij3}x_{j3} \le b_{i3},~~~ \sum _{j=1}^{n} a_{ij1}^{\prime }x_{j1}^{\prime } \le b_{i1}^{\prime },$

$\quad ~~~~~~~~~~~~\sum _{j=1}^{n} a_{ij3}^{\prime }x_{j3}^{\prime } \le b_{i3}^{\prime },$

$\quad ~~~~~~~~~~~~x_{j1}^{\prime } \ge 0,~x_{j1}- x_{j1}^{\prime } \ge 0,~ x_{j2}-x_{j1} \ge 0,$

$\quad ~~~~~~~~~~~~x_{j3}-x_{j2} \ge 0,~x_{j3}^{\prime }-x_{j3} \ge 0,$

$\quad ~~~~~~~~~~~~i=1,2,\dots ,m,~j=1,2,\dots , n$

such that the expressions for $Z_{k1},Z_{k2},Z_{k3},Z_{k1}^{'},Z_{k3}^{'}$ remain the same as given in model (P3).

Theorem 1

The efficient solution of problem (P4) is also an efficient solution for problem (P3). The converse of the statement also holds true.

Proof

Let ${\tilde{x}}^{*}=\{ (x_{j1}^{*},x_{j2}^{*},x_{j3}^{*};x_{j1}^{*\prime },x_{j2}^{*},x_{j3}^{ *\prime }),~ j=1,2, \dots ,n \}$ be an efficient solution of problem (P4). Then, since ${\tilde{x}}^{*}$ is feasible for (P4), therefore, we have

$$\begin{aligned} ~~~~~~~~\sum _{j=1}^{n} a_{ij1}x_{j1}^{*} \le b_{i1},~\sum _{j=1}^{n} a_{ij2}x_{j2}^{*} \le b_{i2},~\sum _{j=1}^{n} a_{ij3}x_{j3}^{*} \le b_{i3},\\ \sum _{j=1}^{n} a_{ij1}^{\prime }x_{j1}^{*\prime } \le b_{i1}^{\prime },~ \sum _{j=1}^{n} a_{ij3}^{\prime }x_{j3}^{*\prime } \le b_{i3}^{\prime },~~i=1,2,\dots ,m, \\ x_{j1}^{*\prime } \ge 0,~x_{j1}^{*}- x_{j1}^{*\prime } \ge 0,~ x_{j2}^{*}-x_{j1}^{*} \ge 0,~~~~~~~~~~~~~~~~~~~~~~ \\ x_{j3}^{*}-x_{j2}^{*} \ge 0,~x_{j3}^{*\prime }-x_{j3}^{*} \ge 0,\quad j=1,2,\dots , n.~~~~~~~~ \end{aligned}$$

Using Sect. 2.3, the above constraints imply that

(i):

$\left( \sum _{j=1}^{n} a_{ij1}x_{j1}^{*},\sum _{j=1}^{n} a_{ij2}x_{j2}^{*}, \sum _{j=1}^{n} a_{ij3}x_{j3}^{*};\right.$ $\left.\sum _{j=1}^{n} a_{ij1}^{\prime }x_{j1}^{*\prime },\sum _{j=1}^{n} a_{ij2}x_{j2}^{*}, \sum _{j=1}^{n} a_{ij3}^{\prime }x_{j3}^{*\prime } \right)$ $\preceq (b_{i1},b_{i2},b_{i3};b_{i1}^{\prime },b_{i2},b_{i3}^{\prime }),~~i=1,2,\dots ,m;~$ and

(ii):

$(x_{j1}^{*},x_{j2}^{*},x_{j3}^{*};x_{j1}^{*\prime },x_{j2}^{*},x_{j3}^{*\prime }) \succeq 0,~~~j=1,2,\dots , n.$

Hence, (i) and (ii) give ${\tilde{x}}^{*}$ is also a feasible solution of the problem (P3). Further, as ${\tilde{x}}^{*}$ is an efficient solution of (P4), therefore, there does not exist any feasible $\tilde{{\bar{x}}}$ such that ${\tilde{Z}}_{k}(\tilde{{\bar{x}}}) \succeq {\tilde{Z}}_{k}({\tilde{x}}^{*}) ~\forall ~k=1,2,\dots ,K$ and ${\tilde{Z}}_{k}(\tilde{{\bar{x}}}) \succ {\tilde{Z}}_{k}({\tilde{x}}^{*})$ for at least one index k, which yields ${\tilde{x}}^{*}$ is an efficient solution of problem (P3) also.

Conversely, let us assume that $\tilde{{\hat{x}}}=\{ ({\hat{x}}_{j1},{\hat{x}}_{j2},{\hat{x}}_{j3}; {\hat{x}}_{j1}^{\prime },{\hat{x}}_{j2},{\hat{x}}_{j3}^{\prime }),~ j=1,2, \dots ,n \}$ be an efficient solution of problem (P3). Then, feasibility of $\tilde{{\hat{x}}}$ for problem (P3) gives

$\sum _{j=1}^{n} \left( a_{ij1} {\hat{x}}_{j1}, a_{ij2}{\hat{x}}_{j2},a_{ij3}{\hat{x}}_{j3}; a_{ij1}^{\prime }{\hat{x}}_{j1}^{\prime }, a_{ij2}{\hat{x}}_{j2}, a_{ij3}^{\prime }{\hat{x}}_{j3}^{\prime } \right)$

$\preceq (b_{i1},b_{i2},b_{i3};b_{i1}^{\prime },b_{i2},b_{i3}^{\prime }),~~i=1,2,\dots ,m;~$ and $({\hat{x}}_{j1},{\hat{x}}_{j2},{\hat{x}}_{j3};{\hat{x}}_{j1}^{\prime },{\hat{x}}_{j2},{\hat{x}}_{j3}^{\prime }) \succeq 0,~~~j=1,2,\dots , n.$ Applying the ordering on TIFNs as defined in Sect. 2.3, the non-negativity condition of TIFNs (Definition 4) and applying the definition of a TIFN (Definition 3), the above set of IF constraints reduces to the crisp constraints:

$$\begin{aligned}\sum _{j=1}^{n} a_{ij1}{\hat{x}}_{j1} \le b_{i1},~ \sum _{j=1}^{n} a_{ij2}{\hat{x}}_{j2} \le b_{i2},~\sum _{j=1}^{n} a_{ij3}{\hat{x}}_{j3} \le b_{i3}, \\ \sum _{j=1}^{n} a_{ij1}^{\prime }{\hat{x}}_{j1}^{\prime } \le b_{i1}^{\prime },~\sum _{j=1}^{n} a_{ij3}^{\prime }{\hat{x}}_{j3}^{\prime } \le b_{i3}^{\prime },\quad i=1,2,\dots ,m, \\ {\hat{x}}_{j1}^{\prime } \ge 0,~{\hat{x}}_{j1}- {\hat{x}}_{j1}^{\prime } \ge 0,~ {\hat{x}}_{j2}-{\hat{x}}_{j1} \ge 0,~~~~~~~~~~~~~~~~~~~~~~~~\\ {\hat{x}}_{j3}-{\hat{x}}_{j2} \ge 0,~{\hat{x}}_{j3}^{\prime }-{\hat{x}}_{j3} \ge 0,\quad j=1,2,\dots , n~~~~~~~~~~~~ \end{aligned}$$

which yield that $\tilde{{\hat{x}}}$ is also feasible for problem (P4). Moreover, since $\tilde{{\hat{x}}}$ is an efficient solution for model (P3), consequently, there does not exist any feasible $\tilde{\dot{x}}$ such that ${\tilde{Z}}_{k}(\tilde{\dot{x}}) \succeq {\tilde{Z}}_{k}(\tilde{{\hat{x}}}) ~\forall ~k=1,2,\dots ,K$ and ${\tilde{Z}}_{k}(\tilde{\dot{x}}) \succ {\tilde{Z}}_{k}(\tilde{{\hat{x}}})$ for at least one index k, which implies $\tilde{{\hat{x}}}$ is also an efficient solution of the problem (P4).

Hence the result.□

3.1 Goal Programming Formulation

Goal programming provides a simple and efficient tool to solve optimization problems having multiple conflicting objectives. It was first introduced by Charnes and Cooper [43] and later on extended by Ijiri [44], Lee [45], and Mohamed [42]. Goal programming essentially gives an easy and compromise algorithm to reach the solution to multiple objective problems by minimizing the deviations between the achievement levels of the objectives and the desired goals set for them. In general, the DM does not know the objective goal values with certainty. Therefore, an imprecise aspiration level is assigned to each of the objectives which are termed fuzzy goals. Let ${\tilde{g}}_k$ be the intuitionistic fuzzy aspiration level assigned to the $k^{th}$ objective ${\tilde{Z}}_k({\tilde{x}})$. Then, these goals are interpreted as:

(i):

${\tilde{Z}}_k({\tilde{x}})\succeq _{IF} {\tilde{g}}_k$ (for maximizing ${\tilde{Z}}_k({\tilde{x}})$);

(ii):

${\tilde{Z}}_k({\tilde{x}}) \preceq _{IF} {\tilde{g}}_k$ (for minimizing ${\tilde{Z}}_k({\tilde{x}})$),

where $"\preceq _{IF}"$ and $"\succeq _{IF}"$ represents the intuitionistic fuzziness in the aspiration goals for the objectives and are defined in Sect. 2.3. These can also be interpreted as “essentially less than” and “essentially greater than”, respectively.

Accordingly, a fuzzy goal programming model for the multiple-objective problem (P4) to find $x_{j1}^{\prime }, x_{j1},x_{j2},x_{j3}, x_{j3}^{\prime },~~j=1,2, \dots , n~$ can be formulated as:

${\textbf {(G1)}}~~{\tilde{Z}}_k ({\tilde{x}}) \succeq _{IF} {\tilde{g}}_k,~~~k=1,2,\dots ,K$

$~~~~~~~~~\text{ subject } \text{ to } \text{ all } \text{ the } \text{ constraints } \text{ of } \text{(P4). }$

Further, let the intuitionistic fuzzy goal for the $k^{th}$ objective ${\tilde{Z}}_k$ be expressed by a TIFN as ${\tilde{g}}_k=(g_{k1},g_{k2},g_{k3};g_{k1}^{\prime },g_{k2},g_{k3}^{\prime })$. Then, using the component-wise ordering, the model (G1) can be re-stated as:

${\textbf {(G2)}}~~$ Find $~x_{j1}^{\prime }, x_{j1},x_{j2},x_{j3}, x_{j3}^{\prime },~~j=1,2, \dots , n~$

$\text{ such } \text{ that }$

$~~~~~~~~~~~Z_{k1} \succeq g_{k1},~ Z_{k2} \succeq g_{k2},~ Z_{k3} \succeq g_{k3},~ Z_{k1}^{\prime } \succeq g_{k1}^{\prime },$

$~~~~~~~~~~~Z_{k3}^{\prime } \succeq g_{k3}^{\prime };~~~k=1,2,\dots ,K$

$~~~~~~~~~~\text{ subject } \text{ to } \text{ all } \text{ the } \text{ constraints } \text{ of } \text{(P4) }$

where $Z_{k1}=\frac{ \sum_{j=1}^{n} c_{j1}^{k} x_{j1}+p_{1}^{k}}{\sum_{j=1}^{n} d_{j3}^{k} x_{j3}+q_{3}^{k}},~Z_{k2}=\frac{\sum_{j=1}^{n} c_{j2}^{k} x_{j2}+p_{2}^{k}}{ \sum_{j=1}^{n} d_{j2}^{k} x_{j2}+q_{2}^{k}},$

$~~~~~~~~~~~~Z_{k3}=\frac{\sum_{j=1}^n c_{j3}^{k} x_{j3}+p_{3}^{k}}{\sum_{j=1}^{n} d_{j1}^{k} x_{j1}+q_{1}^k},~Z_{k1}^{\prime }=\frac{\sum_{j=1}^{n} c_{j1}^{\prime k} x_{j1}^{\prime } +p_{1}^{\prime k}}{\sum_{j=1}^{n} d_{j3}^{\prime k} x_{j3}^{\prime } +q_{3}^{\prime k}},$

$~~~~~~~~~~~~~Z_{k3}^{\prime }=\frac{\sum_{j=1}^{n} c_{j3}^{\prime k} x_{j3}^{\prime } +p_{3}^{\prime k}}{\sum_{j=1}^{n} d_{j1}^{\prime k} x_{j1}^{\prime } +q_{1}^{\prime k}},~~k=1,2, \dots , K.$ Consequently, the problem (G2) involves 5K conflicting constraints associated with the objective goals involving linear fractions. Now, the inequality “$\succeq$” in these 5K constraints is the fuzzification of “$\ge$” which can further be handled using a membership function. The choice of this membership function depends on the DM.

3.2 Meaning of Inequality $(x \succeq r)$ Using a Membership Function

The inequality $x \succeq r$ basically refers to the fuzzy behaviour of inequality $x \ge r$. The logical interpretation of $x \succeq r$ in terms of a membership function is that the DM is always satisfied if $x \ge r$, that is, the membership degree is 1. Let t denotes the maximum tolerance range (decided by the DM), then if $x \le r-t$, then the inequality $x \succeq r$ is never satisfied, that is, the degree of membership is 0, and if $r-t \le x \le r$, then the behaviour of inequality is characterized by a piecewise continuously increasing function. Therefore, the fuzzified inequality $x \succeq r$ can be expressed mathematically in terms of a membership function as follows:

$$\mu (x) = \left\{ \begin{gathered} 1,\quad {\text{if }}\;x \ge r, \hfill \\ \phi (x),\quad {\text{if }}\;r - t \le x \le r, \hfill \\ 0,\quad {\text{if }}\;x \le r - t \hfill \\ \end{gathered} \right.$$

where $\phi (x)$ is the piecewise continuous and increasing function for $x \in [r-t,r]$.

3.3 Linear Membership Functions

In this section, we define the membership function to deal with the 5K conflicting fuzzy objective-constraints of the model (G2). One can take the associated functions to be linear, exponential, parabolic, or hyperbolic. The shape of this membership function characterizes the type of restriction imposed on the respective objective goal by the DM. Here, we choose the linear membership functions for the sake of simplicity. The 5K membership functions $(\mu _k's)$ for the respective goals can be expressed as:

$$\mu _{{k1}} \left( {Z_{{k1}} } \right) = \left\{ \begin{gathered} 1,\quad {\text{if }}\;Z_{{k1}} \ge g_{{k1}} , \hfill \\ \frac{{Z_{{k1}} - l_{{k1}} }}{{g_{{k1}} - l_{{k1}} }},\quad {\text{if }}\;l_{{k1}} \le Z_{{k1}} \le g_{{k1}} , \hfill \\ 0,\quad {\text{if }}\;Z_{{k1}} \le l_{{k1}} \hfill \\ \end{gathered} \right.$$

where $l_{k1}$ is the corresponding lower tolerance limit for the goal $g_{k1}$.

$$\begin{aligned} \mu _{k2}(Z_{k2})={\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{k2} \ge g_{k2},\\ \dfrac{Z_{k2}-l_{k2}}{g_{k2}-l_{k2}}, &{} \text{ if } \ l_{k2} \le Z_{k2} \le g_{k2},\\ 0, &{} \text{ if } \ Z_{k2} \le l_{k2}. \end{array}\right. } \\ \mu _{k3}(Z_{k3})={\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{k3} \ge g_{k3},\\ \dfrac{Z_{k3}-l_{k3}}{g_{k3}-l_{k3}}, &{} \text{ if } \ l_{k3} \le Z_{k3} \le g_{k3},\\ 0, &{} \text{ if } \ Z_{k3} \le l_{k3}. \end{array}\right. } \\ \mu _{k1}^{\prime }(Z_{k1}^{\prime })={\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{k1}^{\prime } \ge g_{k1}^{\prime },\\ \dfrac{Z_{k1}^{\prime }-l_{k1}^{\prime }}{g_{k1}^{\prime }-l_{k1}^{\prime }}, &{} \text{ if } \ l_{k1}^{\prime } \le Z_{k1}^{\prime } \le g_{k1}^{\prime },\\ 0, &{} \text{ if } \ Z_{k1}^{\prime } \le l_{k1}^{\prime }. \end{array}\right. } \\ \mu _{k3}^{\prime }(Z_{k3}^{\prime })={\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{k3}^{\prime } \ge g_{k3}^{\prime },\\ \dfrac{Z_{k3}^{\prime }-l_{k3}^{\prime }}{g_{k3}^{\prime }-l_{k3}^{\prime }}, &{} \text{ if } \ l_{k3}^{\prime } \le Z_{k3}^{\prime } \le g_{k3}^{\prime },\\ 0, &{} \text{ if } \ Z_{k3}^{\prime } \le l_{k3}^{\prime } \end{array}\right. } \end{aligned}$$

where for $k=1,2,\dots ,K;$ $l_{k2}, l_{k3}, l_{k1}^{\prime }$ and $l_{k3}^{\prime }$ are lower tolerance limits for the goals $g_{k2}$, $g_{k3}$, $g_{k1}^{\prime }$ and $g_{k3}^{\prime }$, respectively. The graphical representations of these linear membership functions for the objective goals are given in Figs. 3, 4, 5, 6, and 7.

Therefore, in order to meet the goals decided by the DM, each of the membership degrees needs to be maximized and reach close to the maximum value, that is, unity.

Fig. 3

Linear membership function for $Z_{k1}(x)$

Fig. 4

Linear membership function for $Z_{k2}(x)$

Fig. 5

Linear membership function for $Z_{k3}(x)$

Fig. 6

Linear membership function for $Z_{k1}^{\prime }(x)$

Fig. 7

Linear membership function for $Z_{k3}^{\prime }(x)$

3.4 Expression of Membership Goals

The aim of goal programming is to minimize the deviation between the objective function value $Z_k$ and its aspired goal value $g_k$. This deviation is characterized by two deviational variables $d_k^-$ and $d_k^+$ where $d_k^-$ is the under-deviational variable, given by

$$\begin{aligned} d_k^-= \text{ max }\left\{ 0,\dfrac{g_k-Z_k}{g_k-l_k} \right\} =\dfrac{1}{2(g_k-l_k)}\Big (g_k-Z_k+|g_k-Z_k|\Big ), \end{aligned}$$

and $d_k^+$ is the over-deviational variable defined by

$$\begin{aligned} d_k^+= \text{ max }\left\{ 0,\dfrac{Z_k-g_k}{g_k-l_k}\right\} =\dfrac{1}{2(g_k-l_k)}\Big (Z_k-g_k+|Z_k-g_k|\Big ). \end{aligned}$$

Now, using the fact that the maximum value to be obtained for any membership function is unity, the defined 5K fuzzified inequalities of the model (G2) can be re-interpreted in the form of following equations by associating the two-deviational variables with each membership function:

$$\begin{aligned} \mu _{k1}(Z_{k1})+d_{k1}^--d_{k1}^+=1, \\ \mu _{k2}(Z_{k2})+d_{k2}^--d_{k2}^+=1, \\ \mu _{k3}(Z_{k3})+d_{k3}^--d_{k3}^+=1, \\ \mu _{k1}^{\prime }(Z_{k1}^{\prime })+d_{k1}^{\prime -}-d_{k1}^{\prime +}=1, \\ \mu _{k3}^{\prime }(Z_{k3}^{\prime })+d_{k3}^{\prime -}-d_{k3}^{\prime +}=1. \end{aligned}$$

Further, substituting the expressions for membership functions as linear functions (Sect. 3.3), the above equations become

$$\begin{aligned}&\dfrac{Z_{k1}-l_{k1}}{g_{k1}-l_{k1}}+d_{k1}^--d_{k1}^+=1, \end{aligned}$$

(1)

$$\begin{aligned}&\dfrac{Z_{k2}-l_{k2}}{g_{k2}-l_{k2}}+d_{k2}^--d_{k2}^+=1, \end{aligned}$$

(2)

$$\begin{aligned}&\dfrac{Z_{k3}-l_{k3}}{g_{k3}-l_{k3}}+d_{k3}^--d_{k3}^+=1, \end{aligned}$$

(3)

$$\begin{aligned}&\dfrac{Z_{k1}^{\prime }-l_{k1}^{\prime }}{g_{k1}^{\prime }-l_{k1}^{\prime }}+d_{k1}^{\prime -}-d_{k1}^{\prime +}=1, \end{aligned}$$

(4)

$$\begin{aligned}&\dfrac{Z_{k3}^{\prime }-l_{k3}^{\prime }}{g_{k3}^{\prime }-l_{k3}^{\prime }}+d_{k3}^{\prime -}-d_{k3}^{\prime +}=1 \end{aligned}$$

(5)

where $d_{k1}^-,d_{k2}^-,d_{k3}^-,d_{k1}^{\prime -},d_{k3}^{\prime -}$ and $d_{k1}^+,d_{k2}^+,d_{k3}^+,d_{k1}^{\prime +},d_{k3}^{\prime +}$ with $d_{k1}^- d_{k1}^+=0,~d_{k2}^- d_{k2}^+=0,~d_{k3}^- d_{k3}^+=0,~d_{k1}^{\prime -} d_{k1}^{\prime +}=0,~d_{k3}^{\prime -} d_{k3}^{\prime +}=0,$ represent the under-deviations and over-deviations from the aspired level, respectively.

In this paper, we have used the min-sum approach of goal programming [42], that is, the objective is now to minimize the deviational variables to achieve the desired degree of membership. Further, depending upon the type of optimization problem (max/min problem), the minimization of under- and/or over-deviational variables took place. Since our problem is a maximization problem, hence, only the minimization of under-deviational variables is required to achieve the aspired level. However, any over-deviation is allowed, as they signify the full achievement of the aspired goal. Therefore, the model (G2) is converted by goal programming to a minimization problem of the under-deviational variables, which is described as follows:

$~{\textbf {(G3)}}~\text{ Min }~\sum _{k=1}^K w_k(d_{k1}^-+d_{k2}^-+d_{k3}^-+d_{k1}^{\prime -}+d_{k3}^{\prime -})$

$~~~~~~~~~~~~~\text{s.t.}~~\dfrac{Z_{k1}-l_{k1}}{g_{k1}-l_{k1}}+d_{k1}^--d_{k1}^+=1,$

$~~~~~~~~~~~~~~~~~~~\dfrac{Z_{k2}-l_{k2}}{g_{k2}-l_{k2}}+d_{k2}^--d_{k2}^+=1,$

$~~~~~~~~~~~~~~~~~~~\dfrac{Z_{k3}-l_{k3}}{g_{k3}-l_{k3}}+d_{k3}^--d_{k3}^+=1,$

$~~~~~~~~~~~~~~~~~~~\dfrac{Z_{k1}^{\prime }-l_{k1}^{\prime }}{g_{k1}^{\prime }-l_{k1}^{\prime }}+d_{k1}^{\prime -}-d_{k1}^{\prime +}=1,$

$~~~~~~~~~~~~~~~~~~~\dfrac{Z_{k3}^{\prime }-l_{k3}^{\prime }}{g_{k3}^{\prime }-l_{k3}^{\prime }}+d_{k3}^{\prime -}-d_{k3}^{\prime +}=1,$

$~~~~~~~~~~~~~~~~~~~\sum _{j=1}^{n} a_{ij1}x_{j1} \le b_{i1},~~\sum _{j=1}^{n} a_{ij2}x_{j2} \le b_{i2},$

$~~~~~~~~~~~~~~~~~~~\sum _{j=1}^{n} a_{ij3}x_{j3} \le b_{i3},~~\sum _{j=1}^{n} a_{ij1}^{\prime }x_{j1}^{\prime } \le b_{i1}^{\prime },$

$~~~~~~~~~~~~~~~~~~~ \sum _{j=1}^{n} a_{ij3}^{\prime }x_{j3}^{\prime } \le b_{i3}^{\prime },$

$~~~~~~~~~~~~~~~~~~~x_{j1}^{\prime } \ge 0,~x_{j1}- x_{j1}^{\prime } \ge 0,~ x_{j2}-x_{j1} \ge 0,$

$~~~~~~~~~~~~~~~~~~~x_{j3}-x_{j2} \ge 0,~~x_{j3}^{\prime }-x_{j3} \ge 0,$

$~~~~~~~~~~~~~~~~~~~i=1,2,\dots ,m;~~~j=1,2,\dots , n,$

$~~~~~~~~~~~~~~~~~~~d_{k1}^-,d_{k2}^-,d_{k3}^-,d_{k1}^{\prime -},d_{k3}^{\prime -} \ge 0,$

$~~~~~~~~~~~~~~~~~~~d_{k1}^+,d_{k2}^+,d_{k3}^+,d_{k1}^{\prime +},d_{k3}^{\prime +}\ge 0,$

$~~~~~~~~~~~~~~~~~~~d_{k1}^- d_{k1}^+=0,d_{k2}^- d_{k2}^+=0,d_{k3}^- d_{k3}^+=0,$ $~d_{k1}^{\prime -} d_{k1}^{\prime +}=0,d_{k3}^{\prime -} d_{k3}^{\prime +}=0,~~k=1,2, \dots , K$

where $w_k \ge 0~ (\text{ with }~\sum _{k=1}^K w_k=1),~k=1,2,\dots ,K,$ represent the relative importance of the various objectives involved in the problem (P1).

However, it can be observed that the membership goals in Eqs. (1)–(5) are inherently non-linear in nature and thereby giving rise to a computational issue in obtaining the solution to the problem (G3). To deal with this difficulty, we have presented a linearization technique in the next section.

3.5 Linearization Process of Membership Goals

Here, we consider the membership goal given by Eq. (1) and demonstrate its linearization. The rest of the goals can be treated in a similar manner. The Eq. (1) can be re-written as

$$\begin{aligned} L_{k1}(Z_{k1}-l_{k1})+d_{k1}^--d_{k1}^+=1,~~\text{ where }~~L_{k1}=\dfrac{1}{g_{k1}-l_{k1}} \end{aligned}$$

Substituting the expression for $Z_{k1}$ from model (G2), the above equation becomes

$L_{k1}\left(\sum _{j=1}^n c_{j1}^k x_{j1}+p_{1}^k \right) +d_{k1}^-\left(\sum _{j=1}^n d_{j3}^k x_{j3}+q_{3}^k \right)$

$~~~{}-d_{k1}^+\left(\sum _{j=1}^n d_{j3}^k x_{j3}+q_{3}^k \right) =L_{k1}^{\prime }\left(\sum _{j=1}^n d_{j3}^k x_{j3}+q_{3}^k \right)$ where $L_{k1}^{\prime }=1+L_{k1}l_{k1}$. Hence,

$\sum _{j=1}^n (r_{j1}^k x_{j1}-s_{j3}^k x_{j3} )+d_{k1}^-\left( \sum _{j=1}^n d_{j3}^k x_{j3}+q_{3}^k \right)$

$$\begin{aligned} \sum _{j=1}^n \big (r_{j1}^k x_{j1}-s_{j3}^k x_{j3} \big )+d_{k1}^-\left( \sum _{j=1}^n d_{j3}^k x_{j3}+q_{3}^k \right)-d_{k1}^+\left(\sum _{j=1}^n d_{j3}^k x_{j3}+q_{3}^k \right) =G_{k1} \end{aligned}$$

(6)

where $r_{j1}^k=L_{k1}c_{j1}^k,~s_{j3}^k=L_{k1}^{\prime }d_{j3}^k~~$ and $G_{k1}=L_{k1}^{\prime }q_3^k-L_{k1}p_1^k$.

The expression in (6) is a simplified general form of a membership goal but it is still non-linear in nature. Now, to obtain the linearized expression for (6), we use the following method of change of variables as presented in Pal et al. [13]:

Letting $D_{k1}^-=d_{k1}^-\left(\sum _{j=1}^n d_{j3}^k x_{j3}+q_{3}^k \right) ~~$ and $D_{k1}^+=d_{k1}^+\left(\sum _{j=1}^n d_{j3}^k x_{j3}+q_{3}^k \right)$, the expression (6) is converted to its linear form as

$$\begin{aligned}\sum _{j=1}^n \left( r_{j1}^k x_{j1}-s_{j3}^k x_{j3} \right) +D_{k1}^--D_{k1}^+=G_{k1} \end{aligned}$$

(7)

with $D_{k1}^-,D_{k1}^+ \ge 0$ and $D_{k1}^-D_{k1}^+=0$ since $d_{k1}^-,d_{k1}^+ \ge 0$ and $\sum \nolimits _{j=1}^n d_{j3}^k x_{j3}+q_{3}^k >0$.

Further, the objective involves the minimization of $d_{k1}^-$, that is, the minimization of $D_{k1}^-/\big(\sum \nolimits _{j=1}^n d_{j3}^k x_{j3}+q_{3}^k\big)$, which is also a non-linear one. It may be noted that the value of $d_{k1}^-=0$ in the solution indicates the full achievement of the aspiration level whereas the $d_{k1}^-=1$ represents the zero achievement of the desired goal. So, the restriction $0 \le d_{k1}^- \le 1$, imposes following additional constraint on the model:

$$\begin{aligned} \dfrac{D_{k1}^-}{\sum _{j=1}^n d_{j3}^k x_{j3}+q_{3}^k} \le 1, \end{aligned}$$

$$\begin{aligned} \text{ that } \text{ is, }~~~~ D_{k1}^--\sum _{j=1}^n d_{j3}^k x_{j3} \le q_{3}^k. \end{aligned}$$

(8)

Now, continuing in the similar fashion, we get the following linear forms for the expressions (2)–(5):

$$\begin{aligned}&\sum _{j=1}^n \big (r_{j2}^k x_{j2}-s_{j2}^k x_{j2} \big )+D_{k2}^--D_{k2}^+=G_{k2}, \end{aligned}$$

(9)

$$\begin{aligned}&\sum _{j=1}^n \big (r_{j3}^k x_{j3}-s_{j1}^k x_{j1} \big )+D_{k3}^--D_{k3}^+=G_{k3}, \end{aligned}$$

(10)

$$\begin{aligned}&\sum _{j=1}^n \big (r_{j1}^{\prime k} x_{j1}^{\prime }-s_{j3}^{\prime k} x_{j3}^{\prime } \big )+D_{k1}^{\prime -}-D_{k1}^{\prime +}=G_{k1}^{\prime }, \end{aligned}$$

(11)

$$\begin{aligned}& \sum _{j=1}^n \big (r_{j3}^{\prime k} x_{j3}^{\prime }-s_{j1}^{\prime k} x_{j1}^{\prime } \big )+D_{k3}^{\prime -}-D_{k3}^{\prime +}=G_{k3}^{\prime } \end{aligned}$$

(12)

along-with the additional set of constraints given below:

$$\begin{aligned} D_{k2}^-- \sum _{j=1}^n d_{j2}^k x_{j2} \le q_{2}^k, \end{aligned}$$

(13)

$$\begin{aligned} D_{k3}^-- \sum _{j=1}^n d_{j1}^k x_{j1} \le q_{1}^k, \end{aligned}$$

(14)

$$\begin{aligned} D_{k1}^{\prime -}- \sum _{j=1}^n d_{j3}^{\prime k} x_{j3}^{\prime } \le q_{3}^{\prime k}, \end{aligned}$$

(15)

$$\begin{aligned} D_{k3}^{\prime -}- \sum _{j=1}^n d_{j1}^{\prime k} x_{j1}^{\prime } \le q_{1}^{\prime k}. \end{aligned}$$

(16)

Consequently, the goal programming model (G3) is transformed to the following problem:

${\textbf {(G4)}}~\text{ Find }~~x_{j1},x_{j2},x_{j3},x_{j1}^{\prime },x_{j3}^{\prime }~~$ so as to

$$\text{ Minimize }~~Z=\sum _{k=1}^K w_k(D_{k1}^-+D_{k2}^-+D_{k3}^-+D_{k1}^{\prime -}+D_{k3}^{\prime -})$$

$$\text{ s.t. }~\sum _{j=1}^n \big (r_{j1}^k x_{j1}-s_{j3}^k x_{j3} \big )+D_{k1}^--D_{k1}^+=G_{k1},$$

$$\sum _{j=1}^n \big (r_{j2}^k x_{j2}-s_{j2}^k x_{j2} \big )+D_{k2}^--D_{k2}^+=G_{k2},$$

$$\sum _{j=1}^n \big (r_{j3}^k x_{j3}-s_{j1}^k x_{j1} \big )+D_{k3}^--D_{k3}^+=G_{k3},$$

$$\sum _{j=1}^n \big (r_{j3}^{\prime k} x_{j3}^{\prime }-s_{j1}^{\prime k} x_{j1}^{\prime } \big )+D_{k3}^{\prime -}-D_{k3}^{\prime +}=G_{k3}^{\prime },$$

$$\sum _{j=1}^{n} a_{ij1}x_{j1} \le b_{i1},~~\sum _{j=1}^{n} a_{ij2}x_{j2} \le b_{i2},$$

$$\sum _{j=1}^{n} a_{ij3}x_{j3} \le b_{i3},~~~\sum _{j=1}^{n} a_{ij1}^{\prime }x_{j1}^{\prime } \le b_{i1}^{\prime },$$

$$\sum _{j=1}^{n} a_{ij3}^{\prime }x_{j3}^{\prime } \le b_{i3}^{\prime },\quad i=1,2,\dots ,m,$$

$$D_{k1}^--\sum _{j=1}^n d_{j3}^k x_{j3} \le q_{3}^k,$$

$$D_{k2}^--\sum _{j=1}^n d_{j2}^k x_{j2} \le q_{2}^k,$$

$$D_{k3}^-- \sum _{j=1}^n d_{j1}^k x_{j1} \le q_{1}^k,$$

$$D_{k1}^{\prime -}- \sum _{j=1}^n d_{j3}^{\prime k} x_{j3}^{\prime } \le q_{3}^{\prime k},$$

$$D_{k3}^{\prime -}- \sum _{j=1}^n d_{j1}^{\prime k} x_{j1}^{\prime } \le q_{1}^{\prime k},$$

$$\quad x_{j1}^{\prime } \ge 0,~x_{j1}- x_{j1}^{\prime } \ge 0,~ x_{j2}-x_{j1} \ge 0,$$

$$\quad x_{j3}-x_{j2} \ge 0,~x_{j3}^{\prime }-x_{j3} \ge 0,$$

$$\quad j=1,2,\dots , n,$$

$$\quad D_{k1}^-,D_{k2}^-,D_{k3}^-,D_{k1}^{\prime -},D_{k3}^{\prime -},D_{k1}^+,D_{k2}^+,$$

$$\quad D_{k3}^+,D_{k1}^{\prime +},D_{k3}^{\prime +} \ge 0,\quad k=1,2,\dots ,K.$$

Finally, obtain the optimal solution to the linear optimization problem (G4) using any of the available commercial packages (LINGO/MATLAB/MAPLE).

Fig. 8

Flowchart of the proposed approach

4 Steps of the Proposed Solution Methodology

The present section briefly describes the procedure used in the proposed technique to solve a fully IF-MO-LFP problem. The steps of the proposed approach and its flowchart (Fig. 8) are presented as follows:

Step 1:

Substitute all the parameter values and decision variables as TIFNs in the model (P1).

Step 2:

Apply the arithmetic operations (Sect. 2.2) and ordering from Sect. 2.3 so as to obtain the model (P4).

Step 3:

Set up the aspiration level for each objective function as a TIFN, that is, ${\tilde{g}}_k$, $k=1,2,\dots ,K$ and develop the goal programming model (G2).

Step 4:

Using the membership functions defined in Sect. 3.3, formulate the goal programming constraints (1)–(5).

Step 5:

Apply the linearization process along-with variable transformations as described in Sect. 3.5.

Step 6:

Finally, formulate the weighted goal programming deterministic model (G4).

Step 7:

Solve the crisp linear program (G4) by any of the available commercial packages (MAPLE/LINGO/ MATLAB) to find the global optima of the model. Further, by substituting all the values in the objectives of the problem (P1), we obtain an efficient solution to the problem (P1).

Step 8:

Stop if the DM is satisfied with the solution. Otherwise, change the tolerance limit for the objectives and repeat the process from Step 4.

5 Advantages of the Proposed Technique

The significant merits of the proposed algorithm over existing studies are summarized in Table 2.

Table 2 Advantages of the proposed method

6 Numerical Illustration

In this section, we present a numerical example to demonstrate the steps of the proposed methodology. Consider the following problem having two objectives:

${\mathbf {(M1)}}~\text{ Max }~{\tilde{Z}}_1({\tilde{x}})=\frac{\sum_{j=1}^{2}({\tilde{c}}_{j}^{1} \otimes {\tilde{x}}_{j})\oplus \tilde{\alpha }_{1}}{\sum_{j=1}^{2}({\tilde{d}}_{j}^{1} \otimes {\tilde{x}}_{j}) \oplus \tilde{\beta }_{1}},$

$\quad ~~~~~\text{ Max }~{\tilde{Z}}_{2}({\tilde{x}})=\frac{\sum_{j=1}^{2}({\tilde{c}}_{j}^{2} \otimes {\tilde{x}}_{j})\oplus \tilde{\alpha }_{2}}{\sum_{j=1}^{2}({\tilde{d}}_{j}^{2} \otimes {\tilde{x}}_{j}) \oplus \tilde{\beta }_{2}}$

$\quad ~~~~~~~~~\text{s.t.}~~{\tilde{a}}_{11} \otimes {\tilde{x}}_1 \ominus {\tilde{a}}_{12} \otimes {\tilde{x}}_2 \preceq {\tilde{b}}_1,$

$\quad ~~~~~~~~~~~~~~~{\tilde{x}}_1,~{\tilde{x}}_2~\text{ are } \text{ non-negative } \text{ TIFNs }$

$$\begin{aligned} \text { where}\,\,\,&{\tilde{c}}_1^1=(1,2,3;0,2,4), \quad {\tilde{c}}_2^1 =(5,7,8;3,7,9),\\&{\tilde{d}}_1^1=(1,1,1;0,1,1),\quad {\tilde{d}}_2^1 =(2,3,4;1,3,6),\\&\tilde{\alpha }_1=(0,0,0;0,0,0),\quad \tilde{\beta }_1 =(1,3,5;1,3,6),\\&{\tilde{c}}_1^2=(2,4,5;1,4,5),\quad {\tilde{c}}_2^2 =(3,6,9;1,6,10),\\&{\tilde{d}}_1^2=(2,2,2;1,2,2),\quad {\tilde{d}}_2^2 =(1,3,4;0,3,5),\\&\tilde{\alpha }_2=(0,0,0;0,0,0),\quad \tilde{\beta }_2 =(1,2,2;1,2,4),\\&{\tilde{a}}_{11}=(2,4,6;0,4,8),\quad {\tilde{a}}_{12} =(2,3,4;1,3,5),\\&{\tilde{b}}_{1}=(-5,10,20;-10,10,40). \end{aligned}$$

Step 1 Substituting ${\tilde{x}}_1=(x_{11},x_{12},x_{13};x_{11}^{\prime },x_{12},x_{13}^{\prime })~\text{ and } {\tilde{x}}_2=(x_{21},x_{22},x_{23};x_{21}^{\prime },x_{22},x_{23}^{\prime })$, the model (M1) becomes

${\textbf {(M2)}}~\text{ Max }~{\tilde{Z}}_1({\tilde{x}})=\dfrac{{\tilde{F}}_1({\tilde{x}})}{{\tilde{G}}_1({\tilde{x}})},$

$\quad ~~~~~\text{ Max }~{\tilde{Z}}_2({\tilde{x}})= \dfrac{{\tilde{F}}_2({\tilde{x}})}{{\tilde{G}}_2({\tilde{x}})}$

$\quad ~~\text{ where }~{\tilde{F}}_1({\tilde{x}})=(1,2,3;0,2,4)\otimes (x_{11},x_{12},x_{13};$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~x_{11}^{\prime },x_{12},x_{13}^{\prime }) \oplus (5,7,8;3,7,9)$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~~~\otimes (x_{21},x_{22},x_{23};x_{21}^{\prime },x_{22},x_{23}^{\prime }),$

$\quad ~~~~~~~~~~~~~~~{\tilde{G}}_1({\tilde{x}})=(1,1,1;0,1,1)\otimes (x_{11},x_{12},x_{13};$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~x_{11}^{\prime },x_{12},x_{13}^{\prime }) \oplus (2,3,4;1,3,6)$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~~~\otimes (x_{21},x_{22},x_{23};x_{21}^{\prime },x_{22},x_{23}^{\prime })$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~~~\oplus (1,3,5;1,3,6)$

$\quad ~~~~~~~~~~~~~~~{\tilde{F}}_2({\tilde{x}})=(2,4,5;1,4,5)\otimes (x_{11},x_{12},x_{13};$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~x_{11}^{\prime },x_{12},x_{13}^{\prime }) \oplus (3,6,9;1,6,10)$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~~~\otimes (x_{21},x_{22},x_{23};x_{21}^{\prime },x_{22},x_{23}^{\prime })$

$\quad ~~~~~~~~~~~~~~~{\tilde{G}}_2({\tilde{x}})=(2,2,2;1,2,2)\otimes (x_{11},x_{12},x_{13};$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~x_{11}^{\prime },x_{12},x_{13}^{\prime }) \oplus (1,3,4;0,3,5)$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~~~\otimes (x_{21},x_{22},x_{23};x_{21}^{\prime },x_{22},x_{23}^{\prime })$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~~~\oplus (1,2,2;1,2,4)$

$\quad ~~~~~~~~~\text{s.t.}~(2,4,6;0,4,8)\otimes (x_{11},x_{12},x_{13};x_{11}^{\prime },x_{12},x_{13}^{\prime })\ominus$

$\quad ~~~~~~~~~~~~~~~(2,3,4;1,3,5)\otimes (x_{21},x_{22},x_{23};x_{21}^{\prime },x_{22},x_{23}^{\prime })$

$\quad ~~~~~~~~~~~~~~\preceq (-5,10,20;-10,10,40),$

$\quad ~~~~~~~~~~~~~~~(x_{11},x_{12},x_{13};x_{11}^{\prime },x_{12},x_{13}^{\prime })~\succeq 0,$

$\quad ~~~~~~~~~~~~~~~(x_{21},x_{22},x_{23};x_{21}^{\prime },x_{22},x_{23}^{\prime })~\succeq 0.$

Step 2 Applying the basic arithmetic operations, using the ordering technique and maintaining the form of a TIFN, the model (M2) gets converted into the following problem:

${\textbf {(M3)}}~\text{ Max }~{\tilde{Z}}_1({\tilde{x}})=\left[ \dfrac{x_{11}+5x_{21}}{x_{13}+4x_{23}+5},\dfrac{2x_{12}+7x_{22}}{x_{12}+3x_{22}+3},\right.$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\dfrac{3x_{13}+8x_{23}}{x_{11}+2x_{21}+1};\dfrac{3x_{21}^{\prime }}{x_{13}^{\prime }+6x_{23}^{\prime }+6},$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\left. \dfrac{2x_{12}+7x_{22}}{x_{12}+3x_{22}+3},\dfrac{4x_{13}^{\prime }+9x_{23}^{\prime }}{x_{21}^{\prime }+1} \right]$

$\quad ~~~~~\text{ Max}~~{\tilde{Z}}_2({\tilde{x}})=\left[ \dfrac{2x_{11}+3x_{21}}{2x_{13}+4x_{23}+2},\dfrac{4x_{12}+6x_{22}}{2x_{12}+3x_{22}+2},\right.$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\dfrac{5x_{13}+9x_{23}}{2x_{11}+x_{21}+1}; \dfrac{x_{11}^{\prime }+x_{21}^{\prime }}{2x_{13}^{\prime }+5x_{23}^{\prime }+4},$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\left. \dfrac{4x_{12}+6x_{22}}{2x_{12}+3x_{22}+2},\dfrac{5x_{13}^{\prime }+10x_{23}^{\prime }}{x_{11}^{\prime }+1} \right]$

$\quad ~~~~~~~~~\text{s.t.}~~2x_{11}-4x_{23} \le -5,~~4x_{12}-3x_{22} \le 10,$

$\quad ~~~~~~~~~~~~~~~6x_{13}-2x_{21} \le 20,-5x_{23}^{\prime } \le -10,$

$\quad ~~~~~~~~~~~~~~~8x_{13}^{\prime }-x_{21}^{\prime } \le 40,$

$\quad ~~~~~~~~~~~~~~~x_{11}^{\prime } \ge 0,~x_{11}-x_{11}^{\prime } \ge 0,~x_{12}-x_{11} \ge 0,$

$\quad ~~~~~~~~~~~~~~~x_{13}-x_{12} \ge 0,~x_{13}^{\prime }-x_{13} \ge 0,$

$\quad ~~~~~~~~~~~~~~~x_{21}^{\prime } \ge 0,~x_{21}-x_{21}^{\prime } \ge 0,~x_{22}-x_{21} \ge 0,$

$\quad ~~~~~~~~~~~~~~~x_{23}-x_{22} \ge 0,~x_{23}^{\prime }-x_{23} \ge 0.$

Step 3 Let ${\tilde{g}}_1=(0.05,1,10;0,1,30)$ and ${\tilde{g}}_2=(0.1,1,10;0,1,40)$ be the IF goals for the objectives ${\tilde{Z}}_1$ and ${\tilde{Z}}_2$, respectively. Hence, the equivalent goal programming model becomes

$\quad {\textbf {(M4)}}~~\text{ Find }~~x_{11},x_{12},x_{13},x_{11}^{\prime },x_{13}^{\prime },x_{21},x_{22},x_{23},x_{21}^{\prime },x_{23}^{\prime }$

$\quad ~~\text{ such } \text{ that }$

$\quad ~~~~~~~~~~~~~~~~~~~~~Z_{11}=\dfrac{x_{11}+5x_{21}}{x_{13}+4x_{23}+5} \succeq 0.05,$

$\quad ~~~~~~~~~~~~~~~~~~~~~Z_{12}=\dfrac{2x_{12}+7x_{22}}{x_{12}+3x_{22}+3} \succeq 1,$

$\quad ~~~~~~~~~~~~~~~~~~~~~Z_{13}=\dfrac{3x_{13}+8x_{23}}{x_{11}+2x_{21}+1} \succeq 10,$

$\quad ~~~~~~~~~~~~~~~~~~~~~Z_{11}^{\prime }=\dfrac{3x_{21}^{\prime }}{x_{13}^{\prime }+6x_{23}^{\prime }+6} \succeq 0,$

$\quad ~~~~~~~~~~~~~~~~~~~~~Z_{13}^{\prime }=\dfrac{4x_{13}^{\prime }+9x_{23}^{\prime }}{x_{21}^{\prime }+1} \succeq 30,$

$\quad ~~~~~~~~~~~~~~~~~~~~~Z_{21}=\dfrac{2x_{11}+3x_{21}}{2x_{13}+4x_{23}+2} \succeq 0.1,$

$\quad ~~~~~~~~~~~~~~~~~~~~~Z_{22}=\dfrac{4x_{12}+6x_{22}}{2x_{12}+3x_{22}+2} \succeq 1,$

$\quad ~~~~~~~~~~~~~~~~~~~~~Z_{23}=\dfrac{5x_{13}+9x_{23}}{2x_{11}+x_{21}+1} \succeq 10,$

$\quad ~~~~~~~~~~~~~~~~~~~~~Z_{21}^{\prime }=\dfrac{x_{11}^{\prime }+x_{21}^{\prime }}{2x_{13}^{\prime }+5x_{23}^{\prime }+4} \succeq 0,$

$\quad ~~~~~~~~~~~~~~~~~~~~~Z_{23}^{\prime }=\dfrac{5x_{13}^{\prime }+10x_{23}^{\prime }}{x_{11}^{\prime }+1} \succeq 40,$

$\quad ~~~~~~~~~~~~~~~~~~~~\text{ subject } \text{ to } \text{ all } \text{ the } \text{ constraints } \text{ of } \text{(M3) }.$

Step 4 The linear membership functions for the objective constraints be given as:

$$\begin{aligned} \mu _{11}(Z_{11})={\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{11} \ge 0.05,\\ \dfrac{Z_{11}-0.01}{0.04}, &{} \text{ if } \ 0.01 \le Z_{11} \le 0.05,\\ 0, &{} \text{ if } \ Z_{11} \le 0.01, \end{array}\right. } \\ \mu _{12}(Z_{12})= {\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{12} \ge 1,\\ \dfrac{Z_{12}-0.5}{0.5}, &{} \text{ if } \ 0.5 \le Z_{12} \le 1,\\ 0, &{} \text{ if } \ Z_{12} \le 0.5, \end{array}\right. }~~~~~~~~ \\ \mu _{13}(Z_{13})={\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{13} \ge 10,\\ \dfrac{Z_{13}-5}{5}, &{} \text{ if } \ 5 \le Z_{13} \le 10,\\ 0, &{} \text{ if } \ Z_{13} \le 5, \end{array}\right. }~~~~~~~~~~~~ \\ \mu _{11}^{\prime }(Z_{11}^{\prime })= {\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{11}^{\prime } \ge 0,\\ \dfrac{Z_{11}^{\prime }+0.5}{0.5}, &{} \text{ if } \ -0.5 \le Z_{11}^{\prime } \le 0,\\ 0, &{} \text{ if } \ Z_{11}^{\prime } \le -0.5, \end{array}\right. }~~~ \\ \mu _{13}^{\prime }(Z_{13}^{\prime })= {\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{13}^{\prime } \ge 30,\\ \dfrac{Z_{13}^{\prime }-20}{10}, &{} \text{ if } \ 20 \le Z_{13}^{\prime } \le 30,\\ 0, &{} \text{ if } \ Z_{13}^{\prime } \le 20, \end{array}\right. }~~~~~~~ \\ \mu _{21}(Z_{21})={\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{21} \ge 0.1,\\ \dfrac{Z_{21}-0.05}{0.05}, &{} \text{ if } \ 0.05 \le Z_{21} \le 0.1,\\ 0, &{} \text{ if } \ Z_{21} \le 0.05, \end{array}\right. } \\ \mu _{22}(Z_{22})= {\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{22} \ge 1,\\ \dfrac{Z_{22}-0.5}{0.5}, &{} \text{ if } \ 0.5 \le Z_{22} \le 1,\\ 0, &{} \text{ if } \ Z_{22} \le 0.5, \end{array}\right. }~~~~~ \\ \mu _{23}(Z_{23})={\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{23} \ge 10,\\ \dfrac{Z_{23}-5}{5}, &{} \text{ if } \ 5 \le Z_{23} \le 10,\\ 0, &{} \text{ if } \ Z_{23} \le 5, \end{array}\right. }~~~~~~~~ \\ \mu _{21}^{\prime }(Z_{21}^{\prime })= {\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{21}^{\prime } \ge 0,\\ \dfrac{Z_{21}^{\prime }+0.5}{0.5}, &{} \text{ if } \ -0.5 \le Z_{21}^{\prime } \le 0,\\ 0, &{} \text{ if } \ Z_{21}^{\prime } \le -0.5, \end{array}\right. } \\ \mu _{23}^{\prime }(Z_{23}^{\prime })={\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{23}^{\prime } \ge 40,\\ \dfrac{Z_{23}^{\prime }-30}{10}, &{} \text{ if } \ 30 \le Z_{23}^{\prime } \le 40,\\ 0, &{} \text{ if } \ Z_{23}^{\prime } \le 30. \end{array}\right. }~~~ \end{aligned}$$

Accordingly, formulate the goal programming constraints as:

$$\begin{aligned}&\mu _{11}(Z_{11})+d_{11}^--d_{11}^+=1,\\&\mu _{12}(Z_{12})+d_{12}^--d_{12}^+=1,\\&\mu _{13}(Z_{13})+d_{13}^--d_{13}^+=1,\\&\mu _{11}^{\prime }(Z_{11}^{\prime })+d_{11}^{\prime -}-d_{11}^{\prime +}=1,\\&\mu _{13}^{\prime }(Z_{13}^{\prime })+d_{13}^{\prime -}-d_{13}^{\prime +}=1,\\&\mu _{21}(Z_{21})+d_{21}^--d_{21}^+=1,\\&\mu _{22}(Z_{22})+d_{22}^--d_{22}^+=1,\\&\mu _{23}(Z_{23})+d_{23}^--d_{23}^+=1,\\&\mu _{21}^{\prime }(Z_{21}^{\prime })+d_{21}^{\prime -}-d_{21}^{\prime +}=1,\\&\mu _{23}^{\prime }(Z_{23}^{\prime })+d_{23}^{\prime -}-d_{23}^{\prime +}=1. \end{aligned}$$

Step 5 Using the expressions for various membership functions as described in Step 4 and employing the linearization process (Sect. 3.5), the above constraints can be recast into

$$\begin{aligned} \left. \begin{array}{ll} x_{11}+5x_{21}-0.05x_{13}-0.2x_{23}+D_{11}^--D_{11}^+=0.25, \\ x_{12}+4x_{22}+D_{12}^--D_{12}^+=3, \\ 3x_{13}+8x_{23}-10x_{11}-20x_{21}+D_{13}^--D_{13}^+=10, \\ 3x_{21}^{\prime }+D_{11}^{\prime -}-D_{11}^{\prime +}=0, \\ 4x_{13}^{\prime }+9x_{23}^{\prime }-30x_{21}^{\prime }+D_{13}^{\prime -}-D_{13}^{\prime +}=30, \\ 2x_{11}+3x_{21}-0.2x_{13}-0.4x_{23}+D_{21}^--D_{21}^+=0.2, \\ 2x_{12}+3x_{22}+D_{22}^--D_{22}^+=2, \\ 5x_{13}+9x_{23}-20x_{11}-10x_{21}+D_{23}^--D_{23}^+=10, \\ x_{11}^{\prime }+x_{21}^{\prime }+D_{21}^{\prime -}-D_{21}^{\prime +}=0, \\ 5x_{13}^{\prime }+10x_{23}^{\prime }-40x_{11}^{\prime }+D_{23}^{\prime -}-D_{23}^{\prime +}=40 \\ \end{array} \right\} \end{aligned}$$

(17)

along-with the additional constraints

$$\begin{aligned} \left. \begin{array}{ll} D_{11}^--0.04x_{13}-0.16x_{23} \le 0.2, \\ D_{12}^--0.5x_{12}-1.5x_{22} \le 1.5, \\ D_{13}^--5x_{11}-10x_{21} \le 5, \\ D_{11}^{\prime -}-0.5x_{13}^{\prime }-3x_{23}^{\prime } \le 3, \\ D_{13}^{\prime -}-10x_{21}^{\prime } \le 10, \\ D_{21}^--0.1x_{13}-0.2x_{23} \le 0.1, \\ D_{22}^--x_{12}-1.5x_{22} \le 1, \\ D_{23}^--10x_{11}-5x_{21} \le 5, \\ D_{21}^{\prime -}-x_{13}^{\prime }-2.5x_{23}^{\prime } \le 2, \\ D_{23}^{\prime -}-10x_{11}^{\prime } \le 10. \\ \end{array} \right\} \end{aligned}$$

(18)

Step 6 Hence, the final deterministic weighted goal programming model becomes

${\textbf {(M5)}}~~\text{ Min }~Z=w_1(D_{11}^-+D_{12}^-+D_{13}^-+D_ {11}^{\prime -}+D_{13}^{\prime -})+$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~w_2(D_{21}^-+D_{22}^-+D_{23}^-+D_{21}^{\prime -}+D_{23}^{\prime -})$

$\quad ~~~~~~~~\text{s.t.}~~2x_{11}-4x_{23} \le -5,~~4x_{12}-3x_{22} \le 10,$

$\quad ~~~~~~~~~~~~~~~6x_{13}-2x_{21} \le 20,~~-5x_{23}^{\prime } \le -10,$

$\quad ~~~~~~~~~~~~~~~8x_{13}^{\prime }-x_{21}^{\prime } \le 40,$

$\quad ~~~~~~~~~~~~~~~x_{11}^{\prime } \ge 0,~x_{11}-x_{11}^{\prime } \ge 0,~x_{12}-x_{11} \ge 0,$

$\quad ~~~~~~~~~~~~~~~x_{13}-x_{12} \ge 0,~x_{13}^{\prime }-x_{13} \ge 0,$

$\quad ~~~~~~~~~~~~~~~x_{21}^{\prime } \ge 0,~x_{21}-x_{21}^{\prime } \ge 0,~x_{22}-x_{21} \ge 0,$

$\quad ~~~~~~~~~~~~~~~x_{23}-x_{22} \ge 0,~x_{23}^{\prime }-x_{23} \ge 0,$

$\quad ~~~~~~~~~~~~~~~D_{k1}^-,D_{k2}^-,D_{k3}^-,D_{k1}^{\prime -},D_{k3}^{\prime -} \ge 0,~~k=1,2,$

$\quad ~~~~~~~~~~~~~~\text{ along-with } \text{ the } \text{ set } \text{ of } \text{ constraints } \text{(17) } \text{ and } \text{(18) }.$

Step 7 For the choice of $w_1=w_2=0.5$, solving the linear programming problem (M5) by using the solver "LINGO-17.0", the optimal solution of the problem (M5) is as follows:

$$\begin{aligned} D_{{11}}^{ - } & = D_{{12}}^{ - } = D_{{13}}^{ - } = D_{{11}}^{{\prime - }} = D_{{13}}^{{\prime - }} = 0, \\ D_{{21}}^{ - } & = D_{{22}}^{ - } = D_{{23}}^{ - } = D_{{21}}^{{\prime - }} = D_{{23}}^{{\prime - }} = 0, \\ D_{{11}}^{ + } & = 1.25,D_{{12}}^{ + } = 7.5,D_{{13}}^{ + } = 0,D_{{11}}^{{\prime + }} = 0,D_{{13}}^{{\prime + }} = 8, \\ D_{{21}}^{ + } & = 1.1,D_{{22}}^{ + } = 10.12,D_{{23}}^{ + } = 0,D_{{21}}^{{\prime + }} = 0,D_{{23}}^{{\prime + }} = 5, \\ x_{{11}} & = 1.05,x_{{12}} = 3.4,x_{{13}} = 3.4,x^{\prime}_{{11}} = 0,x^{\prime}_{{13}} = 5, \\ x_{{21}} & = 0.19,x_{{22}} = 1.78,x_{{23}} = 1.78,x^{\prime}_{{21}} = 0,x^{\prime}_{{23}} = 2, \\ \end{aligned}$$

with the optimal objective function value $Z=0$.

Hence, the solution to the problem (M1) is given by

$$\begin{aligned} {\tilde{x}}_1=(1.05,3.4,3.4;0,3.4,5), \\ {\tilde{x}}_2=(0.19,1.78,1.78;0,1.78,2) \end{aligned}$$

with

$$\begin{aligned} \tilde{Z}_{1} & = (0.13,1.6,10.06;0,1.6,38), \\ \tilde{Z}_{2} & = (0.17,1.72,10.04;0,1.72,45). \\ \end{aligned}$$

7 An Application in E-education System

Due to the present prevailing scenario of the COVID-19 pandemic worldwide, the need for drastic advancement in the current education system is of utmost importance to all nations. In this context, a university plans to run some of the programmes/courses using an E-platform via the internet to facilitate a significant number of graduates in distant areas too. In order to achieve this objective, the university has selected two different cities (A and B) covering a wide area to set up various E-learning centres (ELC) in the region to provide direct access of services to students. However, due to various resources and budget limitations, the university has to decide how many ELCs to install in city A and in city B. The university administration had a crude idea about the various involved parameters such as capital requirement, number of targeted graduates, etc. Therefore, from a practical point of view, this ELC set-up model fails to predict the exact values of the problem parameters. Consequently, it is more relevant and promising to express the model parameters as well as the number of ELCs in the form of IFNs. Table 3 summarizes all the data regarding the approximate (IF) capital requirement, the approximate (IF) manpower for ELC routine maintenance, the approximate (IF) number of students served in each city, and some fixed approximate (IF) maintenance costs. The diagrammatic depiction of the outline of the ELC model is shown in Fig. 9. Moreover, according to a survey conducted by the university, the greater manpower demonstrates higher user satisfaction. Further, let ${\tilde{x}}_1$ and ${\tilde{x}}_2$ be the number of ELCs in the form of TIFNs to be established in cities A and B, respectively. The university has following two objectives for establishing the ELCs:

Table 3 Approximate (IF) data for E-learning centres set-up

• 1. The university must install an optimal number of ELCs, in order to provide direct access for students and maintain a high ratio of user satisfaction/investment capital. Mathematically, $\text{Max} \, {\tilde{Z}}_1$= Max $\left[ \dfrac{\text {the \, number \, of \, manpower}}{\text {total \, investment \, budget}} \right]$ $=\text{ Max }~\left[ \dfrac{(2,3,4;1,3,5){\tilde{x}}_1 \oplus (1,3,5;1,3,6){\tilde{x}}_2}{(1,2,3;0,2,4){\tilde{x}}_1 \oplus (2,3,4;1,3,5){\tilde{x}}_2 \oplus (1,2,3;1,2,4)} \right]$

• 2. The university must install an optimal number of ELCs so as to achieve a higher ratio of service to students/investment capital, that is, $\text{Max} \, {\tilde{Z}}_1$= Max $\left[ \dfrac{\text {the \, number \, of \, served \, students}}{\text {total \, investment \, budget}} \right]$ $=\text{ Max }~\left[ \dfrac{(1,3,5;1,3,6){\tilde{x}}_1 \oplus (4,5,6;3,5,6){\tilde{x}}_2}{(1,2,3;0,2,4){\tilde{x}}_1 \oplus (2,3,4;1,3,5){\tilde{x}}_2 \oplus (2,4,6;2,4,8)} \right]$

Due to the limited resources available to the university, the following constraints are imposed on the model of establishing ELCs.

• 1. The total approximate manpower for the smooth maintenance and running of ELCs must not exceed 25 persons.

• 2. The total approximate investment budget must not exceed 20 million dollars.

Fig. 9

Pictorial representation of university ELCs set-up

The mathematical formulation of the problem is given by

${\textbf {(S1)}}~\text{ Max }~{\tilde{Z}}({\tilde{x}})=\left\{ \dfrac{{\tilde{F}}_1({\tilde{x}})}{{\tilde{G}}_1({\tilde{x}})},\dfrac{{\tilde{F}}_2({\tilde{x}})}{{\tilde{G}}_2({\tilde{x}})} \right\}$

$\quad ~\text{ where }~{\tilde{F}}_1({\tilde{x}})=(2,3,4;1,3,5){\tilde{x}}_1 \oplus (1,3,5;1,3,6){\tilde{x}}_2,$

$\quad ~~~~~~~~~~~~~{\tilde{G}}_1({\tilde{x}})=(1,2,3;0,2,4){\tilde{x}}_1 \oplus (2,3,4;1,3,5){\tilde{x}}_2$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~\oplus (1,2,3;1,2,4),$

$\quad ~~~~~~~~~~~~~{\tilde{F}}_2({\tilde{x}})=(1,3,5;1,3,6){\tilde{x}}_1 \oplus (4,5,6;3,5,6){\tilde{x}}_2,$

$\quad ~~~~~~~~~~~~~{\tilde{G}}_2({\tilde{x}})=(1,2,3;0,2,4){\tilde{x}}_1 \oplus (2,3,4;1,3,5){\tilde{x}}_2$

$\quad ~~~~~~~~~~~~~~~~~~~~~~~~~~\oplus (2,4,6;2,4,8)$

$\quad ~~~~~~\text{s.t.}~~(2,3,4;1,3,5){\tilde{x}}_1 \oplus (1,3,5;1,3,6){\tilde{x}}_2$

$\quad ~~~~~~~~~~~~\preceq (10,15,25;8,15,35),$

$\quad ~~~~~~~~~~~~(1,2,3;0,2,4){\tilde{x}}_1 \oplus (2,3,4;1,3,5){\tilde{x}}_2$

$\quad ~~~~~~~~~~~~\preceq (5,10,20;3,10,30),$

$\quad ~~~~~~~~~~~~{\tilde{x}}_1,~{\tilde{x}}_2~\text{ are } \text{ non-negative } \text{ TIFNs. }$

Letting ${\tilde{g}}_1=(0.5,0.8,5;0,0.8,10)$ and ${\tilde{g}}_2=(0.5,1,8;0,1,20)$ along-with the linear membership functions for the objective constraints given by:

$$\begin{aligned} \quad \mu _{11}(Z_{11})={\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{11} \ge 0.5,\\ \dfrac{Z_{11}-0.1}{0.4}, &{} \text{ if } \ 0.1 \le Z_{11} \le 0.5,\\ 0, &{} \text{ if } \ Z_{11} \le 0.1, \end{array}\right. } \\ \quad \mu _{12}(Z_{12})= {\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{12} \ge 0.8,\\ \dfrac{Z_{12}-0.6}{0.2}, &{} \text{ if } \ 0.6 \le Z_{12} \le 0.8,\\ 0, &{} \text{ if } \ Z_{12} \le 0.6, \end{array}\right. } \\ \quad \mu _{13}(Z_{13})={\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{13} \ge 5,\\ \dfrac{Z_{13}-2}{3}, &{} \text{ if } \ 2 \le Z_{13} \le 5,\\ 0, &{} \text{ if } \ Z_{13} \le 2, \end{array}\right. }~~~~~~~~~ \\ \quad \mu _{11}^{\prime }(Z_{11}^{\prime })= {\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{11}^{\prime } \ge 0,\\ \dfrac{Z_{11}^{\prime }+0.5}{0.5}, &{} \text{ if } \ -0.5 \le Z_{11}^{\prime } \le 0,\\ 0, &{} \text{ if } \ Z_{11}^{\prime } \le -0.5, \end{array}\right. } \\ \quad \mu _{13}^{\prime }(Z_{13}^{\prime })= {\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{13}^{\prime } \ge 10,\\ \dfrac{Z_{13}^{\prime }-7}{3}, &{} \text{ if } \ 7 \le Z_{13}^{\prime } \le 10,\\ 0, &{} \text{ if } \ Z_{13}^{\prime } \le 7, \end{array}\right. }~~~~~~~ \\ \quad \mu _{21}(Z_{21})={\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{21} \ge 0.5,\\ \dfrac{Z_{21}-0.2}{0.3}, &{} \text{ if } \ 0.2 \le Z_{21} \le 0.5,\\ 0, &{} \text{ if } \ Z_{21} \le 0.2, \end{array}\right. } \\ \quad \mu _{22}(Z_{22})= {\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{22} \ge 1,\\ \dfrac{Z_{22}-0.8}{0.2}, &{} \text{ if } \ 0.8 \le Z_{22} \le 1,\\ 0, &{} \text{ if } \ Z_{22} \le 0.8, \end{array}\right. }~~~ \\ \quad \mu _{23}(Z_{23})={\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{23} \ge 8,\\ \dfrac{Z_{23}-5}{3}, &{} \text{ if } \ 5 \le Z_{23} \le 8,\\ 0, &{} \text{ if } \ Z_{23} \le 5, \end{array}\right. }~~~~~~~~~ \\ \quad \mu _{21}^{\prime }(Z_{21}^{\prime })= {\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{21}^{\prime } \ge 0,\\ \dfrac{Z_{21}^{\prime }+1}{1}, &{} \text{ if } \ -1 \le Z_{21}^{\prime } \le 0,\\ 0, &{} \text{ if } \ Z_{21}^{\prime } \le -1, \end{array}\right. }~~~~ \\ \quad \mu _{23}^{\prime }(Z_{23}^{\prime })={\left\{ \begin{array}{ll} 1, &{} \text{ if } \ Z_{23}^{\prime } \ge 20,\\ \dfrac{Z_{23}^{\prime }-10}{10}, &{} \text{ if } \ 10 \le Z_{23}^{\prime } \le 20,\\ 0, &{} \text{ if } \ Z_{23}^{\prime } \le 10. \end{array}\right. }~~~ \end{aligned}$$

Applying the steps involved in the algorithm, the final crisp model for problem (S1) becomes

${\textbf {(S2)}}~\text{ Min }~Z=w_1(D_{11}^-+D_{12}^-+D_{13}^-+D_{11}^{\prime -}+D_{13}^{\prime -})+$

$\quad ~~~~~~~~~~~~~~~~~~~~ w_2(D_{21}^-+D_{22}^-+D_{23}^-+D_{21}^{\prime -}+D_{23}^{\prime -})$

$~~~~~~~~~\text{ s.t. }~~2x_{11}+x_{21} \le 10,~~3x_{12}+3x_{22} \le 15,$

$\quad ~~~~~~~~~~~~~4x_{13}+5x_{23} \le 25,~~x_{11}^{\prime }+x_{21}^{\prime } \le 8,$

$\quad ~~~~~~~~~~~~~5x_{13}^{\prime }+6x_{23}^{\prime } \le 35,~~x_{11}+2x_{21} \le 5,$

$\quad ~~~~~~~~~~~~~2x_{12}+3x_{22} \le 10,~~3x_{13}+4x_{23} \le 20,$

$\quad ~~~~~~~~~~~~~x_{21}^{\prime } \le 3,~~4x_{13}^{\prime }+5x_{23}^{\prime } \le 30,$

$\quad ~~~~~~~~~~~~~2x_{11}+x_{21}-1.5x_{13}-2x_{23}+D_{11}^--D_{11}^+=1.5,$

$\quad ~~~~~~~~~~~~~1.4x_{12}+0.6x_{22}+D_{12}^--D_{12}^+=1.6,$

$\quad ~~~~~~~~~~~~~4x_{13}+5x_{23}-5x_{11}-10x_{21}+D_{13}^--D_{13}^+=5,$

$\quad ~~~~~~~~~~~~~x_{11}^{\prime }+x_{21}^{\prime }+D_{11}^{\prime -}-D_{11}^{\prime +}=0,$

$\quad ~~~~~~~~~~~~~5x_{13}^{\prime }+6x_{23}^{\prime }-10x_{21}^{\prime }+D_{13}^{\prime -}-D_{13}^{\prime +}=10,$

$\quad ~~~~~~~~~~~~~x_{11}+4x_{21}-1.5x_{13}-2x_{23}+D_{21}^--D_{21}^+=3,$

$\quad ~~~~~~~~~~~~~x_{12}+2x_{22}+D_{22}^--D_{22}^+=4,$

$\quad ~~~~~~~~~~~~~5x_{13}+6x_{23}-8x_{11}-16x_{21}+D_{23}^--D_{23}^+=16,$

$\quad ~~~~~~~~~~~~~x_{11}^{\prime }+3x_{21}^{\prime }+D_{21}^{\prime -}-D_{21}^{\prime +}=0,$

$\quad ~~~~~~~~~~~~~6x_{13}^{\prime }+6x_{23}^{\prime }-20x_{21}^{\prime }+D_{23}^{\prime -}-D_{23}^{\prime +}=40,$

$\quad ~~~~~~~~~~~~~D_{11}^--1.2x_{13}-1.6x_{23} \le 1.2,$

$\quad ~~~~~~~~~~~~~D_{12}^--0.4x_{12}-0.6x_{22} \le 0.4,$

$\quad ~~~~~~~~~~~~~D_{13}^--3x_{11}-6x_{21} \le 3,$

$\quad ~~~~~~~~~~~~~D_{11}^{\prime -}-2x_{13}^{\prime }-2.5x_{23}^{\prime } \le 2,$

$\quad ~~~~~~~~~~~~~D_{13}^{\prime -}-3x_{21}^{\prime } \le 3,$

$\quad ~~~~~~~~~~~~~D_{21}^--0.9x_{13}-1.2x_{23} \le 1.8,$

$\quad ~~~~~~~~~~~~~D_{22}^--0.4x_{12}-0.6x_{22} \le 0.8,$

$\quad ~~~~~~~~~~~~~D_{23}^--3x_{11}-6x_{21} \le 6,$

$\quad ~~~~~~~~~~~~~D_{21}^{\prime -}-4x_{13}^{\prime }-5x_{23}^{\prime } \le 8,$

$\quad ~~~~~~~~~~~~~D_{23}^{\prime -}-10x_{21}^{\prime } \le 20,$

$\quad ~~~~~~~~~~~~~x_{11}^{\prime } \ge 0,~x_{11}-x_{11}^{\prime } \ge 0,~x_{12}-x_{11} \ge 0,$

$\quad ~~~~~~~~~~~~~x_{13}-x_{12} \ge 0,~x_{13}^{\prime }-x_{13} \ge 0,$

$\quad ~~~~~~~~~~~~~x_{21}^{\prime } \ge 0,~x_{21}-x_{21}^{\prime } \ge 0,~x_{22}-x_{21} \ge 0,$

$\quad ~~~~~~~~~~~~~x_{23}-x_{22} \ge 0,~x_{23}^{\prime }-x_{23} \ge 0,$

$\quad ~~~~~~~~~~~~~D_{k1}^-,D_{k2}^-,D_{k3}^-,D_{k1}^{\prime -},D_{k3}^{\prime -} \ge 0,~~k=1,2.$

Table 4 Comparison of the problem (S1) with existing method

Fig. 10

Comparison of objective function values

For $w_1=w_2=0.5$, the optimal solution of the problem (S2) (using “LINGO-17.0”) is as follows:

$$\begin{aligned} D_{11}^-=8.81,D_{12}^-=D_{13}^-=D_{11}^{\prime -}=D_{13}^{\prime -}=0, \\ D_{21}^-=7.51,D_{22}^-=0,D_{23}^-=7.23,D_{21}^{\prime -}=D_{23}^{\prime -}=0, \\ D_{11}^+=0,D_{12}^+=3.73,D_{13}^+=6.13,D_{11}^{\prime +}=0,D_{13}^{\prime +}=25, \\ D_{21}^+=0,D_{22}^+=1.56,D_{23}^+=D_{21}^{\prime +}=0,D_{23}^{\prime +}=0.66, \\ x_{11}=0.54,x_{12}=3.33,x_{13}=4.85,x_{11}^{\prime }=0,x_{13}^{\prime }=5.66, \\ x_{21}=x_{22}=x_{23}=x_{23}^{\prime }=1.12,x_{21}^{\prime }=0 \end{aligned}$$

with the optimal objective function value $Z=11.77$. Hence, the efficient solution to the problem (S1) is given by

$$\begin{aligned} {\tilde{x}}_1=(0.54,3.33,4.85;0,3.33,5.66)~~\text{ and } \\ {\tilde{x}}_2=(1.12,1.12,1.12;0,1.12,1.12) \end{aligned}$$

giving the objective function values as

$$\begin{aligned} {\tilde{Z}}_1=(0.1,1.11,6.61;0,1.11,35.02)~~\text{ and } \\ {\tilde{Z}}_2=(0.2,1.11,6.48;0,1.11,20.34). \end{aligned}$$

On defuzzifying the obtained IF solution by using the accuracy function (Definition 5), the total number of ELCs to be installed in cities A and B are approximately 3 and 1, respectively. This practical application is modified from the real case given in Arya et al. [23] considering the variables and parameters as IFNs and hence leads to a more significant and generalized modelling. Since there exists no technique to solve the fully IF-MO-LFP problems, therefore, we have compared the obtained solutions with the existing methods for fully fuzzy MOLFP problems. The problem (S1) is solved using the weighted sum approach given by Arya et al. [23] and also solved by employing the proposed solution technique. The defuzzified values of the objective function values obtained by the proposed approach and Arya et al. [23] are tabulated in Table 4. Further, the bar graph (Fig. 10) shows the comparison between the defuzzified values of the objective functions ${\tilde{Z}}_1$ and ${\tilde{Z}}_2$ obtained by the proposed methodology and Arya et al. [23].

Table 4 and Fig. 10 show that the values of both the objectives given by the proposed algorithm are much greater than the corresponding values obtained by Arya et al. [23]. Therefore, our methodology yields better results since the original problem (S1) is a maximization-type optimization problem. This comparison establishes the efficacy and relevancy of the proposed study.

Additionally, several other realistic optimization problems exist in the literature such as sustainable municipal solid waste management problem [2], production planning problem of a company [20], integrated production-transportation problem in a supply chain management of a company [26], the land-use problem of a country [39], and many more which can be constructed in a similar manner under the IF environment and thereby, a parallel efficient solution technique can be formulated using the presented fuzzy-based goal programming approach.

8 Conclusion

LFP problems are a special kind of non-linear optimization problem that aims to optimize the fraction of linear quantities subject to some linear constraints. Furthermore, when a practical situation requires optimizing more than one but conflicting objectives, then the methodologies to solve a MO-LFP problem are invoked. Consequently, in this article, we have formulated a fully IF-MO-LFP problem and proposed an efficient approach to reach the Pareto-optimal solution of the problem. The proposed study provides a more realistic formulation of a fractional optimization problem by incorporating the hesitation and uncertainty in the modelling of the problem. The novelty of the proposed approach is that it unifies the three efficient techniques, namely goal programming, change of variables, and membership function strategy to solve a multi-objective optimization problem. To show the application of the study, a university E-education planning problem is framed in an intuitionistic fuzzy environment and solved using the developed methodology. Moreover, a comparison is carried out between the proposed algorithm and the method given by Arya et al. [23] which proves that the proposed methodology yield better results than the existing studies to solve the MO-LFP problems. Although, the proposed IF-MO-LFP problem is able to solve a number of fractional optimization problems but when the objective function involves the non-linear functions in fractions, then the LFP problem-based solution techniques fail to find an optimal solution. Therefore, in the future, the proposed solution technique can be extended to solve quadratic fractional programming problems, fractional transportation problems using the LR-type IFNs, and non-linear fractional programming problems under the IF environment.