Mixed $H_2/H_\infty$ Fault-Tolerant Sampled-Data Fuzzy Control for Nonlinear Parabolic PDE Systems Under Deception Attacks

Abstract

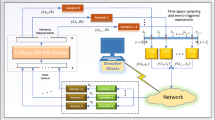
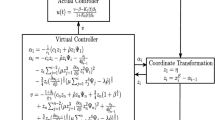
This paper addresses mixed $H_2/H_\infty$ fault-tolerant sampled-data (SD) fuzzy control for nonlinear space-varying parabolic partial differential equation (PDE) system under deception attacks. Firstly, a T–S fuzzy PDE model is given to exactly describe the nonlinear space-varying parabolic PDE system. Secondly, a fault-tolerant SD fuzzy controller via the spatial linear matrix inequalities (SLMIs) is developed based on a Lyapunov functional which is continuous at sampling times but not necessary to be positive definite in sampling intervals such that the closed-loop PDE system is exponentially stable with a mixed $H_2/H_\infty$ performance. Then, to solve the SLMIs, the fault-tolerant SD fuzzy control problem for space-varying parabolic PDE system is formulated as linear matrix inequality feasibility problem. Furthermore, the design condition of the suboptimal mixed $H_2/H_\infty$ fault-tolerant SD controller subject to deception attacks can be derived by considering the property of membership functions. Lastly, two examples are given to illustrate the design method.

Appendices

Appendix A

Proof of Theorem 1

Considering the Lyapunov functional (18), one has

$$\begin{aligned} {\dot{V}}_1(t)\,=\, & {} 2\int _\Omega z^{\mathrm{T}}(x,t)P_1z_t(x,t){\text d}x \end{aligned}$$

(A1)

$$\begin{aligned} {\dot{V}}_2(t)\,=\, & {} 2\int _\Omega z_x^{\mathrm{T}}(x,t)P_2\Upsilon (x) z_{xt}(x,t){\text d}x \end{aligned}$$

(A2)

$$\begin{aligned} {\dot{V}}_3(t)\,=\, & {} 2\psi (t)\int _\Omega {\tilde{z}}^{\mathrm{T}}(x,t)X_1 z_t(x,t){\text d}x\nonumber \\&+2\psi (t)\int _\Omega (z(x,t)-{\tilde{z}}(x,t))^{\mathrm{T}}X_2{\tilde{z}}_t(x,t){\text d}x\nonumber \\&-\int _\Omega {\tilde{z}}^{\mathrm{T}}(x,t)X_1{\tilde{z}}(x,t){\text d}x\nonumber \\&-2\int _\Omega (z(x,t)-{\tilde{z}}(x,t))^{\mathrm{T}}X_2{\tilde{z}}(x,t){\text d}x \end{aligned}$$

(A3)

$$\begin{aligned} {\dot{V}}_4(t)\,=\, & {} -2\delta V_4(t)+\psi (t)\int _\Omega \zeta ^{\mathrm{T}}(x,t)Q\zeta (x,t){\text d}x \nonumber \\&-\int _\Omega \int _{t_k}^{t} \text {e}^{2\delta (\varsigma -t)}\zeta ^{\mathrm{T}}(x,\varsigma )Q\zeta (x,\varsigma )d\varsigma {d}x.~~~~~~~~ \end{aligned}$$

(A4)

Let $\xi (x,t)=[z^{\mathrm{T}}(x,t)\ z^{\mathrm{T}}(x,t_k)\ z_t^{\mathrm{T}}(x,t)~ z_x^{\mathrm{T}}(x,t)]^{\mathrm{T}}$. For any matrices ${\mathcal M}_{ij}\in {\mathbb {R}}^{4n_z\times n_z}$, due to ${\tilde{z}}(x,t)=z(x,t)-z(x,t_k)=\int _{t_k}^{t}z_\varsigma (x,\varsigma )d\varsigma$, we have

$$\begin{aligned} 0\,=\, & {} 2\int _\Omega \sum _{i=1}^r\sum _{j=1}^r \sigma _i(\varrho (x,t))\sigma _j(\varrho (x,t_k)) \xi ^{\mathrm{T}}(x,t){\mathcal M}_{ij}\nonumber \\&~~~~~~~~~\times [{\tilde{z}}(x,t)-\int _{t_k}^{t}z_\varsigma (x,\varsigma )d\varsigma ]{\text d}x. \end{aligned}$$

(A5)

Then, we can derive from the system (19)

$$\begin{aligned} 0=&\;2\int _\Omega \xi ^{\mathrm{T}}(x,t){\mathcal P}\left[ \{\Upsilon (x) z_{x}(x,t)\}_x \right. \nonumber \\&\left. \;+\sum _{i=1}^r\sum _{j=1}^r \sigma _i(\varrho (x,t))\sigma _j(\varrho (x,t_k))(A_i(x)z(x,t) \right. \nonumber \\&\left. \;+G_{1i}(x){\mathcal F}K_jz(x,t_k)-z_t(x,t)\right] {\text d}x\nonumber \\ =&\;2\int _\Omega \xi ^{\mathrm{T}}(x,t){\mathcal P}\{\Upsilon (x) z_{x}(x,t)\}_x {\text d}x\nonumber \\&\;+\int _\Omega \sum _{i=1}^r\sum _{j=1}^r \sigma _i(\varrho (x,t))\sigma _j(\varrho (x,t_k))\nonumber \\&\;\times [\xi ^{\mathrm{T}}(x,t)({\mathcal P}{\mathcal A}_{ij}(x)+{\mathcal A}_{ij}^{\mathrm{T}}(x){\mathcal P}^{\mathrm{T}})\xi (x,t)]. \end{aligned}$$

(A6)

Considering $P_2\Upsilon (x)=\Upsilon (x)P_2^{\mathrm{T}}>0$, we integrate (A6) by parts such that the equalities are obtained as follows:

$$\begin{aligned}&2\int _\Omega \xi ^{\mathrm{T}}(x,t){\mathcal P}\{\Upsilon (x) z_{x}(x,t)\}_{x} {\text d}x\nonumber \\\,=\, & {} -2\int _\Omega \xi _x^{\mathrm{T}}(x,t){\mathcal P}\Upsilon (x) z_{x}(x,t){\text d}x\nonumber \\\,=\, & {} -2\int _\Omega z_x^{\mathrm{T}}(x,t){\mathcal P}_1\Upsilon (x) z_x(x,t){\text d}x \nonumber \\&-2\int _\Omega z_{tx}^{\mathrm{T}}(x,t)P_2\Upsilon (x) z_{x}(x,t){\text d}x\nonumber \\\,=\, & {} -\int _\Omega z_x^{\mathrm{T}}(x,t)\{{\mathcal P}_1 \Upsilon (x)+\Upsilon (x){\mathcal P}_1^{\mathrm{T}}\} z_x(x,t){\text d}x\nonumber \\&-2\int _\Omega z_{xt}^{\mathrm{T}}(x,t)P_2\Upsilon (x) z_{x}(x,t){\text d}x\nonumber \\\,=\, & {} -\int _\Omega z_x^{\mathrm{T}}(x,t)\{{\mathcal P}_1\Upsilon (x)+\Upsilon (x){\mathcal P}_1^{\mathrm{T}}\} z_x(x,t){\text d}x \nonumber \\&-2\int _\Omega z_{x}^{\mathrm{T}}(x,t)P_2\Upsilon (x) z_{xt}(x,t){\text d}x \end{aligned}$$

(A7)

According to (A1)–(A7), one can derive

$$\begin{aligned}&{\dot{V}}(t)+2\delta V(t)\nonumber \\\leqslant & {} \int _\Omega \sum _{i=1}^r\sum _{j=1}^r \sigma _i(\varrho (x,t))\sigma _j(\varrho (x,t_k))\nonumber \\&\times \left\{ \xi ^{\mathrm{T}}(x,t)[\Xi _{1ij}(x)+\psi (t)\Xi _{2,1}]\xi (x,t) \right. \nonumber \\&\left. -\int _{t_k}^{t} \left[ \begin{array}{cc}\xi (x,t) \\ z_\varsigma (x,\varsigma )\end{array}\right] ^{\mathrm{T}} \Xi _{3ij} \left[ \begin{array}{cc}\xi (x,t) \\ z_\varsigma (x,\varsigma )\end{array}\right] d\varsigma \right\} {\text d}x \nonumber \\\,=\,&{}\int _\Omega \sum _{i=1}^r\sum _{j=1}^r \sigma _i(\varrho (x,t))\sigma _j(\varrho (x,t_k)) \nonumber \\&\times \{\frac{1}{h_k}\int _{t_k}^{t} \left[ \begin{array}{cc}\xi (x,t) \\ z_\varsigma (x,\varsigma )\end{array}\right] ^{\mathrm{T}} \Theta _{2ij}(x,h_k) \left[ \begin{array}{cc}\xi (x,t) \\ z_\varsigma (x,\varsigma )\end{array}\right] d\varsigma \nonumber \\&+\frac{\psi (t)}{h_k}\xi ^{\mathrm{T}}(x,t)\Theta _{1ij}(x,h_k)\xi (x,t)\}{\text d}x. \end{aligned}$$

(A8)

Then, from (20), we can have ${\dot{V}}(t)\le 2\delta V(t)$, $t\in [t_k,t_{k+1})$.

Considering $V(t_k)=V_1(t_k)+V_2(t_k)$, we obtain

$$\begin{aligned} V(0)\le & {} \lambda _{\max }(P_1) \Vert z(\cdot ,t_0)\Vert ^2_2\nonumber \\&+\lambda _{\max }(P_2\Upsilon (x)) \Vert z_x(\cdot ,t_0)\Vert ^2_2\nonumber \\\le & {} \kappa \{\Vert z(\cdot ,t_0)\Vert ^2_2+\Vert z_x(\cdot ,t_0)\Vert ^2_2\} \end{aligned},$$

(A9)

where $\kappa >0$ is a scalar. Moreover, one has

$$\begin{aligned} \Vert z(\cdot ,t_k)\Vert ^2_2\le & {} \frac{1}{\lambda _1}e^{-2\delta (t_k-t_0)}V(0)\nonumber \\\le & {} \frac{\kappa }{\lambda _1}\left\{ \Vert z(\cdot ,t_0)\Vert ^2_2 +\Vert z_x(\cdot ,t_0)\Vert ^2_2\right\} e^{-2\delta (t_k-t_0)} \end{aligned}$$

(A10)

in which $\lambda _1=\lambda _{\min }(P_1)$. For any given $t>t_{0}$, there exists a $k_0\in {\mathbb {N}}$ such that $t\in [t_{k_{0}},t_{k_{0+1}})$. According to Lemma 1, the following inequality is derived

$$\begin{aligned} \Vert z(\cdot ,t)\Vert ^{2}_{2}\le & {} d_{0} \Vert z(\cdot ,t_{k_0})\Vert ^2_{2}\nonumber \\\le & {} \frac{\kappa }{\lambda _{1}}e^{2\delta h}\left\{ \Vert z(\cdot ,t_0)\Vert ^2_{2} +\Vert z_x(\cdot ,t_0)\Vert ^2_2\right\} e^{-2\delta (t-t_0)}. \end{aligned}$$

(A11)

Hence, the SD fuzzy system (10) is exponentially stable. $\square$

Appendix B

Proof of Theorem 2

Along the trajectory (10), one derives

$$\begin{aligned} 0=&\;2\int _\Omega \xi ^{\mathrm{T}}(x,t){\mathcal P}\left[ \{\Upsilon (x) z_{x}(x,t)\}_x \right. \nonumber \\&\left. \;+\sum _{i=1}^r\sum _{j=1}^r \sigma _i(\varrho (x,t))\sigma _j(\varrho (x,t_k)) \right. \nonumber \\&\left. \;~\times (A_i(x)z(x,t)+G_{1i}(x)\left( {\mathcal F}K_jz(x,t_k)\right. \right. \nonumber \\&\left. \left. \;~~~~~~~~~~~+\nu (x,t_k)\right) +G_{2i}(x)w(x,t))-z_t(x,t)\right] {\text d}x \nonumber \\ =&\;2\int _\Omega \xi ^{\mathrm{T}}(x,t){\mathcal P}\{\Upsilon (x) z_{x}(x,t)\}_x {\text d}x\nonumber \\&\;+\int _\Omega \sum _{i=1}^r\sum _{j=1}^r \sigma _i(\varrho (x,t))\sigma _j(\varrho (x,t_k))[\xi ^{\mathrm{T}}(x,t)\nonumber \\&\;\times ({\mathcal P}{\mathcal A}_{ij}(x)+{\mathcal A}_{ij}^{\mathrm{T}}(x){\mathcal P}^{\mathrm{T}})\xi (x,t)+2\xi ^{\mathrm{T}}(x,t){\mathcal P}\nonumber \\&\;\times (G_{1i}(x)\nu (x,t_k)+G_{2i}(x)w(x,t))]{\text d}x. \end{aligned}$$

(B1)

Next, according to (8), we have

$$\begin{aligned}&\int _\Omega z^{\mathrm{T}}(x,t_k)H^{\mathrm{T}}Hz(x,t_k){\text d}x\nonumber \\&~~-\int _\Omega \nu ^{\mathrm{T}}(x,t_k)\nu (x,t_k){\text d}x\ge 0. \end{aligned}$$

(B2)

Moreover, one obtains

$$\begin{aligned} ~~\sum _{i=1}^r\sum _{j=1}^r\sigma _i(\varrho (x,t_k))\sigma _j(\varrho (x,t_k))z^{\mathrm{T}}(x,t_k)K_j^{\mathrm{T}}\bar{{\mathcal F}}K_jz(x,t_k)\nonumber \\ \le \frac{1}{2}\sum _{i=1}^r\sum _{j=1}^r\sigma _i(\varrho (x,t_k))\sigma _j(\varrho (x,t_k))z^{\mathrm{T}}(x,t_k)~~~~~~~~\nonumber \\ \times (K_i^{\mathrm{T}}\bar{{\mathcal F}}K_iz(x,t_k)+K_j^{\mathrm{T}}\bar{{\mathcal F}}K_jz(x,t_k))z(x,t_k)~~~~~\nonumber \\ =\sum _{j=1}^r\sigma _j(\varrho (x,t_k))z^{\mathrm{T}}(x,t_k)K_j^{\mathrm{T}}\bar{{\mathcal F}}K_jz(x,t_k)~~~~~~~~~~ \end{aligned}$$

in which $\bar{{\mathcal F}}={\mathcal F}^{\mathrm{T}}{\mathcal F}$.

Then, the $H_\infty$ performance and $H_2$ performance of nonlinear space-varying parabolic PDE systems are analyzed. Firstly, the $H_2$ performance analysis is presented.

(1) $H_2$ performance analysis:

By using (A1)–(A5), (A7), (B1) with $w(x,t)=0$, and (B2), we obtain

$$\begin{aligned}&{\dot{V}}(t)+2\delta V(t)+\Vert C_{m} z(\cdot ,t)\Vert _2^2+\Vert D_{m} u^f(\cdot ,t)\Vert _2^2\nonumber \\\le & {} \int _\Omega \sum _{i=1}^r\sum _{j=1}^r \sigma _i(\varrho (x,t))\sigma _j(\varrho (x,t_k)) \nonumber \\&\times \{\frac{1}{h_k}\int _{t_k}^{t} \left[ \begin{array}{cc}{\tilde{\xi }}(x,t) \\ z_\varsigma (x,\varsigma )\end{array}\right] ^{\mathrm{T}} {\mathcal T}_{2ij}(x,h_k) \left[ \begin{array}{cc}{\tilde{\xi }}(x,t) \\ z_\varsigma (x,\varsigma )\end{array}\right] d\varsigma \nonumber \\&~~~~~~~~~~~+\frac{\psi (t)}{h_k}{\tilde{\xi }}^{\mathrm{T}}(x,t){\mathcal T}_{1ij}(x,h_k){\tilde{\xi }}(x,t)\}{\text d}x \end{aligned},$$

(B3)

where

$$\begin{aligned} {\tilde{\xi }}(x,t)\,=\, & {} [\xi ^{\mathrm{T}}(x,t) ~ \nu ^{\mathrm{T}}(x,t_k)]^{\mathrm{T}}. \end{aligned}$$

It follows from (21) that

$$\begin{aligned} {\mathcal T}_{\iota ij}(x,h)<0 \end{aligned}$$

(B4)

and

$$\begin{aligned} {\mathcal T}_{\iota ij}(x,\epsilon )<0. \end{aligned}$$

(B5)

Then, according to (B4) and (B5), we get

$$\begin{aligned} {\mathcal T}_{\iota ij}(x,h_k)=\frac{h_k-\epsilon }{h-\epsilon }{\mathcal T}_{\iota ij}(x,h) +\frac{h-h_k}{h-\epsilon }{\mathcal T}_{\iota ij}(x,\epsilon )<0. \end{aligned}$$

Therefore, we have the following inequalities:

$$\begin{aligned}&\sum _{i=1}^r\sum _{j=1}^r\sigma _i(\varrho (x,t))\sigma _j(\varrho (x,t_k)){\mathcal T}_{\iota ij}(x,h_k)<0~ \end{aligned},$$

(B6)

where $\iota =1,2$. Next, by (B6), one can have

$$\begin{aligned} {\dot{V}}(t)+2\delta V(t)+\Vert C_{m} z(\cdot ,t)\Vert _2^2+\Vert D_{m} u^f(\cdot ,t)\Vert _2^2\le 0. \end{aligned}$$

(B7)

Integration of inequality (B7) from $t=0$ to $t=t_f$ gives

$$\begin{aligned}&J=\int _0^{t_f}[\Vert C_m z(\cdot ,t)\Vert ^2_2+\Vert D_m u^f(\cdot ,t)\Vert ^2_2]{\text d}t\nonumber \\&~~~~~~~\le V(0)-V(t_f). \end{aligned}$$

(B8)

Then, the following inequality is deduced:

$$\begin{aligned}&J\le V(0)=\int _\Omega z_0^{\mathrm{T}}(x)P_1z_0(x){\text d}x\nonumber \\&~~~~~~~~~~~~~+\int _\Omega (\frac{\partial z_0(x)}{\partial x})^{\mathrm{T}} P_2\Upsilon (x) \frac{\partial z_0(x)}{\partial x}{\text d}x. \end{aligned}$$

(B9)

Next, the $H_2$ performance (22) is obtained from (B9).

(2) $H_\infty$ performance analysis:

By using (A1)–(A5), (A7), (B1), and (B2), one can derive

$$\begin{aligned}&{\dot{V}}(t)+2\delta V(t)+\Vert y(\cdot ,t)\Vert _2^2-\gamma ^2\Vert w(\cdot ,t)\Vert _2^2\nonumber \\\le & {} \int _\Omega \sum _{i=1}^r\sum _{j=1}^r \sigma _i(\varrho (x,t))\sigma _j(\varrho (x,t_k)) \nonumber \\&\times \{\frac{1}{h_k}\int _{t_k}^{t} \left[ \begin{array}{cc}{\hat{\xi }}(x,t) \\ z_\varsigma (x,\varsigma )\end{array}\right] ^{\mathrm{T}} {\mathcal T}_{4ij}(x,h_k) \left[ \begin{array}{cc}{\hat{\xi }}(x,t) \\ z_\varsigma (x,\varsigma )\end{array}\right] d\varsigma \nonumber \\&~~~~~~~~~~~+\frac{\psi (t)}{h_k}{\hat{\xi }}^{\mathrm{T}}(x,t){\mathcal T}_{3ij}(x,h_k){\hat{\xi }}(x,t)\}{\text d}x \end{aligned},$$

(B10)

where

$$\begin{aligned} {\hat{\xi }}(x,t)\,=\, & {} [{\tilde{\xi }}^{\mathrm{T}}(x,t) ~w^{\mathrm{T}}(x,t)]^{\mathrm{T}}. \end{aligned}$$

It follows from (21) that

$$\begin{aligned}&\sum _{i=1}^r\sum _{j=1}^r\sigma _i(\varrho (x,t))\sigma _j(\varrho (x,t_k)){\mathcal T}_{\iota ij}(x,h_k)<0 ~~ \end{aligned},$$

(B11)

where $\iota =3,4$. It is obvious that the inequality is ensured by (B11) as follows:

$$\begin{aligned} {\dot{V}}(t)+2\delta V(t)+\Vert y(\cdot ,t)\Vert _2^2-\gamma ^2\Vert w(\cdot ,t)\Vert _2^2\le 0. \end{aligned}$$

(B12)

Under the zero condition, integration the above inequality from $t=0$ to $t=t_f$ yields

$$\begin{aligned}&\int _0^{t_f}\Vert y(\cdot ,t)\Vert _2^2{\text d}t \le V(0)-V(t_f)\nonumber \\&~~~~~~~~~~~~~~~~~~~~~+\gamma ^2\int _0^{t_f} \Vert w(\cdot ,t)\Vert _2^2{\text d}t. \end{aligned}$$

(B13)

Then, the $H_\infty$ performance (11) holds. $\square$

Appendix C

Proof of Theorem 3

Denote

$$\begin{aligned} W\triangleq & {} {\bar{W}}^{-1}\\ {\bar{P}}_1\triangleq & {} {\bar{W}}^{\mathrm{T}}P_1{\bar{W}},~{\bar{X}}\triangleq {\bar{W}}^{\mathrm{T}}X{\bar{W}}\\ \Lambda _1\triangleq & {} \text {diag} \{{\bar{W}}^{\mathrm{T}}, {\bar{W}}^{\mathrm{T}}, {\bar{W}}^{\mathrm{T}},{\bar{W}}^{\mathrm{T}},I_{n_z},I_{n_z},I_{n_z}\}\\ \Lambda _2\triangleq & {} \text {diag} \{{\bar{W}}^{\mathrm{T}},{\bar{W}}^{\mathrm{T}}, {\bar{W}}^{\mathrm{T}}, {\bar{W}}^{\mathrm{T}},I_{n_z}, {\bar{W}}^{\mathrm{T}},I_{n_z},I_{n_z}\}\\ \Lambda _3\triangleq & {} \text {diag} \{{\bar{W}}^{\mathrm{T}}, {\bar{W}}^{\mathrm{T}}, {\bar{W}}^{\mathrm{T}},{\bar{W}}^{\mathrm{T}},I_{n_z},I_{n_w},I_{n_z},I_{n_z}\}\\ \Lambda _4\triangleq & {} \text {diag} \{{\bar{W}}^{\mathrm{T}},{\bar{W}}^{\mathrm{T}}, {\bar{W}}^{\mathrm{T}}, {\bar{W}}^{\mathrm{T}},I_{n_z},I_{n_w},{\bar{W}}^{\mathrm{T}},I_{n_z},I_{n_z}\}\\ {\bar{Q}}\triangleq & {} \left[ \begin{array}{cc}{\bar{Q}}_{11} &{} {\bar{Q}}_{12} \\ {*} &{}{\bar{Q}}_{22} \end{array}\right] = \left[ \begin{array}{cc}{\bar{W}}^{\mathrm{T}} &{} 0 \\ {*} &{}{\bar{W}}^{\mathrm{T}} \end{array}\right] Q \left[ \begin{array}{cc}{\bar{W}} &{} 0 \\ {*} &{}{\bar{W}} \end{array}\right] \nonumber \\ {\mathcal P}\triangleq & {} \text {diag}\{ W^{\mathrm{T}},\ W^{\mathrm{T}}, \ W^{\mathrm{T}}, \ W^{\mathrm{T}}\}{\mathcal L}\\ {\mathcal L}\triangleq & {} \left[ r_{1}I_{n_z}\ 0_{n_z}\ r_{2}I_{n_z} \ 0_{n_z} \right] ^{\mathrm{T}} \\ \bar{{\mathcal M}}_{ij}\triangleq & {} \text {diag} \{{\bar{W}}^{\mathrm{T}},\ {\bar{W}}^{\mathrm{T}},\ {\bar{W}}^{\mathrm{T}},{\bar{W}}^{\mathrm{T}}\}{\mathcal M}_{ij}{\bar{W}}. \end{aligned}$$

We multiply the left side of SLMIs (20) with $\Lambda _{\iota }$, and multiply the right side of SLMIs (20) with $\Lambda _{\iota }^{\mathrm{T}}$. The proof is complete. $\square$

Appendix D

Proof of Theorem 4

The space-dependent terms are represented by the following form to solve the SLMIs:

$$\begin{aligned} \Upsilon (x)\,=\, & {} \sum _{s=1}^{2^\chi }\omega _s(x)\Upsilon _s,x\in \Omega \nonumber \\ A_i(x)\,=\, & {} \sum _{q=1}^{2^{{\bar{\chi }}}}{\bar{\omega }}_{q}(x)A_{i,q},x\in \Omega \nonumber \\ G_{1i}(x)\,=\, & {} \sum _{v=1}^{2^{{\tilde{\chi }}}}{\tilde{\omega }}_{v}(x)G_{1i,v},x\in \Omega \nonumber \\ G_{2i}(x)\,=\, & {} \sum _{g=1}^{2^{\breve{\chi }}}\breve{\omega }_{g}(x)G_{2i,g},x\in \Omega \end{aligned},$$

(D1)

where $\omega _s(x)$ are deduced via a combination of $\varsigma _{d\varpi }(x)$ in $\Upsilon (x)$ with

$$\begin{aligned} \varsigma _{d1}(x)\,=\, & {} \frac{\gamma (x)-\min \limits _{x\in \Omega }\{\gamma (x)\}}{\max \limits _{x\in \Omega }\{\gamma (x)\}-\min \limits _{x\in \Omega }\{\gamma (x)\}},\\ \varsigma _{d2}(x)\,=\, & {} 1-\varsigma _{d1}(x), \end{aligned}$$

$d\in \{1,2,\ldots ,\chi \}, \varpi =1,2$, $\chi \leqslant n_z^2$ is the number of space-dependent elements of $\Upsilon (x)$. The remaining space-dependent terms are represented in a similar way according to (D1), where ${\bar{\chi }}\leqslant n_z^2$, ${\tilde{\chi }}\leqslant n_zn_u$ , and $\breve{\chi }\leqslant n_zn_w$.

In addition, one obtains

$$\begin{aligned}&\sum \limits _{s=1}^{2^\chi } \omega _s(x) = 1, \omega _s(x) \geqslant 0, s \in {\mathcal U}_1\triangleq \{1,2,\ldots ,2^\chi \},\\&\sum \limits _{q=1}^{2^{{\bar{\chi }}}} {\bar{\omega }}_{q}(x) = 1, {\bar{\omega }}_{q}(x) \geqslant 0,q \in {\mathcal U}_2\triangleq \{1,2,\ldots ,2^{{\bar{\chi }}}\},\\&\sum \limits _{v=1}^{2^{{\tilde{\chi }}}} {\tilde{\omega }}_{v}(x) = 1, {\tilde{\omega }}_{v}(x) \geqslant 0,v \in {\mathcal U}_3\triangleq \{1,2,\ldots ,2^{{\tilde{\chi }}}\},\\&\sum \limits _{g=1}^{2^{\breve{\chi }}} \breve{\omega }_{g}(x) = 1, \breve{\omega }_{g}(x) \geqslant 0,g \in {\mathcal U}_4\triangleq \{1,2,\ldots ,2^{\breve{\chi }}\}. \end{aligned}$$

On the basis of the above analysis, SLMIs (23) can be transformed into LMIs. The proof is complete. $\square$

Appendix E

Proof of Theorem 5

Denote $\vartheta _j(\varrho (x,t))\triangleq \sigma _j(\varrho (x,t_k))-\sigma _j(\varrho (x,t)), t\in [t_k,t_{k+1})$. Note that

$$\begin{aligned}&\sum _{i=1}^r\sum _{j=1}^r\sigma _i(\varrho (x,t))\sigma _j(\varrho (x,t_k))\hat{{\mathcal T}}_{\iota ij}(h_k)\nonumber \\\,=\, & {} \sum _{i=1}^r\sum _{j=1}^r\sigma _i(\varrho (x,t))\{\sigma _j(\varrho (x,t))\hat{{\mathcal T}}_{\iota ij}(h_k)\nonumber \\&+ \vartheta _j(\varrho (x,t))\hat{{\mathcal T}}_{\iota ij}(h_k)\}\nonumber \\\,=\, & {} \sum _{i=1}^r\sum _{j=1}^r\sigma _i(\varrho (x,t))\sigma _j(\varrho (x,t))\hat{{\mathcal T}}_{\iota ij}(h_k)\nonumber \\&+\sum _{i=1}^r\sum _{p=1}^r\sigma _i(\varrho (x,t))\vartheta _p(\varrho (x,t))\hat{{\mathcal T}}_{\iota ip}(h_k)\nonumber \\\,=\, & {} \sum _{i=1}^r\sum _{j=1}^r\sigma _i(\varrho (x,t))\sigma _j(\varrho (x,t))\{\hat{{\mathcal T}}_{\iota ij}(h_k)\nonumber \\&+\sum _{p=1}^r\vartheta _p(\varrho (x,t))\hat{{\mathcal T}}_{\iota ip}(h_k)\}\nonumber \\\,=\, & {} \sum _{i=1}^r \sum _{j=1}^r\sigma _i(\varrho (x,t))\sigma _j(\varrho (x,t))\{\hat{{\mathcal T}}_{\iota ij}(h_k)\nonumber \\&+\sum _{p=1}^r\vartheta _p(\varrho (x,t))\frac{\hat{{\mathcal T}}_{\iota ip}(h_k)+\hat{{\mathcal T}}_{\iota jp}(h_k)}{2}\} \end{aligned}$$

(E1)

and from $\sum _{p=1}^r\vartheta _p(\varrho (x,t))=0$, it is known

$$\begin{aligned}&\sum _{p=1}^r\vartheta _p(\varrho (x,t))\hat{{\mathcal T}}_{\iota ip}(h_k)\nonumber \\&=\sum _{p=1}^r\vartheta _p(\varrho (x,t))\Omega _{\iota ip}(h_k)\nonumber \\&=\sum _{p=1}^{r-1}\vartheta _p(\varrho (x,t))\{\Omega _{\iota ip}(h_k)-\Omega _{\iota ir}(h_k)\} \end{aligned}$$

(E2)

where

$$\begin{aligned} \Omega _{1ip}(h_k)\,=\, & {} \left[ \begin{array}{cccc}\ \Omega _{1ip}^{11} &{}0&{}\Omega _{1ip}^{13}&{}0 \\ {*}&{}0&{}0&{}0\\ {*}&{}{*}&{}0&{}0\\ {*}&{}{*}&{}{*}&{}0\end{array}\right] \nonumber \\ \Omega _{2ip}(h_k)\,=\, & {} \left[ \begin{array}{cccccc}\Omega _{2ip}^{11} &{}0&{}-h_k{\mathcal M}_{ip}&{}~\Omega _{2ip}^{14}&{}0 \\ {*}&{}0&{}0&{}0&{}0\\ {*}&{}{*}&{}0&{}0&{}0\\ {*}&{}{*}&{}{*}&{}0&{}0\\ {*}&{}{*}&{}{*}&{}{*}&{}0\end{array}\right] \nonumber \\ \Omega _{3ip}(h_k)\,=\, & {} \left[ \begin{array}{ccccc}\ \Omega _{3ip}^{11} &{}0&{}0&{}\Omega _{3ip}^{14}&{}0 \\ {*}&{}0&{}0&{}0&{}0\\ {*}&{}{*}&{}0&{}0&{}0\\ {*}&{}{*}&{}{*}&{}0&{}0\\ {*}&{}{*}&{}{*}&{}{*}&{}0\end{array}\right] \nonumber \\ \Omega _{4ip}(h_k)\,=\, & {} \left[ \begin{array}{cccccc}\Omega _{4ip}^{11} &{}0&{}0&{}-h_k{\mathcal M}_{ip}&{}~\Omega _{4ip}^{15}&{}0 \\ {*}&{}0&{}0&{}0&{}0&{}0\\ {*}&{}{*}&{}0&{}0&{}0&{}0\\ {*}&{}{*}&{}{*}&{}0&{}0&{}0\\ {*}&{}{*}&{}{*}&{}{*}&{}0&{}0\\ {*}&{}{*}&{}{*}&{}{*}&{}{*}&{}0\end{array}\right] \nonumber \\ \Omega _{\iota ip}^{11}\,=\, & {} \bar{{\mathcal M}}_{ip}{\mathcal I}_5 +{\mathcal L}G_{1i,v}{\mathcal F}{\bar{K}}_p{\mathcal I}_2\nonumber \\&+{\mathcal I}_5^{\mathrm{T}}\bar{{\mathcal M}}_{ip}^{\mathrm{T}}+{\mathcal I}_2^{\mathrm{T}}{\bar{K}}_p^{\mathrm{T}}{\mathcal F}^{\mathrm{T}}G_{1i,v}^{\mathrm{T}}{\mathcal L}^{\mathrm{T}}\nonumber \\ \Omega _{1ip}^{13}\,=\, & {} \Omega _{2ip}^{14}=[D_m{\mathcal F}{\bar{K}}_p{\bar{W}}{\mathcal I}_2 ~0]^{\mathrm{T}}\nonumber \\ \Omega _{3ip}^{14}\,=\, & {} \Omega _{4ip}^{15}=[D{\mathcal F}{\bar{K}}_p{\bar{W}}{\mathcal I}_2 ~0]^{\mathrm{T}}. \end{aligned}$$

(E3)

Then, one derives

$$\begin{aligned}&\sum _{i=1}^r\sum _{j=1}^r\sigma _i(\varrho (x,t))\sigma _j(\varrho (x,t_k))\hat{{\mathcal T}}_{\iota ij}(h_k)\nonumber \\\,=\, & {} \sum _{i=1}^r\sum _{j=1}^r\sigma _i(\varrho (x,t))\sigma _j(\varrho (x,t))\{\hat{{\mathcal T}}_{\iota ij}(h_k)\nonumber \\&+\sum _{p=1}^{r-1}\vartheta _p(\varrho (x,t)){\tilde{\Omega }}_{\iota ijp}(h_k)\} \end{aligned}$$

(E4)

where ${\tilde{\Omega }}_{\iota ijp}(h_k)=\frac{\Omega _{\iota ip}(h_k)+\Omega _{\iota jp}(h_k)}{2}-\frac{\Omega _{\iota ir}(h_k)+\Omega _{\iota jr}(h_k)}{2}$.

Notice that $|\vartheta _p(\varrho (x,t))|\le \beta _p,~ p=1,2,...,r-1$, $|\sum _{p=1}^{r-1}$ $\vartheta _p(\varrho (x,t))|$ $=|\vartheta _r(\varrho (x,t))|\le \beta _r$. If the following inequalities hold:

$$\begin{aligned}&\sum _{i=1}^r\sum _{j=1}^r\sigma _i(\varrho (x,t))\sigma _j(\varrho (x,t))\{\hat{{\mathcal T}}_{\iota ij}(h_k)\nonumber \\&~~+\sum _{p=1}^{r-1}{\bar{\vartheta }}_p{\tilde{\Omega }}_{\iota ijp}(h_k)\}<0 \end{aligned}$$

(E5)

for any $({\bar{\vartheta }}_1,...,{\bar{\vartheta }}_{r-1}) \in {\mathcal U}\triangleq \{{\bar{\vartheta }}_1,...,{\bar{\vartheta }}_{r-1}|{\bar{\vartheta }}_p \in \{-\beta _p,\beta _p\}\}$. Hence, based on Lemma 2, the Theorem 5 can be derived. The proof is complete. $\square$