1 Introduction

Piezoelectric actuators are widely applied in many micro-positioning applications due to characters of small size, fast response, high stiffness, and large blocking force. However, one main nonlinearity: hysteresis, limits the control performance of the used piezoelectric actuators. Hysteresis is a lag property, and a variety of models as Jiles-Atherton model [1], Duhem model, simple Dahl model, Bouc–Wen model [2], Backlash-Like model, Maxwell model, etc. were proposed to encapsulate this special characteristic of piezoelectric actuators. In the past few years, Preisach model has been adopted for the studies of the system modeling of piezoelectric actuators popularly [3], but the magnetostrictive property let this model be not easily implemented and accurate enough. For precisely approaching the physical behavior of piezoelectric actuators, the intelligent modeling technology provides another solution [4]. Among them, Bouc–Wen model which is with a set of first-order nonlinear differential equations can properly and precisely present the hysteresis behavior of the controlled piezoelectric actuator, and this model provides the advantages of computational simplicity and practical similarity. Besides, a variety of control designs based on linear approximation models of piezoelectric actuators have been proposed, such as proportional-integral-derivative control designs [5], robust control design [6], sliding mode control designs [7, 8], linear model-based adaptive control design [9], and so on in the past two decades. Most of these published papers took linear models with or without hysteresis into account when designing the corresponding controllers, and the linear properties of models and controllers limited their good control performances only in some specific cases. Wear and tear to piezoelectric actuators naturally appear in sliding mode control designs due to the inevitable chattering effect [7, 8]. These linear control designs possess the advantages of an easy to implement control structure and a low calculation consumption. Recently, nonlinear control designs for piezoelectric actuators were proposed [9, 10]. [10] delivered a neural network-based control design which requires a huge convergence time for adjusting weights of the backpropagation neural network, and convergence of the displacement tracking error cannot be guaranteed and proven mathematically. A nonlinear robust fuzzy eliminator with two approximators for learning the disturbed piezoelectric actuator model and eliminating hysteresis is investigated in [9]. In this investigation, positioning performance can be guaranteed and the controlled piezoelectric actuator has an μm positioning accuracy. However, control structure of this fuzzy-based control design is too complex and needs the help of a high performance calculator. Most of these control designs work well when system parameters do not vary within all the control periods. However, parameters of piezoelectric actuators change during executing given missions; hence control performances of the above-mentioned nonlinear control laws are inevitably degraded due to the hysteresis effect and modeling uncertainties. Simultaneously, mitigating the effects of external disturbances is an important task for designs of the nonlinear control laws of piezoelectric actuators as well. For resolving these depicted reasons, a fuzzy-based control law that combines concepts of the Takagi and Sugeno modeling [11] and the robust fuzzy control design is proposed. In this investigation, the nonlinear dynamics of the controlled piezoelectric actuator are firstly approximated by employing the Takagi and Sugeno (TS) fuzzy model. Then, a robust fuzzy-based control law is developed based on this fuzzy model for reducing the trajectory tracking error as small as possible with respect to all bounded desired trajectories. In this study, for simplifying the control structure of this proposed fuzzy-based control method, the trajectory tracking problem of the controlled piezoelectric actuator is transformed into a linear matrix inequality problem (LMIP) which can be solved optimally via using the convex optimization technique of Matlab software [12]. The advantages of this proposed fuzzy-based control method are: a simple and easy to implement fuzzy controller can be obtained, and the robust trajectory tracking performance can be also guaranteed. For verifying the trajectory tracking performance of this proposed fuzzy-based control method, two simulation scenarios are given. This paper is organized as the following: the micrometer level trajectory tracking design problem of piezoelectric actuators is formulated in Sect. 2. The robust fuzzy-based control law is developed in Sect. 3. In Sect. 4, the simulation results of the proposed method with respect to two scenarios are executed. Finally, conclusions are made [13].

2 Problem Formulation

2.1 Hysteresis Behavior of Piezoelectric Actuator

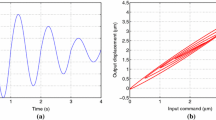
Hysteresis phenomena is a memory-like effect, and this causes an extremely nonlinear relationship between input and output. Therefore, for a certain input, no exclusive output can be obtained. Instead, the output relies on the input history. Piezoelectric actuators naturally possess a hysteresis behavior as shown in Fig. 1 [13]. As mentioned above, the relationship between the control input voltage and output displacement of a controlled piezoelectric actuator is highly nonlinear. This hysteresis behavior will cause an oscillation for the controlled piezoelectric actuator and further results in a 10–15% tracking error.

Fig. 1
figure 1

Hysteresis loop of the piezoelectric actuator

Full size image

2.2 Schematic and Mathematical Model of the Controlled Piezoelectric Actuator

For driving the controlled piezoelectric actuator, two electrodes are installed on the top of A and B surfaces of the piezoelectric element. The deformation of the piezoelectric element can be controlled by applying different input voltages to two electrodes. Based on this property and integrating a fastener to the piezoelectric element, a positioner with the micrometer positioning ability and a higher momentum can be obtained. Figure 2a illustrates the schematic structure of the proposed piezoelectric actuator, and the equivalent model which integrates a linear mass-spring-damping model and a nonlinear model for the controllable piezoelectric element is adopted to present the piezoelectric actuator as Fig. 2a.

Fig. 2
figure 2

a The schematic of the controlled piezoelectric actuator, and b the equivalent model of the controlled piezoelectric actuator

Full size image

For convenience, this investigation adopts the Bouc–Wen model which is mathematically formulated as state-space form, and the nonlinear dynamics of the controlled piezoelectric actuator with the hysteresis behavior in Fig. 1 can be expressed as the following form [14, 15].

$$\left\{ \begin{gathered} m\ddot{x} + c\dot{x} + kx = k(pu - z) \hfill \\ \dot{z} = \alpha p\dot{u} - \beta \left| {\dot{u}} \right|z\left| z \right|^{{n - 1}} - \gamma \dot{u}\left| z \right|^{n} \hfill \\ y = x \hfill \\ \end{gathered} \right.$$
(1)

where m is the mass (kg), c is the damping factor (Ns/m), and k is the stiffness (N/m) of the equivalent mass-spring-damper model of the controlled piezoelectric actuator in Fig. 2b, respectively. The displacement of the fastener in the horizontal axes is denoted by y which is the output position of the piezoelectric actuator. u is the integral control input with the unit: voltage, and p is the piezoelectric coefficient and is a positive constant. The product of the integral control input u and the piezoelectric coefficient p is treated as a force F of the equivalent mass-spring-damper model of the controlled piezoelectric actuator. z is the displacement of the hysteretic loop, and for governing the conversion from elastic to plastic response, n is chosen as 1 [16].

In practice, parameters of nonlinear dynamics of the piezoelectric actuator in Eq. (1) are perturbed, and external disturbances are inevitable; hence parameters of nonlinear dynamics in Eq. (1) can be further reformulated as a nominal part adding a perturbed part as below

$$\left\{ \begin{gathered} m = \overline{m} + \Delta m \hfill \\ k = \overline{k} + \Delta k \hfill \\ p = \overline{p} + \Delta p \hfill \\ \alpha = \overline{\alpha } + \Delta \alpha \hfill \\ \beta = \overline{\beta } + \Delta \beta \hfill \\ \end{gathered} \right.$$
(2)

where \({(}\overline{m},\overline{c},\overline{k},\overline{p},\overline{\alpha },\overline{\beta })\) are nominal terms and \({(}\Delta m,\Delta c,\Delta k,\Delta p,\Delta \alpha ,\Delta \beta )\) are perturbed terms.

Considering the effects of the modeling uncertainties due to variations of dynamics parameters and the bounded external disturbance \(\left\| w \right\| \le B_{w}\), where \(B_{w}\) is a positive constant, the nonlinear dynamics of the piezoelectric actuator in Eq. (1) can be described as

$$(\overline{m} + \Delta m)\ddot{x} + (\overline{c} + \Delta c)\dot{x} + (\overline{k} + \Delta k)x = (\overline{k} + \Delta k)\left[ {(\overline{p} + \Delta p)u - \left( {\overline{z} + \Delta z} \right)} \right] + w$$
(3)

and

$$\dot{z}\; = \;(\overline{\alpha }\; + \;\Delta \alpha )\;(\overline{p} + \Delta p)\dot{u}\; - \;(\overline{\beta } + \Delta \beta )\left| {\dot{u}} \right|z\; - \;(\overline{\gamma } + \Delta \gamma )\dot{u}\left| z \right|$$
(4)

Combining effects of modeling uncertainties which are related to \({(}\Delta m,\Delta c,\Delta k,\Delta p,\Delta \alpha ,\Delta \beta )\) and the bounded external disturbance w, Eqs. (3, 4) can be presented as nonlinear dynamics which is identifiable as below

$$\left\{ \begin{gathered} \overline{m}\ddot{x} + \overline{c}\dot{x} + \overline{k}x = \overline{k}(\overline{p}u - \overline{z}) + w_{1} \hfill \\ \dot{z} = \overline{\alpha }\overline{p}\dot{u} - \overline{\beta }\left| {\dot{u}} \right|z - \overline{\gamma }\dot{u}\left| z \right| + w_{2} \hfill \\ \end{gathered} \right.$$
(5)

where \(w_{1}\) and \(w_{2}\) are sums related to modeling uncertainties and the external disturbance, respectively.

For merging the model of the used piezoelectric element in the second equation of Eq. (5), the first equation in Eq. (5) is differentiated with respect to t. The nonlinear dynamics in Eq. (5) can be then formulated as the following state-space form

$$\begin{gathered} \dot{\tilde{x}}(t) = f \cdot \tilde{x}(t) + g(\tilde{x}(t))\dot{u}(t) + \tilde{w}(t) \hfill \\ \;\;\;\;y = C\tilde{x}(t) \hfill \\ \end{gathered}$$
(6)

where \(\tilde{x}(t) = \left[ {\begin{array}{*{20}c} {x(t)} & {\dot{x}(t)} & {\ddot{x}(t)} & {z(t)} \\ \end{array} } \right]^{T} \in R^{4 \times 1}\) is the state vector, and

$$\begin{gathered} f = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & { - \frac{{\overline{k}}}{{\overline{m}}}} & { - \frac{{\overline{c}}}{{\overline{m}}}} & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right],\;\;g(\tilde{x}(t)) = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\frac{{\overline{k}}}{{\overline{m}}}\left[ {\overline{p} - \overline{\alpha }\overline{p} + \overline{\beta }sign(\dot{u})\overline{z} + \overline{\gamma }\left| {\overline{z}} \right|} \right]} \\ {\overline{\alpha }\overline{p} - \overline{\beta }sign(\dot{u})\overline{z} - \overline{\gamma }\left| {\overline{z}} \right|} \\ \end{array} } \right] \hfill \\ C = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ \end{array} } \right] \hfill \\ \end{gathered}$$

where \(\tilde{w}\left( t \right)\) is the combination of \(w_{1}\), \(w_{2}\) and the unknown bounded external disturbance \(w\). In this study, \(\tilde{w}\left( t \right)\) is assumed as an unknown but bounded function, i.e., \(\left\| {\tilde{w}(t)} \right\| \le \tilde{w}_{{{\text{bound}}}}\), where \(\tilde{w}_{{{\text{bound}}}}\) is a positive constant vector.

2.3 Identification of Piezoelectric Actuator Parameters

Based on the nominal model of the controlled piezoelectric actuator in Eq. (5), the famous particle swarm optimization (PSO) method is employed to search the optimal nominal parameters: \(\overline{m}\), \(\overline{c}\), \(\overline{k}\), \(\overline{p}\), \(\overline{\alpha }\), \(\overline{\beta }\), and \(\overline{\gamma }\) [17].

3 Problem Formulation

For achieving the trajectory tracking design of the controlled piezoelectric actuator in micrometer level, two steps: fuzzy modeling and robust fuzzy control law design, are integrated to construct this proposed nonlinear fuzzy-based control method.

3.1 Takagi and Sugeno Fuzzy Modelling

Takagi and Sugeno (T–S) model is adopted in this investigation for constructing the nonlinear dynamics of the controlled piezoelectric actuator in Eq. (6) by using IF–THEN rules as follows.

Plant Rule \(i\):

$$\begin{array}{*{20}l} {{\text{IF}}} \hfill & {\zeta_{1} (t){\text{ is }}F_{i1} {\text{ and }} \cdots {\text{ and }}\zeta_{g} (t){\text{ is }}F_{ig} ,} \hfill \\ {{\text{THEN}}} \hfill & \begin{gathered} \dot{\tilde{x}} = A_{i} \tilde{x} + B_{i} \dot{u} + \tilde{w}_{i} \hfill \\ y(t) = C_{i} \tilde{x}(t),{\text{ for }}i = 1, \, 2, \, \ldots \, ,L \hfill \\ \end{gathered} \hfill \\ \end{array}$$
(7)

where \(y(t)\) is the system output, \(F_{ig}\) is the fuzzy set of \(\zeta_{g}\), for rule \(i\), L is the number of fuzzy rules, and \(\zeta_{1} ,\zeta_{2} , \cdots ,\zeta_{g}\) are the known fuzzy premise variables.

The overall Takagi and Sugeno fuzzy model in the presence of modeling uncertainties and external disturbance for the controlled piezoelectric actuator can be described as

$$\begin{gathered} \dot{\tilde{x}}(t) = \frac{{\sum\nolimits_{i = 1}^{L} {\mu_{i} \left( {\zeta (t)} \right)\left( {A_{i} \tilde{x}(t) + B_{i} \dot{u}(t)} \right)} }}{{\sum\nolimits_{i = 1}^{L} {\mu_{i} \left( {\zeta (t)} \right)} }} + \tilde{w}_{a} \\ = \sum\nolimits_{i = 1}^{L} {h_{i} \left( {\zeta (t)} \right)\left( {A_{i} \tilde{x}(t) + B_{i} \dot{u}(t)} \right)} + \tilde{w}_{a} \\ \end{gathered}$$
(8)
$$\begin{gathered} y\left( t \right) = \frac{{\sum\nolimits_{i = 1}^{L} {\mu_{i} \left( {\zeta (t)} \right)\left( {C_{i} \tilde{x}(t)} \right)} }}{{\sum\nolimits_{i = 1}^{L} {\mu_{i} \left( {\zeta (t)} \right)} }} \\ = \sum\nolimits_{i = 1}^{L} {h_{i} \left( {\zeta (t)} \right)\left( {C_{i} \tilde{x}(t)} \right)} \\ \end{gathered}$$
(9)

where

$$\mu_{i} \left( {\zeta (t)} \right) = \prod\limits_{j = 1}^{g} {F_{ij} \left( {\zeta_{j} (t)} \right)}$$
(10)
$$h_{i} \left( {\zeta (t)} \right) = \frac{{\mu_{i} \left( {\zeta (t)} \right)}}{{\sum\nolimits_{i}^{L} {\mu_{i} \left( {\zeta (t)} \right)} }}$$
(11)
$$\zeta (t) = [\zeta_{{1}} (t) \, \zeta_{{2}} (t) \, \cdots \, \zeta_{g} (t)]$$
(12)
$$\tilde{w}_{a} = \sum\nolimits_{i = 1}^{L} {h_{i} \left( {\zeta (t)} \right)\tilde{w}_{i} }$$
(13)

The grade of membership \(\zeta_{j}\) in \(F_{ij}\) is denoted by \(F_{ij} \left( {\zeta_{j} \left( t \right)} \right)\), and

$$\mu_{i} \left( {\zeta (t)} \right) \ge 0$$
(14)

and

$$\sum\limits_{i = 1}^{L} {\mu_{i} \left( {\zeta (t)} \right)} > 0$$
(15)

Based on the above definitions, we have

$$\sum\limits_{i = 1}^{L} {h_{i} \left( {\zeta (t)} \right)} = 1$$
(16)

3.2 Robust Fuzzy Control Law Design

Suppose all state variables are fully measurable, a state feedback robust fuzzy controller can be developed based on the proposed Takagi and Sugeno fuzzy model in Eq. (8). Recalling the Takagi and Sugeno model rule in Eq. (7), the corresponding jth control rule has the following form.

Control rule \(j\):

$$\begin{array}{*{20}l} {{\text{IF}}} \hfill & { \, \zeta_{1} \left( t \right)\;{\text{is }}F_{j1} {\text{ and }} \cdots {\text{ and }}\zeta_{g} \left( t \right){\text{ is }}F_{jg} ,} \hfill \\ {{\text{THEN}}} \hfill & { \, \dot{u}(t) = \sum\limits_{j = 1}^{L} {K_{j} \overline{x}(t)} } \hfill \\ \end{array}$$
(17)

The overall robust fuzzy controller is described as

$$\begin{gathered} \dot{u}(t) = \frac{{\sum\nolimits_{j = 1}^{L} {\mu_{j} \left( {\zeta (t)} \right)K_{j} \overline{x}(t)} }}{{\sum\nolimits_{j = 1}^{L} {\mu_{j} \left( {\zeta (t)} \right)} }} \\ = \sum\nolimits_{j = 1}^{L} {h_{j} \left( {\zeta (t)} \right)} K_{j} \overline{x}(t) \\ \end{gathered}$$
(18)

where \(K_{j}\) are the designable control feedback gain, for \(j = 1,2,...,L\).

The overall fuzzy model of the controlled piezoelectric actuator can be further formulated as an augmented state-space form as the following

$$\dot{\overline{x}}(t) = \sum\nolimits_{i = 1}^{L} {\sum\nolimits_{j = 1}^{L} {h_{i} \left( {\zeta (t)} \right)h_{j} \left( {\zeta (t)} \right)\overline{A}_{ij} \overline{x}(t)} } + \overline{w}(t)$$
(19)

where

$$\begin{gathered} \overline{x}(t) = \left[ \begin{gathered} \tilde{x}(t) \\ x_{d} (t) \\ \end{gathered} \right],\overline{w} = \left[ \begin{gathered} \tilde{w}_{a} (t) \\ d(t) \\ \end{gathered} \right] \hfill \\ \overline{A}_{ij} = \left[ {\begin{array}{*{20}c} {A_{i} + B_{i} K_{j} } & { - B_{i} K_{j} } \\ 0 & {A_{d} } \\ \end{array} } \right] \hfill \\ \end{gathered}$$
(20)

For the trajectory tracking problem of the controlled piezoelectric actuator, a time-varying reference model is built up as a proper trajectory generator as the following

$$\dot{x}_{d} = A_{d} x_{d} (t) + d(t)$$
(21)

where \(x_{d} \left( t \right)\), \(A_{d}\) and \(d(t)\) denote the reference states, the particular asymptotically stable matrix, and the bounded reference input, respectively. All states \(x_{d} (t)\), for \(t > 0\) are considered as the desired trajectories for trajectory tracking purposes.

Relating the trajectory tracking error \(\tilde{x}(t) - x_{d} (t)\), an \(H\infty\) trajectory tracking performance index for the trajectory tracking problem of the controlled piezoelectric actuator is defined as below

$$\int_{0}^{{t_{f} }} {(\tilde{x}(t) - x_{d} (t))^{T} Q(\tilde{x}(t) - x_{d} (t)){\text{d}}t} \le r^{2} \int_{0}^{{t_{f} }} {\overline{w}^{T} (t)\overline{w}(t){\text{d}}t}$$
(22)

or

$$\frac{{\int_{0}^{{t_{f} }} {(\tilde{x}(t) - x_{d} (t))^{T} Q(\tilde{x}(t) - x_{d} (t)){\text{d}}t} }}{{\int_{0}^{{t_{f} }} {\overline{w}^{T} (t)\overline{w}(t){\text{d}}t} }} \le r^{2}$$
(23)

where \(Q\) is an adjustable symmetric positive definite matrix, and r is the disturbance attenuation which denotes the level of the worst-case of \(\overline{w}(t)\) can be eliminated.

If we take the initial value \(\overline{x}(0)\) into consideration, the \(H\infty\) trajectory tracking performance index in Eq. (23) can be modified as follows

$$\int_{0}^{{t_{f} }} {\overline{x}^{T} (t)\overline{Q}\overline{x}(t){\text{d}}t} \le \overline{x}^{T} (0)P\overline{x}(0) + r^{2} \int_{0}^{{t_{f} }} {\overline{w}^{T} (t)\overline{w}(t){\text{d}}t}$$
(24)

where \(\overline{x}(t){ = }\left[ {\begin{array}{*{20}c} {\tilde{x}(t)} & {x_{d} (t)} \\ \end{array} } \right]^{T}\), and \(P\) is a symmetric positive-definite matrix. As to \(\overline{Q}\), it is defined as the following

$$\overline{Q} = \left[ {\begin{array}{*{20}c} Q & { - Q} \\ { - Q} & Q \\ \end{array} } \right]$$
(25)

Our design objective is to design a robust fuzzy control law for the augmented system in Eq. (19) to eliminate the effects of modeling uncertainties and external disturbances and simultaneously guarantee the \(H\infty\) trajectory tracking performance in Eq. (24).

Theorem 1

For the nonlinear closed-loop representation of the controlled piezoelectric actuator in Eq. (19), if a positive definite matrix \(\overline{P} = \overline{P}^{T} > 0\) can be obtained by solving the following matrix inequalities.

$$\overline{A}_{ij}^{T} \overline{P} + \overline{P}\overline{A}_{ij} + \frac{1}{{r^{2} }}\overline{P}\overline{P} + \overline{Q} < 0,\;for\;i,j\; = \;1,\;2,\;...,\;L$$
(26)

Then, the \(H\infty\) trajectory tracking performance index in Eq. (24) can be achieved for a prescribed attenuation level \(r\).

The proof is given in Appendix A.

For convenience, \(\overline{P}\) is chosen as

$$\overline{P} = \left[ {\begin{array}{*{20}c} {\overline{P}_{11} } & 0 \\ 0 & {\overline{P}_{22} } \\ \end{array} } \right]$$
(27)

Substituting Eq. (27) into Eq. (26), it yields

$$\left[ {\begin{array}{*{20}c} {\left( {A_{i} + B_{i} K_{j} } \right)^{T} \overline{P}_{11} + \overline{P}_{11} \left( {A_{i} + B_{i} K_{j} } \right) + \frac{1}{{r^{2} }}\overline{P}_{11} \overline{P}_{11} + Q} & { - \overline{P}_{11} B_{i} K_{j} - Q} \\ {\left( { - B_{i} K_{j} } \right)^{T} \overline{P}_{11} - Q} & {A_{d}^{T} \overline{P}_{22} + \overline{P}_{22} A_{d} + \frac{1}{{r^{2} }}\overline{P}_{22} \overline{P}_{22} + Q} \\ \end{array} } \right] < 0$$
(28)

By using Schur complements, Eq. (28) is equivalent to the following LMI’s

$$\left[ {\begin{array}{*{20}c} {M_{11}^{*} } & { - \overline{P}_{11} B_{i} K_{j} - Q} & 0 \\ {\left( { - B_{i} K_{j} } \right)^{T} \overline{P}_{11} - Q} & {A_{d}^{T} \overline{P}_{22} + \overline{P}_{22} A_{d} } & {\overline{P}_{22} } \\ 0 & {\overline{P}_{22} } & { - r^{2} I} \\ \end{array} } \right] < 0$$
(29)

where \(M_{11}^{*} = \left( {A_{i} + B_{i} K_{j} } \right)^{T} \overline{P}_{11} + \overline{P}_{11} \left( {A_{i} + B_{i} K_{j} } \right) + \frac{1}{{r^{2} }}\overline{P}_{11} \overline{P}_{11} + Q\).

Due to \(M_{11}^{*} < 0\), the following inequality can be obtained

$$\left( {A_{i} + B_{i} K_{j} } \right)^{T} \overline{P}_{11} + \overline{P}_{11} \left( {A_{i} + B_{i} K_{j} } \right) + \frac{1}{{r^{2} }}\overline{P}_{11} \overline{P}_{11} + Q < 0$$
(30)

Defining new variables \(W_{11} = \overline{P}_{11}^{ - 1}\) and \(Y_{j} = K_{j} W_{11}\), and multiplying \(W_{11}\) into both side of inequality in Eq. (30), Eq. (30) becomes

$$W_{11} \left( {A_{i} + B_{i} K_{j} } \right)^{T} + \left( {A_{i} + B_{i} K_{j} } \right)W_{11} + \frac{1}{{r^{2} }}I + W_{11} QW_{11} < 0$$
(31)

By using Schur complements, the inequality in Eq. (31) is equivalent to the following LMI’s

$$\left[ {\begin{array}{*{20}c} {W_{11} A_{i}^{T} + \left( {B_{i} Y_{j} } \right)^{T} + A_{i} W_{11} + B_{i} Y_{j} + \frac{1}{{r^{2} }}I} & {W_{11} } \\ {W_{11} } & { - Q^{ - 1} } \\ \end{array} } \right] < 0$$
(32)

\(W_{11} {\text{ and }}Y_{j}\) can be obtained by solving LMI’s in Eq. (32), and we have \(\overline{P}_{11} = W_{11}^{ - 1}\) and \(K_{j} = Y_{j} W_{11}^{ - 1}\). Substituting the solved solutions \(\overline{P}_{11}\) and \(K_{j}\) into the LMI’s in Eq. (29), Eq. (29) thus becomes a standard LMIs. Similarly, \(\overline{P}_{22}\) can be obtained by solving LMIs as well.

Remark 1

If there exist symmetric definite positive solutions \(\overline{P}_{11}\) and \(\overline{P}_{22}\) for LMIs in Eq. (29), then the \(H\infty\) trajectory tracking performance index is achieved with a prescribed attenuation level \(r\).

Remark 2

The \(H\infty\) trajectory tracking problem of the controlled piezoelectric actuator can be reformulated as the following optimization problem.

$$\begin{array}{*{20}l} {\mathop {{\text{Minimize}}}\limits_{{\bar{P}_{{11}} ,\bar{P}_{{22}} }} } \hfill & {r^{2} } \hfill \\ {{\text{Subject to }}} \hfill & \bar{P}_{{11}} = \bar{P}_{{11}}^{T} > 0 \hfill \\ \hfill & {} \bar{P}_{{22}} =\bar{P}_{22}^{T} > 0 \hfill \\ \hfill & {}{\text{LMI's in Eq. 29}} \hfill \\ \end{array}$$
(33)

The \(H\infty\) trajectory tracking performance index can be reduced by minimizing the attenuation level \(r\) in Eq. (33).

Remark 3

The LMIs in Eqs. (29) and (32) above can be solved by the LMI optimization toolbox of MATLAB.

3.2.1 Summary of Design Procedures

  1. (1)

    Select membership functions and construct fuzzy plant rules in Eq. (7).

  2. (2)

    Given an initial attenuation level \(r\).

  3. (3)

    Solve the LMIP in Eq. (32) to obtain \(W_{11}\), \(Y_{j}\); thus, \(\overline{P}_{11} = W_{11}^{ - 1}\) and \(K_{j} = Y_{j} W_{11}^{ - 1}\).

  4. (4)

    Substitute \(\overline{P}_{11}\) and \(K_{j}\) into Eq. (29) and then solve the LMIP in Eq. (29) to obtain \(\overline{P}_{22}\).

  5. (5)

    Decrease \(r\) and repeat Steps 3–5 until \(\overline{P}_{11}\) and \(\overline{P}_{22}\) can not be found.

  6. (6)

    Construct the robust fuzzy controller Eq. (18).

4 Simulation Results

For verifying the trajectory tracking performance of this proposed fuzzy-based control method, two scenarios: a trapezoidal trajectory and a staircase trajectory are adopted. Comparisons of this proposed fuzzy-based control method with respect to the feedback linearization (FL) control method and the robust control method [15] will be discussed in this section. The famous software: MATLAB is adopted to execute simulation results and optimally solve the LMI problem in Eq. (33).

4.1 Fuzzy Modelling Design for the Controlled Piezoelectric Actuator

Recalling the nonlinear dynamics of the controlled piezoelectric actuator in Eq. (6), we have

$$\begin{gathered} \left[ {\begin{array}{*{20}c} {\dot{x}_{1} (t)} \\ {\dot{x}_{2} (t)} \\ {\dot{x}_{3} (t)} \\ {\dot{z}(t)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & { - \frac{{\overline{k}}}{{\overline{m}}}} & { - \frac{{\overline{c}}}{{\overline{m}}}} & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1} (t)} \\ {x_{2} (t)} \\ {x_{3} (t)} \\ {z(t)} \\ \end{array} } \right] \hfill \\ \quad\quad\quad \quad+ \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\frac{{\overline{k}}}{{\overline{m}}}\left[ {\overline{p} - \overline{\alpha }\overline{p} + \overline{\beta }{\text{sign}}(\dot{u})\overline{z} + \overline{\gamma }\left| {\overline{z}} \right|} \right]} \\ {\overline{\alpha }\overline{p} - \overline{\beta }{\text{sign}}(\dot{u})\overline{z} - \overline{\gamma }\left| {\overline{z}} \right|} \\ \end{array} } \right]\dot{u}(t) + \tilde{w}(t) \\ y = x_{1} \\ \end{gathered}$$
(34)

where \(x_{1} (t) = x(t),\;x_{2} (t) = \dot{x}(t),\;x_{3} (t) = \ddot{x}(t)\).

For minimizing the design complexity of the proposed Takagi and Sugeno fuzzy model, as few as possible rules will be chosen. After analysis, 13 fuzzy rules as below are selected.

figure e

For saving pages, details of \((A_{i} ,B_{i} ,C_{i} )\) are omitted.

Select the weighting matrix as

$$Q = \left[ {\begin{array}{*{20}c} {10^{ - 1} } & 0 & 0 \\ 0 & {10^{ - 3} } & 0 \\ 0 & 0 & {10^{ - 9} } \\ \end{array} } \right]$$

and solve the LMI’s in Eq. (29) to obtain \(W_{11}\) and \(Y_{j}\) ( then \(K_{j} = Y_{j} \overline{W}_{11}^{ - 1}\)).

Using the LMI control toolbox of MATLAB [12], the following solutions can be calculated.

\(\bar{W}_{{11}} = \left[ {\begin{array}{*{20}c} {{\text{11}}{\text{.9619}}} & {-{\text{ 332}}{\text{.4268}}} & {-{\text{ 1}}{\text{.2164}} \times {\text{10}}^{4} } \\ {-{\text{ 332}}{\text{.4268}}} & {{\text{4}}{\text{.7537}} \times {\text{10}}^{4} } & {-{\text{ 3}}{\text{.0715}} \times {\text{10}}^{6} } \\ {- {\text{ 1}}{\text{.2164}} \times {\text{10}}^{4} } & {-{\text{ 3}}{\text{.0715}} \times {\text{10}}^{6} } & {{\text{6}}{\text{.1452}} \times {\text{10}}^{8} } \\ \end{array} } \right]\), \(\overline{P}_{11} = \left[ {\begin{array}{*{20}c} {{0}{\text{.1446}}} & {{0}{\text{.0018}}} & {{1}{\text{.1690}} \times {10}^{ - 5} } \\ {{0}{\text{.0018}}} & {{5}{\text{.2651}} \times {10}^{ - 5} } & {{2}{\text{.9812}} \times {10}^{ - 7} } \\ {{1}{\text{.1690}} \times {10}^{ - 5} } & {{2}{\text{.9812}} \times {10}^{ - 7} } & {{3}{\text{.3488}} \times {10}^{ - 9} } \\ \end{array} } \right]\).and

$$\begin{gathered} K_{1} = \left[ {\begin{array}{*{20}c} { - 1.8478 \times 10^{7} } & { - {2}{\text{.2581}} \times 10^{5} } & { - {1}{\text{.4944}} \times 10^{3} } \\ \end{array} } \right],\;K_{2} = \left[ {\begin{array}{*{20}c} { - 2.0498 \times 10^{7} } & { - {2}{\text{.5049}} \times 10^{5} } & { - {1}{\text{.6578}} \times 10^{3} } \\ \end{array} } \right] \hfill \\ K_{3} = \left[ {\begin{array}{*{20}c} { - 2.2970 \times 10^{7} } & { - {2}{\text{.8069}} \times 10^{5} } & { - {1}{\text{.8576}} \times 10^{3} } \\ \end{array} } \right],\;K_{4} = \left[ {\begin{array}{*{20}c} { - 1.9321 \times 10^{7} } & { - {2}{\text{.3611}} \times 10^{5} } & { - {1}{\text{.5626}} \times 10^{3} } \\ \end{array} } \right] \hfill \\ K_{5} = \left[ {\begin{array}{*{20}c} { - 2.0919 \times 10^{7} } & { - {2}{\text{.0256}} \times 10^{5} } & { - {1}{\text{.6917}} \times 10^{3} } \\ \end{array} } \right],\;K_{6} = \left[ {\begin{array}{*{20}c} { - 2.2795 \times 10^{7} } & { - {2}{\text{.7855}} \times 10^{5} } & { - {1}{\text{.8435}} \times 10^{3} } \\ \end{array} } \right] \hfill \\ K_{7} = \left[ {\begin{array}{*{20}c} { - 2.0227 \times 10^{7} } & { - {2}{\text{.4717}} \times 10^{5} } & { - {1}{\text{.6358}} \times 10^{3} } \\ \end{array} } \right],\;K_{8} = \left[ {\begin{array}{*{20}c} { - 2.1355 \times 10^{7} } & { - {2}{\text{.6096}} \times 10^{5} } & { - {1}{\text{.7271}} \times 10^{3} } \\ \end{array} } \right] \hfill \\ K_{9} = \left[ {\begin{array}{*{20}c} { - 2.2623 \times 10^{7} } & { - {2}{\text{.7645}} \times 10^{5} } & { - {1}{\text{.8296}} \times 10^{3} } \\ \end{array} } \right],\;K_{10} = \left[ {\begin{array}{*{20}c} { - 2.1208 \times 10^{7} } & { - {2}{\text{.5916}} \times 10^{5} } & { - {1}{\text{.7151}} \times 10^{3} } \\ \end{array} } \right] \hfill \\ K_{11} = \left[ {\begin{array}{*{20}c} { - 2.1811 \times 10^{7} } & { - {2}{\text{.6653}} \times 10^{5} } & { - {1}{\text{.7639}} \times 10^{3} } \\ \end{array} } \right],\;K_{12} = \left[ {\begin{array}{*{20}c} { - 2.4255 \times 10^{7} } & { - {2}{\text{.7440}} \times 10^{5} } & { - {1}{\text{.8160}} \times 10^{3} } \\ \end{array} } \right] \hfill \\ K_{13} = \left[ {\begin{array}{*{20}c} { - 2.2290 \times 10^{7} } & { - {2}{\text{.7238}} \times 10^{5} } & { - {1}{\text{.8026}} \times 10^{3} } \\ \end{array} } \right] \hfill \\ \end{gathered}$$

Solution for \(\overline{P}_{22}\) can be solved as well as follows

$$\overline{P}_{22} = \left[ {\begin{array}{*{20}c} {{34}{\text{.4379}}} & {{1}{\text{.992}}7} & {{0}{\text{.0226}}} \\ {{1}{\text{.9927}}} & {{0}{\text{.1295}}} & {{0}{\text{.0014}}} \\ {{0}{\text{.0226}}} & {{0}{\text{.0014}}} & {{2}{\text{.4285}} \times 10^{ - 5} } \\ \end{array} } \right]$$

In this investigation, an optimal attenuation level \(r = 0.5\) is searched by decreasing the value of \(r\) from 1 until \(\overline{P}_{22}\) can not be solved from Eq. (29).

Membership functions for Rule 1–13 are selected as Fig. 3.

Fig. 3
figure 3

Membership functions for input variable z

Full size image

4.2 Parameters of the Controlled Piezoelectric Actuator

The nominal model parameters of the controlled piezoelectric actuator can be identified by using particle swarm optimization (PSO) method [15] and listed as Table 1.

Table 1 Nominal parameters for the controlled piezoelectric actuator
Full size table

4.3 Simulation Results

For verifying the trajectory tracking performance of this proposed fuzzy-based control method, this proposed fuzzy-based control law is directly used to control the original system in Eq. (1), and two scenarios are set up as follows:

Scenario 1: A trapezoidal trajectory with an amplitude of ± 10 μm is adopted to test the trajectory tracking performance of this proposed fuzzy-based control method.

Scenario 2: A 2-dimensional staircase trajectory that has the magnitude within [0, 13] is used.

In all of the testing scenarios, 20% of parameter uncertainties and an external disturbance with a magnitude which is 20% of the desired trajectory are randomly added to the model of the controlled piezoelectric actuator in Eq. (1). The initial position of the controlled piezoelectric actuator is set up as 2 μm for these two testing scenarios. Comparisons of tracking accuracy and control consumption of this fuzzy-based control method, the FL control method, and the robust control method will be made in the following.

Remark 1

In the simulations, 20% of parameter uncertainties are not taken into account in the control designs of the FL method and the robust control method because system models are always assumed as exactly known functions for constructing these two nonlinear control methods. Only external disturbances are added to the simulations of these two control methods.

Figures 4 and 5 show us the histories of the trajectories which are controlled by using the FL control method, the robust control method, and this proposed method with respect to Scenario 1. From Figs. 4a, b, and 5, trajectory tracking performances of this proposed method with respect to Scenario 1 outperform those of the FL control method and has a similar control performance as the robust control method in transient response. Under the effect of external disturbance, an overshoot in transient response and a larger error bias in the steady-state response are revealed from the FL control method. Significantly, this proposed fuzzy-based control method possesses precisely trajectory tracking ability than the robust control method and FL control method in steady-state response, and a nanometer-scale tracking accuracy (1.1736 × 10–9 m) can be found from the simulation result of the proposed fuzzy-based control method as shown in Fig. 5b. Tracking error delivered by the proposed method converges to near zero within one second in every turning point even in the presence of 20% modelling uncertainties and 20% external disturbances.

Fig. 4
figure 4

Trajectory tracking histories of this proposed fuzzy-based control method for trapezoidal trajectory: a trajectories, b tracking errors, and c control commands

Full size image
Fig. 5
figure 5

Tracking errors of this proposed fuzzy-based control method, FL control method, and the robust control method for tracking a trapezoidal trajectory: a tracking errors, and b tracking errors in steady-state

Full size image

One more complicated scenario: a staircase trajectory as below, is adopted for the assessment of this proposed fuzzy-based control method. Simulation results of this proposed method, the FL control method, and the robust control method are displayed as Figs. 6 and 7, respectively.

Fig. 6
figure 6

Trajectory tracking histories of this proposed fuzzy-based control method for staircase trajectory: a trajectories, b tracking errors, and c control commands

Full size image
Fig. 7
figure 7

Tracking errors of this proposed fuzzy-based control method for trapezoidal trajectory: a tracking errors, and b tracking errors in steady-state

Full size image

Similarly, this proposed method reveals the advantages of rapid convergence, robustness, and high trajectory tracking accuracy under the effects of hysteresis, modeling uncertainties, and external disturbances with respect to the FL control method and the robust control method.

5 Conclusions

In this study, a controller based on the robust fuzzy control concept is proposed for the micrometer level trajectory tracking problem of the controlled piezoelectric actuators. This proposed fuzzy-based control method has the advantage of being with a simple nonlinear control structure, and this will highly reduce the computation power and difficulty of implementation. For verifying the robustness property and trajectory tracking accuracy of this proposed control method, two scenarios are given. From the demonstrations, the facts indicate that the proposed fuzzy-based control method can precisely derive the piezoelectric actuator which carries a load to move along desired trajectories in the presence of hysteresis effect, modeling uncertainties and external disturbances and simultaneously converges the trajectory tracking errors quickly. From comparisons of this proposed fuzzy-based control method with respect to the feedback linearization control method and the robust control method, it is easy to find out that the feedback linearization control method and robust feedback linearization control method are inferior to this proposed method in trajectory tracking performance.