Business models, consumer data and privacy in platform markets

Abstract

We examine the drivers of the accuracy of the consumer information collected by a digital platform. In an environment where consumers mind their privacy, we compare a pure-intermediation model, where the platform plays a matching function only, by connecting buyers and sellers, with a hybrid business model, where the platform also introduces its private label to compete with third-party sellers. We show that the platform’s incentive to collect demand information in the two models depends on the intensity of intra-platform competition and on its bargaining power vis-à-vis third-party sellers. When end-users perceive the platform’s private label and the third-party sellers’ products as relatively close substitutes (strong intra-platform competition) and the intermediary has a strong bargaining position in the negotiation with the sellers, it tends to acquire less accurate information under the hybrid model than in the pure-intermediation model, at the benefit of consumer privacy. Otherwise, more information is acquired under the hybrid model. These results shed new light on the link between alternative business models, consumer privacy and information collection in the digital sector, and may help explaining why some platforms tend to protect more consumer privacy than others.

1 Introduction

Online platforms are the architects of the digital revolution. Thanks to these platforms, nowadays, consumers and sellers enjoy multiple trading solutions. In addition to meeting physically in stores, they can also trade in a virtual, impersonal, and presumably anonymous world. The reduction of search costs, the increased delivery speed, and higher market transparency are the bright side of this revolution. However, these companies also manage a massive amount of consumer data. Platforms such as Amazon, Apple, and Google, to name a few, collect, package, and disclose users’ data to third parties that use this knowledge for commercial, marketing, and, in the worst case, fraudulent purposes. The information that platforms collect covers a broad spectrum of individual data, ranging from users’ individual characteristics, such as gender, age, and location, to their browsing patterns, prior transactions, social interaction, etc. Platforms can, therefore, forecast consumers’ tastes, habits, and social preferences, and monetize this information through personalized offers.¹ Consumer data may also land in wrong ‘hands’ and be used for illegal purposes that damage consumers and their privacy (e.g., credit card and/or identity cloning). This is allegedly the major dark side of the digital revolution.

A flourishing academic literature has started to investigate the interaction between data management, marketing strategies, and competition in platform markets (see, e.g., Bergemann & Bonatti, 2019; Jullien, 2012; Peitz & Reisinger, 2015, for recent surveys). However, these models are silent on the link between platforms’ business models and the accuracy of the consumer data that they collect and eventually disclose to self-interested third-party sellers.

Notably, while some online businesses have mainly maintained a brokerage activity (e.g., eBay and Google) others operate under hybrid business models and have developed their own private labels to compete with third-party sellers operating through their marketplaces (e.g., Amazon and Apple). Do all these online intermediaries have the same incentives to acquire and disclose users’ personal information? If not, what are the determinants of different approaches to information and privacy management? Is the choice of business model—i.e., pure intermediation vs. hybrid platforms one of these key factors?

In this paper, we study the drivers of the accuracy of the information that digital intermediaries collect and disclose. Specifically, we compare the incentives to collect demand information by a an online intermediary (platform) operating under two alternative business models: a pure-intermediation model, where it plays a matching function only by connecting a third-party seller with buyers, and a hybrid model where, in addition to its traditional middlemen role, the platform also introduces its own private label in the marketplace and competes with the third-party seller distributing through its marketplace. We argue that there is no objective presumption that pure intermediation platforms collect more or less information than hybrid platforms. Platforms’ business model is not neutral to data collection. This observation should be considered carefully by privacy authorities, especially because in the EU the GDPR is based on the ’data minimization principle.’²

We set up a simple duopoly model with linear demand and random willingness to pay (demand intercept). The platform collects information on the demand’s random component and, coherently with recent regulatory trends imposing big tech companies transparency requirements to promote level playing field competition, is mandated to disclose this information to the sellers distributing through its marketplace (including its retail unit when present). Sellers use such information to target quality (or advertising) and prices. The crucial, and somewhat novel, assumption is that disclosing more accurate information directly harms consumers because they mind their privacy.³ To isolate the effects of contractual frictions (e.g., double marginalization) on the platform’s information acquisition problem, in the baseline model we assume efficient contracting—i.e., the platform extracts a fixed share of the seller’s profit.⁴

Within this setting, we show that the platform’s incentive to gather information in the two business models depends on the degree of substitutability between the private label (which is present only under the hybrid model) and the product of the seller distributing through it (intra-platform competition), and the distribution of the bargaining power in the negotiation with the seller. When intra-platform competition is sufficiently intense, and the platform has a strong bargaining position in the negotiation with the seller, it tends to acquire and disclose more accurate information in the pure-intermediation model than in the hybrid model, at the expense of consumers’ privacy. Otherwise, the platform collects and discloses more information when it operates a hybrid model.

Gathering information has two main effects on the platform’s profit. On the one hand, regardless of its business model, the platform is willing to gather information because it allows the sellers active in its marketplace to make more accurate pricing and quality/advertising decisions, generating an extra profit that the platform (partially) extracts at the negotiation stage. On the other hand, since consumers have privacy concerns, gathering information reduces demand because (ceteris paribus) fewer consumers join the platform when they fear that online purchases endanger their privacy.

The first effect described above is present under both business models. The second effect points to less information collection in the hybrid platform than in the pure intermediation model when the private label and the product of the third-party seller are close substitutes and when the bargaining power of the platform is high. This is because when those conditions hold, the hybrid platform can appropriate (via its retailing activity) a larger share of the incremental value generated by each consumer that joins the platform and, therefore, it has a larger incentive to increase demand by protecting privacy. Hence, when the intermediary is in a strong bargaining position and intra-platform competition is strong, hybrid platforms will collect and disclose less information than pure intermediation platforms. The opposite holds otherwise.

Building on these insights, we then explore the determinants of the optimal business model. To begin with, we show that, when both models imply the same level of information accuracy, the platform prefers to operate as a pure intermediary when consumers perceive products as relatively close substitutes and its bargaining power is relatively strong. The intuition is as follows. For given information accuracy, introducing a private label in the marketplace is not worthwhile for the platform if products are close substitutes because competition erodes both the profit earned through its private label and those earned through the intermediation channel. This effect becomes even stronger, in relative terms, when the platform’s bargaining strength rises, because in the pure intermediation model, the platform extracts a relatively higher share of the seller’s profit. Yet, when the information policy differs in the two business models, the result is ambiguous. We find interesting cases in which the hybrid regime maximizes the platform’s profit and vice-versa. The driving forces are again intra-platform competition, which makes the hybrid model relatively less appealing, and the strength of the bargaining position of the third-party seller(s), which makes it more appealing.

These findings generalize to a number of extensions which include alternative demand functions, multiple sellers and decentralized decision making within the platform. Notably, with inefficient contracting (e.g., with ad-valorem and linear per-unit fees) we find that the hybrid model always provides greater incentives to gather information under the hypothesis that the platform makes take-it-or-leave-it offers. While under ad-valorem fees this incentive unambiguously falls with competition, under linear per-unit fees we find a U-shaped relationship between the incentive to collect information and the degree of intra-platform competition. Finally, we show that the effect of the business model on consumer surplus is ambiguous, although positively biased towards the hybrid model in several cases.

2 Related literature

Our work is related to the growing theoretical literature on the economics of privacy and data collection (see Acquisti et al., 2016 for a comprehensive survey of research works on the topic). Especially relevant to our analysis is the work of Evans (2009), who shows that consumers may resist having advertising platforms collecting detailed data about their behavior and government regulation may be called for limiting the ability of advertising intermediaries to collect these data.⁵ Of particular interest is also the work by Kalvenes and Basu (2006) arguing that hybrid platforms may not want to use their private information to gain a competitive advantage over rivals to stimulate participation. Madsen and Vellodi (2021); Lam and Liu (2020), instead, study the entry decision of a platform’s owner in the product space of the complementors (‘hybrid business model’) and the role of individualized information. In contrast to us, both these papers focus on a data dimension that affects sellers and not consumers.

The paper is also related to the extensive literature on multi-sided platforms (see, e.g., Jullien, 2012). In this literature, some authors have analyzed the trade-off between the platform business model and more traditional alternatives. In particular, Hagiu and Wright (2015) analyze the trade-offs that drive an intermediary when choosing between operating as a marketplace, as a reseller or as a hybrid. Along similar lines, Abhishek et al. (2016) identify the conditions under which agency selling (a selling format wherein online retailers allow manufacturers direct access to their consumers) should be preferred to reselling (wholesale pricing), as well as the implications of that choice for market participants (i.e., for competing on-line retailers, manufacturers and consumers). Karle et al. (2020) have more recently argued that the competitive conditions among sellers shape the market structure in platform industries—i.e., agglomeration versus segmentation. Hagiu et al. (2020) study the welfare effects of several policies that may restrict how intermediaries operate, with an emphasis on hybrid intermediaries. In their model third-party sellers also have their own store (direct distribution), where they can set prices in a differentiated way, and have a fraction of captive (single-homing) consumers that will never buy in the marketplace. However, in contrast to our model, in which quality (advertising) is endogenous, they assume that third-party sellers sell a superior product but they produce it at a higher cost than the intermediary. More recently, Anderson and Bedre-Defolie (2021) have identified the negative effects of a hybrid business model for consumers abstracting from privacy related issues. Shopova (2021), instead, studies the incentives of a hybrid platform to offer a low-quality product abstracting, however, from the implications that this strategy has on information and privacy management. None of these papers explores, however, the incentives to collect demand information of a platform operating under alternative business models in an environment where consumers mind their privacy.

3 The baseline model

Players and environmentThis section builds a simple environment to develop and compare two alternative digital business models: a pure- and a hybrid-intermediation model. In both models, there is a platform (P) through which a single seller (S) distributes its product (in the extensions we extend the analysis to $N>1$ sellers). In the pure intermediation model, P only plays a matching function, by connecting the two sides of the market; in the hybrid model, P also develops a private label to compete with S to serve consumers—i.e., there is a duopoly with differentiated products in the final market.

Consumers, information structure and privacy concerns There is a representative consumer who has preferences described by the following utility function

$$\begin{aligned} U(\cdot )\triangleq \underset{\text {Standard Singh-Vives Utility}}{ \underbrace{\sum _{i=1}^{N}\left( A+\theta +x_{i}\right) q_{i}-\frac{1}{2} \sum _{i=1}^{N}q_{i}^{2}-dq_{1}q_{2}-\sum _{i=1}^{N}p_{i}q_{i}}}-\underset{ \text {Privacy Concerns}}{\underbrace{\eta \psi \sum _{i=1}^{N}q_{i}}}, \end{aligned}$$

(1)

where $N=1$ in the pure intermediation model, and $N=2$ in the hybrid model. As a convention, we assume that S supplies product 1 irrespective of the business model, while $P$supplies product 2 when they compete. Hence, in the above expression $q_{1}$ denotes S’s output while $q_{2}$ denotes P ’s output.

The utility function described above can be decomposed in two parts. The first corresponds to the standard (Singh & Vives, 1984) quadratic utility function, which we have chosen for its analytical tractability (i.e., it yields linear demand functions and a tractable expression for consumer surplus). The parameter $d\ge 0$ captures, therefore, the exogenous degree of differentiation between products: the larger d, the closer substitutes products are perceived by consumers. The parameter $A>0$ is an exogenous and deterministic component of the representative consumer’s willingness to pay (the demand intercept); $\theta$ is a zero-mean random variable distributed uniformly on the support $\Theta \triangleq \left[ -\sigma ,\sigma \right]$ , with $\sigma$ capturing the heterogeneity of tastes; $x_{i}\ge 0$ is an endogenous (consumer-surplus enhancing) variable that we interpret as the (observable) quality of each product traded on the platform (e.g., supply of non-market activities such as product description, guarantees, post-sale services, etc.). Alternatively, one can think of $x_{i}$ as being sellers’ advertising intensity—i.e., the extent to which consumers are exposed to ads promoting product i.⁶ Players are uninformed about $\theta$, but P can gather an informative signal. The information policy is ‘all-or-nothing’ (see, e.g., Vives, 1984; Gal-Or, 1985): P receives a signal $s\in \Theta$ which is fully informative of the state $\theta$ with probability $\eta \in \left[ 0,1\right]$, and uninformative otherwise—i.e., with probability $1-\eta$ the state of nature $\theta$ and the signal s are identically and independently distributed.

The second part of the utility function determines consumers’ privacy concerns and represents a novel aspect of our analysis. Following Gal-Or et al. (2018) we assume that tracking and collecting data about users can rise concerns among them. First, although users may benefit from a targeted choice of quality or informative advertising, the resulting loss of privacy may discourage users from adopting the platform (see, e.g., Xu et al., 2012; Tucker, 2014, for empirical studies on targeting and privacy concerns). Second, this information may land in wrong ‘hands’ and be used for illegal purposes that damage consumers (e.g., credit card and/or identity cloning). Hence, we posit that privacy concerns are proportional to the accuracy of the information gathered by P—i.e., the more accurate the information gathered by P, the greater the potential damage consumers face—and proportional to the amount of transactions made by consumers—i.e., the more transactions consumers make, the greater the risk that the information left on the marketplace is misused.⁷ The parameter $\psi \ge 0$ measures the extent of this damage.⁸

The precision $\eta$ of the signal is endogenous and chosen by P at the outset of the game. For simplicity, the cost of gathering information with precision $\eta$ is linear, and denoted by $c\eta$.⁹ Furthermore, we assume that regulatory constraints, imposing non-discriminatory information rules, prevent P from hiding information to S. This hypothesis is in line with many regulatory initiatives aimed at promoting level-playing field competition in digital industry. For example, the CMA has recently created a digital markets unit with the open objective of enforcing a code of conduct based on fair trading, trust, and transparency so to prevent tech giants from discriminating the third-party sellers operating on their platforms/marketplaces at the advantage of their retail harms (e.g., Amazon Retail).¹⁰ As a result, we assume that P and S must have the same information—i.e., P is mandated to fully disclose s regardless of the business model.¹¹

Contracting To focus only on the information management problem faced by the platform, in the baseline model we rule the standard double marginalization arising with per-unit and ad-valorem fees, and simply assume that P appropriates a fraction $b\in \left[ 0,1\right]$ of S’s profit—i.e., P’s negotiation power vis-à-vis S. This assumption reflects the idea of ex-ante contracting and/or efficient bargaining, and it guarantees that when $b\,=\,1$ the platform fully extracts S’s profit.¹² In Sect. 3 (Extensions) we discuss how introducing explicit contractual frictions will alter the equilibrium of the game.

Technology Sellers have linear production technologies with marginal costs of production set to zero. This assumption is without loss of generality given the profit-sharing rule assumed above, but (as we shall discuss) it may not be innocuous when introducing ad-valorem fees.

Providing quality (advertising) is costly and, for tractability, we assume a quadratic cost function $x_{i}^{2}/2$.

Timing and equilibrium concept Following the literature on markets for data (e.g., Bergemann & Bonatti, 2018; Bergemann & Bonatti, 2019; Kastl et al., 2018), we assume that P can commit to an information policy (accuracy) $\eta$.¹³

The timing of the game is as follows:

• P chooses $\eta$—i.e., it commits to deliver some data and related analytics with a certain quality.

• $\theta$ realizes and P observes signal s, which is then disclosed to S.

• Depending on the business model, sellers simultaneously choose qualities and set prices.

• Demand allocates, profits materialize and payments between S and P are made.

The equilibrium concept is Subgame Perfect Nash Equilibrium (SPNE).

Assumptions We assume that $A>\psi +\sigma$ to guarantee positive demand in every state. In addition, we also assume that $d\le \frac{1}{2}$—i.e., competition is not too intense—to guarantee that in the hybrid model prices and qualities are non-negative for every level of $b\in \left[ 0,1\right]$.

3.1 Pure intermediation

Consider first the pure intermediation model—i.e., $q_{2}=0$. The utility function of the representative consumer is

$$\begin{aligned} u\left( \cdot \right) =\left( A+\theta +x_{1}\right) q_{1}-\frac{q_{1}^{2}}{2 }-p_{1}q_{1}-\psi \eta q_{1}. \end{aligned}$$

Optimizing with respect to $q_{1}$, we obtain the following linear demand function conditional on $\theta$

$$\begin{aligned} Q_{1}\left( p_{1},x_{1},\theta \right) =A+\theta +x_{1}-\psi \eta -p_{1}. \end{aligned}$$

Hence, for given signal s disclosed by the platform, the seller solves the following maximization problem

$$\begin{aligned} \max _{x_{1}\ge 0,p_{1}\ge 0}\mathbb {E}\left[ Q_{1}\left( p_{1},x_{1},\theta \right) |s\right] p_{1}-\frac{x_{1}^{2}}{2}, \end{aligned}$$

where, given the all-or-nothing information structure postulated above, the conditional expectation of $\theta$ given$\ s$ is

$$\begin{aligned} \mathbb {E}\left[ \theta |s\right] =\eta s. \end{aligned}$$

Maximizing with respect to $p_{1}$ and $x_{1}$, respectively, we have

$$\begin{aligned} A+\mathbb {E}\left[ \theta |s\right] +x_{1}-\eta \psi -2p_{1}=0, \end{aligned}$$

(2)

and

$$\begin{aligned} p_{1}-x_{1}=0. \end{aligned}$$

(3)

Since consumers value positively quality (advertising), products featuring higher quality (or that are advertised more intensively) will be more expensive—i.e., as $x_{1}$ grows large, $p_{1}$ increases too. Moreover, as privacy concerns become more relevant—i.e., as $\psi$ grows large—the consumers’ willingness to pay drops, which implies a lower price and thus lower quality (advertising).

Solving (2) and (3) simultaneously, it is easy to find the optimal price and the optimal targeting chosen by the seller in the pure-intermediation model—i.e.,

$$\begin{aligned} p_{1}^{*}\left( s\right) =x_{1}^{*}\left( s\right) \triangleq A+\left( s-\psi \right) \eta , \end{aligned}$$

with $p_{1}^{*}\left( s\right) \ge 0$since we assumed $A>\sigma +\psi$.

As intuition suggests, $p_{1}^{*}\left( s\right)$ and $x_{1}^{*}\left( s\right)$ are increasing in s—i.e., the higher the signal, the higher demand (in expected terms), and thus the higher the (equilibrium) price and quality. The effect of $\eta$ is ambiguous and depends on the difference $s-\psi$ which reflects the trade-off between the demand enhancing effect and the privacy concerns. When $\psi>s>0$, privacy concerns are relatively important, hence the price is decreasing in the precision of the information $\eta .$ An interesting aspect to highlight is that quality (advertising intensity) is declining in $\psi$, which suggests that if a platform has a relatively poor reputation for respecting and protecting consumers’ privacy, in equilibrium, the products traded on that platform are of relatively low quality or are advertised less intensively.

Substituting $p_{1}^{*}\left( \cdot \right)$ and $x_{1}^{*}\left( \cdot \right)$into S’s (gross) expected (i.e., signal contingent) profit we have

$$\begin{aligned} \pi ^{*}\left( s\right) \triangleq \frac{\left[ A+\left( s-\psi \right) \eta \right] ^{2}}{2}. \end{aligned}$$

The quadratic structure of the profit function is standard in oligopoly games with linear demand (see, e.g., Vives, 2010). Hence, $\pi ^{*}\left( s\right)$ is convex in s—i.e., firms are risk-lover and their profits increase with the volatility of the signal s. The more volatile the signal, the higher the profit shared by the platform and the seller. Integrating with respect to s, the platform’s expected profit net of the cost of acquiring information is

$$\begin{aligned} \pi ^{*}\left( \eta \right) \triangleq b\int _{-\sigma }^{\sigma }\pi ^{*}\left( s\right) \frac{ds}{2\sigma }-c\eta =b\frac{\eta ^{2}\left( 3\psi ^{2}+\sigma ^{2}\right) +3A\left( A-2\psi \eta \right) }{6}-c\eta , \end{aligned}$$

(4)

which is clearly convex in $\eta$—i.e., P either prefers maximal noise ($\eta =0$) or full accuracy ($\eta =1)$. Hence, P’s problem

$$\begin{aligned} \max _{\eta \in \left[ 0,1\right] }\pi ^{*}\left( \eta \right) , \end{aligned}$$

always features a corner solution—i.e.,

$$\begin{aligned} \eta ^{*}\triangleq \left\{ \begin{array}{c} 1 \\ \in \left[ 0,1\right] \\ 0 \end{array} \begin{array}{l} \Leftrightarrow \pi ^{*}\left( 1\right) >\pi ^{*}\left( 0\right) \\ \Leftrightarrow \pi ^{*}\left( 1\right) =\pi ^{*}\left( 0\right) \\ \Leftrightarrow \pi ^{*}\left( 1\right) <\pi ^{*}\left( 0\right) \end{array} \right. . \end{aligned}$$

Comparing

$$\begin{aligned} \pi ^{*}\left( 1\right) =\frac{b\left( 3\psi ^{2}+\sigma ^{2}+3A\left( A-2\psi \right) \right) }{6}-c, \end{aligned}$$

with

$$\begin{aligned} \pi ^{*}\left( 0\right) =b\frac{A^{2}}{2}, \end{aligned}$$

we can show the following:

Proposition 1

In the pure intermediation model, P chooses $\eta ^{*}=1$ only if

$$\begin{aligned} \psi \le \psi ^{*}\triangleq A-\sqrt{A^{2}-\frac{\sigma ^{2}}{3}}>0, \end{aligned}$$

and if

$$\begin{aligned} c\le c^{*}\triangleq \frac{b\left( \sigma ^{2}-3\psi \left( 2A-\psi \right) \right) }{6}. \end{aligned}$$

Otherwise, $\eta ^{*}=0$.

In addition to the fact that gathering information is costly, there are three additional effects that shape the accuracy of the information collected by P. First, since quality/advertising is costly, gathering more precise information allows P to choose to invest in quality (advertising) more efficiently—i.e., invest in quality when $\theta$ is high. Second, higher accuracy triggers privacy concerns: consumers reduce demand being concerned with their privacy. Third, since the profit function is convex in s, a higher $\eta$ also benefits P because it makes its profits relatively more responsive to s, and thus more volatile.

On the net, the second effect dominates when the privacy concerns are sufficiently strong ($\psi \ge \psi ^{*}$), in which case the platform’s profit is maximized by an uninformative information policy. By contrast, when privacy concerns are not too important ($\psi <\psi ^{*}$ ) gathering information with maximal accuracy is optimal provided that its cost c is not too large—i.e., $c\le c^{*}$. Clearly, the convexity of the profit function with respect to s implies that as demand uncertainty increases (i.e., as $\sigma$ grows large) the thresholds $c^{*}$ and $\psi ^{*}$ rise too, so that acquiring information becomes relatively more valuable. Finally, as intuition suggests, $c^{*}$ is increasing in b, meaning that P has a greater incentive to collect information the larger is the share $b\in \left[ 0,1\right]$ of S’s profit that it can extract.

3.2 Hybrid platform

Consider now a hybrid platform where, in addition to allowing S to match with users, P also competes with it by developing its private label. To simplify, we begin by treating the platform and its (vertically integrated) retailing unit as a unique entity (in the extensions we show that results hold true when this assumption is relaxed).

S’s and P’s demand functions are, respectively,

$$\begin{aligned} q_{1}\left( p_{1},p_{2},x_{1},x_{2},\theta \right) \triangleq \frac{A+\theta -\psi \eta }{1+d}+\frac{x_{1}-p_{1}+d\left( p_{2}-x_{2}\right) }{1-d^{2}}, \\ q_{2}\left( p_{2},p_{1},x_{2},x_{1},\theta \right) \triangleq \frac{A+\theta -\psi \eta }{1+d}+\frac{x_{2}-p_{2}+d\left( p_{1}-x_{1}\right) }{1-d^{2}}. \end{aligned}$$

Hence, conditional on observing signal s, P solves the following maximization problem

$$\begin{aligned} \max _{x_{2}\ge 0,p_{2}\ge 0}\mathbb {E}\left[ q_{2}\left( \cdot \right) |s \right] p_{2}-\frac{x_{2}^{2}}{2}+b\left( \mathbb {E}\left[ q_{1}\left( \cdot \right) |s\right] p_{1}-\frac{x_{1}^{2}}{2}\right) , \end{aligned}$$

whose first-order conditions with respect to $p_{2}$ and $x_{2}$ are, respectively,

$$\begin{aligned} \underset{\text {Standard price-setting rule}}{\underbrace{\frac{A+\left( s-\psi \right) \eta }{1+d}+\frac{x_{2}-dx_{1}-2p_{2}+dp_{1}}{1-d^{2}}}}+ \underset{\text {Cross-demand effect}}{\underbrace{\frac{bd}{1-d^{2}}p_{1}}} =0, \end{aligned}$$

(5)

and

$$\begin{aligned} \underset{\text {Demand-enhancing effect}}{\underbrace{\frac{1}{1-d^{2}}p_{2}} }-\underset{\text {Cost of quality}}{\underbrace{x_{2}}}-\underset{\text { Cross-demand effect}}{\underbrace{\frac{bd}{1-d^{2}}p_{1}}}=0. \end{aligned}$$

(6)

The first-order condition (5) reflects three intuitive economic forces. First, when P increases the price $p_{2}$, it earns a higher profit on the infra-marginal units (i.e., on the consumers that keep purchasing the product even if its price has slightly increased). Second, a higher $p_{2}$ also reduces demand for P’s product, which means a lower sales volume. Third, since prices are strategic complements, a higher $p_{2}$ also boosts S’s profit which, in turn, benefits P because it extracts the share $b\in \left[ 0,1\right]$ of such profit. Notice that when S increases its quality—i.e., when $x_{1}$ increases—P has a weaker incentive to increase its price because the demand for its brand drops further.

The first two terms in condition (6) reflect the same trade-off discussed in the pure intermediation model. The only difference being that the marginal benefit of investing more in quality or advertising (the first term in Eq. 6) now depends, and is increasing, in d—i.e., the closer substitutes products are, the more quality becomes a competitive instrument to gain market share. However, since P partly internalizes S ’s profit, a higher $x_{2}$ also hurts P because it reduces S’s demand, and therefore the profit that they share.

S solves the following maximization problem

$$\begin{aligned} \max _{x_{1}\ge 0,p_{1}\ge 0}\mathbb {E}\left[ q_{1}\left( \cdot \right) |s \right] p_{1}-\frac{x_{1}^{2}}{2}. \end{aligned}$$

The first-order conditions with respect to $p_{1}$ and $x_{1}$ are, respectively,

$$\begin{aligned} \underset{\text {Standard price setting rule}}{\underbrace{\frac{A+\eta \left( s-\psi \right) }{1+d}+\frac{x_{1}-dx_{2}-2p_{1}+dp_{2}}{1-d^{2}}}}=0, \end{aligned}$$

(7)

and

$$\begin{aligned} \underset{\text {Demand-enhancing effect}}{\underbrace{\frac{p_{1}}{1-d^{2}}}} -\underset{\text {Cost of quality}}{\underbrace{x_{1}}}=0. \end{aligned}$$

(8)

The intuition behind these expressions is the same as in the pure-intermediation model. Solving the system of first-order conditions (5)–(8) we can state the following result.

Proposition 2

In the hybrid model, the equilibrium market outcome is such that

$$\begin{aligned}&p_{2}^{\star }\left( s\right) \triangleq \frac{\left( 1-d^{2}\right) \left( 1-d\left( 1+d\right) -d^{2}b\right) }{1-bd^{2}\left( 1-d^{2}\right) -d^{2}\left( 3-d^{2}\right) }\left( A+\eta \left( s-\psi \right) \right) \\&\le p_{1}^{\star }\left( s\right) \triangleq \frac{\left( 1-d^{2}\right) \left( 1-d\left( 1+d\right) \right) }{1-bd^{2}\left( 1-d^{2}\right) -d^{2}\left( 3-d^{2}\right) }\left( A+\eta \left( s-\psi \right) \right) , \end{aligned}$$

with equality only at $b=0$, and

$$\begin{aligned} x_{2}^{\star }\left( s\right) =\frac{1}{1-d^{2}}\left[ p_{2}^{\star }\left( s\right) -bdp_{1}^{\star }\left( s\right) \right] \le x_{1}^{\star }\left( s\right) =\frac{p_{1}^{\star }\left( s\right) }{1-d^{2}}, \end{aligned}$$

with equality holding again at $b=0$ only.

Interestingly, P’s private label is cheaper and features lower quality than S’s product. The reason is straightforward: P has a weaker incentive to invest in quality (or advertising) than S because it internalizes the negative effect of a higher $x_{2}$ on S’s demand. Essentially, P purposefully creates a sort of ‘vertical differentiation’ between its product and S’s product by reducing $x_{2}$, so as to relax competition and increase profits. Clearly, since P invests in quality (or advertising) less than S, product 2 must also be cheaper than product 1.

We can now turn to study the optimal accuracy of the information collected by P.

Lemma 3

There exists a positive function $\Gamma \left( b,d\right)$ such that, conditional on observing signal s, P’s expected profit is

$$\begin{aligned} \pi ^{\star }(s)\triangleq \left[ A+\eta \left( s-\psi \right) \right] ^{2}\Gamma \left( b,d\right) . \end{aligned}$$

Hence, P’s ex-ante expected profit, net of the cost of collecting information with accuracy $\eta$ is

$$\begin{aligned} \pi ^{\star }\left( \eta \right) \triangleq \left( \eta ^{2}\left( 3\psi ^{2}+\sigma ^{2}\right) +3A\left( A-2\psi \eta \right) \right) \Gamma \left( b,d\right) -c\eta . \end{aligned}$$

(9)

Once again, the expected profit features a quadratic structure and is convex in $\eta$ – i.e., P’s problem features corner solutions

$$\begin{aligned} \eta ^{\star }\triangleq \left\{ \begin{array}{l} 1 \\ \in \left[ 0,1\right] \\ 0 \end{array} \begin{array}{c} \Leftrightarrow \pi ^{\star }\left( 1\right) >\pi ^{\star }\left( 0\right) \\ \Leftrightarrow \pi ^{\star }\left( 1\right) =\pi ^{\star }\left( 0\right) \\ \Leftrightarrow \pi ^{\star }\left( 1\right) <\pi ^{\star }\left( 0\right) \end{array} \right. . \end{aligned}$$

The function $\Gamma \left( b,d\right) \ge 0$ is characterized in the Appendix, and is plotted in Fig. 1 (red curve) below in the space $\left( b,d\right) \in \left[ 0,1\right] \times [0,1/2)$.

Fig. 1

Impact of b and d on profits

It can be seen that $\Gamma \left( b,d\right)$ is increasing in b (for given d) and decreasing in d (for given b). Hence, for given information disclosure, P’s expected profit is decreasing with the intensity of competition and increasing with its bargaining power vis-à -vis S.

Comparing

$$\begin{aligned} \pi ^{\star }\left( 1\right) =\left( 3\psi ^{2}+\sigma ^{2}+3A\left( A-2\psi \right) \right) \Gamma \left( b,d\right) -c, \end{aligned}$$

with

$$\begin{aligned} \pi ^{\star }\left( 0\right) =A^{2}\Gamma \left( b,d\right) , \end{aligned}$$

we can state the following.

Proposition 4

In the hybrid model, the optimal accuracy is such that $\eta ^{\star }=1$ only if $\psi \le \psi ^{*}$and if

$$\begin{aligned} c\le c^{\star }\triangleq \left( \sigma ^{2}-3\psi \left( 2A-\psi \right) \right) \Gamma \left( b,d\right) . \end{aligned}$$

Otherwise, $\eta ^{\star }=0$.

The intuition is the same as in the pure intermediation model. As long as privacy concerns are not too strong and gathering information is not too costly, P becomes fully informed. Otherwise, it has no incentive to collect information. Of course, this incentive now depends on the extent to which consumers perceive products as more or less substitutes, and on the share b of S’s profit extracted by P. As noted before, Fig. 1 shows that the incentive to become informed in the hybrid model is decreasing in d and increasing in b.

3.3 The drivers of information accuracy

We can finally study the drivers of the information accuracy in the two business models. As a benchmark, it is useful to start by considering two extreme but interesting scenarios: $b\,=\,0$ so that P does not internalize S ’s profit at all—e.g., because there is a competing platform that stands ready to attract S—and $b\,=\,1$ where P fully internalizes S’s profit—e.g., because P is monopolist in the platform market and S has no other distribution options.

Comparing the thresholds $c^{\star }$ and $c^{*}$, we have the following preliminary lemma:

Lemma 5

Suppose that $\psi \ge \psi ^{*}$, then P does not collect information regardless of the business model. By contrast, for $\psi <\psi ^{*}$, the following holds:

• For $b\rightarrow 0$ the incentive to collect information is stronger in the hybrid model than in the pure intermediation model for every admissible level of d—i.e., $c^{\star }>c^{*}$ for every $d\in [0,\frac{1}{2}).$

• For $b\rightarrow 1$ there exists a value $d^{*}\approx 0.4$ such that the incentive to acquire information is stronger in the pure intermediation model than in the hybrid model if and only if $d\ge d^{*}$, and the opposite is true otherwise—i.e., $c^{\star }\le c^{*}$ iff $d\ge d^{*}$.

This result shows that the relationship between the incentive to collect consumer data and the business model is non-monotonic, and depends both on P’s bargaining power in the negotiation with S and on the intensity of competition.

When b is sufficiently small, $P$gains more from collecting information in the hybrid model than in the pure intermediation model. The intuition is that when P acts as a pure intermediary, its main source of profit is the surplus extracted from S. Clearly, if the share of S’s profit internalized by P is small enough ($b\rightarrow 0$), paying the cost of collecting information is not worthwhile. By contrast, since under the hybrid model, P sells its own product, it has a stronger incentive to collect information even when $b\rightarrow 0$: an informed P can price and target quality/advertising more accurately.

By contrast, when b is sufficiently large, the incentives to collect information in the two business models may reverse depending on the intensity of intra-platform competition, as reflected by the magnitude of the differentiation parameter d. The platform has a stronger incentive to collect information in the pure intermediation model compared to the hybrid model when intra-platform competition is sufficiently intense. To see why, consider the extreme case in which $b=1$—i.e., P fully extracts S’s profit under both models. In the pure-intermediation model, S acts as a monopolist, and collecting information has the exclusive benefit of enabling it to price and invest in quality (advertising) more accurately. The implied extra profit is then fully extracted by P. In the hybrid model, instead, P and S compete fiercely when d is sufficiently large since consumers perceive their goods as relatively close substitutes. In this case, P has a weaker incentive to gather information because when S is uninformed it makes less accurate quality/advertising and price decisions, whereby competing less aggressively with P.

We can now turn study the difference between $c^{\star }$ and $c^{*}$ for every admissible $b\in \left( 0,1\right)$. It is easy to show that

$$\begin{aligned} c^{\star }\gtrless c^{*}\quad \Leftrightarrow \quad \Gamma \left( b,d\right) \gtrless \frac{b}{6}. \end{aligned}$$

Figure 2 below plots the difference $\Gamma _{h}\left( b,d\right) -\frac{b }{6}$ (red curve) in the relevant range of parameters.

Fig. 2

Incentives to invest and business model

The figure shows that the difference $c^{\star }-c^{*}$ is negative when b and d are both sufficiently large. Hence, P has a weaker incentive to collect information in the hybrid model than in the pure intermediation model when intra-platform competition is relatively intense (i.e., when d is sufficiently large) and when the platform has strong bargaining position vis-à-vis the sellers operating through it (i.e., when b is sufficiently large). The following then holds.

Proposition 6

There exists a $d_{0}<\frac{1}{2}$ such that:

• for every $d\le d_{0}$, P has a stronger incentive to collect information in the hybrid model for every $b\in \left[ 0,1\right] .$

• for every $d>d_{0}$, there exists a function $b_{0}\left( d\right) <1$ , with $b_{0}^{\prime }\left( d\right) <0$, such that P has a stronger incentive to collect information in the pure intermediation model if and only if $b\ge b_{0}\left( d\right)$.

The intuition follows from the above discussion.

3.4 Comparison of business models

We now compare the equilibrium outcome across the two regimes. We start by considering how prices and targeting change across the two business models.

• In the hybrid model, regardless of whether P collects information or not, it always charges a price lower than that charged by S in the pure intermediation model. The same holds for the quality choice.

The reason is that in the hybrid model there is intra-platform competition, whereas in the pure intermediation model S is a monopolist.

• In the hybrid model, regardless of whether P collects information or not, S sets a lower price than in the pure intermediation model for low values of d and b. The same holds for the targeting choice.

The reason is that as d grows, in the hybrid model P targets less in order to soften competition, whereby leading S to increase both quality and price.

We can now move to compare P’s profits across business models. Two intuitive effects determine P’s choice. First, under the hybrid model, P introduces its private label and, therefore, (other things being equal) it has an additional source of profit compared to the pure intermediation model in which it only extracts a share of S’s profit. Second, by introducing its private label, P also creates competition in the market, which lowers S’s profit and, hence, the surplus that P can extract from S. When d is small, the first effect dominates. For large d, instead, the effect is ambiguous and depends on b, which de facto measures the weight attributed by P to the loss of profit associated with the intensified competition in the marketplace.

Comparing (4) with (9) it is immediate to see that, for given precision $\eta$, the following is true

$$\begin{aligned} \pi ^{\star }\left( \eta \right) \ge \pi ^{*}\left( \eta \right) \quad \Leftrightarrow \quad \Gamma \left( b,d\right) \ge \frac{b}{6}. \end{aligned}$$

Then, the following can be stated:

Proposition 7

Holding $\eta$ constant across the two business models, P prefers to operate as a pure intermediary when consumers perceive products as relatively close substitutes (d large), and when its bargaining power is relatively strong (b large).

The intuition is as follows. For given information accuracy, introducing a private label in the marketplace is not worthwhile for the platform when P ’s and S’s products are close substitutes because competition erodes both the profit earned through its private label and S’s profit. This effect becomes even stronger, in relative terms, when b grows large because in the pure intermediation model, P extracts a relatively higher share of S ’s monopoly profit.

What happens if the optimal accuracy varies across the two business models? There are two additional effects at play over and above those discussed before. First, other things being equal, the business model that induces information gathering features better targeted pricing and quality, thereby benefitting P. Second, since consumers have privacy concerns, demand falls in the regime in which P is informed, which ceteris paribus lowers its profit.

Bearing these effects in mind, we now investigate each of the two possible scenarios—i.e., $\eta ^{\star }=0<\eta ^{*}=1$ and $\eta ^{\star }=1>\eta ^{*}=0$.

Scenario 1$\ \eta ^{\star }=0<\eta ^{*}=1$. In this case, the relevant difference is

$$\begin{aligned} \pi ^{\star }\left( 0\right) -\pi ^{*}\left( 1\right) \triangleq 3A^{2}\Gamma \left( b,d\right) -\frac{b\left( 3\psi ^{2}+\sigma ^{2}+3A\left( A-2\psi \right) \right) }{6}+c. \end{aligned}$$

This expression is decreasing in $\sigma ^{2}$ and increasing in $\psi$. Intuitively, the higher volatility of demand, the less appealing the hybrid model is when it induces P to be uninformed because it cannot target consumers and price discriminate them. By contrast, the hybrid model becomes more suitable when consumers feature greater privacy concerns. Moreover, since the function $\Gamma \left( b,d\right)$is increasing in b (for given d) and decreasing in d (for given b), the impact of d is negative, meaning that a higher product substitutability tends to reduce the incentive of the platform to adopt a hybrid model: the more competition intra-platform, the lower the incentive to create rivalry with the private label. The effect of b is ambiguous: for given level of product differentiation, the higher the platform’s bargaining power vis-à-vis the seller, the higher its incentive to adopt a hybrid model because it can extract a higher share of the seller’s profit. Yet, the higher b, the greater the incentive to monopolize the market through the choice of a pure intermediation model. This second effect, becomes more prominent when demand is more uncertain (i.e., for higher values of $\sigma ^{2}$) and less prominent when consumers’ privacy concerns are stronger (i.e., for higher values of $\psi$).

Hence, when $b\rightarrow 0$, the platform prefers the hybrid model since the pure-intermediation model guarantees relatively small profits (recall that $\Gamma \left( 0,d\right) >0$). Consider thus the polar case in which $b\rightarrow 1$. In this case, we know that $c^{\star }<c^{*}$ for $\psi \le \psi ^{*}$ and $d\ge d^{*}$. As a result, $\eta ^{\star }=0$ and $\eta ^{*}=1$ for any $c\in \left[ c^{\star },c^{*}\right]$. Figure 3 plots the difference $\pi ^{\star }\left( 0\right) -\pi ^{*}\left( 1\right)$at $c=0$ (which is a conservative scenario since we know that $c>0$ in the region of parameters under consideration) in the space $\left( A,d\right) \in [2,+\infty )\times [d^{*},0.5)$ for $\psi =\sigma =1$ (recall that $A\ge \sigma +\psi$, hence we need $A\ge 2$ ).

Fig. 3

Information acquisition and profits

The figure shows that $\pi ^{\star }\left( 0\right) >\pi ^{*}\left( 1\right)$ in the relevant region of parameters. Hence, for large values of product substitutability, it is well possible that the preferred business model for the platform is the hybrid one and that this model minimizes the incentive to collect and disclose information, whereby protecting privacy. Yet, since $\pi ^{\star }\left( 0\right) -\pi ^{*}\left( 1\right)$ is decreasing in $\sigma ^{2}$ the incentive to choose a hybrid platform and be uninformed drops when the market becomes relatively more volatile—i.e., when $\sigma ^{2}$ rises.¹⁴

Scenario 2$\ \eta ^{\star }=1>\eta ^{*}=0$. In this case, the relevant difference is $\pi ^{*}\left( 0\right) -\pi ^{\star }\left( 1\right)$—i.e., this comparison applies when $d<d^{*}$ and for any $c\in \left[ c^{\star },c^{*}\right]$. It can be checked that

$$\begin{aligned} \pi ^{*}\left( 0\right) -\pi ^{\star }\left( 1\right) \triangleq b\frac{ A^{2}}{2}-\left( 3\psi ^{2}+\sigma ^{2}+3A\left( A-2\psi \right) \right) \Gamma \left( b,d\right) +c, \end{aligned}$$

which, as discussed above, is increasing in d and decreasing in $\psi$ and $\sigma ^{2}$. The impact of b is again ambiguous for the same reasons previously illustrated. For $b\rightarrow 0$, the expression above is clearly negative. Therefore, let us consider again the polar case $b=1$ and $d<d^{*}$ so that $c^{*}>c^{\star }$.Setting $c=0$ as before, in Fig. 4 we plot the above difference in the space $\left( A,d\right) \in [2,+\infty )\times [0,d^{*})$ for $\sigma =\psi =1$.

Fig. 4

Information acquisition and profits

The figure shows that the difference $\pi ^{*}\left( 0\right) -\pi ^{\star }\left( 1\right)$ is always positive for low values of A irrespective of d and for high values of d when A grows large. The reason why the difference is positive for b large is simple: intense intra-platform competition dissipates the sellers’ profits and therefore makes the pure intermediation model more appealing than the hybrid model. The reason why a higher A makes the hybrid model more appealing for intermediate values of d is due to the fact that the representative consumer features preference for variety, hence supplying more than one product in the platform is profitable when the consumer’s willingness to pay is sufficiently high.

3.5 Consumer surplus

What is the effect of the business model on consumer surplus? There are three intuitive effects that shape this relationship. First, recall that the hybrid model is positively biased towards consumer surplus. In fact, under this business model, there is one additional variety compared to the pure intermediation model, and consumers like to have more options (because the Sing and Vives (1984), utility function exhibits preference for variety). Second, irrespective of P’s information policy, the hybrid model yields a more competitive outcome that goes in the direction of increasing consumer surplus. Finally, privacy concerns also matter for consumers—i.e., other things being equal, they prefer the model that minimizes the incentive of the intermediary to collect information.

Building on these insights, in this section, we study the effect of the business model on consumer surplus. To neutralize the effect of product variety, we focus only on product 1 and study the effect of the business model on the part of the (representative) consumer’s expected utility function that pertains to this product, and not P’s product. Of course, it should be noted that such a restriction will somewhat bias results in favor of the pure intermediation model. Specifically, we compare (expected) consumer surplus in the pure intermediation model,

$$\begin{aligned} U(\eta )\triangleq \int _{-{\sigma } }^{\sigma }\mathbb {E}_{s}\left[ \left( A+\theta +x_{1}^{*}\left( s\right) \right) q_{1}^{*}\left( s\right) - \frac{1}{2}q_{1}^{*}\left( s\right) ^{2}-p_{1}^{*}\left( s\right) q_{1}^{*}\left( s\right) -\eta \psi q_{1}^{*}\left( s\right) |\theta \right] \frac{d\theta }{2\sigma }. \end{aligned}$$

(10)

with the following expression,

$$\begin{aligned} V(\eta )\triangleq \int _{-\sigma }^{\sigma }\mathbb {E}_{s}\left[ \left( A+\theta +x_{1}^{\star }\left( s\right) \right) q_{1}^{\star }\left( s\right) -\frac{1}{2}q_{1}^{\star }\left( s\right) ^{2}-p_{1}^{\star }\left( s\right) q_{1}^{\star }\left( s\right) -\eta \psi q_{1}^{\star }\left( s\right) |\theta \right] \frac{d\theta }{2\sigma }, \end{aligned}$$

(11)

which only accounts for the utility that consumers derive from product 1 in the hybrid model as it happens in the pure intermediation model.

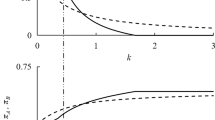
To gain insights on how P’s information policy affects consumer surplus, a first useful exercise is to plot the above expressions for different levels of the cost of privacy $\psi$. Figure 5 shows that they are decreasing in $\eta$for $\psi$ large and increasing or inverted-U shaped for low values of $\psi$.¹⁵

Fig. 5

Simulations of CS for given business model

Under both business models, an information policy with higher accuracy harms consumers when privacy concerns are strong enough ($\psi$ large), whereas a positive level of accuracy benefits consumers when privacy concerns are not too important ($\psi$ sufficiently low). The reason why consumers may prefer to disclose some information about their willingness to pay is clear: this information allows sellers to target price and quality more accurately—i.e., it avoids pricing high and setting quality high when demand is high and vice-versa.

With the above effects in mind, we can now compare expected utilities in the two business model. As before, it is useful to start the analysis by holding the level of accuracy constant across the two business models. Figure 6 simulates the difference $V(\eta )-U(\eta )$ as a function of d for alternative parametric restrictions.

Fig. 6

Difference in CS for given information acquisition decision

Hence, even when neutralizing the effect of the introduction of an additional variety in the hybrid model, conditional on the platform choosing the same information policy in both business models, consumer surplus is higher in the hybrid model than in the pure intermediation model. The reason is simple: for a given accuracy, in the hybrid model, S may loose business to P, which leads to a more competitive outcome.

Figure 7, instead, plots the difference between consumer surplus in the two models for different levels of accuracy.

Fig. 7

Difference in CS for different information acquisition decisions

Panel A shows that the hybrid model still performs better for consumers when $P$does not collect information in the hybrid mode ($\eta ^{\star }=0$ ) and it does so in the pure intermediation model ($\eta ^{*}=1$). Panel B illustrates the opposite scenario in which P collects information in the hybrid model and does not in the pure intermediation model: in this case, the hybrid model under-performs for low levels of d (weak competition or relatively differentiated products), while it still benefits consumers for relatively high values of d (intense competition or relatively close substitutes).

4 Extensions, robustness and further remarks

We now discuss some extensions of the baseline analysis to check its robustness and further issues that have been not addressed in the above analysis.

4.1 Alternative demand function

Instead of assuming the modified version of the Singh and Vives (1984) demand structure used in the baseline model, we consider now the following alternative specification for the representative consumer’s utility function

$$\begin{aligned} U(\cdot )\triangleq \underset{\text {Shubick-Levitan Utility}}{\underbrace{ \sum _{i=1}^{N}\left( A+\theta +x_{i}\right) q_{i}-\frac{d}{2\left( 1+d\right) }\left( \sum _{i=1}^{N}q_{i}\right) ^{2}-\frac{N}{2\left( 1+d\right) }\sum _{i=1}^{N}q_{i}^{2}-\sum _{i=1}^{N}p_{i}q_{i}}}-\underset{ \text {Privacy Concerns}}{\underbrace{\eta \psi \sum _{i=1}^{N}q_{i},}} \end{aligned}$$

where, as before, $N=1$ in the pure intermediation model, and $N=2$ in the hybrid model.

While privacy concerns are still as in the baseline model, the first part of the above expression corresponds to the standard Shubik-Levitan quadratic utility function (see, e.g., Motta, 2004, Ch. 8.4.2.), which is often used in the IO literature as an alternative specification to Singh and Vives (1984). The parameter $d\ge 0$ captures again the degree of product differentiation between products. As in the baseline model, we assume d not too large to avoid corner solutions—i.e., $d\le \frac{5}{2}.$

A somewhat nice property of using this alternative specification is that the analysis of the pure intermediation model does not change since both utility functions yield the same demand when $N=1$. Hence, we focus on the hybrid model. Differentiating the above utility function with respect to quantities and solving the corresponding system of first-order conditions we have the following demand functions

$$\begin{aligned} q_{i}\left( p_{i},p_{j},x_{i},x_{j},\theta \right) \triangleq \frac{A+\theta -\psi \eta +x_{i}-p_{i}}{2}+d\frac{\left( p_{j}-p_{i}\right) -\left( x_{j}-x_{i}\right) }{4}\quad \forall i,j=1,2. \end{aligned}$$

Following again a backward induction approach in solving the game (see the Appendix) we can state the following result.

Proposition 8

There exists a positive function ${\hat{\Gamma }}\left( b,d\right) \ge 0$ such that

$$\begin{aligned} {\hat{\pi }}^{\star }(s)\triangleq \left[ A+\eta \left( s-\psi \right) \right] ^{2}\Gamma _{SL}\left( b,d\right) . \end{aligned}$$

Hence, P’s expected profit net of the cost of collecting information with accuracy $\eta$ is

$$\begin{aligned} {\hat{\pi }}^{\star }\left( \eta \right) \triangleq \left( \eta ^{2}\left( 3\psi ^{2}+\sigma ^{2}\right) +3A\left( A-2\psi \eta \right) \right) \Gamma _{SL}\left( b,d\right) -c\eta . \end{aligned}$$

(12)

The optimal accuracy is such that $\eta ^{\star }=1$ only if $\psi \le \psi ^{*}$ and if

$$\begin{aligned} c\le c_{SL}^{\star }\triangleq \left( \sigma ^{2}-3\psi \left( 2A-\psi \right) \right) \Gamma _{SL}\left( b,d\right) . \end{aligned}$$

Otherwise, $\eta ^{\star }=0$.

The intuition is the same as in the baseline model. Therefore, comparing the outcome above with the results obtained for the pure intermediation model, we have

$$\begin{aligned} c_{SL}^{\star }\gtrless c^{*}\quad \Leftrightarrow \quad \Gamma _{SL}\left( b,d\right) \gtrless \frac{b}{6}. \end{aligned}$$

We can thus state the following.

Proposition 9

When $\psi \ge \psi ^{*}$ the signal is uninformative irrespective of the business model. By contrast, when $\psi <\psi ^{*}$, there exists a threshold $d_{0}\in \left( 0,\frac{5}{2}\right)$ such that:

• if $d\le d_{0}$ then $\eta ^{\star }=1$ and $\eta ^{*}=0$ for every $b\in \left[ 0,1\right] .$

• if $d>d_{0}$ then there exists a function $b_{0}\left( d\right) <1$, with $b_{0}^{\prime }\left( d\right) <0$, such that $\eta ^{\star }=0$ and $\eta ^{*}=1$ if and only if $b\ge b_{0}\left( d\right)$.

This result confirms that the findings of the baseline model extend to different consumer preferences. Figure 8 illustrates the result graphically by plotting the difference $\Gamma _{SL}\left( b,d\right) -\frac{ b}{6}$ (red surface) in the space $\left( b,d\right) \in \left[ 0,1\right] \times [0,\frac{5}{2})$.

Fig. 8

Incentives to acquire information

The figure shows that the difference $c_{SL}^{\star }-c^{*}$ is negative when b and d are both sufficiently large. Hence, P has a weaker incentive to collect information under the hybrid model than in the pure intermediation model when intra-platform competition is relatively intense (i.e., when d is sufficiently large) and when P has strong bargaining position vis-à-vis S (i.e., when b is sufficiently large).

4.2 Decentralized market decisions

So far, we assumed that P and its retail unit (hereafter R) are vertically integrated and that the pricing and the marketing decisions are centralized at the platform level—i.e., they are chosen to maximize P ’s and R’s joint profit. We now assume, on the contrary, that R has full discretion in choosing product 2’s price and quality. As in the baseline model, we posit again the Singh and Vives (1984) utility function.

While the pure intermediation model is unaffected by this hypothesis, in the hybrid model the equilibrium is symmetric because R only cares about product 2’s profit. The optimal accuracy (see the Appendix) is 1 only if $\psi \le \psi ^{*}$ and if

$$\begin{aligned} c\le c_{D}^{\star }\triangleq \left( \sigma ^{2}-3\psi \left( 2A-\psi \right) \right) \Gamma _{D}\left( b,d\right) , \end{aligned}$$

with

$$\begin{aligned} \Gamma _{D}\left( b,d\right) \triangleq \frac{\left( 1+b\right) \left( 1-2d^{2}\right) }{6\left( 1+d\left( 1-d\right) \right) ^{2}}. \end{aligned}$$

In Fig. 9 we compare the incentives to collect information in the two business models by plotting the difference $\Gamma _{D}\left( b,d\right) - \frac{b}{6}$.

Fig. 9

Impact of b and d on the incentive to acquire information

Hence, the qualitative results of the baseline model hold even with vertical delegation. Interestingly, by comparing Figs. 2 and 9 it can be seen that the incentive of the hybrid platform to remain uninformed is stronger when it delegates the pricing and the targeting decisions to the retail unit. In other words, platforms where decision rights are likely to be delegated to their retail units, have weaker incentives to gather and disclose information than platforms featuring a highly hierarchal organization and centralized decision ‘nodes’.

4.3 Multiple sellers

The case of multiple sellers competing in the marketplace is rather intuitive. Consider for example a representative consumer with preferences defined by the following utility function

$$\begin{aligned} U(\cdot )\triangleq \sum _{i=1}^{M}\left( A+\theta +x_{i}\right) q_{i}-\frac{1 }{2}\sum _{i=1}^{M}q_{i}^{2}-d\sum _{j=1}^{M}\sum _{i\ne j}^{M}q_{i}q_{j}-\sum _{i=1}^{M}p_{i}q_{i}-\eta \psi M\sum _{i=1}^{M}q_{i}, \end{aligned}$$

(13)

where $M=N$ in the pure intermediation model, and $M=N+1$ in the hybrid model.¹⁶

Notably, dealing with more than one seller allows us to introduce an aspect that we had neglected so far. Precisely, we now assume that privacy concerns are increasing with the number N of sellers (each denoted by $S_{i}$, with $i=1,..,N$) to which P discloses information (again, we assume no discrimination in the sense that the information collected by P must be disclosed to all sellers listed in the platform).¹⁷ The idea is that the more sellers manage consumer personal data, the more likely it is that some information lands in the wrong hands, whereby hurting consumers.

In this framework, we show (see the Appendix) that when $b,\ d$ and N are sufficiently large, P has no incentive to gather and disclose information in the hybrid model, whereas it gathers information when acting as a pure intermediary. The intuition is essentially the same as in the baseline model. Indeed, an increased number of varieties is just another way of measuring competition within the marketplace: the more varieties there are, the lower will be the market share of each seller, and therefore the more intense competition will be.

One interesting aspect has to do with the impact of the number of varieties on the incentive to gather information within each business model. Two main contrasting forces are at play. First, when the number of varieties increases, other things being equal, the platform is more willing to gather information and allow sellers to make more accurate decisions, so to extract a higher profit from them. Second, recall that in this framework, privacy concerns are increasing in N. Hence, when the number of sellers is too large, gathering information triggers significant privacy concerns, whereby refraining the platform from being informed. When N is small, the first effect dominates; otherwise, the second effect dominates. Hence, while for large values of d the effect of an increase in N is likely to be negative in both business models, for small values of d there is an inverted-U shaped pattern (see the Appendix).

4.4 Endogenous listing fees

So far, we have considered an efficient profit-sharing (bargaining) rule to isolate the effects of information gathering from those of double marginalization. Yet, in reality, platforms charge either per-unit fees (i.e., sellers pay platforms a fee for each unit distributed through the platform) or ad-valorem fees (i.e., they extract a percentage of the price charged to final consumers). In both cases, a double marginalization phenomenon occurs at equilibrium. The extent to which information gathering affects the seller’s incentive to pass on the listing fee to final consumers determines another channel through which the platform’s business model alters the incentive to gather information. In what follows, we discuss how the introduction of these contractual frictions is likely to change our results.

Ad-valorem fee. In the online Appenix we show that with an ad-valorem feee P has a greater incentive to gather information in the hybrid model than in the pure intermediation model, and this incentive drops as products become closer substitutes. The reason is as follows. As standard in the literature, with zero marginal cost downstrea, P fully extracts S ’s revenue with an ad-valorem fee, so that S does not invest in quality/advertising. This fact grants P a competitive advantage in the sense that the demand for its private label is not reduced by the rivals’ investment, and thus the information that it collects will be used only to target quality/advertising of its own brand without fearing that the rival will do the same. Of course, when products become closer substitutes, competition intensifies in the hybrid marketplace and S uses the information received from P to set prices more competitively, thereby mitigating P’s incentive to gather information.

What would happen with a positive marginal cost? In this case, the optimal ad-valorem fee will typically be lower than 1.¹⁸ Therefore, S will earn a positive profit margin and invest (i.e., $x_{2}>0$ ). This will, in turn, spoil P’s competitive advantage discussed above and make results closer to the baseline model. That is, P may have a stronger incentive to acquire information in the pure intermediation model than in the hybrid model when d is sufficiently large: in this case, S will compete more aggressively on both dimensions (marketing and pricing), which may reverse the above result.

Linear per-unit fee The same logic illustrated above applies with a linear per-unit fee. The hybrid model yields a higher incentive to gather information. Interestingly, in contrast to the case of an ad-valorem fee, this difference is U-shaped with respect to d (see the online Appendix). As the degree of product differentiation varies, there are two effects that shape P’s relative incentive to gather information. When products are sufficiently differentiated (d small), an increase in d makes P relatively less willing to gather information under the hybrid model because S will use this information to set price and quality more competitively. When instead products are close substitutes (d large), prices are not too distant one from the other, and P becomes relatively more willing to collect information under the hybrid model because this information will be used by S to target demand and create more vertical differentiation, which ceteris paribus benefits P too.

5 Conclusions

Consumer privacy is at the heart of the policy debate on the benefits and costs of the digital revolution. The extensive use and exchange of consumer data call for a deeper understanding of the forces shaping platforms’ incentives to collect such information.

In this paper, we have contributed to the growing literature on platforms’ organization by investigating the role of business models as drivers of the accuracy of consumer information collected by platforms. We have argued that there is no objective presumption that pure intermediation platforms collect more or less information than hybrid platforms. Platforms’ business model is not neutral to data collection. This observation should be considered carefully by privacy authorities, especially because in the EU the GDPR is based on the ’data minimization principle.’ Specifically, we have concluded that the relationship between the business model and the platform’s incentive to collect consumer information depends on the degree of intra-platform competition and platforms’ bargaining strength vis-à-vis third-party sellers. Pure intermediation platforms are less likely to collect and disclose information than hybrid ones when their bargaining position is not too strong—e.g., because of intense inter-platform competition—and their private labels are highly differentiated from their third-party rivals’ products; the opposite holds otherwise.

We have made a few assumptions to obtain these results and have thus purposefully neglected some relevant aspects of platform markets. For example, we have neglected platform competition and ecosystem effects—e.g., investments made by platforms to benefit all participants to their marketplaces but at the expense of competing platforms. These two aspects are gaining growing importance in online markets, especially regarding the difference between open and closed ecosystems/platforms. We have also assumed away repeated interaction and collusion, a prominent issue in digital markets in light of the recent developments on algorithmic collusion (e.g., Calvano et al., 2020). Finally, while we have primarily focused on an efficient contracting rule to identify the pure relationship between information acquisition and the platform’s business models, our results suggest that the presence of double marginalization (as induced by inefficient contracting rules) may impact such a relationship in a more complex way. All these aspects are on our research agent, and we hope to explore them and other additional interesting elements of platform markets soon.

Appendix

Proof of Proposition 1

Taking the difference between $\pi ^{*}\left( 1\right)$ and $\pi ^{*}\left( 0\right)$, we have

$$\begin{aligned} \pi ^{*}\left( 1\right) -\pi ^{*}\left( 0\right) =\frac{b\left( \sigma ^{2}-3\psi \left( 2A-\psi \right) \right) }{6}-c, \end{aligned}$$

which in the relevant range of parameters is negative if and only if

$$\begin{aligned} \psi \ge \psi ^{*}\triangleq A-\sqrt{A^{2}-\frac{\sigma ^{2}}{3}}. \end{aligned}$$

Hence, $\pi ^{*}\left( 1\right) \ge \pi ^{*}\left( 0\right)$ only if $\psi \le \psi ^{*}$ and if

$$\begin{aligned} c\le c^{*}\triangleq \frac{b\left( \sigma ^{2}-3\psi \left( 2A-\psi \right) \right) }{6}, \end{aligned}$$

which shows the result. $\square$

Proof of Proposition 2

With an hybrid platform, the market equilibrium is obtained by solving the system of first-order conditions (5)–(8). Moreover, it can be shown that

$$\begin{aligned} p_{2}^{\star }\left( s\right) -p_{1}^{\star }\left( s\right) =-\frac{ bd^{2}\left( 1-d^{2}\right) \left( A+\eta \left( s-\psi \right) \right) }{ 1-bd^{2}\left( 1-d^{2}\right) -d^{2}\left( 3-d^{2}\right) }\le 0, \end{aligned}$$

and that

$$\begin{aligned} x_{2}^{\star }\left( s\right) -x_{1}^{\star }\left( s\right) =\frac{1}{ 1-d^{2}}\left( p_{1}^{\star }\left( s\right) -\left( 1+bd\right) p_{2}^{\star }\left( s\right) \right) , \end{aligned}$$

which is negative since $p_{1}^{\star }\left( s\right) \le p_{2}^{\star }\left( s\right) .$ $\square$

Proof of Lemma 3

Conditional on observing signal s, P ’s expected profit is

$$\begin{aligned}\pi ^{\star }(s)&\triangleq \mathbb {E}\left[ q_{2}\left( p_{2}^{\star }\left( s\right) ,p_{2}^{\star }\left( s\right) ,x_{2}^{\star }\left( s\right) ,x_{1}^{\star }\left( s\right) ,\theta \right) |s\right] p_{2}^{\star }\left( s\right) -\frac{x_{2}^{\star }\left( s\right) ^{2}}{2} \\&\quad +b\left[ \mathbb {E}\left[ q_{1}\left( p_{1}^{\star }\left( s\right) ,p_{2}^{\star }\left( s\right) ,x_{1}^{\star }\left( s\right) ,x_{2}^{\star }\left( s\right) ,\theta \right) |s\right] p_{1}^{\star }\left( s\right) - \frac{x_{1}^{\star }\left( s\right) ^{2}}{2}\right] . \end{aligned}$$

It can be shown that

$$\begin{aligned} \pi ^{\star }(s)=\left( A+\eta \left( s-\psi \right) \right) ^{2}\Gamma \left( b,d\right) , \end{aligned}$$

with

$$\begin{aligned}&\Gamma \left( d,b\right) \triangleq \frac{\left( 1-2d^{2}\right) \left( 1-d\left( 1+d\right) \right) ^{2}}{6\left( 1-bd^{2}\left( 1-d^{2}\right) -d^{2}\left( 3-d^{2}\right) \right) ^{2}} \\&\quad +\frac{\left( 1-d\left( 1+d\right) \right) \left( 1-d-5d^{2}+4d^{3}+4d^{4}-2d^{5}\right) b}{6\left( 1-bd^{2}\left( 1-d^{2}\right) -d^{2}\left( 3-d^{2}\right) \right) ^{2}} \\&\quad -\frac{d^{2}\left( 1-2d\right) \left( 1-d\right) ^{2}\left( 1+d\right) ^{2}b^{2}}{6\left( 1-bd^{2}\left( 1-d^{2}\right) -d^{2}\left( 3-d^{2}\right) \right) ^{2}}. \end{aligned}$$

Hence, integrating $\pi ^{\star }(s)$with respect to s we have

$$\begin{aligned} \pi ^{\star }\left( \eta \right) \triangleq \int _{-\sigma }^{\sigma }\pi ^{\star }\left( s\right) \frac{ds}{2\sigma }-c\eta =\left( \eta ^{2}\left( 3\psi ^{2}+\sigma ^{2}\right) +3A\left( A-2\psi \eta \right) \right) \Gamma \left( b,d\right) -c\eta , \end{aligned}$$

which establishes the result. $\square$

Proof of Proposition 4

Comparing $\pi ^{\star }\left( 1\right) \,$with $\pi ^{\star }\left( 0\right)$ we have

$$\begin{aligned} \pi ^{\star }\left( 1\right) -\pi ^{\star }\left( 0\right) =\left( \sigma ^{2}-3\psi \left( 2A-\psi \right) \right) \Gamma \left( b,d\right) -c, \end{aligned}$$

Hence, $\pi ^{\star }\left( 1\right) \ge \pi ^{\star }\left( 0\right)$ only if $\psi \le \psi ^{*}$ and if

$$\begin{aligned} c\le c^{\star }\triangleq \left( \sigma ^{2}-3\psi \left( 2A-\psi \right) \right) \Gamma \left( b,d\right) \text {,} \end{aligned}$$

which concludes the proof. $\square$

Proof of Proposition 6

Showing that if $\psi \ge \psi ^{*}$ then P does not collect information regardless of the business model is straightforward. Consider then $\psi <\psi ^{*}$. Using the expression for $\Gamma \left( d,b\right)$ we have

$$\begin{aligned} \Gamma \left( d,0\right) =\frac{1-2d^{2}}{6\left( 1+d\left( 1-d\right) \right) ^{2}}>0, \end{aligned}$$

which immediately implies that for $b\rightarrow 0$ the incentive to collect information is stronger in the hybrid model than in the pure intermediation model for every admissible level of d.

Next, using the expression for $\Gamma \left( d,b\right)$ again

$$\begin{aligned} \Gamma \left( d,1\right) =\frac{ 2-4d-9d^{2}+18d^{3}+10d^{4}-18d^{5}-5d^{6}+4d^{7}}{6\left( 1-4d^{2}+2d^{4}\right) ^{2}}, \end{aligned}$$

so that, for $\psi \le \psi ^{*}$, it follows that

$$\begin{aligned} c^{\star }\ge c^{*}\quad \Leftrightarrow \quad \Gamma \left( d,1\right) \ge \frac{1}{6}, \end{aligned}$$

which is true for $d\ge d^{*}\approx 0.4$ (as shown in Fig. 2). $\square$

Proof of Corollary 6

The proof follows immediately by inspection of Fig. 2.

Consumer surplus The simulation done for consumer surplus obtains by substituting the equilibrium values of prices and advertising levels into Eqs. (11) and (10). We find that

$$\begin{aligned} U\left( \eta \right) =\frac{\eta +3d^{2}\eta ^{2}-30d\eta -\eta ^{3}+76}{6}, \end{aligned}$$

which is plotted for $\psi =0$ (Panel B.1) and $\psi =1$ (Panel B.2) in Fig. 4.

By the same token we find that, in the same region of parameters,

$$\begin{aligned} V\left( \eta \right) =13.352+0.52763d^{2}\eta ^{2}-5.2763d\eta +\frac{1.3839 }{100}\eta ^{2}, \end{aligned}$$

which is plotted for $\psi =0$ (Panel A.1) and $\psi =1$ (Panel A.2) in Fig. 4.

For alternative values of b, in Fig. 5 we plot the differences

$$\begin{aligned}V\left( 0\right) -U\left( 0\right) &=\tfrac{d^{2}\left( 74+298d+301d^{2}+2d^{3}-76d^{4}\right) \left( 1-d\left( 1+d\right) \right) ^{2}}{6\left( 1+d\right) ^{2}\left( 1-bd^{2}\left( 1-d^{2}\right) -d^{2}\left( 3-d^{2}\right) \right) ^{2}} \\&\quad +\tfrac{2d^{3}\left( 1-d\right) \left( d+1\right) \left( 1-d\left( 1+d\right) \right) \left( 75+76d-74d^{2}-76d^{3}\right) b}{6\left( 1+d\right) ^{2}\left( 1-bd^{2}\left( 1-d^{2}\right) -d^{2}\left( 3-d^{2}\right) \right) ^{2}}-\tfrac{d^{4}\left( 150d+76d^{2}+75\right) \left( 1-d\right) ^{2}\left( 1+d\right) ^{2}b^{2}}{6\left( 1+d\right) ^{2}\left( 1-bd^{2}\left( 1-d^{2}\right) -d^{2}\left( 3-d^{2}\right) \right) ^{2}}, \end{aligned}$$

and

$$\begin{aligned}V\left( 1\right) -U\left( 1\right) &=\tfrac{49d^{2}\left( 1+2d-d^{2}\right) \left( 1-d\left( 1+d\right) \right) ^{2}}{6\left( 1-bd^{2}\left( 1-d^{2}\right) -d^{2}\left( 3-d^{2}\right) \right) ^{2}} \\&\quad +\tfrac{49d^{2}2bd\left( 1+d\right) \left( 1-d\left( 1+d\right) \right) \left( 1-d\right) ^{2}}{6\left( 1-bd^{2}\left( 1-d^{2}\right) -d^{2}\left( 3-d^{2}\right) \right) ^{2}}-\tfrac{49b^{2}d^{4}\left( 1-d\right) ^{2}\left( 1+d\right) ^{2}}{6\left( 1-bd^{2}\left( 1-d^{2}\right) -d^{2}\left( 3-d^{2}\right) \right) ^{2}}. \end{aligned}$$

Finally, for alternative values of b, in Fig. 6 we plot the differences

$$\begin{aligned}V(0)-U(1)&=\tfrac{\left( 27+108d+182d^{2}+244d^{3}+193d^{4}+2d^{5}-49d^{6}\right) \left( 1-d\left( 1+d\right) \right) ^{2}}{6\left( 1-bd^{2}\left( 1-d^{2}\right) -d^{2}\left( 3-d^{2}\right) \right) ^{2}} \\&\quad -\tfrac{2bd^{2}\left( 1-d\right) \left( d+1\right) \left( 1-d\left( 1+d\right) \right) \left( 6d-22d^{2}+47d^{3}+49d^{4}+27\right) .}{6\left( 1-bd^{2}\left( 1-d^{2}\right) -d^{2}\left( 3-d^{2}\right) \right) ^{2}}- \tfrac{b^{2}d^{4}\left( 96d+49d^{2}+48\right) \left( 1-d\right) ^{2}\left( 1+d\right) ^{2}.}{6\left( 1-bd^{2}\left( 1-d^{2}\right) -d^{2}\left( 3-d^{2}\right) \right) ^{2}} \end{aligned}$$

and

$$\begin{aligned}V(1)-U(0)&=-\tfrac{\left( 27+54d-76d^{2}-152d^{3}+76d^{4}\right) \left( 1-d\left( 1+d\right) \right) ^{2}}{6\left( 1-bd^{2}\left( 1-d^{2}\right) -d^{2}\left( 3-d^{2}\right) \right) ^{2}} \\&\quad -\tfrac{2bd^{2}\left( 1-d\right) \left( 1+d\right) \left( -76d+76d^{2}-27\right) \left( 1-d\left( 1+d\right) \right) }{6\left( 1-bd^{2}\left( 1-d^{2}\right) -d^{2}\left( 3-d^{2}\right) \right) ^{2}}- \tfrac{76b^{2}d^{4}\left( 1-d\right) ^{2}\left( d+1\right) ^{2}}{6\left( 1-bd^{2}\left( 1-d^{2}\right) -d^{2}\left( 3-d^{2}\right) \right) ^{2}}. \end{aligned}$$

Proof of Proposition 9

Solving the system of first-order conditions we have

$$\begin{aligned}p_{1}^{\star }\left( s\right)& \triangleq \frac{4\left( 2\left( 3+d\right) +d\left( 1-bd\right) +d\left( b-d\right) \right) }{36+20d+4d\left( 1-bd\right) -d^{2}\left( 3+d\right) }\left( A+\eta \left( s-\psi \right) \right) \\ \le p_{2}^{\star }\left( s\right) &\triangleq \frac{4\left( 2\left( 3+d\right) +d\left( 1-d\right) \right) }{36+20d+4d\left( 1-bd\right) -d^{2}\left( 3+d\right) }\left( A+\eta \left( s-\psi \right) \right) , \end{aligned}$$

$$\begin{aligned}x_{1}^{\star }\left( s\right) &=\frac{12\left( 1+d\right) -4bd\left( 1+d\right) +d^{2}\left( 1-d\right) }{36+20d+4d\left( 1-bd\right) -d^{2}\left( 3+d\right) }\left( A+\eta \left( s-\psi \right) \right) \\ \le x_{2}^{\star }\left( s\right) &=\frac{\left( 2+d\right) \left( 2\left( 3+d\right) +d\left( 1-d\right) \right) }{36+20d+4d\left( 1-bd\right) -d^{2}\left( 3+d\right) }\left( A+\eta \left( s-\psi \right) \right) . \end{aligned}$$

Substituting these values into P’s expected profit, we have

$$\begin{aligned} \pi _{SL}^{\star }\left( \eta \right) \triangleq \left( \eta ^{2}\left( 3\psi ^{2}+\sigma ^{2}\right) +3A\left( A-2\psi \eta \right) \right) \Gamma _{SL}\left( b,d\right) -c\eta \end{aligned}$$

with

$$\begin{aligned}\Gamma _{SL}\left( d,b\right) & \triangleq \frac{\left( d+2\right) \left( 6-d\right) \left( 6+d\left( 3-d\right) \right) ^{2}}{6\left( 36+20d+4d\left( 1-bd\right) -d^{2}\left( 3+d\right) \right) ^{2}} \\&\quad +\frac{\left( 6+d\left( 3-d\right) \right) \left( 2\left( 36+19d\right) +22d\left( 1-d\right) -d^{3}\left( 7-d\right) \right) b}{6\left( 36+20d+4d\left( 1-bd\right) -d^{2}\left( 3+d\right) \right) ^{2}} \\&\quad -\frac{6d^{2}\left( 1+d\right) \left( 3-d\right) b^{2}}{6\left( 36+20d+4d\left( 1-bd\right) -d^{2}\left( 3+d\right) \right) ^{2}}. \end{aligned}$$

The function $\pi _{SL}^{\star }\left( \eta \right)$ is again convex in $\eta$. Hence, comparing $\pi _{SL}^{\star }\left( 1\right)$ with $\pi _{SL}^{\star }\left( 0\right)$ we obtain that $\eta _{h}^{\star }=1$ only if

$$\begin{aligned} \psi \le \psi ^{*}\triangleq A-\sqrt{A^{2}-\frac{\sigma ^{2}}{3}}, \end{aligned}$$

and if

$$\begin{aligned} c\le c_{SL}^{\star }\triangleq \left( \sigma ^{2}-3\psi \left( 2A-\psi \right) \right) \Gamma _{SL}\left( d,b\right) . \end{aligned}$$

The proof of the result is then directly implied by Fig. 8. $\square$

Decentralized decisions and the value of information First, notice that in the pure intermediation model nothing changes. By contrast, in the hybrid model, with decentralized decisions, the equilibrium of the market game is symmetric—i.e.,

$$\begin{aligned} p^{\star }\left( s\right) =\frac{\left( 1-d^{2}\right) \left( 1-d\left( 1+d\right) \right) \left( A+\eta \left( s-\psi \right) \right) }{ 1-d^{2}\left( 3-d^{2}\right) }, \end{aligned}$$

and

$$\begin{aligned} x^{\star }\left( s\right) =\frac{\left( 1-d\left( 1+d\right) \right) \left( A+\eta \left( s-\psi \right) \right) }{1-d^{2}\left( 3-d^{2}\right) }. \end{aligned}$$

Hence,

$$\begin{aligned} \pi _{D}^{\star }(s)\triangleq \mathbb {E}\left[ q_{1}\left( \cdot \right) +bq_{2}\left( \cdot \right) |s\right] p^{\star }\left( s\right) -\left( 1+b\right) \frac{x^{\star }\left( s\right) ^{2}}{2}=\left[ A+\eta \left( s-\psi \right) \right] ^{2}\Gamma _{D}\left( b,d\right) , \end{aligned}$$

with

$$\begin{aligned} \Gamma _{D}\left( d,b\right) =\frac{\left( 1+b\right) \left( 1-2d^{2}\right) }{6\left( 1+d\left( 1-d\right) \right) ^{2}}. \end{aligned}$$

Substituting $p^{\star }\left( s\right)$ and $x^{\star }\left( s\right)$ into $\pi _{D}^{\star }(s)$ and integrating, we have

$$\begin{aligned} \pi _{D}^{\star }(\eta )=\int _{-\sigma }^{\sigma }\pi _{D}^{\star }(s)\frac{ ds}{2\sigma }-c\eta =\left( \eta ^{2}\left( 3\psi ^{2}+\sigma ^{2}\right) +3A\left( A-2\psi \eta \right) \right) \Gamma _{D}\left( d,b\right) -c\eta . \end{aligned}$$

Hence, when P delegates the pricing and advertising decisions to R, it collects and discloses information only if $\psi \le \psi ^{*}$ and if

$$\begin{aligned} c\le c_{D}^{\star }\triangleq \left( \sigma ^{2}-3\psi \left( 2A-\psi \right) \right) \Gamma _{D}\left( d,b\right) . \end{aligned}$$

In Fig. 8 we plot the difference between $\Gamma _{D}\left( d,b\right)$ and $\frac{b}{6}$, which shows immediately that the results of the baseline model hold qualitatively also with decentralized decision making.

Multiple sellersDifferentiating the utility function (13) with respect to quantities, we obtain the following system of first-order conditions

$$\begin{aligned} A+\theta +x_{i}-q_{i}-d\sum \nolimits _{j\ne }q_{j}-p_{i}-\eta M\psi =0\quad \forall i=1,..,M, \end{aligned}$$

whose solution yields the system of direct demand functions

$$\begin{aligned} q_{i}\left( \cdot \right) =\frac{A+\theta -M\psi \eta }{1+\left( M-1\right) d }-\frac{\left( 1+\left( M-2\right) d\right) \left( p_{i}-x_{i}\right) -d\sum \nolimits _{j\ne i}\left( p_{j}-x_{j}\right) }{\left( 1+\left( M-1\right) d\right) \left( 1-d\right) },\quad \forall i=1,..,M. \end{aligned}$$

We assume $A-\sigma -M\psi \ge 0$ to guarantee positive prices and quantities. Recall that $M=N$ in the pure intermediation model, and $M=N+1$ in the hybrid model. For simplicity, assume $b=1$.

Consider first a pure intermediary. Focus on a symmetric equilibrium in which every seller chooses $p^{N}\left( s\right)$ and $x^{N}\left( s\right)$. Seller i solves the following maximization problem

$$\begin{aligned} \max _{p_{i}\ge 0,x_{i}\ge 0}\mathbb {E}\left[ q_{i}\left( \cdot \right) |s \right] p_{i}-\frac{x_{i}^{2}}{2}, \end{aligned}$$

whose first-order conditions with respect to $p_{i}$ and $x_{i}$, are respectively

$$\begin{aligned} \frac{A+\left( s-N\psi \right) \eta }{1+\left( N-1\right) d}-\frac{\left( 1+\left( N-2\right) d\right) \left( 2p^{N}\left( s\right) -x^{N}\left( s\right) \right) -d(N-1)\left( p^{N}\left( s\right) -x^{N}\left( s\right) \right) }{\left( 1+\left( N-1\right) d\right) \left( 1-d\right) }=0, \end{aligned}$$

and

$$\begin{aligned} \frac{1+\left( N-2\right) d}{\left( 1+\left( N-1\right) d\right) \left( 1-d\right) }p^{N}\left( s\right) -x^{N}\left( s\right) =0. \end{aligned}$$

The intuition behind these conditions is the same as in the baseline model, and will be omitted for brevity. The solution is

$$\begin{aligned} p^{N}\left( s\right) =\frac{\left( 1-b\right) \left( 1+b\left( N-1\right) \right) \left( A+\left( s-\psi N\right) \eta \right) }{1-3b\left( 1-b\right) -4b^{2}N+b^{2}N^{2}+2bN}, \end{aligned}$$

$$\begin{aligned} x^{N}\left( s\right) =\frac{\left( 1+b\left( N-2\right) \right) \left( A+\left( s-\psi N\right) \eta \right) }{1-3b\left( 1-b\right) -4b^{2}N+b^{2}N^{2}+2bN}. \end{aligned}$$

Substituting the equilibrium outcomes into P’s expected profit, we have

$$\begin{aligned}&\quad N\int _{-\sigma }^{\sigma }\left\{ \mathbb {E}\left[ q_{i}\left( \cdot \right) |s\right] p_{N}^{*}\left( s\right) -\frac{x_{N}^{*}\left( s\right) ^{2}}{2}\right\} \frac{ds}{2\sigma }-\eta c \\& =\left( \eta ^{2}\left( \sigma ^{2}+3\psi ^{2}N^{2}\right) +3A\left( A-2A\psi N\eta \right) \right) \Gamma _{p}^{N}\left( N,d\right) -c\eta , \end{aligned}$$

with

$$\begin{aligned} \Gamma _{p}\left( N,d\right) \triangleq \frac{\left( 1-d-2Nd^{2}+Nd\right) \left( N+1\right) \left( 1+\left( N-1\right) d\right) }{6\left( 1-d-2Nd^{2}+N^{2}d^{2}+2Nd\right) ^{2}}. \end{aligned}$$

Hence, P collects information only if

$$\begin{aligned} \psi \le \psi _{N}^{*}=\frac{A}{N}-\frac{1}{N}\sqrt{A^{2}-\frac{\sigma ^{2}}{3},} \end{aligned}$$

and if

$$\begin{aligned} c\le c_{N}^{*}\triangleq \left( \sigma ^{2}-3N\psi \left( 2A-N\psi \right) \right) \Gamma \left( N,d\right) . \end{aligned}$$

In the hybrid model there are $N+1$ products distributed through the platform. Consider an equilibrium in which P sets $p_{N+1}^{N}\left( s\right)$ and $x_{N+1}^{N}\left( s\right)$, whereas its N rivals set $p_{h}^{N}\left( s\right)$ and $x_{h}^{N}\left( s\right)$.

The first-order conditions associated with each $S_{i}$’s maximization problem are

$$\begin{aligned} A+\left( s-N\psi \right) \eta =\frac{\left( 1+\left( N-1\right) d\right) \left( 2p_{h}^{N}\left( s\right) -x_{h}^{N}\left( s\right) \right) -d\left( N-1\right) \left( p_{h}^{N}\left( s\right) -x_{h}^{N}\left( s\right) \right) -d\left( p_{N+1}^{N}\left( s\right) -x_{N+1}^{N}\left( s\right) \right) }{1-d }, \end{aligned}$$

and

$$\begin{aligned} \frac{1+\left( N-1\right) d}{\left( 1+Nd\right) \left( 1-d\right) } p_{h}^{N}\left( s\right) -x_{h}^{N}\left( s\right) =0. \end{aligned}$$

P’s maximization problem is, instead,

$$\begin{aligned} \max _{x_{N+1},p_{N+1}}q_{N+1}\left( \cdot \right) p_{N+1}-\frac{x_{N+1}^{2}}{ 2}+\sum \nolimits _{i=1}^{N}\left( q_{i}\left( \cdot \right) p_{h}^{N}\left( s\right) -\frac{x_{h}^{N}\left( s\right) ^{2}}{2}\right) . \end{aligned}$$

Differentiating with respect to $p_{N+1}$ and $x_{N+1}$, the first-order conditions are

$$\begin{aligned} A+\left( s-N\psi \right) \eta -\frac{\left( 1+\left( N-1\right) d\right) \left( 2p_{N+1}^{N}\left( s\right) -x_{N+1}^{N}\left( s\right) \right) -dN\left( p_{h}^{N}\left( s\right) -x_{h}^{N}\left( s\right) \right) }{1-d}+ \frac{bNdp_{h}^{N}\left( s\right) }{1-d}=0, \end{aligned}$$

and

$$\begin{aligned} \frac{1+\left( N-1\right) d}{\left( 1+Nd\right) \left( 1-d\right) } p_{N+1}^{N}\left( s\right) -x_{N+1}^{N}\left( s\right) -\frac{ bNdp_{h}^{N}\left( s\right) }{\left( 1+Nd\right) \left( 1-d\right) }=0. \end{aligned}$$

The economic intuition for these conditions, which we omit for brevity, is straightforward and in line with the reasoning developed in the baseline model. The solution is

$$\begin{aligned}&p_{N+1}^{\star }\left( s\right) =\tfrac{\left( 1-d\right) \left( 1+d+Nd\right) \left( d+3Nd^{2}-Nd+2d^{2}-1\right) \left( A+(s-\psi N)\eta \right) }{ 4Nd^{2}+6Nd^{3}-4Nd^{4}-3N^{2}d^{2}+6N^{2}d^{3}-N^{3}d^{3}+2N^{3}d^{4}-3Nd+4d^{2}-2d^{4}-1 }, \\&p_{h}^{\star }\left( s\right) =\tfrac{\left( 1-b\right) \left( 1+b+Nb\right) \left( b+2Nb^{2}-Nb+b^{2}-1\right) \left( A+(s-\psi N)\eta \right) }{ 4Nb^{2}+6Nb^{3}-4Nb^{4}-3N^{2}b^{2}+6N^{2}b^{3}-N^{3}b^{3}+2N^{3}b^{4}-3Nb+4b^{2}-2b^{4}-1 }, \\&x_{N+1}^{\star }\left( s\right) =\tfrac{\left( 2d+4Nd^{2}-Nd^{3}+N^{2}d^{3}-Nd+d^{2}-d^{3}-1\right) \left( A+(s-\psi N)\eta \right) }{ 4Nd^{2}+6Nd^{3}-4Nd^{4}-3N^{2}d^{2}+6N^{2}d^{3}-N^{3}d^{3}+2N^{3}d^{4}-3Nd+4d^{2}-2d^{4}-1 }, \\&x_{h}^{\star }\left( s\right) =\tfrac{\left( d+2Nd^{2}-Nd+d^{2}-1\right) \left( Nd+1\right) \left( A+(s-\psi N)\eta \right) }{ 4Nd^{2}+6Nd^{3}-4Nd^{4}-3N^{2}d^{2}+6N^{2}d^{3}-N^{3}d^{3}+2N^{3}d^{4}-3Nd+4d^{2}-2d^{4}-1 }. \end{aligned}$$

Hence, substituting for the equilibrium prices and targeting levels, P’s expected profit is

$$\begin{aligned}&\int _{-\sigma }^{\sigma }\left\{ \mathbb {E}\left[ q_{N+1}\left( \cdot \right) |s\right] p_{N+1}^{N}\left( s\right) -\frac{x_{N+1}^{N}\left( s\right) ^{2}}{2}+\sum \nolimits _{i=1}^{N}\left( \mathbb {E}\left[ q_{i}\left( \cdot \right) |s\right] p_{h}^{N}\left( s\right) -\frac{x_{h}^{N}\left( s\right) ^{2}}{2}\right) \right\} \frac{ds}{2\sigma }-c\eta \\&\quad =\left( \eta ^{2}\left( \sigma ^{2}+3\psi ^{2}N^{2}\right) +3A\left( A-2A\psi N\eta \right) \right) \Gamma _{h}\left( N,d\right) -c\eta , \end{aligned}$$

with

$$\begin{aligned}\Gamma _{h}\left( N,d\right) &\triangleq \tfrac{ N-4d-31Nd^{2}+4N^{2}d+4Nd^{3}+79Nd^{4}-34Nd^{5}-46Nd^{6}+12Nd^{7}-N^{2}d^{2}-56N^{2}d^{3}+6N^{3}d^{2}+83N^{2}d^{4} }{6\left( 4Nd^{2}+6Nd^{3}-4Nd^{4}-3N^{2}d^{2}+6N^{2}d^{3}-N^{3}d^{3}+2N^{3}d^{4}-3Nd+4d^{2}-2d^{4}-1\right) ^{2}} \\&\quad -\tfrac{18N^{3}d^{3}-50N^{2}d^{5}+21N^{3}d^{4}-4N^{4}d^{3}+96N^{2}d^{6}-98N^{3}d^{5}+19N^{4}d^{4}+49N^{3}d^{6}-20N^{4}d^{5}-N^{5}d^{4} }{6\left( 4Nd^{2}+6Nd^{3}-4Nd^{4}-3N^{2}d^{2}+6N^{2}d^{3}-N^{3}d^{3}+2N^{3}d^{4}-3Nd+4d^{2}-2d^{4}-1\right) ^{2}} \\&\quad -\tfrac{30N^{3}d^{7}-19N^{4}d^{6}+6N^{5}d^{5}+30N^{4}d^{7}-12N^{5}d^{6}+8N^{5}d^{7}-6Nd+9d^{2}-18d^{3}-10d^{4}+18d^{5}+5d^{6}-4d^{7}-2 }{6\left( 4Nd^{2}+6Nd^{3}-4Nd^{4}-3N^{2}d^{2}+6N^{2}d^{3}-N^{3}d^{3}+2N^{3}d^{4}-3Nd+4d^{2}-2d^{4}-1\right) ^{2} }. \end{aligned}$$

Hence, also in hybrid model, P collects information only if $\psi \le \psi _{N}^{*}\,$and if

$$\begin{aligned} c\le c_{N}^{\star }\triangleq \left( \sigma ^{2}-3N\psi \left( 2A-N\psi \right) \right) \Gamma _{h}\left( N,d\right) . \end{aligned}$$

In Fig. 10 we plot the difference $\Gamma _{h}\left( N,d\right) -\Gamma _{p}\left( N,d\right)$ in the space $\left( N,b\right) \in [0,1/2)\times [1,+\infty )$

Fig. 10

Information acquisition and business model

The figure shows that, for $\alpha ~$large, in the region of parameters where d and N are high, the hybrid platform has a weaker incentive to collect and disclose information than a pure intermediary.

An interesting exercise is to study how the number of varieties affects the overall incentive to gather information. To this purpose, in Fig. 11, we plot the thresholds $c_{N}^{*}$ and $c_{N}^{\star }$ as functions of N for different parameter configurations.

Fig. 11

Simulations of critical costs

For large values of d the effect of an increase in N is negative in both business models, for small values of d there is an inverted-U shaped pattern.