Introduction

Sludge treatment reed bed (STRB) has become an attractive system to dewater and stabilize septage, which is a mixture of excreta and blackwater removed from the septic tanks. STRB is a vegetated granular bed that dewaters the sludge by separating the solids and liquid through gravity drainage and evapotranspiration, and it also promotes microbial-induced mineralization to stabilize the volatile organics in sludge (Nielsen & Stefanakis 2020). The operation of STRBs is simple, in which the sludge is loaded onto the top surface of the reed bed in batches, followed by a resting period to allow sludge dewatering and stabilization. During the treatment, the solids are retained at the top bed surface and form a deposit layer known as sludge residue or sludge deposits, while the water infiltrates and percolates through the granular bed and discharges as leachate (Hu et al. 2021). The STRBs could reduce sludge volume by more than 60% through gravity drainage dewatering, and the leachate was observed with a removal rate of 80% and 90% for total solids and Chemical Oxygen Demand, respectively (Jain et al. 2022). In addition, the loss of moisture content in the sludge deposits via the evapotranspiration (ET) process is also an important dewatering mechanism in STRB to increase the final solids content in the sludge deposits (Trein et al. 2019). Since STRB does not involve any chemicals during the treatment, the dewatered sludge deposits can be safely disposed of or used as fertilizer (Brix 2017).

The sludge dewatering through gravity drainage in STRBs is manifested by water flow through porous media, and its rate significantly depends on the grain size of the porous media used in the reed beds (Kołecka et al. 2016). The coarse-grained material, such as gravel, characterizes high hydraulic conductivity and guarantees excellent dewatering efficiency (Stefanakis 2020). The operating regime also plays an important role in the dewatering performance of STRBs, in which a higher hydraulic load rate (HLR) of raw sludge accelerates the drainage dewatering rate due to a larger head difference created (Osei et al. 2019). However, the sludge deposit accumulation on the reed bed, which is a layer with low effective porosity and hydraulic conductivity, could change the hydraulic behaviour (Molle 2013). Excessive sludge deposits could result in prolonged ponding in STRBs, resulting in the moisture content in sludge deposits being higher than the disposal limit at the end of the resting period (Tan et al. 2023). A study on the complex interactions among hydraulic load, solids load, and deposit layer is then necessary to optimize the operating regime in STRBs to achieve the targeted dewatering efficiency.

A process-based mathematical model is useful for optimizing the operating regime in STRBs. However, the application of the existing dewatering model developed using consolidation theory is limited since it only focuses on optimizing feeding frequency as a function of sludge deposit thickness and evapotranspiration (Uggetti et al. 2012). The water percolation through the reed bed can be simulated by means of a porous media flow model. Several porous media flow models are available to predict the hydraulic behaviour of vertical flow constructed wetland (VFCW), a system similar to STRB but treating the influent with low solid contents such as sewage and combined sewer overflow. Among these models, the model based on the Richards equation has been proven viable for simulating transient variably saturated flow in the wetland bed (Bassetto et al. 2022). However, as the sludge deposit accumulation is insignificant in VFCW due to the low solid contents in the influent, the assumption in these existing models is inadequate for the hydraulic behaviour in STRB. The effect of the sludge deposit layer on the dewatering processes in STRB has not been described using a simulation study. The high accumulation rate of the sludge deposits, which is a function of the solids load onto the reed beds, influences the water infiltration and, thus, the drainage dewatering efficiency. Furthermore, the loss of moisture content in the sludge deposits during the resting period may lead to the formation of cracks, which further alters the hydraulic behaviour, where the water flow tends to be a non-equilibrium, preferential flow across this compacted porous media (Tan et al. 2023).

This study aims to develop a one-dimensional process-based mathematical model to simulate the dewatering mechanism in STRBs with the consideration of the sludge deposit buildup. The proposed model incorporates the dual porosity variably saturated flow model and the Penman–Monteith equation to describe the dewatering through gravity drainage and evapotranspiration, respectively. In addition, the compressible cake filtration (CCF) theory is used to model the accumulation of sludge deposits on the reed bed, and the moving mesh method is adopted as the numerical method to integrate the change of the sludge deposit thickness with the porous flow model. The formulated model is then validated with experimental data from laboratory-scale STRBs treating septage. This study uses a novel numerical modelling approach to understanding the interactions between the sludge dewatering in STRB with respect to the bed characteristics, hydraulic load, and solid load.

Material and methods

Governing equations

Gravity drainage flow

Gravity drainage dewatering is simulated using a porous media flow model. Since the sludge is loaded onto the STRB in batches, the water flow across the reed bed is usually unsaturated. Moreover, the presence of plant rhizomes and sludge deposits creates preferential flow paths in the bed, which leads to the formation of stagnant water and affects the water flow pattern (Li & Yuan 2023). A dual porosity model has been proposed to improve the accuracy of water flow simulation (Tan et al. 2023). This model divides the liquid phase of the porous medium flow into the mobile and immobile regions, and then both regions are correlated using a mass transfer rate. The water flow only occurs in the mobile regions, which is expressed by modified Richards equation as follows:

$$\frac{{\partial \theta_{Mobile} }}{\partial t} = \frac{\partial }{\partial z}\left[ {K\left( {\theta_{Mobile} } \right)\frac{\partial h}{{\partial z}} } \right] - \frac{{\partial K\left( {\theta_{Mobile} } \right)}}{\partial z} --S_{Mobile} - \Gamma_w$$
(1)

where θMobile is the volumetric water content in the mobile region (m3/m3), h is the hydraulic head (m), t is the time (min), z is the vertical coordinate (m, assumed positive upwards), K is the unsaturated hydraulic conductivity (m/min), Гw is the water transfer rate (1/min), and S is the source/sink term (m/min). The source/sink term denotes the additional water due to precipitation or water loss via evapotranspiration.

The unsaturated hydraulic conductivity is determined using van Genuchten's model (VGM), which empirically estimates the unsaturated hydraulic conductivity based on the soil water characteristic curve:

$$\theta = \theta_r + \frac{{\left( {\theta_s - \theta_r } \right)}}{{\left[ {1 + \left( {\alpha \left| h \right|} \right)^n } \right]^m }}$$
(2)
$$K = K_s \left( {\frac{\theta - \theta_r }{{\theta_s - \theta_r }}} \right)^l \left[ {1 - \left( {1 - \left( {\frac{\theta - \theta_r }{{\theta_s - \theta_r }}} \right)^\frac{1}{m} } \right)^m } \right]^2$$
(3)

where θr is the residual water content (m3/m3), θs is the saturated water content (m3/m3), α (1/m), n (–), and m (–) are the empirical van Genuchten's shape parameters of the SWCC, Ks is the saturated hydraulic conductivity (m/min), and l is Mualem's pore connectivity parameter (–).

The stagnant water in the immobile region is described using a mass balance equation as:

$$\frac{{\partial \theta_{Immobile} }}{\partial t} = -S_{Immobile} + \Gamma_w$$
(4)

where θImmobile is the immobile volumetric water content (m3/m3), and SImmobile is the source or sink term of immobile water content (m/min). The mass transfer rate (MTR) between the mobile and immobile regions is estimated according to the gradient of effective saturation. This MTR is a function of a first-order mass transfer coefficient ω (1/min) and saturation level (–), which is expressed as:

$$\Gamma_w = \omega \left( {Se_{Mobile} - Se_{Immobile} } \right)$$
(5)

where the SeMobile (–) and SeImmobile (–) is the effective saturation in the mobile and immobile regions, respectively.

Evapotranspiration

The FAO-56 Penman–Monteith equation (Zotarelli et al. 2015) was adopted to calculate the potential evapotranspiration rate. The FAO-56 Penman–Monteith equation is a simplified attempt to estimate the potential water loss during infiltration within a specific area, and it has been verified feasible in simulating the sludge dewatering in STRB during the resting period (Uggetti et al. 2012). The overall water loss to the atmosphere through evapotranspiration is estimated as follows:

$$ET_o = \frac{1}{\lambda } \left[ { \frac{{\Delta \left( {R_n - G} \right) + \rho_a C_p \frac{{\left( {e_s - e_a } \right)}}{r_a }}}{{\Delta + \gamma \left( {1 + \frac{r_c }{{r_a }} } \right)}}} \right]$$
(6)

where ET0 is the PET rate (mm/s), λ is the latent heat of vaporization (J/g), Rn is the net radiation at the surface (W/m2), G is the soil heat flux (W/m2), ρa is the atmospheric density (kg/m3), Cp is the specific heat of moist air (J/kg/K), es is the saturation vapor pressure at a particular temperature (Pa), ea is the actual vapour pressure (Pa), rc is the crop canopy resistance (m/s), ra is the aerodynamic resistance (m/s), γ is the psychrometric constant (Pa/K), and Δ is the slope of the vapor pressure curve (Pa/K).

However, the Penman–Monteith equation only estimates the total water loss, but in fact, evaporation is limited to the water loss from the water surface, while transpiration may occur from the surface to a certain depth, depending on the root distribution of vegetation. In the proposed model, Beer–Lambert Law (Varado et al. 2006) is used to divide the potential evapotranspiration rate into evaporation and transpiration, where the transpiration is further quantified by coupling the functions of root density distribution and efficiency:

$$T_0 = ET_o \left[ {1 - \exp \left( { - a_{b1} LAI} \right)} \right]$$
(7)
$$E_0 = ET_o \left[ {\exp \left( { - a_{b1} LAI} \right)} \right]$$
(8)

where T0 and E0 are the potential transpiration rate (mm/s) and potential evaporation rate (mm/s), respectively. ab1 is an empirical coefficient (–), and LAI is the leaf area index (–). The leaf area index characterizes the plant canopies as a fraction of the leaf area to the unit surface area.

Formation of sludge deposit layer

The continuous sludge feeding increases the sludge deposit thickness, and the accumulation rate is a function of solid loading. The low effective porosity and hydraulic conductivity in the sludge deposit layer create a flow resistance to the influent, and the thickness and hydraulic characteristics are varied when the sludge deposits are thickened and compressed (Bandelt Riess et al. 2021). This study used compressible cake filtration (CCF) theory to estimate the buildup of sludge deposits, which describes the sludge accumulation rate as a function of the particle retention efficiency on the bed surface (Tien et al. 1997).

The thickness of the sludge deposit layer at the sludge-cake interface, L can be found directly from the sludge deposit growth rate, dL/dt. Thus, by considering the sludge deposit thickness is increased by δL over a time interval of δt, the mass balances of liquid and solids are given as:

$${\text{Liquid}}:\quad \left( {q_{l,c} - q_{l,s} } \right)\delta t = \delta L\left[ {\left( {1 - \varepsilon_c } \right) - \left( {1 - \varepsilon_s } \right)} \right]$$
(9)
$${\text{Solid}}:\quad \left( {q_{s,c} - q_{s,s} } \right)\delta t = \delta L\left( {\varepsilon_c - \varepsilon_s } \right)$$
(10)

where ql,c and ql,s are the liquid fluxes on the cake and sludge sides at the interface (m3/m2s), respectively, qs,c and qs,s are the solid fluxes on the said interface (m3/m2s), respectively, while εc and εs the particle volume fractions on the respective sides of the interface, respectively.

Furthermore, by considering the addition of mass balances for both liquid and solid fluxes in the sludge-cake interface and compared to infiltration flux through the medium, the expression for the change in sludge deposit layer thickness according to Darcy's Law can be written as:

$$\frac{dL}{{dt}} = \frac{\varepsilon_c }{{\varepsilon_c - \varepsilon_s }}\left( {\frac{k}{\mu }\frac{\partial p}{{\partial z}}} \right)_L - q_{l,m}$$
(11)

where k is the cake permeability coefficient (m2), μ is the liquid viscosity (m3/m2s), p is the pressure head (kg/ms2), z is the vertical elevation (m), and ql,m is the permeation flux of filtrate through the medium (m3/m2s).

Numerical implementation

The proposed model integrated conventional and adaptive mesh schemes to simulate the water flow across the sludge deposit layer and reed bed. The fixed mesh method was used for the simulation domain of the reed bed since the top and bottom boundaries remained unchanged over the sludge dewatering process. The formulation of the dual porosity Richards equation model was based on a finite difference approach, where an implicit method was adopted to discretize the time step (∆t) (Dehghan and Shirilord 2020). By coupling the spatial and temporal discretization, the hydraulic head, which is the unknown in the equation, is solved using a modified Picard iteration approach (Tisdell 2019). The water content and flux are then computed by means of the analytical VGM model and Darcy's law, respectively.

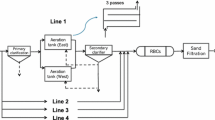
In contrast, the moving mesh method describes the moving boundary of the sludge deposit thickness level above the porous medium that is obtained from the CCF submodel. In the moving mesh method, the mesh equation and solution are varied simultaneously, and the number of nodes remains concentrated in regions of rapidly variated solution (Lee et al. 2015; Tang 2005). Particularly in the Richards equation, this method can discretize the meshes through a velocity-based equation with the finite difference approach to simulate the water flow across the domain with changing mesh sizes (Bruce 2011). In every iteration, the thickness of the newly formed deposit during feeding is estimated from the incoming solids using the CCF submodel, and the increasing thickness is added to the spatial discretization of the sludge deposit layer to describe the effect of deposit formation. The loss of water content through evapotranspiration is estimated from the Penman–Monteith equation, which is considered as a sink term in the model. The schematic flow chart of the proposed model is presented in Fig. 1.

Fig. 1
figure 1

Schematic flow chart of proposed model

Full size image

The initial hydraulic head was input as the initial condition to each node, which was assumed to be in equilibrium along the substrate profile. A flux-controlled (Neumann type) boundary condition was implemented as the upper boundary condition to simulate the feeding period. Meanwhile, the upper boundary condition could be automatically switched to the head-controlled condition (Dirichlet type) to describe the temporary ponding. The lower boundary condition was set to be freely drained.

Laboratory-scale STRB

The proposed model aims to simulate the dewatering efficiency of three laboratory-scale STRBs located at Curtin University Malaysia. The STRBs were constructed in a 55-gallon polyethylene tank with a surface area of 0.2 m2. Each reed bed consists of several layers of the porous medium (0.15 m thick filter layer with crushed stone of 4.75–9.75 mm diameter, 0.10 m thick transition layer with crushed stone of 20.00–37.50 mm diameter, and 0.15 m thick drainage layer with crushed stone of 50.00–60.00 mm diameter). Common reeds (Phragmites karka) were selected as the wetland vegetation in the laboratory-scale system.

The reed bed was loaded with raw septage in batches. The solids loading rate (SLR) used in the experiments are 50 (Bed 1), 100 (Bed 2), and 150 kg/m2/year (Bed 3) with a resting period of 7 days, thus allowing for different hydraulic loads across the feeding cycles. The volume of raw septage was determined based on the concentrations of total solids. In this study, since the raw septage had the same total solids concentration in each feeding cycle, the hydraulic load was the highest in Bed 3, then followed by Bed 2 and Bed 1.

After the feeding, the effluent was collected continuously, and the volume was measured with respect to the time after feeding. The effluent flux (m/min/m2) was then estimated from the volume of collection within the specific time interval as:

$$effluent\,flux = \frac{{V_{ei} }}{A \cdot t_i }$$
(12)

where Vei is the volume of effluent collected (m3) within the time interval, ti (min), and A is the area of the reed bed (m2). In this study, eight sets of data from each reed bed, or a total of twenty-four sets of data, were used to calibrate and validate the proposed model.

Since the reed beds have undergone acclimatization with the designated SLRs, a layer of sludge deposit was formed on the top surface of each bed. The changes in the thickness of the sludge deposit layer were recorded over the feeding and non-feeding periods. The samples of sludge deposit were also collected to measure the total solids (TS) content using the standard methods of ASTM D2216 2019.

Model calibration and validation

The domain of the simulated profile was subdivided into four layers, including a deposit layer, an intermediate layer, a small-sized gravel layer and a medium-sized gravel layer. An intermediate layer of 0.05 m thickness was implemented to describe the transition interface, where the solids passed through the surface might be retained at the upper layer of the granular substrate, resulting in a lower porosity and hydraulic conductivity. Consequently, the thickness of the small-sized gravel layer decreased to 0.10 m, while the thickness of the medium-sized gravel layer remained the same. As the drainage layer only acts as a drain and the overall water retention time is negligibly short, it was excluded from the simulated profile. The feeding duration was fixed to be 3 min, and its rate was described per unit area (surface area = 0.2 m2). The initial hydraulic head is needed to initiate the simulation, which indicates the amount of inherent water content along the reed bed profile.

Several assumptions have been made in the simulation of sludge dewatering in the STRB:

  • The influent was assumed to be distributed uniformly across the reed bed,

  • The initial hydraulic head was assumed to be in an equilibrium state,

  • The influence of vegetation was limited to the root water uptake only,

  • The evapotranspiration rate was assumed to be constant throughout the simulation, and

  • The hydraulic properties of the newly formed deposit were assumed to be the same as the existing sludge deposit.

The hydraulic parameters were calibrated by fitting the simulated results to the measured outflow dynamics as a function of time. The values of hydraulic parameters were calibrated based on the existing values of fine and coarse gravel. It is noted that the value of θs was higher for the coarser gravel due to higher porosity, while the θr was vice versa. Then, α, n, and Ks were proportional to the grain size. As for the sludge deposit layer, the hydraulic parameters were interpolated between the standard parameters of clay and silt (Afrasiabi et al. 2019). According to Kim and Forquet (2016), a large bundle of small pores was found in the sludge deposit layer of VFCWs that retained a significant amount of capillary water, which agreed with the hydraulic properties of clay and silt layers.

The sludge deposit is the layer with the lowest hydraulic conductivity within the reed bed profile, and thus, its saturated hydraulic conductivity (Ks) is the most important parameter of the effluent flux. The Ks of the sludge deposit layer is affected by factors including the sludge deposit thickness, mechanical compression, and moisture content (Höfgen et al. 2019; Khomenko et al. 2019). Therefore, the calibration of this parameter based on the experimental results is essential in the simulation of drainage dewatering performance in STRBs. Table 1 summarizes the values of hydraulic parameters used in the simulation.

Table 1 Hydraulic parameters of sludge deposit layer and reed bed
Full size table

Table 2 presents the values used for the simulation of potential evapotranspiration and sludge accumulation. The values of the parameters in the evapotranspiration module were based on the experimental measurement and literature (Zotarelli et al. 2015). The specific cake resistance was estimated to be equivalent to the values proposed for the biodigester sludge (Prajapati et al. 2023). On the other hand, the viscosity of the sludge was obtained from the findings of Wolski (2021) for the non-conditioned digested sludge. The specific cake resistance and viscosity values were selected based on their similar sludge characteristics. In addition, the sludge density and porosity were determined from the average TS concentration of the raw sludge and sludge deposit, respectively.

Table 2 Inputs for potential evapotranspiration (PET)
Full size table

The accuracy of the proposed model was evaluated using root mean square error (RMSE), which was calculated as follows:

$$RMSE = \sqrt {{\frac{1}{n} \mathop \sum \limits_{i = 1}^n \left( {A_t - P_t } \right)^2 }}$$
(13)

where At is the actual flux in the experiment (m/min), Pt is the predicted value of the simulation (m/min), and n is the number of data sets.

Results and discussions

Drainage dewatering

The drainage dewatering efficiency was evaluated through the volume of the water collected from the laboratory-scale STRBs. Based on the experimental results, the gravity drainage dewatering efficiency was above 70% in all cases, and the average drainage dewatering efficiency was 84.90%, 85.04%, and 83.91% in Bed 1, 2, and 3, respectively. The results emphasize the importance of gravity drainage as the major dewatering mechanism in STRBs. During the gravity dewatering, the retention of solids at the bed surface varied the sludge deposit thickness. According to the experimental results, the low SLR in Bed 1 resulted in a relatively thin sludge deposit layer, as shown in Table 3. In contrast, the thicknesses in the other two beds were similar, which is attributed to the extensive compaction caused by the high hydraulic load in Bed 3.

Table 3 Root Mean Square Error (RMSE) of each case in Bed 1, 2, and 3
Full size table

The Richards equation regards the difference in the hydraulic head as the driven force of the porous flow. Therefore, a greater head difference caused by the high hydraulic load theoretically results in a faster porous flow. The experimental results of the lab-scale STRBs also observed a similar trend. According to the experimental results of Feeding Cycle 2, the peak effluent flux was 2.8 cm/min in Bed 3, which is under the highest SLR and hydraulic load. In contrast, the peak effluent fluxes observed in the same feeding cycle were 1.3 cm/min and 0.3 cm/min in Bed 2 and Bed 1, respectively. However, the peak effluent flux of Bed 1 was higher than that of Bed 2 and 3 in several feeding cycles. It can be attributed to the formation of sludge deposits at the bed surface during the feeding period. The accumulation of sludge deposits is regarded as a crucial factor in the dewatering efficiency of STRBs (Jafari et al. 2019), which reduces water infiltration, subsequently leading to higher retention time and slower effluent flux (Trein et al. 2019).

The proposed model has taken into consideration the influence of sludge deposit accumulation on drainage dewatering efficiency in the reed beds by simulating the sludge accumulation as a function of time with the variation of thickness in the moving mesh layer. The formation of a new sludge deposit was simulated using the CCF submodel regarding the solid load and sludge deposit porosity with the respective fluxes. Typically, the sludge accumulation was most apparent during the feeding stage due to the settling of solid particles during the ponding period (Ahmmed et al. 2022). Then, the compression of the sludge deposit by the surface ponding and water infiltration slowly decreased the sludge thickness (Pergam and Briesen 2023). Meanwhile, the hydraulic parameters were assumed to be the same as the existing sludge deposit layer. The consideration of the increasing sludge deposit thickness using the moving mesh model has delivered a more reliable simulation for the drainage dewatering in STRBs compared to the conventional Richards equation model, as it applied a specific flow resistance caused by the sludge accumulation to avoid the overprediction of water infiltration rate (Khomenko et al. 2019). Figure 2 shows the predicted sludge deposit thickness in Feeding Cycle 2 of Bed 3.

Fig. 2
figure 2

Sludge accumulation in Feeding Cycle 2 of Bed 3

Full size image

In this study, the effluent flux curve is used as the parameter in evaluating the accuracy of the proposed model. Figures 3, 4, and 5 compare the experimental and predicted data of effluent fluxes in Bed 1, 2, and 3, respectively. Table 3 summarizes the RMSE of each simulation. Generally, the RMSE is low compared to the average effluent flux, which shows that the proposed model is promising in predicting the overall drainage dewatering trend in the laboratory-scale STRBs under varying feeding conditions and sludge deposit thickness.

Fig. 3
figure 3

Comparison between actual and predicted effluent fluxes in Bed 1

Full size image
Fig. 4
figure 4

Comparison between actual and predicted effluent fluxes in Bed 2

Full size image
Fig. 5
figure 5

Comparison between actual and predicted effluent fluxes in Bed 3

Full size image

The low-permeable sludge deposits on the top bed surface hindered water infiltration into the reed bed, subsequently forming surface ponding at the early phase of the feeding-resting cycle. As a result, the effluent did not discharge immediately after feeding. Nonetheless, the effluent discharge usually occurred within the first ten minutes after feeding, except for a case with an eighteen-minute delay in Bed 1. The peak effluent flux was recorded after the effluent discharge was observed, followed by a decelerating trend. As a result, the cumulative effluent increased rapidly at the early phase of the feeding-draining cycle and became stable afterwards, where the majority of the effluent discharge was observed within 30–60 min after the feeding. The peak effluent fluxes varied across the cases, but the effluent flux was usually faster in the beds with higher SLRs. This study referred to both the occurrence time and peak flux of effluent discharge as crucial indicators of the drainage flow simulation.

In the proposed model, the effluent flux is determined by the difference in the hydraulic head (h) across the spatial discretion and the hydraulic conductivity of porous media, as described by the Richards equation. Accordingly, the largest head difference created by the high ponding depth at the beginning of the feeding-resting cycle resulted in the peak effluent flux. Then, the continuous effluent discharge reduced the difference in the hydraulic head due to the shallower ponding depth, subsequently decelerating the water percolation flow until the discharge became insignificant. The overall effluent flux curve is similar to the results reported by Nielsen and Stefanakis (2020).

However, the ponding depth was determined by the hydraulic load imposed on the reed bed, which was input as a value for the boundary condition in the simulation. On the other hand, the sludge deposit layer has the lowest hydraulic conductivity across the reed bed profile, and thus, the simulation results showed that only the sludge deposit layer reached saturation. Therefore, the saturated hydraulic conductivity (Ks) of the sludge deposit layer limits the infiltration capacity and, thus, the water percolation flow rate and effluent flux. The Ks of the sludge deposit layer were then calibrated to fit the peak effluent flux of the gravity drainage.

On the other hand, the initial pressure head (h) values were calibrated to match the occurring time of effluent discharge. This value implies the moisture content remained in the bed after the non-feeding period, in which a lower h would result in longer flow delays because the low moisture content in porous media takes longer to reach saturation and, therefore, delays the effluent. Similar to the calibration of peak effluent flux, the Ks of the sludge deposit layer were also crucial to the time of flow occurrence in the simulation, where a higher value leads to a faster water percolation flow and an early effluent discharge. By calibrating the Ks of the sludge deposit layer and initial h to match the peak flux and occurring time of effluent discharge, the overall trend of the drainage dewatering can be promisingly predicted without adjusting other parameters. The low RMSE compared to the average effluent flux for all feeding cycles in this study further reflects the robustness of the proposed model in simulating drainage dewatering under different feeding conditions and sludge deposit thickness without extensive calibration.

Table 3 presents the calibrated h and Ks of each simulation. As mentioned previously, the h and Ks were calibrated to match the occurring time and peak flux of the effluent discharge. Since the occurring time of effluent discharge was consistently short in all beds, the calibrated h was within the range of − 8 and − 15 cm. It shows that as long as the effluent discharge occurs immediately after the feeding, the calibration of this parameter is minimal. However, the calibrated h in the Feeding Cycle 3 of Bed 1 was as low as − 50 cm due to the long delay of effluent discharge. In contrast, the calibrated Ks values varied across the simulation cases. The calibrated Ks ranged from 0.050 to 0.325 cm/min in Bed 1, while the calibrated Ks could reach 1.3 cm/min and 2.6 cm/min in Bed 2 and 3, respectively. This finding reveals that a constant value of Ks was unlikely to match all instances, and thus, the calibration of this parameter is always essential. The thickness, mechanical compression, moisture content, and accumulation of incoming solids are the factors that vary the Ks of the sludge deposit layer (Höfgen et al. 2019; Khomenko et al. 2019; Trein et al. 2019). Moreover, the surface cracks in the sludge deposit layer due to the excessive moisture content lost could drastically change the permeability of the reed bed (Trein et al. 2019). In order to improve modelling accuracy, further study is required to derive an adaptive modelling method for the variations in the Ks of the sludge deposit layer in STRBs.

It was observed that the predicted peak effluent fluxes were lower than the actual effluent flux in several cases, including Feeding Cycles 4 and 6 of Bed 2 and Feeding Cycles 2 and 4 of Bed 3. For example, Fig. 6 shows the effluent flux during the first 30 min in Feeding Cycle 4 of Bed 2, where the peak effluent flux observed in the 4th minute was 60% faster than the nominal effluent flux recorded in the first 10 min. It is attributable to the hydraulic short-circuiting in the reed bed, which was caused by bypassing raw septage through the cracks in the sludge deposit layer that led to a sudden acceleration in the effluent flux (Khomenko et al. 2019). The experimental result also showed that the short-circulating flow occurred under the large hydraulic gradient when the ponding depth was high in the reed beds. A similar pattern of short-circulating flow was observed in the early phase of Feeding Cycles 6 of Bed 2 and Feeding Cycles 2 and 4 of Bed 3. Nonetheless, the short-circulating flow only remained for a very short period, and thus, its effect on the overall drainage dewatering efficiency is neglectable. The simulation was then calibrated to the second-highest effluent flux recorded in these cases.

Fig. 6
figure 6

Short-circulating flow observed in Feeding Cycle 4 of Bed 2

Full size image

Figure 7 illustrates the effluent flux of Feeding Cycle 2 in Bed 1, where the simulation shows a good match with the effluent flux at the beginning phase. After approximately 15 min of the feed-drying cycle, the effluent flux decelerated rapidly, while the effluent flux of the predicted data remained fast. It resulted in a relatively high RMSE of 0.009 compared to an average effluent flux of 0.104 cm/min, where most deviations between the actual and predicted data were attributed to the overestimation of effluent flux at the late phase of the feeding-draining cycle. The difference can be explained by the low drainage dewatering efficiency observed in the experiment, which was only approximately 75%. However, the predicted dewatering efficiency was much higher than the experimental data. Since the Richards equation considers the law of mass conservation while the water loss is assumed to be via evapotranspiration, the proposed model is less efficient in projecting the significant water loss due to the water retention in the reed bed. Although the proposed model has adopted the dual porosity flow model to describe such a water loss, the exchange rate of water content between the mobile and immobile regions in the simulation is insignificant. A further study on the water retention in the reed bed, particularly the sludge deposit layer, is needed to derive a more accurate value for the first-order mass transfer coefficient in simulating the water content in the immobile region. In contrast, the simulation of Feeding Cycle 7 in Bed 1, which had a drainage dewatering efficiency of 92.83%, accurately predicted the effluent flux over the feeding-drying cycle with a RMSE of only 0.002, as shown in Fig. 8.

Fig. 7
figure 7

Bed 1 Feeding Cycle 2

Full size image
Fig. 8
figure 8

Bed 1 Feeding Cycle 7

Full size image

Evapotranspiration

The experimental results revealed that approximately 85% of the liquid content in the raw septage was dewatered through gravity drainage, and the remaining liquid content was expected to be removed via evapotranspiration dewatering. The simulation of water loss through evapotranspiration was included as a sink term in the Richards equation, where it only involved the upper layer in the reed beds. Typically, evapotranspiration is only remarkable when a long resting period is implemented in STRBs (Cascone et al. 2019). Figure 9 shows that the predicted moisture content of the top sludge deposit layer with evapotranspiration has no significant difference from the results without evapotranspiration. The difference in moisture content due to evapotranspiration was only observed in the late phase of the resting period.

Fig. 9
figure 9

Simulation of moisture content with and without evapotranspiration

Full size image

In this simulation study, the tropical climate and the assumption of the low density of vegetation coverage in the laboratory-scale STRB led to an average potential evapotranspiration rate of 0.322 cm/day. The water loss over the resting period of six days was approximately 2 cm, and it could be comparable to drainage dewatering. However, the assumption of mass conservation in the Richards equation led to a low moisture content in the sludge deposit layer. As a result, the predicted evapotranspiration rate imposed on the top layer was as low as 0.013 cm/day, much lower than the gravity drainage dewatering. In fact, higher moisture content was observed in the sludge deposit layer, implying the presence of stagnant water (Ghanbarian 2021). Although the proposed model implemented the dual porosity flow concept for the immobile water content in the reed bed, a further study on the behaviour of water exchange between the mobile and immobile regions is needed to improve the simulation accuracy. Moreover, a study revealed that the deformation of the sludge deposit and possible cracks upon prolonged drying during resting periods have caused direct contact of the sludge deposits in the deeper layer with the atmosphere, further enhancing the sludge dewatering via evapotranspiration (Khomenko et al. 2019). Accordingly, a study on the influence of evaporation on the deeper layer of the sludge deposit layer is necessary, as the current model assumes that evaporation only occurs at the bed surface, which could underestimate the dewatering rate via evapotranspiration.

Conclusion

A one-dimensional process-based mathematical model was successfully developed to simulate the dewatering mechanism in STRBs with the consideration of the sludge deposit accumulation. The compressible cake filtration (CCF) theory was implemented to simulate the accumulation of sludge deposits on the surface of the reed bed, while the varying sludge deposit thickness was accounted for using the moving mesh method. The proposed model also incorporated the dual porosity variably saturated flow model and the Penman–Monteith equation to describe the dewatering through gravity drainage and evapotranspiration, respectively. The results from the model were validated with experimental data from laboratory-scale STRBs treating septage. In particular, integrating a variably saturated flow module with the consideration of evapotranspiration and sludge accumulation delivered a feasible tool to predict the sludge dewatering performance in STRBs under varying solids loads. The findings are as follows:

  • Considering the sludge deposit layer as a specific flow resistance effectively avoids the overprediction of water infiltration rate in the reed bed.

  • The calibrated H ranging from − 8 to − 15 cm has successfully matched the occurring time of the effluent discharge. However, the calibrated Ks varied across the simulation cases, ranging from 0.050 to 2.600 cm/min to fit the actual flux peaks. Hence, the calibration of Ks is necessary for each simulation case.

  • The low overall RMSE of the predicted effluent flux curve highlighted the efficiency of the proposed model in simulating drainage dewatering in STRBs. However, significant deviations were observed in the case with low drainage dewatering efficiency. It can be explained by the assumption of mass conservation in the proposed model, which is less efficient in projecting excessive water retention in STRBs over the feeding-resting cycle.

  • The effect of evapotranspiration was found to be negligibly small in the simulation, while it is only remarkable during a prolonged resting period.

Future studies should focus on the standardization of the value of Ks in the sludge deposit layer to improve the robustness of the model. Further research on the water retention in the reed bed, particularly the sludge deposit layer, is also needed to derive a more accurate value for the first-order mass transfer coefficient in simulating the immobile water content.