Modelling on assessment of flood risk susceptibility at the Jia Bharali River basin in Eastern Himalayas by integrating multicollinearity tests and geospatial techniques

Abstract

Climate change and anthropogenic factors have exacerbated flood risks in many regions across the globe, including the Himalayan foothill region in India. The Jia Bharali River basin, situated in this vulnerable area, frequently experiences high-magnitude floods, causing significant damage to the environment and local communities. Developing accurate and reliable flood susceptibility models is crucial for effective flood prevention, management, and adaptation strategies. In this study, we aimed to generate a comprehensive flood susceptibility zone model for the Jia Bharali catchment by integrating statistical methods with expert knowledge-based mathematical models. We applied four distinct models, including the Frequency Ratio model, Fuzzy Logic (FL) model, Multi-criteria Decision Making based Analytical Hierarchy Process model, and Fuzzy Analytical Hierarchy Process model, to evaluate the flood susceptibility of the basin. The results revealed that approximately one-third of the Jia Bharali basin area fell within moderate to very high flood-prone zones. In contrast, over 50% of the area was classified as low to very low flood-prone zones. The applied models demonstrated strong performance, with ROC-AUC scores exceeding 70% and MAE, MSE, and RMSE scores below 30%. FL and AHP were recommended for application among the models in areas with similar physiographic characteristics due to their exceptional performance and the training datasets. This study offers crucial insights for policymakers, regional administrative authorities, environmentalists, and engineers working in the Himalayan foothill region. By providing a robust flood susceptibility model, the research enhances flood prevention efforts and management, thereby serving as a vital climate change adaptation strategy for the Jia Bharali River basin and similar regions. The findings also have significant implications for disaster risk reduction and sustainable development in vulnerable areas, contributing to the global efforts towards achieving the United Nations' Sustainable Development Goals.

Introduction

Floods stand as one of the gravest natural hazards globally, posing immense challenges for humanity (WHO 2003; Meraj et al. 2013, 2015, 2018; Rahmati et al. 2016; Chakrabortty et al. 2023; Mehravar et al. 2023). Their repercussions include serious injuries, loss of life, extensive infrastructure damage, economic losses, and societal upheavals (Billa et al. 2006; Termah et al. 2018; Mitra et al. 2022). Climate change and the detriments of rapid urbanization and improper land management have recently intensified flood-related devastations in many nations (Caruso 2017; Zadeh et al. 2020; Rani et al. 2023; Choudhury et al. 2023; Saravanan et al. 2023). Consequently, researchers globally are probing into this peril due to its vast socio-economic impacts (Das 2020). India has a very unpredictable monsoon climate. Many rivers run through the entire nation, and a lengthy heavy rain can cause flooding (Sarkar and Mondal 2020; Ghosh 2023). According to reports, approximately 8 Mha of land is influenced by flood hazards each year in India, where approximately 40 Mha are prone to flooding (Sarkar and Mondal 2020). Thus, it is the second most flood affected-nation following Bangladesh. According to statistical information provided by the Central Water Commission of India, between 1953 and 2009, floods in India caused a capital loss of almost 200 billion dollars and the deaths of 92,000 people (CWC 2010). Each year, India accounts for almost 20% of global fatalities due to this catastrophe. Every rainy season in India results in the deaths of about 1500 people, and around three crores of people are affected due to flooding. Hence, effective flood management is essential to minimize damage (Mitra and Das 2022).

India's monsoon climate is highly unpredictable, with numerous rivers running through the country, making it vulnerable to flooding (Sarkar and Mondal 2020). Every year in India, nearly 8 million hectares of land suffer from flood damage, and an estimated 40 million hectares are susceptible to these water-related disasters (Sarkar and Mondal 2020). This positions India as the country most impacted by floods after Bangladesh. Between 1953 and 2009, the economic toll of these floods in India approached 200 billion dollars, leading to the tragic loss of 92,000 lives (CWC 2010). Every year, India accounts for almost 20% of global fatalities due to flooding, with approximately 1500 deaths and around 30 million people affected by flooding during the rainy season (Mitra and Das 2022). Therefore, effective flood susceptibility assessment is crucial to minimize damage (Salvati et al. 2023). Flood calamities cannot be entirely prevented, but appropriate management and mitigation strategies can help reduce the devastation (Lahon et al. 2023a, b). Mitra et al. (2022) suggest that floods can be efficiently reduced or even entirely avoided through geographic assessment. Therefore, the key strategic element of disaster vulnerability reduction strategy is identifying vulnerable areas (Chapi et al. 2017). The usage of geospatial techniques has increased recently, giving vulnerability assessments a new dimension and sound reasoning (Sajan et al. 2022; Debnath et al. 2022; Lahon et al. 2023a, b; Debnath et al. 2023a, b, c; Dutta and Deka 2023; Nath et al. 2023). Geospatial platforms provide an array of tools and algorithms that allow for the execution and adjustment of models geared toward assessing flood vulnerability (Dutta et al. 2023). The outcomes derived from these platforms are often more coherent and widely accepted. Globally, different models are currently applied significantly to analyze flood susceptibility in the GIS environment (Pradhan and Lee 2010; Zaharia et al. 2017; Khosravi et al. 2018, 2019; Tella and Balogun 2020; Sarkar and Mondal 2020). The frequently used models in previous studies are logistic regression (Pradhan and Lee 2010; Al-Juaidi et al. 2018; Liu et al. 2022), Random Forest (RF) (Ghosh and Dey 2021; Hasanuzzaman et al. 2022), Naive Bayes (NB) (Hasanuzzaman et al. 2022), MCDM based VIKOR, TOPSIS, SAW (Khosravi et al. 2019; Mitra and Das 2022), EDAS (Mitra and Das 2022), Dempster Shafer (DS) evidence theory (Pan et al. 2023), decision trees (Pham et al. 2021), index-of-entropy (Wang et al. 2021; Arora et al. 2021; Islam et al. 2022), artificial neural networks (Rahman et al. 2019; Jahangir et al. 2019), Analytic Network Process (ANP) (Solaimani et al. 2022).

Although conventional optimization approaches like linear, nonlinear, and dynamic programming have been used in assessing flood hazards in the past few decades (Olsen et al. 2000; Yazdi and Neyshabouri 2012), frequency ratio (FR) (Rahman et al. 2019; Sarkar and Mondal 2020; Waqas et al. 2021; Ghosh and Dey 2021), Analytical Hierarchy Process (AHP) (Das 2020; Das and Gupta 2021; Mitra et al. 2022; Hasanuzzaman et al. 2022; Choudhury et al. 2022; Gupta and Dixit 2022), and fuzzy logic (FL) (Wang et al. 2019; Tella and Balogun 2020; Ghosh and Dey 2021; Akay 2021; Balogun et al. 2022) models have also considered highly acceptable techniques for hazard assessment studies, these studies demonstrate that flood risk assessment is linked to multidimensional attributes and incorporates spatial elements. Nevertheless, research encounters intrinsic challenges and constraints in pinpointing and measuring flood risk and vulnerability indicators, like terrain, drainage systems, hydrological factors, and weather patterns. These challenges extend to handling ambiguities, assigning suitable importance to various indicators, and confirming the findings' accuracy (Gupta and Dixit 2022). Risk assessment indicators, inherently intricate, encompass ambiguities across temporal and spatial dimensions (Meyer et al. 2009). A significant challenge is collating data for indicators like hydrological, meteorological, and LULC factors. This process demands substantial manpower and extended durations, especially in regions vulnerable to flooding (Emanuelsson et al. 2014; Gupta and Dixit 2022). While most standalone predictive models exhibit certain limitations (Tehrany et al. 2017; Wang et al. 2021), evidence suggests that integrating two or three predictive techniques enhances result accuracy, proving the combined approach superior to singular methods (Chau et al. 2005). Another significant limitation of the previous studies is that they do not consider the spatiotemporal patterns of floods. It has been noted that flood patterns are changing over time due to land use changes, climate change, and other anthropogenic factors (Wang et al. 2019; Singh et al. 2021). Therefore, there is a need for more comprehensive models that can incorporate the spatiotemporal patterns of floods.

It's vital to create models that evaluate the effects of floods on societal structures, economic systems, and the environment. Current models predominantly concentrate on gauging the physical susceptibility of regions, often overlooking the socio-economic implications (Thieken et al. 2005). Population concentration, land utilization trends, and vital infrastructure are pivotal in ascertaining how floods influence society and its economic framework. Therefore, a more comprehensive approach that integrates physical, social, and economic vulnerability factors is needed to assess the overall vulnerability of the areas to floods (Bera et al. 2022). Therefore, using geospatial techniques has significantly improved the vulnerability assessment of floods. However, several challenges and limitations must be addressed to develop more comprehensive and accurate models. The complexity and uncertainty of the flood indicators, the changing spatiotemporal patterns of floods, and the need for more comprehensive models that can integrate physical, social, and economic vulnerability factors are some of the critical challenges that need to be addressed. Future research should focus on developing more comprehensive models that can address these challenges and provide accurate and reliable assessments of the vulnerability of areas to floods.

Numerous global studies currently employ an ensemble of multiple models to produce flood susceptibility maps (Altaf et al. 2013; Rather et al. 2022). For instance, Sahana and Patel (2019) employed the FR and FL model for flood mapping in India's lower Kosi River basin. In contrast, Wang et al. (2021) combined the FR and entropy index with multilayer perception (MLP) and classification and regression tree techniques for their flood mapping. Cui et al. (2023) adopted a cutting-edge hybrid strategy that combined neural networks with genetic quantum ensembles to map floods in China's Tumen River basin. Similarly, Chen et al. (2023) leveraged MLP, LR, SVM, and RF for their flash flood mapping, while Mousavi et al. (2022) compared EBF and WOE with the TOPSIS model in Northern Iran. Furthermore, Ghosh et al. (2022) amalgamated FR, LR, decision tree, and fuzzy logic models for predicting flood vulnerability in India's lower Gangetic plain. Yet, few research efforts have combined both geospatial and statistics-driven methods, specifically the bivariate statistical model (frequency ratio) and a probabilistic mathematical model (fuzzy logic, FL), with dual MCDM strategies (Analytical Hierarchy Process and Fuzzy Analytical Hierarchy Process), as our study has. The frequency ratio (FR) is a straightforward yet potent model, while the FL model, rooted in mathematical uncertainty, excels in tackling intricate problems (Sahana and Patel 2019). Interestingly, some research indicates that bivariate statistical models can occasionally outperform machine learning models, especially if the latter lack extensive training data (Ullah and Zhang 2020; Aditian et al. 2018; Shahabi et al. 2013; Shafapour et al. 2017; Fayaz et al. 2022; Sharma et al. 2023; Tripathi et al. 2023). Alternatively, the decision-making methodology known as multi-criteria decision analysis (MCDA) was designed to solve challenges in operational research, where decision-makers evaluate variables against specified criteria (Tripathi et al. 2022).

The thorough comparison of statistical models and GIS-based MCDM methods in flood areas has not been investigated so much, despite substantial studies and reviews of models and trends of various approaches. Moreover, the AHP and FAHP combo in MCDA is an excellent tool for making precise maps for analyzing flood-prone areas. These methods have several significant benefits, including simplicity of usage and the lack of proportionality of the criteria (Tomar et al. 2021; Sud et al. 2023). It uses various weighting techniques to quantify each aspect influencing the MCDM process. The present research used FR, FL, AHP, and FAHP models to develop a precise flood susceptibility map for the entire Jia Bharali River basin to prevent approaching disasters. The high-magnitude flooding in the foothill region of the Jia Bharali River causes severe damage in the lower reach and is prevalent in the basin. Tezpur, the most inhabited city along the bank of the Jia Bharali River, experiences flooding yearly along with the nearby villages. The lower reach of this basin experienced significant flooding in 1954, 1962, 1972, 1977, 1984, 1988, 1998, 2002, 2004, 2012, 2013, 2015, 2016, 2017, 2018, 2019, 2020, and 2022 over the past half-a-century. It has been noticed that the frequency of the flood has increased significantly in the past two decades compared to the second half of the twentieth century. Therefore, assessment of flood susceptible zones of this basin becomes an important task to reduce the disaster risk. The study aims to utilize sophisticated and well-accepted models to generate a reliable flood susceptibility map for the entire basin. The study results will provide valuable insight to policymakers, regional administrative authorities, environmentalists, and engineers in the Himalayan foothill region for improving their efforts in flood prevention and management and for adapting to the effects of climate change in the Jia Bharali River basin. The novelty of the present research in the case of flood susceptibility assessment is that it is the first time these four statistical and MCDM-based models have been utilized jointly in a river watershed of the Northeastern region of India for the flood susceptibility assessment.

Study area

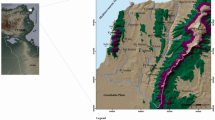
The Jia Bharali basin is located within the coordinates of 26° 37ʹ N to 28° 00ʹ N for latitude and 92° 00ʹ E to 93° 25ʹ E for longitude. It spans an area of 11,716 km². This basin constitutes 6.7% of the total area of the Brahmaputra River System and is shared by the Indian states of Assam and Arunachal Pradesh. The majority of the basin, 10,239.8 km² or 87.4%, lies within the mountainous regions of Arunachal Pradesh. In comparison, the remaining 1476.6 km² or 12.6% is found in the plains of Assam (Fig. 1). The basin's origin is at a height of 4520 m in the Great Himalayan Range. It stretches 247 km through mountainous terrains, valleys, and flatlands before merging with the Brahmaputra. Numerous tributaries emerging from various parts of the Himalayas feed into this river. Notably, its right bank is fed by the Bichom, Nam Sonai, Tipi, Mansiri, and Dharikatitributaries. In contrast, the Pacha, Diju, Papu, Upper Dikrai, Namiri, BorDikrai, and Khari Dikraitributaries join from the left bank. The Jia Bharali is also called the Kameng during most of its 185 km length in Arunachal Pradesh before entering the Brahmaputra plain of Assam. After cutting through the Siwalik Mountain, the river runs into the Brahmaputra plain of Assam near the Bhalukpong. Afterward, the river flows approximately 62 km before the Brahmaputra River (Debnath et al. 2023a, b, c).

Fig. 1

Geographic overview of the study area. a Political map showcasing the Union of India for contextual orientation. b Zoomed-in view of the North-Eastern region of India, highlighting its administrative subdivisions. c Detailed location map pinpointing the specific study area within the North-Eastern region

The study area, a portion of the Brahmaputra Valley, has a subtropical monsoon climate type with moderately warm, humid summers and partly dry winters. The four distinct seasons here in a year are winter, summer or pre-monsoon, monsoon, and retreating monsoon. There is 213 cm of yearly rainfall on average in the research area. The monsoon season, which brings torrential rain, begins in June and often lasts through September. However, it can occasionally extend into mid-October. It is the longest season there and is distinguished by a high level of air humidity, slight fluctuation in temperature, and prolonged rainy days. The monsoon season begins in early June, bringing heavy rains and a significant slowdown in the rise in temperature, with a monthly average temperature of 24.33 °C. The peak month for rainfall is often July, with secondary and tertiary peaks occurring between June and August and May and September, respectively. The first period of rain with an increasing intensity usually happens in April; however, it can also occur seldom in late March or early May. The initial flash flood in the river originates from this phenomenon. The river runs through hills for about three-quarters of its length and traverses plains for the remaining quarter. Most of its tributaries converge with the main river in these plains. The river transports vast amounts of silt from the Tertiary-era Mountains throughout its hilly trajectory. Yet, upon entering the Brahmaputra plains, its speed and sediment transport capacity decrease, slowing notably as it continues downstream. In this context, the river adopts a braided pattern due to sediment accumulation on its bed. The river's path shifts during the monsoon season, driven by its high velocity and increased erosive power. Jia Bharali's depth on the plains is relatively modest due to the dumping of a substantial amount of sediment in the lower course. As a result, during the height of the monsoon, flooding in the nearby areas occurs because of excess water that frequently surpasses the river's capacity to hold it due to excessive rainfall. On both sides of the river, many urban and peri-urban settlement zones are severely impacted by flood conditions.

Methodology

The methodology includes the overall organization of the present research, which comprises creating the flood inventory map, identifying flood-affecting variables and Multicollinearity diagnosis, validation and accuracy analysis or assessment of the flood susceptibility maps, etc. (Table 1). The models adopted to generate the flood susceptible index (FSI) map are MCDM-AHP, FAHP, FR, and FL (Fig. 2).

Table 1 Source of the flood conditioning factors used for the flood susceptibility mapping

Fig. 2

Applied methodology flowchart followed in this research

Generation of the Flood Inventory Map (FIM) Generally, the FIM of a region is made from previous flood data and can be used to predict potential flood events using different models (Ahmed et al. 2022; EI-Magd 2022). The correctness of the previously documented flooding episodes determines the accuracy and dependability of the future flood vulnerability (Sarkar and Mondal 2020). The FIM of the Jia Bharali River Basin was created using the GIS environment with the 2022 severe flood event (https://geoapps.icimod.org). Altogether 200 flood sites/points were collected from the Jia Bharali River basin. These sites/points were randomly classified into two groups, i.e., training and testing data sets, to set up and validate the susceptibility map. Although there is a lack of established guidelines about the assignment of the training and testing points in maximum research, 70% of points are used as a training data set to prepare the FSI map using different models, and the remaining 30% is utilized for validating the output FSI map (Pradhan and Lee 2010; Ahmed et al. 2022). Similarly, in the present research,140 training samples (70%) and 60 training samples (30%) were randomly selected for the FSI modeling and validation, respectively (Sarkar and Mondal 2020).

Method for the preparation of the flood influencing criteria

Generally, creating the FSI map for an area is complicated and comprehensive because it involves many different hydrological and terrain elements. The current investigation picked and generated 13 flood-affecting criteria based on assessments from earlier studies and flood susceptibility models (Janizadeh et al. 2019). These 13 criteria were Elevation (EL), Flow Accumulation (FA), Curvature (CU), Slope (SL), Topographic Ruggedness Index (TRI), Land Use and Land Cover (LULC), Topographic Wetness Index (TWI), Distance from the River (DR), Drainage Density (DD), Geology (GL), Rainfall (RF), Geomorphology (GM), and Soil Texture (ST) (Das 2020; Mitra and Das 2022).

Elevation The elevation of the topography has always been crucial and helpful in creating the FSI map of a region (Ahmed et al. 2022). It is generally recognized as a main factor that triggers floods because lower altitudes are typically linked to considerably larger river discharge and flood more quickly from high water surges. The SRTM (Shuttle Radar Topography Mission) DEM (Digital Elevation Model), which had a 30 m resolution and was obtained from NASA (https://earthexplorer.usgs.gov), was utilized to produce the altitude map of the selected basin (Fig. 3a).

Fig. 3

Flood conditioning factors, a elevation; b slope; c distance from the river; d drainage density; e TWI; f LULC; g Rainfall; h geomorphology; i soil texture; j TRI; k curvature; l geology; m Flow Accumulation

Slope Slope has an essential role in FSI mapping since it clearly illustrates the degree of steepness of the slope. It regulates floodwater movement and direction along with the flow velocity. Water has more time to percolate in areas with gentle slopes because surface runoff is slower and vice versa(Adiat et al. 2012). According to Li et al. (2012), a higher slope area has increased surface flow, but when the slope abruptly declines, a massive volume of water remains immobile, creating a flood situation. The SRTM DEM with 30 m × 30 m grid cells was used to automatically generate the slope angle map, broken down into five categories. In the present study, the angle degrees of slope span from 0° to 86.95°, indicating a low to a very high degree of slope (Fig. 3b).

Curvature In this research, the profile curvature was also taken into account because it considerably impacts the velocity at which water drains off the surface (Ahmed et al. 2022). It replicates the shape of surface topography in any area and defines the degree of slope surface distortion (Das and Gupta 2021). The ArcGIS 10.3 program's Spatial Analyst Tool was used to calculate the curvature of the research region (Fig. 3c). It is assumed that runoff and floods will affect convex surfaces more severely. Negative curvature values indicate concavity in the topography, whereas values near 0 indicate flat terrain and a higher likelihood of floods (Das and Gupta 2021).

Flow accumulation Flow accumulation is considered an essential parameter for flood susceptibility modeling. According to Zhang et al. (2017), the output raster calculates the cumulative water flow as the weighted sum of all cells, which then flows into every down-slope cell. The probability of flooding is enhanced by an increasing flow accumulation value, which indicates a higher probability of water concentration. In the Jia Bharali Rivers, a flow accumulation is very high, particularly vulnerable to flooding (Fig. 3m).

Distance from the river This factor reveals the main paths for flood discharge and spread since excess river water initially reaches adjacent banks. Flood risk in a region increases as the distance from a river decreases, but risk decreases as the distance from the river increases (Shahabi et al. 2021). Numerous studies have shown that flood occurs in local areas in conjunction with inland water bodies (Reager et al. 2014). Nevertheless, this factor is thought to vary depending on the hydro-geomorphic situation and is more region-specific. The distance from the river map of the Jia Bharali basin was generated by the stream network estimated from the SRTM DEM data (Fig. 3c).

Drainage density It is considered the primary regulating element that significantly influences the likelihood of flooding (Gül 2013). According to Kumar et al. (2007), the possibility or risk of a flood is influenced by the drainage density of a certain location since higher drainage density indicates higher surface runoff. It is determined by dividing the sum of the drainage or river lengths in a cell by the area of that cell (Greenbaum 1989; Altaf et al. 2013; Kotecha et al. 2023). The drainage density map of the study region was prepared in ArcGIS 10.7 software, where the drainage network patterns were translated into a quantifiable quantity (Fig. 3d).

Topographic Wetness Index (TWI) This factor is a numerical representation of the flood inundation area. It demonstrates how terrain affects surface runoff. This factor also displays the quantity of flow accumulation in a particular location of the watershed (Ahmed et al. 2022). TWI was initially mentioned by Beven and Kirkby (1979). The following formula (Eq. 1), proposed by Moore et al. (1991), was adopted to calculate TWI:

$$TWI=Ln\left(\frac{{A}_{s}}{tan\beta }\right)$$

(1)

where,${ A}_{s}$ indicates the area under the basin and $\beta$ indicates the slope angle. The TWI value and the likelihood of flooding are inversely associated. The higher the TWI value, the greater the chances of flooding. The TWI value ranged from − 23.89 to 18.22 (Fig. 3e) in the present study.

Topographic Ruggedness Index (TRI) Riley et al. (1999) describe the topographic ruggedness index (TRI) as the altitude difference between DEM cells that are close to one another. It determines the elevation values from the eight cells rapidly encircling the central cell and the difference between those values. This factor heavily depends on the regional terrain condition of a watershed/basin and is also used to assess floods in a region. Generally, a higher TRI value means there is less chance of flooding and the other way around (Ahmed et al. 2022). The TRI map for this investigation was created using the stretch format and had values between 0 and 653 (Fig. 3j).

Land use/land cover Generally, a high density of vegetation reduces the chances of the flood of a region (Altaf et al. 2014; Debnath et al. 2022, 2023a, b, c). Hence, LULC is regarded as one of the essential determinants of the occurrence of floods (Mojaddadi et al. 2017). The surface runoff is high over the concrete surface of the cities due to the low water penetration. Conversely, open or barren land allows water to penetrate and reduces surface runoff. As a result, different land-use types have diverse hydrological responses, increasing the risk of flooding (Das and Gupta 2021). Therefore, there is a significant relation between the frequency of flood occurrences and the pattern of land use, including its dynamics in terms of historical evolution and changes (Sugianto et al. 2022). The supervised classification technique was adopted to create the LULC map of the current study. The map was divided into six (6) classes: water body, settlement, barren terrain, agricultural land, vegetation, and ice/snow cover (Fig. 3f).

Rainfall The rainfall of a region is considered a prime reason for the flood. Even a brief spell of intense rainfall in a region has the potential to result in catastrophic flood conditions. Gridded rainfall data from 2012 and 2022 were gathered from the India Meteorological Department (IMD) (Retrieved from: https://www.imdpune.gov.in) for the JiaBharali river basin. The rainfall map is generated by applying the inverse distance weight (IDW) technique in ArcGIS to interpolate the point characteristics of the rainfall data. The rainfall values were divided into five categories using the ArcGIS software's Natural Breaks (Jenks) feature. The precipitation of the Jia Bharali River catchment area ranges from 1127.58 to 1835.29 mm (Fig. 3g).

Geology A geological characteristic has varied propensities of the lithological components in the hydrological process. Therefore, it is also considered an essential factor in FSI mapping. Spatio-temporal variation of the hydrological characteristics and sediment generation of a drainage basin is significantly controlled by the geology (Rahmati et al. 2016). Low drainage density can be found in highly resistant rocks or porous subsurface areas. Moreover, the development of a drainage pattern in connection to the emergence of a floodplain is also significantly influenced by geology (Ahmed et al. 2021). Additionally, natural factors like the permeability and erodibility of the geological subsoil and the torrential petrographic formations significantly influence the probability of flooding (Gupta and Dixit 2022). The Geological Survey of India (GSI) provided the geological data (retrieved from https://bhukosh.gsi.gov.in/), which was divided into five classes: Quaternary group, Siwalliks, Gondowana, Metamorphites undifferentiated, Sela group (Fig. 3l).

Geomorphology Another critical element for floods is the different geomorphology found in other regions. In general, the river's excess water can spread over low-lying plains quickly, and the loose soil in badlands is eroded with the cumulative flow of water. On the other hand, hilly areas are less likely to flood. The information related to this factor was collected from the GSI, which was categorized as low dissected structural hills and valleys, moderately dissected structural hills and valleys, highly dissected structural hills and valleys, active flood plain, and piedmont alluvial plain (Fig. 3h).

Soil texture This factor plays a considerable role in the local subsurface drainage network, surface flow of water, and moisture contents of a river basin (Ahmed et al. 2022). As a result, soil texture is a key flood hazard factor. The soil information was gathered from the NBSS & LUP District Soil Resource. The soil texture map of the present study region was divided into soil classes: (a) loam, (b) sandy clay loam, and (c) clay (Fig. 3i).

Method of the Multicollinearity testing for the selected flood influencing factors Tolerances, variance inflation factors (VIF), conditional index, and Pearson's correlation coefficients are often used for the multicollinearity tests prior to regression analysis in the susceptibility models (Ahmed et al. 2022). In this study, tolerances and VIF were applied to assess the degree of multicollinearity of the selected 13 flood-affecting elements (Mitra and Das 2022). In statistical evaluations, the VIF (Variance Inflation Factor) gauges the intensity of multicollinearity within the Ordinary Least Squares (OLS) regression framework. This metric serves as an indicator, measuring the extent to which multicollinearity amplifies the variance of an estimated regression coefficient. Duque and Aquino (2019) and Khosravi et al. (2018) proposed that multicollinearity is an issue if any flood-affected elements have total VIF values greater than 9. On the other hand, the presence of a tolerance value smaller than 0.1 is another sign of multicollinearity. Therefore, taking such influencing factors out of the equation is strongly advised before modeling if their VIF values are > 9 and their tolerance is < 0.1. The following formulas (Eqs. 2 and 3) were utilized to compute the VIF values of the chosen flood influencing factors.

$${T}_{i}=1-{{R}_{i}}^{2}$$

(2)

$${VIF}_{i}=\frac{1}{{T}_{i}}$$

(3)

where,${ T}_{i}$ stands for the tolerance value of ith predictor variable; ${VIF}_{i}$ stands for the variance inflation factor of ith predictor variable; ${{R}_{i}}^{2}$ denotes the determination coefficient associated with the regression equation.

Methods for the FSI mapping

Frequency ratio model (bivariate statistical techniques)

It is a subset of bivariate statistical techniques (BST) that evaluates the impact of each sub-category within chosen flood-affecting elements on potential future flooding (Rahmati et al. 2016). The link between flood occurrences and the associated causes is analyzed in order to determine FR. This model can be applied to provide a fundamental geographic evaluation approach to realize the stochastic correlation among the dependent and independent parameters. This statistical model for FSI mapping was used by Lee et al. (2012), Rahmati et al. (2016), Rahman et al. (2019), Sarkar and Mondal (2020), Waqas et al. (2021) and Ghosh and Dey (2021). The FR values were assessed utilizing the following Eq. (4):

$$FR=\frac{\left[\frac{{{\text{N}}}_{\mathrm{pix }}\left({{\text{SX}}}_{{\text{i}}}\right)}{{\sum }_{i=1}^{m}{{\text{SX}}}_{1}}\right]}{\left[\frac{{{\text{N}}}_{\mathrm{pix }}\left({{\text{X}}}_{{\text{j}}}\right)}{{\sum }_{j=1}^{n}{{\text{N}}}_{{\text{pix}}}\left({{\text{X}}}_{{\text{j}}}\right)}\right]}$$

(4)

After calculating the FR values for each class and sub-class (Table 2), the following Eq. (5) was applied for the flood susceptibility mapping.

$${\text{FSI}}={\sum }_{j=1}^{n}{\text{FR}}$$

(5)

where, N_pix(Xj)stands for the count of pixels related to variable X_j, N_pix(SX_i)represents the count of flood-related points within class I of variable X, m signifies the overall number of classes associated with variable X_i, while n is the cumulative total of all factors within the research area.

Table 2 FR and FL assessment of the conditioning factors

Fuzzy Logic model Fuzzy Logic (FL) is a collection of numerical formulas utilized to solve complicated situations. It is a straightforward mathematical technique that is simple to use (Ghosh and Dey 2021). Additionally, any measuring scale's data can be used with it, and experts also regulate the relative weights of each component (Sahana and Patel 2019; Ghosh et al. 2022). The normalized relative weights of the conditioning factors are prepared by applying the fuzzy membership function in a GIS context. The fuzzy overlay function enables the combination of those factors. The values in fuzzy membership normally span from “0” to “1”, where “0” stands for non-membership and “1” stands for significant membership. Sometimes, the membership values also fluctuated between “0” and “1”(Ramesh and Iqbal 2020). However, there are no standardized methods for evaluating the membership function.

In some cases, the values are preferred depending on the subjective assessment, whereas in others, membership values are extracted using statistical processes. The current study extracted the fuzzy membership values using the FR model (Ghosh et al. 2022). (Table 2). Therefore, it is named a Fuzzy Frequency Ratio (FFR) model (Kumar et al. 2016). The calculated FR value of each parameter and its sub-classes were then normalized between “0” (not sensitive to flooding) and “1” (sensitive to flooding) by applying the fuzzy membership function tool in ArcMap 10.7. Additionally, this normalized fuzzy membership analysis reflects the relative weights of every class of flood-influencing elements. Eventually, fuzzy membership data were integrated utilizing the fuzzy overlay analysis tool of ArcMap 10.7 to build the FSImap of the Jia Bharali River basin. Fuzzy AND, fuzzy OR, fuzzy algebraic product, fuzzy algebraic product, and fuzzy gamma operator are some of the operators used in the FL model to execute the overlay function (Ghosh et al. 2022). In this study, each parameter was united by the gamma operator, which ranges between 0.1 and 0.9. This research used a gamma value of 0.9 for the accurate FSI map of the Jia Bharali River basin (Ghosh and Dey 2021). The following Eq. (6) is a mathematical expression of the gamma operator:

$$\mu combination={\left(fuzzy algebric sum\right)}^{\uplambda }\times {(fuzzy algebraic product)}^{\uplambda }$$

(6)

Here, λ represents the chosen factors within the 0 and 1 range; the fuzzy algebraic functions as an ascending relation, whereas the fuzzy algebraic product operates as a descending relation.

Multi-Criteria Decision-Making Based Analytical Hierarchy Process (MCDM-AHP) T. L. Saaty created the MCDM-AHP method in the late 1970s. This model was initially used in the marketing sector (Saaty 1977, 1980). Currently, it is the most used MCDM-based model for weighing or rating the components and their categories (Saaty 1987, 1990). It is an efficient method for solving complex issues (Souissi et al. 2020). This MCDM technique is widely applied for flood vulnerability and susceptibility zone analysis because of its significance and relevance to current situations (Mitra et al. 2022). Therefore, the MCDM-based AHP technique was also adopted in this study to incorporate the selected conditioning elements for flood susceptibility mapping. Concerning their impact on creating the susceptibility mapping, each layer's weight varies. AHP uses pair-wise comparison matrices (PCM) to compare the weights of each class in a single theme layer as well as between different thematic levels. Hence, the relative weight of each factor was computed utilizing the Saaty scale (Saaty 1980), which ranges between 1 and 9 (Table 3). These preferences were determined using the information gathered from literature reviews, field experience, and expert recommendations. It is known as the knowledge-driven technique and is the fundamental and essential phase of this technique (Mitra et al. 2022).

Table 3 Pairwise comparison scale (Saaty 1980)

In the AHP method, a square matrix A = ${(a}_{ij})$ was generated when the n criteria for the flood susceptibility parameters needed to be compared. The following Eq. (7) was applied to calculate the ${a }_{ij}$ aij of the matrix component.

$${a}_{ij}=\frac{1}{{a}_{ij}}$$

(7)

In the case of the PCM, ${a}_{ij}$ adhere to equality, i.e.,${a}_{ij}=\frac{{P}_{i}}{{P}_{j}}$, where ${P}_{i}$ denotes the preference of the alternative $i$ as stated in Eq. (8).

$$A=\left(\begin{array}{ccc}\frac{{P}_{1}}{{P}_{1}}\cdots & \frac{{P}_{1}}{{P}_{j}}\cdots & \frac{{P}_{1}}{{P}_{n}}\cdots \\ \frac{{P}_{i}}{{P}_{1}} 1 & \cdots 1& \cdots \frac{{P}_{i}}{{P}_{n}}\\ \frac{\ddot{{P}_{n}}}{{P}_{1}}\cdots & \cdots \frac{{P}_{n}}{{P}_{j}}& \cdots \frac{{\ddot{P}}_{n}}{{P}_{n}}\end{array}\right)$$

(8)

The PCM of the present study is shown in Table 4.

Table 4 Decision matrix of the conditioning factors for the AHP model

Afterward, the relative ratio scale was computed from the matrix generated by the pair-wise comparison to assign weights or ratings using the following steps:

Step 1: Sum up all the elements in the j column of matrix A using Eq. (9).

$$\frac{{P}_{1}}{{P}_{j}}+ \dots + \frac{{P}_{1}}{{P}_{j}}+ \dots + \frac{{P}_{n}}{{P}_{n}}= \frac{{\sum }_{i=1}^{n}{{\text{P}}}_{{\text{i}}}}{{P}_{j}}$$

(9)

Step 2: Normalised values were calculated (Table 5) using Eq. (10).

Table 5 Conditioning factors for flood susceptibility modelling in the Jia Bharali River Basin

$$\frac{\frac{{P}_{i}}{{P}_{j}}}{\frac{{\sum }_{i=1}^{n}{{\text{P}}}_{{\text{i}}}}{{P}_{j}}}=\frac{{P}_{1}}{{P}_{j}}\times \frac{{P}_{j}}{{\sum }_{i=1}^{n}{{\text{P}}}_{{\text{i}}}}= \frac{{P}_{i}}{{\sum }_{i=1}^{n}{{\text{P}}}_{{\text{i}}}}$$

(10)

Step 3: Calculated the weight or rating $\left({w}_{i}\right)$ using the average of the elements (Table 5) using Eq. (11):

$${W}_{i}=\left(\frac{{P}_{i}}{{\sum }_{i=1}^{n}{{\text{P}}}_{{\text{i}}}}+\dots + \frac{{P}_{i}}{{\sum }_{i=1}^{n}{{\text{P}}}_{{\text{i}}}}\right)\times \frac{1}{n}$$

(11)

Examining judgment consistency is crucial to confirm the reliability and acceptability of the experts' decisions on pair-wise comparison for each conditioning factor (Mitra et al. 2022). The Consistency Ratio (CR) of the MCDM-AHP model was computed by applying the following Eqs. (12, 13) give by Saaty (1988):

$$CR=\frac{CI}{RI}$$

(12)

where, CR is the consistency ratio, CI is the consistency index, and RI is the random index, which is constant and analyzed in the paper of Saaty (1980b). The CI value was computed using the following Eq. (13):

$$CI=\frac{{\uplambda }_{max}-n}{n-1}$$

(13)

where, n stands for the number of components, $\mathrm{\lambda max}$ for the primary eigenvalue of the matrix, which was calculated using Eq. (14).

$${l}_{max}=\sum_{i=1}^{n}\left({W}_{i}\times \frac{{P}_{i}}{{\sum }_{i=1}^{n}{{\text{P}}}_{{\text{i}}}}\right)$$

(14)

The MCDM-AHP model determines the Consistency Ratio (CR) using the random consistency index, as detailed in Table 6. Typically, the model is accepted if the CR is less than 0.10. Higher CR values (> 0.10) result in a recalculation of the entire mathematical model and an adjustment to the relative weights of the characteristics. The Cumulative Consistency ratio for the FSI map of the Jia Bharalibasin is displayed in Table 7. It represents that the decisions taken for each selected factor to produce the FSI map of the river basin chosen using the AHP model are valid and acceptable.

Table 6 Random consistency index (Saaty 1988)

Table 7 Cumulative Consistency check for flood susceptibility assessment in the Jia Bharali Basin

After applying this AHP model to compute weights and ranks of the selected flood conditioning factor and sub-factor (Table 5), the FSI map was generated in ArcGIS 10.7 software utilizing the “raster calculator”. The following Eq. (15) was used to calculate FSI:

$$FSI= {(W}_{i}\times El) +\left({W}_{i}\times Sl\right) + \left({W}_{i}\times DD\right) + \left({W}_{i}\times DR\right)+\left({W}_{i}\times TWI\right) + \left({W}_{i}\times LULC\right) +\left({W}_{i}\times RF\right)+ \left({W}_{i}\times FA\right) + \left({W}_{i}\times ST\right) + \left({W}_{i}\times TRI\right) + \left({W}_{i}\times GM\right) +\left({W}_{i}\times Cu\right) + \left({W}_{i}\times GL\right)$$

(15)

Fuzzy analytical hierarchy process (FAHP)

FAHP performed better than AHP in evaluating and forecasting the flood hazard index (Yang et al. 2013). Since the values provided for each parameter in the AHP approach result from individualized assessments and preferences, they cannot be accurately quantified. Hence, fuzzy set theory can address the problem of uncertainty and calculate human evaluations with the fewest potential errors (Zadeh 1965; Ghosh and Maiti 2021). The core procedures of the FAHP model encompass deriving fuzzy triangular numbers (TFN) from the comparison of the AHP pairwise stage, ascertaining the fuzzy vector weights and factor ordering in a way that influences flooding, and drawing a conclusion (Tella and Balogun 2020; Vilasan and Kapse 2022). Generally, in the FAHP model, TFN is employed to explain the fuzzy membership functions (Table 8). The AHP values were averaged to provide fuzzy numbers that represented the AHP priority after accounting for the decision-makers preferences and the crisp numerical AHP values (Ayhan 2013). The fuzzification method applied in this experiment is shown in Table 9. The steps of the FAHP modeling process are as follows:

Table 8 Fuzzy pairwise scale

Table 9 Matrix for Fuzzy AHP decision related to criteria

Step 1: Comparison of the flood influencing factors. Here, the entire flood influencing parameters in the hierarchy system's dimensions were used to create pair-wise comparison matrices. Afterward, linguistic terms (Eq. 16) were allocated to the pair-wise comparisons in each case to determine which was more important in the two factors or criteria (Chen et al. 2011).

$$\tilde{A} = \left[ {\begin{array}{*{20}c} {\tilde{1}} & {\tilde{a}_{12} } & \cdots & {\tilde{a}_{1n} } \\ {\tilde{a}_{21} } & {\tilde{1}} & \ldots & {\tilde{a}_{2n} } \\ \vdots & \vdots & \ddots & \vdots \\ {\tilde{a}_{n1} } & {a_{n2} } & \cdots & {\tilde{1}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\tilde{1}} & {\tilde{a}_{12} } & \cdots & {\tilde{a}_{1n} } \\ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\tilde{a}_{21} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\tilde{a}_{21} }$}}} & {\tilde{1}} & \ldots & {\tilde{a}_{2n} } \\ \vdots & \vdots & \ddots & \vdots \\ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\tilde{a}_{n1} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\tilde{a}_{n1} }$}}} & {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\tilde{a}_{n2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\tilde{a}_{n2} }$}}} & \cdots & {\tilde{1}} \\ \end{array} } \right]$$

(16)

where, ${\widetilde{a}}_{ij}$ calculate denotes, let $\widetilde{1}$ be (1,1,1) when $i$ equal $j$ (i.e.,$i=j$); if $\widetilde{1}, \widetilde{2,}\widetilde{3,}\widetilde{4,}\widetilde{5,}\widetilde{6 }\widetilde{7,}\widetilde{8,}\widetilde{9}$ calculate that criterion $i$ is comparatively vital to criterion $j$ and then ${\widetilde{1}}^{-1}, {\widetilde{2}}^{-1}, {\widetilde{3}}^{-1},{\widetilde{4}}^{-1},{\widetilde{5}}^{-1},{\widetilde{6}}^{-1},{\widetilde{7}}^{-1},{\widetilde{8}}^{-1},{\widetilde{9}}^{-1}$ calculate that criterion $j$ is relatively crucial to criterion$i$.

Step 2: Geometric mean ${\widetilde{(r}}_{i})$ was applied to estimate the relative weight of each criterion (${\widetilde{w}}_{i}$) (Tables 10 and 11). The following Eqs.(17 and 18) were utilized to determine the geometric mean and fuzzy weight values (Buckley 1985).

$${\widetilde{r}}_{i}={\left({\widetilde{a}}_{i1}\otimes {\widetilde{a}}_{i2}\otimes \dots \otimes {\widetilde{a}}_{in}\right)}^{1/n}$$

(17)

$${\text{and then}}\;\tilde{w}_{i} = \tilde{r}_{i} \otimes \left( {\tilde{r}_{1} \otimes \ldots \otimes \tilde{r}_{n} } \right)^{ - 1} = (lw_{i} , mw_{i} , uw_{i} )$$

(18)

where, ${\widetilde{a}}_{in}$ is the fuzzy comparison value of criteria $i$ to criterion n, ${\widetilde{r}}_{i}$ is the geometric mean (GM) of the fuzzy comparison value (FCV) of criterion to every criterion $i$, ${\widetilde{w}}_{i}$ is the $i$ th criterion fuzzy weight, which can be denoted by a triangular fuzzy number (TFN). Here, ${uw}_{i}, {{mw}_{i, }and lw}_{i}$ denote the upper, middle, and lower fuzzy weight values of the of the $i$ th criterion, respectively.

Table 10 Geometric mean of the fuzzy matrix

Table 11 Fuzzy weight of the flood conditioning factors

To ascertain the final priority for each criterion, the precise numerical value underwent a defuzzification process utilizing the center of area (COA) approach. The average weight (Aw) shown in Table 11 was derived by employing Eq. (19) for the defuzzification process (Chou and Chang 2008).

$${A}_{w}= \frac{{lw}_{i}, {mw}_{i}, {uw}_{i}}{3}$$

(19)

Afterward, ${A}_{w}$ values were normalized using Eq. (20)in order to obtain the normalized average weight $({N}_{w})$.

$${N}_{w}= \frac{{A}_{w}}{{\sum }_{i=1}^{n}{A}_{w}}$$

(20)

After computing the normalized average weight $({N}_{i})$ using the FAHP model, the Flood Susceptibility Index (FSI) was prepared in ArcMap 10.7 by applying the “raster calculator”. The following Eq. (21) was applied to calculate the FSI:

$$FSI=({N}_{w}\times El) +\left({N}_{w}\times Sl\right) + \left({N}_{w}\times DD\right) + \left({N}_{w}\times DR\right)+\left({N}_{w}\times TWI\right) + \left({N}_{w}\times LULC\right) +\left({N}_{w}\times RF\right)+ \left({N}_{w}\times FA\right) + \left({N}_{w}\times ST\right) + \left({N}_{w}\times TRI\right) + \left({N}_{w}\times GM\right) +\left({N}_{w}\times Cu\right) + \left({N}_{w}\times GL\right)$$

(21)

Model validation The reliability and accuracy of any developed model are verified using the model validation process, and it is considered an essential part of the study (Mitra et al. 2022). The process of validating hazard susceptibility models can be done in many ways, but in this work, the FSI map has been validated using ROC-AUC, MAE, MSE, and RMSE. ROC-AUC illustrates the compromise between sensitivity and specificity (Mitra et al. 2022; Gupta and Dixit 2022; Ahmed et al. 2022). On the two-dimensional ROC graph, the $y$-axis stands for sensitivity (true positive rate), and the $x$-axis 1-specificity (false positive rate). The following Eqs. (22 and 23), following Swets (1988), describe the properties of $x$ and $y$ axis:

$$x=1-Specificity=1-\left[\frac{TN}{(TN+FP)}\right]$$

(22)

$$y=Sensitivity=\left[\frac{TN}{(TP-FN)}\right]$$

(23)

where, TN indicates True Negative; TP indicates True Positive; FP indicates False Positive; FN indicates False Negative.

Validations of the generated FSI models were done using the collected testing data. MAE, MSE, and RMSE were computed using the following Eqs to determine the prediction accuracy (Eqs. 24, 25, and 26):

$$MAE=\frac{{\sum }_{i=1}^{n}\left|{X}_{i}-{Y}_{i}\right|}{n}$$

(24)

$$MSE=\frac{{\sum }_{i=1}^{n}{\left({X}_{i}-{Y}_{i}\right)}^{2}}{n}$$

(25)

$$RMSE=\sqrt{\frac{{\sum }_{i=1}^{n}{\left({X}_{i}-{Y}_{i}\right)}^{2}}{n}}$$

(26)

Here, n denotes the sum of the data points, and ${X}_{i}$ and ${Y}_{i}$ for the observed and predicted values, respectively. In every situation, the smallest MAE, MSE, and RMSE value signifies greater model fitness. Greater model fitness is always indicated by lower MAE, MSE, and RMSE values.

Results

Multicollinearity results of the flood influencing factors and flood susceptibility mapping

To screen variables and evaluate the degree of multicollinearity before regression analysis, VIF is utilized. However, VIF alone does not identify which variables impact the dependent variable. To detect the degree of multicollinearity in the susceptibility and vulnerability modeling and to examine the significance of the selected flood-controlling variables, both VIF and tolerance value multicollinearity were obtained. A collinearity issue is generally identified with a VIF value greater than ten and a tolerance value less than 0.1. The VIF and tolerance values for all conditioning factors in this study range between 10 and 0.01 (Table 12), indicating that none of the 13 selected flood conditioning factors have a multicollinearity problem. According to the results, flow accumulation has the highest VIF value (6.67) and the lowest tolerance number (0.15) (Table 7).

Table 12 Multicollinearity test (tolerance and VIF values) of the flood conditioning factors

In this study, 13 flood-controlling factors were used to create an FSI map of the Jia Bharali River basin after identifying the flood-controlling factors through a literature review, analysis of basin conditions, and variable screening using the multicollinearity test. Before the model was executed, the CR of each thematic layer was estimated and found to have reached a reasonable level (< 0.10) of consistency. According to the models' assessment results, rainfall, flow accumulation, elevation, and distance to a stream have the biggest effects on the likelihood of flooding in the Jia Bharali river basin. This finding is consistent with prior research findings, such as Ahmed et al. (2022), Tella and Balogun (2020), and Das and Gupta (2021), which show that flood-controlling parameters, such as rainfall, drainage density, stream distance, LULC, elevation, and slope, have a considerable effect on flood hazards. Recent studies by Gupta and Dixit (2022) and Ahmed et al. (2022) have also concluded that excessive rainfall, distance from streams, LULC, elevation, and slope are the most significant contributing factors to flooding in the Brahmaputra floodplain, while geomorphology, curvature, and geology are less important. Finally, flood risk zones were categorized into five groups, including very low, low, moderate, high, and very high, to group flood risk zones (Fig. 4a–d).

Fig. 4

Flood susceptibility Index of the study area a AHP, b F-AHP, c FR, d FL

The MCDM-based AHP model indicated that the 110 sq km area of the entire Jia Bharali river basin would be “very highly” prone to flood hazard, whereas 2842 sq km would be “highly” sensitive. The FAHP model identified 520 km² and 1379 km² areas as “very high” and “high” flood risk zones (Table 13). In contrast, FR identified 19 km² and 973 km² as a zone with a “very high” and “high” possibility of flooding (Table 13). The Fuzzy Logic model identified 209 km² and 590 km²area of the Jia Bharali River basin in the “very high” and “high” probability of flooding, respectively. Moreover, the FR and FL models mostly highlighted the areas with very low flood hazard susceptibility. The areas were 3307 km² and 7298 km², respectively. The area under the lowland of the river basin and the vicinity of the river both display extremely high and high flood-prone zones. The result shows that as per the AHP, FAHP, FR, and FL models, 23.48, 15.10, 7.89, and 6.35% of areas come under the high to very high flood susceptibility zone, respectively. On the other hand, over 50% of the basin is classified between 'moderate to very low' flood-prone categories. Furthermore, most of the high to very high susceptible areas were found in the foothill region of the Jia Bharali watershed. For all four models, a consistent geographical distribution pattern of flood-prone areas was noticed regarding the area included under the “moderate”, “high”, and “very high” groups. However, in the FR and FL models, the statistics for the “high” and “very high” classifications are marginally lower than the AHP and FAHP models.

Table 13 Extent of areas mapped by the four susceptibility models within the Jia Bharali river basin

The results show that maximum built-up areas of the Jia Bharali River basin were found within the moderate to very high flood possibility zones (Fig. 3f) (Fig. 4a–d). Additionally, it was noticed that the “very high” and “high” susceptibility areas were also prevalent in metropolitan centers in the lower flood plain, whereas the “low” and “very low” susceptibility zones were discovered in hilly and mountainous locations. The prevalence of flood-prone zones in urban areas was also reviewed in the previous studies of Ahmed et al. (2022), Tella and Balogun (2020), and Das and Gupta (2021). According to Ahmed et al. (2022), 0.18 million people globally suffer each year due to flood disasters, notably those who live in thickly inhabited metropolitan centers and those who live closest to the river.

Model validation and evaluation

This research quantitatively validates the model results against the flood inventory map utilizing metrics like ROC-AUC, MAE, MSE, and RMSE. The FSI maps generated using the different models were compared using the validation points with the help of “The ArcSDM” toolbox in ArcMap 10.7 to perform the ROC-AUC. The RUC-AUC curve for FR, FL, AHP, and FAHP has been displayed in Fig. 5. The ROC-AUC demonstrated the efficiency level of the FSI model and classified it into five categories: excellent (> 0.9), accepted (0.8–0.9), good (0.7–0.8), considerable (0.6–0.7), and poor (0.5–0.6). In the present research, the AUC values of the FR, FL, AHP, and FAHP models are 0.900, 0.907, 0.950, and 0.881, respectively. It is simple to draw the conclusion that the models adopted to create the FSI map in this study are reliable and appropriate for identifying flood trends. The ROC-AUC curves suggested that the AHP technique had the maximum accuracy, followed by FL, FR, and FAHP. Therefore, AHP, FR, and FL performed excellently, while FAHP was accepted/very good based on the satisfaction scale. However, MAE, MSE, and RMSE findings for the four individual models are also analyzed in Table 14. The results clearly show that the FL model had the smallest MAE value of 0.1447, the smallest MSE value of 0.4096, and the smallest RMSE of 0.1678 compared to other selected models (Table 14). As a result, it is implied that the FL model had a very good relationship between the actual flood points and the anticipated flood points compared to other models applied in the study. It suggests that AHP and FL models have a very high degree of acceptability along with fewer flaws when modeling flood susceptibility index (FSI).

Fig. 5

ROC-AUC of the Jia Bharali River basin

Table 14 Evaluation of the four susceptibility models' precision for training data via various error metrics

Discussion

In Assam's Brahmaputra valley, floods are a frequent natural disaster (Gupta and Dixit 2022; Debnath et al. 2022). Furthermore, the Jia Bharali River, a north-bank tributary of the Brahmaputra River, is known for its vulnerability to hazards, causing extensive floods and erosion on an annual basis. Therefore, it is necessary to adopt a strategy to cope with floods and other natural disasters to lower the number of fatalities and property losses in hazard-prone areas. As a result, creating flood hazard zone maps becomes the utmost prerequisite because risk assessment heavily relies on them. Therefore, the current work uses innovative and reliable techniques to provide exact data that will aid in future flood management strategies. In this research, the susceptibility areas to the Jia Bharali River basin floods were forecasted using thirteen (13) flood conditioning factors. These variables can influence floods anywhere, and several of their methods are still being researched (Ahmed et al. 2022). The results clearly distinguish the research area's capacities for flood prediction by the affecting factors. The results of the Multicollinearity assessment did not show any of the factors employed in the study to have been eliminated because there were no highly correlated independent variables among the selected flood-influencing factors of the Jia Bharali River basin. The current research uses GIS approaches in conjunction with a model like FR, FL, AHP, and FAHP to recognize the flood susceptible areas of the Jia Bharali River basin. These models are used worldwide to rank the alternatives depending on their performance (Sarkar and Mondal 2020; Lee et al. 2012; Das and Gupta 2021; Mitra et al. 2022; Tella and Balogun 2020). Similar areas fall under the “moderate”, “high”, and “very high” classes in all four models employed in the study, and a consistent geographical pattern of flood sensitivity is evident in the basin. The study area predominantly experiences floods during the monsoon period, as noted by Gupta and Dixit (2022), with the foothill region being particularly affected. The FSI maps of the region further underscore that the foothill areas, significantly those close to the river, fall within the moderate to very high-risk flood zones. Moreover, the “high” susceptible zones of the flood were also seen in the riverine floodplain, where drainage density, flow accumulation, TWI, and rainfall were higher. Flood risk was lower in the upper mountainous catchment of the river due to high elevation, steep slope, low flow accumulation, and drainage density.

Mitra et al. (2022) use the AHP approach to evaluate the Uttar Dinajpur district of West Bengal's flood vulnerability zone. They claimed that in the floodplain region, floods have generally occurred along the riverside area; hence, the very high and high flood susceptibility classes are noticed along the rivers and their adjoining area. Flood conditioning indicators that contribute to the creation of high to very high flood-sensitive zones include lower elevation, a gentler slope, increased drainage density, TWI, and MNDWI. The flood susceptibility zone in Iran's Golastan Province was estimated by Rahmati et al. (2016). They showed that flooding mainly happens close to the river bank and hardly ever far from the rivers. The likelihood of a flood decreases with the increase in elevation and slope angle. Utilizing the FR and FL models, Sahana and Patel (2019) evaluate the Kosi River basin's vulnerability to flooding. The areas that are more susceptible to flooding include those near rivers, areas with greater drainage densities, sections of flat slopes, and low regional elevations. The regions with higher regional elevation, steeper slopes, and sites far from rivers were characteristic of the very low and low susceptibility zones, whilst the moderate susceptibility zone was typically limited to the interfluve areas. Similar results were also found in this research. According to Saikh and Mondal (2023), the model's prediction performance gets better as AUC rises. The AUC is more significant than 0.80–1.00, indicating that the model performance rate is good or excellent, according to the success rate curve's (training dataset and validation dataset) outcome of previous research results on flood susceptibility mapping (Sahana and Patel 2019; Das and Gupta 2021). Similar AUC scores for all models are also shown in this study compared to past research findings.

The ROC-AUC results evaluated that the AHP model correctly recognized the flood hazard zones of the basin (Das and Gupta 2021). As a result, this model is the most effective for the flood-prone zone identification of the Jia Bharali River basin, among other approaches. On the other hand, the FL model demonstrates relatively lower inaccuracy in the created susceptibility map based on MAE, MSE, and RMSE matrices (Lee et al. 2012). In that regard, the FR model is also acceptable for detecting flood-prone areas in the study region. The present research results will be extremely helpful to the local and state authorities of the Jia Bharali River basin. In addition to aiding in creating appropriate precautions to prevent potential danger in the research region, the study will offer many comprehensive ways for decision-makers to mitigate flood risks. The Jia Bharali basin's lower flatland has a history of frequent floods, making it difficult to observe and control post-flood phenomena. The Sonitpur district of Assam is identified as particularly vulnerable to flooding on susceptibility maps. This district experiences the greatest extent of “medium” to “very high” vulnerable zones every year. According to state disaster management assessments, the flood-prone zones of the Jia Bharali River basin include Bokagaon, Bokagaonchapari, Baligaon Miri, Gorali, Kekokali, Kolabari, and No. 2 Miri path area.

Additionally, the Tezpur urban area, considered a cultural town of Assam, is also flood-prone. These areas face floods yearly, and the locals there must deal with recurrent flash floods following each significant downpour during the monsoon season. The river water surges above the danger line and rises to the bank due to heavy rain, causing the river to overflow and erode the riverbanks, demolishing homes and displacing entire populations. Typically, those weaker in society suffer the most (Ahmed et al. 2022). Thousands of people lose their houses and begin living in different camps following the flood every year. The situation worsens for farmers as they cannot transport their crops, and water sources for drinking are flooded. All across the area, roads become clogged and disconnected. Consequently, in the Himalayan foothill area, flooding remains a significant issue (Mitra and Das 2022), leading to substantial setbacks in economic terms and human lives. While floods cannot be entirely avoided, they can be minimized by taking the necessary safety measures (Das and Gupta 2021; Gupta and Dixit 2022). However, this objective becomes more challenging from the perspective of climate change. Thus, accurately identifying this region's susceptible, vulnerable, and risk-prone areas is crucial.

The present study used geospatial technology to assess the spatial–temporal variation of flood susceptibility areas in the Jia Bharali River basin to prioritize flood-prone zones for effective mitigation and sustainable management measures (Meraj et al. 2022). The results of the current research are expected to have a significant impact on global flood hazard analysis research. The novelty of the present research lies in several factors. To begin with, this research marks the inaugural FSI mapping of the Jia Bharali River basin within the Brahmaputra floodplain. Next, unlike prior studies in the Brahmaputra floodplain area (Hazarika et al. 2018; Sharma et al. 2018; Pareta 2021), our study incorporated all crucial factors influencing floods. Finally, a unique combination of geospatial and geostatistical was merged with two MCDM techniques. This integrated approach was applied for the first time in any flood-vulnerable area of India. Another unique aspect of the present study is that it was conducted in a basin where almost 70–75% of the area comes under the Himalayan mountainous region, and the remaining area comes under the plain. Thus, the foothill region is affected by the sudden flow accumulation during the monsoon season, causing floods and havoc in this region. The models and flood-influencing factors adopted in the present study can be considered in any foothill region of the world for flood susceptibility analysis.

Although this study did not face any significant limitations, long-term hydrological data, especially water level and discharge, could have provided more insights and accuracy in flood susceptibility modeling. However, since these data were not available freely due to restrictions from the Central Water Commission of India, they could not be used in this study. Nonetheless, it is recommended to consider long-term water level and discharge data, if available, and prepare a hydrograph and rating curve when conducting flood susceptibility mapping of any region. The findings of this study have several implications for flood risk management and sustainable development in the Jia Bharali River basin and other similar regions. The study identified several flood-prone areas and zones of varying vulnerability, providing a basis for prioritizing mitigation and management measures. The results can guide decision-makers in developing effective flood preparedness and response plans, including constructing appropriate infrastructure such as embankments, flood shelters, and evacuation routes (Meraj et al. 2021). This study underscores the efficacy of geospatial technology and multi-criteria decision-making methods in the realm of flood susceptibility mapping, particularly in regions with limited data. The approach outlined here can be extended to other areas susceptible to floods and various natural calamities, significantly contributing to global hazard analysis and management endeavors. Through its findings, the research offers profound insights into flood risks in the Jia Bharali River basin and emphasizes the need for prioritized mitigation and management strategies. The value of geospatial technology and decision-making methodologies in understanding flood vulnerabilities is further reinforced. Going forward, research efforts should delve into the inclusion of extended hydrological records and investigate the role of emerging technologies in hazard assessment and control.

Conclusion

This investigation into flood susceptibility mapping in the Jia Bharali River Basin serves as a landmark in guiding flood mitigation and management strategies. By harnessing advanced methodologies like AHP, FR, FL, and FAHP, we've showcased their capabilities in furnishing dependable and precise outcomes. Notably, the AHP model emerged as the standout in pinpointing flood-prone zones within the surveyed territory. Our findings underscore the enhanced vulnerability of the lower floodplains and proximal river areas. Critical determinants like flow accumulation, topographical elevation, gradient, drainage density, and variances in precipitation are instrumental in ascertaining the susceptibility of the terrain. While some constraints, like data scarcity, posed challenges, the deployment of robust techniques—Bivariate Statistical, Fuzzy Logic, and MCDA-based strategies—illustrates their potential in flood risk evaluations, especially in regions grappling with data limitations. These insights resonate with flood-exposed locales globally, offering invaluable guidance to policymakers, engineering professionals, conservationists, and regional governance entities in amplifying their flood management and counteractive endeavors. From a broader perspective, the research sheds light on the repercussions of climate variability on flood hazards, accentuating the urgency of adaptive measures to champion the sustainable progression of the Jia Bharali River Basin. However, the study has limitations related to the database, including soil, topography, meteorology, lithology, historical flood events, stream discharge, weightage assignment, and accuracy of RS data. Looking ahead, incorporating heightened sensitivity assessments and cutting-edge machine learning techniques, artificial intelligence (AI), and deep learning (DL) algorithms can further refine the precision and trustworthiness of flood susceptibility delineations. This research underscores the profound implications of sophisticated modeling paradigms in fortifying flood management and preventive initiatives in regions susceptible to such calamities.