Introduction

Monkeypox disease (Mpox) is a disease that infects humans and animals. It is caused by the monkeypox virus (MPV) which belongs to the Orthopoxvirus genus of the Poxviridae family (Kumar et al. 2022). Symptoms of the disease usually start within 1–21 days after exposure (World Health Organization (WHO) 2023a). Common symptoms include a rash, fever, headache, sore throat, muscle aches, back pain, lethargy, and/or swollen lymph nodes (World Health Organization (WHO) 2023a; Thornhill et al. 2022).

In 2022, a global outbreak of mpox occurred with more than 85 thousand cases and 80 deaths reported from 110 countries (Laurenson-Schafer et al. 2023). Before the global outbreak, since the discovery of mpox in 1958, there has been sporadically cases of mpox mainly in Central and East Africa (Peter et al. 2022b). For example, thousands of cases of mpox have been reported annually in the DRC since 2005 (World Health Organization (WHO) 2023a). In 2017, mpox re-emerged in Nigeria and continues to spread among individuals across the country (World Health Organization (WHO) 2023a; Nigeria Centre for Disease Control and Prevention 2023; Alakunle et al. 2020). In recent decades sporadic cases of mpox have been reported in North America, Europe, and the Middle East, linked to tourists (Sah et al. 2022). These examples indicate the importance of controlling the spread of the mpox infections and why there is a need to improve our understanding of its transmission dynamics.

The transmission of mpox can occur in several ways: person-to-person, animal-to-person, animal-to-animal, and person-to-animal (World Health Organization (WHO) 2023b). Person-to-person transmission occurs through close contact with someone who is infected. Similarly, animal-to-animal transmission occurs through close contact of a susceptible animal with an infected animal. Animal-to-person transmission can occur when people come into physical contact with an infected animal such as some species of monkeys or terrestrial rodents (such as the tree squirrel). Physical contact can include through bites or scratches, or during activities such as hunting, skinning, trapping, or cooking. The virus can also be caught through eating infected animals if the meat is not cooked thoroughly (World Health Organization (WHO) 2023b).

Despite the negative impact of mpox globally, the disease has not attracted sufficient attention since its discovery (Dolgopolov et al. 2021). This together with other factors has contributed to a limited understanding of its transmission dynamics (Peter et al. 2022b).

Theoretical studies in the form of mathematical models have been successfully implemented in analysing the dynamics and the control of infectious diseases similar to mpox (Tien and Earn 2010; Wang and Liao 2012; Collins and Duffy 2022; Onuorah et al. 2022). Peter et al. (2022b) used a mathematical model based on the fractional differential equations to analyse the mpox transmission dynamics and Emeka et al. (2018) developed a deterministic mathematical model for mpox and used it to study the effect of infection and vaccination rates on the prevalence of the disease. Alharbi et al. (2022) developed a non-integer model for mpox and studied its qualitative analysis and dynamic behaviour using the fixed-point theorem approach. Al Qurashi et al. (2023) investigated mpox dynamics using a mathematical model in the form of fractional derivative. More studies on the transmission dynamics of mpox using mathematical deterministic models can be found in Bhunu and Mushayabasa (2011) and Peter et al. (2022a)). Important contributions to understanding the transmission dynamics and control of mpox epidemics are provided by these studies. A deterministic model is used in the present study to consider mpox dynamics focused on a Nigerian outbreak. However, as more than one group can be infected by mpox, humans and animals, the results of a deterministic model do not always hold when at the outset the number of people infected is small (Allen and Lahodny Jr 2012). In these cases a stochastic model based on the assumptions of the deterministic model can provide better insights (Lahodny et al. 2015) and this approach is also used here to model the mpox dynamics.

Method

First, a deterministic mathematical model is developed for the transmission dynamics of the monkeypox disease. This model is analysed to understand the possible dynamics and control of mpox. For a situation with more than one infectious group and when the initial number of the infected population is small a stochastic model is more suitable for analysing the dynamics (Allen and Lahodny Jr 2012). Thus, a stochastic version of model (1) is formulated using a continuous-time Markov chain (CTMC) process with discrete population sizes of humans and animals. The probability of mpox disease extinction or persistence using this model is estimated using a multitype branching process.

The deterministic model

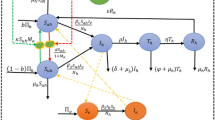
A deterministic mathematical model for mpox that takes into account the major factors that influence its dynamics is proposed. The model comprises two populations: humans and animals. A schematic illustration of this model is given in Fig. 1. The total human population \(N_h\) is further partitioned into four sub-populations namely, susceptible humans \(S_h\), exposed humans \(E_h\), infected humans \(I_h\) and recovered humans \(R_h\) (i.e, \(N_h = S_h + E_h + I_h + R_h\)). Similarly, the total animal population is partitioned into four sub-populations, namely, susceptible animals \(S_a\), exposed animals \(E_a\), infected animals \(I_a\), and recovered animals \(R_a\) (i.e., \(N_a = S_a + E_a + I_a + R_a\)).

Fig. 1
figure 1

Schematic illustration of the mpox model (1)

Full size image

The transmission dynamics within and across each of the sub-populations are formulated mathematically as follows. This formulation is an extension of the model given in (Peter et al. 2022b). Mpox infection may occur through human-to-human transmission, animal-to-animal transmission, animal-to-human transmission, and human-to-animal transmission (World Health Organization (WHO) 2023b). Susceptible human class increases through recruitment at a rate \(\Lambda _h\). Susceptible humans may proceed to the exposed human class upon contracting the disease through human-to-human or animal-to-human transmission at a rate \(\beta _{hh}\) and \(\beta _{ah}\) respectively. Exposed humans move to the infected class at a rate \(\sigma _h\) as they become infectious. The infected humans may die due to the disease at the rate \(\delta _h\) or recover at the rate \(\gamma _h\). Individuals in all the human class may die naturally at a rate \(\mu _h\).

Similarly, for the animal population, we assume that recruitment into the susceptible animal population occurs at a rate \(\Lambda _a\). Susceptible animals may proceed from the susceptible animal class to the exposed animal class upon contracting the disease through animal-to-animal or human-to-animal transmission at a rate \(\beta _{aa}\) and \(\beta _{ha}\) respectively. Exposed animals move to the infected animal class at a rate \(\sigma _a\) as they become infectious. The infected animals die due to the disease at the rate \(\delta _a\) or recover at the rate \(\gamma _a\). Natural death occurs in all the animal class at a rate \(\mu _a\).

Control measures that are capable of reducing the transmission rates are considered in the model by assuming that human-to-human, animal-to-animal, animal-to-human, and human-to-animal transmission can be reduced by a proportion \(c_{hh}, c_{aa}, c_{ah}\) and \(c_{ha}\) respectively through the introduction of the appropriate control measure. Based on these formulations aided by the assumptions above, the following deterministic model for the dynamics and control of mpox disease is developed:

$$\begin{aligned} \frac{dS_h}{dt}=\, & {} \Lambda _h - \frac{(1-c_{hh})\beta _{hh}I_h S_h}{N_h} - \frac{(1-c_{ah})\beta _{ah}I_a S_h}{N_a} - \mu _h S_h, \nonumber \\ \frac{dE_h}{dt}=\, & {} \frac{(1-c_{hh})\beta _{hh}I_h S_h}{N_h} + \frac{(1-c_{ah})\beta _{ah}I_a S_h}{N_a} - (\sigma _h + \mu _h)E_h, \nonumber \\ \frac{dI_h}{dt}=\, & {} \sigma _h E_h - (\gamma _h + \delta _h + \mu _h)I_h, \nonumber \\ \frac{dR_h}{dt}=\, & {} \gamma _h I_h - \mu _h R_h,\nonumber \\ \frac{dS_a}{dt}=\, & {} \Lambda _a - \frac{(1-c_{aa})\beta _{aa} I_a S_a}{N_a} - \frac{(1-c_{ha})\beta _{ha} I_h S_a}{N_h} - \mu _a S_a, \nonumber \\ \frac{dE_a}{dt}=\, & {} \frac{(1-c_{aa})\beta _{aa} I_a S_a}{N_a} + \frac{(1-c_{ha})\beta _{ha} I_h S_a}{N_h} - (\sigma _a + \mu _a )E_a, \nonumber \\ \frac{dI_a}{dt}=\, & {} \sigma _a E_a - (\gamma _a + \delta _a + \mu _a)I_a, \nonumber \\ \frac{dR_a}{dt}=\, & {} \gamma _a I_a - \mu _a R_a. \end{aligned}$$
(1)

The meaning of variables and parameters of model (1) can be found in Tables 1 and 2, respectively.

Table 1 Variables for model (1)
Full size table
Table 2 Parameters for model (1)
Full size table

Deterministic model analyses

The analysis of some important epidemiological features of model (1) are presented in this section. The equations for the dynamics of total human and animal populations from model (1), respectively, are given by

$$\begin{aligned} \frac{dN_h}{dt} = \Lambda _h - \mu _h N_h - \delta _h I_h, \end{aligned}$$
(2)

and

$$\begin{aligned} \frac{dN_a}{dt} = \Lambda _a - \mu _a N_a - \delta _a I_a. \end{aligned}$$
(3)

Thus, the feasible region

$$\begin{aligned} \Omega = \left\{ (S_h, E_h, I_h, R_h, S_a, E_a, I_a, R_a) \in \mathbb {R}_+^8 \vert N_h \le \frac{\Lambda _h}{\mu _h}, ~~ N_a \le \frac{\Lambda _a}{\mu _a} \right\} \end{aligned}$$
(4)

is positively invariant with respect to model (1).

The basic reproduction number

Model (1) has a disease-free equilibrium (DFE) given by

$$\begin{aligned}{} & {} (S_h^0,~ E_h^0, ~I_h^0, ~ R_h^0,~ S_a^0, ~ E_a^0, ~ I_a^0, ~R_a^0) \nonumber \\{} & {} \quad = \left( \frac{\Lambda _h}{\mu _h},~ 0, ~0, ~0, \frac{\Lambda _a}{\mu _a}, ~ 0, ~0, ~0 \right) . \end{aligned}$$
(5)

An important epidemiological threshold quantity for model (1) known as basic reproduction number \((\mathcal {R}_0)\) is calculated via the next-generation matrix approach (van den Driessche and Watmough 2002). The next-generation matrix for the model are given by

$$\begin{aligned} F = \begin{pmatrix} 0 &{} (1-c_{hh})\beta _{hh} &{} 0 &{} \frac{(1-c_{ah})\beta _{ah} S_h^0}{S_a^0} \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} \frac{(1-c_{ha})\beta _{ha} S_a^0}{S_h^0} &{} 0 &{} (1-c_{aa})\beta _{aa}\\ 0 &{} 0 &{} 0 &{} 0 \end{pmatrix}, ~~ V = \begin{pmatrix} \alpha _1 &{} 0 &{} 0 &{} 0 \\ -\sigma _h &{} \alpha _2 &{} 0 &{} 0 \\ 0 &{} 0 &{} \alpha _3 &{} 0\\ 0 &{} 0 &{} -\sigma _a &{} \alpha _4 \end{pmatrix} \end{aligned}$$

where \(\alpha _1 = \sigma _h + \mu _h\), \(\alpha _2 = \gamma _h + \delta _h + \mu _h\), \(\alpha _3 = \sigma _a + \mu _a\) and \(\alpha _4 = \gamma _a + \delta _a+ \mu _a\). The spectral radius of the matrix \(FV^{-1}\) which is the basic reproduction number (\(\mathcal {R}_0\)) is determined as

$$\begin{aligned} \mathcal {R}_0 = \frac{(\mathcal {R}_0^{hh} +\mathcal {R}_0^{aa}) + \sqrt{(\mathcal {R}_0^{hh} - \mathcal {R}_0^{aa})^2 + 4 \mathcal {R}_0^{ah} \mathcal {R}_0^{ha}}}{2}, \end{aligned}$$
(6)

where

$$\begin{aligned} \mathcal {R}_0^{hh}=\, & {} \frac{(1-c_{hh})\beta _{hh} \sigma _h}{\alpha _1 \alpha _2}, ~~~ \mathcal {R}_0^{aa} = \frac{(1-c_{aa})\beta _{aa} \sigma _a}{\alpha _3 \alpha _4}, \nonumber \\ \mathcal {R}_0^{ah}=\, & {} \frac{(1-c_{ah})\beta _{ah}S_h^0 \sigma _a}{\alpha _3 \alpha _4 S_a^0}, ~~\mathcal {R}_0^{ha} = \frac{(1-c_{ha})\beta _{ha} \sigma _h S_a^0}{\alpha _1 \alpha _2 S_h^0}. \end{aligned}$$
(7)

The quantities \(\mathcal {R}_0^{hh}, ~ \mathcal {R}_0^{aa}, ~~ \mathcal {R}_0^{ha}\) and \(\mathcal {R}_0^{ah}\) represent contributions to \(\mathcal {R}_0\) via human-to-human, animal-to-animal, animal-to-human, and human-to-animal transmissions respectively.

Existence of endemic equilibrium

Animal-only endemic equilibrium: This can occur in the system when there are only animal-to-animal infections and no human-to-human infections or animal-to-human infections. The disease endemic equilibrium (EE) for this scenario in model (1) (for \(\delta _a = \delta _h = 0\)) is obtained as

$$\begin{aligned}{} & {} (S_h^*,~ E_h^*, ~I_h^*, ~ R_h^*,~ S_a^*, ~ E_a^*, ~ I_a^*, ~R_a^*) \nonumber \\{} & {} \quad = \left( S_h^0,~ 0, ~0, ~0, \frac{S^0_a}{\mathcal {R}_0^{aa}}, ~\frac{\alpha _4 I_a^*}{\sigma _a}, ~I_a^*, \frac{\gamma _a I_a^*}{\mu _a} \right) , \end{aligned}$$
(8)

where \(I_a^* = \frac{\mu _a\sigma _aS_a^0(\mathcal {R}_0^{aa} - 1)}{ \alpha _3 \alpha _4 \mathcal {R}_0^{aa}}.\) Equation (8) shows that an animal-only endemic equilibrium exists for model (1) whenever \(\mathcal {R}_0^{aa} > 1\) and \(\mathcal {R}_0^{hh} < 1\).

Human-only endemic equilibrium: This can occur in the system when there is only human-to-human infection and no animal-to-animal infection or animal-to-human infections. The EE for this scenario in a model (1) (for \(\delta _a = \delta _h = 0\)) is obtained as

$$\begin{aligned}{} & {} (S_h^*,~ E_h^*, ~I_h^*, ~ R_h^*,~ S_a^*, ~ E_a^*, ~ I_a^*, ~R_a^*) \nonumber \\{} & {} \quad = \left( \frac{S^0_h}{\mathcal {R}_0^{hh}},~ \frac{\alpha _2 I_h^*}{\sigma _h}, ~ I_h^*, ~\frac{\gamma _h I_h^*}{\mu _h}, ~ S_a^0, ~ 0, ~0, ~0 \right) , \end{aligned}$$
(9)

where \(I_h^* = \frac{\mu _h\sigma _hS_h^0(\mathcal {R}_0^{hh} - 1)}{ \alpha _1 \alpha _2 \mathcal {R}_0^{hh}}.\) Similarly, Eq. (9) shows that human-only endemic equilibrium exists for model (1) whenever \(\mathcal {R}_0^{hh} > 1\) and \(\mathcal {R}_0^{aa} < 1\).

Stability analyses

In this section the stability of model (1) about the DFE is presented to illustrate the dynamics of the model about the equilibrium point. The result of the stability analysis is presented in Theorem 1 below.

Theorem 1

The disease-free equilibrium (5) is globally asymptotically stable when \(\mathcal {R}_0<1\).

The proof of Theorem 1 is established using a stability results by Castillo-Chavez et al. (2002), which is stated below.

Lemma 1

Consider a model system written in the form

$$\begin{aligned} \frac{dZ_1}{dt}=\, & {} F(Z_1,Z_2) \nonumber \\ \frac{dZ_2}{dt}=\, & {} G(Z_1,Z_2), ~~ ~~ G(Z_1,0) = 0. \end{aligned}$$
(10)

where \(Z_1 \in \mathbb {R}^m\), \(Z_2 \in \mathbb {R}^n\) and \(Z_0 = (Z_1; 0)\) is an equilibrium of the system. Assume that

  1. (H1)

    For \(\frac{dZ_1}{dt} = F(Z_1, 0)\), \(Z_1^*\) is globally asymptotically stable;

  2. (H2)

    \(G(Z_1, Z_2 ) = A Z_2 - \hat{G}(Z_1,Z_2)\),   \(\hat{G}(Z_1,Z_2)\ge 0\) for \((Z_1,Z_2) \in \Omega ,\) where the Jacobian \(A = \frac{\partial G}{\partial Z_2}(Z_1, 0)\) is a M–matrix (the off-diagonal elements of A are non-negative), and \(\Omega\) is the region where the model makes biological sense.

Then \(Z_0\) is globally asymptotically stable provided that \(\mathcal {R}_0 \le 1\).

Proof

To proof Theorem 1 using Lemma 1, it only required to show that the conditions (H1) and (H2) hold when \(\mathcal {R}_0 \le 1\). In model (1), let \(Z_1 = (S_h(t), R_h(t), S_a(t), R_a(t)),~ Z_2 = (E_h(t), I_h(t), E_a(t), I_a(t))\) and \(Z_1^* = \left( S_h^0, 0, S_a^0, 0\right)\). The system \(G(Z_1,Z_2)\) is given by

$$\begin{aligned} G(Z_1, Z_2 ) = \begin{pmatrix} \frac{(1-c_{hh})\beta _{hh}I_h S_h}{N_h} + \frac{(1-c_{ah})\beta _{ah}I_a S_h}{N_a} - \alpha _1 E_h \\ \sigma _h E_h - \alpha _2 I_h\\ \frac{(1-c_{aa})\beta _{aa} I_a S_a}{N_a} + \frac{(1-c_{ha})\beta _{ha} I_h S_a}{N_h} - \alpha _3 E_a\\ \sigma _a E_a - \alpha _4 I_a \end{pmatrix}. \end{aligned}$$

\(G(Z_1,Z_2)\) can be rewritten in the form

$$\begin{aligned} G(Z_1, Z_2 ) = A Z_2 - \hat{G}(Z_1,Z_2) \end{aligned}$$

where

$$\begin{aligned} A = \begin{pmatrix} \nonumber - \alpha _1 &{} (1-c_{hh})\beta _{hh} &{} 0 &{} \frac{(1-c_{ah})\beta _{ah} S_h^0}{S_a^0} \\ \sigma _h &{} - \alpha _2 &{} 0 &{} 0 \\ 0 &{} \frac{(1-c_{ha})\beta _{ha} S_a^0}{S_h^0} &{} -\alpha _3 &{} (1-c_{aa})\beta _{aa} \\ 0 &{} 0 &{} \sigma _a &{} - \alpha _4 \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} \hat{G}(Z_1,Z_2) = \begin{pmatrix} (1-c_{hh})\beta _{hh} I_h\left( 1 - \frac{S_h}{N_h} \right) + (1-c_{ah})\beta _{ah} I_a\left( \frac{S_h^0}{S_a^0} - \frac{S_h}{N_a} \right) \\ 0 \\ (1-c_{ha})\beta _{ha} I_h\left( \frac{S_a^0}{S_h^0} - \frac{S_a}{N_h} \right) + (1-c_{aa})\beta _{aa} I_a\left( 1 - \frac{S_a}{N_a} \right) \\ 0 \end{pmatrix}. \end{aligned}$$

It is obvious that \(\hat{G}(Z_1,Z_2)\ge 0\), since at DFE \(S_h^0 = N_h \ge S_h\) and \(S_a^0 = N_a \ge S_a\). The global stability of the system

$$\begin{aligned} \frac{dZ_1}{dt} = F(Z_1, 0) = \begin{pmatrix} \Lambda _h - \mu _h S_h \nonumber \\ -\mu _h R_h \nonumber \\ \Lambda _a - \mu _a S_a \nonumber \\ -\mu _a R_a \nonumber \\ \end{pmatrix} \end{aligned}$$

can be easily verified as follows: \(F(Z_1, 0)\) is a system of linear ordinary differential equations, and solving it gives \(S_h(t) = S_h^0 + B_1e^{-\mu _h t}\), \(R_h(t) = R_h(0)e^{-\mu _h t}\), \(S_a(t) = S_a^0 + B_2e^{-\mu _a t}\) and \(R_a(t) = R_a(0)e^{-\mu _a t}\) where \(B_1, B_2\) are constants. Clearly, \((S_h(t), R_h(t), S_a(t), R_a(t)) \longrightarrow (S_h^0, 0, S_a^0, 0)\) as \(t \longrightarrow \infty\). Therefore, \(Z_1^*\) is globally asymptotically stable. Hence, the disease-free equilibrium (5) is globally asymptotically stable when \(\mathcal {R}_0<1\), completing the proof. \(\square\)

The stochastic model

For the stochastic model formulation, we proceed as follows. Let \(S_h(t), E_h(t), I_h(t), R_h(t), E_a(t), I_a(t), I_a(t)\) and \(R_a(t)\) be discrete-valued random variables for the number of susceptible humans, exposed humans, infected humans, recovered humans, susceptible animals, exposed animals, infected animals and recovered animals respectively, each with a finite state space and where time \(t \in [0, \infty )\) is continuous. The same symbols used for the deterministic model (1) are used for the stochastic model for simplicity. Description of the state transitions and rates for the CTMC model are given in Table 3.

Table 3 State transitions and rates for the stochastic model
Full size table

The probability of disease eradication or persistence can be calculated via the multitype branching process approach (Allen and Lahodny Jr 2012; Lahodny et al. 2015). The method is applicable to the infectious populations while the non-infectious populations are assume to be at DFE (Allen and Lahodny Jr 2012).

An estimate for the probability of disease extinction can be obtained from an offspring probability-generating function (pgf) (Allen and Lahodny Jr 2012). When the initial populations of humans and animals are near to the DFE (\(S_h(0) = S_h^0\) and \(S_a(0)= S_a^0\)), the offspring pgfs for \(E_h, I_a, E_a\) and \(I_a\) is calculated using the transition rates in Table 3. For instance, the offspring pgf for \(E_h\) given \(E_h(0) = 1, I_h(0) = 0, E_a(0)= 0\) and \(I_a(0) = 0\) is

$$\begin{aligned} g_1(u_1,u_2,u_3,u_4) = \frac{\sigma _h u_2 + \mu _h}{\sigma _h + \mu _h}. \end{aligned}$$
(11)

The term \(\frac{\sigma _h }{\sigma _h + \mu _h}\) can be interpreted as the probability that an \(E_h\) survives natural death and becomes \(I_h\) which results in \(E_h = 0, I_h = 1, E_a = 0\) and \(I_a = 0\). Also, the term \(\frac{\mu _h }{\sigma + \mu _h}\) is the probability that an \(E_h\) dies due to natural death before becoming \(I_h\). Similarly, the offspring pgf for \(I_h\) given \(E_h(0) = 0, I_h(0) = 1, E_a(0)= 0\) and \(I_a(0) = 0\) is

$$\begin{aligned} g_2(u_1,u_2,u_3,u_4) = \frac{(1-c_{hh})\beta _{hh}u_1u_2 + (1-c_{ha})\beta _{ha}S_{ha}^0u_2u_3 + \alpha _2 }{(1-c_{hh})\beta _{hh} + (1-c_{ha})\beta _{ha}S_{ha}^0 + \alpha _2 }, \end{aligned}$$
(12)

where \(S_{ha}^0 = \frac{S_a^0}{S_h^0}\). The offspring pgf for an \(E_a\) given \(E_h(0) = 0, I_h(0) = 0, E_a(0)= 1\) and \(I_a(0) = 0\) is

$$\begin{aligned} g_3(u_1,u_2,u_3,u_4) = \frac{\sigma _a u_4 + \mu _a}{\sigma _a + \mu _a}. \end{aligned}$$
(13)

The offspring pgf for \(I_a\) given \(E_h(0) = 0, I_h(0) = 0, E_a(0)= 0\) and \(I_a(0) = 1\) is

$$\begin{aligned} g_4(u_1,u_2,u_3,u_4) = \frac{ (1-c_{aa})\beta _{aa}u_3u_4 + (1-c_{ah})\beta _{ah}S_{ah}^0u_1u_4 + \alpha _4 }{(1-c_{aa})\beta _{aa} + (1-c_{ah})\beta _{ah}S_{ah}^0 + \alpha _4}, \end{aligned}$$
(14)

where \(S_{ah}^0 = \frac{S_h^0}{S_a^0}\).

The expectation matrix \(\mathbb {M}\) of the offspring pgfs is defined by

$$\begin{aligned}{} & {} \mathbb {M} = \begin{pmatrix} \frac{\partial g_1}{\partial u_1} ~ &{} \frac{\partial g_2}{\partial u_1} ~&{} \frac{\partial g_3}{\partial u_1} ~ &{} \frac{\partial g_4}{\partial u_1} \\ \\ \frac{\partial g_1}{\partial u_2} ~ &{} \frac{\partial g_2}{\partial u_2} ~&{} \frac{\partial g_3}{\partial u_2} ~ &{} \frac{\partial g_4}{\partial u_2}\\ \\ \frac{\partial g_1}{\partial u_3} ~ &{} \frac{\partial g_2}{\partial u_3} ~&{} \frac{\partial g_3}{\partial u_3} ~ &{} \frac{\partial g_4}{\partial u_3}\\ \\ \frac{\partial g_1}{\partial u_4} ~ &{} \frac{\partial g_2}{\partial u_4} ~&{} \frac{\partial g_3}{\partial u_4} ~ &{} \frac{\partial g_4}{\partial u_4}\\ \end{pmatrix} ~ \text {evalauted ~at} ~ (u_1,u_2,u_3,u_4) \nonumber \\{} & {} \quad = (1,1,1,1). \end{aligned}$$
(15)

Evaluating Eq. (15) gives

$$\begin{aligned} \mathbb {M}=\, & {} \begin{pmatrix} 0 &{} \frac{(1-c_{hh})\beta _{hh}}{(1-c_{hh})\beta _{hh} + (1-c_{ha})\beta _{ha}S_{ha}^0 + \alpha _2 } &{} 0 &{} \frac{ (1-c_{ah})\beta _{ah}S_{ah}^0}{(1-c_{aa})\beta _{aa} + (1-c_{ah})\beta _{ah}S_{ah}^0 + \alpha _4 } \\ \\ \frac{\sigma _h }{\alpha _1}&{} \frac{(1-c_{hh})\beta _{hh} + (1-c_{ha})\beta _{ha}S_{ha}^0 }{(1-c_{hh})\beta _{hh} + (1-c_{ha})\beta _{ha}S_{ha}^0 + \alpha _2 } &{} 0 &{} 0 \\ \\ 0 &{} \frac{(1-c_{ha})\beta _{ha}S_{ha}^0}{(1-c_{hh})\beta _{hh} + (1-c_{ha})\beta _{ha}S_{ha}^0 + \alpha _2} &{} 0 &{} \frac{ (1-c_{aa})\beta _{aa}}{(1-c_{aa})\beta _{aa} + (1-c_{ah})\beta _{ah}S_{ah}^0 + \alpha _4 } \\ \\ 0 &{} 0 &{} \frac{\sigma _a}{\alpha _3} &{} \frac{ (1-c_{aa})\beta _{aa} + (1-c_{ah})\beta _{ah}S_{ah}^0}{(1-c_{aa})\beta _{aa} + (1-c_{ah})\beta _{ah}S_{ah}^0 + \alpha _4 } \\ \end{pmatrix} \nonumber \\=\, & {} \begin{pmatrix} \mathbb {M}_{1} &{} \mathbb {M}_{2}\\ \mathbb {M}_{3} &{} \mathbb {M}_{4} \end{pmatrix}, \end{aligned}$$
(16)

where \(\mathbb {M}_{1}, \mathbb {M}_{2}, \mathbb {M}_{3}\) and \(\mathbb {M}_{4}\), respectively, are 2 by 2 sub-matrices in the upper right, upper left, lower right, and lower left corners of \(\mathbb {M}\).

By taking the basic reproduction numbers into consideration, the matrix (16) can be rewritten as

$$\begin{aligned} \mathbb {M} = \begin{pmatrix} 0 &{} \frac{ \alpha _1 \mathcal {R}_0^{hh}}{\alpha _1 (\mathcal {R}_0^{hh} + \mathcal {R}_0^{ha}) + \sigma _h } &{} 0 &{} \frac{ \alpha _3 \mathcal {R}_0^{ah}}{\alpha _3 (\mathcal {R}_0^{aa} + \mathcal {R}_0^{ah}) + \sigma _a } \\ \\ \frac{\sigma _h }{\alpha _1}&{} \frac{ \alpha _1 ( \mathcal {R}_0^{hh} + \mathcal {R}_0^{ha} )}{\alpha _1 (\mathcal {R}_0^{hh} + \mathcal {R}_0^{ha}) + \sigma _h } &{} 0 &{} 0 \\ \\ 0 &{} \frac{ \alpha _1 \mathcal {R}_0^{ha}}{\alpha _1 (\mathcal {R}_0^{hh} + \mathcal {R}_0^{ha}) + \sigma _h } &{} 0 &{} \frac{ \alpha _3 \mathcal {R}_0^{aa}}{\alpha _3 (\mathcal {R}_0^{aa} + \mathcal {R}_0^{ah}) + \sigma _a } \\ \\ 0 &{} 0 &{} \frac{\sigma _a}{\alpha _3} &{} \frac{ \alpha _3 (\mathcal {R}_0^{aa} + \mathcal {R}_0^{ah} )}{\alpha _3 (\mathcal {R}_0^{aa} + \mathcal {R}_0^{ah}) + \sigma _a } \\ \end{pmatrix}. \end{aligned}$$
(17)

Let \(\rho (\mathbb {M})\) represent the spectral radius of the expectation matrix \(\mathbb {M}\). The magnitude of \(\rho (\mathbb {M})\) shows whether the probability of the disease extinction (\(\mathbb {P}_0\)) is equal to or less than one (Allen and van den Driessche 2013). If \(\rho (\mathbb {M}) \le 1\) (subcritical and critical), then \(\mathbb {P}_0\) becomes one, that is,

$$\begin{aligned} \mathbb {P}_0 = \lim _{t \longrightarrow \infty } \{ \overline{I}(t) = 0 \} = 1, \end{aligned}$$
(18)

where \(\overline{I}(t) = (E_h(t), I_h(t), E_a(t), I_a(t) )^T\) and T is the transpose. However, if \(\rho (\mathbb {M}) >1\), there is a non-zero probability that the disease will persist. Particularly, if \(\rho (\mathbb {M}) > 1\) (supercritical), there exists a fixed point \((u_1, u_2, u_3, u_4)\in (0,1)^4\) of the offspring pgfs, \(g_i(u_1, u_2, u_3, u_4) = u_i\) for \(i = 1, 2, 3, 4\) such that the probability of the disease eradication is given by

$$\begin{aligned} \mathbb {P}_0 = \lim _{t \longrightarrow \infty } \{ \overline{I}(t) = 0 \} = u_1^{e_h}u_2^{i_h}u_3^{e_a}u_4^{i_a} < 1, \end{aligned}$$
(19)

where \(e_h = E_h(0), i_h = I_h(0), e_a = E_a(0)\) and \(i_a = I_a(0)\). The value of \(u_1, u_2, u_3\) and \(u_4\), are the probability of disease extinction for \(E_h, I_h, E_a\) and \(I_a\) respectively. Thus, the probability of a major outbreak or persistence \(\mathbb {P}_m\) can be calculated as

$$\begin{aligned} \mathbb {P}_m = 1 -\mathbb {P}_0. \end{aligned}$$
(20)

The matrix (17) satisfies \(\rho (\mathbb {M}) < 1\) iff the following conditions hold

$$\begin{aligned} \text {trace}(\mathbb {M}_i)< 1 + \text {det}(\mathbb {M}_i) < 2, ~~~ \forall ~~ i = 1, 2, 3, 4. \end{aligned}$$
(21)

To determine if the matrix (17) satisfies the inequality (21), we proceed as follows. Obviously, \(\text {trace}(\mathbb {M}_i) = \text {det}(\mathbb {M}_i) = 0\) for \(i = 2,3\). So \(\mathbb {M}_2\) and \(\mathbb {M}_3\) satisfies condition (21). For \(\mathbb {M}_1\) and \(\mathbb {M}_4\), we have

$$\begin{aligned} \text {trace}(\mathbb {M}_1)=\, & {} \frac{ \alpha _1 (\mathcal {R}_0^{hh} + \mathcal {R}_0^{ha} )}{\alpha _1 (\mathcal {R}_0^{hh} + \mathcal {R}_0^{ha}) + \sigma _h }, \nonumber \\ \text {trace}(\mathbb {M}_4)=\, & {} \frac{ \alpha _3 (\mathcal {R}_0^{aa} + \mathcal {R}_0^{ah} )}{\alpha _3 (\mathcal {R}_0^{aa} + \mathcal {R}_0^{ah}) + \sigma _a }, \nonumber \\ \text {det}(\mathbb {M}_1)=\, & {} \frac{ - \sigma _h \mathcal {R}_0^{hh}}{\alpha _1 (\mathcal {R}_0^{hh} + \mathcal {R}_0^{ha}) + \sigma _h }, \nonumber \\ \text {det}(\mathbb {M}_4)=\, & {} \frac{ -\sigma _a \mathcal {R}_0^{aa} }{\alpha _3 (\mathcal {R}_0^{aa} + \mathcal {R}_0^{ah}) + \sigma _a }. \nonumber \end{aligned}$$
(22)

By algebraic calculations, we obtain that

$$\begin{aligned} \text {trace}(\mathbb {M}_1) - \text {det}(\mathbb {M}_1)=\, & {} \frac{ \alpha _1 (\mathcal {R}_0^{hh} + \mathcal {R}_0^{ha} ) + \sigma _h \mathcal {R}_0^{hh}}{\alpha _1 (\mathcal {R}_0^{hh} + \mathcal {R}_0^{ha}) + \sigma _h }< 1 ~~\text {iff} ~~ \mathcal {R}_0^{hh}< 1, \nonumber \\ \text {trace}(\mathbb {M}_4) - \text {det}(\mathbb {M}_4)=\, & {} \frac{ \alpha _3 (\mathcal {R}_0^{aa} + \mathcal {R}_0^{ah} ) + \sigma _a \mathcal {R}_0^{aa}}{\alpha _3 (\mathcal {R}_0^{aa} + \mathcal {R}_0^{ah}) + \sigma _a }< 1~~ \text {iff} ~~ \mathcal {R}_0^{aa} < 1 \nonumber . \end{aligned}$$
(23)

This shows that the matrix (17) satisfies the conditions (21) iff \(\mathcal {R}_0^{hh} < 1\) and \(\mathcal {R}_0^{aa} < 1\). Thus, \(\rho (\mathbb {M}) < 1\) iff \(\mathcal {R}_0^{hh} < 1\) and \(\mathcal {R}_0^{aa} < 1\).

However, if \(\mathcal {R}_0^{hh} > 1\) and \(\mathcal {R}_0^{aa} > 1\), the fixed points of the offspring pgfs can be calculated by setting \(g_i(u_1, u_2, u_3, u_4) = u_i\), for \(i = 1, 2, 3, 4\). Solving for \(u_i\), from (11)–(14), we obtain

$$\begin{aligned} u_1=\, & {} \frac{\sigma _h u_2 + \mu _h}{\alpha _1},\\ u_3=\, & {} \frac{\sigma _a (d_5u_2 - d_1u_2^2 - d_3) + d_2 \mu _a u_2 }{\alpha _3 d_2 u_2},\\ u_4=\, & {} \frac{d_5u_2 - d_1u_2^2 - d_3 }{d_2 u_2}, \end{aligned}$$
(24)

and \(u_2\) satisfy the equation given by

$$\begin{aligned} a_4u_2^4 + a_3u_2^3 + a_2u_2^2 + a_1u_2 + a_0 = 0, \end{aligned}$$
(25)

where,

$$\begin{aligned} a_4=\, & {} \alpha _1 \sigma _a \alpha _3^2 \sigma _h^2 \mathcal {R}_0^{hh}\left( \mathcal {R}_0^{aa}\mathcal {R}_0^{hh} - \mathcal {R}_0^{ha} \mathcal {R}_0^{ah} \right) ,\\ a_3=\, & {} d_1d_2l_3 + (d_1 + d_5)d_2l_2 - d_1l_1(d_4+d_5),\\ a_2=\, & {} (2d_1d_3 + d_4d_5)l_1 - (d_3 + d_5)d_2l_2 - d_2d_4l_3,\\ a_1=\, & {} d_3 \left[ d_2(l_2 + l_3) - (d_4 + d_5)l_1 \right] ,\\ a_0=\, & {} \alpha _1 \sigma _a \sigma _h^2 \alpha _3^2 \mathcal {R}_0^{aa}, \end{aligned}$$

where, \(d_1 = \alpha _3 \sigma _h \mathcal {R}_0^{hh}, ~~ d_2 = \alpha _1 \sigma _a \mathcal {R}_0^{ha},~~ d_3 = \sigma _h \alpha _3, ~~ d_4 = d_1 + d_3, ~~ d_5 = d_1 + d_2 + d_3, ~~l_1 = \alpha _1 \sigma _a \mathcal {R}_0^{aa}, ~~ l_2 = \alpha _3 \sigma _h \mathcal {R}_0^{ah},~~ l_3 = \sigma _h \alpha _1\).

Results

Sensitivity analyses

Sensitivity analyses, employing the Latin Hypercube Sampling Method (LHSM), are used to determine which parameters have a significant effect on \(\mathcal {R}_0\) from the model (1) dynamics (Chitnis et al. 2008). The partial rank correlation coefficients (PRCCs) of \(\mathcal {R}_0\) are calculated from the LHSM. The sign and value of the PRCC indicates the influence of that parameter on \(\mathcal {R}_0\). Parameters with PRCC values out side the range \(-\) 0.5 to 0.5 are regarded as the most sensitive to \(\mathcal {R}_0\) (Taylor 1990). The influence of each parameter to \(\mathcal {R}_0\) based on the PRCC values are given in Fig. 2.

Fig. 2
figure 2

Tornado plot showing the sensitivity indices of \(\mathcal {R}_0\) with respect to the parameters

Full size image

From Fig. 2, two parameters that are the most sensitive to \(\mathcal {R}_0\) are infection rate of animal to animal transmission \(\beta _{aa}\), followed by the disease-induced death rate of animals \(\delta _a\). The remaining parameters \(\mathcal {R}_0\) in descending order of the magnitude of PRCC are \(\Lambda _a\), \(\gamma _a\), \(\mu _a\), \(c_{aa}\), \(\beta _{ha}\), \(\sigma _h\), \(\beta _{ah}\), \(c_{ah}\), \(\delta _h\), \(\Lambda _h\), \(\gamma _h, \beta _{hh}\), \(\sigma _a\), \(c_{ah}\), \(c_{hh}\) and \(\mu _h\).

Numerical simulation of the deterministic model: a case study of 2022 mpox outbreak in Nigeria

Numerical simulations are used to explore the dynamics of model (1) using data from the 2022 mpox outbreak in Nigeria.

Model fitting and parameter estimation

Most of the the parameters are taken from the literature (Table 4). However, fitting model (1) to the 2022 mpox outbreak in Nigeria is important here and so other parameters, especially the control parameters, are fit to the data obtained from the Nigeria Centre for Disease Control and Prevention (NCDC) Nigeria Centre for Disease Control and Prevention (2023). The fit of the model to the data is given in Fig. 3 and parameter estimates from the fit are presented Table 5.

Table 4 Parameters for model (1)
Full size table
Fig. 3
figure 3

Model fit of the cumulative number of confirm cases of mpox in Nigeria from January to December, 2022

Full size image
Table 5 Estimated parameter values from the model fitting
Full size table

Using these estimated parameters and the parameters in Table 4\(\mathcal {R}_0\) is calculated resulting in \(\mathcal {R}_0 = 1.7\). As \(\mathcal {R}_0 >1\) this result suggests that mpox infections are most likely endemic at present in Nigeria (Tien and Earn 2010). Using the same parameter values, the \(\mathcal {R}_0\) for person-to-person \(\mathcal {R}_0^{hh}\), animal-to-animal \(\mathcal {R}_0^{aa}\), animal-to-person \(\mathcal {R}_0^{ah}\) and person-to-animal transmission \(\mathcal {R}_0^{ha}\) are calculated in the same way to obtain \(\mathcal {R}_0^{hh} = 0.0018\), \(\mathcal {R}_0^{aa} = 1.5600\), \(\mathcal {R}_0^{ah} = 0.8019\) and \(\mathcal {R}_0^{ha} = 0.2984\). Thus, transmission from animals is a primary source of secondary infections in Nigeria and likely to be driving the mpox infections in Nigeria.

Fig. 4
figure 4

Plot illustrating a possible dynamics of mpox disease in Nigeria using model (1)

Full size image

The long term possible dynamics of mpox in Nigeria are given in Fig. 4. Over the next hundred and twenty months, the number of mpox infections are likely to continue to increase.

Effects of control measures using the deterministic model

Fig. 5
figure 5

a Plot showing the effects of reduction in animal-to-animal transmission using control measures \(c_{aa}\). b Plot showing the effects of reduction in animal-to-person transmission using control measures \(c_{ah}\)

Full size image

Figure 5a shows the effects of control measure \(c_{aa}\) in reducing animal-to-animal transmission. From the figure, increasing this control measure decreases the number of mpox infections significantly. Specifically, effective implementation of this control will reduce the number of infected individuals by over 80%.

Similarly, Fig. 5b shows the effects of control measure \(c_{ah}\) in reducing animal-to-human transmission. The figure reveals that increasing the implementation of this control measure decreases the number of individuals infected with mpox. In particular, effective implementation of this control measure leads to possible eradication of the disease.

Fig. 6
figure 6

a Plot showing the effects of reduction in person-to-person transmission using control measures \(c_{hh}\). b Plot showing the effects of reduction in person-to-animal transmission using control measures \(c_{ha}\)

Full size image

Figure 6a, b show the effects of the reduction in person-to-person and person-to-animal transmission using control measures \(c_{hh}\) and \(c_{ha}\). Unlike the previous controls, control measures \(c_{hh}\) and \(c_{ha}\) have less of an effect in reducing mpox infections.

Numerical simulations of the stochastic model

In this section, numerical simulations are considered to explore the dynamics of the stochastic model. The probability of disease extinction when \(\mathcal {R}_0>1\) is estimated for various initial conditions (see Table 6). The Table shows that the probability of disease extinction is less than one when \(\mathcal {R}_0>1\). Increasing the initial number of mpox infections decreases the probability of disease extinction.

Table 6 Probability of disease extinction for various initial conditions
Full size table
Fig. 7
figure 7

Plot showing model results of a single mpox dynamic comparing the stochastic model and deterministic model, where the trajectories with fluctuations represent the dynamics obtained from the stochastic model and the trajectories without fluctuations represent the dynamics obtained from the deterministic model. The initial conditions are 1 and 2 for the exposed/infected human (\(E_h, I_h\)) and exposed/infected animals (\(E_a, I_a\)) respectively

Full size image

Possible dynamics of mpox are presented in Fig. 7 with differences and similarities between the dynamics of the stochastic and deterministic versions shown. For a situation when \(\mathcal {R}_0>1\), mpox is likely to persist. However, unlike the deterministic case when \(\mathcal {R}_0>1\), the probability of disease eradication is not necessarily zero for small numbers of initial exposures or infections (Table 6). For both the deterministic and stochastic models the disease is eradicated for \(\mathcal {R}_0<1\).

Discussion

Mpox is a viral disease that affects humans and animals. The 2022 global outbreak of mpox that resulted in thousand cases and many deaths from 110 countries has drawn the attention of researchers to the disease. Consequently, there is a need to improve on an understanding of the transmission dynamics of mpox, which is necessary for developing better control measures that minimize infections (Dolgopolov et al. 2021). Theoretical studies in the form of mathematical models have been successfully used in analysing the dynamics and control of infectious diseases. In this work, two modelling approaches, deterministic and stochastic, are used to study the dynamics and control of mpox infections.

A deterministic model gives a broad view of scenarios where the disease will persist or be eradicated using the basic reproduction number \(\mathcal {R}_0\). The DFE of a model is shown to be globally asymptotically stable when \(\mathcal {R}_0<1\). Epidemiologically, this means that the diseases could be eradicated, provided that \(\mathcal {R}_0<1\) otherwise, the disease persists. When \(\mathcal {R}_0>1\), endemic equilibria exist in the model. This suggests the possibility of disease persistence when \(\mathcal {R}_0>1\).

A deterministic model, an extension of previously published models, is developed here to study mpox dynamics. This model is then used to consider the 2022 mpox outbreak in Nigeria by fitting it to the cumulative cases of mpox infections from January to December 2022. Some parameters values are taken from the literature while others are used to fit the model to the data. In particular, parameters for the control measures are estimated from the model fitting. Results show that the model is a reasonable fit for the 2022 mpox outbreak (Fig. 3). Using these parameter values, fitted and fixed, the basic reproduction number is \(\mathcal {R}_0 = 1.7\). The Epidemiological implication of this result is that mpox is likely to be endemic in Nigeria which is further illustrated by the long-term dynamics given by the model for mpox in Nigeria (Fig. 4). These results are in agreement with reports that the disease has been present in Nigeria since 2017 (World Health Organization (WHO) 2023b; Nigeria Centre for Disease Control and Prevention 2023).

The deterministic model is also used to consider the major transmission routes for the infection: person-to-person (\(\mathcal {R}_0^{hh}\)), animal-to-animal (\(\mathcal {R}_0^{aa}\)), animal-to-person (\(\mathcal {R}_0^{ah}\)), and person-to-animal (\(\mathcal {R}_0^{ha}\)). The basic reproduction numbers calculated for these transmissions are \(\mathcal {R}_0^{hh} = 0.0018\), \(\mathcal {R}_0^{aa} = 1.5600\), \(\mathcal {R}_0^{ah} = 0.8019\) and \(\mathcal {R}_0^{ha} = 0.2984\). These results show that transmission from animals generates greater secondary infections in Nigeria. Hence, based on these results, transmission from animals is currently driving the mpox epidemic in Nigeria and, therefore, should be the major target of control measures for possible eradication of the disease.

Sensitivity analyses using the Latin Hypercube Sampling method are used to determine the parameters with a high impact on \(\mathcal {R}_0\). Two parameters (i.e, the infection rate from animal-to-animal \(\beta _{aa}\), and the death rate of the animal due to the disease \(\delta _a\)), have the greatest influence on \(\mathcal {R}_0\), at about \(70\%\). These results highlight the importance of the prevalence of the disease in animals.

The results indicate that the disease will remain endemic unless effective control measures are implemented. Thus, the impact of the control measures are explored numerically. The control measures that reduce transmission from animal-to-human (\(c_{ah}\)) and animal-to-animal (\(c_{aa}\)) are shown to have a significant effect in decreasing infections. These results again highlight the importance of the prevalence of the disease in animals.

While the deterministic model provides a broad picture of the dynamics, when there is more than one group of players that can be infectious, as is the case here, the standard results of a deterministic model do not always hold (Allen and Lahodny Jr 2012). For this reason a stochastic model based on the assumptions of the deterministic model was developed to provide better insights (Lahodny et al. 2015). In this stochastic version of the model a multitype branching process is used to estimate the probability of disease eradication or persistence.

Again, even for the stochastic analyses, when \(\mathcal {R}_0<1\), the probability of disease eradication is one. However, when \(\mathcal {R}_0>1\), the probability of disease eradication is less than one but not necessarily zero. Regardless of this fact, considering the low probabilities of disease eradication given in Table 6 it is clear that in most situations that disease persistence is still likely when \(\mathcal {R}_0>1\). Even for the most probable case, with one animal exposed to the virus, the probability of disease persistence is as much as 60%. Thus, control measures that keep \(\mathcal {R}_0<1\) are still strongly recommended for probable eradication of mpox.

The importance of adding the stochastic modelling approach was to ascertain the extent that in this case, with multiple infectious groups, stochasticity might affect the dynamics. Based on the Nigeria outbreak of mpox the deterministic model appears to provide an adequate indication of the disease dynamics. However, the differences between the model results do suggest the importance of a cost analyses. The cost of control implementation could depend on the nuances of the stochastic model. In the case presented this possibility seems unlikely but the approach could be important in other cases where the stochastic model might show significant variation when compared to the deterministic model. Then cost implications for introducing controls could be affected.

For the Nigerian outbreak considered here, both models show the importance of controls that force the reproduction number below unity. This knowledge is important for the effective management of mpox disease outbreaks. In particular, target of controls for the disease in animal hosts are shown here to be important. More importantly, our model formulations could be useful in general for use in making decisions on the effective management of mpox outbreaks in any endemic area.